1 Introduction

Based on the nonlinear relationship between charge q and magnetic flux \(\varphi \), the concept of memristors was first theoretically postulated by Chua [4], which was recognized as the first real-life understanding of the so-called missing fourth circuit element. Subsequently, Chua and Kang extended the idea of memristors to memristive systems and devices in [5]. In a seminal paper that appeared in late 2008, a two-terminal titanium dioxide nanoscale device that exhibited memristive characteristics was unveiled by Hewlett–Packard (HP), which was considered as the starting point for the design of a new class of high-density processors, thus igniting renewed interest in memristors. One immediate application is enabling low-cost technology for nonvolatile memories where future computers will turn on instantly without the usual “booting time” that is currently required in all personal computers. This feature leads to the memristive neural networks have been widely studied in [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30].

Among which, by means of a robust analysis approach, the synchronization control of memristive neural networks was studied in [31], which provides a new method to deal with the switching feature of the connection weights. In [18], a memristive neural network with nonmonotonic piecewise linear activation functions is studied, the coexistence of the multiple equilibrium points for the memristive neural networks is discussed, and then the corresponding sufficient condition of the local mu-stability is given. In [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30], the fractional-order delayed memristive neural networks are invested, and several criteria on state estimation, synchronization, and stabilization are obtained. While, in the above conclusions, one can find that the error system converges to zero as time goes to infinity. In fact, different systems may have different states, which can affect the stability of the error system, thus, the error system tends to a small region will be much more reasonable. This is one of our motivations for researching this article.

Modeling different real-world phenomena, using fractional definitions, has become the most highly appreciated areas of realistic sciences. This is because the nonlocal properties of fractional operator enable these differential models to condense the information, about recent and historical situations. For the last few decades, many advancements have been made in this regard to enhance the definitions and properties of fractional calculus, which enrich the capabilities of fractional differential models by bringing diverse significance. Hence, the behaviors of many fractional differential equations have been studied and various techniques have been developed in [7,8,9,10,11,12,13,14,15,16,17], but still, there are many things that can be done in this area.

Generally speaking, complex-valued system has many different and more complicated properties than real-valued ones. Very recently, a system with quaternion parameters is proposed, which contains one real part and three imaginary parts. Quaternion performed a number of meaningful applications from various areas, such as attitude control, quantum mechanics as well as computer graphics. It should be mentioned that the imaginary parts in a quaternion are not commutative, which makes the studying of the quaternion neural networks much more difficult. Moreover, vector algebra is not a division algebra and suffers from mathematical deficiencies when modeling orientation and rotation. In this case, the quaternion domain offers a convenient and unified way to process 3-D and 4-D signals [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. Therefore, quaternion neural networks are supposed to give further investigation for their broad applications [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23].

The main objective of this paper is to design a new controller that provides a system with the quasi-stability property. In this regard, using contraction mapping theory, a sufficient condition is derived to ensure the existence of the equilibrium point for the memristive neural networks. Subsequently, fractional Laplace transform is utilized to deal with the quasi-stability of the equilibrium point. Here, a vector ordering approach is employed, which can be used to compare the “magnitude” of two different quaternions, and thus, the convex closure proposed by the quaternion connection weights is meaningful.

The remaining paper contains: the basic definitions of the quaternion, the Caputo fractional derivative and the model description of the memristive neural networks. Next, the existence of the equilibrium point and the quasi-stability scheme of the proposed equilibrium point are described in detail. Furthermore, a comprehensive discussion of the a vector ordering approach is imparted. Conclusively, effective outcomes of the whole attempt are transliterated by a simulation.

2 Preliminaries

This section comprises the illustrative preliminaries of the paper, which include some major definitions and properties of the quaternion algebra, caputo derivative and the description of the memristive neural networks.

A quaternion can be described by:

$$\begin{aligned} \begin{aligned} \theta =\theta ^{ R }+ \theta ^{I} i +\theta ^{J} j +\theta ^{K} k, \end{aligned} \end{aligned}$$
(1)

in which, the three imaginary parts i, j, k, are defined as:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} i^2=j^2=k^2=ijk=-1,\\ ij=-ji=k,\\ jk=-kj=i,\\ ki=-ik=j. \end{array} \right. \end{aligned} \end{aligned}$$
(2)

Set \({\mathbb {Q}}\triangleq \{h^{ R }+ h^{I} i +h^{J} j +h^{K} k | h^{ R}, h^{I}, h^{J},h^{K}\in {\mathbb {R}}\}\), the conjugate of h is denoted by \({\bar{\theta }}\), with:

$$\begin{aligned} \begin{aligned} {\bar{\theta }}= \theta ^{R}- \theta ^{I} i -\theta ^{J} j -\theta ^{K} k. \end{aligned} \end{aligned}$$

The modulus of \(\theta \in {\mathbb {Q}}\) is defined as:

$$\begin{aligned} \begin{aligned} |\theta |=\sqrt{\theta {\bar{\theta }}}=\sqrt{(\theta ^{R})^2+(\theta ^{I})^2 +(\theta ^{J})^2 + (\theta ^{K})^2 }. \end{aligned} \end{aligned}$$

Besides, for \(\theta =(\theta _1, \theta _2, \ldots , \theta _n)^T \), set \(|\theta |=(|\theta _1|, |\theta _2|, \ldots , |\theta _n|)^T \) be the modulus of \(\theta \), and \(\Vert \theta \Vert = \Big ( \sum _{p=1}^n |\theta _p|^2\Big )^{ \frac{1}{2} } \) be the norm of \(\theta \).

Definition 2.1

[19] For \(\omega (t)\), \(D_{t_0,t}^{-\epsilon }\) is presented as:

$$\begin{aligned} D_{t_0,t}^{-\epsilon }\omega (t)=\frac{1}{\Gamma (\epsilon )}\int _{t_0}^t(t-\tau )^{\epsilon -1}\omega (\tau )d\tau , \end{aligned}$$

where \(\Gamma (\cdot )\) implies gamma function.

Definition 2.2

[19] The Caputo derivative of \(\omega (t)\) implies:

$$\begin{aligned} {C}^{D_{t_0,t}^{\epsilon }}\omega (t)=D_{t_0,t}^{-(n-\epsilon )}\frac{d^n}{dt^n}\omega (t) =\frac{1}{\Gamma (n-\epsilon )}\int _{t_0}^t(t-\tau )^{n-\epsilon -1}\omega ^{(n)}(\tau )d\tau , \end{aligned}$$

where \(n-1<\epsilon <n\in Z^+\).

In the following lines, \(D^\epsilon \) is short for \({C}^{D_{t_0,t}^{\epsilon }}\).

Lemma 2.1

If \(a=(a_1,\ldots , a_n)\) and \(b=(b_1,\ldots , b_n)\) are sequences of quaternion numbers, then

$$\begin{aligned} \bigg | \sum _{p=1}^n a_p b_p \bigg |^2\le \bigg ( \sum _{p=1}^n | a_p|^2 \bigg ) \bigg ( \sum _{p=1}^n | b_p|^2 \bigg ) \end{aligned}$$

holds, if and only if the sequences a and b are proportional.

Proof

Let \(a= a^R + a^I i + a^J j+ a^K k= (a^R + a^I i) + (a^J + a^K i)j \), thus, a quaternion a can be seen as a complex number, then, based on Lemma 8 in [33], the above inequality is correct. \(\square \)

Lemma 2.2

[23] Set x, \(y\in {\mathbb {Q}}\), \(\varepsilon >0\) be a constant, then

$$\begin{aligned} yx +{\bar{x}}{\bar{y}} \le \varepsilon {\bar{x}} x +\frac{1}{\varepsilon } y{\bar{y}} \end{aligned}$$

holds.

Lemma 2.3

[26] For \(0 < \epsilon \le 1\), \(\forall \tau > 0\), if \(|\arg (\lambda )|> \frac{\pi }{2}\), \(\det (\Delta (t))=0\) has no pure imaginary roots, then the zero root of

$$\begin{aligned} D^\epsilon x(s)=-A x(s)+B x(s-\tau ) \end{aligned}$$

is globally Lyapunov stable, where \(\lambda \) is the eigenvalues of \(-A +B \).

Lemma 2.4

[26] For a model as given below:

$$\begin{aligned} \begin{aligned}&\left\{ \begin{array}{l} D^\epsilon \varsigma (t) \le -\epsilon _1 \varsigma (t)+ \epsilon _2 \varsigma (t-\tau ), \ 0 < \epsilon \le 1, \\ \varsigma (t)=\pi (t), \end{array} \right. \end{aligned} \end{aligned}$$

and a linear system:

$$\begin{aligned} \begin{aligned}&\left\{ \begin{array}{l} D^\epsilon \varrho (t) = -\epsilon _1 \varrho (t)+ \epsilon _2 \varrho (t-\tau ), \ 0 < \epsilon \le 1, \\ \varrho (t)=\pi (t), \end{array} \right. \end{aligned} \end{aligned}$$

where \(\varsigma (t)\), \(\varrho (t)\), \(t\in (0, +\infty )\), are continuous and nonnegative, \(\pi (t)\ge 0\). Then \(\varsigma (t)\le \varrho (t)\), \(\epsilon _1\), \(\epsilon _2>0\).

Definition 2.3

For the system, the trivial solution is quasi-stability, if there has \(\Omega \), when t goes to infinity, the system y(t) converges to a bounded region \(\Omega =\{y(t)\in {\mathbb {Q}} \mid \Vert y(t)\Vert \le \varepsilon \}\) with an error level \(\varepsilon >0\).

In general, the dynamical equation of memristive system with Caputo fractional derivative can be written as:

$$\begin{aligned} \begin{aligned} D^\epsilon x_p(t)=&-d_p x_p(t)+\sum _{q=1}^{n}a_{pq}(x_p(t))f_q(x_{q}(t))\\&+\sum _{q=1}^{n}b_{pq}(x_p(t))f_q(x_{q}(t-\tau )) +J_p , \end{aligned} \end{aligned}$$
(3)

where \(0< \alpha < 1\), \(d_p>0\) is the neuron state, \(a_{pq}(x_p(t))\), \(b_{pq}(x_p(t))\) are the connection weights, \(f_q(\cdot )\) stand for the active functions, \(\tau \) signifies the delay, and \(J_p\) is a external input.

The initial condition of (3) is:

$$\begin{aligned} x_p(t)=\vartheta _p(t), \ \ \ p=1,2,\ldots ,n, \end{aligned}$$

with \(\vartheta _p(0)=0\).

The parameters \(a_{pq}(x_p(t))\), \(b_{pq}(x_p(t))\) in system (3) are defined as:

$$\begin{aligned} \begin{aligned}&a_{pq}(x_p(t)) =\left\{ \begin{array}{l} a_{pq}^{\intercal }=a_{1pq}^R + a_{1pq}^I i+ a_{1pq}^J j+ a_{1pq}^K k, \ \ \ \ |x_p(t)|\le {\mathcal {S}}_p, \\ a_{pq}^{\intercal \intercal }=a_{2pq}^R + a_{2pq}^I i+ a_{2pq}^J j+ a_{2pq}^K k, \ \ \ |x_p(t)|> {\mathcal {S}}_p, \end{array} \right. \\&b_{pq}(x_p(t)) =\left\{ \begin{array}{l} b_{pq}^{\intercal }=b_{1pq}^R + b_{1pq}^I i+ b_{1pq}^J j+ b_{1pq}^K k, \ \ \ \ |x_p(t)|\le {\mathcal {S}}_p, \\ b_{pq}^{\intercal \intercal }=b_{2pq}^R + b_{2pq}^I i+ b_{2pq}^J j+ b_{2pq}^K k, \ \ \ |x_p(t)|> {\mathcal {S}}_p, \end{array} \right. \end{aligned} \end{aligned}$$

where the switching jump \({\mathcal {S}}_p>0\).

\((A_1)\): There exist constants \(m_q, M_q > 0\), such that for \(q=1,2,\ldots ,n\),

$$\begin{aligned} \begin{aligned} |f_q ( x_1 )-f_q ( x_2) | \le m_q | x_1-x_2 |, \ \ \ |f_q ( x ) | \le M_q \end{aligned} \end{aligned}$$

hold.

Definition 2.4

(Generalized Inequalities [12] ) For any cone \(N \subseteq {\mathbb {R}}^n\), the partial ordering relation in \({\mathbb {R}}^n\) is defined as:

  1. (I).
    $$\begin{aligned} \alpha \preceq \beta \Leftrightarrow \beta -\alpha \in N; \end{aligned}$$
  2. (II).
    $$\begin{aligned} \alpha \prec \beta \Leftrightarrow \beta -\alpha \in \text {int} N, \end{aligned}$$

    where \(\text {int} N\) is the interior of N.

Remark 2.1

As one knows, a complex value can be seen as a two-dimensional vector, thus the generalized inequalities can be employed to compare the “magnitude” of two complex values, i.e, if N stands for the first (or fourth) quadrant of the complex plane, then any complex value on its “right” side is greater than it, and the complex number in the “upper right” of a complex value is strictly greater than it.

For example, given two different complex values \(x_1=a_1+b_1 i\), \(x_2=a_2+b_2 i\), then, \(x_2-x_1=a_2-a_1+(b_2-b_1) i\). Now, two cases will be proposed in the following lines: (i) \((a_2-a_1)\cdot (b_2-b_1)\ge 0\), (ii) \((a_2-a_1)\cdot (b_2-b_1)<0\). For the case (i), if \(a_2-a_1>0\), \(b_2-b_1>0\), then \(x_1 \prec x_2\); if \(a_2-a_1= 0\), \(b_2-b_1>0\), or \(a_2-a_1>0\), \(b_2-b_1=0\), then \(x_1 \preceq x_2\); if \(a_2-a_1<0\), \(b_2-b_1<0\), then \(x_1 \succ x_2\); For the case (ii), if \(a_2-a_1>0\), \(b_2-b_1<0\), then \(x_1 \prec x_2\); if \(a_2-a_1<0\), \(b_2-b_1>0\), then \(x_1 \succ x_2\).

For two different quaternions \(x_1=a_1+b_1 i +c_1 j +d_1 k=(a_1+b_1 i)+ (c_1+d_1 i)j\triangleq x_{11} + x_{12} j\), \(x_2=a_2+b_2 i+c_2 j +d_2 k=(a_2+b_2 i)+ (c_2+d_2 i)j\triangleq x_{21} + x_{22} j\), the first step is to compare two pairs of the vectors \(x_{11}\) and \(x_{21}\), \(x_{12}\) and \(x_{22}\), respectively. If \(x_{11} \prec (\succ ) x_{21}\) and \(x_{12} \prec (\succ ) x_{22}\), then \(x_1\prec (\succ ) x_2\); if \(x_{11} \preceq x_{21}\), \(x_{12} \prec x_{22}\), or \(x_{11} \prec x_{21}\), \(x_{12} \preceq x_{22}\), then one has \(x_1\preceq x_2\); if \(x_{11} \preceq (\succeq ) x_{21}\), \(x_{12} \succ (\prec ) x_{22}\), then \(x_1\preceq (\succeq ) x_2\); if \(x_{11} \prec (\succ ) x_{21}\), \(x_{12} \succeq (\preceq ) x_{22}\), then \(x_1\preceq (\succeq ) x_2\).

By applying the above theory, \(\acute{a}_{pq} \), \(\grave{a}_{pq} \), \(\acute{b}_{pq} \) and \(\grave{b}_{pq} \) can be derived correspondingly, thus, system (3) can be written as:

$$\begin{aligned} \begin{aligned} D^\epsilon x_p(t)\in&- d_p x_p(t)+\sum _{q=1}^{n} co [\grave{a}_{pq} , \acute{a}_{pq} ]f_q(x_{q}(t)) +\sum _{q=1}^{n} co [\grave{b}_{pq} , \acute{b}_{pq} ]f_q(x_{q}(t-\tau )) +J_p , \end{aligned} \end{aligned}$$
(4)

where \(\grave{a}_{pq} =\min \{a_{pq}^{\intercal }, a_{pq}^{\intercal \intercal }\}\), \(\acute{a}_{pq} =\max \{a_{pq}^{\intercal }, a_{pq}^{\intercal \intercal }\}\), \(\grave{b}_{pq} =\min \{b_{pq}^{\intercal }, b_{pq}^{\intercal \intercal }\}\), \(\acute{b}_{pq} =\max \{b_{pq}^{\intercal }, b_{pq}^{\intercal \intercal }\}\).

Now, using the differential inclusion, system (3) is developed as:

$$\begin{aligned} \begin{aligned} D^\epsilon x_p(t)=&- d_p x_p(t)+\sum _{q=1}^{n}a^{\prime }_{pq}(t) f_q(x_{q}(t))\\&+\sum _{q=1}^{n}b^{\prime }_{pq}(t) f_q(x_{q}(t-\tau )) +J_p, \ \ \ p=1,2,\ldots ,n, \end{aligned} \end{aligned}$$
(5)

where \(a^{\prime }_{pq}(t) \in co[\grave{a}_{pq} , \acute{a}_{pq} ]\), \(b^{\prime }_{pq}(t) \in co [\grave{b}_{pq} , \acute{b}_{pq} ] \).

3 Quasi-Stability Analysis

The existence and uniqueness of the equilibrium point will be proposed by means of contraction mapping theory. Thenceforth, we exercise the Lyapunov functional and fractional Laplace transform to derive the quasi-stability condition for the equilibrium point.

Theorem 3.1

Under the assumption (\(A_1\)), if the following inequality holds:

$$\begin{aligned} \begin{aligned} 0< \rho =\bigg ( \sum _{p=1}^{n} \sum _{q=1}^{n} \Big ( \frac{ ( | a^{*}_{pq} |+ | b^{*}_{pq} | ) m_q }{d_q}\Big )^2 \bigg )^{\frac{1}{2}}<1, \end{aligned} \end{aligned}$$

then system (3) has a unique equilibrium.

Proof

Let \(u_p^{*}=d_p x_p^{*}\), constructing a mapping \(\Phi : {\mathbb {Q}}^n \rightarrow {\mathbb {Q}}^n \), with:

$$\begin{aligned} \begin{aligned} \Phi _p(u_p)=&\sum _{q=1}^{n}a^{*}_{pq} f_q(\frac{u_{q}}{d_q} )+\sum _{q=1}^{n}b^{*}_{pq} f_q(\frac{u_{q}}{d_q} ) +J_p, \end{aligned} \end{aligned}$$

where \(a^{*}_{pq} \in co [\grave{a}_{pq}, \acute{a}_{pq}] \), \(b^{*}_{pq} \in co [\grave{b}_{pq}, \acute{b}_{pq}] \). \(\square \)

For two different vectors \(u,v\in {\mathbb {Q}}^n\), one has:

$$\begin{aligned} \Vert \Phi (u )-\Phi (v) \Vert&= \bigg ( \sum _{p=1}^{n} (\Phi _p(u_p)-\Phi _p(v_p))\overline{(\Phi _p(u_p)-\Phi _p(v_p))} \bigg )^{\frac{1}{2}}\nonumber \\&= \bigg ( \sum _{p=1}^{n} | \Phi _p(u_p)-\Phi _p(v_p)|^2 \bigg )^{\frac{1}{2}}\nonumber \\&= \bigg ( \sum _{p=1}^{n} \bigg | \sum _{q=1}^{n}a^{*}_{pq} \Big ( f_q(\frac{u_{q}}{d_q} )- f_q(\frac{v_{q}}{d_q} )\Big ) + \sum _{q=1}^{n}b^{*}_{pq} \Big ( f_q(\frac{u_{q}}{d_q} )- f_q(\frac{v_{q}}{d_q} )\Big ) \bigg |^2 \bigg )^{\frac{1}{2}}\nonumber \\&\le \bigg ( \sum _{p=1}^{n} \bigg [ \sum _{q=1}^{n} \Big | {\tilde{a}}_{pq} \Big | \Big | f_q(\frac{u_{q}}{d_q} )- f_q(\frac{v_{q}}{d_q} ) \Big | + \sum _{q=1}^{n} \Big |{\tilde{b}}_{pq} \Big | \Big | f_q(\frac{u_{q}}{d_q} )- f_q(\frac{v_{q}}{d_q} ) \Big | \bigg ]^2 \bigg )^{\frac{1}{2}}\nonumber \\&\le \bigg ( \sum _{p=1}^{n} \bigg [ \sum _{q=1}^{n} \frac{ ( | {\tilde{a}}_{pq} |+ | {\tilde{b}}_{pq} | ) m_q }{d_q} | u_{q}- v_{q} | \bigg ]^2 \bigg )^{\frac{1}{2}}\nonumber \\&\le \bigg ( \sum _{p=1}^{n} \bigg [ \sum _{q=1}^{n} \Big ( \frac{ ( | {\tilde{a}}_{pq} |+ |{\tilde{b}}_{pq} | ) m_q }{d_q}\Big )^2 \sum _{q=1}^{n} | u_{q}- v_{q} |^2 \bigg ] \bigg )^{\frac{1}{2}}\nonumber \\&= \bigg ( \sum _{p=1}^{n} \sum _{q=1}^{n} \Big ( \frac{ ( | {\tilde{a}}_{pq} |+ | {\tilde{b}}_{pq} | ) m_q }{d_q}\Big )^2 \bigg )^{\frac{1}{2}} \Vert u - v \Vert , \end{aligned}$$
(6)

in which, Lemma 2.1 is utilized in the above process, and \({\tilde{a}}_{pq}=\max \{ | a_{pq}^{\intercal }|, |a_{pq}^{\intercal \intercal }| \}\), \({\tilde{b}}_{pq}=\max \{ | b_{pq}^{\intercal }|, |b_{pq}^{\intercal \intercal }| \}\), where \(\mid a_{pq}^{\intercal }\mid =\mid a_{1pq}^R\mid + \mid a_{1pq}^I \mid i+ \mid a_{1pq}^J\mid j+ \mid a_{1pq}^K \mid k\), besides, \(\mid a_{pq}^{\intercal \intercal }\mid \), \(\mid b_{pq}^{\intercal }\mid \), \(\mid b_{pq}^{\intercal \intercal }\mid \) have the same definition.

It follows from the definition of \(\rho \), one has:

$$\begin{aligned} \begin{aligned} \Vert \Phi (u )-\Phi (v) \Vert \le \rho \Vert u - v \Vert , \end{aligned} \end{aligned}$$

which means that \(\Phi \) is a contraction mapping on \({\mathbb {Q}}^n\), thus, system (3) has a unique equilibrium. The proof is thus completed.

Set \(x_p^{*}\) be the equilibrium of system (3), i.e.,

$$\begin{aligned} \begin{aligned} 0=&- d_p x_p^{*} +\sum _{q=1}^{n}a^{*}_{pq} f_q(x_{q}^{*} )+\sum _{q=1}^{n}b^{*}_{pq} f_q(x_{q}^{*}) +J_p, \end{aligned} \end{aligned}$$
(7)

then, shifting the above equilibrium to the origin by \(y_p(t)=x_p(t)- x_p^{*}\), one has:

$$\begin{aligned} \begin{aligned} D^\epsilon y_p(t)=&- d_p y_p(t) +\sum _{q=1}^{n} a^{\prime }_{pq}(t) f_q(x_{q}(t))- \sum _{q=1}^{n}a^{*}_{pq} f_q(x_{q}^{*} ) +\sum _{q=1}^{n}b^{\prime }_{pq}(t) f_q(x_{q}(t-\tau ))\\&-\sum _{q=1}^{n}b^{*}_{pq} f_q(x_{q}^{*})\\ =&- d_p y_p(t) +\sum _{q=1}^{n}( a^{\prime }_{pq}(t) - a^{*}_{pq}) f_q(x_{q}(t))+ \sum _{q=1}^{n}a^{*}_{pq} (f_q(x_{q}(t))- f_q(x_{q}^{*} ) ) \\&+\sum _{q=1}^{n} (b^{\prime }_{pq}(t)- b^{*}_{pq}) f_q(x_{q}(t-\tau )) + \sum _{q=1}^{n} b^{*}_{pq} ( f_q(x_{q}(t-\tau )) - f_q(x_{q}^{*})). \end{aligned} \end{aligned}$$
(8)

In order to stabilization the equilibrium, the following controlled memristive system is necessary:

$$\begin{aligned} D^\epsilon y_p(t) =&- d_p y_p(t) +\sum _{q=1}^{n}( a^{\prime }_{pq}(t) - a^{*}_{pq}) f_q(x_{q}(t))+ \sum _{q=1}^{n}a^{*}_{pq} (f_q(x_{q}(t))- f_q(x_{q}^{*} ) ) \nonumber \\&+\sum _{q=1}^{n} (b^{\prime }_{pq}(t)- b^{*}_{pq}) f_q(x_{q}(t-\tau )) + \sum _{q=1}^{n} b^{*}_{pq} ( f_q(x_{q}(t-\tau )) - f_q(x_{q}^{*}))+ u_p(t)\nonumber \\ \le&- d_p y_p(t) + \sum _{q=1}^{n}a^{*}_{pq} (f_q(x_{q}(t))- f_q(x_{q}^{*} ) ) + \sum _{q=1}^{n}(\acute{a}_{pq} - \grave{a}_{pq}) f_q(x_{q}(t)) \nonumber \\&+ \sum _{q=1}^{n} b^{*}_{pq} ( f_q(x_{q}(t-\tau )) - f_q(x_{q}^{*}))+\sum _{q=1}^{n} (\acute{b}_{pq} - \grave{b}_{pq}) f_q(x_{q}(t-\tau ))+ u_p(t). \end{aligned}$$
(9)

Theorem 3.2

Under the assumption (\(A_1\)), if there exist some positive constants \(\sigma _p\), \(p=1,2,3,4\), such that:

$$\begin{aligned} \begin{aligned} \lambda _{1 } =&\min _p\Big ( 2 d_p + 2 \upsilon _p - \sigma _1 m_p^2 - \frac{1}{\sigma _1 } \sum _{q=1}^{n} {\tilde{a}}_{pq} \bar{{\tilde{a}}}_{pq} - \frac{1}{\sigma _2 } \sum _{q=1}^{n} {\tilde{b}}_{pq} \bar{{\tilde{b}}}_{pq} \\&- \frac{1}{ \sigma _3 } \sum _{q=1}^{n} (\acute{a} _{pq} -\grave{a} _{pq} )(\bar{\acute{a}}_{pq} -\bar{\grave{a}}_{pq} )\\&- \frac{1}{ \sigma _4 } \sum _{q=1}^{n} (\acute{b}_{pq} -\grave{b}_{pq} )(\bar{\acute{b}}_{pq} -\bar{\grave{b}}_{pq} ) \Big )>0,\\ \lambda _{2 } =&\sigma _2 \max _p m_p^2>0,\\ \lambda _{3 } =&\sum _{p=1}^{n} \Big ( \sigma _3 + \sigma _4 \Big ) M^2_p, \ \ \ \lambda _{1 }> \lambda _{2 } \end{aligned} \end{aligned}$$

hold, then the trivial solution of (9) is quasi-stable under the following controller:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} u_p(t)= -\eta _p(t)y_p(t), \\ D^\epsilon \eta _p(t)=\xi _p {\bar{y}}_p(t)y_p(t), \end{array}\right. \end{aligned} \end{aligned}$$
(10)

where \(\eta _p(t)\in {\mathbb {R}} \), and \(\xi _p\) is an arbitrary positive constant. Moreover, system (9) will converges to a small region \(\Omega =\Big \{y_p(t)\in {\mathbb {Q}} \mid \Vert y(t)\Vert \le \sqrt{\frac{ \lambda _{3 }}{ \lambda _{1}- \lambda _{2}} + \varepsilon } \Big \}\).

Proof

Consider the following function:

$$\begin{aligned} \begin{aligned} V(t ) = \sum _{p=1}^n{\bar{y}}_p (t) y_p (t) + \sum _{p=1}^n \frac{1}{ \xi _p}(\eta _p(t)-\upsilon _p)^2. \end{aligned} \end{aligned}$$
(11)

By computing Caputo fractional-order derivative of V(t) from (9), one has:

$$\begin{aligned} D^\epsilon V (t) \le&\sum _{p=1}^n \Big (D^\epsilon {\bar{y}}_p (t)\Big ) y_p (t) + \sum _{p=1}^n {\bar{y}}_p (t) D^\epsilon y_p (t) + \sum _{p=1}^n \frac{2}{ \xi _p}(\eta _p(t)-\upsilon _p) D^\epsilon \eta _p(t) \nonumber \\ \le&\sum _{p=1}^n \Big (- d_p {\bar{y}}_p(t) + \sum _{q=1}^{n} ({\bar{f}}_q(x_{q}(t))-{\bar{f}}_q(x_{q}^{*} ) ){\bar{a}}^{*}_{pq} + \sum _{q=1}^{n}{\bar{f}}_q(x_{q}(t)) (\bar{\acute{a}}_{pq} - \bar{\grave{a}}_{pq}) \nonumber \\&+ \sum _{q=1}^{n} ( {\bar{f}}_q(x_{q}(t-\tau )) - {\bar{f}}_q(x_{q}^{*})){\bar{b}}^{*}_{pq} +\sum _{q=1}^{n} {\bar{f}}_q(x_{q}(t-\tau )) (\bar{\acute{b}}_{pq} - \bar{\grave{b}}_{pq}) + u_p(t) \Big ) y_p (t) \nonumber \\&+ \sum _{p=1}^n {\bar{y}}_p (t) \Big (- d_p y_p(t) + \sum _{q=1}^{n}a^{*}_{pq} (f_q(x_{q}(t))- f_q(x_{q}^{*} ) ) + \sum _{q=1}^{n}(\acute{a}_{pq} - \grave{a}_{pq} ) f_q(x_{q}(t)) \nonumber \\&+ \sum _{q=1}^{n} b^{*}_{pq} ( f_q(x_{q}(t-\tau )) - f_q(x_{q}^{*}))+\sum _{q=1}^{n} (\acute{b}_{pq} - \grave{ b}_{pq} ) f_q(x_{q}(t-\tau )) + u_p(t) \Big )\\&+ \sum _{p=1}^n 2 (\eta _p(t)-\upsilon _p) {\bar{y}}_p(t)y_p(t)\nonumber \\ =&\sum _{p=1}^n \Big [- (2 d_p + 2 \upsilon _p){\bar{y}}_p(t)y_p(t) + \sum _{q=1}^{n} \Big (({\bar{f}}_q(x_{q}(t))-{\bar{f}}_q(x_{q}^{*} ) ){\bar{a}}^{*}_{pq}y_p (t) \nonumber \\&+ {\bar{y}}_p (t) a^{*}_{pq} (f_q(x_{q}(t))- f_q(x_{q}^{*} ) )\Big ) + \sum _{q=1}^{n} \Big ( ( {\bar{f}}_q(x_{q}(t-\tau )) - {\bar{f}}_q(x_{q}^{*})){\bar{b}}^{*}_{pq} y_p (t) \nonumber \\&+ {\bar{y}}_p (t) b^{*}_{pq} ( f_q(x_{q}(t-\tau )) - f_q(x_{q}^{*}))\Big ) + \sum _{q=1}^{n} \Big ({\bar{f}}_q(x_{q}(t)) (\bar{\acute{a}}_{pq} - \bar{\grave{a}}_{pq} ) y_p(t) \nonumber \\&+ {\bar{y}}_p(t) (\acute{a}_{pq} - \grave{ a}_{pq} ) f_q(x_{q}(t)) \Big ) + \sum _{q=1}^{n} \Big ( {\bar{f}}_q(x_{q}(t-\tau )) (\bar{\acute{b}}_{pq} - \bar{\grave{b}}_{pq} ) y_p (t)\nonumber \\&+ {\bar{y}}_p(t)(\acute{b}_{pq} - \grave{ b}_{pq} ) f_q(x_{q}(t-\tau )) \Big ) \Big ], \nonumber \end{aligned}$$
(12)

from Lemma 2.2, there exist four constants \(\sigma _1\), \(\sigma _2\), \(\sigma _3\), \(\sigma _4>0\), such that:

$$\begin{aligned} \begin{aligned}&({\bar{f}}_q(x_{q}(t))-{\bar{f}}_q(x_{q}^{*} ) ) {\bar{a}}^{*}_{pq}y_p (t) + {\bar{y}}_p (t) a^{*}_{pq} (f_q(x_{q}(t))- f_q(x_{q}^{*} ) ) \\ \le&\sigma _1 ({\bar{f}}_q(x_{q}(t))-{\bar{f}}_q(x_{q}^{*} )) (f_q(x_{q}(t))- f_q(x_{q}^{*} ) ) + \frac{1}{\sigma _1 } {\bar{y}}_p (t) a^{*}_{pq} {\bar{a}}^{*}_{pq}y_p (t) \\ \le&\sigma _1 m_q^2 {\bar{y}}_{q}(t) y_{q}(t) + \frac{1}{\sigma _1 } {\bar{y}}_p(t) {\tilde{a}}_{pq} \bar{{\tilde{a}}}_{pq} y_p(t),\\&( {\bar{f}}_q(x_{q}(t-\tau )) - {\bar{f}}_q(x_{q}^{*})){\bar{b}}^{*}_{pq} y_p (t) + {\bar{y}}_p (t) b^{*}_{pq} ( f_q(x_{q}(t-\tau )) - f_q(x_{q}^{*})) \\ \le&\sigma _2 m_q^2 {\bar{y}}_{q}(t-\tau ) y_{q}(t-\tau ) + \frac{1}{\sigma _2 } {\bar{y}}_p(t) {\tilde{b}}_{pq} \bar{{\tilde{b}}}_{pq} y_p(t),\\&{\bar{f}}_q(x_{q}(t)) (\bar{\acute{a}}_{pq} - \bar{\grave{a}}_{pq}) y_p(t)+ {\bar{y}}_p(t) (\acute{a}_{pq} - \grave{ a}_{pq}) f_q(x_{q}(t)) \\ \le&\sigma _3 {\bar{f}}_q(x_{q}(t)) f_q(x_{q}(t)) + \frac{1}{\sigma _3 } {\bar{y}}_p(t) (\acute{a}_{pq} - \grave{ a}_{pq}) (\bar{\acute{a}}_{pq} - \bar{\grave{a}}_{pq}) y_p(t)\\ \le&\sigma _3 M^2_q + \frac{1}{ \sigma _3 } {\bar{y}}_p(t) (\acute{a}_{pq} - \grave{ a}_{pq}) (\bar{\acute{a}}_{pq} - \bar{\grave{a}}_{pq}) y_p(t),\\&{\bar{f}}_q(x_{q}(t-\tau )) (\bar{\acute{b}}_{pq} - \bar{\grave{b}}_{pq}) y_p (t) + {\bar{y}}_p(t)(\acute{b}_{pq} - \grave{ b}_{pq}) f_q(x_{q}(t-\tau )) \\ \le&\sigma _4 M^2_q + \frac{1}{ \sigma _4 } {\bar{y}}_p(t)(\acute{b}_{pq} - \grave{ b}_{pq}) (\bar{\acute{b}}_{pq} - \bar{\grave{b}}_{pq}) y_p(t). \end{aligned} \end{aligned}$$
(13)

\(\square \)

Taking into account of equations (12)-(13), the fractional derivative of V(t) is simplified to the following system:

$$\begin{aligned} \begin{aligned} D^\epsilon V (t) \le&\sum _{p=1}^n \Big [ -{\bar{y}}_p(t) \Big ( 2 d_p + 2 \upsilon _p - \sigma _1 m_p^2 - \frac{1}{\sigma _1 } \sum _{q=1}^{n} {\tilde{a}}_{pq} \bar{{\tilde{a}}}_{pq} - \frac{1}{\sigma _2 } \sum _{q=1}^{n} {\tilde{b}}_{pq} \bar{{\tilde{b}}}_{pq} \\&- \frac{1}{ \sigma _3 } \sum _{q=1}^{n} (\acute{a} _{pq} -\grave{a} _{pq} )(\bar{\acute{a}}_{pq} -\bar{\grave{a}}_{pq} ) - \frac{1}{ \sigma _4 } \sum _{q=1}^{n} (\acute{b}_{pq} -\grave{b}_{pq} )(\bar{\acute{b}}_{pq} -\bar{\grave{b}}_{pq} ) \Big ) \Big ] y_p(t)\\&+ \sigma _2 \sum _{p=1}^n m_p^2 {\bar{y}}_{p}(t-\tau ) y_{p }(t-\tau ) + \sum _{p=1}^{n} \Big ( \sigma _3 + \sigma _4 \Big ) M^2_p, \end{aligned} \end{aligned}$$
(14)

which implies that:

$$\begin{aligned} \begin{aligned} D^\epsilon V (t) \le&- \lambda _{1 } V(t)+ \lambda _{2 } V (t-\tau )+ \lambda _{3 }, \end{aligned} \end{aligned}$$
(15)

i.e.,

$$\begin{aligned} \begin{aligned} D^\epsilon \Big ( V (t) - \frac{ \lambda _{3 }}{ \lambda _{1}- \lambda _{2}} \Big ) \le&-\lambda _{1 }\Big ( V (t) - \frac{ \lambda _{3 }}{ \lambda _{1}- \lambda _{2}} \Big ) + \lambda _{2 } \Big ( V (t-\tau ) - \frac{ \lambda _{3 }}{ \lambda _{1}- \lambda _{2}} \Big ), \end{aligned} \end{aligned}$$
(16)

set \( \omega (t)= V (t) - \frac{ \lambda _{3 }}{ \lambda _{1}- \lambda _{2}}\), then (16) can be rewritten as:

$$\begin{aligned} \begin{aligned} D^\epsilon \omega (t) \le&-\lambda _{1 }\omega (t) + \lambda _{2 } \omega (t-\tau ). \end{aligned} \end{aligned}$$
(17)

Consider the following system:

$$\begin{aligned} D^\epsilon \psi (t )= - \lambda _{1 } \psi (t)+ \lambda _{2 } \psi (t-\tau ), \end{aligned}$$
(18)

in which \(\psi (t )\ge 0\), (18) and V(t) have the identical initial values.

The main contribution of the following lines are proving system (18) is quasi-stable. Employing the Laplace transform on (18) gives:

$$\begin{aligned} \begin{aligned} s^\epsilon \psi (s)-s^{\epsilon -1} \psi (0)=&-\lambda _1\psi (s)+\lambda _2\int _0^{+ \infty }e^{-s t } \psi (t-\tau ) dt\\ =&-\lambda _1\psi (s)+\lambda _2\int _{-\tau }^{+ \infty }e^{-s (\nu +\tau ) } \psi (\nu ) d\nu \\ =&-\lambda _1\psi (s)+\lambda _2e^{-s \tau }\int _{-\tau }^{0}e^{-s \nu } \psi (\nu ) d\nu +\lambda _2e^{-s \tau }\int _{0}^{+\infty }e^{-s \nu } \psi (\nu ) d\nu \\ =&-\lambda _1\psi (s)+\lambda _2e^{-s \tau }\psi (s)+\lambda _2e^{-s \tau }\int _{-\tau }^{0}e^{-s \nu } \psi (\nu ) d\nu , \end{aligned} \end{aligned}$$

which implies:

$$\begin{aligned} \begin{aligned} (s^\epsilon +\lambda _1-\lambda _2e^{-s \tau })\psi (s)=s^{\epsilon -1} \psi (0)+\lambda _2e^{-s \tau }\int _{-\tau }^{0}e^{-s \nu } \psi (\nu ) d\nu , \end{aligned} \end{aligned}$$

thus, the characteristic equation is given by:

$$\begin{aligned} \text {det}(\Delta (s) )= s^\epsilon +\lambda _1-\lambda _2 e^{-s \tau }=0. \end{aligned}$$
(19)

Now, based on Lemma 2.3, one need to prove (19) has no pure imaginary solutions. If \(s= v i=|v|(\cos \frac{\pi }{2}+ i \sin (\pm \frac{\pi }{2}))\) satisfies (19), this means that:

$$\begin{aligned} |v|^\epsilon ( \cos \frac{\epsilon \pi }{2} + i \sin ( \pm \frac{\epsilon \pi }{2}))+\lambda _1-\lambda _2 \cos v \tau + i \lambda _2 \sin v \tau =0, \end{aligned}$$
(20)

thus,

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} |v|^\epsilon \cos \frac{\epsilon \pi }{2}+\lambda _1=\lambda _2 \cos v \tau , \\ |v|^\epsilon \sin ( \pm \frac{\epsilon \pi }{2}) =- \lambda _2 \sin v \tau , \end{array} \right. \end{aligned} \end{aligned}$$

then,

$$\begin{aligned} \begin{aligned} |v|^{2\epsilon }+ 2\lambda _1 \cos \frac{\epsilon \pi }{2} |v|^{ \epsilon } +\lambda _1^2=\lambda _2^2, \end{aligned} \end{aligned}$$
(21)

thus,

$$\begin{aligned} \begin{aligned} \Delta = (2\lambda _1 \cos \frac{\epsilon \pi }{2})^2-4(\lambda _1^2-\lambda _2^2)<0, \end{aligned} \end{aligned}$$

obviously, if \( \lambda _2 < \lambda _1 \sin \frac{\epsilon \pi }{2}\), then (21) has no real roots.

Considering that \( \lambda _2 < \lambda _1 \sin \frac{\epsilon \pi }{2} \le \lambda _1\), thus, the eigenvalues of \( \lambda _2-\lambda _1< 0 \), and this implies \(|\arg ( \lambda ^*)|> \frac{\pi }{2}\), \(\lambda ^*\) is the eigenvalues of \(\lambda _2-\lambda _1\).

Now, based on Lemma 2.3, the zero solution of (18) is global asymptotically stable, i.e., \( \psi (t ) \rightarrow 0\) as \(t \rightarrow \infty \). On the other hand, a straightforward of Lemma 2.4 gives \(0 < \omega (t)\le \psi (t)\), thus \( \omega (t)\rightarrow 0 \) as \(t \rightarrow \infty \). Then, for \(\forall \varepsilon >0\), there has \(T>0\), such that \( \omega (t )< \varepsilon \) as \(t >T \), i.e., \( V (t) \le \frac{ \lambda _{3 }}{ \lambda _{1}- \lambda _{2}} + \varepsilon \) as \(t >T \).

Considering that \( \Vert y(t)\Vert ^2 \le V(t) \), which implies that

$$\begin{aligned} \Vert y(t)\Vert \le \sqrt{\frac{ \lambda _{3 }}{ \lambda _{1}- \lambda _{2}} + \varepsilon }, \ \ \ t >T. \end{aligned}$$

This suggests that unique equilibrium of system (3) is quasi-stable from Definition 2.3. This completes the proof.

Remark 3.1

In this paper, the parameters are taking values in the quaternion field, thus, the closed convex hull consisted by the quaternion-valued can be derived, i.e., one need to compare the “magnitude” of two quaternions. In some existing results [21,22,23,24,25,26,27,28], the quaternion-valued system is transformed into four real number systems, this may undermine the integrity of the quaternion-valued system. To solve such problems, a vector ordering approach is employed, which can be used to compare the “magnitude” of two different quaternions. Moreover, this method provides a new way to study the quaternion-valued neural networks with uncertain terms.

4 Numerical Examples

This section exemplifies our theoretical results with one example.

Example 1

The highlights of this example are to expound the effectiveness of the technical analysis for the quasi-stabilization control of the given system, thus considering system (3) with the following coefficients:

$$\begin{aligned} \begin{aligned}&a_{11}(x_1(t)) =\left\{ \begin{array}{l} 1.5 + 1.6 i+ 1.16 j+ 1.35 k, \ \ \ \ \ |x_1(t)|\le 1, \\ 1.2 + 1.2i+ j+ 1.1 k, \ \ \ \ \ \ \ \ \ \ \ \ \ \ |x_1(t)|> 1, \end{array} \right. \\&a_{12}(x_1(t)) =\left\{ \begin{array}{l} -0.1 -0.1 i-0.12 j-0.11 k, \ \ |x_1(t)|\le 1, \\ -0.2 -0.12 i-0.13 j-0.12 k, |x_1(t)|> 1, \end{array} \right. \\&a_{21}(x_2(t)) =\left\{ \begin{array}{l} -1.1-1.4 i-1.24 j-1.3 k, \ \ \ \ |x_2(t)|\le 1, \\ -1.1- i- j-1.12 k, \ \ \ \ \ \ \ \ \ \ \ \ \ \ |x_2(t)|> 1, \end{array} \right. \\&a_{22}(x_2(t)) =\left\{ \begin{array}{l} 1.2+2.1 i+2.2 j+2.1 k, \ \ \ \ \ \ \ \ \ |x_2(t)|\le 1, \\ 1.7+ 2.15 i+ 2.35 j+2.2 k, \ \ \ \ \ |x_2(t)|> 1, \end{array} \right. \\&b_{11}(x_1(t)) =\left\{ \begin{array}{l} -1.5-1.5 i-1.57 j-1.23 k, \ \ \ |x_1(t)|\le 1, \\ -1.2 -0.9 i-1.35 j-0.89k, \ \ \ |x_1(t)|> 1, \end{array} \right. \\&b_{12}(x_1(t)) =\left\{ \begin{array}{l} - 0.1-0.1 i-0.11 j-0.11 k, \ \ \ |x_1(t)|\le 1, \\ -0.13-0.13 i+0.13 j+0.1 k, \ |x_1(t)|> 1, \end{array} \right. \\&b_{21}(x_2(t)) =\left\{ \begin{array}{l} -0.23-0.53 i-0.3 j-0.57 k, \ |x_2(t)|\le 1, \\ -0.2-0.51 i-0.2 j-0.21 k, \ \ \ |x_2(t)|> 1, \end{array} \right. \\&b_{22}(x_2(t)) =\left\{ \begin{array}{l} -1.9-1.3 i-1.2 j-1.49 k, \ \ \ \ \ |x_2(t)|\le 1, \\ -1.8 -2.9 i- 2.1 j-1.32 k, \ \ \ \ \ |x_2(t)|> 1, \end{array} \right. \end{aligned} \end{aligned}$$

besides, \(d_1\)=\(d_2\)=1.6, the time delay and activation function are \(\tau =0.1\), \(f_q(\cdot )= 0.1\tanh (\cdot ) \), respectively. From the assumption \((A_1)\), it follows that \( M_q =m_q = 0.1 \), with the above-mentioned parameters, the constants \(\sigma _p\) are defined as \(\sigma _1=8\), \(\sigma _2=8\), \(\sigma _3=1\), \(\sigma _4=1\), then according to the conditions derived in Theorem 3.2, one can calculate that:

$$\begin{aligned}&2 d_1 + 2 \upsilon _1 - \sigma _1 m_1^2 - \frac{1}{\sigma _1 } \sum _{q=1}^{2} {\tilde{a}}_{1q} \bar{{\tilde{a}}}_{1q} - \frac{1}{\sigma _2 } \sum _{q=1}^{2} {\tilde{b}}_{1q} \bar{{\tilde{b}}}_{1q} - \frac{1}{ \sigma _3 } \sum _{q=1}^{2} (\acute{a} _{1q} -\grave{a} _{1q} )(\bar{\acute{a}}_{1q} -\bar{\grave{a}}_{1q} )\\&- \frac{1}{ \sigma _4 } \sum _{q=1}^{2} (\acute{b}_{1q} -\grave{b}_{1q} )(\bar{\acute{b}}_{1q} -\bar{\grave{b}}_{1q} ) \\ =&2 \upsilon _1-0.0215>0,\\&2 d_2 + 2 \upsilon _2 - \sigma _1 m_2^2 - \frac{1}{\sigma _1 } \sum _{q=1}^{2} {\tilde{a}}_{2q} \bar{{\tilde{a}}}_{2q} - \frac{1}{\sigma _2 } \sum _{q=1}^{2} {\tilde{b}}_{2q} \bar{{\tilde{b}}}_{2q} - \frac{1}{ \sigma _3 } \sum _{q=1}^{2} (\acute{a} _{2q} -\grave{a} _{2q} )(\bar{\acute{a}}_{2q} -\bar{\grave{a}}_{2q} )\\&- \frac{1}{ \sigma _4 } \sum _{q=1}^{2} (\acute{b}_{2q} -\grave{b}_{2q} )(\bar{\acute{b}}_{2q} -\bar{\grave{b}}_{2q} ) \\ =&2 \upsilon _2-5.2125 >0,\\ \end{aligned}$$
$$\begin{aligned} \begin{aligned} \lambda _{2 } =&\sigma _2 \max _p m_p^2 = 0.08>0,\\ \lambda _{3 } =&( \sigma _3 + \sigma _4 ) \sum _{p=1}^{2} M^2_p =0.04, \end{aligned} \end{aligned}$$

then, set \(\upsilon _1=0.056\), \(\upsilon _2=2.7\), one has: \(\lambda _{1 } = 0.0905\), which implies that \(\lambda _{1 }> \lambda _{2 }\).

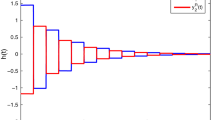
Based on the conclusions derived in Theorem 3.2, one can see that the error system (9) is quasi-stability, and the stability region can be calculated as \( \Vert y(t)\Vert \le \sqrt{\frac{ \lambda _{3 }}{ \lambda _{1}- \lambda _{2}} + \varepsilon }= 1.977 \), where \(\varepsilon =0.1\). Set, \(\xi _1=\xi _2=0.1\). then, one can depict the transient behaviors of the states and the control parameters in Fig. 1, 2, 3, 4, from which it is apparent that the quasi-stability for the system (9) is achieved.

Fig. 1
figure 1

Trajectories of the states \(x^R(t)\) and control parameters \(\eta ^R(t)\)

Full size image
Fig. 2
figure 2

Trajectories of the states \(x^I(t)\) and control parameters \(\eta ^I(t)\)

Full size image
Fig. 3
figure 3

Trajectories of the states \(x^J(t)\) and control parameters \(\eta ^J(t)\)

Full size image
Fig. 4
figure 4

Trajectories of the states \(x^K(t)\) and control parameters \(\eta ^K(t)\)

Full size image

5 Conclusion

In this present work, we discussed the quaternion-valued fractional-order memristive neural networks and its quasi-stability behavior. Using contraction mapping theory, a sufficient condition is derived to ensure the existence of the equilibrium point for the quaternion-valued fractional-order memristive neural networks. Subsequently, the corresponding conclusion is given to ensure the quasi-stability of the derived equilibrium point. What should be mentioned is that, a vector ordering approach is proposed, which provides an effective method to compare the “magnitude” of two different quaternions, thus, the convex closure composed by the quaternion connection weights is meaningful. Finally, a numerical example is given to demonstrate the usefulness of the proposed quasi-stability criteria.

It should be mentioned that although the vector ordering method is employed in this paper, while, some problems should be considered further, for example, is there any other methods to compare the “size” of two different quaternions? Thus, it is also challenging and will be discussed in our future research. Moreover, dynamic behaviors of the fractional-order discrete-time memristive neural networks are also our future works.