Stabilization of a Class of Hybrid Systems by Switching Controllers with Input Constraints

Abstract

In this paper, a hybrid control strategy using appropriate switching between a set of linear controllers is presented for stabilization of a class of hybrid systems with input constraints. The input constraints under consideration are novel reverse polytopic constraints avoiding a set of specified input values. The design procedure of the switching controllers is performed by solving a set of linear matrix inequalities for the full state feedback case and by solving a set of bilinear matrix inequalities for the output feedback case. Under the designed controllers, the closed-loop system is shown to be globally uniformly pre-asymptotically stable if a specific set of matrix inequalities ensuring the existence of a common Lyapunov function are satisfied. To avoid the Zeno behavior, a tunable parameter related to the controller gains is introduced and assessed. It is shown that the proposed switching control is superior to continuous state feedback control with input constraints. In addition, besides continuous linear systems, the proposed control strategy is applicable to hybrid or impulsive systems. Numerical examples are included to illustrate the proposed results.

1 Introduction

1.1 Motivation

Hybrid systems are ubiquitous in realistic systems due to their ability to capture models having state variables that can evolve continuously (flows) and/or discretely (jumps). In recent years, the study of stabilization in hybrid systems has received substantial attention. This is mainly due to the increasing application of digital devices for the control of real systems, such as robotics [9], power systems [7] and chemical processes [25], and also for their flexibility, which allows us to overcome some fundamental limitations of classical control. Particular motivation for the study of switching control with input constraints comes from the fact that switching thrusters with constraints are always employed as actuators, such as hydrazine, cold gas and pulsed plasma thrusters.

1.2 Related Work

Numerous of dynamic systems have the characteristics of continuous-time systems and discrete-time systems, generally referred to as hybrid dynamic systems or simply hybrid systems. During the last years, the research on the analysis and control design of such systems has received the attention of many academics. Recent progress in the development of stability and control theory for hybrid dynamical systems has led to a new framework [8]. In [6], a hybrid feedback control was proposed to trajectory tracking of quadrotor-like vehicles. In addition, the fault detection problem of discrete-time hybrid systems was addressed in [30]. Li et al. [16] studied the set stability of switched Boolean networks with state-based switching. Impulsive system as one of hybrid systems, its stability and controller design have attracted much attention. The controller designs of hybrid impulsive systems were considered in [13, 21, 22, 27]. The authors in [15] derived some sufficient conditions ensuring stability and stabilization of the impulsive systems with unbounded time-varying delay. In [14, 28], synchronization of impulsive networks was addressed. For hybrid systems with input constraints, [1] gave a constructive switching algorithm for finite state machines subject to state and input constraints. By solving two specific linear matrix inequalities, [20] explored stabilization of a class of time-delay hybrid systems with input constraint. The authors in [29] proposed an impulse-based filtering scheme of a class of nonlinear systems over sensor networks based on impulsive control theory and a comparison theorem. In addition, the design of a switched Boolean networks with state and input constraints using the semi-tensor product method was proposed in [17].

Input constraints exist in many actual control systems and pose significant challenges to controller design issues. In recent years, the problem of designing a controller in the presence of input constraints has attracted more and more attention. To guarantee a globally stabilizing control law for arbitrarily small bounds on the input, the system should have no eigenvalues with positive real part [12, 26]. In general, one can describe linear input constraints as a finite number of linear inequalities, which is equivalent to a polyhedron as described in [3]. In Casau et al. [5] proposed a reverse polytopic input constraint model avoiding a specified set of input values where the system states evolve continuously. Such constraints are likely to be applied to quad-rotors that want to avoid free-fall conditions as mentioned in [10]. However, due to limitations in these control methods, it is not appropriate to deal with the above reverse polytopic input constraints. The common input control does not make full use of the input values meeting the constraints, so the control performance is not good. In [18], a switching method among multiple controllers to stabilize a linear system with actuator constraints is proposed. Cai and Mijanovic in [4] provided a switching control methodology to stabilize linear hybrid systems. Such a switching method can jump between various input values that satisfy the constraint, and can improve the control performance. This motivates us to consider switching controllers with input constraints. Inspired by this, we consider the problem of stabilizing a class of hybrid impulsive systems with reverse polytopic input constraints within the hybrid systems framework in [8] and combining the matrix inequality techniques in [2, 11].

1.3 Contributions

Tools for the analysis of stabilization of hybrid systems under switching control with reverse polytopic input constraints are not yet available in the literature. In this paper, we propose such an approach for the stabilization problem of hybrid systems, which are ubiquitous in many cases such as impulsive systems, through switching feedback control while avoiding a prescribed set of input values. The main idea in our control strategy is to ensure that the input constraints are always obeyed through proper switching of a set of controllers. By [19], if each of the designed controllers for subsystems has a common Lyapunov function, then the stability of the closed-loop system is independent of the switching sequence, which is the crux to design the controllers. Then, the control problem can be tackled by solving a set of matrix inequalities. The contributions of this paper include the following:

• We propose switching controllers with input constraints to stabilize a class of hybrid impulsive systems.

• The design procedure of the switching controllers with reverse polytopic constraints is performed by solving a set of linear matrix inequalities for the full state feedback case and by solving a set of bilinear matrix inequalities for the output feedback case.

• We establish conditions for the global uniform pre-asymptotic stability of the closed-loop system and design a parameter $\beta$ related to the controller gains to avoid the Zeno behavior.

1.4 Organization and Notation

The organization of the paper is as follows. We give some preliminaries on hybrid systems in Sect. 2 and present the reverse polytopic constraints in Sect. 3. In Sect. 4, we propose a switching control strategy with input constraints for stabilization of a class of hybrid systems and numerical simulations are also given to verify the results. Finally, Sect. 5 concludes the paper.

Notation In this work, ${\mathbb {R}}^n$ denotes the Euclidean space of dimension n, with the inner product $\langle u,v\rangle ={u}^\top {v}$ and for each ${v}\in {\mathbb {R}}^n$, the induced norm $\mid \!v\!\mid = \sqrt{\langle v,v\rangle }$. ${\mathbb {R}}^{{m}\times {n}}$ denotes ${m}\times {n}$ matrices with real entries. ${\mathbb {R}}$ denotes the set of real number and ${\mathbb {R}}_{\ge 0}:=[0,\infty )$. The interior of a set ${S}\subset {\mathbb {R}}^n$ is denoted by int(S) and its closure is denoted by cl(S). ${\mathbb {N}}$ denotes the set of natural numbers and ${\mathbb {N}}^+$ represents the set of numbers in ${\mathbb {N}}$ that are removed by 0. ${e}_i$ is the unit vector of the ith entry equal to 1 for each ${i}\in \{1,2,\ldots ,{n}\}$ and $\mathbf{1 }_{n}$ denotes a vector where each entry is equal to 1. Succinctly, we say ${u}<{v}$ if ${e}_i^\top {u}<{e}_i^\top {v}$ for each $i\in \{1,2,\ldots ,n\}$. Similarly, there are ${u}>{v}$, ${u}\le {v}$, ${u}\ge {v}$. A set of ${n}\times {n}$ real symmetric matrices with positive eigenvalues is expressed as ${\mathbb {S}}^{n}_{>0}$. For the sake of convenience, we use (u, v) in place of [${u}^\top {v}^\top$]$^\top$, where $({u},{v})\in {\mathbb {R}}^n \times {\mathbb {R}}^m$. For ${M}:{\mathbb {R}}^m\rightrightarrows {\mathbb {R}}^n$, $dom \,{M} = \{{x}\in {\mathbb {R}}^m:{M}(x)\ne \emptyset \}$ and the graph of M is the set $gph \,M=\{(x,y)\in {\mathbb {R}}^m\times {\mathbb {R}}^n:y\in M(x)\}$. Let $\{M_i\}_{i=1}^\infty$ be a sequence of set-valued mappings $M_i:{\mathbb {R}}^m\rightrightarrows {\mathbb {R}}^n$ that is graphically convergent and set $M= gph-lim _{i\rightarrow \infty }M_i$. Given a closed set ${\mathcal {A}}\subset {\mathbb {R}}^n$ and $\mid \!{x}\!\mid _{\mathcal {A}}:= \mathrm {inf}_{y\in {\mathcal {A}}}\mid \!{x}-{y}\!\mid$. A function $\alpha :{\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}_{\ge 0}$ is of class ${\mathcal {K}}$ if it is zero at zero, strictly increasing and continuous. If $\alpha$ is unbounded, we say $\alpha \in {\mathcal {K}}_\infty$. A function $\rho :{\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}_{\ge 0}$ is positive definite (${{\mathcal {P}}}{{\mathcal {D}}}$), written $\rho \in {{\mathcal {P}}}{{\mathcal {D}}}$, if it is continuous, $\rho (s)>0$ for every $s>0$ and $\rho (0)=0$. $\nabla V(x)$ denotes the gradient of a function $V:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ at x.

2 Hybrid Systems

The model of a hybrid system with state space ${\mathbb {R}}^n$ can be represented in the following form

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{\xi }}\in F(\xi ), \qquad&\xi \in {\mathcal {C}}, \\&\xi ^+\in G(\xi ),\qquad&\xi \in {\mathcal {D}}, \end{aligned} \right. \end{aligned}$$

(1)

where $\xi$ denotes the state of the system, ${\mathcal {C}}\subset {\mathbb {R}}^n$ is the flow set, ${F}:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$ is the flow map, ${\mathcal {D}} \subset {\mathbb {R}}^n$ is the jump set and ${G}:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$ is the jump map. A hybrid system with the data as above will be represented by the notation ${\mathcal {H}}:=({\mathcal {C}},{F},{\mathcal {D}},{G})$.

Solutions of continuous-time systems are parameterized by ${t}\in {\mathbb {R}}_{\ge 0}$, in other words, by times, and solutions of discrete-time systems are parameterized by ${j}\in {\mathbb {N}}$, that is, by the number of jumps or discrete steps. For hybrid systems, it is natural to suggest that solutions be parameterized by (t, j), where t denotes flow time and j denotes the jump time, and its domain $\mathrm {dom}\,{\xi }\subset {\mathbb {R}}_{\ge 0}\times {\mathbb {N}}$ is a hybrid time domain [8]: For all $({T},{J})\in$$\mathrm {dom}\;{\xi }$, $\mathrm {dom}\,{\xi }\cap \left( [0,{T}]\times \{0,1,\ldots ,{J}\}\right)$ can be written in the form $\bigcup _{j=0}^{J-1}\left( [t_j,t_{j+1}],j\right)$ for some finite sequence of times $0=t_0\le t_1\le t_2\le \cdots \le t_J$. Given a hybrid time domain E, we have $\mathrm {sup}_tE=\mathrm {sup}\{t\in {\mathbb {R}}_{\ge 0}:\exists \; j\in {\mathbb {N}}\mathrm {\;such\;that\;}(t,j)\in E\}$, $\mathrm {sup}_jE=\mathrm {sup}\{j\in {\mathbb {N}}:\exists \;t\in {\mathbb {R}}_{\ge 0}\mathrm {\;such\; that\;}(t,j)\in E\}$ and $\mathrm {length}(E)=\mathrm {sup}_tE+\mathrm {sup}_jE$. Solution to ${\mathcal {H}}$ that cannot be extended is said to be maximal and it is said to be complete if its domain is unbounded [8, Chapter 2]. Clearly, complete solutions are maximal. A hybrid system ${\mathcal {H}}$ is said to be well posed if it satisfies the following hybrid basic conditions.

Assumption 1

[8] (Hybrid basic conditions)

(A1):

${\mathcal {C}}$ and ${\mathcal {D}}$ are closed subsets of ${\mathbb {R}}^n$;

(A2):

${F}:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$ is outer-semicontinuous and locally bounded relative to ${\mathcal {C}}$, ${\mathcal {C}}\subset \mathrm {dom}\,{F}$, and $F(\xi )$ is convex for every $\xi \in {\mathcal {C}}$;

(A3):

${G}:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$ is outer-semicontinuous and locally bounded relative to ${\mathcal {D}}$, ${\mathcal {D}}\subset \mathrm {dom}\,{G}$.

Definition 1

[8] (Well-posed hybrid system) A hybrid system ${\mathcal {H}}$ is called well posed if the following property holds: Given an arbitrary continuous function $\zeta :{\mathbb {R}}^n\rightarrow {\mathbb {R}}_{\ge 0}$, a decreasing sequence $\{\delta _i\}_{i=1}^\infty$ of numbers in (0, 1) with ${\mathrm{lim}}_{i\rightarrow \infty }\delta _i=0$, and a graphically convergent sequence $\{\phi _i\}_{i=1}^\infty$ of solutions to ${\mathcal {H}}_{\delta _i\zeta }$ with $\mathrm{lim}_{i\rightarrow \infty }\phi _i(0,0)=\epsilon \in {\mathbb {R}}^n$,

(B1):

if the sequence $\{\phi _i\}_{i=1}^\infty$ is locally eventually bounded, then the sequence $\{\mathrm{length}(\phi _i)\}_{i=1}^\infty$ either converges or properly diverges to $\infty$ and $\phi =gph-lim _{i\rightarrow \infty }\phi _i$ is a solution to ${\mathcal {H}}$ with $\phi (0,0)=\epsilon$ and $\mathrm {length}(\phi )=\mathrm {lim}_{i\rightarrow \infty }$$\mathrm {length}(\phi _i)$;

(B2):

if the sequence $\{\phi _i\}_{i=1}^\infty$ is not locally eventually bounded, then there exist the smallest $j^\star \in {\mathbb {N}}$, $t^\star \in {\mathbb {R}}_{>0}$ for which there exist $(t_i,j^\star )\in \mathrm {dom}\;\phi _i$ for all large enough i such that $\mathrm {lim}_{i\rightarrow \infty }t_i=t^\star$ and $\mathrm {lim}_{i\rightarrow \infty }|\phi _i(t_i,j^\star )|=\infty$, and the mapping $\phi =\left( gph-lim _{i\rightarrow \infty }\phi _i\right) |_{t+j<t^\star +j^\star }$ is a maximal solution to ${\mathcal {H}}$ and $\mathrm {lim}_{t\rightarrow t^\star }|\phi (t,j^\star )|=\infty$.

Lemma 1

[8] If a hybrid system ${\mathcal {H}}$ satisfies Hybrid basic conditions, then it is well posed.

The sufficient Lyapunov conditions ensuring the hybrid system ${\mathcal {H}}$ be uniformly globally pre-asymptotically stable are proposed in [8, Theorem 1].

Lemma 2

[8] Consider the hybrid system ${\mathcal {H}}$ in (1) and a closed set ${\mathcal {A}}\subset {\mathbb {R}}^n$. If V is Lyapunov function candidate for ${\mathcal {H}}$ and there exist $\alpha _1,\alpha _2\in {\mathcal {K}}_\infty$ and a function $\rho \in {{\mathcal {P}}}{{\mathcal {D}}}$ such that

$$\begin{aligned}&\alpha _1(\mid \!\xi \!\mid _{\mathcal {A}})\le V(\xi )\le \alpha _2(\mid \!\xi \!\mid _{\mathcal {A}}),\;&\forall \xi \in {\mathcal {C}}\cup {\mathcal {D}}\cup G({\mathcal {D}}), \end{aligned}$$

(2)

$$\begin{aligned}&\langle \nabla V(\xi ),f\rangle \le -\rho (\mid \!\xi \!\mid _{\mathcal {A}}),&\forall \xi \in {\mathcal {C}},\;f\in F(\xi ), \end{aligned}$$

(3)

$$\begin{aligned}&V(g)\le V(\xi ),&\forall \xi \in {\mathcal {D}},\;g\in G(\xi ). \end{aligned}$$

(4)

If for each $r>0$, there exists $\lambda _r\in {\mathcal {K}}_\infty$, $N_r\ge 0$ such that for every solution $\xi$ to the hybrid system ${\mathcal {H}}$, $\mid \!\xi (0,0)\!\mid _{\mathcal {A}}\in (0,r]$, $(t,j)\in \mathrm {dom}\,\xi$, $t+j\ge T^\prime$ imply $t\ge \lambda _r(T^\prime )-N_r$, then ${\mathcal {A}}$ is uniformly globally pre-asymptotically stable.

Note that (3) and (4) ensure that the Lyapunov function candidate does not increase in both the flows and the jumps, respectively. More specific details can be found in [8, Chapter 3] and [23].

In this paper, we consider a class of hybrid impulsive systems given by

$$\begin{aligned} \begin{aligned}&{\left( \begin{array}{c} {\dot{x}}\\ {\dot{\tau }} \end{array} \right) }= F(x,\tau ):={\left( \begin{array}{c} Ax+Bu\\ 1 \end{array} \right) },&\!\!\!(x,\tau )\in {\mathcal {C}}, \\&{\left( \begin{array}{c} x^+\\ \tau ^+ \end{array} \right) }\in G(x,\tau ):={\left( \begin{array}{c} A_dx\\ 0 \end{array} \right) },&\!\!\!(x,\tau )\in {\mathcal {D}}, \\&\;y=Cx, \end{aligned} \end{aligned}$$

(5)

with

$$\begin{aligned}&{\mathcal {C}}:=\{(x,\tau )\in {\mathbb {R}}^{n}\times {\mathbb {R}}:\tau \in [0,\;T]\},\\&{\mathcal {D}}:=\{(x,\tau )\in {\mathbb {R}}^{n}\times {\mathbb {R}}:\tau =T\}, \end{aligned}$$

where ${x}\in {\mathbb {R}}^n$ and $\tau \in [0,\;T]$ are the system states, $T$ is a positive number, $u\in {\mathbb {R}}^p$ denotes the input, $y\in {\mathbb {R}}^m$ denotes the output, $A\in {\mathbb {R}}^{n\times n}$, $B\in {\mathbb {R}}^{n\times p}$, $C\in {\mathbb {R}}^{m\times n}$ and $A_d\in {\mathbb {R}}^{n\times n}$ denotes the parameters of the system.

3 Input Constraints

Denote a polyhedron

$$\begin{aligned} P_{(H,h)}:=\{u\in {\mathbb {R}}^p:Hu\le h\}, \end{aligned}$$

(6)

where $(H,h)\in {\mathbb {R}}^{s\times p}\times {\mathbb {R}}^s$, $p,s\in {\mathbb {N}}^+$. See [3, 5] for more information.

Lemma 3

[5] For all $(H,h)\in {\mathbb {R}}^{s\times p}\times {\mathbb {R}}^s$ with $s,p\in {\mathbb {N}}^+$, and for all $\theta >0$, then

$$\begin{aligned} P_{(H,h)}\cap \mathrm {cl}\left( {\mathbb {R}}^p\setminus P_{(H,h+\mathbf{1 }_s\theta )}\right) = \emptyset . \end{aligned}$$

Lemma 4

[5] Given $(H,h)\in {\mathbb {R}}^{s\times p}\times {\mathbb {R}}^s$ with $s,p\in {\mathbb {N}}^+$, if $P_{(H,h)}$ is bounded, then there exists ${a}\in {\mathbb {R}}^s$ satisfying ${a}>0$, $H^\top {a}=0$, $\mathbf{1 }_s^\top {a}=1$.

Lemma 5

Given finite sets ${\mathcal {W}}\subset {\mathbb {N}}^+$, $(H_i,h_i)\in {\mathbb {R}}^{s_i\times p}\times {{\mathbb {R}}^{s_i}}$ with $s_i,p\in {\mathbb {N}}^+$ and $i\in {\mathcal {W}}$, for all $0<\theta ^-<\theta ^+$, then

$$\begin{aligned} \bigcup \limits _{i\in {\mathcal {W}}}P_{(H_i,h_i+\mathbf{1 }_{s_i}\theta ^-)}\cap \,\mathrm {cl}\left( \bigcap \limits _{i\in {\mathcal {W}}}\left( {\mathbb {R}}^p\setminus P_{(H_i,h_i+\mathbf{1 }_{s_i}\theta ^+)}\right) \right) = \emptyset . \end{aligned}$$

(7)

Proof

Following from the definition in (6), we have that $P_{(H,h+\mathbf{1 }_s\theta ^-)}\subset P_{(H,h+{1}_s\theta ^+)}$, then $P_{(H,h+\mathbf{1 }_s\theta ^-)}\cap \mathrm {cl}\left( {\mathbb {R}}^p\setminus P_{(H,h+\mathbf{1 }_s\theta ^+)}\right) =\emptyset$. Consequently, (7) holds.

In this paper, we consider the reverse polytopic input constraints mentioned in [5]

$$\begin{aligned} u\notin \bigcup \limits _{i\in {\mathcal {W}}}P_{(H_i,h_i)}, \end{aligned}$$

(8)

where $u\in {\mathbb {R}}^p$ is the input of the hybrid system (5) and the index $i\in {\mathcal {W}}$ indicates the ith constraint.

Next, consider an example to illustrate the input constraints mentioned above. $\square$

Example 1

Consider the input of the hybrid system (5) with $p=1$ satisfies the constraint $\mid \!u\!\mid \notin [0.2,0.7]$. This constraint can be written in the form of (8) with $H_1=-H_2=[1\;-1]^\top$, $h_1=h_2=[0.7\;-0.2]^\top$, ${\mathcal {W}}=\{1,2\}$.

4 Controller Design

In this section, for the hybrid system (5) with constraint (8), we aim to design switching controllers ${\mathcal {H}}_c$ ensuring the closed-loop system to be globally uniformly pre-asymptotically stable.

4.1 State Feedback

First, we consider the case of full state feedback controllers with the form

$$\begin{aligned} u=K_q^x x, \end{aligned}$$

(9)

where $u\in {\mathbb {R}}^p$ is the input of (5) that obeys constraint (8) and is also the output of the controllers, $x\in {\mathbb {R}}^n$ is the state of (5) and is also the input of the controllers and controller gain $K_q^x\in {\mathbb {R}}^{p\times n}$ is real for all $q\in {\mathcal {Q}}:=\{1,2,\ldots ,q_{\max }\}$ with $q_{\max }\in {\mathbb {N}}^+$ representing the total number of the controllers. One can switch these controllers suitably by q to guarantee that constraint (8) is satisfied. It is worth noting that the superscript x of $K_q^x$ is the identity of the state feedback rather than the exponential operation.

Given a finite set ${\mathcal {W}}\subset {\mathbb {N}}^+$, $(H_i,h_i)\in {\mathbb {R}}^{s_i\times p}\times {\mathbb {R}}^{s_i}$ with $s_i,p\in {\mathbb {N}}^+$ for all $i\in {\mathcal {W}}$, $\theta ^+>0$ and a set of controllers mentioned in (9), define a multi-valued map

$$\begin{aligned} \varrho (x):=\{q\in {\mathcal {Q}}:K_q^x x\in {\mathcal {C}}^+,\;x\in {\mathbb {R}}^n\}, \end{aligned}$$

where ${\mathcal {C}}^+:=\mathrm {cl}\left( \bigcap \nolimits _{i\in {\mathcal {W}}}\left( {\mathbb {R}}^p\setminus P_{(H_i,h_i+\mathbf{1 }_{s_i}\theta ^+)}\right) \right)$. It follows from Lemma 3 that the function of this map is to pick out the sequence number q of the controller gains that do not violate the given input constraint.

Next, let us revisit (8). To guarantee $K_q^x x\notin \bigcup \nolimits _{i\in {\mathcal {W}}}P_{(H_i,h_i)},$ we design supervisory control among the $q_{\max }$ controllers related to the logic state q. Given $\theta ^+>\theta ^->0$, we design the logic state abiding by the following dynamics

$$\begin{aligned} \begin{aligned}&{\dot{q}}=0,\qquad&q\in {\mathcal {C}}_c,\\&q^+\in \varrho (x),&q\in {\mathcal {D}}_c, \end{aligned} \end{aligned}$$

(10)

where ${\mathcal {C}}_c:=\left\{ q\in {\mathcal {Q}}:K_q^x x\in {\mathcal {C}}^-\right\} ,$${\mathcal {D}}_c:=\left\{ q\in {\mathcal {Q}}:K_q^x x\in {\mathcal {D}}^-\right\} ,$

$$\begin{aligned}&{\mathcal {C}}^-:=\mathrm {cl}\left( \bigcap \limits _{i\in {\mathcal {W}}} \left( {\mathbb {R}}^p\setminus P_{(H_i,h_i+\mathbf{1 }_{s_i}\theta ^-)}\right) \right) , \end{aligned}$$

(11)

$$\begin{aligned}&{\mathcal {D}}^-:=\bigcup \limits _{i\in {\mathcal {W}}}P_{(H_i,h_i +\mathbf{1 }_{s_i}\theta ^-)}. \end{aligned}$$

(12)

Note that ${\mathcal {C}}_c$ and ${\mathcal {D}}_c$ denote the flow set and the jump set, respectively. q keeps constant during flows. The function $\varrho : {\mathbb {R}}^{n}\rightrightarrows {\mathcal {Q}}$ determines the value of the logic state after jumps.

The closed-loop system consisting of (5) and (10) with state space $\varOmega :={\mathbb {R}}^n\times {\mathcal {Q}}\times [0,\;T]$ can be written as the flow dynamics

$$\begin{aligned} \begin{aligned}&\left( \begin{array}{c} {\dot{x}}\\ {\dot{q}}\\ {\dot{\tau }} \end{array} \right) = f(x,q,\tau ):= \left( \begin{array}{c} (A+BK_q^x)x\\ 0\\ 1 \end{array} \right) , \end{aligned} \end{aligned}$$

(13)

with

$$\begin{aligned} (x,q,\tau )\in {\mathcal {C}}:=\left\{ (x,q,\tau )\in \varOmega :x\in {\mathbb {R}}^n,q \in {\mathcal {C}}_c,\tau \in [0,T]\right\} , \end{aligned}$$

and the jump dynamics

$$\begin{aligned} \begin{aligned} \left( \begin{array}{c} x^+\\ q^+\\ \tau ^+ \end{array} \right) \in G_1(x,q,\tau ):= \left( \begin{array}{c} x\\ \varrho (x)\\ \tau \end{array} \right) \quad (x,q,\tau )\in {\mathcal {D}}_1,\\ \left( \begin{array}{c} x^+\\ q^+\\ \tau ^+ \end{array} \right) \in G_2(x,q,\tau ):= \left( \begin{array}{c} A_dx\\ \varrho (x)\\ 0 \end{array} \right) \quad (x,q,\tau )\in {\mathcal {D}}_2,\\ \left( \begin{array}{c} x^+\\ q^+\\ \tau ^+ \end{array} \right) = G_3(x,q,\tau ):= \left( \begin{array}{c} A_dx\\ q\\ 0 \end{array} \right) \quad (x,q,\tau )\in {\mathcal {D}}_3, \end{aligned} \end{aligned}$$

(14)

with

$$\begin{aligned} \begin{aligned}&{\mathcal {D}}_1:=\{(x,q,\tau )\in \varOmega :x\in {\mathbb {R}}^n,q \in {\mathcal {D}}_c,\tau \ne T\},\\&{\mathcal {D}}_2:=\{(x,q,\tau )\in \varOmega :x\in {\mathbb {R}}^n,q \in {\mathcal {D}}_c,\tau =T\},\\&{\mathcal {D}}_3:=\{(x,q,\tau )\in \varOmega :x\in {\mathbb {R}}^n,q\notin {\mathcal {D}}_c,\tau =T\}. \end{aligned} \end{aligned}$$

Denote ${\mathcal {D}}:={\mathcal {D}}_1\cup {\mathcal {D}}_2\cup {\mathcal {D}}_3$ and $G:=G_1\cup G_2\cup G_3$. Then, we call the hybrid system as ${\mathcal {H}}^\star :=({\mathcal {C}},f,{\mathcal {D}},G)$.

4.2 Output Feedback

Next, we consider the case of output feedback controllers with the form

$$\begin{aligned} u=K_q^yy. \end{aligned}$$

The switching control gain $K_q^y\in {\mathbb {R}}^{p\times m}$ will be determined to ensure that the input $u\in {\mathbb {R}}^p$ satisfies constraint (8). Note that although the output feedback is similar to the state feedback in form, the degree of freedom of $K_q^y$ is much smaller than that of $K_q^x$. Hence, the output feedback is only equivalent to part of the state feedback, which results in difficulties to the calculation of gain $K_q^y$. Next, define a multi-valued map

$$\begin{aligned} \varrho (x)=\{q\in {\mathcal {Q}}:K_q^y Cx\in {\mathcal {C}}^+,\;x\in {\mathbb {R}}^n\}. \end{aligned}$$

Then, we can obtain a logic controller similar to (10), where ${\mathcal {C}}_c$ and ${\mathcal {D}}_c$ are now given by

$$\begin{aligned}&{\mathcal {C}}_c=\left\{ q\in {\mathcal {Q}}:K_q^yCx\in {\mathcal {C}}^-\right\} ,\\&{\mathcal {D}}_c=\left\{ q\in {\mathcal {Q}}:K_q^yCx\in {\mathcal {D}}^-\right\} , \end{aligned}$$

where ${\mathcal {C}}^-$ and ${\mathcal {D}}^-$ are defined in (11) and (12), respectively. The flow dynamics of the closed-loop system under the output feedback control is given by

$$\begin{aligned} \begin{aligned} \left( \begin{array}{c} {\dot{x}}\\ {\dot{q}}\\ {\dot{\tau }} \end{array} \right) = f(x,q,\tau ):= \left( \begin{array}{c} (A+BK_q^yC)x\\ 0\\ 1 \end{array} \right) , \end{aligned} \end{aligned}$$

(15)

where $(x,q,\tau )\in {\mathcal {C}}$. Note that the jump dynamics of the closed-loop system is the same as (14). Also, we denote the closed-loop system as ${\mathcal {H}}^\star$.

4.3 Stability Analysis

To properly switch among the controllers with the input constraints, one needs to guarantee that $\varrho (x)\not =\emptyset$, which is equivalent to ${\mathcal {D}}\subset \mathrm {dom}\,G$.

Lemma 6

Given a finite set ${\mathcal {W}}\subset {\mathbb {N}}^+$, $(H_i,h_i)\in {\mathbb {R}}^{s_i\times p}\times {\mathbb {R}}^{s_i}$ for all $i\in {\mathcal {W}}$, $K_q^x\in {\mathbb {R}}^{p\times n}$ (respectively, $K_q^y\in {\mathbb {R}}^{p\times m}$) for all $q\in {\mathcal {Q}}$ and $\theta ^+>\theta ^->0$, if there exists $q^\prime \in {\mathcal {Q}}$ for all $(i,q)\in {\mathcal {W}}\times {\mathcal {Q}}$ such that, for all $k\in {\mathcal {W}}$, there is a solution $\vartheta \ge 0$ to

$$\begin{aligned} \vartheta ^\top \left[ \begin{array}{c} h_i+\mathbf{1 }_{s_i}\theta ^-\\ h_k+\mathbf{1 }_{s_k}\theta ^+ \end{array} \right] <0,\; \vartheta ^\top \left[ \begin{array}{c} H^q_i\\ H^{q^\prime }_k \end{array} \right] =0, \end{aligned}$$

(16)

where $H^q_i:=H_iK_q^x$ (respectively, $H^q_i:=H_iK_q^yC$), then $\varrho (x)\not =\emptyset$.

Proof

The proof follows from that of Lemma 5 in [5].

It is worth mentioning that if Lemma 6 holds, constraint (8) will be satisfied. $\square$

Lemma 7

Given a finite set ${\mathcal {W}}\subset {\mathbb {N}}^+$, $(H_i,h_i)\in {\mathbb {R}}^{s_i\times p}\times {\mathbb {R}}^{s_i}$ for all $i\in {\mathcal {W}}$, $K_q^x\in {\mathbb {R}}^{p\times n}$ (respectively, $K_q^y\in {\mathbb {R}}^{p\times m}$) for all $q\in {\mathcal {Q}}$ and $\theta ^+>\theta ^->0$, if the following conditions

$$\begin{aligned} \vartheta ^\top \left[ \begin{array}{c} h_i+\mathbf{1 }_{s_i}\theta ^-\\ h_k+\mathbf{1 }_{s_k}\theta ^+ \end{array} \right] <0,\; \vartheta ^\top \left[ \begin{array}{c} H^q_i\\ H^{q^\prime }_k \end{array} \right] =0 \end{aligned}$$

hold, where $H^q_i:=H_iK_q^x$ (respectively, $H^q_i:=H_iK_q^yC$), then hybrid system ${\mathcal {H}}^\star$ is well posed. $\square$

Proof

By Lemma 1, to prove that the hybrid system ${\mathcal {H}}^\star$ is well posed, we need to verify the three conditions in Assumption 1. It is easy to prove that ${\mathcal {C}}$ and ${\mathcal {D}}$ are closed sets since ${\mathcal {C}}^-$ and ${\mathcal {D}}^-$ are closed sets. Considering that the flow dynamics of ${\mathcal {H}}^\star$ are determined by the function f, condition (A2) in Assumption 1 degenerates to require that f be continuous. Note that the function f in (13) and f in (15) is obviously continuous. It remains to verify the condition (A3) in Assumption 1. Consider a sequence $\{(x_k,q_k,\tau _k)\}_{k\in {\mathbb {N}}}\in {\mathcal {D}}$ converging to $(x,q,\tau )$ and sequence $\{q_k^\prime \}_{k\in {\mathbb {N}}}$ converging to $q^\prime$ where $q_k^\prime \in \varrho (x_k)$ for all $k\in {\mathbb {N}}$. Suppose that $q^\prime \notin \varrho (x)$, then there exists $\iota \in {\mathcal {W}}$ such that $H_\iota ^{q^\prime }x<h_\iota +{\mathbf {1}}_{s_\iota }\theta ^+$. By continuity, $H_\iota ^{q_k^\prime }x_k<h_\iota +{\mathbf {1}}_{s_\iota }\theta ^+$ holds for sufficiently large k, where $H_\iota ^q$ is defined in Lemma 6. However, this contradicts with $q_k^\prime \in \varrho (x_k)$. Therefore, G is outer-semicontinuous. The property ${\mathcal {D}}\subset \mathrm {dom}\;G$ follows from Lemma 6 and locally bounded follows from the fact that q takes values on a compact set. Therefore, the hybrid system ${\mathcal {H}}^\star$ is well posed if the conditions in Lemma 7 hold. The proof is completed. $\square$

Next, we establish stability conditions of the set ${\mathcal {A}}$ under the controllers above, where the set is given by

$$\begin{aligned} {\mathcal {A}}:=\left\{ (x,q,\tau )\in \varOmega :x=0\right\} . \end{aligned}$$

(17)

The following theorem establishes a sufficient condition for global pre-asymptotic stability.

Theorem 1

Given a finite set ${\mathcal {W}}\subset {\mathbb {N}}^+$, $(H_i,h_i)\in {\mathbb {R}}^{s_i\times p}\times {\mathbb {R}}^{s_i}$ for all $i\in {\mathcal {W}}$, if there exist $K_q^x\in {\mathbb {R}}^{p\times n}$, $P\in {\mathbb {S}}^n_{>0}$ and $\theta ^-,\;\theta ^+\in {\mathbb {R}}$ with $0<\theta ^-<\theta ^+$ such that (16) holds and for all $q\in {\mathcal {Q}}$

$$\begin{aligned}&{A_q^x }^\top P+PA_q^x\in {\mathbb {S}}^n_{<0}, \end{aligned}$$

(18)

$$\begin{aligned}&A_d^\top PA_d-P\in {\mathbb {S}}^n_{\le 0}, \end{aligned}$$

(19)

where $A_q^x:=A+BK_q^x$, then constraint (8) holds and the set ${\mathcal {A}}$ in (17) is globally uniformly pre-asymptotically stable for ${\mathcal {H}}^\star$.

Proof

Since $P\in {\mathbb {S}}^n_{>0}$, the function $V(x,q):=x^\top Px$ is positive definite and satisfies (2) with $\alpha _1(s)=\lambda _{\min }(P)s^2$ and $\alpha _2(s)=\lambda _{\max }(P)s^2$, where $\lambda (P)$ is the eigenvalue of P. By (18), the derivative of V is negative definite relative to (17), and the condition (3) holds, where $\rho (s)=\eta s^2$ with small enough number $\eta >0$. By (19), it is easy to get $(A_dx)^\top P(A_dx)\le x^\top Px$. Then, (4) is satisfied for all jumps. In addition, it follows from Lemma 6 that constraint (8) is satisfied and G always maps the jump set to the flow set using the structure of ${\mathcal {H}}^\star$. Therefore, except for solutions starting at the origin, all jumps are followed by flow dynamics for at least $T_f>0$ units of time similar to [8, Example 3.28]. Then, $(t,j)\in \mathrm {dom}\,x$ implies $j\le 1+t/T_f$. With the addition of $t+j\ge T^\prime$, obtain $t\ge (T_f T^\prime )/(T_f+1)-T_f/(T_f+1)$. Therefore, Lemma 2 applies. $\square$

Remark 1

Theorem 1 shows that for all $q\in {\mathcal {Q}}$, the subsystems of the closed-system have a common Lyapunov function. Then, the stability of the hybrid system ${\mathcal {H}}^\star$ is independent of the switching sequence.

For the case of output feedback, we have a corollary as follows.

Corollary 1

Given a finite set ${\mathcal {W}}\subset {\mathbb {N}}^+$, $(H_i,h_i)\in {\mathbb {R}}^{s_i\times p}\times {\mathbb {R}}^{s_i}$ for all $i\in {\mathcal {W}}$, if there exist $K_q^y\in {\mathbb {R}}^{p\times m}$, $P\in {\mathbb {S}}^n_{>0}$ and $\theta ^-,\;\theta ^+\in {\mathbb {R}}$ with $0<\theta ^-<\theta ^+$ such that (16) holds and for all $q\in {\mathcal {Q}}$

$$\begin{aligned}&{A_q^y }^\top P+PA_q^y\in {\mathbb {S}}^n_{<0}, \end{aligned}$$

(20)

$$\begin{aligned}&A_d^\top PA_d-P\in {\mathbb {S}}^n_{\le 0}, \end{aligned}$$

(21)

where $A_q^y:=A+BK_q^yC$, then constraint (8) is satisfied and the set ${\mathcal {A}}$ in (17) is globally uniformly pre-asymptotically stable for ${\mathcal {H}}^\star$.

Proof

The proof is similar to the proof of Theorem 1. We omit it here.

Note that by Lemma 5 it is indicated that ${\mathcal {C}}^+\cap \;{\mathcal {D}}^-=\emptyset$, and thus, we have $G({\mathcal {D}})\cap {\mathcal {D}}=\emptyset$. Consequently, the Zeno behavior that is prone to occur in the design of hybrid system control laws is avoided. See [8, Chapter 2] and [24, Lemma 2.7]. $\square$

4.4 Calculation of Controller Gains

In this section, we design controllers with ${\mathcal {Q}}=\{1,2\}$ to solve the stabilization problem. By Lemma 4, there exists a vector $v\in {\mathbb {R}}^s$ such that $H^\top v=0$ and $v>0$. In order to simplify the calculation of the controller gains, we introduce the following lemma.

Lemma 8

Let ${\mathcal {Q}}=\{1,2\}$ and find a vector $v\in {\mathbb {R}}^s$ satisfying $H^\top v=0$, $v>0$, for all $\theta ^-,\;\theta ^+\in {\mathbb {R}}$ with $0<\theta ^-<\theta ^+<-\frac{{v_1}^\top h}{{v_1}^\top {\mathbf {1}}_s}$, there exist $\beta _1,\,\beta _2\in {\mathbb {R}}$ with $\beta _1<\beta _2$, for $\beta \in (0,\beta _1)\cup (\beta _2,+\infty )$, if there exists P satisfies Theorem 1 (or Corollary 1, respectively) with $K_2^x=\beta K_1^x$ (or $K_2^y=\beta K_1^y$, respectively), then the set (17) is uniformly pre-asymptotically stable for ${\mathcal {H}}^\star$; in addition, constraint (8) is satisfied, where two maps $v_1$ and $v_2$ are defined as

$$\begin{aligned} \begin{aligned} e^\top _iv_1(v,\theta ^+)=\left\{ \begin{aligned}&e^\top _iv\quad&\mathrm {if}\;e^\top _i(h+{\mathbf {1}}_s\theta ^+)<0\\&0&\mathrm {otherwise} \end{aligned} \right. \\ e^\top _iv_2(v,\theta ^+)=\left\{ \begin{aligned}&e^\top _iv\quad&\mathrm {if}\;e^\top _i(h+{\mathbf {1}}_s\theta ^+)>0\\&0&\mathrm {otherwise} \end{aligned} \right. \end{aligned} \end{aligned}$$

for all $i\in \{1,2,\ldots ,s\}$, and

$$\begin{aligned} \begin{aligned}&\beta _1=\mathrm {min}\left\{ -\frac{v_1^\top (h+\mathbf{1 }_s\theta ^+)}{v_2^\top (h+\mathbf{1 }_s\theta ^-)},\; -\frac{v_1^\top (h+\mathbf{1 }_s\theta ^-)}{v_2^\top (h+\mathbf{1 }_s\theta ^+)} \right\} ,\\&\beta _2=\mathrm {max}\left\{ -\frac{v_2^\top (h+\mathbf{1 }_s\theta ^+)}{v_1^\top (h+\mathbf{1 }_s\theta ^-)},\; -\frac{v_2^\top (h+\mathbf{1 }_s\theta ^-)}{v_1^\top (h+\mathbf{1 }_s\theta ^+)} \right\} . \end{aligned} \end{aligned}$$

(22)

Proof

This proof follows from an application of [5, Corollary 1]. $\square$

Fig. 1

State responses of $x_1$ and $x_2$ without control

Fig. 2

Trajectories of $x_1$, $x_2$ and control input |u| under continuous feedback control with bounded input constraint

Fig. 3

Trajectories of $x_1$, $x_2$ and control input |u| under switching control with input constraint

It is worthy noting that $\beta _1$ and $\beta _2$ in (22) do not depend on the controller gains. Thus, we are able to select $\beta$ prior to the design of the controller gains.

Theorem 2

Given $H_1=-H_2=[1\;-1]^\top$, $h_1=h_2=[{\overline{h}}\;\;{\underline{h}}]^\top$. Let ${\mathcal {Q}}=\{1,2\}$ and find $v\in {\mathbb {R}}^s$ satisfying $H_1^\top v=0$, $v>0$, for all $\theta ^-,\;\theta ^+\in {\mathbb {R}}$ with $0<\theta ^-<\theta ^+<-{\underline{h}}$, there exist $\beta _1,\,\beta _2\in {\mathbb {R}}$ given in (22) with $\beta _1<\beta _2$, for $\beta \in (0,\beta _1)\cup (\beta _2,+\infty )$. For state feedback case with $K_2^x=\beta K_1^x$, if there exists $L\in {\mathbb {S}}_{>0}^n$, $Y\in {\mathbb {R}}^{p\times n}$ satisfies

$$\begin{aligned}&AL+LA^\top +BY+Y^\top B^\top <0, \end{aligned}$$

(23)

$$\begin{aligned}&AL+LA^\top +\beta BY+\beta Y^\top B^\top <0, \end{aligned}$$

(24)

$$\begin{aligned}&\left[ \begin{aligned} -L\quad&LA_d^\top \\ A_dL&-L \end{aligned} \right] \le 0, \end{aligned}$$

(25)

then constraint (8) is satisfied and the set ${\mathcal {A}}$ in (17) is globally uniformly pre-asymptotically stable for ${\mathcal {H}}^\star$; besides, $K_1^x=YL^{-1}$.

Proof

It follows from Lemma 8 that constraint (8) is satisfied since $0<\theta ^-<\theta ^+<-{\underline{h}}$ is equivalent to $0<\theta ^-<\theta ^+<-\frac{{v_1}^\top h}{{v_1}^\top {\mathbf {1}}_s}$ with $v=\mathbf{1 }_s$. By [18, Section 7.2.1], we have that (18) is equivalent to (23) with $L=P^{-1}$ and $Y=K_1^xL$ in the case of $q=1$. Furthermore, we have (24) holds with $q=2$. According to the property of Schur complement, (25) is equivalent to (19). $\square$

Remark 2

We have a standard linear matrix inequality in Theorem 2, so the controller can be designed in two steps, first picking $\beta$ and then solving three linear matrix inequalities. However, for the output feedback case, (20) can only be converted into bilinear matrix inequality, which brings difficulties to the calculation of the controller gains.

The following example is given to illustrate the controller design results for the hybrid systems.

Example 2

Consider the hybrid impulsive system (5) with data

$$\begin{aligned} \begin{aligned}&A=\left[ \begin{array}{c} 0\quad 1\\ 0\quad 0 \end{array} \right] ,\;&B=\left[ \begin{array}{c} 0\\ 1 \end{array} \right] , A_d=\left[ \begin{array}{c} 1.2\quad 0\\ 0\quad 1.2 \end{array} \right] ,\ T=5,\ C=[1\quad 1]. \end{aligned} \end{aligned}$$

Here, we impose the reverse polytopic input constraint with $|u|\notin [0.2,\;0.7]$ as in Example 1. It is straightforward to verify that $H^\top v=0$ with $v=\mathbf{1 }_2^\top$, and then, we have

$$\begin{aligned} \begin{aligned}&v_1=\left\{ \begin{aligned}&[0,1]^\top ,\;\theta ^+\in [0,0.2)\\&[0,0]^\top ,\;\theta ^+\in [0.2,+\infty ), \end{aligned} \right. \\&v_2=\left\{ \begin{aligned}&[1,0]^\top ,\;\theta ^+\in [0,0.2]\\&[1,1]^\top ,\;\theta ^+\in (0.2,+\infty ). \end{aligned} \right. \end{aligned} \end{aligned}$$

Take $\theta ^+=0.1$ and $\theta ^-=0.01$. It follows from Lemma 8 that $\beta \in (0,0.1408)\cup (7.1,+\infty )$. Taking $\beta =7.2$, we find the controller gains $K_1^x=[-0.6917\;-\!1.5264]$ and $K_2^x=[-4.9802\;-\!10.9901]$ by solving a set of linear matrix inequalities (23), (24) and (25). Moreover, we perform simulation experiments using the above data with the initial condition $\left( x_1(0,0),x_2(0,0),q(0,0),\tau (0,0)\right) =(-2.17,1.139,2,0)$. For comparison, we control the hybrid impulsive system (5) under continuous feedback control with input constraint such that $|u|<0.2$ as in [2] and obtain the control gain $K=[-0.0774\;-0.2801]$.

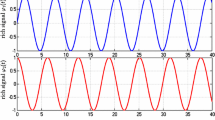
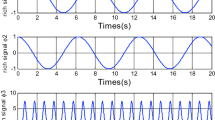
Figure 1 shows the response curves of the system states $x_1$ and $x_2$ without control. Obviously, the system is unstable. Figure 2 shows the response of the system under continuous feedback control in the presence of input constraint. It is observed that the system is stabilized but it spends long time to meet the input constraints. The pink color in the figure denotes the area of $[0.2,\;0.7]$, which is the set of input values to avoid. Figure 3 depicts the response of the system under the switching controllers proposed in this paper. It can be seen that the input constraint $|u|\notin [0.2,\;0.7]$ is satisfied and the quality of control is much better than the continuous feedback control with bounded input constraint.

5 Conclusions

In this paper, we have presented a hybrid switching control strategy for a class of hybrid systems with reverse polytopic input constraints. The controller designs for both the full state feedback case and the output feedback case have been proposed. Sufficient conditions have been established for stability of a closed set of the closed-loop system. The calculation of controller gains has been discussed and numerical examples have been provided to illustrate the proposed results. Future work includes applying the results to general linear/nonlinear hybrid systems with more intricate dynamics, and switching control design for such systems as well as their robust implementation.