1 Introduction

With the development of integrated micro-sensor technology, sensor networks have been applied into many control areas [2, 16, 19, 23]. The problem of state estimation or filtering in dynamical systems has also received increasing attention in the control areas. In particular, many efforts have been devoted to the study of estimation and control over sensor networks [1, 3, 9, 10, 14, 16, 18, 21, 22]. For instance, Based on the Kalman filtering approach, Olfati-Saber and Jalalkamali presented three novel distributed Kalman filtering algorithms for sensor networks in [16]. Calafiorea and Abratea exploited a distributed consensus diffusion scheme that relies only on bidirectional communication among neighbor nodes in [3]. In [18], Shen et al. addressed a new distributed H\(_\infty \) consensus filtering problem over a finite-horizon for sensor networks with multiple missing measurements and designed two kinds of robust distributed filters. In [1], Açıkmeşe et al. proposed a decentralized observer with a consensus filter for discrete-time linear distributed systems and proved the exponential convergence of the state estimating error of the proposed observer.

It is worth noting that most existing works in this area are based on the continuously-measured output of the system under consideration. Such an assumption restrains the applications of digital sensors where often the outputs of many control systems are only available at discrete sampled instants [4]. We believe that results depending on such continuously-measured condition among sensors with limited resources should lead to extensive communication requirements. To reduce the communication cost or bandwidth, the impulsive models or impulsive estimation approaches may be a potential solution [5, 11,12,13, 17]. In an impulsive fashion, the measurements are only sampled at discrete-time instants, which results in impulsive error dynamics. In contrast to continuous-time observers [1, 3, 10, 14, 18], such an impulse-based observers/estimators will save the bandwidth of networks and communication cost among the measured-information transmissions at discrete-time instants. Therefore, we believe that impulse-based estimation methods should play a prominent role in estimation of sensor networks in view of the wide applications of digital sensors and communication networks. However, general results on impulse-based or hybrid estimator design do not seem to have received much attention so far in the context of sensor networks, being the main reason the absence of a proper impulsive control tool for such applications.

By exploiting the impulsive control theory in [20] for such purpose, we are able to establish the following key contributions for the study of target estimation problem of nonlinear systems over sensor networks in an impulsive fashion:

  • A constructive method is developed to handle the impulse-based estimation problem of nonlinear systems over sensor networks, through an array of sensing devices providing time-triggered measurements from the target. We do not assume that the output of the nonlinear system under consideration is measured continuously.

  • In our proposed framework, each sensing device estimates the states of the nonlinear systems and exchanges the estimations within its neighbors.

  • A parameter-dependent Lyapunov function is utilized to ensure the asymptotic convergence of the state estimation error. Based on the Lyapunov function and comparison principle, a generic criterion is presented, where impulsive interval can be time-varying and the introduction of a positive function K(t) makes the conditions more flexible.

  • The proposed results are illustrated through a numerical example and can be applied to synchronization in complex networks.

The organization of the paper is as follows. In Sect. 2, we present needed notations and some preliminaries. Section 3 presents some additional definitions and lemmas in impulsive systems, and proves the stability of the error dynamics of the distributed filters. In Sect. 4, numerical simulations on a four-sensor network are provided to show the effectiveness of the proposed results. Section 5 concludes the paper.

2 System Description and Preliminaries

The notation used in this paper is fairly standard. Specifically, \(\mathbb {R}^{n}\) denotes the n-dimensional real space. \(\mathbb {R}^{+}\) is the set of non-negative real numbers. Denote \(\mathbb {N}_{n}=\{1,2,\ldots ,n\}\). \(A^{\top }\) and \(A^{\text {-1}}\) represents the transpose of matrix A and the inverse of matrix A,  respectively. Given matrices A, B with proper dimensions, \(A\otimes B\) defines the Kronecker product. Given a vector \(x\in {\mathbb {R}^{n}},\)\(x^{\top }\) denotes its transpose. \(\Vert x\Vert =(\sum _{i=1}^{n}x_{i}^{2})^{1/2}\) denotes the Euclidean norm.

The plant is described by the following class of nonlinear systems

$$\begin{aligned} \dot{s}(t) = f(t,s(t)), \end{aligned}$$
(1)

where \(s(t)\in {\mathbb {R}^{n}}\) is the state of the target.

Consider a sensor network of size N and assume that each sensor i can measure partial states of \(s(t)\in {\mathbb {R}^{n}},\) that is,

$$\begin{aligned} y_{i}(t) = C_{i}s(t) \end{aligned}$$
(2)

where \(y_{i}(t)\in \mathbb {R}^{m}\) is the measurement of sensor i on target s(t) and \(C_{i}\in \mathbb {R}^{m\times n}\) (\(i\in \mathbb {N}_{N}\)) are known matrices with appropriate dimensions. We assume \(\text {rank}(C_{i}) = m\), \(i\in \mathbb {N}_{N}\). Notice that each \(y_{i}(t)\) here measures all signals of partial states of the target s(t). However, to reduce the communication cost or bandwidth in sensor networks, the measurements are only sampled at discrete-time instants in our next proposed framework instead of measured continuously.

Note that there are many sensors that can measure the target s(t) from observations \(y_i(t)\), \(i\in \mathbb {N}_{N}\). We assume that the full state is observable through these partial measurements of target s(t). However, how to carry out the data fusion is still a challenging problem if there is not a centralized processor capable of collecting all the measurements from the sensors. Therefore, the objective here is to design an impulse-based distributed filter to track the states of the target s(t).

Assumption 1

[22]. For all \(x, y\in {\mathbb {R}^{n}}\), there exists a constant \(\theta \) such that

$$\begin{aligned} (x-y)^{\top }(f(t,x)-f(t,y))\le \theta (x-y)^{\top }(x-y), \quad \forall t\in \mathbb {R}. \end{aligned}$$

In the sensor network, the information available for the filter on sensor node i comes from not only sensor i but also its neighbors. Motivated by this fact, we can design a filter of the following structure on sensor node i:

$$\begin{aligned} \dot{x}_{i}(t)= & {} \left[ f(t,x_{i}(t))+c\sum \limits _{j\in \mathcal {N}_{i}}G_{ij}(x_{j}(t)-x_{i}(t))\right] ,\quad t\ne \tau _{r},\nonumber \\ \varDelta x_{i}(t)= & {} B_{ir} (C_{i}x_{i}(t)-y_{i}(t)),\quad t=\tau _{r}, i\in \mathbb {N}_{N} \end{aligned}$$
(3)

for \(t\ge 0, r=1,2,\ldots ,\) where \(\mathcal {N}_{i}\) denotes the set of neighbors of sensor node i, \(x_{i}(t)\in {\mathbb {R}^{n}}\) is the state estimate of sensor node i, c is the coupling strength, \(B_{ir}\) is the impulsive control gain with respect to i and r. The time sequence \(\{\tau _{r}\}_{r=1}^{\infty }\) is varying and satisfy \(\tau _{r-1}<\tau _{r},\)\(\lim \nolimits _{r\rightarrow \infty }\tau _{r}=+\infty ,\) and for a given positive constant \(\varepsilon ,\)\(\tau _{2r+1}-\tau _{2r}\le \varepsilon (\tau _{2r}-\tau _{2r-1}),\;\forall r\in \{1,2,\ldots \}.\) Denote \(\varDelta _{1}=\sup _{r}\{\tau _{2r+1}-\tau _{2r}\},\) and \(\varDelta _{2}=\sup _{r}\{\tau _{2r}-\tau _{2r-1}\}\) where \(\varDelta _{1}\) and \(\varDelta _{2}\) are positive. \(\varDelta x_{i}(\tau _{r})=x_{i}(\tau _{r}^{+})-x_{i}(\tau _{r}^{-})\) is the ’jump’ of the state \(x_{i}(t)\) at time \(t=\tau _{r}\) in which \(x_{i}(\tau _{r}^{+})=\lim _{t\searrow \tau _{r}^{+}}x_{i}(t).\) Without loss of generality, we assume that \(\lim _{t\nearrow \tau _{r}^{-}}x_{i}(t)=x_{i}(\tau _{r}),\) which means the solution \(x_{i}(t)\) is continuous from the left. The initial conditions of (3) are given by \(x_{i}(0)=\phi _{i}(0)\in \mathbb {R}^{n},\) where \(\phi _{i}(\cdot )\) represent the initial functions. The coupling matrix \(G=(G_{ij})_{N\times N}\) denotes the Laplacian, where \(G_{ij}=G_{ji}\ge 0\) denotes the coupling coefficient from vertex j to vertex i,  for all \(i\ne j,\) with \(G_{ii}=-\sum _{j=1,j\ne i}^{N}G_{ij}.\) Then, (3) can be written as

$$\begin{aligned} \dot{x}_{i}(t)= & {} \left[ f(t,x_{i}(t))+c\sum \limits _{j=1}^{N}G_{ij}x_{j}(t)\right] ,\quad t\ne \tau _{r},\nonumber \\ \varDelta x_{i}(t)= & {} B_{ir}C_{i}(x_{i}(t)-s(t)),\quad t=\tau _{r}, i\in \mathbb {N}_{N}. \end{aligned}$$
(4)

Letting \(e_{i}(t)=x_{i}(t)-s(t)\), we can obtain the following system that governs the filtering error dynamics for the sensor network:

$$\begin{aligned} \dot{e}_{i}(t)= & {} \left[ f(t,x_{i}(t))-f(t,s(t))+c\sum \limits _{j=1}^{N}G_{ij}e_{j}(t)\right] ,\quad t\ne \tau _{r},\nonumber \\ \varDelta e_{i}(t)= & {} B_{ir}C_{i}e_{i}(t),\quad t=\tau _{r}, i\in \mathbb {N}_{N}. \end{aligned}$$
(5)

The impulse-based control is said to solve the estimation problem if the states between the target and sensors satisfy \( \lim _{t\rightarrow \infty } \Vert x_{i}(t)-s(t)\Vert =0. \)

3 Main Results

In this section, we present impulse-based estimation results for system (1) with N sensors within a given topology. To support our analysis, some additional definitions and lemmas are needed based on the following impulsive differential equations

$$\begin{aligned}&\dot{x}(t) = f(t,x(t)), \quad t\ne \tau _{r},\nonumber \\&\varDelta x(t) = I_{r}(x(t)), \quad t=\tau _{r},\nonumber \\&x(t_{0})= x_{0}, \quad r=1,2,\ldots \end{aligned}$$
(6)

where \(x(t)\in \mathbb {R}^{n}\) is the state variable, \(f: \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}^{n}\) is left continuous function. \(\varDelta x(\tau _{r})=I_{r}(x(\tau _{r}))=x(\tau _{r}^{+})-x(\tau _{r}^{-}),\) in which \(x(\tau _{r}^{+})=\lim _{t\rightarrow \tau _{r}^{+}}x(t),\)\(\lim _{t\rightarrow \tau _{r}^{-}}x(t)=x(\tau _{r})\)\((r=1,2,\ldots ).\) The instant sequence \(\{\tau _{r}\}_{r=1}^{\infty }\) satisfy \(\tau _{r-1}<\tau _{r}\) and \(\lim _{r\rightarrow \infty }\tau _{r}=+\infty .\)

Definition 1

[6] The function \(V: [t_{0},\infty )\times \mathbb {R}^{n}\rightarrow \mathbb {R}^{+}\) belongs to class \(\mathcal {V}_{0}\) if it satisfies the following conditions:

  1. (1)

    the function V is continuous on each of the sets \((\tau _{r-1},\tau _{r}]\times \mathbb {R}^{n}\) and for all \(t\ge t_{0},\)\(V(t,0)\equiv 0;\)

  2. (2)

    V(t, x) is locally Lipschitzian in \(x\in \mathbb {R}^{n};\)

  3. (3)

    for each \(r\in \mathbb {Z},\) there exist finite limits

    $$\begin{aligned}&\lim \limits _{(t,y)\rightarrow (\tau _{r}^{-},x)}V(t,y)=V(\tau _{r}^{-},x)=V(\tau _{r},x), \nonumber \\&\lim \limits _{(t,y)\rightarrow (\tau _{r}^{+},x)}V(t,y)=V(\tau _{r}^{+},x). \end{aligned}$$
    (7)

Definition 2

[20] Let \(V\in \mathcal {V}_{0},\) for \(t\in (\tau _{r-1},\tau _{r}],\) we define

$$\begin{aligned} D^{+}V(t, x(t))=\lim _{h\rightarrow 0^{+}}\sup \frac{1}{h} [V(t+h,x(t+h))-V(t,x(t))]. \end{aligned}$$

The following two lemmas are introduced for self-containedness.

Lemma 1

[20] Assume that the following three conditions

  1. (i)

    \(V:\mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}^{+},\)\(V\in \mathcal {V}_{0},\) then there exists a integer number \(\beta \ge 1,\) such that:

    $$\begin{aligned} K(t)D^{+}V(t,x^{\beta })+D^{+}K(t)V(t,x^{\beta })\le g(t,K(t)V(t,x^{\beta })),\quad t\ne \tau _{r} \end{aligned}$$

    where \(g:\mathbb {R}^{+}\times \mathbb {R}^{+}\rightarrow \mathbb {R}\) is continuous and \(K(t)\ge m>0, \lim _{t\rightarrow \tau _{r}^{-}}K(t)=K(\tau _{r})\), i.e., K(t) is left continuous at \(t=\tau _{r}\) also: \(\lim _{t\rightarrow \tau _{r}^{+}}K(t)\) exists, \(r=1,2,\ldots ,\) and \(D^{+}K(t)=\lim _{h\rightarrow 0^{+}}\sup \frac{1}{h} [K(t+h)-K(t)];\)

  2. (ii)

    \(K(\tau _{r}^{+})V(\tau _{r}^{+},(x+I_{r}(x))^{\beta })\) \( \le \varPsi _{r}(K(\tau _{r})V(\tau _{r},x^{\beta })),r=1,2,\ldots ;\)

  3. (iii)

    \(V(t,0)=0\) and \(\alpha _{1}(\Vert x\Vert ^{\beta })\le V(t,x^{\beta })\) on \(\mathbb {R}^{+}\times \mathbb {R}^{n},\) where \(\alpha _{1}(\cdot )\in \mathcal{K}\) (class of continuous strictly increasing functions \(\alpha _{1}:\mathbb {R}^{+}\rightarrow \mathbb {R}^{+}\) such that \(\alpha _{1}(0)=0\)) are satisfied. Then, the global asymptotic stability of the trivial solution \(\omega =0\) of the comparison system

    $$\begin{aligned}&\dot{\omega }(t)=g(t,\omega (t)), \quad t\ne \tau _{r},\nonumber \\&\omega \left( \tau _{r}^{+}\right) =\varPsi _{r}(\omega (\tau _{r})),\quad t=\tau _{r},\nonumber \\&\omega \left( t_{0}^{+}\right) =\omega _{0}\ge 0, \end{aligned}$$
    (8)

implies global asymptotic stability of the trivial solution of impulsive system (6).

Lemma 2

[20] Let \(g(t,\omega )=\dot{\lambda (}t)\omega ,\)\(\lambda \in C^{1}[\mathbb {R}^{+},\mathbb {R}^{+}],\)\(\varPsi _{r}(\omega )=d_{r}\omega ,\)\(d_{r}\ge 0\) for all \(r=1,2,\ldots .\) Then, the origin of system (6) is globally asymptotically stable if the conditions of Lemma 1 and the following conditions hold:

  1. (i)

    \(\lambda (t)\) is nondecreasing, and \(\lim _{t\rightarrow \tau _{r}}\lambda (t)=\lambda (\tau _{r}),\) i.e. \(\lambda (t)\) is left continuous at \(t=\tau _{r},\) also \(\lim _{t\rightarrow \tau _{r}^{+}}\lambda (t)=\lambda (\tau _{r}^{+})\) exists, for all \(r=1,2,\ldots ;\)

  2. (ii)

    \(\sup _{r}\{d_{r}\exp (\lambda (\tau _{r+1})-\lambda (\tau _{r}^{+}))\}=\epsilon _{0}<\infty ;\)

  3. (iii)

    there exists an \(\mu >1\) such that

    $$\begin{aligned} \lambda (\tau _{2r+3})+\lambda (\tau _{2r+2})+\ln (\mu d_{2r+2}d_{2r+1}) \le \lambda \left( \tau _{2r+2}^{+}\right) +\lambda \left( \tau _{2r+1}^{+}\right) \end{aligned}$$

    holds for all \(d_{2r+1}d_{2r+2}\ne 0,\)\(r=1,2,\ldots ,\) or there exists an \(\mu >1\) such that \(\lambda (\tau _{r+1})+\ln (\mu d_{r+1}d_{r})\le \lambda (\tau _{r}^{+})\) for all k; 

  4. (iv)

    \(V(t,0)=0\) and there exists an \(\alpha _{1}(\cdot )\) in class \(\mathcal{K}\) such that \(\alpha _{1}(\Vert x\Vert )\le V(t,x).\)

Remark 1

Lemma 2 indicates that, global asymptotical stability of the impulsive system (6) not only depends on dynamical characteristic of the system at \(t\ne \tau _{r},\) but also is heavily determined by the impulsive control gain \(d_{r}.\)

Next, we present the main result of this paper.

Theorem 1

Suppose that Assumption 1 holds. The state s(t) of the system (1) can be asymptotically estimated by the impulse-based filter (3) if there exists a constant \(\mu >1\) and a differentiable at \(t\ne \tau _{r}\) and nonincreasing function K(t) which satisfies condition of Lemma 1, such that the following conditions hold:

  1. (C1)

    \((I+B_{ir}C_{i})^{\top }(I+B_{ir}C_{i})\le \gamma _{i}(r) I,\) where \(\gamma _{i}(r)\)\((i\in \mathbb {N}(1,N), r=1,2,\ldots )\) are positive constants;

  2. (C2)
    $$\begin{aligned} \sup \limits _{r}\left\{ \rho (r)\mathrm {exp}\left[ \alpha (\tau _{r+1}-\tau _{r}) +\ln \frac{K(\tau _{r+1})}{K\left( \tau _{r}^{+}\right) } \right] \right\} <\infty , \end{aligned}$$

    where \(\alpha =2\theta +2c\lambda _{M}(G\otimes I_{n}),\)\(\rho (r)=\max _{i}(\gamma _{i}(r))\);

  3. (C3)
    $$\begin{aligned}&\alpha (1+\varepsilon )\varDelta _{2} +\ln \left[ \frac{K(\tau _{2r+3})}{K\left( \tau _{2r+2}^{+}\right) }\right] +\ln \left[ \frac{K(\tau _{2r+2})}{K\left( \tau _{2r+1}^{+}\right) }\right] \nonumber \\&\quad \le -\ln (\mu \rho (2r+2)\rho (2r+1)), \end{aligned}$$
    (9)

    or

    $$\begin{aligned} \alpha \max \{\varDelta _{1},\varDelta _{2}\} +\ln \left[ \frac{K(\tau _{r+1})}{K\left( \tau _{r}^{+}\right) }\right] \le -\ln (\mu \rho (r+1)\rho (r)); \end{aligned}$$
    (10)
  4. (C4)
    $$\begin{aligned} \alpha +\frac{D^{+}K(t)}{K(t)}\ge 0. \end{aligned}$$

Proof

For any \(t>0,\) there exists an integer \(r>0\) such that \(t\in [\tau _{r},\tau _{r+1}).\) Define \(V(t)=\sum _{i=1}^{N}e_{i}^{\top }(t)e_{i}(t)\) and \(W(t)=K(t)V(t).\) By Assumption 1, one can obtain

$$\begin{aligned} e_{i}^{\top }(t)f(t,x_{i}(t))-f(t,s(t)) \le \theta e_{i}^{\top }(t)e_{i}(t). \end{aligned}$$
(11)

Then, computing the derivative of W(t) along with the system (5), we have that for \(t\in [\tau _{r},\tau _{r+1})\)

$$\begin{aligned} \dot{W}(t)= & {} K(t)\sum \limits _{i=1}^{N}\left\{ 2e_{i}^{\top }(t)\left[ f(t,x_{i}(t))-f(t,s(t))+c\sum \limits _{j=1}^{N}G_{ij}e_{j}(t)\right] \right\} +D^{+}KV(t) \nonumber \\\le & {} K(t)\left[ \sum \limits _{i=1}^{N}2\theta e_{i}^{\top }(t)e_{i}(t) +2c\sum \limits _{i=1}^{N}\sum \limits _{j=1}^{N}G_{ij}e_{i}^{\top }(t)e_{j}(t) \right] + D^{+}KV(t) \nonumber \\\le & {} K(t)(2\theta +2c\lambda _{M}(G\otimes I_{n}))\sum \limits _{i=1}^{N} e_{i}^{\top }(t)e_{i}(t) + D^{+}KV(t) \nonumber \\= & {} \left[ \alpha +\frac{\dot{K}(t)}{K(t)} \right] W(t), \end{aligned}$$
(12)

where \(\alpha =2\theta +2c\lambda _{M}(G\otimes I_{n}).\)

When \(t=\tau _{r},\) by means of condition (C1), we have

$$\begin{aligned} W\left( \tau _{r}^{+}\right)= & {} K\left( \tau _{r}^{+}\right) V\left( \tau _{r}^{+}\right) \nonumber \\= & {} K\left( \tau _{r}^{+}\right) \sum \limits _{i=1}^{N}\left[ e_{i}^{\top }(\tau _{r})(I_{n}+B_{ir}C_{i})^{\top }(I_{n}+B_{ir}C_{i})e_{i}^{\top }(\tau _{r}) \right] \nonumber \\\le & {} \max \limits _{i}(\gamma _{i}(r)) K(\tau _{r})V(\tau _{r})\nonumber \\= & {} \rho (r) W(\tau _{r}), \end{aligned}$$
(13)

where \(\rho (r)=\max _{i}(\gamma _{i}(r)).\)

Now consider the following comparison system:

$$\begin{aligned} \dot{\omega }(t)= & {} \left[ \alpha +\frac{\dot{K}(t)}{K(t)} \right] \omega (t), \quad t\ne \tau _{r},\nonumber \\ \omega \left( \tau _{r}^{+}\right)= & {} \rho (r) \omega (\tau _{r}), \quad t=\tau _{r},\nonumber \\ \omega \left( t_{0}^{+}\right)= & {} \omega _{0}\ge 0. \end{aligned}$$
(14)

By letting \(\dot{\lambda (}t)=\alpha +\frac{\dot{K}(t)}{K(t)}\) and \(d_{r}=\rho (r),\) system (14) is in accord with (8). Therefore, condition (ii) in Lemma 2 is guaranteed by condition (C2) in Theorem 1 as a result of

$$\begin{aligned}&\sup \limits _{r}\left\{ \rho (r) \text {exp}\left[ \alpha (\tau _{r+1}-\tau _{r})+\ln \frac{K(\tau _{r+1})}{K\left( \tau _{r}^{+}\right) }\right] \right\} \\&\quad \le \sup _{r}\{\rho (r)\} e^{\alpha }\max \{\varDelta _{1},\varDelta _{2}\}<\infty . \end{aligned}$$

Accordingly, in order to ensure condition (iii) in Lemma 2, we need

$$\begin{aligned}&\int _{\tau _{2r+2}}^{\tau _{2r+3}}\left[ \alpha +\frac{\dot{K}(t)}{K(t)}\right] \mathrm {d}t +\int _{\tau _{2r+1}}^{\tau _{2r+2}}\left[ \alpha +\frac{\dot{K}(t)}{K(t)}\right] \mathrm {d}t\\&\quad +\ln (\mu \rho (2r+2)\rho (2r+1))\le 0, \end{aligned}$$

or

$$\begin{aligned} \int _{\tau _{r}^{+}}^{\tau _{r+1}}\left[ \alpha +\frac{\dot{K}(t)}{K(t)}\right] \mathrm {d}t +\ln (\mu \rho (r+1)\rho (r))\le 0, \end{aligned}$$

where \(\mu >1.\)

After some arrangements, we have that

$$\begin{aligned}&\alpha (\tau _{2r+3}-\tau _{2r+2}) +\alpha (\tau _{2r+2}-\tau _{2r+1}) \nonumber \\&\quad \quad +\ln \left[ \frac{K(\tau _{2r+3})}{K(\tau _{2r+2}^{+})}\right] +\ln \left[ \frac{K(\tau _{2r+2})}{K(\tau _{2r+1}^{+})}\right] \nonumber \\&\quad \quad +\ln (\mu \rho (2r+2)\rho (2r+1)) \nonumber \\&\quad \le \alpha (\varDelta _{1}+\varDelta _{2}) +\ln \left[ \frac{K(\tau _{2r+3})}{K(\tau _{2r+2}^{+})}\right] \nonumber \\&\quad \quad +\ln \left[ \frac{K(\tau _{2r+2})}{K(\tau _{2r+1}^{+})}\right] +\ln (\mu \rho (2r+2)\rho (2r+1)) \nonumber \\&\quad \le \alpha (1+\varepsilon )\varDelta _{2} +\ln \left[ \frac{K(\tau _{2r+3})}{K(\tau _{2r+2}^{+})}\right] \nonumber \\&\quad \quad +\ln \left[ \frac{K(\tau _{2r+2})}{K(\tau _{2r+1}^{+})}\right] +\ln (\mu \rho (2r+2)\rho (2r+1))\le 0 \end{aligned}$$
(15)

or

$$\begin{aligned} \begin{array}{r c ll} &{}&{} \alpha (\tau _{r+1}-\tau _{r}) +\ln \left[ \frac{K(\tau _{r+1})}{K\left( \tau _{r}^{+}\right) }\right] +\ln (\mu \rho (r+1)\rho (r)) \\ &{}&{}\quad \le \alpha \max \{\varDelta _{1},\varDelta _{2}\} +\ln \left[ \frac{K(\tau _{r+1})}{K\left( \tau _{r}^{+}\right) }\right] +\ln (\mu \rho (r+1)\rho (r)) \le 0 \end{array} \end{aligned}$$
(16)

which are guaranteed by the condition (C3) in Theorem 1. Therefore, using the condition (C4) in Theorem 1, all conditions in Lemma 2 are satisfied, which means that the error system (5) is globally asymptotically stable, i.e., all estimating states \(x_{i}(t)\) globally converge to the target s(t). This completes the proof. \(\square \)

Remark 2

It is indicated from Theorem 1 that the estimation of the target (1) not only depends on the dynamical characteristic of each sensor, but also the impulsive control gain \(B_{ir}\) and the impulsive intervals \((\varDelta _{1},\varDelta _{2}).\) Here, \(B_{ir}\) does not require to be symmetric, neither does \(\Vert I+B_{ir}C_{i}\Vert \le 1.\) Thus, our result can be used for a wide class of nonlinear systems. It is also worth noting that impulsive interval here can be time-varying and the introduction of positive function K(t) makes the conditions more flexible, which is different from previous studies on impulsive control [15, 25].

To be convenient, when the impulsive intervals are set to be constant, i.e., \(\varDelta _{1}=\varDelta _{2}\equiv \varDelta \), we have the following corollary.

Corollary 1

Suppose that Assumption 1 holds. The state s(t) of the system (1) can be asymptotically estimated by the impulse-based filter (3) if there exists a constant \(\mu >1\) and a differentiable at \(t\ne \tau _{r}\) and nonincreasing function K(t) which satisfies condition of Lemma 1, such that the following conditions hold:

  1. (C1’)

    \((I+B_{ir}C_{i})^{\top }(I+B_{ir}C_{i})\le \gamma _{i}(r) I,\) where \(\gamma _{i}(r)\)\((i\in \mathbb {N}(1,N), r=1,2,\ldots )\) are positive constants;

  2. (C2’)

    \(\sup \limits _{r}\left\{ \rho (r)\mathrm {exp}\left[ \alpha (\tau _{r+1}-\tau _{r}) +\ln \frac{K(\tau _{r+1})}{K(\tau _{r}^{+})} \right] \right\} <\infty ,\) where \(\alpha =2\theta +2c\lambda _{M}(G\otimes I_{n}),\)\(\rho (r)=\max _{i}(\gamma _{i}(r))\);

  3. (C3’)

    \(\alpha \varDelta +\ln \left[ \frac{K(\tau _{r+1})}{K(\tau _{r}^{+})}\right] \le -\ln (\mu \rho (r+1)\rho (r)); \)

  4. (C4’)

    \(\alpha +\frac{D^{+}K(t)}{K(t)}\ge 0.\)

If \(K(t)\equiv 1\) and the impulsive intervals are fixed to be constant in Theorem 1, then we can obtain the following corollary.

Corollary 2

Suppose that Assumption 1 holds. The state s(t) of the system (1) can be asymptotically estimated by the impulse-based filter (3) if there exists a constant \(\mu >1\) such that the following conditions hold:

  1. (B1)

    \((I+B_{ir}C_{i})^{\top }(I+B_{ir}C_{i})\le \gamma _{i}(r) I,\) where \(\gamma _{i}(r)\)\((i\in \mathbb {N}(1,N), r=1,2,\ldots )\) are positive constants;

  2. (B2)

    \(\sup \limits _{r}\left\{ \rho (r)\mathrm {exp}\left[ \alpha (\tau _{r+1}-\tau _{r})\right] \right\} <\infty ,\) where \(\alpha =2\theta +2c\lambda _{M}(G\otimes I_{n}),\)\(\rho (r)=\max _{i}(\gamma _{i}(r))\);

  3. (B3)

    \(\alpha \varDelta \le -\ln (\mu \rho (r+1)\rho (r))\) and \(\alpha \ge 0.\)

Remark 3

The approach used here can be extended to analyze synchronization in complex networks [24] or asymptotic stability of impulsive control systems with impulses [8]. The method used in [24] can be regarded as a special case of our results if the time-varying positive function K(t) is set to be constant one and the impulsive intervals are fixed to be constant. The nonlinear functions in the system considered in [24] are required to satisfy Lipschitz continuous condition, while the nonlinear function f here only needs to satisfy Assumption 1. In addition, when \(N=1\) (that is, the estimation problem is considered by one sensor node rather than in a network environment) and K(t) is a constant number in Theorem 1, we obtain Theorem 3 of [8]. If a constant number \(\alpha > 0\) and let K(t) satisfy (C3), then \(\ln (K(\tau _{2r+3}){\big /} K(\tau _{2r+2}^{+}))\le 0\) and \(\ln (K(\tau _{2r+2}){\big /}K(\tau _{2r+1}^{+}))\le 0\) as K(t) is nonincreasing function. Hence, condition (22) in [8] cannot be derived from (9). Thus, Theorem 1 is less conservative than Theorem 3 of [8].

Remark 4

The conditions in Theorem 1 are flexible and easy to be verified. Given an arbitrary nonlinear system satisfying Assumption 1 with some constant \(\theta \), impulsive sequence \(\{t_r\}\) and impulsive control gain matrix \(B_{ir}\)\((i\in \mathbb {N}(1,N), r=1,2,\ldots )\) must exist. One can construct the impulse-based filter (3) under some network topology between sensor nodes. Letting the impulsive control gain \(B_{ir}\) satisfies condition (C1) for positive constants \(\gamma _{i}(r)\) and define a positive function K(t) such that (C4) holds. Finally, determine the impulsive interval bounds \(\varDelta _{1}\) and \(\varDelta _{2}\) such that (C2) and (C3) hold. If the impulsive intervals satisfying (C2) and (C3) are not available, one can choose other positive constants \(\gamma _{i}(r)\), impulsive control gains \(B_{ir}\) and the positive function K(t), and redesign the impulsive intervals. In Sect. 4, we provide a way to choose the positive function K(t). At times, one might be interested in a way without choosing the positive function K(t). Such case can be handled by Corollary 2 or Theorem 1 with \(K(t)\equiv 1\).

4 Simulation

In this section, a numerical example is employed to illustrate our results. Simulation results show that the proposed impulse-based filtering scheme is valid.

Example 1

The target model is described by the chaotic Lorenz oscillator described as follows

$$\begin{aligned} \dot{s}_{1}= & {} 10(s_{2}-s_{1}),\nonumber \\ \dot{s}_{2}= & {} 28s_{1}-s_{2}-s_{1}s_{3},\nonumber \\ \dot{s}_{3}= & {} s_{1}s_{2}-\frac{8}{3}s_{3}. \end{aligned}$$
(17)

Since \(s(t)=[s_{1}, s_{2}, s_{3}]^{\top }\) is a chaotic orbit and locates in a bounded region [7], i.e., \(|s_{1}(t)|,|s_{2}(t)|\le M_{1}=28.918,\) and \(|s_{3}(t)|\le M_{2}=56.918,\) for all t, by some arrangements we have \((x-s)^{\top }(f(x)-f(s))\le \theta (x-s)^{\top }(x-s),\) with \(\theta =51.918\). Consider a sensor network of size \(N=4\) with the coupling matrix

$$\begin{aligned}G= \begin{bmatrix} -2&1&0&1\\ 1&-2&1&0\\ 0&1&-2&1\\ 1&1&0&-2 \end{bmatrix}. \end{aligned}$$

Assume that \(y_{1}(t)=0.6s_{1}(t),\)\(y_{2}(t)=0.4s_{2}(t)\) and \(y_{3}(t)=y_{4}(t)=0.5s_{3}(t)\), which implies that each sensor measures different partial states of target. By Theorem 1, to asymptotically estimate the states of system (17), we further need to verify conditions (C1)–(C4). For simplicity, we consider the impulsive control gain \(B_{ir}=-0.8\) all \(i=1,2,3,4,\) and \(r=1,2,\ldots ,\) then \((I+B_{ir}C_{i})^{\top }(I+B_{ir}C_{i})\le \gamma _{i}(r)I=0.78I\) for all \(i\in \mathbb {N}_{4},\) and thus \(\rho (t)=\max _{i}(\gamma _{i}(r))=0.78.\) If we choose \(c=3, \mu =1.1,\)\(\varepsilon =0.5\) and

$$\begin{aligned} K(t)=\left\{ \begin{array}{ll} e^{-r}+1, &{}\quad t=\tau _{r},\\ e^{-t+\tau _{r}-r}+1, &{}\quad t\in (\tau _{r-1},\tau _{r}), \end{array} \right. \end{aligned}$$
(18)

for all \(r=1,2,\ldots ,\) then it can be derived that \(\alpha =2\theta +2c\lambda _{M}(G\otimes I_{n})=103.836.\) Hence, when we choose \(\tau _{2r}-\tau _{2r-1}\le \varDelta _{2}= -\ln (\mu \rho ^{\beta }(2r+2)\rho ^{\beta }(2r+1)) / [\alpha \beta (1+\varepsilon )]=0.0201,\) and \(\tau _{2r+1}-\tau _{2r}\le \varDelta _{1}=0.5\varDelta _{2}\approx 0.01,\) all conditions of Theorem 1 are satisfied, which means the states of the target (17) can be fully estimated under the impulse-based filter. To examine the estimation effects, define the estimation error

$$\begin{aligned} E(t)=\sum \limits _{i=1}^{3} \sqrt{\sum \limits _{j=1}^{N} (x_{ij}(t)-s_{i}(t))^{2}}, \end{aligned}$$
(19)
Fig. 1
figure 1

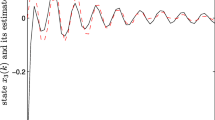
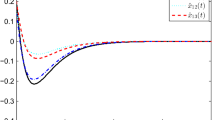
The trajectories of the target states s(t) and the estimated states \(x_{i}(t)\) of all sensors, and the evolutions of the estimation error E(t) defined in (19)

Full size image

which reflects the ensemble of estimation. Each dimension of the target states s(t) and the estimated states \(x_{i}(t)\) of all sensors are depicted in Fig. 1a–c, respectively. Figure 1a shows the time evolutions between the first dimensional state \(s_1(t)\) of target shown in blue and the states \(x_{i1}(t)\) of sensor i, \(i=1,2,3,4\). It is found that all states \(x_{i1}(t)\) finally converge to each other and the state \(s_1(t)\) is estimated after ten seconds. It is also revealed from Fig. 1a that, since only the signal \(s_1(t)\) is measured by sensor 1 which is impulsively and directly acted on the state \(x_{11}(t)\), the state \(x_{11}(t)\) vibrates frequently during the initial times while other three states \(x_{i1}(t)\), \(i=2,3,4\) evolve smoothly. Similarly, Fig. 1b (respectively, Fig. 1c) shows the time evolutions between the state \(s_2(t)\) (respectively, \(s_3(t)\)) of target shown in blue and the states \(x_{i2}(t)\) (respectively, \(x_{i3}(t)\)) of sensor i, \(i=1,2,3,4\). It is shown that the states \(s_2(t)\) and \(s_3(t)\) has been estimated. In addition, due to different measurement information of sensors, the state \(x_{22}(t)\) of sensor 2 vibrates frequently during the initial times in Fig. 1b, and the state \(x_{33}(t)\) of sensor 3 the state \(x_{43}(t)\) of sensor 4 vibrate frequently during the initial times in Fig. 1c. The evolution of estimation error defined in (19) is shown in Fig. 1d. It is shown that the error asymptotically converges to zero, which implies that the impulse-based filter does achieve the estimation of the states of the target.

5 Conclusion

In this paper, we have analyzed the impulse-based estimation problem of nonlinear systems over sensor networks. By constructing a parameter-dependent Lyapunov function and utilizing the comparison system, we have proved the asymptotic convergence of the state estimation error based on the designed impulse-based filter, even when the impulsive controls are imposed in varying intervals. Numerical simulations of coupled Lorenz oscillator have also been provided to verify the usefulness and practicability of proposed theoretical results.