Integral Sliding-Mode Fault-Tolerant Control for Fuzzy Singular Systems with Actuator Saturation

Abstract

In this paper, the $H_\infty$ reliable control problem is investigated for a class of nonlinear singular systems subject to external disturbance and actuator faults and saturations. By means of the Takagi–Sugeno fuzzy model to describe the nonlinear plant, a reliable sliding-mode control scheme is built to compensate for the impact of aforementioned factors on system stability and performance. First, a fuzzy integral sliding function is designed and sufficient conditions are derived such that the sliding-mode dynamics is robustly admissible and satisfies the pre-specified $H_\infty$ disturbance attenuation requirement. Then, by considering the saturation as nonlinear input, an adaptive sliding-mode control law is synthesized to ensure reachability of the specified sliding surface. Finally, the lower-limb rehabilitation system is exploited to validate the effectiveness of the presented controller design methodology.

1 Introduction

Due to its clear ability to describe simultaneously the interrelationship between different components of physical plants, singular system has attracted a great deal of research attention in both theoretical research and application fields related to power systems, mechanical/robotic systems, biological systems, industrial/chemical engineering processes, etc. In studying this class of systems, it turns out that the system regularity and absence of impulses need to be verified [7, 9]. Accordingly, a great deal of work has been devoted to the analysis and synthesis of singular systems [5, 10, 14, 30].

It is worth mentioning that these references are mainly confined to linear singular systems. However, nonlinearities exist commonly in real world and the systems are practically nonlinear. Recognized as an effective tool to approximate smoothly nonlinear systems, Takagi–Sugeno T–S fuzzy model [36] has been recently used to deal with nonlinear complex systems and a rich body of literature has appeared in this field (see [21, 22, 51] and references therein). In this context, the sector nonlinearity approach [37] has been extensively utilized as a systematic way to derive an equivalent T–S fuzzy model of the original nonlinear system. A shortcoming of this approach is that the fuzzy rules number increases exponentially with the number of nonlinearities arising from the original system leading to an increased computational costs. As a tighter nonlinear system representation, T–S fuzzy singular systems have been recently introduced to reduce the number of fuzzy rules and overcome the computational problems [26]. In spite of their complexities, some representative results regarding fuzzy singular systems have been published in the literature (see, for example, [9, 17, 48] and references therein).

On another research front, the implicit assumption that the control systems are fully reliable is not always true since failures may always occur. The failures, generally originating from ageing of sensors and actuators, the abrupt changes of working conditions, the corrosion of the internal components, may result in substantial damage and can even affect dramatically the stability and the performances of the controlled systems. Recently, much attention has been devoted to the fault-tolerant control for many practical engineering systems, such as aircraft, chemical and nuclear power plants. Hence, the fault-tolerant control or the reliable control for dynamic systems has become an important subject in control engineering in order to maintain the overall system stability and an acceptable performance in the face of faults and failures within the system. In fact, substantial progress has been made on this subject and related control schemes ranging from active to passive have been published in the literature. To mention a few, the authors in [50] provide an excellent literature review on fault-tolerant control. The problems of reliable passivity and passification for a singular Markovian system with actuator failure have also been investigated in [43]. In [49], the reliable observer-based control problem of nonlinear systems represented by the switched fuzzy systems with time-varying delay has been developed. The problem of direct adaptive compensation for infinite number of time-varying actuator failures/faults is investigated for fuzzy systems in [19]. Accordingly, the reliable control technique has been applied for many practical systems subject to actuator faults such as an electronic circuit in [41] and a near-space hypersonic vehicle in [42].

Another important problem encountered in practical control systems is the actuator saturation. In fact, actuators cannot provide unlimited amplitude signal due primarily to the physical, safety or technological constraints. However, if this phenomenon is not properly handled, it will inevitably affect the implementation of the designed controller and may even degrade the system performances. Consequently, and in order to handle the actuator saturation, additional constraints on the analysis and design of singular systems are to be taken into account. It is worthwhile pointing out that the saturation control design has increasingly received much attention as one of the most interesting practical problems (see, for example, [2, 31, 46], and the references therein).

Due to its inherent robustness and effectiveness to deal with nonlinear and incompletely modeled systems, sliding-mode control (SMC) scheme has been widely applied to various practical engineering systems. One can refer to [4, 8, 18, 20, 35, 40] and the references therein, as representative work on this topic. The advantages of this control strategy exhibit some results for the class of singular systems. In [11, 44], the SMC with passivity is investigated for singular systems with time-varying delay and nonlinear perturbations. The authors in  [13, 16] studied the SMC for uncertain discrete-time singular systems with delay. The problem of SMC design was also suggested in [15, 25] for fuzzy singular systems. It is worthwhile to mention that SMC has been recently used to cope with actuator faults [1, 32, 45]. In particular, the integral sliding-mode approach has been widely proposed to achieve robustness of the considered system even if the matched conditions are not satisfied. In [26], the observer-based fuzzy integral (SMC) for nonlinear descriptor systems is addressed. For switched systems with partial actuator faults, a sliding-mode control scheme was proposed in [29]. The study of an output feedback control algorithm based on unit vector sliding mode for a class of multivariable systems was presented in [6]. The problem of SMC with passivity for uncertain singular systems with semi-Markov switching and actuator failures is discussed in [12].

It should be noted that there are only a few results concerned with reliable control for systems with simultaneous presence of actuator saturations and faults although such a phenomenon is quite typical in engineering practice. To name just a few, the stochastic reliable control problem for networked control systems (NCSs) subject to actuator failure and input saturation is investigated in [23]. Bustan et al. proposed in [3] a continuous globally stable tracking control algorithm for a spacecraft in the presence of unknown actuator failure, control input saturation. In [39], a reliable robust discrete gain scheduling controller is designed for the systems with input saturation, external disturbance and actuator failures. For a class of singular systems subject to both nonlinear perturbation and actuator saturation, a robust fault-tolerant controller is designed in [53]. To the best of our knowledge, up to now the problem of reliable control for nonlinear singular systems with external disturbance, actuator failures and saturation is still open issue, see unsolved despite its engineering importance in practice.

Motivated by the above discussion, the main purpose of this paper is to pave the way for dealing with the problem of reliable SMC design for real plants with aforementioned environmental constraints. Two difficulties are required to be considered in this study: (1) The switching term of the designed controller has to be synthesized by considering the actuator fault parameters and the saturation as input nonlinearity and (2) to cope with the difficulty of practically knowing the slope parameters of the input nonlinearity and the bounds of the lumped perturbations, the adaptive control should be further addressed. Hence, an adaptive sliding-mode control scheme is to be developed to solve this design problem. The main questions to be addressed in this paper are as follows:

• How to design a suitable sliding surface such that the developed criterion ensures the admissibility of the resulting sliding-mode dynamics and allows us to determine all the sliding function parameters?

• How to synthesize a reliable SMC law to adaptively ensure the sliding-mode phase so as to reject the effect of the external disturbance, actuator failures and saturation on the desired dynamic performance of the system under consideration?

The rest of this paper is outlined as follows: The description of the system and preliminaries are introduced in Sect. 2. Section 3 presents the design procedure of SMC for nonlinear singular systems under consideration. Section 4 is devoted to validate the effectiveness of the proposed control strategy via a simulation study carried out for the lower-limb rehabilitation system. Conclusion remarks are given in Sect. 5.

Notations The notations in this paper are quite standard except where otherwise stated. The superscript ‘T’ stands for matrix transposition and $X\in \mathbb {R}^{n}$ denotes the n-dimensional Euclidean space, while $X\in \mathbb {R}^{n\times m}$ refers to the set of all $n\times m$ real matrices; $X>0$ (respectively, $X\ge 0$) means that matrix X is real symmetric positive definite (respectively, positive semi-definite); I and 0 represent the identity matrix and a zero matrix with appropriate dimension, respectively; $\mathrm{diag}\{\ldots \}$ stands for a block-diagonal matrix; ${{\,\mathrm{sym}\,}}(X)$ stands for $X+X^T$; the notation $\Vert A\Vert$ refers to the norm of a matrix A; and $\Vert \cdot \Vert$ denotes the Euclidean norm of a vector and its induced norm of a matrix. $X_\mu$ represents the convex combination $\sum _{i=1}^{r}\mu _iX_i$; ${X}_{\mu \mu }$ will denote a convex combination of the form $\sum _{i=1}^{r}\sum _{j=1}^{r}\mu _i\mu _jX_{ij }$. In symmetric block matrices or long matrix expressions, we use an asterisk $*$ to represent a term that is induced by symmetry. Matrices, if their dimensions are not explicitly stated, are assumed to be compatible for algebraic operations.

2 System Description and Preliminaries

In this paper, we focus on the T–S fuzzy descriptor system described by the following rule:

$$\begin{aligned}&{\mathbf {R}}_{i}{:}\quad \text {If}~{\theta }_{1}(t)~\text {is}~{F}_{1}^{i}~\text {and}~ \text {If}~{\theta }_{2}(t)~\text {is}~{F}_{2}^{i}\ldots \text {If}~{\theta }_{s}(t)~\text {is}~{F}_{s}^{i}, \quad \text {Then} \nonumber \\&\left\{ \begin{aligned}&E\dot{x}(t)=({A}_{i}+\Delta A_i)x(t)+{{B}_{i}}\big ({ u^{\mathrm{F}}(t)+{f}_{i}({x}(t))+f_a(t)}\big )+{{B}_{wi}} {w}(t)\\&{z}(t)={C}_{i}x(t)\quad i=1,2,\ldots ,r \end{aligned} \right. \end{aligned}$$

(1)

where $x(t)\in {\mathbb {R}}^{n}$ represents the system state; $u^{\mathrm{F}}(t)\in {\mathbb {R}}^{m}$ is the control input subject to actuator faults; ${w}(t)$ refers to the exogenous input subject to $L_2[0,\infty )$; ${f}_{i}({x}(t))$ represents the system nonlinearities; $f_{\mathrm{a}}(t) \in {\mathbb {R}}^{m}$ denotes the unknown additive actuator fault; ${z}(t)\in {\mathbb {R}}^{s}$ denotes the controlled output; $F^i_j$$(j=1\ldots s)$ are fuzzy sets; and $\theta (t)=[{\theta }_{1}(t),\ldots ,{\theta }_{s}(t)]$ is the vector of premise variables. Matrix $E\in {\mathbb {R}}^{n\times n}$ may be singular with ${{\,\mathrm{rank}\,}}(E)=q< n$. $( {A}_{i},{B}_{i}, {B}_{wi} )$ describes the ith local model of the system, and $\Delta A_i$ represents the time-varying uncertainty term satisfying:

$$\begin{aligned} \begin{aligned} \Delta {{A}_{i}}(t)={M}_{i}{\Delta }(t){N}_{i} \end{aligned} \end{aligned}$$

(2)

where ${M}_{i}$ and ${N}_{i}$ are known matrices and $\Delta (t)$ is unknown time-varying matrix function satisfying ${\Delta }^T(t){\Delta }(t)\le I$.

Denote ${\mu }_{i}(\theta (t))$ as the standardized fuzzy basis function defined by

$$\begin{aligned} {\mu }_{i}(\theta (t))&=\frac{\prod ^s_{j=1}F_j^i({\theta }_{j}(t) )}{\sum ^r_{i=1}\prod ^s_{j=1}F_j^i({\theta }_{j}(t) )},\quad i=1,2,\ldots ,r \end{aligned}$$

where $F_j^i({\theta }_{j}(t))$ is the grade of membership of ${\theta }_{j}(t)$ in fuzzy set $F_j^i$. Then, for all t, it can be seen that

$$\begin{aligned} {\mu }_{i}(\theta (t))\ge 0,\quad i=1,2,\ldots ,r\quad \displaystyle \sum _{{i=1}}^{r}{\mu }_{i}(\theta (t))=1. \end{aligned}$$

(3)

Let ${\psi }_{i}(t,{x}(t))={f}_{i}({x}(t))+f_a(t)$. Based on the properties of fuzzy basis functions, the overall T–S dynamical model can be obtained:

$$\begin{aligned} \left\{ \begin{aligned}&E\dot{x}(t) =({A}_\mu +\Delta {A}_\mu )x(t)+{B}_\mu \big ({u^{\mathrm{F}}(t)+{\psi }_\mu (t,{x}(t)) }\big )+{ {B}_{w}}_\mu {w}(t) \\&{z}(t)= {C}_\mu x(t)\end{aligned} \right. \end{aligned}$$

(4)

Without loss of generality, we introduce the following assumptions for technical convenience.

• 1. Matched nonlinearities $\psi _\mu (t,x)$ satisfy the inequality

  $$\begin{aligned} \Vert \psi _\mu (t,x) \Vert \le \rho _0+\rho _1\Vert x\Vert \end{aligned}$$

  (5)

  where $\rho _0$ and $\rho _1$ are positive unknown scalars.

• 2. Exogenous signal ${w}(t)$ is bounded and satisfies

  $$\begin{aligned} \Vert {w}(t)\Vert \le \rho _{2} \end{aligned}$$

  (6)

  where $\rho _{2}$ is an unknown positive real constant.

Remark 1

In [15], it is assumed that the exogenous disturbance is bounded by a known positive function. That is, $\Vert \psi _\mu (t,x) \Vert \le \eta (t,x)$. In practical cases, this assumption is quite restrictive. To relax this restriction, an adaptive SMC scheme will be addressed in this study.

We assume that the actuators suffer from failures. Let $u_l^{\mathrm{F}}(t)$ denote the signal from the actuator that has failed for the control input $u_l(t)$, $l = 1,\ldots ,m$. By taking the effects of actuator fault and saturation, the following model is adopted in this paper:

$$\begin{aligned} \begin{aligned} u^{\mathrm{F}}(t)={R}(t)\sigma ({u}(t)) \end{aligned} \end{aligned}$$

(7)

where $\sigma ({u}(t))$ represents the standard saturation function and ${R}(t)$ is the actuator fault matrix defined as

$$\begin{aligned} {R}(t)={{\,\mathrm{diag}\,}}\big ({{r}_{1}(t),{r}_{2}(t),\ldots ,{r}_{m}(t)}\big ) \end{aligned}$$

(8)

where ${r}_{l}(t),\ (l = 1,\ldots ,m)$ model the degradation level of the ‘l’th actuator. For every fault mode, ${\underline{r}}_{l}$ and ${\bar{r}}_{l}$ represent the lower and upper bounds of ${r}_{l}(t)$, respectively, that is, ${r}_{l}(t)$ satisfying ${\underline{r}}_{l}\le {r}_{l}(t)\le {\bar{r}}_{l}$, $l=1,2\ldots ,m$.

The actuator fault matrix R(t) can be described as

$$\begin{aligned} \begin{aligned} {R}(t)={R}_{ 0}(I+G(t)),\quad \Vert G(t)\Vert \le \Vert Q\Vert \le I \end{aligned} \end{aligned}$$

(9)

where the matrices $R_0$, G(t) and Q are defined as follows:

$$\begin{aligned} \begin{aligned} Q&={{\,\mathrm{diag}\,}}\big ({ {q}_{1}, {q}_{2},\ldots , {q}_{m}}\big ),\quad {R}_{ 0}={{\,\mathrm{diag}\,}}\big ({{r}_{01},{r}_{02},\ldots ,{r}_{0m}}\big ), \\ G(t)&={{\,\mathrm{diag}\,}}\big ({{g}_{1}(t),{g}_{2}(t),\ldots ,{g}_{m}(t)}\big )\\ {q}_{l}&=\dfrac{{\bar{r}}_{l}-{\underline{r}}_{l} }{{\bar{r}}_{l}+{\underline{r}}_{l} },\quad {r}_{ 0l}=\dfrac{{\bar{r}}_{l}+{\underline{r}}_{l} }{2}, \\ {g}_{l}(t)&=\dfrac{{r}_{l}(t) - {r}_{ 0l}}{{r}_{ 0l}},\ (l=1,2\ldots ,m). \end{aligned} \end{aligned}$$

(10)

Remark 2

The above model of actuator failure in (7) covers the normal operation case (as ${\underline{r}}_{l} = {\bar{r}}_{l}=1$) and the partial degradation case (as $0< {\underline{r}}_{l}\le 1$ and ${\bar{r}}_{l}\ge 1$). To design well the sliding-mode control law, this study does not include the complete failure case (${\underline{r}}_{l} = {\bar{r}}_{l}=0$).

The saturation function under consideration can be regarded as a nonlinearity input where each component can be described by the following mathematical model:

$$\begin{aligned} \sigma ({u}_{l}(t)) =\chi ({u}_{l}(t))\cdot {u}_{l}(t) \end{aligned}$$

(11)

where

$$\begin{aligned} \chi ({u}_{l}(t))=&\left\{ \begin{array}{lll} \dfrac{u_{l,\mathrm{{\mathrm{max}}}}}{u_{l}(t)} ,&{}\quad {u}_{l}(t)>{u_{l,\mathrm{{\mathrm{max}}}}}\\ 1, &{}\quad |u_{l}(t) | \le u_{l,\mathrm{{\mathrm{max}}}},\\ -\,\dfrac{u_{l,\mathrm{{\mathrm{max}}}}}{u_{l}(t)} ,&{}\quad {u}_{l}(t)<-{u_{l,\mathrm{{\mathrm{max}}}}}\\ \end{array} \right. \quad l=1,2\ldots ,m \end{aligned}$$

(12)

$u_{l,{\mathrm{max}}}$ is the known bound of ${u}_{l}(t)$, and $\chi ({u}_{l}(t))$ satisfies $0<\alpha \le \chi ({u}_{l}(t))\le 1$.

Substituting (7) in (4), we can get the following system:

$$\begin{aligned}&\left\{ \begin{aligned}&E\dot{x}(t) =({A}_\mu +\Delta {A}_\mu )x(t)+{B}_\mu \Big ({R(t))\sigma ({u}(t))+{\psi }_\mu (t,{x}(t))}\Big )+{ {B}_{w}}_\mu {w}(t) \\&{z}(t)= {C}_\mu x(t)\end{aligned} \right. \end{aligned}$$

(13)

Now, we shall recall the following definitions and lemmas to be used for stating our main results. Consider the following unforced descriptor system:

$$\begin{aligned} E\dot{x}(t)= {A} x(t). \end{aligned}$$

(14)

Definition 1

[7]

• 1. System (14) is said to be regular if $\mathrm{det}\Big ({sE- {A} }\Big )$ is not identically zero.

• 2. System (14) is said to be impulse free if $\deg \Big ({\det \Big ({sE- {A} }\Big )}\Big )={{\,\mathrm{rank}\,}}( E)$.

• 3. System (14) is said to be admissible if it is regular, impulse free and stable.

We end this section by recalling the following lemmas which will be essential to the following development.

Lemma 1

[52] Let $T_0(x)$, $T_1(x)$, $\ldots$, $T_p(x)$ be quadratic function of $x\in \mathbb {R}^n$.

$$\begin{aligned} T_i=x^T{\varPsi }_ix,\ i=1,\ldots p \end{aligned}$$

(15)

Then, the implication

$$\begin{aligned} T_1(x)\le 0,\ \ldots ,\ T_p(x)\le 0\Longrightarrow T_0(x)< 0 \end{aligned}$$

(16)

holds if there exist positive scalars $\tau _i,\ i=1\ldots p$ such that

$$\begin{aligned} {\varPsi }_0-\sum _{i=1}^{p}\tau _i{\varPsi }_i<0. \end{aligned}$$

(17)

Lemma 2

[33] Let M and N be real matrices with appropriate dimensions. Then, for any matrix $\Delta$ satisfying $\Delta ^T\Delta \le I$ and a scalar $\varepsilon >0$,

$$\begin{aligned} \begin{aligned} {{\,\mathrm{sym}\,}}(M\Delta N)\le \varepsilon \textit{MM}^T+\varepsilon ^{-1}{N^T}{}{N}. \end{aligned}&\end{aligned}$$

(18)

Lemma 3

[38] If the following inequalities hold:

$$\begin{aligned}&\begin{aligned}&{\varXi }_{ii}<0\\&\dfrac{1}{r-1}{\varXi }_{ii}+\dfrac{1}{2}\big ({{\varXi }_{ij}+{\varXi }_{ji}}\big )<0, \quad i, j = 1, 2,\ldots , r, i \ne j \end{aligned} \end{aligned}$$

(19)

then the following matrix inequality holds:

$$\begin{aligned} \begin{aligned}&\displaystyle \sum _{{i=1}}^{r}\displaystyle \sum _{{j=1}}^{r}{\mu }_{i}(\theta (t)){\mu }_{j}(\theta (t)){\varXi }_{ij}<0.\\ \end{aligned} \end{aligned}$$

(20)

3 Design and Analysis of SMC

For singular system (13), the main purpose of this work is to synthesize a sliding-mode control law so that the resultant closed-loop system is robustly admissible despite the effect of actuator degradation. This section is devoted to designing the switching manifold and the sliding-mode controller such that the task of this paper is fulfilled. To this end, we choose the following integral sliding-mode surface function:

$$\begin{aligned} s( t) =S_0(E x(t)-E x(0)) -S_0 \int _{{0}}^{t} ({A}_\mu +{B}_\mu {K}_\mu ) x(\tau )\mathrm{d}\tau \end{aligned}$$

(21)

where ${K}_\mu \in {\mathbb {R}}^{m\times n}$ is a real matrix to be designed and $S_0\in {\mathbb {R}}^{m\times n}$ is a constant matrix satisfying $S_0{B}_\mu$ is nonsingular.

According to the SMC theory, when the system trajectories reach the switching surface, it follows that $s(0)= 0$ and ${\dot{s}}(t)= 0$. Thus, by ${\dot{s}}(t)= 0$, we get the equivalent control as

$$\begin{aligned} \begin{aligned} \sigma (u(t))_{\mathrm{eq}}&={K}_\mu x(t)-{\psi }_\mu (t,{x}(t))-({S}_{0}{B}_\mu )^{-1}{S}_{0} \Big ({B_1}_\mu w(t)+\Delta {A}_\mu x(t)\Big ) \end{aligned} \end{aligned}$$

(22)

Substituting (22) into (13), we obtain the sliding mode dynamics

$$\begin{aligned} \begin{aligned} E{\dot{x}}(t)&={{\bar{A}}}_{\mu \mu }(k) x(t)+{\bar{B_1}}_\mu w(t) \end{aligned} \end{aligned}$$

(23)

where ${{\bar{A}}}_{\mu \mu }(k) ={{\bar{A}}}_{\mu \mu } +{\mathbb {S}}_{0}\Delta { A}_\mu$, ${{\bar{A}}}_{\mu \mu }= {A}_\mu +{B}_\mu {K}_\mu$, ${\bar{B_1}}_\mu = {\mathbb {S}}_{0} {B_1}_\mu$ and ${\mathbb {S}}_{0}=I-{B}_\mu ({S}_{0}{B}_\mu )^{-1}{S}_{0}$.

3.1 $H_\infty$ Sliding-Mode Dynamics Analysis

In this subsection, we will pay attention for developing a sufficient condition that ensures sliding-mode dynamics (23) is robustly admissible with $H_\infty$ performance.

Theorem 1

Given a scalar $\gamma > 0$. The system in (23) is robustly $H_\infty$ admissible if there exist matrices $P_i>0$, $S_i$ and $G_l, (l= 1,2)$ and positive scalars $\tau _{ijk}$ and $\varepsilon _i$ such that the following inequalities hold for $i,j,k=1,\ldots , r$:

$$\begin{aligned}&\begin{bmatrix} {{\varPhi }}_{ik}^j&\quad P_k+S_kR^T+{\bar{ A}}_{ik}^T{G}_{2}^T-{G}_{1}&\quad {G}_{1}{\bar{B_1}}_{i}&\quad {C}_{i}^T&\quad \varepsilon _i {G}_{1}{\bar{M}}_{i}&\quad {N}_{i}^T\\ *&\quad -{{\,\mathrm{sym}\,}}{({G}_{2})}&\quad {G}_{2}{\bar{B_1}}_{i}&\quad 0&\quad \varepsilon _i {G}_{2}{\bar{M}}_{i}&\quad 0\\ *&\quad *&\quad -\gamma ^2 I&\quad 0&\quad 0&\quad 0\\ *&\quad *&\quad *&\quad -I&\quad 0&\quad 0\\ *&\quad *&\quad *&\quad *&\quad -\varepsilon _iI&\quad 0\\ *&\quad *&\quad *&\quad *&\quad *&\quad -\varepsilon _iI\\ \end{bmatrix}<0 \end{aligned}$$

(24)

where ${{\varPhi }}_{ik}^j= {{\,\mathrm{sym}\,}}( G_1{\bar{ A}}_{ik})+\sum _{j=1}^{r}\tau _{ijk}E^T[P_k-P_j]E$, ${\bar{ A}}_{ik}={A}_{i}+{B}_{i}{K}_{k}$ and matrix $R \in {\mathbb {R}}^{n\times (n-q)}$ is of full rank such that $R^TE=0$

Proof

The proof of this theorem is divided into two parts. The first one is concerned with the regularity and the impulse-free characterizations, and the second one treats the stability property of system (23). First, we consider the nominal case of (23) (that is, $\Delta {A}_\mu =0$).

Since ${{\,\mathrm{rank}\,}}(E)=q< n$, there always exist two nonsingular matrices ${\mathbb {M}}$ and ${\mathbb {N}}\in {\mathbb {R}}^{ n\times n}$ such that

$$\begin{aligned} \begin{aligned} {\mathbb {E}}&={\mathbb {M}}E{\mathbb {N}}=\begin{bmatrix} {I}_{q}&\quad 0 \\ 0&\quad 0 \end{bmatrix} \end{aligned} \end{aligned}$$

(25)

Then, R can be characterized as $R={\mathbb {M}}^T \begin{bmatrix} 0\\ {{\hat{{\varPhi }}}} \end{bmatrix}$, where ${\hat{{\varPhi }}}\in {\mathbb {R}}^{( n-q)\times ( n-q)}$ is any nonsingular matrix.

We also define

$$\begin{aligned} \begin{aligned} {\hat{A}}_{ik}&={\mathbb {M}}{\bar{ A}}_{ik}{\mathbb {N}}=\begin{bmatrix} {\hat{A}}_{11ik}&\quad {{\hat{A}}_{12ik}} \\ {\hat{A}}_{21ik}&\quad {\hat{A}}_{22ik} \end{bmatrix},&{\hat{P}}_{i}&={\mathbb {M}}^{-T}{P}_{i}{\mathbb {N}}=\begin{bmatrix} {\hat{P}}_{11i}&\quad {\hat{P}}_{12i} \\ {\hat{P}}_{21i}&\quad {\hat{P}}_{22i} \end{bmatrix}, \\ {\hat{S}}_k&={\mathbb {N}}^TS_k=\begin{bmatrix} {\hat{S}}_{11k} \\ {\hat{S}}_{21k} \end{bmatrix},\\ \end{aligned} \end{aligned}$$

(26)

It follows from (24) that

$$\begin{aligned} \begin{bmatrix} {\varPhi }_{ik}^j&\quad P_k+S_kR^T+{\bar{ A}}_{ik}^T{G}_{2}^T-{G}_{1} \\ *&\quad -{{\,\mathrm{sym}\,}}{({G}_{2})} \end{bmatrix}<0 \end{aligned}$$

(27)

Pre- and post-multiplying (27) by $\Big [{I\ {\bar{ A}}_{ik}^T}\Big ]$ and its transpose, respectively, we obtain

$$\begin{aligned} \mathrm{sym}\Big ({S_iR^T{\bar{ A}}_{ik}+{P}_{k}{\bar{ A}}_{ik}}\Big )+\displaystyle \sum _{{j=1}}^{r}\tau _{ijk}E^T[P_k-P_j]E<0 \end{aligned}$$

(28)

Pre- and post-multiplying (28) by ${\mathbb {N}}^T$ and ${\mathbb {N}}$, respectively, the following inequality holds using expressions (25)–(26):

$$\begin{aligned} \begin{aligned} \mathrm{sym}{({\hat{S}}_{21\mu {{\hat{{\varPhi }}}}^T{\hat{A}}_{22\mu \mu }})}<0 \end{aligned} \end{aligned}$$

(29)

Accordingly, ${\hat{A}}_{22\mu \mu }$ is nonsingular and then singular system is regular and impulse free using Definition 1.

To prove the stability of system (23), we choose the following Lyapunov function:

$$\begin{aligned} \begin{aligned} {\mathbf {V}}({x}(t))&=\max \big \{{V}_{1}({x}(t)),{V}_{2}({x}(t)),\ldots , {V}_{r}({x}(t))\big \} \end{aligned} \end{aligned}$$

(30)

where ${V}_{k}({x}(t))= {x}^T(t){P}_{k}^T E{x}(t) ,\quad E^TP_k={P}_{k}^TE>0,\ k=1,2,\ldots , r$.

Evaluating the derivative of ${\mathbf {V}}({x}(t))$ along the solutions of system (23), it yields

$$\begin{aligned} \begin{aligned} {\dot{{\mathbf {V}}}}({x}(t))&={\dot{V}}_k({x}(t)),\ \text {if } E^TP_k\ge E^TP_j \ j,k=1,2,\ldots , r\\&=2{x}^T(t){P}_{k}^T E\dot{x}(t). \end{aligned} \end{aligned}$$

(31)

Define $\xi (t)=\begin{bmatrix} {x}^T(t)&\quad \dot{x}^T(t)E^T \end{bmatrix}^T$. From (23), the following equations hold for any matrices ${G}_{l},\ (l=1,2)$ and $S_k$ with the appropriate dimensions

$$\begin{aligned}&2{\xi }^T(t)[{G}_{1}^T\ {G}_{2}^T]^T [-E\dot{x}(t)+{\bar{ A}}_{\mu \mu } x(t) ]=0,\quad 2{x}^T(t)S_kR^TE\dot{x}(t)=0 \end{aligned}$$

(32)

Considering (31)–(32), we obtain

$$\begin{aligned} \begin{aligned} \dot{{\mathbf {V}}}({x}(t))\le&\xi ^T (t)\displaystyle \sum _{{i=1}}^{r}{\mu }_{i}\left( \begin{bmatrix} \mathrm{sym}\Big ({G_1{\bar{ A}}_{ik}}\Big )&\quad P_k+S_kR^T+{\bar{ A}}_{ik}^T{G}_{2}^T-{G}_{1}\\ *&\quad -{{\,\mathrm{sym}\,}}{({G}_{2})} \end{bmatrix} \right) \xi (t) \end{aligned} \end{aligned}$$

(33)

Using the fact that $E^TP_k\ge E^TP_j$, it is easy to verify that

$$\begin{aligned} \begin{aligned} \xi ^T (t) \begin{bmatrix} E^TP_j -E^TP_k&\quad 0\\ *&\quad 0 \end{bmatrix} \xi (t)<0 \end{aligned} \end{aligned}$$

(34)

From (24), we get

$$\begin{aligned} \begin{bmatrix} {\varPhi }_{ik}^j&\quad P_k+S_kR^T+{\bar{ A}}_{ik}^T{G}_{2}^T-{G}_{1}\\ *&\quad -{{\,\mathrm{sym}\,}}{({G}_{2})} \end{bmatrix}<0 \end{aligned}$$

(35)

From (34) and using Lemma 1, we verify that ${\dot{{\mathbf {V}}}}({x}(t))< 0$ when $\xi ( t ) \ne 0$ , which implies that system (23) is stable.

Let us now analyze the $H_\infty$ performance of system (23). Consider the following performance index:

$$\begin{aligned} \begin{aligned} {J}_{zw}=\int _{{0}}^{\infty }\Big ({ {z}^T(t) {z}(t) -\gamma ^2 {w}^T(t) {w}(t) }\Big )\mathrm{d}t \end{aligned} \end{aligned}$$

(36)

Noting that

$$\begin{aligned} \begin{aligned} {J}_{zw}&=\int _{{0}}^{\infty }\Big ({{z}^T(t) {z}(t) -\gamma ^2 {w}^T(t) {w}(t)+{\dot{{\mathbf {V}}}}(x(t)) }\Big )\mathrm{d}t-\int _{{0}}^{\infty }{\dot{{\mathbf {V}}}}(x(t)) \mathrm{d}t\\&=\int _{{0}}^{\infty }\Big ({{z}^T(t) {z}(t) -\gamma ^2 {w}^T(t) {w}(t)+{\dot{{\mathbf {V}}}}(x(t)) }\Big )\mathrm{d}t-\lim _{t\rightarrow \infty }{\mathbf {V}}(x(t))+{\mathbf {V}}(x(0)) \end{aligned} \end{aligned}$$

(37)

Define ${\zeta }(t)= \begin{bmatrix} { \xi ^T }(t)&\quad {w}^T(t) \end{bmatrix}^T$. The following null equation holds

$$\begin{aligned}&2{\xi }^T(t)[{G}_{1}^T\ {G}_{2}^T\ 0]^T \left[ -E\dot{x}(t)+{\bar{ A}}_{\mu \mu } x(t)+{\bar{B_1}}_\mu w(t) \right] =0 \end{aligned}$$

(38)

By following the same procedure as used above and performing the Schur complement equivalence of (24), we can verify that

$$\begin{aligned} \begin{aligned} {z}^T(t) {z}(t) -\gamma ^2 {w}^T(t) {w}(t)+{\dot{{\mathbf {V}}}}(x(t)) <0 \end{aligned} \end{aligned}$$

(39)

For any zero initial condition, we can deduce from (37) that

$$\begin{aligned} \begin{aligned} {J}_{zw}<0 \end{aligned} \end{aligned}$$

(40)

Therefore, for any $0\ne {w}(t) )$, we have $||{z}(t)||<\gamma ||{w}(t)||$.

Consider now the uncertain case. According to Schur complement and Lemma 2, it is to verify form (24) that

$$\begin{aligned}&\begin{bmatrix} {\bar{{\varPhi }}}_{ik}^j&\quad P_k+S_kR^T+{\bar{ A}}_{ik}^T(k){G}_{2}^T-{G}_{1}&\quad {G}_{1}{\bar{B_1}}_{i}&\quad {C}_{i}^T \\ *&\quad -{{\,\mathrm{sym}\,}}{({G}_{2})}&\quad {G}_{2}{\bar{B_1}}_{i}&\quad 0\\ *&\quad *&\quad -\gamma ^2 I&\quad 0 \\ *&\quad *&\quad *&\quad -I \end{bmatrix}<0 \end{aligned}$$

(41)

where ${\bar{{\varPhi }}}_{ik}^j={{\,\mathrm{sym}\,}}( G_1{\bar{ A}}_{ik}(k))+\sum _{j=1}^{r}\tau _{ijk}E^T[P_k-P_j]E$. Thus, system (23) is robustly stable. This completes the proof. $\square$

Now, we are ready to design the gains $K_i$ in (21) such that sliding-mode dynamics (23) is robustly admissible with $H_\infty$ performance.

Theorem 2

Let $\gamma >0$ and $\lambda _l, (l = 1, 2)$ be given scalars. Sliding-mode dynamics of (23) is robustly admissible with $H_\infty$ performance $\gamma$, if there exist matrices G, $S_i$, $P_i>0$, ${Y}_{i}$ and positive scalars $\tau _{ijk}$ and $\varepsilon _i$, $i,j,k= 1,\ldots ,r$ such that the following LMIs hold : 

$$\begin{aligned}&{{\varOmega }}_{ii}^j<0 \end{aligned}$$

(42)

$$\begin{aligned}&\dfrac{1}{r-1}{{\varOmega }}_{ii}^j+\dfrac{1}{2}({{\varOmega }}_{ik}^j+{{\varOmega }}_{ki})^j<0 ,\quad i\ne k \end{aligned}$$

(43)

where

$$\begin{aligned} {{\varOmega }}_{ik}^j&=\begin{bmatrix} {{\varPhi }}_{ik}^j&\quad P_k+S_kR^T+\lambda _2({A}_{i}G+{B}_{i}{Y}_{k})-\lambda _1{G}_{}^T&\quad \lambda _1G^T{C}_{i}^T&\quad {\bar{B_1}}_{i}&\quad \varepsilon _i \lambda _1G{\bar{M}}_{i}&\quad {N}_{i}^T\\ *&\quad -\lambda _2{{\,\mathrm{sym}\,}}{(G)}&\quad \lambda _2G^T{C}_{i}^T&\quad 0&\quad \varepsilon _i \lambda _2 G{\bar{M}}_{i}&\quad 0\\ *&\quad *&\quad -\gamma ^2 I&\quad 0&\quad 0&\quad 0\\ *&\quad *&\quad *&\quad -I&\quad 0&\quad 0\\ *&\quad *&\quad *&\quad *&\quad -\varepsilon _iI&\quad 0\\ *&\quad *&\quad *&\quad *&\quad *&\quad -\varepsilon _iI\\ \end{bmatrix}, \nonumber \\ {{\varPhi }}_{ik}^j&= \lambda _1{{\,\mathrm{sym}\,}}( {{A}}_{i}G+{B}_{i}{Y}_{k})+\displaystyle \sum _{{j=1}}^{r}\tau _{ijk}E^T[P_k-P_j]E \end{aligned}$$

(44)

Furthermore, ${K}_{i}={Y}_{i}G^{-1}$.

Proof

Under the conditions of the theorem, we can easily verify that matrix G is nonsingular, since ${{\,\mathrm{sym}\,}}{(G)}<0$. Now consider the following singular delay system:

$$\begin{aligned}&\left\{ \begin{aligned}&E^T\dot{\zeta }(t)t ={\bar{A}}_\mu ^T{\zeta }(t)+{C}_{\mu }^T{w}(t)\\&{z}(t) ={\bar{B_w}}_\mu ^T{\zeta }(t)\end{aligned} \right. \end{aligned}$$

(45)

Note that $\mathrm{det}\big ({sE-{\bar{A}}_\mu }\big )=\mathrm{det}\big ({sE^T-{\bar{A}}_\mu ^T}\big )$, and then the pair $\big ({E,{\bar{A}}_\mu }\big )$ is regular, impulse free and stable if and only if the pair $\big ({E^T,{\bar{A}}_\mu ^T}\big )$ is regular, impulse free and stable. Moreover, since $\mathrm{det}\big ({sE-{\bar{A}}_\mu }\big )=0$ and $\mathrm{det}\big ({sE^T-{\bar{A}}_\mu ^T }\big )=0$ have the same solution, and

$$\begin{aligned} \begin{aligned} ||G(s)||_\infty =\sup _{{w}(t)\in L_2[0,\infty ) }\sigma _{{\mathrm{max}}}\Big \{{C\big ({j\omega E-{\bar{A}}_\mu }\big )^{-1}{\bar{B_w}}_\mu }\Big \} \end{aligned} \end{aligned}$$

is equal to

$$\begin{aligned} \begin{aligned} ||H(s)||_\infty =\sup _{{w}(t)\in L_2[0,\infty ) }\sigma _{{\mathrm{max}}}\Big \{{{\bar{B_w}}_\mu ^T\big ({j\omega E^T-{\bar{A}}_\mu ^T}\big )^{-1}C^T}\Big \} \end{aligned} \end{aligned}$$

as long as the regularity, free of impulse and stability with $H_\infty$ performance are concerned, we can consider system (45) instead of (23). Then, applying Theorem 1 to system (45) and setting ${G}_{1}^T=\lambda _1G$ and ${G}_{2}^T=\lambda _2G$, conditions (42)–(43) hold. $\square$

Remark 3

• It is noted that the conditions in Theorem 2 are LMIs if the tuning parameters $\lambda _1$ and $\lambda _2$ are well chosen. Thus, as in [47], the following algorithm is suggested in order to find the optimal values of the tuning parameters $\lambda _1$ and $\lambda _2$.

Step 1 :

Specify the ranges $\lambda _i \in [m_i,\ M_i]$, $i=1,2$ and increments $\Delta \lambda _i$ for $\lambda _i$ so that each $\Delta \lambda _i<M_i-m_i$. Also set $\lambda _1 = m_1$ and $\lambda _2=m_2$.

Step 2 :

Carry out Theorem 2 with specified $\lambda _i$’s.

Step 3 :

If we get a solution in Theorem 2, obtain control gains $K_i$. Otherwise, go to Step 4.

Step 4 :

Change $\lambda _1= \lambda _1+\Delta \lambda _1$. If $\lambda _1>M_1$, change $\lambda _1=m_1$, $\lambda _2= \lambda _2+\Delta \lambda _2$. If $\lambda _2>M_2$, then we have no solution. Otherwise, go to Step 2.

Remark 4

• In order to reduce the effect of the disturbance input, the $H_\infty$ concept is addressed to guarantee the closed-loop system to be admissible within a prescribed disturbance attenuation level $\gamma$.

• To obtain the minimum-allowed $\gamma$ satisfying the LMIs in Theorem 2, the following optimization problem can be solved:

  $$\begin{aligned} \min {\nu =\gamma ^2}\quad \text {subject to LMIs} \, (42)\text {--}(43) \end{aligned}$$

  (46)

  The optimal $H_\infty$ performance is $\gamma =\sqrt{\nu }$.

For comparison purposes, consider the following system where the saturation and the nonlinear disturbance are ignored.

$$\begin{aligned}&\left\{ \begin{aligned}&E\dot{x}(t) =({A}_\mu +\Delta {A}_\mu )x(t)+{B}_\mu R(t){u}(t)+{ {B}_{w}}_\mu {w}(t) \\&{z}(t)= {C}_\mu x(t)\end{aligned} \right.&\end{aligned}$$

(47)

Based on the reliable approach, developed by Wu [43], the following lemma shows how to design a $H_\infty$ reliable controller for (47).

Lemma 4

Given a scalar $\gamma >0$. Then, system (47) is admissible and reliable with $H_\infty$ performance if there exist matrices $P>0$ and $W>0$, a nonsingular matrix S, such that the following set of LMIs hold for $i= 1,\ldots ,r$

$$\begin{aligned}&{\varXi }_{ii}<0 \end{aligned}$$

(48)

$$\begin{aligned}&\dfrac{1}{r-1}{\varXi }_{ii}+\dfrac{1}{2}({\varXi }_{ij}+{\varXi }_{ij})<0 ,\quad i>j \end{aligned}$$

(49)

where

$$\begin{aligned} {\varXi }_{ij}=&\begin{bmatrix} {{\,\mathrm{sym}\,}}( {{A}}_{i}{\varPi }+{B}_{i}R_0{Y}_{j})&\quad {\varPi }^T{C}_{i}^T&\quad {{B_1}}_{i}&\quad \varepsilon _i {\varPi }{M}_{i}&\quad {N}_{i}^T&\quad {B}_{i} W&\quad ({Q}_{0} {R}_{0} {Y}_{j})^T\\ *&\quad -\gamma ^2 I&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ *&\quad *&\quad -I&\quad 0&\quad 0&\quad 0&\quad 0\\ *&\quad *&\quad *&\quad -\varepsilon _iI&\quad 0&\quad 0&\quad 0\\ *&\quad *&\quad *&\quad *&\quad -\varepsilon _iI&\quad 0&\quad 0\\ *&\quad *&\quad *&\quad *&\quad 0&\quad -W&\quad 0\\ *&\quad *&\quad *&\quad *&\quad 0&\quad 0&\quad -W\\ \end{bmatrix} , \end{aligned}$$

(50)

where ${\varPi }=\textit{PE}^T+\textit{SR}^T$ and $R \in {\mathbb {R}}^{n\times (n-q)}$ is of full rank such that $R^TE=0$. Furthermore, ${K}_{i}={Y}_{i}{\varPi }^{-1}$.

3.2 Adaptive SMC Law Synthesis

After establishing the appropriate switching surface (21), an adaptive SMC law will be designed to guarantee the reachability of the specified sliding surface $s(t) = 0$ even though uncertainties and input nonlinearity are present.

The adaptive SMC that achieves the control objective can be designed as:

$$\begin{aligned} u_{l}(t)&=\left\{ \begin{array}{ll} -\,{\hat{\alpha }}(t) {\varPsi }(t)\dfrac{{{\tilde{s}}}_l(t)}{\Vert {{\tilde{s}}}(t)\Vert } ,&{}\quad {\tilde{s}}_{l}(t)>0\\ 0,&{}\quad {\tilde{s}}_{l}(t)=0,\\ -\,{\hat{\alpha }}(t) {\varPsi }(t)\dfrac{{{\tilde{s}}}_l(t)}{\Vert {\tilde{s}}(t)\Vert },&{}\quad {\tilde{s}}_{l}(t)<0 \end{array} \right. \quad l=1,2\ldots ,m \end{aligned}$$

(51)

where ${\tilde{s}}(t)=({S}_{0}{B}_\mu {R}_{0})^Ts(t)$, ${\varPsi }(t)=\dfrac{1}{1-\Vert Q\Vert } ({\varPsi }_0(t)+\epsilon )$, and

$$\begin{aligned} {{\varPsi }}_{0}(t)&= \Vert R_0^{-1}\Vert \Bigg ( \Vert ({S}_{0}{B}_\mu )^{-1}\Vert \Vert {S}_{0}\Vert \Vert {M}_\mu \Vert \Vert {N}_\mu \Vert \Vert {x}(t)\Vert + \Vert {K}_\mu {x}(t)\Vert +{{\hat{\rho }}}_{0} (t) \nonumber \\&\qquad +\,{{\hat{\rho }}}_{1} (t)\Vert x(t)\Vert +\Vert ({S}_{0}{B}_\mu )^{-1}\Vert \Vert {S}_{0}\Vert \Vert {B_1}_\mu \Vert \hat{\rho }_{2} (t) \Bigg ) \end{aligned}$$

(52)

Note that ${\hat{\alpha }}(t)$, ${\hat{\rho }}_{0}(t)$, ${\hat{\rho }}_{1}(t)$ and ${\hat{\rho }}_{2}(t)$ represent the estimate of ${\alpha }(t)$, ${\rho }_{0}(t)$. ${\rho }_{1}(t)$ and ${\rho }_{2}(t)$, respectively. ${\hat{\alpha }}(t)$, ${\hat{\rho }}_{0}(t)$, ${\hat{\rho }}_{1}(t)$ and ${\hat{\rho }}_{2}(t)$ are generated as the solution of the following differential equations:

$$\begin{aligned} \dot{{\hat{\alpha }}}(t)&=\kappa {{\hat{\alpha }}}^3(t){\varPsi }_0(t)\Vert {\tilde{s}}(t)\Vert ,\ \dot{{\hat{\rho }}}_{0}(t) =q_{0}\Vert R_0^{-1}\Vert \Vert {\tilde{s}}(t)\Vert , \nonumber \\ \dot{{\hat{\rho }}}_{1}(t)&=q_{1}\Vert R_0^{-1}\Vert \Vert x(t)\Vert \Vert {\tilde{s}}(t)\Vert \nonumber \\ \dot{{\hat{\rho }}}_{2}(t)&=q_{2}\Vert R_0^{-1}\Vert \Vert \Vert ({S}_{0}{B}_\mu )^{-1}\Vert \Vert {S}_{0}\Vert \Vert {B_1}_\mu \Vert \Vert {\tilde{s}}(t)\Vert \end{aligned}$$

(53)

where ${{\hat{\alpha }}}(0)$, ${{\hat{\rho }}}_{0}(0)$, ${{\hat{\rho }}}_{1}(0)$ and ${{\hat{\rho }}}_{2}(0)$ are bounded positive initial values of ${\hat{\alpha }}(t)$, ${\hat{\rho }}_{0}(t)$, ${\hat{\rho }}_{1}(t)$ and ${\hat{\rho }}_{2}(t)$, respectively, and $\kappa$, $q_{0}$, $q_{1}$, $q_{2}$ and $\epsilon$ are positive constants.

Theorem 3

If the adaptive control input ${u}(t)$ is designed as (51) with adaptive law (53), then the trajectory of system (13) converges to the sliding surface $s(t) = 0$.

Proof

Consider the following Lyapunov function:

$$\begin{aligned} V_s(t)&=\dfrac{1}{2}s^T(t) s(t)+\dfrac{1}{2\kappa } {\tilde{\alpha }}^2(t)+\dfrac{1}{2q_{0}}{\tilde{\rho }}_{0}^2(t) +\dfrac{1}{2q_{1}}{\tilde{\rho }}_{1}^2(t) +\dfrac{1}{2q_{2}} {\tilde{\rho }}_{2}^2(t) \end{aligned}$$

(54)

where ${\tilde{\alpha }}(t)={{\hat{\alpha }}}^{-1}(t) -\alpha$, ${\tilde{\rho }}_{0}(t)={{\hat{\rho }}}_{0}(t) -\rho _{0}$, ${\tilde{\rho }}_{1}(t)=\hat{\rho }_{1}(t) -\rho _{1}$ and ${\tilde{\rho }}_{2}(t)={{\hat{\rho }}}_{2}(t) -\rho _{2}$.

According to Eq. (21), we get

$$\begin{aligned} \begin{aligned} {\dot{s}}(t)&= S_0\Big \{ \big ({{\Delta {A}_{\mu }}(t)-{B}_\mu {K}_\mu }\big ){x}(t))+{B_1}_\mu {w}(t)(t){w}(t) \\&\qquad +\,{B}_\mu \Big ({R(t)\sigma ({u}(t))+{\psi }_\mu (t,{x}(t)) }\Big ) \Big \} \end{aligned} \end{aligned}$$

(55)

By taking the derivative of $V_s(t)$, we get

$$\begin{aligned} {\dot{V}}_s(t)= & {} s^T(t) {\dot{s}}(t)-\dfrac{1}{\kappa } {\tilde{\alpha }}(t)\dfrac{\dot{{{\hat{\alpha }}}}(t)}{ {{{\hat{\alpha }}}}^2(t)}+ \dfrac{1}{q_{0}}{\tilde{\rho }}_{0}(t) \dot{{\hat{\rho }}}_{0}(t)+\dfrac{1}{q_{1}}{\tilde{\rho }}_{1}(t) \dot{{\hat{\rho }}}_{1}(t) +\dfrac{1}{q_{2}}{\tilde{\rho }}_{2}(t) \dot{{\hat{\rho }}}_{2}(t) \nonumber \\= & {} {\tilde{s}}^T(t) \Bigg (\sigma ({u}(t))+G(t)\sigma ({u}(t))+R^{-1}_0\Big (\psi (t,{x}(t))-{K}_\mu {x}(t)\nonumber \\&+\,{R}_{0}^{-1}({S}_{0}{B}_\mu )^{-1}{S}_{0} ({B_1}_\mu {w}(t)+\Delta A_\mu (t) x(t))\Big ) \Bigg ) -{\hat{\alpha }}(t)\tilde{\alpha }(t){{\varPsi }}_{0}\Vert {\tilde{s}}(t)\Vert \nonumber \\&+\,{\tilde{\rho }}_{0}(t)\Vert R_0^{-1}\Vert \Vert {\tilde{s}}(t)\Vert + {\tilde{\rho }}_{1}(t)\Vert R_0^{-1}\Vert \Vert x(t)\Vert \Vert {\tilde{s}}(t)\Vert \nonumber \\&+\,{\tilde{\rho }}_{2}(t)\Vert R_0^{-1}\Vert \Vert \Vert ({S}_{0}{B}_\mu )^{-1}\Vert \Vert {S}_{0}\Vert \Vert {B_1}_\mu \Vert {\tilde{s}}(t)\Vert \nonumber \\\le & {} {\tilde{s}}^T(t) \Big ({ (1-\Vert G(t)\Vert )\sigma ({u}(t))}\Big ) \nonumber \\&+\,\Bigg ({\varPsi }_0(t)-{{\hat{\rho }}}_{0}(t) \Vert R_0^{-1}\Vert + \rho _{0} \Vert R_0^{-1}\Vert -{{\hat{\rho }}}_{1}(t) \Vert R_0^{-1}\Vert \Vert x(t)\Vert \nonumber \\&+\,\rho _{1} \Vert R_0^{-1}\Vert \Vert x(t)\Vert +\hat{\rho }_{2}(t)\Vert R_0^{-1}\Vert \Vert \Vert ({S}_{0}{B}_\mu )^{-1}\Vert \Vert {S}_{0}\Vert \Vert {B_1}_\mu \Vert \nonumber \\&-\,\rho _{2} \Vert R_0^{-1}\Vert \Vert \Vert ({S}_{0}{B}_\mu )^{-1}\Vert \Vert {S}_{0}\Vert \Vert {B_1}_\mu \Vert \Bigg ) \Vert {\tilde{s}}(t)\Vert \nonumber \\&-\,{\hat{\alpha }}(t)\tilde{\alpha }(t){{\varPsi }}_{0}\Vert {\tilde{s}}(t)\Vert +{\tilde{\rho }}_{0}(t)\Vert R_0^{-1}\Vert \Vert {\tilde{s}}(t)\Vert \nonumber \\&+\,{\tilde{\rho }}_{1}(t)\Vert R_0^{-1}\Vert \Vert x(t)\Vert \Vert {\tilde{s}}(t)\Vert \nonumber \\&+\,{\tilde{\rho }}_{2}(t)\Vert R_0^{-1}\Vert \Vert \Vert ({S}_{0}{B}_\mu )^{-1}\Vert \Vert {S}_{0}\Vert \Vert {B_1}_\mu \Vert \Vert {\tilde{s}}(t)\Vert \nonumber \\\le & {} \Big ({1-\Vert Q(t)\Vert }\Big ){\tilde{s}}^T(t) \sigma ({u}(t))+(1-{\hat{\alpha }}(t){\tilde{\alpha }}(t)){{\varPsi }}_{0}\Vert {\tilde{s}}(t)\Vert \end{aligned}$$

(56)

From Eqs. (12) and (51), $u_l(t) > 0$ implies that, for ${\tilde{s}}_{l}(t)>0$,

$$\begin{aligned} \sigma ({u}_{l}(t)){u}_{l}(t)&=-{\hat{\alpha }}(t){{\varPsi }}_{0}(t)\dfrac{{\tilde{s}}_l(t)}{\Vert {\tilde{s}}(t)\Vert }{\sigma }_{l}(t) \nonumber \\&=\chi ({u}_{l}(t)){u}_{l}^{2}(t)\nonumber \\&\ge \alpha {\hat{\alpha }}^2(t){\varPsi }^2(t)\dfrac{{\tilde{s}}_l^2(t)}{\Vert {\tilde{s}}(t)\Vert ^2} \end{aligned}$$

(57)

and for ${\tilde{s}}_{l}(t)<0$,

$$\begin{aligned} \sigma ({u}_{l}(t)){u}_{l}(t)=-{\hat{\alpha }}(t) {\varPsi }(t)\dfrac{{\tilde{s}}_l(t)}{\Vert {\tilde{s}}(t)\Vert }{\sigma }_{l}(t)\ge \alpha {\hat{\alpha }}^2(t) {\varPsi }^2(t)\dfrac{{\tilde{s}}_l^2(t)}{\Vert {\tilde{s}}(t)\Vert ^2} \end{aligned}$$

(58)

From (57) and (58), we can obtain

$$\begin{aligned} {\tilde{s}}_l(t){\sigma }_{l}(t)\le - \alpha {\hat{\alpha }}(t) {\varPsi }(t)\dfrac{{\tilde{s}}_l^2(t)}{\Vert {\tilde{s}}(t)\Vert } \end{aligned}$$

(59)

Hence, we have

$$\begin{aligned} \begin{aligned} \Big ({1-\Vert Q(t)\Vert }\Big ){\tilde{s}}^T(t)\sigma ( u)&=-\Big ({1-\Vert Q(t)\Vert }\Big )\sum _{l=1}^m \alpha {\hat{\alpha }}(t) {\varPsi }(t)\dfrac{{\tilde{s}}_l^2(t)}{\Vert {\tilde{s}}(t)\Vert }\\&=-\alpha {\hat{\alpha }}(t) {\varPsi }_0 (t)\Vert {\tilde{s}}(t)\Vert \end{aligned} \end{aligned}$$

(60)

Substituting (60) into (56), we obtain

$$\begin{aligned} {\dot{V}}_s(t)=&\Big ({{\varPsi }}_{0} -{\hat{\alpha }}(t){\tilde{\alpha }}(t){{\varPsi }}_{0}-\alpha {\hat{\alpha }}(t)({{\varPsi }}_{0}+\epsilon )\Big )\Vert {\tilde{s}}(t)\Vert <0,\quad \forall \Vert s(t)\Vert \ne 0 \end{aligned}$$

(61)

Noting that $\alpha {\hat{\alpha }}(t)+{\hat{\alpha }}(t){\tilde{\alpha }}(t) = 1$ and ${\hat{\alpha }}(t)>0$, it is easy to verify that

$$\begin{aligned} {\dot{V}}_s(t)<0,\quad \forall t> 0 \end{aligned}$$

(62)

Which means that the system trajectories converge to the predefined sliding surface and are restricted to the surface for all subsequent times, thereby completing the proof. $\square$

Remark 5

Due to term $\Vert R_0^{-1}\Vert$ in (52), the complete failure case cannot be considered as mentioned in Remark 2.

Remark 6

It is noted that the sliding-mode controller given in (51) contains the term $\dfrac{{\tilde{s}}(t)}{\Vert {\tilde{s}}(t)\Vert }$ which is ill-defined when $s(t) = 0$. In order to avoid this problem and reduce the effect of chattering caused by the discontinuous controller, a sigmoid-like function $\dfrac{{\tilde{s}}(t)}{\varsigma +\Vert {\tilde{s}}(t)\Vert }$ can be introduced to replace $\dfrac{{\tilde{s}}(t)}{\Vert {\tilde{s}}(t)\Vert }$, where $\varsigma$ is a small positive scalar value.

Remark 7

For singular systems, the existence of the algebraic equation may cause an impulsive behavior of the states unless each control input is continuously differentiable. Besides, the chattering phenomenon produced by the SMC law may destroy the system performances and even damage the actuators. To circumvent this difficulty, the high-order sliding-mode control can be a good issue, which needs to be further investigated, which may be a future direction in our investigation [24, 27].

4 Application to the Lower-Limb Rehabilitation System

In this section, the proposed control scheme is applied to the lower-limb rehabilitation system shown in Fig. 1. The system is governed by the following dynamic model extracted from reference [34]:

$$\begin{aligned} \mathrm {M}(q)\ddot{q}(t)+C(q,{\dot{q}}){\dot{q}}(t)+G(q)q(t)=Ru(t)+Sw(t) \end{aligned}$$

(63)

where $q(t)=[{q}_{1}^T(t)\ {q}_{2}^T(t)]^T$ denotes the generalized coordinates, $u(t) =[C_{M1}(t) \ C_{M2}(t)]^T$ is the input vector and $w(t) =[f_{px}(t) \ C_{pz}(t)]^T$ is the disturbance vector.

Fig. 1

Mechanical scheme of the lower-limb rehabilitation system

The model matrices are defined as.

$$\begin{aligned} \mathrm {M}(q)&=\begin{bmatrix} M + m&\quad -ml \mathrm{sin}(\alpha )\mathrm{sin}(q_2(t))\\ -m \mathrm{sin}(\alpha )\mathrm{sin}(q_2(t))&\quad ml^2 + J+\Delta J \end{bmatrix}, \nonumber \\ C(q,{\dot{q}})&=\begin{bmatrix} 0&\quad -ml \mathrm{sin}(\alpha ){\dot{q}}_2(t) \mathrm{cos}(q_2 (t))\\ 0&\quad 0 \end{bmatrix},\nonumber \\ G(q)&=\begin{bmatrix} 0&\quad 0\\ 0&\quad -ml\mathrm{cos}(\alpha )\dfrac{\mathrm{sin}(q_2(t))}{q_2(t)} \end{bmatrix}, \nonumber \\ R&=\begin{bmatrix} \dfrac{1}{a}&\quad 0\\ 0&\quad 1 \end{bmatrix},\ S=\begin{bmatrix} 1&\quad 0\\ 0&\quad 1 \end{bmatrix} \end{aligned}$$

(64)

with $M=14\,\mathrm{kg}$, $m=4\,\mathrm{kg}$, $J=0.26\,\mathrm{kg}\,\mathrm{m}^2$, $a=0.025$, $l=0.05\,\mathrm{m}$, $\alpha =20^{\circ }$, $\beta =0.01\,\mathrm{m}$ and $h=0.6\,\mathrm{m}$.

Let ${x}_{1}(t)={q}_{1}(t)$, ${x}_{2}(t)={q}_{2}(t)$, ${x}_{3}(t)= { {\dot{q}}}_{1}(t)$, ${x}_{4}(t)= { {\dot{q}}}_{2}(t)$, ${x}_{5}(t)= { \ddot{q}}_{1}(t)$ and ${x}_{6}(t)= { \ddot{q}}_{2}(t)$. Model (63) can be also written as

$$\begin{aligned} \begin{aligned} E{\dot{x}}(t)&= \begin{bmatrix} 0&\quad I&\quad 0\\ 0&\quad 0&\quad I\\ -G(q)&\quad 0&\quad -M(q) \end{bmatrix}x(t)+ \begin{bmatrix} 0\\ 0\\ R \end{bmatrix}\Big ({\sigma ( u(t)) +f(x) }\Big )+ \begin{bmatrix} 0\\ 0\\ S \end{bmatrix}w(t) \end{aligned} \end{aligned}$$

(65)

where $E={{\,\mathrm{diag}\,}}\big ({1,1,1,1,0,0}\big )$, $x(t)=[{x}_{1}(t)\ {x}_{2}(t)\ {x}_{3}(t)\ {x}_{4}(t)\ {x}_{5}(t)\ {x}_{6}(t)]^T$ and $f(x)=-R^{-1}C(q,{\dot{q}}) {\dot{q}}(t)=\begin{bmatrix} f_0x_4^2\mathrm{cos}(x_2)\\0 \end{bmatrix}$.

Assume that $\theta _1(t)= \mathrm{sin}({x}_{2}(t))\in \big [\begin{array}{ll} -1&,\, 1\end{array} \big ]$ and $\theta _2(t)=\dfrac{\mathrm{sin}({x}_{2}(t))}{{x}_{2}(t)}\in \big [\begin{array}{ll} \frac{\mathrm{sin}(\pi /4)}{\pi /4}&,\, 1\end{array} \big ]$.

Using the sector nonlinearity approach, the above nonlinear functions can be rewritten as

$$\begin{aligned}&\left\{ \begin{aligned} {\theta }_{1}(t)&= -{w}_{11}(\theta (t))+ {w}_{12}(\theta (t))\\ {\theta }_{2}(t)&= \frac{\mathrm{sin}(\pi /4)}{\pi /4}{w}_{21}(\theta (t))+ {w}_{22}(\theta (t)) \end{aligned}\right. \end{aligned}$$

(66)

The membership functions are calculated as

$$\begin{aligned}&\left\{ \begin{array}{ll} {w}_{11}(\theta (t))=\dfrac{1-\theta _1(t)}{2},&{}\quad {w}_{12}(\theta (t))=1-{w}_{11}(\theta (t))\\ {w}_{21}(\theta (t))=\dfrac{1-\theta _2(t)}{ 1-\frac{\mathrm{sin}(\pi /4)}{\pi /4}},&{}\quad {w}_{22}(\theta (t))=1-{w}_{21}(\theta (t)) \end{array}\right. \end{aligned}$$

(67)

According to (67), nonlinear systems (65) can be exactly represented by the following T–S fuzzy system with $4=2^2$ rules.

$$\begin{aligned} \left\{ \begin{array}{l} E\dot{x}(t) =\sum _{i=1}^4{\mu }_{i}(\theta (t))({A_i}+\Delta {A_i} )x(t)+{B}\big ({u^{\mathrm{F}}(t)+ \psi (t,{x}(t)) }\big )+{ {B}_{w}}{w}(t) \\ {z}(t) = \sum _{i=1}^4{\mu }_{i}(\theta (t)) C_ix(t)\end{array}\right. \end{aligned}$$

(68)

where

$$\begin{aligned}&\left\{ \begin{aligned} {\mu }_{1}(\theta (t))&=w_{11}(\theta (t))w_{21}(\theta (t)),&\quad {\mu }_{2}(\theta (t))&=w_{11}(\theta (t))w_{22}(\theta (t)),\\ {\mu }_{3}(\theta (t))&=w_{12}(\theta (t))w_{21}(\theta (t)),&\quad {\mu }_{4}(\theta (t))&=w_{12}(\theta (t))w_{22}(\theta (t)) \end{aligned} \right. \end{aligned}$$

(69)

and the numerical values of matrices are as follows:

$$\begin{aligned} \begin{aligned}&{A}_{1}=\begin{bmatrix} 0&\quad I&\quad 0\\ 0&\quad 0&\quad I\\ -\,{G}_{1}&\quad 0&\quad -\,{M}_{1} \end{bmatrix},\ {A}_{2}=\begin{bmatrix} 0&\quad I&\quad 0\\ 0&\quad 0&\quad I\\ -\,{G}_{2}&\quad 0&\quad -\,{M}_{1} \end{bmatrix},\ {A}_{3}=\begin{bmatrix} 0&\quad I&\quad 0\\ 0&\quad 0&\quad I\\ -\,{G}_{1}&\quad 0&\quad -\,{M}_{2} \end{bmatrix}, \\&{A}_{4}=\begin{bmatrix} 0&\quad I&\quad 0\\ 0&\quad 0&\quad I\\ -\,{G}_{2}&\quad 0&\quad -\,{M}_{2} \end{bmatrix} \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&{G}_{1}=\begin{bmatrix} 0&\quad 0\\ 0&\quad -\,1.84 \end{bmatrix},&{M}_{1}=\begin{bmatrix} 18&\quad -\,0.0684\\ -\,0.0684&0.29 \end{bmatrix},&{G}_{2}=\begin{bmatrix} 0&\quad 0\\ 0&\quad -\,0.104 \end{bmatrix}, \\&{M}_{2}=\begin{bmatrix} 18&\quad 0.0684\\ 0.0684&\quad 0.29 \end{bmatrix}. \end{aligned} \end{aligned}$$

In this example, it is assumed that the uncertain parameter matrix function ${\Delta }(t)=0.7+0.3\mathrm{sin}(0.2t)$ and the constant matrices:

$$\begin{aligned} \begin{aligned} M_i&= \begin{bmatrix} 0&\quad 0&\quad 0&\quad 1 \end{bmatrix}^T,&N_i&= \begin{bmatrix} 0&\quad 0&\quad 0&\quad 0.1 \end{bmatrix},\quad i=1,2\ldots ,4 \end{aligned} \end{aligned}$$

Set $S_0=B_0^+$. For given scalars of $\lambda _1=1$ and $\lambda _2=0.35$, the corresponding convex optimization problem (46) (solved using the Yalmip toolbox and the Sdpt3 solver), produces a feasible solution with minimum-allowed $\gamma ^*=0.911$ and the following feedback gain matrices:

$$\begin{aligned} \begin{aligned} K_1&=\begin{bmatrix} -\,10.584&\quad -\,1.0518&\quad -\,2.0261&\quad -\,0.18358&\quad 0.015715&\quad -\,0.015255\\ -\,132.34&\quad -\,15.801&\quad -\,17.552&\quad -\,4.7413&\quad 0.27426&\quad -\,2.327 \end{bmatrix},\\ K_2&=\begin{bmatrix} -\,10.748&\quad -\,1.0702&\quad -\,2.0379&\quad -\,0.18818&\quad 0.020137&\quad -\,0.019633\\ -\,133.94&\quad -\,14.179&\quad -\,20.948&\quad -\,4.0343&\quad -\,0.94344&\quad -\,1.4583 \end{bmatrix},\\ K_3&= \begin{bmatrix} -\,9.8035&\quad -\,0.97517&\quad -\,1.8541&\quad -\,0.16953&\quad 0.044707&\quad -\,0.013411\\ -\,137.38&\quad -\,16.215&\quad -\,18.714&\quad -\,4.6986&\quad 0.10553&\quad -\,2.184 \end{bmatrix},\\ K_4&=\begin{bmatrix} -\,10.196&\quad -\,1.0157&\quad -\,1.9235&\quad -\,0.17836&\quad 0.036194&\quad -\,0.017035\\ -\,130.7&\quad -\,13.845&\quad -\,20.326&\quad -\,3.9507&\quad -\,0.83096&\quad -\,1.4364 \end{bmatrix} \end{aligned} \end{aligned}$$

(70)

The existence of a feasible solution shows that there exists a sliding surface in (21) such that the resulting sliding mode dynamics in (23) is admissible.

It is assumed that $f_0=0.0017$. The actuator faults $f_{\mathrm{a}}(t)= \begin{bmatrix} f_{\mathrm{a}2}^{T}(t)&\quad f_{\mathrm{a}2}^{T}(t) \end{bmatrix}^T$ and the external disturbance input are, respectively, selected as

$$\begin{aligned} f_{\mathrm{a}1} (t)&={\left\{ \begin{array}{ll} 0.1t,&{}\quad 0 \le t \le 2,\\ 0.2, &{}\quad 2< t < 3,\\ 0.1 \mathrm{sin}(10t ) + 0.1\mathrm{cos}(10t ) &{}\quad 3 \le t \le 5\\ \end{array}\right. } \nonumber \\ f_{\mathrm{a}2} (t)&={\left\{ \begin{array}{ll} 0.1 \mathrm{cos}(t),&{}\quad 0 \le t \le 1,\\ 0.1 \mathrm{sin}(10t ) + 0.1 &{}\quad 1 \le t \le 5\\ \end{array}\right. } \end{aligned}$$

(71)

and $w( t ) =\big [\begin{matrix} 0.1\mathrm{sin} ( 3t )e^{-0.01t}&,\ \dfrac{0.1 \mathrm{sin} ( 5t )}{5t+1}\end{matrix} \big ]$.

The saturation levels are ${u}_{ 1, {\mathrm{max}}}=1$ and ${u}_{ 2, {\mathrm{max}}}=5$, and the actuators can have failures with parameters, namely ${\underline{r}}_{1}= 0.2$, ${\underline{r}}_{2}= 0.1$, ${\bar{r}}_{1}= 1.5$, ${\bar{r}}_{2}= 1$, so $R_0 ={{\,\mathrm{diag}\,}}\{0.85,0.55 \}$ and $Q_0 ={{\,\mathrm{diag}\,}}\{0.7647,0.8182 \}$.

For the sake of verifying the effectiveness of the proposed controller, the following parameters and initial conditions are selected in the simulation: $\kappa =0.01$, $q_{0}=0.1$, $q_{1}=0.2$, $q_{2}=0.2$, $\epsilon =35$ and $x(t)=\begin{bmatrix} 0.15&\quad \frac{\pi }{4}&\quad 0&\quad 0&\quad 0 \end{bmatrix}^T$. To prevent the control signal from chattering, we replace $\dfrac{{\tilde{s}}(t)}{\Vert {\tilde{s}}(t)\Vert }$ with $\dfrac{{\tilde{s}}(t)}{0.1+\Vert {\tilde{s}}(t)\Vert }$.

Fig. 2

State trajectories

Fig. 3

State trajectories

Fig. 4

Input trajectories

Fig. 5

Surface trajectories

Fig. 6

Adaptive law ${\hat{\alpha }}(t)$

Fig. 7

Adaptive law ${\hat{\rho }}_0(t)$

To study the effect of actuator failures, we consider a scenario defined by a fault matrix R(t) as

$$\begin{aligned} R(t)={{\,\mathrm{diag}\,}}\{\xi _1(t)+0.7,\xi _2(t)+0.2 \} \end{aligned}$$

(72)

where $1\le t\le 20$ and

$$\begin{aligned} \xi _1(t)={\left\{ \begin{array}{ll} 0.6, &{}\quad \text {if}\ 0\le \mathrm{mod}(t,3 )\le 1\\ -0.4,&{} \quad \text {if}\ 1< \mathrm{mod}(t,3 )\le 2\\ 0.8, &{}\quad \text {if}\ 2< \mathrm{mod}(t,3 )\le 3 \end{array}\right. }&\quad \xi _2(t)={\left\{ \begin{array}{ll} 0.1, &{}\quad \text {if}\ 0\le \mathrm{mod}(t,3 )\le 1\\ 0.2, &{}\quad \text {if}\ 1< \mathrm{mod}(t,3 )\le 2\\ 0.3, &{}\quad \text {if}\ 2< \mathrm{mod}(t,3 )\le 3 \end{array}\right. } \end{aligned}$$

(73)

The numerical simulations are performed for the reliable control mode, where the reliable SMC controller is implemented under the previous failure scenario. The corresponding simulation results are plotted in Figs. 2, 3, 4, 5, 6, 7, 8, 9 and 10.

• Figures 2, 3, 4 and 5 depict, respectively, the system state trajectories, the control input and the resulting sliding surface when the designed control strategy is applied. We observe that the system under consideration is stabilized by using the sliding-mode fault-tolerant controller (51). More precisely, the closed-loop system still maintains some good performance despite the presence of actuator faults and saturation, parameter uncertainties and external disturbances.

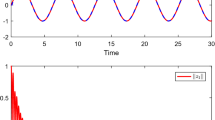
• Figures 6, 7, 8 and 9 show that the adaptive laws converge to some values depending on initial condition values ${{\hat{\alpha }}}(0)$, ${{\hat{\rho }}}_{1}(0)$ and ${{\hat{\rho }}}_{0}(0)$ and the adaptation gains $\kappa$, $q_{0}$, $q_{1}$ and $q_{2}$. However, we can note that ${{\hat{\alpha }}}(t)$, ${{\hat{\rho }}}_{0}(t)$ and ${{\hat{\rho }}}_{1}(t)$ do not necessarily converge to nominal values $\alpha$, $\rho _{0}$, $\rho _{1}$ and $\rho _{2}$, respectively.

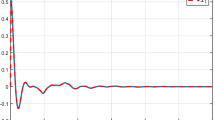
• From Fig. 10, it can be clearly observed that the ratio of $\frac{||{z}(t)||_2}{||{w}(t)||_2}$ under zero initial condition is less than $\gamma = 0.911$.

• It is clear from Fig. 4 that the control signal is chattering free.

Fig. 8

Adaptive law ${\hat{\rho }}_1(t)$

Fig. 9

Adaptive law ${\hat{\rho }}_2(t)$

Fig. 10

Ratio trajectory

Fig. 11

State trajectories using reliable controller (74)

In order to highlight the effectiveness of the proposed control scheme, we will perform a comparison with the method applied in [43]. According to Lemma 4, the minimum allowed $\gamma ^*=0.541$ and the reliable control gains can be computed as

$$\begin{aligned} \begin{aligned} K_1&=\begin{bmatrix} 74.989&\quad -\,6.6756&\quad -\,27.243&\quad -\,1.6557&\quad 0.035945&\quad -\,0.020326\\ -\,4257.5&\quad -\,593.77&\quad -\,679.87&\quad -\,211.11&\quad -\,0.17689&\quad -\,7.176 \end{bmatrix},\\ K_2&=\begin{bmatrix} -\,74.232&\quad -\,6.5933&\quad -\,27.035&\quad -\,1.6323&\quad 0.039699&\quad -\,0.019473\\ -\,4243.4&\quad -\,590.55&\quad -\,669.93&\quad -\,210.87&\quad -\,0.14559&\quad -\,7.1768 \end{bmatrix},\\ K_3&=\begin{bmatrix} -\,75.494&\quad -\,6.7569&\quad -\,27.269&\quad -\,1.6865&\quad 0.036911&\quad -\,0.018333\\ -\,4221.1&\quad -\,590.6&\quad -\,666.33&\quad -\,210.34&\quad 0.26424&\quad -\,7.1648 \end{bmatrix},\\ K_4&=\begin{bmatrix} -\,74.927&\quad -\,6.6994&\quad -\,27.1&\quad -\,1.6717&\quad 0.04065&\quad -\,0.017746\\ -\,4205.3&\quad -\,587.23&\quad -\,655.81&\quad -\,210.06&\quad 0.3122&\quad -\,7.1645 \end{bmatrix} \end{aligned} \end{aligned}$$

(74)

Assume that $f_0=0.4$. Figures 11 and 12 exhibit a comparison of state variable trajectories using the reliable controller designed in (74) and the proposed reliable SMC controller (51). It is observed from the plotted figures that the developed control law leads to avoid divergence of the states and maintain the dynamic stability of the system.

Fig. 12

State trajectories using reliable SMC controller (51)

In conclusion, although the method in [43] proposes an effective reliable control design for linear singular systems with external disturbances, it may not be able to cope with a complex case with nonlinear disturbance and actuator saturation. Thus, the impact of the synthesized control law is evidently quite effective and it can stabilize the underlying system with satisfactory performance.

5 Conclusion

In this paper, we have studied the reliable sliding-mode control problem for a class of nonlinear singular systems described by T–S fuzzy model with external disturbance, actuator failures and saturation. The key features of the proposed approach lie in the design of integral-type sliding surface and the associated adaptive SMC law for the system under consideration. An admissibility criterion with $H_\infty$ performance has been established to ensure the stability of the sliding-mode dynamics enforced on the sliding surface. In addition, the design method can be applied to a wide range of practical systems. Motivated by research developed in [28], the proposed approach will be extended to multi-agent systems in future. Furthermore, the high-order sliding-mode control for nonlinear singular systems will be a challenging issue for our future investigation. Finally, experimental results will be a challenge for solidly convincing the developed results.