1 Introduction

Compared with linear systems, almost all actual industrial systems are nonlinear systems, such as hypersonic aircraft [1], ship autopilot system [2], aircraft flight control system [3], and robotic manipulator system [4]. However, because the analysis of nonlinear systems is far more complicated than linear systems, and there is a lack of effective mathematical tools that can be processed uniformly, there are few results on nonlinear systems compared with linear systems. It was not until the emergence of neural networks (NNs) and fuzzy logic systems (FLSs) that this deadlock was broken. NNs and FLSs have been proven to be a universal approximator that can approximate a continuous unknown nonlinear function with arbitrary precision. Since then, adaptive control methods of unknown nonlinear systems have been extensively developed in [4,5,6,7,8,9,10,11,12,13,14,15,16,17]. For the switched nonlinear systems, an adaptive fuzzy finite-time tracking control approach was investigated in [5]. Based on event triggered, a fuzzy adaptive tracking fixed-time control problem was studied for non-strict-feedback nonlinear systems in [16].

Based on the state-space method, also called the first-order method, all the above control methods are very effective for dealing with the control problems of nonlinear systems, but it requires a system to be a first-order differential system. According to the laws of physics, such as Newton’s laws of motion, Euler’s equations, Lagrange’s equations, Kirchhoff’s law, etc., many models of real industrial systems are higher-order differential equations. For example, the rigid robotic systems were modeled as second-order differential dynamics equations in [18], and single-link flexible manipulators were described as fourth-order differential equations in [19]. The state-space method can solve the control problems of high-order nonlinear systems, but it is necessary to transform the high-order system into a first-order one by lowering the order and maximizing the number of equations, which greatly increases the complexity of the controller design, and the system after processing by maximizing the number of equations, the physical meaning of some states may be lost. How to directly design a simpler controller for high-order systems is more challenging. Professor Guangren Duan first proposed the high-order fully actuated (HOFA) system method, namely the high-order method, which provides a new dawn for the controller design of high-order systems, such as [20,21,22,23,24,25,26,27,28,29]. The adaptive tracking controllers and stabilizing controllers were first designed for three types of high-order system models with parametric uncertainties in [23]. In [24], the high-order backstepping control and robust control approaches were discussed for an uncertain high-order strict-feedback system (SFS), an uncertain second-order SFS, and a single HOFA model with nonlinear uncertainties. Although these results require fault-free operating conditions, but they provide a new idea for directly designing a fault-tolerant controller of high-order unknown nonlinear systems in this paper.

For actual industrial systems, faults are inevitable and unpredictable. Faults may lead to poor control performance and even system instability. Therefore, considering the controller design of the unknown nonlinear system with faults is theoretical and practical significance. Some adaptive control methods of nonlinear systems with faults were investigated in [30,31,32,33]. An adaptive decentralized fault-tolerant control (FTC) approach was proposed for uncertain interconnected nonlinear systems in [31]. In [30,31,32,33], all the control methods only consider linear faults, which are invalid for nonlinear faults. In fact, most faults in practical systems are nonlinear functions of controller u and state x [34,35,36,37,38]. To the best of the authors’ knowledge, so far there are few FTC results that considered nonlinear faults in nonlinear system control. For instance, the FTC algorithm proposed in [39] has solved the control problem of nonlinear systems with affine nonlinear faults, which are functions of the state x. But what about non-affine nonlinear faults, the control methods above are obviously ineffective. For the above literature, all the FTC approaches were studied for first-order nonlinear systems. Therefore, how to directly design an adaptive controller of the high-order nonlinear SFS with non-affine nonlinear faults is still an open problem, which is of great theoretical and practical value.

Based on the above motivation, we study the adaptive tracking FTC method for the high-order nonlinear SFS with non-affine nonlinear faults. The main contributions are summarized as follows:

  1. (1)

    Based on the state-space method, for the control methods of second- or high-order systems in the existing literature, it is all need to converting the system to first-order one. But for actual industrial systems, some states have lost the physical meanings in the process of model transformation. In this paper, the adaptive controller can be designed directly for high-order unknown nonlinear systems, it does not need to convert the high-order system into first-order one. Thus, the proposed high-order backstepping method needs fewer steps than the usual state-space backstepping method; at the same time, the computation complexity has been greatly reduced.

  2. (2)

    For the actual industrial system, faults are inevitable due to some unpredictable reasons. For the existing results on faults, most control methods only consider linear faults [30,31,32,33], and only a few control methods consider affine nonlinear faults [39]. However, in most cases, the faults exhibit non-affine properties. Therefore, it is of practical significance to investigate high-order nonlinear systems with non-affine nonlinear faults. And according to the authors’ knowledge, it is the first time to solve the adaptive fuzzy FTC of high-order nonlinear SFS with non-affine nonlinear faults.

The outline of this paper is state as follows: Sect. 2 provides the problem description and preliminaries. High-order backstepping controller is constructed in Sect. 3. Section 4 shows the stability analysis. Finally, the simulation results and conclusion are provided in Sect. 5 and 6, respectively.

2 Problem Description and Preliminaries

2.1 Problem Formulation

The high-order nonlinear SFS is considered as follows:

$${\left\{ \begin{array}{ll} x_{1}^{\left( q_{1}\right) }=f_{1}(x_{1}^{\left( 0\sim q_{1}-1\right) })+g_{1}(x_{1}^{\left( 0\sim q_{1}-1\right) })x_{2}, \\ x_{2}^{\left( q_{2}\right) }=f_{2}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim 2}\right. )+g_{2}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim 2}\right. )x_{3}, \\ \quad \ \ \ \ \ \ \ \ \ \vdots \\ x_{n-1}^{\left( q_{n-1}\right) }=f_{n-1}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n-1}\right. )+g_{n-1}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n-1}\right. )x_{n}, \\ x_{n}^{\left( q_{n}\right) }=f_{n}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. )+g_{n}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. )u+l\left( t-T_{0}\right) \nu \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) ,\\ y=x_{1}, \end{array}\right. },$$
(1)

where \(x_{i}\in R\), \(i=1,2,\ldots ,n\) are the state variables, \(f_{j}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim j}\right. )\in R\) and \(g_{j}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim j}\right. )\in R\), \(j=1,2\ldots ,n\) denote unknown nonlinear functions and known nonlinear functions, respectively. \(y\in R\) and \(u\in R\) are the output and input of the considered system. It is assumed that \(g_{j}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim j}\right. )\ne 0\). \(\nu \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) \in R\) represents an unknown external disturbance caused by a fault. \(l\left( t-T_{0}\right) \in R\) denotes the time profile of the fault that occurs at some unknown time:

$$l\left( t-T_{0}\right) =\left\{ \begin{array}{ll} 0,&{} t<T_{0}, \\ 1-{\text {e}}^{-\delta \left( t-T_{0}\right) },&{} t\ge T_{0}, \end{array} \right. ,$$
(2)

where \(\delta >0\) is the evolution rate of the unknown fault. The reference signal \(y_{\text {r}}\) is a smooth function, \(y_{\text {r}}\) and its derivatives \({\dot{y}} _{\text {r}},\ldots ,y_{\text {r}}^{(q_{1})}\) are all bounded.

The objective is to construct adaptive fuzzy controller for high-order nonlinear SFS with non-affine nonlinear faults (1), such that the output of the system can track the ideal signal \(y_{\text {r}}\), and the closed-loop system is stable.

Assumption 1

([40]:) For system (1), the inequality

$$\begin{aligned}&\left| f_{n}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. )+l\left( t-T_{0}\right) \nu \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) \right| \\&\quad \le \eta \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) \end{aligned}$$
(3)

holds, where \(\eta \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right)\) is an unknown nonnegative function.

Remark 1

It should be pointed out that almost all the results on adaptive control problems of nonlinear systems are based on the state-space method, i.e., the first-order method. According to the laws of physics, many models of real industrial systems are high-order dynamic differential equations. The state-space method can also solve the control problem of high-order nonlinear systems, but it needs to transform the system into a first-order one first, so this method is relatively cumbersome. In the past 2 years, professor Guangren Duan first proposed the HOFA system method [20,21,22,23,24,25,26,27,28,29]. This method can directly design the controller of the high-order nonlinear system, but it requires the nonlinear function to be known [20, 22,23,24,25,26,27,28]. Due to the natural environment or technical means, many practical systems cannot be accurately modeled. Therefore, it is of great theoretical and practical significance to study the direct design controller of high-order systems with unknown nonlinear functions.

Remark 2

For most of the existing results on adaptive FTC approaches of nonlinear systems, basically only linear faults are considered [30,31,32,33], i.e., lock-in-place model and loss of effectiveness model. Compared to linear faults, there are few results considering nonlinear faults. In fact, most faults in practical systems are nonlinear functions of controller u and state x [39]. The FTC algorithm proposed in [39] has solved the control problem of nonlinear systems with affine nonlinear faults, which are functions of the state x. But what about non-affine faults, the control methods above are obviously ineffective. However, in most cases, the faults exhibit non-affine properties. Therefore, the faults considered in this paper are more general than the above-mentioned results.

2.2 Preliminaries

For convenience, we define the following symbols that can be used in the following paper. \(I_{\text {m}}\) represents the identity matrix, and

$$\begin{aligned}&x^{\left( 0\sim q\right) }=\left[ \begin{array}{c} x \\ {\dot{x}} \\ \vdots \\ x^{\left( q\right) } \end{array} \right] ,\\&\left. x_{k}^{\left( q_{0}\sim q_{k}\right) }\right| _{k=i\sim j}=\left[ \begin{array}{c} x_{i}^{\left( q_{0}\sim q_{k}\right) } \\ x_{i+1}^{\left( q_{0}\sim q_{k}\right) } \\ \vdots \\ x_{j}^{\left( q_{0}\sim q_{k}\right) } \end{array} \right] ,\quad j\ge i,\\&A^{0\sim q-1}=\left[ \begin{array}{cccc} A_{0}&A_{1}&\cdots&A_{q-1} \end{array} \right] ,\\&\varPhi \left( A^{0\sim q-1}\right) =\left[ \begin{array}{cccc} 0 &{} I &{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} I \\ -A_{0} &{} -A_{1} &{} \cdots &{} A_{q-1} \end{array} \right] . \end{aligned}$$

FLSs are used to approximate the unknown nonlinear functions of the system (1). The inference rules of knowledge base are in the following [40]:

\(R^{l}\): If \(x_{1}\) is \(F_{l}^{l}\) and \(x_{2}\) is \(F_{2}^{l}\) and \(\ldots\) and \(x_{n}\) is \(F_{n}^{l}\),

      then y is \(G^{l}\), \(l=1,2,\ldots ,N\), where \(x = [x_{1},\ldots ,x_{n}]^{\text {T}}\) and y are the input and output of an FLS. N is the rules number. Fuzzy sets \(F_{i}^{l}\) and \(G^{l}\) are associated with the fuzzy membership functions \(\mu _{F_{i}^{l}}(x)\) and \(\mu _{G^{l}}(y)\), respectively.

By using product inference, center average defuzzification along with singleton fuzzifier, the FLS is designed as follows:

$$y(x)=\frac{\sum _{l=1}^{N}{\bar{y}}_{l}\prod _{i=1}^{n}\mu _{F_{i}^{l}}(x_{i})}{ \sum _{l=1}^{N}[\prod _{i=1}^{n}\mu _{F_{i}^{l}}(x_{i})]},$$
(4)

where \({\bar{y}}_{l}=\max _{y\in R}\mu _{G^{l}}(y)\).

The fuzzy basis functions are designed as follows:

$$\varphi _{l}=\frac{\prod _{i=1}^{n}\mu _{F_{i}^{l}}(x_{i})}{\sum _{l=1}^{N}\left( \prod _{i=1}^{n} \mu _{F_{i}^{l}}(x_{i})\right) }$$
(5)

then, (4) can be rewritten as \(y(x)=\theta ^{\text {T}}\varphi (x)\), where \(\theta ^{\text {T}}=[{\bar{y}}_{1},{\bar{y}}_{2},\ldots ,{\bar{y}}_{N}]=[\theta _{1},\theta _{2},\ldots , \theta _{N}]\) and \(\varphi (x)=[\varphi _{1}(x),\ldots ,\varphi _{N}(x)]^{\text {T}}\).

Lemma 1

Let \(f\left( x\right)\) be a continuous smooth function defined on a compact set U,  for any positive approximation error \(\varepsilon ,\) there exists a FLS \(\theta ^{\text {T}}\varphi \left( x\right)\) such that

$$\sup _{x\in U}\left| f\left( x\right) -\theta ^{\text {T}}\varphi \left( x\right) \right| \le \varepsilon ,$$
(6)

where \(\varepsilon\) satisfies \(|\varepsilon |\le \varepsilon ^{*},\) \(\varepsilon ^{*}\) is a positive constant.

Proposition 1

([22, 23]:) For an arbitrarily chosen F \(\in R^{q_{i}\times q_{i}},\) all the matrix \(A^{0\sim q_{i}-1}\) and the nonsingular matrix V \(\in R^{q_{i}\times q_{i}}\) satisfying

$$\varPhi \left( A^{0\sim q_{i}-1}\right) =VFV^{-1}$$
(7)

are given by

$$\begin{aligned}&A^{0\sim q_{i}-1}=-ZF^{q_{i}}V^{-1}\left( Z,F\right) , \end{aligned}$$
(8)
$$\begin{aligned}&V\left( Z,F\right) =\left[ \begin{array}{c} Z \\ ZF \\ \vdots \\ ZF^{q_{i}-1} \end{array} \right] , \end{aligned}$$
(9)

where Z \(\in R^{1\times q_{i}}\) is an arbitrary parameter matrix satisfying

$$\det V\left( Z,F\right) \ne 0 .$$
(10)

Then, to solve the matrix \(P\left( A_{i}^{0\sim q_{i}}\right)\) satisfying the following Lyapunov matrix equation (13), some notations related to a square matrix \(\varPhi\) \(\in R^{q_{i}\times q_{i}}\) are introduced as follows:

$$\begin{aligned}&\det \left( sI+\varPhi \right) \triangleq \sum \limits _{i=0}^{q_{i}}c_{i}^{\varPhi }s^{i}, \end{aligned}$$
(11)
$$\begin{aligned}&adj\left( sI+\varPhi ^{\text {T}}\right) \triangleq \sum \limits _{i=0}^{q_{i}-1}C_{i}^{\varPhi }s^{i} . \end{aligned}$$
(12)

Proposition 2

([23]:) If \(\varPhi\) \(\in R^{q_{i}\times q_{i}}\) is Hurwitz, then the following Lyapunov equation

$$\varPhi ^{\text {T}}P+P\varPhi =-I$$
(13)

has a unique solution given by

$$P=\sum \limits _{i=0}^{q_{i}-1}C_{i}^{\varPhi }P_{0}^{-1}\varPhi ^{i}$$
(14)

with

$$P_{0}=\sum \limits _{i=0}^{q_{i}}c_{i}^{\varPhi }\varPhi ^{i}.$$
(15)

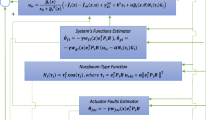
3 High-Order Backstepping Controller Design

Bases on HOFA theory, the backstepping controller design approach can be directly given for the high-order nonlinear SFS (1) without converting the system into a first-order one.

Suppose \(A_{i}^{0\sim q_{i}-1}\in R^{1\times q_{i}}\), \(i=1,2,\ldots ,n\) are a set of matrices which make \(\varPhi (A_{i}^{0\sim q_{i}-1})\in R^{q_{i}\times q_{i}}\), \(i=1,2,\ldots ,n\) stable, and

$$P_{i}\left( A_{i}^{0\sim q_{i}-1}\right) =\left[ \begin{array}{ccc} P_{iF}\left( A_{i}^{0\sim q_{i}-1}\right)&P_{iM}\left( A_{i}^{0\sim q_{i}-1}\right)&P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \end{array} \right] \in R^{q_{i}\times q_{i}}$$

is the unique positive definite solution to the Lyapunov equation:

$$\begin{aligned}&\varPhi ^{\text {T}}\left( A_{i}^{0\sim q_{i}-1}\right) P_{i}\left( A_{i}^{0\sim q_{i}-1}\right) \\&\quad +P_{i}\left( A_{i}^{0\sim q_{i}-1}\right) \varPhi \left( A_{i}^{0\sim q_{i}-1}\right) =-I_{q_{i}}, \end{aligned}$$
(16)

where \(P_{iF}\left( A_{i}^{0\sim q_{i}-1}\right) \in R^{q_{i}\times 1}\) and \(P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \in R^{q_{i}\times 1}\).

For the backstepping control method in this paper, the following first-order filter is introduced

$$l_{i}{\dot{{\bar{\alpha }}}}_{i}+{\bar{\alpha }}_{i}=\alpha _{i},\quad i=2,\ldots ,n,$$
(17)

where \({\bar{\alpha }}_{i}\) is the output, the backstepping virtual controller \(\alpha _{i}\) is the input, and \(l_{i}\) is a positive design parameter.

Let

$$\varpi _{i}={\bar{\alpha }}_{i}-\alpha _{i}$$
(18)

denotes the filter error. Then, it is easy to get

$$l_{i}G_{i}\left( \cdot \right) =l_{i}\dot{\varpi }_{i}+\varpi _{i},$$
(19)

where \(G_{i}\left( \cdot \right)\) represents the continuous function.

Step 1: Let

$$\xi _{1}^{\left( 0\sim q_{1}-1\right) }=x_{1}^{\left( 0\sim q_{1}-1\right) }-y_{\text {r}}^{\left( 0\sim q_{1}-1\right) }$$
(20)

and

$$\xi _{2}^{\left( 0\sim q_{2}-1\right) }=x_{2}^{\left( 0\sim q_{2}-1\right) }- {\bar{\alpha }}_{2}^{\left( 0\sim q_{2}-1\right) }.$$
(21)

(21) can be decomposed into

$$\xi _{2}=x_{2}-{\bar{\alpha }}_{2} ,$$
(22)

then the \(q_{1}\)th derivative of \(\xi _{1}\) is given by

$$\xi _{1}^{\left( q_{1}\right) }=f_{1}(x_{1}^{\left( 0\sim q_{1}-1\right) })+g_{1}(x_{1}^{\left( 0\sim q_{1}-1\right) })\left( \xi _{2}+\varpi _{2}+\alpha _{2}\right) -y_{\text {r}}^{\left( q_{1}\right) }.$$
(23)

Design the first virtual control \(\alpha _{2}\) as follows:

$$\begin{aligned}&\alpha _{2}=-g_{1}^{-1}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) \left( A_{1}^{0\sim q_{1}-1}\xi _{1}^{\left( 0\sim q_{1}-1\right) }\right. \\&\quad \left. +{\hat{\theta }} _{1}^{\text {T}}\varphi _{1}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) -y_{\text {r}}^{\left( q_{1}\right) }\right) . \end{aligned}$$
(24)

Substituting (24) into (23) gives

$$\begin{aligned} \xi _{1}^{\left( q_{1}\right) }= & {} -A_{1}^{0\sim q_{1}-1}\xi _{1}^{\left( 0\sim q_{1}-1\right) }+{\tilde{\theta }}_{1}^{\text {T}}\varphi _{1}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) +\varepsilon _{1} \\&\quad +g_{1}(x_{1}^{\left( 0\sim q_{1}-1\right) })\left( \xi _{2}+\varpi _{2}\right) . \end{aligned}$$
(25)

(25) can be further written as follows:

$${\dot{\xi }}_{1}^{\left( 0\sim q_{1}-1\right) }=\varPhi _{1}\left( A_{1}^{0\sim q_{1}-1}\right) \xi _{1}^{\left( 0\sim q_{1}-1\right) }+\left[ \begin{array}{c} 0 \\ b_{1} \end{array} \right] ,$$
(26)

where

$$b_{1}={\tilde{\theta }}_{1}^{\text {T}}\varphi _{1}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) +\varepsilon _{1}+g_{1}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) \left( \xi _{2}+\varpi _{2}\right) .$$
(27)

Select Lyapunov function candidate as follows:

$$V_{1}=\left( \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}P_{1}\left( A_{1}^{0\sim q_{1}-1}\right) \xi _{1}^{\left( 0\sim q_{1}-1\right) }+{\tilde{ \theta }}_{1}^{\text {T}}{\tilde{\theta }}_{1}.$$
(28)

Differentiating \(V_{1}\) with respect to time produces

$$\begin{aligned}&{\dot{V}}_{1} =\left( {\dot{\xi }}_{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}P_{1}\left( A_{1}^{0\sim q_{1}-1}\right) \xi _{1}^{\left( 0\sim q_{1}-1\right) } \\&\qquad +\left( \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}P_{1}\left( A_{1}^{0\sim q_{1}-1}\right) {\dot{\xi }}_{1}^{\left( 0\sim q_{1}-1\right) }-2 {\tilde{\theta }}_{1}^{\text {T}}{\dot{{\hat{\theta }}}}_{1} \\&\quad =\left( \varPhi _{1}\left( A_{1}^{0\sim q_{1}-1}\right) \xi _{1}^{\left( 0\sim q_{1}-1\right) }+\left[ \begin{array}{c} 0 \\ b_{1} \end{array} \right] \right) ^{\text {T}}P_{1}\left( A_{1}^{0\sim q_{1}-1}\right) \xi _{1}^{\left( 0\sim q_{1}-1\right) } \\&\qquad +\left( \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}P_{1}\left( A_{1}^{0\sim q_{1}-1}\right) \left( \varPhi _{1}\left( A_{1}^{0\sim q_{1}-1}\right) \xi _{1}^{\left( 0\sim q_{1}-1\right) }+\left[ \begin{array}{c} 0 \\ b_{1} \end{array} \right] \right) -2{\tilde{\theta }}_{1}^{\text {T}}{\dot{{\hat{\theta }}}}_{1} \\&\quad =\left( \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}\left( \varPhi _{1}^{\text {T}}\left( A_{1}^{0\sim q_{1}-1}\right) P_{1}\left( A_{1}^{0\sim q_{1}-1}\right) \right. \\&\qquad \left. +P_{1}\left( A_{1}^{0\sim q_{1}-1}\right) \varPhi _{1}\left( A_{1}^{0\sim q_{1}-1}\right) \right) \xi _{1}^{\left( 0\sim q_{1}-1\right) } \\&\qquad +2{\tilde{\theta }}_{1}^{\text {T}}\left( \left( \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) \varphi _{1}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) -{\dot{{\hat{\theta }}}}_{1}\right) \\&\qquad +2\left( \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) g_{1}(x_{1}^{\left( 0\sim q_{1}-1\right) })\left( \xi _{2}+\varpi _{2}\right) \\&\qquad +2\left( \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) \varepsilon _{1}. \end{aligned}$$
(29)

By designing the adaptive law

$${\dot{{\hat{\theta }}}}_{1}=\left( \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) \varphi _{1}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) -\gamma _{1}{\hat{\theta }}_{1}.$$
(30)

\({\dot{V}}_{1}\) can be transformed into

$$\begin{aligned}&{\dot{V}}_{1} =-\left\| \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right\| ^{2}+2\gamma _{1}{\tilde{\theta }}_{1}^{\text {T}}{\hat{\theta }}_{1}+2\left( \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) \varepsilon _{1} \\&\quad +2\left( \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) g_{1}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) \left( \xi _{2}+\varpi _{2}\right) . \end{aligned}$$
(31)

By using the following inequalities:

$$\begin{aligned}&2\left( \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) g_{1}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) \left( \xi _{2}+\varpi _{2}\right) \\&\quad \le \frac{1}{4}\left\| \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right\| ^{2}+8\left\| P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) \right\| ^{2}g_{1}^{2}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) \varpi _{2}^{2} \\&\qquad +8\left\| P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) \right\| ^{2}g_{1}^{2}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) \left\| \xi _{2}^{\left( 0\sim q_{2}-1\right) }\right\| ^{2} \end{aligned}$$
(32)
$$\begin{aligned}&\quad 2\left( \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right) ^{\text {T}}P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) \varepsilon _{1} \\&\quad \le \frac{1}{4}\left\| \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right\| ^{2}+4\left\| P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) \right\| ^{2}\varepsilon _{1}^{*2}. \end{aligned}$$
(33)

(31) becomes

$$\begin{aligned}&{\dot{V}}_{1} \le -\frac{1}{2}\left\| \xi _{1}^{\left( 0\sim q_{1}-1\right) }\right\| ^{2}+2\gamma _{1}{\tilde{\theta }}_{1}^{\text {T}}{\hat{\theta }} _{1}+8\left\| P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) \right\| ^{2}g_{1}^{2}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) \varpi _{2}^{2} \\&\quad +8\left\| P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) \right\| ^{2}g_{1}^{2}\left( x_{1}^{\left( 0\sim q_{1}-1\right) }\right) \left\| \xi _{2}^{\left( 0\sim q_{2}-1\right) }\right\| ^{2}+c_{1}, \end{aligned}$$
(34)

where

$$c_{1}=4\left\| P_{1L}\left( A_{1}^{0\sim q_{1}-1}\right) \right\| ^{2}\varepsilon _{1}^{*2}.$$

Step i: Let

$$\xi _{i}^{\left( 0\sim q_{i}-1\right) }=x_{i}^{\left( 0\sim q_{i}-1\right) }- {\bar{\alpha }}_{i}^{\left( 0\sim q_{i}-1\right) }$$
(35)

\(\xi _{i}^{\left( q_{i}-1\right) }\) can be written as follows:

$$\xi _{i}^{\left( q_{i}-1\right) }=x_{i}^{\left( q_{i}-1\right) }-{\bar{\alpha }} _{i}^{\left( q_{i}-1\right) }.$$
(36)

Differentiating (36) with respect to time, and using (1), yield

$$\xi _{i}^{\left( q_{i}\right) }=f_{i}(x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. )+g_{i}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) x_{i+1}-{\bar{\alpha }}_{i}^{\left( q_{i}\right) }.$$
(37)

Let

$$\xi _{i+1}^{\left( 0\sim q_{i+1}-1\right) }=x_{i+1}^{\left( 0\sim q_{i+1}-1\right) }-{\bar{\alpha }}_{i+1}^{\left( 0\sim q_{i+1}-1\right) }$$
(38)

which can be equivalently decomposed into

$$\xi _{i+1}=x_{i+1}-{\bar{\alpha }}_{i+1}.$$
(39)

Substituting (39) into (37) gives

$$\begin{aligned}&\xi _{i}^{\left( q_{i}\right) } =f_{i}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) -{\bar{\alpha }}_{i}^{\left( q_{i}\right) } \\&\quad +g_{i}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) \left( \xi _{i+1}+\varpi _{i+1}+\alpha _{i+1}\right) . \end{aligned}$$
(40)

By designing the virtual controller \(\alpha _{i+1}\) as follows:

$$\begin{aligned}&\alpha _{i+1} =-\left( g_{i}(x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. )\right) ^{-1}\left( A_{i}^{0\sim q_{i}-1}\xi _{i}^{\left( 0\sim q_{i}-1\right) }\right. \\&\quad \left. +{\hat{\theta }}_{i}^{\text {T}}\varphi \left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) -{\bar{\alpha }}_{i}^{\left( q_{i}\right) }\right) . \end{aligned}$$
(41)

\(\xi _{i}^{\left( q_{i}\right) }\) can be further transformed into the following equation:

$$\begin{aligned}&\xi _{i}^{\left( q_{i}\right) } =-A_{i}^{0\sim q_{i}-1}\xi _{i}^{\left( 0\sim q_{i}-1\right) }+{\tilde{\theta }}_{i}^{\text {T}}\varphi (x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. )+\varepsilon _{i} \\&\quad +g_{i}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) \left( \xi _{i+1}+\varpi _{i+1}\right) . \end{aligned}$$
(42)

Eq (42) can be further rewritten in the state-space form as follows:

$${\dot{\xi }}_{i}^{\left( 0\sim q_{i}-1\right) }=\varPhi _{i}\left( A_{i}^{0\sim q_{i}-1}\right) \xi _{i}^{\left( 0\sim q_{i}-1\right) }+\left[ \begin{array}{c} 0 \\ b_{i} \end{array} \right] ,$$
(43)

where

$$b_{i}={\tilde{\theta }}_{i}^{\text {T}}\varphi \left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) +\varepsilon _{i}+g_{i}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) \left( \xi _{i+1}+\varpi _{i+1}\right) .$$
(44)

Select Lyapunov function candidate as follows:

$$V_{i}=\left( \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}P_{i}\left( A_{i}^{0\sim q_{i}-1}\right) \xi _{i}^{\left( 0\sim q_{i}-1\right) }+\varpi _{i}^{2}+{\tilde{\theta }}_{i}^{\text {T}}{\tilde{\theta }}_{i}.$$
(45)

Taking the derivative of \(V_{i}\) yields

$$\begin{aligned}&{\dot{V}}_{i} =\left( {\dot{\xi }}_{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}P_{i}\left( A_{i}^{0\sim q_{i}-1}\right) \xi _{i}^{\left( 0\sim q_{i}-1\right) }+\left( \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}P_{i}\left( A_{i}^{0\sim q_{i}-1}\right) {\dot{\xi }}_{i}^{\left( 0\sim q_{i}-1\right) } \\&\qquad +2\varpi _{i}\dot{\varpi }_{i}-2{\tilde{\theta }}_{i}^{\text {T}}{\dot{{\hat{\theta }}}}_{i} \\&\quad =\left( \varPhi _{i}\left( A_{i}^{0\sim q_{i}-1}\right) \xi _{i}^{\left( 0\sim q_{i}-1\right) }+\left[ \begin{array}{c} 0 \\ b_{i} \end{array} \right] \right) ^{\text {T}}P_{i}\left( A_{i}^{0\sim q_{i}-1}\right) \xi _{i}^{\left( 0\sim q_{i}-1\right) } \\&\qquad +\left( \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}P_{i}\left( A_{i}^{0\sim q_{i}-1}\right) \left( \varPhi _{i}\left( A_{i}^{0\sim q_{i}-1}\right) \xi _{i}^{\left( 0\sim q_{i}-1\right) }+\left[ \begin{array}{c} 0 \\ b_{i} \end{array} \right] \right) \\&\qquad +2\varpi _{i}\left( G_{i}\left( \cdot \right) -\frac{\varpi _{i}}{l_{i}}\right) -2{\tilde{\theta }} _{i}^{\text {T}}{\dot{{\hat{\theta }}}}_{i} \\&\quad =\left( \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}\left( \varPhi _{i}^{\text {T}}\left( A_{i}^{0\sim q_{i}-1}\right) P_{i}\left( A_{i}^{0\sim q_{i}-1}\right) +P_{i}\left( A_{i}^{0\sim q_{i}-1}\right) \varPhi _{i}\left( A_{i}^{0\sim q_{i}-1}\right) \right) \xi _{i}^{\left( 0\sim q_{i}-1\right) } \\&\qquad +2{\tilde{\theta }}_{i}^{\text {T}}\left( \left( \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \varphi \left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) -{\dot{ {\hat{\theta }}}}_{i}\right) \\&\qquad +2\left( \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) g_{i}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) \left( \xi _{i+1}+\varpi _{i+1}\right) \\&\qquad +2\left( \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \varepsilon _{i}+2\varpi _{i}\left( G_{i}\left( \cdot \right) -\frac{ \varpi _{i}}{l_{i}}\right) . \end{aligned}$$
(46)

The adaptive law is designed as follows:

$${\dot{{\hat{\theta }}}}_{i}=\left( \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \varphi \left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) -\gamma _{i}{\hat{\theta }}_{i} .$$
(47)

Together with (47), (46) is given as follows:

$$\begin{aligned}&{\dot{V}}_{i} =-\left\| \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right\| ^{2}+2\gamma _{i}{\tilde{\theta }}_{i}^{\text {T}}{\hat{\theta }}_{i}+2\varpi _{i}\left( G_{i}\left( \cdot \right) -\frac{\varpi _{i}}{l_{i}}\right) \\&\quad +2\left( \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) g_{i}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) \left( \xi _{i+1}+\varpi _{i+1}\right) \\&\quad +2\left( \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \varepsilon _{i}. \end{aligned}$$
(48)

By using Yang’s inequality, the following inequalities hold:

$$\begin{aligned}&2\left( \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) g_{i}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) \left( \xi _{i+1}+\varpi _{i+1}\right) \\&\quad \le \frac{1}{4}\left\| \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right\| ^{2}+8\left\| P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \right\| ^{2}g_{i}^{2}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) \left\| \xi _{i+1}^{\left( 0\sim q_{i+1}-1\right) }\right\| ^{2} \\&\qquad +8\left\| P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \right\| ^{2}g_{i}^{2}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) \varpi _{i+1}^{2}, \end{aligned}$$
(49)
$$\begin{aligned}&\quad 2\left( \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right) ^{\text {T}}P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \varepsilon _{i} \\&\quad \le \frac{1}{4}\left\| \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right\| ^{2}+4\left\| P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \right\| ^{2}\varepsilon _{i}^{*2}, \end{aligned}$$
(50)
$$\begin{aligned}&\quad 2\varpi _{i}G_{i}\left( \cdot \right) \le \beta +\frac{G_{i}^{2}\left( \cdot \right) \varpi _{i}^{2}}{\beta }. \end{aligned}$$
(51)

Substituting (49)–(51) into (48) yields

$$\begin{aligned}&{\dot{V}}_{i} \le -\frac{1}{2}\left\| \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right\| ^{2}+2\gamma _{i}{\tilde{\theta }}_{i}^{\text {T}}{\hat{\theta }}_{i}-\left( \frac{2}{l_{i}}-\frac{G_{i}^{2}\left( \cdot \right) }{\beta }\right) \varpi _{i}^{2} \\&\quad +8\left\| P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \right\| ^{2}g_{i}^{2}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) \left\| \xi _{i+1}^{\left( 0\sim q_{i+1}-1\right) }\right\| ^{2} \\&\quad +8\left\| P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \right\| ^{2}g_{i}^{2}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i}\right. \right) \varpi _{i+1}^{2}+c_{i}, \end{aligned}$$
(52)

where

$$c_{i}=4\left\| P_{iL}\left( A_{i}^{0\sim q_{i}-1}\right) \right\| ^{2}\varepsilon _{i}^{*2}+\beta .$$
(53)

Step n: Similarly, let

$$\xi _{n}^{\left( 0\sim q_{n}-1\right) }=x_{n}^{\left( 0\sim q_{n}-1\right) }- {\bar{\alpha }}_{n}^{\left( 0\sim q_{n}-1\right) }$$
(54)

which gives

$$\xi _{n}^{\left( q_{n}-1\right) }=x_{n}^{\left( q_{n}-1\right) }-{\bar{\alpha }} _{n}^{\left( q_{n}-1\right) } .$$
(55)

From the system (1), taking the derivative of (55) yields

$$\begin{aligned}&\xi _{n}^{\left( q_{n}\right) } =f_{n}\left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. \right) +g_{n}\left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. \right) u \\&\quad +l\left( t-T_{0}\right) \nu \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) -{\bar{\alpha }}_{n}^{\left( q_{n}\right) }. \end{aligned}$$
(56)

By designing the actual controller

$$\begin{aligned}&u =-\left( g_{n}\left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. \right) \right) ^{-1}\left( A_{n}^{0\sim q_{n}-1}\xi _{n}^{\left( 0\sim q_{n}-1\right) }\right. \\&\quad \left. +{\hat{\theta }}_{n}^{\text {T}}\varphi \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u_{\text {f}}\right) -{\bar{\alpha }}_{n}^{\left( q_{n}\right) }\right), \end{aligned}$$
(57)

then the Eq. (56) can be converted to

$$\begin{aligned}&\xi _{n}^{\left( q_{n}\right) } =-A_{n}^{0\sim q_{n}-1}\xi _{n}^{\left( 0\sim q_{n}-1\right) }+f_{n}\left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. \right) \\&\quad -{\hat{\theta }}_{n}^{\text {T}}\varphi \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u_{\text {f}}\right) +l\left( t-T_{0}\right) \nu \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) . \end{aligned}$$
(58)

Then, it can be converted into a state-space form:

$${\dot{\xi }}_{n}^{\left( 0\sim q_{n}-1\right) }=\varPhi _{n}\left( A_{n}^{0\sim q_{n}-1}\right) \xi _{n}^{\left( 0\sim q_{n}-1\right) }+\left[ \begin{array}{c} 0 \\ b_{n} \end{array} \right] ,$$
(59)

where

$$\begin{aligned}&b_{n} =f_{n}\left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. \right) -{\hat{\theta }}_{n}^{\text {T}}\varphi \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u_{\text {f}}\right) \\&\quad +l\left( t-T_{0}\right) \nu \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) . \end{aligned}$$
(60)

Design the following Lyapunov function

$$V_{n}=\left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{n}\left( A_{n}^{0\sim q_{n}-1}\right) \xi _{n}^{\left( 0\sim q_{n}-1\right) }+\varpi _{n}^{2}+{\tilde{\theta }}_{n}^{\text {T}}{\tilde{\theta }}_{n}.$$
(61)

Differentiating \(V_{n}\) with respect to time produces

$$\begin{aligned}&{\dot{V}}_{n} =\left( {\dot{\xi }}_{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{n}\left( A_{n}^{0\sim q_{n}-1}\right) \xi _{n}^{\left( 0\sim q_{n}-1\right) }+\left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{n}\left( A_{n}^{0\sim q_{n}-1}\right) {\dot{\xi }}_{n}^{\left( 0\sim q_{n}-1\right) } \\&\qquad +2\varpi _{n}\dot{\varpi }_{n}-2{\tilde{\theta }}_{n}^{\text {T}}{\dot{{\hat{\theta }}}}_{n} \\&\quad =\left( \varPhi _{n}\left( A_{n}^{0\sim q_{n}-1}\right) \xi _{n}^{\left( 0\sim q_{n}-1\right) }+\left[ \begin{array}{c} 0 \\ b_{n} \end{array} \right] \right) ^{\text {T}}P_{n}\left( A_{n}^{0\sim q_{n}-1}\right) \xi _{n}^{\left( 0\sim q_{n}-1\right) } \\&\qquad +\left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{n}\left( A_{n}^{0\sim q_{n}-1}\right) \left( \varPhi _{n}\left( A_{n}^{0\sim q_{n}-1}\right) \xi _{n}^{\left( 0\sim q_{n}-1\right) }+\left[ \begin{array}{c} 0 \\ b_{n} \end{array} \right] \right) \\&\qquad +2\varpi _{n}\left( G_{n}\left( \cdot \right) -\frac{\varpi _{n}}{l_{n}}\right) -2{\tilde{\theta }} _{n}^{\text {T}}{\dot{{\hat{\theta }}}}_{n} \\&\quad =\left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}\left( \varPhi _{n}^{\text {T}}\left( A_{n}^{0\sim q_{n}-1}\right) P_{n}\left( A_{n}^{0\sim q_{n}-1}\right) +P_{n}\left( A_{n}^{0\sim q_{n}-1}\right) \varPhi _{n}\left( A_{n}^{0\sim q_{n}-1}\right) \right) \xi _{n}^{\left( 0\sim q_{n}-1\right) } \\&\qquad +2\left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{nL}\left( A_{n}^{0\sim q_{n}-1}\right) \left( f_{n}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. )\right. \\&\qquad \left. -{\hat{\theta }}_{n}^{\text {T}}\varphi \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u_{\text {f}}\right) +l\left( t-T_{0}\right) \nu \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) \right) \\&\qquad +2\varpi _{n}\left( G_{n}\left( \cdot \right) -\frac{\varpi _{n}}{l_{n}}\right) -2{\tilde{\theta }} _{n}^{\text {T}}{\dot{{\hat{\theta }}}}_{n}. \end{aligned}$$
(62)

By using Assumption 1 and Young’s inequality, one has

$$\begin{aligned}&2\left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{nL}\left( A_{n}^{0\sim q_{n}-1}\right) \left( f_{n}\left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. \right) \right. \\&\qquad \left. +l\left( t-T_{0}\right) \nu \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) \right) \\&\quad \le 2\left| \left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{nL}\left( A_{n}^{0\sim q_{n}-1}\right) \right| \left| \eta \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) \right| \\&\quad \le \frac{1}{a}\left( \left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{nL}\left( A_{n}^{0\sim q_{n}-1}\right) \right) ^{2}\eta ^{2}\left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) +a \\&\quad =2\left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{nL}\left( A_{n}^{0\sim q_{n}-1}\right) {\bar{\eta }}\left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) +a, \end{aligned}$$
(63)

where

$$\begin{aligned}&{\bar{\eta }}\left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) \\&\quad =\frac{1}{2a}\left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{nL}\left( A_{n}^{0\sim q_{n}-1}\right) \eta ^{2}\left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) . \end{aligned}$$
(64)

Define the approximation error as follows:

$$\varepsilon _{n}={\bar{\eta }}\left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u\right) -\theta _{n}^{\text {T}}\varphi \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u_{\text {f}}\right) ,$$
(65)

where \(\left| \varepsilon _{n}\right| \le \varepsilon _{n}^{*}\) , \(\varepsilon _{n}^{*}\) being a positive constant, \(u_{\text {f}}\) is the output of filtered signal

$$u_{\text {f}}=H_{\text {L}}\left( s\right) u\approx u$$
(66)

and \(H_{\text {L}}\left( s\right)\) is the Butterworth low-pass filter. Then, (62) is expressed as follows:

$$\begin{aligned}&{\dot{V}}_{n} \le -\left\| \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right\| ^{2}+2\varpi _{n}\left( G_{n}\left( \cdot \right) -\frac{\varpi _{n}}{l_{n}}\right) \\&\quad +2{\tilde{\theta }}_{n}^{\text {T}}\left( \left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{nL}\left( A_{n}^{0\sim q_{n}-1}\right) \varphi \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u_{\text {f}}\right) - {\dot{{\hat{\theta }}}}_{n}\right) \\&\quad +2\left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{nL}\left( A_{n}^{0\sim q_{n}-1}\right) \varepsilon _{n}+a. \end{aligned}$$
(67)

It is true that

$$\begin{aligned}&2\left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{nL}\left( A_{n}^{0\sim q_{n}-1}\right) \varepsilon _{n} \\&\quad \le \frac{1}{2}\left\| \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right\| ^{2}+2\left\| P_{nL}\left( A_{n}^{0\sim q_{n}-1}\right) \right\| ^{2}\varepsilon _{n}^{*2}, \end{aligned}$$
(68)
$$\begin{aligned}&2\varpi _{n}G_{n}\left( \cdot \right) \le \beta +\frac{G_{n}^{2}\left( \cdot \right) \varpi _{n}^{2}}{\beta }. \end{aligned}$$
(69)

By designing the adaptive law

$${\dot{{\hat{\theta }}}}_{n}=\left( \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right) ^{\text {T}}P_{nL}\left( A_{n}^{0\sim q_{n}-1}\right) \varphi \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim n}\right. ,u_{\text {f}}\right) -\gamma _{n}{\hat{\theta }}_{n}$$
(70)

and according to (68) and (69), \({\dot{V}}_{n}\) can be obtained as follows:

$${\dot{V}}_{n}\le -\frac{1}{2}\left\| \xi _{n}^{\left( 0\sim q_{n}-1\right) }\right\| ^{2}+2\gamma _{n}{\tilde{\theta }}_{n}^{\text {T}}{\hat{\theta }}_{n}-\left( \frac{2}{l_{n}}-\frac{G_{n}^{2}\left( \cdot \right) }{\beta }\right) \varpi _{n}^{2}+c_{n},$$
(71)

where

$$c_{n}=2\left\| P_{nL}\left( A_{n}^{0\sim q_{n}-1}\right) \right\| ^{2}\varepsilon _{n}^{*2}+a+\beta .$$

4 Stability Analysis

So far, according to fully actuated system approach, the adaptive tracking FTC has been completed for high-order nonlinear SFS with non-affine nonlinear faults. Then, a theorem can be summarized as follows.

Theorem 1

Consider the fuzzy adaptive tracking control of high-order nonlinear SFS with non-affine nonlinear faults (1), composed of the virtual controllers (24) and (41), the actual controllers (57) and adaptive laws (30), (47), and (70), if there exist the positive design parameters \(\gamma _{i}\) and \(l_{i}\) satisfy \(\frac{1}{2} -\eta _{i}>0\) and \(\frac{2}{l_{i}}-\frac{G_{i}^{2}}{\beta }-\delta _{i}>0\), then all the signals in the closed-loop system are bounded, and the satisfactory tracking control performance is achieved.

Proof

Select the whole Lyapunov function V as follows:

$$V=\sum _{i=1}^{n}V_{i}.$$
(72)

According to the inequalities (34), (52) and (71), the derivative of V can be given as follows:

$$\begin{aligned} {\dot{V}}\le & {} -\sum _{i=1}^{n}\left( \frac{1}{2}-\eta _{i}\right) \left\| \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right\| ^{2}+2\sum _{i=1}^{n}\gamma _{i}{\tilde{\theta }}_{i}^{\text {T}}{\hat{\theta }}_{i} \\&\quad -\sum _{i=2}^{n}\left( \frac{2}{l_{i}}-\frac{G_{i}^{2}\left( \cdot \right) }{\beta }-\delta _{i}\right) \varpi _{i}^{2}+c_{0}, \end{aligned}$$
(73)

where \(c_{0}=\sum _{i=1}^{n}c_{i}\), \(\eta _{1}=0\),

$$\begin{aligned}&\eta _{i}=8\left\| P_{i-1,L}\left( A_{i-1}^{0\sim q_{i-1}-1}\right) \right\| ^{2}g_{i-1}^{2}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i-1}\right. \right) ,\quad i=2,\ldots ,n,\\&\delta _{i}=8\left\| P_{i-1,L}\left( A_{i-1}^{0\sim q_{i-1}-1}\right) \right\| ^{2}g_{i-1}^{2}\left( x_{j}^{\left( 0\sim q_{j}-1\right) }\left| _{j=1\sim i-1}\right. \right) ,\quad i=2,\ldots ,n. \end{aligned}$$

and \(G_{i}\left( \cdot \right)\) satisfy the inequalities \(|G_{i}\left( \cdot \right) | \le {\bar{G}}_{i}\) with \({\bar{G}}_{i}\) being some positive constants. \(\square\)

Based on Young’s inequality, one has

$${\tilde{\theta }}_{i}^{\text {T}}{\hat{\theta }}_{i}={\tilde{\theta }}_{i}^{\text {T}}\left( \theta _{i}-{\tilde{\theta }}_{i}\right) ={\tilde{\theta }}_{i}^{\text {T}}\theta _{i}-{\tilde{ \theta }}_{i}^{\text {T}}{\tilde{\theta }}_{i}\le -\frac{1}{2}{\tilde{\theta }}_{i}^{\text {T}} {\tilde{\theta }}_{i}+\frac{1}{2}\theta _{i}^{\text {T}}\theta _{i}.$$
(74)

Substituting (74) into (73) gives

$$\begin{aligned}&{\dot{V}} \le -\sum _{i=1}^{n}\left( \frac{1}{2}-\eta _{i}\right) \left\| \xi _{i}^{\left( 0\sim q_{i}-1\right) }\right\| ^{2}-\sum _{i=1}^{n}\gamma _{i}{\tilde{\theta }}_{i}^{\text {T}}{\tilde{\theta }}_{i} \\&\qquad -\sum _{i=2}^{n}\left( \frac{2}{l_{i}}-\frac{{\bar{G}}_{i}^{2}}{\beta }-\delta _{i}\right) \varpi _{i}^{2}+\sum _{i=1}^{n}\gamma _{i}\theta _{i}^{\text {T}}\theta _{i}+c_{0} \\&\quad \le -bV+c, \end{aligned}$$
(75)

where \(c=\sum _{i=1}^{n}\gamma _{i}\theta _{i}^{\text {T}}\theta _{i}+c_{0}\)and \(b=\min \left\{ \frac{1}{2}-\eta _{i},\gamma _{i},\frac{2}{l_{i}}-\frac{ {\bar{G}}_{i}^{2}}{\beta }-\delta _{i}\right\}\).

5 Simulation Example

In order to illustrate the effectiveness of the proposed control approach, a numerical example is considered in the following

$${\left\{ \begin{array}{ll} {\ddot{x}}_{1}=f_{1}(x_{1}^{\left( 0\sim 2\right) })+g_{1}(x_{1}^{\left( 0\sim 2\right) })x_{2}, \\ {\ddot{x}}_{2}=f_{2}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim 2}\right. )+g_{2}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim 2}\right. )u+l\left( t-T_{0}\right) \nu \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim 2}\right. ,u\right) , \\ y=x_{1}, \end{array}\right. }$$
(76)

where \(f_{1}(x_{1}^{\left( 0\sim 2\right) })=\sin ({\dot{x}} _{1}){\text {e}}^{-x_{1}^{4}}\), \(f_{2}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim 2}\right. )={\dot{x}}_{2}{\text {e}}^{0.5x_{1}{\dot{x}}_{1}}+{\dot{x}}_{1}\sin \left( x_{1}x_{2}\right)\), \(g_{1}(x_{1}^{\left( 0\sim 2\right) })=2+\sin (x_{1}{\dot{x}}_{1})\), \(g_{2}(x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim 2}\right. )=3+0.5\cos (x_{1}{\dot{x}}_{1})\sin (x_{2}{\dot{x}}_{1})\). Select the fault function as \(\nu \left( x_{i}^{\left( 0\sim q_{i}-1\right) }\left| _{i=1\sim 2}\right. ,u\right) =15(x_{1}{\dot{x}}_{1}x_{2}{\dot{x}} _{2}+\sin (u))+15\), and the time profile of fault as follows:

$$l\left( t-T_{0}\right) =\left\{ \begin{array}{ll} 0,&{} t<T_{0}, \\ 1-{\text {e}}^{-\delta \left( t-T_{0}\right) },&{} t\ge T_{0}, \end{array} \right.$$

where \(\delta =8\) and \(T_{0}=10\) s. The Butterworth low-pass filter is chosen as \(H_{\text {L}}(s)=\frac{1}{s^{2}+1.414s+1}\), and the reference signal is chosen as \(y_{\text {r}}=\sin (t)\).

Choose

$$\begin{aligned}&F_{1}=\left[ \begin{array}{cc} -6 &{} 1 \\ 0 &{} -6 \end{array} \right] ,\quad F_{2}=\left[ \begin{array}{cc} -5 &{} -1 \\ 1 &{} -5 \end{array} \right] ,\\&Z_{1}=\left[ \begin{array}{cc} 1&0 \end{array} \right] ,\quad Z_{2}=\left[ \begin{array}{cc} 1&1 \end{array} \right] \end{aligned}$$

by Proposition 1, we have

$$\begin{aligned}&V_{1}=\left[ \begin{array}{c} Z_{1} \\ Z_{1}F_{1} \end{array} \right] =\left[ \begin{array}{cc} 1 &{} 0 \\ -6 &{} 1 \end{array} \right] ,\\&V_{2}=\left[ \begin{array}{c} Z_{2} \\ Z_{2}F_{2} \end{array} \right] =\left[ \begin{array}{cc} 1 &{} 1 \\ -4 &{} -6 \end{array} \right] \end{aligned}$$

and

$$\begin{aligned}&A_{1}^{0\thicksim 2}=-Z_{1}F_{1}^{2}V_{1}^{-1}=\left[ \begin{array}{cc} 36&12 \end{array} \right] ,\\&A_{2}^{0\thicksim 2}=-Z_{2}F_{2}^{2}V_{2}^{-1}=\left[ \begin{array}{cc} 26&10 \end{array} \right] . \end{aligned}$$

Select the initial values as \(x_{1}\left( 0\right) =x_{2}\left( 0\right) =0\) and \(\theta _{1}^{\text {T}}\left( 0\right) =\theta _{2}^{\text {T}}\left( 0\right) =\left[ 0,0,0,0,0,0,0\right]\), and choose the design parameters as \(\gamma _{1}=\gamma _{2}=60\) and \(l_{2}=0.01\).

Fig. 1
figure 1

Tracking performance trajectories

Full size image
Fig. 2
figure 2

States trajectories

Full size image
Fig. 3
figure 3

Trajectory of control signal u

Full size image
Fig. 4
figure 4

Trajectories of Norm of adaptive laws estimation \(||{\hat{\theta }}_{1}||\) and \(||{\hat{\theta }}_{2}||\)

Full size image
Fig. 5
figure 5

Trajectories of the filter’s input \(\alpha _{2}\) and output \({\bar{\alpha }}_{2}\)

Full size image

By using the proposed fuzzy adaptive tracking control approach of high-order nonlinear SFS with non-affine nonlinear faults, the simulation results are given in Figs. 1. 2, 3, 4, and 5. The tracking trajectories are displayed in Fig. 1. From Fig. 1, it is clearly seen that the proposed control method in this paper has satisfactory tracking control performance. The states trajectories are shown in Fig. 2. Figure 3 shows the response of the adaptive fuzzy tracking controller. The norm of adaptive laws estimation are shown in Fig. 4. The input and output of first-order filter are shown in Fig. 5. Figures 1, 2, 3, 4, and 5 show that the stability of the high-order nonlinear SFS is guaranteed by using the proposed fuzzy adaptive tracking control method. Besides, the tracking control performance is achieved.

6 Conclusion

An novel adaptive fuzzy FTC method has been investigated for high-order nonlinear SFS with non-affine nonlinear fault. The fuzzy logic systems can be used as approximators of unknown nonlinear functions in the system. There was no need to convert a high-order system to first-order one, the controllers have been designed directly for the high-order system, and the control performance can be achieved. In the further, our research scope will be extended to the cooperative control of high-order nonlinear multi-agent systems by using the fully actuated system approach.