1 Introduction

Signal models are often encountered in scientific disciplines and engineering applications. The parameter estimation of signal models is very important, and then many estimation approaches have been presented [32, 41, 42]. As an original way, Fourier analysis plays a key role in signal processing [48, 50]. However, there are certain limitations because the frequencies of the Fourier transform are just a collection of the individual frequencies of the periodic signals. Another classical method is the phase-locked loop technique, which automatically adjusts the frequency by locking the phase between the reference and the internal sine waves. Additionally, a self-correlation phase method [4] has been developed to estimate the frequencies. The parameter estimation methods can be applied to many areas [2, 3, 5, 51].

Many methods can estimate the parameters of the signal models. For example, Stoica et al. [37] used the weighted least squares method to estimate the amplitudes of the sinusoidal signals. The amplitude and frequency of a sine signal were estimated with the property of global convergence in [20]. The amplitude and frequency estimation problem of multiple sine signals was investigated based on the adaptive identifier [21]. Recently, Hou [22] has presented a solution for estimating parameters of a biased multiple sinusoids using a combination of a frequency identifier and gradient algorithms. This paper is devoted to identify the parameters for dual-frequency signals, including the unknown amplitudes, frequencies, and phases.

The iterative methods play an important role not only in finding the solutions of nonlinear matrix equations, but also in deriving parameter estimation algorithms for signal models. Combining with some optimization tools, the iterative methods can be applied to estimate the parameters of the nonlinear systems [9, 34]. For example, Xu [40] derived a Newton iterative algorithm for the parameter estimation of dynamical systems. Ding et al. [12] studied the iterative parameter identification for pseudo-linear systems with ARMA noise using the filtering technique.

As a classical optimization tool, the Newton method is a root-finding algorithm that utilizes the first few terms of the Taylor series of a function in the neighborhood of a suspected root. For a long time, the Newton method has received a great deal of attention, and there have been lots of applications in many fields, such as the minimization and maximization problems, the transcendental equations, the numerical verification for the solutions of nonlinear equations [30, 35, 49].

The previous work in [29, 43] considered the Newton iterative (NI) algorithm for the nonlinear parameter estimation problems. The NI algorithm possesses high parameter estimation accuracy, while the computational cost is large for the reason that the inverse of the Hessian matrix needs to be computed at each iteration, and its components are second-order derivatives. In order to reduce the computational cost, this paper presents a hierarchical least squares and gradient-based iterative (HI) algorithm using the parameter decomposition. The key is to decompose the parameter vector into three parts and to estimate the parameters of each part, so the dimension of the parameter vector is reduced and the computational efficiency and the parameter estimation accuracy are improved.

The rest of this paper is organized as follows. Sections 2 and 3 derive two iterative algorithms based on the gradient search and the Newton search, respectively. Section 4 provides a HI algorithm. Section 5 gives two numerical examples to illustrate the effectiveness of the proposed algorithms. Finally, some conclusions are drawn in Sect. 6.

2 The Gradient-Based Iterative Algorithm

The sine and cosine signals are typical periodic signals, whose waveforms are the sine and cosine curves in mathematics. Many complex signals can be decomposed into numerous sinusoidal signals with different frequencies and amplitudes by the Fourier series [1]. The sine signal differs from the cosine signal by \(\pi /2\) in the initial phase. This paper derives the parameter estimation algorithms for the dual-frequency cosine signals, which can be applied to the sine signals.

Consider the following dual-frequency cosine signal model:

$$\begin{aligned} y(t)=a\cos (\omega _1 t+\phi )+b\cos (\omega _2 t+\psi )+v(t), \end{aligned}$$
(1)

where \(a>0\) and \(b>0\) are the amplitudes, \(\omega _1>0\) and \(\omega _2>0\) are the angular frequencies, \(\phi \) and \(\psi \) are the initial phases, t is a continuous-time variable, y(t) is the observations, and v(t) is a stochastic disturbance with zero mean and variance \(\sigma ^2\).

The actual signals are always interfered with various stochastic noises. In practical engineering, we can only get the discrete observed data. Suppose that the sampled data are \(y(t_i)\), \(i=1,2,3,\ldots ,L\), where \(t_i\) is the sampled time and L denotes the data length.

Use the observed data \(y(t_i)\) and the model output to construct the criterion function

$$\begin{aligned} J_1({\varvec{\theta }}):=\frac{1}{2}\sum ^L_{i=1}\left[ y(t_i)-a\cos (\omega _1t_i+\phi )-b\cos (\omega _2t_i+\psi )\right] ^2. \end{aligned}$$

The criterion function represents the square sum of the errors between the model outputs and the observed data. It is desired that this criterion function is as small as possible, which is equivalent to minimizing \(J_1({\varvec{\theta }})\) and obtaining the estimates of the parameter vector \({\varvec{\theta }}:=[a,b,\omega _1,\omega _2,\phi ,\psi ]^{\tiny \text{ T }}\in {{\mathbb {R}}}^6\).

Letting the partial derivative of \(J_1({\varvec{\theta }})\) with respect to \({\varvec{\theta }}\) gives

$$\begin{aligned} \mathrm{grad}[J_1({\varvec{\theta }})]:= & {} \frac{\partial J_1({\varvec{\theta }})}{\partial {\varvec{\theta }}}\\= & {} \left[ \frac{\partial J_1({\varvec{\theta }})}{\partial a},\frac{\partial {J_1({\varvec{\theta }})}}{\partial b},\frac{\partial J_1({\varvec{\theta }})}{\partial \omega _1},\frac{\partial J_1({\varvec{\theta }})}{\partial \omega _2},\frac{\partial J_1({\varvec{\theta }})}{\partial {\phi }},\frac{\partial J_1({\varvec{\theta }})}{\partial {\psi }}\right] ^{\tiny \text{ T }}\in {{\mathbb {R}}}^6. \end{aligned}$$

Define the stacked observed data \({\varvec{Y}}(L)\) and the stacked information matrix \({\varvec{\varPhi }}({\varvec{\theta }},L)\) as

$$\begin{aligned} {\varvec{Y}}(L):= & {} [y(t_1),y(t_2),\ldots ,y(t_L)]^{\tiny \text{ T }}\in {{\mathbb {R}}}^L,\\ {\varvec{\varPhi }}({\varvec{\theta }},L):= & {} [{\varvec{\varphi }}({\varvec{\theta }},t_1),{\varvec{\varphi }}({\varvec{\theta }},t_2),\ldots ,{\varvec{\varphi }}({\varvec{\theta }},t_L)]^{\tiny \text{ T }}\in {{\mathbb {R}}}^{L\times 6}. \end{aligned}$$

Define the information vector

$$\begin{aligned} {\varvec{\varphi }}({\varvec{\theta }},t_i):= & {} [-\cos (\omega _1t_i+\phi ),-\cos (\omega _2t_i+\psi ),at_i\sin (\omega _1t_i+\phi ),bt_i\sin (\omega _2t_i+\psi ),\\&a\sin (\omega _1t_i+\phi ),\, b\sin (\omega _2t_i+\psi )]^{\tiny \text{ T }}\in {{\mathbb {R}}}^6. \end{aligned}$$

Let \(f(t_i):=a\cos (\omega _1t_i+\phi )+b\cos (\omega _2t_i+\psi )\in {{\mathbb {R}}}\), and the stacked model output vector

$$\begin{aligned} {\varvec{F}}({\varvec{\theta }},L):=\left[ \begin{array}{c} f({\varvec{\theta }},t_1) \\ f({\varvec{\theta }},t_2) \\ \vdots \\ f({\varvec{\theta }},t_L) \end{array}\right] \in {{\mathbb {R}}}^L. \end{aligned}$$

Then, the gradient vector can be expressed as

$$\begin{aligned} \mathrm{grad}[J_1({\varvec{\theta }})]:={\varvec{\varPhi }}^{\tiny \text{ T }}({\varvec{\theta }},L)[{\varvec{Y}}(L)-{\varvec{F}}({\varvec{\theta }},L)]. \end{aligned}$$

Let \(k=1,2,3,\ldots \) be an iterative variable and \({\hat{{\varvec{\theta }}}}_k\) be the estimate of \({\varvec{\theta }}\) at iteration k. The partial derivatives at \({\varvec{\theta }}={\hat{{\varvec{\theta }}}}_{k-1}\) are given by

$$\begin{aligned} \frac{\partial J_1\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) }{\partial a}= & {} -\sum ^L_{i=1}\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) w\left( {\hat{{\varvec{\theta }}}}_{k-1},t_i\right) ,\\ \frac{\partial J_1\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) }{\partial b}= & {} -\sum ^L_{i=1}\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) w\left( {\hat{{\varvec{\theta }}}}_{k-1},t_i\right) ,\\ \frac{\partial J_1\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) }{\partial \omega _1}= & {} \sum ^L_{i=1}{\hat{a}}_{k-1}t_i\sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) w\left( {\hat{{\varvec{\theta }}}}_{k-1},t_i\right) ,\\ \frac{\partial J_1\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) }{\partial \omega _2}= & {} \sum ^L_{i=1}{\hat{b}}_{k-1}t_i\sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) w\left( {\hat{{\varvec{\theta }}}}_{k-1},t_i\right) ,\\ \frac{\partial J_1\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) }{\partial \phi }= & {} \sum ^L_{i=1}{\hat{a}}_{k-1}\sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) w\left( {\hat{{\varvec{\theta }}}}_{k-1},t_i\right) ,\\ \frac{\partial J_1\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) }{\partial \psi }= & {} \sum ^L_{i=1}{\hat{b}}_{k-1}\sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) w\left( {\hat{{\varvec{\theta }}}}_{k-1},t_i\right) ,\\ w\left( {\hat{{\varvec{\theta }}}}_{k-1},t_i\right):= & {} y\left( t_i\right) -{\hat{a}}_{k-1}\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) -{\hat{b}}_{k-1}\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) . \end{aligned}$$

Minimizing \(J_1({\varvec{\theta }})\) and selecting an iterative step size \(\mu _k\geqslant 0\), we can get the gradient-based iterative (GI) algorithm for dual-frequency signal models:

$$\begin{aligned} {\hat{{\varvec{\theta }}}}_k= & {} {\hat{{\varvec{\theta }}}}_{k-1}-\mu _k\mathrm{grad}\left[ J_1\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) \right] \nonumber \\= & {} {\hat{{\varvec{\theta }}}}_{k-1}-\mu _k{\varvec{\varPhi }}^{\tiny \text{ T }}\left( {\hat{{\varvec{\theta }}}}_{k-1},L\right) \left[ {\varvec{Y}}\left( L\right) -{\varvec{F}}\left( {\hat{{\varvec{\theta }}}}_{k-1},L\right) \right] ,\end{aligned}$$
(2)
$$\begin{aligned} {\varvec{Y}}\left( L\right)= & {} \left[ y\left( t_1\right) ,y\left( t_2\right) ,\ldots ,y\left( t_L\right) \right] ^{\tiny \text{ T }},\end{aligned}$$
(3)
$$\begin{aligned} {\varvec{\varPhi }}\left( {\hat{{\varvec{\theta }}}}_{k-1},L\right)= & {} \left[ {\varvec{\varphi }}\left( {\hat{{\varvec{\theta }}}}_{k-1},t_1\right) ,{\varvec{\varphi }}\left( {\hat{{\varvec{\theta }}}}_{k-1},t_2\right) ,\ldots ,{\varvec{\varphi }}\left( {\hat{{\varvec{\theta }}}}_{k-1},t_L\right) \right] ^{\tiny \text{ T }},\end{aligned}$$
(4)
$$\begin{aligned} {\varvec{F}}\left( {\hat{{\varvec{\theta }}}}_{k-1},L\right)= & {} \left[ f\left( {\hat{{\varvec{\theta }}}}_{k-1},t_1\right) ,f\left( {\hat{{\varvec{\theta }}}}_{k-1},t_2\right) ,\ldots ,f\left( {\hat{{\varvec{\theta }}}}_{k-1},t_L\right) \right] ^{\tiny \text{ T }},\end{aligned}$$
(5)
$$\begin{aligned} {\varvec{\varphi }}\left( {\hat{{\varvec{\theta }}}}_{k-1},t_i\right)= & {} \left[ -\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) ,-\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) ,\right. \nonumber \\&{\hat{a}}_{k-1}t_i\sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) ,\nonumber \\&{\hat{b}}_{k-1}t_i\sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) ,{\hat{a}}_{k-1}\sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) ,\nonumber \\&\left. {\hat{b}}_{k-1}\sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \right] ^{\tiny \text{ T }},\end{aligned}$$
(6)
$$\begin{aligned} f\left( {\hat{{\varvec{\theta }}}}_{k-1},t_i\right)= & {} {\hat{a}}_{k-1}\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) +{\hat{b}}_{k-1}\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) ,\end{aligned}$$
(7)
$$\begin{aligned} \mu _k= & {} \arg \min J_1\left( {\hat{{\varvec{\theta }}}}_{k-1}-\mu \mathrm{grad}\left[ J_1\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) \right] \right) ,\end{aligned}$$
(8)
$$\begin{aligned} {\hat{{\varvec{\theta }}}}_k= & {} \left[ {\hat{a}}_k,{\hat{b}}_k,{\hat{\omega }}_{1,k},{\hat{\omega }}_{2,k},{\hat{\phi }}_k,{\hat{\psi }}_k\right] ^{\tiny \text{ T }}. \end{aligned}$$
(9)

\(\mu _k\leqslant \lambda _{\max }^{-1}[{\varvec{\varPhi }}^{\tiny \text{ T }}({\hat{{\varvec{\theta }}}}_{k-1},L){\varvec{\varPhi }}({\hat{{\varvec{\theta }}}}_{k-1},L)]\), where the \(\lambda _{\max }[{\varvec{\varPhi }}^{\tiny \text{ T }}({\hat{{\varvec{\theta }}}}_{k-1},L){\varvec{\varPhi }}({\hat{{\varvec{\theta }}}}_{k-1},L)]\) denotes the maximum eigenvalue of the matrix \([{\varvec{\varPhi }}^{\tiny \text{ T }}({\hat{{\varvec{\theta }}}}_{k-1},L){\varvec{\varPhi }}({\hat{{\varvec{\theta }}}}_{k-1},L)]\). The procedure of the GI algorithm in (2)–(9) for dual-frequency signals is as follows.

  1. 1.

    Let \(k=1\), give a small number \(\varepsilon \) and an integer L, set the initial value \({\hat{{\varvec{\theta }}}}_0=\mathbf{1}_6/p_0\), where \(p_0\) is generally taken as a large positive number, for example, \(p_0=10^6\).

  2. 2.

    Collect the observed data \(y(t_i)\) and \(u(t_i)\), \(i=1,2,\ldots ,L\), form \({\varvec{Y}}(L)\) by (3).

  3. 3.

    Form the information vector \({\varvec{\varphi }}({\hat{{\varvec{\theta }}}}_{k-1},t_i)\) by (6) and the stacked information matrix \({\varvec{\varPhi }}({\hat{{\varvec{\theta }}}}_{k-1},L)\) by (4).

  4. 4.

    Form \(f({\hat{{\varvec{\theta }}}}_{k-1},t_i)\) by (7) and the stacked model output vector \({\varvec{F}}({\hat{{\varvec{\theta }}}}_{k-1},L)\) by (5).

  5. 5.

    Select a largest \(\mu _k\) satisfying (8), and update the estimate \({\hat{{\varvec{\theta }}}}_k\) by (9).

  6. 6.

    Compare \({\hat{{\varvec{\theta }}}}_k\) with \({\hat{{\varvec{\theta }}}}_{k-1}\), if \(\Vert {\hat{{\varvec{\theta }}}}_k-{\hat{{\varvec{\theta }}}}_{k-1}\Vert \geqslant \varepsilon \), then increase k by 1 and go to Step 3; otherwise, obtain the iterative time k and the estimate \({\hat{{\varvec{\theta }}}}_k\) and terminate this procedure.

Remark 1

In fact, the one-dimensional search for finding the best step size \(\mu _k\) needs to solve a complicated nonlinear equation at each iteration, so we cannot obtain the algebraic solution for computing \(\mu _k\) by Eq. (8). To figure out this problem, we can use the cut-and-try method or the Newton iterative method to acquire the approximation. In what follows, we derive a Newton iterative algorithm for estimating the parameters.

3 The Newton Iterative Algorithm

The gradient method requires the first derivative, but the Newton method is quadratically convergent. In order to improve the parameter estimation accuracy, calculating the second partial derivative of the criterion function \(J_1({\varvec{\theta }})\) with respect to \({\varvec{\theta }}\) gives the Hessian matrix

$$\begin{aligned} {\varvec{H}}({\varvec{\theta }}):= & {} \frac{\partial ^2J_1({\varvec{\theta }})}{\partial {\varvec{\theta }}\partial {\varvec{\theta }}^{\tiny \text{ T }}}=\frac{\partial \mathrm{grad}[J_1({\varvec{\theta }})]}{\partial {\varvec{\theta }}^{\tiny \text{ T }}}= \left[ \begin{array}{cccccc} h_{11}({\varvec{\theta }}) &{} h_{12}({\varvec{\theta }}) &{} \cdots &{} h_{16}({\varvec{\theta }})\\ h_{21}({\varvec{\theta }}) &{} h_{22}({\varvec{\theta }}) &{} \cdots &{} h_{26}({\varvec{\theta }})\\ \vdots &{} \vdots &{} &{}\vdots \\ h_{61}({\varvec{\theta }}) &{} h_{62}({\varvec{\theta }}) &{} \cdots &{}h_{66}({\varvec{\theta }}) \end{array}\right] \in {{\mathbb {R}}}^{6\times 6},\\ h_{11}({\varvec{\theta }})= & {} \frac{\partial ^2J_1({\varvec{\theta }})}{\partial a^2} =\sum ^L_{i=1}\cos ^2(\omega _1t_i+\phi ),\\ h_{12}({\varvec{\theta }})= & {} \frac{\partial ^2J_1({\varvec{\theta }})}{\partial a\partial b} =\sum ^L_{i=1}\cos (\omega _1t_i+\phi )\cos (\omega _2t_i+\psi ),\\ h_{13}({\varvec{\theta }})= & {} \frac{\partial ^2J_1({\varvec{\theta }})}{\partial a\partial \omega _1} =\sum ^L_{i=1}t_i\sin (\omega _1t_i+\phi )[y(t_i)-b\cos (\omega _2t_i+\psi )]\\&-\,at_i\sin (2\omega _1t_i+2\phi ),\\ h_{14}({\varvec{\theta }})= & {} \frac{\partial ^2J_1({\varvec{\theta }})}{\partial a\partial \omega _2} =-\sum ^L_{i=1}bt_i\cos (\omega _1t_i+\phi )\sin (\omega _2t_i+\psi ),\\ h_{15}({\varvec{\theta }})= & {} \frac{\partial ^2J_1({\varvec{\theta }})}{\partial a\partial \phi } =\sum ^L_{i=1}\sin (\omega _1t_i+\phi )[y(t_i)-b\cos (\omega _2t_i+\psi )]-\sin (2\omega _1t_i{+}2\phi ),\\ h_{16}({\varvec{\theta }})= & {} \frac{\partial ^2J_1({\varvec{\theta }})}{\partial a\partial \psi } =-\sum ^L_{i=1}b\cos (\omega _1t_i+\phi )\sin (\omega _2t_i+\psi ). \end{aligned}$$

For the sake of brevity, the derivation results of all \(h_{mn}\), \(1=n<m\leqslant 6\) are not listed here, and the rest are presented in (10)–(39). Let \({\hat{{\varvec{\theta }}}}_k:=[{\hat{a}}_k,{\hat{b}}_k,{\hat{\omega }}_{1,k},{\hat{\omega }}_{2,k},{{\hat{\phi }}}_k,{{\hat{\psi }}}_k]^{\tiny \text{ T }}\) be the estimate of \({\varvec{\theta }}\) at iteration k. Based on the Newton search, we can derive the Newton iterative (NI) algorithm for dual-frequency signal models:

$$\begin{aligned} {\hat{{\varvec{\theta }}}}_k= & {} {\hat{{\varvec{\theta }}}}_{k-1}-{\varvec{H}}^{-1}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) \mathrm{grad}\left[ J_1\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) \right] ,\end{aligned}$$
(10)
$$\begin{aligned} {\varvec{Y}}\left( L\right)= & {} \left[ y\left( t_1\right) ,y\left( t_2\right) ,\ldots ,y\left( t_L\right) \right] ^{\tiny \text{ T }},\end{aligned}$$
(11)
$$\begin{aligned} {\hat{{\varvec{\varPhi }}}}_k= & {} {\varvec{\varPhi }}\left( {\hat{{\varvec{\theta }}}}_{k-1},L\right) =\left[ {\varvec{\varphi }}\left( {\hat{{\varvec{\theta }}}}_{k-1},t_1\right) ,{\varvec{\varphi }}\left( {\hat{{\varvec{\theta }}}}_{k-1},t_2\right) ,\ldots ,{\varvec{\varphi }}\left( {\hat{{\varvec{\theta }}}}_{k-1},t_L\right) \right] ^{\tiny \text{ T }},\end{aligned}$$
(12)
$$\begin{aligned} {\hat{{\varvec{F}}}}_k= & {} {\varvec{F}}\left( {\hat{{\varvec{\theta }}}}_{k-1},L\right) =\left[ f\left( {\hat{{\varvec{\theta }}}}_{k-1},t_1\right) ,f\left( {\hat{{\varvec{\theta }}}}_{k-1},t_2\right) ,\ldots ,f\left( {\hat{{\varvec{\theta }}}}_{k-1},t_L\right) \right] ^{\tiny \text{ T }}, \end{aligned}$$
(13)
$$\begin{aligned} {\hat{{\varvec{\varphi }}}}_k\left( t_i\right)= & {} {\varvec{\varphi }}\left( {\hat{{\varvec{\theta }}}}_{k-1},t_i\right) \nonumber \\= & {} \left[ -\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) ,-\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) ,\right. \nonumber \\&{\hat{a}}_{k-1}t_i\sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) ,\nonumber \\&{\hat{b}}_{k-1}t_i\sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) ,{\hat{a}}_{k-1}\sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) ,\nonumber \\&\left. {\hat{b}}_{k-1}\sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \right] ^{\tiny \text{ T }}, \end{aligned}$$
(14)
$$\begin{aligned} {\hat{f}}_k\left( t_i\right)= & {} f\left( {\hat{{\varvec{\theta }}}}_{k-1},t_i\right) \nonumber \\= & {} {\hat{a}}_{k-1}\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) +{\hat{b}}_{k-1}\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(15)
$$\begin{aligned} {\varvec{H}}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \left[ \begin{array}{ccccc} h_{11}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) &{} h_{12}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) &{} \cdots &{} h_{16}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) \\ h_{21}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) &{} h_{22}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) &{} \cdots &{} h_{26}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) \\ \vdots &{} \vdots &{} &{} \vdots \\ h_{61}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) &{} h_{62}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) &{} \cdots &{} h_{66}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) \end{array}\right] ,\end{aligned}$$
(16)
$$\begin{aligned} h_{11}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}\cos ^2\left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) , \end{aligned}$$
(17)
$$\begin{aligned} h_{12}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(18)
$$\begin{aligned} h_{13}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}t_i\sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \left[ y\left( t_i\right) -{\hat{b}}_{k-1}\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \right] \nonumber \\&-\,{\hat{a}}_{k-1}t_i\sin \left( 2{\hat{\omega }}_{1,k-1}t_i+2{\hat{\phi }}_{k-1}\right) , \end{aligned}$$
(19)
$$\begin{aligned} h_{14}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} -\sum ^L_{i=1}{\hat{b}}_{k-1}t_i\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(20)
$$\begin{aligned} h_{15}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}\sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \left[ y\left( t_i\right) -{\hat{b}}_{k-1}\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \right] \nonumber \\&-\,\sin \left( 2{\hat{\omega }}_{1,k-1}t_i+2{\hat{\phi }}_{k-1}\right) , \end{aligned}$$
(21)
$$\begin{aligned} h_{16}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} -\sum ^L_{i=1}{\hat{b}}_{k-1}\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(22)
$$\begin{aligned} h_{22}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}\cos ^2\left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(23)
$$\begin{aligned} h_{23}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} -\sum ^L_{i=1}{\hat{a}}_{k-1}t_i\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) , \end{aligned}$$
(24)
$$\begin{aligned} h_{24}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}t_i\sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \left[ y\left( t_i\right) -{\hat{a}}_{k-1}\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \right] \nonumber \\&-\,{\hat{b}}_{k-1}t_i\sin \left( 2{\hat{\omega }}_{2,k-1}t_i+2{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(25)
$$\begin{aligned} h_{25}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} -\sum ^L_{i=1}{\hat{a}}_{k-1}\sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(26)
$$\begin{aligned} h_{26}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}\sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \left[ y\left( t_i\right) -{\hat{a}}_{k-1}\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \right] \nonumber \\&-\,\sin \left( 2{\hat{\omega }}_{2,k-1}t_i+2{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(27)
$$\begin{aligned} h_{33}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}-{\hat{a}}_{k-1}{\hat{b}}_{k-1}t_i^2\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \nonumber \\&+\,{\hat{a}}_{k-1}t_i^2y\left( t_i\right) \cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \nonumber \\&-\,{\hat{a}}_{k-1}^2t_i^2\cos \left( 2{\hat{\omega }}_{1,k-1}t_i+2{\hat{\phi }}_{k-1}\right) , \end{aligned}$$
(28)
$$\begin{aligned} h_{34}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}{\hat{a}}_{k-1}{\hat{b}}_{k-1}t_i^2\sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(29)
$$\begin{aligned} h_{35}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}-{\hat{a}}_{k-1}{\hat{b}}_{k-1}t_i\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \nonumber \\&+\,{\hat{a}}_{k-1}t_i\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) y\left( t_i\right) \nonumber \\&-\,{\hat{a}}_{k-1}^2t_i\cos \left( 2{\hat{\omega }}_{1,k-1}t_i+2{\hat{\phi }}_{k-1}\right) , \end{aligned}$$
(30)
$$\begin{aligned} h_{36}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}{\hat{a}}_{k-1}{\hat{b}}_{k-1}t_i\sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(31)
$$\begin{aligned} h_{44}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}-{\hat{a}}_{k-1}{\hat{b}}_{k-1}t_i^2\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \nonumber \\&-\,{\hat{b}}_{k-1}^2t_i^2\cos \left( 2{\hat{\omega }}_{2,k-1}t_i+2{\hat{\psi }}_{k-1}\right) \nonumber \\&+\,{\hat{b}}_{k-1}t_i^2\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) y\left( t_i\right) , \end{aligned}$$
(32)
$$\begin{aligned} h_{45}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}{\hat{a}}_{k-1}{\hat{b}}_{k-1}t_i\sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) , \end{aligned}$$
(33)
$$\begin{aligned} h_{46}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}-{\hat{a}}_{k-1}{\hat{b}}_{k-1}t_i\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \nonumber \\&+\,{\hat{b}}_{k-1}t_i\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) y\left( t_i\right) \nonumber \\&-\,{\hat{b}}_{k-1}^2t_i\cos \left( 2{\hat{\omega }}_{2,k-1}t_i+2{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(34)
$$\begin{aligned} h_{55}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}-{\hat{a}}_{k-1}{\hat{b}}_{k-1}\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \nonumber \\&+\,{\hat{a}}_{k-1}\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) y\left( t_i\right) -{\hat{a}}_{k-1}^2\cos \left( 2{\hat{\omega }}_{1,k-1}t_i+2{\hat{\phi }}_{k-1}\right) , \end{aligned}$$
(35)
$$\begin{aligned} h_{56}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}{\hat{a}}_{k-1}{\hat{b}}_{k-1}\sin \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \sin \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(36)
$$\begin{aligned} h_{66}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} \sum ^L_{i=1}-{\hat{a}}_{k-1}{\hat{b}}_{k-1}\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) \nonumber \\&+\,{\hat{b}}_{k-1}\cos \left( {\hat{\omega }}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) y\left( t_i\right) -{\hat{b}}_{k-1}^2\cos \left( 2{\hat{\omega }}_{2,k-1}t_i+2{\hat{\psi }}_{k-1}\right) , \end{aligned}$$
(37)
$$\begin{aligned} h_{mn}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right)= & {} h_{nm}\left( {\hat{{\varvec{\theta }}}}_{k-1}\right) ,\quad 1=n<m\leqslant 6,\end{aligned}$$
(38)
$$\begin{aligned} {\hat{{\varvec{\theta }}}}_k= & {} \left[ {\hat{a}}_k,{\hat{b}}_k,{\hat{\omega }}_{1,k},{\hat{\omega }}_{2,k},{\hat{\phi }}_k,{\hat{\psi }}_k\right] ^{\tiny \text{ T }}. \end{aligned}$$
(39)

The steps of the NI algorithm for computing \({\hat{{\varvec{\theta }}}}_k\) are listed as follows.

  1. 1.

    To initialize, let \(k=1\), \({\hat{{\varvec{\theta }}}}_0=\mathbf{1}_6/p_0\), and give a small number \(\varepsilon \).

  2. 2.

    Collect the observed data \(y(t_i)\) and \(u(t_i)\), \(i=1,2,\ldots ,L\), form \({\varvec{Y}}(L)\) by (11).

  3. 3.

    Form the information vector \({\hat{{\varvec{\varphi }}}}_k(t_i)\) using (14), the stacked information matrix \({\hat{{\varvec{\varPhi }}}}_k\) using (12).

  4. 4.

    Form \({\hat{f}}_k(t_i)\) using (15) and the stacked model output vector \({\hat{{\varvec{F}}}}_k\) using (13).

  5. 5.

    Compute \(h_{mn}({\hat{{\varvec{\theta }}}}_{k-1})\) by (17)–(38), \(1=n<m\leqslant 6\), form the Hessian matrix \({\varvec{H}}({\hat{{\varvec{\theta }}}}_{k-1})\) by (16).

  6. 6.

    Update the estimate \({\hat{{\varvec{\theta }}}}_k\) by (39).

  7. 7.

    Compare \({\hat{{\varvec{\theta }}}}_k\) with \({\hat{{\varvec{\theta }}}}_{k-1}\), if \(\Vert {\hat{{\varvec{\theta }}}}_k-{\hat{{\varvec{\theta }}}}_{k-1}\Vert >\varepsilon \), then increase k by 1, and go to Step 3; otherwise, obtain the estimate \({\hat{{\varvec{\theta }}}}_k\) and terminate this procedure.

Remark 2

The NI algorithm is an effective parameter estimation algorithm; however, it must calculate the inverse of the Hessian matrix at each iteration, which requires much computational cost. The following will derive a hierarchical least squares and gradient-based iterative algorithm, which not only ameliorates the estimation accuracy but also improves the computational efficiency.

4 The Hierarchical Iterative Algorithm

Inspired initially by the hierarchical control for large-scale systems based on the decomposition–coordination principle, we derive a hierarchical identification algorithm for the parameter estimation problem in this paper. According to the parameter decomposition, the original optimization problem is transformed into a combination of the nonlinear optimization and the linear optimization. In this way, the computational complexity is reduced greatly. The hierarchical method can be devoted to signal processing [44, 47], nonlinear systems [26, 31, 52,53,54], and other fields [10, 11, 25].

Define three parameter vectors \({\varvec{{\alpha }}}:=[a,b]^{\tiny \text{ T }}\in {{\mathbb {R}}}^2\), \({\varvec{\omega }}:=[\omega _1,\omega _2]^{\tiny \text{ T }}\in {{\mathbb {R}}}^2\) and \({\varvec{\beta }}:=[\phi ,\psi ]^{\tiny \text{ T }}\in {{\mathbb {R}}}^2\). The information vector with respect to \({\varvec{{\alpha }}}\) can be written as

$$\begin{aligned} {\varvec{\varphi }}_{\alpha }(t_i)=[-\cos (\omega _1t_i+\phi ),-\cos (\omega _2t_i+\psi )]^{\tiny \text{ T }}\in {{\mathbb {R}}}^2. \end{aligned}$$

Define the information matrix with respect to \({\varvec{{\alpha }}}\) as

$$\begin{aligned} {\varvec{\varPhi }}_{\alpha }(L):=[{\varvec{\varphi }}_{\alpha }(t_1),{\varvec{\varphi }}_{\alpha }(t_2),\ldots , {\varvec{\varphi }}_{\alpha }(t_L)]^{\tiny \text{ T }}\in {{\mathbb {R}}}^{2\times L}. \end{aligned}$$

Define three criterion functions:

$$\begin{aligned} J_2({\varvec{{\alpha }}}):= & {} \frac{1}{2}\Vert {\varvec{Y}}(L)-{\varvec{\varPhi }}_{\alpha }(L){\varvec{{\alpha }}}\Vert ^2,\\ J_3({\varvec{\omega }}):= & {} \frac{1}{2}\sum ^L_{i=1}e^2({\varvec{\omega }},t_i),\\ J_4({\varvec{\beta }}):= & {} \frac{1}{2}\sum ^L_{i=1}e^2({\varvec{\beta }},t_i), \end{aligned}$$

where \(e({\varvec{\omega }},t_i)\)=\(e({\varvec{\beta }},t_i)\):=\(y(t_i)-a\cos (\omega _1t_i+\phi )-b\cos (\omega _2t_i+\psi )\). Letting the first-order derivative of \(J_2({\varvec{{\alpha }}})\) with respect to \({\varvec{{\alpha }}}\) be zero, we have

$$\begin{aligned} \frac{\partial J_2({\varvec{{\alpha }}})}{\partial {\varvec{{\alpha }}}}=-{\varvec{\varPhi }}^{\tiny \text{ T }}_{\alpha }(L)[{\varvec{Y}}(L)-{\varvec{\varPhi }}_{\alpha }(L){\varvec{{\alpha }}}]=\mathbf{0}. \end{aligned}$$

The least squares (LS) solution is given by

$$\begin{aligned} {\varvec{{\alpha }}}=[{\varvec{\varPhi }}^{\tiny \text{ T }}_{\alpha }(L){\varvec{\varPhi }}_{\alpha }(L)]^{-1}{\varvec{\varPhi }}_{\alpha }(L){\varvec{Y}}(L). \end{aligned}$$
(40)

Unfortunately, there are the unknown terms \(\omega _1\), \(\omega _2\), \(\phi \), and \(\psi \) in \({\varvec{\varPhi }}_{\alpha }(L)\). The parameter estimates cannot be obtained.

Taking the first-order derivative of \(J_3({\varvec{\omega }})\) with respect to \({\varvec{\omega }}\) gives

$$\begin{aligned} \mathrm{grad}[J_3({\varvec{\omega }})]=\frac{\partial J_3({\varvec{\omega }})}{\partial {\varvec{\omega }}}=\left[ \frac{\partial J_3({\varvec{\omega }})}{\partial \omega _1},\frac{\partial J_3({\varvec{\omega }})}{\partial \omega _2}\right] ^{\tiny \text{ T }}\in {{\mathbb {R}}}^2. \end{aligned}$$

Taking the first-order derivative of \(J_3({\varvec{\beta }})\) with respect to \({\varvec{\beta }}\) gives

$$\begin{aligned} \mathrm{grad}[J_4({\varvec{\beta }})]=\frac{\partial J_4({\varvec{\beta }})}{\partial {\varvec{\beta }}}=\left[ \frac{\partial J_4({\varvec{\beta }})}{\partial \phi },\frac{\partial J_4({\varvec{\beta }})}{\partial \psi }\right] ^{\tiny \text{ T }}\in {{\mathbb {R}}}^2. \end{aligned}$$

Let \({\hat{{\varvec{\omega }}}}_k:=[{\hat{\omega }}_{1,k},{\hat{\omega }}_{2,k}]^{\tiny \text{ T }}\) be the estimate of \({\varvec{\omega }}\) at iteration k and \({\hat{{\varvec{\beta }}}}_k:=[{\hat{\phi }}_k,{\hat{\psi }}_k]^{\tiny \text{ T }}\in {{\mathbb {R}}}^2\) be the estimate of \({\varvec{\beta }}\) at iteration k. The gradient-based iterative (GI) algorithm for estimating the parameter vector \({\varvec{\omega }}\) is given as follows:

$$\begin{aligned} {\hat{{\varvec{\omega }}}}_k= & {} {\hat{{\varvec{\omega }}}}_{k-1}-\nu _k\mathrm{grad}[J_3({\hat{{\varvec{\omega }}}}_{k-1})],\nonumber \\ \mathrm{grad}[J_3({\hat{{\varvec{\omega }}}}_{k-1})]= & {} \left[ \frac{\partial J_3({\hat{{\varvec{\omega }}}}_{k-1})}{\partial \omega _1},\frac{\partial J_3({\hat{{\varvec{\omega }}}}_{k-1})}{\partial \omega _2}\right] ^{\tiny \text{ T }}\in {{\mathbb {R}}}^2. \end{aligned}$$
(41)

and the GI parameter estimation algorithm for estimating the parameter vector \({\varvec{\beta }}\) is given as follows:

$$\begin{aligned} {\hat{{\varvec{\beta }}}}_k= & {} {\hat{{\varvec{\beta }}}}_{k-1}-\lambda _k\mathrm{grad}[J_4({\hat{{\varvec{\beta }}}}_{k-1})],\nonumber \\ \mathrm{grad}[J_4({\hat{{\varvec{\beta }}}}_{k-1})]= & {} \left[ \frac{\partial J_4({\hat{{\varvec{\beta }}}}_{k-1})}{\partial \phi },\frac{\partial J_4({\hat{{\varvec{\beta }}}}_{k-1})}{\partial \psi }\right] ^{\tiny \text{ T }}\in {{\mathbb {R}}}^2, \end{aligned}$$
(42)

where two step sizes \(\nu _k\) and \(\lambda _k\) can be determined by using the one-dimensional search. Here, we replace the unknown parameter vectors \({\varvec{{\alpha }}}\), \({\varvec{\omega }}\), and \({\varvec{\beta }}\) in (40), (41), and (42) with their previous estimates and obtain the hierarchical least squares and gradient-based iterative (HI) algorithm for the dual-frequency signals:

$$\begin{aligned} {\hat{{\varvec{{\alpha }}}}}_k= & {} \left[ {\hat{{\varvec{\varPhi }}}}^{\tiny \text{ T }}_{\alpha ,k-1}\left( L\right) {\hat{{\varvec{\varPhi }}}}_{\alpha ,k-1}\left( L\right) \right] ^{-1}{\hat{{\varvec{\varPhi }}}}_{\alpha ,k-1}\left( L\right) {\varvec{Y}},\end{aligned}$$
(43)
$$\begin{aligned} {\hat{{\varvec{\omega }}}}_k= & {} {\hat{{\varvec{\omega }}}}_{k-1}-\nu _k\mathrm{grad}[J_3\left( {\hat{{\varvec{\omega }}}}_{k-1}\right) ],\end{aligned}$$
(44)
$$\begin{aligned} {\hat{{\varvec{\beta }}}}_k= & {} {\hat{{\varvec{\beta }}}}_{k-1}-\lambda _k\mathrm{grad}[J_4\left( {\hat{{\varvec{\beta }}}}_{k-1}\right) ],\end{aligned}$$
(45)
$$\begin{aligned} {\varvec{Y}}\left( L\right)= & {} [y\left( t_1\right) ,y\left( t_2\right) ,\ldots ,y\left( t_L\right) ]^{\tiny \text{ T }},\end{aligned}$$
(46)
$$\begin{aligned} {\hat{{\varvec{\varPhi }}}}_{\alpha ,k-1}\left( L\right)= & {} \left[ {\hat{{\varvec{\varphi }}}}_{\alpha ,k-1}\left( t_1\right) ,{\hat{{\varvec{\varphi }}}}_{\alpha ,k-1}\left( t_2\right) ,\ldots ,{\hat{{\varvec{\varphi }}}}_{\alpha ,k-1}\left( t_L\right) \right] ^{\tiny \text{ T }},\end{aligned}$$
(47)
$$\begin{aligned} {\hat{{\varvec{\varphi }}}}_{\alpha ,k-1}\left( t_i\right)= & {} \left[ -\cos \left( {\hat{\omega }}_{1,k-1}t_i+{\hat{\phi }}_{k-1}\right) ,-\cos \left( {{\hat{\omega }}}_{2,k-1}t_i+{\hat{\psi }}_{k-1}\right) \right] ^{\tiny \text{ T }},\qquad \end{aligned}$$
(48)
$$\begin{aligned} \mathrm{grad}\left[ J_3\left( {\hat{{\varvec{\omega }}}}_{k-1}\right) \right]= & {} \left[ \frac{\partial J_3\left( {\hat{{\varvec{\omega }}}}_{k-1}\right) }{\partial \omega _1},\frac{\partial J_3\left( {\hat{{\varvec{\omega }}}}_{k-1}\right) }{\partial \omega _2}\right] ^{\tiny \text{ T }},\end{aligned}$$
(49)
$$\begin{aligned} \nu _k= & {} \arg \min J_3\left( {\hat{{\varvec{\omega }}}}_{k-1}-\nu \mathrm{grad}[J_3\left( {\hat{{\varvec{\omega }}}}_{k-1}\right) ]\right) ,\end{aligned}$$
(50)
$$\begin{aligned} \mathrm{grad}\left[ J_4\left( {\hat{{\varvec{\beta }}}}_{k-1}\right) \right]= & {} \left[ \frac{\partial J_4\left( {\hat{{\varvec{\beta }}}}_{k-1}\right) }{\partial \phi },\frac{\partial J_4\left( {\hat{{\varvec{\beta }}}}_{k-1}\right) }{\partial \psi }\right] ^{\tiny \text{ T }},\end{aligned}$$
(51)
$$\begin{aligned} \lambda _k= & {} \arg \min J_4\left( {\hat{{\varvec{\beta }}}}_{k-1}-\lambda \mathrm{grad}\left[ J_4\left( {\hat{{\varvec{\beta }}}}_{k-1}\right) \right] \right) ,\end{aligned}$$
(52)
$$\begin{aligned} {\hat{{\varvec{\theta }}}}_k= & {} \left[ {\hat{{\varvec{{\alpha }}}}}^{\tiny \text{ T }}_k,{\hat{{\varvec{\omega }}}}^{\tiny \text{ T }}_k,{\hat{{\varvec{\beta }}}}^{\tiny \text{ T }}_k\right] ^{\tiny \text{ T }}. \end{aligned}$$
(53)

The steps of the HI algorithm in (43)–(53) for dual-frequency signals are as follows.

  1. 1.

    To initialize, let \(k=1\), \({\hat{{\varvec{{\alpha }}}}}_0=\mathbf{1}_2/p_0\), let \({\hat{{\varvec{\omega }}}}_0\) and \({\hat{{\varvec{\beta }}}}_0\) be small real number vectors, give a small number \(\varepsilon \).

  2. 2.

    Collect the observed data \(y(t_i)\) and \(u(t_i)\), \(i=1,2,\ldots ,L\), and form \({\varvec{Y}}(L)\) by (46).

  3. 3.

    Form the information vector \({\hat{{\varvec{\varphi }}}}_{\alpha ,k-1}(t_i)\) using (48) and the stacked information matrix \({\hat{{\varvec{\varPhi }}}}_{\alpha ,k-1}(L)\) using (47).

  4. 4.

    Compute \(\frac{\partial J_3({\hat{{\varvec{\omega }}}}_{k-1})}{\partial \omega _i}\), \(i=1,2\), using (49) and form \(\mathrm{grad}[J_3(\hat{\varvec{\omega }}_{k-1})]\).

  5. 5.

    Compute \(\frac{\partial J_4(\hat{\varvec{\beta }}_{k-1})}{\partial \phi }\), \(\frac{\partial J_4(\hat{\varvec{\beta }}_{k-1})}{\partial \psi }\) using (51) and form \(\mathrm{grad}[J_4({\hat{{\varvec{\beta }}}}_{k-1})]\).

  6. 6.

    Select the step sizes \(\nu _k\) by (50) and \(\lambda _k\) by (52).

  7. 7.

    Update the estimate \({\hat{{\varvec{{\alpha }}}}}_k\) by (43), update the estimate \({\hat{{\varvec{\omega }}}}_k\) by (44), and update the estimate \({\hat{{\varvec{\beta }}}}_k\) using (45). Form \({\hat{{\varvec{\theta }}}}_k\) using (53).

  8. 8.

    If \(\Vert {\hat{{\varvec{\theta }}}}_k-{\hat{{\varvec{\theta }}}}_{k-1}\Vert >\varepsilon \), then increase k by 1, and go to Step 3; otherwise, obtain the estimate \({\hat{{\varvec{\theta }}}}_k\) and terminate this procedure.

Fig. 1
figure 1

NI and GI estimation errors \(\delta \) versus k

Full size image

5 Examples

Example 1

Consider the following dual-frequency cosine signal model:

$$\begin{aligned} y(t)=1.48\cos (0.2t+2\pi /15)+2.25\cos (0.55t+\pi /4)+v(t). \end{aligned}$$

The parameter vector to be estimated is

$$\begin{aligned} {\varvec{\theta }}=[a, b, \omega _1, \omega _2, \phi , \psi ]^{\tiny \text{ T }}=[1.48, 2.25, 0.20, 0.55, 2\pi /15, \pi /4]^{\tiny \text{ T }}. \end{aligned}$$

In simulation, the white noise signal v(t) with variance \(\sigma ^2=1.00^2\) is added to the cosine combination signal. Set the sampling period \(T=0.01\,{\hbox {s}}\), \(t=nT\), \(n=1,2,3,\ldots \), let the iterative time \(k=500\), the data length \(L=2000\). Apply the GI algorithm and the NI algorithm to estimate the parameter vector \({\varvec{\theta }}\). The parameter estimation errors \(\delta :=\Vert {\hat{{\varvec{\theta }}}}_k-{\varvec{\theta }}\Vert /\Vert {\varvec{\theta }}\Vert \times 100\%\) versus k are illustrated in Fig. 1, and the parameter estimates and their estimation errors are exhibited in Table 1.

Table 1 GI and the NI estimates and errors
Full size table
Fig. 2
figure 2

Measured data \(y(t_i)\) (\(\sigma ^2=1.00^2\))

Full size image

From the comparison of the GI algorithm and the NI algorithm, we can draw the following conclusions:

  • The parameter estimation errors obtained by the GI algorithm and the NI algorithm gradually decrease as iteration k increases.

  • The NI parameter estimates approach their true values only in the dozens of iterations.

  • Table 1 and Fig. 1 show that the NI algorithm has more accurate parameter estimates than those of the GI algorithm under the same condition.

Example 2

Consider the signal model in Example 1. In this simulation, the sampling period is 0.1s and the iterative time \(k=100\); v(t) is the noise with zero mean and variances \(\sigma ^2=0.50^2\) and \(\sigma ^2=1.00^2\), respectively. The distribution of the measured data is shown in Fig. 2.

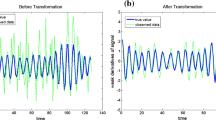
Apply the HI algorithm in (43)–(53) to estimate the parameter vectors \({\varvec{{\alpha }}}\), \({\varvec{\omega }}\), and \({\varvec{\beta }}\) of the dual-frequency signal model. The parameter estimates and errors \(\delta \) are shown in Table 2 and Fig. 3. In order to test the effectiveness of the estimated signal, the actual signal and its estimates are drawn in Fig. 4, where the solid line denotes the actual signal and the dot line denotes its estimates.

Table 2 HI estimates and errors
Full size table
Fig. 3
figure 3

HI estimation errors \(\delta \) versus k

Full size image
Fig. 4
figure 4

Actual signal and its estimates (\(\sigma ^2=1.00^2\))

Full size image

From Fig. 3, we can see that the parameter estimation errors \(\delta \) obtained by the HI algorithm become small with k increasing. As the noise levels decrease, the HI algorithm can give more accurate parameter estimates; see the parameter estimation errors in the last column in Table 2 and the error curves in Fig. 3.

6 Conclusions

This paper presents a hierarchical least squares and gradient-based iterative algorithm to estimate all parameters of dual-frequency signal models from the observed data. The simulation results indicate that the proposed algorithm can improve the parameter estimation accuracy and reduce the computational burden. Similarly, the idea can be extended to estimate the parameters of multi-frequency signals and applied to signal detection and reconstruction, as well as in signal processing. The proposed algorithms in this paper can combine other methods such as the neural network methods [8, 27] and the kernel methods [16, 24] to study parameter identification of different systems [6, 7, 13,14,15, 18, 19, 23, 28, 38, 45, 58] and can be applied to other fields [17, 33, 36, 39, 46, 55,56,57].