1 Introduction

The frequency estimation of multi-sinusoidal signals in additive noise can be easily applied in diverse areas, such as the direction estimation of arrival narrowed sources signals, power supply systems, speech, radar, and sonar signal processing, and biomedical engineering [6, 14, 17, 19, 26, 28]. Given white additive noise, a variety of approaches have been proposed for the frequency estimation problem, and they demonstrate differences in the estimation accuracy and computational complexity. These approaches include fast Fourier transform (FFT), modified iteration scheme algorithm, characteristic polynomial-based methods, and subspace-based methods [4, 5, 15, 17, 18, 26, 27, 29]. The colored additive noise is frequently encountered in practice [10, 22]. Computational methods developed for this scenario include higher-order statistics [7, 22, 23], prefiltering-based ESPRIT [10], and parametric least square estimator [11,12,13, 24]. The least squares (LS) method [2, 3, 20] is the most widely used among these methods, because it is simple and does not require significant prior knowledge in signal statistics. However, just as most of the existing state-of-the-art methods, the LS algorithm suffers from middle or low signal-to-noise ratio (SNR).

The multi-sinusoidal signals generally contain a parsimonious structure with a small number of unit norm sinusoids. Therefore, the sparse representation theory is commonly used in the frequency estimation of multi-sinusoidal signals to obtain the best sparse approximation of the observed signals. For efficient implementation, the orthogonal matching pursuit (OMP) algorithm is a greedy algorithm that iteratively identifies the sinusoidal atom that yields the greatest improvement in approximation quality in the dictionary. The dictionary is generally designed by discretizing the frequency parameter using a grid. When the frequency is roughly discretized, the size of the dictionary will be small, and OMP becomes computationally attractive for identifying the best atom at each iteration. However, it is more likely that the true underlying frequencies lie outside a rougher grid. This is called the “basis mismatch” or “off-grid” effect, which significantly comprises the reconstructing performance. More recent methods, such as gradient basis local search and Newton-basis cyclic refinement [16], have been developed to alleviate the problem.

To enhance the robustness of frequency estimation given noisy signals, this paper introduces the weighted LS optimization with a penalized term of the weak derivation (WD). Mathematically, WD generalizes the concept of derivative for non-differentiable functions. WD has the ability to suppress the noises. The LS criterion is a commonly used criterion which minimizes the sum of the squared residuals between the observed and the fitted values. However, the LS method ignores the connections among the data points, especially for the time series signals. The individual data points are connected with each other through the derivatives of the time-continuous function. Ignoring the connection information may easily lead to overfitting. Therefore, the usage of derivatives has been studied in some system identification tasks [1, 21], and WD has been successfully utilized in the identification of nonlinear dynamic systems and has achieved more accurate approximation [8]. Thus, to some extent, WD can prevent overfitting caused by the LS optimization and can suppress the noise. This proposed LS + WD optimization model is solved by a modified OMP algorithm. In addition, a novel multi-grid dictionary learning (MGDL) strategy is applied to alleviate the possible basis mismatch effect. Each MGDL iteration ranks the atoms by the OMP and then inserts new samples around the frequency vectors corresponding to the top atoms. The proposed method is validated using simulated data with both white and colored noises at different SNRs. Compared to state-of-the-art algorithms, the proposed algorithm can obtain more accurate estimation with higher computational efficiency.

2 Background

2.1 LS Frequency Estimation for Multi-sinusoidal Signals Model

We use \( y(n) \) to denote the observed p-component multi-sinusoidal signal, which is modeled as

$$ y(n) = \sum\limits_{i = 1}^{p} {x_{i}^{ls} \sin (\omega_{i} nt_{s} ) + e(n),\quad n = 1, \ldots ,N,} $$
(1)

where the parameters \( x_{i}^{ls} \) and \( \omega_{i} \) are, respectively, the amplitude and frequency of the i-th component, \( t_{s} \) is the sampling period,\( e(n) \) denotes the additive noise process and \( N \) is the number of samples.

Let

$$ {\mathbf{g}}_{i} = [\begin{array}{*{20}c} {\sin (\omega_{i} \cdot t_{s} )} & {\sin (\omega_{i} \cdot 2t_{s} )} & \cdots & {\sin (\omega_{i} \cdot Nt_{s} )} \\ \end{array} ]^{\text{T}} , $$
(2)

then the LS frequency estimation can be achieved by minimizing the following loss function

$$ \mathop {\hbox{min} }\limits_{{{\mathbf{x}},{\varvec{\upomega}}}} J_{\text{LS}} = \left\| {{\mathbf{y}} - \sum\limits_{i = 1}^{p} {x_{i}^{ls} {\mathbf{g}}_{i} } } \right\|_{2}^{2} , $$
(3)

where \( {\mathbf{y}} = [\begin{array}{*{20}c} {y(1)} & {y(2)} & \cdots & {y(N)} \\ \end{array} ]^{\text{T}} \).

2.2 Weak Derivation

Let \( z \) be a function in the Lebesgue space \( L^{1} ([a,\;b]) \), and \( \varphi (t) \in C_{0}^{\infty } ([a,b]) \) is a smooth function with compact support on \( [a,b] \). Then \( D(z(t)) \) is a weak derivative of \( z(t) \), if \( \int_{a}^{b} {z(t)D(\varphi (t)){\text{d}}t = - \int_{a}^{b} {\varphi (t)D(z(t)){\text{d}}t} } \), and \( D( \cdot ) \) is called the weak derivation operator. An efficient method to calculate \( D(\, \cdot \,) \) was derived in [8].

$$ Dy(n) = y(n) * \frac{\text{d}}{{{\text{d}}n}}\varphi (n), $$
(4)
$$ Dg_{i} (n) = g_{i} (n) * \frac{\text{d}}{{{\text{d}}n}}\varphi (n). $$
(5)

Here, the filter \( \varphi (n) \) is set as a Gaussian function since it is widely used to achieve smoothing effect on the observed signals. \( \frac{\text{d}}{{{\text{d}}n}}\varphi (n) \) is calculated using the first-order difference to approximate the derivative of \( \varphi (n) \).

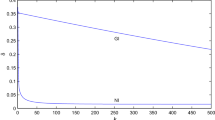
To illustrate the operator D’s ability to suppress the noise, an example with a mixture of three sinusoidal components corrupted by the additive Gaussian noise is shown in Fig. 1. We investigate the noise effect on the signal before and after transformation by the operator D. The left panel indicates that the noise effect on the signal is evident and the discrepancy between the true values and the noisy observed data is huge before transformation. In contrast, the discrepancy is largely reduced after both the true values and the noisy signal are transformed by the operator D. These results indicate that the associated weak derivatives are capable of reducing the noise effect.

Fig. 1
figure 1

An example of multi-sinusoidal signals before and after transformation. The solid line denotes the true values while the dashed line denotes the noisy observed data. a Before transformation, b after transformation by the weak derivative operator

Full size image

3 The Modified OMP Algorithm

3.1 The Weighted Criterion

To enhance the robustness of the algorithm, a LS + WD criterion is introduced to modify the objective function on (3):

$$ J_{{{\text{LS}} + {\text{WD}}}} = \left\| {{\mathbf{y}} - \sum\limits_{i = 1}^{p} {x_{i} {\mathbf{g}}_{i} } } \right\|_{2}^{2} + \mu \left\| {D\left( {{\mathbf{y}} - \sum\limits_{i = 1}^{p} {x_{i} {\mathbf{g}}_{i} } } \right)} \right\|_{2}^{2} . $$
(6)

The first term measures the local approximation error by calculating the difference between the observed and reconstructed signals, while the second term characterizes a more general divergence between the trend of the observed and reconstructed signals. The tradeoff parameter \( \mu \) is applied to balance the importance of the “local error” and the “general error” in the training phase, which can be selected by cross-validation.

Based on the definition of the weak derivatives, minimizing the improved weighted criterion (6) is equivalent to solving a new least squares problem

$$ \left[ {\begin{array}{*{20}c} {\mathbf{y}} \\ {\mu D{\mathbf{y}}} \\ \end{array} } \right] = \sum\limits_{i = 1}^{p} {x_{i} } \left[ {\begin{array}{*{20}c} {{\mathbf{g}}_{i} } \\ {D{\mathbf{g}}_{i} } \\ \end{array} } \right]. $$
(7)

3.2 Modified Orthogonal Matching Pursuit

The classic OMP is an efficient scheme to iteratively solve the LS-type optimization problems by constructing the model term by term. Given discrete observations of the multi-sinusoidal signal \( y(n),n = 1, \ldots ,N \) and the original dictionary \( g_{i} (n),\;n = 1, \ldots ,N \), the discrete forms of (4) and (5) can be written as

$$ Dy(n) = \sum\limits_{k = n}^{{n + n_{0} }} {y(k) \cdot \varphi^{\prime } (n - k)} , $$
$$ Dg_{i} (n) = \sum\limits_{k = n}^{{n + n_{0} }} {g_{i} (k) \cdot \varphi^{\prime } (n - k)} , $$

where \( \varphi^{\prime } ( \cdot ) = \frac{\text{d}}{{{\text{d}}n}}\varphi ( \cdot ) \), \( n_{0} \) is the support of the function \( \varphi ( \cdot ) \), and \( n = 1, \ldots ,N - n_{0} \).

The matrix form of (7) can be written as

$$ {\mathbf{Y}}_{{{\text{LS}} + {\text{WD}}}} = {\mathbf{G}}_{{{\text{LS}} + {\text{WD}}}} {\mathbf{x}}, $$
(8)

where

$$ {\mathbf{Y}}_{{{\text{LS}} + {\text{WD}}}} = [y(1) \cdots y(N)\mu Dy(1) \cdots \mu Dy(N - n_{0} )]^{\text{T}} , $$
(9)
$$ {\mathbf{G}}_{{{\text{LS}} + {\text{WD}}}} = [g_{i} (1) \cdots g_{i} (N)Dg_{i} (1) \cdots Dg_{i} (N - n_{0} )]^{\text{T}} , $$
(10)
$$ and {\mathbf{x}} = [\begin{array}{*{20}c} {x_{1} } & {x_{2} } & \cdots & {x_{{2N - n_{0} }} } \\ \end{array} ]^{\text{T}} . $$

It follows that a classic OMP can be applied to solve (8) by minimizing the loss function (6).

3.3 Multi-grid Dictionary Training Strategy

In the classic OMP, the candidate parameters are typically sampled uniformly using a grid. However, it is rather challenging to select a proper sampling rate. A low-resolution grid with a small sampling rate is likely to cause serious off-grid effect and lead to bad reconstruction performance. On the other hand, a high-resolution dictionary with a large amount of atoms results in a heavy computational burden. Therefore, instead of defining a large size of dictionary, we propose a multi-grid scheme to adaptively refine a coarse dictionary. The coarse dictionary \( {\mathbf{G}}^{(0)} \) is constructed by discretizing the frequency parameters with a sampling rate of 10 within the frequency range of the signal. Table 1 describes the procedure of updating the dictionary \( {\mathbf{G}}^{(l - 1)} \) to \( {\mathbf{G}}^{(l)} \). At steps 1 and 2, OMP is utilized to select the index set \( {\text{ind}}_{l} \) of \( {\mathbf{G}}^{(l - 1)} \), and the size of \( {\text{ind}}_{l} \) is \( nf_{l}^{\text{cand}} \). At step 3, the active frequency set \( \varOmega_{l} \) is a subset of the frequency sampling set \( {\text{fus}}_{l - 1} \) with the indices of \( {\text{ind}}_{l} \). The new frequency set \( {\text{fus}}_{l} \) is obtained at step 4 by inserting new samples in the neighborhood of \( \varOmega_{l} \). Finally, the new dictionary \( {\mathbf{G}}^{(l)} \) can be constructed according to frequency set \( {\text{fus}}_{l} \) based on Eqs. (2) and (10). The iteration terminates when the maximum level is reached.

Table 1 Multi-grid dictionary learning algorithm (MGDL)
Full size table

4 The Modified OMP (MOMP) Algorithm

The modified OMP algorithm for the frequency estimation of multi-sinusoidal signals can be illustrated as Fig. 2.

Fig. 2
figure 2

Algorithm flow chart

Full size image

Initialization: Set hyper-parameters \( \mu \), Gaussian function \( \varphi (n) \) with support \( n_{0} \), original dictionary \( {\mathbf{G}}^{(0)} \) built from the initial frequency set \( {\text{fus}}_{0} = \{ \omega_{1} ,\omega_{2} , \ldots ,\omega_{{nf_{0} }} \} \).

Step 1 Given the current dictionary \( {\mathbf{G}}^{(0)} \), use OMP to obtain a solution \( {\mathbf{x}}^{(0)} \) and \( {\text{fus}}_{1} \).

  1. (1)

    Let \( l = 1 \). For the dictionary \( {\mathbf{G}}^{(0)} \), use the test function to get the new

    $$ {\tilde{\mathbf{G}}}^{(0)} = [{\tilde{\mathbf{g}}}_{1} \cdots {\tilde{\mathbf{g}}}_{{nf_{0} }} ] = \left[ {\begin{array}{*{20}c} {{\mathbf{g}}_{1} } & \cdots & {{\mathbf{g}}_{{nf_{0} }} } \\ {D{\mathbf{g}}_{1} } & \cdots & {D{\mathbf{g}}_{{nf_{0} }} } \\ \end{array} } \right], $$

    with \( {\mathbf{g}}_{i} = [\begin{array}{*{20}c} {\sin (\omega_{i} \cdot t_{s} )} & {\sin (\omega_{i} \cdot 2t_{s} )} & \cdots & {\sin (\omega_{i} \cdot Nt_{s} )} \\ \end{array} ]^{\text{T}} \).

  2. (2)

    For \( {\mathbf{r}}_{0} = {\mathbf{y}} \), \( {\mathbf{Y}}_{{I - {\text{LS}}}}^{0} = [{\tilde{\mathbf{r}}}_{0} ] = \left[ {\begin{array}{*{20}c} {\lambda {\mathbf{r}}_{0} } \\ {\mu D{\mathbf{r}}_{0} } \\ \end{array} } \right] \); therefore, we obtain

    $$ l_{1} = \mathop {\arg \hbox{max} }\limits_{{1 \le j \le n_{M} }} \{ C({\tilde{\mathbf{r}}}_{0} ,{\tilde{\mathbf{g}}}_{j} )\} , $$

    where the function \( C(\; \cdot \;,\; \cdot \;) \) denotes the correlation coefficient. Then, the first orthogonal regressor can be chosen as \( {\mathbf{h}}_{1} = {\mathbf{g}}_{{l_{1} }} \), and the residual vector can be updated as

    $$ {\mathbf{r}}_{1} = {\mathbf{r}}_{0} - \frac{{{\mathbf{r}}_{0}^{\text{T} } {\mathbf{h}}_{1} }}{{{\mathbf{h}}_{1}^{\text{T} } {\mathbf{h}}_{1} }}{\mathbf{h}}_{1} . $$
  3. (3)

    In general, let us assume that at the (m − 1)-th step, a subset \( {\mathbf{G}}_{m - 1}^{{^{(0)} }} \) consisting of \( (m - 1) \) significant bases \( {\mathbf{g}}_{{l_{1} }} ,{\mathbf{g}}_{{l_{2} }} \ldots {\mathbf{g}}_{{l_{m} - 1}} \) has been determined, and these bases have been transformed into a new group of orthogonal basis \( {\mathbf{h}}_{1} , \ldots {\mathbf{h}}_{m - 1} \). Let

    $$ {\mathbf{h}}_{j}^{(m)} = {\mathbf{g}}_{j} - \sum\limits_{k = 1}^{m - 1} {\frac{{{\mathbf{g}}_{j}^{\text{T} } {\mathbf{h}}_{k} }}{{{\mathbf{h}}_{k}^{\text{T} } {\mathbf{h}}_{k} }}} {\mathbf{h}}_{k} , $$
    $$ l_{m} = \mathop {\arg \hbox{max} }\limits_{{j \ne l_{k} ,1 \le j \le m - 1}} \left\{ {C\left( {{\tilde{\mathbf{r}}}_{m - 1} ,\left[ {\begin{array}{*{20}c} {{\mathbf{h}}_{j}^{(m)} } \\ {D{\mathbf{h}}_{j}^{(m)} } \\ \end{array} } \right]} \right)} \right\}, $$

    The m-th significant basis can then be chosen as \( {\mathbf{h}}_{m} = {\mathbf{h}}_{{l_{m} }}^{(m)} \). The residual vector is given by

    $$ {\mathbf{r}}_{m} = {\mathbf{r}}_{m - 1} - \frac{{{\mathbf{r}}_{m - 1}^{\text{T} } {\mathbf{h}}_{m} }}{{{\mathbf{h}}_{m}^{\text{T} } {\mathbf{h}}_{m} }}{\mathbf{h}}_{m} . $$

The algorithm terminates until the maximum level \( nf_{1}^{\text{cand}} \) is reached. Then, \( \varOmega_{1} = \{ \omega_{{l_{1} }} ,\omega_{{l_{2} }} , \ldots \omega_{{l_{{nf_{1}^{\text{cand}} }} }} \} \), so \( {\text{fus}}_{1} \) by inserting new samples in the neighborhood of \( \varOmega_{1} \).

Step 2 Update \( {\mathbf{G}}^{(l)} \) using MGDL strategy in Table 1. Obtain the MOMP solution \( {\mathbf{x}}^{(l)} \) and \( {\text{fus}}_{l + 1} \) at the current dictionary \( {\mathbf{G}}^{(l)} \).

Step 3 If \( l < L - 1 \), use MOMP to update the dictionary; otherwise, terminate the algorithm. At the last iteration, p components are extracted by OMP, and their corresponding frequencies \( {\text{fus}}_{L} \) are the estimated frequencies output by the algorithm.

5 Simulation Results

We use simulation studies to evaluate the performance of the proposed MOMP method compared with five state-of-art methods: MUSIC, OW-HMUSIC [29], OMP, Newtonized OMP (NOMP), and ZZB [18]. The simulation results show that MOMP outperforms the above-mentioned methods given signals with low SNR. All the phases are set to zero in these studies.

5.1 Frequency Estimation of Sinusoidal Signal with White Additive Noise

The MOMP is compared with the other five methods in the frequency estimation of two-component sinusoidal signals polluted by white Gaussian noise:

$$ y(n) = a_{1} \sin (\omega_{1} \cdot nt_{s} ) + a_{2} \sin (\omega_{2} \cdot nt_{s} ) + v(n). $$
(11)

The frequency and amplitude parameters are set as \( \omega_{1} = 0.6,\;\;\omega_{2} = 1.7,\;\;a_{1} = 1,\;\;{\text{and}}\;\;a_{2} = 2 \), respectively. The additive noise \( v(n) \) follows the Gaussian distribution, with mean zero, standard deviation \( \sigma \), and support \( n_{0} = 90 \). The sampling interval \( t_{s} = 0.1 \). A total of 256 data points are generated according to (11). In the MOMP algorithm, the trade-off parameter \( \mu \) is selected from the candidate set \( \{ 0.15,0.2,0.25, \ldots ,0.5\} \) using cross-validation. For MOMP, OMP, and NOMP, the dictionary is constructed by discretizing the frequency parameters with a sampling rate of 10 within \( [0,\pi ] \), and thus the dictionary is of size \( 62 \times 256 \). In ZZB, the stopping criterion parameter \( \tau \) is set as \( \sigma^{ 2} \log N - \sigma^{ 2} \log \log \left( {\frac{1}{{1 - p_{0} }}} \right) \) with \( p_{0} = 10^{ - 2} \). In OW-HMUSIC, the parameter M is set to 100.

To evaluate the robustness of different methods against noise, signals with different SNRs are obtained by properly scaling the noise variance \( \sigma^{ 2} \). The SNR is defined as

$$ {\text{SNR}} = 10\log_{10} \frac{{a_{1}^{2} + a_{2}^{2} }}{{\sigma^{2} }}. $$

We assess the detection result of a method using detection acceptance condition (DAC), which means that we accept a detection only if all the frequencies have been accurately estimated, i.e.,

$$ \hbox{max} (|\omega_{1} - \tilde{\omega }_{1} |,|\omega_{2} - \tilde{\omega }_{2} |) < 0.01. $$

Finally, the detection rate is defined as

$$ {\text{detection}}\;{\text{rate = }}\frac{{{\text{the}}\;{\text{number}}\;{\text{of}}\;{\text{correct}}\;{\text{detection}}}}{{{\text{the}}\;{\text{number}}\;{\text{of}}\;{\text{total}}\;{\text{experiment}}\;{\text{runs}}}}. $$
(12)

The detection rate is a value in [0, 1], with 1 indicating best accuracy. All the presented simulation results are averaged over 100 independent experiments.

The detection rates of MOMP and the other five methods given varying SNRs are shown in Fig. 3. Both the ZZB algorithm and the newly proposed method MOMP are the only two methods that achieve 100% detection rate at SNR = − 1 or 0 dB. However, with the lower SNR (< − 5 dB), the accuracy of ZZB, MUSIC, and OW-HMUSIC decreases greatly and all of their detection rates are smaller than 40%. The detection rate of MOMP is nearly 10% higher than the other methods when SNR < − 5 dB. These results demonstrate the superiority of the proposed MOMP method compared with the other methods, especially when SNR is relatively low.

Fig. 3
figure 3

Detection rate of four methods at different SNRs

Full size image

5.2 Frequency Estimation of Sinusoidal Signal with Stationary Colored Additive Noise

The newly proposed algorithm MOMP can also be used to improve frequency estimation in the existence of the stationary colored additive noise. It was proved that if the additive noise satisfies a certain assumption [11,12,13, 24], the strong consistency or the asymptotic normality results can be obtained [12], even if the noise does not satisfy the standard sufficient condition (Jennrich [9] or Wu [25]) for the least squares estimators to be consistent.

In this experiment, the sinusoidal signal is polluted by colored additive noise, and the two frequency parameters are very close with \( \omega_{1} = 0.63 \) and \( \omega_{2} = 0.66 \). The amplitude parameters are set as \( a_{1} = 1,a_{2} = 2 \). The noise \( v(n) \) is a random variable following the exponential distribution:

$$ v(n) = s_{1} e(n) + s_{2} e(n - 1),e(n)\sim{\text{i}} . {\text{i}} . {\text{d}}.\;{\text{exponential}}\;{\text{distribution}}\;\lambda $$

where \( s_{1} = 2.8,{\kern 1pt} \;s_{2} = 0.2 \), and 256 sample points are generated with sample rate 10. The values of \( \mu \) and \( n_{0} \) are the same as in experiment 1. With the stationary colored additive noise, both MUSIC and OW-HMUSIC can extract only one harmonic component when the two frequencies to be estimated have very close true values. That is, the frequency resolution rates of both methods are significantly decreased with the colored additive noise. Moreover, ZZB cannot detect any harmonic component in this case, because ZZB is specially designed for data with the Gaussian white noise. Therefore, we compare the detection rate of MOMP with that of OMP and NOMP in this experiment.

The MOMP algorithm coupled with the multi-grid approach is applied to estimate the frequency of the sinusoidal signal with 256 samples embedded in the colored additive noise with different SNRs. Here, the SNR is defined as

$$ {\text{SNR}} = 10\log_{10} \left( {\frac{{a_{1}^{2} + a_{2}^{2} }}{{\lambda^{2} (s_{1}^{2} + s_{2}^{2} )}}} \right). $$

Because the frequency parameters in this experiment are not initially in the dictionary, we used the multi-grid procedure presented in Sect. 3.3. Figure 4 illustrates the detection rates of the MOMP, OMP, and NOMP algorithms. All the three methods are able to distinguish the two frequency parameters when the SNR is 5 dB. However, when SNR is decreased to 2 dB, only MOMP is still able to estimate the two frequencies with 100% accuracy, while the accuracy of the other two methods decreases to 95%. The NOMP estimates the frequency with a rate higher than 80% for an SNR more than − 1 dB, while the rate of both OMP and NOMP is almost 60%.

Fig. 4
figure 4

Detection rate of three methods at different SNRs

Full size image

6 Conclusion

Sparse representation is an effective way to solve the frequency estimation problem of the multi-sinusoidal signals. However, when the signals are polluted by additive noise, the commonly used least squares criterion cannot reconstruct the signal well. To address this issue, a new stricter measurement of the residuals is proposed to improve the frequency estimation performance. The weak derivatives of the observed data and the model-predicted values are combined with the classic least square criterion via a weighted parameter to construct an improved weighted criterion.

The MOMP algorithm is proposed to efficiently detect the true underlying frequency. A multi-grid dictionary training strategy is used to assist the selection of dictionary and improve the efficiency of sparse construction. The idea behind the multi-grid approach is to refine the dictionary over several levels of resolution. Simulation results showed that the new algorithm significantly improved the accuracy of frequency estimation.

Despite the good performance of the proposed MOMP algorithm in the simulation, a mathematical proof is in need to guarantee its effectiveness. As a continuous effort, we will analyze the theoretical properties and potential extensions of MOMP in the future work.