New Results on Exponential Stability and Passivity Analysis of Delayed Switched Systems with Nonlinear Perturbations

Abstract

In this paper, we investigate the problem of exponential stability and passivity analysis of a class of switched systems with interval time-varying delays and nonlinear perturbations. By constructing an improved Lyapunov–Krasovskii functional combining with novel refined Jensen-based inequalities, some improved sufficient conditions for exponential stability are proposed for a class of switching signals with average dwell time. Moreover, a new sufficient condition for passivity analysis of switched continuous-time systems with an interval time-varying delay is also derived. These conditions are delay dependent and are given in the form of linear matrix inequalities, which therefore can be efficiently solved by existing convex algorithms. Lastly, four examples are provided to demonstrate the effectiveness of our results.

1 Introduction

During the last decades, switched systems have attracted a lot of research attentions due to the increase in their practical applications (see [23, 44] and the references therein). As well known, the existence of time delays in systems may cause instability and performance degradation of systems. Therefore, many problems concerning delayed switched systems have been investigated in the literature (see [2, 4, 10, 20, 24, 26, 27, 38,39,40,41, 46, 47, 51, 60, 61, 63, 65] and the references therein). For instance, based on the switched Lyapunov functional approach, the authors in [40] investigated the problems of disturbance tolerance and rejection of discrete switched systems with time-varying delay and saturating actuator. Problem of $L_1$ observer design for positive switched linear delay-free systems with observable and unobservable subsystems was considered in [20]. Recently, in [27], the authors have studied the problem of finite-time stability of discrete switched singular positive systems.

On the other hand, as noted by many scholars, nonlinear perturbations are always unavoidable in practical systems. Therefore, the stability analysis of delayed switched systems with nonlinear perturbations has been addressed by many authors. For example, in [24,25,26, 38], by constructing a common Lyapunov–Krasovskii functionals combining with Jensen integral inequality [8], the authors gave some sufficient conditions for exponential stability of switched nonlinear systems with time-varying delay. However, most switched systems do not possess a common Lyapunov–Krasovskii functionals, yet they still may be stable under certain switching laws. Therefore, average dwell time technique is an effective tool for choosing such switching laws [59]. In [47], the average dwell time technique was employed to consider the exponential stability and $L_2$-gain for a switched delay system; however, the results only apply for the slow time-varying case (the derivative of the delay is limited to be less than one). To overcome these disadvantages, based on piecewise descriptor-type Lyapunov–Krasovskii functional and the average dwell time approach, the authors in [11] investigated the problem of exponential stability of switched neutral systems with nonlinear perturbations where the derivative of the discrete delay is larger than one. Noting that, in the majority of the papers which consider the stability analysis of delayed switched nonlinear systems, the delay is assumed to be differential and its derivative is bounded [10, 11, 24,25,26, 38, 39, 61]. Therefore, it is interesting and worthy to investigate the problem of exponential stability of switched nonlinear systems in the case where the time-varying delay function is nondifferentiable.

The problem of passivity and passification of time-delay systems first was considered in [5, 30, 35]. In recent years, the problem has attracted a lot of attentions and many interesting results have been reported in the literature. In [1, 12, 15, 16, 29, 34, 48, 50, 56, 57, 62, 64], passivity of delayed neural networks systems was studied. The problem of passivity and passification of fuzzy systems with time delays was considered in [17, 49, 52]. Some sufficient criteria on passivity of delayed singular systems or singular Markovian systems were proposed in [18, 53,54,55]. Based on using the Lyapunov–Krasovskii stability theory and linear matrix inequality approach, several $H_{\infty }$ control approaches were presented for networked cascade control systems [32, 33]. For linear switched systems without time delay, some interesting results were reported for the problem of passivity and passification of switched discrete-time systems [19] or switched continuous-time systems [6, 66, 67]. By using average dwell time approach, free-weighting matrix method and Jensen’s integral inequality, problems of passivity and passification for a class of uncertain switched systems subject to stochastic disturbance and time-varying delay were considered in [21]. Recently, some delay-dependent stochastic passivity conditions for switched recurrent neural networks have been derived in terms of LMIs in [22] by using the multiple Lyapunov functions method combining with average dwell time approach. The method used in [21, 22] only applies for the slow time-varying case or the fast time-varying case where the lower bound of time-varying delay is zero. However, as noted by many researchers, the time-varying delay may vary within an interval where the lower bound is not restricted to being zero [3] and can be modeled in systems having network-induced communication delays [13]. In addition, the time derivatives of the time-varying delay can be unknown or undefined. Moreover, it has been shown that the conservativeness of the celebrated Jensen’s inequality can be reduced by employing less restrictive inequalities, such as Wirtinger-based integral inequality [42] and refined Jensen-based inequalities [9, 37]. However, the application of those inequalities to solve the problem of passivity analysis of delayed switched nonlinear systems has been fairly overlooked. Therefore, it is important to consider the problem of passivity analysis of switched systems with nondifferentiable interval time-varying delays and nonlinear perturbations by employing some less restrictive inequalities in [9, 37].

Motivated by the above discussions, in this paper, the problems of exponential stability and passivity analysis of switched nonlinear systems with interval time-varying delay are investigated. Four main features of our study are highlighted in the following: (1) By using novel refined Jensen-based inequalities proposed in [9, 37] combining with the reciprocally convex technique [36] when estimating the derivative of the Lyapunov–Krasovskii functional and the average dwell time approach, new exponential stability criterion will be derived in Theorem 1 within the framework of linear matrix inequalities. Note that, in our work, the time-varying delay is not necessarily differentiable. Therefore, our derived result can be applied to switched systems with fast interval time-varying delays; (2) as noted by many authors in the literature [14], in stability problems of switched systems with time-varying delay, to derive less conservative criteria guaranteeing the stability of the switched systems is a key purpose. The maximal allowable upper bound (MAUB) of time delay is one of the important indexes to check conservatism of the proposed condition. Corollary 1 provides an improved result on the exponential stability of delayed switched nonlinear systems for the case where the time derivative of the delay is known, i.e., the rate of change of the delay satisfies an upper bound condition; (3) based on the result of Theorem 1, the problem of passivity analysis of switched systems with interval time-varying delay and nonlinear perturbations will be suggested in Theorem 2; (4) the applicability of the derived analytical results is exemplified by several illustrative examples in comparison with existing results.

Notation

In this paper, we denote by ${\mathbb {R}}^n$ and ${\mathbb {R}}^{n\times m}$, respectively, the n-dimensional space with vector norm $\Vert .\Vert$ and the space of $n\times m$ matrices. For matrices $A,B\in {\mathbb {R}}^{n\times m}$, $\mathrm {diag}\{A,B\}$ denotes the block matrices $\begin{bmatrix}A&0\\0&B\end{bmatrix}$. A matrix P is symmetric positive definite, write $P>0$, if $P^T=P$ and $x^TPx>0$ for all $x\in {\mathbb {R}}^n,\; x\ne 0.$ For a symmetric positive definite matrix Q, we denote maximal eigenvalue by $\lambda _{\max }(Q)$ and minimal eigenvalue by $\lambda _{\min }(Q).$ We use ${\mathbb {S}}^+_n$ to denote the set of symmetric positive definite matrices in ${\mathbb {R}}^{n\times n}$.

2 Preliminaries

Consider the following switched systems with interval time-varying delay and nonlinear perturbations

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t) = A_{ \sigma (t)}x(t) + D_{\sigma (t)}x(t-\tau (t)) + E_{\sigma (t)}\omega (t)+ f_{\sigma (t)}(t, x(t), x(t-\tau (t)), \omega (t)), \\ x_{t_0}(s) = x(t_0 + s) = \phi (s), \quad s \in [-\tau _2, 0],\\ z(t) = M_{\sigma (t)}x(t) + U_{\sigma (t)}x(t-\tau (t)) + W_{\sigma (t)}\omega (t), \end{array}\right. \end{aligned}$$

(1)

where $x(t) \in {\mathbb {R}}^{n}$ is the state vector, $\omega (t) \in {\mathbb {R}}^{m}$ is the external input of the switched system, $z(t) \in {\mathbb {R}}^{m}$ is the output of the system, $\sigma (t):[0, \infty ) \rightarrow {\mathcal {N}}: = \{1, 2, \ldots , N\}$ is the switching signal, $A_i, D_i, E_i, M_i, U_i, W_i, i = 1, \ldots , N,$ are constant known matrices, $\phi (s)$ is a differentiable vector-valued initial function on $[-\tau _2, 0], \tau _2 > 0.$ The nonlinear perturbations $f_i(.), i = 1, \ldots , N,$ satisfy $f_i(t, 0, 0, 0) = 0,$ and

$$\begin{aligned}&f_i^T(t, x(t), x(t-\tau (t)), \omega (t))f_i(t, x(t), x(t-\tau (t)), \omega (t))\nonumber \\&\quad \le x^T(t)L_i^TL_ix(t) + x^T(t-\tau (t))G_i^TG_ix(t-\tau (t)) + \omega ^T(t)H_i^TH_i \omega (t), \end{aligned}$$

(2)

where $L_i, G_i, H_i, i = 1, \ldots , N,$ are known constant matrices. Noting that the assumption on the nonlinear perturbations is widely applicable in practice and considered by many researchers [4, 11, 24,25,26, 65].

In this paper, we assume that the delay $\tau (t)$ is time-varying and satisfies

$$\begin{aligned} 0 \le \tau _{1} \le \tau (t) \le \tau _{2}, \end{aligned}$$

(3)

where $\tau _{1}, \tau _{2}$ are known constants involving the lower bound and the upper bound of the time-varying delay function.

Corresponding to the switching signal $\sigma (t),$ we have the switching sequence

$$\begin{aligned} \{x_{t_0}; (i_0, t_0), \ldots , (i_k, t_k){:}\; i_k \in {\mathcal {N}},~k = 0, 1, \ldots \}, \end{aligned}$$

which means that the $i_k$th subsystem is activated when $t \in [t_k, t_{k+1}).$

To get inside, let us introduce the following definitions and auxiliary lemmas, which are essential in order to derive our main results in this paper.

Definition 1

For any $T_2>T_1 \ge 0,$ let $N_\sigma (T_1, T_2)$ denote the number of switching of $\sigma (t)$ over $(T_1, T_2).$ If $N_\sigma (T_1, T_2) \le N_0 + \frac{T_2-T_1}{T_a}$ holds for $T_a>0, N_0 \ge 0,$ then $T_a$ is called the average dwell time. As commonly used in the literature, we choose $N_0 = 0.$

Definition 2

Switched system (1), with $\omega (t) = 0,$ is said to be exponentially stable under $\sigma (t)$ if the solution $x(t, \phi )$ of the systems (1) satisfies

$$\begin{aligned} \Vert x(t, \phi )\Vert \le \beta \mathrm{e}^{-\alpha (t-t_0)}\Vert x_{t_0}\Vert , \quad \forall t \ge t_0 \end{aligned}$$

for constants $\beta \ge 1, \alpha > 0.$

Definition 3

Switched system (1) is said to be passive if there exists a scalar $\gamma \ge 0$ such that, under zero initial condition, the following inequality holds for all $t_{f}\ge t_0$

$$\begin{aligned} 2\int _{t_0}^{t_{f}}z^{T}(s)\omega (s)\hbox {d}s \ge -\gamma \int _{t_0}^{t_{f}}\omega ^{T}(s)\omega (s)\hbox {d}s. \end{aligned}$$

(4)

The following refined Jensen-based inequalities, which are theoretically shown to encompass the Jensen inequality and Wirtinger-based inequality, were proposed in [9, 37].

Lemma 1

[9, 37] For a given matrix $R\in {\mathbb {S}}^+_n$ and a function $\varphi : [a, b]\rightarrow {\mathbb {R}}^{n}$ whose derivative ${\dot{\varphi }} \in PC([a, b],{\mathbb {R}}^{n})$, the following inequality holds

$$\begin{aligned} \int _{a}^{b}\dot{\varphi }^T(s)R{\dot{\varphi }} (s)\mathrm{d}s \ge \frac{1}{b-a}{\hat{\chi }}^T\overline{R}{\hat{\chi }}, \end{aligned}$$

(5)

where $\overline{R} =\mathrm {diag}\{R, 3R, 5R\}$, ${{\hat{\chi }}}=\begin{bmatrix}\chi _1^T&\chi _2^T&\chi _3^T\end{bmatrix}^T$, and

$$\begin{aligned}&\chi _1=\varphi (b)-\varphi (a),\quad \chi _2=\varphi (b)+\varphi (a)-\frac{2}{b-a}\int _{a}^{b}\varphi (s)\mathrm{d}s\\&\chi _3=\varphi (b)-\varphi (a)+\frac{6}{b-a}\int _{a}^{b}\varphi (s)\mathrm{d}s -\frac{12}{(b-a)^{2}}\int _{a}^{b}\int _{s}^{b}\varphi (u)\mathrm{d}u\mathrm{d}s. \end{aligned}$$

The reciprocally convex combination inequality provided in [36] is used in this paper. This inequality has been improved in [43] and is stated in Lemma 2.

Lemma 2

[43] For given symmetric positive matrices $R_{1} \in {\mathbb {R}}^{n \times n}, R_{2} \in {\mathbb {R}}^{m \times m},$ if there exists a matrix $X \in {\mathbb {R}}^{n \times m}$ such that

$$\begin{aligned} \begin{bmatrix} R_{1}&X \\ *&R_{2} \end{bmatrix} \ge 0 \end{aligned}$$

then the inequality

$$\begin{aligned} \begin{bmatrix} \frac{1}{\gamma }R_{1}&0 \\ 0&\frac{1}{1-\gamma }R_{2} \end{bmatrix} \ge \begin{bmatrix} R_{1}&X \\ *&R_{2} \end{bmatrix} \end{aligned}$$

holds for all $\gamma \in (0, 1).$

3 Exponential Stability Analysis

For the simplicity of matrix representation, $e_i (i=1, \ldots , 11) \in {\mathbb {R}}^{n \times 11n}$ is defined as a block entry matrix. For example, $e_4 = [0\quad 0\quad 0\quad I \quad 0\quad 0\quad 0\quad 0\quad 0\quad 0\quad 0],$ ${\mathscr {A}}=Ae_1 + De_3 + e_{11},$ augmented vector $\chi _0(t)=[\chi _{01}^T(t) \quad \chi _{02}^T(t) \quad \chi _{03}^T(t)]^T$, where

$$\begin{aligned} \chi _{01}(t)&=\begin{bmatrix}x(t)\\ x(t-\tau _{1})\\ x(t-\tau (t))\\ x(t-\tau _{2}) \end{bmatrix},\quad \chi _{02}(t)=\begin{bmatrix}\frac{1}{\tau _1}\int _{t-\tau _1}^{t}x(s)\hbox {d}s\\ \frac{1}{\tau (t)-\tau _1}\int _{t-\tau (t)}^{t-\tau _1}x(s)\hbox {d}s\\ \frac{1}{\tau _2-\tau (t)}\int _{t-\tau _2}^{t-\tau (t)}x(s)\hbox {d}s\end{bmatrix},\\ \chi _{03}(t)&=\begin{bmatrix}\frac{2}{\tau _1^2}\int _{t-\tau _1}^{t}\int _{s}^{t}x(u)\hbox {d}u\hbox {d}s\\ \frac{2}{(\tau (t)-\tau _1)^2}\int _{t-\tau (t)}^{t-\tau _1}\int _{s}^{t-\tau _1}x(u)\hbox {d}u\hbox {d}s\\ \frac{2}{(\tau _2-\tau (t))^2}\int _{t-\tau _2}^{t-\tau (t)}\int _{s}^{t-\tau (t)}x(u)\hbox {d}u\hbox {d}s \\ f(.) \end{bmatrix}, \end{aligned}$$

and matrices

$$\begin{aligned} {{\mathscr {G}}}_1(\tau )&= \left[ e_1^T \quad \tau _1e_5^T \quad (\tau -\tau _1)e_6^T + (\tau _2-\tau )e_7^T \quad 0.5\tau _1^2e_8^T \right] ^T,\\ {{\mathscr {G}}}_2&= \left[ {\mathscr {A}}^T \quad (e_1-e_2)^T \quad (e_2-e_4)^T \quad \tau _1(e_1-e_5)^T\right] ^T,\\ {{\mathscr {G}}}_3&= \left[ e_1^T \quad e_2^T \quad e_5^T \quad e_8^T\right] ^T, \quad {{\mathscr {G}}}_4 = \left[ e_2^T \quad e_3^T \quad e_6^T \quad e_9^T\right] ^T, \quad {{\mathscr {G}}}_5 = \left[ e_3^T \quad e_4^T \quad e_7^T \quad e_{10}^T\right] ^T, \end{aligned}$$

and

$$\begin{aligned}&F=\begin{bmatrix} I_n&-I_n&0&0\\ I_n&I_n&-2I_n&0 \\ I_n&-I_n&6I_n&-6I_n \end{bmatrix},\\&\overline{S} = \mathrm {diag}\left\{ \mathrm{e}^{-\alpha \tau _1}S, 3\mathrm{e}^{-\alpha \tau _1}S, 5\mathrm{e}^{-\alpha \tau _1}S\right\} , \quad \overline{Z} = \mathrm {diag}\left\{ \mathrm{e}^{-\alpha \tau _2}Z, 3\mathrm{e}^{-\alpha \tau _2}Z, 5\mathrm{e}^{-\alpha \tau _2}Z\right\} . \end{aligned}$$

We first consider the nonswitched delay system:

$$\begin{aligned} \dot{x}(t)= & {} Ax(t) + Dx(t-\tau (t)) + f(t, x(t), x(t-\tau (t))),\nonumber \\ x_{t_0}(s)= & {} x(t_0 +s), \quad s \in [-\tau _2, 0], \end{aligned}$$

(6)

where the nonlinear perturbation $f(t, x(t), x(t-\tau (t)))$ satisfies the following condition:

$$\begin{aligned} \begin{aligned}&f^T(t, x(t), x(t-\tau (t)))f(t, x(t), x(t-\tau (t))) \\&\quad \le x^T(t)L^TLx(t) + x^T(t-\tau (t))G^TGx(t-\tau (t)), \end{aligned} \end{aligned}$$

(7)

with L, G are known matrices.

Choose the Lyapunov–Krasovskii candidate of the form

$$\begin{aligned} V(x_t)= & {} \eta ^T(t)P\eta (t) + \int _{t-\tau _1}^t\mathrm{e}^{\alpha (s-t)}x^T(s)Qx(s)\hbox {d}s + \int _{t-\tau _2}^{t-\tau _1}\mathrm{e}^{\alpha (s-t)}x^T(s)Rx(s)\hbox {d}s\nonumber \\&+\, \tau _1\int _{-\tau _1}^0\int _{t+s}^t\mathrm{e}^{\alpha (s-t)}\dot{x}^T(u)S\dot{x}(u)\hbox {d}u\hbox {d}s\nonumber \\&+\, \tau _{12}\int _{-\tau _2}^{-\tau _1}\int _{t+s}^t\mathrm{e}^{\alpha (s-t)}\dot{x}^T(u)Z\dot{x}(u)\hbox {d}u\hbox {d}s, \end{aligned}$$

(8)

where $P\in {\mathbb {S}}^+_{4n}$, $Q, R, S, Z \in {\mathbb {S}}^+_n,$ and

$$\begin{aligned} \tau _{12}&= \tau _2 - \tau _1, \\ \eta (t)&= \left[ x^T(t)\quad \int _{t-\tau _1}^{t}x^T(s)\hbox {d}s\quad \int _{t-\tau _2}^{t-\tau _1}x^T(s)\hbox {d}s\quad \int _{t -\tau _1}^{t}\int _{s}^{t}x^T(u)\hbox {d}u\hbox {d}s\right] ^T. \end{aligned}$$

Then, we have the following lemma.

Lemma 3

Given $\alpha > 0.$ Assume that there exist matrices $P\in {\mathbb {S}}^+_{4n}$, $Q, R, S, Z \in {\mathbb {S}}^+_n$, $X\in {\mathbb {R}}^{3n\times 3n}$, and a scalar $\varepsilon > 0$ such that the following LMIs hold for $\tau \in \{\tau _1, \tau _2\}$

$$\begin{aligned} \Phi&=\begin{bmatrix}\overline{Z}&X \\ X^T&\overline{Z} \end{bmatrix}\ge 0,\end{aligned}$$

(9a)

$$\begin{aligned} \Omega (\tau )&=\Xi _1(\tau )-\Xi _2 -\Gamma ^T \Phi \Gamma < 0. \end{aligned}$$

(9b)

Then, along the trajectory of system (6), we have

$$\begin{aligned} V(x_t) \le \mathrm{e}^{-\alpha (t-t_0)}V(x_{t_0}), \quad \forall t \ge t_0, \end{aligned}$$

(10)

where

$$\begin{aligned} \Xi _1(\tau )&= {\mathscr {G}}_1^T(\tau )P{\mathscr {G}}_2 + {\mathscr {G}}_2^TP\mathscr {G}_1(\tau ) + \alpha {\mathscr {G}}_1^T(\tau )P\mathscr {G}_1(\tau ) + e_1^T(Q + \varepsilon L^TL)e_1\\&\quad + e_2^T\left( \mathrm{e}^{-\alpha \tau _1}R - \mathrm{e}^{-\alpha \tau _1}Q \right) e_2- \mathrm{e}^{-\alpha \tau _2}e_4^TRe_4+ \varepsilon e_3^TG^TGe_3 \\&\quad - \varepsilon e_{11}^Te_{11} + {\mathscr {A}}^T\left( \tau _1^2S + \tau _{12}^2Z \right) {\mathscr {A}},\\ \Xi _2&= {\mathscr {G}}_3^TF^T\overline{S}F{\mathscr {G}}_3, \quad \Gamma = \begin{bmatrix}F{\mathscr {G}}_4 \\ F{\mathscr {G}}_5 \end{bmatrix}. \end{aligned}$$

Proof

With $\varepsilon > 0,$ from (7) we have

$$\begin{aligned} -\varepsilon f^T(.)f(.) + \varepsilon x^T(t)L^TLx(t) + \varepsilon x^T(t-\tau (t))G^TGx(t-\tau (t)) \ge 0. \end{aligned}$$

(11)

Taking derivative of $V(x_t)$ in t and using (11), we obtain

$$\begin{aligned} \dot{V}(x_t) + \alpha V(x_t)\le & {} \chi _0^T(t) \Xi _1(\tau ) \chi _0(t) - \tau _1\mathrm{e}^{-\alpha \tau _1}\int _{t-\tau _1}^t\dot{x}^T(s)S\dot{x}(s)\hbox {d}s\nonumber \\&- \tau _{12}\mathrm{e}^{-\alpha \tau _2}\int _{t-\tau _2}^{t-\tau _1}\dot{x}^T(s)Z\dot{x}(s)\hbox {d}s. \end{aligned}$$

(12)

By applying inequality (5) in Lemma 1, we obtain

$$\begin{aligned} -\tau _1\mathrm{e}^{-\alpha \tau _1}\int _{t-\tau _1}^t\dot{x}^T(s)S\dot{x}(s)\hbox {d}s \le -\chi _0^T(t){\mathscr {G}}_3^TF^T\overline{S}F{\mathscr {G}}_3\chi _0(t) =-\chi _0^T(t)\Xi _2\chi _0(t).\nonumber \\ \end{aligned}$$

(13)

Next, by splitting

$$\begin{aligned}&-\tau _{12}\mathrm{e}^{-\alpha \tau _2}\int _{t-\tau _2}^{t-\tau _1}\dot{x}^T(s)Z\dot{x}(s)\hbox {d}s\\&\quad =-\tau _{12}\mathrm{e}^{-\alpha \tau _2}\int _{t-\tau _2}^{t-\tau (t)}\dot{x}^T(s)Z\dot{x}(s)\hbox {d}s -\tau _{12}\mathrm{e}^{-\alpha \tau _2}\int _{t-\tau (t)}^{t-\tau _1}\dot{x}^T(s)Z\dot{x}(s)\hbox {d}s \end{aligned}$$

the second integral term in (12) can be bounded by (5) and Lemma 2 as follows

$$\begin{aligned} \begin{aligned}&-\tau _{12}\mathrm{e}^{-\alpha \tau _2}\int _{t-\tau _2}^{t-\tau _1}\dot{x}^T(s)Z\dot{x}(s)\hbox {d}s \\&\quad \le -\frac{\tau _{12}}{\tau (t)-\tau _1}\chi _0^T(t){\mathscr {G}}_4^TF^T\overline{Z}F{\mathscr {G}}_4\chi _0(t) -\frac{\tau _{12}}{\tau _2-\tau (t)}\chi _0^T(t){\mathscr {G}}_5^TF^T\overline{Z}F{\mathscr {G}}_5\chi _0(t) \\&\quad =-\chi _0^T(t)\Gamma ^T\begin{bmatrix}\frac{\tau _{12}}{\tau (t)-\tau _1}\overline{Z}&0 \\ 0&\frac{\tau _{12}}{\tau _2-\tau (t)}\overline{Z}\end{bmatrix} \Gamma \chi _0(t)\\&\quad \le - \chi _0^T(t)\Gamma ^T\begin{bmatrix}\overline{Z}&X \\ X^T&\overline{Z}\end{bmatrix} \Gamma \chi _0(t)\\&\quad =-\chi _0^T(t)\Gamma ^T\Phi \Gamma \chi _0(t). \end{aligned} \end{aligned}$$

(14)

Therefore, from (12) to (14), we have

$$\begin{aligned} \dot{V}(x_t) + \alpha V(x_t) \le \chi _0^T(t)\Omega (\tau )\chi _0(t). \end{aligned}$$

(15)

Since $\Omega (\tau )$ is an affine function in $\tau$, $\Omega (\tau )<0$ for all $\tau \in [\tau _1,\tau _2]$ if and only if $\Omega (\tau _1)<0$ and $\Omega (\tau _2)<0$. Therefore, if (9b) holds for $\tau =\tau _1$ and $\tau =\tau _2$ then

$$\begin{aligned} \dot{V}(x_t) + \alpha V(x_t) \le 0, \quad \forall t \ge t_0. \end{aligned}$$

(16)

Integrating this inequality gives (10). $\square$

Consider the following switched system with interval time-varying delay and nonlinear perturbations.

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t) = A_{\sigma (t)}x(t) + D_{\sigma (t)}x(t-\tau (t)) + f_{\sigma (t)}(t, x(t), x(t-\tau (t))),\\ x_{t_0} = x(t_0 +s) = \phi (s), \quad s \in [-\tau _2, 0]. \end{array}\right. \end{aligned}$$

(17)

The following theorem provides an exponential stability condition for the case where the time derivative of the delay is unknown or the time delay is not differentiable.

Theorem 1

Given $\alpha > 0.$ Assume that there exist matrices $P_i = \begin{bmatrix} P_{11}^i&P_{12}^i&P_{13}^i&P_{14}^i \\ P_{21}^i&P_{22}^i&P_{23}^i&P_{24}^i \\ P_{31}^i&P_{32}^i&P_{33}^i&P_{34}^i \\ P_{41}^i&P_{42}^i&P_{43}^i&P_{44}^i\end{bmatrix} \in {\mathbb {S}}^+_{4n}$, $Q_i, R_i, S_i, Z_i \in {\mathbb {S}}^+_n$, $X_i \in {\mathbb {R}}^{3n\times 3n}, (i =1, \ldots , N)$, and scalars $\varepsilon _i > 0, (i =1, \ldots , N)$ such that the following LMIs hold for $\tau \in \{\tau _1, \tau _2\}$

$$\begin{aligned} \Phi ^i&=\begin{bmatrix}\overline{Z}_i&X_i \\ X_i^T&\overline{Z}_i \end{bmatrix}\ge 0, \quad i = 1, \ldots , N,\end{aligned}$$

(18a)

$$\begin{aligned} \Omega ^i(\tau )&=\Xi _1^i(\tau )-\Xi _2^i -\Gamma ^T \Phi ^i \Gamma < 0, \quad i = 1, \ldots , N. \end{aligned}$$

(18b)

Then, system (17) is exponentially stable for any switching signal with average dwell time satisfying

$$\begin{aligned} T_a > T_a^* = \frac{\ln \mu }{\alpha }. \end{aligned}$$

(19)

Moreover, an estimate of state decay is given by

$$\begin{aligned} \Vert x(t, \phi )\Vert \le \sqrt{\frac{b}{a}}\mathrm{e}^{-\lambda (t-t_0)}\Vert x_{t_0}\Vert , \end{aligned}$$

(20)

where $\mu \ge 1$ satisfies

$$\begin{aligned} P_i \le \mu P_j, \quad Q_i \le \mu Q_j, \quad R_i \le \mu R_j, \quad S_i \le \mu S_j, \quad Z_i \le \mu Z_j, \quad \forall i, j \in {\mathcal {N}},\nonumber \\ \end{aligned}$$

(21)

$$\begin{aligned} {\mathscr {A}}_i&= A_ie_1 + D_ie_3 + e_{11} ,\quad \overline{S}_i = \mathrm {diag}\{\mathrm{e}^{-\alpha \tau _1}S_i, 3\mathrm{e}^{-\alpha \tau _1}S_i, 5\mathrm{e}^{-\alpha \tau _1}S_i\}, \quad i = 1, \ldots , N,\\ \overline{Z}_i&= \mathrm {diag}\{\mathrm{e}^{-\alpha \tau _2}Z_i, 3\mathrm{e}^{-\alpha \tau _2}Z_i, 5\mathrm{e}^{-\alpha \tau _2}Z_i \}, \quad i = 1, \ldots , N, \\ \Xi _1^i(\tau )&= {\mathscr {G}}_1^T(\tau )P_i{\mathscr {G}}_2 + {\mathscr {G}}_2^TP_i{\mathscr {G}}_1(\tau ) + \alpha {\mathscr {G}}_1^T(\tau )P_i{\mathscr {G}}_1(\tau ) + e_1^T(Q_i + \varepsilon _i L_i^TL_i)e_1\\&\quad + e_2^T\left( \mathrm{e}^{-\alpha \tau _1}R_i - \mathrm{e}^{-\alpha \tau _1}Q_i \right) e_2 - \mathrm{e}^{-\alpha \tau _2}e_4^TR_ie_4+ \varepsilon _i e_3^TG_i^TG_ie_3 \\&\quad - \varepsilon _i e_{11}^Te_{11} + {\mathscr {A}}_i^T\left( \tau _1^2S_i + \tau _{12}^2Z_i \right) {\mathscr {A}}_i, \quad i = 1, \ldots , N,\\ \Xi _2^i&= {\mathscr {G}}_3^TF^T\overline{S}_iF{\mathscr {G}}_3, \quad i = 1, \ldots , N,\\ \lambda&= \frac{1}{2}\left( \alpha - \frac{\ln \mu }{T_a} \right) , \quad a = \min \limits _{i \in {\mathcal {N}}}\lambda _{\min }(P_{11}^i), \\ b&= \max \limits _{i \in {\mathcal {N}}}\lambda _{\max }(P_i) + \tau _1 \max \limits _{i \in {\mathcal {N}}}\lambda _{\max }(Q_i) + \tau _{12}\max \limits _{i \in {\mathcal {N}}}\lambda _{\max }(R_i) + \frac{1}{2}\max \limits _{i \in {\mathcal {N}}}\tau _1^3\lambda _{\max }(S_i)\\&\quad + \frac{1}{2}\tau _{12}^2(\tau _1 + \tau _2)\max \limits _{i \in {\mathcal {N}}}\lambda _{\max }(Z_i). \end{aligned}$$

Proof

Define the following piecewise Lyapunov–Krasovskii functional

$$\begin{aligned} V(x_t)= & {} V_{\sigma (t)}(x_t) = \eta ^T(t)P_{\sigma (t)}\eta (t) + \int _{t-\tau _1}^t\mathrm{e}^{\alpha (s-t)}x^T(s)Q_{\sigma (t)}x(s)\hbox {d}s\nonumber \\&+ \int _{t-\tau _2}^{t-\tau _1}\mathrm{e}^{\alpha (s-t)}x^T(s)R_{\sigma (t)}x(s)\hbox {d}s+ \tau _1\int _{-\tau _1}^0\int _{t+s}^t\mathrm{e}^{\alpha (s-t)}\dot{x}^T(u)S_{\sigma (t)}\dot{x}(u)\hbox {d}u\hbox {d}s \nonumber \\&+ \tau _{12}\int _{-\tau _2}^{-\tau _1}\int _{t+s}^t\mathrm{e}^{\alpha (s-t)}\dot{x}^T(u)Z_{\sigma (t)}\dot{x}(u)\hbox {d}u\hbox {d}s. \end{aligned}$$

(22)

When $t \in [t_k, t_{k+1}),$ (18a), (18b) and Lemma 3 give

$$\begin{aligned} V(x_t) = V_{\sigma (t)}(x_t) \le \mathrm{e}^{-\alpha (t-t_k)}V_{\sigma (t_k)}(x_{t_k}). \end{aligned}$$

(23)

Using (21) and (23), at switching instant $t_i,$ we have

$$\begin{aligned} V_{\sigma (t_i)}(x_{t_i}) \le \mu V_{\sigma (t_i^-)}(x_{t_i^-}), \quad i = 1, 2, \ldots \end{aligned}$$

(24)

It follows from (23), (24) and the relation $k = N_{\sigma }(t_0, t) \le \frac{t-t_0}{T_a},$ we obtain

$$\begin{aligned} \begin{aligned} V(x_t)&\le \mathrm{e}^{-\alpha (t-t_k)}\mu V_{\sigma (t_k^-)}(x_{t_k^-}) \le \cdots \le \mathrm{e}^{-\alpha (t-t_0)}\mu ^k V_{\sigma (t_0)}(x_{t_0})\\&\le \mathrm{e}^{-\left( \alpha - \frac{\ln \mu }{T_a} \right) (t-t_0)}V_{\sigma (t_0)}(x_{t_0}). \end{aligned} \end{aligned}$$

(25)

By using simple computing, we have

$$\begin{aligned} a\Vert x(t, \phi )\Vert ^2 \le V(x_t), \quad V_{\sigma (t_0)}(x_{t_0}) \le b\Vert x_{t_0}\Vert ^2. \end{aligned}$$

(26)

Combining (25) and (26) leads to

$$\begin{aligned} \Vert x(t, \phi )\Vert ^2 \le \frac{1}{a}V(x_t) \le \frac{b}{a} \mathrm{e}^{-\left( \alpha - \frac{\ln \mu }{T_a} \right) (t-t_0)}\Vert x_{t_0}\Vert ^2. \end{aligned}$$

(27)

Now, it is easy to obtain (20), which completes the proof of this theorem. $\square$

Remark 1

It should be noted that the problem of stability analysis of delayed switched nonlinear systems has been considered in the literature [11, 24,25,26, 38, 65]. However, the shortcoming of the method used in these works is that the delay function is assumed to be differential and its derivative is still bounded. Although it was theoretically and numerically shown that the integral inequalities proposed in [9, 37] give tighter lower bound than the ones based on Jensen’s inequality and its variants [8, 45], particular challenging remains on how to construct a suitable and effective Lyapunov–Krasovskii function for nonlinear delayed switched systems. By using novel refined Jensen-based inequalities proposed in [9, 37] combining with the reciprocally convex technique [36] when estimating the derivative of the Lyapunov–Krasovskii functional and the average dwell time approach, Theorem 1 solves the problem in case where the time derivative of the delay is unknown or the time delay is not differentiable. Therefore, our result may be less conservative than existing results [11, 24,25,26, 38, 65].

When the rate of change of the delay $\tau (t)$ satisfies an upper bound condition, that is $\dot{\tau }(t) \le \delta < 1,$ where $\delta$ is a known constant, the following corollary provides an improved sufficient condition for exponential stability of switched systems with interval time-varying delay and nonlinear perturbations (17). Numerical Example 1 in Sect. 5 will be given to demonstrate the improvement of our results over existing results in the literature.

Corollary 1

Given $\alpha > 0.$ Assume that there exist matrices $P_i = \begin{bmatrix} P_{11}^i&P_{12}^i&P_{13}^i&P_{14}^i \\ P_{21}^i&P_{22}^i&P_{23}^i&P_{24}^i \\ P_{31}^i&P_{32}^i&P_{33}^i&P_{34}^i \\ P_{41}^i&P_{42}^i&P_{43}^i&P_{44}^i \end{bmatrix} \in {\mathbb {S}}^+_{4n}$, $Q_i, R_i, S_i, Z_i, Q_i^d, W_i^d, M_i^d \in {\mathbb {S}}^+_n$, $X_i \in {\mathbb {R}}^{3n\times 3n}, (i =1, \ldots , N)$, and scalars $\varepsilon _i > 0, (i =1, \ldots , N)$ such that the following LMIs hold for $\tau \in \{\tau _1, \tau _2\}$

$$\begin{aligned} \Phi ^i&=\begin{bmatrix}{\overline{Z}}_i&X_i \\ X_i^T&\overline{Z}_i \end{bmatrix}\ge 0, \quad i = 1, \ldots , N,\end{aligned}$$

(28a)

$$\begin{aligned} {\hat{\Omega }}^i(\tau )&={\hat{\Xi }}_1^i(\tau )-\Xi _2^i -\Gamma ^T \Phi ^i \Gamma < 0, \quad i = 1, \ldots , N. \end{aligned}$$

(28b)

Then, system (17) is exponentially stable for any switching signal with average dwell time satisfying

$$\begin{aligned} T_a > T_a^* = \frac{\ln \mu }{\alpha }. \end{aligned}$$

(29)

Moreover, an estimate of state decay is given by

$$\begin{aligned} \Vert x(t, \phi )\Vert \le \sqrt{\frac{\mathbf {b}}{a}}\mathrm{e}^{-\lambda (t-t_0)}\Vert x_{t_0}\Vert , \end{aligned}$$

(30)

where $\mu \ge 1$ satisfies

$$\begin{aligned}&P_i\le \mu P_j,\quad Q_i \le \mu Q_j,\quad R_i \le \mu R_j,\quad S_i \le \mu S_j, Z_i\le \mu Z_j,\quad Q_{i}^d \le \mu Q_{j}^d,\nonumber \\&\quad W_i^d \le \mu W_j^d,\quad M_i^d \le \mu M_j^d,\quad \forall i,\quad j \in {\mathcal {N}}, \end{aligned}$$

(31)

$$\begin{aligned} {\mathscr {A}}_i&= A_ie_1 + D_ie_3 + e_{11} ,\quad \overline{S}_i = \mathrm {diag}\left\{ \mathrm{e}^{-\alpha \tau _1}S_i, 3\mathrm{e}^{-\alpha \tau _1}S_i, 5\mathrm{e}^{-\alpha \tau _1}S_i\right\} , \quad i = 1, \ldots , N,\\ \overline{Z}_i&= \mathrm {diag}\left\{ \mathrm{e}^{-\alpha \tau _2}Z_i, 3\mathrm{e}^{-\alpha \tau _2}Z_i, 5\mathrm{e}^{-\alpha \tau _2}Z_i \right\} , \quad i = 1, \ldots , N, \\ \hat{\Xi }_1^i(\tau )&= {\mathscr {G}}_1^T(\tau )P_i{\mathscr {G}}_2 + {\mathscr {G}}_2^TP_i{\mathscr {G}}_1(\tau ) + \alpha {\mathscr {G}}_1^T(\tau )P_i{\mathscr {G}}_1(\tau ) \\&\quad + e_1^T(Q_i + Q_i^d + \varepsilon _i L_i^TL_i)e_1 \\&\quad + e_2^T\left( \mathrm{e}^{-\alpha \tau _1}R_i - \mathrm{e}^{-\alpha \tau _1}Q_i \right) e_2 - \mathrm{e}^{-\alpha \tau _2}e_4^TR_ie_4\\&\quad + e_3^T\left( \varepsilon _i G_i^TG_i - (1- \delta )\mathrm{e}^{-\alpha \tau _2}Q_{i}^d \right) e_3\\&\quad - \varepsilon _i e_{11}^Te_{11} + \mathrm{e}^{-\alpha \tau _1}e_2^TW_i^de_2 - \mathrm{e}^{-\alpha \tau _2}e_4^TM_i^de_4 \\&\quad + (1-\delta )e_3^T\left( \mathrm{e}^{-\alpha \tau _1}M_i^d -\mathrm{e}^{-\alpha \tau _2}W_i^d \right) e_3\\&\quad + {\mathscr {A}}_i^T\left( \tau _1^2S_i + \tau _{12}^2Z_i \right) \mathcal {A}_i, \quad i = 1, \ldots , N,\\ \Xi _2^i&= {\mathscr {G}}_3^TF^T\overline{S}_iF{\mathscr {G}}_3, \quad i = 1, \ldots , N,\\ \lambda&= \frac{1}{2}\left( \alpha - \frac{\ln \mu }{T_a} \right) , \quad a = \min \limits _{i \in {\mathcal {N}}}\lambda _{\min }\left( P_{11}^i\right) , \\ \mathbf {b}&= \max \limits _{i \in {\mathcal {N}}}\lambda _{\max }(P_i) + \tau _1 \max \limits _{i \in {\mathcal {N}}}\lambda _{\max }(Q_i) + \tau _{12}\max \limits _{i \in {\mathcal {N}}}\lambda _{\max }(R_i) + \frac{1}{2}\max \limits _{i \in {\mathcal {N}}}\tau _1^3\lambda _{\max }(S_i)\\&\quad + \frac{1}{2}\tau _{12}^2(\tau _1 + \tau _2)\max \limits _{i \in {\mathcal {N}}}\lambda _{\max }(Z_i) + \tau _{12}\max \limits _{i \in {\mathcal {N}}}\lambda _{\max }\left( W_i^d\right) + \tau _{12}\max \limits _{i \in {\mathcal {N}}}\lambda _{\max }\left( M_i^d\right) \\&\quad +\tau _{2}\max \limits _{i \in {\mathcal {N}}}\lambda _{\max }(Q_i^d). \end{aligned}$$

Proof

We slightly modify the Lyapunov–Krasovskii functional as follows

$$\begin{aligned} \hat{V}(x_t)= & {} V(x_t) + \int _{t-\tau (t)}^{t}\mathrm{e}^{\alpha (s-t)}x^T(s)Q_{\sigma (t)}^d x(s)\hbox {d}s \\&+ \int _{t-\tau (t)}^{t-\tau _1}\mathrm{e}^{\alpha (s-t)}x^T(s)W_{\sigma (t)}^dx(s)\hbox {d}s \\&+ \int _{t-\tau _2}^{t-\tau (t)}\mathrm{e}^{\alpha (s-t)}x^T(s)M_{\sigma (t)}^dx(s)\hbox {d}s, \end{aligned}$$

where $V(x_t)$ is as defined in the proof of Theorem 1, and then by following the similar lines as in the proof of Theorem 1, the remained processes can be easily derived. $\square$

Remark 2

Recently, the authors in [14, 28] proposed a new integral inequality which covers Wirtinger-based integral inequality [42] and free-weighting-based inequality [58] as special cases. By using the new integral inequality in [14, 28] combining with the reciprocally convex technique [36] when estimating the derivative of the Lyapunov–Krasovskii functional and the average dwell time approach, improvement conditions for exponential stability of switched nonlinear systems with interval time-varying delay can be derived, which will be done in our future works.

4 Passivity Analysis

We first consider the following nonswitched delay system

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t) = Ax(t) + Dx(t-\tau (t)) + E\omega (t) + f(t, x(t), x(t-\tau (t)), \omega (t)),\\ x_{t_0}(s) = x(t_0+s) = \phi (s), \quad s \in [-\tau _2, 0],\\ z(t) = Mx(t) + Ux(t-\tau (t)) + W\omega (t), \end{array}\right. \end{aligned}$$

(32)

where the nonlinear perturbation $f(t, x(t), x(t-\tau (t)), \omega (t))$ satisfies the following condition:

$$\begin{aligned} f^T(.)f(.) \le x^T(t)L^TLx(t) + x^T(t-\tau (t))G^TGx(t-\tau (t)) + \omega ^T(t)H^TH\omega (t) ,\nonumber \\ \end{aligned}$$

(33)

with L, G, H are known matrices.

We denote $e_i = [0_{n \times (i-1)n}\quad I_n \quad 0_{n \times (11-i)n} \quad 0_{n \times m}], (i=1, \ldots , 11), e_{12} = [0_{m \times 11n}\quad I_{m}],$ $\mathtt {A}=Ae_1 + De_3 + e_{11} + Ee_{12},$ augmented vector $\xi _0(t)=[\chi _{01}^T(t) \quad \chi _{02}^T(t) \quad \chi _{03}^T(t) \quad \omega ^T(t)]^T.$

We have the following lemma.

Lemma 4

Given $\alpha > 0.$ Assume that there exist matrices $P\in {\mathbb {S}}^+_{4n}$, $Q, R, S, Z \in {\mathbb {S}}^+_n$, $X\in {\mathbb {R}}^{3n\times 3n}$, and two scalars $\gamma \ge 0, \varepsilon > 0$ such that the following LMIs hold for $\tau \in \{\tau _1, \tau _2\}$

$$\begin{aligned} \Phi&=\begin{bmatrix}\overline{Z}&X \\ X^T&\overline{Z} \end{bmatrix}\ge 0,\end{aligned}$$

(34a)

$$\begin{aligned} \Psi (\tau )&=\Psi _1(\tau )-\Xi _2 -\Gamma ^T \Phi \Gamma < 0. \end{aligned}$$

(34b)

Then, along the trajectory of system (32), we have

$$\begin{aligned} V(x_t) \le \mathrm{e}^{-\alpha (t-t_0)}V(x_{t_0}) - \int _{t_0}^t\mathrm{e}^{-\alpha (t-s)}\varphi (s)\hbox {d}s , \quad \forall t \ge t_0, \end{aligned}$$

(35)

where

$$\begin{aligned} \varphi (s)&= -2z^T(s)\omega (s) - \gamma \omega ^T(s)\omega (s),\\ \Psi _1(\tau )&= {\mathscr {G}}_1^T(\tau )P{\mathscr {G}}_2 + {\mathscr {G}}_2^TP{\mathscr {G}}_1(\tau ) + \alpha {\mathscr {G}}_1^T(\tau )P{\mathscr {G}}_1(\tau ) + e_1^T(Q + \varepsilon L^TL)e_1\\&\quad + e_2^T\left( \mathrm{e}^{-\alpha \tau _1}R - \mathrm{e}^{-\alpha \tau _1}Q \right) e_2- \mathrm{e}^{-\alpha \tau _2}e_4^TRe_4+ \varepsilon e_3^TG^TGe_3 \\&\quad - \varepsilon e_{11}^Te_{11} + \mathtt {A}^T\left( \tau _1^2S + \tau _{12}^2Z \right) \mathtt {A} - e_1^TM^Te_{12} - e_{12}^TMe_1\\&\quad - e_3^TU^Te_{12} - e_{12}^TUe_3 - e_{12}^T\left( \gamma I + W + W^T - \varepsilon H^TH \right) e_{12}. \end{aligned}$$

Proof

The proof is similar to that of Lemma 3. $\square$

Now, we present a sufficient condition for passivity analysis of switched systems with interval time-varying delays and nonlinear perturbations (1).

Theorem 2

Given $\alpha > 0.$ Assume that there exist matrices $P_i = \begin{bmatrix} P_{11}^i&P_{12}^i&P_{13}^i&P_{14}^i \\ P_{21}^i&P_{22}^i&P_{23}^i&P_{24}^i \\ P_{31}^i&P_{32}^i&P_{33}^i&P_{34}^i \\ P_{41}^i&P_{42}^i&P_{43}^i&P_{44}^i \end{bmatrix} \in {\mathbb {S}}^+_{4n}$, $Q_i, R_i, S_i, Z_i \in {\mathbb {S}}^+_n$, $X_i \in {\mathbb {R}}^{3n\times 3n}, (i =1, \ldots , N)$, and scalars $\varepsilon _i > 0, (i =1, \ldots , N), \gamma \ge 0$ such that the following LMIs hold for $\tau \in \{\tau _1, \tau _2\}$

$$\begin{aligned} \Phi ^i&=\begin{bmatrix}\overline{Z}_i&X_i \\ X_i^T&\overline{Z}_i \end{bmatrix}\ge 0, \quad i = 1, \ldots , N,\end{aligned}$$

(36a)

$$\begin{aligned} \Psi ^i(\tau )&=\Psi _1^i(\tau )-\Xi _2^i -\Gamma ^T \Phi ^i \Gamma < 0, \quad i = 1, \ldots , N. \end{aligned}$$

(36b)

Then, system (1) is passive for any switching signal with average dwell time defined by (19), where $\mu \ge 1$ satisfies (21) and

$$\begin{aligned} \mathtt {A}_i&= A_ie_1 + D_ie_3 + e_{11} + E_ie_{12},\\ \Psi _1^i(\tau )&= {\mathscr {G}}_1^T(\tau )P_i{\mathscr {G}}_2 + {\mathscr {G}}_2^TP_i{\mathscr {G}}_1(\tau ) + \alpha {\mathscr {G}}_1^T(\tau )P_i{\mathscr {G}}_1(\tau ) + e_1^T\left( Q_i + \varepsilon _i L_i^TL_i\right) e_1\\&\quad + e_2^T\left( \mathrm{e}^{-\alpha \tau _1}R_i - \mathrm{e}^{-\alpha \tau _1}Q_i \right) e_2 - \mathrm{e}^{-\alpha \tau _2}e_4^TR_ie_4+ \varepsilon _i e_3^TG_i^TG_ie_3 \\&\quad - \varepsilon _i e_{11}^Te_{11} + {\mathtt {A}}_i^T\left( \tau _1^2S_i + \tau _{12}^2Z_i \right) \mathtt {A}_i - e_1^TM_i^Te_{12} - e_{12}^TM_ie_1\\&\quad - e_3^TU_i^Te_{12} - e_{12}^TU_ie_3 - e_{12}^T\left( \gamma I + W_i + W_i^T - \varepsilon _i H_i^TH_i \right) e_{12}. \end{aligned}$$

Proof

When $\omega (t) = 0,$ (36a) and (36b) imply (18a) and (18b). Therefore, from Theorem 1, the system is exponentially stable. To show the passivity analysis of system (1), we choose Lyapunov–Krasovskii functional (22). From (21), we have

$$\begin{aligned} V(x_{t_i}) \le \mu V(x_{t_i^-}), \quad i = 1, 2, \ldots \end{aligned}$$

(37)

For any $t\in [t_k, t_{k+1}),$ noticing (36a), (36b) and from Lemma 4, we have

$$\begin{aligned} V(x_t) \le \mathrm{e}^{-\alpha (t-t_k)}V(x_{t_k}) - \int _{t_k}^t\mathrm{e}^{-\alpha (t-s)}\varphi (s)\hbox {d}s. \end{aligned}$$

(38)

Combining (37) and (38) leads to

$$\begin{aligned} V(x_t)\le & {} \mu V(x_{t_k^-})\mathrm{e}^{-\alpha (t-t_k)}-\int _{t_k}^t\mathrm{e}^{-\alpha (t-s)}\varphi (s)\hbox {d}s\nonumber \\\le & {} \mu ^k V(x_{t_0})\mathrm{e}^{-\alpha (t-t_0)} -\mu ^k\int _{t_0}^{t_1}\mathrm{e}^{-\alpha (t-s)}\varphi (s)\hbox {d}s - \mu ^{k-1}\int _{t_1}^{t_2}\mathrm{e}^{-\alpha (t-s)}\varphi (s)\hbox {d}s\nonumber \\&- \cdots - \int _{t_k}^t\mathrm{e}^{-\alpha (t-s)}\varphi (s)\hbox {d}s \nonumber \\= & {} \mathrm{e}^{-\alpha (t-t_0)+N_{\sigma }(t_0, t)\ln \mu }V(x_{t_0}) - \int _{t_0}^t\mathrm{e}^{-\alpha (t-s)+N_{\sigma }(s, t)\ln \mu }\varphi (s)\hbox {d}s. \end{aligned}$$

(39)

Under zero initial condition, (39) gives

$$\begin{aligned} 0 \le - \int _{t_0}^t\mathrm{e}^{-\alpha (t-s)+N_{\sigma }(s, t)\ln \mu }\varphi (s)\hbox {d}s. \end{aligned}$$

(40)

By virtue of (19), we get $N_{\sigma }(s, t) \le \frac{t-s}{T_a} \le \frac{(t-s)\alpha }{\ln \mu }.$ Therefore, from (40), we have

$$\begin{aligned} -\int _{t_0}^t \varphi (s)\hbox {d}s \ge 0. \end{aligned}$$

Hence

$$\begin{aligned} 2\int _{t_0}^tz^T(s)\omega (s)\hbox {d}s \ge - \gamma \int _{t_0}^t\omega ^T(s)\omega (s)\hbox {d}s. \end{aligned}$$

Thus, in the light of Definition 3, system (1) is passive. The proof of theorem is completed. $\square$

Remark 3

By using novel refined Jensen-based inequalities proposed in [9, 37] combining with the reciprocally convex technique [36] and the average dwell time approach, Theorem 2 derives a new sufficient condition for the problem of passivity analysis of a class of delayed switched nonlinear systems. The proposed criteria are quite general since many factors, such as interval time-varying delay in the state and output, nondifferentiable time-varying delay, are considered. Therefore, the results obtained in this paper generalize and improve those given in the previous literature [21, 22, 66, 67].

5 Numerical Examples

In this subsection, we provide four examples and compare our results with the existing results in the literature to show the effectiveness of ours.

Table 1 Comparing the previous results with our results

Example 1

Consider switched nonlinear system (17) with the following parameters, which first considered in [38]:

$$\begin{aligned} A_1&= \begin{bmatrix} 0.1&-0.001 \\ -0.001&0.15 \end{bmatrix}, \quad D_1 = \begin{bmatrix} -0.7&0.001 \\ 0.001&-0.7 \end{bmatrix},\\ A_2&= \begin{bmatrix} 0.15&-0.001 \\ -0.001&0.05 \end{bmatrix}, \quad D_2 = \begin{bmatrix} -0.6&0.001 \\ 0.001&-0.6 \end{bmatrix}, \end{aligned}$$

and nonlinear perturbations $f_i(.), i = 1, 2,$ satisfy the following condition

$$\begin{aligned} \Vert f_i(t, x(t), x(t-\tau (t)))\Vert \le 0.1\Vert x(t)\Vert + 0.0667\Vert x(t-\tau (t))\Vert ,\quad (i=1,2). \end{aligned}$$

By simple computing, we have

$$\begin{aligned} f_i^T(.)f_i(.) \le x^T(t)(2*0.1^2)x(t) + x^T(t-\tau (t))(2*0.0667^2)x(t-\tau (t)), i =1, 2. \end{aligned}$$

This example has been utilized in many works in the literature to check the superiority of stability criteria for switched system with interval time-varying delay and nonlinear perturbations. Table 1 lists the allowable maximum upper bounds delays (MUBDs) of $\tau _2$ that guarantee the exponential stability for the system with given lower bound $\tau _{1} = 0$ and $\alpha = 0.05, \delta = 0.5$. Comparing with existing results, it is clear that our result has an improvement over those in [24, 26, 38]. On the other hand, when the time-varying delay $\tau (t)$ is nondifferentiable or $\delta$ is unknown, the method reported in [11, 24,25,26, 38] cannot be applied. Notably, by using Theorem 1, conditions (18a) and (18b) are feasible with $\alpha = 0.2, \mu = 1.01, \tau _1 = 0, \tau _2 = 1, \varepsilon _1 = 0.1155, \quad \varepsilon _2 = 0.0997,$ and

$$\begin{aligned} P_1&= \begin{bmatrix} 0.0178&0.0000&-0.0844&-0.0001&-0.0087&-0.0000&0&0 \\ 0.0000&0.0184&-0.0001&-0.0859&-0.0000&-0.0090&0&0 \\ -0.0844&-0.0001&1.0941&-0.0002&0.0148&0.0000&0&0 \\ -0.0001&-0.0859&-0.0002&1.0873&0.0000&0.0158&0&0 \\ -0.0087&-0.0000&0.0148&0.0000&0.0078&0.0000&0&0 \\ -0.0000&-0.0090&0.0000&0.0158&0.0000&0.0081&0&0 \\ 0&0&0&0&0&0&0.6786&0 \\ 0&0&0&0&0&0&0&0.6786 \end{bmatrix},\\ P_2&= \begin{bmatrix} 0.0178&0.0000&-0.0844&-0.0001&-0.0087&-0.0000&0&0 \\ 0.0000&0.0183&-0.0001&-0.0859&-0.0000&-0.0090&0&0 \\ -0.0844&-0.0001&1.0942&-0.0002&0.0149&0.0000&0&0 \\ -0.0001&-0.0859&-0.0002&1.0873&0.0000&0.0158&0&0 \\ -0.0087&-0.0000&0.0149&0.0000&0.0078&0.0000&0&0 \\ -0.0000&-0.0090&0.0000&0.0158&0.0000&0.0081&0&0 \\ 0&0&0&0&0&0&0.6786&0 \\ 0&0&0&0&0&0&0&0.6786 \end{bmatrix},\\ Q_1&= Q_2 = \begin{bmatrix} 0.0717&0.0001 \\ 0.0001&0.0737 \end{bmatrix}, \quad S_1 = S_2 = \begin{bmatrix} 0.0015&0.0000 \\ 0.0000&0.0015 \end{bmatrix}, \\ R_1&= R_2 = \begin{bmatrix} 0.0018&0.0000 \\ 0.0000&0.0022 \end{bmatrix}, \quad Z_1= \begin{bmatrix} 0.0051&-0.0000 \\ -0.0000&0.0056 \end{bmatrix}, \quad Z_2 = \begin{bmatrix} 0.0049&-0.0000 \\ -0.0000&0.0045 \end{bmatrix},\\ X_1&= \begin{bmatrix} -0.0036&0.0000&0.0009&-0.0000&0.0000&0.0000 \\ 0.0000&-0.0039&-0.0000&0.0006&0.0000&0.0000 \\ -0.0008&-0.0000&-0.0007&-0.0000&-0.0006&0.0000 \\ -0.0000&-0.0008&-0.0000&-0.0004&0.0000&-0.0007 \\ 0.0002&-0.0000&0.0007&-0.0000&0.0012&-0.0000 \\ -0.0000&0.0002&-0.0000&0.0008&-0.0000&0.0015 \end{bmatrix}, \\ X_2&= \begin{bmatrix} -0.0032&0.0000&0.0003&0.0000&0.0000&0.0000 \\ 0.0000&-0.0029&0.0000&0.0007&0.0000&0.0001 \\ -0.0009&-0.0000&-0.0004&-0.0000&-0.0005&0.0000 \\ -0.0000&-0.0010&-0.0000&-0.0005&0.0000&-0.0005 \\ 0.0001&-0.0000&0.0007&-0.0000&0.0011&-0.0000 \\ -0.0000&0.0001&-0.0000&0.0005&-0.0000&0.0010 \end{bmatrix}. \end{aligned}$$

Thus, the systems are exponentially stable for any switching signal with an average dwell time of $T_a > T_a^* = 0.0498$ and the solutions $x(t, \phi )$ of the system satisfy the following estimate:

$$\begin{aligned} \Vert x(t, \phi )\Vert \le 7.7530~\mathrm{e}^{-0.0751(t-t_0)}\Vert x_{t_0}\Vert . \end{aligned}$$

5.1 Simulation Results

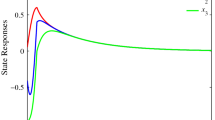
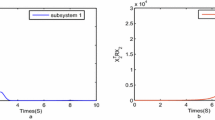
In order to obtain simulation results, the time-varying delay $\tau (t)$ is chosen as $(1-|\sin t|)$. Clearly, the time-varying delay function is nondifferentiable. The perturbation is assumed to be as $f_i(t,x(t),x(t-\tau (t)))= \begin{bmatrix} 0.1\sin ^2t \\ 0.1 \end{bmatrix}x(t)+ \begin{bmatrix} 0.0667\cos ^2t \\ 0.0667 \end{bmatrix}x(t-\tau (t)) (i = 1, 2)$. Figure 1 shows the switching signals of system (17) with two subsystems, while Fig. 2 shows the state response of the considered switched nonlinear system under the designed switching signal depicted in Fig. 1.

Fig. 1

Switching signals of two subsystems

Fig. 2

Responses of state trajectories of the switched nonlinear system with the designed switching signal depicted in Fig. 1

Example 2

Consider switched system (17) with $f_i(.) = 0, (i=1,2)$ as reported in [25, 65] with the parameters

$$\begin{aligned}&N = 2, \quad A_1 = A_2 = \begin{bmatrix} -1&0\\0&-1 \end{bmatrix}, \quad D_1 = \begin{bmatrix} 0&0.5 \\ -1&0 \end{bmatrix}, \quad D_2 = \begin{bmatrix} 0&1 \\ -0.5&0 \end{bmatrix}, \nonumber \\&\quad f_i(.) = 0, (i=1,2). \end{aligned}$$

In order to compare the results in [25, 65], using Theorem 1, the comparison results are listed in Tables 2 and 3 for $\alpha = 0$ and $\alpha = 0.3,$ respectively. Clearly, the results proposed in this paper provide a larger admissible upper bound delay to guarantee the asymptotic or exponential stability of system (17) with $f_i(.) = 0, (i=1,2)$.

Table 2 Comparative results of $\tau _2$ for given $\alpha = 0$ and various $\tau _1$

Table 3 Comparative results of $\tau _2$ for given $\alpha = 0.3$ and various $\tau _1$

5.2 Simulation Results

To obtain simulation results, we choose $\alpha = 0$ and $\tau (t) =1 + 1.5|\sin t|$. Figure 3 shows the switching signals of system (17) with two subsystems, while Fig. 4 shows the state response of the considered switched system under the designed switching signal depicted in Fig. 3.

Fig. 3

Switching signals of two subsystems

Fig. 4

Responses of state trajectories of the switched system with the designed switching signal depicted in Fig. 3

Example 3

Consider a stream water quality dynamic model for Nile River [7, 31] in two modes of operation:

$$\begin{aligned} A_1= & {} \begin{bmatrix} k_{ce}^{1}&0 \\ -k_{de}^{1}&- k_{re}^{1} \end{bmatrix},\quad D_1 = \begin{bmatrix} k_{cd}^{1}&k_{od}^{1} \\ -k_{dd}^{1}&-k_{rd}^{1} \end{bmatrix},\quad f_{1}(.) = 0, \nonumber \\ A_2= & {} \begin{bmatrix} k_{ce}^{2}&0 \\ -k_{de}^{2}&- k_{re}^{2} \end{bmatrix},\quad D_2 = \begin{bmatrix} k_{cd}^{2}&k_{od}^{2} \\ -k_{dd}^{2}&-k_{rd}^{2} \end{bmatrix},\quad f_{2}(.) = 0, \end{aligned}$$

(41)

where $k_{ce}^{i}, k_{de}^{i}, k_{re}^{i}, k_{cd}^{i}, k_{od}^{i}, k_{dd}^{i}, k_{rd}^{i} (i = 1, 2)$ are composite rates. In this example, we assume that the time-varying delay function is nondifferentiable and satisfies condition (3). We now consider the problem of exponential stability for system (37) with the following parameters

$$\begin{aligned} k_{ce}^{1}= & {} 0.1,\quad k_{ce}^{2} = 0.2,\quad k_{de}^{1} = 3,\quad k_{de}^{2} = 4,\quad k_{re}^{1} = k_{re}^{2} = 2, \\ k_{cd}^{1}= & {} -1.55,\quad k_{cd}^{2} = -1.45,\quad k_{od}^{1} = 0.7,\quad k_{od}^{2} = 0.5,\\ k_{dd}^{1}= & {} 0.25,\quad k_{dd}^{2} = 0.15,\quad k_{rd}^{1} = 0.3,\quad k_{rd}^{2} = 0.1. \end{aligned}$$

The upper bounds $\tau _{2}$ for various $\tau _1$ with $\alpha = 0.1, \mu = 1.01$ for exponential stability of system (37) are derived by Theorem 1 in this paper and are listed in Table 4.

5.3 Simulation Results

To obtain simulation results, we choose $\alpha = 0.1$ and $\tau (t) =0.1 + 0.411|\sin t|$. Figure 5 shows the switching signals of system (17) with two subsystems, while Fig. 6 shows the state response of the considered switched system under the designed switching signal depicted in Fig. 5.

Table 4 Upper bound of $\tau _2$ for various $\tau _1$

Fig. 5

Switching signals of two subsystems

Fig. 6

Responses of state trajectories of the switched system with the designed switching signal depicted in Fig. 5

Example 4

Consider the following switched system with interval time-varying delays and nonlinear perturbations (1) with $N = 2,$

$$\begin{aligned} A_1&= \begin{bmatrix} -1&0 \\ 0.5&-1.8 \end{bmatrix}, \quad D_1 = \begin{bmatrix} 0&0.3 \\ -1&0 \end{bmatrix}, \quad E_1 = \begin{bmatrix} 2 \\ 1 \end{bmatrix}, \quad M_1 = \begin{bmatrix} 1&2 \end{bmatrix},\\&\quad U_1 = \begin{bmatrix} -1&2 \end{bmatrix}, \quad W_1 = \begin{bmatrix} 0.2 \end{bmatrix},\\ A_2&= \begin{bmatrix} -0.5&0 \\ 0.9&-2 \end{bmatrix}, \quad D_2 = \begin{bmatrix} 0&0.4 \\ -1&0 \end{bmatrix}, \quad E_2 = \begin{bmatrix} 1\\0 \end{bmatrix}, \quad M_2 = \begin{bmatrix} 1&3 \end{bmatrix}, \\&\quad U_2 = \begin{bmatrix} 2&-2 \end{bmatrix}, \quad W_2 = \begin{bmatrix} 0.5 \end{bmatrix}, \end{aligned}$$

and nonlinear perturbations $f_i(.), i = 1, 2,$ satisfy the following condition

$$\begin{aligned} f_i^T(.)f_i(.)\le & {} x^T(t)0.1^2x(t) + x^T(t-\tau (t))0.2^2x(t-\tau (t)) \\&+~\omega ^T(t)0.3^2\omega (t), \quad i = 1, 2. \end{aligned}$$

The upper bounds $\tau _{2}$ with $\alpha = 0.1, \mu = 2$ for passivity analysis of the system are derived by Theorem 2 in this paper and are listed in Table 5.

Table 5 Upper bound of $\tau _2$ for various $\tau _1$

6 Conclusion

In this paper, the problems of exponential stability and passivity analysis of switched nonlinear systems with interval time-varying delay have been investigated based on average dwell time approach. A novel piecewise Lyapunov–Krasovskii functional has been constructed to derive sufficient delay-dependent conditions. To reduce the conservatism of our results, refined Jensen-based inequalities combining with the reciprocally convex technique have been used to estimate the derivative of the Lyapunov–Krasovskii functional. Numerical examples and simulation results have been provided to show the validity and improvement of our derived results.

Future works can apply the proposed stability analysis method to further consider the problem of dissipativity analysis of various dynamic networks, such as neutral switched systems with interval time-varying mixed delays and nonlinear perturbations, switched neural networks systems with interval time-varying delays, stochastic and Markovian jumping complex systems with interval time-varying delays. To those dynamic networks, in general, constructing a new effective Lyapunov–Krasovskii functional is not an easy task, while the auxiliary function-based integral inequalities [14, 28, 37] can significantly reduce the conservatism of the derived conditions. This also needs to be further investigated in the future works.