Extended Finite-Time Boundedness and Stability for Switched Linear Systems with Large Delay Period

Abstract

In this paper, finite-time stability (FTS) and finite-time boundedness (FTB) are investigated for a class of switched linear systems with large delay period and input disturbances. The limitation of the frequency and the maximum ratio of large delay period are used to guarantee the properties of FTS and FTB. By constructing a piecewise Lyapunov functional with large delay integral terms, sufficient conditions that can guarantee the FTS and FTB are developed in the form of linear matrix inequalities. Two numerical examples are provided to demonstrate the effectiveness of the proposed results.

1 Introduction

Switched system is an important class of hybrid dynamical systems. The primary motivation for studying switched system is from its numerous applications in control of mechanical systems, such as aircraft and air traffic control, automotive industry and many other fields [9, 14, 15]. Many valuable results on switched systems have been developed in the last few decades. Most of the existing results related to stability of switched linear systems focus on the Lyapunov asymptotic stability which is defined over an infinite-time interval [1, 2, 4, 5, 15, 22, 27]. However, in many practical applications, the main concern is the behavior of the system over a fixed time interval. Some early literature related to FTS and FTB can be found in [10, 13, 17, 21]. The FTS problems have attracted scholars’ attention again in recent years such as [6, 7, 12, 16] and [23,24,25,26]. In addition, time-delay phenomena are commonly encountered in various engineering systems, which may degrade the system performance, cause oscillation and even lead to instability [3]. As a result, many research efforts have been devoted to the study of finite-time control for switched linear systems with delay [3, 20].

Note that the aforementioned results are mainly concerned with small delay systems. The study of FTS and FTB problems for switched systems which include both small and large delay subsystems is few focused on, even for the linear cases. Reference [19] is the first work to study the stability of a single linear system which is with large delay period, and the concepts of the length rate and the frequency of large delay period were introduced. Inspired by this, we wish to use the related method proposed in [19] to switched linear delayed systems which consist of both stable and unstable subsystems. To achieve this goal, several problems need to be solved. (1) How to choose Lyapunov functional to eliminate the influence of large delay? (2) How to realize the unity of the Lyapunov functional between the large delay subsystems and small delay one? (3) How to seek switching signal and calculate the ratio at each switching point?

The main task of the paper is to solve the above three problems. The first problem is solved primarily by constructing a new piecewise Lyapunov functional with large delay integral terms (LDITs) to eliminate the influence of large delay. For the second problem, a uniform Lyapunov functional was constructed for both stable and unstable subsystems, though the LDITs are not necessary for stable subsystems. Under the restriction on the maximum ratio between the running time of LDP and SDP, the third problem is effectively solved by introducing some LDITs to the piecewise Lyapunov functional candidate. The adding of LDITs makes the third problem solvable and does not increase the conservativeness of the criterion.

This paper is organized as follows: Sect. 2 gives some useful preliminaries. Section 3 provides the analysis of FTB and FTS for switched linear systems with large delay period, following two simulation examples in Sect. 4. Section 5 concludes this paper.

Notation

Throughout this paper, the notations are standard. $R^+$ stands for the set of all the nonnegative real numbers. $P>0$ denotes a positive definite matrix, and $*$ denotes the symmetric term in a symmetric matrix. $\mathcal {I}=\{0,1,2,\ldots ,L\}$ where $L>1$ is the number of subsystems. $\varOmega =\{R_i, i\in \mathcal {I}\}$ denotes a set of positive definite matrices. $\lambda _{\max }(P)$ and $\lambda _{\min }(P)$ denote the maximum and minimum eigenvalues of symmetric matrix P, respectively. ${\mathcal {N}}$ is used to denote an integer set $\{0,1,2,\ldots \}$.

2 Preliminaries

Consider a class of continuous switched linear systems with time-varying delay in a fixed finite-time interval [0, T]

$$\begin{aligned} \dot{x}(t)= & {} A_{\sigma (t)}x(t)+ A_{d\sigma (t)}x(t-d_{\sigma (t)}(t))+D_{\sigma (t)}\omega (t), \nonumber \\ \ x(t)= & {} \varphi (t),t\in [-h_3,0), \end{aligned}$$

(1)

where the state vector $x(t)\in R^{n}$, the input disturbance $\omega (t)\in R^{m}$ and

$$\begin{aligned}&\int _{0}^\mathrm{T}\omega ^\mathrm{T}(t)\omega (t)\hbox {d}t\le d_\omega ,\quad d_\omega \ge 0. \end{aligned}$$

(2)

$A_{\sigma (t)},A_{d\sigma (t)}$ and $D_{\sigma (t)}$ are known real constant matrices of appropriate dimensions. $\varphi (t):[-h_3, 0]\rightarrow R^n$ is a continuous initial function in which $h_3>0$ is constant. $d_{\sigma (t)}(t)$ denotes the time-varying delay satisfying

$$\begin{aligned} 0\le h_1\le d_{\sigma (t)}(t)\le h_3, \quad \dot{d}_{\sigma (t)}(t)\le d<1. \end{aligned}$$

(3)

The switching signal $\sigma (t):[0,T]\rightarrow \mathcal {I}$ is a piecewise constant function. It is assumed that the system switching is dependent on time. If $t\in [t_k ,t_{k+1})$, we say that the $\sigma (t_k)$th subsystem is active in the running time of $t_{k+1}-t_{k}$, in which $t_k$ stands for the switching instant for $k\in \mathcal {N}$. For simplicity, it is assumed $t_0=0$.

To facilitate the upcoming control design, two assumptions imposed on system (1) are given as follows.

Assumption 1

Switched system (1) is FTB if $d_{\sigma (t)}(t)$ satisfies $h_1\le d_{\sigma (t)}(t)\le h_2<h_3$ for $\forall t\in [0,T]$. Otherwise it is not FTB if $h_2 < d_{\sigma (t)}(t)\le h_3$ for $\forall t\in [0,T]$.

Assumption 2

Switched system (1) with $\omega (t)\equiv 0$ is FTS if $d_{\sigma (t)}(t)$ satisfies $h_1\le d_{\sigma (t)}(t)\le h_2<h_3$ for $\forall t\in [0,T]$. Otherwise it is not FTS if $h_2<d_{\sigma (t)}(t)\le h_3$ for $\forall t\in [0,T]$.

Definition 1

[19] Time interval $[T_1,T_2)$ is called large delay period (LDP) if for $\forall t\in [T_1,T_2)$, $h_2< d_{\sigma (t)}\le h_3$ holds. And it is called small delay period (SDP) if for $\forall t\in [T_1,T_2)$, $h_1\le d_{\sigma (t)}\le h_2$ holds.

Throughout this paper, we allow both the large delay and the small delay subsystems to coexist in system (1). The set of small delay subsystems are denoted by $\mathcal {I}_\mathrm{s}=\{0,2,4,\ldots , L-1\}$. In this case, when $t\in [t_{2k},t_{2k+1})$, $\sigma (t)\in \mathcal {I}_\mathrm{s}$ and $h_1\le d_{\sigma (t)}\le h_2$. The set of large delay subsystems are indicated by $\mathcal {I}_\mathrm{l}=\{1,3,5,\ldots ,L\}$. When $t\in [t_{2k+1},t_{2k+2})$, $\sigma (t)\in \mathcal {I}_\mathrm{l}$ and $h_2< d_{\sigma (t)}\le h_3$ hold. The running time of LDP and SDP is defined as $T_{\mathrm{l}(0,t)}$ and $T_{\mathrm{s}(0,t)}$, respectively. Let $N_{\sigma }(0,t)$ denote the switching times within a finite-time interval [0, t], while $N_{\mathrm{l}}(0,t)$ and $N_{\mathrm{s}}(0,t)$ indicate the switching times of LDP and SDP, respectively.

Definition 2

[25] Given a positive constant $\eta$, the switching signal $\sigma (t)$ in a finite interval $[0,T_\mathrm{f}]$ is said to possess a property of maximum ratio $\eta$ between the running time of LDP and SDP, if $\frac{T_{\mathrm{l}(0,t)}}{T_{\mathrm{s}(0,t)}}\le \eta$ hold for any $t\in [0,T_\mathrm{f}]$. Such a property is called MRRT $\eta$ and expressed as $\sigma _{\eta }$ for simplicity.

Definition 3

[19] For any $T_2>T_1\ge 0$, $F_\mathrm{f}(T_1,T_2)=\frac{N_{\mathrm{l}}(T_1,T_2)}{T_2-T_1}$ is referred to the frequency of LDP in the time interval $[T_1,T_2)$.

Definition 4

Given positive constants $T_\mathrm{f},c_1<c_2$ and $d_\omega \ge 0$, system (1) is extended finite-time boundedness with respect to $(c_1,c_2,\varOmega ,T_\mathrm{f},\sigma _{\eta }, d_\omega )$, if $\sup _{t\in [-h_3,0]}\{x^\mathrm{T}(t)R_{\sigma _{\eta }(t)}x(t),\dot{x}^\mathrm{T}(t)R_{\sigma _{\eta }(t)}\dot{x}(t)\}\le c_1\Longrightarrow {x^\mathrm{T}(t)R_{\sigma _{\eta }(t)}x(t)}\le c_2$ for any $t\in [0,T_\mathrm{f}]$.

Definition 5

[25] Given positive constants $T_\mathrm{f}$ and $c_1<c_2$, system (1) with disturbance $\omega (t)\equiv 0$ is extended FTS with respect to $(c_1,c_2,\varOmega ,T_\mathrm{f},\sigma _{\eta })$, if $\sup _{t\in [-h_3,0]}\{x^\mathrm{T}(t)R_{\sigma _{\eta }(t)}x(t),\dot{x}^\mathrm{T}(t)R_{\sigma _{\eta }(t)}\dot{x}(t)\} \le c_1\Longrightarrow {x^\mathrm{T}(t)R_{\sigma _{\eta }(t)}x(t)}\le c_2$ for any $t\in [0,T_\mathrm{f}]$.

Remark 1

System (1) includes finite-time unbounded subsystems, due to the effect of large delay $d_{\sigma (t)}(t)$, $\sigma (t)\in \mathcal {I}_\mathrm{l}$. Although system (1) can be unbounded if LDP appears in the whole fixed time interval [0, T], it can still be FTB when LDP and SDP alternate appears with a property of MRRT $\eta$. In the present paper, we give a restriction on the maximum length ratio of LDP and the frequency of LDP by which to obtain the FTB and FTS conditions.

3 Stability and Boundedness Analysis

Consider the following time-delay switched systems

$$\begin{aligned} \dot{x}(t)= & {} A_{\sigma (t)}x(t)+ A_{d\sigma (t)}x(t-d_{\sigma (t)}(t))+D_{\sigma (t)}\omega (t), \nonumber \\ \ x(t)= & {} \varphi (t),t\in [-h_2,0], \end{aligned}$$

(4)

in which $\sigma (t)\in \mathcal {I}_\mathrm{s}$, $h_1\le d_{\sigma (t)}(t)\le h_2$ and all the other parameters are the same with system (1). To analyze system (4), the Lyapunov functional candidate is chosen as follows

$$\begin{aligned}&\ V_{1\sigma (t)}(t)=\sum _{i=1}^{7}V_{1\sigma (t)}^{i}(t), \end{aligned}$$

(5)

where

$$\begin{aligned} V_{1\sigma (t)}^{1}(t)= & {} x^\mathrm{T}(t)P_{1\sigma (t)}x(t), \\ V_{1\sigma (t)}^{2}(t)= & {} \int _{t-d_{\sigma (t)}}^\mathrm{T}\hbox {e}^{\alpha _{1\sigma (t)}(s-t)}x^\mathrm{T}(s)Q_{1\sigma (t)}x(s)\hbox {d}s,\\ V_{1\sigma (t)}^{3}(t)= & {} \int _{t-h_2}^{t-h_1}\hbox {e}^{\alpha _{1\sigma (t)}(s-t)}x^\mathrm{T}(s)Q_{2\sigma (t)}x(s)\hbox {d}s,\\ V_{1\sigma (t)}^{4}(t)= & {} \int _{t-h_3}^{t-h_2}\hbox {e}^{\alpha _{1\sigma (t)}(s-t)}x^\mathrm{T}(s)Q_{3\sigma (t)}x(s)\hbox {d}s, \\ V_{1\sigma (t)}^{5}(t)= & {} \int _{-h_2}^{0}\int _{t+\theta }^\mathrm{T}\hbox {e}^{\alpha _{1\sigma (t)}(s-t)}\dot{x}^\mathrm{T}(s)W_{1\sigma (t)}\dot{x}(s)\hbox {d}s\hbox {d}\theta , \\ V_{1\sigma (t)}^{6}(t)= & {} \int _{-h_2}^{-h_1}\int _{t+\theta }^\mathrm{T}\hbox {e}^{\alpha _{1\sigma (t)}(s-t)}\dot{x}^\mathrm{T}(s)W_{2\sigma (t)}\dot{x}(s)\hbox {d}s\hbox {d}\theta , \\ V_{1\sigma (t)}^{7}(t)= & {} \int _{-h_3}^{-h_2}\int _{t+\theta }^\mathrm{T}\hbox {e}^{\alpha _{1\sigma (t)}(s-t)}\dot{x}^\mathrm{T}(s)W_{3\sigma (t)}\dot{x}(s)\hbox {d}s\hbox {d}\theta , \end{aligned}$$

with $P_{1\sigma (t)},Q_{i\sigma (t)},W_{i\sigma (t)}$, $i=1,2,3$ are determined positive definite matrices. In this section, two lemmas which play important roles in the coming FTB and FTS analysis are developed as follows.

Lemma 1

Let $T>0, \sigma (t)=p\in \mathcal {I}_\mathrm{s}, \alpha _{1p}\ge 0, h_3>h_2>h_1\ge 0$ and $d<1$. If there exist positive definite matrices $P_{1p},Q_{ip},W_{ip}, (i=1,2,3)$ which satisfy the following linear matrix inequality

$$\begin{aligned} \varXi _{1p}= \left[ \begin{array}{cccccc} \sum _{1p}&{}\sum _{2p}&{}0&{}\frac{\hbox {e}^{-\alpha _{1p}h_2}}{h_2} W_{1p}&{}0&{}\sum _{3p}\\ * &{}\sum _{4p}&{}0&{}0&{}0&{}\sum _{5p}\\ 0&{}0&{}\sum _{6p}&{}\frac{\hbox {e}^{-\alpha _{1p}h_2}}{h_{12}} W_{2p}&{}0&{}0\\ * &{}0&{}* &{}\sum _{7p}&{}\frac{\hbox {e}^{-\alpha _{1p}h_3}}{h_{23}} W_{3p}&{}0\\ 0&{}0&{}0&{}*&{}\sum _{8p}&{}0\\ *&{}*&{}0&{}0&{}0&{}\sum _{9p} \end{array} \right] <0 , \end{aligned}$$

(6)

where

$$\begin{aligned} \sum \nolimits _{1p}= & {} P_{1p}A_p+A^\mathrm{T}_pP_{1p}+Q_{1p}+\alpha _{1p}P_{1p}-\frac{\hbox {e}^{-\alpha _{1p}h_2}}{h_{2}} W_{1p}+A^\mathrm{T}_p\varDelta _{1p} A_{p},\\ \sum \nolimits _{2p}= & {} P_{1p}A_{dp}+A^\mathrm{T}_p\varDelta _{1p} A_{dp},\quad \sum \nolimits _{3p}=P_{1p}D_{p}+A^\mathrm{T}_p\varDelta _{1p} D_{p},\\ \sum \nolimits _{4p}= & {} -(1-d)\hbox {e}^{-\alpha _{1p}h_2}Q_{1p}+A^\mathrm{T}_{dp}\varDelta _{1p} A_{dp},\\ \sum \nolimits _{5p}= & {} A^\mathrm{T}_{dp}\varDelta _{1p} D_{p}, \quad \sum \nolimits _{6p}=\hbox {e}^{-\alpha _{1p}h_1}Q_{2p}-\frac{\hbox {e}^{-\alpha _{1p}h_2}}{h_{12}} W_{2p},\\ \sum \nolimits _{7p}= & {} \hbox {e}^{-\alpha _{1p}h_2}(Q_{3p}-Q_{2p})-\frac{\hbox {e}^{-\alpha _{1p}h_2}}{h_{2}} W_{1p}-\frac{\hbox {e}^{-\alpha _{1p}h_2}}{h_{12}} W_{2p}-\frac{\hbox {e}^{-\alpha _{1p}h_3}}{h_{23}} W_{3p},\\ \sum \nolimits _{8p}= & {} -\hbox {e}^{-\alpha _{1p}h_3}Q_{3p}-\frac{\hbox {e}^{-\alpha _{1p}h_3}}{h_{23}} W_{3p}, \quad \sum \nolimits _{9p}=D^\mathrm{T}_{p}\varDelta _{1p} D_{p}-S_p,\\ \varDelta _{1p}= & {} h_2W_{1p}+h_{12}W_{2p}+h_{23}W_{3p}, \quad h_{12}=h_2-h_1, \quad h_{23}=h_3-h_2, \end{aligned}$$

then, for $\forall t\in [t_{2k}, t_{2k+1})$, one has

$$\begin{aligned} \ V_{1\sigma (t)}(t)\le & {} \hbox {e}^{-\alpha _{1\sigma (t_{2k})}(t-t_{2k})}V_{1\sigma (t_{2k})}(x(t_{2k}))\nonumber \\&+\int _{t_{2k}}^\mathrm{T}\hbox {e}^{-\alpha _{1\sigma (t_{2k})}(t-s)}\omega ^\mathrm{T}(s)S_{\sigma (t_{2k})}\omega (s)\hbox {d}s. \end{aligned}$$

(7)

Proof

By computing the time derivative of (5) along the trajectory of system (4), it is obtained

$$\begin{aligned} \dot{V}_{1p}^{1}(t)= & {} x^\mathrm{T}(t)\left( P_{1p}A_p+A^\mathrm{T}_pP_{1p}\right) x(t)+x^\mathrm{T}(t)\left( P_{1p}A_{dp}\right) x\left( t-d_p(t)\right) \nonumber \\&+x^\mathrm{T}\left( t-d_{p}(t)\right) \left( A^\mathrm{T}_{dp}P_{1p}\right) x(t)+x^\mathrm{T}(t)\left( P_{1p}D_{p}\right) \omega (t)\nonumber \\&+\omega ^\mathrm{T}(t)\left( D^\mathrm{T}_{p}P_{1p}\right) x(t), \end{aligned}$$

(8)

$$\begin{aligned} \dot{V}_{1p}^{2}(t)\le & {} -\alpha _{1p}V_{1p}^{2}(t)+x^\mathrm{T}(t)Q_{1p}x(t)\nonumber \\&-(1-d)\hbox {e}^{-\alpha _{1p}h_2}x^\mathrm{T}\left( t-d_p(t)\right) Q_{1p}x\left( t-d_p(t)\right) , \end{aligned}$$

(9)

$$\begin{aligned} \dot{V}_{1p}^{3}(t)= & {} -\alpha _{1p}V_{1p}^{3}(t)+\hbox {e}^{-\alpha _{1p}h_1}x^\mathrm{T}\left( t-h_1\right) Q_{2p}x\left( t-h_1\right) \nonumber \\&-\hbox {e}^{-\alpha _{1p}h_2}x^\mathrm{T}\left( t-h_2\right) Q_{2p}x\left( t-h_2\right) , \end{aligned}$$

(10)

$$\begin{aligned} \dot{V}_{1p}^{4}(t)= & {} -\alpha _{1p}V_{1p}^{4}(t)+\hbox {e}^{-\alpha _{1p}h_2}x^\mathrm{T}\left( t-h_2\right) Q_{3p}x\left( t-h_2\right) \nonumber \\&-\hbox {e}^{-\alpha _{1p}h_3}x^\mathrm{T}\left( t-h_3\right) Q_{3p}x\left( t-h_3\right) , \end{aligned}$$

(11)

$$\begin{aligned} \dot{V}_{1p}^{5}(t)\le & {} -\alpha _{1p}V_{1p}^{5}(t)+h_2\dot{x}^\mathrm{T}(t)W_{1p}\dot{x}(t)-\hbox {e}^{-\alpha _{1p}h_2}\int _{t-h_2}^\mathrm{T}\dot{x}^\mathrm{T}(s)W_{1p}\dot{x}(s)\hbox {d}s.\qquad \end{aligned}$$

(12)

Moreover, with Jensen’s inequality [8], we get

$$\begin{aligned} \dot{V}_{1p}^{5}(t)\le & {} -\alpha _{1p}V_{1p}^{5}(t)+h_2\dot{x}^\mathrm{T}(t)W_{1p}\dot{x}(t)\nonumber \\&-\frac{\hbox {e}^{-\alpha _{1p}h_2}}{h_2} \left[ x(t)-x(t-h_2)\right] ^\mathrm{T}W_{1p}\left[ x(t)-x(t-h_2)\right] . \end{aligned}$$

(13)

Similar to the proof of (13), one has

$$\begin{aligned} \dot{V}_{1p}^{6}(t)\le & {} -\alpha _{1p}V_{1p}^{6}(t)+h_{12}\dot{x}^\mathrm{T}(t)W_{2p}\dot{x}(t)\\&-\frac{\hbox {e}^{-\alpha _{1p}h_2}}{h_{12}} \left[ x(t-h_1)-x(t-h_2)\right] ^\mathrm{T}W_{2p}\left[ x(t-h_1)-x(t-h_2)\right] , \qquad \end{aligned}$$

(14)

$$\begin{aligned} \dot{V}_{1p}^{7}(t)\le & {} -\alpha _{1p}V_{1p}^{7}(t)+h_{23}\dot{x}^\mathrm{T}(t)W_{3p}\dot{x}(t)\\&-\frac{\hbox {e}^{-\alpha _{1p}h_3}}{h_{23}} \left[ x(t-h_2)-x(t-h_3)\right] ^\mathrm{T}W_{3p}\left[ x(t-h_2)-x(t-h_3)\right] .\qquad \end{aligned}$$

(15)

Consequently, if inequality (6) holds, (5) and (8)–(15) immediately lead to the following inequality

$$\begin{aligned} \dot{V}_{1p}(t)+\alpha _{1p}V_{1p}(t)-\omega ^\mathrm{T}(t)S_p\omega (t) \le \zeta _p^\mathrm{T}(t)\varXi _{1p}\zeta _p(t)<0, \end{aligned}$$

(16)

in which $\zeta _p(t)=\left[ x^\mathrm{T}(t),x^\mathrm{T}(t-d_p(t)),x^\mathrm{T}(t-h_1),x^\mathrm{T}(t-h_2),x^\mathrm{T}(t-h_3),\omega ^\mathrm{T}(t)\right] ^\mathrm{T}$. By integrating (16) from $t_{2k}$ to t, inequality (7) follows readily. $\square$

Remark 2

Lemma 1 discusses small delay subsystems of system (1). For the small delay case, all LDITs contained $h_3$ are not needed in the traditional constructions of Lyapunov functional [11, 18, 23], while these LDITs are necessary for the Lyapunov functional of Lemma 2 which will be discussed in Remark 3.

Next, consider the following system

$$\begin{aligned}&\dot{x}(t)= A_{\sigma (t)}x(t)+ A_{d\sigma (t)}x(t-d_{\sigma (t)}(t))+D_{\sigma (t)}\omega (t), \nonumber \\&\ x(t)= \varphi (t),t\in [-h_3,0), \end{aligned}$$

(17)

where $\sigma (t)\in \mathcal {I}_\mathrm{l}$, $h_2< d_{\sigma (t)}\le h_3$. For system (17), with the help of determined positive definite matrices $P_{2\sigma (t)},Q_{i\sigma (t)},W_{i\sigma (t)}$ for $i=4,5,6$, choose the Lyapunov functional as

$$\begin{aligned}&\ V_{2\sigma (t)}(t)=\sum _{i=1}^{7}V_{2\sigma (t)}^{i}(t), \end{aligned}$$

(18)

where

$$\begin{aligned} V_{2\sigma (t)}^{1}(t)= & {} x^\mathrm{T}(t)P_{2\sigma (t)}x(t),\\ V_{2\sigma (t)}^{2}(t)= & {} \int _{t-d_{\sigma (t)}}^\mathrm{T}\hbox {e}^{\alpha _{2\sigma (t)}(t-s)}x^\mathrm{T}(s)Q_{4\sigma (t)}x(s)\hbox {d}s,\\ V_{2\sigma (t)}^{3}(t)= & {} \int _{t-h_2}^{t-h_1}\hbox {e}^{\alpha _{2\sigma (t)}(t-s)}x^\mathrm{T}(s)Q_{5\sigma (t)}x(s)\hbox {d}s,\\ V_{2\sigma (t)}^{4}(t)= & {} \int _{t-h_3}^{t-h_2}\hbox {e}^{\alpha _{2\sigma (t)}(t-s)}x^\mathrm{T}(s)Q_{6\sigma (t)}x(s)\hbox {d}s,\\ V_{2\sigma (t)}^{5}(t)= & {} \int _{-h_2}^{0}\int _{t+\theta }^\mathrm{T}\hbox {e}^{\alpha _{2\sigma (t)}(t-s)}\dot{x}^\mathrm{T}(s)W_{4\sigma (t)}\dot{x}(s)\hbox {d}s\hbox {d}\theta , \\ V_{2\sigma (t)}^{6}(t)= & {} \int _{-h_2}^{-h_1}\int _{t+\theta }^\mathrm{T}\hbox {e}^{\alpha _{2\sigma (t)}(t-s)}\dot{x}^\mathrm{T}(s)W_{5\sigma (t)}\dot{x}(s)\hbox {d}s\hbox {d}\theta , \\ V_{2\sigma (t)}^{7}(t)= & {} \int _{-h_3}^{-h_2}\int _{t+\theta }^\mathrm{T}\hbox {e}^{\alpha _{2\sigma (t)}(t-s)}\dot{x}^\mathrm{T}(s)W_{6\sigma (t)}\dot{x}(s)\hbox {d}s\hbox {d}\theta . \end{aligned}$$

Based on the Lyapunov functional specified by (18), the following lemma is achieved.

Lemma 2

Let $T>0, \sigma (t)=q \in \mathcal {I}_\mathrm{l}, \alpha _{2q}\ge 0, h_3>h_2>h_1\ge 0$ and $d<1$. If there exist positive definite matrices $P_{2q},Q_{iq},W_{iq},(i=4,5,6)$, which satisfy the following linear matrix inequality

$$\begin{aligned} \varXi _{2q}= \left[ \begin{array}{cccccc} \sum _{1q}&{}\sum _{2q}&{}0&{}\frac{W_{4q}}{h_2} &{}0&{}\sum _{3q}\\ * &{}\sum _{4q}&{}0&{}0&{}0&{}\sum _{5q}\\ 0&{}0&{}\sum _{6q}&{}\frac{\hbox {e}^{\alpha _{2q}h_1}W_{5q}}{h_{12}} &{}0&{}0\\ * &{}0&{}* &{}\sum _{7q}&{}\frac{\hbox {e}^{\alpha _{2q}h_2} W_{6q}}{h_{23}}&{}0\\ 0&{}0&{}0&{}*&{}\sum _{8q}&{}0\\ *&{}*&{}0&{}0&{}0&{}\sum _{9q} \end{array} \right] <0 , \end{aligned}$$

(19)

where

$$\begin{aligned} \sum \nolimits _{1q}= & {} P_{2q}A_q+A^\mathrm{T}_qP_{2q}+Q_{4q}-\alpha _{2q}P_{2q}-\frac{W_{4q}}{h_{2}} +A^\mathrm{T}_q\varDelta _{2q} A_{q}, \\ \sum \nolimits _{2q}= & {} P_{2q}A_{dq}+A^\mathrm{T}_q\varDelta _{2q} A_{dq},\quad \sum \nolimits _{3q}=P_{2q}D_{q}+A^\mathrm{T}_q\varDelta _{2q} D_{q}, \\ \sum \nolimits _{4q}= & {} -(1-d)\hbox {e}^{\alpha _{2q}h_3}Q_{4q}+A^\mathrm{T}_{dq}\varDelta _{2q} A_{dq}, \\ \sum \nolimits _{5q}= & {} A^\mathrm{T}_{dq}\varDelta _{2q} D_{q},\quad \sum \nolimits _{6q}=\hbox {e}^{\alpha _{2q}h_1}Q_{5q}-\frac{\hbox {e}^{\alpha _{2q}h_1}}{h_{12}} W_{5q},\\ \sum \nolimits _{7q}= & {} -\hbox {e}^{\alpha _{2q}h_2}(Q_{5q}-Q_{6q})-\frac{W_{4q}}{h_{2}} -\frac{\hbox {e}^{\alpha _{2q}h_1}W_{5q}}{h_{12}} -\frac{\hbox {e}^{\alpha _{2q}h_2}W_{6q}}{h_{12}} ,\\ \sum \nolimits _{8q}= & {} -\hbox {e}^{\alpha _{2q}h_3}Q_{6q}-\frac{\hbox {e}^{\alpha _{2q}h_2}W_{6q}}{h_{23}} , \quad \sum \nolimits _{9q}=D^\mathrm{T}_{q}\varDelta _{2q} D_{q}-S_q,\\ \varDelta _{2q}= & {} h_2W_{4q}+h_{12}W_{5q}+h_{23}W_{6q}, \quad h_{12}=h_2-h_1, \quad h_{23}=h_3-h_2, \end{aligned}$$

then, for $\forall t\in [t_{2k+1}, t_{2k+2})$, one has

$$\begin{aligned} V_{2\sigma (t)}(t)\le & {} \hbox {e}^{\alpha _{2\sigma (t_{2k+1})}(t-t_{2k+1})}V_{2\sigma (t_{2k+1})}(x(t_{2k+1}))\nonumber \\&+\int _{t_{2k+1}}^\mathrm{T}\hbox {e}^{\alpha _{2\sigma (t_{2k+1})}(t-s)}\omega ^\mathrm{T}(s)S_{\sigma (t_{2k+1})}\omega (s)\hbox {d}s. \end{aligned}$$

(20)

Proof

The proof of Lemma 2 is similar to that of the Lemma 1. $\square$

Remark 3

Lemma 2 discusses large delay subsystems of system (1). In order to get the delay bound $h_3$ in LMI (19), LDITs are introduced in (18). The LDITs $V_{1\sigma (t)}^4$ and $V_{1\sigma (t)}^7$ defined in $V_{1\sigma (t)}$ are also necessary. In fact, these terms make the corresponding integral parts in $V_{1\sigma (t)}$ and $V_{2\sigma (t)}$ with the same integral. Hence, these terms are critical to make the ratio between $V_{1\sigma (t)}$ and $V_{2\sigma (t)}$ easily calculated at each switching point.

Theorem 1

Consider the continuous time-delay switched system (1), for given positive constants $c_1, c_2, T, d_\omega$, $\alpha _{1p}, \alpha _{2q}, p\in \mathcal {I}_\mathrm{s}, q\in \mathcal {I}_\mathrm{l}$. If there exist positive definite matrices $P_{1p}, Q_{ip}, W_{ip} (i=1,2,3)$, $P_{1q}, Q_{iq}, W_{iq} (i=4,5,6)$ satisfying LMI (6) and (19), then under switching signals (S), system (1) is extended FTB with respect to $(c_1,c_2,\varOmega , T, \sigma _\eta , d_{\omega })$ where

$$\begin{aligned} c_2= & {} \frac{c\hbox {e}^{c_0T}}{\min \left\{ \lambda _{\min }\left\{ R_{\sigma (t)}^{-\frac{1}{2}}P_{1\sigma (t)}R_{\sigma (t)}^{-\frac{1}{2}}\right\} ,\lambda _{\min }\left\{ R_{\sigma (t)}^{-\frac{1}{2}} P_{2\sigma (t)}R_{\sigma (t)}^{-\frac{1}{2}}\right\} \right\} },\\ c_0= & {} \alpha +\frac{(\eta \alpha _{2M}-\alpha _{1m})}{1+\eta }, \quad c=\varLambda c_1+\lambda _8d_\omega ,\\ \varLambda= & {} \lambda _1+(\lambda _2+\lambda _5) h_2 +\hbox {e}^{-\alpha _{1m}h_1}(\lambda _3+\lambda _6)h_{12}+\hbox {e}^{-\alpha _{1m}h_2}(\lambda _4+\lambda _7)h_{23},\\ \lambda _1= & {} \lambda _{\max }\left( R_{\sigma (0)}^{-\frac{1}{2}}P_{1\sigma (0)}R_{\sigma (0)}^{-\frac{1}{2}}\right) ,\quad \lambda _2=\lambda _{\max }\left( R_{\sigma (0)}^{-\frac{1}{2}}Q_{1\sigma (0)}R_{\sigma (0)}^{-\frac{1}{2}}\right) , \\ \lambda _3= & {} \lambda _{\max }\left( R_{\sigma (0)}^{-\frac{1}{2}}Q_{2\sigma (0)}R_{\sigma (0)}^{-\frac{1}{2}}\right) ,\quad \lambda _4=\lambda _{\max }\left( R_{\sigma (0)}^{-\frac{1}{2}}Q_{3\sigma (0)}R_{\sigma (0)}^{-\frac{1}{2}}\right) , \\ \lambda _5= & {} \lambda _{\max }\left( R_{\sigma (0)}^{-\frac{1}{2}}W_{1\sigma (0)}R_{\sigma (0)}^{-\frac{1}{2}}\right) , \quad \lambda _6=\lambda _{\max }\left( R_{\sigma (0)}^{-\frac{1}{2}}W_{2\sigma (0)}R_{\sigma (0)}^{-\frac{1}{2}}\right) , \\ \lambda _7= & {} \lambda _{\max }\left( R_{\sigma (0)}^{-\frac{1}{2}}W_{3\sigma (0)}R_{\sigma (0)}^{-\frac{1}{2}}\right) ,\quad \lambda _8=\lambda _{\max }\left( S_{\sigma (t)}\right) ,\quad \alpha _{1M}=\max \left\{ \alpha _{1\sigma (t)}\right\} , \\ \alpha _{2M}= & {} \max \left\{ \alpha _{2\sigma (t)}\right\} ,\quad \alpha _{1m}=\min \left\{ \alpha _{1\sigma (t)}\right\} ,\quad \alpha _{2m}=\min \left\{ \alpha _{2\sigma (t)}\right\} . \end{aligned}$$

Therein, the switching signals (S) should satisfy the following properties:

$$\begin{aligned}&\frac{T_{\mathrm{l}(0,t)}}{T_{\mathrm{s}(0,t)}}\le \eta , \quad F_\mathrm{f}(0,t)\le \frac{\alpha }{\ln (\mu ^2_M\mu )},\quad \alpha >0,\quad \forall t\in [0,T], \end{aligned}$$

(21)

$$\begin{aligned}&P_{\mathrm{l}m}\le \mu _mP_{hn},\quad Q_{im}\le \mu _mQ_{jn},\quad W_{im}\le \mu _mW_{jn},\nonumber \\&\mu =\hbox {e}^{(\alpha _{1M}+\alpha _{2M})h_3},\quad \mu _m\ge 1, \quad \mu _M=\max \{\mu _m\}, \nonumber \\&\forall l,h\in \{1,2\}, \forall \{i,j\}or\{j,i\}=\{(1,4),(2,5),(3,6)\}, m,n\in \mathcal {I}. \end{aligned}$$

(22)

Proof

Construct piecewise Lyapunov functional candidate as follows

$$\begin{aligned} V_{\sigma (t)}(t)=\left\{ \begin{array}{ll} V_{1\sigma (t)}(t), &{}\quad t\in [t_{2k},t_{2k+1}), \\ V_{2\sigma (t)}(t), &{} \quad t\in [t_{2k+1},t_{2k+2}), \quad k\in \mathcal {N},\\ \end{array}\right. \end{aligned}$$

(23)

where $V_{1\sigma (t)}(t)$ and $V_{2\sigma (t)}(t)$ are defined in (5) and (18), respectively. From (22) and (23), it is easy to see that the switching point satisfies

$$\begin{aligned} V_{1\sigma (t_i)}\le \mu _i V_{2\sigma (t^-_i)},\quad \forall \sigma (t_i)=p\in \mathcal {I}_\mathrm{s}, \quad \sigma (t^-_i)=q\in \mathcal {I}_\mathrm{l} ,\quad i\in \mathcal {N}, \nonumber \\ V_{2\sigma (t_j)}\le \mu \mu _j V_{1\sigma (t^-_j)},\quad \forall \sigma (t_j)=q\in \mathcal {I}_\mathrm{l}, \quad \sigma (t^-_j)=p\in \mathcal {I}_\mathrm{s},\quad j\in \mathcal {N}. \end{aligned}$$

(24)

Consider the piecewise Lyapunov functional (23), from Lemmas 1 and 2, it yields

$$\begin{aligned} V_{\sigma (t)}(t)\le \left\{ \begin{array}{ll} \hbox {e}^{-\alpha _{1\sigma (t_{2k})}(t-t_{2k})}V_{1\sigma (t_{2k})}(x(t_{2k})) \\ \quad +\int _{t_{2k}}^\mathrm{T}\hbox {e}^{-\alpha _{1\sigma (t_{2k})}(t-s)}\omega ^\mathrm{T}(s)S_{\sigma (t_{2k})}\omega (s)\hbox {d}s,&{} \quad t\in [t_{2k},t_{2k+1}),\\ \\ \hbox {e}^{\alpha _{2\sigma (t_{2k+1})}(t-t_{2k+1})}V_{2\sigma (t_{2k+1})}(x(t_{2k+1}))\\ \quad +\int _{t_{2k+1}}^{t}\hbox {e}^{\alpha _{2\sigma (t_{2k+1})}(t-s)}\omega ^\mathrm{T}(s)S_{\sigma (t_{2k+1})}\omega (s)\hbox {d}s,&{}\quad t\in [t_{2k+1}, t_{2k+2}).\\ \end{array}\right. \end{aligned}$$

(25)

Without loss of generality, we assume $t\in [t_{2k+1},t_{2k+2}), k\ge 0, \sigma (t)\in \mathcal {I}_\mathrm{l}$. Based on (23) and (24), along the trajectory of system (1), it derives

$$\begin{aligned} V_{\sigma (t)}(t)\le & {} \mu \mu _{2k+1}\hbox {e}^{\alpha _{2\sigma (t_{2k+1})}(t-t_{2k+1})}V_{1\sigma (t^-_{2k+1})}(x(t^-_{2k+1}))\nonumber \\&+ \int _{t_{2k+1}}^{t}\hbox {e}^{\alpha _{2\sigma (t_{2k+1})}(t-s)}\omega ^\mathrm{T}(s)S_{\sigma (t_{2k+1})}\omega (s)\hbox {d}s\nonumber \\\le & {} \exp (N_{\mathrm{l}}(0,t)\ln \mu + N_{\sigma }(0,t)\ln \mu _M + \alpha _{2M}T_{\mathrm{l}(0,t)} -\alpha _{1m}T_{\mathrm{s}(0,t)})V_{1\sigma (0)}(0) \nonumber \\&+\lambda _{\max }(S_{\sigma (t)})\int _{0}^{t}\exp (N_{\mathrm{l}}(0,t)\ln \mu + N_{\sigma }(0,t)\ln \mu _M + \alpha _{2M}T_{\mathrm{l}(0,s)}\nonumber \\&-\alpha _{1m}T_{\mathrm{s}(0,s)})\omega ^\mathrm{T}(s)\omega (s)\hbox {d}s . \end{aligned}$$

(26)

In view of (21) and $N_{\sigma }(0,t)\le 2N_{\mathrm{l}}(0,t)$, it is easy to see that

$$\begin{aligned}&N_{\mathrm{l}}(0,t)\ln \mu + N_{\sigma }(0,t)\ln \mu _M + \alpha _{2M}T_{\mathrm{l}(0,t)} -\alpha _{1m}T_{\mathrm{s}(0,t)} \nonumber \\&\quad \le (\alpha +\frac{(\eta \alpha _{2M}-\alpha _{1m})}{1+\eta })t=c_0t. \end{aligned}$$

(27)

Then, from (26) and (27), it holds

$$\begin{aligned} V_{\sigma (t)}(t)\le \hbox {e}^{c_0t}V_{1\sigma (0)}(0)+\lambda _{\max }(S_{\sigma (t)})\hbox {e}^{c_0t}d_\omega . \end{aligned}$$

(28)

By virtue of the form of Lyapunov functional and the condition of Theorem 1, one has

$$\begin{aligned} V_{1\sigma (0)}(0)\le & {} \left[ \lambda _1+(\lambda _2+\lambda _5) h_2 +\hbox {e}^{-\alpha _{1m}h_1}(\lambda _3+\lambda _6)h_{12}+\hbox {e}^{-\alpha _{1m}h_2}(\lambda _4+\lambda _7)h_{23}\right] \nonumber \\&\times \sup _{t\in [-h_3,0]}\left\{ x^\mathrm{T}(t)R_{\sigma (t)}x(t),\dot{x}^\mathrm{T}(t)R_{\sigma (t)}\dot{x}(t)\right\} \nonumber \\= & {} \varLambda c_1. \end{aligned}$$

(29)

Substituting (29) into (28) yields

$$\begin{aligned} V_{\sigma (t)}(t)\le \hbox {e}^{c_0t}\varLambda c_1+\lambda _8 \hbox {e}^{c_0t}d_\omega =c\hbox {e}^{c_0t}. \end{aligned}$$

(30)

Noting that $V_{1\sigma (t)}(t)\ge x^\mathrm{T}(t)P_{1\sigma (t)}x(t)$ and $V_{2\sigma (t)}(t)\ge x^\mathrm{T}(t)P_{2\sigma (t)}x(t)$, hence

$$\begin{aligned} x^\mathrm{T}(t)R_{\sigma (t)}x(t) \le c_2. \end{aligned}$$

(31)

This completes the proof of Theorem 1. $\square$

When the input disturbance $\omega (t)$ vanishes, we have another main result in this paper.

Theorem 2

Consider the continuous time-delay switched system (1) with $\omega (t)\equiv 0$, where the parameters are the same with Theorem 1. If there exist positive definite matrices $P_{1p}, Q_{ip}, W_{ip}, (i=1,2,3)$, $P_{1q}, Q_{iq}, W_{iq}, (i=4,5,6)$ satisfying LMI (32) and (33) (all the parameters are defined in Lemmas 1 and 2 with $D_p=D_q=0$)

$$\begin{aligned} \varXi '_{1p}= & {} \left[ \begin{array}{ccccc} \sum _{1p}&{}\sum _{2p}&{}0&{}\frac{\hbox {e}^{-\alpha _{1p}h_2}}{h_2} W_{1p}&{}0\\ * &{}\sum _{4p}&{}0&{}0&{}0\\ 0&{}0&{}\sum _{6p}&{}\frac{\hbox {e}^{-\alpha _{1p}h_2}}{h_{12}} W_{2p}&{}0\\ * &{}0&{}* &{}\sum _{7p}&{}\frac{\hbox {e}^{-\alpha _{1p}h_3}}{h_{23}} W_{3p}\\ 0&{}0&{}0&{}*&{}\sum _{8p} \end{array} \right] <0 , \end{aligned}$$

(32)

$$\begin{aligned} \varXi '_{2q}= & {} \left[ \begin{array}{ccccc} \sum _{1q}&{}\sum _{2q}&{}0&{}\frac{W_{4q}}{h_2} &{}0\\ * &{}\sum _{4q}&{}0&{}0&{}0\\ 0&{}0&{}\sum _{6q}&{}\frac{\hbox {e}^{\alpha _{2q}h_1}W_{5q}}{h_{12}} &{}0\\ * &{}0&{}* &{}\sum _{7q}&{}\frac{\hbox {e}^{\alpha _{2q}h_2} W_{6q}}{h_{23}}\\ 0&{}0&{}0&{}*&{}\sum _{8q} \end{array} \right] <0 , \end{aligned}$$

(33)

then, under the same switching signals (S) with Theorem 1, system (1) is extended FTS with respect to $(c_1,c_2,\varOmega , T, \sigma _\eta )$, where

$$\begin{aligned} c= & {} c_1*\left[ \lambda _1+(\lambda _2+\lambda _5) h_2 +\hbox {e}^{-\alpha _{1m}h_1}(\lambda _3+\lambda _6)h_{12}+\hbox {e}^{-\alpha _{1m}h_2}(\lambda _4+\lambda _7)h_{23}\right] . \end{aligned}$$

Proof

According to Theorem 1, the conclusion is easy to get by letting $\omega (t)\equiv 0$. $\square$

4 Simulation Examples

Example 1

Consider continuous time-delay system (1) with two subsystems

$$\begin{aligned}&\dot{x}(t)= \left[ \begin{array}{cc} -0.2&{} 0\\ 0&{}-0.9 \end{array} \right] x(t)+ \left[ \begin{array}{cc} -0.1&{} 0\\ -0.1&{}-0.1 \end{array} \right] x(t-d_{1}(t))+\left[ \begin{array}{cc} 1, &{} 0\\ 0, &{} 1 \end{array} \right] \omega (t),\nonumber \\&x(t)= [1 ,2]^\mathrm{T}, t\in [-h_2,0], \end{aligned}$$

(34)

$$\begin{aligned}&\dot{x}(t)= \left[ \begin{array}{cc} 0.5&{} -1.5\\ 0.7&{}0.3 \end{array} \right] x(t)+ \left[ \begin{array}{cc} -0.05&{} -0.05\\ -0.03&{}0 \end{array} \right] x(t-d_{2}(t))+\left[ \begin{array}{cc} 1, &{} 0\\ 0, &{} 1 \end{array} \right] \omega (t),\nonumber \\&x(t)= [0 ,1]^\mathrm{T}, t\in [-h_3,0], \end{aligned}$$

(35)

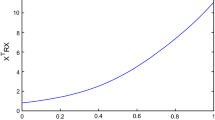
where $d_1(t)=0.2+0.1*\sin (t), \ d_2(t)=0.6+0.3*\sin (t)$ and $\omega (t)=[0.01*\sin (t), 0.02*\cos (2t+1)]^\mathrm{T}$. A straightforward calculation obtains $h_1=0.1, h_2=0.3, h_3=0.9$ and $d=0.3$. The simulation parameters are given as $c_1=5, T=10, R=I$ and $d_\omega =0.1$. In this example, (34) denotes a small delay subsystem 1 and (35) indicates a large delay subsystem 2. Figure 1a, b shows that the subsystems 1 and 2 are bounded and unbounded in time interval [0,10], respectively.

Fig. 1

Time history of $X^\mathrm{T}RX$

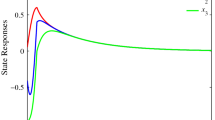
For $\alpha _1=0.01, \alpha _2=0.02, \alpha =0.21, \mu _M=1.21, \eta =0.1764,$ we obtain $P_{1}= \left[ \begin{array}{cc} 1.4086 &{} -0.2167\\ -0.2167 &{} 1.9320 \end{array} \right] ,$ $P_{2}= \left[ \begin{array}{cc} 0.1243 &{} 0.1251\\ 0.1251 &{} 0.2139 \end{array} \right] ,$ $\lambda _1=2.01, \lambda _2 =1.0301, \lambda _3 =0.5867, \lambda _4 = 0.8197, \lambda _5 =0.9878, \lambda _6 =0.6164$, $\lambda _7 =1.6026, \lambda _8 =2.8358$ and $c_2=34.1407$. Given switching signals as shown in Fig. 2, we can see from Fig. 3 that the switched system is bounded in finite-time [0, 10].

Fig. 2

The switching signals

Fig. 3

$X^\mathrm{T}RX$ under switching signals

Example 2

[11] Consider system (1) with

$$\begin{aligned} A_1=A_2= \left[ \begin{array}{cc} -2&{} 0\\ 0&{}-0.9 \end{array} \right] ,\quad A_{d_1}=A_{d_2}=\left[ \begin{array}{cc} -1&{} 0\\ -1&{}-1 \end{array} \right] ,\quad \omega (t)=0. \end{aligned}$$

(36)

For the case of $0\le d_1(t)\le 1.6, d=0.5$ and $T=50$, Table 1 shows all the bounds of $\frac{T_{\mathrm{l}(0,t)}}{T_{\mathrm{s}(0,t)}}$, $F_\mathrm{f}(0,t)$ and maximum allowed delay bound (MADB). It is worth pointing out that MADB obtained in [11] is only 2.04, while our method can achieve the MADB as high as 15. Hence, the method proposed in this paper can provide a large MADB compared with the exiting methods.

Table 1 The bounds of $\frac{T_{\mathrm{l}(0,t)}}{T_{\mathrm{s}(0,t)}}$, $F_\mathrm{f}(0,t)$ and MADB for $0\le d_1(t)\le 1.6$ and $d=0.5$

5 Conclusions

FTB and FTS have been investigated in this paper for a class of switched linear systems with large delay period. Though the subsystems with large delay may be finite-time unbounded, with the help of an appropriate switching signal, the FTB and FTS are still guaranteed under the restriction on frequency and maximum ratio of LDP. By introducing a piecewise Lyapunov functional with large delay integral terms, the LMI conditions are given with the help of Jensen’s inequality. Two numerical examples demonstrate the effectiveness of the proposed method.