1 Introduction

High-resolution (HR) images are always desired in many fields, such as medical image analysis [37], high-definition televisions [33], remote sensing [29] and video surveillance [14]. Super-resolution (SR) algorithms aim to generate an image with higher resolution than the imaging device. Classical methods for SR produce a HR image using multiple degraded low-resolution (LR) images with subpixel alignments between them [15, 27]. In practice multiframe SR techniques are NP-hard due to the unknown registration parameters, inadequate number of LR images and unstable motions between the LR frames [15, 32]. On the other hand, single image SR (SISR) techniques generate a HR image using single subsampled LR image. These algorithms can be grouped into three categories, namely interpolation techniques, machine learning approaches and wavelet-based techniques.

Nearest neighbor, bilinear and bicubic interpolation methods are the simple approaches for SR, but always produce blurred images with ringing and jagged artifacts. Li and Orchard [23] addressed this problem by using the local covariances of an LR image. In Ref. [34], the missing pixels are interpolated in two mutually orthogonal directions and these two estimates are adaptively fused into a single HR image using a local window. Zhang and Wu [36] introduced block-based computation of the unknown pixels by employing autoregressive model. Jing and Wu [22] proposed a different interpolation approach based on the inverse distance weighting method, by introducing a new intensity distance measure. However, the above interpolation methods are used for low computational complexity but not for the performance. Besides, the interpolation techniques are confined to a maximum scaling factor 2 alone.

Machine learning-based SISR approach is a better way to overcome the limitations of interpolation techniques. Most of these algorithms divide the image plane into number of small patches. Prior to the SR reconstruction process, there is a training procedure involved between several HR example image patches and their LR counter parts. Here, SR algorithms rely on the a priori term obtained from the training activity. In the past few years, dictionary learning and sparsity priors are successfully employed in many SISR algorithms. Fadili et al. [11] developed an expectation maximization frame work for image upscaling and image inpainting, where a sparsity prior is enforced on SR reconstruction. This approach proved successful for image inpainting than interpolation. In Ref. [33], a compact dictionary pair is learned for improving the speed of training process.

Dong et al. [8,9,10] further developed example-based techniques by proposing centralized sparse representation and autoregressive model. In addition, Dong et al. [7] used the advantage of self-repeating patterns in natural images by modeling each sparse coefficient as a non-local Gaussian scale mixture with simultaneous sparse coding. He et al. [16] addressed the dictionary learning problem by suggesting a beta process model in a Bayesian frame work. But, the sparsity invariance assumption restricts the idea to the nonzero locations of sparse representation vector. Peleg and Elad [26] solved this issue by implementing a statistical prediction model on the LR-HR sparse representation vectors. This model makes no sparsity invariance assumption. However, it is difficult to achieve similar LR-HR sparse representations in practice. So, a strong regularization technique was used recently in [21, 31] by developing a sparse support regression algorithm from the dictionaries. In addition, Jiang et al. [21] attempted to preserve the geometric structures of HR examples rather than their LR counterparts to avoid the aliasing effect. Recently, an interesting improvement is proposed in [20] for face SR. In addition to the LR patches, HR patch reconstruction component is introduced in the objective function. Most of these machine learning techniques yield better results, but the training step with large database increases the computation time remarkably. In addition, these techniques are limited to a factor 3 enlargement.

On the other hand, wavelet-based SISR techniques play a vital role in super-resolving the images. These techniques also provide significant results by employing self-similarities among the neighboring pixels in the subbands. Recently, many algorithms have been proposed in wavelet domain [3,4,5,6, 17]. In Ref. [5], a resolution enhancement scheme is proposed by employing discrete wavelet transform (DWT) and stationary wavelet transform (SWT). Chavez-Roman and Ponomaryov [4] used sparse mixing estimators to improve the DWT low-frequency subband. This method provides better results with multiple edge preserving stages. Many other wavelet-based techniques, such as lifting wavelet transform (LWT) [6], dual-tree complex wavelet transform (DTCWT) [3] and undecimated DTCWT [17], are also proposed in the context of SR. Similar to the machine learning algorithms, wavelet-based SR techniques also provide superior results. Our work is motivated by the impressive performance of [5], even at large magnification factors. Besides, the computational simplicity enables numerous signal and image processing applications.

In this correspondence, we present a new wavelet-based SISR algorithm. We estimate the initial HR image by implementing covariance-based interpolation algorithm on the input LR image [30]. The initial HR estimate is used in the next stages of our method. We explore the singular value decomposition (SVD) of the initial HR estimate and the low-frequency subband, to generate a new subband. SWT which is adopted in our algorithm for subband decomposition has promising directionality and shift invariance when compared to the traditional wavelet decomposition. All subbands are enhanced by applying the complex diffusion-based shock filter (DBSF). The dual-mode operation of DBSF simultaneously enhances and denoises the subband images [28]. In addition, the nearest neighbor interpolation (NNI) process incorporates the lost edge information into the subband images.

This paper is structured as follows. In Sect. 2, the covariance-based interpolation algorithm is presented. Section 3 describes the DBSF operation in detail. The proposed algorithm is illustrated in Sect. 4. Various experimental results are evaluated in Sect. 5, and finally Sect. 6 concludes this paper.

2 Interpolation Using Local Covariance Estimates

In order to overcome the undesired artifacts of plain linear interpolation techniques, we employ covariance-based interpolation algorithm in our proposal to estimate the initial HR image. The algorithm uses the basic idea of geometric regularity to obtain the linear interpolation coefficients with minimal mean square error [23, 30]. If Y[2m, 2n] denotes the LR image and Y[m, n] denotes the enlarged HR image, then the basic fourth-order interpolation is given as follows [35]:

$$\begin{aligned} Y[2m+1, 2n+1] = \sum _{i, j\in [0, 1]}w[2i+j]\quad Y[2(m+i), 2(n+j)], \end{aligned}$$
(1)

where \(w=[w_0, w_1, w_2, w_3]\) represents the optimal linear interpolation coefficient vector.

Fig. 1
figure 1

Insight into the geometric regularity between LR and HR covariances

Full size image

In general, the linear interpolation is performed in two consecutive steps. Since, the unknown pixels on the HR grid are categorized into two groups, namely \(Y[2m+1, 2n+1]\) and Y[m, n] (\(m+n=\,\)odd) as shown in Fig. 1. First, the missing pixels \(Y[2m+1, 2n+1]\) are computed from Y[2m, 2n] by solving Eq. (1). Second, the rest unknown part Y[m, n] (\(m+n\,=\,\)odd) can be obtained from Y[m, n] (\(m+n=\,\)even) in a similar fashion. However, the two unknown pixel groups \(Y[2m+1, 2n+1]\) and Y[m, n] (\(m+n=\,\)odd) have similar geometric dualities, which are isomorphic up to a scaling factor of \(\sqrt{2}\)    and a rotation of \(45^{\circ }\) [22]. Due to this fact the first group of pixels \(Y[2m+1, 2n+1]\) are only considered in Eq. (1).

The linear interpolation coefficients can be computed from the covariances at higher resolution, based on the assumption that natural images are modeled by local stationary Gaussian process. Thus, from classical Wiener filter theory [19]:

$$\begin{aligned} w={\widetilde{\mathbf{Q }}}^{-1}\widetilde{\mathbf{q }} , \end{aligned}$$
(2)

where \(\widetilde{\mathbf{Q }}=[\widetilde{\mathbf{Q }}_{ij}]\) and \(\widetilde{\mathbf{q }}=[\widetilde{\mathbf{q }}_i]\), \(0\le i, j\le 3\) are the covariances at higher resolution.

Now, the challenge is obtaining the HR covariances when we have only the LR image. This is where geometric duality comes into picture. It links the HR and LR covariances by coupling a pair of pixels along the same direction, and still they are at distinct resolution as shown in Fig. 1. Let x denotes the sampling distance. The normalized covariance is given by \(\widetilde{\mathbf{Q }}(x)\sim \hbox {e}^{\frac{-x^2}{{2\sigma ^2}}}\). Similarly, if d and 2d are the HR and LR sampling distances, then they are related by a quadratic function \(\widetilde{\mathbf{Q }}(d)=\widetilde{\mathbf{Q }}^\frac{1}{4}(2d)\). At higher resolution, the sampling distance, \(d\rightarrow 0\) such that \(\mathbf Q (d)\approxeq \mathbf{Q (2d)}\). Therefore, the HR covariances can be replaced by the corresponding LR covariances.

The LR covariances \(\mathbf Q , \mathbf q \) can be computed by taking a \(N\times N\) local window of the input LR image. Thus, from traditional covariance approach [19]

$$\begin{aligned} \mathbf Q =\frac{1}{N^2}\mathbf{D ^{T}{} \mathbf D } \quad \text{ and } \quad \mathbf q =\frac{1}{N}\mathbf{D ^{T}{} \mathbf b }, \end{aligned}$$
(3)

where \(\mathbf b \) is data vector and \(\mathbf D \) is a \(4\times {N^2}\) data matrix whose columns are the four diagonal neighbors of the elements of the data vector.

By solving Eqs. (1), (2) and (3), the missing pixels on the interlacing lattice are obtained. The interpolated image is used in the next stages of our proposed algorithm.

3 Diffusion-Based Shock Filter (DBSF)

Shock filter was proposed by Osher and Rudin [25], which has a wide range of applications in image enhancement and deblurring. We employ shock filter in our algorithm, to denoise the estimated high-frequency subbands. Besides, the low-frequency subband is also enhanced by operating the shock filter in the edge preserving mode.

Let Y[m, n] be an input image. The shock filter considers it as a time-varying function Y(m, n, k) with k as the time index. Mathematically, shock filter can be evaluated as

$$\begin{aligned} Y_k = {-}{{\mathrm{sign}}}(Y_{\rho \rho })|\nabla Y|, \end{aligned}$$
(4)

where \(Y_k\) denotes the first-order time derivative of the function Y(m, n, k), \(Y_{\rho \rho }\) represents the second derivative of input image with respect to \(\rho \) direction, and \(\nabla Y\) is the corresponding gradient.

This filter fails to preserve edge information, and also it is highly sensitive to noise. The method in [12] addressed these issues by introducing a linear diffusion term to the basic shock filter.

$$\begin{aligned} Y_k = {-}{{\mathrm{sign}}}(Y_{\rho \rho })|\nabla Y| + \lambda Y_{\eta \eta }, \end{aligned}$$
(5)

where \(\lambda >0\) is a weight of the linear diffusion term and \(\eta \) is the direction perpendicular to \(\nabla Y\).

To ensure sharp edges in the output image, the above DBSF can be generalized to complex values [13] with several applications to spectral analysis, as

$$\begin{aligned} Y_k = -\frac{2}{\pi } \arctan \bigg (\delta {{\mathrm{Im}}}\Big (\frac{Y}{\theta }\Big )\bigg )|\nabla Y| + \widetilde{\lambda } Y_{\rho \rho }+ \lambda Y_{\eta \eta } , \end{aligned}$$
(6)

where the parameter \(\delta \) provides control over the slope at zero crossings. \(\lambda \in \mathbb {R}\) and \(\widetilde{\lambda }\in \mathbb {C}\) are the scalar diffusion weights and \(\theta =\arg (\widetilde{\lambda })\).

This complex diffusion-based shock filter can be used for image enhancement by following the first term in Eq. (6) and also for image denoising as a result of the diffusion term. When the diffusion weights are small, the regularized term is suppressed and the process approximates to edge preserving shock filter. For large weights, the diffusion term plays a vital role, resulting a denoising shock filter.

Fig. 2
figure 2

Block diagram of the proposed SR image generation algorithm

Full size image

4 Proposed SR Technique

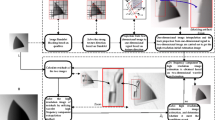
The proposed method can be represented as a block diagram shown in Fig. 2. Initially, we compute the local covariances of the known LR image. Then, the fourth-order interpolation is applied on the input LR image to generate an initial estimate of the unknown HR image. This can be done by exploiting geometric duality between LR covariances and HR covariances as shown in Fig. 1. The covariance-based interpolation process improves the visual quality of the interpolated LR image, but increased computational complexity should be addressed. In order to reduce the computational time, we apply covariance-based interpolation process only to the edge pixels and plain bicubic interpolation to the pixels in smooth regions. Thus, a trade-off is obtained between computational complexity and subjective quality. This mixed interpolation scheme gives favorable outcome when the desired enlargement factor is 2 or less. It is capable of preserving the geometric structures around the edges in an image. In addition, the smoothing effect and ringing artifacts are also minimized. This can not be achieved using traditional interpolation methods. However, the performance of covariance-based interpolation degrades rapidly for higher scaling factors. But HR images with large magnification factors are highly essential to meet the growing demands. So, we further process this initial HR estimate in wavelet domain to add more high-frequency details.

In this correspondence, we choose SWT for subband decomposition of the initial HR estimate. SWT divides an image into four different subbands, termed as approximation \(Y_\mathrm{A}\), horizontal \(Y_\mathrm{H}\), vertical \(Y_\mathrm{V}\) and diagonal \(Y_\mathrm{D}\) coefficients, respectively. Here, the translation invariance property of SWT allows the subband images to have same size as the initial HR estimate. The high-frequency subbands \(Y_\mathrm{H}\), \(Y_\mathrm{V}\) and \(Y_\mathrm{D}\) carry the edge information of the interpolated LR image. But the low-frequency subband \(Y_\mathrm{A}\) contains no edge details; instead, it has the valid illumination information. The SVD of an image holds illumination information, and thus, changing the singular values directly affects the contrast of the edges. The subbands \(Y_\mathrm{H}\), \(Y_\mathrm{V}\) and \(Y_\mathrm{D}\) do not contain any illumination information. Hence, we apply SVD to the initial HR estimate \(Y_0\) and the \(Y_\mathrm{A}\) subband only.

$$\begin{aligned} Y_0 = U_1 {\varSigma }_1 {V_1}^T \quad \text {and} \quad Y_\mathrm{A} = U_2 {\varSigma }_2 {V_2}^T, \end{aligned}$$
(7)

where \(U_1,V_1\) and \(U_2,V_2\) are the unitary matrices of the initial HR estimate and the low-frequency subband, respectively. \({\varSigma }_1, {\varSigma }_2\) are the corresponding singular value matrices, whose diagonal elements are the singular values in the decreasing order.

To preserve the contrast information in the super-resolved image, we modify the low-frequency subband using the initial HR estimate by computing the illumination constant as

$$\begin{aligned} \zeta =\frac{1}{\nu } \frac{\hbox {max}({\varSigma }_1)}{\hbox {max}({\varSigma }_2)}, \end{aligned}$$
(8)

where \(\nu \) is the normalization parameter.Now, the new low-frequency subband is reconstructed as

$$\begin{aligned} \overline{Y}_A = U_2 \overline{{\varSigma }}_2 {V_2}^T, \end{aligned}$$
(9)

where \(\overline{{\varSigma }}_2=\zeta \quad {\varSigma }_2\) is the corrected singular value matrix of the low-frequency subband.

To obtain resolution enhancement with the desired magnification factor, the improved low-frequency subband \(\overline{Y}_\mathrm{A}\) and all the high-frequency subbands \(Y_\mathrm{H}, Y_\mathrm{V}\) and \(Y_\mathrm{D}\) are upscaled using Lanczos kernel. Next, we have applied the DBSF on the interpolated subband images by choosing appropriate diffusion weights. As discussed in Sect. 3, small diffusion weights ensure edge enhancement as dominant mode. On the contrary, large diffusion weights provide image denoising as dominant mode. Thus, we apply enhancement mode shock filter on the low-frequency subband, as it suffers from poor edge information. Similarly, the denoising mode shock filter is used to cater for the artifacts induced by the Lanczos interpolation in the high-frequency subbands.

Fig. 3
figure 3

Ground truth images from left to rightand top to bottom: Lena, Mandrill, Barbara, Lake, Biker, Boat, House, Kid, Plane and Statue

Full size image
Table 1 PSNR (dB) and SSIM values of different SR methods for \(\beta =3\)
Full size table
Table 2 PSNR (dB) and SSIM values of different SR methods for \(\beta =4\)
Full size table
Table 3 Average run times (in seconds) of different SR methods for \(\beta =4\) enlargement
Full size table

Apart from \(Y_\mathrm{A}\) subband, all other subbands contain isolated high-frequency components. In order to preserve the edge information, we employ an edge extraction stage using the high-frequency subbands \(Y_\mathrm{H}\), \(Y_\mathrm{V}\) and \(Y_\mathrm{D}\). The extracted edge details are first interpolated using NNI procedure and then added to the high-frequency subbands [4]. The NNI process alters the intensity values in agreement with the closest neighbor pixels. This process incorporates additional high-frequency information into the subband images. The edge details are computed as,

$$\begin{aligned} E=\sqrt{Y_\mathrm{H}^2+Y_\mathrm{V}^2+Y_\mathrm{D}^2} \quad . \end{aligned}$$
(10)

Finally, all the estimated subbands are combined by applying inverse SWT process. It can be observed that the edge extraction step and the interpolation of SWT subbands effectively preserve the edge information. Besides, the initial HR estimation using local covariances and the SVD-based low-frequency subband modification improves the visual quality of the super-resolved image.

Fig. 4
figure 4

Cropped portions from Lena image by different SR methods for \(\beta =3\) enlargement: a original image, b SME [24], c SCSR [33], d SPM-SR [26], e DWT [2], f DWT-SWT [5], g DWT-Sparse [4], h LWT [1], i DTCWT-NLM [18] and j proposed method

Full size image
Fig. 5
figure 5

Reconstructed images of Lena, Mandrill and Statue by different SR methods for \(\beta =4\) enlargement: a original image, b SME [24], c SCSR [33], d SPM-SR [26], e DWT [2], f DWT-SWT [5], g DWT-Sparse [4], h LWT [1], i DTCWT-NLM [18] and j proposed method

Full size image
Fig. 6
figure 6

Reconstructed images of Kid by different SR methods for \(\beta =4\) enlargement: a original image, b SME [24], c SCSR [33], d SPM-SR [26], e DWT [2], f DWT-SWT [5], g DWT-Sparse [4], h LWT [1], i DTCWT-NLM [18] and j proposed method

Full size image
Fig. 7
figure 7

Reconstructed images of Plane by different SR methods for \(\beta =4\) enlargement: a original image, b SME [24], c SCSR [33], d SPM-SR [26], e DWT [2], f DWT-SWT [5], g DWT-Sparse [4], h LWT [1], i DTCWT-NLM [18] and j proposed method

Full size image
Fig. 8
figure 8

SR results of the proposed method for different scaling factors using Biker image. a, b LR-SR result for \(\beta =2\), c, d LR-SR result for \(\beta =3\), e, f LR-SR result for \(\beta =4\) and g original image

Full size image

5 Experimental Results

To demonstrate the effectiveness of the proposed method over the existing techniques, 10 distinct LR test images are used for comparison. Both gray scale images (Lena, Mandrill, Barbara and Lake) and color images (Biker, Boat, House, Kid, Plane and Statue) are involved. In all our experiments, the SR reconstruction process is directly applied to gray scale images. On the other hand, color images are expressed using RGB color model. But, most of the edge information is present in the luminance channel of an image. Besides, humans are more sensitive to the variations in the luminance channel than to the variations in the color channels. We separate the luminance channel from the given RGB color image by employing YCbCr color model. The SR reconstruction process is applied only to the Y component, while the Cb and Cr components are upscaled using Lanczos interpolation.

The ground truth images used for comparison are shown in Fig. 3. In our simulations, the LR test images are generated by directly downsampling the ground truth images with a scaling factor of \(\beta \) and then super-resolved back using various SR methods. To perform the covariance-based interpolation, we differentiate the edge pixels by choosing gray level threshold \(\hbox {th}=8\). The covariances of the input LR image are estimated using local window of size \(N=9\).

In this paper, we used Bior 1.1 wavelet functions for SWT subband decomposition. The enhancement mode shock filter is operated on the low-frequency subband with \(\lambda =0.01\), \(\widetilde{\lambda }=0.3 \) and \(\delta =0.5\). Similarly, the denoising mode shock filter is operated on high-frequency subbands by choosing \(\lambda =0.9 \), \(\widetilde{\lambda }=0.5 \) and \(\delta =0.1 \). The proposed SR approach and the existing methods are tested using MATLAB 2013b software on Intel(R) Core(TM) i3-2350M CPU with 2.30 GHZ and 4 GB RAM system.

Conventional methods, viz bicubic interpolation (bicubic), direction filtering and data fusion (DFDF) [34], sparse-adaptive mixing estimators (SME) [24], sparse coding-based SR (SCSR) [33], statistical prediction model (SPM-SR) [26] and state-of-the-art methods, such as SR based on wavelet domain interpolation (DWT) [2], resolution enhancement using DWT and SWT (DWT-SWT) [5], SR using DWT and sparse representation (DWT-Sparse) [4], LWT and SWT (LWT) [1], DTCWT and non-local means filter (DTCWT-NLM) [18], are used for the comparison purpose.

Peak signal-to-noise ratio (PSNR) and structured similarity index measure (SSIM) are used to quantitatively asses the super-resolved images. These comparisons are listed in Tables 1 and 2 for \(\beta =3\) and \(\beta =4\), respectively. From these tables, it can be noticed that the proposed method achieves highest average PSNR and SSIM values. Besides, our method is simple and has moderate execution times. In Table 3, we present the average run times of different SR methods for \(\beta =4\) enlargement. It is noticed that Bicubic, DWT [2], DWT-SWT [5], LWT [1] methods can be implemented in less than 5 seconds. The average run time of the proposed method is comparable to DFDF [34], SPM-SR [26], DTCWT-NLM [18], whereas SME [24], SCSR [33] and DWT-Sparse [4] methods consume much time.

In Figs. 4, 5, 6, 7 and 8, a comparative analysis of different SR methods is carried out in terms of subjective visual quality. Figure 4 shows the SR results of cropped Lena for \(\beta =3\), and Figs. 5, 6 and 7 show the SR results of Lena, Mandril, Statue, Kid and Plane for \(\beta =4\). As illustrated in these figures, SME [24], SCSR [33], SPM-SR [26] methods produce blurred edge details and dotted artifacts (e.g., brim of Lena’s hat in Fig. 4c, d). The wavelet-based methods [2, 4, 5, 18] preserve edge information to some extent. However, these methods result in non-uniform illumination in various image regions (e.g., Lena’s hair in Fig. 5e, i). This is mainly because of the direct replacement of low-frequency subband with the input LR image. With SVD-based correction, the proposed method (Figs. 4j, 5j, 6j and 7j) can preserve the contrast. Besides, the edge preservation using the high-frequency subbands generates sharp edges in the SR image. Figure 8 shows the reconstructed SR results of the proposed method for different scaling factors. We can observe that the proposed method yields better visual quality even at large scaling factors. From these tables and figures, it can be noticed that the proposed technique overperforms the conventional and state-of-the-art SR techniques qualitatively as well as quantitatively.

6 Conclusion

A novel cost-effective approach for SISR has been discussed in this paper. Compared to the conventional and state-of-the-art SR methods, our approach has an advantage in terms of preserving the contrast. This is achieved by correcting the SWT low-frequency subband, by employing the SVD. Besides, we do not require any training database for SR reconstruction. The initial HR estimation using covariance-based interpolation and refinement of SWT subbands by DBSF effectively preserves the edge information. The proposed algorithm overperforms the existing SR methods to produce super-resolved image with higher visual quality. Thus, our approach generates HR images using low-cost image acquisition devices, which minimizes the hardware cost significantly.