Design of Time–Frequency Optimal Three-Band Wavelet Filter Banks with Unit Sobolev Regularity Using Frequency Domain Sampling

Abstract

In this paper, we design three-band time–frequency-localized orthogonal wavelet filter banks having single vanishing moment. We propose new expressions to compute mean and variances in time and frequency from the samples of the Fourier transform of the asymmetric band-pass compactly supported wavelet functions. We determine discrete-time filter of length eight that generates the time–frequency optimal time-limited scaling and wavelet functions using cascade algorithm. Time–frequency product (TFP) of a function is defined as the product of its time variance and frequency variance. The TFP of the designed functions is close to 0.25 with unit Sobolev regularity. Three-band filter banks are designed by minimizing a weighted combination of TFPs of wavelets and scaling functions. Interestingly, empirical results show that time–frequency optimal, filter banks of length nine, designed with the proposed methodology, have unit Sobolev regularity, which is maximum achievable with single vanishing moment. Design examples for length six and length nine filter banks are given to demonstrate the effectiveness of the proposed design methodology.

1 Introduction

In the last two decades, the wavelet filter banks have gained a lot of interest to generate wavelet series expansions for finite energy functions. Time–frequency-localized and smooth wavelet basis functions with compact support are important in applications like signal analysis [10] and image coding [26, 39] . Cascade algorithm is used to generate time-limited scaling and wavelet functions from filters of the wavelet filter bank. In cascade algorithm, we first generate the iterated sequence by convolving the upsampled filters [51]. The iterated sequence is interpolated and depending on the convolution sequence of upsampled filters scaling or wavelet function is generated. Under certain conditions, cascade iterations of low-pass filter converge to a unique smooth function $f(t) \in L_2(\mathfrak {R})$ [51]. In all practical applications, finite number of cascade iterations are sufficient to generate wavelet expansion of signal under consideration [5]. For time–frequency analysis of functions $f(t) \in L_2(\mathfrak {R})$, the scaling and wavelet functions must be regular [27] as well as localized simultaneously in time and frequency. Since these functions are generated from cascade iterations of low-pass filter, the low-pass filter can be optimized for time–frequency localization. However, time–frequency-localized low-pass filter do not ensure that scaling function generated at the finite cascade iteration is optimally localized in both time and frequency. In other approach, the scaling function at any ith cascade iteration may be optimized for time–frequency localization with respect to the coefficients of the scaling filter. In cascade algorithm, the iterated sequence is interpolated by normalized and scaled piece-wise constant box function [51]. The frequency variance of the piece-wise constant box function is infinite, and it cannot be used to design time–frequency-localized wavelet basis functions. In this paper, we propose to interpolate the normalized iterated sequence by a smooth-edged normalized box function with finite frequency variance. We determine the Fourier transform of the interpolated function and compute its samples such that sample spacing satisfies the dual of the Nyquist criterion. According to the duality of the Nyquist criterion and spectral sampling theorem [23], under certain conditions, a time-limited function is uniquely determined by the samples of its Fourier transform. We further derive the expressions for mean and variances in time and frequency domain from the samples of the Fourier transform. The developed expressions for variances are subsequently used to minimize variances of scaling or the wavelet function to design time–frequency optimal wavelet filter banks. In the literature, computation of variances in time and frequency from the samples of the band-limited zero-phase function is discussed by Venkatesh et al. [50]. The limitations of variance expressions proposed by them are as follows:

• 1. These expressions are not applicable to time-limited functions.

• 2. These expressions are not applicable to asymmetric functions.

• 3. These expressions are not applicable to band-pass functions.

In this paper, we generalize the expressions proposed by them to arbitrary mean in time and frequency domain. We have used duality and the samples of Fourier transform to extend the expressions of variances proposed by them for band-limited functions to time-limited functions.

Time–frequency localization of a function is often measured by the product of its time variance and frequency variance which is generally called time–frequency product (TFP). Gabor’s uncertainty principle states that functions cannot be well localized in time and frequency simultaneously and that the TFP is bounded below by 0.25 [10]. Chui et al. [6] modified the definition of frequency variance and showed that the same lower bound for the TFP holds even for band-pass functions. Venkatesh et al. [50] studied the limitations of the discrete-time uncertainty principle proposed by Ishii and Furukawa [16] and proposed new expressions for variances from the samples of zero-phase low-pass band-limited functions. In this work, we propose new expressions for mean in time domain and mean in frequency domain from the samples of the Fourier transform of the function and extend the definitions proposed by Venkatesh et al. [50] to asymmetric low-pass and band-pass functions. We design TFP optimal compactly supported scaling and wavelet functions. We further extend the design of TFP optimal functions from orthogonal three-band perfect reconstruction filter bank (PRFB).

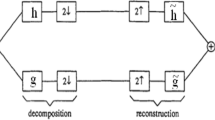
Often, wavelets are constructed from two-band wavelet filter banks. However, wavelets constructed from M-band filter banks exhibit interesting features such as more flexible time–frequency tiling and excellent analysis of narrowband high-frequency signals [11, 40]. M-band filter banks provide orthogonality and linear phase simultaneously, which is not possible in the case of two-band filter banks [7]. M-band orthogonal wavelets can be generated from the regular M-band paraunitary filter banks [40]. Several criteria such as perfect reconstruction (PR), frequency selectivity, coding gain, regularity and time–frequency localization are used for designing filter banks. Various design methods and filter bank structures have been proposed to design regular M-band PRFB [5, 7, 11]. It has been shown by the authors, Shen and Shen [39], Monro and Sherlock [26] and Tay et al. [46] that time–frequency-localized wavelets improve the performance in applications such as image compression and signal analysis. To obtain time–frequency optimal wavelet bases, either the filters of a regular PRFB can be optimized for time–frequency localization [26, 37, 38, 44, 45, 47] or wavelet functions generated by a finite number of cascade iterations of filters can be optimized [21, 36, 54]. Time–frequency optimal M-band filter banks are designed by Tay et al. [48]. In this study, filters are optimized for their time–frequency localization. However, authors have designed only filter banks with an even number of subbands. Haddad et al. [12] evaluate discrete-time and continuous-time uncertainty for some well-known M-band filter banks. To the best of our knowledge, no literature is available on the design of time–frequency optimal M-band wavelet bases with $M>2$, where M is odd. In this paper, we present the design of three-band time–frequency-optimized orthogonal filter banks.

Recently, there have been a lot of research in the area of three-band PRFBs. Three-band filter banks have shown improved performance in digital watermarking [3, 19] and image denoising [55]. A hybrid of two- and three-band filter banks has shown excellent performance in image coding [34]. Many authors have proposed various design methodologies for the design of three-band filter banks. Tilo S. [43], Howlett and Nguyen [15] and Jayawardena [17] proposed three-band biorthogonal wavelet filter banks. Chui and Lian [7], Zhao and Zhao [55], Lizhong and Wang [25] and Lin et al. [24] designed orthogonal wavelet filter banks. However, time–frequency localization is not used as the optimality criterion. The three-band time–frequency-localized orthogonal wavelet filter bank of length six is designed by Bhati et al. [2]. In this study, authors minimized TFP of wavelet and scaling functions employing Gabor’s uncertainty principle [10] for continuous-time function in $L_2(\mathfrak {R})$. Gaussian functions are optimal functions which achieve the lower bound. However, Gaussian functions are not compactly supported in time domain [10]. Venkatesh et al. [50] computed the samples of time–frequency product optimal function which is compactly supported in frequency domain. In this paper, our goal is to design three-band time–frequency optimal orthogonal wavelets with compact support in time domain. We formulate four new expressions that compute the time mean, frequency mean, time variance and frequency variance of compactly supported functions from the samples of the Fourier transform of the function. We design three-band orthogonal time–frequency optimal wavelet filter banks of lengths six and nine. Unlike the methodology in [2], the developed expressions for TFP for time-limited function have been used for design of time–frequency optimal wavelet filter banks. On the other hand, the variance definitions used by Bhati et al. [2] and Xie and Morris [54] involve numerical integration in order to compute variance from the samples of the function. In addition to this, the regularity of filter bank is necessary if we design time–frequency-localized filter bank with the TFP expression used in [2]. In this paper, we have shown that the proposed expression for the TFP eliminates this limitation and even non-regular filter banks can be optimized for time–frequency localization. As an example, we design TFP optimal low-pass scaling function from the scaling filter without zeros on the aliasing frequencies. This scaling function cannot be designed using the TFP expression used in [2].

In this paper, we use dyadic factorization of polyphase matrix proposed by Vaidyanathan [49] for the implementation of orthogonal M-band filter bank. Thus, filter bank regularity and orthogonality, or equivalently, vanishing moments (VMs) are imposed structurally [5]. A parametrization-based technique [54] is used to minimize a weighted summation of TFPs with respect to free parameters to obtain a time–frequency-localized filter bank. We compare length six and length nine filter banks with respect to time–frequency optimality. The proposed design methodology has following features:

• 1. Time–frequency localization measures for time-limited functions are formulated and employed in the design methodology to generate time–frequency optimal wavelet bases with compact support.

• 2. We can design TFP optimal time-limited scaling and wavelet functions using the proposed methodology. These functions can be generated from finite length discrete-time sequences using cascade algorithm.

• 3. We can control the time–frequency products of wavelets by choosing different weights.

• 4. We use dyadic factorization of polyphase matrix proposed by Vaidyanathan [49] for the implementation of orthogonal three-band filter bank which ensures a search over the complete class of finite impulse response (FIR) filter bank for the given length.

• 5. Single VM and orthogonality constraints are imposed structurally [5], and therefore, the filter bank design problem becomes an unconstrained optimization problem.

• 6. It is well known that the maximum Sobolev regularity that can be achieved with single VM is one [13]. We found that all filter banks of length nine with single VM designed in this paper have Sobolev regularity of one. Thus, the proposed methodology designs maximal Sobolev regularity filter banks with single VM provided sufficient number of degrees of freedom are available.

• 7. Unlike Daubechies [8] and Strang [41] conditions of regularity, the proposed design methodology provides direct and arbitrary fine control on the frequency variance of the scaling function.

• 8. M-band, time–frequency optimal, wavelet filter banks can be designed with the proposed methodology with M odd or even.

The rest of the paper is organized as follows. In Sect. 2, we derive the expressions for mean and variances for asymmetric band-pass time-limited functions from the samples of the Fourier transform of the function. Section 3 illustrates a method to compute the Fourier transform of the scaling and wavelet function at the ith cascade iteration. Samples of the Fourier transform are then used to obtain the TFP of scaling and wavelet functions. In Sect. 4, we use the proposed measure for TFP and the cascade algorithm to design TFP optimal scaling and wavelet functions. Three-band time–frequency optimal, orthogonal, single VM, length six and length nine filter banks are designed in Sect. 5. Finally, results and conclusions are given in Sects. 6 and 7, respectively.

2 Computation of Time and Frequency Variances from Samples of Fourier Transform

According to the dual of the Nyquist criterion, under certain conditions, a time-limited function is uniquely determined by the samples of its Fourier transform [23]. In this section, our goal is to develop time and frequency variance expressions for time-limited functions using samples of the Fourier transform of the function. We briefly present the methodology proposed by Venkatesh et al. [50], to compute the variances from the samples of the zero-phase low-pass band-limited function. We show that duality can be used to extend the expressions proposed by them for band-limited functions to time-limited functions. In this section, we formulate four expressions that compute the time mean, frequency mean, time variance and frequency variance from the samples of the Fourier transform of a time-limited function.

Let $f(t) \in L_2(\mathfrak {R})$ be a real function and $F({\varOmega })$ is its Fourier transform. Let $E=||f(t)||_2^2$ is the energy of the function. The time variance $\hat{\triangle }_{t}^{2}$ and frequency variance $\hat{\triangle }_{{\varOmega }}^{2}$ of f(t), centered in time and frequency at $\mu _t$ and $\mu _{\varOmega }$, respectively, are defined as [31, 53],

$$\begin{aligned} \mu _t(f(t))= & {} \frac{1}{E}\int _{t=-\infty }^{\infty } t{|f(t)|}^2 \hbox {d}t \end{aligned}$$

(1)

$$\begin{aligned} \hat{\triangle }_{t}^{2}(f(t))= & {} \frac{1}{E}\int _{t=-\infty }^{\infty } {|(t-\mu _t)f(t)|}^2 \hbox {d}t \end{aligned}$$

(2)

$$\begin{aligned} \triangle _{t}^{2}(f(t))= & {} \frac{1}{E}\int _{t=-\infty }^{\infty } {|tf(t)|}^2 \hbox {d}t \end{aligned}$$

(3)

$$\begin{aligned} \mu _{\varOmega }(f(t))= & {} \frac{1}{\pi E}\int _{{\varOmega }=0}^{\infty } {\varOmega }{|F({\varOmega })|}^2 \hbox {d}{\varOmega }\end{aligned}$$

(4)

$$\begin{aligned} \hat{\triangle }_{{\varOmega }}^2(f(t))= & {} {\frac{1}{\pi E}\int _{{\varOmega }=0}^{\infty } {|({\varOmega }-\mu _{\varOmega })F({\varOmega })|^2} \hbox {d}{\varOmega }} \end{aligned}$$

(5)

$$\begin{aligned} {\triangle }_{{\varOmega }}^{2}(f(t))= & {} \frac{1}{2\pi E}\int _{{\varOmega }=-\infty }^{\infty } {|{\varOmega }F({\varOmega })|}^2 \hbox {d}{\varOmega }\end{aligned}$$

(6)

It should be noted that,

$$\begin{aligned} \hat{\triangle }_{t}^{2}(f(t))= & {} \triangle _{t}^{2}(f(t))- (\mu _{t}(f(t)))^2 \end{aligned}$$

(7)

$$\begin{aligned} \hat{\triangle }_{{\varOmega }}^{2}(f(t))= & {} \triangle _{{\varOmega }}^{2}(f(t))- (\mu _{{\varOmega }}(f(t)))^2 \end{aligned}$$

(8)

2.1 Computation of Time and Frequency Variances of Zero-Phase Low-Pass Band-Limited Functions from Samples

Venkatesh et al. [50] attempted to interpolate the samples of band-limited function, using an interpolation scheme and then measured its continuous-time time variance and frequency variance. The proposed expressions are consistent with traditional continuous-time definitions of variances; however, the expressions developed are applicable only to zero-phase, low-pass, band-limited functions. If the time center $\mu _t$ of the low-pass function is not zero, i.e., if the function is not symmetric then proposed measures require a modification which is suggested in this section. Similarly, the measure proposed by them cannot be used for computing variances of band-pass functions. In this section, we have proposed a measure to compute variances of band-pass functions.

2.1.1 Brief of Venkatesh et al. Work [50]

Real-world signals such as speech and image have a spectrum which is negligibly small beyond a certain frequency. Such signals can be modeled as band-limited functions. The Shannon–Whittaker theorem [28] facilitates the processing of band-limited continuous-time signals on a computer, taking its discrete-time samples. It states that under certain conditions, the band-limited signal can be uniquely represented by its discrete samples. Intuitively, continuous-time and discrete-time variances for band-limited functions must be the same [50]. Let,

$$\begin{aligned} D_n^2=\sum _{n=-\infty }^{\infty } n^2|f[n]|^2 \end{aligned}$$

and

$$\begin{aligned} D_\omega ^2=\frac{1}{2\pi }\int _{-\pi }^{\pi } \omega ^2|F(e^{j\omega })|^2\hbox {d}\omega \end{aligned}$$

represent the time variance and frequency variance of the normalized sequence f[n], respectively, where $f(nT_s)$ are samples of zero-phase low-pass band-limited function f(t) [16]. Then, it is observed that $D_n^2 \ne \triangle _t^2(f(t))$ and $D_\omega ^2 \ne \triangle _{\varOmega }^2(f(t))$ even for band-limited functions. Venkatesh et al. [50] proposed new definitions for discrete-time variances that remove this inconsistency between the existing discrete-time definitions $\left( D_n^2 \hbox {and} D_\omega ^2 \right)$ and continuous-time definitions. Results have been demonstrated for standard test functions like band-limited triangular and half-cosine functions. Further, they computed the samples of TFP optimal zero-phase low-pass band-limited functions.

They interpolate the samples $f(kT_s)$, $k \in \mathbb {Z}$ of the band-limited function $f(t) \in L_2(\mathfrak {R})$, that satisfies the following condition,

$$\begin{aligned} F({\varOmega })=0, ~\forall ~ |{\varOmega }| \ge \sigma \end{aligned}$$

assuming sampling interval $T_s<\pi /\sigma$. Standard sinc interpolation cannot be used as the time variance of the sinc function is infinite. They refine the spectrum of the sinc function by modifying discontinuous edges to smooth edges as shown in Fig. 1 and propose $G({\varOmega })$,

$$\begin{aligned} G({\varOmega })={\left\{ \begin{array}{ll} \frac{T_s}{2}\left[ \cos \left( \frac{\pi ({\varOmega }+ \sigma )}{\epsilon }\right) +1\right] &{} ~~:~~ {-\sigma - \epsilon \le {\varOmega }< -\sigma } \\ T_s &{} ~~:~~ {-\sigma \le {\varOmega }\le \sigma }\\ \frac{T_s}{2}\left[ \cos \left( \frac{\pi ({\varOmega }- \sigma )}{\epsilon }\right) +1\right] &{} ~~:~~ {\sigma < {\varOmega }\le \sigma + \epsilon } \\ 0 &{} ~~:~~ \text {elsewhere} \end{array}\right. } \end{aligned}$$

(9)

Fig. 1

Fourier transform $G({\varOmega })$ of band-limited interpolating function [50]

as the Fourier transform of the interpolating function. In (9), the parameter $\epsilon$ controls the transition band of $G({\varOmega })$. The interpolated function f(t) is then substituted in (3), and it is shown that $\triangle _t^2(f(kT_s))$ in terms of the samples is given by,

$$\begin{aligned} \triangle _t^2(f(kT_s))=\frac{1}{2\pi E}\sum _{n \in {\mathbb {Z}}}\sum _{m \in {\mathbb {Z}}}f(nT_s)f(mT_s)\bigg (\frac{m^2+n^2}{2}T_s^2{ A}(m,n) +{B}(m,n)\bigg ) \end{aligned}$$

(10)

where

$$\begin{aligned}&{ A}(m,n)=2\sigma T_s^2\delta _{mn} \\&\quad +\,\frac{T_s^2(-1)^{(m-n)}}{2}\left[ \epsilon \frac{\sin ((m-n)T_s\epsilon )}{(m-n)T_s\epsilon } +\frac{\sin ((m-n)T_s\epsilon )}{2}\frac{2(m-n)T_s}{{(\frac{\pi }{\epsilon })}^2-(m-n)^2T_s^2}\right] \\&\quad +\,\frac{T_s^2(-1)^{(m-n)}}{2}\left[ \epsilon \frac{\sin ((m-n)T_s\epsilon )}{(m-n)T_s\epsilon } \left( 1-\frac{\frac{1}{2}}{\left[ 1-{(\frac{(m-n)T_s\epsilon }{2\pi })}^2\right] }\right) \right] \end{aligned}$$

and,

$$\begin{aligned} {B}(m,n)= & {} \frac{1}{4\epsilon }\frac{\sin ((m-n)T_s\epsilon )}{(m-n)T_s\epsilon }\frac{T_s^2\pi ^2(-1)^{m-n}}{\left[ 1-{\left( \frac{(m-n)T_s\epsilon }{2\pi }\right) }^2\right] }\\ \sigma= & {} \frac{\pi }{T_s}-\epsilon . \end{aligned}$$

Let $F(\hbox {e}^{j\omega })$ represent the discrete-time fourier transform (DTFT) of samples $f(kT_s)$ given in [28],

$$\begin{aligned} F(\hbox {e}^{j\omega })=\sum _{k=-\infty }^{\infty } f(kT_s)\hbox {e}^{-j\omega k} \end{aligned}$$

The Fourier transform $F({\varOmega })$ of band-limited function f(t) and DTFT $F(\hbox {e}^{j\omega })$ are related by [28],

$$\begin{aligned} F({\varOmega })={\left\{ \begin{array}{ll} T_sF(\hbox {e}^{j{\varOmega }T_s}) &{} ~~:~~ \forall |{\varOmega }| \le \frac{\pi }{T_s} \\ 0 &{} ~~:~~ \text {elsewhere} \end{array}\right. } \end{aligned}$$

(11)

They substitute $F({\varOmega })$ from (11) in (6) and show that $\triangle _{\varOmega }^2(f(kT_s))$ is given by,

$$\begin{aligned} \triangle _{\varOmega }^2(f(kT_s))= & {} \frac{1}{2\pi T_sE}\bigg [ \frac{2 \pi ^3}{3}\sum _{n \in \mathbb {Z}} f^2(nT_s) \nonumber \\&+\,{\sum _{n \in \mathbb {Z}}\sum _{m \in \mathbb {Z}}}_{m \ne n}\frac{4\pi (-1)^{(m-n)}}{(m-n)^2}f(mT_s)f(nT_s)\bigg ] \end{aligned}$$

(12)

Let $\mathbf{f}$ be the column vector of samples $f(kT_s)$. Then, $\triangle _t^2(f(kT_s))$ and $\triangle _{\varOmega }^2(f(kT_s))$ can be represented as,

$$\begin{aligned} \triangle _t^2(\mathbf{f})=\frac{1}{2 \pi E}(\mathbf{f}^H \mathbf{S}_v \mathbf{f}) \end{aligned}$$

(13)

$$\begin{aligned} \triangle _{\varOmega }^2(\mathbf{f})=\frac{1}{2 \pi T_sE}(\mathbf{f}^H \mathbf{B}_v \mathbf{f}) \end{aligned}$$

(14)

where

$$\begin{aligned} { S}_v(m,n)=\frac{m^2+n^2}{2}T_s^2{ A}(m,n)+{ B}(m,n) \end{aligned}$$

and,

$$\begin{aligned} { B}_v(m,n)={\left\{ \begin{array}{ll} \frac{2\pi ^3}{3} &{} ~~:~~ m=n \\ \frac{4\pi (-1)^{m-n}}{(m-n)^2} &{} ~~:~~ m \ne n \end{array}\right. } \end{aligned}$$

(15)

Here, H represents the Hermitian transpose. In the next section, we work with functions which are not necessarily centered in time domain and frequency domain both. We derive the expressions for $\mu _t(\mathbf{f})$, $\mu _{\varOmega }(\mathbf{f})$, $\hat{\triangle }_{t}^{2}(\mathbf{f})$ and $\hat{\triangle }_{{\varOmega }}^{2}(\mathbf{f})$ in terms of samples $\mathbf{f}$ of the band-limited function.

2.2 Expressions for Mean and Variance in Time and Frequency for Band-Limited Functions From Samples

2.2.1 Time Center

Time center or mean in time $\mu _t$ of a function $f(t) \in L_2(\mathfrak {R})$ is defined in (1). We first interpolate the samples $f(nT_s)$, $n \in \mathbb {Z}$, sampled at $T_s<\frac{\pi }{\sigma }$, using an interpolation scheme proposed by Venkatesh et al. [50] and obtain the continuous-time function. The interpolation scheme is given by,

$$\begin{aligned} f(t)=\sum _{n=-\infty }^{\infty } f(nT_s)g(t-nT_s) \end{aligned}$$

(16)

where the Fourier transform $G({\varOmega })$ of the band-limited function g(t) is given by (9). Then, as shown in ‘Appendix’ section Mean in Time From Samples of Band-limited Function, $\mu _t(\mathbf{f})$ is given by,

$$\begin{aligned} \mu _t(\mathbf{f})=\frac{1}{2\pi E}(\mathbf{f}^H \mathbf{S}_\mu \mathbf{f}) \end{aligned}$$

(17)

where

$$\begin{aligned} \mathbf{S}_\mu =\mathbf{{C_1}}+\mathbf{{C_2}}+nT_s\mathbf{A} \end{aligned}$$

[m, n]th element of matrices are given as follows.

$$\begin{aligned} { C}_1(m,n)= & {} \frac{j}{4}\frac{\pi ^2T_s^2\hbox {e}^{j(-\pi +T_s\epsilon )(m-n)}(3\pi ^2\hbox {e}^{-jT_s(m-n)\epsilon } + { K}_1(m,n))}{{ K}_2(m,n)}\\ { C}_2(m,n)= & {} \frac{-j}{4}\frac{\pi ^2T_s^2\hbox {e}^{-j(-\pi +T_s\epsilon )(m-n)}(3\pi ^2\hbox {e}^{jT_s(m-n)\epsilon } + { K}_1(m,n))}{{ K}_2(m,n)}\\ { K}_1(m,n)= & {} 5\pi ^2 - 2T_s^2{(m-n)}^2\epsilon ^2\\ { K}_2(m,n)= & {} T_s^4(m-n)^4\epsilon ^4 - 5\pi ^2T_s^2(m-n)^2\epsilon ^2 + 4\pi ^4 \end{aligned}$$

2.2.2 Time Variance

Venkatesh et al. [50] strictly assumed a real-valued function with zero mean in time, and their definition can be used to compute the time variance of time-centered, symmetric, low-pass functions. For functions, which are not time-centered, time variance $\hat{\triangle }_{t}^{2}(\mathbf{f})$ is defined in (7), where $\triangle _{t}^{2}(\mathbf{f})$ and $\mu _t(\mathbf{f})$ are given by (13) and (17), respectively.

2.2.3 Frequency Center

Frequency center or mean frequency of real-valued low-pass functions is zero. The mean frequency, $\mu _{\varOmega }$, of a band-pass function can be obtained from its positive frequency spectrum. The mean frequency is defined in (4). As shown in ‘Appendix’ Mean in Frequency From Samples of Band-limited Function, $\mu _{{\varOmega }}(\mathbf{f})$ is given by,

$$\begin{aligned} \mu _{{\varOmega }}(\mathbf{f})=\frac{1}{\pi E}\left( \mathbf{f}^H \mathbf{B}_\mu \mathbf{f}\right) \end{aligned}$$

(18)

where

$$\begin{aligned} { B}_\mu (m,n)=-\frac{[(-1)^{(m-n)}(-1+\pi j (m-n))+1]}{{(m-n)}^2} \end{aligned}$$

For $m=n$

$$\begin{aligned} { B}_\mu (m,n)=\pi ^2 /2 \end{aligned}$$

2.2.4 Frequency Variance

Frequency variance $\hat{\triangle }_{\varOmega }^{2}(\mathbf{f})$ of a band-pass function is given by (8), where $\triangle _{\varOmega }^2(\mathbf{f})$ and $\mu _{\varOmega }(\mathbf{f})$ are given by (14) and (18), respectively.

2.3 Expressions for Mean and Variance of Compactly Supported Functions in Time and Frequency from Samples of Fourier Transform

Let ${\hat{\mathbf{f}}}$ be a column vector and represent the samples ${F}(k {\varOmega }_s)$ of the Fourier transform ${F}({\varOmega })$, where ${\varOmega }_s$ denotes the sample spacing in frequency domain. Then, energy $E=\frac{{\varOmega }_s}{2 \pi }{\hat{\mathbf{f}}}^H{\hat{\mathbf{f}}}$. Let ${\mu }_t^{'}({\hat{\mathbf{f}}})$, $\mu _{\varOmega }^{'}({\hat{\mathbf{f}}})$, $\triangle _{t}^{2^{'}}({\hat{\mathbf{f}}})$, $\triangle _{{\varOmega }}^{2^{'}}({\hat{\mathbf{f}}})$ denote the time-limited equivalent of measures ${\mu }_t(\mathbf{f})$ $\mu _{\varOmega }(\mathbf{f})$, $\triangle _{t}^{2}(\mathbf{f})$, $\triangle _{{\varOmega }}^{2}(\mathbf{f})$ for band-limited functions, respectively. Note that we can obtain frequency variance (6) from the expression for time variance (3) by the substitution $f(t)={F(t)}/{\sqrt{2\pi }}$. Here, $F({\varOmega })$ represents the Fourier transform of f(t). In terms of the samples, the substitution is represented by $\mathbf{f}={\hat{\mathbf{f}}}/{\sqrt{2\pi }}$ and $T_s={\varOmega }_s$. The substitution is used in the expression for $\triangle _t^2(\mathbf{f})$ to compute $\triangle _{\varOmega }^{2^{'}}({\hat{\mathbf{f}}})$ for time-limited functions. Similarly, the expression for the measure $\triangle _{\varOmega }^2(\mathbf{f})$ is used to compute $\triangle _t^{2^{'}}({\hat{\mathbf{f}}})$ for time-limited functions. Let $\mathbf{S}^{'}_\mu$, $\mathbf{S}^{'}_v$ and $\mathbf{B}^{'}_v$ represent the matrices in (13), (14) and (17) with sampling time $T_s$ substituted by ${\varOmega }_s$. Then,

$$\begin{aligned} \triangle _{t}^{2^{'}}({\hat{\mathbf{f}}})= & {} \frac{1}{4\pi ^2 {\varOmega }_s E}({\hat{\mathbf{f}}}^H \mathbf{B}^{'}_v {\hat{\mathbf{f}}}) \end{aligned}$$

(19)

$$\begin{aligned} \triangle _{{\varOmega }}^{2^{'}}({\hat{\mathbf{f}}})= & {} \frac{1}{4\pi ^2 E}\left( {\hat{\mathbf{f}}}^H \mathbf{S}^{'}_v {\hat{\mathbf{f}}}\right) \end{aligned}$$

(20)

$$\begin{aligned} \mu _{\varOmega }^{'}({\hat{\mathbf{f}}})= & {} \frac{1}{4\pi ^2 E^{'}}\left( {\hat{\mathbf{f}}}^H \mathbf{S}^{'}_\mu {\hat{\mathbf{f}}}\right) \end{aligned}$$

(21)

$$\begin{aligned} \mu _{t}^{'}({\hat{\mathbf{f}}})= & {} \frac{{\varOmega }_s^2}{4\pi ^2 E}\left( {\hat{\mathbf{f}}}^H \mathbf{R} {\hat{\mathbf{f}}}\right) \end{aligned}$$

(22)

The scaling and wavelet functions are low-pass and band-pass functions, respectively. Mean frequency of band-pass functions is given by (21), where ${\hat{\mathbf{f}}}$ represents the samples of spectrum for positive frequencies and the normalization using $E^{'}=E/2$ and the computation of the matrix $\mathbf{S}^{'}_\mu$ must be done accordingly. Mean in time $\mu _{t}^{'}({\hat{\mathbf{f}}})$ of the asymmetric function is given by (22). The expression for the matrix $\mathbf{R}$ in (22) is derived in ‘Appendix’ Mean of Time-limited Functions From the Samples of Fourier transform. Since the mean frequency of the real-valued low-pass scaling function is zero, the frequency variance of the scaling function is given by $\triangle _{\varOmega }^{2^{'}}({\hat{\mathbf{f}}})$. However, mean in time of scaling and wavelet functions may be nonzero and the time variance $\hat{\triangle }_t^{2^{'}}({\hat{\mathbf{f}}})$ for both the functions is given by,

$$\begin{aligned} \hat{\triangle }_t^{2^{'}}({\hat{\mathbf{f}}})=\triangle _{t}^{2^{'}}({\hat{\mathbf{f}}})-\left( \mu _{t}^{'}({\hat{\mathbf{f}}})\right) ^2 \end{aligned}$$

(23)

Similarly, the frequency variance $\hat{\triangle }_{{\varOmega }}^{2^{'}}({\hat{\mathbf{f}}})$ of the band-pass wavelet function is given by,

$$\begin{aligned} \hat{\triangle }_{{\varOmega }}^{2^{'}}({\hat{\mathbf{f}}})=\triangle _{{\varOmega }}^{2^{'}}({\hat{\mathbf{f}}})-\left( \mu _{{\varOmega }}^{'}({\hat{\mathbf{f}}})\right) ^2 \end{aligned}$$

(24)

Note that, ${\hat{\mathbf{f}}}$ in (24) represents the samples of spectrum for positive frequencies.

In the next section, we calculate the Fourier transform of wavelet and scaling functions at the ith cascade iteration and compute the samples of the Fourier transform with sample spacing ${\varOmega }_s$ that satisfies the dual of the Nyquist criterion. According to the dual of the Nyquist criterion, the Fourier transform of time-limited functions with support s, i.e.,

$$\begin{aligned} f(t)=0~~: ~~\forall ~ |t|>s \end{aligned}$$

can be reconstructed from the samples of the Fourier transform if the sample spacing ${\varOmega }_s < \pi /s$ [23].

3 Time–Frequency Product of Functions Generated by the Cascade Algorithm

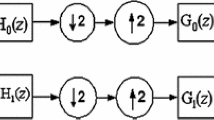
The scaling function $\phi (t)$ and wavelet functions $\psi _k(t)$ for M-band wavelet filter bank are given by [52],

$$\begin{aligned} \phi (t)=\sqrt{M}\sum _n g_0[n]\phi (Mt-n)\\ \psi _k(t)=\sqrt{M}\sum _n g_k[n]\phi (Mt-n) \end{aligned}$$

where $k=1,2,\ldots ,M-1$. $g_0[n]$ and $g_k[n]$ represent low-pass and high-pass filters, respectively. The cascade algorithm is used to generate scaling and wavelet functions from the iterations of discrete-time filters of the PRFB [52]. Let $g_0^i[n]$, represents the normalized iterated sequence. Then,

$$\begin{aligned} g_0^i[n]=g_0[n]*g_0[n/M]*g_0[n/M^2]*\cdots *g_0[n/M^{i-1}] \end{aligned}$$

(25)

where $g_0[n/N]$ represents the up-sampled sequence obtained by inserting $(N-1)$ zeros between each of the samples of $g_0[n]$ and $*$ represents the convolution operation. Let L be the length of the scaling filter $g_0[n]$. Then, length $L^{(i)}$ of the iterated sequence $g_0^i[n]$ for two-band filter banks is given by Vetterli [52]. For M-band filter banks $L^{(i)}$ can be given by,

$$\begin{aligned} L^{(i)}=\bigg [\frac{M^i-1}{M-1}(L-1)+1\bigg ]. \end{aligned}$$

Fig. 2

Interpolating function b(t): Samples generated by cascade iterations are interpolated using the time-limited function b(t)

Let $B(j{\varOmega })$ represents the Fourier transform of the normalized interpolating smooth Box function b(t) shown in Fig. 2. It is normalized in energy by substituting $A=1/\sqrt{\tau }$. A Box function with discontinuous edges cannot be used for interpolation as its frequency variance is infinite. Interpolating the iterated sequence $g_0^i[n\tau ]$ with the interpolating function $b(t-\frac{\tau }{2})$, with $\epsilon \rightarrow 0$ and $\tau =\frac{1}{M^i}$, we get the scaling function $\phi ^i(t)$ given by,

$$\begin{aligned} \phi ^i(t)=\sum _{n=0}^{L^{(i)}-1} g_0^i(n\tau )b\left( t-\frac{\tau }{2}-n\tau \right) \end{aligned}$$

(26)

Using the convolution property of the Fourier transform, the Fourier transform of the scaling function, ${{\varPhi }}^{(i)}({\varOmega })$, at the ith iteration, is given by,

$$\begin{aligned} {{\varPhi }}^{(i)}({\varOmega })=G_0^{(i)}(\hbox {e}^{j{\varOmega }\tau })B(j{\varOmega })\hbox {e}^{\frac{-j{\varOmega }\tau }{2}} \end{aligned}$$

(27)

where

$$\begin{aligned} G_0^{(i)}(\hbox {e}^{j\omega })=G_0(\hbox {e}^{j\omega })G_0(\hbox {e}^{jM\omega })\ldots G_0(\hbox {e}^{jM^{i-1}\omega }) \end{aligned}$$

and,

$$\begin{aligned} B(j{\varOmega })=\frac{A_1+B_1}{{\varOmega }(\pi ^2-\epsilon ^2{\varOmega }^2)}+\frac{A\tau \sin ({\varOmega }\tau /2)}{({\varOmega }\tau /2)} \end{aligned}$$

where

$$\begin{aligned} A_1= & {} \pi ^2A[\sin ({\varOmega }\epsilon +{\varOmega }\tau /2)-\sin ({\varOmega }\tau /2)]\\ B_1= & {} 2A\epsilon ^2{\varOmega }^2\sin ({\varOmega }\tau /2) \end{aligned}$$

Note that if $G_0(\hbox {e}^{j0})=\sqrt{3}$, then ${\varPhi }^{(i)}(0)=1$. Similarly, ${{\varPsi }_k}^{(i)}({\varOmega })$ is given by,

$$\begin{aligned} {{\varPsi }_k}^{(i)}({\varOmega })=G_k^{(i)}(\hbox {e}^{j{\varOmega }\tau })B(j{\varOmega })\hbox {e}^{\frac{-j{\varOmega }\tau }{2}} \end{aligned}$$

(28)

where

$$\begin{aligned} G_k^{(i)}(\hbox {e}^{j\omega })=G_0(\hbox {e}^{j\omega })G_0(\hbox {e}^{jM\omega }) \ldots G_0\left( \hbox {e}^{jM^{i-2}\omega }\right) G_k\left( \hbox {e}^{jM^{i-1}\omega }\right) \end{aligned}$$

Since the support of scaling and wavelet functions at the ith iteration is [0, s], where $s=L^{(i)}\tau$, we sample ${{\varPhi }_0}^{(i)}({\varOmega })$,${{\varPsi }_1}^{(i)}({\varOmega })$ and ${{\varPsi }_2}^{(i)}({\varOmega })$ at the sample spacing ${\varOmega }_s$ that satisfies,

$$\begin{aligned} {\varOmega }_s<\frac{\pi }{s} \end{aligned}$$

and compute time and frequency variances from the samples using the measures (23) and (24), respectively. It should be noted that we are interpolating normalized iterated sequence in (25) with normalized smooth-edge box function b(t) and therefore ${{\varPhi }}^{(i)}({\varOmega }) \in L_2(\mathfrak {R})$ and ${{\varPsi }_k}^{(i)}({\varOmega }) \in L_2(\mathfrak {R})$ [18]. To obtain the TFP, we multiply the time variance and the frequency variance of the function. Figures 3 and 4 show the samples of Fourier transforms of the scaling and wavelet functions, respectively, for length six Daubechies (db) orthonormal maximally flat filter.

Fig. 3

Samples of fourier transform of db3 scaling function

Fig. 4

Samples of fourier transform of db3 wavelet function

For the rest of the paper, we assume $M=3$ and $i=4$ unless otherwise stated. We introduce short notations for the TFP of the scaling and wavelet function computed from the proposed method. The scaling function $\phi ^i(t)$ is generated using the filter $g_0[n]$. Therefore, its TFP is denoted by $\hat{\triangle }_t^{2^{'}}\hat{\triangle }_{\varOmega }^{2^{'}}(g_0[n])$. The wavelet function $\psi _k^i(t)$ is generated using filters $g_0[n]$ and $g_k[n]$. Therefore, the TFP of the wavelet function is denoted by $\hat{\triangle }_t^{2^{'}}\hat{\triangle }_{\varOmega }^{2^{'}}(g_0[n],g_k[n])$.

4 Design of Time–Frequency Product Optimal Time-Limited Scaling and Wavelet Functions from Discrete-Time Sequences

Venkatesh et al. [50] computed the samples of TFP optimal band-limited function. In this section, we design the TFP optimal time-limited scaling and wavelet function. For the given scaling filter $g_0[n]$, we first compute the samples of the Fourier transform of the scaling function using (27). The samples of the Fourier transform are the used to determine time variance and frequency variance using (23) and (24), respectively. To compute the TFP $\hat{\triangle }_t^{2^{'}}\hat{\triangle }_{\varOmega }^{2^{'}}(g_0[n])$, we multiply time variance and frequency variance. To design TFP optimal time-limited scaling function, we minimize the objective function $\hat{\triangle }_t^{2^{'}}\hat{\triangle }_{\varOmega }^{2^{'}}(g_0[n])$ with respect to $g_0[n]$. The unconstrained optimization problem is given by,

$$\begin{aligned} \begin{aligned}&\underset{g_0[n]}{\text {minimize}}&\hat{\triangle }_t^{2^{'}}\hat{\triangle }_{\varOmega }^{2^{'}}(g_0[n]) \end{aligned} \end{aligned}$$

(29)

It is found that, starting from $g_0[n]=[1~ 1~ 1~ 1~ 1~ 1~ 1~ 1]$ or any other random initial point for $g_0[n]$, the optimization problem (29) generates the unique TFP optimal length eight normalized scaling filter given in the first column of Table 1 and scaling function is shown in Fig. 5. For two-band filter banks, Rioul [35] has shown that continuity of scaling function implies zeros on aliasing frequencies of scaling filter. Pole-zero map of optimized scaling filter $g_0[n]$ confirms that there are zeros at aliasing frequencies $\omega =\pm \frac{2 \pi }{3}$.

Table 1 Normalized filter coefficients that generate time–frequency optimal time-limited scaling and wavelet function

Fig. 5

TFP optimal time-limited scaling filter is computed by solving the unconstrained optimization problem in (29). Figure shows the corresponding scaling function. TFP of the function is 0.25154005. Scaling filter coefficients are given in first column of Table 1

Let $p_0[n]$ represents the filter coefficients in Table 1. We design the TFP optimal time-limited wavelet function by minimizing the objective function $\hat{\triangle }_t^{2^{'}}\hat{\triangle }_{\varOmega }^{2^{'}}(p_0[n],g_1[n])$. The expression (28) is used to compute the samples of the Fourier transform of wavelet function. The samples of the Fourier transform are then used to determine time variance and frequency variance using (23) and (24), respectively. The constrained optimization problem is given by,

(30)

Second column of Table 1 gives the optimized filter coefficients for $g_1[n]$ for the optimization problem in (30). Figure 6 shows the corresponding wavelet function.

Fig. 6

TFP optimal time-limited wavelet function is designed by solving the constrained optimization problem in (30). Figure shows the TFP optimal wavelet function. TFP of the function is 0.338491717. Corresponding high-pass filter coefficients $g_1[n]$ are given in second column of Table 1

5 Design of Time–Frequency-Localized Three-Band Orthogonal Single Vanishing Moment Wavelet Filter Bank

The M-band orthogonal filter bank in its canonical form is represented by [49],

$$\begin{aligned} \mathbf{h}(z)=[H_0(z) \ H_1(z) \ \ldots \ H_{M-1}(z)]^T \end{aligned}$$

The analysis filters $\mathbf{h}(z)$ can be obtained from the analysis polyphase matrix, $\mathbf{E}(z)$ using $\mathbf{h}(z)=\mathbf{E}(z^{M})\mathbf{e}(z)$, where $\mathbf{e}(z)=[1 \ z^{-1} \ \ldots \ z^{-(M-1)}]^T$ [49]. An M-band filter bank is said to be orthogonal and K-regular, if it satisfies $<h_i[-n],h_j[n-Mk]>=\delta (i-j)\delta (k)$ or equivalently, $\mathbf{E}(z)\mathbf{E}^T(z^{-1})=\mathbf{I}$, and if low-pass filter has K zeros [5] at $\omega _k=2\pi m/M$ for $m=1,2, \ldots M-1$. K-regular low-pass filter can be given by,

$$\begin{aligned} H_0(z)=\bigg (\frac{1+z^{-1}+ \cdots +z^{-(M-1)}}{M}\bigg )^K Q(z). \end{aligned}$$

It means that $H_0(z)$ is $(K-1)$th-order flat at aliasing frequencies. For an orthogonal filter bank, K regularity implies $H_0(\hbox {e}^{j0})=\sqrt{M}$ and each high-pass filter has K VMs [29]. We must note that regularity of $H_0(z)$ does not guarantee any degree of differentiability of the scaling or wavelet function, and the regularity of filter bank is not sufficient for regularity of functions generated from cascade iterations [51]. Even if the scaling filter satisfies the necessary and sufficient condition for convergence of cascade iterations in $L_2(\mathfrak {R})$ [42], it does not ensure regularity more than that of the box function. Let p[n] represents the autocorrelation of the sequence q[n] such that $Q(e^{j0})=1$. The transition matrix is given by $[\mathbf{T}_\mathbf{Q}]_{ij}=Mp[Mi-j]$ [5, 41]. Let $\lambda (\mathbf{T}_\mathbf{Q})$ denote the eigenvalues of the matrix $[\mathbf{T}_\mathbf{Q}]$. For orthogonal filter banks $\lambda (\mathbf{T}_\mathbf{{H_0}}) \le 1$ [41]. Sobolev regularity or $L_2$ differentiability [13, 27] of a scaling function $\phi (t)$ is defined as the smallest real number $S_\mathrm{max}$ such that for all $s < S_\mathrm{max}$, $\int _{-\infty }^{\infty } (1+{\varOmega }^2)^s|{\varPhi }({\varOmega })|^2 d{\varOmega }< \infty$. Note that $S_\mathrm{max}=K-\frac{\log |\lambda _\mathrm{max}(\mathbf{T}_\mathbf{Q}) |}{2\log (M)}$, and it is completely determined by the scaling filter $H_0(z)$ [5, 13]. $S_\mathrm{max} = 0.5$ for the Haar filter bank [33, 42] and $S_\mathrm{max} > 0.5$ ensures the regularity of scaling and wavelet functions to be more than that of the box function. Interestingly, it is found that $S_\mathrm{max} > 0.5$ for all the filter banks designed in this paper. It can be noted that scaling filter $g_0[n]$ in Table 1 has unit Sobolev regularity. Since the wavelet is a linear combination of the dilates and translates of the scaling function, regularity of the wavelet is same as the scaling function.

In the proposed design method, rather than representing a filter bank in its canonical form, we use the dyadic factorization of polyphase matrix proposed by Vaidyanathan [5, 49]. The use of the dyadic framework has a number of advantages over the canonical form. The key benefit is that orthogonality condition is automatically satisfied and explicit optimization constraints are not required. This greatly reduces the complexity of the constrained optimization problem and converts it into an unconstrained optimization problem.

5.1 Design Methodology for TFP Optimal Three-Band Orthogonal Single Vanishing Moment Wavelet Filter Bank

To design time–frequency optimal three-band orthogonal wavelet bases, we minimize a weighted sum of TFPs of wavelets and scaling functions with respect to filter coefficients, under orthogonality and VM constraint. The optimization problem is given by,

$$\begin{aligned} \begin{aligned} \underset{[h_0[n],h_1[n],h_2[n]]}{\text {minimize}}&w_0\rho _0(h_0[n])+ w_1\rho _1(h_0[n],h_1[n])+ w_2\rho _2(h_0[n],h_2[n]) \\ \text {subject to}&<h_i[-n],h_j[n-3k]>=\delta (i-j)\delta (k)~~i,j=0,1,2 \\&H_0(\hbox {e}^{j2\pi /3})=H_0(\hbox {e}^{j4\pi /3})=0 \end{aligned} \end{aligned}$$

(31)

where

$$\begin{aligned} \rho _0(h_0[n])= & {} \hat{\triangle }_t^{2^{'}}\hat{\triangle }_{\varOmega }^{2^{'}}(h_0[n])\\ \rho _1(h_0[n],h_1[n])= & {} \hat{\triangle }_t^{2^{'}}\hat{\triangle }_{\varOmega }^{2^{'}}(h_0[n],h_1[n])\\ \rho _2(h_0[n],h_2[n])= & {} \hat{\triangle }_t^{2^{'}}\hat{\triangle }_{\varOmega }^{2^{'}}(h_0[n],h_2[n]) \end{aligned}$$

To design three-band filter banks, we have employed the parametrization technique given by Lizhong et al. [25] and Vaidyanathan [49]. The parameters have been optimized to obtain TFP optimal wavelets and scaling function. The degree-one paraunitary building block $\mathbf{V}_\mathbf{m}(z)$ is given by [49],

$$\begin{aligned} \mathbf{V}_\mathbf{m}(z)= & {} \mathbf{I}-\mathbf{v}_\mathbf{m}{} \mathbf{v}_\mathbf{m}^T+z^{-1}{} \mathbf{v}_\mathbf{m}{} \mathbf{v}_\mathbf{m}^T\\ ||\mathbf{v}_\mathbf{m}||= & {} 1 \end{aligned}$$

where $\mathbf{v}_\mathbf{m}$ is a column vector of size [M, 1]. For the design of three-band orthogonal filter bank, we choose the following parametrization [25] for $\mathbf{v}_\mathbf{m}$.

$$\begin{aligned} \mathbf{v}_\mathbf{m}(\theta _1,\theta _2)=[\cos (\theta _1)\cos (\theta _2)~~~ \cos (\theta _1)\sin (\theta _2)~~~ \sin (\theta _1)]^T \end{aligned}$$

Note that any degree-N paraunitary polyphase matrix $\mathbf{E}(z)$ can be factored as [49]

$$\begin{aligned} \mathbf{E}(z)=\mathbf{V}_\mathbf{N}(z)\mathbf{V}_\mathbf{N-1}(z) \ldots \mathbf{V}_\mathbf{1}(z)\mathbf{E}_\mathbf{0} \end{aligned}$$

where $\mathbf{E}_\mathbf{0}$ is a unitary factor which can be further parameterized using Householder [5] or Given’s rotation building blocks [25]. Irrespective of the above two choices, three degrees of freedom are available for the unitary factor $\mathbf{E}_\mathbf{0}$ [49] and two degrees of freedom for each dyadic block $\mathbf{V}_\mathbf{m}(z)$. Thus, in order to span the complete class of $(3N+3)$ length orthogonal filter bank, $\mathbf{E}(z)$ or $\mathbf{h}(z)$, $(2N+3)$ degrees of freedom are available without redundancy [49]. Two degrees of freedom are consumed in imposing one VM. Thus, $(2N+1)$ degrees of freedom are available for time–frequency optimization. For details on imposing regularity using the matrix $\mathbf{{E_0}}$, reader is suggested to refer previous work [2]. We optimize the free trigonometric variables $\theta$ of the filter bank to obtain a time–frequency-localized orthogonal wavelet filter bank.

6 Results and Discussion

To validate the proposed measures for time and frequency variances of asymmetric time-limited low-pass and band-pass functions, we compare the TFP computed through expressions developed by us with that of Haddad et al. [12] for length six Daubechies and Coiflet filter banks. The results are reported in Table 2. We have used seven cascade iterations to compute the results in Table 2. It demonstrates that proposed expressions for variances for asymmetric time-limited low-pass and band-pass functions give comparable results.

We study the effect of length of filter banks and weight schemes on time–frequency localization and Sobolev regularity. We present five design examples with different weight schemes each for length six and length nine filter banks. We minimize the objective function in (31) and generate the filter banks that jointly minimizes TFPs of scaling and wavelet functions. Tables 3, 4, 5 and 6 give filter coefficients for optimized filter banks for given weights. Figures 7 and 8 show the scaling and wavelet function plots of TFP optimal length nine and length six filter banks, respectively. TFP of scaling and wavelet functions is given in Tables 8 and 9. The results in Tables 8 and 9 demonstrate that as we increase the filter length, the lesser value of TFP can be achieved for scaling as well as wavelet functions. Eigenvalues of Lawton’s matrix $\mathbf{T}_{\mathbf{H}_\mathbf{0}}$ [54] in Table 7 show that the designed filter banks satisfy the necessary and sufficient condition for convergence of cascade iterations in $L_2(\mathfrak {R})$. It should be noted that all the low-pass filters have almost same filter coefficients for the given length.

Table 2 Comparison with Haddad’s [12] measure

Table 3 Weights and filter coefficients for length six filter bank

Table 4 Weights and filter coefficients for length six filter bank

Table 5 Weights and filter coefficients for length nine filter bank

Table 6 Weights and filter coefficients for length nine filter bank

Fig. 7

TFP optimized functions for length nine filter bank corresponding to weights $w_0=1/3, w_1=1/3, w_2=1/3$. a Scaling function. b Wavelet1 function. c Wavelet2 function

Fig. 8

TFP optimized functions for length six filter bank corresponding to weights $w_0=1/3, w_1=1/3, w_2=1/3$. a Scaling function. b Wavelet1 function. c Wavelet2 function

Table 7 Eigenvalues of Lawton’s matrix $\mathbf{T}_\mathbf{H_0}$

Table 8 TFP and Sobolev regularity of designed length nine filter banks

Table 9 TFP and Sobolev regularity of designed length six filter banks

Optimization problems considered in the paper are nonlinear, and the final solution of any problem will depend on the chosen initial guess [9]. The proposed expression for the TFP is a function of the number of cascade iterations used to generate the samples of the function. As the number of iterations increase, the number of samples increases and that further increases the computational time and memory requirement. However, it is found that designed length six and length nine filter banks are invariably regular with Sobolev index $S_\mathrm{max} > 0.5$, irrespective of the initial chosen solution, weights and the number of cascade iterations (Tables 8, 9).

Designed length nine and length six filter banks have Sobolev regularity of 0.99 and 0.88, respectively. Empirically, we found that the PRFB realization using dyadic decomposition of polyphase matrix exhibits a particular property that relates frequency variance of the generated scaling function and the objective function in (31). It is observed that minimizing the objective function in (31) minimizes the frequency variance of the scaling function irrespective of the chosen initial point.

As frequency variance of scaling function decreases, the decay of Fourier transform becomes faster and scaling function becomes smoother or regular. In the proposed framework of dyadic factorization of polyphase matrix, functions generated from filter banks have upper bound on their smoothness or Sobolev regularity. This upper bound is imposed by the number of degrees of freedom available for time–frequency optimization. The maximum Sobolev regularity of the scaling function that can be achieved with single VM is one [13]. Thus, the value of upper bound increases with number of degrees of freedom and it saturates to unity in case of single VM filter banks. As an example, for length nine filter bank, Figures 9 and 10 show that frequency variance of the scaling function decreases with the objective function in (31) and Sobolev regularity reaches to the maximum of one. Since number of degrees of freedom is only three for length six filter banks, the Sobolev regularity saturates to 0.88. However, in case of length nine filter banks five degrees of freedom are available and the Sobolev regularity reaches to the maximum of one. Note that there may exist PRFB structures in which minimizing the TFP do not minimize frequency variance and the maximal Sobolev regularity achieved will depend on the structure of the PRFB and other design constraints.

Fig. 9

Frequency variance of scaling function with respect to number of optimization iterations while minimizing objective function in (31) for length nine filter bank. The figure demonstrates that frequency variance of scaling function decreases with objective function

Fig. 10

Sobolev regularity of scaling function with respect to number of optimization iterations while minimizing objective function in (31) for length nine filter bank. The figure demonstrates that Sobolev regularity saturates to unity

Based on the empirical results, we conjecture that the time–frequency optimal, single VM filter banks, designed with the proposed time–frequency expressions and the framework of dyadic factorization of polyphase matrix, always lead to unit Sobolev regularity of functions, if sufficient number of degrees of freedom are available. In case of three-band, time–frequency optimal, orthogonal, single VM filter banks, five degrees of freedom of the dyadic structure are sufficient enough to achieve unit Sobolev regularity. Thus, the proposed methodology designs maximal Sobolev regularity filter banks with single vanishing moment. Since the optimization problem is nonlinear, it is important to note that maximal Sobolev regularity do not imply global maxima.

Functions with finite frequency variance cannot be discontinuous. Thus, finite frequency variance of a function is sufficient to ensure its continuity. A new design methodology for M-band biorthogonal filter bank can be proposed in which frequency variance of analysis and synthesis scaling function is constrained to be less than any arbitrary value and TFP, coding gain, stop band and pass band energy or any other objective function of analysis and/or synthesis filter bank can be optimized. Unlike Daubechies [8] and Strang [41] conditions of regularity, the proposed design methodology provides direct and arbitrary fine control on the frequency variance of the scaling function.

Mean and variances are first and second moments of energy of a function. In the literature, there exist many time–frequency inequalities that relate energy of the function with other time frequency measures that involves higher moments of energy of Fourier transform. Consider the theorem [14, p. 221] given below which states that finite value of the product of time variance and higher moments of energy of Fourier transform implies $f(t) \in L_2(\mathfrak {R})$.

$\mathbf{Theorem}$: Suppose that $1 < p,q < \infty$ and $U({\varOmega })$, v(t) are nonnegative weight functions. Set $||f(t)||_{L_v^p}=(|||f(t)|^pv||_{L^1})^{1/p}$. If there is a constant $C>0$ such that, for $f(t) \in {L_v^p}(\mathfrak {R})$, $||F({\varOmega })||_{L_U^q} \le C||f(t)||_{L_v^p}$ holds, then,

$$\begin{aligned} ||F(j{\varOmega })||^2 \le 2C\bigg ({\bigg [\int |{\varOmega }F({\varOmega })|^{q}U({\varOmega })^{-q}\hbox {d}{\varOmega }\bigg ]}^{1/q}{\bigg [\int |tf(t)|^p v(t)\hbox {d}t\bigg ]}^{1/p}\bigg )\nonumber \\ \end{aligned}$$

(32)

For our discussion, we assume, $p=2,q=2$ and $U({\varOmega })=1/({\varOmega }^N)$. First integral on the right side involves the energy of Fourier transform of the $(N+1)$th derivative of f(t). For $N=0$ and $v(t)=1$, right side becomes the product of square root of time variance and frequency variance. Finite value of the product at right-hand side in the inequality (32) not only ensure finite energy but also smoothness or differentiability of function f(t). A design methodology can be proposed in which $(N+1)$th differentiability of the scaling function is imposed by minimizing the product of time variance and higher moments of energy of Fourier transform of the function. Note that regularity order of more than two in higher-order M-band filter banks is not known [5].

Three-band filter banks perform better than two-band filter banks in extracting features of 1D or higher-dimensional signals. For example, two level wavelet transform decomposition using two- and three-band filter banks generate three and five decorrelated subbands, respectively. The energy of decorrelated subbands can be used for the classification of signals. Thus, designed three-band filter banks has applications in discriminating 1D signals like electroencephalogram (EEG) [30], electrocardiogram (ECG) [20] and classification [4] and segmentation [22] of 2D signals with low- and high-frequency content. The designed time–frequency-localized filter banks may find applications in content-based image retrieval [32] and fingerprint recognition [1].

7 Conclusion

We have obtained explicit expressions for the mean in time and the mean in frequency for asymmetric band-pass time-limited functions from the samples of the Fourier transform of the function. The variance expressions proposed by Venkatesh et al. [50] for zero-phase low-pass band-limited functions are extended to asymmetric band-pass time-limited functions. We designed time–frequency-localized time-limited wavelets and scaling functions without orthogonality constraint. The time–frequency product of the designed functions is close to 0.25 with unit Sobolev regularity. We determine discrete-time filter of length eight that generates the time–frequency optimal time-limited function using cascade algorithm with scaling factor of three. The proposed measures for variances are used to design time–frequency-localized orthogonal three-band wavelet filter banks. Filter banks with length six and nine are designed, and it is shown that better joint localization can be achieved by increasing the filter length. We have proposed a single vanishing moment wavelet filter bank design methodology with maximal Sobolev regularity.

Appendix

1.1 Mean in Time from Samples of Band-Limited Function

In this appendix, we derive the expression for mean in time $\mu _t$ for real-valued band-limited function $f(t) \in L_2(\mathfrak {R})$ in terms of samples $f(nT_s)$ sampled at $T_s < \frac{\pi }{\sigma }$. Substituting f(t) from (16) in (1), we get

$$\begin{aligned} \mu _t= \frac{1}{E}\int _{t=-\infty }^{\infty } \bigg [\left( t\sum f(mT_s)g(t-mT_s)\right) \left( \sum f(nT_s)g(t-nT_s)\right) \hbox {d}t \bigg ] \end{aligned}$$

where $m,n \in Z$. or,

$$\begin{aligned} \mu _t= \frac{1}{E} \sum \sum f(mT_s)f(nT_s) \bigg [ \int _{t=-\infty }^{\infty } tg(t-mT_s)g(t-nT_s)\hbox {d}t \bigg ] \end{aligned}$$

Let $H_1({\varOmega })$ and $H_2({\varOmega })$ are Fourier transforms of $tg(t-nT_s)$ and $g(t-mT_s)$, respectively. Then, using generalized Parseval’s theorem,

$$\begin{aligned} \int _{t=-\infty }^{\infty } tg(t-mT_s)g(t-nT_s)\hbox {d}t =\frac{1}{2\pi }\int _{{\varOmega }=-\infty }^{\infty } H_1({\varOmega })H_2^{*}({\varOmega })\hbox {d}{\varOmega }\end{aligned}$$

Thus,

$$\begin{aligned} \mu _t= \frac{1}{2\pi E} \sum \sum f(mT_s) f(nT_s) \int _{-\infty }^{\infty } H_1({\varOmega })H_2^{*}({\varOmega }) \hbox {d}{\varOmega }\end{aligned}$$

(33)

Since $G({\varOmega })$ is differentiable, the Fourier transform $H_1({\varOmega })$ and $H_2({\varOmega })$ is given by

$$\begin{aligned} H_1({\varOmega })= & {} j\frac{\hbox {d}}{\hbox {d}{\varOmega }}\left[ G({\varOmega })\hbox {e}^{-j{\varOmega }nT_s}\right] =j\frac{\hbox {d}G({\varOmega })}{\hbox {d}{\varOmega }}\hbox {e}^{-j{\varOmega }n T_s} +nT_sG({\varOmega })\hbox {e}^{-j{\varOmega }n T_s}\\ H_2({\varOmega })= & {} G({\varOmega })\hbox {e}^{-j{\varOmega }mT_s} \end{aligned}$$

Since $G({\varOmega })$ is a real function,

$$\begin{aligned} H_2^{*}({\varOmega })=G({\varOmega })\hbox {e}^{j{\varOmega }mT_s} \end{aligned}$$

Then,

$$\begin{aligned} H_1({\varOmega })H_2^{*}({\varOmega })=\bigg [ jG({\varOmega })\frac{\hbox {d}G({\varOmega })}{\hbox {d}{\varOmega }} +(nT_s)|G({\varOmega })|^2 \bigg ] \hbox {e}^{j{\varOmega }(m-n)T_s} \end{aligned}$$

To simplify the integral in (33), define the integrals $I_1$ and $I_2$ as,

$$\begin{aligned} I_1(m,n)=\int _{{\varOmega }=-\infty }^{\infty } jG({\varOmega })\frac{\hbox {d}G({\varOmega })}{\hbox {d}{\varOmega }} \hbox {e}^{j{\varOmega }(m-n)T_s}\hbox {d}{\varOmega }\end{aligned}$$

and,

$$\begin{aligned} I_2(m,n)=\int _{{\varOmega }=-\infty }^{\infty } (nT_s)|G({\varOmega })|^2\hbox {e}^{j{\varOmega }(m-n)T_s} \hbox {d}{\varOmega }\end{aligned}$$

Differentiating $G({\varOmega })$ in (9), we get,

$$\begin{aligned} \frac{\hbox {d}G({\varOmega })}{\hbox {d}{\varOmega }}={\left\{ \begin{array}{ll} \frac{-T_s\pi }{2\epsilon }\sin \left( \frac{\pi ({\varOmega }+\sigma )}{\epsilon }\right) &{} ~~:~~ -\sigma - \epsilon \le {\varOmega }< -\sigma \\ \frac{-T_s\pi }{2\epsilon }\sin \left( \frac{\pi ({\varOmega }-\sigma )}{\epsilon }\right) &{} ~~:~~ \sigma < {\varOmega }\le \sigma + \epsilon \\ 0 &{} ~~:~~ \text {elsewhere}. \end{array}\right. } \end{aligned}$$

Split the integral $I_1$ into $C_1$ and $C_2$ corresponding to frequency range $-\sigma - \epsilon \le {\varOmega }< -\sigma$ and $\sigma < {\varOmega }\le \sigma + \epsilon$. Let $I_1(m,n)=C_1(m,n)+C_2(m,n)$, where

$$\begin{aligned}&C_1(m,n)\\&\,=\int _{-\sigma -\epsilon }^{-\sigma } j\bigg [\frac{T_s}{2}\left( \cos \left( \frac{\pi ({\varOmega }+ \sigma )}{\epsilon }\right) +1\right) \left( \frac{-T_s\pi }{2\epsilon }\sin \left( \frac{\pi ({\varOmega }+\sigma )}{\epsilon }\right) \right) \hbox {e}^{j{\varOmega }(m-n)T_s}\hbox {d}{\varOmega }\bigg ]\\&C_2(m,n)\\&\,=\int _{\sigma }^{\sigma +\epsilon } j \bigg [ \frac{T_s}{2}\left( \cos \left( \frac{\pi ({\varOmega }- \sigma )}{\epsilon }\right) +1\right) \left( \frac{-T_s\pi }{2\epsilon }\sin \left( \frac{\pi ({\varOmega }-\sigma )}{\epsilon }\right) \right) \hbox {e}^{j{\varOmega }(m-n)T_s}\hbox {d}{\varOmega }\bigg ] \end{aligned}$$

Solving the above integrals and substituting $\sigma =\frac{\pi }{T_s}-\epsilon$, we get

$$\begin{aligned} C_1= & {} \frac{j\pi ^2T_s^2\hbox {e}^{j(-\pi +T_s\epsilon )(m-n)}\left( 3\pi ^2\hbox {e}^{-jT_s(m-n)\epsilon } + 5\pi ^2 - 2T_s^2{(m-n)}^2\epsilon ^2\right) }{4\left( T_s^4(m-n)^4\epsilon ^4 - 5\pi ^2T_s^2(m-n)^2\epsilon ^2 + 4\pi ^4\right) }\\ C_2= & {} \frac{-j}{4}\frac{\pi ^2T_s^2\hbox {e}^{-j(-\pi +T_s\epsilon )(m-n)}\left( 3\pi ^2\hbox {e}^{jT_s(m-n)\epsilon } + 5\pi ^2 - 2T_s^2(m-n)^2\epsilon ^2\right) }{T_s^4(m-n)^4\epsilon ^4 - 5\pi ^2T_s^2(m-n)^2\epsilon ^2 + 4\pi ^4} \end{aligned}$$

Let

$$\begin{aligned} I_2(m,n)=\int _{{\varOmega }=-\infty }^{\infty } (nT_s)|G({\varOmega })|^2\hbox {e}^{j{\varOmega }(m-n)T_s} \hbox {e}{\varOmega }=nT_sA \end{aligned}$$

then A is given by [50],

$$\begin{aligned} A(m,n)= & {} 2\sigma T_s^2\delta _{mn}+ \frac{T_s^2(-1)^{(m-n)}}{2}\bigg (\epsilon \frac{\sin ((m-n)T_s\epsilon )}{(m-n)T_s\epsilon } \\&+\,\frac{\sin ((m-n)T_s\epsilon )}{2}\frac{2(m-n)T_s}{{(\frac{\pi }{\epsilon })}^2-(m-n)^2T_s^2}\bigg )\\&+\,\frac{T_s^2(-1)^{(m-n)}}{2}\left( \epsilon \frac{\sin ((m-n)T_s\epsilon )}{(m-n)T_s\epsilon }\left( 1-\frac{\frac{1}{2}}{\left[ 1-{\left( \frac{(m-n)T_s\epsilon }{2\pi }\right) }^2\right] }\right) \right) \end{aligned}$$

Thus,

$$\begin{aligned} \mu _t= \frac{1}{2\pi E}\sum _{m \in \mathbb {Z}} \sum _{n \in \mathbb {Z}} f(mT_s)f(nT_s)(C_1(m,n)+C_2(m,n)+nT_sA(m,n)) \end{aligned}$$

or,

$$\begin{aligned} \mu _t=\frac{1}{2\pi E}(\mathbf{f}^H \mathbf{S}_\mu \mathbf{f}) \end{aligned}$$

where

$$\begin{aligned} S_\mu (m,n)=C_1(m,n)+C_2(m,n)+nT_sA(m,n) \end{aligned}$$

1.2 Mean in Frequency from Samples of Band-Limited Function

Mean frequency of band-pass function $f(t) \in L_2(\mathfrak {R})$ can be obtained from its spectrum for positive frequencies. It is defined by (4). Since we have to compute $\mu _{{\varOmega }}$ from the samples of band-limited function f(t), representing Fourier transform $F({\varOmega })$ in terms of DTFT $F(\hbox {e}^{j\omega })$, and using the relation ${\varOmega }=\frac{\omega }{T_s}$, we have

$$\begin{aligned} F({\varOmega }) ={\left\{ \begin{array}{ll} T_sF(\hbox {e}^{j{\varOmega }T_s}) &{} ~~:~~ {\forall |{\varOmega }| \le \frac{\pi }{T_s}}\\ 0 &{} ~~:~~ \text {elsewhere}. \end{array}\right. } \end{aligned}$$

(34)

Substituting for $F({\varOmega })$ from (34) in the expression for $\mu ({\varOmega })$, we get

$$\begin{aligned} \mu _{{\varOmega }}=\frac{1}{\pi E} \int _{\omega =0}^{\pi } \omega {|F(\hbox {e}^{j\omega )}|}^2 \hbox {d}\omega \end{aligned}$$

(35)

Since f[n] is a real-valued sequence, we have

$$\begin{aligned} |F(\hbox {e}^{j\omega })|^2=F(\hbox {e}^{j\omega })F(\hbox {e}^{j\omega })^* =\left( \sum _{n \in Z} f[n]\hbox {e}^{-jn\omega }\right) \left( \sum _{m \in Z} f[m]\hbox {e}^{jm\omega }\right) \end{aligned}$$

(36)

Substituting $|F(\hbox {e}^{j\omega })|^2$ from (36) in (35), we get

$$\begin{aligned} \mu _{{\varOmega }}= & {} \frac{1}{\pi E} \int _{\omega =0}^{\pi } \omega \left( \sum _{m \in Z} f[m]\hbox {e}^{jm\omega }\right) \left( \sum _{n \in Z} f[n]\hbox {e}^{-jn\omega }\right) \hbox {d}\omega \\= & {} \frac{1}{\pi E} \sum \sum f[m]f[n] \int _{\omega =0}^{\pi } \omega \hbox {e}^{j\omega (m-n)} \hbox {d}\omega \end{aligned}$$

or,

$$\begin{aligned} \mu _{{\varOmega }}=\frac{1}{\pi E}(\mathbf{f}^H \mathbf{B}_v \mathbf{f}) \end{aligned}$$

where

$$\begin{aligned} {B}_v(m,n)=\int _{\omega =0}^{\pi } \omega {\hbox {e}^{j\omega (m-n)}} \hbox {d}\omega =-\frac{[(-1)^{(m-n)}(-1+\pi j (m-n))+1]}{{(m-n)}^2} \end{aligned}$$

Note that for $m=n$,

$$\begin{aligned} {B}_\mu (m,n)=\pi ^2 /2 \end{aligned}$$

1.3 Mean of Time-Limited Functions from the Samples of Fourier Transform

For a real-valued function $f(t) \in L_2(\mathfrak {R})$, mean in time $\mu _t$ is defined as

$$\begin{aligned} \mu _t= \frac{1}{E}\int _{t=-\infty }^{\infty } (t{f(t)})({f(t)})^* \hbox {d}t \end{aligned}$$

The Dual of (34) is given by,

$$\begin{aligned} f(t) ={\left\{ \begin{array}{ll} \frac{{\varOmega }_s}{2\pi }\sum _{k=-\infty }^{\infty } F(k{\varOmega }_s)\hbox {e}^{jk{\varOmega }_s t} &{} ~~:~~ {\forall |{\varOmega }| \le \frac{\pi }{T_s}}\\ 0 &{} ~~:~~ \text {elsewhere}. \end{array}\right. } \end{aligned}$$

(37)

Then,

$$\begin{aligned} \mu _t=\frac{1}{E} \int _{t=-\pi /{\varOmega }_s}^{\pi /{\varOmega }_s} \bigg [t{\bigg (\frac{{\varOmega }_s}{2\pi }\sum _m F(m{\varOmega }_s)\hbox {e}^{jm{\varOmega }_s t}\bigg )}\bigg ] \bigg [{\bigg (\frac{{\varOmega }_s}{2\pi }\sum _n F(n{\varOmega }_s)\hbox {e}^{jn{\varOmega }_s t}\bigg )}\bigg ]^* \hbox {d}t \end{aligned}$$

or,

$$\begin{aligned} \mu _t= \frac{{\varOmega }_s^2}{4\pi ^2 E} \sum _m \sum _n F(m{\varOmega }_s) F(n{\varOmega }_s)^* \int _{t=-\pi /{\varOmega }_s}^{\pi /{\varOmega }_s} t{ \hbox {d}^{j{\varOmega }_s(m-n) t}} \hbox {d}t \end{aligned}$$

Let

$$\begin{aligned}&\int _{t=-\pi /{\varOmega }_s}^{\pi /{\varOmega }_s} [t{ \hbox {e}^{j{\varOmega }_s(m-n) t}}] \hbox {d}t=2j\bigg [\frac{\sin (\pi (m-n)) - \pi (m-n)\cos (\pi (m-n))}{((m-n){\varOmega }_s)^2}\bigg ]\\&\quad =R(m,n) \end{aligned}$$

Then,

$$\begin{aligned} \mu _t=\frac{{\varOmega }_s^2}{4\pi ^2 E}({\hat{\mathbf{f}}}^H \mathbf{R} {\hat{\mathbf{f}}}) \end{aligned}$$

Note that for $m=n$,

$$\begin{aligned} R(m,n)=0 \end{aligned}$$