An Eigenfilter-Based Approach to the Design of Time-Frequency Localization Optimized Two-Channel Linear Phase Biorthogonal Filter Banks

Abstract

We present a novel eigenfilter-based approach to the design of time-frequency optimized, linear-phase, biorthogonal FIR filter banks. We first design a linear-phase, low-pass analysis filter, followed by a complementary linear-phase, low-pass synthesis filter. The optimality criterion used is uncertainty-based time-frequency localization, where the objective function is a convex combination of time variance and frequency variance of the respective filters. The objective function to be minimized is formulated in a convex-quadratic form and the perfect reconstruction (PR) and vanishing moment (VM) conditions are imposed in the eigen design of filters as a set of linear equality constraints. The PR and VM conditions are expressed in the time domain matrix formulation, so that these can directly be incorporated into the eigenfilter design. Using the Rayleigh principle, the optimal filter is obtained as an eigenvector corresponding to the minimum eigenvalue of the real symmetric positive-definite matrix associated with the optimization criterion. Thus, our formulation reduces the design problem of time-frequency optimal filter banks to an eigenfilter-based problem. Furthermore, the filter banks designed in this manner are found to be regular and are valid candidates for wavelet filter banks, allowing for the construction of linear phase wavelets. We present a few examples to show that the smooth wavelets can be constructed using the proposed method.

1 Introduction

The eigenfilter approach [25, 30] is an efficient and popular method to design digital filters with a quadratic optimization criterion. Slepian [25] introduced the notion which formed a precursor to the eigenfilter design. He designed a real window with minimum stop-band energy called a prolate spheroidal wave sequence. In designing the prolate spheroidal wave sequence, the objective function $\phi$, which is the energy of the sequence in the frequency range $\sigma \le \omega \le \pi$ for, $0<\sigma <\pi$ is expressed in quadratic form and the optimization problem has been formalized as follows:

$$\begin{aligned}&\underset{\mathbf {a}}{\text {minimize}} \qquad \phi =\mathbf {a}^{T}\mathbf {Pa} \\&\text {subject to} \qquad \mathbf {a}^{T}\mathbf {a}=1, \end{aligned}$$

where $\mathbf {P}$ is a real, symmetric, and positive-definite matrix and $\mathbf {a}$ is a real-valued vector. The optimal sequence, which minimizes the cost function is the eigenvector $\mathbf {a}$ of the matrix $\mathbf {P}$ corresponding to its smallest eigenvalue. The constraint $\mathbf {a}^{T}\mathbf {a}=1$ is imposed to avoid trivial solutions. The “eigenfilter” method proposed by Tkacenko et al. [30] involves designing of an optimal finite impulse response (FIR) filter directly, instead of using the windowing method. Similar to the prolate spheroidal window sequence design, the filter is obtained as the eigenvector of a real symmetric positive-definite matrix. In the eigenfilter approach, the objective is to minimize the error between the desired frequency response and the frequency response of the filter to be designed. Recently, eigenfilter-based methods have also been used by Andrew et al. [1] as well as Jain and Crochiere [15] to design filter banks. They proposed a technique to design quadrature mirror filter banks (QMF) using an eigenfilter-based approach. Patil et al. [20] proposed another design method, combining the complementary filter technique with the eigenfilter approach, for linear phase two-channel PR filter banks. Using Bernstein polynomials, Cooklev et al. [5] proposed an eigenfilter based approach for designing a half-band polynomial, the factorization of which yields both orthogonal and biorthogonal filter banks. In all these eigenfilter-based designs of filter banks [1, 5, 15, 20] discussed above, the optimizing criterion is a combination of the pass-band and stop-band error between desired and actual frequency response of filters.

It is well known that wavelets can be generated from iterations of these filter banks. Wavelet transforms are used in joint time-frequency analysis due to their superior time-frequency localization over other transforms [11]. Time-frequency localization of wavelet filters also plays a pertinent role in various signal processing applications. Abundant literature is available for designing optimal filter banks using a variety of optimizing criteria such as ripples in the pass-band and stop-band, pass-band and stop-band energy, frequency selectivity, flatness at particular frequency, regularity, orthogonality, linearity of phase, and energy compaction. However, surprisingly the literature on the design of optimal time-frequency localized wavelet filter banks is relatively scant, and filter banks are seldom designed with an objective of minimizing joint time-frequency localization. This is despite the fact that in certain signal processing applications such as feature extraction, image enhancement, edge detection, and image segmentation; time-frequency localization appears promising [35, 36]. It is shown by the authors in [35, 36] that the filters, designed to achieve simultaneous concentration in time and frequency, are very effective in feature extraction, image compression, and image segmentation. Furthermore, it is reported by Monro and Sherlock [16] that the filter banks designed taking the time-frequency localization into account exhibit good performance in image compression applications. This motivates us to design wavelet filter banks with good time-frequency localization.

We are interested in designing optimal filter banks using an eigenfilter approach instead of a parametrization approach. This is because the eigenfilter-based methods are numerically efficient, and one can incorporate both time domain and frequency domain constraints easily. The eigenfilter method gives a global solution. Using this approach, we can design orthogonal as well as biorthogonal filters banks. The eigenfilter formulation can be extended to design M-band and 2-D filter banks. These advantages justify the use of the eigenfilter approach.

Ample literature is available on the design of filters using the eigenfilter approach. However, to the best of our knowledge, no description is available on the design of biorthogonal wavelet filter banks using the eigenfilter-based formulation, wherein the optimality criterion is associated with the time-frequency uncertainty of the filters.

Haddad et al. [12] present time-frequency localization properties of discrete-time sequences (filters), filter banks, wavelets, and several other signal decomposition techniques in view of the uncertainty principle. They evaluate time-frequency localization of filter banks and orthogonal wavelets. However, no design methodology is suggested to design wavelets and filter banks possessing good time-frequency localization. Morris and Xie [17, 37] design time-frequency-localized orthonormal wavelets via optimization of the lattice parameters of the paraunitary filter banks. Caglar et al. [3] design optimal orthogonal filter banks keeping the optimality criterion as a combination of coding gain, aliasing energy, and VM; but the time-frequency localization is not considered explicitly. Sharma et al. [24] design linear phase biorthogonal filter banks, wherein the optimality criterion is the product of the time variance and frequency variance of wavelet bases. The wavelet filter banks are designed using a parameterization technique, and the authors have not used an eigenfilter approach. However, in this paper, we present the eigenfilter approach due to its obvious advantages instead of parameterization techniques for designing time-frequency localized filter banks. Furthermore, we optimize the time-frequency localization of filters of underlying PR filter banks, whereas in [24], the authors attempt to optimize time-frequency localization of wavelet bases. In the inspiring work reported by Tay [27, 29], author designs a special class of linear phase biorthogonal filter banks called half-band pair filter banks (HBPF) [22], employing a measure called balanced-uncertainty metric proposed by Monro and Sherlock [16], which is a weighted summation of the time variance and frequency variance of the filter to be designed. The author uses parametric Bernstein polynomials to optimize filter coefficients. A similar kind of cost function is also used by us. However, we present an eigenfilter based approach for designing the general class of linear-phase biorthogonal filter banks with the desired degree of the regularity. Furthermore, in [27, 29] the authors do not present any lower bound on the metric used. We establish a lower bound on the objective measure used by us to design filters. In the motivating work [34, 35], Wilson and Granlund design filters with optimal time-frequency localization. However, authors have not addressed the design of PR filter banks. Furthermore, the measure of frequency localization used is different from what we have used in our designs. Recently, Parhizkar et al. [19] used the notion of the periodic frequency spread, suggested by Breitenberger [2], to design optimal time-frequency sequences [19]. However, Parhizkar et al. [19] do not address the issue of optimal PR filter bank design.

In this paper, we present a method for designing linear phase biorthogonal wavelet filter banks. The method proposed is a combination of the eigenfilter-based formulation and the complementary filter bank design technique. We first design a linear phase, low-pass analysis filter using the eigenfilter-based formulation. The filter is designed with the objective of minimizing its joint time-frequency localization subject to the constraint of desired number of VMs. Then follows the design of the complementary synthesis, linear phase, low-pass filter with the objective of minimizing time-frequency localization subject to the constraints of PR and VMs. The objective function is a convex combination of the time variance and frequency variance of filters to be designed, which has been formulated in a quadratic form which involves a real, symmetric, positive-definite matrix. In view of the well-known Rayleigh principle [13], the optimal filter is obtained as the eigenvector corresponding to the smallest eigenvalue of this matrix. The PR and VM constraints are formulated as a set of linear equations so that they can readily be incorporated in the eigen design problem. The important features of our design method are as follows:

• The objective function as well as PR and VM constraints are formulated in the time domain. Here time-domain formulation implies a form, which directly employs filter coefficients and does not use any parameterization.

• We can design filters with as many VMs as desired.

• The solution of the optimization problem is global, stable and does not need manual intervention for initial guess.

• Filter banks designed using the proposed method are found to be regular, and it is observed that smooth wavelets can be constructed via iterations of the designed filter bank, using the cascade algorithm.

• We also establish an inequality, which poses a lower bound on the uncertainty-based time-frequency measure used by us.

• We can control the time and frequency localization of the analysis and synthesis filters independently and arbitrarily. It is possible to design completely time localized and frequency localized filters using the proposed method.

• Our method is neither an iterative method, unlike methods proposed by Andrew et al. [1] as well as Jain and Crochiere [15] nor requires factorization of half-band polynomials unlike the method of Cooklev [5].

• In the eigenfilter-based design of filter banks in [1, 5, 15, 20], the optimizing criterion is a combination of the pass-band and stop-band errors between desired and actual frequency response of the filter. However, we have used a convex combination of Gabor’s uncertainty-based time variance and frequency variance of the filters as our optimality criterion.

We have also compared the time-frequency localization properties of the optimal filter banks designed by us, with time-frequency properties of the filter bank designed by Tay [29] and the popular CDF-9/7 filter bank. It has been shown that the time-frequency localization of the optimal filter bank designed by us is superior to that of others.

The paper is organized as follows. The Sect. 2 gives a brief overview of two-channel perfect reconstruction filter banks and uncertainty-based time-frequency measures for continuous-time signals and discrete-time sequences. Section 3 explains the uncertainty principle in the context of the quantum harmonic oscillator’s eigenvalue problem and its relationship with the objective function (criterion) used by us. The lower bound on the objective function is established. In this Section, we derive the framework for the eigenfilter-based design of time-frequency localization optimized filter banks. In Sect. 4, we present the proposed design methodology in detail. In Sect. 5, we give several design examples including construction of wavelets via iterations of the designed filter banks.

We use following notations: Boldfaced lowercase letters $\mathbf{a}$ represent vectors, and bold-faced uppercase letters $\mathbf {A}$ are used for matrices. $\mathbf {A}^{T}$denotes the transpose of the matrix $\mathbf {A}$. The notation $\left\langle \mathbf {x,y} \right\rangle$ represents the dot product of vectors $\mathbf {x}$ and $\mathbf {y}$.

2 Background

2.1 Perfect Reconstruction Filter Banks

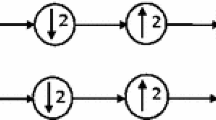
A two-channel filter bank is shown in Fig. 1. The filters $H_{0}(z)$ and $H_{1}(z)$ are analysis low-pass and high-pass filters, respectively. Similarly, $F_{0}(z)$ and $F_{1}(z)$ denote synthesis filters. The choice of high-pass filters given in (1) ensures alias cancellation.

$$\begin{aligned} H_{1}(z)=z^{-1}F_{0}(-z)\quad F_{1}(z)=zH_{0}(-z) \end{aligned}$$

(1)

Defining the product filter as

$$\begin{aligned} P(z)=H_0(z)F_0(z) \end{aligned}$$

(2)

The perfect reconstruction (half band) condition can be expressed as

$$\begin{aligned} P(z)+P(-z)=2 \end{aligned}$$

(3)

Equality (3) implies that the product filter $P(z)$ is a symmetric (zero phase) polynomial in $z$, whose coefficients corresponding to even powers of $z$ are zero, except for the term ($z^0$) which carries a coefficient 1. Hence, the design of two-channel PR filter bank reduces to the design of the half band filter $P(z)$. Several techniques are available to design perfect reconstruction filter banks. The design techniques for two-channel PR filter banks can broadly be divided into the following categories: Factorizing a Lagrange half-band polynomial (LHBP) [4, 33], Lattice and lifting structures in the polyphase domain [18, 31, 32], and Complementary filter design method [33]. Recently, the eigenfilter-based approach has also been used for designing PR filter banks by Patil et al. [20]. In the complementary design method, a valid analysis filter is first independently designed. For the given analysis filter, the synthesis filter is designed by imposing the PR condition. However, the designed filters are not necessarily optimal in any sense. In this paper, optimal filter banks are designed by blending the complementary filter design method and the eigenfilter approach. Furthermore, the design of wavelet filter banks is also equivalent to the design of PR filter banks except that the former must satisfy regularity constraints in order to ensure the convergence of wavelets and scaling functions in $L_{2}(\mathbb {R})$. Wavelets can be constructed from iterations of two-channel PR filter banks using the cascade algorithm [33].

Fig. 1

Two-channel 1D filter bank

2.2 Time-Frequency Localization and Uncertainty Principle

2.2.1 Uncertainty in continuous-time domain

In this subsection, we describe, in brief, the time-frequency localization measures and associated uncertainty principles for continuous-time and discrete-time signals. Gabor’s uncertainty principle essentially states: “A signal cannot be localized simultaneously in time and frequency arbitrarily.”

Let $f(x)$ be a real valued, even symmetric function in $L_{2}(\mathbb {R})$ with unity norm, i.e., $\int _{-\infty }^{+\infty }|f(x)|^{2}dx=1$. According to Gabor’s uncertainty principle [9]

$$\begin{aligned} \left\{ \int _{\mathbb {R}}x^{2}|f(x)|^{2}dx\right\} \times \left\{ \frac{1}{2\pi }\int _{\mathbb {R}}\Omega ^{2}|F(\Omega )^{2}|d\Omega \right\} \ge \frac{1}{4}, \end{aligned}$$

(4)

where $F(\Omega )=\int _{\mathbb {R}}f(x)e^{-j\Omega x}dx$ is the Fourier transform of $f(x)$. In (4), equality is achieved only for Gaussian signals. Inequality (4) implies that the time-frequency product of a signal $f(x)$, given by $\triangle _{f}=\sigma _{x}^{2}\sigma _{\Omega }^{2}$, is bounded below by $0.25$. Where $\sigma _{x}^{2}=\int _{\mathbb {R}}x^{2}\left| f\left( x\right) \right| ^{2}dx$ and $\sigma _{\Omega }^{2}=\frac{1}{2\pi }\int _{\mathbb {R}}\Omega ^{2}|F(\Omega )^{2}|d\Omega$ are time spread and frequency spread of the signal $f(x)$, respectively.

2.2.2 Uncertainty in discrete-time domain

In this subsection, we give a brief overview of the time-frequency localization and uncertainty principle associated with discrete-time signals. There are several notions [2, 7, 8, 12, 14, 23, 25] of uncertainty measures associated with simultaneous time-frequency localization for discrete-time sequences; however, all these measures are not necessarily variance or spread based. In this paper, we shall consider the measure given in [12, 14], which can be considered as an extension of the continuous-time measure explained above.

Let $h(n)$ be a real valued, even symmetric, discrete-time sequence in $l^{2}\left( \mathbb {Z}\right)$ normalized as, $\sum _{n=-\infty }^{\infty }\left| h\left( n\right) \right| ^{2}=1$, and, let $H\left( \omega \right) =\sum _{n=-\infty }^{\infty }h\left( n\right) e^{-j\omega n}$ be the Discrete-Time Fourier Transform (DTFT) of the sequence $h(n)$. The time variance, $\sigma _n^2$, and the frequency variance, $\sigma _{\omega }^2$, of the sequence are defined as [12, 14].

$$\begin{aligned} \sigma _{n}^{2}&= \sum _{n=-\infty }^{\infty }n^{2}\left| h\left( n\right) \right| ^{2}\end{aligned}$$

(5)

$$\begin{aligned} \sigma _{\omega }^{2}&= \frac{1}{2\pi }\int _{-\pi }^{\pi }\omega ^{2}\left| H\left( \omega \right) \right| ^{2}d \omega \end{aligned}$$

(6)

The time-frequency product (TFP) or uncertainty product of the sequence $h(n)$ denoted by $\triangle _{h}$ is lower bounded by the inequality

$$\begin{aligned} \triangle _{h}=\sigma _{n}^{2}\sigma _{\omega }^{2}\ge \frac{\left( 1-\left| H\left( \pi \right) \right| ^2\right) ^{2}}{4} \end{aligned}$$

(7)

In the case of discrete sequences, the lower bound is not fixed unlike the time-frequency product of continuous-time signals. It can reduce to zero, which is obvious from the inequality (7). It is interesting to note that if the low-pass sequence has a null at $\omega =\pi$ then the lower bound on the time-frequency product is the same as that for the continuous-time signal [12], i.e., $\triangle _{h}=\sigma _{n}^{2}\sigma _{\omega }^{2}\ge 0.25$. Thus, the Heisenberg uncertainty principle for discrete-time sequences in $l_{2}\left( \mathbb {Z}\right)$ can be expressed as follows:

$$\begin{aligned} \triangle _{h}=\sigma _n^2\sigma _{\omega }^2\ge 0.25,\; H\left( \pi \right) =0. \end{aligned}$$

(8)

An important point to note is that $H\left( \pi \right)$ is invariably $0$, for low-pass filters of an underlying regular wavelet filter bank. Therefore, for the class of sequences corresponding to low-pass filters of regular wavelet filter banks, inequality (8) holds true. This allows us to use this uncertainty measure for regular filter banks. For more details readers are referred to the work of Haddad et al. [12].

3 Problem Formulation

3.1 Our Optimality Criterion and its Merits

Gabor’s uncertainty inequality, as given in (4), is well known. It poses a lower bound on the ‘product’ of the time localization and frequency localization of a function. The important but relatively less explored equivalent of uncertainty principle is the eigenvalue problem corresponding to the quantum harmonic oscillator. This form of uncertainty principle presents a lower bound on the ‘summation’ of the potential energy and kinetic energy of the oscillator. The signal processing equivalent of the uncertainty principle, which poses the lower bound on the summation of time variance and frequency variance of a signal, or a sequence, is presented in this subsection.

The energy state of the quantum harmonic oscillator is characterized by an operator called the Hamiltonian [10]

$$\begin{aligned} \mathbb {H}:=x^{2}-\left( \frac{d}{dx}\right) ^{2} \end{aligned}$$

(9)

In the right side of (9), the first and second terms represent potential and kinetic energy operators, respectively. The corresponding Hamiltonian eigenvalue problem (or Schrodinger equation) is given as follows:

$$\begin{aligned} \mathbb {H}f=x^{2}f-\frac{d^{2}f}{dx^{2}}=\lambda f \end{aligned}$$

(10)

A remarkable property of a quantum harmonic oscillator is that the eigenvalues of (10) are of the form; $\lambda _{n}=2\left( n+\frac{1}{2}\right) , n\in \{0,1,2,\cdots \}$. The eigenfunctions corresponding to $\lambda _n$ are $f_{n}(x)=kH_{n}(x)e^{-\frac{x^{2}}{2}},k\in \mathbb {R}$. Where $H_{n}(x)=(-1)^{n}e^{x^{2}}\left( \frac{d}{dx}\right) ^{n}e^{-x^{2}}$ are Hermite polynomials of the order $n$.

Here, we present the signal processing interpretation of the uncertainty principle related to the eigenvalue problem of the harmonic oscillator.

On taking the dot product of both sides of (10) with $f\in L_{2}(\mathbb {R}),$ we obtain the relation

$$\begin{aligned} \left\langle x^{2}f-\frac{d^{2}f}{dx^{2}},f\right\rangle =\lambda E, \end{aligned}$$

(11)

where $E=\left\langle f,f\right\rangle$ is the $L_{2}$ norm of the signal $f$. Since, the eigenvalues of the (10) are equal to or greater than $1$. Therefore, from (11), we infer

$$\begin{aligned} \lambda E=\left\langle x^{2}f-\frac{d^{2}f}{dx^{2}},f\right\rangle \ge E \end{aligned}$$

(12)

Assuming $f$ is normalized such that $\left\langle f,f\right\rangle =1$, then from (12)

$$\begin{aligned} \left\langle x^{2}f,f\right\rangle +\left\langle -\frac{d^{2}f}{dx^{2}},f\right\rangle \ge 1 \end{aligned}$$

(13)

The first term on the left-hand side of the inequality (13) represents the time variance and second term denotes frequency variance of the real, symmetric signal $f\in L_{2}(\mathbb {R})$, whose energy is normalized to $1$. The eigenvalue $\lambda$ represents the sum of the time variance and frequency variance of the signal $f$.

Using Parseval’s theorem, the inequality (13) can be expanded as

$$\begin{aligned}&\displaystyle \int _{\mathbb {R}}x^{2}|f(x)|^{2}dx+\int _{\mathbb {R}}|f'(x)|^{2}dx\ge 1\end{aligned}$$

(14)

$$\begin{aligned}&\displaystyle \sigma _{x}^{2}+\sigma _{\Omega }^{2}\ge 1 \end{aligned}$$

(15)

which essentially states that the sum of the time variance and frequency variance of a real, symmetric signal $f(x)\in L_{2}(\mathbb {R})$ is lower bounded by 1. The equality is achieved only in the case of the Gaussian signal. The condition (15) associated with a quantum harmonic oscillator can also be deduced from the Heisenberg’s uncertainty principle as follows:

According to the Heisenberg uncertainty [9],

$$\begin{aligned} \int _{\mathbb {R}}x^{2}|f(x)|^{2}dx\int _{\mathbb {R}}|f'(x)|dx=\sigma _{x}^{2}\sigma _{\Omega }^{2}\ge \frac{1}{4} \end{aligned}$$

(16)

Using the inequality of arithmetic and geometric mean (AM-GM inequality), which states that the arithmetic mean $(AM)$ of two non-negative real numbers a and b is greater than or equal to their geometric mean $(GM)$

$$\begin{aligned} \frac{a+b}{2}\ge \sqrt{ab} \end{aligned}$$

(17)

and following (16), we have

$$\begin{aligned} \frac{\sigma _{x}^{2}+\sigma _{\Omega }^{2}}{2}\ge \sigma _{x}\sigma _{\Omega }\ge \frac{1}{2} \end{aligned}$$

(18)

Hence, we deduce

$$\begin{aligned} \sigma _{x}^{2}+\sigma _{\Omega }^{2}\ge 1 \end{aligned}$$

(19)

On the parallel lines, using the uncertainty principle for discrete-time sequences given in (8) and AM-GM inequality (20), we arrive at an important inequality associated with discrete-time sequences

$$\begin{aligned} \frac{\sigma _{n}^{2}+\sigma _{\omega }^{2}}{2}\geqslant \sigma _{n}\sigma _{\omega }\geqslant \frac{1}{2} \end{aligned}$$

(20)

Implying

$$\begin{aligned} \sigma _{n}^{2}+\sigma _{\omega }^{2}\ge 1 \end{aligned}$$

(21)

We use the summation form (21) of the uncertainty measure instead of the product form (8), for designing filter banks. The, justification for using the measure is motivated at the end of this subsection. Now, we establish an inequality, which imposes a lower bound on the objective criterion used by us.

Let us consider a convex combination of the time variance and frequency variance of a discrete time sequence $f\in l_{2}(\mathbb {Z})$

$$\begin{aligned} \phi =\alpha \sigma _{n}^{2}+(1-\alpha )\sigma _{\omega }^{2}, \, \alpha \in [0,1] \end{aligned}$$

(22)

Invoking AM-GM inequality (17)

$$\begin{aligned} \phi =\alpha \sigma _{n}^{2}+(1-\alpha )\sigma _{\omega }^{2}\ge 2\sigma _{n}\sigma _{\omega }\sqrt{\alpha (1-\alpha )} \end{aligned}$$

(23)

Using the uncertainty inequality (8) for the class of sequences in $l_{2}(\mathbb {Z})$ having the spectrum null at $\omega =\pi$ and (23), we obtain

$$\begin{aligned} \alpha \sigma _{n}^{2}+(1-\alpha )\sigma _{\omega }^{2}\ge 2\sigma _{n}\sigma _{\omega }\sqrt{\alpha (1-\alpha )}\ge \sqrt{\alpha (1-\alpha )} \end{aligned}$$

Thus, we have an important inequality

$$\begin{aligned} \phi =\alpha \sigma _{n}^{2}+(1-\alpha )\sigma _{\omega }^{2}\ge \sqrt{\alpha (1-\alpha )} \end{aligned}$$

(24)

For $\alpha =\frac{1}{2}$, the inequality (24) boils down to the inequality (21). We use a convex combination of the time variance and frequency variance as our objective function in designing filter banks. (We abbreviate the convex combination of the time variance and frequency variance as “CCTFV”). The inequality (24) poses the lower bound on the objective function $\phi$ used by us. The rationale to minimize CCTFV instead of TFP in designing the filter bank is twofold.

• 1. We design filter banks using the eigenfilter-based approach due to its obvious advantage as mentioned in the Sect. 1. The eigenfilter-based optimization method can be used to design optimal filters provided the objective measure is a quadratic function of the design variables of the form $\mathbf {a}^{T}\mathbf {P}\mathbf {a}$, where P is a real, symmetric, and positive-definite matrix and $\mathbf {a}$ is a real vector containing design variables. Unfortunately, the time-frequency product $\sigma _{n}^{2}\sigma _{\omega }^{2}$ cannot be expressed in the quadratic form. However, we have derived and explained, in the next Sect. 3.2 that the objective measure CCTFV, as given in (22), can be cast in the desired convex-quadratic form. This enables us to employ the eigenfilter approach.

• 2. To design wavelet filter banks, Tay [29] used a criterion called balanced uncertainty (BU), which is a weighted sum of the time variance and frequency variance of wavelet filters to be designed. Tay [29] reported that the sum of time variance and frequency variance is a better measure than the product of time variance and frequency variance because different wavelet filters with vastly different time variance and frequency variance give the same time-frequency product. Moreover, the product measure does not give any control on time localization and frequency localization individually.

3.2 Formulation of the Objective Function in Quadratic Form

Let $h(n)$ denote the impulse response of a zero phase, low-pass, real-valued FIR filter of length $2N+1$, such that $h(n) \ne 0$, only in the range $-N\le n \le N$. Its DTFT denoted by $H(\omega )$ can be given as

$$\begin{aligned} H(\omega )=h(0)+2\sum _{n=1}^{N}h(n)\cos (\omega n) \end{aligned}$$

(25)

Defining the vectors $\mathbf {a,c}\in \mathbb {R}^{(N+1)}$

$$\begin{aligned} \mathbf {a}&=\left[ \begin{array}{ccccc} h(0)&h(1)&\ldots&h(N-1)&h(N)\end{array}\right] ^{T},\, N\in \mathbb {N}\end{aligned}$$

(26)

$$\begin{aligned} \mathbf {c}(\omega )&=\left[ \begin{array}{ccccc} 1&2\cos (\omega )&\ldots&2\cos (N\omega )\end{array}\right] ^{T},\omega \in [0,\pi ] \end{aligned}$$

(27)

The vector $\mathbf{f}$ is obtained from the first derivative of the vector $\mathbf {c}$, i.e.,

$$\begin{aligned} \mathbf {f}(\omega )=\frac{d}{d\omega }\mathbf {c(\omega )} \end{aligned}$$

Thus, we obtain

$$\begin{aligned} \mathbf {f}(\omega )=\left[ \begin{array}{ccccc} 0&-2\sin (\omega )&-4\sin (2\omega )&\ldots&-2N\sin (N\omega )\end{array}\right] ^{T} \end{aligned}$$

(28)

The frequency response $H(\omega )$ and its derivative $H^{'}(\omega )$ can be expressed as

$$\begin{aligned} H\mathbf {(\omega )}&= \mathbf{a^{T}c(\omega )}\end{aligned}$$

(29)

$$\begin{aligned} H\mathbf {'(\omega )}&= \mathbf {\frac{d}{d\omega }}H(\omega )\mathbf {=a^{T}\frac{d}{d\omega }c(\omega )=a^{\mathbf {T}}}\mathbf {f(\omega )} \end{aligned}$$

(30)

The frequency variance of a real-valued zero phase, sequence $h(n)$ in $l_{2}(\mathbb {Z})$ normalized to unit energy is given by (6). On substituting (29) in (6), we obtain

$$\begin{aligned} \sigma _{\omega }^{2}=\mathbf {a^{T}}\left\{ \int _{0}^{\pi }\omega ^{2}\mathbf{c}(\omega )\mathbf{c}^\mathbf{T}(\omega )\frac{\mathbf{d}\omega }{\pi }\right\} \mathbf{a} \end{aligned}$$

(31)

The equality (31) can be expressed as $\sigma _{\omega }^{2}=\mathbf {a^{T}}\mathbf {Q}\mathbf {a}$, where $\mathbf {Q}=\int _{0}^{\pi }\omega ^{2}\mathbf {c}(\omega )\mathbf {c}^{\mathbf {T}}(\omega )\frac{d\omega }{\pi }$. The matrix $\mathbf {Q}$ is a real, symmetric, positive-definite matrix of the order $(N+1)\times (N+1)$ due to the fact that $\sigma _{\omega }^{2}=\mathbf {a^{T}Qa>} 0$ for each $\mathbf {a}\in \mathbb {R}^{N+1}$. The $(k,l)^{th}$ element of the matrix $\mathbf {Q}$ is given as

$$\begin{aligned}{}[\mathbf {Q}]_{k,l}={\left\{ \begin{array}{ll} \frac{\pi ^{2}}{3} &{} k=l=0\\ \frac{2 \pi ^{2}}{3}+\frac{1}{k^2} &{} k=l,\; except\; k=l=0\\ \frac{4(-1)^{k+l}}{(k+l)^2} &{} k=0\; or\; l=0,\; except\; k=l=0\\ 8(-1)^{k+l}\frac{(k^{2}+l^{2})}{(k^{2}-l^{2})^{2}} &{} otherwise \end{array}\right. } \end{aligned}$$

(32)

where $0\le k,l\le N$. The derivation of (32) is given in the Appendix.

The time variance of a real-valued zero phase, sequence $h(n)$ in $l_{2}(\mathbb {Z})$ normalized to unit energy is given by (5). Using Parseval’s theorem, we obtain from (5)

$$\begin{aligned} \sigma _{n}^{2}=\frac{1}{\pi }\int _{0}^{\pi }\left| \frac{d}{d\omega }\mathbf {H}(\omega )\right| ^{2}d\omega \end{aligned}$$

(33)

On substituting (30) in (33), we get

$$\begin{aligned} \sigma _{n}^{2}=\mathbf {a^{T}\left\{ \mathbf {\int _{0}^{\pi }}\mathbf {f(\omega )f^{T}(\omega )\frac{d\omega }{\pi }}\right\} }\mathbf {a} \end{aligned}$$

(34)

Hence, $\sigma _n^2$ can be expressed as $\sigma _{n}^{2}=\mathbf {a^{T}Pa}$, where $\mathbf {P}=\int _{0}^{\pi }\mathbf {f(\omega )f^{T}(\omega )\frac{d\omega }{\pi }}$. The matrix $\mathbf {P}$ is a real, symmetric, positive-definite matrix of the size $(N+1)\times (N+1)$.

The $(k,l)^{th}$ element of $\mathbf {P}$ is given by

$$\begin{aligned}{}[\mathbf {P}]_{k,l}=&2k^{2}\delta (k-l),\; k,l\in \{0,1,\cdots ,(N-1)\} \end{aligned}$$

(35)

Thus, $\mathbf {P}$ is a diagonal matrix, with non-negative, real entries. The derivation of (35) is given in the Appendix.

Now we define the objective function $\phi$ to be minimized, which is a convex combination of the time variance and frequency variance (CCTFV) of the filter as

$$\begin{aligned} \phi =\alpha \sigma _{n}^{2}+(1-\alpha )\sigma _{\omega }^{2}, \,\alpha \in [0,1], \end{aligned}$$

(36)

where $\alpha$ is a trade-off factor between the time variance $\sigma _n^2$ and frequency variance $\sigma _{\omega }^2$.

The equality (36) can be expressed in the following convex quadratic form

$$\begin{aligned} \mathbf {\phi }&= \alpha \mathbf {a^{T}}\mathbf {P}\mathbf {a+(1-\alpha )a^{T}}\mathbf {Q}\mathbf {a}\nonumber \\&= \mathbf {a^{T}\{\alpha P+(1-\alpha )Q\}a}\mathbf =\mathbf {a^{T}Ra}, \end{aligned}$$

(37)

where $\mathbf {\mathbf {R}=\alpha \mathbf {P}+(1-\alpha )\mathbf {Q}}$ is a real, symmetric, positive-definite matrix of order $(N+1)\times (N+1)$ and $\mathbf {a}\in \mathbf {R}^{(N+1)}$ is a unit norm vector. Using the Rayleigh Principle [13], the optimum filter, which minimizes $\phi$ is obtained as the eigenvector of $\mathbf {R}$, corresponding to its smallest eigen value. Note, our aim is not only to design the finite length filters, which minimize the objective function but which also satisfy constraints of vanishing moments and perfect reconstruction. In order to absorb these constraints in the eigenfilter design, it is mandatory that the constraints be expressed in the form $\mathbf {Ca}=\mathbf {0}$ as described by Pie et al. [21]. In the next section, we present how to formalize PR and VM conditions in the desired form to unable us to incorporate them in eigenfilter design.

3.3 Constraints on the Lengths of Filters

In this paper, we shall consider the design of the odd-length symmetric filters, i.e., type-1 FIR filters only, although the design methodology can be used for even length symmetric filters also. In this section, we present the constraints on the length of filters to be designed. In the case of odd-length, linear phase biorthogonal filter banks, the choice of lengths of filters is constrained by the fact that the lengths of analysis and synthesis filters differ by an odd multiple of two, and the sum of the lengths of analysis and synthesis low-pass filter must be $4m, m\in \mathbb {N}$ [33].

In order to obtain some freedom to optimize the filter coefficients and to ensure existence of the solution of the optimization problem, the length of filters should be chosen so as to satisfy the aforementioned fact along with additional constraints presented in this subsection. Let $h_0(n)$ denote a symmetric low-pass analysis filter such that $h_0(n)=0$, for $|n|>P$, i.e., the length $L_A$ of the $h_0(n)$ is $2P+1$. Let $f_0(n)$ denote the symmetric low-pass synthesis filter such that $f_0(n)=0$, for $|n|> Q$, i.e., the length $L_S$ of the $f_0(n)$ is $2Q+1$. The sum of the length of the analysis and synthesis low-pass filters must be $4m, m\in \mathbb {N}$, i.e., $L_{A}+L_{S}=2P+1+2Q+1=4m$. It follows

$$\begin{aligned} P+Q=2m-1,\, m\in \mathbb {N} \end{aligned}$$

(38)

Thus, the first constraint on choice of lengths of the filter is that $P+Q$ be odd.

Let us assume the analysis low-pass filter $H_{0}(z)$ has $2M_{A}$ number of vanishing moments, i.e., the filter has $2M_{A}$ zeros at $z=-1$ and synthesis low-pass filter $F_{0}(z)$ has $2M_{S}$ number of vanishing moments. To obtain some freedom to optimize the filter coefficients $h_{0}(n)$, the length of the analysis filter should be chosen such that inequality

$$\begin{aligned} P>M_{A} \end{aligned}$$

(39)

is satisfied. Thus, the degrees of freedom available to design the filter is $P-M_{A}$. The filter corresponding to $P=M_{A}$ is the binomial filter. In order to obtain some freedom to optimize filter coefficients of the synthesis filter $f_{0}(n)$, the length must be chosen so as to satisfy the condition

$$\begin{aligned} Q>\left\{ \left( \frac{P+Q-1}{2}\right) +M_{S}\right\} \end{aligned}$$

(40)

In which case, the degrees of freedom available to design the filter are $\left\{ Q-\left( \frac{(P+Q-1)}{2}+M_{S}\right) \right\}$. If one chooses $Q=\left\{ \left( \frac{P+Q-1}{2}\right) +M_{S}\right\}$, there exists a unique solution but there is no freedom left to optimize the filter coefficients. No solution exists for the length corresponding to $Q<\left\{ \left( \frac{P+Q-1}{2}\right) +M_{S}\right\}$.

3.4 Imposing Linear Constraints in Eigen Design Formulation

Linear constraints of the form $\mathbf {C}\mathbf {a}=\mathbf {d}$ can be incorporated into eigenfilter design of FIR filters, where the vector $\mathbf {a}$ contains the filter coefficients. The matrix $\mathbf {C}$ is a rectangular matrix having constant elements and the vector $\mathbf {d}$ is an arbitrary vector having constant elements. To impose the linear constraint

$$\begin{aligned} \mathbf {C}\mathbf {a}=\mathbf {0} \end{aligned}$$

(41)

a method, given by Pei et al. [21], is used in this paper.

From Eq. (41), we infer that $\mathbf {a}$ is in the null space of $\mathbf {C}$. Therefore, $\mathbf {a}$ can be expressed as [13]

$$\begin{aligned} \mathbf {a}=\mathbf {U}\mathbf {b}, \end{aligned}$$

(42)

where $\mathbf {U}$ is a rectangular unitary matrix, i.e., $\mathbf {UU^{T}}=\mathbf {I}$

The columns of $\mathbf {U}$ form an orthogonal basis for the null space of $\mathbf {C}$, and $\mathbf {b}$ is an arbitrary vector. The objective function $\phi$, as given in (37), can be expressed as

$$\begin{aligned} \phi =\mathbf {a}^{T}\mathbf {R}\mathbf {a=\mathbf {b}^{T}\mathbf {U^{T}RU}\mathbf {b}=\mathbf {b^{T}S}\mathbf {b}}, \end{aligned}$$

(43)

where $\mathbf {S=U^{T}RU}$ is a real symmetrical matrix of the order $(N+1)\times (N+1)$. Using the Rayleigh theorem [13], the optimal $\mathbf {b}$ is obtained as the eigenvector of the matrix $\mathbf {S}$, corresponding to its minimum eigenvalue. Having obtained the optimal $\mathbf {b},$ the optimal $\mathbf {a}$ can be obtained using $\mathbf {a}=\mathbf {U}\mathbf {b}$.

3.5 Framework for Imposing PR and VMs Condition in Time Domain

In this subsection we present how PR and VM conditions can be expressed as a set of linear equations in the time domain.

3.5.1 Perfect reconstruction condition

In case of two-channel filter banks, the condition of perfect reconstruction is equivalent to biorthogonality. In this subsection, we describe how to impose PR conditions as a set of linear constraints in the eigen-design of the synthesis low-pass filter $F_{0}(z)$.

The half-band condition (3) on the product filter $P(z)$ can be expressed in the time domain as

$$\begin{aligned} p(2n)&= f_{0}(0)h_{0}(2n)+\sum _{k=1}^{Q}{\displaystyle f_{0}(k)\{h_{0}(2n-k)+h_{0}(2n+k)\}} \nonumber \\&= 0 \; \text{ for } 1\le n\le \left( \frac{P+Q-1}{2}\right) , \end{aligned}$$

(44)

where $p(n)$ is normalized such that $p(0)=1$. We express the condition (44) in the form $\mathbf {B}\mathbf {a}=\mathbf {0}$, in order to be able to assimilate it in the eigen filter design. The $\mathbf {a}\in \mathbb {R}^{(Q+1)}$ containing the filter coefficients $f_{0}(n)$, for $0\le n\le Q$, and $\mathbf {B\in \mathbb {R}^{\left( \frac{P+Q-1}{2}\right) \times (Q+1)}}$. The $(k,l)^{th}$ element of matrix $\mathbf {B}$ is obtained as

$$\begin{aligned}{}[\mathbf {B}]_{k,l}={\left\{ \begin{array}{ll} h_{0}[2k+2] &{} l=0 \\ h_{0}[2(k+1)-l]+h_{0}[2(k+1)+l] &{} 1\le l\le Q, \end{array}\right. } \end{aligned}$$

(45)

where $0\le k<\left\{ \left( \frac{P+Q-1}{2}\right) -1 \right\}$. Note, here $h_{0}(n)=h_{0}(-n), 0 \le n \le P$ and $h_{0}(n)=0, |n|>P$. In the above formulation, the condition $p(0)=1$ is not included explicitly. The condition is absorbed in normalizing the energy of the filter.

3.5.2 Vanishing Moment Condition

In certain applications, specially in the design of wavelet filter banks, we require the low-pass filters to be regular. A low-pass filter $H_{0}(z)$ is said to be $K$-regular if it has $K$ multiple zeros at $z=-1$. Since we also want to design wavelets from the filter banks designed by us we will impose certain additional conditions on PR filter banks to enable them to be valid candidates for wavelet filter banks. The design of wavelet filter banks is equivalent to the design of PR filter banks, except that the former must satisfy vanishing moment or regularity constraints in order to ensure construction of regular wavelets and scaling functions. In this paper, $K$-regular low-pass filters are said to have $K$ vanishing moments (VMs). In our design, VM constraints are imposed in the time-domain matrix form $\mathbf {Ab=0}$ as explained below.

Let we impose $2M_{A}$ zeros at $z=-1$ on the low-pass filter $H_{0}(z)$ having $2P+1$ non-zero taps. Then the impulse response of the filter $h_{0}(n)$ satisfies the equality

$$\begin{aligned} \sum _{n=-P}^{P}n^{K}(-1)^{n}h_{0}(n)=0,\ \mathrm{for}\ K=0,1,2,\ldots 2M_{A}-1 \end{aligned}$$

(46)

Note, in case of odd length filters, zeros at $z=-1$ always occur in pairs.

Since $h_{0}(n)$ is a zero phase filter, the condition (46) boils down to

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{0}(0)+2\sum \nolimits _{n=1}^{P}(-1)^{n}h_{0}(n)=0 \\ 2\sum \nolimits _{n=1}^{P}n^{2K}(-1)^{n}h_{0}(n)=0\text{, } K=1,2,\ldots M_{A}-1 \end{array}\right. } \end{aligned}$$

(47)

The conditions (47) can be expressed in the form $\mathbf {Ab}=\mathbf {0}$. Where, the vector $\mathbf {b}$, defined as $\mathbf {b} =[h_{0}(0)\, h_{0}(1)\cdots \, h_{0}(P-1)\,h_{0}(P)]^{T}\in \mathbb {R}^{(P+1)}$, contains filter coefficients $h_{0}(n)$, for $0\le n\le P$, and $\mathbf {A}\in \mathbb {R}^{(M_{A})\times (P+1)}$. The $(k,l)^{th}$ element of matrix $\mathbf {A}$ is obtained as follows:

$$\begin{aligned}{}[\mathbf{A}]_{k,l}={\left\{ \begin{array}{ll} 1 &{} k\!=\!l\!=\!0\\ 2(l)^{2k}(-1)^{l} &{} l\!\in \!\{0,1,2,\cdots , P\},\;k\!\in \!\{0,1,2,\cdots , M_{A}\!-\!1\}\backslash \{k\!=\!l\!=\!0\} \end{array}\right. }\nonumber \\ \end{aligned}$$

(48)

4 Design Method

In this section, we present a method to design linear phase PR wavelet filter banks using a combination of the eigenfilter-based approach and the complementary filter bank design technique. The analysis and the synthesis filters are designed with the objective of minimizing the time-frequency localization measure CCTFV subject to constraints of VMs and/or PR, using the eigenfilter-based approach. The objective measure CCTFV is formulated in the quadratic form ${\phi =\mathbf{a}^{T}\mathbf{Ra}}$, where $\mathbf {R}$ is a real symmetric positive-definite matrix. Perfect reconstruction and vanishing moments conditions are incorporated in the the eigenfilter design by casting the constraints in the form $\mathbf {Ca}=\mathbf {0}$ [21], where $\mathbf {C}$ is a constant matrix and $\mathbf {a}$ is a constant vector associated to the filter coefficients. The optimal filter is obtained as the eigenvector of the matrix $\mathbf {S}$ associated with the objective measure and the constraits, as given in (43).

We first design an optimal analysis low-pass filter $H_{0}(z)$ using the eigenfilter approach taking CCTFV as minimizing objective measure subject to the constraints of VMs. The filter $H_0(z)$ cannot be an arbitrary filter. It ought to be a valid analysis filter of the underlying PR filter bank. A condition given by Vetterli and Herley [33] states that the analysis filter $H_{0}(z)$ has a complementary-synthesis filter $F_{0}(z)$ if and only if its two-polyphase components are coprime. The validity is checked explicitly, using the Proposition 4.3 given by Vetterli and Herley [33] which states that a filter $H_{0}(z)$ has a complementary filter, if and only if, it has no pair of zeros at $z=\gamma$ and $z=-\gamma$. The absence of zero pairs of the form $(\gamma ,-\gamma )$ ensures that polyphase components of $H_{0}(z)$ are coprime. Having obtained the valid analysis low-pass filter $H_{0}(z)$, we proceed to design the optimal complementary synthesis low-pass filter $F_{0}(z)$ with the objective of minimizing CCTFV subject to the constraints of VMs and PR. High-pass filters $F_{1}(z)$ and $H_{1}(z)$ are obtained by quadrature conjugation of low-pass filters $H_{0}(z)$ and $F_{0}(z)$, respectively.

We also construct wavelets from iterations of the filters of the corresponding wavelet filter banks. To construct wavelets from the filter banks, the cascade algorithm given by Vetterli and Herley [33] is used. However, all PR two-channel biorthogonal filter banks cannot yield regular wavelets and scaling functions. In order to ensure that the designed filter bank corresponds to a valid wavelet filter bank, we use the necessary and sufficient condition given by Strang [26]. This condition essentially states that the wavelet $\psi (t)$ and the scaling function $\phi (t)$ converge into $L_{2}(\mathbb {R})$ if and only if the absolute values of all eigenvalues of the transition matrix $\mathbf {T}$, which is defined below, are less than 1 (except for the simple eigenvalue 1). The Transition matrix is defined as

$$\begin{aligned} \mathbf {T}=\left( \downarrow 2\right) 2\mathbf {HH}^{T}, \end{aligned}$$

(49)

where $\left( \downarrow 2\right)$ denotes downsampling-by-$2$ operator. The $(k,l)^{th}$ element of the Toeplitz matrix $\mathbf {H}$ is given as $[\mathbf {H}]_{k,l}=h_{0}(k-l)$, $h_{0}(n)$ is the filter coefficients of the low-pass filter of the underlying biorthogonal filter bank, normalized to $\sum _{n}h_{0}(n)=1$. Note, for biorthogonal filter banks we have to explicitly check the eigenvalues of the transition matrices corresponding to both the analysis and the synthesis sides of the filter bank. The flow chart which delineates the design methodology is given in the Fig. 2.

Fig. 2

Flow Chart for the Design Method

In the later part of this section, we present how the design problem of the analysis and synthesis filter can be formulated as a constrained optimization problem and how to obtain optimal time-frequency localized filters using the eigenfilter technique.

4.1 Design of Analysis filter

• 1. First we fix the lengths and numbers of vanishing moments for the analysis and synthesis filters by choosing appropriate values of $P,Q,M_{A}$, and $M_{S}$ such that constraints given on the lengths in the Sect. 3.3 are satisfied. We also choose the value of the time-frequency trade-off factor $\alpha ,\,0\le \alpha \le 1$ for the analysis as well as the synthesis filters. The design of the analysis low-pass filter $h_0(n)$ has been cast as a constrained optimization (minimization) problem

  $$\begin{aligned}&\underset{\mathbf {h}}{\text {minimize}}\quad \phi =\mathbf {h}^{T}\mathbf {Rh}\\&\text {subject to} \quad \mathbf {Ah}=\mathbf {0},\;\mathbf {h}^{T}\mathbf {h}=1 \end{aligned}$$

  where $\phi$ is the objective function CCTFV (37). The matrix $\mathbf {R}\in \mathbb {R}^{(P+1)\times (P+1)}$ is a real, symmetric positive-definite matrix. The set of linear equation $\mathbf {Ah}=\mathbf {0}$ corresponds to VM constraints, $\mathbf A \in \mathbb {R}^{M_A\times (P+1)}$ is the matrix as defined in (48), and $\mathbf {h}\in \mathbb {R}^{(P+1)}$ contains the filter coefficients $h_{0}(n)$ for $0\le n\le P$.

• 2. The optimal vector $\mathbf {h}$ is obtained as the eigenvector of the matrix $\mathbf {S}$, as defined in (43), corresponding to its minimum eigenvalue. The matrix $\mathbf {S}$ is constructed using the method given in the Sect. 3.4. The vector $\mathbf {h}$ contains $P+1$ coefficients of the filter $h_{0}(n)$ for $0\le n\le P.$ The remaining $P$ coefficients can be deduced from symmetry. Having obtained the filter coefficients $h_{0}(n)$, we explicitly verify that $H_{0}(z)$ does not have any pair of zeros at $z=\gamma$ and $z=-\gamma ,$ which ensures that two-polyphase components of $H_{0}(z)$ are relatively coprime and therefore it is a valid filter (for PR filter bank). In fact, it is observed that filters designed by taking the cost function (37) are “almost always” valid for all values of time-frequency trade-off factor $\alpha$ except for $\alpha =0$, in which case all zeros of $H_{0}(z)$ lie on the unit circle.

We would like to note that a filter from the well-known biorthogonal filter banks such as CDF-9/7 [4] can also be chosen as the analysis filter, and we can design a complementary-synthesis filter for this given analysis filter. For example, in design Example 1 given in the Sect. 5, we chose 7-tap filter of the CDF-9/7 filter banks as our analysis filter and design the optimal complementary-synthesis filter.

4.2 Design of Synthesis Filter

• 1 For the given (designed) analysis low-pass filter, the design of the complementary, synthesis, low-pass filter can also be formulated as a constrained optimization problem

  $$\begin{aligned}&\underset{\mathbf {g}}{\text {minimize}}\quad \phi =\mathbf {g}^{T}\mathbf {Rg} \\&\text {subject to} \quad \mathbf {Ag}=\mathbf {0},\;\mathbf {Bg}=\mathbf {0},\;\mathbf {g}^{T}\mathbf {g}=1, \end{aligned}$$

  where $\phi$, matrices $\mathbf {R}\in \mathbb {R}^{(Q+1)\times (Q+1)}$ and $\mathbf {A}\in \mathbb {R}^{M_S\times (Q+1)}$ are exactly same as defined for the design of the analysis filter. The set of linear equations $\mathbf {Bg}=\mathbf {0}$ represents PR constraints, where the matrix $\mathbf {B\in \mathbb {R}^{\left( \frac{P+Q-1}{2}\right) \times (Q+1)}}$, defined in (45), corresponds to $\left( \frac{P+Q-1}{2}\right)$ number of PR linear constraints.

• 2. The vector $\mathbf {g}$ corresponding to the optimal filter is obtained in the exactly similar way as that of the analysis filter using the method described in the Sect. 3.4. The vector $\mathbf {g}$ contains $Q+1$ coefficients of filter $f_{0}(n)$ for $0\le n\le Q.$ The remaining $Q$ coefficients can be deduced from symmetry.

Having designed both the analysis and the synthesis filters, we check the eigen values of the transition matrices, as defined in (49), for both the analysis as well as the synthesis sides of the underlying filter bank, in order to ensure the convergence of the wavelets and the scaling functions in $L_2(\mathbb {R})$. If the filter bank satisfies the validity condition, wavelets are constructed using the cascade algorithm. In all the design examples presented by us, the filter banks satisfy the condition and therefore the corresponding wavelets converge in $L_{2}(\mathbb {R})$.

5 Design Examples and Results

In this section, we present a few design examples to show the effectiveness of the proposed eigenfilter-based design methodology. We also present time-frequency measures of the optimal filter banks designed by us in this section.

Example 1

In this example, we compare time-frequency localization properties of the popular CDF-9/7 filter bank and the optimal time-frequency localized 13/7 filter bank designed by us. The analysis filter has not been designed rather we take the 7-tap filter of CDF-9/7 filter bank as our analysis filter $h_{0}(n)$. We design only the complementary-synthesis filter $f_{0}(n)$ of length $13$ for the given analysis filter by choosing the design parameters as $Q=6$, $2M_S=2$, and $\alpha =.5$. The value of $\alpha$ indicates that time localization and frequency localization are given same weightage in the optimization process. It is to be noted that in CDF-9/7 filter bank, both the analysis and synthesis filter have four vanishing moments. To obtain some degrees of freedom to optimize the filter coefficients, the length and number of vanishing moments are chosen to be $13$ and $2$, respectively. The degrees of freedom are used to optimize time-frequency localization of the filter. Interestingly, the time-frequency localization of the optimal length-$13$ filter designed by us has better time-frequency localization than that of the length-$9$ filter of the CDF-9/7 filter bank. In Table 1, we compare the time-frequency localization of the $9$-tap filter of CDF-9/7 and $13$-tap filter of the optimal $13/7$ filter bank deigned by us. From Table 1, it is clear that the product of the time variance and frequency variance of the optimal length-$13$ filter is lesser than that of the length-$9$ filter of the CDF-9/7 filter bank. The frequency response plots for $H_{0}(\omega )$ and $F_{0}(\omega )$ are shown in Fig. 3g and h, respectively. The pole-zero plots for $H_{0}(z)$ and $F_{0}(z)$ are shown in Fig. 3e and f, respectively. The filter coefficients $h_{0}(n)$ and $f_{0}(n)$ are given in Table 2.

Table 1 Time-frequency Properties: Example-1

Table 2 Filter Coefficients of Design Examples

Fig. 3

Example-1

Example 2

This example demonstrates the fact that filter banks designed by us are optimally time-frequency localized. It is shown that the time-frequency localization property of the optimal filter bank designed by us is superior to the property of time-frequency optimized filter bank deigned by Tay [29]. This example also testifies that we can construct smooth wavelets and scaling functions from iterations of the filter bank designed by the proposed method. For the sake of comparison we choose the length of filters and number of VMs exactly same as that of the filters of the $11/25$ filter bank deigned by Tay [29] in the Example 1. For the analysis filter, the design parameters are as follows: $L_A=11$, $2M_A=4$, and trade-off factor $\alpha =5/6$. For the synthesis filter, we choose $L_S=25$, $2M_S=4$, and $\alpha =10/11$. Note that in this example, we choose different values of the trade-off factor $\alpha$ for the analysis and synthesis filters, which indicates that time and frequency localization is not given the same weightage in the optimization process. In the Table 3, we compare the time-frequency localization of the optimal $11/25$ filter bank deigned by us and $11/25$ time-frequency optimized filter bank designed by Tay [29] in the Example 1. It is clear from the table that time-frequency product of the analysis as well as the synthesis filters designed by us is superior. The frequency response plots for $H_{0}(\omega )$ and $F_{0}(\omega )$ are shown in Fig. 4g and h, respectively. The pole-zero plots for $H_{0}(z)$ and $F_{0}(z)$ are shown in Fig. 4e and f, respectively. From the iteration of these filters, scaling functions and wavelets are constructed using the cascade algorithm. The wavelets and scaling functions are found to be regular. The analysis scaling function and wavelet are shown in Fig. 4a and b, respectively. The synthesis scaling function and wavelet are shown in Fig. 4c and d, respectively. Figure 4 exhibits that designed wavelets and scaling functions are reasonably smooth. The filter coefficients $h_{0}(n)$ and $f_{0}(n)$ are given in Table 2.

Table 3 Time-frequency Properties: Example-2

Fig. 4

Example-2

Example 3

This example justifies the fact that we can control time-frequency localization of the analysis and synthesis filter independently and arbitrarily. It is possible to design the optimal time localized and optimal frequency localized filters. In this example, we design optimally time-localized analysis filters without taking into account the frequency localization. On the other hand, the synthesis filter designed is optimally frequency localized, i.e., time localization is not taken into account in the optimization process. For the analysis filter, the deign parameters are as follows: $L_A=11$, $2M_A=6$, and $\alpha =1$. The synthesis filter is designed with $L_S=25$, $2M_S=6$, and $\alpha =0$. The frequency response plots for $H_{0}(\omega )$ and $F_{0}(\omega )$ are shown in Fig. 5g and h, respectively. The pole-zero plots for $H_{0}(z)$ and $F_{0}(z)$ are shown in Fig. 5e and f, respectively. From the iteration of these filters, scaling functions and wavelets are constructed using the cascade algorithm. The wavelets and scaling functions are found to be regular. Analysis scaling function and wavelet are shown in Fig. 5a and b, respectively. Synthesis scaling function and wavelet are shown in Fig. 5c and d, respectively. From the Fig. 5, it is clear that the wavelets and scaling functions designed by us are smooth. The filter coefficients $h_{0}(n)$ and $f_{0}(n)$ are given in Table 2. Time-frequency properties of filters are given in the Table 4.

Fig. 5

Example-3

Table 4 Time-frequency Properties: Example-3

6 Conclusion

In this paper, we present an eigenfilter-based approach to design time-frequency optimized linear phase biorthogonal two-channel filter banks. We also impose desired degree of flatness at $\omega =0$ (regularity) in the transfer function of the low-pass analysis as well as synthesis filters. We have shown that regular wavelets can be constructed from the iterations of the designed filter banks. We have demonstrated that it is possible to control time localization and frequency localization of the analysis and synthesis filters independently. This method can also be extended to design of M-channel, 1-D, and 2-D filter banks. The method can be extended to design filter banks, wherein the optimality criterion is a combination of time-frequency localization, pass-band error, and stop-band error. In addition, the study of trade-offs among time localization, frequency localization, stop-band error, and pass-band error can be extended further.

Appendices

Appendix

Derivation of Matrix Formulation for Time and Frequency Variance for Real Symmetric Discrete-Time Sequences

1.1 Frequency Variance Measure

From the Eq. (31) the frequency variance of the zero phase, low-pass, real FIR filter $h(n)$ of length $2N+1$, $N\in \mathbb {N}$ is given by

$$\begin{aligned} \sigma _{\omega }^{2}=\mathbf {a^{T}}\mathbf {Q}\mathbf {a}, \end{aligned}$$

(50)

where the matrix $\mathbf {Q}$ and the vector $\mathbf {a}$ are defined in the Eqs. (31) and (26), respectively. We define the matrix $\mathbf {E}$ as

$$\begin{aligned} \mathbf {E}=\omega ^{2}\left[ \begin{array}{c} 1\\ 2\cos (\omega )\\ 2\cos (2\omega )\\ \vdots \\ 2\cos (N\omega )\end{array}\right] \left[ \begin{array}{ccccc} 1&2\cos (\omega )&2\cos (2\omega )&\dots&2\cos (N\omega )\end{array}\right] \end{aligned}$$

(51)

The matrix $\mathbf {E}$ can also be expressed as follows:

$$\begin{aligned} \mathbf {E}(\omega )=\omega ^{2}\mathbf {c}(\omega )\mathbf {c}^{T}(\omega ) \end{aligned}$$

(52)

The vector $\mathbf {c}(\omega )$ is defined in (27). The $(k,l)^{th}$ element of the matrix $\mathbf {E}$ is given as

$$\begin{aligned}{}[\mathbf {E}]_{k,l}={\left\{ \begin{array}{ll} \omega ^{2} &{} k=l=0\\ \omega ^{2}\{\cos (k+l)\omega +\cos (k-l)\omega \} &{} k=0\; \text{ or }\; l=0\; \text{ except }\; k=l=0 \\ 2\omega ^{2}\{\cos (k+l)\omega +\cos (k-l)\omega \} &{} otherwise \end{array}\right. }\quad \quad \nonumber \\ \end{aligned}$$

(53)

where $0 \le k,l \le N$. The matrix $\mathbf {Q}$ corresponding to the frequency variance is related to the matrix $\mathbf {E}$ as

$$\begin{aligned} \mathbf {Q}(\omega )=\frac{1}{\pi }\int _{0}^{\pi }\mathbf {E}(\omega )d\omega \end{aligned}$$

(54)

The $(k,l)^{th}\;\text{ element }$ of the matrix $\mathbf {Q}$ can be given as

$$\begin{aligned}{}[\mathbf {Q}]_{k,l}={\left\{ \begin{array}{ll} \frac{1}{\pi }\int _{0}^{\pi }\omega ^{2}d\omega =\frac{\pi ^{2}}{3} &{} k=l=0\\ \frac{1}{\pi }\int _{0}^{\pi }4\omega ^{2}\cos ^2(k\omega )d\omega =\frac{2\pi ^{2}}{3}+\frac{1}{k^2} &{} k=l\; except\; k=l=0 \end{array}\right. } \end{aligned}$$

(55)

$$\begin{aligned}{}[\mathbf {Q}]_{k,l}={\left\{ \begin{array}{ll} \int _{0}^{\pi }\omega ^{2}[\cos (k+l)\omega +\cos (k-l)\omega ]\frac{d\omega }{\pi } &{} k=0\; or \; l\!=\!0\; except\; k\!=\!l\!=\!0\!\!\!\\ \int _{0}^{\pi }2\omega ^{2}[\cos (k+l)\omega +\cos (k-l)\omega ]\frac{d\omega }{\pi } &{} 1\le k,l \le N,\; except\; k=l \end{array}\right. }\nonumber \\ \end{aligned}$$

(56)

In order to evaluate the integrals in the Eq. (56), we substitute $k+l=m$ and $k-l=s$. Thus (56) boils down to

$$\begin{aligned}{}[\mathbf {Q}]_{k,l}={\left\{ \begin{array}{ll} \int _{0}^{\pi }\omega ^{2}[\cos (m\omega )+\cos (s\omega )]\frac{d\omega }{\pi } &{} k=0\; or \; l=0\; except\; k=l=0\\ \int _{0}^{\pi }2\omega ^{2}[\cos (m\omega )+\cos (s\omega )]\frac{d\omega }{\pi } &{} 1\le k,l \le N,\; except\; k=l \end{array}\right. }\nonumber \\ \end{aligned}$$

(57)

The indefinite integral $I=\int \omega ^{2}\cos (m\omega )d\omega$ is evaluated as

$$\begin{aligned} I&= \int \omega ^{2}\cos (m\omega )d\omega \nonumber \\&= \frac{\omega ^{2}\sin (m\omega )}{m}+\frac{2\omega \cos (m\omega )}{m^{2}}-\frac{2\sin (m\omega )}{m^{2}}, m\ne 0 \end{aligned}$$

(58)

On substituting limits in the integral of the expression (58) we get

$$\begin{aligned} \int _{0}^{\pi }\omega ^{2}\cos (m\omega )d\omega =\frac{2\pi (-1)^{m}}{m^{2}},\;m \ne 0 \end{aligned}$$

(59)

Using (59), (57), and (55), we obtain

$$\begin{aligned}{}[\mathbf {Q}]_{k,l}={\left\{ \begin{array}{ll} \frac{\pi ^{2}}{3} &{} k=l=0\\ \frac{2 \pi ^{2}}{3}+\frac{1}{k^2} &{} k=l\; except\; k=l=0\\ \frac{4(-1)^{k+l}}{(k+l)^2} &{} k=0\; or\; l=0,\; except\; k=l=0\\ 8(-1)^{k+l}\frac{(k^{2}+l^{2})}{(k^{2}-l^{2})^{2}} &{} otherwise \end{array}\right. } \end{aligned}$$

(60)

where $0\le k,l\le N$.

1.2 Time Variance Measure

From the Eq. (34) the time variance of the zero phase, low-pass, real FIR filter $h(n)$ of length $2N+1$, $N\in \mathbb {N}$ is expressed as

$$\begin{aligned} \sigma _{n}^{2}=\mathbf {a^{T}Pa}, \end{aligned}$$

(61)

where the matrix $\mathbf {P}$ and the vector $\mathbf {a}$ are defined in the Eqs. (34) and (26), respectively. We define the matrix $\mathbf {F}$ as

$$\begin{aligned} \mathbf {F}=\left[ \begin{array}{c} 0\\ -2\sin (\omega )\\ -4\sin (2\omega )\\ \vdots \\ -2N\sin (N\omega )\end{array}\right] \left[ \begin{array}{ccccc} 0&-2\sin (\omega )&-4\sin (2\omega )&\dots&-2N\sin (N\omega )\end{array}\right] \end{aligned}$$

(62)

$$\begin{aligned} \mathbf {F}=\mathbf {f}(\omega )\mathbf {f^{T}}(\omega ) \end{aligned}$$

The vector $\mathbf {f}(\omega )$ is defined in (28). The $(k,l)^{th}$ element of the matrix $\mathbf {F}$ is given as

$$\begin{aligned}{}[\mathbf {F}]_{k,l}=4kl\sin (k\omega )\sin (l\omega ) \end{aligned}$$

The matrix $\mathbf {P}$ corresponding to time variance is related to the matrix $\mathbf {F}$ as

$$\begin{aligned} \mathbf {P}(\omega )=\frac{1}{\pi }\int _{0}^{\pi }\mathbf {F}(\omega )d\omega \end{aligned}$$

The $(k,l)^{th}$ element of matrix $\mathbf {P}$ is

$$\begin{aligned}{}[\mathbf {P}]_{k,l}&= \frac{1}{\pi }\int _{0}^{\pi }4kl\sin (k\omega )\sin (l\omega )d\omega \nonumber \\&= \frac{1}{\pi }\int _{0}^{\pi }kl[2\cos (k-l)\omega -2\cos (k+l)\omega ]d\omega \end{aligned}$$

(63)

In order to evaluate the integral in the Eq. (63), we substitute $k+l=m$ and $k-l=s$. Thus (63) boils down to

$$\begin{aligned}{}[\mathbf {P}]_{k,l}=\frac{1}{\pi }\int _{0}^{\pi }kl\{2\cos (s\omega )-2\cos (m\omega )\}d\omega \end{aligned}$$

(64)

The value of the integral $\frac{1}{\pi }\int _{0}^{\pi }\cos (m\omega )d\omega$ is evaluated as

$$\begin{aligned} \frac{1}{\pi }\int _{0}^{\pi }\cos (m\omega )d\omega =0,m\ne 0 \end{aligned}$$

(65)

Using (65) and (64), we get

$$\begin{aligned}{}[\mathbf {P}]_{k,l}={\left\{ \begin{array}{ll} 0 &{} k \ne l \\ 2k^{2} &{} k=l \end{array}\right. } \end{aligned}$$

(66)

Thus, the matrix $\mathbf {P}$ can be expressed as

$$\begin{aligned} \mathbf {[P]}_{k,l}=2k^{2}\delta (k-l),0\le k,l\le N \end{aligned}$$

It is to be noted that the matrix $\mathbf {P}$ can be obtained directly using (5) in time domain; however, for the sake of completeness we derived the matrix $\mathbf {P}$ using frequency-domain approach and Parseval’s identity.