1 Introduction

Due to the increasing scale of control systems, faults are prone to occur in these systems. Faults may lead to degradation or instability for the whole system, even catastrophic consequences if they cannot be detected and treated in time. Therefore, it is becoming a hot topic on how to improve safety and reliability of control systems [5]. Fault detection and isolation (FDI) of dynamic systems has received great attention and is developing rapidly based on this [10]. In the last few decades, the model-based FDI has been successfully applied to real systems [12, 28, 30], whose basic idea is to employ a residual signal to detect faults [14]. The existing model-based FDI methods can be classified into the following three types according to different residual generation forms: the observer method, the parity space method, and the parameter estimation method. Among them, the observer method is the most popular one and has received much attention in the existing literature. For the latest advance in observer designing, we refer to [31, 32]. Plentiful and substantial achievements for observer-based FDI can be found in several excellent books [4, 7] and survey papers [10, 14, 15].

It should be noted that FDI only uses the residual signal to indirectly determine whether system is faulty or not. Compared with FDI, fault estimation is more difficult and challenging. The shape and magnitude of a fault can be obtained directly through fault estimation, and thus, an intuitive understanding of faults can be realized. The observer-based fault estimation has been widely studied for this reason. To name a few, the fault estimation problem of dynamic systems is studied in [1, 13, 19, 21, 26, 29], whereas only linear systems are considered. As most of actual systems are subject to nonlinearities, therefore the study for fault estimation of nonlinear systems is of both theoretical and practical significance. To the best of the authors’ knowledge, the fault estimation problem of nonlinear systems has not been deeply studied due to its complexity. For example, the fault estimation problem of nonlinear systems is studied in [11, 16, 23] by adaptive observers, but adaptive observers often use indirect residual information to estimate the fault. In fact, it is difficult to achieve high accuracy of fault estimation by this method. A neural network observer is employed to estimate the fault of a class of nonlinear systems in [25], but how to choose the parameters of neural network is still lack of a unified scientific basis. In addition, high accuracy of fault estimation is achieved by sliding mode observer in [9], and further study can be seen in [6, 17, 24, 27]. Nevertheless, sliding mode observer needs a high-frequency switch to achieve sliding mode dynamic, which requires much energy, also brings about chattering inevitably, and easily excites the unmodeled dynamic of the observer error dynamic system. The unknown input (fault) estimation was studied in [22] by a second-order sliding mode observer based on the super-twisting algorithm. However, not only the gain values of sliding mode observer are obtained through the geometric method, but also the studied system needs to be linear.

Motivated by above analyses, this paper aims to present a second-order sliding mode observer to estimate the fault of a class of nonlinear systems using the super-twisting algorithm. The proposed second-order sliding mode observer has two features: (1) The undesirable chattering caused by traditional sliding mode observer is avoidable, and then fault estimation can be stably obtained, which overcomes the shortcomings of traditional sliding mode observer; and (2) The advantage of traditional sliding mode observer, which can achieve high accuracy of fault estimation, is retained. To eliminate the cumbersome stability proving process of the super-twisting algorithm using the geometric method [18], a Lyapunov function in [20] is adopted.

Subsequent sections of the paper are organized as follows. In Sect. 2, the nonlinear system is described and proper coordinate transformations are employed to decouple the fault. The second-order sliding mode observer is designed in Sect. 3. Estimation of the fault is achieved in Sect. 4. The proposed method is applied to a rot-arm problem in Sect. 5. Finally, Sect. 6 draws the conclusion for the whole paper.

Throughout the paper, \(A>0\) represents \(A\) is a symmetric positive definite matrix; \(\Vert A\Vert \) represents the Euclidean norm of vector \(A\) or Frobenius norm of matrix \(A\); \(\lambda _{\text {min}}(A)\) and \(\lambda _{\text {max}}(A)\) represent the minimum and maximum eigenvalue of matrix \(A\), respectively; \(A^{+}\) is the left pseudo-inverse of matrix \(A\); \(I_{n}\) represents the \(n\)th-order identity matrix; the superscripts T and -1 stand for the matrix transpose and inverse, respectively; \(\mathbb {R}^{n}\) denotes an \(n\)-dimensional Euclidean space.

2 System Description

Consider the following nonlinear continuous-time system with actuator fault

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}}(t) = Ax(t) + Bu(t)+Eg(x)+Df(t)\text {,} \\ y(t) = Cx(t), \\ \end{array} \right. \end{aligned}$$
(1)

where \(x\in \mathbb {R}^{n}, y\in {{\mathbb {R}}^{p}},u\in {{\mathbb {R}}^{m}}\) denote the state, measurement output and control input, respectively; \(g\) is the nonlinear vector function, satisfying Lipschitz condition, i.e., \(\left\| g\left( x \right) -g\left( {\hat{x}} \right) \right\| \le {{L}_{g}}\left\| x-\hat{x} \right\| \), where \(L_{g}>0\) is the Lipschitz constant. \(f\in {{\mathbb {R}}^{q}}\) represents the actuator fault, which satisfies \(\left\| {\dot{f}} \right\| \le \delta \), \(\delta \in \left( 0,\infty \right) \). \(A,\text { }B,\text { }C,\text { }D,\text { }E\) are matrices of appropriate dimension, where \(D\) is the matrix with full column rank.

First of all, the following assumptions and definition are given.

Assumption 1

The matrix \(CD\) is full column rank, i.e., \(\text {rank}\left( CD \right) =\text {rank}\left( D \right) =q\).

Assumption 2

The invariant zeros of the triple \(\left( A,D,C \right) \) are in the open left-hand complex plane, i.e.,

$$\begin{aligned} \text {rank}\left[ \begin{array}{c@{\quad }c} s{{I}_{n}}-A &{} D \\ C &{} 0 \\ \end{array} \right] =n+\text {rank}\left( D \right) \end{aligned}$$

for arbitrary complex number \(s\) with nonnegative real part.

Definition 1

[3] Consider the following dynamic system

$$\begin{aligned} \dot{x}=h\left( x \right) , \end{aligned}$$
(2)

where \(x\in U,\text { }x\left( 0 \right) ={{x}_{0}}\), and \(h:U\rightarrow {{\mathbb {R}}^{n}}\) is continuous on an open neighborhood \(U\subset {{\mathbb {R}}^{n}}\) of the origin. The zero solution of system (2) is finite-time convergent if there exists an open neighborhood \({{U}_{0}}\subset U\) of the origin and a function \({{T}_{m}}:{{U}_{0}}\backslash \left\{ 0 \right\} \rightarrow \left( 0,\infty \right) \), such that \(\forall {{x}_{0}}\in {{U}_{0}}\), the solution trajectory \(x\left( t,{{x}_{0}} \right) \) of system (2) starting from the initial point \({{x}_{0}}\in {{U}_{0}}\backslash \left\{ 0 \right\} \) is well defined and unique in forward time for \(t\in \left[ 0,{{T}_{m}}\left( {{x}_{0}} \right) \right) \) and \({{\lim }_{t\rightarrow {{T}_{m}}\left( {{x}_{0}} \right) }}x\left( t,{{x}_{0}} \right) =0\). Then, \({{T}_{m}}\left( {{x}_{0}} \right) \) is called the settling time. The zero solution of system (2) is finite-time stable if it is Lyapunov stable and finite-time convergent.

The following lemma is useful to prove that the zero solution of system (2) is finite-time stable.

Lemma 1

[2] Suppose there exists a continuously differentiable function \(V:U\rightarrow \mathbb {R}\), real numbers \(c>0\) and \(\beta \in \left( 0,1 \right) \), and a neighborhood \({{U}_{0}}\subset U\) of the origin such that \(V\) is positive definite on \({{U}_{0}}\) and \(\dot{V}+c{{V}^{\beta }}\) along system (2) is negative semidefinite on \({{U}_{0}}\). Then the zero solution of system (2) is finite-time stable.

If the nonlinear system (1) satisfies the above assumptions, the actuator fault \(f\) can be decoupled by appropriate coordinate transformations, and then fault estimation can be conveniently obtained. From the coordinate transformation \(\bar{x}=\left( \bar{x}_{1}^{\text {T}},\bar{x}_{2}^{\text {T}} \right) =Tx\) in [8, 9], the following system is inferred from the original system (1). For clarity, we omit the time parameter \(t\) in the following development, e.g., \(x\left( t \right) \) is denoted as \(x\), \(y\left( t \right) \) is denoted as \(y\), etc.

$$\begin{aligned}&{{\dot{\bar{x}}}_{1}}={{A}_{11}}{{\bar{x}}_{1}}+{{A}_{12}}{{\bar{x}}_{2}}+{{B}_{1}}u+{{g}_{1}}\left( {\bar{x}} \right) , \end{aligned}$$
(3)
$$\begin{aligned}&\left\{ \begin{array}{l} {{\dot{\bar{x}}}_{2}} = {{A}_{21}}{{{\bar{x}}}_{1}}+{{A}_{22}}{{{\bar{x}}}_{2}}+{{B}_{2}}u+{{g}_{2}}\left( {\bar{x}} \right) +{{D}_{2}}f, \\ y = {{C}_{2}}{{{\bar{x}}}_{2}}, \\ \end{array} \right. \end{aligned}$$
(4)

where \({{\bar{x}}_{1}}\in {{\mathbb {R}}^{n-p}},{{\bar{x}}_{2}}\in {{\mathbb {R}}^{p}}\), \(\left[ \begin{matrix} {{g}_{1}}\left( {\bar{x}} \right) \\ {{g}_{2}}\left( {\bar{x}} \right) \\ \end{matrix} \right] =TEg\left( {{T}^{-1}}\bar{x} \right) \), and

$$\begin{aligned}&\left[ \begin{matrix} {{A}_{11}} &{} {{A}_{12}} \\ {{A}_{21}} &{} {{A}_{22}} \\ \end{matrix} \right] =TA{{T}^{-1}},\text { }\left[ \begin{matrix} {{B}_{1}} \\ {{B}_{2}} \\ \end{matrix} \right] =TB, \\&\left[ \begin{matrix} 0 &{} {{C}_{2}} \\ \end{matrix} \right] =C{{T}^{-1}},\text { }\left[ \begin{matrix} 0 \\ {{D}_{2}} \\ \end{matrix} \right] =TD, \end{aligned}$$

where \({{D}_{2}}=\left[ \begin{matrix} {{0}_{\left( p-q \right) \times q}} \\ {{{\bar{D}}}_{2}} \\ \end{matrix} \right] \), \({{\bar{D}}_{2}}\in {{\mathbb {R}}^{q\times q}}\), \({{\bar{D}}_{2}}\) and \({{C}_{2}}\) are both invertible.

Introducing a further coordinate transformation \(w=S\bar{x}\) for system (3)–(4) with \(S=\left[ \begin{matrix} {{I}_{n-p}} &{} L \\ 0 &{} {{I}_{p}} \\ \end{matrix} \right] \), where \(L=\left[ \begin{matrix} {\bar{L}} &{} 0 \\ \end{matrix} \right] \), \(\bar{L}\in {{\mathbb {R}}^{\left( n-p \right) \times \left( p-q \right) }}\), then

$$\begin{aligned} {{\dot{w}}_{1}}= & {} \left( {{A}_{11}}+L{{A}_{21}} \right) {{w}_{1}}+\left[ {{A}_{12}}+L{{A}_{22}}-\left( {{A}_{11}}+L{{A}_{21}} \right) L \right] {{w}_{2}}\nonumber \\&\quad +\left( {{B}_{1}}+L{{B}_{2}} \right) u+\left[ {{I}_{n-p}}\text { }L \right] TEg\left( {T}^{-1}{{S}^{-1}}w \right) ,\end{aligned}$$
(5)
$$\begin{aligned}&\left\{ \begin{array}{l} {{\dot{w}}_{2}} = {{A}_{21}}{{w}_{1}}+\left( {{A}_{22}}-{{A}_{21}}L \right) {{w}_{2}}+{{B}_{2}}u+{{g}_{2}}\left( {{S}^{-1}}w \right) +{{D}_{2}}f, \\ y={{C}_{2}}{{w}_{2}}. \\ \end{array} \right. \end{aligned}$$
(6)

In the following section, an observer will be designed for system (5)–(6), and the stability of the observer error dynamic system will be proved.

3 Observer Designing

The following observer is designed for system (5)–(6),

$$\begin{aligned}&{{\dot{\hat{w}}}_{1}}=\left( {{A}_{11}}+L{{A}_{21}} \right) {{\hat{w}}_{1}}+\left[ {{A}_{12}}+L{{A}_{22}}-\left( {{A}_{11}}+L{{A}_{21}} \right) L \right] C_{2}^{-1}y\nonumber \\&\quad +\left( {{B}_{1}}+L{{B}_{2}} \right) u+\left[ {{I}_{n-p}}\text { }L \right] TEg\left( {T}^{-1}{{S}^{-1}}\hat{w} \right) , \end{aligned}$$
(7)
$$\begin{aligned}&\left\{ \begin{array}{l} {{{\dot{\hat{w}}}}_{2}}= {{A}_{21}}{{{\hat{w}}}_{1}}+\left( {{A}_{22}}-{{A}_{21}}L \right) C_{2}^{-1}y+{{B}_{2}}u+{{g}_{2}}\left( {{S}^{-1}}\hat{w} \right) +\upsilon , \\ \hat{y}={{C}_{2}}{{{\hat{w}}}_{2}}, \\ \end{array} \right. \end{aligned}$$
(8)

where \(\hat{w}={{\left[ {{{\hat{w}}}_{1}},{{w}_{2}} \right] }^{\text {T}}}\). Note that \(\hat{w}\) does not represent the state estimation \({{\left[ {{{\hat{w}}}_{1}},{{{\hat{w}}}_{2}} \right] }^{\text {T}}}\). Define \({{e}_{y}}=\hat{y}-y\), \({{e}_{1}}={{\hat{w}}_{1}}-{{w}_{1}},\text { }{{e}_{2}}={{\hat{w}}_{2}}-{{w}_{2}}\), then \({{e}_{y}}={{C}_{2}}\left( {{{\hat{w}}}_{2}}-{{w}_{2}} \right) ={{C}_{2}}{{e}_{2}}\). As \({{C}_{2}}\) is invertible, then \({{e}_{2}}\) can be obtained as \({{e}_{2}}=C_{2}^{-1}{{e}_{y}}\). The second-order sliding mode item \(\upsilon \) is expressed as

$$\begin{aligned} \left\{ \begin{array}{l} \upsilon \left( t \right) ={{\upsilon }_{1}}\left( t \right) +{{\upsilon }_{2}}\left( t \right) , \\ {{\upsilon }_{1}}\left( t \right) =-{{k}_{1}}\left| {e}_{2}\right| ^{1/2}\text {sgn} \left( {{e}_{2}} \right) ,\\ {{{\dot{\upsilon }}}_{2}}\left( t\right) =-{{k}_{2}}\text {sgn}\left( {{e}_{2}} \right) , \end{array} \right. \end{aligned}$$

where \({\left| {{e}_{2}} \right| }^{1/2}\text {sgn} \left( {{e}_{2}} \right) \) can be written in component-wise as

$$\begin{aligned} {\left| {{e}_{2}} \right| }^{1/2}\text {sgn} \left( {{e}_{2}} \right) ={{\left[ \begin{matrix} {\left| {{e}_{21}} \right| }^{1/2}\text {sgn} \left( {{e}_{21}} \right) \text{, }\ &{} \ldots \text{, }\ &{} {\left| {{e}_{2p}} \right| }^{1/2}\text {sgn} \left( {{e}_{2p}} \right) \\ \end{matrix} \right] }^{\text {T}}}. \end{aligned}$$

The parameters \({{k}_{1}}\) and \({{k}_{2}}\) are the gain values to be designed later, and sgn represents the sign function.

Sliding mode surface is designed as

$$\begin{aligned} {{e}_{2}}\text {=}0. \end{aligned}$$
(9)

From the definition of \({{e}_{1}}\), \({{e}_{2}}\) and (5)–(8), the observer error dynamic system is given by

$$\begin{aligned} {{\dot{e}}_{1}}= & {} \left( {{A}_{11}}+L{{A}_{21}} \right) {{e}_{1}}+\left[ {{I}_{n-p}}\text { }L \right] TE\left[ g\left( {T}^{-1}{{S}^{-1}}\hat{w} \right) -g\left( {T}^{-1}{{S}^{-1}}w \right) \right] , \end{aligned}$$
(10)
$$\begin{aligned} {{\dot{e}}_{2}}= & {} {{A}_{21}}{{e}_{1}}+{{g}_{2}}\left( {{S}^{-1}}\hat{w} \right) -{{g}_{2}}\left( {{S}^{-1}}w \right) +\upsilon -{{D}_{2}}f. \end{aligned}$$
(11)

By computation, it shows that \({{S}^{-1}}\hat{w}-{{S}^{-1}}w=\left[ \begin{matrix} {{I}_{n-p}} &{} -L \\ 0 &{} {{I}_{p}} \\ \end{matrix} \right] \left[ \begin{matrix} {{{\hat{w}}}_{1}}-{{w}_{1}} \\ {{w}_{2}}-{{w}_{2}} \\ \end{matrix} \right] =\left[ \begin{matrix} {{e}_{1}} \\ 0 \\ \end{matrix} \right] \), then \(\left\| {{S}^{-1}}\hat{w}-{{S}^{-1}}w \right\| =\left\| {{e}_{1}} \right\| \).

Theorem 1

Given the nonlinear system (1) with Assumptions 1–2, the observer error dynamic system (10) is asymptotically stable, and \({{e}_{1}}\) satisfies \(\left\| {{e}_{1}}\left( t \right) \right\| \le N\left\| {{e}_{1}}\left( 0 \right) \right\| \exp \left( -{\alpha t}/{2}\; \right) \) if the following matrix inequality

$$\begin{aligned} {{\bar{A}}^{\text {T}}}{{\bar{R}}^{\text {T}}}+\bar{R}\bar{A}+\frac{1}{\varepsilon }\bar{R}{{\bar{R}}^{\text {T}}}+\varepsilon {{\left( {{L}_{g}} \right) }^{2}}{{\left\| TE \right\| }^{2}}{{\left\| {{T}^{-1}} \right\| }^{2}}{{I}_{n-p}}+\alpha R<0 \end{aligned}$$
(12)

is established. Where \(\varepsilon ,\text { }\alpha \) are positive numbers, \(N=\sqrt{\frac{{{\lambda }_{\max }}\left( R \right) }{{{\lambda }_{\min }}\left( R \right) }}\), \(\bar{R}=R\left[ {{I}_{n-p}}\text { }L \right] \), \(\bar{A}={{\left[ \begin{matrix} A_{11}^{\text {T}} &{} A_{21}^{\text {T}} \\ \end{matrix} \right] }^{\text {T}}} \), and \(R\in {{\mathbb {R}}^{\left( n-p \right) \times \left( n-p \right) }}\) is a symmetric positive definite matrix.

Proof

Consider the Lyapunov function \(V=e_{1}^{\text {T}}R{{e}_{1}}\). Differentiating \(V\) with respect to time yields

$$\begin{aligned} \dot{V}= & {} e_{1}^{\text {T}}\left[ {{\left( {{A}_{11}}+L{{A}_{21}} \right) }^{\text {T}}}R+R\left( {{A}_{11}}+L{{A}_{21}} \right) \right] {{e}_{1}} \\&\quad +\,2{{\left( R{{e}_{1}} \right) }^{\text {T}}}\left[ {{I}_{n-p}}\text { }L \right] TE\left[ g\left( {{T}^{-1}}{{S}^{-1}}\hat{w} \right) -g\left( {{T}^{-1}}{{S}^{-1}}w \right) \right] \\= & {} e_{1}^{\text {T}}\left( {{{\bar{A}}}^{\text {T}}}{{{\bar{R}}}^{\text {T}}}+\bar{R}\bar{A} \right) {{e}_{1}}+2{{\left( {{{\bar{R}}}^{\text {T}}}{{e}_{1}} \right) }^{\text {T}}}TE\left[ g\left( {{T}^{-1}}{{S}^{-1}}\hat{w} \right) -g\left( {{T}^{-1}}{{S}^{-1}}w \right) \right] . \end{aligned}$$

By the inequality \(2{{X}^{\text {T}}}Y\le \frac{1}{\varepsilon }{{X}^{\text {T}}}X+\varepsilon {{Y}^{\text {T}}}Y\), it yields that

$$\begin{aligned} \dot{V}= & {} e_{1}^{\text {T}}\left( {{{\bar{A}}}^{\text {T}}}{{{\bar{R}}}^{\text {T}}}+\bar{R}\bar{A} \right) {{e}_{1}}+2{{\left( {{{\bar{R}}}^{\text {T}}}{{e}_{1}} \right) }^{\text {T}}}TE\left[ g\left( {{T}^{-1}}{{S}^{-1}}\hat{w} \right) -g\left( {{T}^{-1}}{{S}^{-1}}w \right) \right] \\\le & {} e_{1}^{\text {T}}\left( {{{\bar{A}}}^{\text {T}}}{{{\bar{R}}}^{\text {T}}}+\bar{R}\bar{A} \right) {{e}_{1}}+\frac{1}{\varepsilon }e_{1}^{\text {T}}\bar{R}{{{\bar{R}}}^{\text {T}}}{{e}_{1}}+\varepsilon \left\{ TE\left[ g\left( {{T}^{-1}}{{S}^{-1}}\hat{w} \right) \right. \right. \\&\left. \left. -g\left( {{T}^{-1}}{{S}^{-1}}w \right) \right] \right\} ^{\text {T}}\left\{ TE\left[ g\left( {{T}^{-1}}{{S}^{-1}}\hat{w} \right) -g\left( {{T}^{-1}}{{S}^{-1}}w \right) \right] \right\} \\\le & {} e_{1}^{\text {T}}\left( {{{\bar{A}}}^{\text {T}}}{{{\bar{R}}}^{\text {T}}}+\bar{R}\bar{A} \right) {{e}_{1}}+\frac{1}{\varepsilon }e_{1}^{\text {T}}\bar{R}{{{\bar{R}}}^{\text {T}}}{{e}_{1}}+\varepsilon {{\left( {{L}_{g}} \right) }^{2}}{{\left\| TE \right\| }^{2}}{{\left\| {{T}^{-1}} \right\| }^{2}}{{\left\| {{e}_{1}} \right\| }^{2}} \\= & {} e_{1}^{\text {T}}\left[ {{{\bar{A}}}^{\text {T}}}{{{\bar{R}}}^{\text {T}}}+\bar{R}\bar{A}+\frac{1}{\varepsilon }\bar{R}{{{\bar{R}}}^{\text {T}}}+\varepsilon {{\left( {{L}_{g}} \right) }^{2}}{{\left\| TE \right\| }^{2}}{{\left\| {{T}^{-1}} \right\| }^{2}}{{I}_{n-p}} \right] {{e}_{1}}. \end{aligned}$$

From the inequality (12), then \(\dot{V}\le -\alpha e_{1}^{\text {T}}R{{e}_{1}}=-\alpha V\), so system (10) is asymptotically stable. As \(\dot{V}\le -\alpha V\), then there exists a positive \(N\) such that

$$\begin{aligned} \left\| {{e}_{1}}\left( t \right) \right\| \le N\left\| {{e}_{1}}\left( 0 \right) \right\| \exp \left( -{\alpha t}/{2}\; \right) , \end{aligned}$$

where \(N=\sqrt{\frac{{{\lambda }_{\max }}\left( R \right) }{{{\lambda }_{\min }}\left( R \right) }}\). The poof is complete. \(\square \)

From Sect. 2, we know \(\bar{x}={{S}^{-1}}w\), and let \(\hat{\bar{x}}={{S}^{-1}}\hat{w}\) for simplicity. Denoting \({{g}_{2}}\left( \hat{w},w \right) ={{g}_{2}}\left( {{S}^{-1}}\hat{w} \right) -{{g}_{2}}\left( {{S}^{-1}}w \right) \), it follows that

$$\begin{aligned} {{{\dot{g}}}_{2}}\left( \hat{w},w \right)= & {} \frac{\text {d}{{g}_{2}}}{\text {d}x}\left| _{x=\hat{\bar{x}}} \right. \dot{\hat{\bar{x}}}-\frac{\text {d}{{g}_{2}}}{\text {d}x}\left| _{x=\bar{x}} \right. \dot{\bar{x}} \\= & {} \frac{\text {d}{{g}_{2}}}{\text {d}x}\left| _{x=\hat{\bar{x}}} \right. \dot{\hat{\bar{x}}}-\frac{\text {d}{{g}_{2}}}{\text {d}x}\left| _{x=\bar{x}} \right. \dot{\hat{\bar{x}}}+\frac{\text {d}{{g}_{2}}}{\text {d}x}\left| _{x=\bar{x}} \right. \dot{\hat{\bar{x}}}-\frac{\text {d}{{g}_{2}}}{\text {d}x}\left| _{x=\bar{x}} \right. \dot{\bar{x}} \\= & {} \left[ \frac{\text {d}{{g}_{2}}}{\text {d}x}\left| _{x=\hat{\bar{x}}} \right. -\frac{\text {d}{{g}_{2}}}{\text {d}x}\left| _{x=\bar{x}} \right. \right] \dot{\hat{\bar{x}}}+\frac{\text {d}{{g}_{2}}}{\text {d}x}\left| _{x=\bar{x}} \right. \left( \dot{\hat{\bar{x}}}-\dot{\bar{x}} \right) , \end{aligned}$$

and consequently

$$\begin{aligned} \left\| {{{\dot{g}}}_{2}}\left( \hat{w},w \right) \right\| \le {{L}_{\frac{\text {d}{{g}_{2}}}{\text {d}x}}}\left\| {{e}_{1}} \right\| \left\| {\dot{\hat{\bar{x}}}} \right\| +{{L}_{{{g}_{2}}}}\left\| {{{\dot{e}}}_{1}} \right\| . \end{aligned}$$
(13)

where \({{L}_{\frac{\text {d}{{g}_{2}}}{\text {d}x}}}\) and \({{L}_{{{g}_{2}}}}\) are the Lipschitz constant of the vector functions \(\frac{\text {d}{{g}_{2}}}{\text {d}x}\) and \(g_{2}\). From (10), it follows that

$$\begin{aligned} \begin{aligned} \left\| {{{\dot{e}}}_{1}} \right\|&=\left\| \left( {{A}_{11}}+L{{A}_{21}} \right) {{e}_{1}}+\left[ {{I}_{n-p}}\text { }L \right] TE\left[ g\left( {T}^{-1}{{S}^{-1}}\hat{w} \right) -g\left( {T}^{-1}{{S}^{-1}}w \right) \right] \right\| \\&\le \left\| {{A}_{11}}+L{{A}_{21}} \right\| \left\| {{e}_{1}} \right\| +{{L}_{g}}\left\| \left[ {{I}_{n-p}}\text { }L \right] TE \right\| \left\| {{T}^{-1}} \right\| \left\| {{e}_{1}} \right\| \\&=\left( \left\| {{A}_{11}}+L{{A}_{21}} \right\| +{{L}_{g}}\left\| \left[ {{I}_{n-p}}\text { }L \right] TE \right\| \left\| {{T}^{-1}} \right\| \right) \left\| {{e}_{1}} \right\| . \end{aligned} \end{aligned}$$
(14)

To facilitate the subsequent analysis, let \(\omega ={{A}_{21}}{{e}_{1}}-{{D}_{2}}f+{{g}_{2}}\left( {{S}^{-1}}\hat{w} \right) -{{g}_{2}}\left( {{S}^{-1}}w \right) \). From (13)–(14), it implies

$$\begin{aligned} \left\| {\dot{\omega }} \right\|\le & {} \left\| {{A}_{21}} \right\| \left\| {{{\dot{e}}}_{1}} \right\| +\left\| {{D}_{2}} \right\| \left\| {\dot{f}} \right\| +\left\| {{{\dot{g}}}_{2}}\left( \hat{w},w \right) \right\| \\\le & {} \left\| {{A}_{21}} \right\| \left( \left\| {{A}_{11}}+L{{A}_{21}} \right\| +{{L}_{g}}\left\| \left[ {{I}_{n-p}}\text { }L \right] TE \right\| \left\| {{T}^{-1}} \right\| \right) \left\| {{e}_{1}} \right\| +\left\| {{D}_{2}} \right\| \delta \\&\quad +\,{{L}_{\frac{\text {d}{{g}_{2}}}{\text {d}x}}}\left\| {{e}_{1}} \right\| \left\| {\dot{\hat{\bar{x}}}} \right\| +{{L}_{{{g}_{2}}}}\left( \left\| {{A}_{11}}+L{{A}_{21}} \right\| +{{L}_{g}}\left\| \left[ {{I}_{n-p}}\text { }L \right] TE \right\| \left\| {{T}^{-1}} \right\| \right) \left\| {{e}_{1}} \right\| \\\le & {} \left[ \left( \left\| {{A}_{21}} \right\| +{{L}_{{{g}_{2}}}} \right) \left( \left\| {{A}_{11}}+L{{A}_{21}} \right\| +{{L}_{g}}\left\| \left[ {{I}_{n-p}}\text { }L \right] TE \right\| \left\| {{T}^{-1}} \right\| \right) \!+\!{{L}_{\frac{\text {d}{{g}_{2}}}{\text {d}x}}}\left\| {\dot{\hat{\bar{x}}}} \right\| \right] \\&\cdot N\left\| {{e}_{1}}\left( 0 \right) \right\| \exp \left( -{\alpha t}/{2}\; \right) \!+\!\left\| {{D}_{2}} \right\| \delta . \end{aligned}$$

Choose

$$\begin{aligned} \gamma= & {} \left[ \left( \left\| {{A}_{21}} \right\| +{{L}_{{{g}_{2}}}} \right) \left( \left\| {{A}_{11}}+L{{A}_{21}} \right\| +{{L}_{g}}\left\| \left[ {{I}_{n-p}}\text { }L \right] TE \right\| \left\| {{T}^{-1}} \right\| \right) +{{L}_{\frac{\text {d}{{g}_{2}}}{\text {d}x}}}\left\| {\dot{\hat{\bar{x}}}} \right\| \right] \\&\cdot N\left\| {{e}_{1}}\left( 0 \right) \right\| \exp \left( -{\alpha t}/{2}\; \right) +\left\| {{D}_{2}} \right\| \delta , \end{aligned}$$

then

$$\begin{aligned} \left\| {\dot{\omega }} \right\| \le \gamma . \end{aligned}$$
(15)

Theorem 2

Under Assumptions 1–2, the observer error dynamic system (11) is finite-time stable if the parameters \({k}_{1}\) and \({k}_{2}\) satisfy the condition

$$\begin{aligned} {{k}_{1}}>0,\text { }{{k}_{2}}>\frac{2{{\gamma }^{2}}}{k_{1}^{2}}+\gamma . \end{aligned}$$
(16)

Proof

Denote

$$\begin{aligned} \varphi =\omega -\int _{0}^{t}{{{k}_{2}}\text {sgn} \left( {{e}_{2}} \right) \text {d}\tau }, \end{aligned}$$
(17)

then the observer error dynamic system (11) turns into the following form

$$\begin{aligned} {{\dot{e}}_{2}}= & {} -{{k}_{1}}{\left| {{e}_{2}} \right| }^{1/2}\text {sgn} \left( {{e}_{2}} \right) +\varphi , \end{aligned}$$
(18)
$$\begin{aligned} \dot{\varphi }= & {} -{{k}_{2}}\text {sgn} \left( {{e}_{2}} \right) +\dot{\omega }. \end{aligned}$$
(19)

Define \(z={{\left[ \sigma ,\text { }\varphi \right] }^{\text {T}}}\), where \(\sigma ={\left| {{e}_{2}} \right| }^{1/2}\text {sgn} \left( {{e}_{2}} \right) \), then component-wise of \(z\) is \({{z}_{i}}={{\left[ {\left| {{e}_{2i}} \right| }^{1/2}\text {sgn} \left( {{e}_{2i}} \right) ,\text { }{{\varphi }_{i}} \right] }^{\text {T}}}\text {, }i=1,2,\ldots ,p\); \(\omega \) can be written in component-wise as \(\omega ={{\left[ {{\omega }_{1}},{{\omega }_{2}},\ldots ,{{\omega }_{p}} \right] }^{\text {T}}}\). \(\square \)

Once the finite-time stability of the error dynamic system (18)–(19) is proved, then the finite-time stability of the observer error dynamic system (11) will be got.

Consider the Lyapunov function

$$\begin{aligned} {{V}_{i}}={{z}_{i}}^{\text {T}}P{{z}_{i}},\text { }i=1,2,\ldots ,p, \end{aligned}$$

where \(P=\frac{1}{2}\left[ \begin{matrix} 4{{k}_{2}}+k_{1}^{2} &{} \text {-}{{k}_{1}} \\ \text {-}{{k}_{1}} &{} 2 \\ \end{matrix} \right] \), as \({{k}_{1}},\text { }{{k}_{2}}>0\), then \(P>0\).

The derivative of \({{V}_{i}}\) is

$$\begin{aligned} {\dot{V}}_{i}=-\frac{1}{{\left| {{e}_{2i}}\right| }^{1/2}}{{z}_{i}}^{\text {T}}Q{{z}_{i}}+{{\dot{\omega }}_{i}}{{a}^{\text {T}}}{{z}_{i}}, \end{aligned}$$
(20)

where \(Q=\frac{{{k}_{1}}}{2}\left[ \begin{matrix} 2{{k}_{2}}+k_{1}^{2} &{} \text {-}{{k}_{1}} \\ \text {-}{{k}_{1}} &{} 1 \\ \end{matrix} \right] ,\text { }{{a}^{\text {T}}}=\left[ \begin{matrix} -{{k}_{1}} &{} 2 \\ \end{matrix} \right] \). Computation shows that

$$\begin{aligned} {{\dot{\omega }}_{i}}{{a}^{\text {T}}}{{z}_{i}}=\frac{1}{{\left| {{e}_{2i}} \right| }^{1/2}}\left( {{z}_{i}}^{\text {T}}{{M}_{i}^{\text {T}}}P{{z}_{i}}+{{z}_{i}}^{\text {T}}PM_{i}{{z}_{i}} \right) . \end{aligned}$$
(21)

where \(M_{i}=\left[ \begin{matrix} 0 &{} 0 \\ {{{\dot{\omega }}}_{i}}\text {sgn} ({{e}_{2i}}) &{} 0 \\ \end{matrix} \right] \).

By (20)–(21), it yields that

$$\begin{aligned} {{{\dot{V}}}_{i}}= & {} -\frac{1}{{\left| {{e}_{2i}} \right| }^{1/2}}{{z}_{i}}^{\text {T}}Q{{z}_{i}}+{{{\dot{\omega }}}_{i}}{{a}^{\text {T}}}{{z}_{i}} \\= & {} -\frac{1}{{\left| {{e}_{2i}} \right| }^{1/2}}{{z}_{i}}^{\text {T}}\left( Q-{{M}_{i}^{\text {T}}}P-PM_{i} \right) {{z}_{i}} \\= & {} -\frac{1}{{\left| {{e}_{2i}} \right| }^{1/2}}{{z}_{i}}^{\text {T}}\tilde{Q}_{i}{{z}_{i}}, \end{aligned}$$

where

$$\begin{aligned} \tilde{Q}_{i}=\frac{{{k}_{1}}}{2}\left[ \begin{array}{cc} 2{{k}_{2}}+k_{1}^{2}+2{{{\dot{\omega }}}_{i}}\text {sgn} ({{e}_{2i}}) &{} \text {-}{{k}_{1}}-\frac{2{{{\dot{\omega }}}_{i}}\text {sgn} ({{e}_{2i}})}{{{k}_{1}}} \\ \text {-}{{k}_{1}}-\frac{2{{{\dot{\omega }}}_{i}}\text {sgn} ({{e}_{2i}})}{{{k}_{1}}} &{} 1 \\ \end{array} \right] . \end{aligned}$$

Let

$$\begin{aligned} {{\tilde{Q}}_{0i}}=\left[ \begin{array}{c@{\quad }c} 2{{k}_{2}}+k_{1}^{2}+2{{{\dot{\omega }}}_{i}}\text {sgn} ({{e}_{2i}}) &{} \text {-}{{k}_{1}}-\frac{2{{{\dot{\omega }}}_{i}}\text {sgn} ({{e}_{2i}})}{{{k}_{1}}} \\ \text {-}{{k}_{1}}-\frac{2{{{\dot{\omega }}}_{i}}\text {sgn} ({{e}_{2i}})}{{{k}_{1}}} &{} 1 \\ \end{array} \right] . \end{aligned}$$

As \({{k}_{1}}>0\), if \({{\tilde{Q}}_{0i}}>0\), then \(\tilde{Q}_{i}>0\). The necessary and sufficient condition for \({{\tilde{Q}}_{0i}}>0\) is

$$\begin{aligned} 2{{k}_{2}}+k_{1}^{2}+2{{\dot{\omega }}_{i}}\text {sgn} ({{e}_{2i}})>0\quad \text {and }\quad \text {det }{{\tilde{Q}}_{0i}}>0. \end{aligned}$$
(22)

By simplifying, then (22) is equivalent to

$$\begin{aligned} {{k}_{2}}>-\frac{k_{1}^{2}}{2}-{{\dot{\omega }}_{i}}\text {sgn} ({{e}_{2i}})\quad \text { and}\quad {{k}_{2}}>\frac{2{{{\dot{\omega }}}_{i}}^{2}}{k_{1}^{2}}+{{\dot{\omega }}_{i}}\text {sgn} ({{e}_{2i}}). \end{aligned}$$
(23)

From (15)–(16), we know (23) is satisfied, then \({{\tilde{Q}}_{0i}}>0\), so \(\tilde{Q}_{i}>0\).

On the other hand, it is easy to obtain

$$\begin{aligned} {{\lambda }_{\min }}\left( P \right) {{\left\| {{z}_{i}} \right\| }^{2}}\le {{V}_{i}}={{z}_{i}}^{\text {T}}P{{z}_{i}}\le {{\lambda }_{\max }}\left( P \right) {{\left\| {{z}_{i}} \right\| }^{2}}. \end{aligned}$$
(24)

Thus,

$$\begin{aligned} {\left| {{e}_{2i}} \right| }^{1/2}\le \left\| {{z}_{i}} \right\| \le \frac{{{V}_{i}}^{1/2}}{{{\left[ {{\lambda }_{\min }}\left( P \right) \right] }^{1/2}}}, \end{aligned}$$
(25)

where \({{\left\| {{z}_{i}} \right\| }^{2}}={{\left| {{\sigma }_{i}} \right| }^{2}}+{{\left| {{\varphi }_{i}} \right| }^{2}}\).

By (24)–(25), one can get

$$\begin{aligned} \begin{aligned} {{{\dot{V}}}_{i}}&=-\frac{1}{{\left| {{e}_{2i}} \right| }^{1/2}}{{z}_{i}}^{\text {T}}\tilde{Q}_{i}{{z}_{i}} \\&\le -\frac{1}{{\left| {{e}_{2i}} \right| }^{1/2}}{{\lambda }_{\min }}\left( {\tilde{Q}_{i}} \right) {{\left\| {{z}_{i}} \right\| }^{2}}\\&\le -\mu _{i} {{V}_{i}}^{1/2}, \end{aligned} \end{aligned}$$
(26)

where \(\mu _{i}=\frac{{\left[ {{\lambda }_{\min }}\left( P \right) \right] }^{1/2}{\lambda }_{\min }\left( {\tilde{Q}_{i}} \right) }{{{{\lambda }_{\max }}\left( P \right) }}\).

By (26) and Lemma 1, \(e_{2}\) and \(\varphi \) converge to zero in finite time, so the observer error dynamic system (11) is finite-time stable. This completes the proof.

Remark 1

By the Lyapunov function, the parameters \({{k}_{1}}\) and \({{k}_{2}}\) are derived to guarantee the finite-time stability of the observer error dynamic system (11). The cumbersome proving process for the stability of the super-twisting algorithm by the geometric method [18] is also avoidable.

4 Fault Estimation

Based on the above section, the actuator fault estimation will be achieved by the second-order sliding mode observer in this section. The conclusion is stated as follows.

Theorem 3

If system (1) satisfies assumptions 1–2, the parameters \({k}_{1}\) and \({k}_{2}\) satisfy (16), then the actuator fault of system (1) can be estimated as

$$\begin{aligned} \hat{f}=-D_{2}^{+}\int _{0}^{t}{{{k}_{2}}\text {sgn} \left( {{e}_{2}} \right) \text {d}\tau }. \end{aligned}$$
(27)

Proof

From Theorem 2, \(\varphi \) converges to zero in finite time. According to (17), it follows that

$$\begin{aligned} \omega -\int _{0}^{t}{{{k}_{2}}\text {sgn} \left( {{e}_{2}} \right) \text {d}\tau }\rightarrow 0. \end{aligned}$$

Substituting \(\omega ={{A}_{21}}{{e}_{1}}-{{D}_{2}}f+{{g}_{2}}\left( {{S}^{-1}}\hat{w} \right) -{{g}_{2}}\left( {{S}^{-1}}w \right) \) yields

$$\begin{aligned} {{A}_{21}}{{e}_{1}}-{{D}_{2}}f+{{g}_{2}}\left( {{S}^{-1}}\hat{w} \right) -{{g}_{2}}\left( {{S}^{-1}}w \right) -\int _{0}^{t}{{{k}_{2}}\text {sgn} \left( {{e}_{2}} \right) \text {d}\tau }\rightarrow 0. \end{aligned}$$
(28)

\(\square \)

As the observer error dynamic system (10) is asymptotically stable from Theorem 1, then \({{e}_{1}}\) converges to zero, thus \({{g}_{2}}\left( {{S}^{-1}}\hat{w} \right) -{{g}_{2}}\left( {{S}^{-1}}w \right) \longrightarrow 0\), so the estimation expression of actuator fault \(f\) can be inferred from (28) as \(\hat{f}=-D_{2}^{+}\int _{0}^{t}{{{k}_{2}}\text {sgn} \left( {{e}_{2}} \right) \text {d}\tau }\). Hence, the conclusion follows.

Remark 2

From (27), only the deviation between the output of the second-order sliding mode observer (8) and the output of the system (1) is needed to estimate the actuator fault \(f\) of system (1), so the fault estimation can be implemented online.

Remark 3

As the second-order sliding term \(-{{k}_{2}}\int _{0}^{t}{\text {sgn} \left( {{e}_{2}} \right) \text {d}\tau }\) is continuous, the actuator fault estimation expression (27) can avoid chattering caused by traditional sliding mode observer [9, 27].

5 Simulation Results

Consider the single link flexible joint robot arm described by [16]

$$\begin{aligned} \left\{ \begin{aligned} {{{\dot{\theta }}}_{m}}&={{\omega }_{m}}, \\ {{{\dot{\omega }}}_{m}}&=\frac{k}{{{J}_{m}}}\left( {{\theta }_{1}}-{{\theta }_{m}} \right) -\frac{b}{{{J}_{m}}}{{\omega }_{m}}+\frac{{{K}_{\tau }}}{{{J}_{m}}}u, \\ {{{\dot{\theta }}}_{1}}&={{\omega }_{1}}, \\ {{{\dot{\omega }}}_{1}}&=\frac{k}{{{J}_{1}}}\left( {{\theta }_{1}}-{{\theta }_{m}} \right) -\frac{mgh}{{{J}_{1}}}\sin \left( {{\theta }_{1}} \right) , \\ \end{aligned}\right. \end{aligned}$$
(29)

where \({{\theta }_{m}}\) and \({{\omega }_{m}}\) are the angular position and velocity of the motor; \({{\theta }_{1}}\) and \({{\omega }_{1}}\) are the angular position and velocity of the link. \({{J}_{m}}\) and \({{J}_{1}}\) are inertia of the motor and the link, respectively, \(k\) is the elastic constant, \(m\) is the link mass, the length of the link is given by 2\(h\), \(b\) is the viscous friction coefficient, \({{K}_{\tau }}\) is the amplifier gain, and \(g\) is the acceleration due to gravity. It is assumed that the motor position, motor velocity, and the sum of link velocity and link position are measured.

Let \({{x}^{\text {T}}}=\left( {{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}} \right) =\left( {{\theta }_{m}},{{\omega }_{m}},{{\theta }_{1}},{{\omega }_{1}} \right) \), then the robot system (29) is in the form of (1). Its system matrices are stated as follows [16] \(A=\left[ \begin{matrix} 0 &{}\quad \! 1 &{}\quad \! 0 &{}\quad \! 0 \\ -48.6 &{}\quad \! -1.25 &{}\quad \! 48.6 &{}\quad \! 0 \\ 0 &{}\quad \! 0 &{}\quad \! 0 &{}\quad \! 10 \\ 1.95 &{}\quad \! 0 &{}\quad \! -1.95 &{}\quad \! 0 \\ \end{matrix} \right] \), \(B=\left[ \begin{matrix} 0 \\ 21.6 \\ 0 \\ 0 \\ \end{matrix} \right] \), \(C=\left[ \begin{matrix} 1 &{}\quad \! 0 &{}\quad \! 0 &{}\quad \! 0 \\ 0 &{}\quad \! 1 &{}\quad \! 0 &{}\quad \! 0 \\ 0 &{}\quad \! 0 &{}\quad \! 1 &{}\quad \! 1 \\ \end{matrix} \right] \), \(E={{I}_{4}}\).

Taking into account the actuator fault occurs in the control input channel, then \(D=B\), and the Lipschitz nonlinear item

$$\begin{aligned} g\left( x \right) =\left[ \begin{matrix} 0 \\ 0 \\ 0 \\ -0.333\sin {{x}_{3}} \\ \end{matrix} \right] . \end{aligned}$$

Introducing the coordinate transformation

$$\begin{aligned} T=\left[ \begin{matrix} 0 &{}\quad \! 0 &{}\quad \! 0.7071 &{}\quad \! -0.7071 \\ 0 &{}\quad \! 0 &{}\quad \! 1 &{}\quad \! 1 \\ 1 &{}\quad \! 0 &{}\quad \! 0 &{}\quad \! 0 \\ 0 &{}\quad \! 1 &{}\quad \! 0 &{}\quad \! 0 \\ \end{matrix} \right] , \end{aligned}$$

then in the new coordinate, system matrices become

Nonlinear term

$$\begin{aligned} g\left( {{T}^{-1}}\bar{x} \right) =\left[ \begin{array}{c} {g}_{1} \\ \hline {g}_{2} \end{array}\right] =\left[ \begin{array}{c} 0.2355\sin \left( 0.7071{{{\bar{x}}}_{1}}+0.5{{{\bar{x}}}_{2}} \right) \\ \hline -0.333\sin \left( 0.7071{{{\bar{x}}}_{1}}+0.5{{{\bar{x}}}_{2}} \right) \\ 0 \\ 0 \end{array}\right] . \end{aligned}$$

Through the coordinate transformation \(T\), the original system (1) has become the form of (5) and (6), so the coordinate transformation \(S={{I}_{4}}\).

Take \(\alpha =1.05\), the Lipschitz constant \({{L}_{g}}=0.333\), \(\delta =0.024\pi \), the matrix \(L=\left[ \begin{matrix} 0 &{} 0 &{} 0 \\ \end{matrix} \right] \). By solving matrix inequality (12), \(\varepsilon =1,\text { }R=1\) can be obtained.

It can be easily shown that \(\text {rank}\left( CD \right) =\text {rank}\left( D \right) =1\), and the triple \(\left( A,D,C \right) \) does not possess any invariant zeros, then Assumptions 1–2 are satisfied. The initial states of system (1) are \(x\left( 0 \right) =\left[ \begin{matrix} 0.25 &{} -0.08 &{} 0.23 &{} -0.15 \\ \end{matrix} \right] ^{\text {T}}\), by the coordinate transformation \(T\), then \(\bar{x}\left( 0 \right) =\left[ \begin{matrix} 0.2687 &{} 0.08 &{} 0.25 &{} -0.08 \\ \end{matrix} \right] ^{\text {T}}\), and the initial conditions for observer are set as \(\hat{\bar{x}}\left( 0 \right) =\left[ \begin{matrix} 0 &{} 0 &{} 0 &{} 0 \\ \end{matrix} \right] ^{\text {T}}\). Simulation step is set as 0.001s.

Consider the actuator occurring the following incipient fault

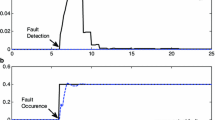
$$\begin{aligned} f\left( t \right) =\left\{ \begin{array}{l@{\quad }l} 0,&{}0\le t<1.5; \\ 0.012\sin 2\pi t\cos \pi t,&{} 1.5\le t\le 8. \\ \end{array} \right. \end{aligned}$$

Figures 1, 2, 3, and 4 show the actual states (dash line) and their estimates (solid line). From Figs. 1, 2, 3 and 4, the designed observer can trace the states very well (in order to make the estimation errors clear, the local amplification of Figs. 2 and 3 near the initial time is shown). The simulation in Fig. 5a shows that the proposed second-order sliding mode observer based on the super-twisting algorithm (SOSMOSTA) can achieve fault estimation rapidly and stably, whereas in Fig. 5b, it shows that traditional sliding mode observer (TSMO) [9, 27] cannot reconstruct the fault signal very well in Fig. 5b, which needs the high-frequency switch compared with the proposed method in the paper.

Fig. 1
figure 1

The system state \({{\bar{x}}_{1}}\) and its estimation \({{\hat{\bar{x}}}_{1}}\)

Full size image
Fig. 2
figure 2

The system state \({{\bar{x}}_{2}}\) and its estimation \({{\hat{\bar{x}}}_{2}}\)

Full size image
Fig. 3
figure 3

The system state \({{\bar{x}}_{3}}\) and its estimation \({{\hat{\bar{x}}}_{3}}\)

Full size image
Fig. 4
figure 4

The system state \({{\bar{x}}_{4}}\) and its estimation \({{\hat{\bar{x}}}_{4}}\)

Full size image
Fig. 5
figure 5

a Fault estimation based on SOSMOSTA. b Fault estimation based on TSMO

Full size image

6 Conclusions

In this paper, the actuator fault of a class of Lipschitz nonlinear systems is estimated by the proposed second-order sliding mode observer based on the super-twisting algorithm, which avoids chattering, and can estimate the fault stably. The stability of the observer error dynamic system is proved by the Lyapunov function. Fault estimation can be calculated online by the deviation between the output of the second-order sliding mode observer and the output of the system. Simulation of a robotic arm system shows the effectiveness of the proposed approach. Extension of the proposed method to robust fault estimation for uncertain nonlinear systems is an interesting problem for further study.