1 Introduction

In many modeling problems of physical processes, a 2D representation is needed such as energy exchanging process and electricity transmission [15]. 2D systems have attracted considerable research attention in control theory and practice over the past few decades due to their wide applications such as multi-dimensional digital filtering, linear image processing, signal processing, and process control [9, 15, 22]. 2D systems can be represented by different models such as the Roesser model, Fornasini–Marchesini model and Attasi model. Some important problems such as realization, reachability, stability, stabilization and minimum energy control have been extensively investigated [8, 16].

On the other hand, a considerable interest has been devoted to the research of switched systems during the recent decades. A switched system comprises a family of subsystems described by continuous or discrete-time dynamics, and a switching law that specifies the active subsystem at each instant of time. Apart from the switching strategy to improve control performance [7, 26], switched systems also arise in many engineering applications, for example, in motor engine control, constrained robotics and networked control systems [1, 4, 36]. Many techniques are effective tools dealing with switched systems, such as common quadratic Lyapunov function method, multiple Lyapunov function method, and average dwell time approach [6, 20, 21, 24, 30].

It is well known that the switching phenomenon may also occur in practical 2D systems, for example, the thermal processes in chemical reactors, heat exchangers and pipe furnaces with multiple modes, can be expressed by a 2D switched system. So 2D switched systems have also attracted considerable research attention. There are a few reports on 2D discrete switched systems, Benzaouia et al. firstly considered 2D switched systems with arbitrary switching sequences [2], where the process of switching was considered as a Markovian jumping one. Furthermore, they investigated the stabilizability problem of discrete 2D switched systems in [3]. Recently, the exponential stability and stabilization of the discrete 2D switched system in Roesser model was firstly investigated via the average dwell time approach in [29]. H 2 control problem for 2D switched systems in Roesser model was addressed in [11].

However, perturbations and uncertainties widely exist in the practical systems. In some cases, the perturbations can be merged into the disturbance, which can be supposed to be bounded in the appropriate norms. A main advantage of H ∞ control is that its performance specification takes into account the worst case performance of the system in terms of energy gain. This is more appropriate for system robustness analysis and robust control under modeling uncertainties and disturbances than other performance specifications. Recently, the problems of robust H ∞ control and filtering for 2D systems have been studied by many researchers [13, 14, 17, 19, 27, 32–34]. The same problems of switched systems have also been studied in [18, 25, 28, 35]. H ∞ control problem for 2D switched systems in Roesser model have been investigated in [10]. However, to the best of our knowledge, the dynamic output feedback H ∞ control problem of 2D switched systems in FM LSS model has not yet been fully investigated, which motivates this present study.

In this paper, we are interested in H ∞ control problem of discrete 2D switched systems described by the FM LSS model. The main theoretical contributions are twofold: (1) Sufficient conditions are proposed to guarantee the exponential stability with a prescribed weighted H ∞ disturbance attenuation level for the 2D switched system by using the average dwell time approach. (2) The corresponding output feedback controller is designed to achieve the prescribed weighted H ∞ disturbance attenuation level γ. It should be noted that these conditions are presented in the form of a set of LMIs (linear matrix inequalities).

This paper is organized as follows. In Sect. 2, the problem formulation and some necessary lemmas are given. In Sect. 3, the weighted H ∞ performance analysis and control problems are addressed by the average dwell time approach. Two examples are provided to illustrate the effectiveness of the proposed approach in Sect. 4. Concluding remarks are given in Sect. 5.

Notations

Throughout this paper, the superscript “T” denotes the transpose, and the notation X≥Y (X>Y) means that matrix X−Y is positive semi-definite (positive definite, respectively). ∥ ⋅ ∥ denotes the Euclidean norm. I represents the identity matrix. \(\operatorname {diag}\{ a_{i} \}\) denotes a diagonal matrix with the diagonal elements a i , i=1,2,…,n. X −1 denotes the inverse of X. The asterisk ∗ in a matrix is used to denote the term that is induced by symmetry. R n denotes the n dimensional vector. For a matrix P, λ min(P) means the smallest eigenvalue of P and λ max(P) means the largest eigenvalue of P. The set of all nonnegative integers is represented by Z +. The l 2 norm of a 2D signal w(i,j) is given by

$$\Vert w \Vert _{2} = \sqrt{\sum_{i = 0}^{\infty } \sum_{j =0}^{\infty } \bigl\Vert w ( i,j ) \bigr\Vert ^{2}} $$

where w(i,j) belongs to l 2{[0,∞),[0,∞)}.

2 Problem Formulation and Preliminaries

Consider the following FM LSS model for a 2D switched system:

$$\begin{aligned} x(i + 1,j + 1) =& A_{1}^{\sigma (i + j + 1)}x(i,j + 1) + A_{2}^{\sigma (i + j + 1)}x(i+ 1,j) \\ &{}+ B_{1}^{\sigma (i + j+ 1)}w(i,j + 1) + B_{2}^{\sigma (i + j + 1)}w(i +1,j), \\ z(i,j) =& H^{\sigma (i + j)}x(i,j) + L^{\sigma (i + j)}w(i,j), \end{aligned}$$
(1)

where x(i,j)∈R n is the state vector, \(w( i,j ) \in R^{n_{w}}\) is the noise input which belongs to l 2{[0,∞),[0,∞)}, z(i,j)∈R d is the controlled output. i and j are integers in Z +. \(\sigma( i + j ):Z_{ + } \to\underline{N} = \{ 1,2,\ldots,N \}\) is the switching signal. N is the number of subsystems. σ(i+j)=k, \(k \in\underline{N}\), means that the kth subsystem is active at the instant i+j. \(A_{1}^{k}\), \(A_{2}^{k}\), \(B_{1}^{k}\), \(B_{2}^{k}\), H k, L k are constant matrices with appropriate dimensions.

In the paper, the switch can be assumed to occur only at each sampling points of i or j. The switching sequence can be described as

$$ \bigl( m_{0},\sigma( m_{0} ) \bigr), \bigl( m_{1},\sigma( m_{1} ) \bigr),\ldots, \bigl( m_{\pi},\sigma( m_{\pi } ) \bigr),\ldots $$
(2)

with m π =i π +j π , π=0,1,2,…,m π denotes the πth switching instant.

Remark 1

As stated in literature [3, 29], the 2D system causality imposes an increment depending only on i+j, thus the value of the switching signal can be assumed to be only dependent upon i+j and the switching sequence can be expressed as (2).

Remark 2

System (1) is of significance because it can be used to describe the relation between voltage and current in a long transmission line with multiple modes, some multi-mode processes of gas absorption, water stream heating, air drying, and some thermal processes with multiple subsystems, for example in chemical reactors, heat exchangers and pipe furnaces.

Remark 3

If there is only one subsystem in system (1), it will degenerate to the following 2D system in FM LSS model [31]:

$$\begin{aligned} x(i + 1,j + 1) =& A_{1}x(i,j + 1) + A_{2}x(i + 1,j)\\ &{} + B_{1}w(i,j + 1) + B_{2}w(i + 1,j), \\ z ( i,j ) =& Hx ( i,j ) + Lw ( i,j ). \end{aligned}$$

Therefore, the addressed system (1) can be viewed as an extension of 2D FM LSS systems to switched systems. In other words, system (1) not only represents the well-known 2D FM LSS model [31], but also describes the 2D FM LSS system with certain switching property, which demonstrates that system (1) is rational.

For 2D discrete switched system (1), we consider a finite set of initial conditions, that is, there exist positive integers z 1 and z 2 such that

$$ \left \{ \begin{array}{l} x ( 0,j ) = v_{j}, \quad \forall 0 \le j \le z_{2}, \\ x ( i,0 ) = w_{i}, \quad \forall 0 \le i \le z_{1}, \\ v_{0} = w_{0}, \quad i = j = 0 , \\ x ( 0,j ) = 0, \quad \forall j > z_{2}, \\ x ( i,0 ) = 0, \quad \forall i > z_{1} \\ \end{array} \right . $$
(3)

where z 1<∞ and z 2<∞ are positive integers, v j and w i are given vectors.

Denote ∥x(i,j)∥ r =sup{∥x(i,j)∥:i+j=r,i≤z 1,j≤z 2}. We give the following definitions.

Definition 1

System (1) is said to be exponentially stable under σ(i+j) if for a given z≥0, there exist positive constants c and ξ, such that

$$ \sum_{i + j = D} \bigl\Vert x ( i,j ) \bigr\Vert ^{2} \le\xi e^{ -c ( D - z )}\sum_{i + j = z} \bigl\Vert x ( i,j ) \bigr\Vert _{r}^{2} $$
(4)

holds for all D≥z.

Remark 4

From Definition 1, it is easy to see that when z is given, \(\sum_{i + j = z} \| x( i,j ) \|_{r}^{2}\) will be bounded, and ∑ i+j=D ∥x(i,j)∥2 will tend to be zero exponentially as D goes to infinity, which also means that ∥x(i,j)∥ will tend to be zero exponentially.

Definition 2

For a given scalar γ>0, system (1) is said to have a weighted disturbance attenuation level γ under switching signal σ(i+j) if it satisfies the following conditions:

  1. (1)

    when w(i,j)=0, system (1) is asymptotically stable or exponentially stable;

  2. (2)

    under the zero-boundary condition, we have

    $$ \sum_{i = 0}^{\infty } \sum_{j = 0}^{\infty } \bigl( \lambda^{i + j}\| \overline{z} \|_{2}^{2} \bigr) < \gamma^{2}\sum_{i = 0}^{\infty } \sum_{j = 0}^{\infty } \| \overline{w} \|_{2}^{2}, \quad \forall 0 \ne w \in l_{2}\bigl\{ [ 0,\infty),[ 0,\infty) \bigr\} $$
    (5)

    where 0<γ<1 and the l 2-norm of 2D discrete signal z(i,j) and w(i,j) are defined as

    $$ \begin{aligned} \|\overline{z}\|^2_2 =& \bigl\| z( i+1,j )\bigr\| ^2_2 + \bigl\| z( i,j+1 )\bigr\| ^2_2, \\ \|\overline{w}\|^2_2 =& \bigl\| w( i+1,j )\bigr\| ^2_2 + \bigl\| w( i,j+1 )\bigr\| ^2_2. \end{aligned} $$
    (6)

Definition 3

[29]

For any i+j=D≥z=i z +j z , let N σ (z,D) denote the switching number of σ(⋅) on an interval [z,D). If

$$ N_{\sigma } ( z,D ) \le N_{0} + \frac{D - z}{\tau _{a}} $$
(7)

holds for given N 0≥0 and τ a ≥0, then the constant τ a is called the average dwell time and N 0 is the chatter bound.

Lemma 1

[5]

For a given matrix , where S 11 and S 22 are square matrices, the following conditions are equivalent.

  1. (i)

    S<0;

  2. (ii)

    S 11<0, \(S_{22} - S_{12}^{T}S_{11}^{ - 1}S_{12} < 0\);

  3. (iii)

    S 22<0, \(S_{11} - S_{12}S_{22}^{ - 1}S_{12}^{T} < 0\).

Lemma 2

Consider 2D discrete switched system (1) with w(i,j)=0, for a given positive constant λ<1, if there exist a set of positive-definite symmetric matrices G k∈R n×n, \(k \in\underline{N}\), such that

$$ W^{k} = \lambda \left [ \begin{array}{c@{\quad }c} \alpha G^{k} & 0 \\ 0 & (1 - \alpha)G^{k} \\ \end{array} \right ] - A^{kT}G^{k}A^{k} > 0, $$
(8)

where

$$A^{k} = \bigl[ A_{1}^{k} \quad A_{2}^{k} \bigr],\quad 0 <\alpha < 1, $$

then, the system is exponentially stable for any switching signal with the average dwell time satisfying

$$ \tau_{a} > \tau_{a}^* = \frac{\ln\mu}{-\!\ln\lambda }, $$
(9)

where μ≥1 satisfies

$$ G^{k} \le\mu G^{l}, \quad \forall k, \ l \in\underline{N}. $$
(10)

Proof

Without loss of generality, we assume that the kth subsystem is active. For the kth subsystem, we consider the following Lyapunov function candidate:

$$ V^{k} ( i,j ) = x^{T} ( i,j )G^{k}x ( i,j ) $$
(11)

where G k is an n×n positive-definite matrix for any \(k\in\underline{N}\), and thus

$$V^{k}( i,j ) > 0\quad \mathrm{for} \ x ( i,j )\ne 0 $$

and

$$V^{k}( i,j ) = 0\quad \mathrm{only} \ \mathrm{when} \ x ( i,j )=0. $$

Then we have

$$\begin{aligned} & V^{k} ( i + 1,j + 1 ) - \lambda \bigl[ \alpha V^{k} ( i,j+ 1 ) + ( 1 - \alpha )V^{k} ( i +1,j ) \bigr] \\ &\quad = - \left [ \begin{array}{c@{\quad }c} x^{T} ( i,j + 1) & x^{T} ( i + 1,j ) \\ \end{array} \right ] \\ &\qquad {}\times \left \{\lambda \left [ \begin{array}{c@{\quad }c} \alpha G^{k} & 0 \\ 0 & ( 1 -\alpha )G^{k} \\ \end{array} \right ] - A^{kT}G^{k}A^{k} \right \} \left [\begin{array}{c} x ( i,j + 1 ) \\ x ( i +1,j ) \\ \end{array} \right ] \\ &\quad = - \left [ \begin{array}{c@{\quad }c} x^{T} ( i,j + 1 ) & x^{T} ( i+ 1,j ) \\ \end{array} \right ]W^{k} \left [ \begin{array}{c} x (i,j + 1 ) \\ x ( i + 1,j ) \\ \end{array} \right ] \end{aligned}$$
(12)

where \(A^{k} = [ A_{1}^{k} \ A_{2}^{k} ]\), 0<λ<1, and 0<α<1.

From (8), we get

$$ V^{k} ( i + 1,j + 1 ) \le\lambda \bigl[ \alpha V^{k} ( i,j + 1 ) + ( 1 - \alpha )V^{k} ( i + 1,j ) \bigr]. $$
(13)

The equality holds only if

$$V^{k} ( i + 1,j + 1 ) = V^{k} ( i + 1,j ) = V^{k} ( i,j + 1 ) = 0. $$

It follows from (13) that

$$ \sum_{i + j = M + 1} V^{k} ( i,j ) \le\lambda\sum_{i + j = M} V^{k} ( i,j ). $$
(14)

Now let υ=N σ (z,D) denote the switching number of σ(⋅) on an interval [z,D), and let m κ−υ+1<m κ−υ+2<⋯<m κ−1<m κ denote the switching points of σ(⋅) over the interval [z,D), thus, for D∈[m κ ,m κ+1), we have from (14)

$$ \sum_{i + j = D} V^{\sigma (m_{\kappa } )} ( i,j ) <\lambda^{D - m_{\kappa }} \sum_{i + j = m_{\kappa }} V^{\sigma (m_{\kappa } )} ( i,j ). $$
(15)

Using (10) and (11), at switching instant m κ =i+j, we have

$$ \sum_{i + j = m_{\kappa }} V^{\sigma (m_{\kappa })} ( i,j ) \le\mu\sum_{i + j = m_{\kappa }} V^{\sigma( m_{\kappa - 1} )} ( i,j ). $$
(16)

In addition, according to Definition 3, it follows that

$$ \upsilon = N_{\sigma} ( z,D ) \le N_{0} +\frac{D - z}{\tau _{a}}. $$
(17)

Therefore, the following inequality can be obtained easily:

$$\begin{aligned} \sum_{i + j = D} V^{\sigma (m_{\kappa })} ( i,j ) <& \lambda^{D - m_{\kappa }}\sum_{i + j = m_{\kappa }} V^{\sigma (m_{\kappa } )} ( i,j ) \le\mu\lambda^{D - m_{\kappa }}\sum_{i + j = m_{\kappa }^{ - }} V^{\sigma (m_{\kappa - 1} )} ( i,j ) \\ < &\mu\lambda^{D - m_{\kappa }}\sum_{i + j = m_{\kappa - 1}} V^{\sigma (m_{\kappa - 1} )} ( i,j ) \lambda^{m_{\kappa } - m_{\kappa - 1}} \\ \le & \cdots \\ < &\mu^{\nu - 1}\lambda^{D - m_{\kappa - v + 1}} \sum_{i + j =m_{\kappa - v + 1}} V^{\sigma (m_{\kappa - v + 1})} ( i,j ) \\ < & \mu^{\nu }\lambda^{D -m_{\kappa - v + 1}} \sum_{i + j = z} V^{\sigma (z )} (i,j ) \lambda^{m_{\kappa - v + 1} - z} \\ \le &\mu^{\nu }\lambda^{D - z}\sum_{i + j = z} V^{\sigma (z )} ( i,j ). \end{aligned}$$
(18)

Inequality (18) can be rewritten as follows:

$$ \sum_{i + j = D} V^{\sigma (m_{\kappa } )} ( i,j ) \le e^{ - ( \frac{-\ln \mu }{\tau _{a}} - \ln \lambda ) ( D - z )}\sum_{i + j = z} V^{\sigma (z)} ( i,j). $$
(19)

In the view of (11), there exist two positive constants a and b (a≤b) such that

$$ \sum_{i + j = D} V^{\sigma (m_{\kappa } )}( i,j ) \ge a\sum _{i + j = D} \bigl\| x( i,j ) \bigr\| ^{2}, \qquad \sum_{i + j = z} V^{\sigma (z )}( i,j ) \le b\sum_{i + j = z} \bigl\| x( i,j ) \bigr\| ^{2} $$
(20)

where \(a = \min _{k \in \underline{N}}\lambda_{\min}(G^{k})\), \(b = \max _{k \in \underline{N}}\lambda_{\max}(G^{k})\).

Combining (19) and (20), it is easy to get

$$ \sum _{i + j = D} \bigl\| x( i,j ) \bigr\| ^{2} \le \frac{b}{a} e^{-(\frac{-\ln\mu}{\tau _a}- \ln \lambda )(D-z)} \sum_{i + j = z} \bigl\| x( i,j ) \bigr\| ^{2}. $$
(21)

By Definition 1, we know that if \(-\frac{\ln\mu}{\tau _{a}}- \ln \lambda >0\), that is \(\tau_{a}>\tau_{a}^{*} = \frac{\ln\mu}{-\ln\lambda }\), the 2D discrete switched system is exponentially stable.

The proof is completed. □

Remark 5

Note that when μ=1 in (9), (10) turns out to be G k=G l, \(\forall k,l \in\underline{N}\). In the case, we have \(\tau_{a} >\tau_{a}^{*} = 0\), which means that the switching signal can be arbitrary.

3 Main Results

3.1 H ∞ Performance Analysis

In this section, we focus on the H ∞ performance analysis of the 2D switched systems. The following theorem presents sufficient conditions which can guarantee that system (1) is exponentially stable and has a prescribed weighted H ∞ disturbance attenuation level γ.

Theorem 1

For given positive scalars γ and 0<α<1, if there exist symmetric and positive-definite matrices G p>0, \(p\in \underline{N}\), such that

$$\begin{aligned} & \left [ \begin{array}{@{}ccccccc@{}} - G^{p} & G^{p}A_{1}^{p} & G^{p}A_{2}^{p} & G^{p}B_{1}^{p} & G^{p}B_{2}^{p} & 0 & 0 \\ * & - \lambda\alpha G^{p} & 0 & 0 & 0 & H^{pT} & 0 \\ * & * & - \lambda(1 \!- \alpha)G^{p} & 0 & 0 & 0 & H^{pT} \\ * & * & * & - \gamma^{2}I & 0 & L^{pT} & 0 \\ * & * & * & * & - \gamma^{2}I & 0 & L^{pT} \\ * & * & * & * & * & - I & 0 \\ * & * & * & * & * & * & - I \\ \end{array} \right ] {<}\, 0, \\ &\quad \forall p\,{\in}\, \underline{N} \end{aligned}$$
(22)

then, 2D switched system (1) is exponentially stable and has a prescribed weighted H ∞ disturbance attenuation level γ for any switching signals with average dwell time satisfying (9), where μ≥1 satisfies (10).

Proof

It is an obvious fact that (22) implies that inequality (8) holds. By Lemma 2, we can find that system (1) is exponentially stable when w(i,j)=0. Now we are in a position to prove that system (1) has a prescribed weighted H ∞ performance γ for any nonzero w(i,j)∈l 2{[0,∞),[0,∞)}.

To establish the weighted H ∞ performance, we choose the same Lyapunov functional candidate as in (11) for system (1). Following the proof line of Lemma 2, we can get

$$V^{p}( i + 1,j + 1 ) \le\lambda\bigl[ \alpha V^{p}( i,j + 1 ) + ( 1 -\alpha)V^{p}( i + 1,j ) \bigr] + \gamma^{2} \overline {w}^{T}\overline {w} -\overline {z}^{T}\overline {z}, $$

with

$$\overline {z} = \bigl[{z}^T( i,j + 1 )\quad {z}^T( i + 1,j )\bigr]^T, \qquad \overline {w} = \bigl[{w}^T( i,j + 1 )\quad {w}^T( i + 1,j )\bigr]^T, $$

if

$$ \varPsi < 0 $$
(23)

where

$$\begin{aligned} &\varPsi =\left [ \begin{array}{c} A_{1}^{pT} \\ A_{2}^{pT} \\ B_{1}^{pT} \\ B_{2}^{pT} \\ \end{array} \right ] G^{p} \left [ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} A_{1}^{p} & A_{2}^{p} & B_{1}^{p} & B_{2}^{p} \\ \end{array} \right ] \\ & \quad \phantom{\varPsi} + \left [ \!\begin{array}{c@{\ }c@{\ }c@{\ }c} H^{pT}\!H^{p} \!- \alpha\lambda G^{p} & 0 & H^{pT}\!L^{p} & 0 \\ * & H^{pT}\!H^{p} \!- ( 1 \!- \alpha)\lambda G^{p} & 0 & H^{pT}\!L^{p} \\ * & * & - \gamma^{2}I + L^{pT}\!L^{p} & 0 \\ * & * & * & - \gamma^{2}I + L^{pT}\!L^{p} \\ \end{array} \!\right ],\\ &\quad \forall p\,{\in}\, \underline{N}. \end{aligned}$$

Using Lemma 1 to (23), we can get the equivalent inequality as follows:

$$\begin{aligned} & \left [ \begin{array}{c@{\ }c@{\ }c@{\ }c@{\ }c} - (G^{p})^{ - 1} & A_{1}^{p} & A_{2}^{p} & B_{1}^{p} & B_{2}^{p} \\ A_{1}^{pT} & H^{pT}H^{p} - \lambda\alpha G^{p} & 0 & H^{pT}L^{p} & 0 \\ A_{2}^{pT} & 0 & H^{pT}H^{p} - \lambda(1 - \alpha)G^{p} & 0 & H^{pT}L^{p} \\ B_{1}^{pT} & L^{pT}H^{p} & 0 & - \gamma^{2}I + L^{pT}L^{p} & 0 \\ B_{2}^{pT} & 0 & L^{pT}H^{p} & 0 & - \gamma^{2}I + L^{pT}L^{p} \\ \end{array} \right ] \\ &\quad < 0. \end{aligned}$$
(24)

Pre- and post-multiplying (24) by \(\operatorname {diag}( G^{p},I,I,I,I )\), we obtain

$$\begin{aligned} & \left [ \begin{array}{c@{\ }c@{\ }c@{\ }c@{\ }c} - G^{p} & G^{p}A_{1}^{p} & G^{p}A_{2}^{p} & G^{p}B_{1}^{p} & G^{p}B_{2}^{p} \\ A_{1}^{pT}G^{p} & H^{pT}H^{p} - \lambda\alpha G^{p} & 0 & H^{pT}L^{p} & 0 \\ A_{2}^{pT}G^{p} & 0 & H^{pT}H^{p} - \lambda(1 - \alpha)G^{p} & 0 & H^{pT}L^{p} \\ B_{1}^{pT}G^{p} & L^{pT}H^{p} & 0 & - \gamma^{2}I + L^{pT}L^{p} & 0 \\ B_{2}^{pT}G^{p} & 0 & L^{pT}H^{p} & 0 & - \gamma^{2}I + L^{pT}L^{p}\\ \end{array} \right ] \\ &\quad < 0. \end{aligned}$$
(25)

Then using Lemma 1, we find that (22) is equivalent to (25).

Thus it can be obtained from (22) that

$$\begin{aligned} &V^{p}( i + 1,j + 1 ) - \lambda\bigl[ \alpha V^{p}( i,j +1 ) + ( 1 - \alpha)V^{p}( i + 1,j ) \bigr] \\ &\quad {} - \gamma^{2}\overline {w}^{T}\overline {w} + \overline {z}^{T}\overline {z} < 0. \end{aligned}$$
(26)

Then we have

$$\begin{aligned} V^{p}( i + 1,j + 1 ) <& \lambda\bigl[ \alpha V^{p}( i,j + 1) + ( 1 - \alpha)V^{p}( i + 1,j ) \bigr] \\ & {}+ \gamma^{2} \overline {w}^{T}\overline {w} - \overline {z}^{T}\overline {z}. \end{aligned}$$
(27)

Let

$$ \varGamma( i + j + 1 ) = \| \overline {z} \|_{2}^{2} - \gamma^{2}\| \overline {w} \|_{2}^{2} = \left \| \begin{array}{c} z( i + 1,j ) \\ z( i,j + 1 )\\ \end{array} \right \|_{2}^{2} - \gamma^{2} \left \| \begin{array}{c} w( i + 1,j ) \\ w( i,j + 1 ) \\ \end{array} \right \|_{2}^{2}. $$
(28)

Summing up both sides of (27) from (D−2) to 0 with respect to j and 0 to (D−2) with respect to i, respectively, and applying the zero-boundary condition, one gets

$$\begin{aligned} &\sum_{i + j = D} V^{\sigma (m_{\kappa })} ( i,j ) \\ & \quad < \lambda\sum_{i + j = D - 1} V^{\sigma( m_{\kappa } )} ( i,j ) - \sum_{i + j = D - 2}\varGamma ( i,j ) \\ & \quad < \lambda^{D - m_{\kappa }}\sum_{i + j = m_{\kappa }} V^{\sigma (m_{\kappa } )} ( i,j ) - \sum_{m = m_{\kappa } - 1}^{D - 2} \sum_{i + j = m} \lambda^{D - 2 - i - j}\varGamma ( i,j ) \\ & \quad \le \mu\lambda^{D - m_{\kappa }}\sum_{i + j = (m_{\kappa } )^{ - }} V^{\sigma (m_{\kappa - 1} )} ( i,j ) - \sum_{m = m_{\kappa } - 1}^{D - 2} \sum_{i+ j = m} \lambda^{D - 2 - i - j}\varGamma ( i,j ) \\ & \quad < \sum_{i +j = m_{\kappa } - 1} \mu\lambda^{D - ( m_{\kappa } - 1)} V^{\sigma (m_{\kappa - 1} )} ( i,j ) -\mu\lambda^{D - m_{\kappa }} \sum_{i + j = m_{\kappa } - 2}\varGamma ( i,j ) \\ &\qquad {}- \sum_{m = m_{\kappa } - 1}^{D - 2} \sum_{i +j = m} \lambda^{D - 2 - i - j}\varGamma ( i,j ) \\ & \quad = \sum_{i + j = m_{\kappa } - 1} \mu^{N_{\sigma } ( i + j,D )}\lambda^{D -( m_{\kappa } - 1 )} V^{\sigma (m_{\kappa - 1})} ( i,j ) \\ &\qquad {} - \sum_{m = m_{\kappa } - 2}^{D - 2} \sum_{i+ j = m} \mu^{N_{\sigma } ( i + j + 1,D )}\lambda^{D - 2 - i- j}\varGamma ( i,j) \\ & \quad < \sum_{i + j = m_{\kappa - 1}} \mu^{N_{\sigma } ( i + j,D )} \lambda^{D - m_{\kappa -1}}V^{\sigma (m_{\kappa - 1} )} ( i,j ) \\ &\qquad {}- \sum_{m = m_{\kappa - 1} - 1}^{D - 2} \sum_{i + j = m} \mu^{N_{\sigma} ( i + j + 1,D )}\lambda^{D - 2 - i - j}\varGamma ( i,j) \\ & \quad \le \sum_{i + j = ( m_{\kappa - 1} )^{ - }} \mu^{N_{\sigma } ( i + j - 1,D )}\lambda^{D - m_{\kappa -1}} V^{\sigma (m_{\kappa - 2} )} ( i,j ) \\ &\qquad {}-\sum_{m = m_{\kappa - 1} - 1}^{D - 2} \sum_{i + j = m} \mu^{N_{\sigma} ( i + j + 1,D )}\lambda^{D - 2 - i - j}\varGamma ( i,j) \\ & \quad < \cdots \\ & \quad < \sum_{i + j = 1} \mu^{N_{\sigma } ( i + j,D )} \lambda^{D -1}V^{\sigma (1 )}( i,j ) \\ &\qquad {}- \sum_{m = 0}^{D - 2} \sum_{i + j= m} \mu^{N_{\sigma } ( i + j + 1,D )}\lambda^{D - 2 - i -j} \varGamma( i,j ). \end{aligned}$$
(29)

Under the zero-initial condition, we have

$$ \sum_{i + j = 1} \mu^{N_{\sigma } ( i + j,D )} \lambda^{D -1}V^{\sigma (1 )}(i,j ) = 0 . $$
(30)

Thus, we have

$$ \sum_{m = 0}^{D - 2} \sum_{i + j = m} \mu^{N_{\sigma } ( i + j +1,D )} \lambda^{D - 2 - i - j}\varGamma( i,j ) <- \sum_{i + j = D} V^{\sigma (m_{\kappa } )}( i,j ) < 0. $$
(31)

Multiplying the both sides of (31) by \(\mu^{ - N_{\sigma } ( 1,D )}\), we can get the following inequality:

$$ \sum_{m = 0}^{D - 2} \sum_{i + j = m} \!\mu^{ - N_{\sigma } ( 1,i +j + 1 )} \lambda^{D - 2 - i - j}\| \overline {z} \|_{2}^{2} < \sum_{m =0}^{D - 2} \sum_{i + j = m} \!\mu^{ - N_{\sigma } ( 1,i + j + 1)} \lambda^{D - 2 - i - j}\| \overline {w} \|_{2}^{2} . $$
(32)

Noting N σ (1,i+j+1)≤(i+j)/τ a , and using (9), we have

$$ \mu^{ - N_{\sigma } ( 1,i + j + 1 )} = e^{ - N_{\sigma } ( 1,i + j + 1 ) \ln \mu } \ge e^{ ( i + j )\ln \lambda }. $$
(33)

Thus

$$\begin{aligned} &\sum_{m = 0}^{D - 2} \sum_{i + j = m} e^{ ( i + j )\ln\lambda }\lambda^{D - 2 - i - j} \| \overline {z}\|_{2}^{2} < \sum_{m = 0}^{D- 2}\sum_{i + j = m} \mu^{ - N_{\sigma } ( 1,i + j + 1)}\lambda^{D - 2 - i - j} \| \overline {w} \|_{2}^{2} \end{aligned}$$
(34)
$$\begin{aligned} &\quad \Rightarrow\quad \sum_{m = 0}^{D - 2} \sum_{i + j = m} \lambda^{D - 2}\| \overline {z} \|_{2}^{2} < \gamma^{2}\sum_{m = 0}^{D - 2} \sum_{i + j = m} \lambda^{D - 2 - i - j}\| \overline {w}\|_{2}^{2} \\ &\quad \Rightarrow\quad \sum_{D = 2}^{\infty } \sum_{m = 0}^{D - 2} \sum_{i + j =m} \lambda^{D - 2}\| \overline {z} \|_{2}^{2} < \gamma^{2}\sum_{D = 2}^{\infty} \sum_{m = 0}^{D - 2} \sum_{i + j = m} \lambda^{D - 2 - i - j}\| \overline {w} \|_{2}^{2} \\ &\quad \Rightarrow\quad \sum_{m = 0}^{\infty } \sum_{i + j = m} \lambda^{i + j} \| \overline {z} \|_{2}^{2} \sum_{D = 2 + m}^{\infty } \lambda^{D - 2 - m} < \gamma^{2}\sum_{m = 0}^{\infty } \sum_{i + j = m} \| \overline {w} \|_{2}^{2} \sum_{D = 2 + m}^{\infty } \lambda^{D - 2 - m} \\ &\quad \Rightarrow\quad \frac{1}{1 - \lambda} \sum_{m = 0}^{\infty } \sum_{i + j =m} \lambda^{i + j}\| \overline {z}\|_{2}^{2} < \gamma^{2}\frac{1}{1 -\lambda} \sum_{m = 0}^{\infty } \sum_{i + j = m} \| \overline {w} \|_{2}^{2} \\ &\quad \Rightarrow\quad \sum_{m = 0}^{\infty } \sum_{i + j = m} \lambda^{i + j} \| \overline {z} \|_{2}^{2} < \gamma^{2}\sum_{m = 0}^{\infty } \sum_{i + j = m} \| \overline {w} \|_{2}^{2} \\ &\quad \Rightarrow\quad \sum_{i = 0}^{\infty } \sum_{j = 0}^{\infty } \lambda^{i +j} \| \overline {z}\|_{2}^{2} < \gamma^{2}\sum_{i = 0}^{\infty } \sum_{j =0}^{\infty } \| \overline {w} \|_{2}^{2}. \end{aligned}$$
(35)

According to Definition 3, we can see that system (1) is exponentially stable and has a prescribed weighted H ∞ disturbance attenuation level γ.

The proof is completed. □

3.2 H ∞ Control Problem

In this subsection, we shall deal with the H ∞ control problem of 2D switched systems via dynamic output feedback. Our purpose is to design a dynamic output feedback controller such that the closed-loop system is exponentially stable and has a specified weighted H ∞ disturbance attenuation level γ.

Consider the following discrete 2D switched plant in the FM LSS model:

$$\begin{aligned} x ( i + 1,j + 1 ) =& A_{1}^{\sigma (i +j+1 )}x ( i,j + 1 ) +A_{2}^{\sigma (i+ j+1 )}x ( i + 1,j ) \\ &{}+ B_{11}^{\sigma (i + j+1 )}w ( i,j + 1 )+ B_{12}^{\sigma (i + j+1 )}w( i + 1,j ) \\ &{}+ B_{21}^{\sigma (i + j+1)}u ( i,j + 1 )+ B_{22}^{\sigma (i + j+1 )}u( i + 1,j ), \\ z( i,j ) =& C_{1}^{\sigma (i +j)}x ( i,j ) + D_{11}^{\sigma (i +j)} w ( i,j ) + D_{12}^{\sigma (i +j)} u ( i,j ) , \\ y( i,j ) =& C_{2}^{\sigma (i +j)}x ( i,j ) + D_{21}^{\sigma (i +j)} w ( i,j ) + D_{22}^{\sigma (i +j)} u ( i,j ) \end{aligned}$$
(36)

where x(i,j)∈R n, \(w( i,j ) \in R^{n_{w}}\), u(i,j)∈R m, z(i,j)∈R d and \(y( i,j ) \in R^{n_{y}}\) are, respectively, the state, the disturbance input, the control input, the controlled output, and the measurement output of the plant, i and j are integers in Z +. \(A_{1}^{k}\), \(A_{2}^{k}\), \(B_{11}^{k}\), \(B_{12}^{k}\), \(B_{21}^{k}\), \(B_{22}^{k}\), \(C_{1}^{k}\), \(C_{2}^{k}\), \(D_{11}^{k}\), \(D_{12}^{k}\), \(D_{21}^{k}\), \(D_{22}^{k}\) with \(k\,{\in}\, \underline{N}\) are constant matrices with appropriate dimensions. We make no assumption on the statistics of the disturbance input signal w(i,j) other than that it is energy bounded, i.e., ∥w∥2<∞. Without loss of generality, we assume \(D_{22}^{k}=0\) for \(\forall k\,{\in}\, \underline{N}\).

Introduce the following output feedback controller of order n c :

$$\begin{aligned} x_{c} ( i + 1,j + 1 ) =& A_{c1}^{\sigma ( i + j + 1 )} x_{c}( i,j + 1 ) + A_{c2}^{\sigma( i + j + 1 )}x_{c} ( i + 1,j ) \\ &{}+B_{c1}^{\sigma (i + j + 1 )} y ( i,j + 1 ) + B_{c2}^{\sigma (i + j + 1 )}y( i + 1,j ), \\ u( i,j ) =& C_{c}^{\sigma (i +j)}x_{c} ( i,j ) + D_{c}^{\sigma (i +j)} y ( i,j ) \end{aligned}$$
(37)

where \(x_{c} \in R^{n_{c}}\).

The closed-loop system consisting of the plant (36) and the controller (37) is of the form

$$\begin{aligned} \overline {x} ( i + 1,j + 1 ) =& \overline {A}_{1}^{\sigma ( i + j + 1 )} \overline {x} ( i,j + 1) + \overline {A}_{2}^{\sigma (i + j + 1 )}\overline {x} ( i + 1,j ) \\ &{}+ \overline {B}_{1}^{\sigma (i + j + 1)}w ( i,j + 1 ) + \overline {B}_{2}^{\sigma (i + j + 1)}w ( i + 1,j ), \\ z( i,j ) =& \overline {C}^{\sigma (i + j )}\overline {x}( i,j ) + \overline {D}^{\sigma (i + j )}w( i,j ) \end{aligned}$$
(38)

where \(\overline {x} ( i,j) = [x^{T}(i,j) \ x^{T}_{c}(i,j)]^{T}\) and

$$\begin{aligned} \overline {A}_{1}^{\sigma ( i + j + 1 )} =& \left [\begin{array}{c@{\quad }c} A_{1}^{\sigma ( i + j + 1 )} + B_{21}^{\sigma (i + j + 1)} D_{c}^{\sigma (i +j+1)} & B_{21}^{\sigma (i + j + 1)} C_{c}^{\sigma ( i + j +1)}\\ B_{c1}^{\sigma (i +j+1)}C_{2}^{\sigma (i +j+1)} & A_{c1}^{\sigma ( i + j + 1 )} \end{array} \right ],\\ \overline {A}_{2}^{\sigma ( i + j + 1 )} =& \left [\begin{array}{c@{\quad }c} A_{2}^{\sigma ( i + j + 1)} + B_{22}^{\sigma (i + j + 1)} D_{c}^{\sigma (i +j+1)} & B_{21}^{\sigma (i + j + 1)} C_{c}^{\sigma ( i + j +1)}\\ B_{c2}^{\sigma (i +j+1)}C_{2}^{\sigma (i +j+1)} & A_{c2}^{\sigma ( i + j + 1)} \end{array} \right ],\\ \overline {B}_{1}^{\sigma ( i + j + 1 )} =& \left [\begin{array}{c} {B}_{11}^{\sigma (i + j + 1)} + {B}_{21}^{\sigma (i + j + 1)} D_{c}^{\sigma (i +j+1)}D_{21}^{\sigma (i +j+1)}\\ B_{c1}^{\sigma (i +j+1)}D_{21}^{\sigma (i +j+1)} \end{array} \right ], \\ \overline {B}_{2}^{\sigma ( i + j + 1 )} =& \left [\begin{array}{c} {B}_{12}^{\sigma (i + j + 1)} + {B}_{22}^{\sigma (i + j + 1)} D_{c}^{\sigma (i +j+1)}D_{21}^{\sigma (i +j+1)}\\ B_{c2}^{\sigma (i +j+1)}D_{21}^{\sigma (i +j+1)} \end{array} \right ], \\ \overline {C}^{\sigma ( i + j )} =& \bigl[\begin{array}{c@{\quad }c} C_{1}^{\sigma ( i + j )} + D_{12}^{\sigma (i +j)}D_{c}^{\sigma (i +j)} C_{2}^{\sigma ( i + j )} & D_{12}^{\sigma (i +j)}C_{c}^{\sigma ( i + j )} \end{array}\bigr], \\ \overline {D}^{\sigma ( i + j )} =& D_{11}^{\sigma (i +j)}+ D_{12}^{\sigma (i +j)}D_{c}^{\sigma (i +j)} D_{21}^{\sigma (i +j)}. \end{aligned}$$

For the closed-loop system (38), we state the 2D H ∞ control problem as: find a 2D dynamic output feedback controller of the form in (37) for the 2D plant (36) such that the closed-loop system (38) has a specified weighted H ∞ disturbance attenuation level γ. The controller design procedure is provided in the following theorem.

Theorem 2

For given positive scalars γ and 0<α<1, if there exist symmetric and positive-definite matrices R p>0, S p>0 and matrices \(\varPsi^{p}_{1}\), \(\varPsi^{p}_{2}\), \(\varPhi^{p}_{1}\), \(\varPhi^{p}_{2}\), \(D^{p}_{c}\), Z p, \(p\,{\in}\, \underline{N}\), such that

$$ \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} - Y^{p}_{F} & Y^{p}_{A_{1}} & Y^{p}_{A_{2}} & Y^{pT}_{B_{1}} & Y^{pT}_{B_{2}} & 0 & 0 \\ * & - \lambda \alpha Y^{p}_{F} & 0 & 0 & 0 & Y^{pT}_{c} & 0 \\ * & * & - \lambda (1 - \alpha)Y^{p}_{F} & 0 & 0 & 0 & Y^{pT}_{c} \\ * & * & * & - \gamma^{2}I & 0 & \overline {D}^{pT} & 0 \\ * & * & * & * & - \gamma^{2}I & 0 & \overline {D}^{pT} \\ * & * & * & * & * & - I & 0 \\ * & * & * & * & * & * & - I \\ \end{array} \right ] {<}\, 0, \quad \forall p\,{\in}\, \underline{N} $$
(39)

with

$$\begin{aligned} Y^{p}_{F} =& \left [ \begin{array}{c@{\quad }c} R^{p} & I \\ I & S^{p} \\ \end{array} \right ], \qquad \overline {D}^{p} = D_{11}^{p} + D_{12}^{p}D_{c}^{p}D_{21}^{p}, \\ Y_{A_{1}}^{p} =& \left [ \begin{array}{c@{\quad }c} A_{1}^{p}R^{p} + B_{21}^{p}Z^{p} & A_{1}^{p} + B_{21}^{p}D_{c}^{p}C_{2}^{p} \\ \varPhi_{1}^{p} & S^{p}A_{1}^{p} + \varPsi_{1}^{p}C_{2}^{p} \\ \end{array} \right ], \\ Y_{A_{2}}^{p} =& \left [ \begin{array}{c@{\quad }c} A_{2}^{p}R^{p} + B_{22}^{p}Z^{p} & A_{2}^{p} + B_{22}^{p}D_{c}^{p}C_{2}^{p} \\ \varPhi_{2}^{p} & S^{p}A_{2}^{p} + \varPsi_{2}^{p}C_{2}^{p} \\ \end{array} \right ], \\ Y_{B_{1}}^{p} =& \bigl[ \begin{array}{c@{\quad }c} B_{11}^{pT} + D_{21}^{pT}D_{c}^{pT}B_{21}^{pT} & B_{11}^{pT}S^{p} + D_{21}^{pT}\varPsi_{1}^{pT} \\ \end{array} \bigr], \\ Y_{B_{2}}^{p} =& \bigl[ \begin{array}{c@{\quad }c} B_{12}^{pT} + D_{21}^{pT}D_{c}^{pT}B_{22}^{pT} & B_{12}^{pT}S^{p} + D_{21}^{pT}\varPsi_{2}^{pT} \\ \end{array} \bigr], \\ Y_{c}^{p} =& \left [ \begin{array}{c@{\quad }c} C_{1}^{p}R^{p} + D_{12}^{p}Z^{p} & C_{1}^{p} + D_{12}^{p}D_{c}^{p}C_{2}^{p} \\ \end{array} \right ], \end{aligned}$$

then 2D switched closed-loop system (38) is exponentially stable and has a prescribed weighted H ∞ disturbance attenuation level γ for any switching signals with the average dwell time satisfying

$$ \tau_{a} > \tau_{a}^* = \frac{\ln\mu}{-\ln\lambda } $$
(40)

where Σ p Λ pT=I−R p S p, R p Λ p+Σ p U p=0, Σ pT S p+V p Λ pT=0, and μ≥1 satisfies

$$ \left [\begin{array}{c@{\quad }c} R^{q} & \varSigma^{q}\\ \varSigma^{qT} & V^{q} \end{array} \right ] <\mu \left [\begin{array}{c@{\quad }c} R^{p} & \varSigma^{p}\\ \varSigma^{pT} & V^{p} \end{array} \right ], \quad \forall p,q \in\underline{N}. $$
(41)

And the controller parameters can be obtained as follows:

$$ \begin{aligned} C_{c}^{p} &= \bigl(Z^{p} - D_{c}^{p}C_{2}^{p}R^{p}\bigr)\bigl( \varSigma^{p} \bigr)^{ - T} , \\ B_{c1}^{p} &= \bigl( \varLambda^{p} \bigr)^{ - 1} \bigl( \varPsi_{1}^{p} -S^{P}B_{21}^{p}D_{c}^{p} \bigr), \qquad B_{c2}^{p} = \bigl( \varLambda^{p} \bigr)^{ - 1} \bigl(\varPsi_{2}^{p} - S^{p}B_{22}^{p}D_{c}^{p} \bigr), \\ A_{c1}^{p} &= \bigl( \varLambda^{p}\bigr)^{ - 1} \bigl( \varPhi_{1}^{p} - S^{p}\bigl(A_{1}^{p} + B_{21}^{p}D_{c}^{p}C_{2}^{p}\bigr)R^{^{p}} - S^{p}B_{21}^{p}C_{c}^{p}\varSigma^{pT} \\ &\quad {}- \varLambda^{p}B_{c1}^{p}C_{2}^{p}R^{p} \bigr) \bigl( \varSigma^{p} \bigr)^{ - T} , \\ A_{c2}^{p} &= \bigl( \varLambda^{p} \bigr)^{ - 1} \bigl( \varPhi_{2}^{p} - S^{p}\bigl(A_{1}^{p} + B_{22}^{p}D_{c}^{p}C_{2}^{p}\bigr)R^{^{p}} + S^{p}B_{22}^{p}C_{c}^{p}\varSigma^{pT} \\ &\quad {} + \varLambda^{p}B_{c2}^{p}C_{2}^{p}R^{p} \bigr) \bigl( \varSigma^{p} \bigr)^{ - T}. \end{aligned} $$
(42)

Proof

By applying Theorem 1 to the closed-loop system (38), the controller solves the 2D switched H ∞ control problem if the following matrix inequalities hold

$$\begin{aligned} & \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} - X^{p} & X^{p}\overline {A}_{1}^{p} & X^{p}\overline {A}_{2}^{p} & X^{p}\overline {B}_{1}^{p} & X^{p}\overline {B}_{2}^{p} & 0 & 0 \\ * & - \lambda\alpha X^{p} & 0 & 0 & 0 & \overline {C}^{pT} & 0 \\ * & * & - \lambda(1 - \alpha)X^{p} & 0 & 0 & 0 & \overline {C}^{pT} \\ * & * & * & - \gamma^{2}I & 0 & \overline {D}^{pT} & 0 \\ * & * & * & * & - \gamma^{2}I & 0 & \overline {D}^{pT} \\ * & * & * & * & * & - I & 0 \\ * & * & * & * & * & * &- I \\ \end{array} \right ] {<}\, 0, \\ &\quad \forall p\,{\in}\, \underline{N}. \end{aligned}$$
(43)

Pre- and post-multiplying (43) by \(\operatorname {diag}( ( X^{p} )^{ - 1},( X^{p} )^{ -1}, ( X^{p} )^{ - 1},I,I,I,I )\) leads to

$$\begin{aligned} & \left [ \begin{array}{c@{\ }c@{\ }c@{\ }c@{\ }c@{\ }c@{\ }c} - ( X^{p} )^{ - 1} & \overline {A}_{1}^{p}( X^{p} )^{ - 1} & \overline {A}_{2}^{p}( X^{p} )^{- 1} & \overline {B}_{1}^{p} & \overline {B}_{2}^{p} & 0 & 0 \\ * & - \lambda\alpha( X^{p} )^{ - 1} & 0 & 0 & 0 & ( X^{p} )^{ -1}\overline {C}^{pT} & 0 \\ * & * & - \lambda(1 - \alpha)( X^{p} )^{ - 1} & 0 & 0 & 0 & ( X^{p} )^{ - 1}\overline {C}^{pT} \\ * & * & * & - \gamma^{2}I & 0 & \overline {D}^{pT} & 0 \\ * & * & * & * & - \gamma^{2}I & 0 & \overline {D}^{pT} \\ * & * & * & * & * & - I & 0 \\ * & * & * & * & * & * & - I\\ \end{array} \right ] < 0, \\ &\quad \forall p\,{\in}\, \underline{N}. \end{aligned}$$
(44)

Definite F p=(X p)−1, we can obtain

$$\begin{aligned} &\left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} - F^{p} & \overline {A}_{1}^{p}F^{p} & \overline {A}_{2}^{p}F^{p} & \overline {B}_{1}^{p} & \overline {B}_{2}^{p} & 0 & 0 \\ * & - \alpha F^{p} & 0 & 0 & 0 & F^{p}\overline {C}^{pT} & 0 \\ * & * & - (1 - \alpha)F^{p} & 0 & 0 & 0 & F^{p}\overline {C}^{pT} \\ * & * & * & - \gamma^{2}I & 0 & \overline {D}^{pT} & 0 \\ * & * & * & * & - \gamma^{2}I & 0 & \overline {D}^{pT} \\ * & * & * & * & * & - I & 0 \\ * & * & * & * & * & * & - I \\ \end{array} \right ] {<}\, 0, \\ &\quad \forall p\,{\in}\, \underline{N}. \end{aligned}$$
(45)

Partition F p and (F p)−1 as

$$ F^{p} = \left [\begin{array}{c@{\quad }c} R^{p} & \varSigma^{p}\\ \varSigma^{pT} & V^{p} \end{array} \right ], \qquad \bigl(F^{p}\bigr)^{-1} = \left [\begin{array}{c@{\quad }c} S^{p} & \varLambda ^{p}\\ \varLambda^{pT} & U^{p} \end{array} \right ], $$
(46)

where R p,S p,U p,V p∈R n×n. It is easy to show from (46) that Σ p Λ pT=I−R p S p.

Set

$$\begin{aligned} \varOmega^{p} =& \left [ \begin{array}{c@{\quad }c} I & S^{p} \\ 0 & \varLambda^{pT} \\ \end{array} \right ]^{T}, \qquad Z^{p} = D_{c}^{p}C^{p}R^{p} + C_{c}^{p}\varSigma^{pT} , \\ \varPsi_{1}^{p} =& S^{p}B_{21}^{p}D_{c}^{p} + \varLambda^{p}B_{c1}^{p}, \qquad \varPsi_{2}^{p} = S^{p}B_{22}^{p}D_{c}^{p} + \varLambda^{p}B_{c2}^{p} , \\ \varPhi_{1}^{p} =& S^{p} \bigl(A_{1}^{p} + B_{21}^{p}D_{c}^{p}C_{2}^{p}\bigr)R^{^{p}} + S^{p}B_{21}^{p}C_{c}^{p}\varSigma^{pT} + \varLambda^{p}B_{c1}^{p}C_{2}^{p}R^{p} \\ &{} + \varLambda^{p}A_{c1}^{p}\varSigma^{pT} , \\ \varPhi_{2}^{p} =& S^{p}\bigl(A_{1}^{p} + B_{22}^{p}D_{c}^{p}C_{2}^{p}\bigr)R^{^{p}} + S^{p}B_{22}^{p}C_{c}^{p}\varSigma^{pT} + \varLambda^{p}B_{c2}^{p}C_{2}^{p}R^{p} \\ &{} + \varLambda^{p}A_{c2}^{p}\varSigma^{pT} . \end{aligned}$$

Pre- and post-multiplying (45) \(\operatorname {diag}(\varOmega^{pT},\varOmega^{pT},\varOmega^{pT},I,I,I,I)\) and \(\operatorname {diag}(\varOmega^{p},\varOmega^{p}, \varOmega^{p}, I,I,I,I)\), respectively, we have

$$\begin{aligned} & \left [ \!\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} - \varOmega^{pT}F^{p}\varOmega^{p} & \varOmega^{pT}\overline {A}_{1}^{p}F^{p}\varOmega^{p} & \varOmega^{pT}\overline {A}_{2}^{p}F^{p}\varOmega^{p} & \varOmega^{pT}\overline {B}_{1}^{p} \\ * & - \lambda\alpha\varOmega^{pT}F^{p}\varOmega^{p} & 0 & 0 \\ * & * & -\lambda(1-\alpha)\varOmega^{pT}F^{p}\varOmega^{p} & 0 \\ * & * & * & - \gamma^{2}I \\ * & * & * & * \\ * & * & * & * \\ * & * & * & * \\ \end{array} \right . \\ & \qquad \qquad \qquad \quad \left . \!\begin{array}{c@{\quad }c@{\quad }c} \varOmega^{pT}\overline {B}_{2}^{p} & 0 & 0\\ 0 & \varOmega^{pT}F^{p}\overline {C}^{pT} & 0\\ 0 & 0 & \varOmega^{pT}F^{p}\overline {C}^{pT}\\ 0 & \overline {D}^{pT} & 0\\ - \gamma^{2}I & 0 & \overline {D}^{pT}\\ * & - I & 0\\ * & * & - I \\ \end{array}\!\right ] \\ &\quad < 0 \end{aligned}$$
(47)

with

$$\begin{aligned} \varOmega^{pT}F^{p}\varOmega^{p} =& \left [ \begin{array}{c@{\quad }c} R^{p} & I \\ I & S^{p} \\ \end{array} \right ] , \\ \varOmega^{pT}\overline {A}_{1}^{p}F^{p}\varOmega^{p} =& \left [ \begin{array}{c@{\quad }c} A_{1}^{p}R^{p} + B_{21}^{p}Z^{p} & A_{1}^{p} + B_{21}^{p}D_{c}^{p}C_{2}^{p} \\ \varPhi_{1}^{p} & S^{p}A_{1}^{p} +\varPsi_{1}^{p}C_{2}^{p} \\ \end{array} \right ] , \\ \varOmega^{pT}\overline {A}_{2}^{p}F^{p}\varOmega^{p} =& \left [ \begin{array}{c@{\quad }c} A_{2}^{p}R^{p} + B_{22}^{p}Z^{p} & A_{2}^{p} + B_{22}^{p}D_{c}^{p}C_{2}^{p} \\ \varPhi_{2}^{p} & S^{p}A_{2}^{p} +\varPsi_{2}^{p}C_{2}^{p} \\ \end{array} \right ] , \\ \overline {B}_{1}^{pT}\varOmega^{p} =& \bigl[ \begin{array}{c@{\quad }c} B_{11}^{pT} +D_{21}^{pT}D_{c}^{pT}B_{21}^{pT} & B_{11}^{pT}S^{p} + D_{21}^{pT}\varPsi_{1}^{pT} \\ \end{array} \bigr] , \\ \overline {B}_{2}^{pT}\varOmega^{p} =& \bigl[ \begin{array}{c@{\quad }c} B_{12}^{pT} +D_{21}^{pT}D_{c}^{pT}B_{22}^{pT} & B_{12}^{pT}S^{p} + D_{21}^{pT}\varPsi_{2}^{pT} \\ \end{array} \bigr] , \\ \overline {C}^{p}F^{p}\varOmega^{p} =& \bigl[ \begin{array}{c@{\quad }c} C_{1}^{p}R^{p} + D_{12}^{p}Z^{p} & C_{1}^{p} + D_{12}^{p}D_{c}^{p}C_{2}^{p} \\ \end{array} \bigr] . \end{aligned}$$

Then we take

$$\begin{aligned} Y_{F}^{p} =& \varOmega^{pT}F^{p}\varOmega^{p}, \qquad Y_{A_{1}}^{p} = \varOmega^{pT}\overline {A}_{1}^{p}F^{p}\varOmega^{p}, \qquad Y_{A_{2}}^{p} = \varOmega^{pT}\overline {A}_{2}^{p}F^{p}\varOmega^{p} , \\ Y_{B_{1}}^{p} =& \overline {B}_{1}^{pT}\varOmega^{p}, \qquad Y_{B_{2}}^{p} = \overline {B}_{2}^{pT}\varOmega^{p}, \qquad Y_{c}^{p} = \overline {C}^{p}F^{p}\varOmega^{p} . \end{aligned}$$

The condition (39) can be obtained.

Suppose that the LMIs (39) admits feasible solutions R p>0, S p>0, \(D_{c}^{p}\), \(\varPsi_{1}^{p}\), \(\varPsi_{2}^{p}\), \(\varPhi_{1}^{p}\), \(\varPhi_{2}^{p}\) and Z p with \(p \in\underline{N}\). Since \(Y_{F}^{p} > 0\), Σ p Λ pT=I−R p S p is non-singular. Therefore, invertible matrices Σ p and Λ p can be computed. Then, U p and V p can be computed from R p Λ p+Σ p U p=0 and Σ pT S p+V p Λ pT=0, respectively. We can find that the positive scalar μ≥1 can be obtained by solving (41), then the average dwell time τ a can be obtained from (40). And the rest of the controller parameters \(A_{c1}^{p}\), \(A_{c2}^{p}\), \(B_{c1}^{p}\), \(B_{c2}^{p}\), \(C_{c}^{p}\) with \(p\in\underline{N}\) can be obtained by solving (42).

This completes the proof. □

Remark 6

If there is only one subsystem in system (36), it will degenerate to be a general 2D FM LSS model which is a special one of 2D switched systems. Theorem 2 is also applicable for 2D FM LSS systems, which means that our results are more general than the ones just for 2D FM LSS systems. Compared with the existing result in the literature [10], we get sufficient conditions of output feedback H ∞ stabilization instead of state feedback H ∞ stabilization.

4 Examples

In this section, we shall illustrate the results developed earlier via two examples. All simulations are performed with LMI control toolbox [12].

Example 1

This numerical example demonstrates the design of a 2D H ∞ controller for the following 2D switched system of type (36) with two subsystems:

Subsystem 1:

$$\begin{aligned} A_{1}^{1} =& \left [ \begin{array}{c@{\quad }c} - 0.2450 & 0.0307 \\ - 0.1444 & 0.0008 \\ \end{array} \right ], \qquad A_{2}^{1} = \left [ \begin{array}{c@{\quad }c} - 0.2860 & 0.1800 \\ -0.1435 & - 0.4601 \\ \end{array} \right ] , \\ B_{11}^{1} =& \left [ \begin{array}{c} 0.8392 \\ 0.6288 \\ \end{array} \right ], \qquad B_{12}^{1} = \left [ \begin{array}{c} 1.0322 \\ 0.2071 \\ \end{array} \right ], \\ B_{21}^{1} =& \left [ \begin{array}{c} 0.1338 \\ 1.0708 \\ \end{array} \right ], \qquad B_{22}^{1} = \left [ \begin{array}{c} 0.6298 \\ 0.9778 \\ \end{array} \right ] , \\ C_{1}^{1} =& [ \begin{array}{c@{\quad }c} 0.005 & 0.1 \\ \end{array} ], \qquad C_{2}^{1} = [ \begin{array}{c@{\quad }c} 1 & 10 \\ \end{array} ], \\ D_{11}^{1} =& 0.3, \qquad D_{12}^{1} = 0.1, \qquad D_{21}^{1} = 0.03, \qquad D_{22}^{1} = 0 . \end{aligned}$$

Subsystem 2:

$$\begin{aligned} A_{1}^{2} =& \left [ \begin{array}{c@{\quad }c} - 0.2450 & 0.0008 \\ - 0.1444 & 0.0307 \\ \end{array} \right ], \qquad A_{2}^{2} = \left [ \begin{array}{c@{\quad }c} - 0.2860 & - 0.4601 \\ -0.1435 & 0.1800 \\ \end{array} \right ] , \\ B_{11}^{2} =& \left [ \begin{array}{c} 0.8392 \\ 0.2071 \\ \end{array} \right ], \qquad B_{12}^{2} = \left [ \begin{array}{c} 1.0322 \\ 0.9778 \\ \end{array} \right ], \\ B_{21}^{2} =& \left [ \begin{array}{c} 0.1338 \\ 0.6288 \\ \end{array} \right ], \qquad B_{22}^{2} = \left [ \begin{array}{c} 0.6298 \\ 1.0708 \\ \end{array} \right ] , \\ C_{1}^{2} =& [ \begin{array}{c@{\quad }c} 0.1 & 0.005 \\ \end{array} ], \qquad C_{2}^{2} = [ \begin{array}{c@{\quad }c} 10 & 1 \\ \end{array} ], \\ D_{11}^{2} =& 0.3, \qquad D_{12}^{2} = 0.1, \qquad D_{21}^{2} = 0.03, \qquad D_{22}^{2} = 0 . \end{aligned}$$

Take λ=0.75, α=0.6 and γ=10, according to Theorem 2, solving (39) gives rise to the following solutions:

$$\begin{aligned} R^{1} =& \left [ \begin{array}{c@{\quad }c} 197.2681 & - 103.3501 \\ - 103.3501 & 65.6891 \\ \end{array} \right ], \qquad R^{2} = \left [ \begin{array}{c@{\quad }c} 15.7966 & - 17.5360 \\ - 17.5360 & 54.3629 \\ \end{array} \right ], \\ S^{1} =& \left [ \begin{array}{c@{\quad }c} 154.9188 & - 128.5563 \\ - 128.5563 & 244.3175 \\ \end{array} \right ], \qquad S^{2} = \left [ \begin{array}{c@{\quad }c} 112.7032 & - 126.8899 \\ - 126.8899 & 213.6495 \\ \end{array} \right ], \\ \varPhi_{1}^{1} =& \left [ \begin{array}{c@{\quad }c} - 0.4870 & - 0.0077 \\ - 0.6565 & 0.1357 \\ \end{array} \right ], \qquad \varPhi_{1}^{2} = \left [ \begin{array}{c@{\quad }c} -0.4834 & 0.1163 \\ 0.3148 & 0.1961 \\ \end{array} \right ], \\ \varPhi_{2}^{1} =& \left [ \begin{array}{c@{\quad }c} - 0.2485 & 0.1995 \\ 0.3106 & - 0.4696 \\ \end{array} \right ], \qquad \varPhi_{2}^{2} = \left [ \begin{array}{c@{\quad }c} 0.0730 & - 0.2655 \\ - 0.4215 & 0.0970 \\ \end{array} \right ], \\ Z^{1} =& [ \begin{array}{c@{\quad }c} 24.3453 & - 11.2155 \\ \end{array} ], \qquad Z^{2} = [ \begin{array}{c@{\quad }c} -2.6035 & 18.2364 \\ \end{array} ], \\ D_{c}^{1} =& 0.0528, \qquad D_{c}^{2} = 0.0506 , \\ \varPsi_{1}^{1} =& \left [ \begin{array}{c} 8.6536 \\ 3.7301 \\ \end{array} \right ], \qquad \varPsi_{1}^{2} = \left [ \begin{array}{c} 1.0636 \\ - 0.3689 \\ \end{array} \right ], \\ \varPsi_{2}^{1} =& \left [ \begin{array}{c} - 22.8833 \\ 57.4539 \\ \end{array} \right ], \qquad \varPsi_{2}^{2} = \left [ \begin{array}{c} 3.0049 \\ - 1.7051\\ \end{array} \right ] . \end{aligned}$$

Then, U p and V p with p∈2 can be computed

$$\begin{aligned} U^{1} =& \left [ \begin{array}{c@{\quad }c} 0.0031 & - 0.0012 \\ - 0.0012 & 0.0157 \\ \end{array} \right ], \qquad U^{2} = \left [\begin{array}{c@{\quad }c} 0.0034 & 0.0007 \\ 0.0007 & 0.0377 \\ \end{array} \right ], \\ V^{1} =& 10^{7} \times \left [ \begin{array}{c@{\quad }c} 2.3565 & 0.0085 \\ 0.0085 & 0.0044 \\ \end{array} \right ], \qquad V^{2} = 10^{6} \times \left [ \begin{array}{c@{\quad }c} 5.2571 & - 0.0140 \\ - 0.0140 & 0.0067 \\ \end{array} \right ]. \end{aligned}$$

The positive scalar μ=2.3834 can be obtained by solving (41), then \(\tau_{a}^{*} = 3.0191\) can be obtained from (40). And the rest of the controller parameters \(A_{c1}^{p}\), \(A_{c2}^{p}\), \(B_{c1}^{p}\), \(B_{c2}^{p}\), \(C_{c}^{p}\) with p∈2 can be obtained by solving (42)

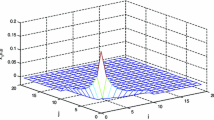
$$\begin{aligned} A_{c1}^{1} =& \left [ \begin{array}{c@{\quad }c} -0.0589 & 0.2202 \\ 0.0094 & 0.2275 \\ \end{array} \right ], \qquad A_{c2}^{1} = \left [ \begin{array}{c@{\quad }c} - 0.1526 & 1.6987 \\ 0.0025 & 0.4386 \\ \end{array} \right ], \\ B_{c1}^{1} =& \left [ \begin{array}{c} 7.2039 \\ - 3.6735 \\ \end{array} \right ], \qquad B_{c2}^{1} = \left [ \begin{array}{c} -51.2096 \\ - 15.7511 \\ \end{array} \right ], \\ C_{c}^{1} =& [ \begin{array}{c@{\quad }c} -0.0003 & 0.0025 \\ \end{array} ], \quad D_{c}^{1} = 0.0505; \\ A_{c1}^{2} =& \left [ \begin{array}{c@{\quad }c} 0.2216 & 0.3603 \\ 0.0183 & 0.0229 \\ \end{array} \right ], \qquad A_{c2}^{2} = \left [ \begin{array}{c@{\quad }c} 0.2808 & - 0.2963 \\ 0.03499 & 0.3633 \\ \end{array} \right ], \\ B_{c1}^{2} =& \left [ \begin{array}{c} 7.6501 \\ - 0.2021 \\ \end{array} \right ], \qquad B_{c2}^{2} = \left [ \begin{array}{c} 11.1692 \\ - 0.2422 \\ \end{array} \right ], \\ C_{c}^{2} =& [ \begin{array}{c@{\quad }c} 0.0015 & 0.0025 \\ \end{array} ], \qquad D_{c}^{2} = 0.0488. \end{aligned}$$

Choosing τ a =4, the simulation results are shown in Figs. 1, 2 and 3, where the boundary condition of the system is

$$\begin{aligned} x( i,j ) =& \frac{1}{50( j + 1 )}, \quad \forall 0 \le j \le 20, \ i = 0, \\ x( i,j ) =& \frac{1}{50( i + 1 )}, \quad \forall 0 \le i \le 20, \ j = 0, \end{aligned}$$

and w(i,j)=0.5exp(−0.025π(i+j)). It can be seen from Figs. 1–3 that the system is exponentially stable. Furthermore, when the boundary condition is zero, by computing, we get \(\sum_{i = 0}^{\infty} \sum_{j = 0}^{\infty} \lambda^{i + j}\| \overline {z} \|_{2}^{2} = 0.2741\) and \(\sum_{i = 0}^{\infty } \sum_{j = 0}^{\infty } \| \overline {w} \|_{2}^{2} = 14.6952\), and it satisfies the condition (2) in Definition 2. It can be seen that the system has a weighted H ∞ disturbance attenuation level γ=10.

Fig. 1
figure 1

Response of state x 1(i,j)

Full size image
Fig. 2
figure 2

Response of state x 2(i,j)

Full size image
Fig. 3
figure 3

Switching signal

Full size image

Example 2

It is known that some dynamical processes in gas absorption, water stream heating and air drying can be described by the Darboux equation [23]. Now we consider a dynamical process with multiple subsystems:

$$ \frac{\partial ^{2}s ( x,t )}{\partial x\partial t} = a_{1}^{\sigma (x,t )} \frac{\partial s ( x,t)}{\partial t} + a_{2}^{\sigma (x,t )} \frac{\partial s ( x,t )}{\partial x} +a_{0}^{\sigma (x,t )} + b^{\sigma (x,t )}f ( x,t ) $$
(48)

where s(x,t) is an unknown function at x(space)∈[0,x f ] and t(time)∈[0,∞), \(a_{0}^{\sigma (x,t)}\), \(a_{1}^{\sigma (x,t )}\), \(a_{2}^{\sigma (x,t )}\) and b σ(x,t) are real coefficients with σ(x,t) being the switching signal, and f(x,t) is the input function. Define

$$r ( x,t ) = \frac{\partial s ( x,t )}{\partial t} - a_{2}^{\sigma (x,t )}s ( x,t ) $$

and x T(i,j)=[r T(i,j) s T(i,j)], where x(i,j)=x(iΔx,jΔt). It is easy to verify that Eq. (48) can be converted into a 2D switched FM LSS model of the form (36) when without disturbance input:

$$\begin{aligned} A_{1}^{\sigma (i,j )} =& \left [ \begin{array}{c@{\quad }c} 1 + a_{1}^{\sigma (i,j )}\varDelta x & ( a_{1}^{\sigma (i,j )}a_{2}^{\sigma (i,j )} + a_{0}^{\sigma (i,j )} )\varDelta x \\ 0 & 0 \\ \end{array} \right ], \qquad A_{2}^{\sigma (i,j )} = \left [ \begin{array}{c@{\quad }c} 0 & 0 \\ \varDelta t & 0 \\ \end{array} \right ], \\ B_{21}^{\sigma (i,j )} =& \left [ \begin{array}{c@{\quad }c} b^{\sigma( i,j )}\varDelta x \\ 0 \\ \end{array} \right ], \qquad B_{22}^{\sigma (i,j )} = \left [ \begin{array}{c} 0 \\ 0 \\ \end{array} \right ]. \end{aligned}$$

It should be noted that the value of σ(i,j) depends on i+j, so σ(i,j) can be written as σ(i+j). Now we assume that the 2D switched system has two subsystems with \(a_{0}^{1} = 0.2\), \(a_{0}^{2} = 0.3\), \(a_{1}^{1} = - 10\), \(a_{1}^{2} = - 8\), \(a_{2}^{1} = - 1\), \(a_{2}^{2} = - 2\), b 1=10, b 2=8, Δx=0.1 and Δt=0.5. Taking the noise input w(i,j)=0.5exp(−0.025π(i+j)), we can get a 2D switched discrete system in the form of (36) with parameters as follows:

Subsystem 1:

$$\begin{aligned} A_{1}^{1} =& \left [ \begin{array}{c@{\quad }c} 0 & 1.02 \\ 0 & 0 \\ \end{array} \right ], \qquad A_{2}^{1} = \left [ \begin{array}{c@{\quad }c} 0 & 0 \\ 0.5 & 0 \\ \end{array} \right ], \\ B_{11}^{1} =& \left [ \begin{array}{c} 0.1 \\ 0 \\ \end{array} \right ], \qquad B_{12}^{1} = \left [\begin{array}{c} 0 \\ 0.1 \\ \end{array} \right ], \qquad B_{21}^{1} = \left [ \begin{array}{c} 1 \\ 0 \\ \end{array} \right ], \qquad B_{22}^{1} = \left [ \begin{array}{c} 0 \\ 0 \\ \end{array} \right ], \\ C_{1}^{1} =& [ \begin{array}{c@{\quad }c} 1 & 10 \\ \end{array} ], \qquad C_{2}^{1} = [\begin{array}{c@{\quad }c} 1 & 10 \\ \end{array} ], \\ D_{11}^{1} =& 0.3, \qquad D_{12}^{1} = 0.1 , \qquad D_{21}^{1} = 0.03, \qquad D_{22}^{1} = 0 . \end{aligned}$$

Subsystem 2:

$$\begin{aligned} A_{1}^{2} =& \left [ \begin{array}{c@{\quad }c} 0.2 & 1.63 \\ 0 & 0 \\ \end{array} \right ], \qquad A_{2}^{2} = \left [ \begin{array}{c@{\quad }c} 0 & 0 \\ 0.5 & 0 \\ \end{array} \right ], \\ B_{11}^{2} =& \left [ \begin{array}{c} 0.2 \\ 0 \\ \end{array} \right ], \qquad B_{12}^{2} = \left [ \begin{array}{c} 0 \\ 0.05 \\ \end{array} \right ], \qquad B_{21}^{2} = \left [ \begin{array}{c} 0.8 \\ 0 \\ \end{array} \right ], \qquad B_{22}^{2} = \left [ \begin{array}{c} 0 \\ 0 \\ \end{array} \right ], \\ C_{1}^{2} =& [ \begin{array}{c@{\quad }c} 1 & 10 \\ \end{array} ], \qquad C_{2}^{2} = [ \begin{array}{c@{\quad }c} 1 & 10 \\ \end{array} ], \\ D_{11}^{2} =& 0.3,\qquad D_{12}^{2} = 0.1, \qquad D_{21}^{2} = 0.03, \qquad D_{22}^{2} = 0 . \end{aligned}$$

Take λ=0.75, α=0.6 and γ=10. According to Theorem 2, we can get a 2D switched output feedback controller of the form (37) with

$$\begin{aligned} A_{c1}^{1} =& \left [ \begin{array}{c@{\quad }c} -0.0097 & - 0.0384 \\ 0.0027 & 0.0106 \\ \end{array} \right ], \qquad A_{c2}^{1} = \left [ \begin{array}{c@{\quad }c} -1.0313 & - 3.9227 \\ 0.3267 & 1.0533 \\ \end{array} \right ], \\ B_{c1}^{1} =& \left [ \begin{array}{c} 18.7114 \\ - 5.1523 \\ \end{array} \right ], \qquad B_{c2}^{1} = \left [ \begin{array}{c} 1.6242 \\ 5.5622 \\ \end{array} \right ], \\ C_{c}^{1} =& 10^{ - 5} \times[ \begin{array}{c@{\quad }c} -0.9527 & 0.7637 \\ \end{array} ], \qquad D_{c}^{1} = - 0.1045; \\ A_{c1}^{2} =& 10^{ - 3} \times \left [ \begin{array}{c@{\quad }c} - 0.0143 & 0.5437 \\ 0.0789 & - 0.7291 \\ \end{array} \right ], \qquad A_{c2}^{2} = \left [ \begin{array}{c@{\quad }c} -2.8819 & - 2.9440 \\ 4.4824 & 3.6717 \\ \end{array} \right ], \\ B_{c1}^{2} =& \left [ \begin{array}{c} 1.1809 \\ - 1.6818 \\ \end{array} \right ], \qquad B_{c2}^{2} = \left [ \begin{array}{c} 2.4408 \\ 1.6085 \\ \end{array} \right ], \\ C_{c}^{2} =& 10^{ - 4} \times[ \begin{array}{c@{\quad }c} -0.1480 & - 0.1306 \\ \end{array} ], \qquad D_{c}^{2}= - 0.2062. \end{aligned}$$

Thus the system can be H ∞ stabilized via the designed controller.

5 Conclusions

This paper has investigated the problems of stability and weighted H ∞ disturbance attenuation performance analysis for 2D discrete switched systems described by the FM LSS model. An exponential stability criterion is obtained via the average dwell time approach. Some sufficient conditions for the existence of weighted H ∞ disturbance attenuation level γ for the considered system are derived in terms of LMIs. In addition, a 2D dynamic output feedback controller is designed to solve the H ∞ control problem. Finally, two examples are also given to illustrate the applicability of the proposed results.