State Feedback $H_\infty$ Control For 2-D Switched Delay Systems with Actuator Saturation in the Second FM Model

Abstract

This paper is concerned with the problem of state feedback $H_\infty$ stabilization of discrete two-dimensional switched delay systems with actuator saturation represented by the second Fornasini and Marchesini state-space model. Firstly, the saturation behavior is described with the help of the convex hull representation, and a sufficient condition for asymptotical stability of the closed-loop system is proposed in terms of linear matrix inequalities via the multiple Lyapunov functional approach. Then, a state feedback controller is designed to guarantee the $H_\infty$ disturbance attenuation level of the corresponding closed-loop system. Finally, two examples are provided to validate the proposed results.

1 Introduction

Two-dimensional (2-D) systems are gaining momentum due to their extensive applications such as in signal processing, linear image processing, multi-dimensional digital filtering, electricity transmission, energy exchange processes and process control [15, 32, 36]. 2-D systems are different in a sense from one-dimensional (1-D) systems, since information is propagated along two independent directions. 2-D systems can be represented by different models such as the Rosser model, Fornasini and Marchesini (FM) model and Attasi model [1, 20, 39]. Several significant results on the issues of stability analysis and controller synthesis of 2-D systems are available in the literature (see for instance [4, 9, 25, 33, 34, 37, 41, 47] and the references therein). Moreover, researchers in [13, 22, 23] presented useful results on stability and controller design of linear repetitive process.

In practical control systems, time delay is inevitable. For instance, time delay exists if there is transmission of information between different parts of the system. Time delay may greatly influence the stability of a system and sometimes may give rise to periodic oscillations in the system. Stability and stabilization of 1-D delayed systems were well addressed in [38, 40, 46]. The problems of stability analysis and controller design of 2-D systems with time delay have been investigated in [6, 19, 44, 48]. The $H_\infty$ control problem of 2-D systems with and without delays was studied in [24, 45].

On the other hand, the actuator may be subject to saturation due to the existence of physical, technological or even safety constraints [8]. Actuator saturation may degrade the system performance and even lead to instability. The issues of stability and stabilization of 2-D systems with state or actuator saturation have been addressed in [7, 10, 14, 30, 35].

In past few decades, control community has paid considerable attention to switched control systems, because such systems are not only academically challenging but also practically important [31]. A switched system belongs to a special class of hybrid systems which consist of several subsystems described by differential/difference equations, along with a switching law specifying the switching between subsystems. Recently, the stability of 2-D switched systems via common Lyapunov function and multiple Lyapunov function approaches has been studied by Benzaouia et al. [2, 3]. The stability and stabilization of 2-D switched systems were investigated by utilizing the average dwell time approach [27–29, 42]. State feedback and output feedback $H_\infty$ stabilization problems of 2-D switched delay-free systems were investigated in [16, 17]. Moreover, the dynamic output feedback $H_\infty$ stabilization problem for 2-D switched systems with constant delay was investigated in [18]. However, to the best of our knowledge, the issue of control for 2-D switched systems with time-varying delay and actuator saturation has not been fully investigated, which motivates our current study.

In this paper, the $H_\infty$ control problem of 2-D discrete switched systems with time-varying delay and actuator saturation represented by the second FM model is studied. Main contributions of this paper can be summarized as follows: (1) A new delay-dependent stability condition of 2-D switched delayed systems is derived by utilizing the multiple Lyapunov functional approach; and (2) $H_\infty$ disturbance attenuation performance of the 2-D switched delay systems in the presence of actuator saturation is developed and the corresponding controller gains are obtained.

The remainder of this paper is organized as follows. In Sect. 2, problem formulation and some necessary lemmas are given. In Sect. 3, main results are presented. In Sect. 4, two examples are given to show the effectiveness of the proposed results. In Sect. 5, concluding remarks are given.

Notations: Throughout this paper, the superscript “$T$” denotes the transpose, and $\left\| \cdot \right\|$ denotes the Euclidean norm. $I$ represents the identity matrix with appropriate dimension. The set of all nonnegative integers is represented by $Z_{+}.\, \mathrm{sat}\left( \cdot \right)$ denotes the saturation function, and $\mathrm{diag}\left\{ {a_i } \right\}$ denotes a diagonal matrix with the diagonal elements $a_i ,\,i=1,2,...,n.\, X^{-1}$ denotes the inverse of $X$. The asterisk ${*}$ in a matrix is used to denote the term that is induced by symmetry. The $l_2$-norm of a 2-D signal $w(i,j)\in R^{n},\, i,j\in Z_+$, is given by

$$\begin{aligned} \left\| w \right\| _2 =\sqrt{\sum _{i=0}^\infty {\sum _{j=0}^\infty {\left[ {w^{T}\left( {i,j} \right) w\left( {i,j} \right) } \right] }}}. \end{aligned}$$

We say $w(i,j)$ belongs to $l_2 \left\{ {\left[ {0,\infty } \right) ,\left[ {0,\infty } \right) } \right\}$ if $\left\| w \right\| _2 <\infty$.

2 Problem Formulation and Preliminaries

Consider the following discrete 2-D switched delay system with actuator saturation in the second FM model:

$$\begin{aligned} x(i+1,j+1)&= A_1^{\sigma (i,j+1)} x(i,j+1)+A_2^{\sigma (i+1,j)} x(i+1,j)\nonumber \\&+A_{d1}^{\sigma (i,j+1)} x(i-d_1 (i),j+1) \nonumber \\&+A_{d2}^{\sigma (i+1,j)} x(i+1,j-d_2 (j))+B_1^{\sigma (i,j+1)} w(i,j+1) \nonumber \\&+B_2^{\sigma (i+1,j)} w(i+1,j) \nonumber \\&+E_1^{\sigma (i,j+1)} \mathrm{sat}(u(i,j+1))+E_2^{\sigma (i+1,j)} \mathrm{sat}(u(i+1,j)),\qquad \end{aligned}$$

(1a)

$$\begin{aligned} z\left( {i,j} \right)&= G^{\sigma (i,j)}x\left( {i,j} \right) +L^{\sigma (i,j)}w\left( {i,j} \right) +F^{\sigma (i,j)}\mathrm{sat}(u(i,j)), \end{aligned}$$

(1b)

where $x\left( {i,j} \right) \in R^{n}$ is a state vector, $w\left( {i,j} \right) \in R^{q}$ is the noise input which belongs to $l_2 \left\{ {\left[ {0,\infty } \right) ,\left[ {0,\infty } \right) } \right\} ,\, u(i,j)\in R^{m}$ is the control input, and $z(i,j)\in R^{g}$ is the controlled output. $i$ and $j$ are integers in $Z_+ .\, \sigma (i,j):Z_+ \times Z_+ \rightarrow \underline{N}=\left\{ {1,2,...,N} \right\}$ is the switching signal with $N$ being the number of subsystems. $A_1^k ,\,A_2^k ,\, A_{d1}^k ,\, A_{d2}^k ,\, B_1^k ,\, B_2^k ,\, E_1^k , \,E_2^k , \,G^{k}, \,L^{k}$ and $F^{k}$, $k\in \underline{N}$, are constant matrices with appropriate dimensions. $d_1 (i)$ and $d_2 (j)$ are delays along the horizontal and vertical directions, respectively, and satisfy

$$\begin{aligned} \underline{d}{_1} \le d_1 (i)\le \bar{{d}}_1 , \underline{d}{_2} \le d_2 (j)\le \bar{{d}}_2 , \end{aligned}$$

(2)

where $\underline{d}{_1} ,\, \bar{{d}}_1 ,\, \underline{d}{_2}$ and $\bar{{d}}_2$ represent the lower and upper bounds on the horizontal and vertical directions, respectively.

Remark 1

When there is only one subsystem, i.e., $N=1$, system (1) reduces to the following 2-D system

$$\begin{aligned} x(i+1,j+1)&= A_1 x(i,j+1)+A_2 x(i+1,j)+A_{d1} x(i-d_1 (i),j+1) \nonumber \\&+A_{d2} x(i+1,j-d_2 (j))+B_1 w(i,j+1)+B_2 w(i+1,j) \nonumber \\&+E_1 \mathrm{sat}(u(i,j+1))+E_2 \mathrm{sat}(u(i+1,j)), \end{aligned}$$

(3a)

$$\begin{aligned} z\left( {i,j} \right)&= Gx\left( {i,j} \right) +Lw\left( {i,j} \right) +F\mathrm{sat}(u(i,j)). \end{aligned}$$

(3b)

Therefore, the addressed system (1) can be viewed as an extension of 2-D systems to switched systems.

For system (1), we consider a finite set of initial conditions, that is, there exist positive integers $z_1 <\infty$ and $z_2 <\infty$ such that

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} x(i,j)=h_{ij} , \quad \forall 0\le j\le z_1,\,\, i=-\bar{d_{1}}, -\bar{{d}}_1 +1,\ldots ,0, \\ x(i,j)=v_{ij} , \quad \forall 0\le i\le z_2 ,\,\, j=-\bar{d_{2}}, -\bar{{d}}_2 +1,\ldots ,0, \\ h_{00} =v_{00} ,\\ x(i,j)=0, \quad \forall j>z_1 , \,\,i=-\bar{d{_1}} ,-\bar{d{_1}} +1,\ldots ,0, \\ x(i,j)=0, \quad \forall i>z_2 , \,\,j=-\bar{d{_2}} ,-\bar{d{_2}} +1,\ldots ,0,\\ \end{array} \right. \end{aligned}$$

where $h_{ij}$ and $v_{ij}$ are given vectors.

The saturation function $\mathrm{sat}\left( \cdot \right) :R^{m}\rightarrow R^{m}$ is defined as

$$\begin{aligned} \mathrm{sat}\left( u \right) =\left[ \mathrm{sat}\left( {u{_1}} \right) \, \mathrm{sat}\left( {u{_2}} \right) \, \cdots \,\mathrm{sat}\left( {u{_m}} \right) \right] ^{T}, \end{aligned}$$

(4)

where $u=\left[ {u{_1}} \, {u{_2}} \,\cdots \,{u{_m}} \right] ^{T}\,\in R^{m}$, and $\mathrm{sat}\left( {u{_s}} \right) =\mathrm{sign}\left( {u{_s}} \right) \min \left\{ {1,\left| {u{_s}} \right| } \right\} ,\, s=1,2,\ldots ,m$.

Implementing the control law $u\left( {i,j} \right) =K^{\sigma (i,j)}x\left( {i,j} \right)$ to system (1) leads to the following closed-loop system:

$$\begin{aligned} x(i+1,j+1)&= A_1^{\sigma (i,j+1)} x(i,j+1)+A_2^{\sigma (i+1,j)} x(i+1,j) \nonumber \\&+A_{d1}^{\sigma (i,j+1)} x(i-d_1 (i),j+1) \nonumber \\&+A_{d2}^{\sigma (i+1,j)} x(i+1,j-d_2 (j))+B_1^{\sigma (i,j+1)} w(i,j+1) \nonumber \\&+B_2^{\sigma (i+1,j)} w(i+1,j) \nonumber \\&+E_1^{\sigma (i,j+1)} \mathrm{sat}(K^{\sigma (i,j+1)}x(i,j+1)) \nonumber \\&+E_2^{\sigma (i+1,j)} \mathrm{sat}(K^{\sigma (i+1,j)}x(i+1,j)), \end{aligned}$$

(5a)

$$\begin{aligned} z\left( {i,j} \right)&= G^{\sigma (i,j)}x\left( {i,j} \right) +L^{\sigma (i,j)}w\left( {i,j} \right) +F^{\sigma (i,j)}\mathrm{sat}\left( {K^{\sigma (i,j)}x\left( {i,j} \right) } \right) .\nonumber \\ \end{aligned}$$

(5b)

Let $\Xi$ be the set of all diagonal matrices in $R^{m\times m}$ with diagonal elements that are either $1$ or $0$. For example, if $m=2$, then

$$\begin{aligned} \Xi =\left\{ D{_1} ,D{_2} ,D{_3} ,D{_4} \right\} =\left\{ \! \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} \left[ \begin{array}{l@{\quad }l} 0&{} 0 \\ 0&{} 0 \\ \end{array} \right] ,&{} \left[ \begin{array}{l@{\quad }l} 0&{} 0 \\ 0&{} 1 \\ \end{array} \right] ,&{} \left[ \begin{array}{l@{\quad }l} 1&{} 0 \\ 0&{} 0 \\ \end{array} \right] ,&{} \left[ \begin{array}{l@{\quad }l} 1&{} 0 \\ 0&{} 1 \\ \end{array} \right] \\ \end{array} \!\right\} . \end{aligned}$$

There are $2^{m}$ elements $D{_p}$ in $\Xi$, and for every $p=1,\ldots ,2^{m},\,D_{p}^{-}=I_{m}-D_{p}$ is also an element in $\Xi$.

For a positive definite matrix $P\in R^{n\times n}$ and a scalar $\delta >0$, an ellipsoid $\Omega \left( {P,\delta }\right)$ is defined as:

$$\begin{aligned} \Omega \left( {P,\delta } \right) =\left\{ {x\left( {i,j} \right) \in R^{n}:x\left( {i,j} \right) ^{T}Px\left( {i,j} \right) \le \delta } \right\} . \end{aligned}$$

For a matrix $H\in R^{m\times n}$, the polyhedral set $L\left( H\right)$ is defined as:

$$\begin{aligned} L\left( H \right) :=\left\{ {x\left( {i,j} \right) \in R^{n}:\left| {H_s x\left( {i,j} \right) } \right| \le 1,\; \quad s=1,2,\ldots ,m} \right\} . \end{aligned}$$

where $H{_s}$ is the $s$th row of the matrix $H$.

Remark 2

In this paper, the switch among different modes can be assumed to occur at each of the sampling points of $i$ or $j$. It should be observed that the value of $\sigma (i,j)$ only depends upon $i+j$ (see the Refs. [3, 42]).

Definition 1

[1] System (5) with $w(i,j)=0$ is asymptotically stable under switching signal $\sigma (i,j)$, if $\mathop {\lim }\limits _{i+j\rightarrow \infty } x(i,j)=0$.

Definition 2

System (5) is said to have a prescribed $H_\infty$ disturbance attenuation level $\gamma$ under switching signal $\sigma (i,j)$, if it satisfies the following conditions:

• (1) When $w(i,j)=0$, system (5) is asymptotically stable;

• (2) Under zero boundary condition, it holds that

$$\begin{aligned} J_0 =\mathop {\sup }\limits _{0\ne \left( {i,j} \right) \in l_2 } \frac{\left\| {\bar{{z}}} \right\| _2^2}{\left\| {\bar{{w}}} \right\| _2^2 }<\gamma ^{2}, \end{aligned}$$

(6)

where $\left\| {\bar{{z}}} \right\| _2^2 =\left\| {z(i,j+1)} \right\| _2^2 +\left\| {z(i+1,j)} \right\| _2^2$ and $\left\| {\bar{{w}}} \right\| _2^2 =\left\| {w(i,j+1)} \right\| _2^2 +\left\| {w(i+1,j)} \right\| _2^2$.

Lemma 1

[5] For a given matrix $S=\left[ \begin{array}{ll} {S_{11} }&{} {S_{12}} \\ {S_{12}^T }&{} {S_{22}} \\ \end{array}\right]$, where $S_{11}$ and $S_{22}$ are square matrices, the following conditions are equivalent:

• (1) $S<0;$

• (2) $S_{11} <0,\, S_{22} -S_{12}^T S_{11}^{-1} S_{12} <0;$

• (3) $S_{22} <0,\, S_{11} -S_{12} S_{22}^{-1} S_{12}^T <0.$

Lemma 2

[26] Given $K\in R^{m\times n}$ and $H\in R^{m\times n}$, then

$$\begin{aligned} \mathrm{sat}\left( {Kx\left( {i,j} \right) } \right) \in co\left\{ {\left( {D{_p} K+D_p^- H} \right) x\left( {i,j} \right) ,\; \quad p=1,2,\ldots ,2^{m}} \right\} \end{aligned}$$

(7)

for all $x\left( {i,j} \right) \in R^{n}$ satisfying $\left| {H_s x\left( {i,j} \right) } \right| \le 1$ for $s=1,2,\ldots ,m$, where $H_s$ is the $s$th row of the matrix $H$ and $co\{\cdot \}$ is the convex hull.

When $x(i,j)\in L\left( {H^{\sigma (i,j)}} \right)$, it follows from Lemma 2 that

$$\begin{aligned}&\mathrm{sat}\left( {K^{\sigma (i,j)}x\left( {i,j} \right) } \right) \in co\left\{ \left( {D_p K^{\sigma (i,j)}+D{_p}{^-} H^{\sigma (i,j)}} \right) x\left( {i,j} \right) ,\;\right. \nonumber \\&\quad \left. p=1,2,\ldots ,2^{m} \right\} , \end{aligned}$$

(8)

then substituting (8) into system (5) and noticing the relationship between convex combination and its vertex, we can obtain the following representation for $p=1,2,\ldots ,2^{m}$

$$\begin{aligned} x(i+1,j+1)&= A_{1p}^{\sigma (i,j+1)} x(i,j+1)+A_{2p}^{\sigma (i+1,j)} x(i+1,j) \nonumber \\&+A_{d1}^{\sigma (i,j+1)} x(i-d_1 (i),j+1) \nonumber \\&+A_{d2}^{\sigma (i+1,j)} x(i+1,j-d_2 (j))+B_1^{\sigma (i,j+1)} w(i,j+1) \nonumber \\&+B_2^{\sigma (i+1,j)} w(i+1,j), \end{aligned}$$

(9a)

$$\begin{aligned} z\left( {i,j} \right)&= G_p^{\sigma (i,j)} x(i,j)+L^{\sigma (i,j)}w\left( {i,j} \right) , \end{aligned}$$

(9b)

where

$$\begin{aligned} A_{1p}^{\sigma (i,j+1)}&= A_1^{\sigma (i,j+1)} +E_1^{\sigma (i,j+1)} D_p K^{\sigma (i,j+1)}+E_1^{\sigma (i,j+1)} D_p^- H^{\sigma (i,j+1)},\\ A_{2p}^{\sigma (i+1,j)}&= A_2^{\sigma (i+1,j)} +E_2^{\sigma (i+1,j)} D_p K^{\sigma (i+1,j)}+E_2^{\sigma (i+1,j)} D_p^- H^{\sigma (i+1,j)},\\ G_p^{\sigma (i,j)}&= G^{\sigma (i,j)}+F^{\sigma (i,j)}D_p K^{\sigma (i,j)}+F^{\sigma (i,j)}D_p^- H^{\sigma (i,j)}. \end{aligned}$$

3 Main Results

In this section, we focus upon the controller design of 2-D discrete switched system (1) to ensure the asymptotical stability and $H_\infty$ performance of the closed-loop system (5).

3.1 Stability Analysis

In this subsection, a sufficient condition for asymptotical stability of system (5) is obtained via the multiple Lyapunov functional approach.

Theorem 1

Consider system (5) with $w(i,j)=0$, if there exist symmetric positive definite matrices $P_{h}^{k},\, P_{v}^{k},\, Q{_h} ,\, Q{_v} ,\, W_h ,\, W{_v} ,\, R{_h} ,\, R{_v} ,\, X=\left[ \begin{array}{ll} X_{11}&{} X_{12} \\ *&{} X_{22} \\ \end{array} \right] ,\, Y=\left[ \begin{array}{ll} Y_{11}&{}Y_{12} \\ *&{} Y_{22} \\ \end{array} \right]$ and any matrices $N_1 =\left[ \begin{array}{l} N_{11} \\ N_{12} \\ \end{array} \right] , \, N_2 =\left[ \begin{array}{l} N_{21} \\ N_{22} \\ \end{array} \right] ,\, S_1 =\left[ \begin{array}{l} S_{11} \\ S_{12} \\ \end{array} \right] ,\, S_2 =\left[ \begin{array}{l} S_{21} \\ S_{22} \\ \end{array} \right]$ and $H^{k}$ with appropriate dimensions, $k\in \underline{N}$, such that

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\Gamma _{11}}&{} 0&{} {\Gamma _{13}}&{} 0&{} {-N_{21}}&{} 0&{} {A_{1p}^{lT} (P_h^k +P_v^k )}&{} {\sqrt{\bar{{d}}_1}(A_{1p}^{lT} -I)R_h}&{} {\sqrt{\bar{{d}}_2 }A_{1p}^{lT} R_v} \\ *&{} {\Gamma _{22} }&{} 0&{} {\Gamma _{24} }&{} 0&{} {-S_{21} }&{} {A_{2p}^{lT} (P_h^k +P_v^k )}&{} {\sqrt{\bar{{d}}_1 }A_{2p}^{lT} R_h }&{} {\sqrt{\bar{{d}}_2 }(A_{2p}^{lT} -I)R_v } \\ *&{} *&{} {\Gamma _{33} }&{} 0&{} {-N_{22} }&{} 0&{} {A_{d1}^{lT} (P_h^k +P_v^k )}&{} {\sqrt{\bar{{d}}_1 }A_{d1}^{lT} R_h }&{} {\sqrt{\bar{{d}}_2 }A_{d1}^{lT} R_v } \\ *&{} *&{} *&{} {\Gamma _{44} }&{} 0&{} {-S_{22} }&{} {A_{d2}^{lT} (P_h^k +P_v^k )}&{} {\sqrt{\bar{{d}}_1 }A_{d2}^{lT} R_h }&{} {\sqrt{\bar{{d}}_2 }A_{d2}^{lT} R_v } \\ *&{} *&{} *&{} *&{} {-W_h }&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} {-W_v }&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} {-(P_h^k +P_v^k )}&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-R_h }&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-R_v } \\ \end{array} \right] <0,\nonumber \\&\qquad p=1,2,\ldots ,2^{m},\,\forall k,l\in \underline{N}, \end{aligned}$$

(10)

$$\begin{aligned}&\left[ \begin{array}{l@{\quad }l} X&{} {N_1 } \\ *&{} {R_h }\\ \end{array} \right] \ge 0, \quad \left[ \begin{array}{l@{\quad }l} X&{} {N_2} \\ *&{} {R_h} \\ \end{array} \right] \ge 0, \quad \left[ \begin{array}{l@{\quad }l} Y&{} {S_1}\\ *&{} {R_v} \\ \end{array} \right] \ge 0, \quad \left[ \begin{array}{l@{\quad }l} Y&{} {S_2} \\ *&{} {R_v} \\ \end{array} \right] \ge 0, \end{aligned}$$

(11)

$$\begin{aligned}&\Omega \left( {P_h^k +P_v^k ,1} \right) \subset L\left( {H^{k}} \right) , \quad k\in \underline{N}, \end{aligned}$$

(12)

where

$$\begin{aligned} \Gamma _{11}&= -P_h^l +W_h +(\bar{{d}}_1 -{d}_1 +1)Q_h +N_{11} +N_{11}^T +\bar{{d}}_1 X_{11} ,\\ \Gamma _{22}&= -P_v^l +W_v +(\bar{{d}}_2 -{d}_2 +1)Q_v +S_{11} +S_{11}^T +\bar{{d}}_2 Y_{11} ,\\ \Gamma _{33}&= -Q_h +N_{22} +N_{22}^T -N_{12} -N_{12}^T +\bar{{d}}_1 X_{22} ,\quad \Gamma _{44} =-Q_v +S_{22} +S_{22}^T -S_{12}\\&-S_{12}^T +\bar{{d}}_2 Y_{22} ,\\ \Gamma _{13}&= N_{12}^T -N_{11} +N_{21} +\bar{{d}}_1 X_{12} , \quad \Gamma _{24} =-S_{11} +S_{12}^T +S_{21} +\bar{{d}}_2 Y_{12} , \end{aligned}$$

then the system is asymptotically stable for all switching sequence $\sigma (i,j)$ and initial states satisfying $\hbox {T}(\phi _h,\phi _v )\le 1$, where

$$\begin{aligned} \hbox {T}(\phi _h ,\phi _v )&= \phi _h^2 (\mathop {\max }\limits _{k\in \underline{N}} \{\lambda _{\max } (P_h^k )\}+\bar{{d}}_1 \lambda _{\max } (Q_h )+\bar{{d}}_1 \lambda _{\max } (W_h )+\tau _{1h} \lambda _{\max } (Q_h)\nonumber \\&+\tau _{2h} \lambda _{\max } (R_h )) +\phi _v^2 (\mathop {\max }\limits _{k\in \underline{N}} \{\lambda _{\max } (P_v^k )\}+\bar{{d}}_2 \lambda _{\max } (Q_v )+\bar{{d}}_2 \lambda _{\max } (W_v )\nonumber \\&+\tau _{1v} \lambda _{\max } (Q_v) +\tau _{2v} \lambda _{\max } (R_v )), \end{aligned}$$

(13)

and

$$\begin{aligned} \phi _h&= \mathop {\max }\limits _{-\bar{{d}}_1 \le \xi _h \le 0} \sum _{j=0}^{z_1 } {\left\| {x(-\xi _h ,j)} \right\| } , \quad \phi _v =\mathop {\max }\limits _{-\bar{{d}}_2 \le \xi _v \le 0} \sum _{i=0}^{z_2 } {\left\| {x(i,-\xi _v )} \right\| },\\&\quad \tau _{1h} =0.5(\bar{{d}}_1 -\underline{d}_1 )(\bar{{d}}_1 -1+\underline{d}_1 ), \tau _{2h} =0.5\bar{{d}}_1 (1+\bar{{d}}_1 ), \\&\quad \tau _{1v} =0.5(\bar{{d}}_2 -\underline{d}_2 )(\bar{{d}}_2 -1+\underline{d}_2 ), \quad \tau _{2v} =0.5\bar{{d}}_2 (1+\bar{{d}}_2). \end{aligned}$$

Proof

When $x(i,j)\in \mathop \cap \limits _{k=1}^N \Omega (P_h^k +P_v^k ,\;1)$, it can be obtained from (12) that $x(i,j)\in L\left( {H^{k}} \right)$, $\forall k\in \underline{N}$, then by Lemma 2, we get (8).

At first, we consider the following Lyapunov candidate functional

$$\begin{aligned} V(i,j)=V_{\sigma (i,j)} (i,j)=V_{\sigma (i,j)}^h (i,j)+V_{\sigma (i,j)}^v (i,j), \end{aligned}$$

(14)

with

$$\begin{aligned} V_k^h (i,j)&= x(i,j)^{T}P_h^k x(i,j)\!+\!\sum _{r=i-d_1 (i)}^{i-1} {x(r,j)^{T}Q_h } x(r,j)\\&+\sum _{r=i-\bar{{d}}_1 }^{i-1} {x(r,j)^{T}W_h } x(r,j)+\sum _{s=-\bar{{d}}_1 +1}^{-\underline{d}_1 } \sum _{r=i+s}^{i-1} {x(r,j)^{T}Q_h } x(r,j)\\&+\sum _{s=-\bar{{d}}_1 +1}^0{\sum _{r=i+s-1}^{i-1} {\eta (r,j)^{T}R_h } \eta (r,j),\quad \forall k\in \underline{N},}\\ V_k^v (i,j)&= x(i,j)^{T}P_v^k x(i,j)\!+\!\sum _{t=j-d_2 (j)}^{j-1} {x(i,t)^{T}Q_v } x(i,t)\!+\!\sum _{t=j-\bar{{d}}_2 }^{j-1} {x(i,t)^{T}W_v } x(i,t)\\&+\sum _{s=-\bar{{d}}_2 +1}^{-\underline{d}_2} \sum _{t=j+s}^{j-1} {x(i,t)^{T}Q_v } x(i,t)\\&+\sum _{s=-\bar{{d}}_2 +1}^0{\sum _{t=j+s-1}^{j-1} {\delta (i,t)^{T}R_v } \delta (i,t),\quad \forall k\in \underline{N},}\\ \eta (r,j)&= x(r+1,j)-x(r,j), \quad \delta (i,t)=x(i,t+1)-x(i,t). \end{aligned}$$

Without lose of generality, it is assumed that the $k$th and the $l$th subsystems are activated at points $(i+1, j+1)$ and $(i, j+1)$, respectively. The increment $\Delta V(i+1,j+1)$ along the trajectory of system (5) with $w(i,j)=0$ satisfies,$\forall x(i,j)\in \mathop \cap \limits _{k=1}^N \Omega (P_h^k +P_v^k ,\;1)$,

$$\begin{aligned}&\Delta V(i+1,j+1)=V_k^h (i+1,j+1)+V_k^v (i+1,j+1) \nonumber \\&\qquad -V_l^h(i,j+1)-V_l^v (i+1,j) \le x(i+1,j+1)^{T}P_h^k x(i+1,j+1)\nonumber \\&\qquad -x(i,j+1)^{T}P_h^l x(i,j+1) +x(i,j+1)^{T}Q_h x(i,j+1)\nonumber \\&\qquad -x(i-d_1 (i),j+1)^{T}Q_h x(i-d_1 (i),j+1)\nonumber \\&\qquad +\sum _{r=i+1-\bar{{d}}_1 }^{i-\underline{d}_1 } {x(r,j+1)^{T}Q_h } x(r,j+1) +x(i,j+1)^{T}W_h x(i,j+1)\nonumber \\&\qquad -x(i-\bar{{d}}_1 ,j+1)^{T}W_h x(i-\bar{{d}}_1 ,j+1) +(\bar{{d}}_1 -\underline{d}_1 )x(i,j+1)^{T}\nonumber \\&\quad \quad \times Q_h x(i,j+1)-\sum _{r=i+1-\bar{{d}}_1 }^{i-\underline{d}_1 } {x(r,j+1)^{T}Q_h x(r,j+1)} \nonumber \\&\quad \quad +\,\bar{{d}}_1 \eta (i,j+1)^{T}R_h \eta (i,j+1)-\sum _{r=i-\bar{{d}}_1 }^{i-1} {\eta (r,j+1)^{T}R_h \eta (r,j+1)} \nonumber \\&\quad \quad +\,x(i+1,j+1)^{T}P_v^k x(i+1,j+1)-x(i+1,j)^{T}P_v^l x(i+1,j) \nonumber \\&\quad \quad +\,x(i+1,j)^{T}Q_v x(i+1,j) -x(i+1,j-d_2 (j))^{T}Q_v x(i+1,j-d_2 (j))\nonumber \\&\quad \quad +\,\sum _{t=j+1-\bar{{d}}_2 }^{j-\underline{d}_2 } {x(i+1,t)^{T}Q_v } x(i+1,t) +x(i+1,j)^{T}W_v x(i+1,j)\nonumber \\&\quad \quad -\,x(i+1,j-\bar{{d}}_2 )^{T}W_v x(i+1,j-\bar{{d}}_2 )+(\bar{{d}}_2 -\underline{d}_2 )x(i+1,j)^{T} \nonumber \\&\quad \quad \times Q_v x(i+1,j)-\sum _{t=j+1-\bar{{d}}_2 }^{j-\underline{d}_2 } {x(i+1,t)^{T}Q_v x(i+1,t)} \nonumber \\&\quad \quad +\,\bar{{d}}_2 \delta (i+1,j)^{T}R_v \delta (i+1,j)-\sum _{t=j-\bar{{d}}_2 }^{j-1} {\delta (i+1,t)^{T}R_v \delta (i+1,t)} \nonumber \\&\quad \le \mathop {\max }\limits _{p=1,2,\cdots ,2^{m}} \left\{ {\chi (i,j)^{T}(\Psi +\Theta ^{T}(P_h^k +P_v^k )\Theta )\chi (i,j)} \right\} \nonumber \\&\quad \quad +\,\bar{{d}}_1 \eta (i,j+1)^{T}R_h \eta (i,j+1)-\sum _{r=i-\bar{{d}}_1 }^{i-1} {\eta (r,j+1)^{T}R_h \eta (r,j+1)} \nonumber \\&\quad \quad +\,\bar{{d}}_2 \delta (i+1,j)^{T}R_v \delta (i+1,j)-\sum _{t=j-\bar{{d}}_2 }^{j-1} {\delta (i+1,t)^{T}R_v \delta (i+1,t)} , \end{aligned}$$

(15)

where

$$\begin{aligned} \chi (i,j)&= \left[ {\chi _1 (i,j)^{T}}\, {\chi _2 (i,j)^{T}} \right] ^{T},\\ \chi _1 (i,j)&= \left[ {x(i,j+1)^{T}}\, {x(i+1,j)^{T}}\, {x(i-d_1 (i),j+1)^{T}} \right] ^{T},\\ \chi _2 (i,j)&= \left[ {x(i+1,j-d_2 (j))^{T}}\, {x(i-\bar{{d}}_1 ,j+1)^{T}}\, {x(i+1,j-\bar{{d}}_2 )^{T}} \right] ^{T},\\ \Psi&= \mathrm{diag}\{\Psi _{11} ,\Psi _{22} ,-Q_h ,-Q_v ,-W_h ,-W_v \}, \quad \Psi _{11} =-P_h^l\\&\quad +W_h +(\bar{{d}}_1 -{d}_1 +1)Q_h ,\\ \Psi _{22}&= -P_v^l +W_v +(\bar{{d}}_2 -{d}_2 +1)Q_v , \quad \Theta =\left[ \begin{array}{llllll} {A_{1p}^l }&{A_{2p}^l }&{A_{d1}^l}&{A_{d2}^l}&0&0 \end{array}\right] . \end{aligned}$$

The following equations hold for any matrices $N_1^ =\left[ \begin{array}{l} N_{11} \\ N_{12} \\ \end{array} \right] ,\, N_2 =\left[ \begin{array}{l} N_{21} \\ N_{22} \\ \end{array} \right] ,\, S_1 =\left[ \begin{array}{l} S_{11} \\ S_{12} \\ \end{array} \right]$ and $S_2 =\left[ \begin{array}{l} S_{21} \\ S_{22} \\ \end{array} \right]$ with appropriate dimensions:

$$\begin{aligned} 0&= 2\zeta _1 \left( {i,j} \right) ^{T}N_1 \left[ \! {x\left( {i,j\!+\!1} \right) \!-\!x\left( {i\!-\!d_1 (i),j\!+\!1} \!\right) \!-\!\sum _{r=i-d_1 (i)}^{i-1} {\eta (r,j+1)} } \!\right] \!, \end{aligned}$$

(16)

$$\begin{aligned} 0&= 2\zeta _1 \left( {i,j} \right) ^{T}N_2 \left[ \! {x\left( {i\!-\!d_1 (i),j\!+\!1} \right) \!-\!x(i\!-\!\bar{{d}}_1 ,j\!+\!1)\!-\!\sum _{r=i-\bar{{d}}_1 }^{i-d_1 (i)-1} {\eta (r,j\!+\!1)} } \!\right] , \end{aligned}$$

(17)

$$\begin{aligned} 0&= 2\zeta _2 \left( {i,j} \right) ^{T}S_1 \left[ {x\left( {i\!+\!1,j} \right) \!-\!x\left( {i\!+\!1,j\!-\!d_2 (j)} \right) \!-\!\sum _{t=j-d_2 (j)}^{j-1} {\delta (i\!+\!1,t)} } \!\right] \!, \end{aligned}$$

(18)

$$\begin{aligned} 0&= 2\zeta _2 \left( {i,j} \right) ^{T}S_2 \left[ {x\left( {i\!+\!1,j\!-\!d_2 (j)} \right) \!-\!x(i\!+\!1,j\!-\!\bar{{d}}_2 )\!-\!\sum _{t=j-\bar{{d}}_2 }^{j-d_2 (j)\!-\!1} {\delta (i\!+\!1,t)} } \!\right] \!,\nonumber \\ \end{aligned}$$

(19)

where

$$\begin{aligned} \zeta _1 (i,j)^{T}&= [ {x(i,j+1)^{T}}\, {x(i-d_1 (i),j+1)^{T}]},\\ \zeta _2 (i,j)^{T}&= {[x(i+1,j)^{T}}\, {x(i+1,j-d_2 (j))^{T}]}. \end{aligned}$$

On the other hand, for any matrices $X=\left[ \begin{array}{ll} X_{11} &{} X_{12} \\ *&{} X_{22} \\ \end{array} \right] >0$ and $Y=\left[ {{\begin{array}{ll} Y_{11} &{} Y_{12} \\ *&{} Y_{22} \\ \end{array}}} \right] \!>\!0$, the following equations hold:

$$\begin{aligned} 0&= \bar{{d}}_1 \zeta _1 \left( {i,j} \right) ^{T}X\zeta _1 \left( {i,j} \right) -\sum _{r=i-d_1 (i)}^{i-1} {\zeta _1 \left( {i,j} \right) ^{T}X\zeta _1 \left( {i,j} \right) } \nonumber \\&-\sum _{r=i-\bar{{d}}_1}^{i-d_1 (i)-1} {\zeta _1 \left( {i,j} \right) ^{T}X\zeta _1 \left( {i,j} \right) } , \end{aligned}$$

(20)

$$\begin{aligned} 0&= \bar{{d}}_2 \zeta _2 \left( {i,j} \right) ^{T}Y\zeta _2 \left( {i,j} \right) -\sum _{t=j-d_2 (j)}^{j-1} {\zeta _2 \left( {i,j} \right) ^{T}Y\zeta _2 \left( {i,j} \right) } \nonumber \\&-\sum _{t=j-\bar{{d}}_2}^{j-d_2 (j)-1} {\zeta _2 \left( {i,j} \right) ^{T}Y\zeta _2 \left( {i,j} \right) } . \end{aligned}$$

(21)

Adding the terms on the right-hand sides of Eqs. (16–21) to (15) allows us to write (15) as

$$\begin{aligned}&\Delta V(i+1,j+1)\le \mathop {\max }\limits _{p=1,2,\cdots ,2^{m}} \left\{ {\chi (i,j)^{T}\Psi _p \chi (i,j)} \right\} \\&\quad -\sum _{r=i-d_1 (i)}^{i-1} {\left[ \begin{array}{l@{\quad }l} {\zeta _1 \left( {i,j} \right) } \\ {\eta (r,j+1)} \\ \end{array} \right] ^{T}} \left[ \begin{array}{l@{\quad }l} X&{} {N_1} \\ *&{} {R_h} \\ \end{array} \right] \left[ \begin{array}{l@{\quad }l} {\zeta _1 \left( {i,j} \right) } \\ {\eta (r,j+1)} \\ \end{array} \right] \\&\quad -\sum _{r=i-\bar{{d}}_1 }^{i-d_1 (i)-1} {\left[ \begin{array}{l@{\quad }l} {\zeta _1 \left( {i,j} \right) } \\ {\eta (r,j+1)} \\ \end{array} \right] ^{T}} \left[ \begin{array}{l@{\quad }l} X&{} {N_2} \\ *&{} {R_h } \\ \end{array} \right] \left[ \begin{array}{l@{\quad }l} {\zeta _1 \left( {i,j} \right) } \\ {\eta (r,j+1)} \\ \end{array} \right] \\&\quad -\sum _{t=j-d_2 (j)}^{j-1} {\left[ \begin{array}{ll} {\zeta _2 \left( {i,j} \right) } \\ {\delta (i+1,t)} \\ \end{array} \right] } ^{T} \left[ \begin{array}{l@{\quad }l} Y&{} {S_1} \\ *&{} {R_v } \\ \end{array} \right] \left[ \begin{array}{l@{\quad }l} {\zeta _2 \left( {i,j} \right) } \\ {\delta (i+1,t)} \\ \end{array}\ \right] \\&\quad -\sum _{t=j-\bar{{d}}_2 }^{j-d_2 (j)-1} {\left[ \begin{array}{ll} {\zeta _2 \left( {i,j} \right) } \\ {\delta (i+1,t)} \\ \end{array} \right] } ^{T}\left[ \begin{array}{l@{\quad }l} Y&{} {S_2} \\ *&{} {R_v} \\ \end{array} \right] \left[ \begin{array}{l@{\quad }l} {\zeta _2 \left( {i,j} \right) } \\ {\delta (i+1,t)} \\ \end{array} \right] , \end{aligned}$$

where $\Psi _p =\Psi +\Theta ^{T}(P_h^k +P_v^k )\Theta +\left[ \begin{array}{ll} \Sigma {_1}{^T}&{}\Sigma {_2}{^T} \\ \end{array} \right] \left[ \begin{array}{ll} {\bar{d{_1}}} R{_h}&{} 0 \\ 0&{} {\bar{d{_2}}} R{_v} \\ \end{array} \right] \left[ \begin{array}{ll} \Sigma {_1}&{} \Sigma {_2} \\ \end{array} \right] ,$

$$\begin{aligned} \Sigma {_1} \!=\!\left[ {A_{1p}^l -I}\quad {A_{2p}^l}\quad {A_{d1}^l}\quad {A_{d2}^l}\quad 0\quad 0 \right] ,\quad \! \Sigma {_2} \!=\!\left[ {A_{1p}^l}\quad {A_{2p}^l -I}\quad {A_{d1}^l}\quad {A_{d2}^l}\quad 0\quad 0 \!\right] \!. \end{aligned}$$

Applying Lemma 1, it follows from LMI (10) that $\Psi _p <0$, and from (11), we have

$$\begin{aligned} \Delta V(i+1,j+1)<0, \quad \forall x(i,j)\in \mathop \cap \limits _{k=1}^N \Omega (P_h^k +P_v^k ,\;1). \end{aligned}$$

(22)

For any $r>z=\max (z_1 ,z_2 )$, it follows from (3) that $V^{h}(0,r)=V^{v}(r,0)=0$, then summing up terms on both sides of (22) from $r-1$ to $0$ with respect to $j$ and $0$ to $r-1$ with respect to $i$, one gets

$$\begin{aligned} \sum _{i+j=r} V (i,j)&= V^{h}(0,r)+V^{h}(1,r-1)+V^{h}(2,r-2)+\cdots +V^{h}(r-1,1) \nonumber \\&+V^{h}(r,0)+V^{v}(0,r)+V^{v}(1,r-1)+V^{v}(2,r-2)+\cdots +V^{v}(r-1,1) \nonumber \\&+V^{v}(r,0) \nonumber \\&< V^{h}(0,r-1)+V^{v}(0,r-1)+V^{h}(1,r-2)+V^{v}(1,r-2) \nonumber \\&+\cdots +V^{h}(r-1,0)+V^{v}(r-1,0) \nonumber \\&= \sum _{i+j=r-1} {V(i,j)} <\cdots <\sum _{i+j=z} V (i,j). \end{aligned}$$

(23)

It can be obtained from (23) that

$$\begin{aligned} \sum _{i+j=1} V (i,j)&< V(0,0)+V^{h}(0,1)+V^{v}(1,0)\\&= \sum _{j=0}^1 {V^{h}(0,j)} +\sum _{i=0}^1 {V^{v}(i,0)}\\&\le \sum _{j=0}^{z_1 } {V^{h}(0,j)} +\sum _{i=0}^{z_2 } {V^{v}(i,0)} ,\\ \sum _{i+j=2} V (i,j)&< \sum _{i+j=1} {V(i,j)} +V_h (0,2)+V_v (2,0)\\&< V(0,0)+V^{h}(0,1)+V^{v}(1,0)+V^{h}(0,2)+V^{v}(2,0)\\&\le \sum _{j=0}^{z_1 } {V^{h}(0,j)} +\sum _{i=0}^{z_2 } {V^{v}(i,0)} . \end{aligned}$$

Similarly, we can get, $\forall i+j=r\in Z_+$,

$$\begin{aligned}&x(i,j)^{T}(P_h^{\sigma (i,j)} +P_v^{\sigma (i,j)} )x(i,j) \\&\quad \le \sum _{i+j=r} V (i,j) \\&\quad \le \sum _{j=0}^{z_1 } {V^{h}(0,j)} +\sum _{i=0}^{z_2 } {V^{v}(i,0)} \\&\quad \le \phi _h^2 (\mathop {\max }\limits _{k\in \underline{N}} \{\lambda _{\max } (P_h^k )\}+\bar{{d}}_1 \lambda _{\max } (Q_h )+\bar{{d}}_1 \lambda _{\max } (W_h )+\tau _{1h} \lambda _{\max } (Q_h) \\&\quad \quad +\,\tau _{2h} \lambda _{\max } (R_h )) +\phi _v^2 (\mathop {\max }\limits _{k\in \underline{N}} \{\lambda _{\max } (P_v^k )\}+\bar{{d}}_2 \lambda _{\max } (Q_v )+\bar{{d}}_2 \lambda _{\max } (W_v )\\&\qquad +\,\tau _{1v} \lambda _{\max } (Q_v) +\tau _{2v} \lambda _{\max } (R_v )) \\&\quad =\hbox {T}(\phi _h ,\phi _v ). \end{aligned}$$

If $\hbox {T}(\phi {_h} ,\phi {_v})\le 1$, then $x(i,j)^{T}(P{_h}{^k} +P{_v}{^k})x(i,j)\le 1$ is satisfied for all $k\in \underline{N}$. Therefore, all the trajectories of $x(i,j)$ starting from $\hbox {T}(\phi _h ,\phi _v )\le 1$ will remain within $\mathop \cap \nolimits _{k=1}^N \Omega (P_h^k +P_v^k ,\,1)$. Moreover, system (5) with $w(i,j)=0$ is asymptotically stable for any switching sequences and initial conditions satisfying $\hbox {T}(\phi _h ,\phi _v )\le 1$.

This completes the proof. $\square$

3.2 $H_\infty$ Performance Analysis

In this subsection, $H_\infty$ performance analysis of system (5) with $w\left( {i,j} \right)$ satisfying $\left\| {\bar{{w}}} \right\| _2 \le \alpha$ is developed.

Theorem 2

Let $\alpha$ and $\gamma$ be given scalars. If there exist symmetric positive definite matrices $P_h^k , \,P{_v}{^k} , \,Q_h ,\, Q_v,\,W_h,\, W_v ,\, R_h ,\,R_v ,\, X=\left[ \begin{array}{ll} X_{11} &{} X_{12} \\ *&{} X_{22} \\ \end{array} \right] >0,\, Y=\left[ \begin{array}{ll} Y_{11} &{} Y_{12} \\ *&{} Y_{22} \\ \end{array} \right] >0$, and any matrices $N_1 =\left[ \begin{array}{l} N_{11} \\ N_{12} \\ \end{array} \right] , \, N_2 =\left[ \begin{array}{l} N_{21} \\ N_{22} \\ \end{array} \right] ,\, S_1 =\left[ \begin{array}{l} S_{11} \\ S_{12} \\ \end{array} \right] ,\, S_2 =\left[ \begin{array}{l} S_{21} \\ S_{22} \\ \end{array} \right]$ and $H^{k}$ with appropriate dimensions, $k\in \underline{N}$, such that

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\bar{{\Gamma }}_{11} }&{} 0&{} {\Gamma _{13} }&{} 0&{} {-N_{21} }&{} 0&{} {G_p^{lT} L^{l}}&{} 0&{} {\Gamma _{19} }&{} {\Gamma _{10} }&{} {\sqrt{\bar{{d}}_2 }A_{1p}^{lT} R_v } \\ *&{} {\bar{{\Gamma }}_{22} }&{} 0&{} {\Gamma _{24} }&{} 0&{} {-S_{21} }&{} 0&{} {G_p^{lT} L^{l}}&{} {\Gamma _{29} }&{} {\sqrt{\bar{{d}}_1 }A_{2p}^{lT} R_h }&{} {\Gamma _{20} } \\ *&{} *&{} {\Gamma _{33} }&{} 0&{} {-N_{22} }&{} 0&{} 0&{} 0&{} {\Gamma _{39} }&{} {\sqrt{\bar{{d}}_1 }A_{d1}^{lT} R_h }&{} {\sqrt{\bar{{d}}_2 }A_{d1}^{lT} R_v } \\ *&{} *&{} *&{} {\Gamma _{44} }&{} 0&{} {-S_{22} }&{} 0&{} 0&{} {\Gamma _{49} }&{} {\sqrt{\bar{{d}}_1 }A_{d2}^{lT} R_h }&{} {\sqrt{\bar{{d}}_2 }A_{d2}^{lT} R_v } \\ *&{} *&{} *&{} *&{} {-W_h }&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} {-W_v }&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} {\Gamma _{77} }&{} 0&{} {\Gamma _{79} }&{} {\sqrt{\bar{{d}}_1 }B_1^{lT} R_h }&{} {\sqrt{\bar{{d}}_2 }B_1^{lT} R_v } \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} {\Gamma _{88} }&{} {\Gamma _{89} }&{} {\sqrt{\bar{{d}}_1 }B_2^{lT} R_h }&{} {\sqrt{\bar{{d}}_2 }B_2^{lT} R_v } \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-\Gamma _{99} }&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-R_h }&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-R_v } \\ \end{array}\right] <0, \nonumber \\&\qquad p=1,2,\ldots ,2^{m}, \quad \forall k,l\in \underline{N}, \end{aligned}$$

(24)

$$\begin{aligned}&\left[ \begin{array}{l@{\quad }l} X&{} {N_1} \\ *&{} {R_h} \\ \end{array} \right] \ge 0, \quad \left[ \begin{array}{l@{\quad }l} X&{} {N_2} \\ *&{} {R_h} \\ \end{array} \right] \ge 0, \quad \left[ \begin{array}{l@{\quad }l} Y&{} {S_1} \\ *&{} {R_v} \\ \end{array} \right] \ge 0, \quad \left[ \begin{array}{l@{\quad }l} Y&{} {S_2} \\ *&{} {R_v} \\ \end{array} \right] \ge 0, \end{aligned}$$

(25)

$$\begin{aligned}&\Omega \left( {P_h^k +P_v^k ,1+\gamma ^{2}\alpha ^{2}} \right) \subset L\left( {H^{k}} \right) , \quad k\in \underline{N}, \end{aligned}$$

(26)

where

$$\begin{aligned} \bar{{\Gamma }}_{11}&= G_p^{lT} G_p^l -P_h^l +W_h +(\bar{{d}}_1 -\underline{d}_1 +1)Q_h +N_{11} +N_{11}^T +\bar{{d}}_1 X_{11} ,\\ \bar{{\Gamma }}_{22}&= G_p^{lT} G_p^l -P_v^l +W_v +(\bar{{d}}_2 -\underline{d}_2 +1)Q_v +S_{11} +S_{11}^T +\bar{{d}}_2 Y_{11} , \\&\Gamma _{77} =\Gamma _{88} =L^{lT}L^{l}-\gamma ^{2}I,\\ \Gamma _{19}&= A_{1p}^{lT} (P_h^k +P_v^k ), \quad \Gamma _{29} =A_{2p}^{lT} (P_h^k +P_v^k ), \quad \Gamma _{39} =A_{d1}^{lT} (P_h^k +P_v^k ),\\&\Gamma _{49} =A_{d2}^{lT} (P_h^k +P_v^k ), \quad \Gamma _{79} =B_1^{lT} (P_h^k +P_v^k ), \quad \Gamma _{89} =B_2^{lT} (P_h^k +P_v^k ), \\&\Gamma _{99} =P_h^k +P_v^k ,\\ \Gamma _{10}&= \sqrt{\bar{{d}}_1 }(A_{1p}^{lT} -I)R_h , \quad \Gamma _{20} =\sqrt{\bar{{d}}_2 }(A_{2p}^{lT} -I)R_v, \end{aligned}$$

then system (5) has a prescribed $H_\infty$ disturbance attenuation level $\gamma$ for all switching sequence $\sigma (i,j)$ and initial states satisfying $\hbox {T}(\phi _h ,\phi _v )\le 1$, where $\hbox {T}(\phi _h ,\phi _v)$ is given by (13).

Proof

When $x(i,j)\in \mathop \cap \limits _{k=1}^N \Omega (P_h^k +P_v^k ,\;1+\gamma ^{2}\alpha ^{2})$, it can be obtained from (26) that $x(i,j)\in L\left( {H^{k}} \right) ,\, \forall k\in \underline{N}$, then by Lemma 2, we get (8). Since (10–12) can be deduced from (24–26), by Theorem 1, we can obtain from (24–26) that system (5) with $w(i,j)=0$ is asymptotically stable for any switching sequences and initial conditions satisfying $\hbox {T}(\phi _h ,\phi _v )\le 1$.

To establish the $H_\infty$ performance of system (5), we consider

$$\begin{aligned} \Upsilon (i,j)=\Delta V(i+1,j+1)+\bar{{z}}(i,j)^{T}\bar{{z}}(i,j)-\gamma ^{2}\bar{{w}}(i,j)^{T}\bar{{w}}(i,j), \end{aligned}$$

(27)

where $\bar{z}(i,j)=\left[ \begin{array}{ll} {z(i,j+1)^{T}}&{z(i+1,j)^{T}}\end{array} \right] ^{T}$ and $\bar{w}(i,j)=\big [\begin{array}{ll} {w(i,j+1)^{T}}&{w(i+1,j)^{T}}\end{array} \big ]^{T}$.

Following the procedure of the proof of Theorem 1, $\forall x(i,j)\in \mathop \cap \nolimits _{k=1}^N \Omega (P_h^k +P_v^k ,\;1 +\gamma ^{2}\alpha ^{2})$, we can obtain

$$\begin{aligned} \Upsilon (i,j)&\le \mathop {\max }\limits _{p=1,2,\cdots ,2^{m}} \left\{ {\bar{{\chi }}(i,j)^{T}\bar{{\Psi }}_p \bar{{\chi }}(i,j)} \right\} \nonumber \\&-\sum _{r=i-d_1 (i)}^{i-1} {\left[ \begin{array}{l} {\zeta _1 \left( {i,j} \right) } \\ {\eta (r,j+1)} \end{array} \right] ^{T}} \left[ \begin{array}{l@{\quad }l} X&{} {N_1} \\ *&{} {R_h} \\ \end{array} \right] \left[ \begin{array}{l} {\zeta _1 \left( {i,j} \right) } \\ {\eta (r,j+1)} \\ \end{array} \right] \nonumber \\&-\sum _{r=i-\bar{{d}}_1 }^{i-d_1 (i)-1} {\left[ \begin{array}{l} {\zeta _1 \left( {i,j} \right) } \\ {\eta (r,j+1)} \\ \end{array} \right] ^{T}} \left[ \begin{array}{l@{\quad }l} X&{} {N_2} \\ *&{} {R_h} \\ \end{array} \right] \left[ \begin{array}{l} {\zeta _1 \left( {i,j} \right) } \\ {\eta (r,j+1)} \\ \end{array} \right] \nonumber \\&-\sum _{t=j-d_2 (j)}^{j-1} {\left[ \begin{array}{l} {\zeta _2 \left( {i,j} \right) } \\ {\delta (i+1,t)} \\ \end{array} \right] } ^{T} \left[ \begin{array}{l@{\quad }l} Y&{} {S_1 } \\ *&{} {R_v } \\ \end{array} \right] \left[ \begin{array}{l} {\zeta _2 \left( {i,j} \right) } \\ {\delta (i+1,t)} \\ \end{array} \right] \nonumber \\&-\sum _{t=j-\bar{{d}}_2 }^{j-d_2 (j)-1} {\left[ \begin{array}{l} {\zeta _2 \left( {i,j} \right) } \\ {\delta (i+1,t)} \\ \end{array} \right] } ^{T} \left[ \begin{array}{l@{\quad }l} Y&{} {S_2} \\ *&{} {R_v} \\ \end{array} \right] \left[ \begin{array}{l} {\zeta _2 \left( {i,j} \right) } \\ {\delta (i+1,t)} \\ \end{array} \right] , \end{aligned}$$

(28)

where

$$\begin{aligned} \bar{{\chi }}(i,j)&= \left[ {\chi _1 (i,j)^{T}}\, {\chi _2 (i,j)^{T}}\, {w(i,j)^{T}} \right] ^{T}, \quad \bar{{\Theta }}=\left[ \Theta \, {B_1^l}\, {B_2^l} \right] , \\ \bar{{\Psi }}_p&= \bar{{\Psi }}+\bar{{\Theta }}^{T}(P_h^k +P_v^k)\bar{{\Theta }}+\left[ \bar{{\Sigma }}{_1}{^T}\, \bar{{\Sigma }}{_2}{^T} \right] \left[ \begin{array}{l@{\quad }l} {\bar{{d}}_1 R_h }&{} 0\\ 0&{} {\bar{{d}}_{2} R_{v}} \end{array} \right] \left[ {\bar{{\Sigma }}_1 }\, {\bar{{\Sigma }}_2 } \right] , \\ \bar{{\Sigma }}_1&= \left[ \begin{array}{l@{\quad }l@{\quad }l} {\Sigma _1 }&{B_1^l }&{B_2^l }\end{array} \right] , \quad \bar{{\Sigma }}_2 =\left[ \begin{array}{l@{\quad }l@{\quad }l} {\Sigma _2 }&{B_1^l }&{B_2^l} \end{array}\right] , \quad \bar{{\Psi }}=\mathrm{diag}\left\{ {\Psi ,\Gamma _{77} ,\Gamma _{88} } \right\} . \end{aligned}$$

By Lemma 1, LMI (24) is equivalent to $\bar{{\Psi }}_p <0$, and from (25), we have

$$\begin{aligned} \Upsilon (i,j)=\Delta V(i+1,j+1)+\bar{{z}}(i,j)^{T}\bar{{z}}(i,j)-\gamma ^{2}\bar{{w}}(i,j)^{T}\bar{{w}}(i,j)<0, \end{aligned}$$

(29)

that is

$$\begin{aligned} \bar{{z}}(i,j)^{T}\bar{{z}}(i,j)-\gamma ^{2}\bar{{w}}(i,j)^{T}\bar{{w}}(i,j)<-\Delta V(i+1,j+1). \end{aligned}$$

(30)

For any $\left\| {\bar{{w}}} \right\| _2 \le \alpha$, we obtain from (30) that

$$\begin{aligned} \sum _{i+j=r} V (i,j)<\sum _{i+j=z} V (i,j)+\gamma ^{2}\alpha ^{2}, \quad \forall r>z=\max (z_1 ,z_2 ). \end{aligned}$$

(31)

It follows from $\hbox {T}(\phi _h , \phi _v )\le 1$ and (31) that $x(i,j)^{T}(P_h^k +P_v^k )x(i,j)\le 1+\gamma ^{2}\alpha ^{2}$, $\forall k\in \underline{N}$. Thus, all the trajectories of system (5) starting from $\hbox {T}(\phi _h , \phi _v )\le 1$ will remain within $\mathop \cap \limits _{k=1}^N \Omega (P_h^k +P_v^k ,1+\gamma ^{2}\alpha ^{2})$.

On the other hand, we can obtain form (31) that

$$\begin{aligned} \sum _{i+j=0}^\infty {(\bar{{z}}(i,j)^{T}\bar{{z}}(i,j)-\gamma ^{2}\bar{{w}}(i,j)^{T}\bar{{w}}(i,j))} <\sum _{i+j=0}^\infty {(-\Delta V(i+1,j+1))} . \end{aligned}$$

(32)

Under zero boundary conditions, it can be obtained from (32) that

$$\begin{aligned} \sum _{i+j=0}^\infty {\bar{{z}}(i,j)^{T}\bar{{z}}(i,j)} <\sum _{i+j=0}^\infty {\gamma ^{2}\bar{{w}}(i,j)^{T}\bar{{w}}(i,j)} , \end{aligned}$$

(33)

which implies

$$\begin{aligned} \left\| {\bar{{z}}} \right\| _2^2 <\gamma ^{2}\left\| {\bar{{w}}} \right\| _2^2 . \end{aligned}$$

This completes the proof. $\square$

3.3 $H_\infty$ Controller Design

In this subsection, a sufficient condition for finding the controller gains is obtained in terms of LMIs.

Theorem 3

Consider system (1), for given scalars $\alpha$ and $\gamma$, and matrices $J>0,\, U>0$ and $Z>0$; if there exist symmetric positive definite matrices $P_h^k,\, P_v^k ,\, Q_h ,\, Q_v ,\, W_h ,\, W_v ,\, R_h ,\, R_v ,\, X=\left[ \begin{array}{ll} X_{11}&{} X_{12} \\ *&{} X_{22} \\ \end{array} \right] ,\, Y=\left[ \begin{array}{ll} Y_{11} &{} Y_{12} \\ *&{} Y_{22} \\ \end{array}\right]$ and any matrices $K^{k},\, H^{k},\, N_1 =\left[ \begin{array}{l} N_{11} \\ N_{12} \\ \end{array} \right] ,\, N_2 =\left[ \begin{array}{l} N_{21} \\ N_{22} \\ \end{array} \right] ,\, S_1 =\left[ \begin{array}{l} S_{11} \\ S_{12} \\ \end{array} \right]$ and $S_2 =\left[ \begin{array}{l} S_{21} \\ S_{22} \\ \end{array} \right]$ with appropriate dimensions, $k\in \underline{N}$, such that (25) and the following LMIs hold:

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\bar{{\Gamma }}_{11} }&{} 0&{} {\Gamma _{13} }&{} 0&{} {-N_{21} }&{} 0&{} 0&{} 0&{} {A_{1p}^{lT} }&{} {\psi _1 }&{} {\sqrt{\bar{{d}}_2 }A_{1p}^{lT} }&{} 0&{} {G_p^{lT} } \\ *&{} {\bar{{\Gamma }}_{22} }&{} 0&{} {\Gamma _{24} }&{} 0&{} {-S_{21} }&{} 0&{} 0&{} {A_{2p}^{lT} }&{} {\sqrt{\bar{{d}}_1 }A_{2p}^{lT} }&{} {\psi _2 }&{} {G_p^{lT} }&{} 0 \\ *&{} *&{} {\Gamma _{33} }&{} 0&{} {-N_{22} }&{} 0&{} 0&{} 0&{} {A_{d1}^{lT} }&{} {\sqrt{\bar{{d}}_1 }A_{d1}^{lT} }&{} {\sqrt{\bar{{d}}_2 }A_{d1}^{lT} }&{} 0&{} 0 \\ *&{} *&{} *&{} {\Gamma _{44} }&{} 0&{} {-S_{22} }&{} 0&{} 0&{} {A_{d2}^{lT} }&{} {\sqrt{\bar{{d}}_1 }A_{d2}^{lT} }&{} {\sqrt{\bar{{d}}_2 }A_{d2}^{lT} }&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} {-W_h }&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} {-W_v }&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} {-\gamma ^{2}I}&{} 0&{} {B_1^{lT} }&{} {\sqrt{\bar{{d}}_1 }B_1^{lT} }&{} {\sqrt{\bar{{d}}_2 }B_1^{lT} }&{} 0&{} {L^{lT}} \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-\gamma ^{2}I}&{} {B_2^{lT} }&{} {\sqrt{\bar{{d}}_1 }B_2^{lT} }&{} {\sqrt{\bar{{d}}_2 }B_2^{lT} }&{} {L^{lT}}&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {\psi _3 }&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {\psi _4 }&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {\psi _5 }&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-I}&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-I} \\ \end{array} \right] <0, \nonumber \\&\quad p=1,2,\ldots ,2^{m}, \quad \forall k,l\in \underline{N}, \end{aligned}$$

(34)

$$\begin{aligned}&\left[ \begin{array}{cc} \eta &{} {H_s^k } \\ *&{} {P_h^k +P_v^k } \\ \end{array} \right] \ge 0, \quad k\in \underline{N}, \quad s=1,2,\ldots ,m, \end{aligned}$$

(35)

where

$$\begin{aligned} A_{1p}^l&= A_1^l +E_1^l D_p K^{l}+E_1^l D_p^- H^{l}, \quad A_{2p}^l =A_2^l +E_2^l D_p K^{l}+E_2^l D_p^- H^{l},\\ \psi _1&= \sqrt{\bar{{d}}_1 }(A_{1p}^{lT} -I), \quad \psi _2 =\sqrt{\bar{{d}}_2 }(A_{2p}^{lT} -I), \quad \psi _3 =J^{T}(P_h^k +P_v^k )J-2J,\\ \psi _4&= U^{T}R_h U-2U, \quad \psi _5 =Z^{T}R_v Z-2Z, \quad \eta =1/(1+\gamma ^{2}\alpha ^{2}),\\ G_p^l&= G^{l}+F^{l}D_p K^{l}+F^{l}D_p^- H^{l}, \quad k,l\in \underline{N}, \end{aligned}$$

then the closed-loop system (5) has a prescribed $H_\infty$ disturbance attenuation level $\gamma$ for all switching sequence $\sigma (i,j)$ and initial states satisfying $\hbox {T}(\phi _h ,\phi _v )\le 1$, where $\hbox {T}(\phi _h ,\phi _v)$ is given by (13).

Proof

By Lemma 1, (35) is equivalent to (26). Pre- and post-multiplying (24) by $\mathrm{diag}\left\{ {I,I,I,I,I,I,I,I,(P_h^k +P_v^k )^{-1},(R_h )^{-1},(R_v )^{-1}} \right\}$ and applying Lemma 1, we obtain

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\bar{{\Gamma }}_{11} }&{} 0&{} {\Gamma _{13} }&{} 0&{} {-N_{21} }&{} 0&{} 0&{} 0&{} {A_{1p}^{lT} }&{} {\psi _1 }&{} {\sqrt{\bar{{d}}_2 }A_{1p}^{lT} }&{} 0&{} {G_p^{lT} } \\ *&{} {\bar{{\Gamma }}_{22} }&{} 0&{} {\Gamma _{24} }&{} 0&{} {-S_{21} }&{} 0&{} 0&{} {A_{2p}^{lT} }&{} {\sqrt{\bar{{d}}_1 }A_{2p}^{lT} }&{} {\psi _2 }&{} {G_p^{lT} }&{} 0 \\ *&{} *&{} {\Gamma _{33} }&{} 0&{} {-N_{22} }&{} 0&{} 0&{} 0&{} {A_{d1}^{lT} }&{} {\sqrt{\bar{{d}}_1 }A_{d1}^{lT} }&{} {\sqrt{\bar{{d}}_2 }A_{d1}^{lT} }&{} 0&{} 0 \\ *&{} *&{} *&{} {\Gamma _{44} }&{} 0&{} {-S_{22} }&{} 0&{} 0&{} {A_{d2}^{lT} }&{} {\sqrt{\bar{{d}}_1 }A_{d2}^{lT} }&{} {\sqrt{\bar{{d}}_2 }A_{d2}^{lT} }&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} {-W_h }&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} {-W_v }&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} {-\gamma ^{2}I}&{} 0&{} {B_1^{lT} }&{} {\sqrt{\bar{{d}}_1 }B_1^{lT} }&{} {\sqrt{\bar{{d}}_2 }B_1^{lT} }&{} 0&{} {L^{lT}} \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-\gamma ^{2}I}&{} {B_2^{lT} }&{} {\sqrt{\bar{{d}}_1 }B_2^{lT} }&{} {\sqrt{\bar{{d}}_2 }B_2^{lT} }&{} {L^{lT}}&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {\bar{{\psi }}_3 }&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {\bar{{\psi }}_4 }&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {\bar{{\psi }}_5 }&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-I}&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-I} \\ \end{array}\right] <0, \nonumber \\&\quad p=1,2,\ldots ,2^{m}, \quad \forall k,l\in \underline{N}, \end{aligned}$$

(36)

where $\bar{{\psi }}_3 =(P_h^k +P_v^k )^{-1},\, \bar{{\psi }}_4 =(R_h )^{-1}$ and $\bar{{\psi }}_5 =(R_v )^{-1}$.

For any matrices $J>0,\, U>0$ and $Z>0$, we have

$$\begin{aligned}&J^{T}(P_h^k +P_v^k )J\ge 2J-(P_h^k +P_v^k )^{-1}, \quad U^{T}R_h U\ge 2U-(R_h )^{-1}, \\&\quad Z^{T}R_v Z\ge 2Z-(R_v )^{-1}. \end{aligned}$$

Then (36) holds if (34) is satisfied.

This completes the proof. $\square$

Remark 3

Some previous results on $H_\infty$ controller design of 2-D switched systems can be seen in [16–18]; however, time-varying delay and actuator saturation, which add difficulties in designing the controller, were not taken into account in these papers. In the present paper, a new Lyapunov functional, which can lead to less conservative results, is proposed to deal with the time-varying delay, and the convex hull technique is utilized to handle the actuator saturation.

Remark 4

It should be noted that the conditions (25), (34) and (35) are in the form of LMIs, which can be conveniently solved via LMI toolbox or Sedumi and Yalmip in MATLAB [5, 21]. From Theorem 3, we can see that the controller gain matrices $K^{k}(k\in \underline{N})$ can be directly obtained by solving LMIs (25), (34) and (35).

We present the procedure for construction of the desired controller as follows:

• Step 1. Input the matrices $A_1^k,\, A_2^k ,\, A_{d1}^k ,\, A_{d2}^k ,\,B_1^k ,\, B_2^k ,\, E_1^k ,\, E_2^k ,\, G^{k},\, L^{k}$ and $F^{k},\, \forall k\in \underline{N}$.

• Step 2. Choose the appropriate parameters $\underline{d}_1 ,\, \bar{{d}}_1 ,\, \underline{d}_2 ,\, \bar{{d}}_2 ,\, \alpha ,\, \gamma$ and matrices $J>0,\, U>0,\, Z>0$.

• Step 3. By solving LMIs (25, 34–35), one can obtain $P_h^k ,\, P_v^k ,\, H^{k},\, Q_h ,\, Q_v , W_h ,\, W_v ,\, R_h,$ $R_v ,\, X,\, Y,\, N_1$, $N_2 ,\, S_1 ,\, S_2$ and controller gain matrices $K^{k} \,(k\in \underline{N})$ directly.

4 Simulation Examples

In this section, we present two examples to illustrate the effectiveness of the proposed approach.

Example 1

Consider system (1) with parameters as follows:

Subsystem 1:

$$\begin{aligned} A_1^1&= \left[ \begin{array}{l@{\quad }l} {0.12}&{} 0 \\ 0&{} {0.1} \\ \end{array} \right] , \quad A_2^1 =\left[ \begin{array}{l@{\quad }l} 0&{} {0.01} \\ 0&{} 0 \\ \end{array}\right] , \quad A_{d1}^1 =\left[ \begin{array}{l@{\quad }l} 0&{} {0.1} \\ 0&{} 0 \\ \end{array} \right] , \\&A_{d2}^1 =\left[ \begin{array}{l@{\quad }l} {0.025}&{} 0 \\ {0.024}&{} 0 \\ \end{array} \right] ,\quad B_1^1 =\left[ \begin{array}{l} {0.012} \\ {0.01} \\ \end{array} \right] ,\\ B_2^1&= \left[ \begin{array}{l} {0.014} \\ 0 \\ \end{array}\right] , \quad E_1^1 =\left[ \begin{array}{l} 4 \\ 4 \\ \end{array}\right] , \quad E_2^1 =\left[ \begin{array}{l} {0.012} \\ {0.01} \\ \end{array} \right] , \quad G^{1}=\left[ \begin{array}{l@{\quad }l} {0.06}&{} {0.06} \\ \end{array} \right] ,\\&L^{1}=0.1, \quad F^{1}=0.02. \end{aligned}$$

Subsystem 2:

$$\begin{aligned} A{_1}{^2}&= \left[ \begin{array}{l@{\quad }l} 0&{} {0.2} \\ 0&{} {0.1} \\ \end{array}\right] , \quad A_2^2 =\left[ \begin{array}{l@{\quad }l} 0&{} 0 \\ {0.02}&{} 0 \\ \end{array} \right] , \quad A_{d1}^2 =\left[ \begin{array}{l@{\quad }l} 0&{} {0.022} \\ 0&{} 0 \\ \end{array}\right] ,\\&A_{d2}^2 =\left[ \begin{array}{l@{\quad }l} {0.03}&{} 0 \\ 0&{} {0.03} \\ \end{array}\right] ,\\ B_1^2&= \left[ \begin{array}{l} {0.01} \\ 0 \\ \end{array} \right] , \quad B_2^2 =\left[ \begin{array}{l} 0 \\ {0.02} \\ \end{array} \right] , \quad E_1^2 =\left[ \begin{array}{l} {0.02} \\ {0.01} \\ \end{array} \right] , \quad E_2^2 =\left[ \begin{array}{l} {0.01} \\ {-0.02} \\ \end{array} \right] ,\\&G^{2}=\left[ \begin{array}{l@{\quad }l} {0.08}&{} {0.08} \\ \end{array} \right] ,\\ L^{2}&= 0.2, \quad F^{2}=0.04, \quad d_1 (i)=2+\sin \left( {\frac{\pi i}{2}} \right) , \quad d_2 (j)=2+\sin \left( {\frac{\pi j}{2}} \right) . \end{aligned}$$

In this example, it can be obtained that $\underline{d}_1 =1,\, \bar{{d}}_1 =2,\, \underline{d}_2 =1$ and $\bar{{d}}_2 =2$. Take $\alpha =0.1,\, \gamma =1,\, J=\mathrm{diag}\{3,3\},\,U=\mathrm{diag}\{22,15\}$ and $Z=\mathrm{diag}\{30,17\}$. Then solving LMIs in Theorem 3 via LMI toolbox gives rise to

$$\begin{aligned} P{_h}{^1}&= \left[ \begin{array}{l@{\quad }l} {{960.5559}}&{} {{0.0028}} \\ {{0.0028}}&{} {{963.9219}} \\ \end{array} \right] , \quad P{_v}{^1} =\left[ \begin{array}{l@{\quad }l} {{174.0246}}&{} {{0.0011}} \\ {{0.0011}}&{} {{174.0281}} \\ \end{array} \right] ,\\&R{_v} =\left[ \begin{array}{l@{\quad }l} {{0.0348}}&{} {{0.0002}} \\ {{0.0002}}&{} {{0.0556}} \\ \end{array} \right] ,\\ P{_h}{^2}&= \left[ \begin{array}{l@{\quad }l} {{960.5601}}&{} {-0.0111} \\ {-0.0111}&{} {{963.9559}} \\ \end{array} \right] , \quad P_v^2 =\left[ \begin{array}{l@{\quad }l} {{0.6020}} &{} {{0.0003}} \\ {{0.0003}}&{} {{0.6015}} \\ \end{array}\right] ,\\&R_h =\left[ \begin{array}{l@{\quad }l} {{1.5097}}&{} {{0.0001}} \\ {{0.0001}}&{} {{1.0079}} \\ \end{array} \right] ,\\ Q{_h}&= \left[ \begin{array}{l@{\quad }l} {{240.2770 }}&{} {-0.0003} \\ {-0.0003}&{} {{241.6877}} \\ \end{array} \right] , \quad N_{11} =\left[ \begin{array}{l@{\quad }l} {-1.2861}&{} {-0.0001}\\ {-0.0001}&{} {-0.8684} \\ \end{array}\right] ,\\&N_{12} =\left[ \begin{array}{l@{\quad }l} {{1.8503}}&{} {{0.0002}} \\ {{0.0002}}&{} {{1.2446}} \\ \end{array} \right] ,\\ N_{21}&= \left[ \begin{array}{l@{\quad }l} {-0.0030}&{} {{0.0000}} \\ {{0.0000}}&{} {-0.0012} \\ \end{array} \right] , \quad W_v =\left[ \begin{array}{l@{\quad }l} {{0.1651 }}&{} {-0.0003} \\ {-0.0003}&{} {{0.1693}} \\ \end{array} \right] ,\\&Q_v =\left[ \begin{array}{l@{\quad }l} {{0.1048 }}&{} {-0.0004}\\ {-0.0004}&{} {{0.0811}} \\ \end{array} \right] ,\\ N_{22}&= \left[ \begin{array}{l@{\quad }l} {-1.8097}&{} {-0.0002} \\ {-0.0002}&{} {-1.2252} \\ \end{array} \right] , \quad S_{11} =\left[ \begin{array}{l@{\quad }l} {-0.0042}&{} {0.0000} \\ {-0.0002}&{} {-0.0072} \\ \end{array}\right] ,\\&S_{12} =\left[ \begin{array}{l@{\quad }l} {{0.0216}}&{} {{0.0003}} \\ {{0.0000}}&{} {{0.0362}} \\ \end{array} \right] ,\\ S_{21}&= \left[ \begin{array}{l@{\quad }l} {-0.0022}&{} {-0.0001} \\ {0.0001}&{} {-0.0025} \\ \end{array} \right] , \quad S_{22} =\left[ \begin{array}{l@{\quad }l} {-0.0223}&{} {-0.0001} \\ {-0.0001}&{} {-0.0369} \\ \end{array} \right] ,\\&W_h =\left[ \begin{array}{l@{\quad }l} {{146.9101}}&{} {{0.0000}} \\ {{0.0000}}&{} {{146.8795}} \\ \end{array}\right] ,\\ H^{1}&= \left[ \begin{array}{l@{\quad }l} {-0.0013}&{} {-0.0003} \\ \end{array} \right] , \quad H^{2}=\left[ \begin{array}{l@{\quad }l} {-\hbox {0.0047}}&{} {-0.0078} \\ \end{array} \right] ,\\ K^{1}&= \left[ \begin{array}{l@{\quad }l} {-0.0072}&{} {-0.0023} \\ \end{array} \right] , \quad K^{2}=\left[ \begin{array}{l@{\quad }l} {-1.0114}&{} {-2.1390} \\ \end{array}\right] . \end{aligned}$$

Figures 1 and 2 depict the trajectories of the two states $x_1 (i,j)$ and $x_2 (i,j)$, respectively. The corresponding switching signal is represented by Fig. 3, where the initial states are

$$\begin{aligned}&x\left( {i,j} \right) =\left[ \begin{array}{l@{\quad }l} {\frac{1}{5\left( {j+1} \right) }}&\frac{1}{5\left( {j+1} \right) } \end{array}\right] ^{T},\,\,\forall 0\le j\le 10,\,i=0,\\&x\left( {i,j} \right) =\left[ \begin{array}{l@{\quad }l} {\frac{1}{5\left( {i+1} \right) }}&\frac{1}{5\left( {i+1} \right) } \end{array}\right] ^{T},\,\,\forall 0\le i\le 10,\,j=0, \end{aligned}$$

and the disturbance is $w\left( {i,j} \right) =0.1\exp \left( {-0.25\pi \left( {i+j} \right) } \right)$.

Fig. 1

State trajectory of $x_1 (i,j)$

Fig. 2

State trajectory of $x_2 (i,j)$

Fig. 3

Switching signal

Form Figs. 1, 2 and 3, it can be observed that the closed-loop system is asymptotically stable.

Example 2

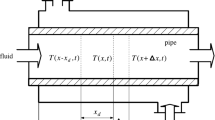
Let us consider the thermal processes in chemical reactors, heat exchangers and pipe furnaces, which can be expressed by the following partial differential equation (PDE) [43]:

$$\begin{aligned} \frac{\partial T\left( {x,t} \right) }{\partial x}&= -\frac{\partial T\left( {x,t} \right) }{\partial t}-a_0^{\sigma \left( {x,t} \right) } T\left( {x,t} \right) +a_1^{\sigma \left( {x,t} \right) } T(x,t-d(t)) \nonumber \\&+\, e^{\sigma \left( {x,t} \right) }\mathrm{sat}(u(x,t)), \end{aligned}$$

(37)

where $T$(${x,t}$) is the temperature at $x\left( {\hbox {space}} \right) \in [0,x_f ]$ and $t\left( {\hbox {time}} \right) \in [0,\infty ),\, a_0^{\sigma \left( {x,t} \right) }$, $a_1^{\sigma \left( {x,t} \right) }$ and $e^{\sigma \left( {x,t} \right) }$ are real coefficients with $\sigma \left( {x,t} \right)$ being the switching signal, and $u(x,t)$ is the input function.

Digitally based control law design and implementation require the construction of an appropriate approximation of the dynamics by difference equations. If a direct discretization method is applied to spatiotemporal dynamics, there is the need to ensure numerical stability by selection of the sampling period(s) [11, 12]. In this paper, we will use the Crank–Nicholson discretization method to guarantee the unconditional numerical stability.

Introduce the following approximations

$$\begin{aligned}&\frac{\partial T(x,t)}{\partial t}\approx \frac{T(i,j+1)-T(i,j)}{\Delta t}, \quad \frac{\partial T(x,t)}{\partial x}\approx \frac{T(i,j)-T(i-1,j)}{\Delta x},\\&\quad u(x,t)\approx u(i,j), \end{aligned}$$

where $T\left( {i,j} \right) =T\left( {i\Delta x,j\Delta t} \right) ,\, u\left( {i,j} \right) =u\left( {i\Delta x,j\Delta t} \right) ,\, \Delta t$ and $\Delta x$ are time and space discretization periods, respectively.

The discrete approximation to the dynamics of (37) can be written in the form of (1) with

$$\begin{aligned} A_1^{\sigma \left( {i,j} \right) }&= \left[ \begin{array}{l@{\quad }l} 0&{} 1 \\ 0&{} 0 \\ \end{array} \right] , \quad A_2^{\sigma \left( {i,j} \right) } =\left[ \begin{array}{l@{\quad }l} 0&{} 0 \\ {\frac{\Delta t}{\Delta x}}&{} {1-\frac{\Delta t}{\Delta x}-a_0^{\sigma \left( {i,j} \right) } \Delta t} \\ \end{array} \right] , \quad A_{d1}^{\sigma (i,j)} =\left[ \begin{array}{l@{\quad }l} 0&{} 0 \\ 0&{} 0 \\ \end{array}\right] ,\\ E_1^{\sigma \left( {i,j} \right) }&= \left[ \begin{array}{l@{\quad }l} 0 \\ 0 \\ \end{array} \right] , \quad E_2^{\sigma \left( {i,j} \right) } =\left[ \begin{array}{l@{\quad }l} 0 \\ {e^{\sigma \left( {i,j} \right) }\Delta t} \\ \end{array} \right] , \quad A_{d2}^{\sigma (i,j)} =\left[ \begin{array}{l@{\quad }l} 0&{} 0 \\ 0&{} {-a_1^{\sigma \left( {i,j} \right) } \Delta t} \\ \end{array} \right] .\\ \end{aligned}$$

Since the limits $\mathop {\lim }\limits _{\Delta t\rightarrow 0} \frac{T(i,j+1)-T(i,j)}{\Delta t}$ and $\mathop {\lim }\limits _{\Delta x\rightarrow 0} \frac{T(i,j)-T(i-1,j)}{\Delta x}$ are first-order derivative when $\Delta t$ and $\Delta x$ are infinitely small, the discretizations of $\frac{\partial T(x,t)}{\partial t}$ and $\frac{\partial T(x,t)}{\partial x}$ are consistent. Moreover, the discretization of the above PDE will converge to the true solution if the resulting difference equation is stable [11, 12].

Now we assume that the 2-D switched system has two subsystems with $a_0^1 =2,\,a_0^2 =3,\, a_1^1 =0.2,\, a_1^2 =0.3,\, e^{1}=1,\, d(t)=1+\sin \left( {\frac{\pi t}{2}} \right) ,\, e^{2}=1.5$. The time and space discretization periods are chosen as $\Delta x=0.3$ and $\Delta t=0.2$. By considering the $H_\infty$ disturbance attenuation, the thermal process is modeled in the form of (1) with parameters as follows:

Subsystem 1:

$$\begin{aligned} A_1^1&= \left[ \begin{array}{l@{\quad }l} 0&{} 1 \\ 0&{} 0 \\ \end{array} \right] , \quad A_2^1 =\left[ \begin{array}{l@{\quad }l} 0&{} 0 \\ {0.6}&{} {0.07} \\ \end{array} \right] , \quad A_{d1}^1 =\left[ \begin{array}{l@{\quad }l} 0&{} 0 \\ 0&{} 0 \\ \end{array} \right] , \quad A_{d2}^1 =\left[ \begin{array}{l@{\quad }l} 0&{} 0 \\ 0&{} {-0.04} \\ \end{array} \right] ,\\&B_1^1 =\left[ \begin{array}{l} {0.3} \\ 0 \\ \end{array} \right] ,\\ B_2^1&= \left[ \begin{array}{l@{\quad }l} {0.2} \\ 0 \\ \end{array} \right] , \quad E_1^1 =\left[ \begin{array}{l@{\quad }l} 0 \\ 0 \\ \end{array} \right] , \quad E_2^1 =\left[ \begin{array}{l@{\quad }l} 0 \\ {0.2} \\ \end{array} \right] , \quad G^{1}=\left[ \begin{array}{l@{\quad }l} {0.01}&{} {0.03} \\ \end{array} \right] , \quad L^{1}=0.3,\\&F^{1}=0.01. \end{aligned}$$

Subsystem 2:

$$\begin{aligned} A_1^2&= \left[ \begin{array}{l@{\quad }l} 0&{} 1 \\ 0&{} 0 \\ \end{array} \right] , \quad A_2^2 =\left[ \begin{array}{l@{\quad }l} 0&{} 0 \\ {0.6}&{} {0.27} \\ \end{array} \right] , \quad A_{d1}^2 =\left[ \begin{array}{l@{\quad }l} 0&{} 0 \\ 0&{} 0 \\ \end{array} \right] , \quad A_{d2}^2 =\left[ \begin{array}{l@{\quad }l} 0&{} 0 \\ 0&{} {-0.06} \\ \end{array} \right] ,\\&B_1^2 =\left[ \begin{array}{l} {0.01} \\ 0 \\ \end{array} \right] ,\\ B_2^2&= \left[ \begin{array}{l} {0.1} \\ 0 \\ \end{array} \right] , \quad E_1^2 =\left[ \begin{array}{l} 0 \\ 0 \\ \end{array} \right] , \quad E_2^2 =\left[ \begin{array}{l} 0 \\ {0.3} \\ \end{array} \right] , \quad G^{2}=\left[ \begin{array}{l@{\quad }l} {0.03}&{} {0.04} \\ \end{array} \right] , \quad L^{2}=0.1,\\&F^{2}=0.03. \end{aligned}$$

Take $\alpha =0.1,\, \gamma =1,\,J=\mathrm{diag}\{3,3\},\, U=\mathrm{diag}\{22,15\}$ and $Z=\mathrm{diag}\{30,17\}$, then solving LMIs in Theorem 3 leads to

$$\begin{aligned} P_h^1&= \left[ \begin{array}{l@{\quad }l} {{836.5842}}&{} {-0.0663} \\ {-0.0663}&{} {{842.4002}} \\ \end{array} \right] , \quad P_v^1 =\left[ \begin{array}{l@{\quad }l} {{151.9147}}&{} {-0.0339} \\ {-0.0339}&{} {{151.8327}} \\ \end{array} \right] ,\\&R_v =\left[ \begin{array}{l@{\quad }l} {{0.0331}}&{} {{0.0047}} \\ {{0.0047}}&{} {{0.0534}} \\ \end{array} \right] ,\\ P_h^2&= \left[ \begin{array}{l@{\quad }l} {{836.5847}}&{} {-0.0667} \\ {-0.0667}&{} {{842.4990}} \\ \end{array} \right] , \quad P_v^2 =\left[ \begin{array}{l@{\quad }l} {{0.6163 }}&{} {{0.0043}} \\ {{0.0043}}&{} {{0.4656}} \\ \end{array} \right] ,\\&R_h =\left[ \begin{array}{l@{\quad }l} {{1.5779}}&{} {{0.0006}} \\ {{0.0006}}&{} {{0.8604}} \\ \end{array} \right] ,\\ Q_h&= \left[ \begin{array}{l@{\quad }l} {{208.9666 }}&{} {-0.0002} \\ {-0.0002}&{} {{210.9341}} \\ \end{array}\right] , \quad N_{11} =\left[ \begin{array}{l@{\quad }l} {-1.3381}&{} {-0.0005} \\ {-0.0005}&{} {-0.7457} \\ \end{array}\right] ,\\ N_{12}&= \left[ \begin{array}{l@{\quad }l} {{1.9287}}&{} {{0.0007}} \\ {{0.0007}}&{} {{1.0685}} \\ \end{array} \right] , \quad N_{21} =\left[ \begin{array}{l@{\quad }l} {-0.0042}&{} {{0.0000}} \\ {0.0000}&{} {-0.0010} \\ \end{array} \right] ,\\&W_v =\left[ \begin{array}{l@{\quad }l} {{0.1277}}&{} {-0.0079} \\ {-0.0079}&{} {{0.1417}} \\ \end{array}\right] ,\\ Q_v&= \left[ \begin{array}{l@{\quad }l} {{0.0768}}&{} {-0.0077} \\ {-0.0077}&{} {{0.0538}} \\ \end{array} \right] , \quad N_{22} =\left[ \begin{array}{l@{\quad }l} {-1.8767}&{} {-0.0006} \\ {-0.0006}&{} {-1.0519} \\ \end{array} \right] ,\\&S_{11} =\left[ \begin{array}{l@{\quad }l} {-0.0042}&{} {-0.0048} \\ {-0.0019}&{} {-0.0096} \\ \end{array} \right] ,\\ S_{12}&= \left[ \begin{array}{l@{\quad }l} {{0.0261}}&{} {{0.0024}} \\ {{0.0038}}&{} {{0.0379}} \\ \end{array}\right] , \quad S_{21} =\left[ \begin{array}{l@{\quad }l} {{0.0026}}&{} {{0.0025}} \\ {{0.0007}}&{} {-0.0017} \\ \end{array} \right] ,\\&S_{22} =\left[ \begin{array}{l@{\quad }l} {-0.0263}&{} {-0.0036} \\ {-0.0030}&{} {-0.0384} \\ \end{array} \right] ,\\ W_h&= \left[ \begin{array}{l@{\quad }l} {{128.2301}}&{} {{0.0004}} \\ {{0.0004}}&{} {{128.1792}} \\ \end{array} \right] , \quad H^{1}=\left[ \begin{array}{l@{\quad }l} {-0.5314}&{} {{0.0842}} \\ \end{array} \right] ,\\&H^{2}=\left[ \begin{array}{l@{\quad }l} {-{0.2045}}&{} {-{0.0127}} \\ \end{array} \right] ,\\ K^{1}&= \left[ \begin{array}{l@{\quad }l} {-2.9025}&{} {{0.6451}} \\ \end{array} \right] , \quad K^{2}=\left[ \begin{array}{l@{\quad }l} {-1.9294}&{} {-0.2250} \\ \end{array} \right] . \end{aligned}$$

Choosing the initial states

$$\begin{aligned} x\left( {i,j} \right)&= \left[ \begin{array}{l@{\quad }l} {\frac{1}{20\left( {j+1} \right) }}&{} \frac{1}{20\left( {j+1} \right) } \\ \end{array} \right] ^{T},\,\,\,\,\forall 0\le j\le 10,\;i=0,\\ x\left( {i,j} \right)&= \left[ \begin{array}{l@{\quad }l} {\frac{1}{20\left( {i+1} \right) }}&{} {\frac{1}{20\left( {i+1} \right) }} \\ \end{array} \right] ^{T},\,\,\,\,\forall 0\le i\le 10,\;j=0, \end{aligned}$$

and the disturbance $w\left( {i,j} \right) =0.1\exp \left( {-0.25\pi \left( {i+j} \right) } \right)$, state trajectories of $x_1 (i,j)$ and $x_2 (i,j)$ are shown in Figs. 4 and 5, respectively, and Fig. 6 shows the switching signal. It can be seen from Figs. 4, 5 and 6 that the resulting difference equation is asymptotically stable, which implies that the true solution of the above PDE asymptotically converges to zero. This demonstrates the effectiveness of the proposed method.

Fig. 4

State trajectory of $x_1 (i,j)$

Fig. 5

State trajectory of $x_2 (i,j)$

Fig. 6

Switching signal

5 Conclusions

This paper has investigated the state feedback $H_\infty$ stabilization problem of 2-D discrete switched systems with actuator saturation. A new sufficient condition for asymptotical stability of the closed-loop system has been obtained. A state feedback $H_\infty$ controller has been proposed such that the closed-loop system is asymptotically stable and achieves a prescribed disturbance attenuation level $\gamma$. Two examples have been provided to show the effectiveness of the proposed approach.