On the impact of spatial heterogeneity and drift rate in a three-patch two-species Lotka–Volterra competition model over a stream

Abstract

In this paper, we study a three-patch two-species Lotka–Volterra competition patch model over a stream network. The individuals are subject to both random and directed movements, and the two species are assumed to be identical except for the movement rates. The environment is heterogeneous, and the carrying capacity is lager in upstream locations. We treat one species as a resident species and investigate whether the other species can invade or not. Our results show that the spatial heterogeneity of environment and the magnitude of the drift rates have a large impact on the competition outcomes of the stream species.

1 Introduction

The species living in stream environment is subject to both passive random movement and directed drift [47]. Intuitively, the drift will carry individuals to the downstream end, which may be crowded or hostile. However, random dispersal may drive the individuals to the upper stream locations, which are usually more favorable for the species [23]. Therefore, the joint impact of both undirectional and directed dispersal rates on the population dynamics of the species is usually complicated and has attracted increasing research interests recently [22, 25, 34, 40,41,42, 47].

Dispersal has profound effects on the distribution and abundance of organisms, and understanding the mechanisms for the evolution of dispersal is a fundamental question related to dispersal [26]. In the seminal works of Hastings [19] and Dockery et al. [15], it has been shown that in a spatially heterogeneous environment, when two competing species are identical except for the random dispersal rate, evolution of dispersal favors the species with a smaller dispersal rate. However, in an advective environment when individuals are subject to both undirectional random dispersal and directed movement, species with a faster dispersal rate can be selected [3, 4, 11].

Two-species reaction–diffusion–advection competition models of the following form have been proposed to study the evolution of dispersal for stream species [28, 34,35,36, 38, 43, 48, 49, 51,52,53]:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t=d_1u_{xx}-q_1 u_x+u[r(x)-u-v], &{}0<x<l,\;\;t>0,\\ v_t=d_2v_{xx}-q_2 v_x+v[r(x)-u-v], &{}0<x<l,\;\;t>0,\\ d_1u_x(0,t)-q_1 u(0,t)=d_2v_x(0,t)-q_2 v(0,t)=0, &{}t>0, \\ d_1u_x(l,t)-q_1 u(l,t)=d_2v_x(l,t)-q_2 v(l,t)=0, &{}t>0,\\ u(x,0), v(x, 0)\ge (\not \equiv )0, &{}0<x<l. \end{array}\right. } \end{aligned}$$

(1.1)

In [28, 34, 49], the authors have treated species u as a resident species and studied the conditions under which the species u only semitrivial equilibrium is stable/unstable. Various results on the global dynamics of (1.1) are presented in [36, 38, 43, 52, 53]. In particular, if r(x) is constant, the works [36, 38, 53] show that the species with a larger diffusion rate and/or a smaller advection rate wins the competition. If r(x) is a decreasing function, the authors in [37, 52] use $q_1$ and $q_2$ as bifurcation parameters to study the global dynamics of (1.1) and the related results will be discussed later (see Remark 3.14).

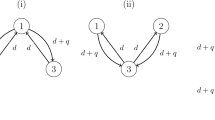
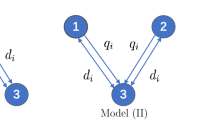
To study the evolution of dispersal in a river network, the authors in [23, 24] propose and investigate three-patch two-species Lotka–Volterra competition models. Let $\varvec{u}=(u_1, u_2, u_3)$ and $\varvec{v}=(v_1, v_2, v_3)$ be the population density of two competing species, respectively, where $u_i$ and $v_i$ are the densities in patch i. Suppose that the dispersal patterns of the individuals and the configuration of the patches are shown in Fig. 1.

Fig. 1

A stream with three patches, where d is the random movement rate and q is the directed drift rate. Patch 1 is the upstream end, and patch 3 is the downstream end

The competition patch model over the stream network in Fig. 1 (with $r_1=r_2=r_3$) in [23, 24] is:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\textrm{d}u_i}{\textrm{d}t}=\displaystyle \sum _{j=1}^{3} (d_1 D_{ij}+q_1Q_{ij})u_j+r_iu_i\left( 1-\frac{u_i+v_i}{k_i}\right) , &{}i=1,2,3,\;\;t>0,\\ \displaystyle \frac{\textrm{d}v_i}{\textrm{d}t}=\displaystyle \sum _{j=1}^{3}(d_2 D_{ij}+q_2Q_{ij})v_j+r_iv_i\left( 1-\frac{u_i+v_i}{k_i}\right) ,&{}i=1,2,3,\;\; t>0, \\ \varvec{u}(0)=\varvec{u}_0\ge (\not \equiv )\;\varvec{0},\; \varvec{v}(0)=\varvec{v}_0\ge (\not \equiv )\; \varvec{0}, \end{array}\right. } \end{aligned}$$

(1.2)

where $d_1$ and $d_2$ are random movement rates; $q_1$ and $q_2$ are directed movement rates; $\varvec{r}=(r_1, r_2, r_3)$ is the growth rate; $\varvec{k}=(k_1, k_2, k_3)$ is the carrying capacity; and two $3\times 3$ matrices $D=(D_{ij})$ and $Q=(Q_{ij})$ represent the random movement pattern and directed drift pattern of individuals, respectively, where

$$\begin{aligned} D=\begin{bmatrix} -1 &{} 1 &{}0 \\ 1&{}-2&{} 1\\ 0&{}1 &{} -1 \\ \end{bmatrix},\;\;Q=\begin{bmatrix} -1 &{} 0 &{}0 \\ 1&{}-1&{} 0\\ 0&{}1 &{} 0\\ \end{bmatrix}. \end{aligned}$$

(1.3)

We can write the model as

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\textrm{d}u_1}{\textrm{d}t}=-(d_1+q_1)u_1+d_1u_2+r_1u_1\left( 1-\displaystyle \frac{u_1+v_1}{k_1}\right) ,\\ \displaystyle \frac{\textrm{d}u_2}{\textrm{d}t}=(d_1+q_1)u_1-(2d_1+q_1)u_2+d_1u_3+r_2u_2\left( 1-\displaystyle \frac{u_2+v_2}{k_2}\right) ,\\ \displaystyle \frac{\textrm{d}u_3}{\textrm{d}t}=(d_1+q_1)u_2-d_1u_3+r_3u_3\left( 1-\displaystyle \frac{u_3+v_3}{k_3}\right) ,\\ \displaystyle \frac{\textrm{d}v_1}{\textrm{d}t}=-(d_2+q_2)v_1+d_2v_2+r_1v_1\left( 1-\displaystyle \frac{u_1+v_1}{k_1}\right) ,\\ \displaystyle \frac{\textrm{d}v_2}{\textrm{d}t}=(d_2+q_2)v_1-(2d_2+q_2)v_2+d_2v_3+r_2v_2\left( 1-\displaystyle \frac{u_2+v_2}{k_2}\right) ,\\ \displaystyle \frac{\textrm{d}v_3}{\textrm{d}t}=(d_2+q_2)v_2-d_2v_3+r_3v_3\left( 1-\displaystyle \frac{u_3+v_3}{k_3}\right) ,\\ \varvec{u}(0)=\varvec{u}_0\ge (\not \equiv )\;\varvec{0},\;\varvec{v}(0)=\varvec{v}_0\ge (\not \equiv )\;\varvec{0}. \end{array}\right. } \end{aligned}$$

(1.4)

We assume $d_1, d_2, q_1, q_2>0$ and $r_i, k_i>0$ for $i=1, 2, 3$. We adopt the same assumption in [23] on $\varvec{k}=(k_1, k_2, k_3)$:

$(\textbf{H})$:

$k_1> k_2> k_3>0$.

Biologically, $(\mathbf {}{H})$ means that the upstream locations are more favorable for both species.

Two-species Lotka–Volterra competition patch models have attracted many research interests recently. Model (1.2) with n patches in spatially homogeneous environment (i.e., $r_1=\dots =r_n$ and $k_1=\dots =k_n$) has been considered in our earlier papers [7, 10], but many techniques and results there cannot be generalized to the situation when $k_1=\dots =k_n$ is not assumed. The authors in [18, 45] have studied the global dynamics of model (1.2) with two patches and $q:=q_1=q_2$. They have showed that there exists a critical drift rate such that below it the species with a smaller dispersal rate wins the competition, while above it the species with a larger dispersal rate wins. In a competition model with two patches, the authors in [12, 17, 32] have showed that the species with more evenly distributed resources has less competition advantage. In [8], the global dynamics of a Lotka–Volterra competition patch model is classified under some assumptions on patches, which requires $d_1/q_1=d_2/q_2$ in terms of (1.2). For more studies on competition patch models, we refer to the works [2, 5, 6, 27, 30, 33, 44, 46, 50].

We will take an adaptive dynamics approach [14, 16] to analyze (1.4) by viewing species $\varvec{u}$ as the resident species and species $\varvec{v}$ as the mutant species. Model (1.4) has two semitrivial equilibria $(\varvec{u}^*,\varvec{0})$ and $(\varvec{0},\varvec{v}^*)$. We fix parameters $d_1$ and $q_1$ and vary $d_2$ and $q_2$. We show that there exists a curve $q=q_{\varvec{u}}^*(d)$ dividing the $(d_2, q_2)$-plane into two regions such that $(\varvec{u}^*, \varvec{0})$ is stable if and only if $(d_2, q_2)$ is above the curve. Our results complement those in [23] by defining and analyzing the curve $q=q_{\varvec{u}}^*(d)$ and obtaining the global dynamics of model (1.4). In particular, we show that if $q_1<{\underline{q}}$ the curve $q=q_{\varvec{u}}^*(d)$ is bounded (see Fig. 3) and if $q_1>{{\overline{q}}}$ it is unbounded (see Fig. 4). This result is in sharp contrast with the corresponding one for the model in spatially homogeneous environment ($k_1=k_2=k_3$) [7], where the curve $q=q_{\varvec{u}}^*(d)$ is always unbounded. We give explicitly parameter ranges for competitive exclusion and conditions for coexistence/bistability in three cases ($q_1<{\underline{q}}$, ${\underline{q}}\le q_1\le {{\overline{q}}}$ and $q_1>{{\overline{q}}}$). Our results show that the magnitude of the drift rates and the spatial heterogeneity of environment have a large impact on the competition outcomes of the stream species.

Our paper is organized as follows. In Sect. 2, we list some preliminary results. In Sect. 3, we state the main results on model (1.4). We give some conclusive remarks and numerical simulations in Sect. 4. The proofs of the main results are presented in Sect. 5. In the Appendix, we show the relations of ${\underline{q}}$, ${{\overline{q}}}$, and $q_0$. These relations are implicitly included in the main results, and we prove them for reader’s convenience.

2 Preliminary

Let $A=(a_{ij})_{n\times n}$ be a square matrix with real entries, $\sigma (A)$ be the set of all eigenvalues of A, and s(A) be the spectral bound of A, i.e., $s(A)=\max \{\textrm{Re} \lambda : \lambda \in \sigma (A)\}$. The matrix A is called irreducible if it cannot be placed into block upper triangular form by simultaneous row and column permutations and essentially nonnegative if $a_{ij}\ge 0$ for all $1\le i, j\le n$ and $i\ne j$. By the Perron–Frobenius theorem, if A is irreducible and essentially nonnegative, then s(A) is an eigenvalue of A (called the principal eigenvalue of A), which is the unique eigenvalue associated with a nonnegative eigenvector. The following result on the monotonicity of spectral bound can be found in [1, 9]:

Lemma 2.1

Let $A=(a_{ij})_{n\times n}$ be an irreducible and essentially nonnegative matrix and $M=\text {diag}(m_i)$ be a real diagonal matrix. If $s(A)=0$, then

$$\begin{aligned} \displaystyle \frac{\textrm{d}}{\textrm{d}\mu } s(\mu A+M)\le 0 \end{aligned}$$

for $\mu \in (0, \infty )$ and the inequality is strict except for the case $m_1=\cdots =m_n$. Moreover,

$$\begin{aligned} \lim _{\mu \rightarrow 0}s(\mu A+M)=\max _{1\le i\le n}\{m_i\} \;\; \text {and} \;\; \lim _{\mu \rightarrow \infty }s(\mu A+M)=\sum _{i=1}^n{\theta _im_i}, \end{aligned}$$

where $\theta _i\in (0, 1)$, $1\le i\le n$, is determined by A and $\displaystyle \sum _{i=1}^n{\theta _i}=1$ (if A has each column sum equaling zero, then $\varvec{\theta }=(\theta _1,\dots ,\theta _n)^T$ is a positive eigenvector of A corresponding to eigenvalue 0).

Let $\varvec{m}=(m_1, m_2, m_3)$ be a real vector. We write $\varvec{m}\gg \varvec{0}$ if $m_i>0$ for all $i=1, 2, 3$, and $\varvec{m}>\varvec{0}$ if $\varvec{m}\ge \varvec{0}$ and $\varvec{m}\ne \varvec{0}$. Matrix $dD+qQ+\text {diag}(m_i)$ is irreducible and essentially nonnegative for any $d, q>0$, where D and Q are defined by (1.3). By the Perron–Frobenius theorem, $s\left( dD+qQ+\text {diag}(m_i)\right)$ is the principal eigenvalue of the following eigenvalue problem:

$$\begin{aligned} \displaystyle \sum _{j=1}^{3}(dD_{ij}+qQ_{ij})\phi _j+m_i\phi _i=\lambda \phi _i, \;\;i=1, 2, 3. \end{aligned}$$

(2.1)

We need to consider the following single-species patch model:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\textrm{d}u_i}{\textrm{d}t}=\displaystyle \sum _{j=1}^{3}(dD_{ij}+qQ_{ij})u_j+r_iu_i\left( 1-\frac{u_i}{k_i}\right) ,&{}i=1,2,3,\;\;t>0,\\ \varvec{u}(0)=\varvec{u}_0>\varvec{0}. \end{array}\right. } \end{aligned}$$

(2.2)

The global dynamics of (2.2) is as follows:

Lemma 2.2

Let D and Q be defined in (1.3), $\varvec{r}, \varvec{k}\gg \varvec{0}$, $d>0$, and $q\ge 0$. Then, model (2.2) admits a unique positive equilibrium $\varvec{u}^*\gg \varvec{0}$, which is globally asymptotically stable.

Proof

By [13, 31, 39], it suffices to show that $\varvec{0}$ is unstable, i.e.,

$$\begin{aligned} s:=s\left( dD+qQ+\text {diag}(r_i)\right) >0. \end{aligned}$$

Let $\phi ^T=(\phi _1, \phi _2, \phi _3)^T\gg \varvec{0}$ with $\sum _{i=1}^3\phi _i=1$ be the positive eigenvector of $dD+qQ+\text {diag}(r_i)$ corresponding to s. Multiplying (1, 1, 1) to the left of $dD\phi +qQ\phi +\text {diag}({r_i})\phi =s\phi$, we get $s=\sum _{i=1}^3{{r_i\phi _i}}>0$. This proves the result. $\square$

By Lemma 2.2, model (1.4) has two semitrivial equilibria $(\varvec{u}^*, \varvec{0})$ and $(\varvec{0}, \varvec{v}^*)$, where $\varvec{u}^* (\text {resp., }\varvec{v}^*)\gg \varvec{0}$ is the positive equilibrium of (2.2) with (d, q) replaced by $(d_1, q_1)$ (resp., $(d_2, q_2)$). Linearizing model (1.4) at $(\varvec{u}^*,\varvec{0})$, we can easily see that its stability is determined by the sign of $\lambda _1\left( d_2,q_2,\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right)$, which is the principal eigenvalue of the following eigenvalue problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda \phi _1=-(d_2+q_2)\phi _1+d_2\phi _2+r_1\left( 1-\displaystyle \frac{u^*_1}{k_1}\right) \phi _1,\\ \lambda \phi _2=(d_2+q_2)\phi _1-(2d_2+q_2)\phi _2+d_2\phi _3+r_2\left( 1-\displaystyle \frac{u^*_2}{k_2}\right) \phi _2,\\ \lambda \phi _3=(d_2+q_2)\phi _2-d_2\phi _3+r_3\left( 1-\displaystyle \frac{u^*_3}{k_3}\right) \phi _3. \end{array}\right. } \end{aligned}$$

(2.3)

In particular, $(\varvec{u}^*,\varvec{0})$ is locally asymptotically stable if $\lambda _1\left( d_2,q_2,\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) <0$ and unstable if $\lambda _1\left( d_2,q_2,\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) >0$. Here, we abuse the notation by denoting $\varvec{1}-{\varvec{u}^*}/{\varvec{k}}:=(1-u_1^*/k_1, 1-u_2^*/k_2, 1-u_3^*/k_3)$.

3 Main results

We fix $d_1, q_1>0, \varvec{r}, \varvec{k}\gg \varvec{0}$ and view species $\varvec{u}$ as the resident species and $\varvec{v}$ as the mutant species. We investigate the dynamics of model (1.4) varying $(d_2, q_2)$. For this purpose, we divide the first quadrant of the (d, q)-plane into six regions:

$$\begin{aligned} \begin{aligned} G_{11}:=&\left\{ (d,q):\; d\ge d_1,q\ge \frac{q_1}{d_1}d,(d,q)\ne (d_1,q_1)\right\} ,\\ G_{12}:=&\left\{ (d,q):\; 0<d<d_1,q\ge q_1\right\} ,\\ G_{13}:=&\left\{ (d, q):\; d\ge d_1,q_1\le q< \frac{q_1}{d_1}d,(d,q)\ne (d_1,q_1)\right\} ,\\ G_{21}:=&\left\{ (d,q):\; 0<d \le d_1,0<q\le \displaystyle \frac{q_1}{d_1}d,(d,q)\ne (d_1,q_1)\right\} ,\\ G_{22}:=&\left\{ (d,q):\; d>d_1,0<q\le q_1\right\} ,\\ G_{23}:=&\left\{ (d,q):\; 0<d\le d_1,\frac{q_1}{d_1}d<q\le q_1,(d,q)\ne (d_1,q_1)\right\} . \end{aligned} \end{aligned}$$

(3.1)

Fig. 2

Illustration of the six regions of (d, q)-plane

For readers’ convenience, we graph the six regions in Fig. 2.

3.1 Invasion curve

We consider the local stability of $(\varvec{u}^*,\varvec{0})$ in this subsection. Biologically, if $(\varvec{u}^*,\varvec{0})$ is stable, then a small amount of species $\varvec{v}$ cannot invade species $\varvec{u}$; if $(\varvec{u}^*,\varvec{0})$ is unstable, then a small amount of species $\varvec{v}$ may be able to invade species $\varvec{u}$. We prove that there exists a curve $q=q_{\varvec{u}}^*(d)$ in the (d, q)-plane such that $(\varvec{u}^*,\varvec{0})$ is locally asymptotically stable if $(d_2, q_2)$ is above the curve and $(\varvec{u}^*,\varvec{0})$ is unstable if it is below the curve. To this end, we define

$$\begin{aligned} d^*={\left\{ \begin{array}{ll} \infty ,&{}\text {if}\;\;\sum _{i=1}^3 r_i\left( 1-\frac{u_i^*}{k_i}\right) \ge 0,\\ d_0,&{}\text {if}\;\; \sum _{i=1}^3 r_i\left( 1-\frac{u_i^*}{k_i}\right) < 0, \end{array}\right. } \end{aligned}$$

(3.2)

where $d=d_0>0$ is the unique root of $\lambda _1(d, 0, \varvec{1}-\varvec{u^*/k})=0$ if $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) < 0$ (see the existence of $d_0$ in Lemma 5.2). We have the following result about the local stability/instability of the semitrivial equilibrium $(\varvec{u}^*,\varvec{0})$:

Theorem 3.1

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$. Then, there exists a continuous function $q=q_{\varvec{u}}^*(d): (0, d^*)\rightarrow {\mathbb {R}}_+$ passing through $(d_1, q_1)$ such that the following statements hold for model (1.4):

• (i) If $(d_2, q_2)\in S_1$, then the semitrivial equilibrium $(\varvec{u}^*,\varvec{0})$ is locally asymptotically stable;

• (ii) If $(d_2, q_2)\in S_2$, then the semitrivial equilibrium $(\varvec{u}^*,\varvec{0})$ is unstable.

Here, $S_1\cup S_2$ is a partition of the first quadrant of the (d, q)-plane defined as follows:

$$\begin{aligned} \begin{aligned} S_1:=&\left\{ (d,q):\; 0<d<d^*,\;\;q>q_{\varvec{u}}^*(d)\right\} \cup S_1^*,\\ S_2:=&\left\{ (d,q):\;0<d<d^*,\;0<q<q_{\varvec{u}}^*(d)\right\} , \end{aligned} \end{aligned}$$

(3.3)

where

$$\begin{aligned} S^*_1={\left\{ \begin{array}{ll} \left\{ (d,q):d\ge d^*,\;\;q>0\right\} , &{}\;\;\text {if}\;\;d^*\ne \infty ,\\ \emptyset , &{}\;\;\text {if}\;\;d^*=\infty .\\ \end{array}\right. } \end{aligned}$$

(3.4)

Remark 3.2

We call the curve in the first quadrant of (d, q)-plane defined by the function $q=q_{\varvec{u}}^*(d)$ in Theorem 3.1 the invasion curve. This curve consists with all the points $(d, q_{\varvec{u}}^*(d))$ such that $\lambda _1(d, q_{\varvec{u}}^*(d), \varvec{1}-{\varvec{u}^*}/{\varvec{k}})=0$, i.e., $(\varvec{u}^*,\varvec{0})$ is linearly neutrally stable. The invasion curve divides the first quadrant into $S_1\cup S_2$, where $S_1$ is the region above the curve and $S_2$ is the region below it. By Theorem 3.1, $(\varvec{u}^*,\varvec{0})$ is locally asymptotically stable if $(d_2, q_2)\in S_1$ and unstable if $(d_2,q_2)\in S_2$.

In the following of this paper, we denote

$$\begin{aligned} \begin{aligned}&{\underline{q}}:=\min \left\{ \displaystyle \frac{r_1}{k_1}(k_1-k_2),\displaystyle \frac{r_3}{k_3}(k_2-k_3)\right\} ,\\&{{\overline{q}}}:=\max \left\{ \displaystyle \frac{r_1}{k_1}(k_1-k_2),\displaystyle \frac{r_3}{k_3}(k_2-k_3)\right\} . \end{aligned} \end{aligned}$$

(3.5)

We take ${\underline{q}}$ and ${{\overline{q}}}$ as the threshold values for the drift rates. Specifically, if a drift rate is below ${\underline{q}}$ (above ${{\overline{q}}}$), we call it a slow (large) drift; if a drift rate is between ${\underline{q}}$ and ${{\overline{q}}}$, we call it an intermediate drift. These definitions coincide with those in [23] if $r_1=r_2=r_3$. It turns out that the magnitude of drift rate $q_1$ will have a large impact on the shape of the invasion curve and the dynamics of the model.

We have the following result about the invasion curve:

Proposition 3.3

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$. Let $S_1$ and $S_2$ be defined in Theorem 3.1. Then, the following statements hold:

• (i) $G_{11}\subset S_1$ and $G_{21}\subset S_2$;

• (ii) If $q_1>{{\overline{q}}}$, then $G_{12}\subset S_1$ and $G_{22}\subset S_2$;

• (iii) If $q_1<{\underline{q}}$, then $G_{13}\subset S_1$ and $G_{23}\subset S_2$

We explore further properties of the invasion curve:

Proposition 3.4

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$. Let $q=q_{\varvec{u}}^*(d): (0, d^*)\rightarrow {\mathbb {R}}_+$ be defined in Theorem 3.1. Then, the following statements hold:

• (i) $\lim _{d\rightarrow 0}q_{\varvec{u}}^*(d)=q_0$, where

  $$\begin{aligned} q_0=\max \left\{ r_1\left( 1-\frac{u_1^*}{k_1}\right) ,\ r_2\left( 1-\frac{u_2^*}{k_2}\right) \right\} ; \end{aligned}$$

  (3.6)

• (ii) If $q_1<{\underline{q}}$, then

  $$\begin{aligned} d^*=d_0\;\;\text {and}\;\; \lim _{d\rightarrow d^*} q_{\varvec{u}}^*(d)=0; \end{aligned}$$

  (3.7)

• (iii) If $q_1>{{\overline{q}}}$, then

  $$\begin{aligned} d^*=\infty \;\;\text {and}\;\;\lim _{d\rightarrow \infty } \displaystyle \frac{q_{\varvec{u}}^*(d)}{d}=\theta \end{aligned}$$

  (3.8)

  for some $\theta \in \left( 0,{q_1}/{d_1}\right)$;

• (iv) If ${\underline{q}}\le q\le {{\overline{q}}}$, then (3.7) holds when $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) < 0$, (3.8) holds with $\theta \in \left( 0,{q_1}/{d_1}\right)$ when $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) > 0$, and (3.8) holds with $\theta =0$ when $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) =0$.

Remark 3.5

By Propositions 3.3 and 3.4, the invasion curve lies in $G_{12}\cup G_{22}$ when the drift rate $q_1$ is small, and it lies in $G_{13}\cup G_{23}$ when $q_1$ is large. Moreover, if $q_1$ is small, the invasion curve is defined on a bounded interval $(0, d_0)$; if $q_1$ is large, it is defined on $(0, \infty )$ and has a slant asymptote $q=\theta d$ for some $\theta \in (0, q_1/d_1)$.

3.2 Competitive exclusion

In this subsection, we study the global dynamics of model (1.4) and find some parameter ranges of $(d_2, q_2)$ such that competitive exclusion happens. The relations of ${\underline{q}}$, ${{\overline{q}}}$ and $q_0$ are implicitly included in the results below. However, for reader’s convenience, we include the proof in the Appendix.

Firstly, we consider the small drift case, i.e., $q_1<{\underline{q}}$.

Theorem 3.6

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$ with $q_1<{\underline{q}}$. Then, the following statements hold:

• (i) If $(d_2,q_2)\in G_{21}\cup G_{23}$, then the semitrivial equilibrium $(\varvec{0},\varvec{v}^*)$ of (1.4) is globally asymptotically stable;

• (ii) If $(d_2,q_2)\in G_{11}\cup G_{12}^*\cup G_{13}$, then the semitrivial equilibrium $(\varvec{u}^*,\varvec{0})$ of (1.4) is globally asymptotically stable.

Here, $G_{12}^*$ is defined by

$$\begin{aligned} G^*_{12}=\{(d_2,q_2): (d_2,q_2)\in G_{12},q_2>{{\overline{q}}}\}. \end{aligned}$$

(3.9)

Fig. 3

Illustration of the results for the case $q_1<{\underline{q}}$. If $(d_2, q_2)$ is above the curve $q=q_{\varvec{u}}^*(d)$, then $(\varvec{u}^*,\varvec{0})$ is stable; and if $(d_2, q_2)$ is under the curve, then $(\varvec{u}^*,\varvec{0})$ is unstable. If $(d_2,q_2)\in G_{21}\cup G_{23}$, $(\varvec{0},\varvec{v}^*)$ is globally asymptotically stable; if $(d_2,q_2)\in G_{11}\cup G_{12}^*\cup G_{13}$, $(\varvec{u}^*,\varvec{0})$ is globally asymptotically stable

Remark 3.7

Our results on model (1.4) for the small drift rate case are summarized in Fig. 3. We have proved that competitive exclusion appears if $(d_2, q_2)$ falls into the blue and yellow regions of Fig. 3.

Next, we consider the large drift case, i.e., $q_1>{{\overline{q}}}$.

Theorem 3.8

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$ with $q_1>{{\overline{q}}}$. Then, the following statements hold:

• (i) If $(d_2,q_2)\in G_{21}\cup G_{22}\cup G_{23}^*$, then the semitrivial equilibrium $(\varvec{0},\varvec{v}^*)$ is globally asymptotically stable;

• (ii) If $(d_2,q_2)\in G_{11}\cup G_{12}$, then the semitrivial equilibrium $(\varvec{u}^*,\varvec{0})$ is globally asymptotically stable.

Here, $G_{23}^*$ is defined by

$$\begin{aligned} G_{23}^*=\{(d_2,q_2):(d_2,q_2)\in G_{23},q_2<{\underline{q}}\}. \end{aligned}$$

(3.10)

Remark 3.9

Our results on model (1.4) for the large drift rate case are summarized in Fig. 4. Different from the small drift rate case, the invasion curve is unbounded. Again, we are able to prove that competitive exclusion happens if $(d_2, q_2)$ falls into the blue and yellow regions of Fig. 4.

Then, we consider the intermediate drift case, i.e., ${\underline{q}}\le q_1\le {{\overline{q}}}$, and we have the following results on the global dynamics of model (1.4).

Theorem 3.10

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$ with ${\underline{q}}\le q_1\le {{\overline{q}}}$. Let $G_{12}^*$ be defined by (3.9) and $G_{23}^*$ be defined by (3.10). Then, the following statements hold:

• (i) If $(d_2,q_2)\in G_{21}\cup G_{23}^*$, then the semitrivial equilibrium $(\varvec{0},\varvec{v}^*)$ is globally asymptotically stable;

• (ii) If $(d_2,q_2)\in G_{11}\cup G^*_{12}$, then the semitrivial equilibrium $(\varvec{u}^*,\varvec{0})$ is globally asymptotically stable.

Fig. 4

Illustration of the results for the case $q_1>{\overline{q}}$. If $(d_2, q_2)$ is above the curve $q=q_{\varvec{u}}^*(d)$, then $(\varvec{u}^*,\varvec{0})$ is stable; and if $(d_2, q_2)$ is under the curve, then $(\varvec{u}^*,\varvec{0})$ is unstable. If $(d_2,q_2)\in G_{21}\cup G_{22}\cup G_{23}^*$, $(\varvec{0},\varvec{v}^*)$ is globally asymptotically stable; and if $(d_2,q_2)\in G_{11}\cup G_{12}$, $(\varvec{u}^*,\varvec{0})$ is globally asymptotically stable

Fig. 5

Illustration of the results for the case ${\underline{q}}\le q_1\le {\overline{q}}$. If $(d_2,q_2)\in G_{21}\cup G_{23}^*$, $(\varvec{0},\varvec{v}^*)$ is globally asymptotically stable; and if $(d_2,q_2)\in G_{11}\cup G^*_{12}$, $(\varvec{u}^*,\varvec{0})$ is globally asymptotically stable

Remark 3.11

Our results on model (1.4) for the intermediate drift rate case are summarized in Fig. 5. In this case, the invasion curve may be defined on either a bounded or an unbounded interval. However, we know that it must locate between the yellow and blue regions in Fig. 5, where competitive exclusion happens.

In view of Theorems 3.6, 3.8, and 3.10, the global dynamics of model (1.4) in $G_{11}\cup G_{21}$ is independent of $q_1$:

Corollary 3.12

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$. Then, the following statements hold:

• (i) If $(d_2,q_2)\in G_{11}$, then the semitrivial equilibrium $(\varvec{u}^*,\varvec{0})$ is globally asymptotically stable;

• (ii) If $(d_2,q_2)\in G_{21}$, then the semitrivial equilibrium $(\varvec{0},\varvec{v}^*)$ is globally asymptotically stable.

More importantly, we have the following result about the evolution of random dispersal and directed drift rates.

Corollary 3.13

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$. Then, the following statements hold:

• (i) Fix $d_1=d_2$. If $q_1<q_2$, then the semitrivial equilibrium $(\varvec{u}^*,\varvec{0})$ is globally asymptotically stable; If $q_1>q_2$, then the semitrivial equilibrium $(\varvec{0},\varvec{v}^*)$ is globally asymptotically stable;

• (ii) Fix $q_1=q_2<{\underline{q}}$. If $d_1<d_2$, then the semitrivial equilibrium $(\varvec{u}^*,\varvec{0})$ is globally asymptotically stable; If $d_1>d_2$, then the semitrivial equilibrium $(\varvec{0}, \varvec{v}^*)$ is globally asymptotically stable;

• (iii) Fix $q_1=q_2>{{\overline{q}}}$. If $d_1<d_2$, then the semitrivial equilibrium $(\varvec{0}, \varvec{v}^*)$ is globally asymptotically stable; If $d_1>d_2$, then the semitrivial equilibrium $(\varvec{u}^*, \varvec{0})$ is globally asymptotically stable.

Remark 3.14

By Corollary 3.13, the species with a smaller drift rate tends to have competitive advantage. If the drift rate is small, the species with smaller random dispersal rate has competitive advantage; if the drift rate is large, larger random dispersal rate is favored. We remark that Corollary 3.13 (i) was proved in [37] for the PDE case, and the corresponding results of 3.13 (ii)–(iii) for the PDE case in [37] are as follows: if $d_1>d_2$, then there exists ${{\overline{q}}}(d_1,d_2)$ (resp. ${\underline{q}}(d_1,d_2)$) such that $(\varvec{u}^*, \varvec{0})$ (resp. $(\varvec{0}, \varvec{v}^*)$) is globally asymptotically stable for $q_1=q_2>{{\overline{q}}}(d_1,d_2)$ (resp. $q_1=q_2<{\underline{q}}(d_1,d_2)$).

3.3 Coexistence and bistability

If $(d_2, q_2)$ is in the blank regions of Figs. 3, 4 and 5, we show that bistability and coexistence may occur. To this end, we explore the stability/instability of the semitrivial equilibrium $(\varvec{0},\varvec{v}^*(d_2,q_2))$ along the invasion curve $q_2=q_{\varvec{u}}^*(d_2)$. Let

$$\begin{aligned} {\hat{\lambda }}_1(d_2):=\lambda _1\left( d_1,q_1,\varvec{1}-\frac{{\varvec{v}^*}\left( d_2,q_{\varvec{u}}^*(d_2)\right) }{\varvec{k}}\right) . \end{aligned}$$

(3.11)

Then, ${\hat{\lambda }}_1(d_1)=0$, the semitrivial equilibrium $(\varvec{0},\varvec{v}^*(d_2,q^*_{\varvec{u}}(d_2)))$ is stable if ${\hat{\lambda }}_1(d_2)<0$, and $(\varvec{0},\varvec{v}^*(d_2,q^*_{\varvec{u}}(d_2)))$ is unstable if ${\hat{\lambda }}_1(d_2)>0$. The following result for the large drift case can be proved similarly as [7, Theorem 5.4], so we omit the proof here.

Theorem 3.15

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$ with $q_1>{{\overline{q}}}$. Let $q=q_{\varvec{u}}^*(d): (0, \infty )\rightarrow {\mathbb {R}}_+$ be defined in Theorem 3.1 and Proposition 3.4 (iii). Then, for any $d_2>0$, the following statements hold:

• (i) If ${\hat{\lambda }}_1(d_2)<0$, then

  $$\begin{aligned} {{\hat{q}}}(d_2):=\inf \left\{ q>0: \ q>q_{\varvec{u}}^*(d_2)\ \text {and} \ \lambda _1\left( d_1,q_1,\varvec{1}-\frac{{\varvec{v}^*}\left( d_2,q\right) }{\varvec{k}}\right) \ge 0\right\} \end{aligned}$$

  exists and satisfies

  $$\begin{aligned} {\left\{ \begin{array}{ll} {{\hat{q}}}(d_2)\in \left( q_{\varvec{u}}^*(d_2),q_1 \right) \;\;&{}\text {for}\;\; d_2<d_1,\\ {{\hat{q}}}(d_2)\in \left( q_{\varvec{u}}^*(d_2),\displaystyle \frac{q_1}{d_1}d_2\right) \;\;&{}\text {for}\;\; d_2>d_1. \end{array}\right. } \end{aligned}$$

  (3.12)

  Moreover, for any $q_2\in (q_{\varvec{u}}^*(d_2), {{\hat{q}}}(d_2))$, both semitrivial equilibria $(\varvec{u}^*,\varvec{0})$ and $(\varvec{0}, \varvec{v}^*)$ are locally asymptotically stable and model (1.4) admits an unstable positive equilibrium.

• (ii) If ${\hat{\lambda }}_1(d_2)>0$, then

  $$\begin{aligned} {{\hat{q}}}(d_2):=\sup \left\{ q>0:\ q<q_{\varvec{u}}^*(d_2)\ \text {and}\ \lambda _1\left( d_1,q_1,\varvec{1}-\frac{{\varvec{v}^*}\left( d_2,q\right) }{\varvec{k}}\right) \le 0\right\} \end{aligned}$$

  exists and satisfies

  $$\begin{aligned} {\left\{ \begin{array}{ll} {{\hat{q}}}(d_2)\in \left( \displaystyle \frac{q_1}{d_1}d_2, q_{\varvec{u}}^*(d_2)\right) \;\; &{}\text {for}\;\; d_2<d_1,\\ {{\hat{q}}}(d_2)\in \left( q_1, q_{\varvec{u}}^*(d_2)\right) \;\;&{}\text {for}\;\; d_2>d_1. \end{array}\right. } \end{aligned}$$

  Moreover, for any $q_2\in ({{\hat{q}}}(d_2),q_{\varvec{u}}^*(d_2))$, both semitrivial equilibria $(\varvec{u}^*,\varvec{0})$ and $(\varvec{0}, \varvec{v}^*)$ are unstable and model (1.4) admits a stable positive equilibrium.

Remark 3.16

In (ii) when both semitrivial equilibria are unstable, we may conclude that the solutions are uniform persistent. If ${\underline{q}}\le q_1\le {{\overline{q}}}$ (the intermediate drift case), Theorem 3.15 (i)–(ii) holds for any $d_2<d_1$, and we omit the statement to save space here.

The small drift rate case will be handled slightly different from the large drift rate case. For any $\theta >0$, by Lemma 2.1 and Proposition 3.3 (ii), the line $q=d\theta$ and the invasion curve $q=q_{\varvec{u}}^*(d)$ have exactly one intersection point $(d^*(\theta ), d^*(\theta )\theta )$. So we can reparameterize the invasion curve as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} d=d^*(\theta ),\\ q=q^*(\theta )=d^*(\theta )\theta , \end{array}\right. } \;\; \theta >0. \end{aligned}$$

(3.13)

Let

$$\begin{aligned} {\tilde{\lambda }}_1(\theta ):=\lambda _1\left( d_1,q_1,\varvec{1}-\frac{{\varvec{v}^*}\left( d^*(\theta ),q^*(\theta )\right) }{\varvec{k}}\right) , \;\;\theta >0. \end{aligned}$$

(3.14)

Then, the semitrivial equilibrium $(\varvec{0},\varvec{v}^*\left( d^*(\theta ),q^*(\theta )\right) )$ is stable if ${\tilde{\lambda }}_1(\theta )<0$ and unstable if ${\tilde{\lambda }}_1(\theta )>0$. Noticing that $q_{\varvec{u}}^*(d_1)=q_1$, we have $d^*(q_1/d_1)=d_1$ and

$$\begin{aligned} {\tilde{\lambda }}_1\left( {q_1}/{d_1}\right) =\lambda _1\left( d_1, q_1, \varvec{1}-\frac{{\varvec{v}^*}\left( d_1,q_1\right) }{\varvec{k}}\right) =0. \end{aligned}$$

Theorem 3.17

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$ with $0<q_1<{\underline{q}}$. Then, for any $\theta >0$, the following statements hold:

• (i) If ${\tilde{\lambda }}_1(\theta )<0$, then

  $$\begin{aligned} {{\tilde{d}}}^*(\theta ):=\inf \left\{ d>0: \ d>d^*(\theta )\ \text {and} \ \lambda _1\left( d_1,q_1,\varvec{1}-\frac{{\varvec{v}^*}\left( d,d\theta \right) }{\varvec{k}}\right) \ge 0\right\} \end{aligned}$$

  exists with $d^*(\theta )<{{\tilde{d}}}^*(\theta )$ such that for any $(d_2,q_2)$ with $q_2=d_2\theta$ and $d^*(\theta )<d_2<{{\tilde{d}}}^*(\theta )$ both semitrivial equilibria $(\varvec{u}^*,\varvec{0})$ and $(\varvec{0}, \varvec{v}^*)$ are locally asymptotically stable and model (1.4) admits an unstable positive equilibrium.

• (ii) If ${\tilde{\lambda }}_1(\theta )>0$, then

  $$\begin{aligned} {{\tilde{d}}}^*(\theta ):=\sup \left\{ d>0: \ d<d^*(\theta )\ \text {and} \ \lambda _1\left( d_1,q_1,\varvec{1}-\frac{{\varvec{v}^*}\left( d, d\theta \right) }{\varvec{k}}\right) \le 0\right\} \end{aligned}$$

  exists with ${{\tilde{d}}}^*(\theta )<d^*(\theta )$ such that for any $(d_2,q_2)$ with $q_2=d_2\theta$ and ${{\tilde{d}}}^*(\theta )<d_2< d^*(\theta )$ both semitrivial equilibria $(\varvec{u}^*,\varvec{0})$ and $(\varvec{0}, \varvec{v}^*)$ are unstable and model (1.4) admits a stable positive equilibrium.

Moreover, ${{\tilde{d}}}^*(\theta )$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} ({{\tilde{d}}}^*(\theta ),{{\tilde{d}}}^*(\theta )\theta )\in G_{12}\;\;\text {if}\;\; \displaystyle \theta >\frac{q_1}{d_1},\\ ({{\tilde{d}}}^*(\theta ),{{\tilde{d}}}^*(\theta )\theta )\in G_{22}\;\;\text {if}\;\; 0<\theta <\displaystyle \frac{q_1}{d_1}.\\ \end{array}\right. } \end{aligned}$$

(3.15)

Proof

We prove (i), and (ii) can be proved similarly. Fix $\theta >0$. Suppose ${\tilde{\lambda }}_1(\theta )<0$. Let

$$\begin{aligned} A=\left\{ d>0: \ d>d^*(\theta )\ \text {and} \ \lambda _1\left( d_1,q_1,\varvec{1}-\frac{{\varvec{v}^*}\left( d,d\theta \right) }{\varvec{k}}\right) \ge 0\right\} . \end{aligned}$$

By Theorem 3.6 (ii), $(\varvec{0},\varvec{v}^*)$ is unstable or neutrally stable if $(d_2, q_2)\in G_{11}\cup G_{13}$, which yields $A\ne \emptyset$. Since ${\tilde{\lambda }}_1(\theta )<0$, there exists $\epsilon _0>0$ such that

$$\begin{aligned} \lambda _1\left( d_1,q_1,\varvec{1}-\frac{{\varvec{v}^*}\left( d^*(\theta )+\epsilon , \theta (d^*(\theta )+\epsilon )\right) }{\varvec{k}}\right)<0, \ \ \text {for any } 0<\epsilon <\epsilon _0. \end{aligned}$$

Therefore, ${{\tilde{d}}}^*(\theta )$ exists with $d^*(\theta )<{{\tilde{d}}}^*(\theta )$.

If $(d_2,q_2)$ satisfies $q_2=d_2\theta$ and ${{\tilde{d}}}^*(\theta )<d_2< d^*(\theta )$, by the definition of ${{\tilde{d}}}^*(\theta )$, we have

$$\begin{aligned} \lambda _1\left( d_1,q_1,\varvec{r-v^*}(d_2,q_2)\right) <0, \end{aligned}$$

which means that $(\varvec{0}, \varvec{v}^*)$ is locally asymptotically stable. By Theorem 3.1, $(\varvec{u}^*,\varvec{0})$ is also locally asymptotically stable. By the monotone dynamical system theory [20, 21, 46], model (1.4) admits an unstable positive equilibrium. Finally, it is easy to see that (3.15) holds by Theorem 3.6. $\square$

4 Discussions and numerical simulations

In this section, we discuss the results of the paper and present some numerical simulations.

4.1 Impact of spatial heterogeneity

If the environment is homogeneous, i.e., assumption (H) is replaced by $k_1=k_2=k_3$, model (1.4) with n patches has been investigated in our recent paper [7]. The main results in [7] are summarized in Fig. 6. In particular, we prove that the invasion curve is between the lines $q=q_1$ and $q=q_1d/d_1$, $(\varvec{u}^*, \varvec{0})$ is globally asymptotically stable in $G_1$, and $(\varvec{0}, \varvec{v}^*)$ is globally asymptotically stable in $G_2$. These results are independent of the magnitude of drift rate $q_1$ and are similar to the large drift rate case in this paper. Biologically, the downstream end is crowded due to the drift and thereby less friendly compared with the upstream end. If the environment perturbs from being uniformly distributed and the upstream locations become advantageous, e.g., assumption (H) holds, then a larger drift rate may compensate for it. This may explain why the homogeneous environment case is similar to the larger drift case in this paper.

Fig. 6

Illustration of the main results for (1.4) with $k_1=k_2=k_3$ in [7]. The blue cure is the invasion curve, which always lies between the lines $q=q_1$ and $q=q_1d/d_1$. Moreover, $(\varvec{u}^*,\varvec{0})$ is globally asymptotically stable if $(d_2, q_2)\in G_1$, and $(\varvec{0},\varvec{v}^*)$ is globally asymptotically stable if $(d_2, q_2)\in G_2$

4.2 Impact of drift rate

By Propositions 3.4 and 3.13, if the drift rate $q_1$ is small ($q_1<{\underline{q}}$), the invasion curve $q=q^*_{\varvec{u}}(d)$ is defined on a bounded interval and the species with a smaller random dispersal rate is advantageous; if $q_1$ is large ($q_1>{{\overline{q}}}$), the invasion curve is unbounded with a slant asymptote $q=\theta d$ for some $\theta >0$ and larger random dispersal rate is favored. The results for the small drift rate case align with the ones in the seminal works [15, 19], which claim that the species with a smaller random dispersal rate will always out-compete the other one in a spatial heterogeneous environment, when both species randomly move in space and are different only by the movement rate. When the drift rate becomes large, the outcomes of the competition change dramatically, and the species with a larger dispersal rate may win the competition.

Fig. 7

The invasion curve for different values of $q_1$. Here, $\varvec{k}=(5, 3, 1)$, $\varvec{r}=(1, 2, 1)$, and $d_1=1$. The threshold values for the drift rates are ${\underline{q}}=0.4$ and ${{\overline{q}}}=2$

We numerically explore the impact of the drift rate $q_1$ on the shape of the invasion curve $q=q^*_{\varvec{u}}(d)$. Fix $\varvec{k}=(5, 3, 1)$, $\varvec{r}=(1, 2, 1)$, and $d_1=1$. Then, we can compute the threshold values for the drift rates: ${\underline{q}}=0.4$ and ${{\overline{q}}}=2$. In Fig. 7, we plot the invasion curves for $q_1=0.2, 0.5, 1.2, 4$. If $q_1=0.2$ or 0.5, the invasion curves seem to be bounded with $\partial _d q^*_{\varvec{u}}(d_1)<0$, which indicates that a smaller random dispersal rate is favored when $q_1=q_2$ and $d_1\approx d_2$. In sharp contrast, if $d_1=1.2$ or 4, the invasion curves seem to be unbounded with $\partial _d q^*_{\varvec{u}}(d_1)>0$. This simulation also shows that the invasion curve can be bounded or unbounded for the intermediate drift case (${\underline{q}}<q_1<{\overline{q}}$).

4.3 Bistability and coexistence phenomena

Let $d_1=1, q_1=1.5$, $\varvec{r}=(3,7,3)$, and $\varvec{k}=(5,3,1)$. We graph the invasion curve $(d^*(\theta ), q^*(\theta ))$ and ${\tilde{\lambda }}(\theta )$ in Fig. 8. The stability of $(\varvec{0}, \varvec{v}^*)$ when $(d_2, q_2)=(d^*(\theta ), q^*(\theta ))$ is determined by the sign of ${\tilde{\lambda }}(\theta )$. In Fig. 8, we can see that ${\tilde{\lambda }}(\theta )$ changes sign, which means that both bistability and coexistence are possible. Indeed, if we choose $(d_2, q_2)=(3.088, 1.239)$, which is slightly below the invasion curve, then both $(\varvec{u}^*, \varvec{0})$ and $(\varvec{0}, \varvec{v}^*)$ are locally asymptotically stable. As shown in Fig. 9, if the initial data are $(\varvec{u}(0),\varvec{v}(0))=((0.1, 0.1, 0.1), (5, 5, 5))$, then the solution of (1.4) converges to $(\varvec{0}, \varvec{v}^*)$; if the initial data are $(\varvec{u}(0),\varvec{v}(0))=((5, 5, 5), (0.1, 0.1, 0.1))$, then the solution converges to $(\varvec{u}^*, \varvec{0})$. Finally, we choose $(d_2, q_2)=(10.28, 0.03)$, which is slightly above the invasion curve ($(\varvec{u}^*, \varvec{0})$ is unstable). Since ${\tilde{\lambda }}$ is positive, $(\varvec{0}, \varvec{v}^*)$ is also unstable, and the model has at least one stable positive equilibrium. We graph the solution of (1.4) for initial data $(\varvec{u}(0), \varvec{v}(0))=((5, 5, 5), (5, 5, 5))$ and the solution seems to converge to a positive equilibrium, see Fig. 10.

Fig. 8

a The invasion curve $(d^*(\theta ), q^*(\theta ))$ when $d_1=1$, $q_1=1.5$, $\varvec{r}=(3,7,3)$, and $\varvec{k}=(5,3,1)$. b The sign of the curve $\tilde{\lambda }_1(\theta )$ determines the stability of $(\varvec{0},\varvec{v}^*)$ when $(d_2, q_2)=(d^*(\theta ), q^*(\theta ))$

Fig. 9

Solutions of (1.4) with $d_1=1$, $q_1=1.5$, $d_2=3.088$, $q_2=1.239$, $\varvec{r}=(3,7,3)$, $\varvec{k}=(5,3,1)$. For a, b, the initial data are $\varvec{u}(0)=(0.1,0.1,0.1)$ and $\varvec{v}(0)=(5,5,5)$, and species $\varvec{v}$ wins the competition; for c, d, the initial data are $\varvec{u}(0)=(5,5,5)$ and $\varvec{v}(0)=(0.1,0.1,0.1)$, and species $\varvec{u}$ wins the competition

Fig. 10

Solution of (1.4) with $d_1=1$, $q_1=1.5$, $d_2=10.28$, $q_2=0.03$, $\varvec{r}=(3,7,3)$, $\varvec{k}=(5,3,1)$, and the initial data are $\varvec{u}(0)=(5,5,5)$ and $\varvec{v}(0)=(5,5,5)$. The two species seem to coexist

4.4 Evolutionarily singular strategies

We formulate a conjecture based on Corollary 3.13 about the existence of an evolutionarily stable strategy (ESS) for the diffusion rate, which may distinguish the 2-patch model from the 3-patch model.

We fix $q_2=q_1>0$ and view the diffusion rate as an evolutionary strategy of the species. By Corollary 3.13 when ${\underline{q}}<{{\overline{q}}}$, we conjecture that there exists ${\underline{q}}\le q_*< q^*\le {{\overline{q}}}$ such that if $q<{\underline{q}}$, then the slower diffuser always wins the competition; if $q>q_*$, then the faster diffuser prevails; if $q_1\in (q_*, q^*)$, there exists a unique $d^*(q_1)>0$ such that $d_1=d^*(q_1)$ is an evolutionarily singular strategy with the asymptotic limits:

$$\begin{aligned} \lim _{q_1\rightarrow q_*^+}d^*(q_1)=0,\ \ \lim _{q_1\rightarrow {q^*}^-}d^*(q_1)=+\infty ; \end{aligned}$$

or

$$\begin{aligned} \lim _{q_1\rightarrow q_*^+}d^*(q_1)=+\infty ,\ \ \lim _{q_1\rightarrow {q^*}^-}d^*(q_1)=0. \end{aligned}$$

Moreover, we conjecture that the singular strategy is an ESS in the former case but not in the latter case (Fig. 11).

We provide some numerical evidence to support the conjecture below. Since

$$\begin{aligned} \lambda _1\left( d_1,q_1,\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) =0, \end{aligned}$$

the sign of

$$\begin{aligned} {\mathcal {S}}(d_1,q_1):=\left. \frac{\partial \lambda _1\left( d,q_1,\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) }{\partial d}\right| _{d=d_1} \end{aligned}$$

is crucial to determine which strategy is favored when $d_2\approx d_1$: if ${\mathcal {S}}(d_1,q_1)<0$ the slow diffuser is favored; if ${\mathcal {S}}(d_1,q_1)>0$ the faster diffuser is favored. By Corollary 3.13, ${\mathcal {S}}(d_1,q_1)$ changes signs. In particular, if $q_1<{\underline{q}}$, ${\mathcal {S}}(d_1,q_1)<0$ and if $q_1>{\underline{q}}$, ${\mathcal {S}}(d_1,q_1)>0$. We numerically solve ${\mathcal {S}}(d_1,q_1)=0$ and plot the solution in Fig. 11, which consists with a curve $d_1=d^*(q_1)$, where $q_1\in (q_*, q^*)$. In the left figure, the sign of ${\mathcal {S}}(d_1,q_1)$ changes from negative to positive when moving from above to below the curve. This suggests that the diffusion rate $d_1=d^*$ may be an ESS for $q\in (q_*, q^*)$. In the right figure, opposite phenomenon appears when crossing the curve and we suspect that the singular strategy is not an ESS in this case.

Fig. 11

The sign of ${\mathcal {S}}(d_1,q_1)$, where ${\mathcal {S}}(d_1,q_1)<0$ in the dark blue region and ${\mathcal {S}}(d_1,q_1)>0$ in the light blue region. Left figure: $\varvec{r}=(3,7,3)$, $\varvec{k}=(5,3,1)$; right F $\varvec{r}=(50,3,3)$, $\varvec{k}=(5,3,1)$

We remark such an intermediate diffusion rate $d_1=d^*$ as an ESS does not appear in the corresponding 2-patch model. For the 2-patch model, as proved in [18, 45] (see [23, Theorem 1]), there exists a critical value $q_*$ such that if $q_1=q_2<q_*$ then $d_1=0$ is an ESS; if $q_1=q_2>q_*$ then $d_1=\infty$ is an ESS. We also note that if ${\underline{q}}={{\overline{q}}}$ in the 3-patch model, then the curve $d_1=d^*(q_1)$ is a vertical line and an intermediate ESS also does not exists (which is similar to the 2-patch case).

Finally, we conjecture that the results in this paper hold for the N-patch model. Our results for 3-patch model are based on the monotonicity of the semitrivial equilibrium (see Lemma 5.1 (iii)–(iv)), which we cannot prove for the N-patch model. Similarly, if the movement rates among patches are not homogeneous (i.e., the off-diagonal entries of D and Q are not 1 s), it is also not trivial to show how the movement rates affect the monotonicity of the semitrivial equilibrium.

5 Proofs for the invasion curve

In this section, we present the proofs of the results on the invasion curve $q_{\varvec{u}}^*(d)$. We begin with an analysis on $\varvec{u}^*$. A similar result of the following lemma when $r_1=r_2=r_3$ except for the sign of $\sum _{i=1}^3r_i\left( 1-{u^*_i}/{k_i}\right)$ can be found in [23].

Lemma 5.1

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, $d_1>0$, and $q_1\ge 0$. Then, the following statements on $\varvec{u}^*$ hold:

• (i) $d_1u_{i+1}^*-(d_1+q_1)u_i^*<0$ for $i=1,2$;

• (ii) $u^*_1<k_1$ and $u^*_3>k_3$;

• (iii) If $q_1>{{\overline{q}}}$, then $u^*_1<u^*_2<u^*_3$ and $\sum _{i=1}^3r_i\left( 1-\frac{u^*_i}{k_i}\right) >0$;

• (iv) If $q_1<{\underline{q}}$, then $u^*_1>u^*_2>u^*_3$ and $\sum _{i=1}^3r_i\left( 1-\frac{u^*_i}{k_i}\right) <0$.

Proof

By (1.4), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} d_1u^*_2-(d_1+q_1)u^*_1=-r_1u^*_1\left( 1-\displaystyle \frac{u^*_1}{k_1}\right) ,\\ \left( d_1u_3^*-(d_1+q_1)u^*_2\right) -\left( d_1u_2^*-(d_1+q_1)u^*_1\right) =-r_2u^*_2\left( 1-\displaystyle \frac{u^*_2}{k_2}\right) ,\\ d_1u_3^*-(d_1+q_1)u^*_2=r_3u^*_3\left( 1-\displaystyle \frac{u^*_3}{k_3}\right) .\\ \end{array}\right. } \end{aligned}$$

(5.1)

Suppose to the contrary that $d_1u^*_2-(d_1+q_1)u^*_1\ge 0$. Then, by the first equation of (5.1), we have $u_2^*\ge u_1^*\ge k_1$. This, together with assumption $(\textbf{H})$ and the second equation of (5.1), implies that $d_1u_3^*-(d_1+q_1)u^*_2>0$ and $u_3^*>k_3$, which contradicts the third equation of (5.1). Therefore, we have $d_1u^*_2-(d_1+q_1)u^*_1<0$. Similarly, we can prove $d_1u_3^*-(d_1+q_1)u^*_2<0$. This proves (i). By (i) and the first and third equations of (5.1), we can easily obtain (ii).

The proof of (iv) is similar to that of (iii), so we only prove (iii) here. Suppose $q_1>{{\overline{q}}}$. We rewrite (5.1) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} d_1(u^*_2-u^*_1)=-r_1u^*_1\left( 1-\displaystyle \frac{q_1}{r_1}-\displaystyle \frac{u^*_1}{k_1}\right) ,\\ d_1(u^*_3-u^*_2)-(d_1+q_1)(u^*_2-u^*_1)=-r_2u^*_2\left( 1-\displaystyle \frac{u^*_2}{k_2}\right) ,\\ -(d_1+q_1)(u^*_3-u^*_2)=-r_3u^*_3\left( 1+\displaystyle \frac{q_1}{r_3}-\displaystyle \frac{u^*_3}{k_3}\right) .\\ \end{array}\right. } \end{aligned}$$

(5.2)

Suppose to the contrary that $u^*_1\ge u^*_2$. Then, by the first equation of (5.2), we have $k_1-\displaystyle \frac{q_1k_1}{r_1}-u^*_1\ge 0$. Since $q_1>\displaystyle \frac{r_1}{k_1}(k_1-k_2)$, we obtain

$$\begin{aligned} k_2>k_1-\displaystyle \frac{q_1k_1}{r_1}\ge u_1^*\ge u_2^*. \end{aligned}$$

Then, by the second equation of (5.2), we get $u^*_2>u^*_3$. This, combined with $q_1>\displaystyle \frac{r_3}{k_3}(k_2-k_3)$, yields

$$\begin{aligned} k_3\left( 1+\displaystyle \frac{q_1}{r_3}\right)>k_2>u^*_2>u^*_3, \end{aligned}$$

which contradicts the last equation of (5.2). This proves $u^*_1< u^*_2$.

Suppose to the contrary that $u^*_2\ge u^*_3$. Then, by the last equation of (5.2), we have $u_3^*\ge k_3\left( 1+\displaystyle \frac{q_1}{r_3}\right)$. By $q_1>{{\overline{q}}}$, we obtain

$$\begin{aligned} u_2^*\ge u_3^*\ge k_3\left( 1+\displaystyle \frac{q_1}{r_3}\right)>k_2>k_1-\frac{q_1k_1}{r_1}. \end{aligned}$$

Then, by the second equation of (5.2), we have $u_1^*>u_2^*$. By the first equation of (5.2), we get

$$\begin{aligned} 0>d_1(u^*_2-u^*_1)=-r_1u^*_1\left( 1-\displaystyle \frac{q_1}{r_1}-\displaystyle \frac{u^*_1}{k_1}\right) >0, \end{aligned}$$

which is a contradiction. This proves $u_2^*<u_3^*$.

Dividing the ith equation of (5.2) by $u_i^*$, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} -(d_1+q_1)+d_1\displaystyle \frac{u^*_{2}}{u^*_1}+r_1\left( 1-\displaystyle \frac{u_1^*}{k_1}\right) =0,\\ (d_1+q_1)\left( \displaystyle \frac{u^*_{1}}{u^*_2}-1\right) -d_1\left( 1-\displaystyle \frac{u^*_{3}}{u^*_2}\right) +r_2\left( 1-\displaystyle \frac{u_2^*}{k_2}\right) =0,\\ (d_1+q_1) \displaystyle \frac{u^*_{2}}{u^*_3}-d_1 +r_3\left( 1-\displaystyle \frac{u_3^*}{k_3}\right) =0. \end{array}\right. } \end{aligned}$$

(5.3)

Adding up the equations in (5.3), we obtain

$$\begin{aligned} \begin{aligned}&\sum _{i=2}^{3} \left( (d_1+q_1)\left( \frac{u_{i-1}^*}{u_i^* }-1\right) +d_1\left( \frac{u_{i}^*}{u_{i-1}^*}-1\right) \right) +\sum _{i=1}^3 r_i\left( 1-\frac{u_i^*}{k_i}\right) \\&\quad =\sum _{i=2}^{3}\frac{(u_{i-1}^*-u_i^*)((d_1+q_1)u_{i-1}^*-d_1u_i^*)}{u_{i-1}^*u_i^*}+ \sum _{i=1}^3r_i\left( 1-\frac{u^*_i}{k_i}\right) =0. \end{aligned} \end{aligned}$$

(5.4)

Then, by (i) and $u_1^*<u_2^*<u_3^*$, we have $\sum _{i=1}^3r_i\left( 1-\frac{u^*_i}{k_i}\right) >0$. This proves (iii). $\square$

5.1 Proof of Theorem 3.1

We prove the existence of the invasion curve $q=q_{\varvec{u}}^*(d)$ in this subsection.

Lemma 5.2

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$. Then, the following statements hold about the semitrivial equilibrium $(\varvec{u}^*, \varvec{0})$ of (1.4):

• (i) If $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) \ge 0$, then for any $d>0$ there exists $q_{\varvec{u}}^*(d)>0$ such that $\lambda _1\left( d,q_{\varvec{u}}^*(d), \varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) =0$, $\lambda _1\left( d,q, \varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) <0$ for all $q>q_{\varvec{u}}^*(d)$, and $\lambda _1\left( d,q, \varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) >0$ for all $q<q_{\varvec{u}}^*(d)$;

• (ii) If $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) < 0$, then there exists $d_0>0$ such that $\lambda _1(d_0,0,\varvec{1}-{\varvec{u}^*}/{\varvec{k}})=0$, $\lambda _1(d,0,\varvec{1}-{\varvec{u}^*}/{\varvec{k}})<0$ for all $d>d_0$, and $\lambda _1(d,0,\varvec{1}-{\varvec{u}^*}/{\varvec{k}})>0$ for all $d<d_0$. Moreover, the following results hold:

${\mathrm{(ii_1)}}$:

For any $d\in (0,d_0)$, there exists $q_{\varvec{u}}^*(d)>0$ such that the statement in $\mathrm{(i)}$ holds;

${\mathrm{(ii_2)}}$:

For any $d\in [d_0, \infty )$, we have $\lambda _1(d,q,\varvec{1}-{\varvec{u}^*}/{\varvec{k}})< 0$ for all $q>0$.

Proof

For simplicity, we denote $\lambda _1(d,q):=\lambda _1\left( d,q,\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right)$. An essential step of the proof is to show the following claim.

Claim 1: Fixing $d>0$, equation $\lambda _1(d, q)=0$ has at most one root for $q\in [0, \infty )$.

Proof of Claim: Let $\varvec{\psi }$ be the positive eigenvector corresponding to $\lambda _1(d,q)$ with $\sum _{i=1}^3\psi _i=1$. Then, we have

$$\begin{aligned} \lambda _1(d,q)\psi _i=d\sum _{j=1}^3 D_{ij}\psi _j+q\sum _{j=1}^3 Q_{ij}\psi _j+r_i\left( 1-\frac{u_i^*}{k_i}\right) \psi _i, \;\;i=1,2,3. \end{aligned}$$

(5.5)

Differentiating (5.5) with respect to q and denoting $'=\partial /\partial q$, we obtain

$$\begin{aligned} \lambda _1'\psi _i+\lambda _1\psi '_i=d\sum _{j=1}^3 D_{ij}\psi '_j+\sum _{j=1}^3 Q_{ij}\psi _j+q\sum _{j=1}^3 Q_{ij}\psi '_j+r_i\left( 1-\frac{u_i^*}{k_i}\right) \psi '_i, \;\;i=1,2,3. \end{aligned}$$

(5.6)

Multiplying (5.5) by $\psi _i'$ and (5.6) by $\psi _i$ and taking the difference of them, we have

$$\begin{aligned} \lambda _1'\psi ^2_i=\sum _{j=1}^3 (dD_{ij}+qQ_{ij})(\psi _i\psi '_j-\psi _i'\psi _j)+\sum _{j=1}^3 Q_{ij}\psi _i\psi _j, \;\;i=1,2,3. \end{aligned}$$

(5.7)

Motivated by [7, Eq. (3.7)], we introduce $(\beta _1,\beta _2,\beta _3)=\left( 1,{d}/(d+q), d^2/(d+q)^2\right)$. Multiplying (5.7) by $\beta _i$ and summing up in i, we obtain

$$\begin{aligned} \lambda _1' \sum _{i=1}^3 \beta _i \psi _i^2 =\sum _{i=1}^{2}\left( \frac{d}{d+q}\right) ^{i-1}\left( -\psi _i+\frac{d}{d+q}\psi _{i+1}\right) \psi _i. \end{aligned}$$

(5.8)

Suppose $\lambda _1\left( d,{{\tilde{q}}}\right) =0$ for some ${{\tilde{q}}}\ge 0$. By Lemma 5.1 (ii), we see that

$$\begin{aligned} \begin{aligned}&d\psi _{2}-(d+{{\tilde{q}}})\psi _{1}=-\psi _1r_1\left( 1-\frac{u^*_1}{k_1}\right)<0,\\&d\psi _{3}-(d+{{\tilde{q}}})\psi _{2}=\psi _3r_1\left( 1-\frac{u^*_3}{k_3}\right) <0. \end{aligned} \end{aligned}$$

Therefore, by (5.8), we have $\lambda '(d, {{\tilde{q}}})<0$. This proves the claim.

According to the claim, whether the equation $\lambda _1(d, q)=0$ has a root in q is determined by the sign of $\lambda _1(d, 0)$ and $\lim _{q\rightarrow \infty }\lambda _1(d,q)$.

Claim 2: $\lim _{q\rightarrow \infty }\lambda _1(d,q)<0$.

Proof of claim: Adding up all the equations of (5.5), we have

$$\begin{aligned} \lambda _1(d,q)=\sum _{i=1}^3r_i\left( 1-\frac{u_i^*}{k_i}\right) \psi _i, \end{aligned}$$

(5.9)

which implies that $\lambda _1(d,q)$ is bounded for $d,q>0$. So up to a subsequence, we may assume $\lim _{q\rightarrow \infty }\varvec{\psi }=\tilde{\varvec{\psi }}$. Dividing (5.5) by q and taking $q\rightarrow \infty$, we obtain

$$\begin{aligned} \sum _{i=1}^3Q_{ij}{\tilde{\psi }}_{j}=0,\;\;i=1,2,3, \end{aligned}$$

which yields $\tilde{\varvec{\psi }}=(0,0,1)^T$. Then, taking $q\rightarrow \infty$ in (5.9), we have

$$\begin{aligned} \lim _{q\rightarrow \infty }\lambda _1(d,q)=r_3\left( 1-\frac{u_3^*}{k_3}\right) <0, \end{aligned}$$

where we have used Lemma 5.1 (ii) in the last step. This proves the claim.

By Lemma 2.1, $\lambda _1(d, 0)$ is strictly decreasing in d with

$$\begin{aligned} \lim _{d\rightarrow 0}\lambda (d,0)=\max _{1\le i\le 3}r_i\left( 1-\frac{u_i^*}{k_i}\right) >0\;\; \text {and}\;\; \lim _{d\rightarrow \infty }\lambda (d,0)=\displaystyle \frac{1}{3}\sum _{i=1}^3 r_i\left( 1-\frac{u_i^*}{k_i}\right) , \end{aligned}$$

where we have used Lemma 5.1 (ii) again to see that $1-u_1^*/k_1>0$. Now, the desired results follow from this and Claims 1 and 2. $\square$

We are ready to prove Theorem 3.1.

Proof of Theorem 3.1

Let $d_0$ be defined in Lemma 5.2, $d^*$ be defined by (3.2), and $q=q^*_{\varvec{u}}(d): (0, d^*)\rightarrow {\mathbb {R}}_+$ be defined in Lemma 5.2. Then, Theorem 3.1 (i)–(ii) follows from Lemmas 5.1–5.2 and the fact that the stability/instability of $(\varvec{u}^*, \varvec{0})$ is determined by the sign of $\lambda _1\left( d,q, \varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right)$. The continuity of $q=q^*_{\varvec{u}}(d)$ follows from $\partial _q \lambda _1\left( d,q^*_{\varvec{u}}(d), \varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) <0$ (Claim 1 of Lemma 5.2) and the implicit function theorem. $\square$

5.2 Proof of Propositions 3.3 and 3.4

First, we prove the following useful result:

Lemma 5.3

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$. Then, we have

$$\begin{aligned} \lambda _1\left( d_2,q_2,\varvec{1}-\frac{\varvec{u}^*}{\varvec{k}}\right) \ne 0, \end{aligned}$$

if one of the following conditions holds:

• (i) $(d_2,q_2)\in G_{11}\cup G_{21}$;

• (ii) $q_1>{{\overline{q}}}$ and $(d_2,q_2)\in G_{12}\cup G_{22}$;

• (iii) $q_1<{\underline{q}}$ and $(d_2,q_2)\in G_{13}\cup G_{23}$.

Proof

Suppose to the contrary that $\lambda _1\left( d_2,q_2,\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) =0$, and let $\varvec{\phi }\gg 0$ be a corresponding eigenvector. Note that $\lambda _1\left( d_1,q_1,\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) =0$ with a corresponding eigenvector $\varvec{u}^*$. Let

$$\begin{aligned} {\tilde{f}}_0={{\tilde{f}}}_3=0,\;\;{{\tilde{g}}}_0={{\tilde{g}}}_3=0, \end{aligned}$$

and

$$\begin{aligned} {{\tilde{f}}}_j=d_1 u^*_{j+1}-(d_1+q_1)u_j^*,\;\;{{\tilde{g}}}_j=d_2\phi _{j+1}-(d_2+q_2)\phi _j, \;\; j=1, 2. \end{aligned}$$

(5.10)

Then, we have

$$\begin{aligned}&{{\tilde{f}}}_{j}-{{\tilde{f}}}_{j-1}=-r_ju^*_j\left( 1-\displaystyle \frac{u_j^*}{k_j}\right) ,\;\;\;j=1,2,3, \end{aligned}$$

(5.11a)

$$\begin{aligned}&{{\tilde{g}}}_{j}-{{\tilde{g}}}_{j-1}=-r_j\phi _j\left( 1-\displaystyle \frac{u_j^*}{k_j}\right) ,\;\;\;j=1,2,3. \end{aligned}$$

(5.11b)

Using similar arguments as in [7, Lemma 5.7], we can show

$$\begin{aligned} \sum _{j=1}^{2}\left[ (d_1-d_2)(\phi _{j+1}-\phi _j)-(q_1-q_2)\phi _j\right] {{\tilde{f}}}_j{\displaystyle \frac{d_1^j}{\left( d_1+q_1\right) ^{j+1}}}=0, \end{aligned}$$

(5.12)

and

$$\begin{aligned} \sum _{k=1}^{2}\left[ (d_2-d_1)(u^*_{j+1}-u^*_j)-(q_2-q_1)u^*_j\right] {{\tilde{g}}}_j{\displaystyle \frac{d_2^j}{\left( d_2+q_2\right) ^{j+1}}}=0. \end{aligned}$$

(5.13)

Indeed, multiplying (5.11a) by $\left( \displaystyle \frac{d_1}{d_1+q_1}\right) ^j\phi _j$, and summing up from $j=1$ to $j=3$, we have

$$\begin{aligned} \begin{aligned}&-\sum _{j=1}^3r_ju^*_j\phi _j\left( 1-\displaystyle \frac{u_j^*}{k_j}\right) \left( \frac{d_1}{d_1+q_1}\right) ^j\\&\quad =\sum _{j=1}^{3}\left( {{\tilde{f}}}_j-{{\tilde{f}}}_{j-1}\right) \phi _j\left( \frac{d_1}{d_1+q_1}\right) ^j\\&\quad ={{\tilde{f}}}_3\phi _3\left( \frac{d_1}{d_1+q_1}\right) ^3-{{\tilde{f}}}_{0}\phi _1\left( \frac{d_1}{d_1+q_1}\right) +\sum _{j=1}^{2}{{\tilde{f}}}_j\displaystyle \left( \frac{d_1}{d_1+q_1}\right) ^j\left( \phi _j-\displaystyle \frac{d_1}{d_1+q_1}\phi _{j+1}\right) \\&\quad =-\sum _{j=1}^{2}(d_1\phi _{j+1}-(d_1+q_1)\phi _j){{\tilde{f}}}_j\displaystyle \frac{d_1^j}{\left( d_1+q_1\right) ^{j+1}}, \end{aligned} \end{aligned}$$

(5.14)

where we have used ${{\tilde{f}}}_3={{\tilde{f}}}_0=0$ in the last step. Similarly, multiplying (5.11b) by $\left( \displaystyle \frac{d_1}{d_1+q_1}\right) ^ju^*_j$ and summing up from $j=1$ to $j=3$, we obtain

$$\begin{aligned} \begin{aligned} -\sum _{j=1}^3r_ju^*_j\phi _j\left( 1-\displaystyle \frac{u_j^*}{k_j}\right) \left( \frac{d_1}{d_1+q_1}\right) ^j =-\sum _{j=1}^{2} {{\tilde{g}}}_j{{\tilde{f}}}_j\displaystyle \frac{d_1^j}{\left( d_1+q_1\right) ^{j+1}}. \end{aligned} \end{aligned}$$

(5.15)

Taking the difference of (5.14) and (5.15), we obtain (5.12). Similarly, we can prove (5.13).

By Lemma 5.1 (i)–(ii) and (5.11b), we have ${{\tilde{f}}}_j, {{\tilde{g}}}_j<0$ for $j=1,2$. Now we obtain a contradiction for each of (i)–(iii).

(i) We only consider the case $(d_2,q_2)\in G_{21}$, since the case $(d_2,q_2)\in G_{11}$ can be studied similarly. Suppose $(d_2,q_2)\in G_{21}$. Then, we have $d_2\le d_1, q_2\le q_1d_2/d_1$, and $(d_1, q_1)\ne (d_2, q_2)$. If $d_1\ne d_2$, then it is easy to check that

$$\begin{aligned} \displaystyle \frac{q_1-q_2}{d_1-d_2}\ge \displaystyle \frac{q_2}{d_2}. \end{aligned}$$

(This inequality can be found in [53, Lemma 2.4].) This, together with ${{\tilde{g}}}_1,{{\tilde{g}}}_2<0$, yields

$$\begin{aligned} (d_1-d_2)(\phi _{j+1}-\phi _j)-(q_1-q_2)\phi _j<0,\;\; j=1,2. \end{aligned}$$

(5.16)

If $d_1=d_2$, then $q_1>q_2$ and (5.16) also holds. Then, by ${{\tilde{f}}}_1,{{\tilde{f}}}_2<0$ and (5.12), we have

$$\begin{aligned} 0<\sum _{j=1}^{2}\left[ (d_1-d_2)(\phi _{j+1}-\phi _j)-(q_1-q_2)\phi _j\right] {{\tilde{f}}}_j{\displaystyle \frac{d_1^j}{\left( d_1+q_1\right) ^{j+1}}}=0, \end{aligned}$$

which is a contradiction.

(ii) We only need to obtain a contradiction for the case $(d_2,q_2)\in G_{22}$, since the case $(d_2, q_2)\in G_{12}$ can be studied similarly. Suppose $(d_2,q_2)\in G_{22}$. Then, we have $d_2>d_1$ and $q_2\le q_1$. By Lemma 5.1 (i), we have $u_1^*<u_2^*<u^*_3$, which implies that

$$\begin{aligned} (d_2-d_1)(u^*_{j+1}-u^*_j)-(q_2-q_1)u^*_j>0, \ \ j=1, 2. \end{aligned}$$

This, combined with ${{\tilde{g}}}_1, {{\tilde{g}}}_2<0$ and (5.13), gives a contradiction.

(iii) We only obtain a contradiction for the case $(d_2,q_2)\in G_{23}$, since the case $(d_2,q_2)\in G_{13}$ can be studied similarly. Suppose $(d_2,q_2)\in G_{23}$. Then, we have $d_2\le d_1$, $q_2\le q_1$, and $(d_1, q_1)\ne (d_2, q_2)$. By Lemma 5.1 (ii), we have $u_1^*>u_2^*>u^*_3$, which implies that

$$\begin{aligned} (d_2-d_1)(u^*_{j+1}-u^*_j)-(q_2-q_1)u^*_j>0, \ \ j=1, 2. \end{aligned}$$

This combined with ${{\tilde{g}}}_1, {{\tilde{g}}}_2<0$ and (5.13) gives a contradiction. $\square$

We are ready to prove Propositions 3.3 and 3.4.

Proof of Proposition 3.3

(i) We only prove the case $G_{21}\subset S_2$, (i.e., $(\varvec{u}^*,\varvec{0})$ is unstable for $(d_2,q_2)\in G_{21}$), since the case $G_{11}\subset S_1$ can be proved similarly. To avoid confusion, we denote $\varvec{u}^*$ by $\varvec{u}^*_{\varvec{k}}$. It is easy to see that $\varvec{u}^*_{\varvec{k}}$ depends continuously on $\varvec{k}$.

Suppose $(d_2, q_2)\in G_{21}$. We need to prove that $\lambda _1\left( d_2,q_2,\varvec{1}-{\varvec{u}^*_{\varvec{k}}}/{\varvec{k}}\right) >0$. Suppose to the contrary that $\lambda _1\left( d_2,q_2,\varvec{1}-{\varvec{u}^*_{\varvec{k}}}/{\varvec{k}}\right) \le 0$. By Lemma 5.3, we must have $\lambda _1\left( d_2,q_2,\varvec{1}-{\varvec{u}^*_{\varvec{k}}}/{\varvec{k}}\right) < 0$. By [7, Theorem 4.2], we have $\lambda _1\left( d_2,q_2,\varvec{1}-{\varvec{u}^*_{\varvec{k}'}}/{\varvec{k}'}\right) >0$, where $\varvec{k}'=(k_3,k_3,k_3)$.

Let $\Lambda (s):=\lambda _1\left( d_2,q_2,\varvec{1}-{\varvec{u}^*_{\varvec{k}_1(s)}}/{\varvec{k}_1(s)}\right)$, where $\varvec{k}_1(s)=s\varvec{k}+(1-s)\varvec{k}'$ satisfies (H) for any $s\in [0, 1]$. Since

$$\begin{aligned} \Lambda (1)=\lambda _1\left( d_2,q_2,\varvec{1}-\frac{\varvec{u}^*_{\varvec{k}}}{\varvec{k}}\right) <0\;\;\text { and}\;\; \Lambda (0)=\lambda _1\left( d_2,q_2,\varvec{1}-\frac{\varvec{u}^*_{\varvec{k}'}}{\varvec{k}'}\right) >0, \end{aligned}$$

there exists $s_0\in (0,1)$ such that $\Lambda (s_0)=0$, which contradicts Lemma 5.3.

(ii) By [7, Theorem 4.2], if $(d_2,q_2)\in G_{22}$, then $\lambda _1\left( d_2,q_2,\varvec{1}-{\varvec{u}^*_{\varvec{k}'}}/{\varvec{k}'}\right) >0$; and if $(d_2,q_2)\in G_{12}$, then $\lambda _1\left( d_2,q_2,\varvec{1}-{\varvec{u}^*_{\varvec{k}'}}/{\varvec{k}'}\right) <0$, where $\varvec{k}'=(k_3,k_3,k_3)$. Then, using similar arguments as (i), we can prove (ii).

(iii) Let $\varvec{\psi }$ be the positive eigenvector corresponding to $\lambda _1:=\lambda _1\left( d_2,q_1,\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right)$ with $\sum _{i=1}^3\psi _i=1$. Then, we have

$$\begin{aligned} \lambda _1\psi _i=d_2\sum _{j=1}^3 D_{ij}\psi _j+q_1\sum _{j=1}^3Q_{ij}\psi _j+r_i\left( 1-\frac{u_i^*}{k_i}\right) \psi _i, \;\;i=1,2,3. \end{aligned}$$

(5.17)

Differentiating (5.5) with respect to $d_2$ and denoting $'=\partial /\partial d_2$, we obtain

$$\begin{aligned} \lambda _1'\psi _i+\lambda _1\psi '_i=d_2\sum _{j=1}^3 D_{ij}\psi '_j+\sum _{j=1}^3 D_{ij}\psi _j+q_1\sum _{j=1}^3Q_{ij}\psi '_j+r_i\left( 1-\frac{u_i^*}{k_i}\right) \psi '_i, \;\;i=1,2,3. \end{aligned}$$

(5.18)

Multiplying (5.17) by $\psi _i'$ and (5.18) by $\psi _i$ and taking the difference of them, we have

$$\begin{aligned} \lambda _1'\psi ^2_i=\sum _{j=1}^3 (d_2D_{ij}+q_1Q_{ij})(\psi _i\psi '_j-\psi _i'\psi _j)+\sum _{j=1}^3 D_{ij}\psi _i\psi _j, \;\;i=1,2,3. \end{aligned}$$

(5.19)

Similar to the proof of Lemma 5.2, let $(\beta _1,\beta _2,\beta _3)=\left( 1,{d_2}/(d_2+q_1), d_2^2/(d_2+q_1)^2\right)$. Multiplying (5.19) by $\beta _i$ and adding up them in i, we obtain

$$\begin{aligned} \lambda _1' \sum _{i=1}^3 \beta _i \psi _i^2 =\sum _{i=1}^{2}\left( \frac{d_2}{d_2+q_1}\right) ^{i-1}\left( -\psi _i+\frac{d_2}{d_2+q_1}\psi _{i+1}\right) (\psi _i-\psi _{i+1}). \end{aligned}$$

(5.20)

Note that $\lambda _1\left( d_1,q_1,\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) =0$ with a corresponding eigenvector $(u_1^*, u^*_2, u_3^*)^T$. Moreover, by Lemma 5.1, we have $d_1u_{i+1}^*-(d_1+q_1)u_i^*<0$ for $i=1, 2$ and $u_1^*>u^*_2>u_3^*$. Then, it follows from (5.20) that

$$\begin{aligned} \left. \frac{\partial \lambda _1\left( d_2,q_1,\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) }{\partial d_2}\right| _{d_2=d_1}<0. \end{aligned}$$

(5.21)

This implies that $\lambda _1\left( d_2,q_1,\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) >0$ if $0<d_1-d_2\ll 1$ and $\lambda _1\left( d_2,q_1,\varvec{1}-\frac{\varvec{u}^*}{\varvec{k}}\right) <0$ if $0<d_2-d_1\ll 1$. Then, by Lemma 5.3, we have $G_{13}\subset S_1$ and $G_{23}\subset S_2$. $\square$

Remark 5.4

A similar inequality of (5.21) is proved in [23], and we include the proof for completeness here.

Proof of Proposition 3.4

For any $0<d<d^*$, let $\varvec{\psi }$ be the eigenvector corresponding to $\lambda _1\left( d,q_{\varvec{u}}^*(d),\varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) =0$ with $\varvec{\psi }\gg 0$ and $\sum _{i=1}^3\psi _i=1$. Then,

$$\begin{aligned} d\sum _{j=1}^3 D_{ij}\psi _j+q_{\varvec{u}}^*(d)\sum _{j=1}^3 Q_{ij}\psi _j+r_i\left( 1-\frac{u_i^*}{k_i}\right) \psi _i=0, \;\;i=1,2,3. \end{aligned}$$

(5.22)

(i) Up to a subsequence, we may assume $\lim _{d\rightarrow 0}\varvec{\psi }=\tilde{\varvec{\psi }}$ for some $\tilde{\varvec{\psi }}\ge \varvec{0}$ and $\sum _{i=1}^3{\tilde{\psi }}_i=1$. We first claim that $q_{\varvec{u}}^*(d)$ is bounded for $d\in (0,\delta )$ with $\delta \ll 1$. If it is not true, then dividing (5.22) by $q_{\varvec{u}}^*(d)$ and taking $d\rightarrow 0$, we have

$$\begin{aligned} \sum _{j=1}^3Q_{ij}{\tilde{\psi }}_{j}=0,\;\;i=1,2,3, \end{aligned}$$

(5.23)

which yields $\tilde{\varvec{\psi }}=(0,0,1)^T$. Adding up all the equations of (5.22) and taking $d\rightarrow 0$ in (5.24), we have

$$\begin{aligned} \sum _{i=1}^3r_i\left( 1-\frac{u_i^*}{k_i}\right) {\tilde{\psi }}_i=0, \end{aligned}$$

(5.24)

and consequently, $k_3-u_3^*=0$, which contradicts Lemma 5.1 (ii). This proves the claim. By the claim, up to a subsequence, we may assume $\lim _{d\rightarrow 0}q^*(\theta )={{\tilde{q}}}_0\in [0,\infty )$. Consequently, for sufficiently small $\epsilon >0$, there exists ${{\bar{d}}}>0$ such that $q_{\varvec{u}}^*(d)<{{\tilde{q}}}_0+\epsilon$ for all $0<d<{{\bar{d}}}$. It follows from Lemma 5.2 that

$$\begin{aligned} \lambda _1\left( d, {{\tilde{q}}}_0+\epsilon , \varvec{1}-\frac{\varvec{u}^*}{\varvec{k}}\right) <0 \end{aligned}$$

(5.25)

for all $0<d<{{\bar{d}}}$. Hence,

$$\begin{aligned} \begin{aligned}&\lim _{d\rightarrow 0}\lambda _1\left( d, {{\tilde{q}}}_0+\epsilon , \varvec{1}-\frac{\varvec{u}^*}{\varvec{k}}\right) \\&\quad =\displaystyle \max \left\{ r_1\left( 1-\frac{u_1^*}{k_1}\right) -({{\tilde{q}}}_0+\epsilon ),r_2\left( 1-\frac{u_2^*}{k_2}\right) -({{\tilde{q}}}_0+\epsilon ),r_3\left( 1-\frac{u_3^*}{k_3}\right) \right\} \le 0.\\ \end{aligned} \end{aligned}$$

Since $k_3-u_3^*=0$ and $\epsilon >0$ was arbitrary,

$$\begin{aligned} \displaystyle \max \left\{ r_1\left( 1-\frac{u_1^*}{k_1}\right) -{{\tilde{q}}}_0,r_2\left( 1-\frac{u_2^*}{k_2}\right) -{{\tilde{q}}}_0\right\} \le 0. \end{aligned}$$

(5.26)

Therefore, we have ${{\tilde{q}}}_0\ge q_0>0$. Similarly, we can prove ${{\tilde{q}}}_0\le q_0$. This proves (i).

Now we prove (ii)–(iv). If we show that (3.7) holds when $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) < 0$, (3.8) holds with $\theta \in (0,q_1/d_1)$ when $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) > 0$, and (3.8) holds with $\theta =0$ when $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) =0$. Then, (iv) holds and (ii)–(iii) follow from Theorem 5.1 (iii)–(iv).

By Lemma 5.2 (i), the function $q=q_{\varvec{u}}^*(d)$ is defined for $d\in (0,\infty )$ when $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) \ge 0$. We claim that ${q_{\varvec{u}}^*(d)}/{d}$ is bounded for $d\in (\delta ,\infty )$ for any fixed $\delta >1$. If it is not true, up to a subsequence, we may assume

$$\begin{aligned} \lim _{d\rightarrow \infty }\displaystyle \frac{q_{\varvec{u}}^*(d)}{d}=\infty \;\; \text {and}\;\;\lim _{d\rightarrow \infty } \varvec{\psi }=\hat{\varvec{\psi }} \end{aligned}$$

for some $\hat{\varvec{\psi }}\ge \varvec{0}$ and $\sum _{i=1}^3{\hat{\psi }}_i=1$. Then, dividing (5.22) by $q_{\varvec{u}}^*(d)$ and taking $d\rightarrow \infty$, we can obtain a contradiction using similar arguments as in the proof of (i). Therefore, ${q_{\varvec{u}}^*(d)}/{d}$ is bounded for $d\in (\delta ,\infty )$. Then, using similar arguments as in the proof of [7, Proposition 4.4], we can show that (3.8) holds with $\theta \in (0,q_1/d_1)$ when $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) > 0$, and (3.8) holds with $\theta =0$ when $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) =0$.

By Lemma 5.2 (ii), the function $q=q_{\varvec{u}}^*(d)$ is defined for $d\in (0,d_0)$ when $\sum _{i=1}^3 r_i\left( 1-{u_i^*}/{k_i}\right) < 0$. Using similar arguments as in (i), we can show that $q_{\varvec{u}}^*(d)$ is bounded for $d\in (d_0-\delta ,d_0)$ for some $\delta \ll 1$. Then, up to a subsequence, we may assume

$$\begin{aligned} \lim _{d\rightarrow d_0} q_{\varvec{u}}^*(d)=\eta \;\;\text {and}\;\;\lim _{d\rightarrow d_0} \varvec{\psi }=\varvec{\psi }^* \end{aligned}$$

for some ${\varvec{\psi }^*}\ge \varvec{0}$ and $\sum _{i=1}^3\psi ^*_i=1$. Taking $d\rightarrow d_0$ in (5.22), we see that

$$\begin{aligned} d_0\sum _{j=1}^3 D_{ij}\psi ^*_j+\eta \sum _{j=1}^3 Q_{ij}\psi ^*_j+r_i\left( 1-\frac{u_i^*}{k_i}\right) \psi ^*_i=0, \;\;i=1,2,3, \end{aligned}$$

(5.27)

which yields $\lambda _1\left( d_0,\eta , \varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) =0$. By the proof of Lemma 5.2, $\lambda _1\left( d_0,q, \varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) =0$ has at most one root for $q\in [0,\infty )$. Since $\lambda _1\left( d_0,0, \varvec{1}-{\varvec{u}^*}/{\varvec{k}}\right) =0$, we must have $\eta =0$. This proves (3.7). $\square$

6 Proofs for the competitive exclusion results

Let $(\varvec{u},\varvec{v})$ be a positive equilibrium of model (1.4). Define

$$\begin{aligned} \begin{aligned}&f_0=f_3=0,\;\;g_0=g_3=0,\\&f_j=d_1u_{j+1}-(d_1+q_1)u_j,\;\;g_j=d_2v_{j+1}-(d_2+q_2)v_j,\;\; j=1,2. \end{aligned} \end{aligned}$$

(6.1)

Clearly, we have

$$\begin{aligned} f_{j}-f_{j-1}=-r_ju_j\left( 1-\displaystyle \frac{u_j+v_j}{k_j}\right) ,\;\;\;j=1,2,3, \end{aligned}$$

(6.2)

and

$$\begin{aligned} g_{j}-g_{j-1}=-r_jv_j\left( 1-\displaystyle \frac{u_j+v_j}{k_j}\right) ,\;\;\;j=1,2,3. \end{aligned}$$

(6.3)

Then, we have the following result about the sign of $f_j,g_j$, $j=1,2$.

Lemma 6.1

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1, q_1, d_2, q_2>0$. If $(\varvec{u},\varvec{v})$ is a positive equilibrium of model (1.4), then we have $f_1,g_1,f_2,g_2<0$.

Proof

First we prove $f_1<0$. Suppose to the contrary that $f_1\ge 0$. By (6.2) and (6.3), we have $k_1-u_1-v_1\le 0$ and $g_1\ge 0$. Since $f_1,g_1\ge 0$, we have $u_2>u_1$ and $v_2>v_1$. This combined with $(\textbf{H})$ implies that $k_2-u_2-v_2<0$. Then, by (6.2) and (6.3) again, we obtain that $f_2,g_2>0$ and $k_3-u_3-v_3<0$, which contradicts (6.2) with $j=3$. Therefore, we have $f_1<0$. Consequently, by (6.2) and (6.3) with $j=1$, we have $g_1<0$. Using similar arguments, we can prove $f_2,g_2<0$. $\square$

The following result is similar to [7, Lemma 5.7] with $j=1$ and $j=n=3$ (see also the proof of Lemma 5.3). Thus, we omit the proof.

Lemma 6.2

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1, q_1, d_2, q_2>0$. If $(\varvec{u},\varvec{v})$ is a positive equilibrium of model (1.4), then the following equations hold:

$$\begin{aligned} \sum _{j=1}^{2}\left[ (d_1-d_2)(v_{j+1}-v_j)-(q_1-q_2)v_j\right] f_j{\displaystyle \frac{d_1^j}{\left( d_1+q_1\right) ^{j+1}}}=0, \end{aligned}$$

(6.4)

and

$$\begin{aligned} \sum _{j=1}^{2}\left[ (d_2-d_1)(u_{j+1}-u_j)-(q_2-q_1)u_j\right] g_k{\displaystyle \frac{d_2^j}{\left( d_2+q_2\right) ^{j+1}}}=0. \end{aligned}$$

(6.5)

An essential step to prove the competitive exclusion results for model (1.4) is to show the nonexistence of positive equilibrium:

Lemma 6.3

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$. Let $G^*_{12}$ and $G_{23}^*$ be defined by (3.9) and (3.10), respectively. Then, model (1.4) admits no positive equilibrium, if one of the following conditions holds:

• (i) $(d_2,q_2)\in G_{11}\cup G_{21}$;

• (ii) $q_1>{{\overline{q}}}$ and $(d_2,q_2)\in G_{12}\cup G_{22}\cup G_{23}^*$;

• (iii) $q_1<{\underline{q}}$ and $(d_2,q_2)\in G_{13}\cup G_{23}\cup G^*_{12}$.

• (iv) ${\underline{q}}\le q_1\le {{\overline{q}}}$ and $(d_2,q_2)\in G^*_{12}\cup G_{23}^*$;

Proof

Suppose to the contrary that model (1.4) admits a positive equilibrium $(\varvec{u},\varvec{v})$. Then, we will obtain a contradiction for each of the cases (i)–(iv).

(i) We only consider the case $(d_2,q_2)\in G_{21}$. Since the nonlinear terms of (1.4) are symmetric, the case $(d_2,q_2)\in G_{11}$ can be proved similarly. Suppose $(d_2,q_2)\in G_{21}$. Then, we have $d_2\le d_1, q_2\le q_1d_2/d_1$ and $(d_1, q_1)\ne (d_2, q_2)$. First, we claim that

$$\begin{aligned} (d_1-d_2)(v_{j+1}-v_j)-(q_1-q_2)v_j<0\;\;\text {for}\;\; j=1,2. \end{aligned}$$

(6.6)

Indeed if $d_1=d_2$, then $q_1>q_2$ and (6.6) holds. If $d_1>d_2$, then it is easy to check that

$$\begin{aligned} \displaystyle \frac{q_1-q_2}{d_1-d_2}\ge \displaystyle \frac{q_2}{d_2}. \end{aligned}$$

(This inequality is in [53, Lemma 2.4]). This, combined with $g_1,g_2<0$, proves (6.6). Then, by $f_1, f_2<0$ and (6.4), we have

$$\begin{aligned} 0<\sum _{j=1}^{2}\left[ (d_1-d_2)(v_{j+1}-v_j)-(q_1-q_2)v_j\right] f_j{\displaystyle \frac{d_1^j}{\left( d_1+q_1\right) ^{j+1}}}=0, \end{aligned}$$

which is a contradiction.

(ii) We first consider the case $(d_2,q_2)\in G_{22}$. Since the nonlinear terms of (1.4) are symmetric, the case $(d_2,q_2)\in G_{12}$ can be proved similarly. Suppose $(d_2, q_2)\in G_{22}$. Then, $d_2>d_1$ and $q_2\le q_1$. By (1.4), we have

$$\begin{aligned}&d_1(u_2-u_1)=-r_1u_1\left( 1-\displaystyle \frac{q_1}{r_1}-\displaystyle \frac{u_1+v_1}{k_1}\right) ,\end{aligned}$$

(6.7a)

$$\begin{aligned}&d_2(v_2-v_1)=-r_1v_1\left( 1-\displaystyle \frac{q_2}{r_1}-\displaystyle \frac{u_1+v_1}{k_1}\right) ,\end{aligned}$$

(6.7b)

$$\begin{aligned}&(d_1+q_1)(u_1-u_2)-d_1(u_2-u_3)=-r_2u_2\left( 1-\displaystyle \frac{u_2+v_2}{k_2}\right) ,\end{aligned}$$

(6.7c)

$$\begin{aligned}&(d_2+q_2)(v_1-v_2)-d_2(v_2-v_3)=-r_2v_2\left( 1-\displaystyle \frac{u_2+v_2}{k_2}\right) ,\end{aligned}$$

(6.7d)

$$\begin{aligned}&(d_1+q_1)(u_2-u_3)=-r_3u_3\left( 1+\displaystyle \frac{q_1}{r_3}-\displaystyle \frac{u_3+v_3}{k_3}\right) ,\end{aligned}$$

(6.7e)

$$\begin{aligned}&(d_2+q_2)(v_2-v_3)=-r_3u_3\left( 1+\displaystyle \frac{q_2}{r_3}-\displaystyle \frac{u_3+v_3}{k_3}\right) . \end{aligned}$$

(6.7f)

Then, we show that $u_1<u_2<u_3$. Suppose to the contrary that $u_1\ge u_2$. Then, by (6.7a), we see that

$$\begin{aligned} u_1+v_1\le k_1-\displaystyle \frac{q_1k_1}{r_1}\le k_1-\displaystyle \frac{q_2k_1}{r_1}, \end{aligned}$$

where we have used $q_2\le q_1$ in the last inequality. This, combined with (6.7b), implies that $v_1\ge v_2$. Noticing that

$$\begin{aligned} q_1>{{\overline{q}}}\ge \displaystyle \frac{r_1}{k_1}(k_1-k_2), \end{aligned}$$

we have

$$\begin{aligned} u_2+v_2\le u_1+v_1\le k_1-\displaystyle \frac{q_1k_1}{r_1} <k_2, \end{aligned}$$

and consequently $u_3<u_2$ and $v_3<v_2$ by (6.7c) and (6.7d). This, combined with $q_1>{{\overline{q}}}$, implies that

$$\begin{aligned} u_3+v_3<u_2+v_2<k_2<k_3+\displaystyle \frac{k_3q_1}{r_3}, \end{aligned}$$

which contradicts (6.7e). Similarly, we can show that $u_2<u_3$. So, $u_1<u_2<u_3$, which leads to

$$\begin{aligned} (d_2-d_1)(u_{j+1}-u_j)-(q_2-q_1)u_j>0, \ \ j=1, 2. \end{aligned}$$

Then, by Lemma 6.1 and (6.5), we have

$$\begin{aligned} 0>\sum _{j=1}^{2}\left[ (d_2-d_1)(u_{j+1}-u_j)-(q_2-q_1)u_j\right] g_j{\displaystyle \frac{d_2^j}{\left( d_2+q_2\right) ^{j+1}}}=0, \end{aligned}$$

which is a contradiction.

Now suppose that $(d_2,q_2)\in G_{23}^*$. Then, $q_2<{\underline{q}}$ and $(d_1,q_1)\in {\hat{G}}_{13}$, where

$$\begin{aligned} {{\hat{G}}}_{13}:=\{(d, q):\; d\ge d_2,q_2\le q< \frac{q_2}{d_2}d,(d,q)\ne (d_2,q_2)\}. \end{aligned}$$

(6.8)

Since the nonlinear terms of (1.4) are symmetric, this case can be proved similarly as the case $(d_2,q_2)\in G_{13}$ (the proof is immediately below).

(iii) Suppose that $(d_2,q_2)\in G_{13}$. Then, we have $d_2\ge d_1$, $q_1\le q_2\le q_1d_2/d_1$, and $(d_1, q_1)\ne (d_2, q_2)$. We show that $u_1>u_2>u_3$. Suppose to the contrary that $u_1\le u_2$. Then, by (6.7a) and $q_2\ge q_1$, we have

$$\begin{aligned} u_1+v_1\ge k_1-\displaystyle \frac{q_1k_1}{r_1}>k_1-\displaystyle \frac{q_2k_1}{r_1}. \end{aligned}$$

This, combined with (6.7b), yields $v_1\le v_2$. Noting that

$$\begin{aligned} q_1<{\underline{q}}<\frac{r_1}{k_1}(k_1-k_2), \end{aligned}$$

we have

$$\begin{aligned} k_2<k_1-\frac{q_1k_1}{r_1}\le u_1+v_1\le u_2+v_2. \end{aligned}$$

Then, by (6.7c) and (6.7d), we have $u_3>u_2$ and $v_3>v_2$. Since $q_1<{\underline{q}}$, we have

$$\begin{aligned} k_3+\frac{k_3q_1}{r_3}<k_2<u_2+v_2<u_3+v_3, \end{aligned}$$

which contradicts (6.7e). Similarly, we can show $u_2>u_3$. Therefore, we have $u_1>u_2>u_3$ and

$$\begin{aligned} (d_2-d_1)(u_{j+1}-u_{j})-(q_2-q_1)u_j<0,\;\;j=1,2. \end{aligned}$$

Then, it follows from Lemma 6.1 and (6.5) that

$$\begin{aligned} 0<\sum _{j=1}^{2}\left[ (d_2-d_1)(u_{j+1}-u_j)-(q_2-q_1)u_j\right] g_j{\displaystyle \frac{d_2^j}{\left( d_2+q_2\right) ^{j+1}}}=0, \end{aligned}$$

which is a contradiction.

For the case $(d_2,q_2)\in G_{23}$, using similar arguments as above, we can obtain $v_1>v_2>v_3$, which leads to

$$\begin{aligned} (d_1-d_2)(v_{j+1}-v_j)-(q_1-q_2)v_j<0, \ \ j=1, 2. \end{aligned}$$

This, combined with Lemma 6.1 and (6.4), implies that

$$\begin{aligned} 0<\sum _{j=1}^{2}\left[ (d_1-d_2)(v_{j+1}-v_j)-(q_1-q_2)v_j\right] f_j{\displaystyle \frac{d_1^j}{\left( d_1+q_1\right) ^{j+1}}}=0, \end{aligned}$$

which is a contradiction.

Next suppose that $(d_2,q_2)\in G_{12}^*$. Then, $q_2>{{\overline{q}}}$ and $(d_1,q_1)\in {\hat{G}}_{22}$, where

$$\begin{aligned} {{\hat{G}}}_{22}:=\{(d,q):\; d>d_2,0<q\le q_2\}. \end{aligned}$$

Since the nonlinear terms of (1.4) are symmetric, this case can be proved similarly the case $(d_2,q_2)\in G_{22}$ in (ii).

(iv) If $(d_2,q_2)\in G_{23}^*$, the proof is similar to the corresponding case in (ii). If $(d_2,q_2)\in G_{12}^*$, the proof is similar to the corresponding case in (iii). $\square$

We are ready to prove Theorems 3.6, 3.8 and 3.10.

Proof of Theorem 3.6

(i) Suppose that $q_1<{\underline{q}}$ and $(d_2,q_2)\in G_{21}\cup G_{23}$. By Lemma 6.3 (i) and (iii), model (1.4) admits no positive equilibrium. By Theorem 3.3 (i) and (iii), $(\varvec{u}^*, \varvec{0})$ is unstable. Then, it follows from the monotone dynamical system theory [20, 21, 29, 46] that $(\varvec{u}^*,\varvec{0})$ is globally asymptotically stable.

(ii) Suppose that $q_1<{\underline{q}}$ and $(d_2,q_2)\in G_{11}\cup G_{12}^*$. By Lemma 6.3 (i) and (iii), model (1.4) admits no positive equilibrium. By the monotone dynamical system theory [20, 21, 29, 46], it suffices to show that $(\varvec{0},\varvec{v}^*)$ is unstable. If $(d_1,q_1)\in G_{12}^*$, then $q_2>{{\overline{q}}}$ and $(d_1,q_1)\in {{\tilde{G}}}_{22}:=\{(d,q):d>d_2,0<q\le q_2\}$. Since the nonlinear terms of model (1.4) are symmetric, it follows from Proposition 3.3 (ii) that $(\varvec{0},\varvec{v}^*)$ is unstable. If $(d_2,q_2)\in G_{11}$, then $(d_1,q_1)\in {{\tilde{G}}}_{21}$, where

$$\begin{aligned} {{\tilde{G}}}_{21}:=\left\{ (d,q):0<d \le d_2,0<q\le \displaystyle \frac{q_2}{d_2}d,(d,q)\ne (d_2,q_2)\right\} . \end{aligned}$$

Similarly, it follows from Proposition 3.3 (i) that $(\varvec{0},\varvec{v}^*)$ is unstable.

Finally, suppose that $q_1<{\underline{q}}$ and $(d_2,q_2)\in G_{13}$. By Proposition 3.3 (iii), $(\varvec{u}^*, \varvec{0})$ is locally asymptotically stable. By Lemma 6.3 (iv), model (1.4) admits no positive equilibrium. If $(\varvec{0}, \varvec{v}^*)$ is locally asymptotically stable, then model (1.4) admits one unstable positive steady state, which is a contradiction. If $(\varvec{0}, \varvec{v}^*)$ is unstable, then the monotone dynamical system theory [20, 21, 29, 46] implies that $(\varvec{u}^*, \varvec{0})$ is globally asymptotically stable. If $(\varvec{0}, \varvec{v}^*)$ is neutrally stable, by [29, Theorem 1.4], $(\varvec{u}^*, \varvec{0})$ is globally asymptotically stable. This proves (ii). $\square$

Proof of Theorems 3.8 and 3.10

We only need to prove the case $(d_2,q_2)\in G_{23}^*$, since the other cases can be proved using similar arguments in the proof of Theorem 3.6. If $(d_2,q_2)\in G_{23}^*$, then $q_2<{\underline{q}}$ and $(d_1,q_1)\in {{\hat{G}}}_{13}$, where

$$\begin{aligned} {{\hat{G}}}_{13}:=\{(d, q):\; d\ge d_2,q_2\le q< \frac{q_2}{d_2}d,(d,q)\ne (d_2,q_2)\}. \end{aligned}$$

Since the nonlinear terms of model (1.4) are symmetric, it follows from Theorem 3.6 (ii) that $(\varvec{0},\varvec{v}^*)$ is globally asymptotically stable. $\square$

Appendix

In the Appendix, we study the relations of ${{\overline{q}}}$, ${\underline{q}}$ and $q_0$. For convenience, we recall the definition of ${{\overline{q}}}$, ${\underline{q}}$ and $q_0$:

$$\begin{aligned}&{{\overline{q}}}=\max \left\{ \displaystyle \frac{r_1}{k_1}(k_1-k_2),\displaystyle \frac{r_3}{k_3}(k_2-k_3)\right\} ,\end{aligned}$$

(6.9a)

$$\begin{aligned}&{\underline{q}}=\min \left\{ \displaystyle \frac{r_1}{k_1}(k_1-k_2),\displaystyle \frac{r_3}{k_3}(k_2-k_3)\right\} ,\end{aligned}$$

(6.9b)

$$\begin{aligned}&q_0=\max \left\{ r_1\left( 1-\frac{u_1^*}{k_1}\right) , r_2\left( 1-\frac{u_2^*}{k_2}\right) \right\} . \end{aligned}$$

(6.9c)

Lemma 6.4

Suppose that $(\textbf{H})$ holds, $\varvec{r}\gg \varvec{0}$, and $d_1,q_1>0$. Then, the following statements hold:

• (i) If $q_1<{\underline{q}}$, then $q_0>q_1$;

• (ii) If $q_1>{{\overline{q}}}$, then $q_0<q_1$;

• (iii) If $q_1>{\underline{q}}$, then $q_0>{\underline{q}}$;

• (iv) If $q_1<{{\overline{q}}}$, then $q_0<{{\overline{q}}}$.

Proof

By (5.10) and (5.11) and Lemma 5.1 (i), we have

$$\begin{aligned}&{{\tilde{f}}}_1=d_1u_{2}^*-(d_1+q_1)u_1^*=-r_1u_1^*\left( 1-\frac{u_1^*}{k_1}\right) <0,\end{aligned}$$

(6.10a)

$$\begin{aligned}&{{\tilde{f}}}_2=d_1u_3^*-(d_2+q_2)u_2^*=r_3\left( 1-\frac{u_3^*}{k_3}\right) <0,\end{aligned}$$

(6.10b)

$$\begin{aligned}&{{\tilde{f}}}_2-{{\tilde{f}}}_1=-r_2u_2^*\left( 1-\frac{u_2^*}{k_2}\right) , \end{aligned}$$

(6.10c)

which will be used in the proof below.

(i) By Lemma 5.1 (iv), we have $u^*_1>u^*_2>u^*_3$. This, together with (6.9c) and (6.10a), implies that

$$\begin{aligned} q_0\ge r_1\left( 1-\frac{u_1^*}{k_1}\right) =\frac{(d_1+q_1)u^*_1-d_1u^*_2}{u^*_1}=d_1\left( 1-\frac{u^*_2}{u^*_1}\right) +q_1>q_1. \end{aligned}$$

(6.11)

(ii) By Lemma 5.1 (iii), we have $u^*_1<u^*_2<u^*_3$. Then, by (6.10a) again, we obtain

$$\begin{aligned} r_1\left( 1-\frac{u_1^*}{k_1}\right) =d_1\left( 1-\frac{u^*_2}{u^*_1}\right) +q_1<q_1. \end{aligned}$$

(6.12)

By (6.10c), we obtain that

$$\begin{aligned} \begin{aligned} r_2\left( 1-\frac{u_2^*}{k_2}\right) =&\displaystyle \frac{\left( (d_1+q_1)u^*_2-d_1u_3^*\right) +{{\tilde{f}}}_1}{u^*_2}\\ =&d_1\left( 1-\frac{u^*_3}{u^*_2}\right) +\frac{{{\tilde{f}}}_1}{u^*_2}+q_1<q_1, \end{aligned} \end{aligned}$$

(6.13)

where we have used (6.10c) and $u_2^*<u_3^*$ in the last step. It follows from (6.9c), (6.12) and (6.13) that $q_0<q_1$.

(iii) We divide the proof into three cases:

$$\begin{aligned} (\textrm{A1})\;\;u_1^*<k_2, \;\;(\textrm{A2})\;\; u^*_1\ge u^*_2,\;\;(\textrm{A3})\;\; k_2\le u_1^*<u_2^*. \end{aligned}$$

For case (A1), we see from (6.9b) and (6.9c) that

$$\begin{aligned} q_0\ge r_1\left( 1-\frac{u_1^*}{k_1}\right) >\displaystyle \frac{r_1}{k_1}(k_1-k_2)\ge {\underline{q}}. \end{aligned}$$

For case (A2), we see from (6.9c) and (6.10a) that

$$\begin{aligned} q_0\ge r_1\left( 1-\frac{u_1^*}{k_1}\right) =d_1\left( 1-\frac{u^*_2}{u^*_1}\right) +q_1\ge q_1>{\underline{q}}. \end{aligned}$$

Now we consider (A3). Suppose to the contrary that $q_0\le {\underline{q}}$. This, combined with (6.9b) and (6.9c), yields

$$\begin{aligned} r_1\left( 1-\frac{u_1^*}{k_1}\right) \le q_0\le {\underline{q}}\le \frac{r_3}{k_3}\left( k_2-k_3\right) . \end{aligned}$$

(6.14)

Noticing that $u_2^*>k_2$, we see from (6.10c) that

$$\begin{aligned} {{\tilde{f}}}_2-{{\tilde{f}}}_1=d_1(u^*_3-u^*_2)-(d_1+q_1)(u^*_2-u^*_1)=-r_2u^*_2\left( 1-\displaystyle \frac{u^*_2}{k_2}\right) >0. \end{aligned}$$

(6.15)

Since $u^*_1< u^*_2$, we see from (6.15) that $u^*_2< u^*_3$. Then, we have

$$\begin{aligned} 0>{{\tilde{f}}}_2>{{\tilde{f}}}_1\;\;\text {and}\;\;k_2\le u^*_1< u^*_2< u^*_3, \end{aligned}$$

(6.16)

which yields

$$\begin{aligned} -\displaystyle \frac{{{\tilde{f}}}_2}{u^*_3}<-\displaystyle \frac{{{\tilde{f}}}_1}{u^*_1}. \end{aligned}$$

(6.17)

This, together with (6.16), (6.10a) and (6.10b), implies that

$$\begin{aligned} r_1\left( 1-\frac{u^*_1}{k_1}\right) =-\displaystyle \frac{{{\tilde{f}}}_1}{u^*_1}>-\displaystyle \frac{{{\tilde{f}}}_2}{u^*_3}=\displaystyle \frac{r_3}{k_3}\left( u^*_3-k_3\right) >\displaystyle \frac{r_3}{k_3}\left( k_2-k_3\right) , \end{aligned}$$

which contradicts (6.14). Therefore, $q_0>{\underline{q}}$ for case (A3).

(iv) We first show that

$$\begin{aligned} r_1\left( 1-\frac{u_1^*}{k_1}\right) <{{\overline{q}}}, \end{aligned}$$

(6.18)

and the proof is divided into three cases:

$$\begin{aligned} (\textrm{B1})\;\;u^*_1> k_2,\;\;(\textrm{B2})\;\;u_1^*\le u_2^*,\;\;(\textrm{B3})\;\; k_2\ge u^*_1> u^*_2. \end{aligned}$$

For case (B1), we have

$$\begin{aligned} r_1\left( 1-\frac{u_1^*}{k_1}\right) <\frac{r_1}{k_1}(k_1-k_2)\le {{\overline{q}}}. \end{aligned}$$

For case (B2), we see from (6.10a) that

$$\begin{aligned} r_1\left( 1-\frac{u_1^*}{k_1}\right) =d_1\left( 1-\frac{u^*_2}{u^*_1}\right) +q_1\le q_1<{{\overline{q}}}. \end{aligned}$$

(6.19)

For case (B3), using similar arguments as the above case (A3), we have

$$\begin{aligned} 0>{{\tilde{f}}}_1>{{\tilde{f}}}_2\;\;\text {and}\;\;k_2\ge u^*_1> u^*_2> u^*_3. \end{aligned}$$

This, combined with (6.10a) and (6.10b), implies that

$$\begin{aligned} r_1\left( 1-\frac{u_1^*}{k_1}\right) =-\frac{{{\tilde{f}}}_1}{u^*_1}<-\frac{{{\tilde{f}}}_2}{u^*_1}<-\frac{{{\tilde{f}}}_2}{u^*_3} =r_3\left( \frac{u_3^*}{k_3}-1\right) <\frac{r_3}{k_3}(k_2-k_3)\le {{\overline{q}}}. \end{aligned}$$

Then, we show that

$$\begin{aligned} r_2\left( 1-\frac{u_2^*}{k_2}\right) <{{\overline{q}}}, \end{aligned}$$

(6.20)

and the proof is also divided into three cases:

$$\begin{aligned} (\textrm{C1})\;\;u^*_2\le u_3^*,\;\;(\textrm{C2})\;\;u_2^*> u_3^*\ge k_2,\;\;(\textrm{C3})\;\; u_2^*> u_3^*\;\;\text {and}\;\;k_2>u_3^*. \end{aligned}$$

For case (C1), we see from (6.13) that

$$\begin{aligned} r_2\left( 1-\frac{u_2^*}{k_2}\right)<q_1<{{\overline{q}}}. \end{aligned}$$

For case (C2), we have

$$\begin{aligned} r_2\left( 1-\frac{u_2^*}{k_2}\right)<0<{{\overline{q}}}. \end{aligned}$$

For case (C3), we see from (6.10) that

$$\begin{aligned} r_2\left( 1-\frac{u_2^*}{k_2}\right) =\frac{{{\tilde{f}}}_1-{{\tilde{f}}}_2}{u^*_2}<-\frac{{{\tilde{f}}}_2}{u^*_2}<-\frac{{{\tilde{f}}}_2}{u^*_3} =\frac{r_3}{k_3}\left( u^*_3-k_3\right) <\frac{r_3}{k_3}\left( k_2-k_3\right) \le {{\overline{q}}}. \end{aligned}$$

By (6.18) and (6.20), we see that (iv) holds. $\square$

Remark 6.5

By ${\underline{q}}\le {{\overline{q}}}$ and Lemma 6.4, we see that if $q_1< {\underline{q}}$, then $q_1<q_0<{{\overline{q}}}$; if $q_1> {{\overline{q}}}$, then ${\underline{q}}<q_0<q_1$; and if ${\underline{q}}<q_1<{{\overline{q}}}$, then ${\underline{q}}<q_0<{{\overline{q}}}$.