1 Introduction

The impact of resource distributions on the persistence of a single species has been studied extensively (e.g., Cantrell and Cosner 1989, 2004; Berestycki et al. 2005; Lou 2006; Cantrell and Cosner 1998). Lou (2006) observed that if the dynamics of the species is modeled by a reaction-diffusion model with logistic type nonlinearity, the total biomass of the species may exceed the carrying capacity. Later, the ratio of total biomass over carrying capacity was studied both theoretically and experimentally (Bai et al. 2016; DeAngelis et al. 2016; Inoue and Kuto 2021; Liang and Lou 2012; Zhang et al. 2015, 2017). The distributions to maximize the growth rate (Cantrell and Cosner 1989, 1991; Lamboley et al. 2016; Lou and Yanagida 2006) and the total biomass (Ding et al. 2010; Mazari et al. 2020, 2022; Mazari and Ruiz-Balet 2021; Nagahara and Yanagida 2018) have been to shown to be of bang-bang type. Similar maximizing total biomass problems have been studied for patch models with logistic growth and random movement (Liang and Zhang 2021; Nagahara et al. 2021).

Resource allocations may also affect the interactions of multiple species (He and Ni 2013, 2016a, b, 2017; Lin et al. 2014; Gourley and Kuang 2005; Wei and Liu 2021). In a two-patch Lotka–Volterra competition model, it was shown that the species with a more heterogeneous distribution of resources will never lose the competition (Lin et al. 2014; Gourley and Kuang 2005). Similarly, in a two species reaction-diffusion competition model, it was shown that a species with a heterogeneous spatial distribution of resources will outcompete a species with homogeneously distributed resources (He and Ni 2016a). Meanwhile, when both species have a heterogeneous distribution of resources, the slower dispersing species wins competition (He and Ni 2017). For reaction-diffusion models it has also been shown that, when the carrying capacity is proportional to the growth rate, there is no optimal form of resource allocation (Hutson et al. 2003). Meanwhile, Mazari showed that the species whose resource allocation results in the largest total biomass wins the competition when the diffusion rate is large in a competition model with multiple species (Mazari 2019).

Our study is motivated by a series of recent works on metapopulation models in stream environments, where the individuals have both random movement and directed drift. In Nguyen et al. (2023), we considered the impact of the distribution of resources on the persistence of a single stream species. In particular, we showed that to maximize the total biomass one should concentrate the resources on the upstream ends while to maximize the growth rate of the population one may need to concentrate the resources on the downstream ends. In Jiang et al. (2020, 2021), the authors studied the joint impact of the diffusion rate, advection rate and network topology on the competition outcome of two stream species in a three patch Lotka–Volterra competition model whose patches are constructed as shown in Fig. 1. When there are n patches aligned along a line, the results in Chen et al. (2022, 2022, 2023) showed that the magnitude of movement rates, the convexity of the drift rates and the population loss rate at the downstream end can significantly alter the competition outcome of two species. For works on reaction-diffusion-advection models for stream species, we refer the interested readers to Lam et al. (2016); Lou and Lutscher (2014); Lou and Zhou (2015); Lutscher et al. (2006); Pachepsky et al. (2005); Speirs and Gurney (2001); Vasilyeva and Lutscher (2012); Wang et al. (2019); Yan et al. (2022); Zhou et al. (2021) and the references therein.

Motivated by the aforementioned studies, we consider the following two-species n-patch Lotka–Volterra competition model in stream environment:

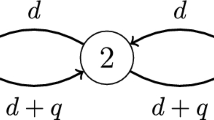
$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{du_i}{dt}=\displaystyle \sum _{j=1}^{n} (d D_{ij}+qQ_{ij})u_j+r_iu_i\left( 1-\frac{u_i+v_i}{k}\right) , &{}i=1,\dots ,n,\;\;t>0,\\ \displaystyle \frac{dv_i}{dt}=\displaystyle \sum _{j=1}^{n} (d D_{ij}+qQ_{ij})v_j+s_iv_i\left( 1-\frac{u_i+v_i}{k}\right) , &{}i=1,\dots ,n,\;\;t>0,\\ \varvec{u}(0)=\varvec{u}_0\ge (\not \equiv ) \varvec{0}, \; \varvec{v}(0)=\varvec{v}_0\ge (\not \equiv ) \varvec{0}. \end{array}\right. }\nonumber \\ \end{aligned}$$
(1.1)

Here the vectors \(\varvec{u}=(u_1, \dots , u_n)\) and \(\varvec{v}=(v_1, \dots , v_n)\) denote the densities of two competing stream species at each patch location. The nonnegative vectors \(\varvec{r}=(r_1, \dots , r_n)\) and \(\varvec{s}=(s_1, \dots , s_n)\) are the growth rates of \(\varvec{u}\) and \(\varvec{v}\), respectively, and the carrying capacity is assumed to be a positive constant k for all the patches. Two \(n\times n\) matrices \(D=(D_{ij})\) and \(Q=(Q_{ij})\) represent the random movement pattern and directed drift pattern of individuals respectively. For the three network configurations with \(n=3\) in Fig. 1 (see Jiang et al. 2020, 2021), the corresponding matrices D and Q are as follows:

  • Case 1:

    $$\begin{aligned} D=\begin{bmatrix} -2 &{} 1 &{}1 \\ 1&{}-1&{} 0\\ 1&{}0 &{} -1 \\ \end{bmatrix},\;\;Q=\begin{bmatrix} -2 &{} 0 &{}0 \\ 1&{}0&{} 0\\ 1&{}0 &{} 0\\ \end{bmatrix}; \end{aligned}$$
    (1.2)

  • Case 2:

    $$\begin{aligned} D=\begin{bmatrix} -1 &{} 0 &{}1 \\ 0&{}-1&{} 1\\ 1&{}1 &{} -2 \\ \end{bmatrix},\;\;Q=\begin{bmatrix} -1 &{} 0 &{}0 \\ 0&{}-1&{} 0\\ 1&{}1 &{} 0\\ \end{bmatrix}; \end{aligned}$$
    (1.3)

  • Case 3:

    $$\begin{aligned} D=\begin{bmatrix} -1 &{} 1 &{}0 \\ 1&{}-2&{} 1\\ 0&{}1 &{} -1 \\ \end{bmatrix},\;\;Q=\begin{bmatrix} -1 &{} 0 &{}0 \\ 1&{}-1&{} 0\\ 0&{}1 &{} 0\\ \end{bmatrix}. \end{aligned}$$
    (1.4)
Fig. 1
figure 1

A stream with three patches, where d is the random movement rate and q is the directed drift rate. i Patch 1 is the upstream end and patches 2 and 3 are the downstream ends. ii Patches 1 and 2 are the upstream ends and patch 3 is the downstream end. iii Patch 1 is the upstream end and patch 3 is the downstream end

Full size image

Our objective is to determine how the distribution of resources for each species, as determined by \({\varvec{r}}\) and \({\varvec{s}}\), impact competitive outcomes for model (1.1). We make the assumption that the resources are proportional to the growth rate in each patch and the two species \(\varvec{u}\) and \(\varvec{v}\) have the same amount of resources, i.e.

$$\begin{aligned} \sum _{i=1}^n r_i=\sum _{i=1}^n s_i=r>0. \end{aligned}$$

We show that if the resources of species \(\varvec{u}\) are distributed to maximize its biomass, i.e. all resources are distributed in the most upstream patches (see Nguyen et al. 2023), while the resources of species \(\varvec{v}\) are not, then species \(\varvec{u}\) always wins the competition. For example, for configuration (i) in Fig. 1, such a distribution of species \(\varvec{u}\) corresponds to \(\varvec{r}=(r, 0, 0)\) while the distribution of species \(\varvec{v}\) satisfies \(\varvec{s}\ne (r,0,0)\).

Our paper is organized as follows. In Section 2, we present some preliminary results which follow from existing theory. In Section 3, we consider the three-node stream networks shown in Fig. 1. For each of these configurations we show that a species whose resources are distributed so that their total biomass is maximized in the absence of competition is able to out-compete a species whose resources are not optimally distributed. In Section 4, we extend these results to apply to n-patch stream networks.

2 Preliminaries

Let \(\varvec{w}=(w_1, \dots , w_n)\) be a real vector. We write \(\varvec{w}\gg \varvec{0}\) if \(w_i>0\) for all \(i=1, \dots , n\), and \(\varvec{w}>\varvec{0}\) if \(\varvec{w}\ge \varvec{0}\) but \(\varvec{w}\ne \varvec{0}\). Let \(A=(a_{ij})_{n\times n}\) be a real square matrix. Let \(\sigma (A)\) be the set of all eigenvalues of A, and s(A) be the spectral bound of A, i.e.

$$\begin{aligned} s(A)=\max \{\textrm{Re} \lambda : \lambda \in \sigma (A)\}. \end{aligned}$$

The matrix A is called irreducible if it cannot be placed into block upper triangular form by simultaneous row and column permutations and essentially nonnegative if \(a_{ij}\ge 0\) for all \(1\le i, j\le n\) such that \(i\ne j\). By the Perron-Frobenius Theorem, if A is irreducible and essentially nonnegative, then \(\lambda _1=s(A)\) is a simple eigenvalue of A. Moreover, \(\lambda _1\) (called the principal eigenvalue of A) is associated with an eigenvector whose components are all positive, which is the unique eigenvalue associated with a nonnegative eigenvector.

Before studying the two species competition model, we revisit the following single species meta-population model:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{du_i}{dt}=\displaystyle \sum _{j=1}^{n}l_{ij} u_j+r_iu_i\left( 1-\frac{u_i}{k_i}\right) ,&{}i=1,\dots ,n,\;\;t>0,\\ \varvec{u}(0)=\varvec{u}_0>\varvec{0}. \end{array}\right. } \end{aligned}$$
(2.1)

Here, \(\varvec{u}=(u_1, \dots , u_n)\) is the density of a meta-population living in n-patches; \(\varvec{k}=(k_1, \dots , k_n)\) is the carrying capacity; \(\varvec{r}=(r_1, \dots , r_n)\) is the growth rate. The coefficients \(\ell _{ij}\ge 0\) denote the movement rate of the individuals from patch j to patch i for \(1\le i,j\le n\) and \(i\not = j\); \(l_{ii}=-\sum _{j\ne i} l_{ji}\) is the total movement rate out from patch i. Then the \(n\times n\) connection matrix L is of the form

$$\begin{aligned} L:=\begin{pmatrix} -\sum _j \ell _{j1} &{} \ell _{12} &{} \cdots &{} \ell _{1n}\\ \ell _{21} &{} -\sum _j \ell _{j2} &{} \cdots &{} \ell _{2n}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \ell _{n1} &{} \ell _{n2} &{} \cdots &{} -\sum _j \ell _{jn} \end{pmatrix}. \end{aligned}$$
(2.2)

It is easy to see that \((1,1, \dots , 1)\) is a left eigenvector of L corresponding to eigenvalue 0. We always assume that L is irreducible. By the Perron-Frobenius Theorem, 0 is the principal eigenvalue of L.

We can associate L with a weighted, directed graph (digraph) \({\mathcal {G}}\) consisting of n nodes (each node i in \({\mathcal {G}}\) corresponds to patch i). In \({\mathcal {G}}\), there is a directed edge (arc) from node j to node i if and only if \(\ell _{ij}>0\). The couple \(({\mathcal {G}}, L)\) is called the movement network associated with (2.1).

The global dynamics of (2.1) are well-known:

Lemma 2.1

(Cosner 1996; Li and Shuai 2010; Lu and Takeuchi 1993; Takeuchi 1996) Suppose that L is essentially nonnegative and irreducible matrix that is defined in (2.2). If \(\varvec{r}>\varvec{0}\) and \(\varvec{k}\gg \varvec{0}\), then model (2.1) has a unique positive equilibrium, which is globally asymptotically stable.

By Lemma 2.1, model (1.1) has two semitrivial equilibria \(E_1:=(\varvec{u}^*, \varvec{0})\) and \(E_2:=(\varvec{0}, \varvec{v}^*)\). By the well-known monotone dynamical system theory (Hess 1991; Hsu et al. 1996; Lam and Munther 2016; Smith 1995), the global dynamics of (1.1) is closely related to the local properties of its equilibria. Denote \(X={\mathbb {R}}_+^n\times {\mathbb {R}}_+^n\). Let \(\le _K\) be the order in X induced by the cone \(K={\mathbb {R}}_+^n\times \{-{\mathbb {R}}_+^n\}\). Then if \(\varvec{x}=(\bar{\varvec{u}}, \bar{\varvec{v}}), \varvec{y}=(\tilde{\varvec{u}}, \tilde{\varvec{v}})\in X\), we write \(\varvec{x}\le _K \varvec{y}\) if \(\bar{\varvec{u}}\le \tilde{\varvec{u}}\) and \(\bar{\varvec{v}}\ge \tilde{\varvec{v}}\); \(\varvec{x}<_K \varvec{y}\) if \(\varvec{x}\le _K \varvec{y}\) and \(\varvec{x}\ne \varvec{y}\). We utilize the following result later (this result is proved in Smith (1995) for the case \(n=2\) first but it holds for any \(n\ge 2\) (Smith 1995, Page 70)):

Lemma 2.2

(Smith 1995, Theorem 4.4.2) Suppose that \(E_1\) is linearly unstable. Then one of the following holds:

  1. (i)

    \(E_2\) attracts all solutions with initial data \((\varvec{u}_0,\varvec{v}_0)\in X\) satisfying \(\varvec{v}_0>0\). In this case, \(E_2\) is linearly stable or neutrally stable;

  2. (ii)

    There exists a positive equilibrium E satisfying \(E_2\ll _K E\ll _K E_1\) such that E attracts all solutions with initial data \((\varvec{u}_0, \varvec{v}_0)\in X\) satisfying \(E\le _K (\varvec{u}_0, \varvec{v}_0)<_K E_1\).

By Lemma 2.2, if \(E_2\) is linearly unstable and the model has no positive equilibrium, then \(E_1\) is globally attractive. It is easy to see that the stability of \(E_1\) is determined by the sign of \(\lambda _1(\varvec{s}, \varvec{u}^*)\), which is the principal eigenvalue of the matrix \(dD+qQ+\text {diag}(s_i(1-u^*_i/k))\): if \(\lambda _1(\varvec{s}, \varvec{u}^*)<0\), \(E_1\) is locally asymptotically stable; if \(\lambda _1(\varvec{s}, \varvec{u}^*)>0\), \(E_1\) is unstable; if \(\lambda _1(\varvec{s}, \varvec{u}^*)=0\), \(E_1\) is linearly neutrally stable. Similarly, the local stability of \(E_2\) is determined by the sign of \(\lambda _1(\varvec{r}, \varvec{v}^*)\), which is the principal eigenvalue of the matrix \(dD+qQ+\text {diag}(r_i(1-v^*_i/k))\).

3 Stream networks of three nodes

In this section, we consider model (1.1) for the three-node stream networks shown in Fig. 1. Here we provide detailed analysis for configuration (i), with analogous results for configurations (ii) and (iii) provided in the appendix. Our results state that a species whose resources are concentrated on the upstream end will have the competitive advantage. In particular, for configuration (i) we show that if \(\varvec{r}=(r, 0, 0)\) and \(\varvec{s}\ne \varvec{r}\), then species \(\varvec{u}\) always wins the competition.

We first prove the following lemma which is used to show that model (1.1) does not have a positive equilibrium.

Lemma 3.1

Suppose that D and Q are given by (1.2). Let \(\varvec{r}=(r, 0, 0)\) and \(\varvec{s}=(s_1, s_2, s_3)>\varvec{0}\) with \(\varvec{s}\ne \varvec{r}\) and \(\sum _{i=1}^3 s_i=r>0\). If \((\varvec{u}, \varvec{v})\) is a positive equilibrium of (1.1), then \(u_1+v_1<k\), \(u_2+v_2>k\) and \(u_3+v_3>k\).

Proof

Suppose that \((\varvec{u}, \varvec{v})\) is a positive equilibrium of (1.1). Then \((\varvec{u}, \varvec{v})\) satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle 0=\displaystyle \sum _{j=1}^{3} (d D_{ij}+qQ_{ij})u_j+r_iu_i\left( 1-\frac{u_i+v_i}{k}\right) , &{}i=1,2,3,\\ \displaystyle 0=\displaystyle \sum _{j=1}^{3} (d D_{ij}+qQ_{ij})v_j+s_iv_i\left( 1-\frac{u_i+v_i}{k}\right) , &{}i=1,2,3. \end{array}\right. } \end{aligned}$$
(3.1)

Let \(w_i:=u_i+v_i\) for \(i=1, 2, 3\). Adding each corresponding pair of equations above, we have

$$\begin{aligned} 0= & {} -(d+q)w_1+dw_2-(d+q)w_1+dw_3+(r_1u_1+s_1v_1)\left( 1-\frac{w_1}{k} \right) , \nonumber \\ 0= & {} (d+q)w_1-dw_2+(r_2u_2+s_2v_2)\left( 1-\frac{w_2}{k} \right) , \nonumber \\ 0= & {} (d+q)w_1-dw_3+(r_3u_3+s_3v_3)\left( 1-\frac{w_3}{k} \right) . \end{aligned}$$
(3.2)

We prove that \(w_2=u_2+v_2 >k\) by contradiction. Assume to the contrary that \(w_2\le k\). Then by the second equation of (3.2), we have

$$\begin{aligned} (d+q)w_1-dw_2 = -(r_2u_2+s_2v_2)\left( 1-\frac{w_2}{k} \right) \le 0. \end{aligned}$$

This implies

$$\begin{aligned} w_1\le \frac{d}{d+q} w_2\le \frac{d}{d+q}k<k. \end{aligned}$$

By \(r_1=r>0\) and the first equation of (3.2), we have

$$\begin{aligned} (d+q)w_1 - dw_3 = -(d+q)w_1+dw_2 + (r_1u_1+s_1v_1)\left( 1-\frac{w_1}{k} \right) . \end{aligned}$$

Since we have shown that \((d+q)w_1 - dw_2 \le 0\) and \(w_1 <k\), we must have \((d+q)w_1-dw_3>0\). Thus

$$\begin{aligned} w_3 < \frac{d+q}{d} w_1 \le \frac{d+q}{d}\frac{d}{d+q}k = k. \end{aligned}$$

This further implies

$$\begin{aligned} (d+q)w_1 - dw_3 +(r_3u_3+s_3v_3)\left( 1-\frac{w_3}{k} \right) > 0, \end{aligned}$$

which contradicts the third equation of (3.2). Therefore, we must have \(u_2+v_2>k\). Similarly, we have \(u_3+v_3>k\).

Since \(\varvec{s}\ne \varvec{r}\), either \(s_2\ne 0\) or \(s_3\ne 0\). Without loss of generality, say \(s_2\ne 0\). Then by the second equation of (3.2) and \(w_2>k\), \((d+q)w_1-dw_2>0\). By the third equation of (3.2) and \(w_3>k\), we have \((d+q)w_1-dw_3\ge 0\). Finally by the first equation of (3.2) and \(s_1>0\), we have \(w_1=u_1+v_1<k\). \(\square \)

Next, in Lemma 3.3 we make use of the following well-known result (e.g., see (Berman and Plemmons 1994, Corollary 2.1.5)) to prove the non-existence of a positive equilibrium.

Lemma 3.2

Suppose that P and Q are \(n\times n\) real-valued matrices, P is essentially nonnegative, Q is nonnegative and nonzero, and \(P+Q\) is irreducible. Then, \(s(P+Q)>s(P)\).

Lemma 3.3

Suppose that D and Q are given by (1.2). Let \(\varvec{r}=(r, 0, 0)\) and \(\varvec{s}=(s_1, s_2, s_3)>\varvec{0}\) with \(\varvec{s}\ne \varvec{r}\) and \(\sum _{i=1}^3 s_i=r>0\). Then model (1.1) has no positive equilibrium.

Proof

Suppose to the contrary that \((\varvec{u}, \varvec{v})\) is a positive equilibrium of (1.1). Then \((\varvec{u}, \varvec{v})\) satisfies (3.1). By the first equation of (3.1), \(\varvec{u}\) is a positive eigenvector of matrix \(M_1:=dD+qQ+\text {diag}(r_i(1-(u_i+v_i)/k))\) corresponding with eigenvalue 0. By the Perron-Frobenius Theorem, we must have \(s(M_1)=0\). Similarly, \(\varvec{v}\) is a positive eigenvector of matrix \(M_2:=dD+qQ+\text {diag}(s_i(1-(u_i+v_i)/k))\) corresponding with eigenvalue 0 and \(s(M_2)=0\). By the assumptions on \(\varvec{r}\) and \(\varvec{s}\) and Lemma 3.1, we have

$$\begin{aligned} r_1\left( 1-\frac{u_1+v_1}{k}\right) >s_1\left( 1-\frac{u_1+v_1}{k}\right) \end{aligned}$$

and

$$\begin{aligned} 0=r_i\left( 1-\frac{u_i+v_i}{k}\right) \ge s_i\left( 1-\frac{u_i+v_i}{k}\right) , \ i=2, 3. \end{aligned}$$

Therefore, by Lemma 3.2, we must have \(s(M_1)>s(M_2)\), which is a contradiction. This proves the result. \(\square \)

In the following two lemmas, we show that the semitrivial equilibrium \(E_2\) is always unstable.

Lemma 3.4

Suppose that D and Q are given by (1.2). Let \(\varvec{s}=(s_1, s_2, s_3)\ge \varvec{0}\) with \(s_2>0\) or \(s_3>0\). Then the semitrivial equilibrium \(E_2=(\varvec{0}, \varvec{v}^*)\) satisfies \(v^*_1<k\).

Proof

We observe that \(\varvec{v}^*\) must satisfy

$$\begin{aligned} 0= \sum _{j=1}^3(dD_{ij}+qQ_{ij})v^*_j + s_iv_i^*\left( 1-\frac{v_i^*}{k}\right) , \ \ i=1, 2, 3. \end{aligned}$$

That is

$$\begin{aligned} 0= & {} -(d+q)v_1^*+dv_2^*-(d+q)v^*_1+dv^*_3+s_1v^*_1\left( 1-\frac{v^*_1}{k} \right) , \nonumber \\ 0= & {} (d+q)v^*_1-dv^*_2+s_2v^*_2\left( 1-\frac{v^*_2}{k} \right) , \nonumber \\ 0= & {} (d+q)v^*_1-dv^*_3+s_3v^*_3\left( 1-\frac{v^*_3}{k} \right) . \end{aligned}$$
(3.3)

Assume to the contrary that \(v_1^*\ge k\). By the first equation of (3.3), either \((d+q)v^*_1-dv^*_2\le 0\) or \((d+q)v^*_1-dv^*_3\le 0\). Without loss of generality, say \(s_2>0\). If \((d+q)v^*_1-dv^*_2\le 0\), then by the second equation of (3.3), we have \(v^*_2\le k\). This implies

$$\begin{aligned} (d+q)v^*_1-dv^*_2\ge (d+q)k-dk>0, \end{aligned}$$
(3.4)

which is a contradiction. Hence, \((d+q)v^*_1-dv^*_3\le 0\). If \(s_3>0\), the third equation of (3.3) implies \(v^*_3\le k\). Then,

$$\begin{aligned} (d+q)v^*_1-dv^*_3\ge (d+q)k-dk>0, \end{aligned}$$

which is a contradiction. If \(s_3=0\), then \((d+q)v^*_1-dv^*_3=0\). Again by \(v_1^*\ge k\) and the first equation of (3.3), \((d+q)v^*_1-dv^*_2\le 0\). This leads to contradiction by the second equation of (3.3) and (3.4). \(\square \)

Lemma 3.5

Suppose that D and Q are given by (1.2). Let \(\varvec{r}=(r, 0, 0)\) and \(\varvec{s}=(s_1, s_2, s_3)>\varvec{0}\) with \(\varvec{s}\ne \varvec{r}\) and \(\sum _{i=1}^3 s_i=r\). Then the semitrivial equilibrium \(E_2=(\varvec{0}, \varvec{v}^*)\) is unstable and the semitrivial equilibrium \(E_1=(\varvec{u}^*, \varvec{0})\) is stable for model (1.1).

Proof

The stability of \(E_2\) is determined by the sign of \(\lambda _1(\varvec{r}, \varvec{v}^*)\), which is the principal eigenvalue of \(dD+qQ+\text {diag}(r_i(1-v^*_i/k))\). By the assumptions on \(\varvec{r}\) and Lemma 3.4, we have

$$\begin{aligned} r_1\left( 1-\frac{v^*_1}{k}\right) >0 \end{aligned}$$

and

$$\begin{aligned} r_i\left( 1-\frac{v^*_i}{k}\right) =0, \ i=2, 3. \end{aligned}$$

Therefore, by Lemma 3.2, we must have \(\lambda _1(\varvec{r}, \varvec{v}^*)>s(dD+qQ)=0\). Hence, \(E_2\) is unstable.

The stability of \(E_1\) is determined by the sign of \(\lambda _1(\varvec{s}, \varvec{u}^*)\), which is the principal eigenvalue of \(dD+qQ+\text {diag}(s_i(1-u^*_i/k))\). By Nguyen et al. (2023), we have \(\varvec{u}^*=(k, (d+q)k/d, (d+q)k/d)\). So,

$$\begin{aligned} s_1\left( 1-\frac{u^*_1}{k}\right) =0, \end{aligned}$$

and

$$\begin{aligned} s_i\left( 1-\frac{u^*_i}{k}\right) \le 0, \ i=2, 3, \end{aligned}$$

with at least one strict sign by the assumption on \(\varvec{s}\). Therefore, by Lemma 3.2, we must have \(\lambda _1(\varvec{s}, \varvec{u}^*)<s(dD+qQ)=0\). Hence, \(E_1\) is stable. \(\square \)

By the theory of monotone dynamical systems (Lemma 2.2) and Lemmas 3.3 and 3.5, we obtain the following result:

Theorem 3.6

Suppose that D and Q are given by (1.2). Let \(\varvec{r}=(r, 0, 0)\) and \(\varvec{s}=(s_1, s_2, s_3)>\varvec{0}\) with \(\varvec{s}\ne \varvec{r}\) and \(\sum _{i=1}^3 s_i=r>0\). Then the semitrivial equilibrium \(E_1=(\varvec{u}^*, \varvec{0})\) is globally asymptotically stable for model (1.1).

4 Stream networks of n nodes

In this section, we generalize the results in Sect. 3 to a certain type of network of n nodes. We recall the definition of stream networks of n nodes in Nguyen et al. (2023).

Definition 4.1

Let G be a directed graph, and denote the set of nodes of G by V. Consider a function \(f: V\rightarrow {\mathbb {Z}}_{\ge 0}\). For each node i, we call f(i) the level of the node and (G, f) a leveled graph if the following assumptions are satisfied

  1. (i)

    For each \(0\le k\le \max _{i\in V}\{f(i)\}\), there exists a node j such that \(f(j)=k\).

  2. (ii)

    For each pair of nodes i and j, there is no edge between i and j if \(|f(i)-f(j)|\ne 1\).

We use level graphs to describe a type of stream network, where the nodes in further downstream positions have larger levels. The left digraph in Fig. 2 is a leveled graph while the right digraph is not.

Fig. 2
figure 2

The left digraph is a leveled graph with level function \(f(1)=0, f(2)=f(3)=1, f(4)=2\). The right digraph cannot be a leveled graph for any choice of level function

Full size image

Definition 4.2

(Nguyen et al. 2023) Consider a graph G with level function f and connection matrix L. We say that (G, f, L) is a homogeneous flow stream network if the following assumptions are satisfied:

  1. (i)

    The matrix L is irreducible.

  2. (ii)

    If there is an edge from node i to node j, then there is also an edge from node j to node i.

  3. (iii)

    If there is an edge from node i to node j, then the weight is \(\ell _{ij} = d+q\) if \(f(j)-f(i)=1\) (i.e. the edge is from an upstream to a downstream node) and \(\ell _{ij}=d\) if \(f(i)-f(j)=1\) (i.e. the edge is from a downstream to an upstream node). Here, d and q are positive constants.

The connection matrix L of a homogeneous flow stream network can be written as \(L=dD+qQ\). We recall the following result about the positive eigenvector of L proved in Nguyen et al. (2023).

Lemma 4.3

Let (G, f, L) be a homogeneous flow stream network. Let \(\varvec{v}\) be the solution to \(L\varvec{v}=(dD+qQ)\varvec{v} = 0\). Then the eigenvector \(\varvec{v}\) writes, up to a constant multiple, as

$$\begin{aligned} v_i = \left( \frac{d+q}{d}\right) ^{f(i)}. \end{aligned}$$

Let \(\varvec{u}^*=(u_1^*, \dots , u_n^*)\) be the positive equilibrium of

$$\begin{aligned} \displaystyle \frac{du_i}{dt}=\displaystyle \sum _{j=1}^{n}(dD_{ij}+qQ_{ij})u_j+r_iu_i\left( 1-\frac{u_i}{k}\right) , \ \ i=1,\dots , n,\;\;t>0. \end{aligned}$$
(4.1)

The total biomass \({\mathcal {K}}\) of \(\varvec{u}^*\) is defined as \({\mathcal {K}}:=\sum _{i=1}^n u_i^*\). We also recall the following theorem in Nguyen et al. (2023) about the total biomass \({\mathcal {K}}\):

Theorem 4.4

Let (G, f, L) be a homogeneous flow stream network, where \(L=dD+qQ\). Suppose that \(\varvec{r}=(r_1,\dots , r_n)>\varvec{0}\) with \(\sum _{i=1}^nr_i=r>0\) and \(k>0\). Then the total biomass \({\mathcal {K}}\) of the positive equilibrium of (4.1) has the upper bound

$$\begin{aligned} {\mathcal {K}} \le { k}\sum _{i=1}^n \left( 1+\frac{q}{d}\right) ^{f(i)}. \end{aligned}$$

Moreover, the maximum is achieved as the upper bound when \(r_i=0\) for any node i with positive level, i.e. \(f(i)>0\). In this case, \(u_i^*=k(\frac{d+q}{d})^{f(i)}\).

The main result we prove in this section is the following, which states that to gain a competitive advantage in a homogeneous flow stream network one needs to distribute all the resources to the upstream ends, i.e. nodes with level 0.

Theorem 4.5

Let (G, f, L) be a homogeneous flow stream network, where \(L=dD+qQ\). Let \(k>0\) and \(\varvec{r}, \varvec{s}>\varvec{0}\) such that \(\sum _{i=1}^n r_i=\sum _{i=1}^n s_i=r>0\). Suppose that \(r_i=0\) for any node i with \(f(i)>0\) and there exists at least one node \(i_0\) with \(f(i_0)>0\) such that \(s_{i_0}>0\). Then the semitrivial equilibrium \(E_1=(\varvec{u}^*, \varvec{0})\) is globally asymptotically stable for (1.1).

4.1 Proof of Theorem 4.5

Suppose to the contrary that \((\varvec{u},\varvec{v})\) is a positive equilibrium of (1.1). Let \(w_i^*=u_i+v_i\) for each \(i=1, \dots , n\). To show the non-existence of a positive equilibrium \(E^*\), we recall the sign pattern approach used in Nguyen et al. (2023). We associate the stream network with a sign pattern graph. The nodes of the sign pattern graph are the same as the nodes in the stream network, but additionally we assign each node i in the sign pattern graph with a sign based on the value of \(w_i^*\):

$$\begin{aligned} \text {sign}(\text {node } i) = {\left\{ \begin{array}{ll} + \quad &{}\text {if} \quad w_i^*<k {\quad \text {and} \quad r_i>0 \text { or } s_i>0}\\ - \quad &{}\text {if} \quad w_i^*>k {\quad \text {and} \quad r_i>0 \text { or } s_i>0}\\ 0 \quad &{}\text {if} \quad w_i^*=k\\ 0^+ \quad &{}\text {if} \quad w_i^*<k \quad \text {and} \quad r_i=s_i=0\\ 0^- \quad &{}\text {if} \quad w_i^*>k \quad \text {and} \quad r_i=s_i=0.\\ \end{array}\right. } \end{aligned}$$

Next, if there is an edge between node i and an adjacent, downstream node j in the stream network, we draw an edge between node i and node j in the sign pattern graph as follows:

  1. 1.

    There is a directed edge from node i to node j (adjacent, downstream of node i), denoted \(i\rightarrow j\), if

    $$\begin{aligned} (d+q)w_i^* > dw_j^*. \end{aligned}$$
  2. 2.

    There is a directed edge from node j to node i (adjacent, downstream of node i), denoted \(j\rightarrow i\), if

    $$\begin{aligned} (d+q)w_i^* < dw_j^*. \end{aligned}$$
  3. 3.

    There is an undirected edge between node i and node j, denoted \(i - j\), if

    $$\begin{aligned} (d+q)w_i^* = dw_j^*. \end{aligned}$$

The edges in the sign pattern graph describe the net flow between adjacent nodes in the stream network.

Lemma 4.6

For any \((+)\) node, there must be at least one directed edge out of the node. For any \((-)\) node, there must be at least one directed edge into the node. For any \((0),(0^+),(0^-)\) node, either all edges connected to the node are undirected, or there must be at least one edge into and one edge out of the node.

Proof

Suppose node i has sign \((+)\). We add the equations of \(u_i\) and \(v_i\) to obtain

$$\begin{aligned} 0= & {} \sum _{j: f(j)-f(i)=1}(dw_j^* - (d+q)w_i^*) + \sum _{j: f(j)-f(i)=-1}((d+q)w_j^* - dw_i^*)\\{} & {} + (r_iu_i+s_iv_i)\bigg (1-\frac{w_i^*}{k}\bigg ). \end{aligned}$$

Since \(w_i^* < k\), there must be a negative term in the sum above corresponding to a node j adjacent to node i. It is easy to check that whether j is upstream or downstream of i we always have an edge \(i\rightarrow j\) in the sign pattern graph. We can repeat the same argument for the nodes with sign \((-), (0), (0^+), (0^-)\). \(\square \)

Lemma 4.7

If \(i-j\) or \(i\rightarrow j\), then

$$\begin{aligned} w_i^* \ge \bigg (\frac{d+q}{d}\bigg )^{f(i)-f(j)}w_j^*. \end{aligned}$$

Proof

If node i is upstream of node j, we have \(f(i)-f(j)=-1\). Since \(i-j\) or \(i\rightarrow j\), by the way we assign edges to the sign pattern graph we must have

$$\begin{aligned} w_i^* \ge \frac{d}{d+q} w_j^* = \bigg (\frac{d+q}{d}\bigg )^{f(i)-f(j)}w_j^*. \end{aligned}$$

If node i is downstream of node j, we have \(f(i)-f(j)=1\). Since \(i-j\) or \(i\rightarrow j\), again we have

$$\begin{aligned} w_i^* \ge \frac{d+q}{d} w_j^* = \bigg (\frac{d+q}{d}\bigg )^{f(i)-f(j)}w_j^*. \end{aligned}$$

\(\square \)

The following corollary follows directly from Lemma 4.7.

Corollary 4.8

If node i is downstream of node j (i.e. \(f(i)-f(j)=1\)) and \(i-j\) or \(i\rightarrow j\) then \(w_i^* > w_j^*\).

Corollary 4.9

If there is a path from node i to node j, i.e. there exist nodes \(i_1,i_2,\dots ,i_h\) such that \(i - (or\rightarrow ) i_1 - (or\rightarrow ) \dots - (or\rightarrow ) i_h - (or\rightarrow ) j\), then

$$\begin{aligned} w_i^* \ge \bigg (\frac{d+q}{d}\bigg )^{f(i)-f(j)}w_j^*. \end{aligned}$$

The equality happens when all edges are undirectedly connected.

Proof

We apply Lemma 4.7 repeatedly

$$\begin{aligned} w_i^*&\ge \bigg (\frac{d+q}{d}\bigg )^{f(i)-f(i_1)}w_{i_1}^*\\&\quad \ge \bigg (\frac{d+q}{d}\bigg )^{f(i)-f(i_1)}\bigg (\frac{d+q}{d}\bigg )^{f(i_1)-f(i_2)}w_{i_2}^*\\&\quad \vdots \\&\quad \ge \bigg (\frac{d+q}{d}\bigg )^{f(i)-f(i_1)+f(i_1)-f(i_2)+\dots +f(i_h)-f(j)}w_j^*\\&\quad = \bigg (\frac{d+q}{d}\bigg )^{f(i)-f(j)}w_j^*. \end{aligned}$$

Since each equality happens when the corresponding edge is −, the overall equality happens when all the edges in the path are −. \(\square \)

Corollary 4.10

If there is a cycle \(i - (or\rightarrow ) i_1 - (or\rightarrow ) \dots - (or\rightarrow ) i_h - (or\rightarrow ) i\), then all the edges in the cycle must be −.

Proof

The proof follows directly from Corollary 4.9 where we set \(j=i\). \(\square \)

Lemma 4.11

For any i such that \(f(i)=0\) (i.e. the most upstream nodes) and \(r_i>0\), we have \(w_i^* \le k\).

Proof

Assume by contradiction that there exists a node i such that \(f(i)=0\), \(r_i>0\) and \(w_i^* >k\). Then node i has \((-)\) sign and by Lemma 4.6, there must exist a node \(i_1\) such that \(i_1\rightarrow i\). Since node i is a most upstream node, node \(i_1\) must be downstream of it and thus by Corollary 4.8, we must have \(w_{i_1}^*> w_i^* >k\), thus node \(i_1\) has either sign \((-)\) or \((0^-)\).

Since there is already an edge out of node \(i_1\), this means there exists a node \(i_2\) such that \(i_2 \rightarrow i_1\). This gives us a path from \(i_2\) to i and thus by Corollary 4.9 we must have

$$\begin{aligned} w_{i_2}^* \ge \bigg (\frac{d+q}{d}\bigg )^{f(i_2)-f(i)}w_i^* = \bigg (\frac{d+q}{d}\bigg )^{f(i_2)}w_i^* >k. \end{aligned}$$

since \(f(i)=0\). Thus again we must have \(i_2\) has either sign \((-)\) or \((0^-)\).

For each index \(h\ge 3\), we can repeat the argument to obtain node \(i_h\) such that \(i_h \rightarrow i_{h-1}\) and node \(i_h\) has either sign \((-)\) or \((0^-)\). Since the number of nodes is finite, the above process must stop after a finite number of steps. This is only possible if we have a cycle. However, since all edges in this cycle are directed, we reach a contradiction based on Corollary 4.10. \(\square \)

Lemma 4.12

Let (G, f, L) be a homogeneous flow stream network, where \(L=dD+qQ\). Let \(k>0\) and \(\varvec{r}, \varvec{s}>\varvec{0}\) such that \(\sum _{i=1}^n r_i=\sum _{i=1}^n s_i=r>0\). Suppose that \(r_i=0\) for any node i with \(f(i)>0\) and there exists at least one node \(i_0\) with \(f(i_0)>0\) such that \(s_{i_0}>0\). Then a positive equilibrium \(E^*\) does not exist.

Proof

Suppose by contradiction that a positive equilibrium \(E^*\) exists. From the assumption on \(\varvec{r}\), there must exists a node i with \(f(i)=0\) and \(r_i>0\). Taking the sum of all \(du_i/dt\), at the positive equilibrium, we must have

$$\begin{aligned} 0 = \sum _{i:f(i)=0, r_i>0} r_i u_i\bigg (1-\frac{w_i^*}{k}\bigg ). \end{aligned}$$
(4.2)

From Lemma 4.11, for any i such that \(f(i)=0\) and \(r_i>0\) we must have \(w_i^*\le k\). From this fact and equation (4.2), we have \(w_i^*=k\) for any i such that \(f(i)=0\) and \(r_i>0\).

Without loss of generality, suppose that \(f(1)=0\) and \(r_1>0\). From the argument above, \(w_1^*=k\) and node 1 has sign (0). If there is a node j adjacent to node 1 such that \(j\rightarrow 1\), then repeating the argument in Lemma 4.11, we have a cycle which leads to a contradiction. Since there is no directed edge into node 1, from Lemma 4.6, all edges connected to node 1 must be undirected. Let \(j_1,\dots ,j_h\) denote the nodes adjacent to node 1. Then from Corollary 4.8, they must have sign \((-)\) or \((0^-)\).

We will show again that all edges connected to node \(j_1\) must be undirected, and a similar argument can be applied to show all edges connected to nodes \(j_1,\dots ,j_h\) are undirected. Assume by contradiction that not all edges connected to node \(j_1\) are undirected. Since node \(j_1\) has sign \((-)\) or \((0^-)\), from Lemma 4.6 there must be a directed edge into node \(j_1\) from another node \(j'\). However, that means there is a path \(j' \rightarrow j_1 - 1\). From Corollary 4.9 we have

$$\begin{aligned} w_{j'}^* >\bigg (\frac{d+q}{d}\bigg )^{f(j')-f(1)} w^*_1 = \bigg (\frac{d+q}{d}\bigg )^{f(j')} w^*_1\ge w^*_1 = k, \end{aligned}$$

and thus node \(j'\) has sign \((-)\) or \((0^-)\) and there is a directed edge into it. We repeat the argument in Lemma 4.11, which leads to a cycle and thus a contradiction.

The same argument can be repeated, and since the stream network is strongly connected, we have all edges in the sign pattern graph must be undirected. Thus all nodes aside from the most upstream nodes must have sign \((-)\) or \((0^-)\). Since there exists \(i_0\) such that \(f(i_0)>0\) and \(s_{i_0}>0\), there must be at least one node with sign \((-)\). Taking the sum of all equations for \(u_i\) and \(v_i\), we have

$$\begin{aligned} 0=\sum _{i=1}^n (r_iu_i+s_iv_i)\bigg (1-\frac{w_i^*}{k}\bigg ). \end{aligned}$$

However, since there is at least one node with sign \((-)\) and no node with sign \((+)\), the right hand side of the equation above must be strictly negative, which is a contradiction. Thus a positive equilibrium \(E^*\) does not exists. \(\square \)

The proof of the following result is similar to that of Theorem 4.4. We include it here for the sake of completeness.

Lemma 4.13

Let (G, f, L) be a homogeneous flow stream network, where \(L=dD+qQ\). Suppose \(\varvec{k}=(k, \dots , k)\) with \(k>0\) and \(\varvec{s}>\varvec{0}\). Let \(\varvec{v}^*=(v^*_1, \dots , v^*_n)\) be the positive equilibrium of (2.1). If there exists at least one node \(i_0\) with \(f(i_0)>0\) such that \(s_{i_0}>0\), then \(v^*_i<k\) for all node i with \(f(i)=0\).

Proof

Since \(L=dD+qQ\) is essentially nonnegative and irreducible, by Smith (1995, Theorem 4.1.1), the solutions of (1.1) induce a strongly monotone dynamical system: if \(\varvec{u}_1(0)>\varvec{u}_2(0)\) then the corresponding solutions satisfy \(\varvec{u}_1(t)\gg \varvec{u}_2(t)\) for all \(t>0\). By Lemma 4.3, \(dD+qQ\) has a positive eigenvector \(\varvec{v}=(v_1, \dots , v_n)\) such that \(v_i=1\) if \(f(i)=0\) for all \(i=1, \dots , n\). Moreover, \(v_i>1\) if \(f(i)>0\). Define \(\bar{\varvec{u}}=k\varvec{v}\). Since \(\bar{\varvec{u}}\) is an eigenvector of \(dD+qQ\) corresponding to eigenvalue 0, we have

$$\begin{aligned} 0\ge s_i{\bar{u}}_i\left( 1-\frac{{\bar{u}}_i}{k}\right) = \sum _{j=1}^n (dD_{ij}+qQ_{ij}){\bar{u}}_j+s_i{\bar{u}}_i\left( 1-\frac{{\bar{u}}_i}{k}\right) , \ \ i=1,\dots , n. \end{aligned}$$

Moreover, the \(i_0\)-th inequality is strict since \(s_{i_0}>0\) and \(v_{i_0}>1\). Hence, the solution \(\varvec{u}(t)\) of (1.1) with initial condition \(\varvec{u}(0)=\varvec{{\bar{u}}}\) is strictly decreasing and converges to an equilibrium (Smith 1995, Proposition 3.2.1), which is the positive equilibrium \(\varvec{v}^*\) by Lemma 2.1. Hence, \(\varvec{v}^*\ll \bar{\varvec{u}}\). In particular, \(v_i^*<k\) if \(f(i)=0\). \(\square \)

We are now ready to prove that \(E_2\) is unstable.

Lemma 4.14

Let (G, f, L) be a homogeneous flow stream network, where \(L=dD+qQ\). Let \(k>0\) and \(\varvec{r}, \varvec{s}>\varvec{0}\) such that \(\sum _{i=1}^n r_i=\sum _{i=1}^n s_i=r>0\). Suppose that \(r_i=0\) for any node i with \(f(i)>0\) and there exists at least one node \(i_0\) with \(f(i_0)>0\) such that \(s_{i_0}>0\). Then the semitrivial equilibrium \(E_2=(\varvec{0}, \varvec{v}^*)\) of (1.1) is unstable and the semitrivial equilibrium \(E_1=(\varvec{u}^*, \varvec{0})\) of (1.1) is stable.

Proof

To see that \(E_2\) is unstable, it suffices to show \(\lambda _1:=\lambda _1(\varvec{r}, \varvec{v}^*)>0\), where \(\lambda _1(\varvec{r}, \varvec{v}^*)\) is the principal eigenvalue of the matrix \(dD+qQ+\text {diag}(r_i(1-v^*_i/k))\). Let \(\varvec{\varphi }=(\varphi _1, \dots , \varphi _n)\) be a positive eigenvector corresponding with \(\lambda _1\). Then,

$$\begin{aligned} \lambda _1 \varphi _i=\sum _{j=1}^n (dD_{ij}+qQ_{ij})\varphi _j+r_i\left( 1-\frac{v_i^*}{k}\right) \varphi _i. \end{aligned}$$

Adding up all the equations and noticing that each column sum of \(dD+qQ\) is zero, we obtain

$$\begin{aligned} \lambda _1 \sum _{i=1}^n \varphi _i= & {} \sum _{i=1}^n r_i\left( 1-\frac{v_i^*}{k}\right) \varphi _i \\= & {} \sum _{i:\ f(i)=0} r_i\left( 1-\frac{v_i^*}{k}\right) \varphi _i, \end{aligned}$$

where we used the assumption that \(r_i=0\) if \(f(i)>0\) in the last step. By Lemma 4.13, \(v_i^*<k\) if \(f(i)=0\). Therefore, we have \(\lambda _1>0\).

The stability of \(E_1\) is determined by the sign of \(\lambda _1(\varvec{s}, \varvec{u}^*)\), which is the principal eigenvalue of \(dD+qQ+\text {diag}(s_i(1-u^*_i/k))\). By Theorem 4.4, we have \( u_i^*=k(\frac{d+q}{d})^{f(i)}\). So we have

$$\begin{aligned} s_i\left( 1-\frac{u^*_i}{k}\right) =0, \ \forall i \text { such that } f(i)=0 \end{aligned}$$

and

$$\begin{aligned} s_i\left( 1-\frac{u^*_i}{k}\right) \le 0, \ \forall i \text { such that } f(i)>0, \end{aligned}$$

with at least one strict sign due to the assumption on \(\varvec{s}\). Therefore, by Lemma 3.2, we must have \(\lambda _1(\varvec{s}, \varvec{u}^*)<s(dD+qQ)=0\). Hence, \(E_1\) is stable. \(\square \)

Finally, Theorem 4.5 follows from Lemmas 2.2, 4.12, and 4.14.