Stability for a nonlinear hyperbolic equation with time-dependent coefficients and boundary damping

Abstract

In this paper, we prove a stability result for a nonlinear wave equation, defined in a bounded domain of ${\mathbb {R}}^N$, $N\ge 2$, with time-dependent coefficients. The smooth boundary of $\Omega$ is $\Gamma =\Gamma _0\cup \Gamma _1$ such that $\Sigma ={\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1\ne \emptyset$. On $\Gamma _0$ we consider the homogeneous Dirichlet boundary condition and on $\Gamma _1$ we consider the Neumann boundary condition with damping term. The presence of time-dependent coefficients and, moreover, of the singularities generated by the condition $\Sigma \ne \emptyset$ brings some technical difficulties. The tools are the combination of appropriate functional with the techniques due to Bey, Loheac, and Moussaoui [2] and new technical arguments.

1 Introduction

This paper is concerned with the study of the decay rates of the energy associated with the following hyperbolic equation with boundary damping

$$\begin{aligned} \left\{ \begin{aligned}&K(x,t)u_{tt} -A(t)u+F(x,t,u,\nabla u) =0\,\, \hbox {in }\Omega \times (0,\infty )\\&u=0 \,\,\hbox {on } \Gamma _0 \times (0,\infty )\\&\frac{\partial u}{\partial \nu _A}+\beta (x)u_t=0 \,\,\hbox {on } \Gamma _1 \times (0,\infty )\\&u(x,0)=u_0(x),\, u_t(x,0)=u_1(x), \, x\in \Omega , \end{aligned} \right. \end{aligned}$$

(1.1)

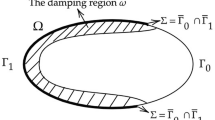
where $\Omega \subset {\mathbb {R}}^N$, $N\ge 2$, is a bounded open set with boundary $\Gamma =\Gamma _0\cup \Gamma _1$, meas$(\Gamma _0)$ and meas$(\Gamma _1)$ are positive and such that ${\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1\ne \emptyset$. The sets $\Gamma _0$ and $\Gamma _1$ are specified below;

$$\begin{aligned} A(t)u=\sum _{j=1}^N\frac{\partial }{\partial x_j}\left( a(x,t)\frac{\partial u}{\partial x_j}\right) , \end{aligned}$$

here $a:{\overline{\Omega }}\times (0,\infty )\rightarrow {\mathbb {R}}$ is a known function; $\nabla$ is the gradient operator in the spatial variable;

$$\begin{aligned} \frac{\partial u}{\partial \nu _A}=\sum _{j=1}^Na(x,t)\frac{\partial u}{\partial x_j}\nu _j, \end{aligned}$$

is the conormal derivative of u with respect to A, $\nu =(\nu _1,\nu _2,\ldots ,\nu _N)$ is the normal unit vector to $\Gamma$; $K:\Omega \times (0,\infty )\rightarrow {\mathbb {R}}$, $F:{\overline{\Omega }}\times [0,\infty )\times {\mathbb {R}}^{N+1}\rightarrow {\mathbb {R}}$, and $\beta :\Omega \rightarrow {\mathbb {R}}$ are known functions; and $u_0$ and $u_1$ are the initial data.

Problems concerning the wave equation with nonconstant coefficient in the principal part have been called the attention of many researchers. We start calling the attention to the important paper Yao [27] where the author studied the boundary exact controllability for the following problem

$$\begin{aligned} \left\{ \begin{aligned}&u_{tt} -\sum _{i,j=1}^N\frac{\partial }{\partial x_i} \left( a_{ij}(x)\frac{\partial u}{\partial x_j} \right) =0 \,\, \text{ in } \Omega \times (0,T) \\&u(x,0)=u_0(x),\, u_t(x,0)=u_1(x), \, x\in \Omega , \\&u=0\quad \text{ in } \Gamma _1\times (0,T),\quad y=v\quad \text{ in } \Gamma _0\times (0,T), \end{aligned} \right. \end{aligned}$$

(1.2)

where $v\in L^2(0,T;L^2(\Gamma _0))$ is the control function. The observability inequalities were established by the Riemannian geometry method under some geometric condition for the Dirichlet problem and for the Neumann problem. The Riemannian geometry method was used by Liu, Li, and Yao [25] to prove the decay of the energy associated with a wave equation with variable coefficients in an exterior domain. The damping was considered on a portion the boundary and also in a portion of the interior of the domain. See also Yao [28,29,30].

When the wave motion holds in an inhomogeneous medium context, the coefficient of $u_{tt}$ is not constant with respect to the spatial variable. A natural way to prove the stability of the problem is use the tools of Microlocal Analysis. A good description of this tools concerning a linear problem can be found in the lecture note due to Burq and Gérard [4]. Nonlinear problems was studied by Cavalcanti et al. [1, 6,7,8,9]. We would like to highlight the work of Cavalcanti et al. [5] where was studied the problem

$$\begin{aligned} \left\{ \begin{aligned}&\displaystyle {\rho (x)u_{tt}-\text{ div }(K(x)\nabla u)+f(u)+a(x)g(u_t)=0}\,\, \text{ in }\,\Omega \times (0,\infty ),\\&u=0\,\, \text{ on }\,\Gamma _0\times (0,\infty ),\\&u(x,0)=u_0(x), \, u_t(x,0)=u_1(x),\,\, x\in \Omega . \end{aligned} \right. \end{aligned}$$

(1.3)

The use of Microlocal Analysis tools brings us two main assumptions. The first one involves the geometric control condition and the second one involves a unique continuation result for the main operator associated with the problem. Problem in inhomogeneous medium and with dynamical boundary conditions was studied by Coclite, G. Goldstein, and J. Goldstein [11]. Results concerning dynamical boundary conditions can be found in the works of Coclite, G. Goldstein, and J. Goldstein [12,13,14], Coclite et al. [15,16,17] and references therein. See also the more recent works of Coclite et al. [18, 19] where the authors studied problems concerning Neumann boundary conditions and discontinuous sources.

When the coefficients are time-dependent the problem becomes more delicate. Indeed, it is well know that the semigroups arguments can not be used. Moreover, the Microlocal Analysis tools also are not appropriate. In [10], using the Faedo–Galerkin method, Cavalcanti, Domingos Cavalcanti, and Soriano proved an existence and uniqueness result to problem (1.1) when the assumption

$$\begin{aligned} {\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1=\emptyset \end{aligned}$$

(1.4)

is in place. Using an appropriate Lyapunov functional they also proved that the energy decay exponentially.

It is well know that assumption (1.4) allows us to use elliptic results which give us regularity on the solution. When this assumption is not in place, we have some delicate technical difficulties which need to be overcome. In the two- and three- dimensional case the tool to overcome the loss of regularity was introduced by Grisvard [21], see also Grisvard [22, 23]. Indeed, he states that a weak solution u of an associate elliptic problem can be split into $u_R$ and $u_S$, where $u_R\in H^2(\Omega )$ and $u_S$ is given by

$$\begin{aligned} u_S = \sum _{x\in \Sigma }\rho (r,\theta )\sqrt{r}\sin \left( \frac{\theta }{2}\right) , \end{aligned}$$

here $(r,\theta )$ is a coordinate system with center in ${\tilde{x}}\in \Sigma$ and $\rho$ and an appropriate smooth function with compact support with $0\le \rho \le 1$. This decomposition allows us to estimate some integrals that are in place due to the presence of singularities.

The ideas of Grisvard was extended to ${\mathbb {R}}^N$, $N\ge 3$, by Bey, Loheac, and Moussaoui [2]. In fact, they proved a theorem which gives as a decomposition of the solution into two functions $u_R$ and $u_S$ with $u_S$ write as in Grisvard case. Moreover, they give a response to the control of $\nabla u$ in a tangential direction. Bey, Loheac, and Moussaoui also proved a stability result to a problem involving the linear wave equation. Problems with singularities also was studied by Cornilleau, Loheac, and Osses [20]. In [20] the authors studied the boundary stabilization of the wave equation by means of a linear or nonlinear Neumann feedback. We highlight that the stability results of [2] and [20] are concerning the wave equation with constant coefficients in the principal operator.

The main goal of the present paper is to study problem (1.1) without assumption (1.4). This work extend the stability results of [2] and [20] to a time-dependent coefficient case. The ideas of Grisvard [21] and, mainly, of Bey, Loheac, and Moussaoui [2] combined with the techniques of Cavalcanti, Domingos Cavalcanti and Soriano [10] are the key to prove our main result.

The difficulties of the present paper are as follows: due to the general assumptions on K and a we do not have control on the derivative of the functional energy. In fact, we do not have the traditional energy identity which is an important tool to prove stability results. This problem combined with the presence of singularities, generated by the change of boundary conditions, brings some technical difficulties which needs to be overcome.

Finally, we also would like to cite the works of Liu and Yao [24], Boiti and Manfrin [3], and Reissig and Smith [26] where the authors studied the wave equation with time-dependent coefficients. In [24] Liu and Yao deal with boundary exact controllability for the dynamics governed by the wave equation subject to Neumann boundary controls. In [3] the authors study the asymptotic behavior of the energy to the Cauchy problem for wave equations with time-dependent propagation speed (i.e., the function which multiply the Laplace operator is time-dependent). $L^p-L^q$ estimates for wave equation with time-dependent propagation speed was studied in [26].

Our paper is organized as follows. In section 2 we present the notations and the assumptions. We also enunciate the existence and uniqueness result. The theorem which gives us the stability also is enunciated in section 2. Finally, in section 3 we prove the stability result, our main result.

2 Preliminaries and existence theorem

Let us denote by $\Vert \cdot \Vert _{L^2(\Omega )}$ the usual norm in the Hilbert space $L^2(\Omega )$ endowed with the inner product $(u,v)_{L^2(\Omega )}=\mathop {\int }\limits _{\Omega }u(x)v(x)\,dx$. We also consider the subspace of $H^1(\Omega )$, denoted by V, as the closure of $C^1({\overline{\Omega }})$ such that $u_{|_{\Gamma _0}}=0$ in the strong topology of $H^1(\Omega )$, i.e.,

$$\begin{aligned} V=\overline{\{u\in C^1({\overline{\Omega }});\,u_{|_{\Gamma _0}}=0\}}^{H^1(\Omega )}. \end{aligned}$$

We have that the Poincaré Inequality holds in V, thus there exists a positive constant $c_p$ such that

$$\begin{aligned} \Vert \nabla u\Vert _{L^2(\Omega )}\le c_p\Vert u\Vert _{L^2(\Omega )}, \end{aligned}$$

for all $u\in V$. Therefore, the space V can be endowed with the norm, $\Vert \nabla \cdot \Vert _{L^2(\Omega )}$, induced by the inner product

$$\begin{aligned} (u,v)_V=(\nabla u,\nabla v)_{L^2(\Omega )}, \end{aligned}$$

which is equivalent to usual norm of $H^1(\Omega )$.

Let $x_0$ a fixed point of ${\mathbb {R}}^N$. We define

$$\begin{aligned} m(x)=(x-x_0)\cdot \nu , \end{aligned}$$

for all $x\in {\mathbb {R}}^N$. We consider that the boundary $\Gamma$ of $\Omega$ is given by

$$\begin{aligned} \Gamma _0 = \{ x\in \Gamma ;\,m\cdot \nu < 0 \} \quad \text{ and } \quad \Gamma _1 = \{ x\in \Gamma ;\,m\cdot \nu \ge 0 \}. \end{aligned}$$

Below, we introduce the assumption on the function F. Our prototype of function F is given by $F(x,t,u,\nabla u)=|u|^{\gamma }u+\vartheta (t) \sum _{j=1}^N\sin \left( \frac{\partial u}{\partial x_j}\right)$, where $\vartheta$ is a regular function.

Assumption 1

We suppose that $F:{\overline{\Omega }}\times [0,\infty )\times {\mathbb {R}}^{N+1}\rightarrow {\mathbb {R}}$ is continuously differentiable and that there exist positive constants $C_0$ and $C_1$ such that

$$\begin{aligned} |F(x,t,\xi ,\varsigma )|\le & {} C_0(1+|\xi |^{\gamma +1}+|\varsigma |),\\ |F_t(x,t,\xi ,\varsigma )|\le & {} C_0(1+|\xi |^{\gamma +1}+|\varsigma |), \\ |F_{\xi }(x,t,\xi ,\varsigma )|\le & {} C_0(1+|\xi |^{\gamma }),\\ |F_{\varsigma _j}(x,t,\xi ,\varsigma )|\le & {} C_1,\,\,\text{ for } j=1,2,\ldots , N, \end{aligned}$$

for all $(x,t,\xi ,\varsigma )\in {\overline{\Omega }}\times [0,\infty )\times {\mathbb {R}}^{N+1}$, where $\gamma >0$, if $N=2$ and $0<\gamma \le \frac{N}{N-2}$, if $N\ge 3$, and $\varsigma =(\varsigma _1,\ldots ,\varsigma _N)$. Moreover, we suppose that there exists a function $C\in L^{\infty }(0,\infty )\cap L^1(0,\infty )$ such that

$$\begin{aligned} F(x,t,\xi ,\varsigma )\eta \ge |\xi |^{\gamma }\xi \eta -C(t)(1+|\eta ||\varsigma |), \end{aligned}$$

for all $(x,t,\xi ,\varsigma )\in {\overline{\Omega }}\times [0,\infty )\times {\mathbb {R}}^{N+1}$ and for all $\eta \in {\mathbb {R}}$;

$$\begin{aligned} F(x,t,\xi ,\varsigma )m\cdot \varsigma \ge |\xi |^{\gamma }\xi m\cdot \varsigma -C(t)(1+|\varsigma ||m\cdot \varsigma |), \end{aligned}$$

for all $(x,t,\xi ,\varsigma )\in {\overline{\Omega }}\times [0,\infty )\times {\mathbb {R}}^{N+1}$. We also suppose that there exist positive constant $D_1$ and $D_2$ such that

$$\begin{aligned} ( F(x,t,\xi ,\varsigma ) - F(x,t,{\hat{\xi }},{\hat{\varsigma }}) ) (\eta -{\hat{\eta }}) \ge -D_1 (|\xi |^{\gamma } -|{\hat{\xi }}|^{\gamma }) |\xi -{\hat{\xi }}| |\eta -{\hat{\eta }}| -D_2 |\varsigma -{\hat{\varsigma }}| |\eta -{\hat{\eta }}|, \end{aligned}$$

for all $(x,t,\xi ,\varsigma ),(x,t,{\hat{\xi }},{\hat{\varsigma }})\in {\overline{\Omega }}\times [0,\infty )\times {\mathbb {R}}^{N+1}$ and $\eta ,{\hat{\eta }}\in \mathbb { R}$.

Next, we write the assumptions on the functions K and a.

Assumption 2

We suppose that $K,a:{\overline{\Omega }}\times (0,\infty )\rightarrow {\mathbb {R}}$ satisfies

$$\begin{aligned} K\in & {} W^{1,\infty }(0,\infty ; C^1({\overline{\Omega }})),\\ a\in & {} W^{1,\infty }(0,\infty ; C^1({\overline{\Omega }}))\cap W^{2,\infty }(0,\infty ; L^{\infty }(\Omega ))\\ K_t,a_t\in & {} L^1(0,\infty ; L^{\infty }(\Omega )), \end{aligned}$$

Moreover, we suppose that there exist constants $K_0$ and $a_0$ such that

$$\begin{aligned} K>k_0>0\quad \text{ and }\quad a>a_0>0\quad \text{ in } \Omega \times (0,\infty ). \end{aligned}$$

Finally, in this paper we consider the case $\beta (x)=m(x)$, for all $x\in {\overline{\Omega }}$.

Now, we can enunciate an existence and uniqueness theorem. The proof is exactly the same of Theorem 2.1 of [10]. But, we highlight that, since in our case ${\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1\ne \emptyset$, we cannot use elliptic regularity arguments and to conclude that $u(t)\in H^2(\Omega )$ (as it was used in [10]).

Theorem 2.1

(Existence and uniqueness of solution) Suppose that Assumptions 1 and 2 hold. For each initial data $(u_0,u_1)\in H^2(\Omega )\times H^2(\Omega )$ satisfying $\frac{\partial u_0}{\partial \nu _A}+\beta (x)u_1=0$, there exist a unique solution of (1.1) in the class

$$\begin{aligned} u\in W^{1,\infty }_{loc}(0,\infty ;V)\cap W^{2,\infty }_{loc}(0,\infty ,L^2(\Omega )). \end{aligned}$$

(2.5)

$\square$

We define the energy associated with problem (1.1) by

$$\begin{aligned} E(t)=\frac{1}{2}\left( \mathop {\int }\limits _{\Omega }K u_t^2\,dx+\mathop {\int }\limits _{\Omega }a|\nabla u|^2\,dx\right) +\frac{1}{\gamma +2}\mathop {\int }\limits _{\Omega }|u|^{\gamma +2}\,dx. \end{aligned}$$

(2.6)

Moreover, for each $\varepsilon >0$, we define the perturbed energy by

$$\begin{aligned} E_{\varepsilon }(t)=E(t)+\varepsilon \Psi (t), \end{aligned}$$

(2.7)

where

$$\begin{aligned} \Psi (t)=2\mathop {\int }\limits _{\Omega }Ku_t m\cdot \nabla u\,dx +\theta \mathop {\int }\limits _{\Omega }Ku_t u\,dx, \end{aligned}$$

(2.8)

here $\theta$ is an appropriate positive constant.

Due to the presence of singularities, initially it is necessary to work away of these points. Therefore, first we define

$$\begin{aligned} \Sigma ={\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1. \end{aligned}$$

Now, let $\delta >0$ a small and fixed number. We consider

$$\begin{aligned} B_{\delta }=\bigcup _{x\in \Sigma }B(x,\delta ), \end{aligned}$$

where $B(x,\delta )=\{y\in \Omega ;\,\Vert x-y\Vert <\delta \}$. The boundary of $B_{\delta }$ is denoted by $\partial B_{\delta }$. We work in the following subset of $\Omega$:

$$\begin{aligned} \Omega _{\delta }=\Omega \setminus B_{\delta }. \end{aligned}$$

Its boundary $\partial \Omega _{\delta }$ is denoted by

$$\begin{aligned} \partial \Omega _{\delta }=\partial \Omega _{\delta }^D\cup \partial \Omega _{\delta }^N\cup (\partial B_{\delta }\cap \Omega ), \end{aligned}$$

where

$$\begin{aligned} \partial \Omega _{\delta }^D=\partial \Omega _{\delta }\cap \Gamma _0 \quad \text{ and }\quad \partial \Omega _{\delta }^N=\partial \Omega _{\delta }\cap \Gamma _1. \end{aligned}$$

See Figures 1 and 2.

Fig. 1

A prototype of the domain: ${\mathbb {R}}^2$ case

Fig. 2

The sets $\partial \Omega _{\delta }^N$, $\partial \Omega _{\delta }^D$, $\partial B_{\delta }\cap \Omega$, and $\Sigma$ in the ${\mathbb {R}}^3$ case

We define the energy associated with problem (1.1) and to $\Omega _{\delta }$ by

$$\begin{aligned} E_{\Omega _{\delta }}(t) = \frac{1}{2}\left( \mathop {\int }\limits _{\Omega _{\delta }}K u_t^2\,dx +\mathop {\int }\limits _{\Omega _{\delta }}a|\nabla u|^2\,dx\right) +\frac{1}{\gamma +2}\mathop {\int }\limits _{\Omega _{\delta }}|u|^{\gamma +2}\,dx. \end{aligned}$$

(2.9)

Finally, for each $\varepsilon >0$, we define the perturbed energy associated with $\Omega _{\delta }$ by

$$\begin{aligned} E_{\delta ,\varepsilon }(t)=E_{\Omega _{\delta }}(t)+\varepsilon \Psi _{\delta }(t), \end{aligned}$$

(2.10)

where

$$\begin{aligned} \Psi _{\delta }(t)=2\mathop {\int }\limits _{\Omega _{\delta }}Ku_t m\cdot \nabla u\,dx +\theta \mathop {\int }\limits _{\Omega _{\delta }}Ku_t u\,dx. \end{aligned}$$

(2.11)

We have the following lemma connecting E(t) with $E_{\Omega _{\delta }}(t)$.

Lemma 2.1

It holds

$$\begin{aligned} E_{\Omega _{\delta }}(t)\rightarrow E(t) \quad \text{ and }\quad \Psi _{\delta }(t)\rightarrow \Psi (t), \end{aligned}$$

as $\delta \rightarrow 0$. Therefore,

$$\begin{aligned} E_{\delta ,\varepsilon }(t)\rightarrow E_{\varepsilon }(t), \end{aligned}$$

(2.12)

as $\delta \rightarrow 0$.

Proof

It follows Lebesgue converge theorem. $\square$

To prove the stability result, it is necessary the following assumption (this assumption also was used by Bey, Loheac, and Moussaoui [2] and Grisvard [21]).

Assumption 3

We denote by $\tau$ the unit tangent vector to $\Gamma$ and normal to $\Sigma$ pointing towards the exterior of $\Gamma _1$, from $\Gamma _1$ to $\Gamma _0$. We suppose that

$$\begin{aligned} m(x)\cdot \tau (x)<0, \end{aligned}$$

for all $x\in \Sigma$.

See Figure 3.

Fig. 3

Examples of domain $\Omega$ and a $x_0$ satisfying Assumption 3

Theorem 2.2

Assume that assumptions 1, 2,  and 3 hold and let E(t) the energy associated with (1.1). Assume that there exist positive constants $\alpha$, r, $\epsilon$, and $\theta _0$ such that for all t sufficiently large, it holds

$$\begin{aligned} \mathop {\int }\limits _0^te^{\epsilon \theta _0s }\varphi (s)\,ds \le \alpha t^r, \end{aligned}$$

(2.13)

where

$$\begin{aligned} \varphi (t)= & {} \frac{r_1}{a_0}\Vert a_t(t)\Vert _{L^{\infty }(\Omega )} +\left( \frac{1}{k_0}+C_2\varepsilon \right) r_1\Vert K_t(t)\Vert _{L^{\infty }(\Omega )} +\varepsilon \left( C_3\Vert \nabla a(t)\Vert _{L^{\infty }(\Omega )} +C_5\Vert \nabla K(t)\Vert _{L^{\infty }(\Omega )} \right) \nonumber \\&+ \left\{ [1+\varepsilon (2+\theta )]\text{ meas }(\Omega ) +\frac{4r_1}{\sqrt{k_0a_0}} +\varepsilon (C_4+C_7)r_1 \right\} C(t), \end{aligned}$$

(2.14)

where $C_2,\ldots ,C_7$ and $r_1$ are known constants, then the energy decay exponentially, i.e., there exist positive constants $\beta _1$ and $\beta _2$ such that

$$\begin{aligned} E(t) \le \beta _1\left( E(0) + \alpha t^r \right) e^{-\beta _2t} \end{aligned}$$

(2.15)

It is possible to verify that the energy $E_{\Omega _{\delta }}(t)$ and the perturbed energy $E_{\delta ,\varepsilon }(t)$ are equivalent. Precisely, there exists a positive constant $r_0$ such that

$$\begin{aligned} |E_{\delta ,\varepsilon }(t)-E_{\Omega _{\delta }}(t)|\le \varepsilon r_0 E_{\Omega _{\delta }}(t), \end{aligned}$$

(2.16)

for all $t\ge 0$ and for all $\varepsilon >0$.

Moreover, there exists a positive constant $r_1$ such that

$$\begin{aligned} E_{\Omega _{\delta }}(t)\le r_1, \end{aligned}$$

(2.17)

for all $t\ge 0$.

Next lemma gives us a kind of inequality of energy. We observe that this lemma does not allow us to conclude that the energy decay. It holds because the assumptions of K and a are very general.

Lemma 2.2

Let $E_{\Omega _{\delta }}(t)$ the energy of (1.1) associated with $\delta$. The following inequality holds

$$\begin{aligned} E_{\Omega _{\delta }}'(t)\le & {} -\mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu u_t^2\,d\Gamma -\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A} u_t\,d\Gamma \nonumber \\&+C(t)\mathop {\int }\limits _{\Omega _{\delta }}(1+|u_t||\nabla u|)\,dx +\frac{1}{2}\mathop {\int }\limits _{\Omega _{\delta }}K_t u_t^2\,dx +\frac{1}{2}\mathop {\int }\limits _{\Omega _{\delta }}a_t |\nabla u|^2\,dx. \end{aligned}$$

(2.18)

Proof

Multiplying (1.1) by $u_t$ and integrating over $\Omega _{\delta }$, we have

$$\begin{aligned}&\frac{1}{2}\frac{d}{dt} \left( \mathop {\int }\limits _{\Omega _{\delta }}K u_t^2\,dx +\mathop {\int }\limits _{\Omega _{\delta }}a|\nabla u|^2\,dx \right) +\mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu u_t^2\,d\Gamma +\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A} u_t\,d\Gamma \nonumber \\&\quad +\mathop {\int }\limits _{\Omega _{\delta }}F(u) u_t\,dx -\frac{1}{2}\mathop {\int }\limits _{\Omega _{\delta }}K_t u_t^2\,dx -\frac{1}{2}\mathop {\int }\limits _{\Omega _{\delta }}a_t |\nabla u|^2\,dx =0. \end{aligned}$$

(2.19)

From this and observing Assumption 1, we obtain (2.18). $\square$

3 Stability theorem proof

Proof of Theorem 2.2

Differentiating $\Psi _{\delta }(t)$ and observing (1.1), we have

$$\begin{aligned} \Psi _{\delta }'(t)= & {} 2\mathop {\int }\limits _{\Omega _{\delta }}K_tu_t m\cdot \nabla u\,dx -2\mathop {\int }\limits _{\Omega _{\delta }}A(t)u \, m\cdot \nabla u\,dx -2\mathop {\int }\limits _{\Omega _{\delta }}F(x,t,u,\nabla u) m\cdot \nabla u\,dx +2\mathop {\int }\limits _{\Omega _{\delta }}K u_t m\cdot \nabla u_t\,dx \\&+\theta \mathop {\int }\limits _{\Omega _{\delta }}K_tu_t u\,dx +\theta \mathop {\int }\limits _{\Omega _{\delta }}Ku_t^2\,dx -\theta \mathop {\int }\limits _{\Omega _{\delta }}uA(t)u \,dx -\theta \mathop {\int }\limits _{\Omega _{\delta }}F(x,t,u,\nabla u)u\,dx. \end{aligned}$$

From this and using Assumption 1, we infer

$$\begin{aligned} \Psi _{\delta }'(t)\le & {} 2\mathop {\int }\limits _{\Omega _{\delta }}K_tu_t m\cdot \nabla u\,dx -2\mathop {\int }\limits _{\Omega _{\delta }}A(t)u \, m\cdot \nabla u\,dx -2\mathop {\int }\limits _{\Omega _{\delta }}|u|^{\gamma }u\, m\cdot \nabla u\,dx -2C(t)\mathop {\int }\limits _{\Omega _{\delta }}(1+|\nabla u|) |m\cdot \nabla u|\,dx \nonumber \\&+2\mathop {\int }\limits _{\Omega _{\delta }}K u_t m\cdot \nabla u_t\,dx +\theta \mathop {\int }\limits _{\Omega _{\delta }}K_tu_t u\,dx +\theta \mathop {\int }\limits _{\Omega _{\delta }}Ku_t^2\,dx \nonumber \\&-\theta \mathop {\int }\limits _{\Omega _{\delta }}uA(t)u \,dx -\theta \mathop {\int }\limits _{\Omega _{\delta }}|u|^{\gamma +2}\,dx +\theta C(t)\mathop {\int }\limits _{\Omega _{\delta }}(1+|u||\nabla u|) \,dx. \end{aligned}$$

(3.20)

Now, we are going to estimate the right-hand side of (3.20).

Estimate for $-2\mathop {\int }\limits _{\Omega _{\delta }}A(t)u \, m\cdot \nabla u\,dx$. Using Gauss theorem, we have

$$\begin{aligned} -2\mathop {\int }\limits _{\Omega _{\delta }}A(t)u \, m\cdot \nabla u\,dx =-\mathop {\int }\limits _{\Omega _{\delta }} a\, m\cdot \nabla (|\nabla u|^2)\,dx -2\mathop {\int }\limits _{\Omega _{\delta }}a|\nabla u|^2\,dx +2\mathop {\int }\limits _{\partial \Omega _{\delta }}\frac{\partial u}{\partial \nu _A} m\cdot \nabla u\,d\Gamma . \end{aligned}$$

(3.21)

Using Gauss theorem one more time, we obtain

$$\begin{aligned} \mathop {\int }\limits _{\Omega _{\delta }} a\, m\cdot \nabla (|\nabla u|^2)\,dx = -\mathop {\int }\limits _{\Omega _{\delta }} \nabla a\cdot m |\nabla u|^2\,dx -n\mathop {\int }\limits _{\Omega _{\delta }} a|\nabla u|^2\,dx +\mathop {\int }\limits _{\partial \Omega _{\delta }} a\, m\cdot \nu |\nabla u|^2\,d\Gamma . \end{aligned}$$

(3.22)

Combining (3.21) with (3.22), we have

$$\begin{aligned} -2\mathop {\int }\limits _{\Omega _{\delta }}A(t)u \, m\cdot \nabla u\,dx= & {} (n-2)\mathop {\int }\limits _{\Omega _{\delta }}a|\nabla u|^2\,dx +\mathop {\int }\limits _{\Omega _{\delta }} \nabla a\cdot m |\nabla u|^2\,dx \nonumber \\&+2\mathop {\int }\limits _{\partial \Omega _{\delta }}\frac{\partial u}{\partial \nu _A} m\cdot \nabla u\,d\Gamma -\mathop {\int }\limits _{\partial \Omega _{\delta }} a\, m\cdot \nu |\nabla u|^2\,d\Gamma . \end{aligned}$$

(3.23)

Estimate for $-2\mathop {\int }\limits _{\Omega _{\delta }}|u|^{\gamma }u\, m\cdot \nabla u\,dx$. We have that

$$\begin{aligned} -2\mathop {\int }\limits _{\Omega _{\delta }}|u|^{\gamma }u\, m\cdot \nabla u\,dx= & {} -\frac{2}{\gamma +2}\mathop {\int }\limits _{\Omega _{\delta }}\nabla (|u|^{\gamma +2})\cdot m \,dx \nonumber \\= & {} \frac{2n}{\gamma +2}\mathop {\int }\limits _{\Omega _{\delta }}|u|^{\gamma +2} \,dx -\frac{2}{\gamma +2}\mathop {\int }\limits _{\partial \Omega _{\delta }}m\cdot \nu |u|^{\gamma +2} \,d\Gamma . \end{aligned}$$

(3.24)

Estimate for $2\mathop {\int }\limits _{\Omega _{\delta }}K u_t m\cdot \nabla u_t\,dx$. We observe that

$$\begin{aligned} 2\mathop {\int }\limits _{\Omega _{\delta }}K u_t m\cdot \nabla u_t\,dx= & {} \mathop {\int }\limits _{\Omega _{\delta }}K m\cdot \nabla u_t^2\,dx \nonumber \\= & {} -\mathop {\int }\limits _{\Omega _{\delta }}(\nabla K\cdot m)u_t^2\,dx -n\mathop {\int }\limits _{\Omega _{\delta }}K u_t^2\,dx +2\mathop {\int }\limits _{\partial \Omega _{\delta }}m\cdot \nu K u_t^2\,d\Gamma . \end{aligned}$$

(3.25)

Estimate for $-\theta \mathop {\int }\limits _{\Omega _{\delta }}uA(t)u \,dx$. Using Gauss theorem, we obtain

$$\begin{aligned} -\theta \mathop {\int }\limits _{\Omega _{\delta }}uA(t)u \,dx =-\theta \mathop {\int }\limits _{\Omega _{\delta }}a|\nabla u|^2 \,dx +\theta \mathop {\int }\limits _{\partial \Omega _{\delta }}\frac{\partial u}{\partial \nu _A}u \,d\Gamma . \end{aligned}$$

(3.26)

Substituting (3.21)–(3.26) into (3.20), we have

$$\begin{aligned} \Psi _{\delta }'(t)\le & {} 2\mathop {\int }\limits _{\Omega _{\delta }}K_tu_t m\cdot \nabla u\,dx - [\theta -(n-2)]\mathop {\int }\limits _{\Omega _{\delta }}a|\nabla u|^2\,dx +\mathop {\int }\limits _{\Omega _{\delta }} \nabla a\cdot m |\nabla u|^2\,dx \nonumber \\&-\left( \theta - \frac{2n}{\gamma +2} \right) \mathop {\int }\limits _{\Omega _{\delta }}|u|^{\gamma +2} \,dx -2C(t)\mathop {\int }\limits _{\Omega _{\delta }}(1+|\nabla u|) |m\cdot \nabla u|\,dx -\mathop {\int }\limits _{\Omega _{\delta }}(\nabla K\cdot m)u_t^2\,dx \nonumber \\&-(n-\theta )\mathop {\int }\limits _{\Omega _{\delta }}K u_t^2\,dx +\theta \mathop {\int }\limits _{\Omega _{\delta }}K_tu_t u\,dx +\theta C(t)\mathop {\int }\limits _{\Omega _{\delta }}(1+|u||\nabla u|) \,dx \nonumber \\&+2\mathop {\int }\limits _{\partial \Omega _{\delta }}\frac{\partial u}{\partial \nu _A} m\cdot \nabla u\,d\Gamma -\mathop {\int }\limits _{\partial \Omega _{\delta }} a\, m\cdot \nu |\nabla u|^2\,d\Gamma -\frac{2}{\gamma +2}\mathop {\int }\limits _{\partial \Omega _{\delta }}m\cdot \nu |u|^{\gamma +2} \,d\Gamma \nonumber \\&+2\mathop {\int }\limits _{\partial \Omega _{\delta }}m\cdot \nu K u_t^2\,d\Gamma +\theta \mathop {\int }\limits _{\partial \Omega _{\delta }}\frac{\partial u}{\partial \nu _A}u \,d\Gamma . \end{aligned}$$

(3.27)

Now, we are going to estimate the integrals over $\partial \Omega _{\delta }$. Observing that $u=0$ on $\Gamma _0$, we have

$$\begin{aligned} m\cdot \nabla u=m\cdot \frac{\partial u}{\partial \nu } \quad \text{ and }\quad |\nabla u|^2=\left( \frac{\partial u}{\partial \nu }\right) ^2 \,\,\text{ on }\,\,\Gamma _0. \end{aligned}$$

From this and observing the boundary condition on $\Gamma _1$, we infer

$$\begin{aligned} 2\mathop {\int }\limits _{\partial \Omega _{\delta }}\frac{\partial u}{\partial \nu _A} m\cdot \nabla u\,d\Gamma= & {} 2\mathop {\int }\limits _{\partial \Omega _{\delta }^D} a m\cdot \nu \left( \frac{\partial u}{\partial \nu }\right) ^2\,d\Gamma \nonumber \\&-2\mathop {\int }\limits _{\partial \Omega _{\delta }^N} m\cdot \nu u_t \, m\cdot \nabla u\,d\Gamma +2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \frac{\partial u}{\partial \nu _A} m\cdot \nabla u\,d\Gamma . \end{aligned}$$

(3.28)

For the second integral on $\partial \Omega _{\delta }$, we have

$$\begin{aligned} -\mathop {\int }\limits _{\partial \Omega _{\delta }} a\, m\cdot \nu |\nabla u|^2\,d\Gamma= & {} -\mathop {\int }\limits _{\partial \Omega _{\delta }^D} a\, m\cdot \nu \left( \frac{\partial u}{\partial \nu }\right) ^2\,d\Gamma \nonumber \\&-\mathop {\int }\limits _{\partial \Omega _{\delta }^N} a\, m\cdot \nu |\nabla u|^2\,d\Gamma -\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } a\, m\cdot \nu |\nabla u|^2\,d\Gamma . \end{aligned}$$

(3.29)

Moreover, since $m\cdot \nu \ge 0$ on $\Gamma _1$, we obtain

$$\begin{aligned} -\frac{2}{\gamma +2}\mathop {\int }\limits _{\partial \Omega _{\delta }}m\cdot \nu |u|^{\gamma +2} \,d\Gamma \le -\frac{2}{\gamma +2}\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu |u|^{\gamma +2} \,d\Gamma . \end{aligned}$$

(3.30)

We also have,

$$\begin{aligned} 2\mathop {\int }\limits _{\partial \Omega _{\delta }}m\cdot \nu K u_t^2\,d\Gamma = 2\mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu K u_t^2\,d\Gamma + 2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu K u_t^2\,d\Gamma \end{aligned}$$

(3.31)

and

$$\begin{aligned} \theta \mathop {\int }\limits _{\partial \Omega _{\delta }}\frac{\partial u}{\partial \nu _A}u \,d\Gamma = -\theta \mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu u_tu \,d\Gamma + \theta \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A}u \,d\Gamma . \end{aligned}$$

(3.32)

Combining (3.27)–(3.32), we infer

$$\begin{aligned} \Psi _{\delta }'(t)\le & {} 2\mathop {\int }\limits _{\Omega _{\delta }}K_tu_t m\cdot \nabla u\,dx - [\theta -(n-2)]\mathop {\int }\limits _{\Omega _{\delta }}a|\nabla u|^2\,dx +\mathop {\int }\limits _{\Omega _{\delta }} \nabla a\cdot m |\nabla u|^2\,dx \nonumber \\&-\left( \theta - \frac{2n}{\gamma +2} \right) \mathop {\int }\limits _{\Omega _{\delta }}|u|^{\gamma +2} \,dx -2C(t)\mathop {\int }\limits _{\Omega _{\delta }}(1+|\nabla u|) |m\cdot \nabla u|\,dx -\mathop {\int }\limits _{\Omega _{\delta }}(\nabla K\cdot m)u_t^2\,dx \nonumber \\&-(n-\theta )\mathop {\int }\limits _{\Omega _{\delta }}K u_t^2\,dx +\theta \mathop {\int }\limits _{\Omega _{\delta }}K_tu_t u\,dx +\theta C(t)\mathop {\int }\limits _{\Omega _{\delta }}(1+|u||\nabla u|) \,dx \nonumber \\&-2\mathop {\int }\limits _{\partial \Omega _{\delta }^N} m\cdot \nu u_t \, m\cdot \nabla u\,d\Gamma -\mathop {\int }\limits _{\partial \Omega _{\delta }^N} a\, m\cdot \nu |\nabla u|^2\,d\Gamma +2\mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu K u_t^2\,d\Gamma -\theta \mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu u_tu \,d\Gamma \nonumber \\&+2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \frac{\partial u}{\partial \nu _A} m\cdot \nabla u\,d\Gamma -\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } a\, m\cdot \nu |\nabla u|^2\,d\Gamma -\frac{2}{\gamma +2}\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu |u|^{\gamma +2} \,d\Gamma \nonumber \\&+ 2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu K u_t^2\,d\Gamma + \theta \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A}u \,d\Gamma . \end{aligned}$$

(3.33)

Recovering the energy on $\Omega _{\delta }$. We observe that

$$\begin{aligned}&- [\theta -(n-2)]\mathop {\int }\limits _{\Omega _{\delta }}a|\nabla u|^2\,dx -\left( \theta - \frac{2n}{\gamma +2} \right) \mathop {\int }\limits _{\Omega _{\delta }}|u|^{\gamma +2} \,dx -(n-\theta )\mathop {\int }\limits _{\Omega _{\delta }}K u_t^2\,dx \nonumber \\&\quad \le -\min \left\{ 2[\theta -(n-2)],2(n-\theta ),2n-(\gamma +2)\theta \right\} E_{\Omega _{\delta }}(t) :=-C_1 E_{\Omega _{\delta }}(t). \end{aligned}$$

(3.34)

Moreover,

$$\begin{aligned}&2\mathop {\int }\limits _{\Omega _{\delta }}K_tu_t m\cdot \nabla u\,dx \le \frac{4}{\sqrt{k_0a_0}}\max _{x\in {\overline{\Omega }}}\left\{ |m(x)|\right\} \Vert k_t(t)\Vert _{L^{\infty }(\Omega )}E_{\Omega _{\delta }}(t) :=C_2\Vert K_t(t)\Vert _{L^{\infty }(\Omega )} E_{\Omega _{\delta }}(t), \end{aligned}$$

(3.35)

$$\begin{aligned}&\mathop {\int }\limits _{\Omega _{\delta }} \nabla a\cdot m |\nabla u|^2\,dx \le \frac{2}{a_0} \max _{x\in {\overline{\Omega }}}\left\{ |m(x)|\right\} \Vert \nabla a(t)\Vert _{L^{\infty }(\Omega )}E_{\Omega _{\delta }}(t) := C_3\Vert \nabla a(t)\Vert _{L^{\infty }(\Omega )}E_{\Omega _{\delta }}(t), \nonumber \\&\quad -2C(t)\mathop {\int }\limits _{\Omega _{\delta }}(1+|\nabla u|) |m\cdot \nabla u|\,dx \le 2\text{ meas }(\Omega )C(t) +4\max _{x\in {\overline{\Omega }}}\left\{ |m(x)|\right\} C(t)E_{\Omega _{\delta }}(t) \end{aligned}$$

(3.36)

$$\begin{aligned}&:=2\text{ meas }(\Omega )C(t) +C_4C(t)E_{\Omega _{\delta }}(t), \end{aligned}$$

(3.37)

$$\begin{aligned}&-\mathop {\int }\limits _{\Omega _{\delta }}(\nabla K\cdot m)u_t^2\,dx \le \frac{2}{k_0}\max _{x\in {\overline{\Omega }}}\left\{ |m(x)|\right\} \Vert \nabla K(t)\Vert _{L^{\infty }(\Omega )}E_{\Omega _{\delta }}(t) :=C_5\Vert \nabla K(t)\Vert _{L^{\infty }(\Omega )}E_{\Omega _{\delta }}(t), \end{aligned}$$

(3.38)

$$\begin{aligned}&\theta \mathop {\int }\limits _{\Omega _{\delta }}K_tu_t u\,dx \le 4\theta \sqrt{\frac{c_p}{a_0k_0}}\Vert K_t(t)\Vert _{L^{\infty }(\Omega )}E_{\Omega _{\delta }}(t) :=\theta C_6 \Vert K_t(t)\Vert _{L^{\infty }(\Omega )}E_{\Omega _{\delta }}(t), \nonumber \\&\quad \theta C(t)\mathop {\int }\limits _{\Omega _{\delta }}(1+|u||\nabla u|) \,dx \le \theta \text{ meas }(\Omega )C(t) +4\theta \frac{\sqrt{c_p}}{a_0}C(t)E_{\Omega _{\delta }}(t) \end{aligned}$$

(3.39)

$$\begin{aligned}&:=\theta \text{ meas }(\Omega )C(t) +C_7C(t)E_{\Omega _{\delta }}(t). \end{aligned}$$

(3.40)

Using estimates (3.34)–(3.40) in (3.33), we obtain

$$\begin{aligned} \Psi _{\delta }'(t)\le & {} -C_1 E_{\Omega _{\delta }}(t) +\lambda (t) E_{\Omega _{\delta }}(t) +(2+\theta )\text{ meas }(\Omega )C(t) \nonumber \\&-2\mathop {\int }\limits _{\partial \Omega _{\delta }^N} m\cdot \nu u_t \, m\cdot \nabla u\,d\Gamma -\mathop {\int }\limits _{\partial \Omega _{\delta }^N} a\, m\cdot \nu |\nabla u|^2\,d\Gamma +2\mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu K u_t^2\,d\Gamma -\theta \mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu u_tu \,d\Gamma \nonumber \\&+2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \frac{\partial u}{\partial \nu _A} m\cdot \nabla u\,d\Gamma -\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } a\, m\cdot \nu |\nabla u|^2\,d\Gamma -\frac{2}{\gamma +2}\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu |u|^{\gamma +2} \,d\Gamma \nonumber \\&+ 2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu K u_t^2\,d\Gamma + \theta \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A}u \,d\Gamma , \end{aligned}$$

(3.41)

where

$$\begin{aligned} \lambda (t) = (C_2+\theta C_6)\Vert K_t(t)\Vert _{L^{\infty }(\Omega )} +C_3\Vert \nabla a(t)\Vert _{L^{\infty }(\Omega )} +(C_4+C_7)C(t) +C_5\Vert \nabla K(t)\Vert _{L^{\infty }(\Omega )}. \end{aligned}$$

Estimate for the integrals on $\partial \Omega _{\delta }^N$. We have

$$\begin{aligned}&-2\mathop {\int }\limits _{\partial \Omega _{\delta }^N} m\cdot \nu u_t \, m\cdot \nabla u\,d\Gamma \le \frac{1}{a_0} \left( \max _{x\in {\overline{\Omega }}}\left\{ |m(x)|\right\} \right) ^2 \mathop {\int }\limits _{\partial \Omega _{\delta }^N} m\cdot \nu u_t^2\,d\Gamma +\mathop {\int }\limits _{\partial \Omega _{\delta }^N} m\cdot \nu a |\nabla u|^2\,d\Gamma , \end{aligned}$$

(3.42)

$$\begin{aligned}&-\theta \mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu u_tu \,d\Gamma \le \frac{\theta ^2}{2a_0 \sigma } \mathop {\int }\limits _{\partial \Omega _{\delta }^N} m\cdot \nu u_t^2\,d\Gamma +\sigma E_{\Omega _{ \delta }}(t), \end{aligned}$$

(3.43)

for all $\sigma >0$ constant. We also obtain that

$$\begin{aligned} 2\mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu K u_t^2\,d\Gamma \le 2\Vert K\Vert _{L^{\infty }(\Omega \times (0,\infty ))}\mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu u_t^2\,d\Gamma . \end{aligned}$$

(3.44)

Therefore,

$$\begin{aligned} \Psi _{\delta }'(t)\le & {} -(C_1-\sigma ) E_{\Omega _{\delta }}(t) +\lambda (t) E_{\Omega _{\delta }}(t) +(2+\theta )\text{ meas }(\Omega )C(t) +C_8\mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu u_t^2\,d\Gamma \nonumber \\&+2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \frac{\partial u}{\partial \nu _A} m\cdot \nabla u\,d\Gamma -\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } a\, m\cdot \nu |\nabla u|^2\,d\Gamma -\frac{2}{\gamma +2}\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu |u|^{\gamma +2} \,d\Gamma \nonumber \\&+ 2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu K u_t^2\,d\Gamma + \theta \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A}u \,d\Gamma , \end{aligned}$$

(3.45)

where

$$\begin{aligned} C_8 = \frac{1}{a_0} \left( \max _{x\in {\overline{\Omega }}}\left\{ |m(x)|\right\} \right) ^2 +\frac{\theta ^2}{2a_0 \sigma } +2\Vert K\Vert _{L^{\infty }(\Omega \times (0,\infty ))}. \end{aligned}$$

Observing Lemma 2.2, (3.45) and the definition of $E_{\delta ,\varepsilon }(t)$, we have

$$\begin{aligned} E_{\delta ,\varepsilon }'(t)\le & {} -\mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu u_t^2\,d\Gamma -\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A} u_t\,d\Gamma \nonumber \\&+C(t)\mathop {\int }\limits _{\Omega _{\delta }}(1+|u_t||\nabla u|)\,dx +\frac{1}{2}\mathop {\int }\limits _{\Omega _{\delta }}K_t u_t^2\,dx +\frac{1}{2}\mathop {\int }\limits _{\Omega _{\delta }}a_t |\nabla u|^2\,dx \nonumber \\&+\varepsilon \left[ -(C_1-\sigma ) E_{\Omega _{\delta }}(t) +\lambda (t) E_{\Omega _{\delta }}(t) +(2+\theta )\text{ meas }(\Omega )C(t) +C_8\mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu u_t^2\,d\Gamma \right. \nonumber \\&+2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \frac{\partial u}{\partial \nu _A} m\cdot \nabla u\,d\Gamma -\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } a\, m\cdot \nu |\nabla u|^2\,d\Gamma -\frac{2}{\gamma +2}\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu |u|^{\gamma +2} \,d\Gamma \nonumber \\&\left. + 2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu K u_t^2\,d\Gamma + \theta \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A}u \,d\Gamma \right] . \end{aligned}$$

(3.46)

We have that

$$\begin{aligned}&C(t)\mathop {\int }\limits _{\Omega _{\delta }}(1+|u_t||\nabla u|)\,dx +\frac{1}{2}\mathop {\int }\limits _{\Omega _{\delta }}K_t u_t^2\,dx +\frac{1}{2}\mathop {\int }\limits _{\Omega _{\delta }}a_t |\nabla u|^2\,dx \\&\quad \le J(t)E_{\Omega _{\delta }}(t)+ C(t)\text{ meas }(\Omega ), \end{aligned}$$

where

$$\begin{aligned} J(t) = \frac{\Vert a_t(t)\Vert _{L^{\infty }(\Omega )}}{a_0}+\frac{\Vert K_t(t)\Vert _{L^{\infty }(\Omega )}}{k_0}+\frac{4}{\sqrt{k_0a_0}}C(t). \end{aligned}$$

Thus,

$$\begin{aligned} E_{\delta ,\varepsilon }'(t)\le & {} -\varepsilon (C_1-\sigma ) E_{\Omega _{\delta }}(t) +(J(t)+\varepsilon \lambda (t)) E_{\Omega _{\delta }}(t) +[1+\varepsilon (2+\theta )]\text{ meas }(\Omega )C(t) \\&-(1-\varepsilon C_8)\mathop {\int }\limits _{\partial \Omega _{\delta }^N}m\cdot \nu u_t^2\,d\Gamma +\Lambda _{\delta }(t)+\Xi _{\delta }(t), \end{aligned}$$

where

$$\begin{aligned} \Lambda _{\delta }(t)= \varepsilon \left[ 2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \frac{\partial u}{\partial \nu _A} m\cdot \nabla u\,d\Gamma -\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } a\, m\cdot \nu |\nabla u|^2\,d\Gamma \right] \end{aligned}$$

(3.47)

and

$$\begin{aligned} \Xi _{\delta }(t)= & {} \varepsilon \left[ -\frac{2}{\gamma +2}\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu |u|^{\gamma +2} \,d\Gamma + 2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu K u_t^2\,d\Gamma \right. \nonumber \\&\left. + \theta \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A}u \,d\Gamma \right] -\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A} u_t\,d\Gamma . \end{aligned}$$

(3.48)

Choosing $n-2<\theta <n$ and, after this, $\sigma =\frac{C_1}{4}$ and $\varepsilon <\frac{1}{C_8}$, we infer

$$\begin{aligned} E_{\delta ,\varepsilon }'(t) \le -\frac{\varepsilon C_1}{4} E_{\Omega _{\delta }}(t) +(J(t)+\varepsilon \lambda (t)) E_{\Omega _{\delta }}(t) +[1+\varepsilon (2+\theta )]\text{ meas }(\Omega )C(t) +\Lambda _{\delta }(t) +\Xi _{\delta }(t). \end{aligned}$$

(3.49)

From this, using (2.16), and as

$$\begin{aligned} \varphi (t) = (J(t)+\varepsilon \lambda (t)) r_1 +[1+\varepsilon (2+\theta )]\text{ meas }(\Omega )C(t) \end{aligned}$$

(see (2.14)) we obtain

$$\begin{aligned} E_{\delta ,\varepsilon }'(t) \le -\frac{\varepsilon C_1}{8} E_{\delta ,\varepsilon }(t) +\varphi (t) +\Lambda _{\delta }(t) +\Xi _{\delta }(t), \end{aligned}$$

(3.50)

for $\varepsilon >0$ small enough. Thus,

$$\begin{aligned} \frac{d}{dt} \left( E_{\delta ,\varepsilon }(t) e^{\frac{\varepsilon C_1t}{8}} \right) \le e^{\frac{\varepsilon C_1t}{8}} \left( \varphi (t) +\Lambda _{\delta }(t) +\Xi _{\delta }(t) \right) . \end{aligned}$$

(3.51)

Integrating from 0 to t, we obtain

$$\begin{aligned} E_{\delta ,\varepsilon }(t) \le E_{\delta ,\varepsilon }(0) e^{-\frac{\varepsilon C_1t}{8}} + \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}}\left( \varphi (s)+\Lambda _{\delta }(s)+\Xi _{\delta }(s)\right) \,ds \right) e^{-\frac{\varepsilon C_1t}{8}}. \end{aligned}$$

(3.52)

From this and using Assumption 2.13, we conclude that

$$\begin{aligned} E_{\delta ,\varepsilon }(t) \le E_{\delta ,\varepsilon }(0) e^{-\frac{\varepsilon C_1t}{8}} + \alpha t^re^{-\frac{\varepsilon C_1t}{8}} + \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}}[\Lambda _{\delta }(s)+\Xi _{\delta }(s)]\,ds \right) e^{-\frac{\varepsilon C_1t}{8}}. \end{aligned}$$

(3.53)

Estimate for $\left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}}\Lambda _{\delta }(s)\,ds \right) e^{-\frac{\varepsilon C_1t}{8}}$. First, we consider the two-dimensional case. For each ${\tilde{x}}\in \Sigma$, we denote by ${\tilde{\nu }}=\nu ({\tilde{x}})$ and ${\tilde{\tau }}=\tau ({\tilde{x}})$ the unit normal vector pointing towards the exterior and the tangent vector of $\Sigma$, respectively. We consider ${\tilde{\tau }}$ from $\Gamma _1$ to $\Gamma _0$. Using coordinate system $({\tilde{x}},{\tilde{\nu }},{\tilde{\tau }})$, it is possible to verify that

$$\begin{aligned} 2\frac{\partial u}{\partial \nu _A} m\cdot \nabla u - a\, m\cdot \nu |\nabla u|^2 = \frac{a}{4\delta }{\tilde{m}}\cdot {\tilde{\tau }} -\frac{a}{4}\nu \cdot {\tilde{\tau }}. \end{aligned}$$

See Figures 4 and 5.

Fig. 4

The vectors $\nu$, $\tau$, ${\tilde{\nu }}$, and ${\tilde{\tau }}$ in the ${\mathbb {R}}^2$ case

Fig. 5

The vectors $\nu$, $\tau$, ${\tilde{\nu }}$, and ${\tilde{\tau }}$ in the ${\mathbb {R}}^3$ case

Observing that

$$\begin{aligned} \frac{1}{\pi \delta } \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } a\,d\Gamma \rightarrow a({\tilde{x}}):={\tilde{a}}, \end{aligned}$$

as $\delta \rightarrow \infty$, we infer

$$\begin{aligned} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \left( 2\frac{\partial u}{\partial \nu _A} m\cdot \nabla u - a\, m\cdot \nu |\nabla u|^2 \right) \,d\Gamma \rightarrow \frac{\pi }{4}{\tilde{a}}\,{\tilde{m}}\cdot {\tilde{\tau }}, \end{aligned}$$

(3.54)

as $\delta \rightarrow 0$. As Assumption 3 is in place and since $a\ge 0$, we conclude that the integral converges to a negative number.

Now, we consider the case in ${\mathbb {R}}^N$, with $N\ge 3$. For each $x\in \partial \Omega _{\delta }\cap \Omega$, there exists $({\tilde{x}},{\tilde{\nu }},{\tilde{\tau }})$ such that x is into the plane defined by $({\tilde{x}},{\tilde{\nu }},{\tilde{\tau }})$. Moreover, there exists an arc of circumference $\gamma ({\tilde{x}},\delta )$ into this plane such that $x\in \gamma ({\tilde{x}},\delta )$. Thus, writing

$$\begin{aligned} \nabla u=\nabla _2 u+\nabla _T u, \end{aligned}$$

(3.55)

where $\nabla _2 u$ is into the plan describe above and $\nabla _T u$ is orthogonal to $\nabla _2 u$, we have

$$\begin{aligned} \nabla _T u\cdot \nabla _2 u=0 \quad \text{ and }\quad |\nabla u|^2=|\nabla _2 u|^2+|\nabla _T u|^2. \end{aligned}$$

Therefore,

$$\begin{aligned}&\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \left( 2\frac{\partial u}{\partial \nu _A}m\cdot \nabla u -a \,m\cdot \nu |\nabla u|^2 \right) \,d\Gamma \nonumber \\&\quad =\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \left[ 2a(\nabla _2 u+\nabla _T u)\cdot \nu \,m\cdot (\nabla _2 u+\nabla _T u) -a\,m\cdot \nu (|\nabla _2 u|^2+|\nabla _T u|^2) \right] \,d\Gamma \nonumber \\&\quad =\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \left( 2a\nabla _T u\cdot \nu \,m\cdot \nabla _T u -a\,m\cdot \nu |\nabla _T u|^2 \right) \,d\Gamma \nonumber \\&\qquad +\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \left( 2a\nabla _2 u\cdot \nu \,m\cdot \nabla _2 u -a\,m\cdot \nu |\nabla _2 u|^2 \right) \,d\Gamma \nonumber \\&\qquad +2\mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } a\left( \nabla _T u\cdot \nu \,m\cdot \nabla _2 u +\nabla _2 u\cdot \nu \,m\cdot \nabla _T u \right) \,d\Gamma . \end{aligned}$$

(3.56)

Using the first part of Theorem 4 of [2], we have

$$\begin{aligned} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \left( 2a\nabla _T u\cdot \nu \,m\cdot \nabla _T u -a\,m\cdot \nu |\nabla _T u|^2 \right) \,d\Gamma \rightarrow 0, \end{aligned}$$

(3.57)

as $\delta \rightarrow 0$.

Next step is to estimate the second integral of the right side of (3.56). From Theorem 4 of [2], we have that u can be written locally as a sum of regular part with a singular part

$$\begin{aligned} \Phi ({\tilde{x}})u_S(x-{\tilde{x}}), \end{aligned}$$

where $\Phi$ is locally in $H^{\frac{1}{2}}(\Sigma )$ and $u_S$ is given by

$$\begin{aligned} u_S(r,w,t)=c(t)r^{\frac{1}{2}}\varrho \sin \Big (\frac{w}{2}\Big ), \end{aligned}$$

(3.58)

where $\varrho \in C^{\infty }$ with compact support and such that $\varrho =1$ into a neighborhood of zero and supp($\varrho$)$\subset [-\varrho _0,\varrho _0]\subset (-1,1)$, with $\varrho _0>0$ small enough. As in the two-dimensional case, using the coordinate system ${\tilde{x}},{\tilde{\nu }},{\tilde{\tau }}$ we obtain

$$\begin{aligned} 2a\nabla _2 u_S\cdot \nu \,m\cdot \nabla _2 u_S -a\,m\cdot \nu |\nabla _2 u_S|^2 =\frac{a}{4\delta }{\tilde{m}}\cdot {\tilde{\tau }}-\frac{a}{4}\nu \cdot {\tilde{\tau }}. \end{aligned}$$

Integrating over the arc $\gamma ({\tilde{x}},\delta )$ and taking the limit as $\delta \rightarrow 0$, as in (3.54), we infer

$$\begin{aligned} \mathop {\int }\limits _{\gamma ({\tilde{x}},\delta )} \left( 2a\nabla _2 u_S\cdot \nu \,m\cdot \nabla _2 u_S -a\,m\cdot \nu |\nabla _2 u_S|^2 \right) \,d\Gamma \rightarrow \frac{\pi }{4}{\tilde{a}}\,{\tilde{m}}\cdot {\tilde{\tau }}, \end{aligned}$$

(3.59)

as $\delta \rightarrow 0$. Using Assumption 3, we infer that this integral converges to a negative number. Therefore, using Fubini’s theorem, we conclude that the second integral of the right-hand side of (3.56) converges to a negative number.

Finally, we are going to estimate the last integral of the right-hand side of (3.56). Using Hölder’s inequality, we have

$$\begin{aligned} 2\mathop {\int }\limits _{\gamma ({\tilde{x}},\delta )} a\left( \nabla _T u\cdot \nu \,m\cdot \nabla _2 u +\nabla _2 u\cdot \nu \,m\cdot \nabla _T u \right) \,d\Gamma \le C \left( \mathop {\int }\limits _{\gamma ({\tilde{x}},\delta )} |\nabla _T u|^2 \,d\Gamma \right) ^{\frac{1}{2}} \left( \mathop {\int }\limits _{\gamma ({\tilde{x}},\delta )} |\nabla _2 u|^2 \,d\Gamma \right) ^{\frac{1}{2}}. \end{aligned}$$

From Theorem 4 of [2], we have

$$\begin{aligned} \left( \mathop {\int }\limits _{\gamma ({\tilde{x}},\delta )} |\nabla _T u|^2 \,d\Gamma \right) ^{\frac{1}{2}} \rightarrow 0, \end{aligned}$$

as $\delta \rightarrow 0$, using the decomposition described above, we infer

$$\begin{aligned} \left( \mathop {\int }\limits _{\gamma ({\tilde{x}},\delta )} |\nabla _2 u|^2 \,d\Gamma \right) ^{\frac{1}{2}} \le C\mathop {\int }\limits _0^{2\pi } \frac{1}{\sqrt{\delta }} \,ds =C\sqrt{\delta }\rightarrow 0, \end{aligned}$$

as $\delta \rightarrow 0$. Therefore,

$$\begin{aligned} 2\mathop {\int }\limits _{\gamma ({\tilde{x}},\delta )} a\left( \nabla _T u\cdot \nu \,m\cdot \nabla _2 u +\nabla _2 u\cdot \nu \,m\cdot \nabla _T u \right) \,d\Gamma \rightarrow 0, \end{aligned}$$

(3.60)

as $\delta \rightarrow 0$. Thus, (3.60) and Fubini’s theorem allow us to conclude that the third integral of the right-hand side of (3.56) converges to zero.

Therefore, we infer

$$\begin{aligned} \Lambda _{\delta }(t) = \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega } \left( 2\frac{\partial u}{\partial \nu _A}m\cdot \nabla u -a \,m\cdot \nu |\nabla u|^2 \right) \,d\Gamma \rightarrow \alpha , \end{aligned}$$

as $\delta \rightarrow 0$, where $\alpha \le 0$ is a real number. At this moment, we consider two cases $\alpha <0$ and $\alpha =0$. If $\alpha <0$, then there exists $\delta _1>0$ such that

$$\begin{aligned} \Lambda _{\delta }(t) <0, \end{aligned}$$

(3.61)

for all $\delta <\delta _1$. Therefore,

$$\begin{aligned} \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}}\Lambda _{\delta }(s)\,ds \right) e^{-\frac{\varepsilon C_1t}{8}} <0, \end{aligned}$$

(3.62)

for all $\delta <\delta _1$. We conclude that term (3.62) can be removed of (3.53), when $\delta \rightarrow 0$.

If $\alpha =0$, then we consider two subcases. First, if there exists a positive $\delta _2$ such that

$$\begin{aligned} \Lambda _{\delta }(t) <0, \end{aligned}$$

(3.63)

for all $\delta <\delta _2$, then we take the same way of the case $\alpha <0$. On the other hand, if there exists a positive $r_1$ such that

$$\begin{aligned} \Lambda _{\delta }(t) >0, \end{aligned}$$

(3.64)

for all $\delta <r_2$, then

$$\begin{aligned} 0 \le \mathop {\int }\limits _0^t \left( e^{\frac{\varepsilon C_1s}{8}} \Lambda _{\delta }(s) \right) \,ds e^{-\frac{\varepsilon C_1t}{8}} \le \mathop {\int }\limits _0^t \Lambda _{\delta }(s)\,ds \rightarrow 0, \end{aligned}$$

(3.65)

as $\delta \rightarrow 0$. Therefore, in this case the term also goes to 0.

Thus, we conclude that

$$\begin{aligned} \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}}\Lambda _{\delta }(s)\,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \rightarrow 0, \end{aligned}$$

(3.66)

as $\delta \rightarrow 0$.

Estimate for $\left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}}\Xi _{\delta }(s)\,ds \right) e^{-\frac{\varepsilon C_1t}{8}}$. Using the decomposition described above as

$$\begin{aligned} u=u_R+u_S, \end{aligned}$$

(3.67)

where $u_R$ is the regular part of u and $u_S$ is the singular one, we have

$$\begin{aligned}&\left| 2\left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu K(x,s) |u_t(x,s)|^2\,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \right| \nonumber \\&\quad \le C \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }|m\cdot \nu | (u_R)_t^2\,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \nonumber \\&\qquad + C \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }|m\cdot \nu | (u_S)_t^2\,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}}. \end{aligned}$$

(3.68)

From Lebesgue convergence theorem, we have

$$\begin{aligned} \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }|m\cdot \nu | (u_R)_t^2\,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \rightarrow 0, \end{aligned}$$

(3.69)

as $\delta \rightarrow 0$. Now, observing (3.58), we have

$$\begin{aligned} \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\gamma ({\tilde{x}},\delta )}|m\cdot \nu | (u_S)_t^2\,d\Gamma \,ds e^{-\frac{\varepsilon C_1t}{8}} \le C \mathop {\int }\limits _0^{2\pi } \sqrt{\delta }\,ds \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}}\,ds\, e^{-\frac{\varepsilon C_1t}{8}} \le C \delta ^{\frac{3}{2}} \rightarrow 0, \end{aligned}$$

(3.70)

as $\delta \rightarrow 0$. From this and using the Fubini’s theorem, we have that the last integral of (3.68) goes to zero, as $\delta \rightarrow 0$. Summarizing, (3.68)–(3.70) give us that

$$\begin{aligned} 2\left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu K(x,s) |u_t(x,s)|^2\,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \rightarrow 0, \end{aligned}$$

(3.71)

as $\delta \rightarrow 0$.

On the other hand, using decomposition (3.67), we have

$$\begin{aligned}&\left| \frac{2}{\gamma +2}\left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu |u(x,s)|^{\gamma +2}\,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \right| \nonumber \\&\quad \le C \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }|m\cdot \nu | |u_R|^{\gamma +2}\,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \nonumber \\&\qquad + C \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }|m\cdot \nu | |u_S|^{\gamma +2}\,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}}. \end{aligned}$$

(3.72)

From Lebesgue convergence theorem, we have

$$\begin{aligned} \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }|m\cdot \nu | |u_R|^{\gamma +2}\,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \rightarrow 0, \end{aligned}$$

(3.73)

as $\delta \rightarrow 0$. Now, observing (3.58), we have

$$\begin{aligned} \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\gamma ({\tilde{x}},\delta )}|m\cdot \nu | |u_S|^{\gamma +2}\,d\Gamma \,ds e^{-\frac{\varepsilon C_1t}{8}} \le C\mathop {\int }\limits _0^{2\pi } \delta ^{\frac{\gamma +2}{2}}\,ds \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}}\,ds\, e^{-\frac{\varepsilon C_1t}{8}} \le C \delta ^{\frac{\gamma +4}{2}} \rightarrow 0, \end{aligned}$$

(3.74)

as $\delta \rightarrow 0$. From this and using the Fubini’s theorem, we have that the last integral of (3.68) goes to zero, as $\delta \rightarrow 0$. Summarizing, (3.72)–(3.74) give us that

$$\begin{aligned} \frac{2}{\gamma +2}\left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }m\cdot \nu |u(x,s)|^{\gamma +2}\,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \rightarrow 0, \end{aligned}$$

(3.75)

as $\delta \rightarrow 0$.

On the other hand, using the decomposition of u into a regular and a singular part and (3.55), we have that

$$\begin{aligned}&\left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A}u \,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \nonumber \\&\quad = \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }a \nabla _T u\cdot \nu u_R \,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} + \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }a \nabla _2 u\cdot \nu u_S \,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \nonumber \\&\qquad + \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }a \nabla _2 u \cdot \nu u_R \,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} + \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }a \nabla _T u\cdot \nu u_S \,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \nonumber \\&\quad \le C\sqrt{\delta }. \end{aligned}$$

(3.76)

From Lebesgue convergence theorem, we have

$$\begin{aligned} \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }a \nabla _T u\cdot \nu u_R \,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \rightarrow 0, \end{aligned}$$

(3.77)

as $\delta \rightarrow 0$. Making calculus analogous to the preview ones, we infer

$$\begin{aligned}&\left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }a \nabla _2 u\cdot \nu u_S \,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \le C \delta \rightarrow 0, \end{aligned}$$

(3.78)

$$\begin{aligned}&\left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }a \nabla _2 u \cdot \nu u_R \,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \le C \sqrt{\delta } \rightarrow 0, \end{aligned}$$

(3.79)

$$\begin{aligned}&\left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }a \nabla _T u\cdot \nu u_S \,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \le C \delta ^{\frac{3}{2}} \rightarrow 0, \end{aligned}$$

(3.80)

as $\delta \rightarrow 0$.

Therefore,

$$\begin{aligned} \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A}u \,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \rightarrow 0, \end{aligned}$$

(3.81)

as $\delta \rightarrow 0$.

Analogously,

$$\begin{aligned} \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}} \mathop {\int }\limits _{\partial \Omega _{\delta }\cap \Omega }\frac{\partial u}{\partial \nu _A} u_t \,d\Gamma \,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \rightarrow 0, \end{aligned}$$

(3.82)

as $\delta \rightarrow 0$.

From (3.71), (3.75), (3.81), and (3.82), we conclude that

$$\begin{aligned} \left( \mathop {\int }\limits _0^t e^{\frac{\varepsilon C_1s}{8}}\Xi _{\delta }(s)\,ds \right) e^{-\frac{\varepsilon C_1t}{8}} \rightarrow 0, \end{aligned}$$

(3.83)

as $\delta \rightarrow 0$.

Returning to the estimate of $E_{\delta ,\varepsilon }(t)$. Observing Lemma 2.2, (3.53), (3.66), and (3.83), we infer

$$\begin{aligned} E_{\varepsilon }(t) \le \left( E_{\varepsilon }(0) + \alpha t^r \right) e^{-\frac{\varepsilon C_1t}{8}}, \end{aligned}$$

(3.84)

for all $t\ge 0$. From (3.84) and using (2.16), we conclude that (2.15) holds. $\square$