Exponential Decay for a Time-Varying Coefficients Wave Equation with Dynamic Boundary Conditions

Abstract

We consider a wave equation with variable coefficients in time and space in a bounded domain $\Omega$ which has the smooth boundary $\Gamma =\Gamma _0\cup \Gamma _1$ such that ${\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1\ne \emptyset$. We study this system that has a homogeneous Dirichlet boundary on $\Gamma _0$ and a dynamic boundary on $\Gamma _1$. The innovation of the paper lies in the coefficients which depends on the time variable and the singularities generated by changing the boundary conditions along the interface, thus we need some special techniques to deal with these difficulties. Under some geometric assumptions, the exponential decay result of the system is established by the Riemannian geometry method and the energy perturbation method.

1 Introduction

Let $\Omega$ be a bounded domain in $R^n$ $(n\ge 2)$ which has a boundary $\Gamma =\Gamma _0\cup \Gamma _1$ of class $C^2$. Here meas($\Gamma _0$) and meas($\Gamma _1$) are positive and $\Sigma ={\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1\ne \emptyset$. Let $\omega$ be an open neighborhood of the part $\Gamma _1$ of the boundary that is supposed to be connected and meas$({\overline{\omega }}\cap \Gamma _0)>0$ (see Fig. 1).

Fig. 1

An example of domain $\Omega$ satisfying the required geometrical assumptions for $n=2$

Here $\nu =(\nu _1,\cdots ,\nu _n)$ represents the outward unit vector normal to $\Gamma$. We denote the gradient and the divergence by $\nabla$ and ${\textrm{div}}$ respectively, and the tangential-gradient and the tangential-divergence by $\nabla _T$ and ${\textrm{div}}_T$ respectively in the Eucliden metric. In this paper, we study the following problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle u_{tt}+{\mathcal {A}}(x,t)u+b(x)u_t=0 &{} \text{ in } \ \Omega \times R^+, \\ \displaystyle u=0 &{} \text{ on } \ \Gamma _0\times R^+, \\ \displaystyle u_{tt}+\frac{\partial u}{\partial \nu _{\mathcal {A}}}+{\mathcal {A}}_T(x,t)u+u_t=0 &{} \text{ on } \ \Gamma _1\times R^+,\\ \displaystyle u(x,0)=u_0(x),\ \ u_{t}(x,0)=u_1(x) &{} \text{ in } \ \Omega , \end{array}\right. } \end{aligned}$$

(1.1)

where

$$\begin{aligned} \displaystyle b(x)=b_0,\ \ \ x\in \omega , \end{aligned}$$

and $b_0\!>\!0$ is a constant. The initial data $u_0$ and $u_1$ are in suitable function spaces. The second-order differential operators ${\mathcal {A}}(x,t)$ and ${\mathcal {A}}_T(x,t)$ are given by

$$\begin{aligned} {\mathcal {A}}(x,t)u:= & {} -\beta (t){\textrm{div}}(A(x)\nabla u),\\ {\mathcal {A}}_T(x,t)u:= & {} -\beta (t){\textrm{div}}_T\left( A(x)|_{\Gamma _1}\nabla _Tu\right) , \end{aligned}$$

in which $\beta \in W^{1,\infty }(0,\infty )$ is a given function and $A(x)=(a_{ij}(x))_{n\times n}$ are symmetric and positive definite matrices functions with $a_{ij}(x)\in C^{\infty }(R^n)$, and the operators also satisfy the uniform ellipticity conditions

$$\begin{aligned} \displaystyle \sum _{i,j=1}^na_{ij}(x)\xi _i\xi _j\ge \lambda \sum _{i=1}^n\xi _i^2,\ \ \ x\in {\overline{\Omega }},\ 0\ne (\xi _1,\xi _2,...,\xi _n)^T\in R^n, \end{aligned}$$

for some constant $\lambda >0$. And

$$\begin{aligned} \displaystyle \frac{\partial u}{\partial \nu _{{\mathcal {A}}}}=\beta (t)\sum _{i,j=1}^na_{ij}(x)\frac{\partial u}{\partial x_j}\nu _i=\beta (t)A(x)\nabla u\cdot \nu \end{aligned}$$

is the outer normal derivative.

Since the boundaries $\Gamma _0$ and $\Gamma _1$ satisfy $\Sigma ={\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1\ne \emptyset$, the singularities occur when the boundary conditions change from $\Gamma _0$ to $\Gamma _1$. We cannot get the regularity of solution by the elliptic results, so we have to use some technicalities to overcome this difficulty. For the two-dimensional case, we can refer to the method in [1] to deal with the problem of lack of regularity, and for more on this can be seen in [2, 3]. The main idea in these papers is to divide the weak solution u corresponding to the elliptic problem into two parts that the regular part and the singular part. More precisely, they decompose the solution into

$$\begin{aligned} u:=u_1+u_2, \end{aligned}$$

where $u_1\in H^2(\Omega )$ and $u_2$ is given by

$$\begin{aligned} u_2:=\sum _{x\in \Sigma }\rho (r,\theta )\sqrt{r}\sin \left( \frac{\theta }{2}\right) , \end{aligned}$$

here $(r,\theta )$ is a coordinate system centered on $x\in \Sigma$ and $\rho$ is an appropriately smooth function with a compact support satisfying $0\le \rho \le 1$. This decomposition of u allows us to estimate some integrals that resulting from the existence of singularities. For the case of higher dimensions ($n\ge 3$), Bey et al. [4] extended the above results, and [4, Theorem 4] is very important and helpful for the proof of our stability. Later, Cornilleau et al. [5] further developed the results of [4] and considered the possible singularities in which they changed the boundary conditions along the interface $\Sigma ={\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1$. They assumed a partition $(\Gamma _0, \Gamma _1)$ of $\Gamma =\partial \Omega$ such that

• $\Sigma ={\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1$ is a $C^3$-manifold of dimension $n-2$,

• $(x-x_0)\cdot \nu =0$ on $\Sigma$, where $x_0\in R^n$ is a fixed point,

• $\Gamma \cap \varpi$ is a $C^3$-manifold of dimension $n-1$,

• ${\mathcal {H}}^{n-1}(\Gamma _0)>0$,

where $n\!\ge \!2$ is the dimension of $\Omega$, $\varpi$ is a suitable neighborhood of $\Sigma$ and ${\mathcal {H}}^{n-1}$ denotes the usual $(n\!-\!1)$-dimensional Hausdorff measure. Under a simple geometrical condition concerning the orientation of the boundary, they obtained the stability results for systems with linear or nonlinear Neumann feedbacks.

It is worth noting that [4] and [5] mentioned here are the literature for the constant coefficients. For the variable coefficients case, we can refer to [6] which extended the stability results of [5] to a time-dependent coefficients case. In [6] Cavalcanti et al. concerned the following hyperbolic equation with boundary damping

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle K(x,t)u_{tt}-A(t)u+F(x,t,u,\nabla u)=0 &{} \text{ in } \ \Omega \times R^+, \\ \displaystyle u=0 &{} \text{ on } \ \Gamma _0\times R^+, \\ \displaystyle \frac{\partial u}{\partial \nu _A}+\beta (x)u_t=0 &{} \text{ on } \ \Gamma _1\times R^+, \end{array}\right. } \end{aligned}$$

where $\Omega \subset R^n$ ($n\ge 2$) is a bounded open set with the boundary $\Gamma =\Gamma _0\cup \Gamma _1$ such that ${\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1\ne \emptyset$. Let $x_0\in R^n$ be a fixed point, the sets $\Gamma _0$ and $\Gamma _1$ given by

$$\begin{aligned} \Gamma _0=\{x\in \Gamma :\ (x-x_0)\cdot \nu <0\}\ \ \ {\textrm{and}}\ \ \ \Gamma _1=\{x\in \Gamma :\ (x-x_0)\cdot \nu \ge 0\}. \end{aligned}$$

Under some assumptions about the functions F, K and A, the authors obtained the exponential decay result by using the energy method.

Our work changes part of the boundary conditions in the above reference, that is, we study the influence of the dynamic boundary on the stability of system. This type of boundary condition takes acceleration into account on the boundary to affect the stability and the exact controllability of elastic structures. In [7], Li et al. considered the following one-dimensional system

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle u_{tt}-u_{xx}=0, &{} x\in (0,1),\ t\ge 0, \\ \displaystyle u(0,t)=0, &{} t\ge 0, \\ \displaystyle \kappa u_{tt}(1,t)+\frac{\partial u}{\partial \nu }(1,t)+u_t(1,t)=0, &{} t\ge 0. \end{array}\right. } \end{aligned}$$

At $\kappa =1$, they got the optimal polynomial decay result, even though the system is exponentially stable if $\kappa =0$. Thus, for the study of dynamic boundary, it not only is very important for theoretical significance, but also is a good reference for some practical applications. This kind of boundary is suitable for dynamic vibration modeling of linear viscoelastic rods and beams with attached masses at their free ends, we refer to the reference [8,9,10,11,12,13]. These questions are common in analyzing the mechanical behavior of any structure with elongated members attached to smaller, heavier objects, for example, a structure consisting of robotic arms attached to satellites. For early studies of the system with dynamic boundary conditions we can refer to [14,15,16]. [16] was devoted to study of the following damped Cauchy-Ventcel problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle u_{tt}+{\mathcal {A}}(x)u+a(x)g_1(u_t)=0 &{} \text{ in } \ \Omega \times R^+, \\ \displaystyle u=v &{} \text{ on } \ \Gamma \times R^+, \\ \displaystyle u=0 &{} \text{ on } \ \Gamma _0\times R^+, \\ \displaystyle v_{tt}+\frac{\partial u}{\partial \nu _{\mathcal {A}}}+{\mathcal {A}}_T(x)v+g_2(v_t)=0 &{} \text{ on } \ \Gamma _1\times R^+, \end{array}\right. } \end{aligned}$$

where there exists a vector field H such that

$$\begin{aligned} \Gamma _1=\{x\in \Gamma :\ H\cdot \nu >0\} \ \ \ {\textrm{and}}\ \ \ {\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1=\emptyset . \end{aligned}$$

The uniform energy decay rate for the above problem was established by Riemannian geometry method which was first introduced by Yao [17] to study the exact controllability of wave equation with variable coefficients. For more information about the variable coefficients that are only related to the space variable, we can refer to [18,19,20,21,22,23] and the references in them.

While for the time-varying coefficients case, we can refer to [24,25,26,27]. In [25], Liu considered the mixed problem

$$\begin{aligned} u_{tt}+{\mathcal {A}}(x,t)u=0, \end{aligned}$$

with Neumann boundary control

$$\begin{aligned} \displaystyle \frac{\partial u}{\partial \nu _{\mathcal {A}}}=v\ \ \ \text{ on } \ \Gamma , \end{aligned}$$

or Dirichlet boundary control

$$\begin{aligned} \displaystyle u=v\ \ \ \text{ on } \ \Gamma _0\ \ \ {\textrm{and}}\ \ \ u=0\ \ \ \text{ on } \ \Gamma _1, \end{aligned}$$

where ${\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1=\emptyset$ and v is a suitable control function. The observability inequalities were established by the Riemannian geometry method under some geometric conditions. For more on time-dependent linear operators, evolution families, and evolution equations and their applications, we refer the reader to [28, 29] and the references therein.

Inspired by the above literature, in this paper we mainly study the system (1.1) with the assumption

$$\begin{aligned} {\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1\ne \emptyset . \end{aligned}$$

In fact, there are two main difficulties in our work. First, because the coefficients are related to the time variable, we cannot accurately estimate the positive and negative properties of the derivative of the energy functional, which makes it impossible to get the stability results of the system by traditional methods. Second, we lose the regularity of solution due to the existence of singularities. So for these two main difficulties, we need more skills to deal with system (1.1) to get the decay result that we want.

The paper is organized as follows. Section 2 presents the notations and some assumptions that we need to follow. By using the semigroup method, we give the well-posedness result in Sect. 3. In Sect. 4, we obtain the exponential decay estimate of the energy. Finally, a concluding remark is stated in Sect. 5.

2 Preliminaries

In this section, we present some materials and assumptions used in this paper. $\displaystyle L^2(\cdot )$ and $\displaystyle H^1(\cdot )$ denote the usual Sobolev spaces. $\displaystyle \Vert \cdot \Vert _2$ and $\displaystyle \Vert \cdot \Vert _{2,\Gamma _1}$ are the norms in the $\displaystyle L^2(\Omega )$ and $\displaystyle L^2(\Gamma _1)$, respectively. For simplicity, we write $\displaystyle \Vert \cdot \Vert$ and $\displaystyle \Vert \cdot \Vert _{\Gamma _1}$ instead of $\displaystyle \Vert \cdot \Vert _2$ and $\Vert \cdot \Vert _{2,\Gamma _1}$, respectively. Let C denote various positive constants which may be different at different occurrences.

Denote

$$\begin{aligned} H_{\Gamma _0}^1(\Omega ):=\left\{ u\in H^1(\Omega ):u|_{\Gamma _0}=0\right\} . \end{aligned}$$

Since the Poincaré inequality holds in $\displaystyle H_{\Gamma _0}^1(\Omega )$, then the apace $\displaystyle H_{\Gamma _0}^1(\Omega )$ can be endowed with the norm $\displaystyle \Vert \nabla \cdot \Vert$, which is equivalent to usual norm of $\displaystyle H^1(\Omega )$.

2.1 Riemannian Notations

We define

$$\begin{aligned} g(x)=(g_{ij}(x))=A^{-1}(x),\ \ \ x\in R^n, \end{aligned}$$

as a Riemannian metric on $R^n$ and consider the couple $(R^n,g)$ as a Riemannian manifold with the inner product and the norm

$$\begin{aligned} \langle X,Y\rangle _g=(A^{-1}(x)X,Y)=A^{-1}(x)X\cdot Y,\ \ \ |X|_g^2=\langle X,X\rangle _g,\ \ \ X,Y\in R_x^n, \end{aligned}$$

where $(\cdot ,\cdot )$ is the Euclidean product of $R^n$. For any $C^1$ function w, we define

$$\begin{aligned} \displaystyle \nabla _gw=A(x)\nabla w,\ \ \ |\nabla _gw|_g^2=\sum _{i,j=1}^na_{ij}(x)w_{x_i}w_{x_j},\ \ \ x\in R^n, \end{aligned}$$

where $\nabla _g$ is the gradient of the metric g. Denote by D the Levi-Civita connection in the Riemannian metric g and let H be a vector field on $R^n$, then for each $x\in R^n$, the covariant differential DH of H determines a bilinear form on $R^n\times R^n$:

$$\begin{aligned} DH(X,Y)=\langle D_YH,X\rangle _g,\ \ \ X,Y\in R_x^n, \end{aligned}$$

where $D_YH$ is the covariant derivative of the vector field H with respect to Y. Next we give the following lemma that provides some further relationships between the Riemannian metric g and the Euclidean metric.

Lemma 2.1

[17] Let $f\in C^2\left( {\overline{\Omega }}\right)$ and H be vector field. Then, with the references to the above notations, we have

• (i) $\displaystyle H(f)=\left\langle \nabla _gf,H\right\rangle _g=\nabla f\cdot H$,

• (ii) $\displaystyle \left\langle \nabla _gf,\nabla _g(H(f))\right\rangle _g=DH\left( \nabla _gf,\nabla _gf\right) +\frac{1}{2}{\textrm{div}}\left( |\nabla _gf|_g^2H\right) -\frac{1}{2}|\nabla _gf|_g^2{\textrm{div}}H$,

where ${\textrm{div}}H$ is the divergence of the vector field H in the Euclidean metric.

2.2 Assumptions

(H1) Assume that $\beta (t)\in W_{loc}^{1,\infty }(0,\infty ),\ \beta '(t)\in L^1(0,\infty )$ and

$$\begin{aligned} \beta (t)\ge \beta _0>0,\ \ \ t\ge 0, \end{aligned}$$

where $\beta _0$ is some positive constant.

(H2) [30] Let H be a vector field on Riemannian manifold $(R^n,g)$, there exists a continuous function $\sigma (x)$ such that

$$\begin{aligned} DH(X,X)=\sigma (x)|X|_g^2,\ \ \ X\in R_x^n,\ \ \ x\in {\overline{\Omega }}, \end{aligned}$$

and denote $\displaystyle \sigma _1=\min _{x\in {\overline{\Omega }}}\sigma (x)>0$ and $\displaystyle \sigma _2=\max _{x\in {\overline{\Omega }}}\sigma (x)$. Moreover, assuming that the vector field H satisfies

$$\begin{aligned} H\cdot \nu \le 0\ \ \ {\textrm{for}}\ x\in \Gamma _0, \end{aligned}$$

and

$$\begin{aligned} H\cdot \nu >0\ \ \ {\textrm{for}}\ x\in \Gamma _1. \end{aligned}$$

Remark 2.2

The vector field H in assumption (H2), which called the escape vector field and firstly introduced by [31] as a checkable assumption. The existence of the vector field H depends on the Riemannian curvature of the metric g. In [32], we know that if assumption (H2) holds, then GCC (Geometric Control Condition) holds. And for the constant coefficients case i.e. considering ${\mathcal {A}}(x,t)\!=-\!\Delta$, many papers always take $H\!=\!x\!-\!x_0$ where $x_0\!\in \!R^n$ is a fixed point and $x\!\in \!\Gamma$.

2.3 Main Results

Consider the phase space

$$\begin{aligned} {\mathcal {H}}:=H_{\Gamma _0}^1(\Omega )\times L^2(\Omega )\times H^1(\Gamma _1)\times L^2(\Gamma _1), \end{aligned}$$

endowed with the inner product

$$\begin{aligned}&\left\langle (w_1,w_2,w_3,w_4)^T,(v_1,v_2,v_3,v_4)^T\right\rangle _{{\mathcal {H}}}\nonumber \\&\quad =\int \nolimits _{\Omega }\left[ \beta (t)\nabla _g w_1\nabla v_1+w_2v_2\right] dx+\int \nolimits _{\Gamma _1}\left[ \beta (t)(\nabla _T)_g w_3(\nabla _T)v_3+w_4v_4\right] d\Gamma . \end{aligned}$$

(2.1)

where $(\nabla _T)_gw=A(x)|_{\Gamma _1}(\nabla _T)w$ for any $C^1$ function w. Taking $\displaystyle U(t)=(u,u_t,\gamma _1(u),\gamma _1(u_t))^T$ with the trace operator $\displaystyle \gamma _1(\cdot )=\cdot |_{\Gamma _1}$, the system (1.1) can be rewritten by

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{dU}{dt}={\mathbb {A}}(t)U,\ \ \ \ \ \ t>0,\\ \displaystyle U(0)=U_0=(u_0,u_1,\gamma _1(u_0),\gamma _1(u_1))^T,\\ \end{array}\right. \end{aligned}$$

(2.2)

where the time-dependent linear operators ${\mathbb {A}}(t)$ have the form

$$\begin{aligned} {\mathbb {A}}(t)\left( \begin{matrix}u\\ \varphi \\ v\\ \psi \\ \end{matrix}\right) =\left( \begin{matrix}\varphi \\ -{\mathcal {A}}(x,t)u-b(x)\varphi \\ \psi \\ \displaystyle -\frac{\partial v}{\partial \nu _{\mathcal {A}}}-{\mathcal {A}}_T(x,t)v-\psi \\ \end{matrix}\right) , \end{aligned}$$

with domain

$$\begin{aligned} D({\mathbb {A}}(t))= & {} D({\mathbb {A}}(0))=\left( H^2(\Omega )\cap H_{\Gamma _0}^1(\Omega )\right) \times H_{\Gamma _0}^1(\Omega )\\{} & {} \times \left( H^2(\Gamma _1)\cap H^1(\Gamma _1)\right) \times H^1(\Gamma _1),\ \ \ t\ge 0, \end{aligned}$$

which means D(A(t)) do not depend on t.

Now, we state the well-posedness result for the Cauchy problem (2.2), which ensures that the system (1.1) is globally well-posed.

Theorem 2.3

Suppose that $({{\textbf {H1}}})$ and $({{\textbf {H2}}})$ hold. Then for any $U_0\in {\mathcal {H}}$, the problem (2.2) admits a unique solution U(t) such that

$$\begin{aligned} U(t)\in C(R_+;{\mathcal {H}}). \end{aligned}$$

Further, assuming

$$\begin{aligned} \left( A(x)|_{\Gamma _1}H,\tau \right) \le 0,\ \ \ x\in \Sigma , \end{aligned}$$

(2.3)

where $\tau$ is the unit tangent vector pointing towards the exterior of $\Gamma _1$, from $\Gamma _1$ to $\Gamma _0$. In fact, for $A(x)=I$, this geometric assumption (2.3) is the same as in [4, 5] when taking the vector field $H=x-x_0$ where $x_0\in R^n$ is a fixed point and $x\in \Sigma$.

Define the associated energy of system (1.1) by

$$\begin{aligned} E(t):=\frac{1}{2}\left\{ \Vert u_t\Vert ^2+\beta (t)\int \nolimits _{\Omega }|\nabla _g u|_g^2dx+\Vert u_t\Vert _{\Gamma _1}^2+\beta (t)\int \nolimits _{\Gamma _1}|(\nabla _T)_g u|_g^2d\Gamma \right\} , \end{aligned}$$

(2.4)

according to the inner product of state space ${\mathcal {H}}$. Our main decay result can be given as follows

Theorem 2.4

Assume that (H1), (H2) and (2.3) hold and there exist positive constants $C_2$, $\alpha$ and m such that for all t sufficiently large, it holds

$$\begin{aligned} \int \nolimits _0^t e^{C_2s}|\beta '(s)|ds\le \alpha t^m. \end{aligned}$$

(2.5)

Then the energy decay exponentially, i.e.,

$$\begin{aligned} E(t)\le C\left( E(0)+\alpha t^m\right) e^{-C_2t}. \end{aligned}$$

Remark 2.5

For assumption (2.5), we give the following two examples for the function $\beta (s)$.

Example $({\textrm{i}})$. Let $\displaystyle \beta (s)=ae^{-bs}+\beta _0$ with $a>0$ and $b\ge C_2>0$. It is obviously that taking $\beta$ to satisfy $({\textbf {H1}})$. By direct calculation, we have

$$\begin{aligned} |\beta '(s)|=abe^{-bs}, \end{aligned}$$

and

$$\begin{aligned} \int \nolimits _0^t e^{C_2s}|\beta '(s)|ds\le C\int \nolimits _0^t e^{-(b-C_2)s}ds. \end{aligned}$$

Therefore, there exist positive constants $\alpha$ and m such that for all t sufficiently large, (2.5) holds.

Example $({\textrm{ii}})$. Let $\displaystyle \beta (s)=se^{-as}+\beta _0$ with $a\ge C_2>0$. It is obviously that taking $\beta$ to satisfy $({\textbf {H1}})$. By direct calculation, we have

$$\begin{aligned} \beta '(s)=(1-as)e^{-as}, \end{aligned}$$

and

$$\begin{aligned} \int \nolimits _0^t e^{C_2s}|\beta '(s)|ds\le C\int \nolimits _0^t(1+|s|)e^{-(a-C_2)s}ds. \end{aligned}$$

Therefore, there exist positive constants $\alpha$ and m such that for all t sufficiently large, (2.5) holds.

3 Well-Posedness

In this section, we study the existence and uniqueness of the solution to system (1.1), that is, using the semigroup method to prove Theorem 2.3.

Proof of Theorem 2.3

This proof is divided into four main steps.

Step 1. The first step is to prove that the linear operators ${\mathbb {A}}(t)$ are dissipative. Indeed, let $U=(v_1,v_2,v_3,v_4)^T\in D({\mathbb {A}}(0))$, using (2.1) and the fact of $v_1=v_3,\ v_2=v_4\ {\textrm{on}}\ \Gamma _1$, we have

$$\begin{aligned} \begin{aligned} \langle {\mathbb {A}}(t)U,U\rangle _{{\mathcal {H}}}=\,&\int \nolimits _{\Omega }\left[ \beta (t)\nabla _g v_2\nabla v_1-({\mathcal {A}}(x,t)v_1+b(x)v_2)v_2\right] dx\\&+\int \nolimits _{\Gamma _1}\left[ \beta (t)(\nabla _T)_g v_4(\nabla _T)v_3-\left( \frac{\partial v_3}{\partial \nu _{\mathcal {A}}}+{\mathcal {A}}_T(x,t)v_3+v_4\right) v_4\right] d\Gamma \\ =\,&-b_0\int \nolimits _\omega |v_2|^2dx-\int \nolimits _{\Gamma _1}|v_4|^2d\Gamma \\ \le \,&0, \end{aligned} \end{aligned}$$

which yields the operators ${\mathbb {A}}(t)$ are dissipative.

Step 2. In this step, we prove the surjection of the operators $\displaystyle I-{\mathbb {A}}(t)$, where I stands for the identity operator. In fact, set $\displaystyle F=(f_1,f_2,f_3,f_4)^T\in {\mathcal {H}}$, we will prove that there exists $\displaystyle U=(v_1,v_2,v_3,v_4)^T$ such that

$$\begin{aligned} \left( I-{\mathbb {A}}(t)\right) U=F, \end{aligned}$$

which is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle v_1-v_2=f_1 &{} \text{ in } \ H_{\Gamma _0}^1(\Omega ), \\ \displaystyle v_2+{\mathcal {A}}(x,t)v_1+b(x)v_2=f_2 &{} \text{ in } \ L^2(\Omega ), \\ \displaystyle v_3-v_4=f_3 &{} \text{ in } \ H^1(\Gamma _1),\\ \displaystyle v_4+\frac{\partial v_3}{\partial \nu _{\mathcal {A}}}+{\mathcal {A}}_T(x,t)v_3+v_4=f_4 &{} \text{ in } \ L^2(\Gamma _1). \end{array}\right. } \end{aligned}$$

(3.1)

From the first and third equations of (3.1), we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle v_2=v_1-f_1, \\ \displaystyle v_4=v_3-f_3.\\ \end{array}\right. } \end{aligned}$$

(3.2)

Substituting the equations of (3.2) into the second and the forth equations of (3.1), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle v_1+{\mathcal {A}}(x,t)v_1+b(x)v_1=f_1+f_2+b(x)f_1, \\ \displaystyle 2v_3+\frac{\partial v_3}{\partial \nu _{\mathcal {A}}}+{\mathcal {A}}_T(x,t)v_3=2f_3+f_4. \end{array}\right. } \end{aligned}$$

(3.3)

This is an elliptic system of two equations. For $(\varphi _1,\psi _1),\ (\varphi _2,\psi _2)\in H_{\Gamma _0}^1(\Omega )\times H^1(\Gamma _1)$, we introduce the following bilinear form

$$\begin{aligned} \begin{aligned} B((\varphi _1,\psi _1),(\varphi _2,\psi _2))=\,&\int \nolimits _{\Omega }\left[ \varphi _1\varphi _2+\beta (t)\nabla _g\varphi _1\nabla \varphi _2+b(x)\varphi _1\varphi _2\right] dx\\&+\int \nolimits _{\Gamma _1}\left[ 2\psi _1\psi _2+\beta (t)(\nabla _T)_g\psi _1(\nabla _T)\psi _2\right] d\Gamma . \end{aligned} \end{aligned}$$

It is easy to show that $B((\varphi _1,\psi _1),(\varphi _2,\psi _2))$ is a bounded bilinear form and

$$\begin{aligned} B((\varphi _1,\psi _1),(\varphi _1,\psi _1))= & {} \int \nolimits _{\Omega }\left[ |\varphi _1|^2+\beta (t)|\nabla _g\varphi _1|_g^2+b(x)|\varphi _1|^2\right] dx\\{} & {} +\int \nolimits _{\Gamma _1}\left[ 2|\psi _1|^2+\beta (t)|(\nabla _T)_g\psi _1|_g^2\right] d\Gamma , \end{aligned}$$

is coercive. Then by using the conditions of $v_1=v_3,\ \varphi =\psi \ {\textrm{on}}\ \Gamma _1$, we can find $(v_1,v_3)\in H_{\Gamma _0}^1(\Omega )\times H^1(\Gamma _1)$, such that for all $(\varphi ,\psi )\in H_{\Gamma _0}^1(\Omega )\times H^1(\Gamma _1)$, the following holds

$$\begin{aligned} B((v_1,v_3),(\varphi ,\psi ))=\int \nolimits _{\Omega }[f_1+f_2+b(x)f_1]\varphi dx+\int \nolimits _{\Gamma _1}(2f_3+f_4)\psi d\Gamma . \end{aligned}$$

Therefore, the system (3.3) admits a unique weak solution $(v_1,v_3)\in H_{\Gamma _0}^1(\Omega )\times H^1(\Gamma _1)$ by the well-known Lax-Milgram theorem. And we deduce from (3.2) that $\displaystyle v_2\in H_{\Gamma _0}^1(\Omega ) (\hookrightarrow L^2(\Omega ))$ and $\displaystyle v_4\in H^1(\Gamma _1) (\hookrightarrow L^2(\Gamma _1))$. This implies that $U\in {\mathcal {H}}$ which gives us the desired solution.

Step 3. Define a vector valued function $h:R_+\rightarrow {\mathcal {H}}$ with $h(t)={\mathbb {A}}(t)U$. We will prove in this step that h is differentiable and its Frechet derivative is the vector valued function

$$\begin{aligned} h'(t) =\left( \begin{matrix}0\\ -{\mathcal {A}}'(x,t)u\\ 0\\ \displaystyle -{\mathcal {A}}_T'(x,t)v\\ \end{matrix}\right) , \end{aligned}$$

where

$$\begin{aligned} {\mathcal {A}}'(x,t)u=-\beta '(t){\textrm{div}}(A(x)\nabla u), \end{aligned}$$

and

$$\begin{aligned} {\mathcal {A}}_T'(x,t)v=-\beta '(t){\textrm{div}}_T(A(x)|_{\Gamma _1}\nabla _Tv). \end{aligned}$$

Indeed, it is quite obvious that $h'(t)\in {\mathcal {H}}$ for $t\ge 0$. And for any $t, \tau \ge 0$ with $t\ne \tau$, we have

$$\begin{aligned} \frac{h(t)-h(\tau )}{t-\tau }=\frac{1}{t-\tau }\left( \begin{matrix}0\\ -[{\mathcal {A}}(x,t)-{\mathcal {A}}(x,\tau )]u\\ 0\\ \displaystyle -[{\mathcal {A}}_T(x,t)-{\mathcal {A}}_T(x,\tau )]v\\ \end{matrix}\right) . \end{aligned}$$

Then

$$\begin{aligned} \frac{h(t)-h(\tau )}{t-\tau }-h'(t)=\left( \begin{matrix}0\\ \displaystyle -\left[ \frac{{\mathcal {A}}(x,t)-{\mathcal {A}}(x,\tau )}{t-\tau }-{\mathcal {A}}'(x,t)\right] u\\ 0\\ \displaystyle -\left[ \frac{{\mathcal {A}}_T(x,t)-{\mathcal {A}}_T(x,\tau )}{t-\tau }-{\mathcal {A}}_T'(x,t)\right] v\\ \end{matrix}\right) , \end{aligned}$$

which yields

$$\begin{aligned} \left\| \frac{h(t)-h(\tau )}{t-\tau }-h'(t)\right\| _{{\mathcal {H}}}&=\ \left\| -\left[ \frac{{\mathcal {A}}(x,t)-{\mathcal {A}}(x,\tau )}{t-\tau }-{\mathcal {A}}'(x,t)\right] u\right\| \\&\quad +\left\| -\left[ \frac{{\mathcal {A}}_T(x,t)-{\mathcal {A}}_T(x,\tau )}{t-\tau }-{\mathcal {A}}_T'(x,t)\right] v\right\| _{\Gamma _1}\\&=\ \left\| \left( \frac{\beta (t)-\beta (\tau )}{t-\tau }-\beta '(t)\right) {\textrm{div}}\nabla _gu\right\| \\&\quad +\left\| \left( \frac{\beta (t)-\beta (\tau )}{t-\tau }-\beta '(t)\right) {\textrm{div}}_T(\nabla _T)_gv\right\| _{\Gamma _1}.\\ \end{aligned}$$

We have

$$\begin{aligned} \lim _{t\rightarrow \tau }\left\| \frac{h(t)-h(\tau )}{t-\tau }-h'(t)\right\| _{{\mathcal {H}}}=0. \end{aligned}$$

Hence according to the chapters 5 of Pazy’s book [33], we define the solution operators of the initial value problem

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{d{\widetilde{U}}}{dt}={\mathbb {A}}(t){\widetilde{U}}\ \ \ \ \ \ 0\le s<t\le T,\\ \displaystyle {\widetilde{U}}(s)={\widetilde{U}}_1,\\ \end{array}\right. \end{aligned}$$

(3.4)

by

$$\begin{aligned} W(t,s){\widetilde{U}}_1={\widetilde{U}}(t),\ \ \ 0\le s<t\le T, \end{aligned}$$

where ${\widetilde{U}}(t)$ is the solution of (3.4) and W(t, s) is a two parameter family of operators. Then, the evolution equation (2.2) has a unique mild solution

$$\begin{aligned} U(t)=W(t,0)U_0,\ \ \ \ t\in [0,T_{\textrm{max}}). \end{aligned}$$

Step 4. Let us show that $T_{\textrm{max}}=\infty$. From the definition of energy (2.4), we have

$$\begin{aligned} E'(t)=\frac{1}{2}\beta '(t)\left\{ \int \nolimits _{\Omega }|\nabla _g u|_g^2dx+\int \nolimits _{\Gamma _1}|(\nabla _T)_g u|_g^2d\Gamma \right\} -b_0\int \nolimits _{\omega }u_t^2dx-\int \nolimits _{\Gamma _1}u_t^2d\Gamma , \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} |E'(t)|&\le \ \frac{|\beta '(t)|}{2}\left\{ \int \nolimits _{\Omega }|\nabla _g u|_g^2dx+\int \nolimits _{\Gamma _1}|(\nabla _T)_g u|_g^2d\Gamma \right\} \\&\le \ \frac{|\beta '(t)|\beta (t)}{2\beta _0}\left\{ \int \nolimits _{\Omega }|\nabla _g u|_g^2dx+\int \nolimits _{\Gamma _1}|(\nabla _T)_g u|_g^2d\Gamma \right\} \\&\le \ \frac{|\beta '(t)|}{\beta _0}E(t). \end{aligned} \end{aligned}$$

The above inequality gives

$$\begin{aligned} -\frac{|\beta '(t)|}{\beta _0}E(t)\le E'(t)\le \frac{|\beta '(t)|}{\beta _0}E(t). \end{aligned}$$

(3.5)

Let

$$\begin{aligned} \beta _1=\int \nolimits _0^\infty \frac{|\beta '(s)|}{\beta _0}ds, \end{aligned}$$

we have

$$\begin{aligned} e^{-\beta _1}E(0)\le E(t)\le e^{\beta _1}E(0),\ \ \ t\in [0,T_{\textrm{max}}). \end{aligned}$$

(3.6)

Then using (2.1), (2.4) and (3.6), we have

$$\begin{aligned} \begin{aligned} \Vert U\Vert _{{\mathcal {H}}}^2=2E(t)\le 2e^{\beta _1}E(0),\ \ \ t\in [0,T_{\textrm{max}}), \end{aligned} \end{aligned}$$

where $\displaystyle U=(u,u_t,\gamma _1(u),\gamma _1(u_t))^T\in {\mathcal {H}}$. Therefore, the local solution cannot blow-up in finite time and it follows that $T_{\textrm{max}}=\infty$. $\square$

Remark 3.1

It is worth noting that in this paper we assumes that ${\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1\ne \emptyset$, so we cannot use the elliptic regularity argument to get $u\in H^2(\Omega )$ and $\gamma _1(u)\in H^2(\Gamma _1)$ from

$$\begin{aligned} {\mathcal {A}}(x,t)u\in L^2(\Omega )\ \ \ {\textrm{and}}\ \ \ {\mathcal {A}}_T(x,t)\gamma _1(u)\in L^2(\Gamma _1). \end{aligned}$$

Then, for the more regular initial data $U_0\in D({\mathbb {A}}(0))$, we do not have a more regular solution $U\in C(R_+;D({\mathbb {A}}(0)))\cap C^1(R_+;{\mathcal {H}})$.

4 Decay Result

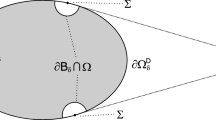
Because of the existence of singularities, we need to avoid them in the following work. As in [6], let $\delta >0$ be a small and fixed constant and consider

$$\begin{aligned} B_\delta =\bigcup _{x\in \Sigma }B(x,\delta ), \end{aligned}$$

where $B(x,\delta )=\{y\in \Omega :|x-y|<\delta \}$. Denote

$$\begin{aligned} \Omega _\delta =\Omega \setminus B_\delta . \end{aligned}$$

Fig. 2

The new domain $\Omega _\delta$ for $n=2$

Next, we will study the stability result of the corresponding system in $\Omega _\delta$ (see Fig. 2), whose boundary is defined as

$$\begin{aligned} \partial \Omega _\delta ={\widetilde{\Gamma }}_0\cup {\widetilde{\Gamma }}_1\cup \Gamma _\delta , \end{aligned}$$

where

$$\begin{aligned} {\widetilde{\Gamma }}_0=\partial \Omega _\delta \cap \Gamma _0,\ \ \ {\widetilde{\Gamma }}_1=\partial \Omega _\delta \cap \Gamma _1, \end{aligned}$$

and

$$\begin{aligned} \Gamma _\delta =\partial B_\delta \cap \Omega . \end{aligned}$$

Then the system (1.1) is transformed into the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle u_{tt}+{\mathcal {A}}(x,t)u+b(x)u_t=0 &{} \text{ in } \ \Omega _\delta \times R^+, \\ \displaystyle u=0 &{} \text{ on } \ {\widetilde{\Gamma }}_0\times R^+, \\ \displaystyle u_{tt}+\frac{\partial u}{\partial \nu _{\mathcal {A}}}+{\mathcal {A}}_T(x,t)u+u_t=0 &{} \text{ on } \ {\widetilde{\Gamma }}_1\times R^+. \end{array}\right. } \end{aligned}$$

(4.1)

Define the energy associated with the problem (4.1) in $\Omega _\delta$ by

$$\begin{aligned}{} & {} E_\delta (t):=\frac{1}{2}\left\{ \int \nolimits _{\Omega _\delta }|u_t|^2dx \right. \nonumber \\{} & {} \quad \left. +\beta (t)\int \nolimits _{\Omega _\delta }|\nabla _g u|_g^2dx+\int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2d\Gamma +\beta (t)\int \nolimits _{{\widetilde{\Gamma }}_1}|(\nabla _T)_g u|_g^2d\Gamma \right\} , \end{aligned}$$

(4.2)

then by a simple calculation, we have

$$\begin{aligned} E'_\delta (t)= & {} \frac{1}{2}\beta '(t)\left\{ \int \nolimits _{\Omega _\delta }|\nabla _g u|_g^2dx+\int \nolimits _{{\widetilde{\Gamma }}_1}|(\nabla _T)_g u|_g^2d\Gamma \right\} -b_0\int \nolimits _{\omega }u_t^2dx\nonumber \\{} & {} -\int \nolimits _{{\widetilde{\Gamma }}_1}u_t^2d\Gamma +\int \nolimits _{\Gamma _\delta }\frac{\partial u}{\partial \nu _{\mathcal {A}}}u_td\Gamma . \end{aligned}$$

(4.3)

Lemma 4.1

The functional

$$\begin{aligned} \Phi _\delta (t):=\int \nolimits _{\Omega _\delta }u_tudx+\int \nolimits _{{\widetilde{\Gamma }}_1}u_tud\Gamma \end{aligned}$$

(4.4)

satisfies

$$\begin{aligned} \begin{aligned}&\Phi '_\delta (t)\le \ -\left( 1-\frac{b_0C_p\varepsilon _1}{\lambda \beta _0}-\frac{C_t\varepsilon _2}{\lambda \beta _0}\right) \int \nolimits _{\Omega _\delta }\beta (t)|\nabla _gu|_g^2dx-\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)|(\nabla _T)_gu|_g^2d\Gamma \\&\quad +\left( 1+\frac{b_0}{4\varepsilon _1}\right) \int \nolimits _{\Omega _\delta }|u_t|^2dx+\left( 1+\frac{1}{4\varepsilon _2}\right) \int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2d\Gamma +\int \nolimits _{\Gamma _\delta }\frac{\partial u}{\partial \nu _{\mathcal {A}}}ud\Gamma , \end{aligned} \end{aligned}$$

(4.5)

where $\varepsilon _1$ and $\varepsilon _2$ are some positive constants, $C_t$ is the smallest possible positive constant produced by the trace theorem and Poincar$\acute{e}$ inequality and $C_p>0$ is the Poincar$\acute{e}$ optimal embedding constant.

Proof

Taking the derivative of (4.4) with respect to the variable t and using (4.1) and Green formula yield

$$\begin{aligned} \begin{aligned} \Phi '_\delta (t)&=\ \int \nolimits _{\Omega _\delta }|u_t|^2dx+\int \nolimits _{\Omega _\delta }u_{tt}udx+\int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2d\Gamma +\int \nolimits _{{\widetilde{\Gamma }}_1}u_{tt}ud\Gamma \\&=\ \int \nolimits _{\Omega _\delta }|u_t|^2dx+\int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2d\Gamma \\&\quad -\int \nolimits _{\Omega _\delta }\left[ {\mathcal {A}}(x,t)u+b(x)u_t\right] udx-\int \nolimits _{{\widetilde{\Gamma }}_1}\left[ \frac{\partial u}{\partial \nu _{\mathcal {A}}}+{\mathcal {A}}_T(x,t)u+u_t\right] ud\Gamma \\&=\ \int \nolimits _{\Omega _\delta }|u_t|^2dx+\int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2d\Gamma -\int \nolimits _{\Omega _\delta }\beta (t)|\nabla _gu|_g^2dx-\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)|(\nabla _T)_gu|_g^2d\Gamma \\&\quad -\int \nolimits _{\Omega _\delta }b(x)u_tudx-\int \nolimits _{{\widetilde{\Gamma }}_1}u_tud\Gamma +\int \nolimits _{\Gamma _\delta }\frac{\partial u}{\partial \nu _{\mathcal {A}}}ud\Gamma . \end{aligned} \end{aligned}$$

(4.6)

Making use of Young’s inequality, Poincaré inequality, the trace theorem and (H1), we have

$$\begin{aligned} \begin{aligned} \left| \int \nolimits _{\Omega _\delta }b(x)u_tudx\right| \le \ {}&b_0\int \nolimits _{\Omega _\delta }|u_tu|dx\\ \le \ {}&\frac{b_0}{4\varepsilon _1}\int \nolimits _{\Omega _\delta }|u_t|^2dx+b_0\varepsilon _1\int \nolimits _{\Omega _\delta }|u|^2dx\\ \le \ {}&\frac{b_0}{4\varepsilon _1}\int \nolimits _{\Omega _\delta }|u_t|^2dx+\frac{b_0C_p\varepsilon _1}{\lambda \beta _0}\int \nolimits _{\Omega _\delta }\beta (t)|\nabla _gu|_g^2dx, \end{aligned} \end{aligned}$$

(4.7)

and

$$\begin{aligned} \begin{aligned} \left| \int \nolimits _{{\widetilde{\Gamma }}_1}u_tud\Gamma \right| \le \ {}&\int \nolimits _{{\widetilde{\Gamma }}_1}|u_tu|d\Gamma \\ \le \,&\frac{1}{4\varepsilon _2}\int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2d\Gamma +\frac{C_t\varepsilon _2}{\lambda \beta _0}\int \nolimits _{\Omega _\delta }\beta (t)|\nabla _gu|_g^2dx. \end{aligned} \end{aligned}$$

(4.8)

Thus, taking (4.7) and (4.8) into (4.6), (4.5) is obtained. $\square$

Lemma 4.2

Suppose that H is the vector field defined in assumption $({\textbf {H2}})$, and define $H_T =H-(H\cdot \nu )\nu$. Then, the functional

$$\begin{aligned} \Psi _\delta (t):=2\int \nolimits _{\Omega _\delta }u_tH(u)dx+2\int \nolimits _{{\widetilde{\Gamma }}_1}u_tH_T(u)d\Gamma \end{aligned}$$

(4.9)

satisfies

$$\begin{aligned} \begin{aligned} \Psi '_\delta (t)\le \,&-(n\sigma _1-b_0\epsilon _1)\int \nolimits _{\Omega _\delta }|u_t|^2dx-(c_\sigma -\epsilon _2)\int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2d\Gamma \\&+\left( n\sigma _2-2\sigma _1+\frac{\max _{x\in {\bar{\Omega }}_\delta }|H|^2b_0}{2\lambda \beta _0\epsilon _1}\right) \int \nolimits _{\Omega _\delta }\beta (t)|\nabla _gu|_g^2dx\\&+\left( \frac{\Vert \nabla _TA\Vert _{L^\infty \left( {\widetilde{\Gamma }}_1\right) }\max _{x\in \bar{{\widetilde{\Gamma }}}_1}|H_T|}{\lambda }+\frac{\max _{x\in \bar{{\widetilde{\Gamma }}}_1}|H_T|^2}{2\lambda \beta _0\epsilon _2}-c_\sigma \right) \int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)|(\nabla _T)_gu|_g^2d\Gamma \\&+\int \nolimits _{{\widetilde{\Gamma }}_1}\left[ |u_t|^2+\frac{\beta (t)}{|\nu _{{\mathcal {A}}}|_g^2}\left| \frac{\partial u}{\partial \nu _{{\mathcal {A}}}}\right| ^2\right] H\cdot \nu d\Gamma \\&+\int \nolimits _{\Gamma _\delta }[|u_t|^2-\beta (t)|\nabla _gu|_g^2]H\cdot \nu d\Gamma +2\int \nolimits _{\Gamma _\delta }\frac{\partial u}{\partial \nu _{\mathcal {A}}}H(u)d\Gamma , \end{aligned} \end{aligned}$$

(4.10)

where $\epsilon _1$, $\epsilon _2$ and $c_\sigma$ are some positive constants.

Proof

Taking the derivative of (4.9) with respect to the variable t and using (4.1) and Green formula yield

$$\begin{aligned} \Psi '_\delta (t)=\,&2\int \nolimits _{\Omega _\delta }u_tH(u_t)dx+2\int \nolimits _{\Omega _\delta }u_{tt}H(u)dx\nonumber \\&+2\int \nolimits _{{\widetilde{\Gamma }}_1}u_tH_T(u_t)d\Gamma +2\int \nolimits _{{\widetilde{\Gamma }}_1}u_{tt}H_T(u)d\Gamma \nonumber \\ =\,&\int \nolimits _{\Omega _\delta }H(u_t^2)dx-2\int \nolimits _{\Omega _\delta }\left[ {\mathcal {A}}(x,t)u+b(x)u_t\right] H(u)dx\nonumber \\&+\int \nolimits _{{\widetilde{\Gamma }}_1}H_T(u_t^2)d\Gamma -2\int \nolimits _{{\widetilde{\Gamma }}_1}\left[ \frac{\partial u}{\partial \nu _{\mathcal {A}}}+{\mathcal {A}}_T(x,t)u+u_t\right] H_T(u)d\Gamma \nonumber \\ =\,&\int \nolimits _{\Omega _\delta }H(u_t^2)dx-2\int \nolimits _{\Omega _\delta }\beta (t)\nabla _gu\nabla (H(u))dx+2\int \nolimits _{\partial \Omega _\delta }\frac{\partial u}{\partial \nu _{\mathcal {A}}}H(u)d\Gamma \\&-2\int \nolimits _{\Omega _\delta }b(x)u_tH(u)dx+\int \nolimits _{{\widetilde{\Gamma }}_1}H_T(u_t^2)d\Gamma -2\int \nolimits _{{\widetilde{\Gamma }}_1}\frac{\partial u}{\partial \nu _{\mathcal {A}}}H_T(u)d\Gamma \nonumber \\&-2\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)(\nabla _T)_gu\nabla _T(H_T(u))d\Gamma -2\int \nolimits _{{\widetilde{\Gamma }}_1}u_tH_T(u)d\Gamma .\nonumber \end{aligned}$$

(4.11)

We begin to deal with the terms on the right of (4.11). Since the assumption (H2), we have

$$\begin{aligned} n\sigma _1\le {\textrm{div}}H\le n\sigma _2, \end{aligned}$$

then there are positive constants $c_\sigma$ and $C_\sigma$ such that

$$\begin{aligned} c_\sigma \le {\textrm{div}}_TH_T\le C_\sigma . \end{aligned}$$

Using the divergence theorem, (H2) and the fact of $H_T\cdot \nu =0$, we have

$$\begin{aligned}&\int \nolimits _{\Omega _\delta }H(u_t^2)dx+\int \nolimits _{{\widetilde{\Gamma }}_1}H_T(u_t^2)d\Gamma \nonumber \\&\quad =\ \int \nolimits _{\Omega _\delta }{\textrm{div}}(u_t^2H)dx-\int \nolimits _{\Omega _\delta } |u_t|^2{\textrm{div}}Hdx-\int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2{\textrm{div}}_T H_Td\Gamma \nonumber \\&\quad =\ \int \nolimits _{\partial \Omega _\delta }|u_t|^2H\cdot \nu d\Gamma -\int \nolimits _{\Omega _\delta } |u_t|^2{\textrm{div}}Hdx-\int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2{\textrm{div}}_T H_Td\Gamma \nonumber \\&\quad \le \ \int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2H\cdot \nu d\Gamma +\int \nolimits _{\Gamma _\delta }|u_t|^2H\cdot \nu d\Gamma \nonumber \\&\quad \quad -n\sigma _1\int \nolimits _{\Omega _\delta } |u_t|^2dx-c_\sigma \int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2d\Gamma . \end{aligned}$$

(4.12)

Using Lemma 2.1 and (H2), we get

$$\begin{aligned} \begin{aligned}&-2\int \nolimits _{\Omega _\delta }\beta (t)\nabla _gu\nabla (H(u))dx-2\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)(\nabla _T)_gu\nabla _T(H_T(u))d\Gamma \\&\quad =\ -2\int \nolimits _{\Omega _\delta }\beta (t)\langle \nabla _gu,\nabla _g(H(u))\rangle _gdx\\&\quad \quad -\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)A(x)|_{\Gamma _1}\nabla _T\left( |\nabla _Tu|^2\right) \cdot H_Td\Gamma -2\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)|(\nabla _T)_gu|_g^2{\textrm{div}}_T H_Td\Gamma \\&\quad =\ -2\int \nolimits _{\Omega _\delta }\beta (t)DH(\nabla _gu,\nabla _gu)dx-\int \nolimits _{\partial \Omega _\delta }\beta (t)|\nabla _gu|_g^2H\cdot \nu d\Gamma \\&\quad \quad +\int \nolimits _{\Omega _\delta }\beta (t)|\nabla _gu|_g^2{\textrm{div}}Hdx\\&\quad \quad +\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)\left( \nabla _TA(x)|_{\Gamma _1}\right) |\nabla _Tu|^2\cdot H_Td\Gamma -\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)|(\nabla _T)_gu|_g^2{\textrm{div}}_TH_Td\Gamma \\&\quad \le \ \left( n\sigma _2-2\sigma _1\right) \int \nolimits _{\Omega _\delta }\beta (t)|\nabla _gu|_g^2dx-\int \nolimits _{\partial \Omega _\delta }\beta (t)|\nabla _gu|_g^2H\cdot \nu d\Gamma \\&\quad \quad +\left( \frac{\Vert \nabla _TA(x)|_{\Gamma _1}\Vert _{L^\infty \left( {\widetilde{\Gamma }}_1\right) }\max _{x\in \bar{{\widetilde{\Gamma }}}_1}|H_T|}{\lambda }-c_\sigma \right) \int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)|(\nabla _T)_gu|_g^2d\Gamma . \end{aligned} \end{aligned}$$

(4.13)

And using Young’s inequality, we have

$$\begin{aligned} \begin{aligned} -2\int \nolimits _{\Omega _\delta }b(x)u_tH(u)dx\le \,&2b_0\int \nolimits _{\Omega _\delta }|u_tH(u)|dx\\ \le \,&b_0\epsilon _1\int \nolimits _{\Omega _\delta }|u_t|^2dx+\frac{\max _{x\in {\bar{\Omega }}_\delta }|H|^2b_0}{2\lambda \beta _0\epsilon _1}\int \nolimits _{\Omega _\delta }\beta (t)|\nabla _gu|_g^2dx, \end{aligned} \end{aligned}$$

(4.14)

and

$$\begin{aligned} \begin{aligned} -2\int \nolimits _{{\widetilde{\Gamma }}_1}u_tH_T(u)dx \le \epsilon _2\int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2dx+\frac{\max _{x\in \bar{{\widetilde{\Gamma }}}_1}|H_T|^2}{2\lambda \beta _0\epsilon _2}\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)|(\nabla _T)_gu|_g^2d\Gamma , \end{aligned} \end{aligned}$$

(4.15)

where $\epsilon _1>0$ and $\epsilon _2>0$ are some constants. Substituting (4.12)–(4.15) into (4.11), we obtain

$$\begin{aligned} \Psi '_\delta (t)\le \,&-(n\sigma _1-b_0\epsilon _1)\int \nolimits _{\Omega _\delta }|u_t|^2dx-(c_\sigma -\epsilon _2)\int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2d\Gamma \nonumber \\&+\left( n\sigma _2-2\sigma _1+\frac{\max _{x\in {\bar{\Omega }}_\delta }|H|^2b_0}{2\lambda \beta _0\epsilon _1}\right) \int \nolimits _{\Omega _\delta }\beta (t)|\nabla _gu|_g^2dx\nonumber \\&+\Bigg (\frac{\Vert \nabla _TA(x)|_{\Gamma _1}\Vert _{L^\infty \left( {\widetilde{\Gamma }}_1\right) }\max _{x\in \bar{{\widetilde{\Gamma }}}_1}|H_T|}{\lambda }\nonumber \\&+\frac{\max _{x\in \bar{{\widetilde{\Gamma }}}_1}|H_T|^2}{2\lambda \beta _0\epsilon _2} -c_\sigma \Bigg )\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)|(\nabla _T)_gu|_g^2d\Gamma \nonumber \\&+\int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2H\cdot \nu d\Gamma -2\int \nolimits _{{\widetilde{\Gamma }}_1}\frac{\partial u}{\partial \nu _{\mathcal {A}}}H_T(u)d\Gamma +\int \nolimits _{\Gamma _\delta }|u_t|^2H\cdot \nu d\Gamma \nonumber \\&-\int \nolimits _{\partial \Omega _\delta }\beta (t)|\nabla _gu|_g^2H\cdot \nu d\Gamma +2\int \nolimits _{\partial \Omega _\delta }\frac{\partial u}{\partial \nu _{\mathcal {A}}}H(u)d\Gamma . \end{aligned}$$

(4.16)

Now, we are going to estimate the integrals over $\partial \Omega _\delta$. On ${\widetilde{\Gamma }}_0\cup {\widetilde{\Gamma }}_1$, we have

$$\begin{aligned} |\nabla _gu|_g^2=\frac{1}{|\nu _{{\mathcal {A}}}|_g^2}\left| \frac{\partial u}{\partial \nu _{{\mathcal {A}}}}\right| _g^2+|(\nabla _T)_gu|_g^2, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial u}{\partial \nu _{{\mathcal {A}}}}H(u)=\frac{\partial u}{\partial \nu _{{\mathcal {A}}}}H_T(u)+\frac{\beta (t)}{|\nu _{{\mathcal {A}}}|_g^2}\left| \frac{\partial u}{\partial \nu _{{\mathcal {A}}}}\right| _g^2H\cdot \nu . \end{aligned}$$

Since $u=u_t=0$ on ${\widetilde{\Gamma }}_0$, it hold that

$$\begin{aligned} \frac{\partial u}{\partial \nu _{{\mathcal {A}}}}H(u)=\beta (t)|\nabla _gu|_g^2H\cdot \nu ,\ \ \ x\in {\widetilde{\Gamma }}_0, \end{aligned}$$

then

$$\begin{aligned} \begin{aligned}&-\int \nolimits _{\partial \Omega _\delta }\beta (t)|\nabla _gu|_g^2H\cdot \nu d\Gamma +2\int \nolimits _{\partial \Omega _\delta }\frac{\partial u}{\partial \nu _{\mathcal {A}}}H(u)d\Gamma \\&\quad =\ \int \nolimits _{{\widetilde{\Gamma }}_0}\beta (t)|\nabla _gu|_g^2H\cdot \nu d\Gamma \\&\quad \quad +\int \nolimits _{{\widetilde{\Gamma }}_1}\left[ 2\frac{\partial u}{\partial \nu _{\mathcal {A}}}H_T(u)-\beta (t)|(\nabla _T)_gu|_g^2H\cdot \nu +\frac{\beta (t)}{|\nu _{{\mathcal {A}}}|_g^2}\left| \frac{\partial u}{\partial \nu _{{\mathcal {A}}}}\right| ^2H\cdot \nu \right] d\Gamma \\&\quad \quad -\int \nolimits _{\Gamma _\delta }\beta (t)|\nabla _gu|_g^2H\cdot \nu d\Gamma +2\int \nolimits _{\Gamma _\delta }\frac{\partial u}{\partial \nu _{\mathcal {A}}}H(u)d\Gamma . \end{aligned} \end{aligned}$$

(4.17)

Combining (4.16) and (4.17), we infer that

$$\begin{aligned} \Psi '_\delta (t) \le \,&-(n\sigma _1-b_0\epsilon _1)\int \nolimits _{\Omega _\delta }|u_t|^2dx -(c_\sigma -\epsilon _2)\int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2d\Gamma \nonumber \\&+\left( n\sigma _2-2\sigma _1 +\frac{\max _{x\in {\bar{\Omega }}_\delta }|H|^2b_0}{2\lambda \beta _0\epsilon _1}\right) \int \nolimits _{\Omega _\delta }\beta (t)|\nabla _gu|_g^2dx\nonumber \\&+\Bigg (\frac{\Vert \nabla _TA(x)|_{\Gamma _1}\Vert _{L^\infty \left( {\widetilde{\Gamma }}_1\right) }\max _{x\in \bar{{\widetilde{\Gamma }}}_1}|H_T|}{\lambda }\nonumber \\&+\frac{\max _{x\in \bar{{\widetilde{\Gamma }}}_1}|H_T|^2}{2\lambda \beta _0\epsilon _2} -c_\sigma \Bigg )\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)|(\nabla _T)_gu|_g^2d\Gamma +\int \nolimits _{{\widetilde{\Gamma }}_0}\beta (t)|\nabla _gu|_g^2H\cdot \nu d\Gamma \nonumber \\&+\int \nolimits _{{\widetilde{\Gamma }}_1}\left[ |u_t|^2-\beta (t)|(\nabla _T)_gu|_g^2+\frac{\beta (t)}{|\nu _{{\mathcal {A}}}|_g^2}\left| \frac{\partial u}{\partial \nu _{{\mathcal {A}}}}\right| ^2\right] H\cdot \nu d\Gamma \nonumber \\&+\int \nolimits _{\Gamma _\delta }\left[ |u_t|^2-\beta (t)|\nabla _gu|_g^2\right] H\cdot \nu d\Gamma +2\int \nolimits _{\Gamma _\delta }\frac{\partial u}{\partial \nu _{\mathcal {A}}}H(u)d\Gamma . \end{aligned}$$

(4.18)

Therefore, using (H2), we obtain (4.10). $\square$

Next we define the perturbed energy associated with $\Omega _\delta$ by

$$\begin{aligned} E_{\delta ,\theta }(t):=NE_\delta (t)+\Phi _\delta (t)+\theta \Psi _\delta (t), \end{aligned}$$

(4.19)

where N and $\theta$ are some positive constants.

Lemma 4.3

If

$$\begin{aligned} E_\delta \rightarrow E,\ \ \ \Phi _\delta \rightarrow \Phi \ \ \ {\textrm{and}}\ \ \ \Psi _\delta \rightarrow \Psi ,\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0, \end{aligned}$$

then

$$\begin{aligned} E_{\delta ,\theta }\rightarrow E_\theta ,\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0, \end{aligned}$$

where

$$\begin{aligned} \Phi (t):= & {} \int \nolimits _{\Omega }u_tudx+\int \nolimits _{\Gamma _1}u_tud\Gamma ,\\ \Psi (t):= & {} 2\int \nolimits _{\Omega }u_tH(u)dx+2\int \nolimits _{\Gamma _1}u_tH_T(u)d\Gamma , \end{aligned}$$

and

$$\begin{aligned} E_\theta (t):=NE(t)+\Phi (t)+\theta \Psi (t). \end{aligned}$$

Proof

Using Lebesgue dominated convergence theorem, we can easily obtain Lemma 4.3. $\square$

Obviously, for N large enough, we have

$$\begin{aligned} E_\delta \sim E_{\delta ,\theta }. \end{aligned}$$

Moreover, due to (3.6), there exists a positive constant $\beta _2$ such that

$$\begin{aligned} E_\delta (t)\le \beta _2,\ \ \ t\ge 0. \end{aligned}$$

(4.20)

Proof of Theorem 2.4

Differentiating (4.19) and taking (4.3), (4.5) and (4.10) into it, we have

$$\begin{aligned} E'_{\delta ,\theta }(t)=\,&NE'_\delta (t)+\Phi '_\delta (t)+\theta \Psi '_\delta (t)\nonumber \\ \le \,&-\left[ Nb_0+(n\sigma _1-b_0\epsilon _1)\theta -\left( 1+\frac{b_0}{4\varepsilon _1}\right) \right] \int \nolimits _{\Omega _\delta }|u_t|^2dx\nonumber \\&-\left[ N+(c_\sigma -\epsilon _2)\theta -\left( 1+\frac{1}{4\varepsilon _2}\right) -C_H\theta \right] \int \nolimits _{{\widetilde{\Gamma }}_1}|u_t|^2d\Gamma \nonumber \\&-\Bigg [\left( 1-\frac{b_0C_p\varepsilon _1}{\lambda \beta _0}-\frac{C_t\varepsilon _2}{\lambda \beta _0}\right) \nonumber \\&-\left( n\sigma _2-2\sigma _1 +\frac{\max _{x\in {\bar{\Omega }}_\delta }|H|^2b_0}{2\lambda \beta _0\epsilon _1}+C_H\right) \theta \Bigg ]\int \nolimits _{\Omega _\delta }\beta (t)|\nabla _gu|_g^2dx\nonumber \\&-\Bigg [1-\Bigg (\frac{\Vert \nabla _TA\Vert _{L^\infty \left( {\widetilde{\Gamma }}_1\right) }\max _{x\in \bar{{\widetilde{\Gamma }}}_1}|H_T|}{\lambda }\nonumber \\&+\frac{\max _{x\in \bar{{\widetilde{\Gamma }}}_1}|H_T|^2}{2\lambda \beta _0\epsilon _2}-c_\sigma \Bigg )\theta \Bigg ]\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)|(\nabla _T)_gu|_g^2d\Gamma \nonumber \\&+\frac{N|\beta '(t)|}{2\beta _0}\int \nolimits _{\Omega _\delta }\beta (t)|\nabla _gu|_g^2dx+\frac{N|\beta '(t)|}{2\beta _0}\int \nolimits _{{\widetilde{\Gamma }}_1}\beta (t)|(\nabla _T)_gu|_g^2d\Gamma \nonumber \\&+N\int \nolimits _{\Gamma _\delta }\frac{\partial u}{\partial \nu _{\mathcal {A}}}u_td\Gamma +\int \nolimits _{\Gamma _\delta }\frac{\partial u}{\partial \nu _{\mathcal {A}}}ud\Gamma \nonumber \\&+\theta \int \nolimits _{\Gamma _\delta }\left[ |u_t|^2-\beta (t)|\nabla _gu|_g^2\right] H\cdot \nu d\Gamma +2\theta \int \nolimits _{\Gamma _\delta }\frac{\partial u}{\partial \nu _{\mathcal {A}}}H(u)d\Gamma , \end{aligned}$$

(4.21)

where $C_H>0$ is some constant depending on H. Thus, we choose $\varepsilon _1$, $\varepsilon _2$, $\epsilon _1$ and $\epsilon _2$ small enough such that

$$\begin{aligned}{} & {} n\sigma _1-b_0\epsilon _1>0,\\{} & {} c_\sigma -\epsilon _2>0, \end{aligned}$$

and

$$\begin{aligned} 1-\frac{b_0C_p\varepsilon _1}{\lambda \beta _0}-\frac{C_tC_p\varepsilon _2}{\lambda \beta _0}>0. \end{aligned}$$

Fixing them, choosing $\theta$ sufficiently small and N lager enough such that

$$\begin{aligned} c_1:= & {} \left( 1-\frac{b_0C_p\varepsilon _1}{\lambda \beta _0}-\frac{C_t\varepsilon _2}{\lambda \beta _0}\right) -\left( n\sigma _2-2\sigma _1+\frac{\max _{x\in {\bar{\Omega }}_\delta }|H|^2b_0}{2\lambda \beta _0\epsilon _1}\right) \theta>0,\\ c_2:= & {} 1-\left( \frac{\Vert \nabla _TA\Vert _{L^\infty \left( {\widetilde{\Gamma }}_1\right) }\max _{x\in \bar{{\widetilde{\Gamma }}}_1}|H_T|}{\lambda } +\frac{\max _{x\in \bar{{\widetilde{\Gamma }}}_1}|H_T|^2}{2\lambda \beta _0\epsilon _2}-c_\sigma \right) \theta>0,\\ c_3:= & {} Nb_0+(n\sigma _1-b_0\epsilon _1)\theta -\left( 1+\frac{b_0}{4\varepsilon _1}\right) >0, \end{aligned}$$

and

$$\begin{aligned} c_4:=N+(c_\sigma -\epsilon _2)\theta -\left( 1+\frac{1}{4\varepsilon _2}\right) -C_H\theta >0. \end{aligned}$$

Therefore, combining (4.20) and (4.21) we obtain

$$\begin{aligned} \begin{aligned} E'_{\delta ,\theta }(t) \le \,&-C_1E_\delta (t)+C|\beta '(t)|+\theta \Theta _\delta (t)+\Lambda _\delta (t), \end{aligned} \end{aligned}$$

(4.22)

where

$$\begin{aligned} C_1:= & {} \min \left\{ c_1,c_2,c_3,c_4\right\} >0,\\ \Theta _\delta (t):= & {} \int \nolimits _{\Gamma _\delta }\left[ 2\frac{\partial u}{\partial \nu _{\mathcal {A}}}H(u)-\beta (t)|\nabla _gu|_g^2 H\cdot \nu \right] d\Gamma , \end{aligned}$$

and

$$\begin{aligned} \Lambda _\delta (t):=\int \nolimits _{\Gamma _\delta }\left[ \frac{\partial u}{\partial \nu _{\mathcal {A}}}u+N\frac{\partial u}{\partial \nu _{\mathcal {A}}}u_t+\theta |u_t|^2H\cdot \nu \right] d\Gamma . \end{aligned}$$

Then, integrating (4.22) from 0 to t, we obtain

$$\begin{aligned} \begin{aligned} E_{\delta ,\theta }(t)\le C\left[ E_{\delta ,\theta }(0)+\int \nolimits _0^te^{C_2s}|\beta '(s)|ds+\int \nolimits _0^te^{C_2s}\left[ \Theta _\delta (s)+\Lambda _\delta (s)\right] ds\right] e^{-C_2t}, \end{aligned} \end{aligned}$$

(4.23)

where $\displaystyle C_2>0$ is some constant.

$\bullet$ Estimate for $\displaystyle L_\delta (t):=\displaystyle \int \nolimits _0^te^{C_2s}\Theta _\delta (s)ds$

(i) For $n=2$, at each point $\displaystyle {\tilde{x}}\in \Sigma$, we can build the vectors $\displaystyle {\tilde{\nu }}=\nu ({\tilde{x}})$ and $\displaystyle {\tilde{\tau }}=\tau ({\tilde{x}})$ which depend on ${\tilde{x}}$ and $\Omega$. ${\tilde{\nu }}$ is the unit normal vector pointing towards the exterior and ${\tilde{\tau }}$ is the tangent vector pointing towards from $\Gamma _1$ to $\Gamma _0$. If $\delta$ is small enough, each point $\displaystyle x\in \Gamma _\delta$ belongs to one and only one coordinate system $\displaystyle ({\tilde{x}},{\tilde{\nu }},{\tilde{\tau }})$ and x belongs to some arc of circle $\displaystyle \partial B({\tilde{x}},\delta )$ contained in this coordinate system (see Fig. 3).

Fig. 3

The vectors $\nu$, $\tau$, ${\tilde{\nu }}$ and ${\tilde{\tau }}$ for $n=2$

We decompose the solution

$$\begin{aligned} u(x)=u_1(x)+u_2(x):=u_1(x)+\eta ({\tilde{x}})U_2(x-{\tilde{x}}), \end{aligned}$$

where $\displaystyle u_1\in H^2(\Omega )$, $\eta$ is locally in $\displaystyle H^{\frac{1}{2}}(\Sigma )$ and $U_2$ is given by

$$\begin{aligned} U_2(x-{\tilde{x}})=U_2(r,\theta )=\rho (r)\sqrt{r}\sin \left( \frac{\theta }{2}\right) , \end{aligned}$$

where $\rho$ is a $\displaystyle C^\infty$-function with compact support such that $\displaystyle \rho (r)=1$ in some neighbourhood of 0 and $\displaystyle {\textrm{supp}}(\rho )\subset [-\varrho ,\varrho ]\subset (-1,1)$, where $\varrho >0$ is as small as we want. Then, using coordinate in $({\tilde{x}},{\tilde{\nu }},{\tilde{\tau }})$, similar to [4], we have

$$\begin{aligned} 2\frac{\partial U_2}{\partial \nu _{\mathcal {A}}}H(U_2)-\beta (t)|\nabla _gU_2|_g^2 H\cdot \nu =\frac{\beta (t)A(x)}{4}\left( \frac{1}{\delta }{\tilde{H}}\cdot {\tilde{\tau }}-\nu \cdot {\tilde{\tau }}\right) , \end{aligned}$$

(4.24)

where ${\tilde{H}}=H({\tilde{x}})$ with ${\tilde{H}}\cdot {\tilde{\nu }}=0$. When $\delta \rightarrow 0$, $\partial B({\tilde{x}},\delta )$ behaves as a half-circle, then we obtain

$$\begin{aligned} \frac{1}{\pi \delta }\int \nolimits _{\partial B({\tilde{x}},\delta )}A(x)d\Gamma \rightarrow A({\tilde{x}})={\tilde{A}}\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned}$$

Integrating (4.24) along $\partial B({\tilde{x}},\delta )$, we get

$$\begin{aligned} \int \nolimits _{\partial B({\tilde{x}},\delta )}\left[ 2\frac{\partial U_2}{\partial \nu _{\mathcal {A}}}H(U_2)-\beta (t)|\nabla _gU_2|_g^2 H\cdot \nu \right] d\Gamma \rightarrow \frac{\pi \beta (t)}{4}{\tilde{A}}{\tilde{H}}\cdot {\tilde{\tau }}\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned}$$

Therefore, integrating the regular part of solution $u_1$ on $\partial B({\tilde{x}},\delta )$ and using Cauchy-Schwarz inequality, Lebesgue dominated convergence theorem, (2.3) and the compactness of function $\rho$, we obtain that $L_\delta (t)$ has a limit of non-positive number as $\delta \rightarrow 0$.

(ii) For $n\ge 3$, when $\delta$ is small enough, we also know that each point $\displaystyle x\in \Gamma _\delta$ belongs to one and only one plane defined by $\displaystyle ({\tilde{x}},{\tilde{\nu }},{\tilde{\tau }})$, and x belongs to some arc of circle $\displaystyle l({\tilde{x}},\delta )$ contained in this plane (the figure is similar to Fig. 3).

Firstly, just like in the case of $n=2$, we write

$$\begin{aligned} u(x)=u_1(x)+u_2(x), \end{aligned}$$

then

$$\begin{aligned}&\int \nolimits _{\partial B({\tilde{x}},\delta )}\left[ 2\frac{\partial u}{\partial \nu _{\mathcal {A}}}H(u)-\beta (t)|\nabla _gu|_g^2H\cdot \nu \right] d\Gamma \\&\quad =\ \int \nolimits _{\partial B({\tilde{x}},\delta )}\beta (t)A(x)\left[ 2\nabla u\cdot \nu \nabla u\cdot H-|\nabla u|^2H\cdot \nu \right] d\Gamma \\&\quad =\ \int \nolimits _{\partial B({\tilde{x}},\delta )}\beta (t)A(x)\left[ 2\nabla (u_1+u_2)\cdot \nu \nabla (u_1+u_2)\cdot H-|\nabla (u_1+u_2)|^2H\cdot \nu \right] d\Gamma \\&\quad =\ \underbrace{\int \nolimits _{\partial B({\tilde{x}},\delta )}\beta (t)A(x)\left[ 2\nabla u_1\cdot \nu \nabla u_1\cdot H-|\nabla u_1|^2H\cdot \nu \right] d\Gamma }_{I_\delta (\nabla u_1)}\\&\quad \quad +\underbrace{\int \nolimits _{\partial B({\tilde{x}},\delta )}\beta (t)A(x)\left[ 2\nabla u_2\cdot \nu \nabla u_2\cdot H-|\nabla u_2|^2H\cdot \nu \right] d\Gamma }_{I_\delta (\nabla u_2)}\\&\quad \quad +2\underbrace{\int \nolimits _{\partial B({\tilde{x}},\delta )}\beta (t)A(x)\left[ \nabla u_1\cdot \nu \nabla u_2\cdot H+\nabla u_2\cdot \nu \nabla u_1\cdot H-\nabla u_1\cdot \nabla u_2H\cdot \nu \right] d\Gamma }_{J_\delta (\nabla u_1,\nabla u_2)}. \end{aligned}$$

Since $u_1\in H^2(\Omega )$ and meas$(\partial B({\tilde{x}},\delta ))\rightarrow 0$ as $\delta \rightarrow 0$ and using the regularity of $\beta (t)$ and A(x), it is easy to get

$$\begin{aligned} I_\delta (\nabla u_1)\rightarrow 0\ \ \ {\textrm{as}}\ \delta \rightarrow 0. \end{aligned}$$

Further, let us do the decomposition of $\nabla u_2$:

$$\begin{aligned} \nabla u_2=\nabla _Xu_2+\nabla _2u_2, \end{aligned}$$

where $\nabla _2u_2$ belongs to the plane $({\tilde{x}},{\tilde{\nu }},{\tilde{\tau }})$ defined above and $\nabla _Xu_2$ is orthogonal to $\nabla _2u_2$, i.e.,

$$\begin{aligned} \nabla _Xu_2\cdot \nabla _2u_2=0\ \ \ {\textrm{and}}\ \ \ |\nabla u_2|^2=|\nabla _Xu_2|^2+|\nabla _2u_2|^2. \end{aligned}$$

Then

$$\begin{aligned} \int \nolimits _{\partial B({\tilde{x}},\delta )}|\nabla u_2|^2d\Gamma =\int \nolimits _{\partial B({\tilde{x}},\delta )}|\nabla _Xu_2|^2d\Gamma +\int \nolimits _{\partial B({\tilde{x}},\delta )}|\nabla _2u_2|^2d\Gamma . \end{aligned}$$

Thanks to the first part of Theorem 4 in [4] and the Lebesgue dominated convergence theorem, we get

$$\begin{aligned} \int \nolimits _{\partial B({\tilde{x}},\delta )}|\nabla _Xu_2|^2d\Gamma \rightarrow 0\ \ \ {\textrm{as}}\ \delta \rightarrow 0. \end{aligned}$$

And as $u_2(x)=\eta ({\tilde{x}})U_2(x-{\tilde{x}})$, using the Fubini’s theorem, we have

$$\begin{aligned} \int \nolimits _{\partial B({\tilde{x}},\delta )}|\nabla _2 u_2|^2d\Gamma =\int \nolimits _\Sigma \eta ^2\int \nolimits _{l({\tilde{x}},\delta )}|\nabla _2U_2|^2dld\Gamma ({\tilde{x}}), \end{aligned}$$

and know that this integral is bounded using $\eta \in H^{\frac{1}{2}}(\Sigma )$ and the definition of $U_2$. So we can end up with

$$\begin{aligned} \int \nolimits _{\partial B({\tilde{x}},\delta )}|\nabla u_2|^2d\Gamma \le C. \end{aligned}$$

Therefore, making use of Cauchy-Schwarz inequality, we obtain

$$\begin{aligned} |J_\delta (\nabla u_1,\nabla u_2)|\le C\left( \int \nolimits _{\partial B({\tilde{x}},\delta )}|\nabla u_1|^2d\Gamma \right) ^{\frac{1}{2}}\left( \int \nolimits _{\partial B({\tilde{x}},\delta )}|\nabla u_2|^2d\Gamma \right) ^{\frac{1}{2}}. \end{aligned}$$

It tends to zero since the first term vanishes as $\delta \rightarrow 0$ and the second one is bounded. And finally we start to deal with the term $I_\delta (\nabla u_2)$. Similar to the above process, we decompose $\nabla u_2$ and have

$$\begin{aligned} I_\delta (\nabla u_2) =\,&\underbrace{\int \nolimits _{\partial B({\tilde{x}},\delta )}\beta (t)A(x)[2\nabla _Xu_2\cdot \nu \nabla _Xu_2\cdot H-|\nabla _Xu_2|^2]d\Gamma }_{I_\delta (\nabla _Xu_2)}\\&+\underbrace{\int \nolimits _{\partial B({\tilde{x}},\delta )}\beta (t)A(x)[2\nabla _2u_2\cdot \nu \nabla _2u_2\cdot H-|\nabla _2u_2|^2H\cdot \nu ]d\Gamma }_{I_\delta (\nabla _2u_2)}\\&+2\underbrace{\int \nolimits _{\partial B({\tilde{x}},\delta )}\beta (t)A(x)[\nabla _Xu_2\cdot \nu \nabla _2u_2\cdot H+\nabla _2u_2\cdot \nu \nabla _Xu_2\cdot H]d\Gamma }_{J_\delta (\nabla _Xu_2,\nabla _2u_2)}. \end{aligned}$$

As above, $I_\delta (\nabla _Xu_2)\rightarrow 0$ as $\delta \rightarrow 0$. Since

$$\begin{aligned} |J_\delta (\nabla _Xu_2,\nabla _2u_2)|\le C\left( \int \nolimits _{\partial B({\tilde{x}},\delta )}|\nabla _Xu_2|^2d\Gamma \right) ^{\frac{1}{2}}\left( \int \nolimits _{\partial B({\tilde{x}},\delta )}|\nabla _2u_2|^2d\Gamma \right) ^{\frac{1}{2}}, \end{aligned}$$

we have the first term vanishes as $\delta \rightarrow 0$ and the second one is bounded, thus we obtain $J_\delta (\nabla _Xu_2,\nabla _2u_2)$ tends to zero. For $I_\delta (\nabla _2u_2)$, as the case of $n=2$, we also have

$$\begin{aligned} 2\nabla _2U_2\cdot \nu \nabla _2U_2\cdot H-|\nabla _2U_2|^2H\cdot \nu =\frac{1}{4}\left( \frac{1}{\delta }{\tilde{H}}\cdot {\tilde{\tau }}-\nu \cdot {\tilde{\tau }}\right) , \end{aligned}$$

and

$$\begin{aligned} \int \nolimits _{l({\tilde{x}},\delta )}\beta (t)A(x)[2\nabla _2U_2\cdot \nu \nabla _2U_2\cdot H-|\nabla _2U_2|^2H\cdot \nu ]dl\rightarrow \frac{\pi \beta (t)}{4}{\tilde{A}}{\tilde{H}}\cdot {\tilde{\tau }}\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned}$$

In other words, this integral term on $l({\tilde{x}},\delta )$ is bounded. Then, the dominated convergence theorem can be used to get

$$\begin{aligned} I_\delta (\nabla _2u_2)\rightarrow \frac{\pi \beta (t)}{4}\int \nolimits _\Sigma \eta ^2{\tilde{A}}{\tilde{H}}\cdot {\tilde{\tau }}d\Gamma ({\tilde{x}})\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned}$$

Therefor, using the assumption (2.3), we know that $I_\delta (\nabla _2u_2)$ converges to a non-positive number.

In conclusion, we infer

$$\begin{aligned} \Theta _\delta (t)\rightarrow \zeta \ \ \ {\textrm{as}}\ \ \delta \rightarrow 0, \end{aligned}$$

where $\zeta \le 0$ is a real number. When $\zeta <0$, then there exists $\delta _1>0$ such that

$$\begin{aligned} \Theta _\delta (t)<0,\ \ \ \delta <\delta _1, \end{aligned}$$

and

$$\begin{aligned} L_\delta (t)=\displaystyle \int \nolimits _0^te^{C_2s}\Theta _\delta (t)ds<0. \end{aligned}$$

When $\zeta =0$, we need to talk about two cases. One case is that there exists a positive constant $\delta _2$ such that

$$\begin{aligned} \Theta _\delta (t)<0,\ \ \ \delta <\delta _2. \end{aligned}$$

Then the process is the same as $\zeta <0$. The other case is that there exists a positive constant $\delta _3$ such that

$$\begin{aligned} \Theta _\delta (t)>0,\ \ \ \delta <\delta _3. \end{aligned}$$

Then

$$\begin{aligned} 0\le L_\delta (t)e^{-C_2t}=\int \nolimits _0^te^{C_2s}\Theta _\delta (s)dse^{-C_2t}\le \int \nolimits _0^t\Theta _\delta (s)ds\rightarrow 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0, \end{aligned}$$

i.e.,

$$\begin{aligned} L_\delta (t)\equiv 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned}$$

Thus, we get

$$\begin{aligned} L_\delta (t)\le 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned}$$

(4.25)

$\bullet$ Estimate for $M_\delta (t):=\displaystyle \int \nolimits _0^te^{C_2s}\Lambda _\delta (s)ds$

Just like we did above, we split u into two parts, this is,

$$\begin{aligned} u(x)=u_1(x)+u_2(x), \end{aligned}$$

where $\displaystyle u_1\in H^2(\Omega )$ is the regular part and $u_2=\eta \cdot U_2$ is the singular part, then

$$\begin{aligned} \begin{aligned}&\int \nolimits _{\partial B({\tilde{x}},\delta )}\frac{\partial u}{\partial \nu _{\mathcal {A}}}ud\Gamma \\&\quad =\, \int \nolimits _{\partial B({\tilde{x}},\delta )}\beta (t)A(x)(\nabla u_1+\nabla u_2)\cdot \nu (u_1+u_2)d\Gamma \\&\quad =\, \int \nolimits _{\partial B({\tilde{x}},\delta )}\beta (t)A(x)[\nabla u_1\cdot \nu u_1+\nabla u_2\cdot \nu u_2+\nabla u_1\cdot \nu u_2+\nabla u_2\cdot \nu u_1]d\Gamma .\\ \end{aligned} \end{aligned}$$

(4.26)

Using Cauchy-Schwarz inequality and the above results, we have

$$\begin{aligned}{} & {} \int \nolimits _{\partial B({\tilde{x}},\delta )}\nabla u_1\cdot \nu u_1d\Gamma \rightarrow 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0, \end{aligned}$$

(4.27)

$$\begin{aligned}{} & {} \int \nolimits _{\partial B({\tilde{x}},\delta )}\nabla u_2\cdot \nu u_2d\Gamma \rightarrow 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0, \end{aligned}$$

(4.28)

$$\begin{aligned}{} & {} \int \nolimits _{\partial B({\tilde{x}},\delta )}\nabla u_1\cdot \nu u_2d\Gamma \rightarrow 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0, \end{aligned}$$

(4.29)

and

$$\begin{aligned} \begin{aligned} \int \nolimits _{\partial B({\tilde{x}},\delta )}\nabla u_2\cdot \nu u_1d\Gamma \rightarrow 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned} \end{aligned}$$

(4.30)

Taking (4.27)–(4.30) into (4.26) and using Lebesgue dominated convergence theorem allow us to get

$$\begin{aligned} \begin{aligned} \int \nolimits _0^te^{C_2s}\int \nolimits _{\partial B({\tilde{x}},\delta )}\frac{\partial u}{\partial \nu _{\mathcal {A}}}ud\Gamma ds\rightarrow 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned} \end{aligned}$$

(4.31)

Analogously,

$$\begin{aligned} \begin{aligned} \int \nolimits _0^te^{C_2s}\int \nolimits _{\partial B({\tilde{x}},\delta )}\frac{\partial u}{\partial \nu _{\mathcal {A}}}u_td\Gamma ds\rightarrow 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned} \end{aligned}$$

(4.32)

On the other hand, using the decomposition of u into a regular part and a singular part, we have

$$\begin{aligned}&\int \nolimits _0^te^{C_2s}\int \nolimits _{\partial B({\tilde{x}},\delta )}|u_t|^2H\cdot \nu d\Gamma ds\\&\quad =\ \int \nolimits _0^te^{C_2s}\int \nolimits _{\partial B({\tilde{x}},\delta )}|u_{1,t}|^2H\cdot \nu d\Gamma ds+\int \nolimits _0^te^{C_2s}\int \nolimits _{\partial B({\tilde{x}},\delta )}|u_{2,t}|^2H\cdot \nu d\Gamma ds. \end{aligned}$$

From the dominated convergence theorem, we have

$$\begin{aligned} \int \nolimits _0^te^{C_2s}\int \nolimits _{\partial B({\tilde{x}},\delta )}|u_{1,t}|^2H\cdot \nu d\Gamma ds\rightarrow 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned}$$

As

$$\begin{aligned} \int \nolimits _{l({\tilde{x}},\delta )}|u_{2,t}|^2H\cdot \nu dl\le C\int \nolimits _0^{2\pi }\int \nolimits _0^\delta r^{\frac{1}{2}}drd\theta \le C\delta ^{\frac{3}{2}}, \end{aligned}$$

we get

$$\begin{aligned} \int \nolimits _0^te^{C_2s}\int \nolimits _{\partial B({\tilde{x}},\delta )}|u_{2,t}|^2H\cdot \nu d\Gamma ds\rightarrow 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned}$$

Then it follows

$$\begin{aligned} \begin{aligned} \int \nolimits _0^te^{C_2s}\int \nolimits _{\partial B({\tilde{x}},\delta )}|u_t|^2H\cdot \nu d\Gamma ds\rightarrow 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned} \end{aligned}$$

(4.33)

Therefore, combining (4.31)–(4.33), we get

$$\begin{aligned} M_\delta (t)=\displaystyle \int \nolimits _0^te^{C_2s}\Lambda _\delta (s)ds\rightarrow 0\ \ \ {\textrm{as}}\ \ \delta \rightarrow 0. \end{aligned}$$

(4.34)

In conclusion, let $\delta \rightarrow 0$ and taking (4.25) and (4.34) into (4.23), we have

$$\begin{aligned} {\mathcal {E}}_\theta (t)\le C\left( {\mathcal {E}}_\theta (0)+\int \nolimits _0^t e^{C_2s}|\beta '(s)|ds\right) e^{-C_2t}. \end{aligned}$$

Then, using the energy equivalence relation and (2.5), we get

$$\begin{aligned} E(t)\le C\left( E(0)+\alpha t^m\right) e^{-C_2t}. \end{aligned}$$

Thus, we complete the proof of Theorem 4.4. $\square$

5 Conclusions

In this paper, we present a study on the stability of a time-varying coefficients wave equation in the bounded domain $\Omega$. The smooth boundary of $\Omega$ is $\Gamma =\Gamma _0\cup \Gamma _1$ such that $\Sigma ={\overline{\Gamma }}_0\cap {\overline{\Gamma }}_1\ne \emptyset$. We consider that a homogeneous Dirichlet boundary on $\Gamma _0$ and a dynamic boundary with damping term on $\Gamma _1$. Since the coefficients depends on the time variable and the singularities are generated by changing the boundary conditions along the interface, these bring no small difficulty to our proof, so some special techniques are needed to deal with these problems. Under the appropriate geometric assumptions, the exponential decay result of the system is established by the Riemannian geometry method and the energy perturbation method.

There are many other issues associated with this type of problem, but we have not studied them here.

• (i) The geometric conditions (H2) and (2.3) are essential in the proof of our exponential stability result, but their necessity leads us to exclude many mathematical models of interest that should also be uniformly stable.

• (ii) We assume that there are no external forces acting on the system or its boundary other than friction. If there is thermal force in system, can the energy still be uniformly stable? What if there is a nonlinear negative source term on $\Gamma _1$?