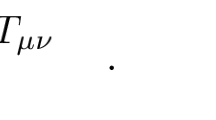Global Nonlinear Stability of Large Dispersive Solutions to the Einstein Equations

Abstract

We extend the monumental result of Christodoulou–Klainerman on the global nonlinear stability of the Minkowski spacetime to the global nonlinear stability of a class of large dispersive spacetimes. More precisely, we show that any regular future causally geodesically complete, asymptotically flat solution to the Einstein-scalar field system which approaches the Minkowski spacetime sufficiently fast for large times is future globally nonlinearly stable. Combining our main theorem with results of Luk–Oh, Luk–Oh–Yang and Kilgore, we prove that a class of large data spherically symmetric dispersive solutions to the Einstein-scalar field system are globally nonlinearly stable with respect to small non-spherically symmetric perturbations. This, in particular, gives the first construction of an open set of large asymptotically flat initial data for which the solutions to the Einstein-scalar field system are future causally geodesically complete.

1 Introduction

The Minkowski spacetime $({\mathbb {R}}^{3+1}, m)$ with metric

$$\begin{aligned} m=-{\text {d}}t^2+\sum _{i=1}^3 ({\text {d}}x^i)^2 \end{aligned}$$

(1.1)

is a special solution to the Einstein equations

$$\begin{aligned} Ric_{\mu \nu }-\frac{1}{2} g_{\mu \nu }R=2 {\mathbb {T}}_{\mu \nu } \end{aligned}$$

in vacuum, i.e., when ${\mathbb {T}}_{\mu \nu }\equiv 0$. A monumental result in general relativity is the nonlinear stability of Minkowski spacetime, proved by Christodoulou–Klainerman in 1993:

Theorem 1.1

(Christodoulou–Klainerman [13]). Minkowski spacetime is globally nonlinearly stable for the Einstein vacuum equations $Ric_{\mu \nu }=0$.

In slightly more precise terms, given asymptotically flat initial data satisfying the constraint equations which are sufficiently close to the Minkowskian initial data, the maximal globally hyperbolic development to the Einstein vacuum equations is causally geodesically complete, remains close to the Minkowski spacetime and “approaches the Minkowski spacetime at large times.”

A more restricted result, for which the initial data are posed on a hyperboloid,¹ was previously proven by Friedrichs [21]. Variations, simplifications and generalizations of the Christodoulou–Klainerman result have subsequently been achieved by various authors. We refer the readers to [6, 22, 24, 35, 38, 43, 45, 46] for extensions and simplifications, and to [5, 6, 20, 28, 38, 47, 48, 59, 62, 65] for results with various matter models. See also the related works [9, 10, 27]. We highlight, in particular, the work of Lindblad–Rodnianski [45, 46] as it is the most relevant to the present work. They gave an alternative proof of the stability of Minkowski spacetime in a wave coordinate system. Besides simplifying the original proof [13], their argument extends to the Einstein-scalar field system for which in addition to the Lorentzian manifold $({\mathcal {M}},g)$, there is a real-valued scalar field $\phi :{\mathcal {M}}\rightarrow {\mathbb {R}}$, such that the following system of equations are satisfied:

$$\begin{aligned} {\left\{ \begin{array}{ll} Ric_{\mu \nu }-\frac{1}{2} g_{\mu \nu }R=2 {\mathbb {T}}_{\mu \nu },\\ {\mathbb {T}}_{\mu \nu }=\partial _\mu \phi \partial _\nu \phi -\frac{1}{2} g_{\mu \nu }(g^{-1})^{\alpha \beta }\partial _\alpha \phi \partial _\beta \phi ,\\ \Box _g\phi :=\frac{1}{\sqrt{-\det g}}\partial _\alpha ((g^{-1})^{\alpha \beta }\sqrt{-\det g}\partial _\beta \phi )=0. \end{array}\right. } \end{aligned}$$

(1.2)

We summarize the Lindblad–Rodnianski theorem for the Einstein-scalar field system as follows:

Theorem 1.2

(Lindblad–Rodnianski [46]). Minkowski spacetime is globally nonlinearly stable for the Einstein-scalar field system (1.2).

The main mechanism for the stability of Minkowski spacetime is a combination of the dispersive nature of the equations and the special structure in the nonlinearity. In this paper, we generalize Theorems 1.1 and 1.2 to a larger class of asymptotically flat spacetime, where smallness is not required. As is well known, general large data solutions to the Einstein equations may be incomplete [8, 12, 51, 54]. However, we show that as long as we have a background “dispersive” solution which is geodesically complete and converging to the Minkowski spacetime sufficiently fast, then any sufficiently small perturbations will also be dispersed. In particular, in an appropriately chosen system of coordinates, the nonlinearity has a special structure such that any small perturbations of the initial data to the background solution lead to a geodesically complete spacetime which again converges to the Minkowski spacetime for large times. We summarize our theorem as follows:

Theorem 1.3

(Main theorem, first version). Any sufficiently regular, future causally geodesically complete and asymptotically flat² solution to the Einstein-scalar field equations that approaches the Minkowski spacetime sufficiently fast is future globally nonlinearly stable.

We will make precise in what sense the solution is required to approach Minkowski spacetime in later sections (see, in particular, Sect. 3). See Theorems 3.6 and 5.2 for more precise statements. Let us point out the obvious fact that Theorem 1.3 generalizes Theorems 1.1 and 1.2.

Unlike Theorems 1.1 and 1.2, our main result does not require the background solution to be small. The natural question is then whether there exist spacetimes satisfying the assumptions of Theorem 1.3. We will particularly consider examples which are spherically symmetric. In a previous work [49], we showed that as long as a spherically symmetric “asymptotically flat” solution to the Einstein-scalar field system satisfies a weak qualitative “BV local scattering condition,” then they in fact satisfy quantitative inverse polynomial decay estimates. In a subsequent joint work with Yang [50], we also demonstrated the existence of solutions which scatter locally in the BV norm with arbitrarily large BV norms,³ so that the solution verifies the decay estimates in [49]. Very recently, Kilgore [32] proved that after constructing a suitable gauge, a subclass of the large BV solutions constructed in [50] in fact also satisfies the estimates required in the assumptions of Theorem 1.3. We therefore obtain

Corollary 1.4

(Combining Theorem 1.3 with [32, 49, 50]). There exist spherically symmetric solutions to the Einstein-scalar field system with large initial data which obey the assumptions of Theorem 1.3 and are therefore future globally nonlinearly stable.

As a consequence, there exists an open set of large initial data for the Einstein-scalar field system such that the maximal Cauchy development is future causally geodesically complete.

While [32] only verifies the assumptions of Theorem 1.3 toward the future, one expects that a subclass of the spacetime in [50] in fact obey the assumptions of Theorem 1.3 both toward the future and the past. In particular, this would give an open set of solutions which are future and past causally geodesically complete.

In addition to Corollary 1.4, we mention two other potential applications of Theorem 1.3.

• Klainerman–Nicolo [35] provided an alternative proof of the stability of Minkowski spacetimes for the Einstein vacuum equations restricted to the causal future of a domain near the asymptotically flat end. Their proof uses the double null foliation gauge, which allows all the estimates to be localized to the causal future of the asymptotically flat region and can therefore be applied to large initial data to show that there exists “a non-empty piece of future null infinity.” Our main theorem could potentially be used to give a different proof of the result in [35] and also to generalize⁴ it to the Einstein-scalar field system

• In [12], Christodoulou constructed spacetimes which are past causally geodesically complete while trapped surfaces form dynamically in the future so that the spacetimes are future causally geodesically incomplete. (See also the very recent [39] for a construction which moreover contains a black hole region in the future.) One expects that after introducing an appropriate gauge, Theorem 1.3 can in principle be used to show that these spacetimes are asymptotically stable toward the past.

Our proof is based on estimating the difference of the metric components and the scalar field with their background values in a generalized wave coordinate gauge. The estimates make use of the decay of the background solutions. As one would expect from [45, 46], both the decay of the background solutions and the decay of the perturbed solutions are borderline. Thus, we need to make use of the weak null condition as in [45, 46]. Unlike in [45, 46], however, we are dealing with a large data stability problem, and we need to avoid that the energy grows as a large power of t. To achieve this, we exploit the weak null condition in our energy estimates (as opposed to just in the $L^\infty$ estimates as in [45, 46]) and also need to localize our estimates in various regions of spacetime. In particular, all of these features require us to choose our generalized wave gauge condition to be adapted to the background solution and moreover also to take into account the perturbation of the ADM mass. In this gauge, we are able to have good control of the null hypersurfaces of the metric which is crucial for us to localize our estimates in various regions of the spacetime. This allows us to fully exploit the weak null structure in the Einstein-scalar field system for a large data stability problem. We will explain all these issues in Sect. 1.3.

The remainder of the introduction is organized as follows. First, we discuss some stability results in the spirit of Theorem 1.3 for related quasilinear wave equations in Sect. 1.1. Afterward, we will then give a more detailed outline of the ideas of the proof in Sect. 1.2. Finally, we end our introduction with an outline of the remainder of the paper in Sect. 1.3.

1.1 Global Existence and Stability of Solutions for Quasilinear Wave Equations

The problem of the global nonlinear stability of the Minkowski spacetime can be viewed in the larger context of small data global existence for small data for nonlinear wave equations. It is well known that in $3+1$ dimensions, the dispersion of the linear wave equation is barely insufficient to obtain small data global existence for wave equations with a quadratic nonlinearity. Counterexamples were first given by John [29]. For a large class of quasilinear wave equations including the compressible Euler equation, it is known that arbitrarily small initial data may lead to the formation of shocks [1, 2, 11, 14, 26, 55, 60].

On the other hand, since the seminal work of Klainerman [34], it is well known that a small data global existence result can be obtained if the quadratic nonlinearity obeys the classical null condition. An independent alternative proof was also given by Christodoulou [7]. We cannot do justice to the large literature on related problems, but will simply point out that similar results have been obtained on more general asymptotically flat manifolds [64], domains in the exterior of obstacles [52, 53], as well as in multiple-speed problems [57, 58] including that of elasticity [56].

Motivated by the problem of small-data global existence for the Einstein equations in the wave coordinate gauge, Lindblad–Rodnianski introduced the notion of the weak null condition [44], which generalizes the classical null condition. A quasilinear system of wave equations is said to satisfy the weak null condition if the corresponding asymptotic system (see Hörmander [25]) has global solutions. Under suitable additional structural assumptions of the equations, small data to quasilinear systems satisfying the weak null condition lead to global solutions. This is in particular the case for the Einstein vacuum equations or the Einstein-scalar field system in the wave coordinate gauge, which was crucially used in the Lindblad–Rodnianski proof of the stability of Minkowski spacetime. [45, 46]. In addition, small data global existence has been proven for a number of other quasilinear systems satisfying the weak null condition; see for instance [19, 23, 30, 31, 41, 42].

In the context of nonlinear wave equations, our main theorem (Theorem 1.3) can be viewed as a stability theorem for large solutions to nonlinear wave equations with sufficiently fast decay. Such results were first obtained by Alinhac [3] for quasilinear wave equations satisfying a classical null condition. This was extended in the work of Yang [66] to equations with time-dependent non-decaying coefficients satisfying a classical null condition. The works [3, 66] use that under the classical null condition, there is effectively additional decay for the solutions. In contrast, in our present work, only a weak null condition holds; see Sect. 1.2.

As mentioned earlier, our result can be specialized to study the solutions in a neighborhood of a class of spherically symmetric solutions to the Einstein-scalar field system (see Corollary 1.4). This result has parallels with global existence theorems for nonlinear wave equations in a neighborhood of symmetric solutions. For instance, Krieger showed that two-dimensional spherically symmetric wave maps⁵$:{\mathbb {R}}^{2+1}\rightarrow {\mathbb {H}}^2$ are stable [36] using the precise asymptotics of the exactly spherically symmetric solutions proven by Christodoulou–Tahvildar-Zadeh [15]. We refer the readers also to the work of Andréasson–Ringström [4] for the Einstein–Vlasov system in the cosmological setting in which the authors studied the stability of a class of global ${\mathbb {T}}^2$-symmetric spacetimes.

1.2 Strategy of the Proof

Our proof, following the main strategy in [45, 46], is based on controlling the metric and the scalar field (and their derivatives) in an appropriately chosen generalized wave coordinate system. In such a coordinate system, the metric and the scalar field satisfy a quasilinear system of wave equations with a weak null condition and our goal is to control the difference of the metric and the scalar field with their background values using this system of wave equations. We will call the background solution $(g_B,\phi _B)$. Define h and $\beta$, respectively, to be appropriate⁶ differences of the metric and the scalar field with their background values. In contrast to the small data problem (i.e., the stability of Minkowski spacetime in Theorems 1.1 and 1.2), the equations in our problem contain linear terms in the $(h,\beta )$ with coefficients that are large and are associated with the background solution $g_B$ and $\phi _B$. In the following, we will in particular explain how these additional terms can be handled.

This section is organized as follows: We begin in Sect. 1.2.1 recalling the decay properties of solutions to the wave equation and the (weak) null condition. In Sect. 1.2.2, we discuss the decay condition that can be expected for the background solution (which for example holds for the spherically symmetric dispersive solutions of [32]). We also explain the relevance of the decay properties of the background to our problem at hand. In Sect. 1.2.3, we then study a model semilinear problem, which captures some of the analytic difficulties for the Einstein-scalar field system, and explain how a large data stability problem can be treated for that model. In Sect. 1.2.4, we then discuss the similarities of the Einstein-scalar field system and the said model problem, but we also emphasize the additional difficulties that arise in the case of the Einstein-scalar field system. In Sect. 1.2.5, we introduce the main new ideas of the paper and discuss how by choosing an appropriate generalized wave coordinate gauge, we can on the one hand treat the difficulties associated with the difference of the ADM masses and on the other hand introduce a localization to fully exploit the weak null structure present in the Einstein-scalar field system. The remaining subsections discuss more technical aspects of the proof. Namely, in Sect. 1.2.6 we explain how to perform the localization to different regions of spacetimes; in Sect. 1.2.7, we discuss the treatment of the quasilinear error terms; in Sect. 1.2.8, we conclude by discussing the higher order error terms and the hierarchy of estimates that are introduced to tackle them.

1.2.1 The Classical Null Condition and the Weak Null Condition

We quickly recall the classical null condition and the weak null condition for quasilinear wave equations in $(3+1)$ dimensions. The key issue is that solutions to the linear wave equation only have uniform $O(\frac{1}{1+t})$ decay, which is barely non-integrable and in general leads to finite-time blowup for small data solutions.

On the other hand, as is by now very well understood, in addition to the uniform $O(\frac{1}{1+t})$ decay, we have

• additional decay in the variable $|t-|x||$, i.e., the sharp $\frac{1}{1+t}$ decay is only saturated when $t\sim |x|$; and

• derivatives which are tangential to the outgoing light cone—which we denote by ${\bar{\partial }}$—decay faster.

The classical null condition requires that in quadratic terms in the nonlinearity, at least of the derivative is a good ${\bar{\partial }}$. Thus, this gives better decay so that small data always lead to global solutions. This structure also allows one to prove a large data stability result, as long as the background large solution obeys “wave-like” estimates.

The Einstein equation in wave coordinates, however, violates the classical null condition. Nonetheless, as shown in the work of Lindblad–Rodnianski [45, 46], they satisfy the weak null condition. The simplest model problem to capture the structure of the semilinear terms is the system

$$\begin{aligned} {\left\{ \begin{array}{ll} \Box \phi =0,\\ \Box \psi =(\partial _t\phi )^2. \end{array}\right. } \end{aligned}$$

(1.3)

It is clear⁷ that both global existence for small data and also global stability for large data solutions hold for (1.3). While this system does not satisfy the classical null condition, there is a reductive structure, i.e., one can first solve the first equation in (1.3) and then solve the second equation in (1.3). It should be noted that even in the small data case, $\psi$ would not have the decay as for solutions to the linear wave equation, but has a logarithmic correction.

Similar ideas of using a reductive structure allow one to consider the following less simplistic model problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} \Box \phi =Q(\phi ,\psi )=\partial \phi {\bar{\partial }}\psi +\partial \psi {\bar{\partial }}\phi ,\\ \Box \psi =(\partial _t\phi )^2. \end{array}\right. } \end{aligned}$$

(1.4)

where Q is a classical null form such that there is at least one good derivative. For the system (1.4), small data global existence holds (and follows ). For this system of equation, a reductive structure can still be exploited to obtain global stability of large data solutions, as long as the background solution is assumed to obey “wave-like” estimates, i.e., it has $O(\frac{1}{1+t})$ decay with improved decay in $||x|-t|$ and for the ${\bar{\partial }}$ derivatives.

We will sketch a proof of stability for large solutions to (1.4) in Sect. 1.2.3, after discussing in Sect. 1.2.2 the decay that we can expect for the background solutions. We note already that while part of our paper is to generalize the proof for (1.4) to the Einstein-scalar field system, a perhaps more important part is to understand why (1.4) is a reasonable toy model for the problem at hand. We will postpone the latter discussion to Sects. 1.2.4 and 1.2.5.

1.2.2 Decay Conditions for the Background Solution

Since the main difference between our problem and the stability of Minkowski spacetime is the extra terms associated with the background $g_B$ and $\phi _B$, it is important to understand their decay properties. Indeed, if these terms decay like⁸,⁹$|\partial g_B|+|\partial \phi _B|\lesssim \frac{1}{(1+t)^{1+}}$, then because they are integrable in time, they can be controlled by a Grönwall-type argument. The remaining (small) nonlinear terms can then be treated as in the proof of the stability of Minkowski spacetime.

However, since $g_B$ and $\phi _B$ themselves are solutions to the the Einstein-scalar field system, we can at best expect “wave-like” estimates. In particular, the uniform-in-time decay estimate is no better than $O(\frac{1}{1+t})$. Here are the decay estimates that are reasonable for the background solution.

• The derivatives of $g_B$ and $\phi _B$ obey the following uniform-in-time decay for some (small) $\gamma >0$:

  $$\begin{aligned} |\partial g_B|(t,x) + |\partial \phi _B|(t,x) \lesssim \frac{1}{(1+t)(1+|t - |x||)^{\gamma }}. \end{aligned}$$

  This captures both the uniform-in-time $O(\frac{1}{1+t})$ decay and the improvement away from the light cone $\{(t,x): t = |x|\}$ typical of solutions to the wave equation.

• Just as for the solutions to wave equation, the “good derivatives” ${\bar{\partial }}$—those that are tangential to the light cone—of $g_B$ and $\phi _B$ decay better. For some (small) $\gamma >0$, we have

  $$\begin{aligned} | {\bar{\partial }}g_B| + |{\bar{\partial }}\phi _B|\lesssim \frac{1}{(1+t)^{1+\gamma }} \end{aligned}$$

• Higher-order versions of the above estimates still holds after differentiating with the Minkowskian commuting vector fields.¹⁰

• So that we can localize our solutions (see Sect. 1.2.5), we need to choose a gauge for the background solution such that some of the components of $h_B:=g_B-m$ decay faster than $\frac{1}{1+t}$ and in fact has a decay that is integrable in time. More precisely, let $L=\partial _t+\partial _r$ and ${\mathcal {T}}$ be a spanning set of vectors tangent to the Minkowskian outgoing light cone, we choose $h_B$ such that for some (small) $\gamma >0$,

  $$\begin{aligned} |h_B|_{L{\mathcal {T}}}(t,x):=\sum _{V\in {\mathcal {T}}} |L^\alpha V^{\beta } (h_B)_{\alpha \beta }|(t,x)\lesssim \frac{1}{(1+t)^{1+\gamma }}. \end{aligned}$$

  However, in this gauge, general components of the background metric decay slower, namely

  $$\begin{aligned} |h_B|(t,x) \lesssim \frac{\log (2+t+|x|)}{1+t+|x|} \end{aligned}$$

For the precise assumptions, see Definition 3.1. By the results of [32, 49, 50], all these decay estimates are indeed satisfied by the class of spherically symmetric BV-scattering solutions to the Einstein-scalar field system considered in Corollary 1.4.

1.2.3 Toy Model Problem (1.4)

We now sketch a proof of the stability of large data dispersive solutions for the toy model (1.4) introduced earlier. Consider a background global solution to (1.4) with the property that for $|I|\le 10$, there exists some small $\gamma >0$ so that

$$\begin{aligned}&|\partial \Gamma ^I\phi _B|\lesssim \frac{1}{(1+t)(1+||x|-t|)^\gamma },\quad |\partial \Gamma ^I\psi _B|\lesssim \frac{1}{(1+t)(1+||x|-t|)^\gamma },\nonumber \\&|{\bar{\partial }}\Gamma ^I\phi _B|+|{\bar{\partial }}\Gamma ^I\psi _B|\lesssim \frac{1}{(1+t)^{1+\gamma }}. \end{aligned}$$

(1.5)

Here, $\Gamma$ are the Minkowskian commuting vector fields, which generate symmetries of the d’Alembertian on the Minkowski spacetime (see Definition 2.1). These assumptions are exactly consistent with those in Sect. 1.2.2.

To prove the stability of such solutions, one combines the following three types of estimates: the weighted energy estimates, the Klainerman–Sobolev inequality and the $L^\infty -L^\infty$ ODE estimate of [40]. First, we have the energy estimates for solutions to $\Box \xi =F$ whenever $t_2\ge t_1\ge 0$:

$$\begin{aligned} \begin{aligned} E(t_2;t_1;\xi )&:=\sup _{t'\in [t_1,t_2]}\int _{\{t'\}\times {\mathbb {R}}^3} w(|x|-t')|\partial \xi |^2(t',x)\,{\text {d}}x\\&\quad +\int _{t_1}^{t_2} \int _{\{t'\}\times {\mathbb {R}}^3} w'(|x|-t')|{\bar{\partial }}\xi |^2(t',x)\,{\text {d}}x\, {\text {d}}t'\\&\lesssim \int _{\{t_1\}\times {\mathbb {R}}^3} w(|x|-t_1)|\partial \xi |^2(t_1,x)\,{\text {d}}x\\&\quad +\left( \int _{t_1}^{t_2} \left( \int _{\{t'\}\times {\mathbb {R}}^3} w(|x|-t')|F(t',x)|^2\,{\text {d}}x\right) ^{\frac{1}{2}} {\text {d}}t'\right) ^2. \end{aligned} \end{aligned}$$

(1.6)

where $w(q):={\left\{ \begin{array}{ll} 1+(1+|q|)^{1+2\gamma } &{}\text{ if } q\ge 0\\ 1+(1+|q|)^{-\frac{\gamma }{2}} &{}\text{ if } q< 0. \end{array}\right. }$. The weight w in the energy estimates, already introduced in [45, 46], serves the double purpose of giving decay in $||x|-t|$ when $|x|\ge t$ and also giving a positive bulk term on the left-hand side which gives better control of the good derivatives terms $|{\bar{\partial }}\xi |$.

The energy estimate is applied to derivatives of $\xi$ with respect to $\Gamma$, which has the property that $[\Box ,\Gamma ]=c\Box$ for some constant c. Moreover, the energy of the $\Gamma$-differentiated quantities gives rise to the decay estimates due to the following Klainerman–Sobolev inequalities (see Propositions 7.1, 11.8 and Lemma 18.1), which hold for all sufficiently regular functions $\xi$:

$$\begin{aligned}&\sup _{x}|\partial \xi (t,x)|(1+t+|x|)(1+||x|-t|)^{\frac{1}{2}} w(|x|-t)^{\frac{1}{2}}\nonumber \\&\quad \le C\sum _{|I|\le 3}\Vert w^{\frac{1}{2}}(|\cdot |-t)\partial \Gamma ^I\xi (t,\cdot ) \Vert _{L^2({\mathbb {R}}^3)} , \end{aligned}$$

(1.7)

$$\begin{aligned}&\sup _{x}\left( |{\bar{\partial }}\xi (t,x)|(1+t+|x|)^2\!+\!|\xi (t,x)|(1+t+|x|)\right) (1+||x|-t|)^{-\frac{1}{2}} w(|x|-t)^{\frac{1}{2}}\nonumber \\&\quad \le C\sum _{|I|\le 4}\sup _{0\le \tau \le t}\Vert w^{\frac{1}{2}}(|\cdot |-\tau )\partial \Gamma ^I\xi (\tau ,\cdot ) \Vert _{L^2({\mathbb {R}}^3)} . \end{aligned}$$

(1.8)

The third ingredient that we need is the following $L^\infty -L^\infty$ estimate (see Proposition 11.10), which holds for solutions to $\Box \xi =F$:

$$\begin{aligned} \begin{aligned}&\sup _x(1+t)|\partial \xi (t,x)| \lesssim \sup _{0\le \tau \le t}\sum _{|I|\le 1}\Vert \Gamma ^I\xi (\tau ,\cdot )\Vert _{L^\infty ({\mathbb {R}}^3)}\\&\quad +\int _0^t \left( (1+\tau )\Vert F(\tau ,\cdot )\Vert _{L^\infty ({\mathbb {R}}^3)}+\sum _{|I|\le 2}(1+\tau )^{-1}\Vert \Gamma ^I\xi (\tau ,\cdot )\Vert _{L^\infty ({\mathbb {R}}^3)}\right) {\text {d}}\tau .\nonumber \end{aligned}\\ \end{aligned}$$

(1.9)

After introducing the basic tools, let us return to the problem of stability of large solutions to (1.4). Defining ${{\bar{\phi }}}=\phi -\phi _B$ and ${{\bar{\psi }}}=\psi -\psi _B$, using the bounds (1.5) for the background solution and only writing a few typical terms to simplify the exposition,¹¹ we have roughly

$$\begin{aligned} {\left\{ \begin{array}{ll} |\Box \Gamma ^I{{\bar{\phi }}}|&{}\lesssim \frac{|\partial \Gamma ^I{{\bar{\phi }}}|+|\partial \Gamma ^I{{\bar{\psi }}}|}{(1+t)^{1+\gamma }}+\frac{|{\bar{\partial }}\Gamma ^I{{\bar{\phi }}}|+|{\bar{\partial }}\Gamma ^I{{\bar{\psi }}}|}{(1+t)(1+||x|-t|)^\gamma }+|\partial \Gamma ^I{{\bar{\phi }}}||{\bar{\partial }}{{\bar{\psi }}}|+|\partial {{\bar{\phi }}}||{\bar{\partial }}\Gamma ^I{{\bar{\psi }}}|+\cdots ,\\ |\Box {{\bar{\psi }}}|&{}\lesssim \frac{|\partial \Gamma ^I{{\bar{\phi }}}|}{1+t}+|\partial \Gamma ^I{{\bar{\phi }}}||\partial {{\bar{\phi }}}|+\cdots .\nonumber \end{array}\right. }\!\!\!\!\!\!\\ \end{aligned}$$

(1.10)

Assume now that the initial perturbations are small, i.e., $\sum _{|I|\le 10} (E(0;0;\Gamma ^I{{\bar{\psi }}})+E(0;0;\Gamma ^I{{\bar{\phi }}}))\le \epsilon ^2$. We first note that by a standard Cauchy stability argument, for every $T>0$ (after choosing $\epsilon$ smaller) there exists $C_T>0$ such that $\sum _{|I|\le 10} (E(T;0;\Gamma ^I{{\bar{\psi }}})+E(T;0;\Gamma ^I{{\bar{\phi }}}))\le C_T\epsilon ^2$. We then make the bootstrap assumptions $\sum _{|I|\le 10} (E(t;0;\Gamma ^I{{\bar{\psi }}})+E(t;0;\Gamma ^I{{\bar{\phi }}}))\le \epsilon (1+t)^{\delta }$ for $\delta \ll \gamma$. The bootstrap assumption implies some pointwise bounds using (1.7) and (1.8) so that we can bound the first equation in (1.10) by

$$\begin{aligned} |\Box \Gamma ^I{{\bar{\phi }}}|\lesssim \frac{|\partial \Gamma ^I{{\bar{\phi }}}|+|\partial \Gamma ^I{{\bar{\psi }}}|}{(1+t)^{1+\gamma }}+\frac{|{\bar{\partial }}\Gamma ^I{{\bar{\phi }}}|+|{\bar{\partial }}\Gamma ^I{{\bar{\psi }}}|}{(1+t)^{1-\delta }(1+||x|-t|)^\gamma }+\cdots . \end{aligned}$$

(1.11)

We now apply the energy estimates (1.6) to (1.11) with $t\ge T>0$ and T sufficiently large to be chosen. Noticing that the term on $\{t=T\}$ can be controlled by the Cauchy stability argument described above, we then get

$$\begin{aligned} \begin{aligned}&\,\sum _{|I|\le 10}\sup _{t'\in [T,t]} E(t';T;\Gamma ^I{{\bar{\phi }}})\\&\quad \lesssim \,C_T\epsilon ^2+\sum _{|I|\le 10}\left( \int _T^t \frac{\left( \int _{\{t'\}\times {\mathbb {R}}^3} w(|x|-t')(|\partial \Gamma ^I{{\bar{\phi }}}|^2(t',x)+|\partial \Gamma ^I{{\bar{\psi }}}|^2(t',x)\,{\text {d}}x\right) ^{\frac{1}{2}}}{(1+t')^{1+\gamma }} {\text {d}}t'\right) ^2 \\&\qquad +\sum _{|I|\le 10}\left( \int _T^t \left( \int _{\{t'\}\times {\mathbb {R}}^3} \frac{w(|x|-t')(|{\bar{\partial }}\Gamma ^I{{\bar{\phi }}}|^2(t',x)+|{\bar{\partial }}\Gamma ^I{{\bar{\psi }}}|^2(t',x))}{(1+t')^{2-2\delta }(1+||x|-t'|)^{2\gamma }}\,{\text {d}}x\right) ^{\frac{1}{2}} {\text {d}}t'\right) ^2\\&\quad \lesssim \,C_T\epsilon ^2+T^{-\gamma }\sum _{|I|\le 10}\sup _{t'\in [T,t]} (E(t';T;\Gamma ^I{{\bar{\phi }}})+E(t';T;\Gamma ^I{{\bar{\psi }}})) \\&\qquad +\left( \int _T^t \int _{\{t'\}\times {\mathbb {R}}^3} \frac{w(|x|-t')(|{\bar{\partial }}\Gamma ^I{{\bar{\phi }}}|^2(t',x)+|{\bar{\partial }}\Gamma ^I{{\bar{\psi }}}|^2(t',x))}{(1+t')^{1-\gamma -2\delta }(1+||x|-t'|)^{2\gamma }}\,{\text {d}}x {\text {d}}t'\right) \left( \int _T^t \frac{{\text {d}}t'}{(1+t')^{1+\gamma }}\right) \\&\quad \lesssim \,C_T\epsilon ^2+T^{-\gamma }\sum _{|I|\le 10}\sup _{t'\in [T,t]} (E(t';T;\Gamma ^I{{\bar{\phi }}})+E(t';T;\Gamma ^I{{\bar{\psi }}}))\\&\quad \lesssim C_T\epsilon ^2+T^{-\gamma }\sum _{|I|\le 10}\sup _{t'\in [T,t]}E(t';T;\Gamma ^I{{\bar{\psi }}}).\nonumber \end{aligned}\!\!\!\!\!\!\\ \end{aligned}$$

(1.12)

where we have used $\frac{w(|x|-t')}{(1+t')^{1-\gamma -2\delta }(1+||x|-t'|)^{2\gamma }}\lesssim w'(|x|-t')$ and the very last estimate is achieved by choosing T sufficiently large and absorbing the term $T^{-\gamma }\sum _{|I|\le 10}\sup _{t'\in [T,t]} E(t;T;\Gamma ^I{{\bar{\phi }}})$ to the left-hand side. On the other hand, applying (1.9) to (1.11) (for $|I|=0$) and using the bootstrap assumption together with (1.7) and (1.8) to control the terms on the right-hand side, we get

$$\begin{aligned} \sup _x|\partial {{\bar{\phi }}}|(t,x)\lesssim \frac{\epsilon }{1+t}. \end{aligned}$$

Plugging this into the second equation in (1.10) and applying the energy estimate (1.6) (again using the estimates from Cauchy stability on the constant T-hypersurface), we get

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le 10}\sup _{t'\in [T,t]} E(t';T;\Gamma ^I{{\bar{\psi }}})\\&\quad \lesssim \, C_T\epsilon ^2+\sum _{|I|\le 10}\left( \int _T^t \frac{(\int _{\{t'\}\times {\mathbb {R}}^3} w(|x|-t')|\partial \Gamma ^I{{\bar{\phi }}}|^2(t',x)\,\hbox {d}x)^{\frac{1}{2}}}{(1+t')} \hbox {d}t'\right) ^2\\&\quad \lesssim \, C_T\epsilon ^2\log ^2(2+t)+T^{-\gamma }\sum _{|I|\le 10}\left( \int _T^t \frac{E(t';T;\Gamma ^I{{\bar{\psi }}})^{\frac{1}{2}}}{(1+t')} \hbox {d}t'\right) ^2,\nonumber \end{aligned}\\ \end{aligned}$$

(1.13)

where in the last line we have plugged in (1.12) and the $C_T\epsilon ^2\log ^2(2+t)$ term arises from $C_T\epsilon ^2(\int _T^t \frac{{\text {d}}t'}{1+t'})^2$. Taking square root of (1.13), choosing T sufficiently large (depending on $\delta$) and using Grönwall’s inequality, we thus get

$$\begin{aligned} \sum _{|I|\le 10}\sup _{t'\in [T,t]} E(t';T;\Gamma ^I{{\bar{\psi }}})\lesssim C_T\epsilon ^2 (1+t)^{\frac{\delta }{2}}. \end{aligned}$$

Plugging this back into (1.12), we then obtain

$$\begin{aligned} \sum _{|I|\le 10}\sup _{t'\in [T,t]} E(t';T;\Gamma ^I{{\bar{\phi }}})\lesssim C_T\epsilon ^2 (1+t)^{\frac{\delta }{2}}. \end{aligned}$$

Now fix $T>0$ so that the above argument goes through. We can then choose $\epsilon >0$ to be sufficiently small and improve the bootstrap assumption.

In the above argument, we see that while all the estimates are coupled and have to be treated via a bootstrap argument, one can exploit the reductive structure in the sense that by first treating the estimates for ${{\bar{\phi }}}$, we can obtain the crucial smallness factor $T^{-\gamma }$ (see (1.12)). Moreover, we can close the argument allowing the energy to grow with a slow rate.¹²

1.2.4 Weak Null Condition for the Einstein-Scalar Field System

As shown in [45, 46], the Einstein-scalar field system has a weak null structure similar to that in the model problem (1.3). This thus gives hope to generalizing the small data results of [45, 46] to the stability of large data solutions. However, there is an additional difficulty that the weak null structure of the semilinear terms in [45, 46] is not manifest in the wave equations for the components of the metric in Cartesian coordinates. To reveal the weak null structure, on the one hand one needs to use the wave coordinate condition and on the other hand one also needs to project the equation to vector fields¹³$\mathbf{E^\mu }\in \{L,{\underline{L}},E^1,E^2,E^3\}$ adapted to the Minkowskian light cone.

To explain more precisely the structure of the semilinear terms, let us first consider the setting of [45, 46] in which the wave coordinate condition holds. We first note that the terms in the equation for ${\widetilde{\Box }}_g g_{\mu \nu }$ take the form $(g^{-1})(g^{-1})(\partial g)(\partial g)$ or $(\partial \phi )(\partial \phi )$. The most difficult terms in [45, 46] are those which are quadratic in the derivatives, i.e., either the $(\partial \phi )^2$ terms or the metric terms with $g^{-1}$ replaced by m. This is because the remaining terms are at least cubic and are easier to control. In our setting, since we have a large background solution, $g^{-1}-m$ is only linear in the perturbation. However, for the linear terms, we can exploit the decay of $(\partial g_B)^2$ of the background solution and these terms are also easier to treat. We will therefore restrict our attention in this subsection only to the quadratic semilinear terms in the derivatives.

For these quadratic semilinear terms in the equation for ${\widetilde{\Box }}_g g_{\mu \nu }$, it was shown in [45, 46] that while some of the terms obey the classical null condition, the following terms violate it:

$$\begin{aligned} \frac{1}{4} m^{\alpha \alpha '}\partial _\mu g_{\alpha \alpha '} m^{\beta \beta '}\partial _\nu g_{\beta \beta '}-\frac{1}{2} m^{\alpha \alpha '}\partial _\mu g_{\alpha \beta } m^{\beta \beta '}\partial _\nu g_{\alpha ' \beta '}-4\partial _\mu \phi \partial _\nu \phi . \end{aligned}$$

(1.14)

Notice that if (1.14) is contracted with $\mathbf{E}^\mu , \mathbf{E}^\nu \in \{L,{\underline{L}},E^1,E^2,E^3\}$ with $\mathbf{E}^\mu \ne {\underline{L}}$ and $\mathbf{E}^\nu \ne {\underline{L}}$, then we have at least one good ${\bar{\partial }}$ derivative and the quadratic term behaves essentially as a term obeying the null condition. Therefore, the “bad” terms only appear in the equation ${\underline{L}}^\mu {\underline{L}}^\nu {\widetilde{\Box }}_g g_{\mu \nu }$. Using the properties of the vector fields $\{L,{\underline{L}},E^1,E^2,E^3\}$ in Minkowski spacetime, we thus have

$$\begin{aligned} |{\underline{L}}^\mu {\underline{L}}^\nu {\widetilde{\Box }}_g g_{\mu \nu }|\lesssim |\partial h|_{{\mathcal {T}}{\mathcal {U}}}|\partial h|_{{\mathcal {T}}{\mathcal {U}}}+|\partial h|_{LL}|\partial h|+|\partial \phi ||\partial \phi |+\dots , \end{aligned}$$

(1.15)

where we have defined the notation for projection to $\mathbf{E}^\mu$ by

$$\begin{aligned} |\partial p|^2_{{\mathcal {V}}{\mathcal {W}}}:=\sum _{U\in {\mathcal {U}},V\in {\mathcal {V}},W\in {\mathcal {W}}}|(\partial _\gamma p_{\alpha \beta })V^{\alpha }W^{\beta }U^\gamma |^2, \end{aligned}$$

with ${\mathcal {T}}:=\{L,E^1,E^2,E^3\}$, ${\mathcal {U}}:=\{L,{\underline{L}},E^1,E^2,E^3\}$, $L=\{L\}$ and ${\mathcal {V}}$, ${\mathcal {W}}$ can be any of these sets. To proceed, it was observed in [45, 46] that by using the wave coordinate condition ${\widetilde{\Box }}_g x^{\mu }=0$, one can rewrite the derivatives of some components of the metric as the good ${\bar{\partial }}$ derivative of some other components of the metric. Namely,

$$\begin{aligned} |\partial h|_{L{\mathcal {T}}} \lesssim |{\bar{\partial }}h|+\text{ quadratic } \text{ terms }. \end{aligned}$$

(1.16)

In particular, since $L\in {\mathcal {T}}$, this gives good control of $|\partial h|_{LL}$ and using (1.15) together with the above observations, we have the system

$$\begin{aligned} {\left\{ \begin{array}{ll} |{\underline{L}}^\mu {\underline{L}}^\nu {\widetilde{\Box }}_g g_{\mu \nu }|\lesssim |\partial h|_{{\mathcal {T}}{\mathcal {U}}}|\partial h|_{{\mathcal {T}}{\mathcal {U}}}+|\partial \phi ||\partial \phi |+\text{ good } \text{ terms },\\ \sum _{V\in {\mathcal {T}},\,W\in {\mathcal {U}}}|V^\mu W^\nu {\widetilde{\Box }}_g g_{\mu \nu }|=\text{ good } \text{ terms },\\ \Box _g\phi =0, \end{array}\right. } \end{aligned}$$

which almost obeys a reductive structure analogous to (1.4), except for the need to commute ${\widetilde{\Box }}_g$ and the projection to V and W in the second equation.

1.2.5 Localization to the Wave Zone, Projection to Vector Fields Adapted to Minkowskian Null Cone and a Generalized Wave Coordinate Condition

One of the difficulties in exploiting the reductive structure for the semilinear terms is that the projection to $\mathbf{E}^\mu$ does not commute with¹⁴${\widetilde{\Box }}_g$. One of the key insights in [45, 46] is that one can in fact prove $L^\infty$ estimates capturing this reductive structure without commuting the projection to $\mathbf{E}^\mu$ with ${\widetilde{\Box }}_g$. More precisely, they adapted a strategy that treats all components on an equal footing in the energy estimates and allow the energy to grow with a slow $(1+t)^{C\epsilon }$ rate. At the same time, they applied an independent estimate, which is an extension of (1.9) to the quasilinear setting, for the $L^\infty$ decay. This independent $L^\infty -L^\infty$ estimate exploits the reductive structure without commutation and gives the sharp $L^\infty$ decay rates. It is precisely because of this sharp $L^\infty$ decay estimates that it is possible to control the growth of the energy.

However, in the setting of our paper, as we have already seen in the model problem in Sect. 1.2.3, it is important to capture the reductive structure also in $L^2$. Indeed, if we only capture the reductive structure at the $L^\infty$ level, then the energy grows as $(1+t)^C$ and we will not be able to close the bootstrap. We therefore also need to capture the reductive structure when proving the energy estimates.

The main observation in this paper is that we can divide the spacetime into various regions.¹⁵ First, as mentioned in Sect. 1.2.2, while the background solution does not have better than $O(\frac{1}{1+t})$ uniform decay, it decays better in $|x|-t$ as $|x|-t\rightarrow \pm \infty$. Therefore, in the region where $||x|-t|$ is large, this is similar to the small data problem and it suffices to use the reductive structure in $L^\infty$ as in [45, 46]. In the remaining region, which has a finite $||x|-t|$-range, we show that the commutator of ${\widetilde{\Box }}_g$ with the projection to $\mathbf{E}^\mu$ is in fact controllable. More precisely, the most slowly-decaying term in the commutator only contains good derivatives,¹⁶ and takes the form $\frac{|{\bar{\partial }}\Gamma ^I h|}{|x|}$. These terms can therefore be controlled using the good bulk term for $|{\bar{\partial }}\Gamma ^I h|$ in the energy estimates (recall (1.6)). Notice that the weight $w'(|x|-t)$ in the good bulk term in (1.6) degenerates as $|x|-t\rightarrow \pm \infty$—it is therefore important that we apply this estimate only in a region with some cutoff in the $||x|-t|$-length.¹⁷

The above discussion relies on the possibility to localize our estimates near spacelike and timelike infinities, as well as near the wave zone. However, there is another obstacle in order to carry out the localization of the estimates into different regions as outlined above. Even for small perturbations of the Minkowski spacetime in wave coordinates, the null hypersurfaces of the nonlinear spacetime diverge from that of the background spacetime logarithmically. In our setting, if such divergences occur, constant $(|x|-t)$-hypersurfaces will potentially¹⁸ be timelike, which does not allow us to localize the energy estimates into regions as described above. As a consequence, we need to use a carefully chosen generalized wave coordinate condition such that the constant $(|x|-t)$-hypersurfaces approaches null as $t\rightarrow \infty$.

This is achieved in two parts: First, we need to choose a coordinate system for the background solution such that the outgoing null hypersurfaces are “well approximated” by hypersurfaces with constant $|x|-t$ values. This is achieved by choosing the background gauge such that the components $|h_B|_{L{\mathcal {T}}}$ have improved decay (see discussions in Sect. 1.2.2). Second, we need to pick a gauge for the perturbed solution such that outgoing null hypersurfaces are again well-approximated constant $(|x|-t)$-hypersurfaces.

Dealing with the second point above is closely related to the “problem of mass,” i.e., the difficulties created by the long range effect of slow decay of the mass term when carrying out the estimates. In particular, the mass term gives infinite energy for an $L^2$ norm of the type that is used in (1.6) (see also the statement of Theorem 5.2). In [46], this is dealt with by approximating the contribution of mass by a term $\chi (r)\chi (\frac{t}{r})\frac{M}{r}\delta _{\mu \nu }$, where $\chi$ is an appropriate cutoff function. This choice, while sufficient for the purpose of [45, 46], leads to a logarithmic divergence of the null hypersurfaces. Instead, we approximate the contribution of the mass by the metric $h_S$, to be defined in Definition 3.2. We then decompose the metric as $g=g_B+h_S+h$ so that h has finite weighted energy and can be controlled using energy estimates. The key point of the choice $h_S$ is that the components $|h_S|_{L{\mathcal {T}}}=0$ and therefore the constant $(|x|-t)$-hypersurfaces approach null as $t\rightarrow \infty$, as long as we can show that $|h|_{L{\mathcal {T}}}$ is also sufficiently well behaved. However, the issue now is that unlike $\frac{M}{r}$, the components of $h_S$ are not solutions to the wave equation. We therefore need to modify the choice of our generalized wave gauge and to impose $\Box _g x^\mu = {\mathcal {G}}^\mu _B+{\mathcal {G}}^\mu _S$, where ${\mathcal {G}}^\mu _B$ is the gauge contribution from the background $g_B$ and ${\mathcal {G}}^\mu _S$ is chosen to cancel with the highest order contribution of $\Box _{m+h_S} x^\mu$ for large |x| (see precise definitions in (4.2)).

Recall from our earlier discussions in Sect. 1.2.4 that the wave coordinate condition is also used to handle some semilinear terms¹⁹ in [45, 46]. As we just discussed, this is replaced by a generalized wave condition involving ${\mathcal {G}}^\mu _B$ and ${\mathcal {G}}^\mu _S$ in our setting. When applying this condition to obtain improved estimates for the derivatives of the good components $|\partial h|_{L {\mathcal {T}}}$, there are extra terms coming from ${\mathcal {G}}^\mu _S$ of order $O(\frac{\epsilon \log (2+t+|x|)}{1+t+|x|})$ (see for example (8.1)), which is insufficient to close the estimates. Nevertheless, one finds a crucial cancellation in the terms $O(\frac{\epsilon \log (2+t+|x|)}{1+t+|x|})$ so that (1.16) still holds with some additional controllable error terms. This cancellation can be traced back to the fact that the approximate mass term $h_S$ is (at the highest order) chosen to be isometric to the Schwarzschild metric, which is itself a solution to the Einstein equations (see Proposition 9.3).

1.2.6 Localized Energy Estimates

Let us elaborate slightly further the localization procedure that we mentioned above. The key point is to use the fact that for every fixed $U\in {\mathbb {R}}$, there exists $T_U\ge 0$ such that the set ${\mathcal {B}}_U:=\{t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}=U \}$ is spacelike when restricted to $t\ge T_U$. To see this, it suffices to show that along every fixed ${\mathcal {B}}_U$, $|g-m|_{L{\mathcal {T}}}(t,x)\lesssim _U \frac{1}{(1+t)^{1+\frac{\gamma }{2}}}$. This decay is achieved by a combination²⁰ of the choice of the background gauge, the choice of $h_S$ (and the generalized wave coordinate condition) and also the decay for $|h|_{L{\mathcal {T}}}$. The decay for $|h_B|_{L{\mathcal {T}}}$ and $|h_S|_{L{\mathcal {T}}}$ has already been briefly discussed in previous subsections. The decay for $|h|_{L{\mathcal {T}}}$, on the other hand, is proven by using the generalized wave coordinate condition, which gives an analogue of (1.16) and implies an estimate $|\partial h|_{L{\mathcal {T}}}(t,x)\lesssim \frac{\epsilon (1+||x|-t|)^{\frac{3\gamma }{8}}}{w(|x|-t)^{\frac{1}{2}}(1+t+|x|)^{1+\frac{\gamma }{2}}}$. This can then be integrated along radial constant $(t+|x|)$-curves to give $|h|_{L{\mathcal {T}}}(t,x)\lesssim \frac{\epsilon (1+||x|-t|)^{\frac{1}{2}+\gamma }}{w(|x|-t)^{\frac{1}{2}}(1+t+|x|)^{1+\frac{\gamma }{2}}}$ (see the proof of Proposition 18.14). Therefore, on each fixed ${\mathcal {B}}_U$, we have the desired decay estimate.

Once we have this decay estimate for $|g-m|_{L{\mathcal {T}}}$, we can then prove the standard $(|x|-t)$-weighted energy estimates of the form (1.6) and note that the contributions on the set ${\mathcal {B}}_U\cap \{t\ge T\}$ have favorable signs (see the proof Proposition 11.3). This then allows the estimates to be localized to the future or past of ${\mathcal {B}}_U\cap \{t\ge T\}$, as long as $T>0$ is sufficiently large.

1.2.7 Commutators and Higher-Order Estimates

In this section and Sect. 1.2.8, we further discuss some technical difficulties which are already present in [45, 46], and can be treated with only minor modifications.

Up to this point, the discussions focused on the semilinear error terms, especially those that do not obey a classical null condition. In addition to those, there are also the quasilinear error terms. In particular, the most difficult error terms arise from the commutation of ${\widetilde{\Box }}_g$ and the Minkowskian vector fields $\Gamma$. It turns out that after choosing the gauge as described in Sect. 1.2.5, these error terms in the large data setting can also be treated in a similar manner as in [45, 46].

Writing $H^{\alpha \beta }:=(g^{-1})^{\alpha \beta }-m^{\alpha \beta }$, where m is the Minkowski metric, the commutators are given by $[{\widetilde{\Box }}_g, \Gamma ]=[\Box _m,\Gamma ]+(-\Gamma H^{\alpha \beta }+H^{\alpha \gamma }(\partial _\gamma \Gamma ^\beta )+H^{\beta \gamma }(\partial _\gamma \Gamma ^\alpha ))\partial _\alpha \partial _\beta$. As pointed out in [45, 46], for $\Gamma$ a Minkowskian commuting vector field²¹$L^\sigma L^\gamma (m_{\alpha \sigma }\partial _\gamma \Gamma ^\alpha )=0$ and therefore either there is a good derivative in the commutator term or we have to control²²$|H|_{L{\mathcal {T}}}$ and $|\Gamma H|_{LL}$. To this end, we need improved decay²³ for $|g-m|_{L{\mathcal {T}}}$ and $\sum _{|I|=1}|\Gamma ^I(g-m)|_{LL}$ (see Proposition 7.3). For the zeroth-order derivative, as we explained near the end of Sect. 1.2.5, this can be obtained precisely due to the choice of our gauge condition and the generalized wave coordinate condition. It turns out that similar ideas can be extended to control $|\Gamma (g-m)|_{LL}$ due to properties of the Minkowskian commuting vector fields.

Notice that, however, this improved decay no longer holds for $\sum _{|I|=2}|\Gamma ^I h|_{LL}$ and $\sum _{|I|=1}|\Gamma ^I h|_{L{\mathcal {T}}}$. As a consequence, for higher commutations, the good structure for the commutator terms only occurs at the top order and there are lower-order terms which do not have a good structure. As we will explain further below, in order to deal with this issue, for every higher derivative that we take, we prove energy estimates that grow with a slightly higher power in t.

1.2.8 Hierarchy of Estimates

In the discussions above, we saw that both the semilinear terms and the commutator terms have a good null-or-reductive structure. However, we have in fact only discussed this good structure at the top order of derivatives and there are in fact terms which are lower order in derivatives and do not have any good structure. We have already discussed one source of such terms near end of Sect. 1.2.7, which comes from the commutation of ${\widetilde{\Box }}_g$ and $\Gamma$.

More precisely, when considering the equation for |I| $\Gamma$ derivatives, in addition to the top order terms which verify the structure we mentioned earlier, we have some additional terms which are lower order in the number of derivatives:

$$\begin{aligned} \begin{aligned} |{\widetilde{\Box }}_g \Gamma ^I h|&\lesssim \, \text{ Top } \text{ order } \text{ terms }+\sum _{|J_1|+|J_2|\le |I|-1}\left( |\partial \Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|+\frac{|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|}{1+||x|-t|}\right) \\&\quad +\sum _{|J|\le |I|-1}\frac{\log (2+t+|x|)|\partial \Gamma ^J h|}{(1+t+|x|)}+\cdots , \end{aligned} \end{aligned}$$

where $\dots$ denotes some lower-order terms that can be treated similarly that we suppress for the exposition.²⁴ Notice that the logarithm growth in the last term is due to the fact that our background metric only obeys the estimate²⁵$|\Gamma ^J h_B|\lesssim \frac{\log (2+t+|x|)|\partial \Gamma ^J h|}{(1+t+|x|)}$.

This difficulty was already present in [45, 46] and was handled by proving a hierarchy of estimates. In our setting, we will introduce a similar hierarchy. More precisely, we make use of the fact that the terms without a good structure are lower order in terms of derivatives and inductively prove estimates which are worse in terms of the time decay for every additional derivative that we take. We will choose small parameters $\delta$ and $\delta _0$ with $\delta \ll \delta _0$. We then prove energy estimates such that for the k-th derivative²⁶ the energy grows as $\epsilon (1+t)^{(2k+5)\delta _0}$. For the decay estimate, we likewise allow some loss in t for every derivative, but quantified with the smaller parameter $\delta$. Namely, we prove for $k\le \lfloor \frac{N}{2}\rfloor +1$ that

$$\begin{aligned}&\sum _{|I|\le k}\sup _{\begin{array}{c} \tau \in [0,t]\\ x\in {\mathbb {R}}^3 \end{array}}(1+\tau +|x|)(1+||x|-t|)^{\frac{1}{2}-\frac{\gamma }{4}} w(|x|-t)^{\frac{1}{2}}(|\partial \Gamma ^Ih|+|\partial \Gamma ^I\beta |)(\tau ,x)\\&\qquad \lesssim \epsilon (1+t)^{2^k\delta }. \end{aligned}$$

Notice that unlike in [45, 46], our bad lower-order error terms are no longer quadratically small, but nonetheless the hierarchy of estimates fit well with an induction argument in which when we consider an estimate with k derivatives, either we have some additional smallness arising from the good structure of the equation at the top order, or we have error terms which depend on at most $k-1$ derivatives.

For such a scheme to work, we need to follow two important facts: Firstly, the proof of the decay estimates is essentially independent of the loss in t in the energy. This is achieved, as in [45, 46], using an independent ODE argument to derive an estimate similar to (1.9). Secondly, while we allow the estimates to have a small loss in the powers of t for both the energy and the pointwise estimates, in the lowest order it is important that we prove the sharp decay estimates $|\partial h|_{{\mathcal {T}}{\mathcal {U}}}+|\partial \beta |\lesssim \frac{\epsilon }{1+t}$. These sharp estimates play a crucial role in recovering the energy estimates.

This concludes the discussion of the main difficulties and ideas in the proof of the main theorem.

1.3 Outline of the Paper

We end the introduction with an outline of the remainder of the paper.

• We introduce our notations in Sect. 2.

• In Sect. 3, we give a precise statement of our main theorem (see Theorem 3.6).

• In Sect. 4, we introduce the gauge condition and recast the equations as a system of quasilinear wave equations. In Sect. 5, we once again rephrase our main theorem (see Theorem 5.2), but not in terms of the system of quasilinear wave equations.

• In Sect. 6, we introduce the bootstrap assumptions; in Sect. 7, we then derive preliminary bounds which follow immediately from the bootstrap assumptions.

• In Sect. 8, we further analyze our gauge condition. Using in particular results in Sects. 7 and 8, we give the first pointwise estimates for the RHS of the equations for h and $\beta$ in Sects. 9 and 10, respectively. In particular, it is here that we derive the weak null structure of the equations.

• In the remaining sections prove the main estimates needed for the proof of the main theorem.

  • In Sect. 11, we collect linear estimates for the wave equation on curved background.

  • In Sect. 12, we divide the spacetime into 4 regions; we then prove the $L^2$-energy estimates in different regions of the spacetime. The finite-t region is treated by Cauchy stability in Sect. 13. In Sect. 14 we give some general estimates to be used in all the remaining regions. Then, in Sects. 15, 16 and 17, we prove estimates in the region near spatial infinity, near null infinity and near timelike infinity, respectively.

  • Finally, we improve the bootstrap assumptions by proving $L^\infty$ estimates in Sect. 18 and conclude the proof.

2 Notations

In this section, we define the necessary notations that we will use in this paper. In our setting, we have a coordinate system $(t,x^1,x^2,x^3)$ on the manifold-with-boundary $[0,\infty )\times {\mathbb {R}}^3$. We will frequently use $x^0$ and t interchangeably. Moreover, r will denote the function $r=\sqrt{\sum _{i=1}^3(x^i)^2}$. The lower case Latin indices $i,j\in \{1,2,3\}$ are reserved for the spatial coordinates, while the lower case Greek indices $\alpha ,\beta \in \{0,1,2,3\}$ are used for all the spacetime coordinates.

First, we define the following:

Definition 2.1

Let the Minkowskian commuting vector fields to be the set of vector fields

$$\begin{aligned} \left\{ \partial _\mu ,\,x^i\partial _j-x^j\partial _i,\,t\partial _i+x^i\partial _t,\,S:=t\partial _t+\sum _{i=1}^3x^i\partial _i\right\} \end{aligned}$$

defined with respect to the coordinate system $(t,x^1,x^2,x^3)$.

In the remainder of the paper, we will use $\Gamma$ to denote a general Minkowskian commuting vector field. For a multi-index²⁷$I=(i_1,i_2,\dots ,i_{|I|})$, $\Gamma ^I$ will denote a product of |I| Minkowskian commuting vector field. More precisely, order the 11 distinct Minkowskian commuting vector fields above as $\Gamma _{(1)}$, $\Gamma _{(2)}$, ..., $\Gamma _{(11)}$. Then, for $(i_1,i_2,\dots ,i_{|I|})\in \{1,2,\dots , 11\}^{|I|}$, $\Gamma ^I=\Gamma _{(i_1)}\Gamma _{(i_2)}\cdots \Gamma _{(i_{|I|})}$.

We also define the vector fields $\{L,{\underline{L}},E^1,E^2,E^3\}$ as follows:

Definition 2.2

Let $\partial _r=\sum _{i=1}^3\frac{x^i}{r}\partial _i$. Define

$$\begin{aligned} L=\partial _t+\partial _r,\quad {\underline{L}}=\partial _t-\partial _r. \end{aligned}$$

We will also define the vector fields $\{E^1,E^2,E^3\}:=\{\frac{x^2}{r}\partial _3-\frac{x^3}{r}\partial _2,\,\frac{x^1}{r}\partial _3-\frac{x^3}{r}\partial _1,\,\frac{x^1}{r}\partial _2-\frac{x^2}{r}\partial _1\}$ tangent²⁸ to the coordinate 2-spheres given by constant r-value. We will use capital Latin indexed $E^A$ to denote an element of $\{E^1,E^2,E^3\}$ and use small Greek indexed and bold $\mathbf{E}^\mu$ to denote an element of the set $\{L,{\underline{L}},E^1,E^2,E^3\}$.

We will also use the coordinates $(s,q,\omega ):=(s,q,\theta ,\varphi )$, where $\omega =(\theta ,\varphi )$ are the usual polar coordinates and (s, q) are defined by

Definition 2.3

$$\begin{aligned} s=t+r,\quad q=r-t. \end{aligned}$$

As a consequence, we have²⁹

$$\begin{aligned} \partial _s=\frac{1}{2}(\partial _t+\partial _r),\quad \partial _q=\frac{1}{2}(\partial _r-\partial _t). \end{aligned}$$

Remark 2.4

Notice the different normalizations of the coordinate vector field $(\partial _s,\partial _q)$ and $(L,{\underline{L}})$.

Remark 2.5

For convenience, we will also use the notation say $q_1=r-t_1$ when $t_1$ is a chosen value of the coordinate function t.

The introduction of these vector fields is important for two reasons. First, the solution has better decay properties when it is differentiated with respect to the “good derivatives” $(L, E^1, E^2, E^3)$. Second, when projected to these vector fields, some “good components” of the metric decay better than the others.

We use the following notations for derivative for a scalar function $\xi$:

Definition 2.6

• (1) General derivatives are denoted by

  $$\begin{aligned} |\partial \xi |^2 := (\partial _t\xi )^2 + \sum _{i=1}^3(\partial _i\xi )^2. \end{aligned}$$

• (2) To capture the improved decay with respect to the “good derivatives,” we define

  

  and

  

• (3) Finally, spatial derivatives are denoted by

  $$\begin{aligned} |\nabla \xi |^2:=\sum _{i=1}^3|\partial _i\xi |^2. \end{aligned}$$

  We will also use the multi-index notation $\nabla ^I$ in a similar manner as that for $\Gamma ^I$ defined above.

We next define the notation for projection to $\mathbf{E}^\mu \in \{L,{\underline{L}},E^1,E^2,E^3\}$ that will be useful in capturing the improved decay for certain components of the metric. First, we introduce the convention that for any 2-tensors, indices are raised and lowered with respect to the Minkowski metric (1.1). We make the following definition for the norms of tensors:

Definition 2.7

Given a 2-tensor p, define

$$\begin{aligned} |p|^2=\sum _{0\le \mu ,\nu \le 3}|p_{\mu \nu }|^2. \end{aligned}$$

We also make the following definitions:

Definition 2.8

Let ${\mathcal {T}}=\{L,E^1,E^2,E^3\}$ and ${\mathcal {U}}=\{L,{\underline{L}},E^1,E^2,E^3\}$. We also abuse notation slightly to denote by L the single element set $\{L\}$. For any two of these family ${\mathcal {V}}$ and ${\mathcal {W}}$ and any 2-tensor p, define

$$\begin{aligned}&|p|^2_{{\mathcal {V}}{\mathcal {W}}}:=\sum _{V\in {\mathcal {V}},W\in {\mathcal {W}}}|p_{\alpha \beta }V^{\alpha }W^{\beta }|^2,\\&|\partial p|^2_{{\mathcal {V}}{\mathcal {W}}}:=\sum _{U\in {\mathcal {U}},V\in {\mathcal {V}},W\in {\mathcal {W}}}|(\partial _\gamma p_{\alpha \beta })V^{\alpha }W^{\beta }U^\gamma |^2,\\&|{\bar{\partial }}p|^2_{{\mathcal {V}}{\mathcal {W}}}:=\sum _{T\in {\mathcal {T}},V\in {\mathcal {V}},W\in {\mathcal {W}}}|(\partial _\gamma p_{\alpha \beta })V^{\alpha }W^{\beta }T^\gamma |^2. \end{aligned}$$

Most importantly, notice that the vector fields contracted outside the differentiation (in a way similar to [45, 46]).

Remark 2.9

We will in particular use the notation introduced in Definition 2.8 for $\Gamma ^I h$. Here, we view $(\Gamma ^I h)_{\mu \nu }$ as a 2-tensor where each component with respect to the coordinate system $(t,x^1,x^2,x^3)$ is simply given by the component-wise derivative by $\Gamma ^I$.

Remark 2.10

We will use the convention that indices are raised and lowered using the Minkowski metric m. In particular, Definitions 2.7 and 2.8 apply to contravariant 2-tensors as well as covariant 2-tensors.

We now define the some notations for the subsets of the spacetime that we consider.

$$\begin{aligned}&\Sigma _{\tau }:=\{(t,x): t=\tau \},\\&D_{\tau }:=\{(t,x):t=\tau ,\,\frac{t}{2}\le |x|\le 2t\}, \\&{\mathcal {R}}_1:= \{(t,x):t\le T\},\\&{\mathcal {R}}_2:=\left\{ (t,x):t\ge T,\,t-|x|-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U_2 \right\} ,\,{\mathcal {R}}_{2,\tau }:={\mathcal {R}}_2\cap \Sigma _\tau ,\\&{\mathcal {R}}_3:=\left\{ (t,x):t\ge T,\,U_2\le t-|x|-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U_3 \right\} ,\,{\mathcal {R}}_{3,\tau }:={\mathcal {R}}_3\cap \Sigma _\tau ,\\&{\mathcal {R}}_4:=\left\{ (t,x):t\ge T,\,t-|x|-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\ge U_3 \right\} ,\,{\mathcal {R}}_{4,\tau }:={\mathcal {R}}_4\cap \Sigma _\tau ,\\&{\mathcal {B}}_U:=\left\{ (t,x):t-|x|-\frac{1}{(1+t)^{\frac{\gamma }{4}}}=U\right\} , \end{aligned}$$

where $U_1,\,U_2,\,U_3\in {\mathbb {R}}$ are constants. We will also use the notation ${\mathcal {R}}$ to denote either one of the regions ${\mathcal {R}}_2$, ${\mathcal {R}}_3$ or ${\mathcal {R}}_4$.

Let us collect here a few more pieces of notations that will be used. For metrics, m denotes the Minkowski metric (see (1.1)); $g_B$ denotes the background metric we perturb against; $h_B:=g_B-m$; g denotes the unknown metric; $h_S$ is given in Definition 3.2; $g_S:=m+h_S$ and $h:=g-m-h_B-h_S$. We will also use the following conventions for the inverse metrics: $H^{\alpha \beta }:=(g^{-1})^{\alpha \beta }-m^{\alpha \beta }$ and $H_B^{\alpha \beta }:=(g_B^{-1})^{\alpha \beta }-m^{\alpha \beta }$.

For the scalar field, $\phi$ denotes the unknown scalar field in the spacetime; $\phi _B$ is the background scalar field; $\beta :=\phi -\phi _B$.

We next introduce our conventions for integration. On $\Sigma _\tau$ or its subsets (e.g., ${\mathcal {R}}_{2,\tau }$, ${\mathcal {R}}_{3,\tau }$ and ${\mathcal {R}}_{4,\tau }$), unless otherwise stated, we integrate with respect to ${\text {d}}x:= {\text {d}}x^1{\text {d}}x^2{\text {d}}x^3=r^2\sin \theta \, {\text {d}}\theta \, {\text {d}}\varphi$. In a spacetime region, unless otherwise stated, we integrate with respect to ${\text {d}}x\, {\text {d}}t$. On ${\mathcal {B}}_U\cap \{t_1\le t\le t_2\}$, we will integrate with respect to the measure ${\text {d}}x$, which is defined as follows: For $\Phi (t):=t-\frac{1}{(1+t)^{\frac{\gamma }{4}}}$, $\int _{{\mathcal {B}}_U\cap \{t_1\le t\le t_2\}} F\,{\text {d}}x:=\int _{{\mathcal {B}}_U\cap \{t_1\le t\le t_2\}} F(t=\Phi ^{-1}(|x|+U),x)\,{\text {d}}x^1\, {\text {d}}x^2\, {\text {d}}x^3$, where $F(t=\Phi ^{-1}(|x|+U),x)$ is considered as a function of $x^1$, $x^2$ and $x^3$. Frequently, when there is no danger of confusion, we suppress the explicit dependence of the integrand on the variables of integration. For instance, when F is a function of spacetime, $\int _T^t \int _{\Sigma _\tau } F\,{\text {d}}x\, {\text {d}}\tau$ always implicitly means $\int _T^t \int _{\Sigma _\tau } F(\tau ,x)\,{\text {d}}x\, {\text {d}}\tau$.

Finally, we introduce the convention that in the remainder of the paper, $x \lesssim y$ denotes the inequality $x\le By$ for some constant B. This constant B will eventually be allowed to depend only on the constants C, $\gamma _0$, N in Definition 3.1, the constants $\gamma$ in Definition 3.5 and also the constants $\delta _0$, $\delta$ that we will introduce in the proof.

3 Assumptions on the Background Solution and Second Version of Main Theorem

With the above definitions, we can describe the class of background metrics that we study. We consider a background Lorentzian metric $g_B$ on a manifold-with-boundary diffeomorphic to $[0,\infty )\times {\mathbb {R}}^3$ settling to Minkowski spacetime with a precise rate. On this manifold-with-boundary, there is also a real-valued function $\phi$ which decays to 0 with a rate. The metric $g_B$ and the scalar field $\phi$ together satisfy the Einstein-scalar field system. More precisely, we define

Definition 3.1

Let $\gamma _0>0$ be a real number and $N\ge 11$ be an integer. A spacetime $({\mathcal {M}}=[0,\infty )\times {\mathbb {R}}^3,g_B)$ with a scalar field $\phi _B:{\mathcal {M}}\rightarrow {\mathbb {R}}$ is a dispersive spacetime solution of size $(C,\gamma _0,N)$ if

• (1) (Solution to the Einstein scalar field system) The triple $({\mathcal {M}},g_B,\phi _B)$ is a solution to the Einstein-scalar field system.

• (2) (Limiting to Minkowski space) There exists a global system of coordinate $(t,x^1,x^2,x^3)$ such that with respect to this coordinate system, the metric takes the form

  $$\begin{aligned} g_B-m = h_B, \end{aligned}$$

  where

  $$\begin{aligned} m=-{\text {d}}t^2+\sum _{i=1}^3({\text {d}}x^i)^2 \end{aligned}$$

  is the Minkowski metric and $h_B$ obeys the bound

  $$\begin{aligned} |\Gamma ^I h_B|\le \frac{C\log (2+s)}{1+s} \end{aligned}$$

  for $|I|\le N+1$, where $\Gamma$’s are the Minkowskian commuting vector fields.

• (3) (Decay for derivatives of metric) For $|I|\le N+1$, we have

  $$\begin{aligned} |\partial \Gamma ^I h_B|\le \frac{C}{(1+s)(1+|q|)^{\gamma _0}} \end{aligned}$$

  for any combinations of Minkowskian commuting vector fields $\Gamma$.

• (4) (Improved decay for “good derivatives” of metric) For $|I|\le N+1$, we have

  $$\begin{aligned} |{{\bar{\partial }}} \Gamma ^I h_B|\le \frac{C}{(1+s)^{1+\gamma _0}} \end{aligned}$$

  for any combinations of Minkowskian commuting vector fields $\Gamma$.

• (5) (Improved decay for “good components” of the metric) For $|I|\le 1$, the following components satisfy better bounds:

  $$\begin{aligned} \sum _{|I|\le 1}|\Gamma ^I h_B|_{LL}+|h_B|_{L{\mathcal {T}}}\le \frac{C}{(1+s)^{1+\gamma _0}} \end{aligned}$$

  for any Minkowskian commuting vector field $\Gamma$.

• (6) (Decay for the scalar field) For $|I| \le N+1$, we have

  $$\begin{aligned} |\partial \Gamma ^I \phi _B|\le \frac{C}{(1+s)(1+|q|)^{\gamma _0}},\quad |{{\bar{\partial }}}\Gamma ^I \phi _B|\le \frac{C}{(1+s)^{1+\gamma _0}} \end{aligned}$$

  for any combinations of Minkowskian commuting vector fields $\Gamma$.

• (7) (Uniform Lorentzian assumption of $g_B$) The metric $g_B$ is everywhere Lorentzian with uniformly bounded inverse:

  $$\begin{aligned} |g_B^{-1}|\le C. \end{aligned}$$

  (3.1)

  Let $({\hat{g}}_B)_{ij}$ be the restriction of the metric $g_B$ on the tangent space to the constant t-hypersurfaces (where $i,j=1,2,3$). $({\hat{g}}_B)_{ij}$ satisfies the condition that for any $\xi _i$,

  $$\begin{aligned} C^{-1}|\xi |^2\le \sum _{i,j=1}^3 ({\hat{g}}_B^{-1})^{ij}\xi _i\xi _j\le C|\xi |^2, \end{aligned}$$

  (3.2)

  where

  $$\begin{aligned} |\xi |^2:=(\xi _1)^2+(\xi _2)^2+(\xi _3)^2. \end{aligned}$$

  Also, the spacetime gradient of t is timelike and satisfies

  $$\begin{aligned} (g_B^{-1})^{00}=(g_B^{-1})^{\alpha \beta }\partial _\alpha t\partial _\beta t\le -C^{-1}<0. \end{aligned}$$

  (3.3)

• (8) (Almost wave coordinate condition) For $|I|\le N+1$, the global coordinate functions satisfy the estimate³⁰

  $$\begin{aligned} |\Gamma ^I(\Box _{g_B} x^{\mu })|\le \frac{C\log (2+s)}{(1+s)^2}. \end{aligned}$$

  Here, $\Box _{g_B}$ is the Laplace–Beltrami operator associated with the metric $g_B$, i.e., 

  $$\begin{aligned} \Box _{g_B}:= \frac{1}{\sqrt{-\det g_B}}\partial _\alpha \left( (g_B^{-1})^{\alpha \beta }\sqrt{-\det g_B}\partial _\beta \cdot \right) . \end{aligned}$$

For a fixed dispersive spacetime $({\mathcal {M}},g_B,\phi _B)$, we will define a class of admissible perturbations for which we will show that their maximal globally hyperbolic future developments are future causally geodesically complete and such that the metrics (resp. scalar fields) are globally close to $g_B$ (resp. $\phi _B$). Recall that an initial data set to the Einstein scalar field system consists of a quintuplet $(\Sigma ,{\hat{g}},{\hat{k}},{\hat{\phi }},{\hat{\psi }})$, where $(\Sigma ,{\hat{g}})$ is a Riemannian 3-manifold, ${\hat{k}}$ is a symmetric 2-tensor and ${\hat{\phi }}$ and ${\hat{\psi }}$ are real valued functions on $\Sigma$. Moreover, for $\mathbf{N}$ being the unit future-directed normal to $\Sigma$ in ${\mathcal {M}}$, the following constraint equations are satisfied:

$$\begin{aligned} \begin{aligned} R_{{\hat{g}}}+(\text{ tr}_{{{\hat{g}}}} {{\hat{k}}})^2-|{{\hat{k}}}|_{{\hat{g}}}^2&=4 {\mathbb {T}}(\mathbf{N},\mathbf{N}),\\ \text{ div}_{{\hat{g}}} {{\hat{k}}}-{{\hat{\nabla }}} (\text{ tr}_{{{\hat{g}}}} {{\hat{k}}})&=2{\mathbb {T}}(\mathbf{N},\cdot ), \end{aligned} \end{aligned}$$

where ${{\hat{\nabla }}}$ is defined as the Levi-Civita connection induced by ${{\hat{g}}}$. The celebrated theorems³¹ of Choquet–Bruhat [16] and Choquet–Bruhat–Geroch [17] show that there exists a unique maximal globally hyperbolic future development $({\mathcal {M}},g,\phi )$ to the initial data which solves the Einstein-scalar field system such that $\Sigma$ is an embedded hypersurface in ${\mathcal {M}}$ with ${\hat{g}}$ and ${\hat{k}}$ being the induced first and second fundamental forms. Moreover, $\phi \restriction _{\Sigma }={\hat{\phi }}$ and $\mathbf{N}\phi \restriction _{\Sigma }={\hat{\psi }}$.

Before we proceed to define the class of admissible perturbations, we need to first introduce another piece of notation.

Definition 3.2

Let ${\tilde{h}}_S$ be defined by

$$\begin{aligned}&({\tilde{h}}_S)_{00}=\frac{2M}{r},\quad ({\tilde{h}}_S)_{0i}=0, \\&({\tilde{h}}_S)_{ij}=-\frac{4M\log (r-2M)}{r}\delta _{ij}-\frac{x_i x_j}{r^2}\left( \frac{2M}{r}-\frac{4M\log (r-2M)}{r}\right) \end{aligned}$$

and define $h_S$ by

$$\begin{aligned} h_S=\chi (r)\chi \left( \frac{r}{t}\right) {\tilde{h}}_S, \end{aligned}$$

where $\chi (s)$ is a smooth cutoff function such that it takes value 1 when $s\ge \frac{3}{4}$ and equals to 0 when $s\le \frac{1}{2}$.

Remark 3.3

Notice that for r sufficiently large, $m+h_S$ is just the Schwarzschild metric (with mass M) written in a non-standard coordinate system up to error terms of order $\frac{\log r}{r^2}$. $h_S$ is introduced so as to capture the behavior of mass at infinity.

Remark 3.4

Notice that for $h_S$ defined above, we have

$$\begin{aligned} |\Gamma ^I h_S|\lesssim \frac{|M| \log (2+s)}{1+s},\quad |\partial \Gamma ^I h_S|\lesssim \frac{|M|\log (2+s)}{(1+s)^2} \end{aligned}$$

for³²$|I|\le N+1$. Moreover,

$$\begin{aligned} (h_S)_{LL}=(h_S)_{LE^A}=0. \end{aligned}$$

Hence, $h_S$ satisfies

$$\begin{aligned} |h_S|_{L{\mathcal {T}}} =0 . \end{aligned}$$

Moreover, a direct computation shows that the LL-component of the $\Gamma$ derivative also vanishes:

$$\begin{aligned} |\Gamma h_S|_{LL} =0. \end{aligned}$$

Notice, however, that this property fails for the general $L{\mathcal {T}}$-component or for higher $\Gamma$ derivatives.

We now define the class of admissible perturbations:

Definition 3.5

Let $\epsilon >0$ and $\gamma >0$ be real numbers and $N\ge 11$ be an integer. An initial data set $(\Sigma ,{\hat{g}},{\hat{k}},{\hat{\phi }},{\hat{\psi }})$ is an $(\epsilon ,\gamma ,N)$-admissible perturbation to a dispersive spacetime $({\mathcal {M}},g_B,\phi _B)$ if

• $\Sigma$ is diffeomorphic to ${\mathbb {R}}^3$.

• There is a coordinate system $(x^1,x^2,x^3)$ on $\Sigma$ such that with respect to this coordinate system, we have

  $$\begin{aligned} {\hat{g}}=g_B\restriction _{\Sigma }+h_S\restriction _{\Sigma }+{{\hat{h}}}, \end{aligned}$$

  (3.4)

  where the parameter M in the definition of $h_S$ satisfies

  $$\begin{aligned} |M|\le \epsilon , \end{aligned}$$

  and ${{\hat{h}}}$ obeys the estimates

  $$\begin{aligned} \sum _{|I|\le N}\Vert (1+r)^{\frac{1}{2}+\gamma +|I|}\nabla \nabla ^I {\hat{h}}\Vert _{L^2(\Sigma )}\le \epsilon . \end{aligned}$$

  (3.5)

• In the coordinate system $(x^1,x^2,x^3)$, the second fundamental form verifies the estimates

  $$\begin{aligned} \sum _{|I|\le N-1}\Vert (1+r)^{\frac{1}{2}+\gamma +|I|}\nabla ^I ({\hat{k}}-(k_B)\restriction _{\{t=0\}})\Vert _{L^2(\Sigma )}\le \epsilon . \end{aligned}$$

  (3.6)

• In the coordinate system $(x^1,x^2,x^3)$, ${\hat{\phi }}$ and ${\hat{\psi }}$ obey the bounds

  $$\begin{aligned} \begin{aligned}&\sum _{|I|\le N}\Vert (1+r)^{\frac{1}{2}+\gamma +|I|}\nabla \nabla ^I ({{\hat{\phi }}}-(\phi _B)\restriction _{\{t=0\}})\Vert _{L^2(\Sigma )}\\&\quad +\sum _{|I|\le N-1}\Vert (1+r)^{\frac{1}{2}+\gamma +|I|}\nabla ^I ({{\hat{\psi }}}-(\partial _t\phi _B)\restriction _{\{t=0\}})\Vert _{L^2(\Sigma )}\le \epsilon . \end{aligned} \end{aligned}$$

  (3.7)

Our main result can be summarized in the following theorem:

Theorem 3.6

(Main theorem, second version). Let $N\ge 11$ and $0<\gamma ,\gamma _0\le \frac{1}{8}$. For every dispersive spacetime solution $({\mathcal {M}},g_B,\phi _B)$ of size $(C,\gamma _0,N)$, there exists $\epsilon =\epsilon (C,\gamma ,\gamma _0,N)>0$ sufficiently small such that for all $(\epsilon ,\gamma ,N)$-admissible perturbations of $({\mathcal {M}}_0,g_B,\phi _B)$, the maximal globally hyperbolic future development is future causally geodesically complete and the spacetime remains close to $({\mathcal {M}}_0,g_B,\phi _B)$ in a suitable³³ sense.

Remark 3.7

Without loss of generality, we can assume that $\gamma =\gamma _0$. We make this assumption from now on.

Remark 3.8

(Strongly asymptotically flat spacetimes (cf. [13])). A smooth initial data set $(\Sigma ,{\hat{g}},{\hat{k}},{\hat{\phi }},{\hat{\psi }})$ is said to be strongly asymptotically flat (with one end) if there exists a compact set $K\subset \Sigma$ such that $\Sigma \setminus K$ is diffeomorphic to³⁴${\mathbb {R}}^3\setminus \overline{B(0,1)}$ and there exists a system of coordinates $(x^1, x^2, x^3)$ in a neighborhood of infinity such that as $r:=\sqrt{\sum _{i=1}^3 (x^i)^2}\rightarrow \infty$, we have³⁵, for $\alpha =\frac{3}{2}$ and for some $M>0$,

$$\begin{aligned}&{\hat{g}}_{ij}=\left( 1+\frac{M}{r}\right) \delta _{ij}+o_{\infty }(r^{-\alpha }),\quad {\hat{k}}_{ij}=o_{\infty }(r^{-\alpha -1}), \nonumber \\&{\hat{\phi }}=o_{\infty }(r^{-\alpha }),\quad {\hat{\psi }}=o_{\infty }(r^{-\alpha -1}). \end{aligned}$$

(3.8)

Theorem 3.6 only requires weaker asymptotics at spatial infinity than strong asymptotic flatness for both the background solution and the perturbation, with $\alpha$ above replaced by any real number greater than 1. Notice that the metric in Theorem 3.6 does not have the form as in (3.8). However, as we will see in the next remark below, the different forms of the metric are equivalent after a change of coordinates.

Remark 3.9

(Relation of $h_S$ to the mass term). We show that the term $h_S$ is related to the mass term in (3.8). More precisely, suppose we have a coordinate system $({\tilde{x}}^1,{\tilde{x}}^2,{\tilde{x}}^3)$ on $\Sigma ={\mathbb {R}}^3$ such that with respect to this coordinate system, the intrinsic metric ${\hat{g}}$ on $\Sigma$ takes the form

$$\begin{aligned} {\hat{g}}_{{{\tilde{i}}}{{\tilde{j}}}}=\delta _{{{\tilde{i}}}{{\tilde{j}}}}+\chi ({{\tilde{r}}})\frac{M}{{{\tilde{r}}}}\delta _{{{\tilde{i}}}{{\tilde{j}}}}+{\tilde{h}}_{{{\tilde{i}}}{{\tilde{j}}}}, \end{aligned}$$

where ${\tilde{h}}=o_{\infty }(r^{-\alpha })$. Then, for

$$\begin{aligned} {\tilde{r}}^2:=\sum _{i=1}^3 ({\tilde{x}}^i)^2, \end{aligned}$$

we can introduce the change of coordinates

$$\begin{aligned} x^i=\chi ({\tilde{r}})\frac{{\tilde{x}}^i}{{\tilde{r}}}\big ({\tilde{r}}+2M\log ({{\tilde{r}}}-2M)\big ) \end{aligned}$$

so that the metric takes the form of

$$\begin{aligned} {\hat{g}}_{ij}=\delta _{ij}+(h_S)_{ij}+h \end{aligned}$$

where $h=o_{\infty }(r^{-\alpha }\log (2+r))$.

4 Basic Setup and Gauge Condition

In this section, we write the Einstein scalar field system in terms of a system of quasilinear wave equations. To this end, we introduce a generalized wave gauge. As mentioned before, we cannot use the standard wave gauge for our problem at hand but will need to carefully design a generalized wave gauge to capture the mass at infinity. In particular, this gauge will allow us to localize near the “wave zone” in order to capture the reductive structure of the Einstein scalar field system at the $L^2$ level.

We now define the generalized wave gauge that we will work with: We impose the following condition:

$$\begin{aligned} \Box _{g}x^{\mu }={\mathcal {G}}^\mu ={\mathcal {G}}^\mu _B+{\mathcal {G}}^\mu _S \end{aligned}$$

(4.1)

where³⁶

$$\begin{aligned} {\mathcal {G}}^\mu _B=\Box _{g_B}x^{\mu },\quad {\mathcal {G}}^0_S=0,\quad {\mathcal {G}}^i_S=-\chi (r)\chi (\frac{r}{t})\left( \frac{4M\log (r-2M)}{r^2}\right) \frac{x^i}{r}. \end{aligned}$$

(4.2)

One easily checks that the condition (4.1) can also be rephrased as

$$\begin{aligned}&\partial _{\alpha }((g^{-1})^{\alpha \beta }\sqrt{|\det g|})=\sqrt{|\det g|}{\mathcal {G}}^{\beta }, \end{aligned}$$

(4.3)

$$\begin{aligned}&(g^{-1})^{\alpha \beta }\partial _{\alpha }g_{\beta \mu }-\frac{1}{2} (g^{-1})^{\alpha \beta }\partial _{\mu }g_{\alpha \beta }=-g_{\mu \nu }{\mathcal {G}}^{\nu }, \end{aligned}$$

(4.4)

or

$$\begin{aligned} \partial _{\alpha }(g^{-1})^{\alpha \nu }-\frac{1}{2}g_{\alpha \beta }(g^{-1})^{\mu \nu }\partial _{\mu }(g^{-1})^{\alpha \beta }={\mathcal {G}}^{\nu }. \end{aligned}$$

We can write down the Einstein-scalar field equations under the generalized wave coordinate condition. We introduce the reduced wave operator

$$\begin{aligned} {\widetilde{\Box }}_g:=(g^{-1})^{\alpha \beta }\partial ^2_{\alpha \beta }. \end{aligned}$$

The components of the metric g satisfy a system of wave equations whose principal part is the reduced wave operator. More precisely,

Proposition 4.1

Let $(g,\phi )$ be a solution to the Einstein-scalar field system together with the generalized wave coordinate condition

$$\begin{aligned} \Box _g x^{\mu }={\mathcal {G}}^\mu . \end{aligned}$$

Then, $g_{\mu \nu }$ and $\phi$ solve the following system of equations:

$$\begin{aligned} {\widetilde{\Box }}_g g_{\mu \nu }:= & {} (g^{-1})^{\alpha \beta }\partial _{\alpha \beta }^2 g_{\mu \nu }\\= & {} P(\partial _\mu g,\partial _\nu g)+Q_{\mu \nu }(\partial g,\partial g)+T_{\mu \nu }(\partial \phi ,\partial \phi )+G_{\mu \nu }(g,{\mathcal {G}}), \end{aligned}$$

and

$$\begin{aligned} \Box _g \phi =0, \end{aligned}$$

where P denotes the term

$$\begin{aligned} P(\partial _\mu g,\partial _\nu g)= & {} \frac{1}{4} (g^{-1})^{\alpha \alpha '}\partial _\mu g_{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _\nu g_{\beta \beta '}\\&-\frac{1}{2} (g^{-1})^{\alpha \alpha '}\partial _\mu g_{\alpha \beta }(g^{-1})^{\beta \beta '}\partial _\nu g_{\alpha ' \beta '}, \end{aligned}$$

Q is given by

$$\begin{aligned} \begin{aligned} Q_{\mu \nu }(\partial g,\partial g)=\,\,&\partial _{\alpha }g_{\beta \mu } (g^{-1})^{\alpha \alpha '} (g^{-1})^{\beta \beta '}\partial _{\alpha '}g_{\beta '\nu }-(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\\&\qquad (\partial _{\alpha }g_{\beta \mu }\partial _{\beta '}g_{\alpha '\nu }-\partial _{\beta '}g_{\beta \mu }\partial _\alpha g_{\alpha '\nu })\\&+(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _\mu g_{\alpha '\beta '}\partial _\alpha g_{\beta \nu }-\partial _\alpha g_{\alpha '\beta '}\partial _\mu g_{\beta \nu })\\&+(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _\nu g_{\alpha '\beta '}\partial _\alpha g_{\beta \mu }-\partial _\alpha g_{\alpha '\beta '}\partial _\nu g_{\beta \mu })\\&+\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\beta '} g_{\alpha \alpha '}\partial _\mu g_{\beta \nu }-\partial _\mu g_{\alpha \alpha '}\partial _{\beta '} g_{\beta \nu })\\&+\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\beta '} g_{\alpha \alpha '}\partial _\nu g_{\beta \mu }-\partial _\nu g_{\alpha \alpha '}\partial _{\beta '}g_{\beta \mu }), \end{aligned} \end{aligned}$$

T is the following term involving the scalar field

$$\begin{aligned} T_{\mu \nu }(\partial \phi ,\partial \phi )=-4\partial _{\mu }\phi \partial _\nu \phi , \end{aligned}$$

and G is the following term which arises from the choice of gauge condition:

$$\begin{aligned} \begin{aligned} G_{\mu \nu }(g,{\mathcal {G}})=&-\partial _\mu (g_{\nu \lambda } {\mathcal {G}}^{\lambda })-\partial _\nu (g_{\mu \lambda } {\mathcal {G}}^{\lambda })-{\mathcal {G}}^{\alpha }\partial _\alpha g_{\mu \nu }- g_{\alpha \nu } g_{\beta \mu } {\mathcal {G}}^\alpha {\mathcal {G}}^{\beta }. \end{aligned} \end{aligned}$$

(4.5)

Proof

First, notice that the Einstein-scalar field system (1.2) is equivalent to

$$\begin{aligned} Ric_{\mu \nu }=2 \partial _\mu \phi \partial _\nu \phi . \end{aligned}$$

(4.6)

To see this, we take the trace of (1.2) to get

$$\begin{aligned} -R=2\partial ^\alpha \phi \partial _\alpha \phi -4 \partial ^{\alpha }\phi \partial _{\alpha }\phi =-2 \partial ^{\alpha }\phi \partial _{\alpha }\phi . \end{aligned}$$

Hence,

$$\begin{aligned} Ric_{\mu \nu }- g_{\mu \nu } \partial ^{\alpha }\phi \partial _{\alpha }\phi =2 {\mathbb {T}}_{\mu \nu }=2\partial _\mu \phi \partial _\nu \phi -g_{\mu \nu } \partial ^{\alpha }\phi \partial _{\alpha }\phi , \end{aligned}$$

which implies the conclusion.

Now, in order to derive the equation, we simply need to write out the Ricci curvature in terms of the metric and then insert the generalized wave coordinate condition. This is similar to the derivation in [45]. Since in our setting we have a different gauge condition, we include the proof for completeness.

Define³⁷$\mathbf{\Gamma }^\lambda _{\mu \nu }:= \frac{1}{2} (g^{-1})^{\lambda \sigma }(\partial _{\mu }g_{\nu \sigma }+\partial _{\nu }g_{\mu \sigma }-\partial _\sigma g_{\mu \nu })$. The Ricci curvature is given by

$$\begin{aligned} Ric_{\mu \nu }=\underbrace{\partial _{\alpha }\mathbf{\Gamma }^\alpha _{\mu \nu }-\partial _{\nu }\mathbf{\Gamma }^\alpha _{\alpha \mu }}_{=:\hbox {I}}+\underbrace{\mathbf{\Gamma }^{\alpha }_{\mu \nu }{} \mathbf{\Gamma }^{\beta }_{\alpha \beta } -\mathbf{\Gamma }^{\alpha }_{\mu \beta } \mathbf{\Gamma }^{\beta }_{\nu \alpha }}_{=:\hbox {II}}. \end{aligned}$$

(4.7)

By (4.4), we have

$$\begin{aligned} \partial _\mu \left( (g^{-1})^{\alpha \beta }\partial _{\alpha } g_{\beta \nu }-\frac{1}{2} (g^{-1})^{\alpha \beta }\partial _{\nu } g_{\alpha \beta }\right) =-\partial _\mu (g_{\nu \alpha }{\mathcal {G}}^{\alpha }). \end{aligned}$$

Therefore, using the identity $\partial (g^{-1})^{\alpha \beta }=-(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial g_{\alpha '\beta '}$, we have

$$\begin{aligned} \begin{aligned} -\partial _\mu \left( g_{\nu \lambda }{\mathcal {G}}^{\lambda }\right) =&(g^{-1})^{\alpha \beta }\partial ^2_{\alpha \mu } g_{\beta \nu }-\frac{1}{2} (g^{-1})^{\alpha \beta }\partial ^2_{\mu \nu } g_{\alpha \beta }\\&-(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _\mu g_{\alpha '\beta '}\left( \partial _{\alpha } g_{\beta \nu }-\frac{1}{2}\partial _{\nu } g_{\alpha \beta }\right) . \end{aligned} \end{aligned}$$

Expanding term I in (4.7) using the above identity (and also its analogue with $\mu$ and $\nu$ switched), we have

$$\begin{aligned}&\partial _{\alpha }{} \mathbf{\Gamma }^\alpha _{\mu \nu }-\partial _{\nu }{} \mathbf{\Gamma }^\alpha _{\alpha \mu }\nonumber \\&\quad =\frac{1}{2}(g^{-1})^{\alpha \beta }(\partial ^2_{\alpha \mu } g_{\beta \nu }+\partial ^2_{\alpha \nu } g_{\beta \mu }-\partial ^2_{\alpha \beta } g_{\mu \nu })\nonumber \\&\qquad -\frac{1}{2} (g^{-1})^{\alpha \beta }(\partial ^2_{\nu \alpha }g_{\beta \mu }+\partial ^2_{\nu \mu }g_{\alpha \beta }-\partial ^2_{\nu \beta }g_{\alpha \mu })\nonumber \\&\qquad -\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _{\alpha } g_{\alpha '\beta '}(\partial _{\mu } g_{\beta \nu }+\partial _{\nu } g_{\beta \mu }-\partial _{\beta } g_{\mu \nu })\nonumber \\&\qquad +\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _{\nu } g_{\alpha '\beta '}(\partial _{\alpha }g_{\beta \mu }+\partial _{\mu }g_{\alpha \beta }-\partial _{\beta }g_{\alpha \mu })\nonumber \\&\quad =-\frac{1}{2}(g^{-1})^{\alpha \beta }\partial ^2_{\alpha \beta } g_{\mu \nu }-\frac{1}{2}\partial _{\mu }(g_{\nu \lambda }{\mathcal {G}}^{\lambda })-\frac{1}{2}\partial _{\nu }(g_{\mu \lambda }{\mathcal {G}}^{\lambda })\nonumber \\&\qquad +\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _\mu g_{\alpha '\beta '}\left( \partial _{\alpha } g_{\beta \nu }-\frac{1}{2}\partial _{\nu } g_{\alpha \beta }\right) \nonumber \\&\qquad +\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _\nu g_{\alpha '\beta '}\left( \partial _{\alpha } g_{\beta \mu }-\frac{1}{2}\partial _{\mu } g_{\alpha \beta }\right) \nonumber \\&\qquad -\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _{\alpha } g_{\alpha '\beta '}(\partial _{\mu } g_{\beta \nu }+\partial _{\nu } g_{\beta \mu }-\partial _{\beta } g_{\mu \nu })\nonumber \\&\qquad +\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _{\nu } g_{\alpha '\beta '}(\partial _{\alpha }g_{\beta \mu }+\partial _{\mu }g_{\alpha \beta }-\partial _{\beta }g_{\alpha \mu }). \end{aligned}$$

(4.8)

Collecting the quadratic terms in the derivatives of g in (4.8), we get

$$\begin{aligned}&\partial _{\alpha }{} \mathbf{\Gamma }^\alpha _{\mu \nu }-\partial _{\nu }{} \mathbf{\Gamma }^\alpha { }_{\alpha \mu }\nonumber \\&\quad =-\frac{1}{2}(g^{-1})^{\alpha \beta }\partial ^2_{\alpha \beta } g_{\mu \nu }-\frac{1}{2}\partial _{\mu }(g_{\nu \lambda }{\mathcal {G}}^{\lambda })-\frac{1}{2}\partial _{\nu }(g_{\mu \lambda }{\mathcal {G}}^{\lambda })\nonumber \\&\qquad +\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _\mu g_{\alpha '\beta '}\partial _{\alpha } g_{\beta \nu }\nonumber \\&\qquad +\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _\nu g_{\alpha '\beta '}(2\partial _{\alpha }g_{\beta \mu }-\partial _{\beta }g_{\alpha \mu })\nonumber \\&\qquad -\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _{\alpha } g_{\alpha '\beta '}(\partial _{\mu } g_{\beta \nu }+\partial _{\nu } g_{\beta \mu }-\partial _{\beta } g_{\mu \nu })\nonumber \\&\quad =-\frac{1}{2}(g^{-1})^{\alpha \beta }\partial ^2_{\alpha \beta } g_{\mu \nu }-\frac{1}{2}\partial _{\mu }(g_{\nu \lambda }{\mathcal {G}}^{\lambda })-\frac{1}{2}\partial _{\nu }(g_{\mu \lambda }{\mathcal {G}}^{\lambda })\nonumber \\&\qquad +\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _\mu g_{\alpha '\beta '}\partial _{\alpha } g_{\beta \nu }-\partial _\alpha g_{\alpha '\beta '}\partial _{\mu } g_{\beta \nu })\nonumber \\&\qquad +\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _\nu g_{\alpha '\beta '}\partial _{\alpha }g_{\beta \mu }-\partial _\alpha g_{\alpha '\beta '}\partial _{\nu }g_{\beta \mu })\nonumber \\&\qquad +\underbrace{\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _\alpha g_{\alpha '\beta '}\partial _{\beta } g_{\mu \nu }}_{=:\hbox {III}}. \end{aligned}$$

(4.9)

Expanding term II (4.7), we get

$$\begin{aligned}&\mathbf{\Gamma }^{\alpha }_{\mu \nu }{} \mathbf{\Gamma }^{\beta }_{\alpha \beta } -\mathbf{\Gamma }^{\alpha }_{\mu \beta } \mathbf{\Gamma }^{\beta }_{\alpha \nu }\nonumber \\&\quad =\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\mu }g_{\alpha '\nu }+\partial _\nu g_{\alpha '\mu }-\partial _{\alpha '}g_{\mu \nu })\partial _{\alpha }g_{\beta \beta '}\nonumber \\&\qquad -\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\mu }g_{\alpha '\beta }+\partial _\beta g_{\alpha '\mu }-\partial _{\alpha '}g_{\mu \beta })(\partial _{\alpha }g_{\nu \beta '}+\partial _\nu g_{\alpha \beta '}-\partial _{\beta '} g_{\alpha \nu })\nonumber \\&\quad =\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\mu }g_{\alpha '\nu }\partial _{\alpha }g_{\beta \beta '}+\partial _\nu g_{\alpha '\mu }\partial _{\alpha }g_{\beta \beta '}-\partial _{\alpha '}g_{\mu \nu }\partial _{\alpha }g_{\beta \beta '})\nonumber \\&\qquad -\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\mu }g_{\alpha '\beta }\partial _{\alpha }g_{\nu \beta '}+\partial _\beta g_{\alpha '\mu }\partial _{\alpha }g_{\nu \beta '}-\partial _{\alpha '}g_{\mu \beta }\partial _{\alpha }g_{\nu \beta '})\nonumber \\&\qquad -\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\mu }g_{\alpha '\beta }\partial _\nu g_{\alpha \beta '}+\partial _\beta g_{\alpha '\mu }\partial _\nu g_{\alpha \beta '}-\partial _{\alpha '}g_{\mu \beta }\partial _\nu g_{\alpha \beta '})\nonumber \\&\qquad +\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\mu }g_{\alpha '\beta }\partial _{\beta '} g_{\alpha \nu }+\partial _\beta g_{\alpha '\mu }\partial _{\beta '} g_{\alpha \nu }-\partial _{\alpha '}g_{\mu \beta }\partial _{\beta '} g_{\alpha \nu })\nonumber \\&\quad =\underbrace{\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\mu }g_{\alpha '\nu }\partial _{\alpha }g_{\beta \beta '}+\partial _\nu g_{\alpha '\mu }\partial _{\alpha }g_{\beta \beta '}-\partial _{\alpha '}g_{\mu \nu }\partial _{\alpha }g_{\beta \beta '})}_{=:\hbox {IV}}\nonumber \\&\qquad \underbrace{-\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _{\alpha '}g_{\mu \beta }\partial _{\beta '} g_{\alpha \nu }}_{=:\hbox {V}}+\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _{\alpha '}g_{\mu \beta }\partial _{\alpha }g_{\nu \beta '}\nonumber \\&\qquad -\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _{\mu }g_{\alpha '\beta }\partial _\nu g_{\alpha \beta '}. \end{aligned}$$

(4.10)

Further expanding III in (4.9) using (4.4), we get

$$\begin{aligned} \begin{aligned} \hbox {III}&=\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _\alpha g_{\alpha '\beta '}\partial _{\beta } g_{\mu \nu }\\&=\frac{1}{2}(g^{-1})^{\beta \beta '}\left( \frac{1}{2}(g^{-1})^{\alpha \alpha '}\partial _{\beta '} g_{\alpha \alpha '}-g_{\beta '\alpha }{\mathcal {G}}^{\alpha }\right) \partial _{\beta } g_{\mu \nu }\\&=\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _{\beta '} g_{\alpha \alpha '}\partial _{\beta } g_{\mu \nu }-\frac{1}{2}{\mathcal {G}}^{\beta }\partial _{\beta } g_{\mu \nu }. \end{aligned} \end{aligned}$$

(4.11)

Using (4.4), IV in (4.10) can be expressed as

$$\begin{aligned} \hbox {IV}&=\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\mu }g_{\alpha '\nu }\partial _{\alpha }g_{\beta \beta '}+\partial _\nu g_{\alpha '\mu }\partial _{\alpha }g_{\beta \beta '}-\partial _{\alpha '}g_{\mu \nu }\partial _{\alpha }g_{\beta \beta '})\nonumber \\&=\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\mu }g_{\alpha '\nu }\partial _{\alpha }g_{\beta \beta '}-\partial _{\alpha }g_{\alpha '\nu }\partial _{\mu }g_{\beta \beta '})\nonumber \\&\quad +\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _\nu g_{\alpha '\mu }\partial _{\alpha }g_{\beta \beta '}-\partial _\alpha g_{\alpha '\mu }\partial _{\nu }g_{\beta \beta '})\nonumber \\&\quad +\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\alpha }g_{\alpha '\nu }\partial _{\mu }g_{\beta \beta '}+\partial _\alpha g_{\alpha '\mu }\partial _{\nu }g_{\beta \beta '}-\partial _{\alpha '}g_{\mu \nu }\partial _{\alpha }g_{\beta \beta '})\nonumber \\&=\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\mu }g_{\alpha '\nu }\partial _{\alpha }g_{\beta \beta '}-\partial _{\alpha }g_{\alpha '\nu }\partial _{\mu }g_{\beta \beta '})\nonumber \\&\quad +\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _\nu g_{\alpha '\mu }\partial _{\alpha }g_{\beta \beta '}-\partial _\alpha g_{\alpha '\mu }\partial _{\nu }g_{\beta \beta '})\nonumber \\&\quad +\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _\nu g_{\alpha \alpha '}\partial _{\mu }g_{\beta \beta '}\nonumber \\&\quad +\frac{1}{4}(g^{-1})^{\beta \beta '}(-g_{\nu \alpha }{\mathcal {G}}^\alpha \partial _{\mu }g_{\beta \beta '}-g_{\mu \alpha }{\mathcal {G}}^\alpha \partial _{\nu }g_{\beta \beta '})\nonumber \\&\quad -\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _{\alpha '}g_{\mu \nu }\partial _{\alpha }g_{\beta \beta '}. \end{aligned}$$

(4.12)

We then expand the term V in (4.10) using (4.4):

$$\begin{aligned} \begin{aligned} \hbox {V}&=-\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _{\alpha '}g_{\mu \beta }\partial _{\beta '} g_{\alpha \nu }\\&=-\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\alpha '}g_{\mu \beta }\partial _{\beta '} g_{\alpha \nu }-\partial _{\beta '}g_{\mu \beta }\partial _{\alpha '} g_{\alpha \nu }) \\&\quad -\frac{1}{2}\left( \frac{1}{2}(g^{-1})^{\beta \beta '}\partial _{\mu }g_{\beta \beta '}-g_{\mu \beta }{\mathcal {G}}^{\beta }\right) \left( \frac{1}{2}(g^{-1})^{\alpha \alpha '}\partial _{\nu } g_{\alpha \alpha '}-g_{\nu \alpha }{\mathcal {G}}^{\alpha }\right) \\&=-\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\alpha '}g_{\mu \beta }\partial _{\beta '} g_{\alpha \nu }-\partial _{\beta '}g_{\mu \beta }\partial _{\alpha '} g_{\alpha \nu }) \\&\quad -\frac{1}{8}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _{\mu }g_{\beta \beta '}\partial _{\nu } g_{\alpha \alpha '}\\&\quad +\frac{1}{4}(g^{-1})^{\beta \beta '}\partial _{\mu }g_{\beta \beta '}g_{\nu \alpha }{\mathcal {G}}^{\alpha }+\frac{1}{4}(g^{-1})^{\alpha \alpha '}\partial _{\nu }g_{\alpha \alpha '}g_{\mu \beta }{\mathcal {G}}^{\beta }-\frac{1}{2}g_{\nu \alpha } g_{\mu \beta } {\mathcal {G}}^{\beta } {\mathcal {G}}^{\alpha }.\nonumber \end{aligned}\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(4.13)

Adding (4.11), (4.12) and (4.13) yields

$$\begin{aligned} \begin{aligned}&{\text {III + IV + V}}\\&=-\frac{1}{2}{\mathcal {G}}^{\beta }\partial _{\beta } g_{\mu \nu }+\frac{1}{8}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}\partial _\nu g_{\alpha \alpha '}\partial _{\mu }g_{\beta \beta '}\\&\qquad +\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\mu }g_{\alpha '\nu }\partial _{\alpha }g_{\beta \beta '}-\partial _{\alpha }g_{\alpha '\nu }\partial _{\mu }g_{\beta \beta '})\\&\qquad +\frac{1}{4}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _\nu g_{\alpha '\mu }\partial _{\alpha }g_{\beta \beta '}-\partial _\alpha g_{\alpha '\mu }\partial _{\nu }g_{\beta \beta '})\\&\qquad -\frac{1}{2}(g^{-1})^{\alpha \alpha '}(g^{-1})^{\beta \beta '}(\partial _{\alpha '}g_{\mu \beta }\partial _{\beta '} g_{\alpha \nu }-\partial _{\beta '}g_{\mu \beta }\partial _{\alpha '} g_{\alpha \nu })-\frac{1}{2}g_{\nu \alpha } g_{\mu \beta } {\mathcal {G}}^{\beta } {\mathcal {G}}^{\alpha }.\nonumber \end{aligned}\!\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(4.14)

Combining (4.6), (4.7), (4.9), (4.10) and (4.14), multiplying by 2 and re-arranging yield the desired result. $\square$

Given an $(\epsilon ,\gamma ,N)$-admissible perturbation of a dispersive spacetime solution $({\mathcal {M}},g_B,\phi _B)$ of size $(C,\gamma , N)$, we show that we can impose the condition (4.1) on the initial data.

Proposition 4.2

Given a dispersive spacetime solution $({\mathcal {M}},g_B,\phi _B)$ of size $(C,\gamma ,N)$, there exist $\epsilon =\epsilon (C,\gamma ,N)$ such that for every $(\epsilon ,\gamma ,N)$-admissible perturbation, one can prescribe the spacetime metric g and its time derivative $\partial _t g$ on the hypersurface $\{t=0\}$ such that the following hold:

• (1) g can be decomposed as

  $$\begin{aligned} g=m+h_B+h_S+h, \end{aligned}$$

• (2) the restriction of g on the tangent space of $\{t=0\}$ coincides with ${\hat{g}}$;

• (3) the second fundamental form of the hypersurface $\{t=0\}$ coincides with ${\hat{k}}$;

• (4) g satisfies the generalized wave coordinate condition (4.1) initially on $\{t=0\}$;

• (5) h obeys the following estimates on the initial hypersurface $\{t=0\}$:

  $$\begin{aligned} \Vert (1+r)^{\frac{1}{2}+|I|+\gamma }\partial \partial ^I h\Vert _{L^2(\{t=0\})}\lesssim \epsilon . \end{aligned}$$

  (4.15)

Proof

Recall our convention that $i,j,m,n=1,2,3$. The initial data for $g_{ij}$ are given by the condition

$$\begin{aligned} g_{ij}\restriction _{\{t=0\}}={\hat{g}}_{ij}. \end{aligned}$$

We thus need to impose $g_{00}$, $g_{0i}$ and $\partial _t g_{\mu \nu }$ in a way that the generalized wave condition is verified and that the second fundamental form of the solution $g_{\mu \nu }$ coincides with the prescribed ${\hat{k}}$. To this end, we first impose³⁸

$$\begin{aligned} g_{00}\restriction _{\{t=0\}}=(g_B)_{00}\restriction _{\{t=0\}}+(h_S)_{00},\quad g_{0i}\restriction _{\{t=0\}}=(g_B)_{0i}\restriction _{\{t=0\}}. \end{aligned}$$

(4.16)

We then impose the condition³⁹

$$\begin{aligned} \begin{aligned} 2{\hat{k}}_{ij}=\,\,&\mathbf{N} g_{ij}\restriction _{\{t=0\}}-\frac{g_{i0,j}+g_{j0,i}}{\sqrt{-g_{00}+({\hat{g}}^{-1})^{mn}g_{0m}g_{0n}}}\restriction _{\{t=0\}}\\&\quad + \frac{({\hat{g}}^{-1})^{kl}g_{0l}(g_{ik,j}+g_{jk,i})}{\sqrt{-g_{00}+({\hat{g}}^{-1})^{mn}g_{0m}g_{0n}}}\restriction _{\{t=0\}}, \end{aligned} \end{aligned}$$

(4.17)

where the future-directed unit normal $\mathbf{N}$ is given by

$$\begin{aligned} \mathbf{N}=\frac{1}{\sqrt{-g_{00}+({\hat{g}}^{-1})^{mn}g_{0m}g_{0n}}}(\partial _t-g_{0j}({\hat{g}}^{-1})^{ij}\partial _i). \end{aligned}$$

Notice that by (4.16) and the fact that ${\hat{g}}$ is Riemannian, we have $-g_{00}+({\hat{g}}^{-1})^{ij}g_{0i}g_{0j}>0$ and thus $\mathbf{N}$ is well defined. In particular, (4.17) determines $\partial _tg_{ij}\restriction _{\{t=0\}}$ (since all remaining terms are previous prescribed). Finally, the $\partial _t$ derivatives of $g_{0\nu }$ can then given by (4.4). More precisely, by taking $\mu =i$ in (4.4), we show that $\partial _t g_{0i}$ can be defined by⁴⁰

$$\begin{aligned} (g^{-1})^{00}\partial _t g_{0 i} =\,&-(g^{-1})^{0j}\partial _t g_{ij}-(g^{-1})^{0j}\partial _j g_{0i}-(g^{-1})^{jk}\partial _j g_{ki}\nonumber \\&+\,\frac{1}{2} (g^{-1})^{\alpha \beta }\partial _i g_{\alpha \beta }-g_{i\nu }{\mathcal {G}}^{\nu }. \end{aligned}$$

(4.18)

By taking $\mu =0$ in (4.4), $\partial _t g_{00}$ can be defined by

$$\begin{aligned} \begin{aligned}&\frac{1}{2} (g^{-1})^{00}\partial _t g_{00}\\&\quad =-(g^{-1})^{0i}\partial _t g_{i0}- (g^{-1})^{0i}\partial _i g_{00}- (g^{-1})^{ij}\partial _ig_{j0}+ \frac{1}{2}(g^{-1})^{ij}\partial _t g_{ij}\qquad \\&\qquad + (g^{-1})^{0i}\partial _t g_{0i}-g_{0\nu }{\mathcal {G}}^{\nu }. \end{aligned}\nonumber \\ \end{aligned}$$

(4.19)

By construction, the conditions (1)–(4) in the statement of the proposition hold. We now check that h defined above satisfies the bound (4.15). In the case that all derivatives falling on h are spatial derivatives, the bound for $h_{ij}$ follows from (3.5) and that for $h_{0\mu }$ follows from (4.16).

In the case that exactly one time derivative falls on h, we take (4.17), (4.18), (4.19) and subtract off the corresponding equation for the background metric $g_B=m+h_B$. (Recall that ${\mathcal {G}}^\mu ={\mathcal {G}}_B^\mu +{\mathcal {G}}_S^{\mu }$, where ${\mathcal {G}}_B^\mu$ is given exactly by the generalized wave coordinate condition for the background metric $g_B$.) For $\partial _th_{ij}$ and $\partial _t h_{00}$, the desired estimate then follows from (3.5), (3.6), the estimate $|\partial ^I{\mathcal {G}}_S|\lesssim \frac{\epsilon \chi (r)\log r}{(1+r)^{2+|I|}}$ for ${\mathcal {G}}^i_S$ and the fact that ${\mathcal {G}}^0_S=0$.

For $\partial _t h_{0i}$, however, we note that each of the terms in (4.18) does not have sufficient decay in r. Nevertheless, by the definition of $h_S$ and ${\mathcal {G}}_S$, we have the exact cancellation that allows us to conclude⁴¹

$$\begin{aligned} \left| -(m^{-1})^{jk}\partial _j (h_S)_{ki}+\frac{1}{2} (m^{-1})^{\alpha \beta }\partial _i (h_S)_{\alpha \beta }-m_{i\nu }{\mathcal {G}}_S^{\nu }\right| \lesssim \frac{\epsilon \log (2+r)}{(1+r)^3}.\nonumber \\ \end{aligned}$$

(4.20)

Similar cancellations occur for higher spatial derivatives, see Proposition 8.1. This allows us to obtain the desired estimate for $\partial _t h_{0i}$ and its weighted spatial derivatives.

Finally, in the cases where there are at least two time derivatives falling on h, we need to use the equation in Proposition 4.1 to express time derivatives in terms of spatial derivatives. The calculations are largely similar to that in Sect. 9 and will be omitted. It is important to note, however, that as above, we need a crucial cancellation between the most slowly decaying terms (see Proposition 9.2). $\square$

5 Third Version of Main Theorem

In Proposition 4.1, we have shown that under the generalized wave coordinate condition (4.1), the Einstein scalar field system reduces to a system of quasilinear wave equations. As is well known, if we solve the system of quasilinear wave equations in Proposition 4.1 with initial data satisfying the constraint equations and the generalized wave coordinate conditions, then the constraint equations and the generalized wave coordinate conditions are propagated and the solution is therefore a genuine solution to the Einstein scalar field system.

In view of this, we can now rephrase our main theorem (Theorem 3.6) as a result on the global existence of solutions to a system of quasilinear wave equations. Before we proceed, we need one more notation:

Definition 5.1

Let⁴²

$$\begin{aligned} w(q)={\left\{ \begin{array}{ll} 1+(1+|q|)^{1+2\gamma } &{}\text{ if } q\ge 0\\ 1+(1+|q|)^{-\frac{\gamma }{2}} &{}\text{ if } q< 0. \end{array}\right. } \end{aligned}$$

Our main theorem can be stated as follows:⁴³

Theorem 5.2

(Main theorem, third version). Let $N\ge 11$, $0<\gamma \le \frac{1}{8}$ and $({\mathcal {M}},g_B,\phi _B)$ be a dispersive spacetime solution of size $(C,\gamma ,N)$. Then, there exists $\epsilon _0=\epsilon _0(C,\gamma ,N)$ such that if the initial data to the system of equations in Proposition 4.1 together with the wave equation

$$\begin{aligned} \Box _g \phi =0 \end{aligned}$$

satisfy the constraint equations, the generalized wave coordinate condition (4.1) and the smallness assumptions

$$\begin{aligned} \sum _{|I|\le N}\Vert (1+r)^{\frac{1}{2}+|I|+\gamma }\partial \nabla ^I h\Vert _{L^2(\{t=0\})}\le \epsilon \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le N}\Vert (1+r)^{\frac{1}{2}+\gamma +|I|}\nabla \nabla ^I ({{\hat{\phi }}}-(\phi _B)\restriction _{\{t=0\}})\Vert _{L^2(\{t=0\})}\\&\quad +\sum _{|I|\le N-1}\Vert (1+r)^{\frac{1}{2}+\gamma +|I|}\nabla ^I ({{\hat{\psi }}}-(\partial _t\phi _B)\restriction _{\{t=0\}})\Vert _{L^2(\{t=0\})}\le \epsilon \end{aligned} \end{aligned}$$

with $|x|^{1+\gamma }|h|,\,|x|^{1+\gamma }|{{\hat{\phi }}}|\rightarrow 0$ as $|x|\rightarrow \infty$ and $\epsilon <\epsilon _0$, then the unique solution to this system of equations is global in time. Moreover, for $\beta :=\phi -\phi _B$, the solution obeys the following estimates:

$$\begin{aligned} \sum _{|I|\le N}\big (\Vert w^{\frac{1}{2}}\partial \Gamma ^I h\Vert _{L^2(\{t=\tau \})}+\Vert w^{\frac{1}{2}}\partial \Gamma ^I \beta \Vert _{L^2(\{t=\tau \})}\big )\lesssim \epsilon (1+\tau )^{\delta _1}, \end{aligned}$$

(5.1)

where $\delta _1>0$ is a small constant which can be chosen to be arbitrary small as long as $\epsilon$ is also chosen to be accordingly small. The implicit constant in the above estimate depends on C, $\gamma$ and $\delta _1$.

Remark 5.3

(Initial bounds in $L^2$ for the $\Gamma ^I$ derivatives). By using equation (4.1) for $g_{\mu \nu }$ and the equation $\Box _g \phi =0$ for $\phi$, it is easy to obtain also the $L^2$ bound for the $\Gamma$ derivatives,

$$\begin{aligned} \begin{aligned} \sum _{|I|\le N}\Vert (1+r)^{\frac{1}{2}+\gamma }\partial \Gamma ^I h\Vert _{L^2(\{t=0\})}&+\sum _{|I|\le N}\Vert (1+r)^{\frac{1}{2}+\gamma }\partial \Gamma ^I \beta \Vert _{L^2(\{t=0\})}\lesssim \epsilon , \end{aligned} \end{aligned}$$

where the implicit constant is independent of $\epsilon$ as long as $\epsilon \le {\tilde{\epsilon }}_0$, with ${\tilde{\epsilon }}_0$ depending only on C, $\gamma$ and N. In order to derive this bound, we need in particular to use the properties of $h_B$ (at $\{t=0\}$) given in Definition 3.1 and the properties of $h_S$ proven in Proposition 9.2.

Remark 5.4

(Initial bounds in $L^\infty$). As an immediate consequence of the assumptions above and standard Gagliardo–Nirenberg theorems, we have

$$\begin{aligned} \sum _{|I|\le N-2}\left( \Vert (1+r)^{1+\gamma }\Gamma ^I h\Vert _{L^\infty (\{t=0\})}+\Vert (1+r)^{1+\gamma }\Gamma ^I \beta \Vert _{L^\infty (\{t=0\})}\right) \lesssim \epsilon . \end{aligned}$$

Remark 5.5

(Theorem 5.2 implies Theorem 3.6). Given an $(\epsilon ,\gamma ,N)$-admissible perturbation in the sense of Definition 3.5, by Proposition 4.2, the initial data for h can be imposed to satisfy the generalized wave coordinate condition (4.1) such that the bounds in the assumptions of Theorem 5.2 are verified (after potentially changing $\epsilon$ by a constant factor). The definition of the initial data set also guarantees that the constraint equations are satisfied.

By Theorem 5.2, we therefore have a solution which is global-in-t-time in the generalized wave coordinate system $(t,x^1,x^2,x^3)$. Finally, it remains to show that the spacetime is indeed future causally geodesically complete. However, this step is standard given the estimates that are established in Theorem 5.2. We omit the details and refer the readers for example to [50].

6 Main Bootstrap Assumptions

We begin the proof of Theorem 5.2. The proof proceeds via a bootstrap argument. By standard methods (see also Theorem 13.2), we know that there exists a local solution and it suffices to prove a priori estimates for $h_{\alpha \beta }:=g_{\alpha \beta }-m_{\alpha \beta }-(h_B)_{\alpha \beta }-(h_S)_{\alpha \beta }$ and $\beta :=\phi -\phi _B$.

Fix $\delta _0>0$ be a small constant satisfying⁴⁴

$$\begin{aligned} 0<\delta _0\le \frac{\gamma }{1000 N}. \end{aligned}$$

(6.1)

We will make bootstrap assumptions on the $L^\infty$ norms of h and its derivatives. First, we assume the following for the derivatives of h:

$$\begin{aligned} \sup _{t,x}\sum _{|I|\le \lfloor \frac{N}{2}\rfloor } (1+s)^{1-\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}|\partial \Gamma ^I h (t,x)|\le \epsilon ^{\frac{1}{2}} \end{aligned}$$

(6.2)

and

$$\begin{aligned} \sup _{t,x}\sum _{|I|\le \lfloor \frac{N}{2}\rfloor } (1+s)^{2-\delta _0}(1+|q|)^{-\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}|{{\bar{\partial }}} \Gamma ^I h (t,x)|\le \epsilon ^{\frac{1}{2}}, \end{aligned}$$

(6.3)

where w(q) is defined in Definition 5.1. For the first derivative of h, we further assume a refined estimate for all but one component. More precisely, we make the bootstrap assumption⁴⁵

$$\begin{aligned} \sup _{t,x}(1+s)|\partial h(t,x)|_{{\mathcal {T}}{\mathcal {U}}}\le \epsilon ^{\frac{1}{2}}. \end{aligned}$$

(6.4)

We then introduce the following bootstrap assumptions on the $L^\infty$ norm of $\Gamma ^I h$:

$$\begin{aligned} \sup _{t,x}\sum _{|I|\le \lfloor \frac{N}{2}\rfloor } (1+s)^{1-\delta _0}(1+|q|)^{-\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}|\Gamma ^I h (t,x)|\le \epsilon ^{\frac{1}{2}}. \end{aligned}$$

(6.5)

Finally, we introduce⁴⁶ the bootstrap assumptions for $h_{L{\mathcal {T}}}$ and $(\Gamma h)_{LL}$:

$$\begin{aligned} \sup _{t,x}(1+s)^{1+\frac{\gamma }{2}}(1+|q|)^{-\frac{1}{2}-\gamma }w(q)^{\frac{1}{2}}\left( |h (t,x)|_{L{\mathcal {T}}}+\sum _{|I|\le 1}|\Gamma ^I h(t,x)|_{LL}\right) \le \epsilon ^{\frac{1}{2}}.\nonumber \\ \end{aligned}$$

(6.6)

In addition to the bootstrap assumptions for the metric components, we also need bootstrap assumptions for the scalar field. More precisely, for $\beta :=\phi -\phi _B$, we make the following bootstrap assumptions, which can be thought of as analogues of (6.2), (6.3) and (6.4):

$$\begin{aligned} \sup _{t,x}\sum _{|I|\le \lfloor \frac{N}{2}\rfloor } (1+s)^{1-\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}|\partial \Gamma ^I \beta (t,x)|\le \epsilon ^{\frac{1}{2}} \end{aligned}$$

(6.7)

and

$$\begin{aligned} \sup _{t,x}\sum _{|I|\le \lfloor \frac{N}{2}\rfloor } (1+s)^{2-\delta _0}(1+|q|)^{-\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}|{{\bar{\partial }}} \Gamma ^I \beta (t,x)|\le \epsilon ^{\frac{1}{2}} \end{aligned}$$

(6.8)

and

$$\begin{aligned} \sup _{t,x}(1+s)|\partial \beta (t,x)|\le \epsilon ^{\frac{1}{2}}, \end{aligned}$$

(6.9)

where w(q) is defined in Definition 5.1.

We will improve all of the above bootstrap assumptions, i.e., we show that (6.2)–(6.9) all hold with a better constant (see Proposition 18.14 at the very end of the proof of Theorem 5.2).

Remark 6.1

(Choice of parameters $\gamma$, $\delta _0$, $\delta$, T, $U_2$, $U_3$, $\epsilon$). We now discuss the choice of various smallness parameters in the problem, some of which have already been introduced above, and the order in which they are chosen. $\gamma$ is given in Theorem 5.2 and is required to obey $0<\gamma \le \frac{1}{8}$. $\delta _0$, which appears in the bootstrap assumptions above and is used to measure the “loss” in the decay rate, is chosen to satisfy⁴⁷ (6.1). It will be considered a fixed constant in the course of the proof. After $\delta _0$ is fixed, we choose $U_2$ and $U_3$, which will appear in the definition of the partition of the spacetime (see Sect. 12), so that $|U_2|$ and $|U_3|$ are large. After that, we choose T to be large. We then choose $\delta$, which is used for the improved pointwise estimates (see Proposition 18.13), to be small. Finally, we choose $\epsilon$, which measures the size of the data, to be small.

7 Preliminary Bounds

In this section, we collect some preliminary bounds. After stating some standard facts regarding the Minkowskian commuting vector fields (Propositions 7.1, 7.2), we then turn to some estimates for $g^{-1}$ and its derivatives using the assumptions on the background metric (Definition 3.1) and the bootstrap assumptions.

We now turn to the details. First, we have the following proposition regarding the decay that one can obtain using the Minkowskian commuting vector fields:

Proposition 7.1

For every scalar function $\xi$,

$$\begin{aligned} (1+t+|q|)|{\bar{\partial }}\xi |(t,x)+(1+|q|)|\partial \xi |(t,x)\lesssim \sum _{|I|=1}|\Gamma ^I\xi |(t,x). \end{aligned}$$

Proof

See Lemma 5.1 in [46]. $\square$

Next, we have a proposition regarding the commutation of $\partial$ and $\Gamma$:

Proposition 7.2

$$\begin{aligned}{}[\partial _\mu ,\Gamma ]=^{(\Gamma )}c_{\mu }{ }^{\nu } \partial _\nu , \end{aligned}$$

where $|{ }^{(\Gamma )}c|\lesssim 1$ and $^{(\Gamma )}c_{LL}=0$ for every Minkowskian commuting vector field $\Gamma$.

Proof

This is a direct computation. $\square$

To conclude this section, we prove the following bounds on the inverses of g and $g_B$:

Proposition 7.3

Define⁴⁸$H^{\alpha \beta }=(g^{-1})^{\alpha \beta }-m^{\alpha \beta }$ and $H_B^{\alpha \beta }=(g_B^{-1})^{\alpha \beta }-m^{\alpha \beta }$. Define also $H_{\alpha \beta }=m_{\alpha \mu }m_{\beta \nu }H^{\mu \nu }$. Then, for $|I|\le N$, H, $H_B$ and $H-H_B$ obey the following estimates:

$$\begin{aligned}&|\Gamma ^I H|(t,x)\lesssim \frac{\log (2+s)}{1+s}+\sum _{|J|\le |I|}|\Gamma ^J h|(t,x), \end{aligned}$$

(7.1)

$$\begin{aligned}&|\Gamma ^I H_B|(t,x)\lesssim \frac{\log (2+s)}{1+s}, \end{aligned}$$

(7.2)

and

$$\begin{aligned} |\Gamma ^I (H-H_B)|(t,x)\lesssim \frac{\epsilon \log (2+s)}{1+s}+\sum _{|J|\le |I|}|\Gamma ^J h|(t,x). \end{aligned}$$

(7.3)

Moreover, we have the following improved estimates for the “good components” of H:

$$\begin{aligned}&|H|_{L{\mathcal {T}}}(t,x)+\sum _{|I|\le 1}|\Gamma ^I H|_{LL}(t,x)\lesssim \frac{(1+|q|)^{\frac{1}{2}+\gamma }}{(1+s)^{1+\frac{\gamma }{2}}w(q)^{\frac{1}{2}}}, \end{aligned}$$

(7.4)

$$\begin{aligned}&|\Gamma ^I H|_{LL}(t,x)\lesssim \frac{\log (2+s)}{1+s}+|\Gamma ^I h|_{LL}(t,x)+\sum _{|J|\le |I|}\frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}|\Gamma ^J h|(t,x)}{(1+s)^{1-\delta _0}w(q)^{\frac{1}{2}}},\nonumber \\ \end{aligned}$$

(7.5)

as well as

$$\begin{aligned} |\Gamma ^I (H-H_B)|_{LL}(t,x)\lesssim & {} \frac{\epsilon \log (2+s)}{1+s}+|\Gamma ^I h|_{LL}(t,x)\nonumber \\&+\sum _{|J|\le |I|} \frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}|\Gamma ^J h|(t,x)}{(1+s)^{1-\delta _0}w(q)^{\frac{1}{2}}}. \end{aligned}$$

(7.6)

Proof

If s is small, the estimates in the proposition are much easier to prove based on (3.1). We will therefore only treat the case where s is large.

Proof of (7.1)–(7.3) for $|I|=0$

We begin with (7.1)–(7.3), first starting with the $|I|=0$ case. We use the following easy fact: Suppose A is a matrix such that $A^{-1}$ has bounded Frobenius norm, i.e., $\Vert A^{-1}\Vert \le C$ and B is a matrix with Frobenius norm $\Vert B\Vert \le a$. Then, for every constant C, there exists $a_0$ sufficiently small such that whenever $a\le a_0$, we have

$$\begin{aligned} \Vert (A+B)^{-1}-(A^{-1}-A^{-1}BA^{-1})\Vert \lesssim \Vert B\Vert ^2. \end{aligned}$$

(7.7)

Taking $A=m$ and $B=h_B+h_S+h$, we obtain the bound

$$\begin{aligned} |(g^{-1})^{\alpha \beta }-m^{\alpha \beta }+m^{\alpha \mu }(h_B+h_S+h)_{\mu \nu }m^{\beta \nu }|\lesssim (|h_B|+|h_S|+|h|)^2 \end{aligned}$$

for s sufficiently large, which implies⁴⁹

$$\begin{aligned} |H_{\alpha \beta }-h_{\alpha \beta }|\lesssim \frac{\log ^2(2+s)}{(1+s)^2}+|(h_S)_{\alpha \beta }|+|(h_B)_{\alpha \beta }|+|h|^2\lesssim \frac{\log (2+s)}{1+s}+|h|^2,\nonumber \\ \end{aligned}$$

(7.8)

where we have used $|h_S|+|h_B|\lesssim \frac{\log (2+s)}{1+s}.$ A similar argument using (7.7) with $A=m$ and $B=h_B$ shows that

$$\begin{aligned} |H_B|\lesssim \frac{\log (2+s)}{1+s}. \end{aligned}$$

(7.9)

To estimate $H-H_B$, we again return to (7.7) and this time let $A=g_B$ and $B=h_S+h$. Since $h_S$ and h both have small $L^\infty$ norms, we can ignore to terms that are quadratic or higher and obtain

$$\begin{aligned} |H-H_B|\lesssim |h_S|+|h|\lesssim \frac{\epsilon \log (2+s)}{1+s}+|h|. \end{aligned}$$

(7.10)

By (7.8), (7.9) and (7.10), we have thus obtained (7.1), (7.2) and (7.3) in the $|I|=0$ case.

Proof of (7.1)–(7.3) for general $|I|\le N$

In order to estimate the derivatives of the inverse of g and $g_B$, we iterate the following formula:

$$\begin{aligned} \partial A^{-1}=-A^{-1}(\partial A) A^{-1} \end{aligned}$$

to obtain the following expression:

$$\begin{aligned}&\Gamma ^I H=\Gamma ^I g^{-1}\nonumber \\&\qquad \qquad =-g^{-1}(\Gamma ^I (h_S+h_B+h)) g^{-1}\nonumber \\&\qquad \qquad +\sum _{\begin{array}{c} J_1+J_2=I\\ J_1,J_2\ne 0 \end{array}}g^{-1}(\Gamma ^{J_1} (h_S+h_B+h)) g^{-1}(\Gamma ^{J_2} (h_S+h_B+h)) g^{-1}\nonumber \\&\qquad -\sum _{\begin{array}{c} J_1+J_2+J_3=I\\ J_1,J_2,J_3\ne 0 \end{array}}g^{-1}(\Gamma ^{J_1} (h_S+h_B+h)) g^{-1}(\Gamma ^{J_2} (h_S+h_B+h)) g^{-1}(\Gamma ^{J_3} (h_S\nonumber \\&\qquad +h_B+h)) g^{-1}+\cdots \end{aligned}$$

(7.11)

Here, for a given multi-index $I=(i_1,i_2,\dots ,i_N)$, $\{J_1+J_2=I,\,J_1,J_2\ne 0\}$ denotes the set of all $J_1$, $J_2$ such that $J_1$ is an ordered $N_1$-sub-tuple of I (for some $0<N_1<N$) and $J_2$ is an ordered $(N-N_1)$-tuple given by removing $J_1$ from I. The set $\{J_1+J_2+J_3=I,\,J_1,J_2,J_3\ne 0\}$ (and the higher-order analogues) is defined in a similar manner.

Recall from the bootstrap assumption (6.5) that $\Gamma ^J h$ are bounded for $|J|\le \lfloor \frac{N}{2}\rfloor$. This, together with the bounds for $g^{-1}$ derived from (7.8), allows us to bound all terms that are quadratic or higher in h both those which are linear. We thus have

$$\begin{aligned} |\Gamma ^I H|\lesssim \sum _{|J|\le |I|}(|\Gamma ^J h_S|+|\Gamma ^J h_B|+|\Gamma ^J h|), \end{aligned}$$

from which (7.1) follows. Similarly, we prove (7.2) by

$$\begin{aligned} |\Gamma ^I H_B|\lesssim \sum _{|J|\le |I|}|\Gamma ^J h_B|\lesssim \frac{\log (2+s)}{1+s}. \end{aligned}$$

We now turn to the difference $H-H_B$, i.e., the proof of (7.3). Using (7.11) for both H and $H_B$ and taking the difference, we have

$$\begin{aligned} \begin{aligned} |\Gamma ^I(H-H_B)|\lesssim&\sum _{|J|\le |I|}\left( |\Gamma ^J h_S|+|\Gamma ^J h|+|H-H_B||\Gamma ^J h_B|\right) \\ \lesssim&\frac{\epsilon \log (2+s)}{1+s}+\sum _{|J|\le |I|}|\Gamma ^J h|, \end{aligned} \end{aligned}$$

where in the last line we have used (7.10) and the bounds for $|\Gamma ^J h_S|$ and $|\Gamma ^J h_B|$. This thus gives (7.3).

Proof of ( 7.4 )

We now turn to the proof of the improved estimates for certain components for $\Gamma ^I H$. When $|I|=0$, we use (7.8) and the triangle inequality to obtain the following bound for $|H|_{L{\mathcal {T}}}$:

$$\begin{aligned} \begin{aligned} |H|_{L{\mathcal {T}}}&\lesssim |h|_{L{\mathcal {T}}}+\frac{\log ^2(2+s)}{(1+s)^2}+|h_S|_{L{\mathcal {T}}}+|h_B|_{L{\mathcal {T}}}+|h|^2\\&\lesssim \frac{(1+|q|)^{\frac{1}{2}+\gamma }}{w(q)^{\frac{1}{2}}(1+s)^{1+\frac{\gamma }{2}}}. \end{aligned} \end{aligned}$$

(7.12)

Here, we have used the bounds for $|h|_{L{\mathcal {T}}}$, $|h_B|_{L{\mathcal {T}}}$ and $|h_S|_{L{\mathcal {T}}}$ from the bootstrap assumption (6.6), Definition 3.1 and Remark 3.4, respectively. We have also used the bound for |h| in the bootstrap assumption (6.5).

We also show that the LL component of $\Gamma ^I H$ is better behaved. Using (7.11), we get

$$\begin{aligned} \begin{aligned} |\Gamma ^I H|_{LL}&\lesssim |\Gamma ^I h_S|_{LL}+|\Gamma ^I h_B|_{LL}+|\Gamma ^I h|_{LL}+|H|(|\Gamma ^I h_S|+|\Gamma ^I h_B|+|\Gamma ^I h|)\\&\qquad \quad \quad +\sum _{|J_1|+|J_2|\le |I|}(|\Gamma ^{J_1} h_S|+|\Gamma ^{J_1} h_B|+|\Gamma ^{J_1} h|)(|\Gamma ^{J_2} h_S|\\&\quad \qquad \quad +|\Gamma ^{J_2} h_B| +|\Gamma ^{J_2} h|). \end{aligned} \end{aligned}$$

(7.13)

For $|I|\le 1$, we have

$$\begin{aligned} |\Gamma ^I h_S|_{LL}+|\Gamma ^I h_B|_{LL}\lesssim \frac{1}{(1+s)^{1+\frac{\gamma }{2}}}. \end{aligned}$$

Using this together with the bootstrap assumptions (6.5) and (6.6), we have

$$\begin{aligned} \sum _{|I|\le 1}|\Gamma ^I H|_{LL}\lesssim \frac{(1+|q|)^{\frac{1}{2}+\gamma }}{w(q)^{\frac{1}{2}}(1+s)^{1+\frac{\gamma }{2}}}. \end{aligned}$$

(7.14)

(7.12) and (7.14) together imply (7.4).

Proof of ( 7.5 )

It suffices to consider $|I|> 1$. Returning again to (7.13), we first use the weaker bounds for $|\Gamma ^I h_S|_{LL}$ and $|\Gamma ^I h_B|_{LL}$ for $|I|> 1$:

$$\begin{aligned} |\Gamma ^I h_S|_{LL}+|\Gamma ^I h_B|_{LL}\lesssim \frac{\log (2+s)}{1+s}. \end{aligned}$$

Using also the bootstrap assumption (6.5), we get (7.5).

Proof of ( 7.6 )

Finally, we prove the estimates for $|\Gamma ^I(H-H_B)|_{LL}$. We again use (7.11) and subtract from it the corresponding equation for $g_B$. Using (7.1), (7.3) and the bootstrap assumption (6.5), we get

$$\begin{aligned} \begin{aligned}&|\Gamma ^I(H-H_B)|_{LL}\\&\quad \lesssim |\Gamma ^I h|_{LL}+|\Gamma ^I h_S|_{LL}\\&\qquad +\sum _{|J_1|+|J_2|\le |I|}(|\Gamma ^{J_1} h|\\&\qquad +|\Gamma ^{J_1} h_S|+|H-H_B|)(|H|+|\Gamma ^{J_2} h_S|+|\Gamma ^{J_2} h_B|+|\Gamma ^{J_2} h|)\\&\quad \lesssim \frac{\epsilon \log (2+s)}{1+s}+|\Gamma ^I h|_{LL}+\sum _{|J|\le |I|} \frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}|\Gamma ^J h|}{(1+s)^{1-\delta _0}w(q)^{\frac{1}{2}}}. \end{aligned} \end{aligned}$$

This proves (7.6) and thus concludes the proof of the proposition. $\square$

8 Generalized Wave Coordinate Condition

Recall that the metric g satisfies the condition

$$\begin{aligned} (g^{-1})^{\alpha \beta }\frac{\partial }{\partial x^\alpha }g_{\beta \mu }-\frac{1}{2} (g^{-1})^{\alpha \beta }\frac{\partial }{\partial x^\mu }g_{\alpha \beta }=-g_{\mu \nu }{\mathcal {G}}^{\nu }, \end{aligned}$$

(8.1)

where ${\mathcal {G}}^\mu ={\mathcal {G}}_B^\mu +{\mathcal {G}}_S^\mu$, ${\mathcal {G}}_B^\mu =\Box _{g_B} x^\mu$ is given by the choice of coordinates for the background solution and ${\mathcal {G}}_S$ is given explicitly as in (4.2) by

$$\begin{aligned} {\mathcal {G}}^0_S=0,\quad {\mathcal {G}}^i_S=-\chi (r)\chi (\frac{r}{t})\left( \frac{4M\log (r-2M)}{r^2}\right) \frac{x^{i}}{r} \end{aligned}$$

In this section, we show that (8.1) allows us to rewrite $|\partial \Gamma ^I h|_{L{\mathcal {T}}}$ in terms of better behaved quantities which either have a “good derivative” ${\bar{\partial }}$ or are lower order in terms of derivatives. This follows closely the ideas in [45, 46]. We show that while we use generalized wave coordinates instead of wave coordinates in our setting, the most slowly decaying terms cancel and the methods for dealing with the “bad derivatives” of the “good components” still apply.

As a preliminary step, we need a calculation about $h_S$ and ${\mathcal {G}}_S$, which is a more general version of the estimate (4.20). More precisely, we have

Proposition 8.1

The following estimate holds for all I with a constant that may depend on |I|:

$$\begin{aligned}&\left| \Gamma ^I\left( m^{\alpha \beta }\frac{\partial }{\partial x^\alpha }(h_S)_{\beta \mu }-\frac{1}{2} m^{\alpha \beta }\frac{\partial }{\partial x^\mu }(h_S)_{\alpha \beta }+m_{\mu \nu } {\mathcal {G}}_S^{\nu }\right) \right| (t,x)\\&\qquad \lesssim {\left\{ \begin{array}{ll} \frac{\epsilon \log (2+s)}{(1+s)^3} &{}{\text {if }}q\ge 0\\ \frac{\epsilon (1+|q|)\log (2+s)}{(1+s)^3} &{}{\text {if }}q< 0. \end{array}\right. } \end{aligned}$$

Proof

Recall from Definition 3.2 that ${\tilde{h}}_S$ is defined by

$$\begin{aligned}&({\tilde{h}}_S)_{00}=\frac{2M}{r},\quad ({\tilde{h}}_S)_{0i}=0,\\&({\tilde{h}}_S)_{ij}=-\frac{4M\log (r-2M)}{r}\delta _{ij}-\frac{x_i x_j}{r^2}\left( \frac{2M}{r}-\frac{4M\log (r-2M)}{r}\right) \end{aligned}$$

and $h_S$ is defined by

$$\begin{aligned} h_S=\chi (r)\chi \left( \frac{r}{t}\right) {\tilde{h}}_S. \end{aligned}$$

Recalling also the definition in (4.2), we can write ${\mathcal {G}}_S$ as

$$\begin{aligned} {\mathcal {G}}_S^\mu =\chi (r)\chi \left( \frac{r}{t}\right) \tilde{{\mathcal {G}}}_S^\mu ,\quad \text{ where }\quad \tilde{{\mathcal {G}}}_S^0=0,\quad \tilde{{\mathcal {G}}}_S^i=-\left( \frac{4M\log (r-2M)}{r^2}\right) \frac{x^i}{r}.\nonumber \\ \end{aligned}$$

(8.2)

Given the above definitions, we have the basic estimate that $|\partial \Gamma ^I {\tilde{h}}_S|+|\Gamma ^I\tilde{{\mathcal {G}}}_S|\lesssim \frac{\log (2+s)}{(1+s)^2}$ for all⁵⁰I. This is of course not sufficient to conclude the proposition and indeed we will need the cancellation between various terms.

To proceed, first, it is easy to observe that the $\Gamma ^I$ derivatives of $\chi (r)\chi (\frac{r}{t})$ are bounded and supported in the region $\{r\ge \frac{1}{2}\}\cap \{\frac{1}{2}\le \frac{r}{t}\le \frac{3}{4}\}$. In particular, this region is a subset of $\{q<0\}$ and we also have $1\lesssim \frac{(1+|q|)}{(1+s)}$. Therefore, using the basic estimate above, all the terms with at least one $\Gamma$ differentiating $\chi (r)\chi (\frac{r}{t})$ obey the desired estimate.

It thus remains to control

$$\begin{aligned} \left| \Gamma ^I\left( m^{\alpha \beta }\frac{\partial }{\partial x^\alpha }({{\tilde{h}}}_S)_{\beta \mu }-\frac{1}{2} m^{\alpha \beta }\frac{\partial }{\partial x^\mu }({{\tilde{h}}}_S)_{\alpha \beta }+m_{\mu \nu } \tilde{{\mathcal {G}}}_S^{\nu }\right) \right| (t,x) \end{aligned}$$

(8.3)

in the region $\{r\ge \frac{1}{2}\}\cap \{r\ge \frac{t}{2}\}$. In the case where $\mu =0$, the above term vanishes identically. We now compute (8.3) in the case where $i=1,2,3$. We will use the following simple facts:

$$\begin{aligned}&\frac{\partial }{\partial x^i} r=\frac{x^i}{r},\quad \frac{\partial }{\partial x^i}\left( \frac{x^j}{r}\right) =\left( \frac{\delta _{ij}}{r}-\frac{x^i x^j}{r^3}\right) ,\nonumber \\&\sum _{i=1}^3\frac{\partial }{\partial x^i}\left( \frac{x^i}{r}\right) =\frac{2}{r},\quad \sum _{j=1}^3\left( \frac{x^j}{r}\right) \frac{\partial }{\partial x^j}\left( \frac{x^i}{r}\right) =0. \end{aligned}$$

(8.4)

For $i=1,2,3$, we have

$$\begin{aligned} \begin{aligned}&m^{\alpha \beta }\frac{\partial }{\partial x^\alpha }({{\tilde{h}}}_S)_{\beta i}\\&\quad =\delta ^{jk}\frac{\partial }{\partial x^j} \left( -\frac{4M\log (r-2M)}{r}\delta _{ik}-\frac{x^i x^k}{r^2}\left( \frac{2M}{r}-\frac{4M\log (r-2M)}{r}\right) \right) \\&\quad =\left( -\frac{4M}{r(r-2M)}+\frac{4M\log (r-2M)}{r^2}\right) \frac{x^i}{r}\\&\qquad -\frac{x^i}{r}\left( -\frac{2M}{r^2}-\frac{4M}{r(r-2M)}+\frac{4M\log (r-2M)}{r^2}\right) \\&\qquad -\frac{2 x^i}{r^2}\left( \frac{2M}{r}-\frac{4M\log (r-2M)}{r}\right) \\&\quad =\frac{8M x^i\log (r-2M)}{r^3}-\frac{2Mx^i}{r^3} \end{aligned} \end{aligned}$$

(8.5)

and

$$\begin{aligned}&\frac{1}{2} m^{\alpha \beta }\frac{\partial }{\partial x^i}({{\tilde{h}}}_S)_{\alpha \beta }\nonumber \\&\quad =-\frac{1}{2} \frac{\partial }{\partial x^i}({{\tilde{h}}}_S)_{00}+\frac{1}{2} \delta ^{jk}\frac{\partial }{\partial x^i}({{\tilde{h}}}_S)_{jk}\nonumber \\&\quad =-\frac{1}{2} \frac{\partial }{\partial x^i}\frac{2M}{r}+\frac{1}{2}\delta ^{jk}\frac{\partial }{\partial x^i}\left( -\frac{4M\log (r-2M)}{r}\delta _{jk}\right. \nonumber \\&\qquad \left. -\frac{x^j x^k}{r^2}\left( \frac{2M}{r}-\frac{4M\log (r-2M)}{r}\right) \right) \nonumber \\&\quad =\frac{M x^i}{r^3}+\frac{3}{2} \left( -\frac{4M}{r(r-2M)}+\frac{4M\log (r-2M)}{r^2}\right) \frac{x^i}{r}\nonumber \\&\qquad -\frac{1}{2}\left( -\frac{2M}{r^2}-\frac{4M}{r(r-2M)}+\frac{4M\log (r-2M)}{r^2}\right) \frac{x^i}{r}\nonumber \\&\quad =\frac{2 M x^i}{r^3}-\frac{4Mx^i}{r^2(r-2M)}+\frac{4Mx^i\log (r-2M)}{r^3}. \end{aligned}$$

(8.6)

Subtracting (8.6) from (8.5), we get

$$\begin{aligned} \begin{aligned} m^{\alpha \beta }\frac{\partial }{\partial x^\alpha }({{\tilde{h}}}_S)_{\beta i}-\frac{1}{2} m^{\alpha \beta }\frac{\partial }{\partial x^i}({{\tilde{h}}}_S)_{\alpha \beta } =&\frac{4M x^i\log (r-2M)}{r^3}\\&-\frac{4Mx^i}{r^3}+\frac{4Mx^i}{r^2(r-2M)}.\nonumber \end{aligned}\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(8.7)

On the other hand,

$$\begin{aligned} -\frac{4Mx^i}{r^3}+\frac{4Mx^i}{r^2(r-2M)}=\frac{4Mx^i(r-(r-2M))}{r^3(r-2M)}=\frac{8M^2 x^i}{r^3(r-2M)}. \end{aligned}$$

(8.8)

Recalling the definition of $\tilde{{\mathcal {G}}}_S$ in (8.2) and using (8.7) and (8.8), we thus obtain

$$\begin{aligned} m^{\alpha \beta }\frac{\partial }{\partial x^\alpha }({{\tilde{h}}}_S)_{\beta i}-\frac{1}{2} m^{\alpha \beta }\frac{\partial }{\partial x^i}({{\tilde{h}}}_S)_{\alpha \beta }+m_{i\nu } \tilde{{\mathcal {G}}}_S^{\nu }=\frac{8M^2 x^i}{r^3(r-2M)}, \end{aligned}$$

which immediately implies (in the region $r\ge \frac{t}{2}$) that

$$\begin{aligned} \left| \Gamma ^I\left( m^{\alpha \beta }\frac{\partial }{\partial x^\alpha }({{\tilde{h}}}_S)_{\beta i}-\frac{1}{2} m^{\alpha \beta }\frac{\partial }{\partial x^i}({{\tilde{h}}}_S)_{\alpha \beta }+m_{i\nu } \tilde{{\mathcal {G}}}_S^{\nu }\right) \right| (t,x)\lesssim \frac{\epsilon }{(1+s)^3}. \end{aligned}$$

We have thus estimated (8.3). This concludes the proof of the proposition. $\square$

We now move on to use the generalized wave coordinate condition to bound the “good components” of the metric. First, we prove an estimate for $|\partial h|_{L{\mathcal {T}}}$:

Proposition 8.2

$|\partial h|_{L{\mathcal {T}}}$ satisfies the estimate

$$\begin{aligned} \begin{aligned}&|\partial h|_{L{\mathcal {T}}}(t,x)\\&\quad \lesssim |{{\bar{\partial }}} h|(t,x)+\frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}+\frac{\log (2+s)}{1+s}|\partial h|(t,x)\\&\qquad +\frac{1}{(1+s)(1+|q|)^{\gamma }}|h|(t,x)+|h||\partial h|(t,x). \end{aligned} \end{aligned}$$

Proof

As a first step, we start from the wave coordinate condition (8.1) and subtract off the contributions from the corresponding wave coordinate conditions for $h_B$ and $h_S$. More precisely, we now use $g^{-1}=(g_B)^{-1}+(H-H_B)$ to rewrite (8.1) as follows:

$$\begin{aligned}&(g_B^{-1})^{\alpha \beta }\frac{\partial }{\partial x^\alpha }(h_B+h_S+h)_{\beta \mu }-\frac{1}{2} (g_B^{-1})^{\alpha \beta }\frac{\partial }{\partial x^\mu }(h_B+h_S+h)_{\alpha \beta }+g_{\mu \nu }{\mathcal {G}}^{\nu }\nonumber \\&\quad =O((H-H_B)\cdot \partial (h_B+h_S+h)). \end{aligned}$$

(8.9)

By definition of ${\mathcal {G}}_B$, we have

$$\begin{aligned} (g_B^{-1})^{\alpha \beta }\frac{\partial }{\partial x^\alpha }(h_B)_{\beta \mu }-\frac{1}{2} (g_B^{-1})^{\alpha \beta }\frac{\partial }{\partial x^\mu }(h_B)_{\alpha \beta }+(g_B)_{\mu \nu }{\mathcal {G}}_B^{\nu }=0. \end{aligned}$$

(8.10)

Therefore, subtracting (8.10) from (8.9), we obtain

$$\begin{aligned} \begin{aligned}&(g_B^{-1})^{\alpha \beta }\frac{\partial }{\partial x^\alpha }(h_S+h)_{\beta \mu }-\frac{1}{2} (g_B^{-1})^{\alpha \beta }\frac{\partial }{\partial x^\mu }(h_S+h)_{\alpha \beta }+(h_S)_{\mu \nu }{\mathcal {G}}_B^{\nu }\\&\qquad +h_{\mu \nu }{\mathcal {G}}_B^{\nu }+g_{\mu \nu }{\mathcal {G}}_S^{\nu }\\&\quad =O((H-H_B)\cdot \partial (h_B+h_S+h)). \end{aligned}\nonumber \\ \end{aligned}$$

(8.11)

Next, we subtract

$$\begin{aligned} m^{\alpha \beta }\frac{\partial }{\partial x^\alpha }(h_S)_{\beta \mu }-\frac{1}{2} m^{\alpha \beta }\frac{\partial }{\partial x^\mu }(h_S)_{\alpha \beta }+m_{\mu \nu } {\mathcal {G}}_S^{\nu } \end{aligned}$$

from the left-hand side of (8.11) and use Proposition 8.1 to conclude

$$\begin{aligned} \begin{aligned}&(g_B^{-1})^{\alpha \beta }\frac{\partial }{\partial x^\alpha }h_{\beta \mu }-\frac{1}{2} (g_B^{-1})^{\alpha \beta }\frac{\partial }{\partial x^\mu }h_{\alpha \beta }+(h_S)_{\mu \nu }{\mathcal {G}}_B^{\nu }+h_{\mu \nu }{\mathcal {G}}_B^{\nu }\\&\quad =O((H-H_B)\cdot \partial (h_B+h_S+h))+O(H_B \cdot \partial h_S)\\&\qquad +O((h_B+h_S+h)\cdot {\mathcal {G}}_S)+O\left( \frac{\epsilon (1+|q|)\log (2+s)}{(1+s)^3w(q)^{\frac{1}{1+2\gamma }}}\right) . \end{aligned}\nonumber \\ \end{aligned}$$

(8.12)

We now rewrite (8.12), viewing $m^{\alpha \beta }\frac{\partial }{\partial x^\alpha }h_{\beta \mu }-\frac{1}{2} m^{\alpha \beta }\frac{\partial }{\partial x^\mu }h_{\alpha \beta }$ as the main term. More precisely, we write (8.12) as follows:

$$\begin{aligned} \hbox {Main}+\hbox {Error}_1+\hbox {Error}_2= & {} \hbox {Error}_3+\hbox {Error}_4+\hbox {Error}_5\nonumber \\&+O\left( \frac{\epsilon (1+|q|)\log (2+s)}{(1+s)^3w(q)^{\frac{1}{1+2\gamma }}}\right) , \end{aligned}$$

(8.13)

where

$$\begin{aligned}&\hbox {Main}:=m^{\alpha \beta }\frac{\partial }{\partial x^\alpha }h_{\beta \mu }-\frac{1}{2} m^{\alpha \beta }\frac{\partial }{\partial x^\mu }h_{\alpha \beta },\end{aligned}$$

(8.14)

$$\begin{aligned}&\hbox {Error}_1:=O(h_B\cdot \partial h), \end{aligned}$$

(8.15)

$$\begin{aligned}&\hbox {Error}_2:=O((h+h_S)\cdot {\mathcal {G}}_B), \end{aligned}$$

(8.16)

$$\begin{aligned}&\hbox {Error}_3:=O((H-H_B)\cdot \partial (h_B+h_S+h)) \end{aligned}$$

(8.17)

$$\begin{aligned}&\hbox {Error}_4:=O(H_B \cdot \partial h_S), \end{aligned}$$

(8.18)

$$\begin{aligned}&\hbox {Error}_5:=O((h_B+h_S+h)\cdot {\mathcal {G}}_S). \end{aligned}$$

(8.19)

The term $O\left( \frac{\epsilon (1+|q|)\log (2+s)}{(1+s)^3w(q)^{\frac{1}{1+2\gamma }}}\right)$ in (8.13) is clearly acceptable. We now show that the main term indeed gives the desired control up to some acceptable error terms and that all the error terms are controllable. We first estimate the terms in (8.15)–(8.19). To that end, recall from Definitions 3.1 and 3.2 and the estimate (7.2) that

$$\begin{aligned}&|h_S|\lesssim \frac{\epsilon \log (2+s)}{1+s},\quad |h_B|\lesssim \frac{\log (2+s)}{1+s},\quad |H_B|\lesssim \frac{\log (2+s)}{1+s}, \\&|\partial h_S|\lesssim \frac{\epsilon \log (2+s)}{(1+s)^2},\quad |\partial h_B|\lesssim \frac{1}{(1+s)(1+|q|)^{\gamma }}; \end{aligned}$$

and by (8) in Definition 3.1 and the definition in (8.1), we have

$$\begin{aligned} |{\mathcal {G}}_B|\lesssim \frac{\log (2+s)}{(1+s)^2},\quad |{\mathcal {G}}_S|\lesssim \frac{\epsilon \log (2+s)}{(1+s)^2}. \end{aligned}$$

Therefore,

$$\begin{aligned}&\hbox {Error}_1\lesssim \frac{\log (2+s)}{1+s}|\partial h|,\nonumber \\&\hbox {Error}_2\lesssim \frac{\log (2+s)}{(1+s)^2}|h|+\frac{\epsilon \log ^2(2+s)}{(1+s)^3}, \end{aligned}$$

(8.20)

$$\begin{aligned}&\hbox {Error}_4\lesssim \frac{\epsilon \log ^2(2+s)}{(1+s)^3},\nonumber \\&\hbox {Error}_5\lesssim \frac{\epsilon \log ^2(2+s)}{(1+s)^3}+\frac{\epsilon \log (2+s)}{(1+s)^2}|h|.\nonumber \\ \end{aligned}$$

(8.21)

For the term $\hbox {Error}_3$, recall from (7.3) in Proposition 7.3 that we have

$$\begin{aligned} |H-H_B|\lesssim \frac{\epsilon \log (2+s)}{1+s}+| h|. \end{aligned}$$

Therefore,

$$\begin{aligned} \hbox {Error}_3\lesssim \frac{\epsilon \log (2+s)}{(1+s)^2(1+|q|)^{\gamma }}+\frac{\log (2+s)}{1+s}|\partial h|+\frac{1}{(1+s)(1+|q|)^{\gamma }}|h|+|h||\partial h|.\nonumber \\ \end{aligned}$$

(8.22)

Combining the estimates from (8.13), (8.20), (8.21) and (8.22), we obtain

$$\begin{aligned} \begin{aligned} |\hbox {Main}|=&\left| m^{\alpha \beta }\frac{\partial }{\partial x^\alpha }h_{\beta \mu }-\frac{1}{2} m^{\alpha \beta }\frac{\partial }{\partial x^\mu }h_{\alpha \beta }\right| \\ \lesssim&\frac{\epsilon \log (2+s)}{(1+s)^2(1+|q|)^\gamma }+\frac{\log (2+s)}{1+s}|\partial h|+\frac{1}{(1+s)(1+|q|)^{\gamma }}|h|+|h||\partial h|.\nonumber \end{aligned}\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(8.23)

We now contract the index $\mu$ in (8.23) with L and $E^A$. The term $|\frac{1}{2} L^{\mu } m^{\alpha \beta }\frac{\partial }{\partial x^\mu }h_{\alpha \beta }|$ and $|\frac{1}{2} (E^A)^{\mu } m^{\alpha \beta }\frac{\partial }{\partial x^\mu }h_{\alpha \beta }|$ can be controlled by a good derivative, i.e., 

$$\begin{aligned} \left| \frac{1}{2} L^{\mu } m^{\alpha \beta }\frac{\partial }{\partial x^\mu }h_{\alpha \beta }\right| ,\,\left| \frac{1}{2} (E^A)^{\mu } m^{\alpha \beta }\frac{\partial }{\partial x^\mu }h_{\alpha \beta }\right| \lesssim \left| {{\bar{\partial }}} h\right| . \end{aligned}$$

We now consider $m^{\alpha \beta }\frac{\partial }{\partial x^\alpha }h_{\beta \mu }$ contracted with $L^\mu$ or $(E^A)^\mu$. Writing $m^{\alpha \beta }=-L^{(\alpha }{\underline{L}}^{\beta )}+\sum _{A=1}^3 (E^A)^{\alpha } (E^A)^{\beta }$, we notice that in each case there is exactly one term on the left-hand side with a bad derivative, i.e., the term $L^\alpha L^\beta \partial _q h_{\alpha \beta }$ or $L^\alpha (E^A)^\beta \partial _q h_{\alpha \beta }$. These are exactly the $|\partial _q h|_{L{\mathcal {T}}}$ terms that we want to control. As a result, we get

$$\begin{aligned} |\partial _q h|_{L{\mathcal {T}}}\lesssim & {} |{{\bar{\partial }}} h|+\frac{\epsilon \log (2+s)}{(1+s)^2(1+|q|)^\gamma }+\frac{\log (2+s)}{1+s}|\partial h|\\&+\frac{1}{(1+s)(1+|q|)^{\gamma }}|h|+|h||\partial h|. \end{aligned}$$

This implies the desired conclusion. $\square$

We can also use the condition (8.1) to obtain an estimate for the bad derivative of the LL component of higher derivatives of h. However, in this case, there are commutator terms containing bad derivative of bad components of the lower derivatives. More precisely, we have

Proposition 8.3

The following estimate holds for the components $(\Gamma ^I h)_{LL}$ for all $|I|\le N$:

$$\begin{aligned} \begin{aligned}&|\partial \Gamma ^I h|_{LL}(t,x)\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}+\frac{\log (2+s)}{(1+s)(1+|q|)^\gamma }\sum _{|J|\le |I|}|\Gamma ^J h|(t,x)\\&\qquad +\frac{\log (2+s)}{1+s}\sum _{|J|\le |I|}|\partial \Gamma ^J h|(t,x)+\sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|(t,x)\\&\qquad +\sum _{|J|\le |I|}|{\bar{\partial }}\Gamma ^J h|(t,x)+\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|(t,x). \end{aligned} \end{aligned}$$

Proof

Using (8.1) and arguing as in the proof of Proposition 8.2, we obtain the following analogue of (8.13), except that now the error terms also have up to |I| derivatives:

$$\begin{aligned} \begin{aligned}&\left| \Gamma ^I\left( m^{\alpha \beta }\partial _{\alpha }h_{\beta \mu }-\frac{1}{2} m^{\alpha \beta }\partial _{\mu }h_{\alpha \beta }\right) \right| \\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}+\hbox {Error}_1+\hbox {Error}_2+\hbox {Error}_3+\hbox {Error}_4, \end{aligned}\nonumber \\ \end{aligned}$$

(8.24)

where

$$\begin{aligned}&\hbox {Error}_1:=\sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}h_B||\partial \Gamma ^{J_2} h|, \end{aligned}$$

(8.25)

$$\begin{aligned}&\hbox {Error}_2:=\sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}h||\Gamma ^{J_2} {\mathcal {G}}_B|, \end{aligned}$$

(8.26)

$$\begin{aligned}&\hbox {Error}_3:=\sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}(H-H_B)||\partial \Gamma ^{J_2} (h_B+h_S+h)| \end{aligned}$$

(8.27)

$$\begin{aligned}&\hbox {Error}_4:=\sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}h||\Gamma ^{J_2} {\mathcal {G}}_S|. \end{aligned}$$

(8.28)

Notice that compared to (8.13), we have not write explicitly the terms that are products of “explicit quantities,” i.e., $h_S$, $h_B$, ${\mathcal {G}}_B$, ${\mathcal {G}}_S$: These terms can clearly be dominated up a constant by $\frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}$ in exactly the same manner as in the proof of Proposition 8.2.

By Definitions 3.1 and 3.2; (4.2) and (7.2), we have

$$\begin{aligned}&\sum _{|J|\le |I|}|\Gamma ^J h_S|\lesssim \frac{\epsilon \log (2+s)}{1+s},\quad \sum _{|J|\le |I|}|\Gamma ^J h_B|\lesssim \frac{\log (2+s)}{1+s},\\&\sum _{|J|\le |I|}|\Gamma ^J H_B|\lesssim \frac{\log (2+s)}{1+s},\\&\sum _{|J|\le |I|}|\partial \Gamma ^J h_S|\lesssim \frac{\epsilon \log (2+s)}{(1+s)^2},\quad \sum _{|J|\le |I|}|\partial \Gamma ^J h_B|\lesssim \frac{1}{(1+s)(1+|q|)^{\gamma }}; \\&\sum _{|J|\le |I|}|\Gamma ^J {\mathcal {G}}_B|\lesssim \frac{\log (2+s)}{(1+s)^2},\quad \sum _{|J|\le |I|}|\Gamma ^J {\mathcal {G}}_S|\lesssim \frac{\epsilon \log (2+s)}{(1+s)^2}. \end{aligned}$$

Therefore,

$$\begin{aligned}&\hbox {Error}_1\lesssim \frac{\log (2+s)}{1+s}\sum _{|J|\le |I|}|\partial \Gamma ^J h|,\quad \hbox {Error}_2\lesssim \frac{\log (2+s)}{(1+s)^2}\sum _{|J|\le |I|}|\Gamma ^J h|,\nonumber \\ \end{aligned}$$

(8.29)

$$\begin{aligned}&\hbox {Error}_4\lesssim \frac{\epsilon \log (2+s)}{(1+s)^2}\sum _{|J|\le |I|}|\Gamma ^{J}h|. \end{aligned}$$

(8.30)

For $\hbox {Error}_3$, we apply (7.3) and the above estimates to obtain

$$\begin{aligned} \hbox {Error}_3&\lesssim \sum _{|J_1|+|J_2|\le |I|}\left( \frac{\epsilon \log (2+s)}{1+s}+|\Gamma ^{J_1} h|\right) \left( \frac{1}{(1+s)(1+|q|)^{\gamma }}+|\partial \Gamma ^{J_2}h|\right) \nonumber \\&\lesssim \frac{\epsilon \log (2+s)}{(1+s)^2(1+|q|)^{\gamma }}+\frac{\epsilon \log (2+s)}{1+s}\sum _{|J|\le |I|}|\partial \Gamma ^{J} h|\nonumber \\&\quad +\frac{1}{(1+s)(1+|q|)^{\gamma }}\sum _{|J|\le |I|}|\Gamma ^{J} h|+\sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1} h||\partial \Gamma ^{J_2}h|.\nonumber \\ \end{aligned}$$

(8.31)

Combining (8.24), (8.29), (8.30) and (8.31), we thus obtain

$$\begin{aligned}&\left| \Gamma ^I\left( \underbrace{m^{\alpha \beta }\partial _{\alpha }h_{\beta \mu }}_{=:A}-\underbrace{\frac{1}{2} m^{\alpha \beta }\partial _{\mu }h_{\alpha \beta }}_{=:B}\right) \right| \nonumber \\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}+\frac{\log (2+s)}{(1+s)(1+|q|)^\gamma }\sum _{|J|\le |I|}|\Gamma ^J h|\nonumber \\&\qquad +\frac{\log (2+s)}{1+s}\sum _{|J|\le |I|}|\partial \Gamma ^J h| +\sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|.\qquad \end{aligned}$$

(8.32)

We now contract the left-hand side of (8.32) with $L^\mu$ and study the resulting expression. In particular, we want to keep track of the structure of the terms after commuting $\Gamma ^I$ with $\partial$. We first control the contraction the term A in (8.32) with $L^\mu$. Given⁵¹$I=(i_1,\dots ,i_{|I|})$, using the notation in Proposition 7.2, we have

$$\begin{aligned}&|L^\mu \Gamma ^I (m^{\alpha \beta }\partial _{\alpha } h_{\beta \mu })-L^\mu ( m^{\alpha \beta } \partial _\alpha (\Gamma ^Ih)_{\beta \mu })|\nonumber \\&\quad \lesssim \sum _{n=1}^{|I|}|L^\mu m^{\alpha \beta } ({ }^{\Gamma _{(i_n)}}c_{\alpha }{ }^\nu )\partial _\nu (\Gamma _{(i_1)}\cdots \Gamma _{(i_{n-1})}\Gamma _{(i_{n+1})}\cdots \Gamma _{(i_{|I|})}h)_{\beta \mu }|\nonumber \\&\qquad +\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|. \end{aligned}$$

(8.33)

By Proposition 7.2, $c_{LL}=0$. Using also $m^{\alpha \beta }=-L^{(\alpha } {\underline{L}}^{\beta )}+\sum _{A=1}^3 (E^A)^\alpha (E^A)^\beta$, we therefore have

$$\begin{aligned}&|L^\mu m^{\alpha \beta } ({ }^{\Gamma _{(i_n)}}c_{\alpha }{ }^\nu )\partial _\nu (\Gamma _{(i_1)}\cdots \Gamma _{(i_{n-1})}\Gamma _{(i_{n+1})}\cdots \Gamma _{(i_{|I|})}h)_{\beta \mu }|\nonumber \\&\qquad \lesssim \sum _{|J|\le |I|-1} \left( |{\bar{\partial }}\Gamma ^J h|+|\partial \Gamma ^J h|_{L{\mathcal {T}}}\right) . \end{aligned}$$

(8.34)

On the other hand, using again $m^{\alpha \beta }=-L^{(\alpha } {\underline{L}}^{\beta )}+\sum _{A=1}^3 (E^A)^\alpha (E^A)^\beta$, we get

$$\begin{aligned} |L^\mu ( m^{\alpha \beta } \partial _\alpha (\Gamma ^Ih)_{\beta \mu })+\frac{1}{2} L^\mu {\underline{L}}^{\alpha } L^\beta \partial _\alpha (\Gamma ^I h)_{\beta \mu }|\lesssim |{\bar{\partial }}\Gamma ^I h|. \end{aligned}$$

(8.35)

Combining (8.33), (8.34) and (8.35), we therefore obtain

$$\begin{aligned}&|L^\mu \Gamma ^I (m^{\alpha \beta }\partial _{\alpha } h_{\beta \mu })+\frac{1}{2} L^\mu {\underline{L}}^{\alpha } L^\beta \partial _\alpha (\Gamma ^I h)_{\beta \mu }|\nonumber \\&\quad \lesssim \sum _{|J|\le |I|} |{\bar{\partial }}\Gamma ^J h|+\sum _{|J|\le |I|-1}|\partial \Gamma ^J h|_{L{\mathcal {T}}}+\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|.\qquad \end{aligned}$$

(8.36)

We now turn to the contraction of the term B in (8.32) with $L^\mu$. Using Proposition 7.2, we have

$$\begin{aligned} \left| L^\mu \left( \frac{1}{2} m^{\alpha \beta }\Gamma ^I\partial _{\mu }h_{\alpha \beta }-\frac{1}{2} m^{\alpha \beta }\partial _{\mu }(\Gamma ^Ih)_{\alpha \beta }\right) \right| \lesssim \sum _{|J|\le |I|-1}|{\bar{\partial }}\Gamma ^J h|+\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|,\nonumber \\ \end{aligned}$$

(8.37)

which then implies

$$\begin{aligned} |L^\mu m^{\alpha \beta }\Gamma ^I\partial _{\mu }h_{\alpha \beta }|\lesssim \sum _{|J|\le |I|}|{\bar{\partial }}\Gamma ^J h|+\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|. \end{aligned}$$

(8.38)

Combining (8.32), (8.36) and (8.38), we thus obtain

$$\begin{aligned} \begin{aligned}&|\partial \Gamma ^I h|_{LL}\lesssim |L^\mu {\underline{L}}^{\alpha } L^\beta \partial _\alpha (\Gamma ^I h)_{\beta \mu }|+|{\bar{\partial }}\Gamma ^I h|\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}+\frac{\log (2+s)}{(1+s)(1+|q|)^\gamma }\sum _{|J|\le |I|}|\Gamma ^J h|+\frac{\log (2+s)}{1+s}\sum _{|J|\le |I|}|\partial \Gamma ^J h|\\&\qquad +\sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|+\sum _{|J|\le |I|}|{\bar{\partial }}\Gamma ^J h|\\&\qquad +\sum _{|J|\le |I|-1} |\partial \Gamma ^J h|_{L{\mathcal {T}}}+\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|.\nonumber \end{aligned}\\ \end{aligned}$$

(8.39)

To proceed, we need an estimate for $\sum _{|J|\le |I|-1} |\partial \Gamma ^J h|_{L{\mathcal {T}}}$. Clearly, $\sum _{|J|\le |I|-1} |\partial \Gamma ^J h|_{LL}$ can be controlled in an identical manner as in (8.39), with I replaced by J for some $|J|\le |I|-1$. It thus remains to control $\sum _{|J|\le |I|-1} |\partial \Gamma ^J h|_{LA}$, for which we have used the convention

$$\begin{aligned} |\partial \Gamma ^J h|_{LA}:=\sum _{B=1}^3 \sum _{U\in {\mathcal {U}}}|L^\alpha (E^B)^\beta U^\gamma \partial _\gamma (\Gamma ^J h)_{\alpha \beta }|. \end{aligned}$$

To estimate this term, we first use $m^{\alpha \beta }=-L^{(\alpha } {\underline{L}}^{\beta )}+\sum _{A=1}^3 (E^A)^\alpha (E^A)^\beta$ to get

$$\begin{aligned} \begin{aligned}&\left| \frac{1}{2}(E^B)^\mu {\underline{L}}^{\alpha } L^{\beta }\partial _\alpha (\Gamma ^J h)_{\beta \mu } +(E^B)^\mu \Gamma ^J\left( m^{\alpha \beta }\partial _{\alpha }h_{\beta \mu }-\frac{1}{2} m^{\alpha \beta }\partial _{\mu }h_{\alpha \beta }\right) \right| \\&\quad \lesssim \sum _{|J'|\le |J|}|{\bar{\partial }}\Gamma ^{J'} h|+\sum _{|J'|\le |J|-1}|\partial \Gamma ^{J'} h|.\nonumber \end{aligned}\\ \end{aligned}$$

(8.40)

Then, contracting the left-hand side of (8.32) with $E^B$ (with I replaced by J) and using (8.40), we obtain

$$\begin{aligned} \begin{aligned}&|\partial \Gamma ^J h|_{LA} \lesssim \sum _{B=1}^3|(E^B)^\mu {\underline{L}}^{\alpha } L^{\beta }\partial _\alpha (\Gamma ^J h)_{\beta \mu }|+\sum _{|J'|\le |J|}|{\bar{\partial }}\Gamma ^{J'} h|\\&\quad \lesssim \sum _{B=1}^3\left| (E^B)^\mu \left( \Gamma ^J\left( m^{\alpha \beta }\partial _{\alpha }h_{\beta \mu }-\frac{1}{2} m^{\alpha \beta }\partial _{\mu }h_{\alpha \beta }\right) \right) \right| \\&\qquad +\sum _{|J'|\le |J|}|{\bar{\partial }}\Gamma ^{J'} h|+\sum _{|J'|\le |J|-1}|\partial \Gamma ^{J'} h|\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}+\frac{\log (2+s)}{(1+s)(1+|q|)^\gamma }\sum _{|J'|\le |J|}|\Gamma ^{J'} h|\\&\qquad +\frac{\log (2+s)}{1+s}\sum _{|J'|\le |J|}|\partial \Gamma ^{J'} h|+\sum _{|J_1|+|J_2|\le |J|}|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|\\&\qquad +\sum _{|J'|\le |J|}|{\bar{\partial }}\Gamma ^{J'} h|+\sum _{|J'|\le |J|-1} |\partial \Gamma ^{J'} h|. \end{aligned} \end{aligned}$$

This implies

$$\begin{aligned} \begin{aligned}&\sum _{|J|\le |I|-1}|\partial \Gamma ^J h|_{LA} \\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}+\frac{\log (2+s)}{(1+s)(1+|q|)^\gamma }\sum _{|J|\le |I|-1}|\Gamma ^J h|\\&\qquad +\frac{\log (2+s)}{1+s}\sum _{|J|\le |I|-1}|\partial \Gamma ^J h|\\&\qquad +\sum _{|J_1|+|J_2|\le |I|-1}|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|+\sum _{|J|\le |I|-1}|{\bar{\partial }}\Gamma ^J h|+\sum _{|J|\le |I|-2} |\partial \Gamma ^J h|.\nonumber \end{aligned}\\ \end{aligned}$$

(8.41)

Combining (8.39) and (8.41), we therefore obtain

$$\begin{aligned} \begin{aligned}&|\partial \Gamma ^I h|_{LL}\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}+\frac{\log (2+s)}{(1+s)(1+|q|)^\gamma }\sum _{|J|\le |I|}|\Gamma ^J h|\\&\qquad +\frac{\log (2+s)}{1+s}\sum _{|J|\le |I|}|\partial \Gamma ^J h|+\sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|\\&\qquad +\sum _{|J|\le |I|}|{\bar{\partial }}\Gamma ^J h|+\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|. \end{aligned} \end{aligned}$$

$\square$

9 Equations for h

In order to obtain estimates for the metric g, we will bound $h:=g-m-h_B-h_S$. To this end, we need to subtract the equations for metric $g_B$ of the background solution from the metric g of the unknown spacetime to derive a wave equation for h. Our goal in this section is to obtain a form of all the terms that appear in the equations for ${\widetilde{\Box }}_g \Gamma ^I h$ (see Propositions 9.15, 9.18). We will then use these equations to control $\Gamma ^Ih$ in the remainder of the paper. We begin with a preliminary proposition:

Proposition 9.1

The inhomogeneous terms in the equation for ${\widetilde{\Box }}_g \Gamma ^I h$ contain the following terms:

$$\begin{aligned}&-\Gamma ^I({\widetilde{\Box }}_g (h_S)_{\mu \nu }-G_{\mu \nu }(g,{\mathcal {G}}_S)), \end{aligned}$$

(9.1)

$$\begin{aligned}&\Gamma ^I(G_{\mu \nu }(g,{\mathcal {G}}_B)-G_{\mu \nu }(g_B,{\mathcal {G}}_B)), \end{aligned}$$

(9.2)

$$\begin{aligned}&-\Gamma ^I\left( 2g_{\alpha \nu }g_{\beta \mu }{\mathcal {G}}_B^{(\alpha } {\mathcal {G}}_S^{\beta )}\right) , \end{aligned}$$

(9.3)

$$\begin{aligned}&[{\widetilde{\Box }}_g,\Gamma ^I] h, \end{aligned}$$

(9.4)

$$\begin{aligned}&-\Gamma ^I ({\widetilde{\Box }}_g h_B-{\widetilde{\Box }}_{g_B} h_B), \end{aligned}$$

(9.5)

$$\begin{aligned}&\Gamma ^I\left( Q_{\mu \nu }(g,g;\partial g,\partial g)-Q_{\mu \nu }(g_B,g_B;\partial g_B,\partial g_B)\right) , \end{aligned}$$

(9.6)

$$\begin{aligned}&\Gamma ^I\left( P_{\mu \nu }(g,g;\partial g,\partial g)-P_{\mu \nu }(g_B,g_B;\partial g_B,\partial g_B)\right) , \end{aligned}$$

(9.7)

$$\begin{aligned}&\Gamma ^I\left( T_{\mu \nu }(\partial \phi ,\partial \phi )-T_{\mu \nu }(\partial \phi _B,\partial \phi _B)\right) . \end{aligned}$$

(9.8)

Proof

$g_{\mu \nu }$ and $(g_B)_{\mu \nu }$ both satisfy equations of the form as given in Proposition 4.1. Taking the difference of these equations, we obtain

$$\begin{aligned} \Gamma ^I({\widetilde{\Box }}_g g_{\mu \nu }-{\widetilde{\Box }}_{g_B} (g_B)_{\mu \nu })= & {} \text{(9.6) }+\text{(9.7) }+\text{(9.8) }\\&+\Gamma ^I\left( G_{\mu \nu }(g,{\mathcal {G}})-G_{\mu \nu }(g_B,{\mathcal {G}}_B)\right) .\nonumber \\ \end{aligned}$$

(9.9)

We first expand the terms on the left-hand side of (9.9):

$$\begin{aligned} \begin{aligned}&\Gamma ^I({\widetilde{\Box }}_g g_{\mu \nu }-{\widetilde{\Box }}_{g_B} (g_B)_{\mu \nu })\\&\quad =\Gamma ^I({\widetilde{\Box }}_g h_{\mu \nu })+\Gamma ^I({\widetilde{\Box }}_g (h_B)_{\mu \nu }-{\widetilde{\Box }}_{g_B} (h_B)_{\mu \nu })+\Gamma ^I({\widetilde{\Box }}_g (h_S)_{\mu \nu })\\&\quad =\underbrace{{\widetilde{\Box }}_g (\Gamma ^Ih_{\mu \nu })}_{=:\hbox {I}}-\underbrace{([{\widetilde{\Box }}_g, \Gamma ^I] h_{\mu \nu })}_{=:\hbox {II}}+\underbrace{\Gamma ^I({\widetilde{\Box }}_g (h_B)_{\mu \nu }-{\widetilde{\Box }}_{g_B} (h_B)_{\mu \nu })}_{=:\hbox {III}}+\underbrace{\Gamma ^I({\widetilde{\Box }}_g (h_S)_{\mu \nu })}_{=:\hbox {IV}}.\nonumber \end{aligned}\\ \end{aligned}$$

(9.10)

Notice now that I is the main term, II is the term (9.4) and III is the term (9.5). The term IV will be taken into account later (after combining with what will be called VII in (9.12)).

To compute the last term on the right-hand side of (9.9), we first observe from (4.5) that $G_{\mu \nu }(g,{\mathcal {G}})$ is linear in ${\mathcal {G}}$ except for the term $-g_{\alpha \nu }g_{\beta \mu }{\mathcal {G}}^{\alpha }{\mathcal {G}}^{\beta }$. Therefore,

$$\begin{aligned} G_{\mu \nu }(g,{\mathcal {G}})=G_{\mu \nu }(g,{\mathcal {G}}_B)+G_{\mu \nu }(g,{\mathcal {G}}_S)-2g_{\alpha \nu }g_{\beta \mu }{\mathcal {G}}_B^{(\alpha } {\mathcal {G}}_S^{\beta )}. \end{aligned}$$

This implies

$$\begin{aligned} \begin{aligned}&\Gamma ^I\left( G_{\mu \nu }(g,{\mathcal {G}})-G_{\mu \nu }(g_B,{\mathcal {G}}_B)\right) \\&\quad =\underbrace{\Gamma ^I\left( G_{\mu \nu }(g,{\mathcal {G}}_B)-G_{\mu \nu }(g_B,{\mathcal {G}}_B)\right) }_{=:\hbox {V}}-\underbrace{2\Gamma ^I\left( g_{\alpha \nu }g_{\beta \mu }{\mathcal {G}}_B^{(\alpha } {\mathcal {G}}_S^{\beta )}\right) }_{=:\hbox {VI}}+\underbrace{\Gamma ^I \left( G_{\mu \nu }(g,{\mathcal {G}}_S)\right) }_{=:\hbox {VII}}.\nonumber \end{aligned}\\ \end{aligned}$$

(9.11)

V gives the term (9.2) and VI gives the term (9.3). Finally, combining IV from (9.11) and VII from (9.12) gives (9.1). $\square$

Given Proposition 9.1, our goal in the remainder of this section is therefore to further estimate each of the terms (9.1)–(9.8). In the process of estimating these terms, we will be using the bootstrap assumptions in Sect. 6. We will control these terms in the order that they appeared in Proposition 9.1. For the convenience of the readers, let us mention the proposition in which each of these terms will be estimated: (9.1) will be estimated in Proposition 9.3; (9.2) will be bounded in Proposition 9.4; (9.3) will be estimated in Proposition 9.5; (9.4) will be controlled in Proposition 9.7; (9.5) will be bounded in Proposition 9.8; and (9.6) will be estimated in Proposition 9.12. The terms (9.7) and (9.8) will be bounded in separately for the general case (in which one has a bad term with “insufficient decay”) and for the ${\mathcal {T}}{\mathcal {U}}$ components. For (9.7), they will be carried out in Propositions 9.13 and 9.16, respectively, while for (9.8), they will be carried out in Propositions 9.14 and 9.17, respectively.

We now control the contribution from the $h_S$ term, i.e., (9.1). First, we have the following preliminary bound:

Proposition 9.2

For every quadruple of nonnegative integers $(k_0,k_1,k_2,k_3)$, $g_S:=m+h_S$ obeys the following estimates:⁵²

$$\begin{aligned}&|\partial _t^{k_0}\partial _{x_1}^{k_1}\partial _{x_2}^{k_2}\partial _{x_3}^{k_3}\big (\Box _m (g_S)_{\mu \nu }+m_{\mu \lambda }\partial _\nu {\mathcal {G}}^{\lambda }_S+m_{\nu \lambda }\partial _\mu {\mathcal {G}}^{\lambda }_S\big )|\nonumber \\&\qquad \lesssim \frac{\epsilon }{(1+s)^{4+k_0+k_1+k_2+k_3}},\quad \text{ for } q\ge 0; \end{aligned}$$

(9.12)

and

$$\begin{aligned}&|\partial _t^{k_0}\partial _{x_1}^{k_1}\partial _{x_2}^{k_2}\partial _{x_3}^{k_3}\big (\Box _m (g_S)_{\mu \nu }+m_{\mu \lambda }\partial _\nu {\mathcal {G}}^{\lambda }_S+m_{\nu \lambda }\partial _\mu {\mathcal {G}}^{\lambda }_S\big )|\\&\qquad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^{3+k_0+k_1+k_2+k_3}},\quad \text{ for } q< 0. \end{aligned}$$

Proof

We recall from Definition 3.2 that $h_S$ is given⁵³ by $h_S:=\chi (r)\chi (\frac{r}{t}){\tilde{h}}_S,$ with $({\tilde{h}}_S)_{00}:=\frac{2M}{r},\quad ({\tilde{h}}_S)_{0i}:=0$, $({\tilde{h}}_S)_{ij}:=-\frac{4M\log (r-2M)}{r}\delta _{ij}-\frac{x_i x_j}{r^2}(\frac{2M}{r}-\frac{4M\log (r-2M)}{r})$. Recall moreover from (4.2) that ${\mathcal {G}}^\mu _S:=\chi (r)\chi (\frac{r}{t})\tilde{{\mathcal {G}}}^\mu _S$, where $\tilde{{\mathcal {G}}}^0_S:=0$ and $\tilde{{\mathcal {G}}}^i_S:=-\left( \frac{4M\log (r-2M)}{r^2}\right) \frac{x^i}{r}$.

We first prove the desired estimate for $q\ge 0$. In this region, the cutoff function $\chi (\frac{r}{t})$ is identically 1. Moreover, if any of the derivatives fall on $\chi (r)$, the resulting term is compactly supported in spacetime and clearly obeys the desired estimates. We can therefore carry out the computations suppressing the cutoff functions, i.e., we only need to estimate ${\tilde{h}}_S$ and $\tilde{{\mathcal {G}}}^i_S$.

We first deal with the simple cases where at least one of the indices $\mu$ or $\nu$ is 0. For $\mu =\nu =0$, the desired inequality is trivial as $\Box _m \big (\frac{1}{r}\big )=0$ and ${\mathcal {G}}_S^0=0$. For $\mu =0$ and $\nu =i$, we have $(g_{S})_{0i}={\mathcal {G}}_S^0=\partial _0 \tilde{{\mathcal {G}}}_S^i=0$. We therefore also have the desired conclusion in this case. + It thus remains to check the case $\mu =i$ and $\nu =j$. We first have⁵⁴

$$\begin{aligned}&\Box _m \left( -\frac{4M\log (r-2M)}{r}\delta _{ij}\right) \nonumber \\&\quad =-\delta _{ij}\left( \partial _r^2+\frac{2}{r}\partial _r\right) \frac{4M\log (r-2M)}{r}\nonumber \\&\quad =-\delta _{ij}\left( \partial _r\left( \frac{4M}{r(r-2M)}-\frac{4M\log (r-2M)}{r^2}\right) \right. \nonumber \\&\qquad \left. +\frac{2}{r}\left( \frac{4M}{r(r-2M)}-\frac{4M\log (r-2M)}{r^2}\right) \right) \nonumber \\&\quad =\frac{4M}{r(r-2M)^2}\delta _{ij}. \end{aligned}$$

(9.13)

To compute $\Box _m \big (\frac{x^i x^j}{r^2}(\frac{4M\log (r-2M)}{r}-\frac{2M}{r})\big )$, notice that in terms of the polar coordinates $(r,\theta ,\varphi )$, $\frac{x^i x^j}{r^2}$ is a function of the angular variables alone and $\frac{4M\log (r-2M)}{r}-\frac{2M}{r}$ is a function of r alone. We then compute the $\Box _m$ of the angular part and the radial part separately to get

$$\begin{aligned} \begin{aligned} \Box _m \frac{x^i x^j}{r^2}=&\sum _{k=1}^3\left( \frac{x^j}{r}\right) \partial _k^2\left( \frac{x^i}{r}\right) +\sum _{k=1}^3\left( \frac{x^i}{r}\right) \partial _k^2\left( \frac{x^j}{r}\right) +2\sum _{k=1}^3\left( \partial _k \frac{x^i}{r}\right) \left( \partial _k \frac{x^j}{r}\right) \\ =&\sum _{k=1}^3\frac{x^j}{r}\partial _k\left( \frac{\delta _{ik}}{r}-\frac{x^ix^k}{r^3}\right) +\sum _{k=1}^3\frac{x^i}{r}\partial _k\left( \frac{\delta _{jk}}{r}-\frac{x^jx^k}{r^3}\right) \\&\qquad +2\left( \frac{\delta _{ik}}{r}-\frac{x^ix^k}{r^3}\right) \left( \frac{\delta _{jk}}{r}-\frac{x^jx^k}{r^3}\right) \\ =&-\frac{2 x^ix^j}{r^4}-\frac{4x^ix^j}{r^4}+\frac{2x^ix^j}{r^4}+\frac{2\delta _{ij}}{r^2}-\frac{2x^ix^j}{r^4}=\frac{2}{r^2}\delta _{ij}-\frac{6 x^i x^j}{r^4}.\nonumber \end{aligned}\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(9.14)

and

$$\begin{aligned} \begin{aligned} \Box _m \left( \frac{4M\log (r-2M)}{r}-\frac{2M}{r}\right) =-\frac{4M}{r(r-2M)^2}. \end{aligned} \end{aligned}$$

(9.15)

Notice that the term (9.15) was computed using (8.4) and the term (9.16) was calculated in a similar manner as (9.14). Therefore, by combining (9.15) and (9.16), we have

$$\begin{aligned}&\Box _m \left( -\frac{x^i x^j}{r^2}\left( \frac{2M}{r}-\frac{4M\log (r-2M)}{r}\right) \right) \nonumber \\&\quad =\Box _m \left( \frac{x^i x^j}{r^2}\left( \frac{4M\log (r-2M)}{r}-\frac{2M}{r}\right) \right) \nonumber \\&\quad =\left( \Box _m \frac{x^i x^j}{r^2}\right) \left( \frac{4M\log (r-2M)}{r}-\frac{2M}{r}\right) \nonumber \\&\qquad +\frac{x^i x^j}{r}\left( \Box _m\left( \frac{4M\log (r-2M)}{r}-\frac{2M}{r}\right) \right) \nonumber \\&\quad =\left( \frac{2}{r^2}\delta _{ij}-\frac{6 x^i x^j}{r^4}\right) \left( \frac{4M\log (r-2M)}{r}-\frac{2M}{r}\right) -\frac{4Mx^i x^j}{r^3(r-2M)^2}\nonumber \\&\quad = \left( -\frac{4M}{r^3}+\frac{8 M\log (r-2M)}{r^3}\right) \delta _{ij}+\frac{8 M x^i x^j}{r^5}\nonumber \\&\qquad -\frac{24 M x^i x^j\log (r-2M)}{r^5}-\frac{16M^2 x^i x^j (r-M)}{r^5(r-2M)^2}. \end{aligned}$$

(9.16)

Adding (9.14) and (9.17), and recalling the definition of $({\tilde{h}}_S)_{ij}$, we have

$$\begin{aligned}&\Box _m ({\tilde{h}}_S)_{ij}\nonumber \\&\quad = \frac{8 M\log (r-2M)}{r^3}\delta _{ij}+\frac{8 M x^i x^j}{r^5}-\frac{24 M x^i x^j\log (r-2M)}{r^5}\nonumber \\&\qquad +\frac{16 M^2(r-M)}{r^3(r-2M)^2}\left( \delta _{ij}-\frac{x^i x^j}{r^2}\right) . \end{aligned}$$

(9.17)

On the other hand, by the definition of $\tilde{{\mathcal {G}}}_S$, we have

$$\begin{aligned} \begin{aligned}&m_{i\lambda }\partial _j \tilde{{\mathcal {G}}}_S^\lambda =m_{j\lambda }\partial _i \tilde{{\mathcal {G}}}_S^\lambda \\&\quad =-\frac{4 M\log (r-2M)}{r^3}\delta _{ij}-\frac{x^i x^j}{r^4}\left( \frac{4M}{r-2M}-\frac{12 M\log (r-2M)}{r}\right) \\&\quad =-\frac{4 M\log (r-2M)}{r^3}\delta _{ij}-\frac{x^i x^j}{r^5}(4M-12 M\log (r-2M))-\frac{8 M^2 x^i x^j}{r^5 (r-2M)}.\nonumber \end{aligned}\\ \end{aligned}$$

(9.18)

Combining (9.18) and (9.19), we obtain

$$\begin{aligned} \begin{aligned} \Box _m ({\tilde{h}}_S)_{ij}+m_{i\lambda }\partial _j \tilde{{\mathcal {G}}}^{\lambda }_S+m_{j\lambda }\partial _i {\mathcal {G}}^{\lambda }_S =&\frac{16 M^2(r-M)}{r^3(r-2M)^2}\left( \delta _{ij}-\frac{x^i x^j}{r^2}\right) -\frac{16 M^2 x^i x^j}{r^5 (r-2M)}. \end{aligned} \end{aligned}$$

Using the fact that $t\le r$ in the region $q\ge 0$, it is clear that all derivatives of the right-hand side obey bounds as in the right-hand side of (9.13). We thus obtain (9.13) for $(\mu ,\nu )=(i,j)$.

Finally, we consider the case $q<0$. For this estimate, we simply need to note that on the support of $\chi (\frac{r}{t})$, using the notation $\partial ^k=\partial _t^{k_0}\partial _{x_1}^{k_1}\partial _{x_2}^{k_2}\partial _{x_3}^{k_3}$ and $|k|=k_0+k_1+k_2+k_3$, we have $|\partial ^k \chi (\frac{r}{t})|\lesssim \frac{1}{(1+s)^{|k|}}$, $|\partial ^k {\tilde{h}}_S|\lesssim \frac{\epsilon \log (2+s)}{(1+s)^{|k|+1}}$ and $|\partial ^k \mathcal {{\tilde{G}}}^{\lambda }_S|\lesssim \frac{\epsilon \log (2+s)}{(1+s)^{|k|+2}}$. Using these estimates to bound each of the terms,⁵⁵ we obtain the desired result. $\square$

Using this, we obtain the following bounds for the term (9.1):

Proposition 9.3

For $|I|\le N$, $g_S=m+h_S$ obeys the following estimates. In the region $q\ge 0$, we have

$$\begin{aligned} \begin{aligned}&|\Gamma ^I({\widetilde{\Box }}_g (g_S)_{\mu \nu }-G_{\mu \nu }(g,{\mathcal {G}}_S))|\\&\quad \lesssim \frac{\epsilon \log ^2 (2+s)}{(1+s)^3(1+|q|)^{\gamma }}+\sum _{|J|\le |I|}\left( \frac{\epsilon \log (2+s)|\partial \Gamma ^J h|}{(1+s)^2}+\frac{\epsilon \log (2+s)|\Gamma ^J h|}{(1+s)^3}\right) . \end{aligned} \end{aligned}$$

In the region $q< 0$, we have

$$\begin{aligned} \begin{aligned}&|\Gamma ^I({\widetilde{\Box }}_g (g_S)_{\mu \nu }-G_{\mu \nu }(g,{\mathcal {G}}_S))|\\&\quad \lesssim \frac{\epsilon \log ^2 (2+s)}{(1+s)^{3}}+\sum _{|J|\le |I|}\left( \frac{\epsilon \log (2+s)|\partial \Gamma ^J h|}{(1+s)^2}+\frac{\epsilon \log (2+s)|\Gamma ^J h|}{(1+s)^3}\right) . \end{aligned} \end{aligned}$$

Proof

We recall the definition of the term $G_{\mu \nu }(g,{\mathcal {G}}_S)$:

$$\begin{aligned} \begin{aligned} G_{\mu \nu }(g,{\mathcal {G}}_S)=&-\partial _\mu (g_{\nu \lambda } {\mathcal {G}}_S^{\lambda })-\partial _\nu (g_{\mu \lambda } {\mathcal {G}}_S^{\lambda })-{\mathcal {G}}_S^{\alpha }\partial _\alpha g_{\mu \nu }- g_{\alpha \nu } g_{\beta \mu } {\mathcal {G}}_S^\alpha {\mathcal {G}}_S^{\beta }. \end{aligned} \end{aligned}$$

By the bound

$$\begin{aligned} \sum _{|J|\le |I|}|\partial \Gamma ^J g|\lesssim \frac{\log (2+s)}{(1+s)(1+|q|)^{\gamma }}+\sum _{|J|\le |I|}|\partial \Gamma ^J h| \end{aligned}$$

and the fact that

$$\begin{aligned} \sum _{|J|\le |I|}|\Gamma ^J{\mathcal {G}}_S^\lambda |\lesssim \frac{\epsilon \log (2+s)}{(1+s)^2}, \end{aligned}$$

(9.19)

we have

$$\begin{aligned} |\Gamma ^I({\mathcal {G}}^{\lambda }_S\partial _\mu g_{\nu \lambda })|+|\Gamma ^I({\mathcal {G}}^{\alpha }_S\partial _\alpha g_{\mu \nu })|\lesssim \frac{\epsilon \log ^2 (2+s)}{(1+s)^{3}(1+|q|)^{\gamma }}+\sum _{|J|\le |I|}\frac{\epsilon \log (2+s)|\partial \Gamma ^J h|}{(1+s)^2}. \end{aligned}$$

On the other hand, using (9.20) again, we have

$$\begin{aligned} |\Gamma ^I(g_{\alpha \nu } g_{\beta \mu } {\mathcal {G}}_S^\alpha {\mathcal {G}}_S^{\beta })|\lesssim \frac{\epsilon ^2\log (2+s)}{(1+s)^4}. \end{aligned}$$

Therefore, we get

$$\begin{aligned} \begin{aligned}&|\Gamma ^I(G_{\mu \nu }(g,{\mathcal {G}}_S)+g_{\mu \lambda }\partial _\nu {\mathcal {G}}^{\lambda }_S+g_{\nu \lambda }\partial _\mu {\mathcal {G}}^{\lambda }_S)|\\&\quad \lesssim \frac{\epsilon \log ^2 (2+s)}{(1+s)^{3}(1+|q|)^{\gamma }}+\sum _{|J|\le |I|}\frac{\epsilon \log (2+s)|\partial \Gamma ^J h|}{(1+s)^2}. \end{aligned} \end{aligned}$$

(9.20)

We recall that $|\Gamma ^J(g_{\mu \nu }-m_{\mu \nu })|\lesssim \frac{\log (2+s)}{1+s}+\sum _{|J'|\le |J|}|\Gamma ^{J'} h|$. Moreover, we have $|\Gamma ^J(\partial _{\sigma }{\mathcal {G}}^{\lambda }_S)|\lesssim \frac{\epsilon \log (2+s)}{(1+s)^3}$ using the definition of ${\mathcal {G}}_S$. They imply

$$\begin{aligned} \begin{aligned}&|\Gamma ^I(m_{\mu \lambda }\partial _\nu {\mathcal {G}}^{\lambda }_S+m_{\nu \lambda }\partial _\mu {\mathcal {G}}^{\lambda }_S-g_{\mu \lambda }\partial _\nu {\mathcal {G}}^{\lambda }_S-g_{\nu \lambda }\partial _\mu {\mathcal {G}}^{\lambda }_S)|\\&\quad \lesssim \frac{\epsilon \log ^2 (2+s)}{(1+s)^{4}}+\sum _{|J|\le |I|}\frac{\epsilon \log (2+s)|\Gamma ^J h|}{(1+s)^3}. \end{aligned} \end{aligned}$$

(9.21)

We now apply Proposition 9.2 to obtain

$$\begin{aligned} |\Gamma ^I\big (\Box _m (g_S)_{\mu \nu }+m_{\mu \lambda }\partial _\nu {\mathcal {G}}^{\lambda }_S+m_{\nu \lambda }\partial _\mu {\mathcal {G}}^{\lambda }_S\big )|\lesssim {\left\{ \begin{array}{ll} \frac{\epsilon }{(1+s)^4} &{}\text{ if } q\ge 0\\ \frac{\epsilon \log (2+s)}{(1+s)^3} &{}\text{ if } q< 0.\nonumber \end{array}\right. }\\ \end{aligned}$$

(9.22)

Finally, using (7.1) in Proposition 7.3, we have

$$\begin{aligned} |\Gamma ^I({\widetilde{\Box }}_g (g_S)_{\mu \nu }-{\widetilde{\Box }}_m (g_S)_{\mu \nu })|\lesssim \frac{\epsilon \log ^2 (2+s)}{(1+s)^4}+\sum _{|J|\le |I|}\frac{\epsilon \log (2+s)|\Gamma ^J h|}{(1+s)^3}.\nonumber \\ \end{aligned}$$

(9.23)

Combining (9.21), (9.22), (9.23) and (9.24) gives the desired conclusion of the proposition. $\square$

We now consider the other term where the gauge condition enters, i.e., the term (9.2) which involves the term ${\mathcal {G}}_B$:

Proposition 9.4

For $|I|\le N$, we have the following bound for (9.2):

$$\begin{aligned} \begin{aligned}&|\Gamma ^I(G_{\mu \nu }(g,{\mathcal {G}}_B)-G_{\mu \nu }(g_B,{\mathcal {G}}_B))|\\&\quad \lesssim \frac{\epsilon \log ^2 (2+s)}{(1+s)^3(1+|q|)}+\sum _{|J|\le |I|}\left( \frac{\log (2+s)|\partial \Gamma ^J h|}{(1+s)^2}+\frac{\log (2+s)| \Gamma ^J h|}{(1+s)^2(1+|q|)}\right) . \end{aligned} \end{aligned}$$

Proof

Recall that

$$\begin{aligned} \begin{aligned} G_{\mu \nu }(g,{\mathcal {G}}_B)=&-\partial _\mu (g_{\nu \lambda } {\mathcal {G}}_B^{\lambda })-\partial _\nu (g_{\mu \lambda } {\mathcal {G}}_B^{\lambda })-{\mathcal {G}}_B^{\alpha }\partial _\alpha g_{\mu \nu }- g_{\alpha \nu } g_{\beta \mu } {\mathcal {G}}_B^\alpha {\mathcal {G}}_B^{\beta }. \end{aligned} \end{aligned}$$

We therefore have to control the following terms:

$$\begin{aligned}&|\Gamma ^I ((\partial g-\partial g_B) {\mathcal {G}}_B)|,\quad |\Gamma ^I ((g-g_B) \partial {\mathcal {G}}_B)|, \\&|\Gamma ^I ((g-g_B) g_B{\mathcal {G}}_B{\mathcal {G}}_B)|,\quad |\Gamma ^I ((g-g_B)(g-g_B){\mathcal {G}}_B{\mathcal {G}}_B)|. \end{aligned}$$

By the definition of dispersive spacetimes ((8) of Definition 3.1), we have

$$\begin{aligned} \sum _{|J|\le |I|}|\Gamma ^J{\mathcal {G}}_B|\lesssim \frac{\log (2+s)}{(1+s)^2}. \end{aligned}$$

Using Proposition 7.1, this implies

$$\begin{aligned} \sum _{|J|\le |I|}|\Gamma ^J\partial {\mathcal {G}}_B|\lesssim \frac{\log (2+s)}{(1+s)^2(1+|q|)}. \end{aligned}$$

Moreover, since $g=g_B+h_S+h$, we have

$$\begin{aligned} \sum _{|J|\le |I|}|\Gamma ^J(g-g_B)|\lesssim \sum _{|J|\le |I|}|\Gamma ^J h|+\frac{\epsilon \log (2+s)}{1+s} \end{aligned}$$

and

$$\begin{aligned} \sum _{|J|\le |I|}|\Gamma ^J\partial (g-g_B)|\lesssim \sum _{|J|\le |I|}|\partial \Gamma ^J h|+\frac{\epsilon \log (2+s)}{(1+s)^2}. \end{aligned}$$

The conclusion follows after combining these estimates and using the bootstrap assumption (6.5) for the quadratic terms in h. $\square$

The next term to be controlled is (9.3), which can be bounded as follows:

Proposition 9.5

For $|I|\le N$, the following estimate holds:

$$\begin{aligned} \begin{aligned} |\Gamma ^I(g_{\alpha \nu }g_{\beta \mu }{\mathcal {G}}_B^{(\alpha }{\mathcal {G}}_S^{\beta )})|\lesssim \frac{\epsilon \log ^2(2+s)}{(1+s)^4}+\sum _{|J|\le |I|}\frac{\epsilon \log ^2(2+s)}{(1+s)^4}|\Gamma ^J h|. \end{aligned} \end{aligned}$$

Proof

By (8) in Definition 3.1 and the formula in (4.2), we have the pointwise estimates

$$\begin{aligned} \sum _{|J|\le |I|}|\Gamma ^J {\mathcal {G}}_B|\lesssim \frac{\log (2+s)}{(1+s)^2},\quad \sum _{|J|\le |I|}|\Gamma ^J {\mathcal {G}}_S|\lesssim \frac{\epsilon \log (2+s)}{(1+s)^2}. \end{aligned}$$

The conclusion is therefore implied by the simple bound $\sum _{|J|\le |I|}|\Gamma ^J g|\lesssim 1+\sum _{|J|\le |I|}|\Gamma ^J h|$ together with the bootstrap assumption (6.5). $\square$

We now turn to the commutator term (9.4). To estimate this term, we need the following estimate in Corollary 12.3 in Appendix A in [46] for the commutator between ${\widetilde{\Box }}_g$ and $\Gamma$. Observe from the formula that one of the following three scenarios occur: Either there is a good (LL- or $L{\mathcal {T}}$-) component of H or there is extra $\frac{1}{1+s}$ decay or the term is lower order in terms of derivatives.

Proposition 9.6

The following commutation formula holds for any scalar function $\xi$:

$$\begin{aligned} \begin{aligned}&|{\widetilde{\Box }}_g \Gamma ^I\xi -{\hat{\Gamma }}^I {\widetilde{\Box }}_g \xi |\\&\quad \lesssim \frac{1}{1+s}\sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|} |\Gamma ^{J_1} H| |\partial \Gamma ^{J_2}\xi |\\&\qquad +\frac{1}{1+|q|}\sum _{|J_2|\le |I|}\left( \sum _{|J_1|+(|J_2|-1)_+\le |I|}|\Gamma ^{J_1} H|_{LL}\right. \\&\qquad \left. +\sum _{|J_1'|+(|J_2|-1)_+\le |I|-1}|\Gamma ^{J_1'} H|_{L{\mathcal {T}}} +\sum _{|J_1''|+(|J_2|-1)_+\le |I|-2}|\Gamma ^{J_1''} H|\right) |\partial \Gamma ^{J_2} \xi |, \end{aligned} \end{aligned}$$

where⁵⁶${\hat{\Gamma }}={\left\{ \begin{array}{ll} \Gamma +2 &{} {\text {if }} \Gamma =S\\ \Gamma &{} {\text {otherwise}} \end{array}\right. }$. Here, $(|K|-1)_+=|K|-1$ if $|K|\ge 1$ and $(|K|-1)_+=0$ if $|K|=0$.

Applying this commutation formula for each component $h_{\mu \nu }$, we obtain the following bound for (9.4):

Proposition 9.7

For $|I|\le N$, the following estimates hold:

$$\begin{aligned} \begin{aligned}&|[{\widetilde{\Box }}_g,\Gamma ^I] h|\\&\quad \lesssim \sum _{|J|\le |I|-1}|\Gamma ^J{\widetilde{\Box }}_g h|+\sum _{|J|\le |I|}\frac{|\partial \Gamma ^J h|}{(1+s)^{1+\frac{\gamma }{2}}}+\sum _{|J|\le |I|}\frac{|\Gamma ^J h|}{(1+s)^{2-2\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}}\\&\qquad +\sum _{|J|\le |I|-1}\frac{\log (2+s)|\partial \Gamma ^J h|}{(1+s)(1+|q|)}+\sum _{|J|\le |I|-1}\frac{|\Gamma ^J h|}{(1+s)(1+|q|)^{1+\gamma }}\\&\qquad +\sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|}\frac{|\Gamma ^{J_1} h|_{LL}|\partial \Gamma ^{J_2} h|}{1+|q|}+\sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ \max \{|J_1|,|J_2|\}\le |I|-1 \end{array}}\frac{|\Gamma ^{J_1} h||\partial \Gamma ^{J_2} h|}{1+|q|}. \end{aligned} \end{aligned}$$

Proof

First, notice that

$$\begin{aligned} |[{\widetilde{\Box }}_g,\Gamma ^I] h|\lesssim |{\widetilde{\Box }}_g \Gamma ^I h-{\hat{\Gamma }}^I {\widetilde{\Box }}_g h|+\sum _{|J|\le |I|-1}|\Gamma ^J{\widetilde{\Box }}_g h|. \end{aligned}$$

(9.24)

It therefore suffices to control $|{\widetilde{\Box }}_g \Gamma ^I h-{\hat{\Gamma }}^I {\widetilde{\Box }}_g h|$, for which we can apply Proposition 9.6 to each component of $h_{\mu \nu }$. We now control each of the four terms from Proposition 9.6 using Proposition 7.3. We have the following estimate for the first term:

$$\begin{aligned}&\frac{1}{1+s}\sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|} |\Gamma ^{J_1} H| |\partial \Gamma ^{J_2} h|\nonumber \\&\quad \lesssim \sum _{|J|\le |I|}\frac{\log (2+s)|\partial \Gamma ^J h|}{(1+s)^2}+\sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|}\frac{|\Gamma ^{J_1} h||\partial \Gamma ^{J_2} h|}{1+s}\nonumber \\&\quad \lesssim \sum _{|J|\le |I|}\frac{\log (2+s)|\partial \Gamma ^J h|}{(1+s)^2}+\sum _{|J|\le |I|}\frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}|\partial \Gamma ^{J} h|}{(1+s)^{2-\delta _0}w(q)^{\frac{1}{2}}}\nonumber \\&\qquad +\sum _{|J|\le |I|}\frac{|\Gamma ^J h|}{(1+s)^{2-\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}}. \end{aligned}$$

(9.25)

where in the first inequality we have used (7.1) in Proposition 7.3 and in the last inequality we have used the bootstrap assumptions (6.2) and (6.5). Here, notice in particular that at least one of the terms has at most $\lfloor \frac{N}{2}\rfloor$ $\Gamma$’s, which allows us to apply the bootstrap assumptions.

For the second term, we use (7.4) and (7.5) in Proposition 7.3 to get

$$\begin{aligned} \begin{aligned}&\frac{1}{1+|q|}\sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|}|\Gamma ^{J_1} H|_{LL}|\partial \Gamma ^{J_2} h|\\&\quad \lesssim \sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|}\frac{|\Gamma ^{J_1} h|_{LL}|\partial \Gamma ^{J_2} h|}{1+|q|}+\sum _{|J|= |I|}\frac{|\partial \Gamma ^J h|}{(1+s)^{1+\frac{\gamma }{2}}}\\&\qquad +\sum _{|J|\le |I|-1}\frac{\log (2+s)|\partial \Gamma ^J h|}{(1+s)(1+|q|)}\\&\qquad +\sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|}\frac{|\Gamma ^{J_1}h||\partial \Gamma ^{J_2} h|}{(1+s)^{1-\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}}\\&\quad \lesssim \sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|}\frac{|\Gamma ^{J_1} h|_{LL}|\partial \Gamma ^{J_2} h|}{1+|q|}+\sum _{|J|= |I|}\frac{|\partial \Gamma ^J h|}{(1+s)^{1+\frac{\gamma }{2}}}\\&\qquad +\sum _{|J|\le |I|-1}\frac{\log (2+s)|\partial \Gamma ^J h|}{(1+s)(1+|q|)}+\sum _{|J|\le |I|}\frac{|\Gamma ^J h|}{(1+s)^{2-2\delta _0}(1+|q|)^{1-\frac{\gamma }{2}}w(q)}.\nonumber \end{aligned}\!\!\!\!\!\!\!\\ \end{aligned}$$

(9.26)

In the last step above, we have used the bootstrap assumptions (6.2) and (6.5).

We now turn to the third term. Using (7.1) and (7.4) in Proposition 7.3 to control $|H|_{L{\mathcal {T}}}$, we obtain

$$\begin{aligned}&\frac{1}{1+|q|}\sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|-1}|\Gamma ^{J_1} H|_{L{\mathcal {T}}}|\partial \Gamma ^{J_2} h|\nonumber \\&\quad \lesssim \sum _{|J|=|I|}\frac{|H|_{L{\mathcal {T}}}|\partial \Gamma ^I h|}{1+|q|}+\sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ \max \{|J_1|,|J_2|\}\le |I|-1 \end{array}}\frac{|\Gamma ^{J_1} H||\partial \Gamma ^{J_2} h|}{1+|q|}\nonumber \\&\quad \lesssim \sum _{|J|=|I|}\frac{|\partial \Gamma ^J h|}{(1+s)^{1+\frac{\gamma }{2}}(1+|q|)^{\frac{1}{2}-\gamma }w(q)^{\frac{1}{2}}}+\sum _{|J|\le |I|-1}\frac{\log (2+s)|\partial \Gamma ^J h|}{(1+s)(1+|q|)}\nonumber \\&\qquad +\sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ \max \{|J_1|,|J_2|\}\le |I|-1 \end{array}}\frac{|\Gamma ^{J_1} h||\partial \Gamma ^{J_2} h|}{1+|q|}. \end{aligned}$$

(9.27)

Finally, notice that the last term in Proposition 9.6 does not contain the highest-order contribution, i.e., we have $|J_1|,|J_2|\le |I|-1$. We use (7.1) in Proposition 7.3 to get

$$\begin{aligned} \begin{aligned}&\frac{1}{1+|q|}\sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|-2}|\Gamma ^{J_1} H||\partial \Gamma ^{J_2} h|\\&\quad \lesssim \sum _{|J|\le |I|-1}\frac{\log (2+s)|\partial \Gamma ^J h|}{(1+s)(1+|q|)}+\sum _{|J_1|+|J_2|\le |I|-1}\frac{|\Gamma ^{J_1} h||\partial \Gamma ^{J_2} h|}{1+|q|}. \end{aligned}\nonumber \\ \end{aligned}$$

(9.28)

The conclusion follows after combining (9.25), (9.26), (9.27), (9.28) and (9.29). $\square$

We turn to the estimates for the term (9.5):

Proposition 9.8

The following estimates hold for (9.5) for $|I|\le N$, :

$$\begin{aligned} \begin{aligned}&|\Gamma ^I({\widetilde{\Box }}_g h_B-{\widetilde{\Box }}_{g_B} h_B)|\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2(1+|q|)^{1+\gamma }}+\frac{|\Gamma ^I h|_{LL}}{(1+s)(1+|q|)^{1+\gamma }}\\&\qquad +\sum _{|J|\le |I|}\frac{|\Gamma ^J h|}{(1+s)^{2-\delta _0}(1+|q|)^{\frac{1}{2}+\frac{3\gamma }{4}}w(q)^{\frac{1}{2}}}+\sum _{|J|\le |I|-1}\frac{|\Gamma ^J h|}{(1+s)(1+|q|)^{1+\gamma }}. \end{aligned} \end{aligned}$$

Moreover, we have the following improved bound for the case $|I|=0$:

$$\begin{aligned} |{\widetilde{\Box }}_g h_B-{\widetilde{\Box }}_{g_B} h_B|\lesssim \frac{\epsilon }{(1+s)^{2+\frac{\gamma }{2}}(1+|q|)^{\frac{1}{2}}w(q)^{\frac{1}{2}}}. \end{aligned}$$

(9.29)

Proof

In order to control the difference of ${\widetilde{\Box }}_g$ and ${\widetilde{\Box }}_{g_B}$, we will apply the estimates for $H-H_B$ given by (7.3) and (7.6) in Proposition 7.3. Notice that in order to control this difference, we need a total of $N+2$ derivatives of $h_B$ and this is precisely the reason that we assume in Definition 3.1 that the background spacetime $({\mathcal {M}}, g_B,\phi _B)$ has one extra degree of differentiability compared to that of $({\mathcal {M}}, g, \phi )$.

We now turn to the proof of the estimates. First, we have the bound

$$\begin{aligned} \begin{aligned}&|\Gamma ^I({\widetilde{\Box }}_g h_B-{\widetilde{\Box }}_{g_B} h_B)|\\&\quad \lesssim \sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ |J_1|\le |I|-1 \end{array}}|\Gamma ^{J_1} (H-H_B)||\partial ^2\Gamma ^{J_2} h_B|\nonumber \\&\qquad +|\Gamma ^I (H-H_B)|_{LL}|\partial ^2 h_B|+|\Gamma ^I (H-H_B)||{{\bar{\partial }}} \partial h_B|. \end{aligned}\\ \end{aligned}$$

(9.30)

Using Proposition 7.1 and the assumptions on $h_B$ in Definition 3.1, we have

$$\begin{aligned} \sum _{|J|\le |I|}|\partial ^2\Gamma ^J h_B|\lesssim \sum _{|J|\le |I|+1}\frac{|\partial \Gamma ^J h_B|}{1+|q|}\lesssim \frac{1}{(1+s)(1+|q|)^{1+\gamma }} \end{aligned}$$

(9.31)

and

$$\begin{aligned} \sum _{|J|\le |I|}|{{\bar{\partial }}}\partial \Gamma ^J h_B|\lesssim \sum _{|J|\le |I|+1}\frac{|\partial \Gamma ^J h_B|}{1+s}\lesssim \frac{1}{(1+s)^2(1+|q|)^{\gamma }}. \end{aligned}$$

(9.32)

On the other hand, (7.3) in Proposition 7.3 implies that

$$\begin{aligned} |\Gamma ^J (H-H_B)|\lesssim \frac{\epsilon \log (2+s)}{1+s}+\sum _{|J'|\le |J|}|\Gamma ^{J'} h| \end{aligned}$$

and (7.5) in Proposition 7.3 implies that

$$\begin{aligned} |\Gamma ^I (H-H_B)|_{LL}\lesssim \frac{\epsilon \log (2+s)}{1+s}+|\Gamma ^I h|_{LL}+\sum _{|J|\le |I|}\frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}|\Gamma ^J h|}{(1+s)^{1-\delta _0}w(q)^{\frac{1}{2}}}. \end{aligned}$$

Combining these estimates and substituting into (9.31) yield the first conclusion of the proposition.

Finally, for the improved estimate in the case $|I|=0$, notice that for $|I|=0$, the first term on the right-hand side of (9.31) is absent, i.e.,

$$\begin{aligned} \begin{aligned} |{\widetilde{\Box }}_g h_B-{\widetilde{\Box }}_{g_B} h_B| \lesssim&|H-H_B|_{LL}|\partial ^2 h_B|+|H-H_B||{{\bar{\partial }}} \partial h_B|. \end{aligned} \end{aligned}$$

(9.33)

Using the estimates (7.4) and (7.6) in Proposition 7.3 and the bootstrap assumption (6.6), we have

$$\begin{aligned} \begin{aligned} |H-H_B|_{LL}\lesssim \frac{\epsilon (1+|q|)^{\frac{1}{2}+\gamma }}{(1+s)^{1+\frac{\gamma }{2}}w(q)^{\frac{1}{2}}} \end{aligned} \end{aligned}$$

(9.34)

and

$$\begin{aligned} \begin{aligned} |H-H_B|\lesssim \frac{\epsilon (1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}}{(1+s)^{1-\delta _0}w(q)^{\frac{1}{2}}}. \end{aligned} \end{aligned}$$

(9.35)

We now substitute the bounds (9.32), (9.33), (9.35), (9.36) into (9.34) to get

$$\begin{aligned} |{\widetilde{\Box }}_g h_B-{\widetilde{\Box }}_{g_B} h_B|\lesssim \frac{\epsilon }{(1+s)^{2+\frac{\gamma }{2}}(1+|q|)^{\frac{1}{2}}w(q)^{\frac{1}{2}}}+\frac{\epsilon (1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}}{(1+s)^{3-\delta _0}(1+|q|)^{\gamma }w(q)^{\frac{1}{2}}}. \end{aligned}$$

The claimed estimate for the $|I|=0$ case thus follows after noting that for $\delta _0$ satisfying (6.1), we have $1-\delta _0-\frac{\gamma }{2}>1-\frac{3\gamma }{4}$. $\square$

We now turn to the quadratic terms in $\partial g$, i.e., (9.6) and (9.7). First, we deal with the terms Q for which a null structure is present, i.e. we control the term (9.6). Before we deal with these terms, we first need a discussion on some standard facts about the classical null forms on Minkowski spacetime.

Definition 9.9

We say ${\widetilde{Q}}(\xi ,\eta )=A^{\alpha \beta }\partial _\alpha \xi \partial _\beta \eta$ is a classical null form if $A^{\alpha \beta }$ are constants satisfying $A^{\alpha \beta }X_{\alpha }X_{\beta }$ whenever $X_0^2=X_1^2+X_2^2+X_3^2$.

It is a standard easy fact that every classical null forms can be controlled by a product where at least one of the derivatives is a good derivative ${\bar{\partial }}$:

Lemma 9.10

If ${\widetilde{Q}}(\xi ,\eta )$ is a classical null form, then

$$\begin{aligned} |{\widetilde{Q}}(\xi ,\eta )|\lesssim |\partial \xi ||{\bar{\partial }}\eta |+|{\bar{\partial }}\xi ||\partial \eta |. \end{aligned}$$

The final fact that we need about classical null forms is that they commute well with the Minkowskian vector fields:

Lemma 9.11

Let ${\widetilde{Q}}(\xi ,\eta )$ be a classical null form and $\Gamma$ be a Minkowskian commuting vector field. Then,

$$\begin{aligned} \Gamma {\widetilde{Q}}(\xi ,\eta )={\widetilde{Q}}(\Gamma \xi ,\eta )+{\widetilde{Q}}(\xi ,\Gamma \eta )+{\widetilde{Q}}'(\xi ,\eta ), \end{aligned}$$

where ${\widetilde{Q}}'(\xi ,\eta )$ is also a classical null form.

Using Lemmas 9.10 and 9.11, we can now proceed to estimate the term (9.6). More precisely, we have

Proposition 9.12

For $|I|\le N$, we have

$$\begin{aligned} \begin{aligned}&|\Gamma ^I(Q_{\mu \nu }(g,g;\partial g,\partial g)-Q_{\mu \nu }(g_B,g_B;\partial g_B,\partial g_B))|\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^3(1+|q|)^{\gamma }}+\sum _{|J|\le |I|}\left( \frac{|\partial \Gamma ^J h|}{(1+s)^{1+\gamma }}\right. \\&\qquad \left. +\frac{|{{\bar{\partial }}} \Gamma ^J h|}{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}+\frac{|\Gamma ^J h|}{(1+s)^{2-2\delta _0}(1+|q|)^{2\gamma +2\delta _0}}\right) . \end{aligned} \end{aligned}$$

Proof

By the triangle inequality and using the bootstrap assumptions (6.5) together with Proposition 7.3 to bound the higher-order terms, it suffices to control the following terms:

$$\begin{aligned}&\Gamma ^I(Q_{\mu \nu }(m,m;\partial h_*,\partial h)), \end{aligned}$$

(9.36)

$$\begin{aligned}&\sum _{|J_1|+|J_2|+|J_3|\le |I|}(1+|\Gamma ^{J_1} H|)|\partial \Gamma ^{J_2} h_*||\partial \Gamma ^{J_3} h_S|, \end{aligned}$$

(9.37)

$$\begin{aligned}&\sum _{|J_1|+|J_2|+|J_3|\le |I|}|\Gamma ^{J_1} H||\partial \Gamma ^{J_2} h_*||\partial \Gamma ^{J_3} h|, \end{aligned}$$

(9.38)

$$\begin{aligned}&\sum _{|J_1|+|J_2|+|J_3|\le |I|}|\Gamma ^{J_1}(H-H_B)||\partial \Gamma ^{J_2} h_*||\partial \Gamma ^{J_3}h_*|, \end{aligned}$$

(9.39)

where we have used the notation $h_*\in \{h_S,h_B,h\}$. We briefly explain the estimates for these terms before turning to the details. First, notice that since we are taking the difference of a g term and a $g_B$ term, every term in the resulting expression must have at least one factor of $\partial \Gamma ^J h$, $\partial \Gamma ^J h_S$ or $\Gamma ^J (H-H_B)$. Now, in order to estimate these terms, we observe that as long as the term is cubic (i.e., the terms (9.39), (9.40)), there is enough decay to guarantee that it obeys the desired estimates. Turning to the quadratic terms, if one of the factors is $h_S$ (i.e., the terms in (9.38) arising from the 1 in the first pair of brackets or the terms in (9.37) where $h_*=h_S$), then we can use the better decay properties of $\partial \Gamma ^J h_S$ to show that these terms are also acceptable. The main term is therefore the quadratic terms (9.37) where $h_*\in \{h_B,h\}$. For these terms, we use the fact that $Q_{\mu \nu }(m,m;\cdot ,\cdot )$ is a classical null form and can be controlled using Lemmas 9.10 and 9.11.

We now turn to the details of the estimates of these terms:

Estimates for ( 9.37 )

Again, it is easy to check that $Q_{\mu \nu }(m,m; \cdot ,\cdot )$ is a classical null form. Using Lemmas 9.10 and 9.11 on classical null forms, we have

$$\begin{aligned} \Gamma ^I(Q_{\mu \nu }(m,m;\partial h_*,\partial h))\lesssim \sum _{|J_1|+|J_2|\le |I|} (|{{\bar{\partial }}} \Gamma ^{J_1} h_*||\partial \Gamma ^{J_2} h|+|\partial \Gamma ^{J_1} h_*||{{\bar{\partial }}} \Gamma ^{J_2} h|).\nonumber \!\!\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(9.40)

First, if $h_*\in \{h_S,h_B\}$, we can simply use the bound

$$\begin{aligned}&\sum _{|J|\le N}|{{\bar{\partial }}}\Gamma ^J h_*|\lesssim \frac{1}{(1+s)^{1+\gamma }}, \end{aligned}$$

(9.41)

$$\begin{aligned}&\sum _{|J|\le N}|\partial \Gamma ^J h_*|\lesssim \frac{1}{(1+s)(1+|q|)^{\gamma }}. \end{aligned}$$

(9.42)

Combining (9.41), (9.42) and (9.43), we have thus shown that in the case $h_*\in \{h_S,h_B\}$, (9.37) obeys bounds as stated in the proposition. Now, turning to the case $h_*=h$, notice that since $|I|\le N$, we have $\min \{J_1,J_2\}\le \lfloor \frac{N}{2}\rfloor$. Therefore, by the bootstrap assumption (6.2), (6.3)

$$\begin{aligned}&\sum _{|J|\le N}|{{\bar{\partial }}}\Gamma ^{\min \{J_1,J_2\}} h|\lesssim \frac{1}{(1+s)^{1+\gamma }}, \end{aligned}$$

(9.43)

$$\begin{aligned}&\sum _{|J|\le N}|\partial \Gamma ^{\min \{J_1,J_2\}} h|\lesssim \frac{1}{(1+s)^{1-\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}}. \end{aligned}$$

(9.44)

(9.41), (9.44) and (9.45) clearly imply the desired bounds in the case $h_*=h$.

Estimates for ( 9.38 )

We first consider the case where $h_*=h$. Using the bound

$$\begin{aligned} |\partial \Gamma ^{J_3}h_S|\lesssim \frac{\epsilon \log (2+s)}{(1+s)^2}, \end{aligned}$$

and (7.1) in Proposition 7.3, we have

$$\begin{aligned}&\sum _{|J_1|+|J_2|+|J_3|\le |I|}(1+|\Gamma ^{J_1} H|)|\partial \Gamma ^{J_2}h||\partial \Gamma ^{J_3}h_S|\\&\qquad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2}\sum _{|J_1|+|J_2|\le |I|}(1+ |\Gamma ^{J_1} h|)|\partial \Gamma ^{J_2} h|. \end{aligned}$$

If $|J_1|\le |J_2|$, this can be controlled using the bootstrap assumption (6.5) by

$$\begin{aligned} \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2}\sum _{|J_2|\le |I|}|\partial \Gamma ^{J_2} h|, \end{aligned}$$

which is acceptable. On the other hand, if $|J_1|\ge |J_2|$, we bound the above expression using the bootstrap assumption (6.2) by

$$\begin{aligned} \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2}\sum _{|J_2|\le |I|}|\partial \Gamma ^{J_2} h|+\frac{\epsilon \log (2+s)}{(1+s)^{3-\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}}\sum _{|J_1|\le |I|} |\Gamma ^{J_1} h|, \end{aligned}$$

which is also acceptable.

We now turn to the case $h_*\in \{h_B,h_S\}$. For these terms, we can apply the $L^\infty$ bound to $|\partial \Gamma ^{J_2}h_*||\partial \Gamma ^{J_3}h_S|$ and to obtain

$$\begin{aligned} \sum _{|J_2|+|J_3|\le N}|\partial \Gamma ^{J_2}h_*||\partial \Gamma ^{J_3}h_S|\lesssim \frac{\epsilon \log (2+s)}{(1+s)^3(1+|q|)^{\gamma }}. \end{aligned}$$

On the other hand, by (7.1) in Proposition 7.3, we have

$$\begin{aligned} \sum _{|J_1|\le |I|}(1+|\Gamma ^{J_1} H|)\lesssim 1+\sum _{|J|\le |I|} |\Gamma ^J h|. \end{aligned}$$

Combining these estimates, we obtain

$$\begin{aligned}&\sum _{|J_1|+|J_2|+|J_3|\le |I|}(1+|\Gamma ^{J_1} H|)|\partial \Gamma ^{J_2}h_*||\partial \Gamma ^{J_3}h_S|\\&\qquad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^3(1+|q|)^{\gamma }}\left( 1+\sum _{|J|\le |I|} |\Gamma ^J h|\right) . \end{aligned}$$

This clearly obeys the bounds stated in the proposition. Notice that here we do not need to use any structure of the quadratic form Q.

Estimates for ( 9.39 )

Since this is a cubic term, we do not need to exploit any structure of the nonlinearity. We can assume without loss of generality that in the case $h_*=h$, we have $|J_2|\le |J_3|$. Therefore, we have the pointwise bound

$$\begin{aligned} |\partial \Gamma ^{J_2}h_*|\lesssim \frac{1}{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}. \end{aligned}$$

Therefore, when combining this estimate with (7.1) in Proposition 7.3, we get

$$\begin{aligned} \begin{aligned}&\sum _{|J_1|+|J_2|+|J_3|\le |I|}|\Gamma ^{J_1} H||\partial \Gamma ^{J_2}h_*||\partial \Gamma ^{J_3} h|\\&\quad \lesssim \sum _{|J_3|\le |I|}\frac{\log (2+s)}{1+s}\frac{|\partial \Gamma ^{J_3}h|}{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}\\&\qquad +\sum _{|J_1|+|J_3|\le |I|}\frac{|\Gamma ^{J_1}h||\partial \Gamma ^{J_3}h|}{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}. \end{aligned} \end{aligned}$$

(9.45)

The first term in (9.46) is clearly acceptable. For the second term, we consider the cases $|J_1|\le |J_3|$ and $|J_1|>|J_3|$ separately. In the case $|J_1|\le |J_3|$, by the bootstrap assumption (6.5), the second term on the right-hand side of (9.46) is bounded by

$$\begin{aligned} \lesssim \sum _{|J|\le |I|}\frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}-\gamma -\delta _0}|\partial \Gamma ^{J}h|}{(1+s)^{2-2\delta _0}w(q)^{\frac{1}{2}}}. \end{aligned}$$

This is acceptable since $1-\gamma -2\delta _0>\frac{1}{2}+\frac{\gamma }{4}-\gamma -\delta _0$ for $\delta _0$ satisfying (6.1). In the case $|J_1|> |J_3|$, by the bootstrap assumption (6.2), the second term on the right-hand side of (9.46) is instead bounded by

$$\begin{aligned} \lesssim \sum _{|J|\le |I|}\frac{|\Gamma ^{J}h|}{(1+s)^{2-2\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}+\gamma +\delta _0}w(q)^{\frac{1}{2}}}, \end{aligned}$$

which is also acceptable.

Estimates for ( 9.40 )

Finally, in order to control (9.40), we can assume that both instances of $h_*$ are in fact $h_B$ for otherwise, this can be bounded in a similar manner as (9.38) and (9.39). We can therefore use the pointwise bound (see Definition 3.1)

$$\begin{aligned} \sum _{|J_2|+|J_3|\le N}|\partial \Gamma ^{J_2}h_B||\partial \Gamma ^{J_3}h_B|\lesssim \frac{1}{(1+s)^2(1+|q|)^{2\gamma }}. \end{aligned}$$

Then, using the bound for $\Gamma ^{J_1}(H-H_B)$ in (7.3) in Proposition 7.3, we get

$$\begin{aligned} \begin{aligned}&\sum _{|J_1|+|J_2|+|J_3|\le |I|}|\Gamma ^{J_1}(H-H_B)||\partial \Gamma ^{J_2} h_*||\partial \Gamma ^{J_3}h_*|\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^3(1+|q|)^{2\gamma }}+\sum _{|J|\le |I|}\frac{|\Gamma ^J h|}{(1+s)^2(1+|q|)^{2\gamma }}, \end{aligned} \end{aligned}$$

which is acceptable. $\square$

We then turn to the remaining quadratic terms P in $\partial g$ for which the classical null condition is violated. While the classical null condition is violated, as observed by Lindblad–Rodnianski, there is a weak null structure which can be exploited. Here, we in particular need to make use of the generalized wave coordinate condition and Proposition 8.3.

Proposition 9.13

For $|I|\le N$, we have

$$\begin{aligned} \begin{aligned}&|\Gamma ^I(P(g,g;\partial _\mu g,\partial _{\nu } g)-P(g_B,g_B;\partial _\mu g_B,\partial _{\nu } g_B))|\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^{3-\delta _0}(1+|q|)^{\delta _0} w(q)^{\frac{\gamma }{1+2\gamma }}}+|\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}|\partial h|_{{\mathcal {T}}{\mathcal {U}}}+\frac{|\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}}{(1+s)(1+|q|)^\gamma }\\&\qquad +\sum _{|J|\le |I|}\frac{|\partial \Gamma ^J h|}{(1+s)^{1+\gamma }}+\sum _{|J|\le |I|-1}\frac{|\partial \Gamma ^J h|}{(1+s)(1+|q|)^{\gamma }}\\&\qquad +\sum _{|J|\le |I|}\frac{|{\bar{\partial }}\Gamma ^J h|}{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}+\sum _{|J|\le |I|}\frac{\log (2+s)|\Gamma ^J h|}{(1+s)^{2-2\delta _0}(1+|q|)^{\gamma +2\delta _0}}\\&\qquad +\sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ \max \{|J_1|,|J_2|\}\le |I|-1 \end{array}}|\partial \Gamma ^{J_1} h||\partial \Gamma ^{J_2} h|. \end{aligned} \end{aligned}$$

Proof

Notice that in the proof of Proposition 9.12, among the terms (9.37), (9.38), (9.39) and (9.40), we have only used the null structure of $Q_{\mu \nu }$ in the bounds for the term (9.37):

$$\begin{aligned} \Gamma ^I(Q(m,m;\partial _\mu h_*,\partial _{\nu } h)). \end{aligned}$$

Therefore, we can now focus our attention to the term⁵⁷

$$\begin{aligned} \Gamma ^I(P(m,m;\partial _\mu h_*,\partial _{\nu } h)), \end{aligned}$$

since all the remaining terms can be bounded analogously as in Proposition 9.12. Moreover, we can make a further reduction and assume that $h_*\in \{h,h_B\}$, since if $h_*=h_S$, we have better decay for $|\partial \Gamma ^J h_S|$ and the term can be controlled in the same way as the first term in (9.38). Recalling the structure of the term P, we therefore have to bound the two terms

$$\begin{aligned} \left| \Gamma ^I\left( m^{\alpha \alpha '}\partial _\mu (h_*)_{\alpha \alpha '}m^{\beta \beta '}\partial _\nu h_{\beta \beta '}\right) \right| \end{aligned}$$

(9.46)

and

$$\begin{aligned} \left| \Gamma ^I\left( m^{\alpha \alpha '}\partial _\mu (h_*)_{\alpha \beta }m^{\beta \beta '}\partial _\nu h_{\alpha ' \beta '}\right) \right| . \end{aligned}$$

(9.47)

First, notice that for the terms in (9.47) and (9.48) in which we do not have the highest derivatives $\partial \Gamma ^I h$, we can simply estimate by naive bound

$$\begin{aligned} \lesssim \sum _{|J|\le |I|-1}\frac{|\partial \Gamma ^J h|}{(1+s)(1+|q|)^{\gamma }}+\sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ \max \{|J_1|,|J_2|\}\le |I|-1 \end{array}}|\partial \Gamma ^{J_1} h||\partial \Gamma ^{J_2} h|,\nonumber \\ \end{aligned}$$

(9.48)

which is acceptable. In the first term above, we have used the bounds in Definition 3.1 to control $\partial \Gamma ^J h_B$.

It therefore remains to consider the highest-order terms in h, i.e., when we have $\partial \Gamma ^I h$. Noticing that $m^{{\underline{L}}{\underline{L}}}=m^{{\underline{L}}A}=0$, we must have one of the following two scenarios: Either we do not have the ${\underline{L}}{\underline{L}}$ component in either of the factors, i.e.,

$$\begin{aligned} |\partial h_*|_{{\mathcal {T}}{\mathcal {U}}}|\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}} \end{aligned}$$

(9.49)

or the ${\underline{L}}{\underline{L}}$ component is coupled with a “good” LL component, i.e.,

$$\begin{aligned} |\partial h_*|_{LL}|\partial \Gamma ^I h|_{{\underline{L}}{\underline{L}}}+|\partial h_*|_{{\underline{L}}{\underline{L}}}|\partial \Gamma ^I h|_{LL}. \end{aligned}$$

(9.50)

In the first case, i.e., (9.50), we have the bound

$$\begin{aligned} |\partial h_*|_{{\mathcal {T}}{\mathcal {U}}}|\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}\lesssim |\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}\left( |\partial h|_{{\mathcal {T}}{\mathcal {U}}}+\frac{1}{(1+s)(1+|q|)^\gamma }\right) . \end{aligned}$$

(9.51)

In the second case, i.e., (9.51), we first note that by Definition 3.1, we have

$$\begin{aligned} |h_B|_{LL}+|\Gamma h_B|_{LL}\lesssim \frac{1}{(1+s)^{1+\gamma }}. \end{aligned}$$

By Proposition 7.1, we have

$$\begin{aligned} |\partial ((h_B)_{LL})|\lesssim \frac{1}{(1+s)^{1+\gamma }(1+|q|)}. \end{aligned}$$

Now, notice that $\partial _q$ commutes with the projection onto L, therefore we have

$$\begin{aligned} |\partial h_B|_{LL}\lesssim \frac{1}{(1+s)^{1+\gamma }(1+|q|)}+|{\bar{\partial }}h_B|\lesssim \frac{1}{(1+s)^{1+\gamma }}, \end{aligned}$$

(9.52)

using again Definition 3.1.

Now, we use Propositions 8.2 and 8.3 to control the terms $|\partial h|_{LL}$ and $|\partial \Gamma ^I h|_{LL}$. More precisely, by Proposition 8.2 and the bootstrap assumptions (6.2), (6.3) and (6.5), we have

$$\begin{aligned} \begin{aligned} |\partial h|_{LL} \lesssim&\frac{\epsilon ^{\frac{1}{2}} }{(1+s)^{1+\gamma }} \end{aligned} \end{aligned}$$

(9.53)

Therefore, by (9.53) and (9.54), the first term in (9.51) can be controlled by

$$\begin{aligned} |\partial h_*|_{LL}|\partial \Gamma ^I h|_{{\underline{L}}{\underline{L}}}\lesssim \frac{|\partial \Gamma ^I h|}{(1+s)^{1+\gamma }}, \end{aligned}$$

(9.54)

which is acceptable.

It now remains to control the second term in (9.51). By Proposition 8.3, we have

$$\begin{aligned}&|\partial \Gamma ^I h|_{LL}\nonumber \\&\quad \lesssim \underbrace{\frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}}_{=:\hbox {I}}+\underbrace{\frac{\log (2+s)}{(1+s)(1+|q|)^\gamma }\sum _{|J|\le |I|}|\Gamma ^J h|}_{=:\hbox {II}}\nonumber \\&\qquad +\underbrace{\frac{\log (2+s)}{1+s}\sum _{|J|\le |I|}|\partial \Gamma ^J h|}_{=:\hbox {III}}+\underbrace{\sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|}_{=:\hbox {IV}}+\underbrace{\sum _{|J|\le |I|}|{\bar{\partial }}\Gamma ^J h|}_{=:\hbox {V}}\nonumber \\&\qquad +\underbrace{\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|}_{=:\hbox {VI}}. \end{aligned}$$

(9.55)

On the other hand, we have the naive bound

$$\begin{aligned} |\partial h_*|_{{\underline{L}}{\underline{L}}}\lesssim \frac{1}{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}. \end{aligned}$$

(9.56)

This is already sufficient to control the terms I, II, III and V in (9.56) since

$$\begin{aligned} \begin{aligned}&\frac{\left( {\text {I + II + III + V}} \right) }{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^{3-\delta _0}(1+|q|)^{\gamma +\delta _0} w(q)^{\frac{\gamma }{1+2\gamma }}}\\&\qquad +\sum _{|J|\le |I|}\frac{\log (2+s)|\Gamma ^J h|}{(1+s)^{2-2\delta _0}(1+|q|)^{\gamma +2\delta _0}}\\&\qquad +\sum _{|J|\le |I|}\frac{|\partial \Gamma ^J h|}{(1+s)^{1+\gamma }}\\&\qquad +\sum _{|J|\le |I|} \frac{|{\bar{\partial }}\Gamma ^J h|}{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}, \end{aligned} \end{aligned}$$

(9.57)

which is acceptable.

For the term IV, since either $|J_1|\le \lfloor \frac{N}{2} \rfloor$ or $|J_2|\le \lfloor \frac{N}{2} \rfloor$, we have

$$\begin{aligned}&|\partial h_*|_{{\underline{L}}{\underline{L}}}\times (\hbox {IV})\nonumber \\&\quad \lesssim |\partial h_*|_{{\underline{L}}{\underline{L}}} \left( \frac{\epsilon ^{\frac{1}{2}}(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}}{(1+s)^{1-\delta _0}w(q)^{\frac{1}{2}}}\sum _{|J|\le |I|}|\partial \Gamma ^J h|\right. \nonumber \\&\qquad \left. +\frac{\epsilon ^{\frac{1}{2}}}{(1+s)^{1-\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}}\sum _{|J|\le |I|}|\Gamma ^J h|\right) \nonumber \\&\quad \lesssim \frac{\epsilon ^{\frac{1}{2}}(1+|q|)^{\frac{1}{2}-\frac{3\gamma }{4}-\delta _0}}{(1+s)^{2-2\delta _0}w(q)^{\frac{1}{2}}}\sum _{|J|\le |I|}|\partial \Gamma ^J h|\nonumber \\&\qquad +\frac{\epsilon ^{\frac{1}{2}}}{(1+s)^{2-2\delta _0}(1+|q|)^{\frac{1}{2}+\frac{3\gamma }{4}+\delta _0}w(q)^{\frac{1}{2}}}\sum _{|J|\le |I|}|\Gamma ^J h|, \end{aligned}$$

(9.58)

where we have used the bootstrap assumptions (6.2) and (6.5) as well as (9.57). This bound is acceptable since $1-2\delta _0-\gamma >\frac{1}{2}+\frac{3\gamma }{4}+\delta _0$ and $\frac{1}{2}+\frac{3\gamma }{4}+\delta _0 >\gamma +2\delta _0$ for $\delta _0$ satisfying (6.1).

Finally, the term VI in (9.56) requires the application of the slightly more refined estimate separating the contributions from $|\partial h|$ and $|\partial h_B|$:

$$\begin{aligned} |\partial h_*|_{{\underline{L}}{\underline{L}}}\lesssim \frac{1}{(1+s)(1+|q|)^{\gamma }}+|\partial h| \end{aligned}$$

from which we obtain

$$\begin{aligned} \begin{aligned}&|\partial h_*|_{{\underline{L}}{\underline{L}}}\times (\hbox {VI})\\&\quad \lesssim \frac{1}{(1+s)(1+|q|)^{\gamma }}\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|+\sum _{|J|\le |I|-2}|\partial h||\partial \Gamma ^J h|, \end{aligned} \end{aligned}$$

(9.59)

which is acceptable.

Combining (9.56), (9.58), (9.59) and (9.60), we have thus shown that $|\partial h_*|_{{\underline{L}}{\underline{L}}}|\partial \Gamma ^I h|_{LL}$ is acceptable. Combining this with (9.50), (9.52) and (9.55), we have therefore proven that the terms (9.47) and (9.48) can be dominated by terms on the right-hand side of the statement of the proposition.

As mentioned in the beginning of the proof of the proposition, the terms other than (9.47) and (9.48) are either cubic or contain a factor of $\partial \Gamma ^J h_S$. They can therefore be controlled in an identical manner as (9.38), (9.39) and (9.40) in the proof of Proposition 9.12. Therefore, we have

$$\begin{aligned} \begin{aligned}&|\text{ Cubic } \text{ terms }|+|\text{ Quadratic } \text{ terms } \text{ containing } \partial \Gamma ^Jh_S|\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^3 (1+|q|)^{\gamma }}+\sum _{|J|\le |I|}\left( \frac{|\partial \Gamma ^J h|}{(1+s)^{1+\gamma }}\right. \\&\qquad \left. +\frac{|{{\bar{\partial }}} \Gamma ^J h|}{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}+\frac{|\Gamma ^J h|}{(1+s)^{2-2\delta _0}(1+|q|)^{2\gamma +2\delta _0}}\right) . \end{aligned} \end{aligned}$$

This concludes the proof of the proposition.

$\square$

Finally, we bound the last term in Proposition 9.1, namely (9.8). Since this term is only quadratic and there are no contributions from the metric terms, it is easy to see that we have the following bound.

Proposition 9.14

Denote $\beta :=\phi -\phi _B$. For $|I|\le N$, the following estimate holds:

$$\begin{aligned} \begin{aligned}&\left| \Gamma ^I\left( T_{\mu \nu }(\partial \phi ,\partial \phi )-T_{\mu \nu }(\partial \phi _B,\partial \phi _B)\right) \right| \\&\quad \lesssim \sum _{|J|\le |I|}\frac{|\partial \Gamma ^J\beta |}{(1+s)(1+|q|)^{\gamma }}+\sum _{|J_1|+|J_2|\le |I|}|\partial \Gamma ^{J_1}\beta ||\partial \Gamma ^{J_2}\beta |. \end{aligned} \end{aligned}$$

Proof

After using (6) in Definition 3.1, this is straightforward. $\square$

Using the above propositions, we obtain

Proposition 9.15

For $|I|\le N$, the right-hand side of the equation for $\Gamma ^I h$ can be decomposed into the following terms:

$$\begin{aligned} |{\widetilde{\Box }}_g\Gamma ^I h| \lesssim {\mathfrak {I}}_I + {\mathfrak {G}}_I + {\mathfrak {B}}_I + {\mathfrak {T}}_I + {\mathfrak {L}}_I + {\mathfrak {W}}_I + {\mathfrak {N}}_I, \end{aligned}$$

where each of these terms is defined as follows:

$$\begin{aligned}&{\mathfrak {I}}_I(t,x):= \frac{\epsilon \log ^2 (2+s)}{(1+s)^2(1+|q|)w(q)^{\frac{\gamma }{1+2\gamma }}},\\&{\mathfrak {G}}_I(t,x):= \sum _{|J|\le |I|}\frac{|\Gamma ^J h|_{LL}}{(1+s)(1+|q|)^{1+\gamma }}+\sum _{|J|\le |I|}\frac{\left( |{\bar{\partial }}\Gamma ^J h|+|{\bar{\partial }}\Gamma ^J \beta |\right) }{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}, \\&{\mathfrak {B}}_I(t,x):= |\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}|\partial h|_{{\mathcal {T}}{\mathcal {U}}}+\frac{\left( |\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}+|\partial \Gamma ^I\beta |\right) }{(1+s)(1+|q|)^{\gamma }}+|\partial \Gamma ^I \beta ||\partial \beta |, \\&{\mathfrak {T}}_I(t,x):= \sum _{|J|\le |I|}\frac{\left( |\partial \Gamma ^J h|+|\partial \Gamma ^J\beta |\right) }{(1+s)^{1+\frac{\gamma }{2}}}, \\&{\mathfrak {L}}_I(t,x):= \sum _{|J|\le |I|-1}\left( \frac{\log (2+s)\left( |\partial \Gamma ^J h|+|\partial \Gamma ^J\beta |\right) }{(1+s)(1+|q|)^{\gamma }}+\frac{|\Gamma ^J h|}{(1+s)(1+|q|)^{1+\gamma }}\right) , \\&{\mathfrak {W}}_I(t,x):= \sum _{|J|\le |I|}\frac{\log (2+s)|\Gamma ^J h|}{(1+s)^{2-2\delta _0}(1+|q|)^{\gamma +2\delta _0}}, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {\mathfrak {N}}_I(t,x)&:= \sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ \max \{|J_1|,|J_2|\}\le |I|-1 \end{array}}\left( |\partial \Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|+|\partial \Gamma ^{J_1}\beta ||\partial \Gamma ^{J_2}\beta |+\frac{|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|}{1+|q|}\right) \\&\quad +\sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|}\frac{|\Gamma ^{J_1} h|_{LL}|\partial \Gamma ^{J_2} h|}{1+|q|}. \end{aligned} \end{aligned}$$

We will call these terms the inhomogeneous term, the good term, the bad term, the top order term, the lower-order term, the potential term and the nonlinear term, respectively. Moreover, when $|I|=0$, in addition to the bounds above, we also have

$$\begin{aligned} {\mathfrak {I}}_0(t,x)\lesssim \frac{\epsilon \log ^2(2+s)}{(1+s)^{2+\frac{\gamma }{2}}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{2}-\delta _0}w(q)^{\frac{1}{2}}}. \end{aligned}$$

Proof

It suffices to show that the right-hand side of Propositions 9.3, 9.4, 9.5, 9.7, 9.8, 9.12, 9.13 and 9.14 can be controlled by the terms as stated in this proposition. We will briefly indicate how to bound the terms from each of these propositions:

Terms from Proposition 9.3

Note that the first terms are different for $q\ge 0$ and $q<0$, while the second and third terms are the same. Combining the estimates for the first terms for $q\ge 0$ and $q<0$, we have a term

$$\begin{aligned} \frac{\epsilon \log ^2(2+s)}{(1+s)^3w(q)^{\frac{\gamma }{1+2\gamma }}}, \end{aligned}$$

which can be dominated by ${\mathfrak {I}}_I$. The second term can be bounded by ${\mathfrak {T}}_I$, while the third term can be estimated by ${\mathfrak {W}}_I$.

Terms from Proposition 9.4

Similar to terms from Proposition 9.3, the first term can be controlled by ${\mathfrak {I}}_I$; the second term by ${\mathfrak {T}}_I$; and the third term by ${\mathfrak {W}}_I$.

Terms from Proposition 9.5

The first term can be bounded by ${\mathfrak {I}}_I$, and the second term can be controlled by ${\mathfrak {W}}_I$.

Terms from Proposition 9.7

The first term on the right-hand side of Proposition 9.7, i.e., $\sum _{|J|\le |I|-1} |\Gamma ^J {\widetilde{\Box }}_g h|$ contains all the terms in Proposition 9.1 (with I replaced by J for $|J|\le |I|-1$) except for (9.4). All these terms are controlled in the rest of the proof of the present proposition. We now move to the remaining terms. The second and third terms can be bounded by ${\mathfrak {T}}_I$, ${\mathfrak {W}}_I$, respectively. The fourth and fifth terms can be estimated by ${\mathfrak {L}}_I$. Finally, the sixth and seventh terms can be controlled by ${\mathfrak {N}}_I$.

Terms from Proposition 9.8

The first to fourth terms are controlled by ${\mathfrak {I}}_I$, ${\mathfrak {G}}_I$, ${\mathfrak {W}}_I$ and ${\mathfrak {L}}_I$, respectively.

Terms from Proposition 9.12

The four terms in Proposition 9.12 can be controlled by ${\mathfrak {I}}_I$, ${\mathfrak {T}}_I$, ${\mathfrak {G}}_I$ and ${\mathfrak {W}}_I$, respectively.

Terms from Proposition 9.13

The first term can be controlled by ${\mathfrak {I}}_I$. The second and third terms are bounded by ${\mathfrak {B}}_I$. The fourth, fifth, sixth, seventh and eighth terms can be estimated by ${\mathfrak {T}}_I$, ${\mathfrak {L}}_I$, ${\mathfrak {G}}_I$, ${\mathfrak {W}}_I$ and ${\mathfrak {N}}_I$, respectively.

Terms from Proposition 9.14

The first term can be estimated by ${\mathfrak {B}}_I$, while the second term can be controlled by ${\mathfrak {B}}_I$ and ${\mathfrak {N}}_I$.

The case $|I|=0$

Finally, we show the improved estimate for the ${\mathfrak {I}}_0$ term. Indeed, we check that for most of the contributions to ${\mathfrak {I}}_I$, we have better decay in s. More precisely, the contributions to ${\mathfrak {I}}_I$ from Proposition 9.3, 9.4, 9.5, 9.12, 9.13 can be bounded above by

$$\begin{aligned} \frac{\epsilon \log ^2(1+s)}{(1+s)^{3-\delta _0}}. \end{aligned}$$

The only contribution to ${\mathfrak {I}}_I$ for which we do not have such good estimates is therefore the term in Proposition 9.8. On the other hand, by Proposition 9.8, in the case $|I|=0$, we have the improved estimate (9.30). The conclusion hence follows. $\square$

Notice that if we naively apply Grönwall’s inequality, the bad term ${\mathfrak {B}}_I$ would in particular force the energy to grow like $(1+t)^C$ for some large constant C except in the regions where |q| is large. We therefore need to further exploit the structure of the Einstein equations to get better bounds in the region where |q| is finite. To this end, we recall that the only contributions to the term ${\mathfrak {B}}_I$ are from (9.7) and (9.8) and we therefore need more refined estimate compared to Propositions 9.13 and 9.14, which will be carried out in Propositions 9.16 and 9.17:

Proposition 9.16

Projecting to the vector fields $\{L,{\underline{L}}, E^1, E^2, E^3\}$, we have the following bounds for the term (9.7): If $\mathbf{E}^\mu , \mathbf{E}^\nu \in \{L,{\underline{L}}, E^1, E^2, E^3\}$ such that $\mathbf{E}^\mu \ne {\underline{L}}^\mu$ or $\mathbf{E}^\nu \ne {\underline{L}}^\nu$,

$$\begin{aligned}&|\mathbf{E}^\mu \mathbf{E}^\nu \Gamma ^I(P_{\mu \nu }(g,g;\partial _{\mu } g,\partial _{\nu } g)-P_{\mu \nu }(g_B;g_B;\partial _{\mu } g_B,\partial _{\nu } g_B))| \\&\qquad \lesssim {\mathfrak {I}}_I+{\mathfrak {G}}_I+{\mathfrak {T}}_I+{\mathfrak {L}}_I+{\mathfrak {W}}_I+{\mathfrak {N}}_I. \end{aligned}$$

Proof

We revisit the proof of Proposition 9.13. Arguing as in the proof of Proposition 9.13 it suffices to control the terms (9.47) and (9.48) where $h_*\in \{h,h_B\}$ and all the $\Gamma$ derivatives fall on h, i.e., we have $\partial \Gamma ^I h$. For these terms, if $\mathbf{E}^\mu \ne {\underline{L}}^\mu$ or $\mathbf{E}^\nu \ne {\underline{L}}^\nu$, then at least one of the derivatives is a good derivatives, and we can therefore bound them by

$$\begin{aligned} \lesssim |{\bar{\partial }}\Gamma ^I h|(|\partial h|+|\partial h_B|)+|\partial \Gamma ^I h|(|{\bar{\partial }} h|+|{\bar{\partial }} h_B|)\lesssim {\mathfrak {G}}_I+{\mathfrak {T}}_I. \end{aligned}$$

$\square$

Proposition 9.17

Projecting to the vector fields $\{L,{\underline{L}}, E^1, E^2, E^3\}$, we have the following bounds for the term (9.8): If $\mathbf{E}^\mu , \mathbf{E}^\nu \in \{L,{\underline{L}}, E^1, E^2, E^3\}$ such that $\mathbf{E}^\mu \ne {\underline{L}}^\mu$ or $\mathbf{E}^\nu \ne {\underline{L}}^\nu$,

$$\begin{aligned} |\mathbf{E}^\mu \mathbf{E}^\nu \Gamma ^I(T_{\mu \nu }(\partial \phi ,\partial \phi )-T_{\mu \nu }(\partial \phi _B,\partial \phi _B))| \lesssim {\mathfrak {I}}_I+{\mathfrak {G}}_I+{\mathfrak {T}}_I+{\mathfrak {L}}_I+{\mathfrak {W}}_I+{\mathfrak {N}}_I. \end{aligned}$$

Proof

We revisit the proof of Proposition 9.14, keeping track more carefully the terms:

$$\begin{aligned} \begin{aligned}&-\Gamma ^I(T_{\mu \nu }(\partial \phi ,\partial \phi )-T_{\mu \nu }(\partial \phi _B,\partial \phi _B))\\&\quad =4\Gamma ^I\left( \partial _\mu \phi _B\partial _\nu \beta +\partial _\mu \beta \partial _\nu \phi _B+\partial _\mu \beta \partial _\nu \beta \right) \\&\quad =4\left( \underbrace{\left( \partial _\mu \phi _B\right) \left( \partial _\nu \Gamma ^I\beta \right) +\left( \partial _\mu \Gamma ^I\beta \right) \left( \partial _\nu \phi _B\right) +\left( \partial _\mu \Gamma ^I\beta \right) \left( \partial _\nu \beta \right) +\left( \partial _\mu \beta \right) \left( \partial _\nu \Gamma ^I\beta \right) }_{\text{ Main } \text{ term }}\right) \\&\qquad +\underbrace{O\left( \sum _{|J|\le |I|-1}\frac{|\partial \Gamma ^{J}\beta |}{(1+s)(1+|q|)^{\gamma }}\right) }_{\hbox {Error}_1}+\underbrace{O\left( \sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ \max \{|J_1|,\,|J_2|\}\le |I|-1 \end{array}}|\partial \Gamma ^{J_1}\beta ||\partial \Gamma ^{J_2}\beta |\right) }_{\hbox {Error}_2}. \end{aligned} \end{aligned}$$

$\hbox {Error}_1$ and $\hbox {Error}_2$ can be controlled by ${\mathfrak {L}}_I$ and ${\mathfrak {N}}_I$, respectively. If we are contracting with $\mathbf{E}^\mu$ and $\mathbf{E}^\nu$ such that at least one of them is in $\{L,E^1,E^2,E^3\}$, then the main term has at least one good derivative, i.e., it can be bounded by

$$\begin{aligned} \begin{aligned}&|{\bar{\partial }}\Gamma ^I\beta ||\partial \phi _B|+|\partial \Gamma ^I\beta ||{\bar{\partial }}\phi _B|+|\partial \Gamma ^I\beta ||{\bar{\partial }}\beta |+|{\bar{\partial }}\Gamma ^I\beta ||\partial \beta |\\&\quad \lesssim \frac{|{\bar{\partial }}\Gamma ^I\beta |}{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}+\frac{|\partial \Gamma ^I\beta |}{(1+s)^{1+\gamma }}, \end{aligned} \end{aligned}$$

where we have used the bootstrap assumptions (6.7) and (6.8) together with (6) in Definition 3.1. It is then easy to check that these two terms can be dominated by ${\mathfrak {G}}_I$ and ${\mathfrak {T}}_I$, respectively. $\square$

As a consequence of Propositions 9.16 and 9.17, we thus obtain that the following components of ${\widetilde{\Box }}_g\Gamma ^I h$ are better behaved in the sense that the bad term ${\mathfrak {B}}_I$ is absent:

Proposition 9.18

Projecting to the vector fields $\{L,{\underline{L}}, E^1, E^2, E^3\}$, we have the following bounds for $|{\widetilde{\Box }}_g \Gamma ^I h |$: If $\mathbf{E}^\mu , \mathbf{E}^\nu \in \{L,{\underline{L}}, E^1, E^2, E^3\}$ such that $\mathbf{E}^\mu \ne {\underline{L}}^\mu$ or $\mathbf{E}^\nu \ne {\underline{L}}^\nu$,

$$\begin{aligned} |({\widetilde{\Box }}_g \Gamma ^I h)_{\mu \nu } \mathbf{E}^{\mu } \mathbf{E}^{\nu }|\lesssim {\mathfrak {I}}_I+{\mathfrak {G}}_I+{\mathfrak {T}}_I+{\mathfrak {L}}_I+{\mathfrak {W}}_I+{\mathfrak {N}}_I. \end{aligned}$$

In other words, compared to Proposition 9.15, the term ${\mathfrak {B}}_I$ is absent.

Proof

Returning to the proof of Proposition 9.15, one sees that the only contributions for the term ${\mathfrak {B}}_I$ come from the terms (9.7) and (9.8). The conclusion thus follows from Propositions 9.16 and 9.17. $\square$

10 Equation for the Scalar Field

In order to close the estimates for the Einstein scalar field system, we need to control the scalar field in addition to the metric. In this section, we derive an analogue of Proposition 9.15 for $\Gamma ^I\beta$, in which we estimate $|{\widetilde{\Box }}_g\Gamma ^I \beta |$. Since the scalar wave equation is considerable simpler, the derivation of this analogous result is also simpler. We note that the terms in Proposition 10.1 are similar to those in Proposition 9.15—indeed most terms are subsets of those in Proposition 9.15. Most importantly, however, notice that there is no analogue of the term ${\mathfrak {B}}_I$ in Proposition 10.1.

Proposition 10.1

For $|I|\le N$ and $\beta :=\phi -\phi _B$, the right-hand side of the equation for $\Gamma ^I\beta$ can be decomposed into the following terms:

$$\begin{aligned} |{\widetilde{\Box }}_g \Gamma ^I \beta |\lesssim {\mathfrak {I}}_I^{(\phi )}+{\mathfrak {G}}_I^{(\phi )}+{\mathfrak {T}}_I^{(\phi )}+{\mathfrak {L}}_I^{(\phi )}+{\mathfrak {W}}_I^{(\phi )}+{\mathfrak {N}}_I^{(\phi )}, \end{aligned}$$

where

$$\begin{aligned}&{\mathfrak {I}}_I^{(\phi )}(t,x):= \frac{\epsilon \log ^2 (2+s)}{(1+s)^2(1+|q|)w(q)^{\frac{\gamma }{1+2\gamma }}}, \\&{\mathfrak {G}}_I^{(\phi )}(t,x):= \sum _{|J|\le |I|}\frac{|\Gamma ^J h|_{LL}}{(1+s)(1+|q|)^{1+\gamma }}, \\&{\mathfrak {T}}_I^{(\phi )}(t,x):= \sum _{|J|\le |I|}\frac{|\partial \Gamma ^J\beta |}{(1+s)^{1+\frac{\gamma }{2}}}, \\&{\mathfrak {L}}_I^{(\phi )}(t,x):= \sum _{|J|\le |I|-1}\left( \frac{\log (2+s)|\partial \Gamma ^J\beta |}{(1+s)(1+|q|)^{\gamma }}+\frac{|\Gamma ^J h|}{(1+s)(1+|q|)^{1+\gamma }}\right) , \\&{\mathfrak {W}}_I^{(\phi )}(t,x):= \sum _{|J|\le |I|}\frac{\log (2+s)|\Gamma ^J h|}{(1+s)^{2-2\delta _0}(1+|q|)^{\gamma +2\delta _0}}, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {\mathfrak {N}}_I^{(\phi )}(t,x)&:= \sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ \max \{|J_1|,|J_2|\}\le |I|-1 \end{array}}\frac{|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}\beta |}{1+|q|}\\&\quad +\sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|}\frac{|\Gamma ^{J_1} h|_{LL}|\partial \Gamma ^{J_2} \beta |}{1+|q|}. \end{aligned} \end{aligned}$$

As in Proposition 9.15, we will call these terms the inhomogeneous term, the good term, the top order term, the lower order term, the potential term and the nonlinear term, respectively. Moreover, when $|I|=0$, in addition to the bounds above, we also have

$$\begin{aligned} {\mathfrak {I}}_0^{(\phi )}(t,x)\lesssim \frac{\epsilon \log ^2(2+s)}{(1+s)^{2+\frac{\gamma }{2}}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{2}-\delta _0}w(q)^{\frac{1}{2}}}. \end{aligned}$$

Importantly, notice that for the equation of the scalar field, there are no bad terms, i.e., there are no analogue of the term ${\mathfrak {B}}_I$ in Proposition 9.15.

Proof

Subtracting the equation $\Box _{g_B}\phi _B=0$ from $\Box _g\phi =0$ and rewriting⁵⁸$\Box _g={\widetilde{\Box }}_g+(\Box _g-{\widetilde{\Box }}_g)$ (and similarly for $\Box _{g_B}$), we obtain

$$\begin{aligned} \begin{aligned} 0&=\Gamma ^I\left( \Box _g\phi -\Box _{g_B}\phi _B\right) \\&=\underbrace{ {\widetilde{\Box }}_g \Gamma ^I\beta }_{=:\hbox {I}}-\underbrace{ [{\widetilde{\Box }}_g,\Gamma ^I] \beta }_{=:\hbox {II}}+\underbrace{(\Gamma ^I\Box _g\beta -\Gamma ^I{\widetilde{\Box }}_g\beta )}_{=:\hbox {III}}\\&\quad +\underbrace{\Gamma ^I({\widetilde{\Box }}_g-{\widetilde{\Box }}_{g_B})\phi _B}_{=:\hbox {IV}}+\underbrace{\Gamma ^I\left( \left( (\Box _g-{\widetilde{\Box }}_g)-(\Box _{g_B}-{\widetilde{\Box }}_{g_B})\right) \phi _B\right) }_{=:\hbox {V}}.\nonumber \end{aligned}\\ \end{aligned}$$

(9.60)

I is the main term. We thus need to control the remaining terms. For II, we apply Proposition 9.6, use the bootstrap assumptions (6.2)–(6.6) and (6.7)–(6.8) and argue as in Proposition 9.7 to obtain

$$\begin{aligned} \begin{aligned} |\hbox {II}|&\lesssim \sum _{|J|\le |I|-1}|\Gamma ^J{\widetilde{\Box }}_g \beta |+\sum _{|J|\le |I|}\frac{|\partial \Gamma ^J \beta |}{(1+s)^{1+\frac{\gamma }{2}}}\\&\quad +\sum _{|J|\le |I|}\frac{|\Gamma ^J h|}{(1+s)^{2-2\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}}\\&\quad +\sum _{|J|\le |I|-1}\frac{\log (2+s)|\partial \Gamma ^J \beta |}{(1+s)(1+|q|)}+\sum _{|J|\le |I|-1}\frac{|\Gamma ^J h|}{(1+s)(1+|q|)^{1+\gamma }}\\&\quad +\sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |{I}|}\frac{|\Gamma ^{J_1} h|_{LL}|\partial \Gamma ^{J_2} \beta |}{1+|q|}\\&\quad +\sum _{\begin{array}{c} |J_1|+|J_2|\le |{I}|\\ \max \{|J_1|,|J_2|\}\le |I|-1 \end{array}}\frac{|\Gamma ^{J_1} h||\partial \Gamma ^{J_2} \beta |}{1+|q|}.\nonumber \end{aligned}\\ \end{aligned}$$

(10.1)

For the term IV, we use the bootstrap assumptions (6.2)–(6.6) and (6.7)–(6.8) and argue as in Proposition 9.8 to obtain

$$\begin{aligned} \begin{aligned} |\hbox {IV}|&\lesssim \frac{\epsilon \log (2+s)}{(1+s)^2(1+|q|)^{1+\gamma }}+\frac{|\Gamma ^I h|_{LL}}{(1+s)(1+|q|)^{1+\gamma }}\\&\quad +\sum _{|J|\le |I|}\frac{|\Gamma ^J h|}{(1+s)^{2-\delta _0}(1+|q|)^{\frac{1}{2}+\frac{3\gamma }{4}}w(q)^{\frac{1}{2}}}+\sum _{|J|\le |I|-1}\frac{|\Gamma ^J h|}{(1+s)(1+|q|)^{1+\gamma }}.\nonumber \end{aligned}\\ \end{aligned}$$

(10.2)

For the terms III and V in (10.1), notice that by (4.3), for any scalar function $\xi$, we have

$$\begin{aligned} (\Box _g-{\widetilde{\Box }}_g)\xi =({\mathcal {G}}_S^\mu +{\mathcal {G}}_B^\mu )\partial _\mu \xi ,\quad (\Box _{g_B}-{\widetilde{\Box }}_{g_B})\xi ={\mathcal {G}}_B^\mu \partial _\mu \xi . \end{aligned}$$

(10.3)

Therefore, by (9.20) and (8) in Definition 3.1, we have

$$\begin{aligned} \begin{aligned} |\hbox {III}|\lesssim \sum _{|J_1|+|J_2|\le |I|} (|\Gamma ^{J_1}{\mathcal {G}}_S|+|\Gamma ^{J_1}{\mathcal {G}}_B|)|\partial \Gamma ^{J_2}\beta |\lesssim \frac{\log (2+s)}{(1+s)^2}\sum _{|J|\le |I|}|\partial \Gamma ^J\beta |.\nonumber \end{aligned}\\ \end{aligned}$$

(10.4)

Finally, for the term V, we have by (10.4) that

$$\begin{aligned} \left( (\Box _g-{\widetilde{\Box }}_g)-(\Box _{g_B}-{\widetilde{\Box }}_{g_B})\right) \phi _B={\mathcal {G}}_S^{\mu }\partial _\mu \phi _B. \end{aligned}$$

Therefore, by (9.20) and (6) in Definition 3.1,

$$\begin{aligned} |\hbox {V}|\lesssim \sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}{\mathcal {G}}_S^{\mu }||\partial \Gamma ^{J_2}\phi _B|\lesssim \frac{\epsilon \log (2+s)}{(1+s)^3(1+|q|)^{\gamma }}. \end{aligned}$$

(10.5)

Combining (10.1), (10.2), (10.3), (10.5) and (10.6), we thus obtain the desired conclusion. $\square$

11 Linear Estimates

In this section, we prove some linear estimates for the wave equation on the curved background $({\mathcal {M}},g)$ where g satisfies the bootstrap assumptions (6.2)–(6.6). These include the energy estimates, the Hardy inequalities and various pointwise decay estimates. Many of these estimates are already present in the works of Lindblad–Rodnianski [45, 46], but since we need various refinements and localized versions in our setting, we include the proofs for completeness.

11.1 Energy Estimates

In this subsection, we derive the energy estimates. We first recall the energy estimates (Lemma 6.1 in [46]).

Proposition 11.1

Suppose $H^{\alpha \beta }=(g^{-1})^{\alpha \beta }-m^{\alpha \beta }$ satisfies $|H|\le \frac{1}{2}$ in $\{t_1\le t\le t_2\}\times {\mathbb {R}}^3$. Then, for every solution $\xi$ to

$$\begin{aligned} {\widetilde{\Box }}_g\xi =F \end{aligned}$$

with $\xi$ decaying sufficiently fast as $|x|\rightarrow \infty$, we have the following estimate:

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _{t_2}} (|\partial _t\xi |^2+|\nabla \xi |^2) w(q_2)\,{\text {d}}x+2\int _{t_1}^{t_2}\int _{\Sigma _t}|{\bar{\partial }}\xi |^2(t,x) w'(q)\,{\text {d}}x\,{\text {d}}t\\&\quad \le 4\int _{\Sigma _{t_1}} (|\partial _t\xi |^2+|\nabla \xi |^2) w(q_1)\,{\text {d}}x\\&\qquad +2\int _{t_1}^{t_2}\int _{\Sigma _t}|2(\partial _{\alpha }H^{\alpha \beta })\partial _{\beta }\xi \partial _t\xi -(\partial _tH^{\alpha \beta })\partial _\alpha \xi \partial _{\beta }\xi +2F\partial _t\xi |w(q)\,{\text {d}}x\,{\text {d}}t\\&\qquad +2\int _{t_1}^{t_2}\int _{\Sigma _t}|H^{\alpha \beta }\partial _{\alpha }\xi \partial _{\beta }\xi +2\left( \frac{x_i}{r}H^{i\beta }-H^{0\beta }\right) \partial _\beta \xi \partial _t\xi |w'(q)\,{\text {d}}x\,{\text {d}}t. \end{aligned} \end{aligned}$$

Here, we recall from Remark 2.5 that we have used the notation $q_1:=r-t_1$, $q_2:=r-t_2$

Under the bootstrap assumptions (6.2)–(6.6), we show that the estimate in Proposition 11.1 implies the energy estimates in Proposition 11.2. This proposition can be thought of as the analogue of Proposition 6.2 in [46], which uses the structure of the terms on the right-hand side of the estimate in Proposition 11.1. In the scenario of the present paper, it is in particular important that we require $|h_B|_{L{\mathcal {T}}}$ to have better decay to avoid the term

$$\begin{aligned} \int _0^t\int _{\Sigma _t} \frac{|\partial \xi |^2}{1+t} \,{\text {d}}x\,{\text {d}}t. \end{aligned}$$

Proposition 11.2

Suppose g satisfies the bootstrap assumptions (6.2)–(6.6). Then there exists $T>0$ sufficiently large such that for $T\le t_1<t_2$ and for every solution $\xi$ to

$$\begin{aligned} {\widetilde{\Box }}_g\xi =F \end{aligned}$$

with $\xi$ decaying sufficiently fast as $|x|\rightarrow \infty$, we have the following estimate:

$$\begin{aligned} \begin{aligned}&\left( \int _{\Sigma _{t_2}} (|\partial _t\xi |^2+|\nabla \xi |^2)w(q_2)\,{\text {d}}x\right) ^{\frac{1}{2}}+\left( \int _{t_1}^{t_2}\int _{\Sigma _t}|{\bar{\partial }}\xi |^2w'(q)\,{\text {d}}x\,{\text {d}}t\right) ^{\frac{1}{2}}\\&\quad \lesssim \left( \int _{\Sigma _{t_1}} (|\partial _t\xi |^2+|\nabla \xi |^2)w(q_1)\,{\text {d}}x\right) ^{\frac{1}{2}}+\int _{t_1}^{t_2}\left( \int _{\Sigma _t}|F|^2 w(q)\,{\text {d}}x \right) ^{\frac{1}{2}}\,{\text {d}}t. \end{aligned} \end{aligned}$$

Proof

By choosing T sufficiently large, Definition 3.1, (7.1) and (6.5) imply that $|H|\le \frac{1}{2}$ and hence Proposition 11.1 apply. The main point is that for each of the terms $H\partial \xi \partial \xi$ and $\partial H\partial \xi \partial \xi$ on the right-hand side of the energy estimate in Proposition 11.1, we can show that one of the following three possibilities holds: Either we have a good derivative on $\xi$, i.e., ${\bar{\partial }}\xi$, or we have a good derivative on H, i.e., ${\bar{\partial }}H$; or we have a good component of H, i.e., $H_{LL}$ or $(\partial H)_{LL}$. This observation is, of course, already present in [45, 46]. Here, we show that this structure together with our bootstrap assumptions give the claimed energy estimates. In particular, our gauge choice guarantees that the term $\int _0^t\int _{\Sigma _t} \frac{|\partial \xi |^2}{1+t} \,{\text {d}}x\,{\text {d}}t$ is absent.

We now turn to the details. We first show that the terms $H\partial \xi \partial \xi$ and $\partial H\partial \xi \partial \xi$ have the structure that we mentioned above. More precisely, we have

$$\begin{aligned} |(\partial _{\alpha }H^{\alpha \beta })\partial _{\beta }\xi \partial _t\xi |&\lesssim (|\partial H|_{LL}+|{\bar{\partial }}H|)|\partial \xi |^2+|\partial H||{\bar{\partial }}\xi ||\partial \xi |, \end{aligned}$$

(10.6)

$$\begin{aligned} |(\partial _tH^{\alpha \beta })\partial _\alpha \xi \partial _{\beta }\xi |&\lesssim |\partial H|_{LL}|\partial \xi |^2+|\partial H||{\bar{\partial }}\xi ||\partial \xi |, \end{aligned}$$

(11.1)

$$\begin{aligned} |H^{\alpha \beta }\partial _{\alpha }\xi \partial _{\beta }\xi |&\lesssim |H|_{LL}|\partial \xi |^2+|H||{\bar{\partial }}\xi ||\partial \xi |, \end{aligned}$$

(11.2)

$$\begin{aligned} \left| \left( \frac{x_i}{r}H^{i\beta }-H^{0\beta }\right) \partial _\beta \xi \partial _t\xi \right|&\lesssim |H|_{LL}|\partial \xi |^2+|H||{\bar{\partial }}\xi ||\partial \xi |. \end{aligned}$$

(11.3)

(11.1)–(11.3) can be proven in a similar manner by writing $m^{\alpha \alpha '}m^{\beta \beta '}H_{\alpha '\beta '}$ and using $m^{\alpha \beta }=-L^{(\alpha }{\underline{L}}^{\beta )}+\sum _{A=1}^3(E^A)^\alpha (E^A)^\beta$; we omit the details. For (11.4), notice that $\frac{x_i}{r}H^{i\beta }-H^{0\beta }=m^{\beta \beta '}L^\alpha H_{\alpha \beta '}$.

Now, we apply the estimates for $\sum _{|I|\le 1} |\Gamma ^I h|$ from Proposition 7.3 together with the bootstrap assumptions (6.2)–(6.6) and Proposition 7.1 to get⁵⁹

$$\begin{aligned}&|H|\lesssim \frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}}{(1+t)^{1-\delta _0}},\quad |\partial H|\lesssim \frac{1}{(1+t)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}},\quad |{{\bar{\partial }}} H|\lesssim \frac{1}{(1+t)^{1+\frac{\gamma }{2}}},\\&|H|_{LL}\lesssim \frac{(1+|q|)^{\frac{1}{2}+\gamma }}{(1+t)^{1+\frac{\gamma }{2}}},\quad |\partial H|_{LL}\lesssim \frac{1}{(1+t)^{1+\frac{\gamma }{2}}}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} |(\partial _{\alpha }H^{\alpha \beta })\partial _{\beta }\xi \partial _t\xi |+|(\partial _tH^{\alpha \beta })\partial _\alpha \xi \partial _{\beta }\xi |\lesssim \frac{|\partial \xi |^2}{(1+t)^{1+\frac{\gamma }{2}}}+\frac{|{\bar{\partial }}\xi ||\partial \xi |}{(1+t)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}} \end{aligned}$$

and

$$\begin{aligned}&|H^{\alpha \beta }\partial _{\alpha }\xi \partial _{\beta }\xi |+|\left( \frac{x_i}{r}H^{i\beta }-H^{0\beta }\right) \partial _\beta \xi \partial _t\xi |\\&\qquad \lesssim \frac{(1+|q|)^{\frac{1}{2}+\gamma }|\partial \xi |^2}{(1+t)^{1+\frac{\gamma }{2}}}+\frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}|{\bar{\partial }}\xi ||\partial \xi |}{(1+t)^{1-\delta _0}}. \end{aligned}$$

We now plug these estimates into the energy estimates in Proposition 11.1. Since $w'(q)\lesssim \frac{w(q)}{1+|q|}$, we have

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _{t_2}} (|\partial _t\xi |^2+|\nabla \xi |^2)w(q_2)\,{\text {d}}x+\int _{t_1}^{t_2}\int _{\Sigma _t}|{\bar{\partial }}\xi |^2w'(q)\,{\text {d}}x\,{\text {d}}t\\&\quad \lesssim \int _{\Sigma _{t_1}} (|\partial _t\xi |^2+|\nabla \xi |^2)w(q_1)\,{\text {d}}x+\int _{t_1}^{t_2}\int _{\Sigma _t}|F||\partial \xi |w(q)\,{\text {d}}x\,{\text {d}}t\\&\qquad +\int _{t_1}^{t_2}\int _{\Sigma _t}\left( \frac{|\partial \xi |^2}{(1+t)^{1+\frac{\gamma }{2}}}+\frac{|{\bar{\partial }}\xi ||\partial \xi |}{(1+t)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}\right) w(q)\,{\text {d}}x\,{\text {d}}t.\nonumber \end{aligned}\\ \end{aligned}$$

(11.4)

To control the last term, we use the bound $w\lesssim w'(1+|q|)^{1+\frac{\gamma }{2}}$, which implies after using the Hölder’s inequality

$$\begin{aligned} \begin{aligned}&\int _{t_1}^{t_2}\int _{\Sigma _{t}}\frac{|{\bar{\partial }}\xi ||\partial \xi |}{(1+t)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}w(q)\,{\text {d}}x\,{\text {d}}t\\&\quad \lesssim \left( \int _{t_1}^{t_2}\int _{\Sigma _{t}}\frac{|\partial \xi |^2 w(q)(1+|q|)^{1+\frac{\gamma }{2}}}{(1+t)^{2-2\delta _0}(1+|q|)^{2\gamma +2\delta _0}}\,{\text {d}}x\,{\text {d}}t\right) ^{\frac{1}{2}}\left( \int _{t_1}^{t_2}\int _{\Sigma _{t}}\frac{|{\bar{\partial }}\xi |^2 w(q)}{(1+|q|)^{1+\frac{\gamma }{2}}}\,{\text {d}}x\,{\text {d}}t\right) ^{\frac{1}{2}}\\&\quad \lesssim \left( \int _{t_1}^{t_2}\frac{{\text {d}}t}{(1+t)^{1+\frac{3\gamma }{4}}}\right) ^{\frac{1}{2}}\left( \sup _{t_1\le t\le t_2}\int _{\Sigma _{t}} |\partial \xi |^2 w(q)\,{\text {d}}x \right) ^{\frac{1}{2}}\left( \int _{t_1}^{t_2}\int _{\Sigma _t}|{\bar{\partial }}\xi |^2w'(q)\,{\text {d}}x\,{\text {d}}t\right) ^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

Notice that by taking T large and $T\le t_1\le t_2$, the quantity $\big (\int _{t_1}^{t_2}\frac{{\text {d}}t}{(1+t)^{1+\frac{3\gamma }{4}}}\big )^{\frac{1}{2}}$ is bounded by a small constant and we can absorb this term to the left-hand side of (11.5). Therefore, we have

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _{t_2}} (|\partial _t\xi |^2+|\nabla \xi |^2)w(q_2)\,{\text {d}}x+\int _{t_1}^{t_2}\int _{\Sigma _t}|{\bar{\partial }}\xi |^2w'(q)\,{\text {d}}x\,{\text {d}}t\\&\quad \lesssim \int _{\Sigma _{t_1}} (|\partial _t\xi |^2+|\nabla \xi |^2)w(q_1)\,{\text {d}}x+\int _{t_1}^{t_2}\int _{\Sigma _t}|F||\partial \xi |w(q)\,{\text {d}}x\,{\text {d}}t\\&\qquad +\int _{t_1}^{t_2}\int _{\Sigma _t}\frac{|\partial \xi |^2}{(1+t)^{1+\frac{\gamma }{2}}}w(q)\,{\text {d}}x\,{\text {d}}t. \end{aligned}\nonumber \\ \end{aligned}$$

(11.5)

Applying the Grönwall’s inequality to (11.6), we get

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _{t_2}} (|\partial _t\xi |^2+|\nabla \xi |^2)w(q_2)\,{\text {d}}x+\int _{t_1}^{t_2}\int _{\Sigma _t}|{\bar{\partial }}\xi |^2w'(q)\,{\text {d}}x\,{\text {d}}t\\&\quad \lesssim \int _{\Sigma _{t_1}} (|\partial _t\xi |^2+|\nabla \xi |^2)w(q_1)\,{\text {d}}x+\int _{t_1}^{t_2}\int _{\Sigma _t}|F||\partial \xi |w(q)\,{\text {d}}x\,{\text {d}}t. \end{aligned}\nonumber \\ \end{aligned}$$

(11.6)

Finally, applying Hölder’s inequality to the last term and absorbing $\sup _{t\in [t_1,t_2]}\int _{\Sigma _{t}} |\partial \xi |^2w(q)\,{\text {d}}x$ to the left-hand side, we obtain the desired conclusion. $\square$

Unlike [46], we will also need energy estimates that are localized in various regions of the spacetime. To describe this localization, we introduce the hypersurface ${\mathcal {B}}_U$ defined by

$$\begin{aligned} {\mathcal {B}}_U=\left\{ t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}=U \right\} . \end{aligned}$$

Under the bootstrap assumptions (6.2)–(6.6) for the metric g, we can show that for every fixed U, there exists T sufficiently large such that the restriction of ${\mathcal {B}}_U$ to $t\ge T$ is spacelike. In particular, this allows us to prove energy estimates in a region localized to the future of the $\{t=T\}$ hypersurface and to the past of ${\mathcal {B}}_U$. More precisely, we have

Proposition 11.3

For every fixed $U\in {\mathbb {R}}$, there exists $T>0$ sufficiently large such that if

$$\begin{aligned} {\widetilde{\Box }}_g\xi =F \end{aligned}$$

for $|\xi |$ decaying sufficiently fast in r initially and g obeying the bootstrap assumptions (6.2)–(6.6), then

$$\begin{aligned}&\left( \int _{\Sigma _{t_2}\cap \{t_2-r-\frac{1}{(1+t_2)^{\frac{\gamma }{4}}}\le U\}} |\partial \xi |^2 w(q_2)\,{\text {d}}x\right) ^{\frac{1}{2}}\\&\qquad +\left( \int _{t_1}^{t_2}\int _{\Sigma _t\cap \{t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U\}}|{\bar{\partial }}\xi |^2w'(q)\,{\text {d}}x\,{\text {d}}t\right) ^{\frac{1}{2}}\\&\qquad +\left( \int _{{\mathcal {B}}_U\cap \{t_1\le t\le t_2\}}(|{\bar{\partial }}\xi |^2+\frac{|\partial \xi |^2}{(1+t)^{\frac{\gamma }{4}+1}}) w(q)\,{\text {d}}x\right) ^{\frac{1}{2}}\\&\quad \lesssim \left( \int _{\Sigma _{t_1}\cap \{t_1-r-\frac{1}{(1+t_1)^{\frac{\gamma }{4}}}\le U\}} |\partial \xi |^2 w(q_1)\,{\text {d}}x\right) ^{\frac{1}{2}}\\&\qquad +\int _{t_1}^{t_2}\left( \int _{\Sigma _t\cap \{t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U\}}|F|^2w(q)\,{\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}t \end{aligned}$$

for $T\le t_1< t_2$.

Proof

We first compute that

$$\begin{aligned}&{\widetilde{\Box }}_g\xi \,w(q) \partial _t\xi =(g^{-1})^{\alpha \beta } \partial _{\alpha } \partial _{\beta } \xi \, w(q) \partial _{t} \xi \\&\quad = \partial _{j} ((g^{-1})^{j \beta } \partial _{\beta } \xi \partial _{t} \xi w(q) ) + \partial _{t} \Big ( (g^{-1})^{0 \beta } \partial _{\beta } \xi \partial _{t} \xi w(q) - \frac{1}{2} (g^{-1})^{\alpha \beta } (\partial _{\alpha } \xi \partial _{\beta } \xi ) w(q) \Big ) \\&\qquad - \partial _{\alpha } (g^{-1})^{\alpha \beta } \partial _{\beta } \xi \partial _{t} \xi w(q) + \frac{1}{2} (\partial _{t}(g^{-1})^{\alpha \beta }) (\partial _{\alpha } \xi \partial _{\beta } \xi ) w(q) \\&\qquad + \frac{1}{2} (g^{-1})^{\alpha \beta } \partial _{\alpha } \xi \partial _{\beta } \xi \partial _{t} w(q) - (g^{-1})^{\alpha \beta } \partial _{\beta } \xi \partial _{t} \xi \partial _{\alpha } w(q). \end{aligned}$$

Taking this identity and integrating by parts in the region $\{(t,x^1,x^2,x^3): t_1\le t\le t_2,\,t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U\}$, we obtain

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _{t_2}\cap \{t_2-r-\frac{1}{(1+t_2)^{\frac{\gamma }{4}}}\le U\}} \left( -(g^{-1})^{0 \beta } \partial _{\beta } \xi \partial _{t} \xi + \frac{1}{2} (g^{-1})^{\alpha \beta } (\partial _{\alpha } \xi \partial _{\beta } \xi )\right) w(q_2) \,{\text {d}}x\\&\qquad +\int _{{\mathcal {B}}_U\cap \{t_1\le t\le t_2\}} \left( -(g^{-1})^{0\beta }\partial _\beta \xi \partial _t\xi +\frac{1}{2} (g^{-1})^{\alpha \beta }\partial _{\alpha }\xi \partial _{\beta }\xi \right. \\&\qquad \left. +\frac{x_j (g^{-1})^{j\beta }\partial _{\beta }\xi \partial _t\xi }{r(1+\frac{\gamma }{4(1+t)^{\frac{\gamma }{4}+1}})}\right) w(q)\, {\text {d}}x\\&\quad =\int _{\Sigma _{t_1}\cap \{t_1-r-\frac{1}{(1+t_1)^{\frac{\gamma }{4}}}\le U\}} \left( -(g^{-1})^{0 \beta } \partial _{\beta } \xi \partial _{t} \xi + \frac{1}{2} (g^{-1})^{\alpha \beta } (\partial _{\alpha } \xi \partial _{\beta } \xi )\right) w(q_1)\, {\text {d}}x\\&\qquad +\int _{t_1}^{t_2}\int _{\Sigma _t\cap \{t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U\}} \left( - \partial _{\alpha } (g^{-1})^{\alpha \beta } \partial _{\beta } \xi \partial _{t} \xi w(q)\right. \\&\qquad \left. + \frac{1}{2} (\partial _{t}(g^{-1})^{\alpha \beta }) (\partial _{\alpha } \xi \partial _{\beta } \xi ) -\partial _t\xi F\right) w(q) \, {\text {d}}x\,{\text {d}}t\\&\qquad + \int _{t_1}^{t_2}\int _{\Sigma _t\cap \{t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U\}}\left( \frac{1}{2} (g^{-1})^{\alpha \beta } \partial _{\alpha } \xi \partial _{\beta } \xi \partial _{t} w(q) \right. \\&\qquad \left. - (g^{-1})^{\alpha \beta } \partial _{\beta } \xi \partial _{t} \xi \partial _{\alpha } w(q)\right) \,{\text {d}}x\,{\text {d}}t.\nonumber \end{aligned}\\ \end{aligned}$$

(11.7)

We now show that the boundary term on $B_U$ has a sign. First, we expand this term

(11.8)

Now, by (7.1) and (7.4), the bootstrap assumption (6.5), and (11.3) and (11.4),

$$\begin{aligned} \begin{aligned}&|-H^{0\beta }\partial _\beta \xi \partial _t\xi +\frac{1}{2} H^{\alpha \beta }\partial _{\alpha }\xi \partial _{\beta }\xi +\frac{x_j H^{j\beta }\partial _{\beta }\xi \partial _t\xi }{r(1+\frac{\gamma }{4(1+t)^{\frac{\gamma }{4}+1}})}|\\&\quad \lesssim |H^{\alpha \beta }\partial _{\alpha }\xi \partial _{\beta }\xi |+|(H^{0\beta }-\frac{x_j}{r} H^{j\beta })\partial _{\beta }\xi \partial _t\xi |+\frac{|H|}{(1+t)^{\frac{\gamma }{4}+1}(1+\frac{\gamma }{4(1+t)^{\frac{\gamma }{4}+1}})}|\partial \xi |^2\\&\quad \lesssim \left( |H|_{LL}+\frac{|H|}{2\gamma +8(1+t)^{\frac{\gamma }{4}+1}}\right) |\partial \xi |^2+|H||{\bar{\partial }}\xi ||\partial \xi |\\&\quad \lesssim \frac{(1+|U|)^{\frac{1}{2}+\gamma }}{(1+t)^{1+\frac{\gamma }{2}}}|\partial \xi |^2+\frac{|{\bar{\partial }}\xi |^2}{(1+t)^{\frac{\gamma }{2}}}\\&\quad \ll \frac{|\partial \xi |^2}{(1+t)^{\frac{\gamma }{4}+1}}+|{\bar{\partial }}\xi |^2 \end{aligned}\nonumber \\ \end{aligned}$$

(11.9)

if T is chosen to be sufficiently large depending on U. Therefore, returning to (11.9), we obtain

$$\begin{aligned} \begin{aligned}&\int _{B_U\cap \{t_1\le t\le t_2\}} \left( -(g^{-1})^{0\beta }\partial _\beta \xi \partial _t\xi +\frac{1}{2} (g^{-1})^{\alpha \beta }\partial _{\alpha }\xi \partial _{\beta }\xi +\frac{x_j (g^{-1})^{j\beta }\partial _{\beta }\xi \partial _t\xi }{r(1+\frac{\gamma }{4(1+t)^{\frac{\gamma }{4}+1}})}\right) w(q)\, {\text {d}}x\\&\quad > rsim \int _{B_U\cap \{t_1\le t\le t_2\}} \left( |{\bar{\partial }}\xi |^2+\frac{\gamma |\partial _q\xi |^2}{\gamma +4(1+t)^{\frac{\gamma }{4}+1}} \right) w(q)\, {\text {d}}x,\nonumber \end{aligned}\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(11.10)

for T sufficiently large. The other boundary terms on $\Sigma _{t_1}$ and $\Sigma _{t_2}$ in (11.8) can be easily be controlled since $|H|\le \frac{1}{2}$ (which holds for T sufficiently large by (7.1) and (6.5)) implies

$$\begin{aligned} \frac{1}{2} ((\partial _t\xi )^2+|\nabla \xi |^2)\le -(g^{-1})^{00}(\partial _t\xi )^2+(g^{-1})^{ij}(\partial _i\xi )(\partial _j\xi )\le 2((\partial _t\xi )^2+|\nabla \xi |^2).\nonumber \\ \end{aligned}$$

(11.11)

Next, we write $(g^{-1})^{\alpha \beta }=m^{\alpha \beta }+H^{\alpha \beta }$ and consider the contributions from the Minkowski metric $m^{\alpha \beta }$ in the last line of (11.8):

$$\begin{aligned} \begin{aligned}&-\int _{t_1}^{t_2}\int _{\Sigma _t\cap \{t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U\}}\left( \frac{1}{2} m^{\alpha \beta } \partial _{\alpha } \xi \partial _{\beta } \xi \partial _{t} w(q) - m^{\alpha \beta } \partial _{\beta } \xi \partial _{t} \xi \partial _{\alpha } w(q)\right) \,{\text {d}}x\,{\text {d}}t\\&\quad > rsim \int _{t_1}^{t_2}\int _{\Sigma _t\cap \{t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U\}} |{\bar{\partial }}\xi |^2 w'(q)\,{\text {d}}x\,{\text {d}}t. \end{aligned} \end{aligned}$$

(11.12)

Therefore, substituting (11.11), (11.12) and (11.13) into (11.8), we obtain

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _{t_2}\cap \{t_2-r-\frac{1}{(1+t_2)^{\frac{\gamma }{4}}}\le U\}} (|\partial _t\xi |^2+|\nabla \xi |^2)w(q_2)\,{\text {d}}x\\&\qquad +\int _{t_1}^{t_2}\int _{\Sigma _t\cap \{t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U\}}|{\bar{\partial }}\xi |^2w'(q)\,{\text {d}}x\,{\text {d}}t\\&\qquad +\int _{B_U\cap \{t_1\le t\le t_2\}} \left( |{\bar{\partial }}\xi |^2+\frac{\gamma |\partial _q\xi |^2}{\gamma +4(1+t)^{\frac{\gamma }{4}+1}} \right) w(q)\, {\text {d}}x\\&\quad \lesssim \int _{\Sigma _{t_1}\cap \{t_1-r-\frac{1}{(1+t_1)^{\frac{\gamma }{4}}}\le U\}} (|\partial _t\xi |^2+|\nabla \xi |^2)w(q_1)\,{\text {d}}x\\&\qquad +\int _{t_1}^{t_2}\int _{\Sigma _t\cap \{t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U\}}|2(\partial _{\alpha }H^{\alpha \beta })\partial _{\beta }\xi \partial _t\xi \\&\qquad -(\partial _tH^{\alpha \beta })\partial _\alpha \xi \partial _{\beta }\xi +2F\partial _t\xi |w(q)\,{\text {d}}x\,{\text {d}}t\\&\qquad +\int _{t_1}^{t_2}\int _{\Sigma _t\cap \{t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U\}}|H^{\alpha \beta }\partial _{\alpha }\xi \partial _{\beta }\xi \\&\qquad +2\left( \frac{x_i}{r}H^{i\beta }-H^{0\beta }\right) \partial _\beta \xi \partial _t\xi |w'(q)\,{\text {d}}x\,{\text {d}}t. \end{aligned} \end{aligned}$$

Finally, we need to control the terms on the last two lines which are quadratic in $\partial \xi$. Of course, these terms are the same as those in Proposition 11.1 and as shown in the proof of Proposition 11.2, they have a favorable structure. We can then control them in an identical manner as in the proof of Proposition 11.2 after choosing T to be larger if necessary. $\square$

There are obvious variations of Propositions 11.2 and 11.3 which allow us to also localize the future of ${\mathcal {B}}_{U'}$. We summarize them below. Their proofs are completely analogous to Propositions 11.2 and 11.3.

Proposition 11.4

For every fixed $U'<U$, there exists $T>0$ sufficiently large such that if

$$\begin{aligned} {\widetilde{\Box }}_g\xi =F \end{aligned}$$

for $|\xi |$ decaying sufficiently fast in r initially and g obeying the bootstrap assumptions (6.2)–(6.6), then

$$\begin{aligned}&\left( \int _{\Sigma _{t_2}\cap \{U'\le t_2-r-\frac{1}{(1+t_2)^{\frac{\gamma }{4}}}\le U\}} |\partial \xi |^2 w(q_2)\,{\text {d}}x\right) ^{\frac{1}{2}}\\&\qquad +\left( \int _{t_1}^{t_2}\int _{\Sigma _t\cap \{U'\le t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U\}}|{\bar{\partial }}\xi |^2w'(q)\,{\text {d}}x\,{\text {d}}t\right) ^{\frac{1}{2}}\\&\qquad +\left( \int _{{\mathcal {B}}_U\cap \{t_1\le t\le t_2\}}(|{\bar{\partial }}\xi |^2+\frac{|\partial \xi |^2}{(1+t)^{\frac{\gamma }{4}+1}}) w(q)\,{\text {d}}x\right) ^{\frac{1}{2}}\\&\quad \lesssim \left( \int _{\Sigma _{t_1}\cap \{U'\le t_1-r-\frac{1}{(1+t_1)^{\frac{\gamma }{4}}}\le U\}} |\partial \xi |^2 w(q_1)\,{\text {d}}x\right) ^{\frac{1}{2}}+\left( \int _{{\mathcal {B}}_{U'}\cap \{t_1\le t\le t_2\}}\bigg (|{\bar{\partial }}\xi |^2 \right. \\&\qquad \left. +\frac{|\partial \xi |^2}{(1+t)^{\frac{\gamma }{4}+1}}\bigg ) w(q)\,{\text {d}}x\right) ^{\frac{1}{2}}\\&\qquad +\int _{t_1}^{t_2}\left( \int _{\Sigma _t\cap \{U'\le t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U\}}|F|^2 w(q)\,{\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}t \end{aligned}$$

for $T\le t_1\le t_2$.

Proof

The proof is identical to that of Proposition 11.3 and will be omitted. We only note that by a similar argument as (11.9) and (11.10), we can bound the term on ${\mathcal {B}}_{U'}$ by

$$\begin{aligned} \int _{{\mathcal {B}}_{U'}\cap \{t_1\le t\le t_2\}}\left( |{\bar{\partial }}\xi |^2+\frac{|\partial \xi |^2}{(1+t)^{\frac{\gamma }{4}+1}}\right) \,{\text {d}}x \end{aligned}$$

after choosing T to be sufficiently large. $\square$

Similar, an analogous theorem holds if we only have a boundary ${\mathcal {B}}_{U'}$ in the past of the region:

Proposition 11.5

For every $U'\in {\mathbb {R}}$, there exists $T>0$ sufficiently large such that if

$$\begin{aligned} {\widetilde{\Box }}_g\xi =F \end{aligned}$$

for $|\xi |$ decaying sufficiently fast in r initially and g obeying the bootstrap assumptions (6.2)–(6.6), then

$$\begin{aligned}&\left( \int _{\Sigma _{t_2}\cap \{U'\le t_2-r-\frac{1}{(1+t_2)^{\frac{\gamma }{4}}}\}} |\partial \xi |^2 w(q_2)\,{\text {d}}x\right) ^{\frac{1}{2}}\\&\qquad +\left( \int _{t_1}^{t_2}\int _{\Sigma _t\cap \{U'\le t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\}}|{\bar{\partial }}\xi |^2w'(q)\,{\text {d}}x\,{\text {d}}t\right) ^{\frac{1}{2}}\\&\quad \lesssim \left( \int _{\Sigma _{t_1}\cap \{U'\le t_1-r-\frac{1}{(1+t_1)^{\frac{\gamma }{4}}}\}} |\partial \xi |^2 w(q_1)\,{\text {d}}x\right) ^{\frac{1}{2}}\\&\qquad +\left( \int _{{\mathcal {B}}_{U'}\cap \{t_1\le t\le t_2\}}(|{\bar{\partial }}\xi |^2+\frac{|\partial \xi |^2}{(1+t)^{\frac{\gamma }{4}+1}}) w(q)\,{\text {d}}x\right) ^{\frac{1}{2}}\\&\qquad +\int _{t_1}^{t_2}\left( \int _{\Sigma _t\cap \{U'\le t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\}}|F|^2 w(q)\,{\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}t \end{aligned}$$

for $T\le t_1\le t_2$.

11.2 Hardy Inequality

In [46], a |q|-weighted Hardy inequality is proved: The main novelty is that the weights in |q| are used instead of the r weights in the classical Hardy inequality. This is useful in the setting of [46] as there is “insufficient r decay” near the wave zone (i.e., when t and r are comparable). In our setting, we also need a similar version of the |q|-weighted Hardy inequality except that we also need to localize it to an annulus $\{R_1\le r\le R_2\}$, where $R_1$ and $R_2$ satisfy $0\le R_1<R_2 \le \infty$. More precisely, we have

Proposition 11.6

The following inequality holds for any $0\le \alpha \le 2$, $\mu _1>-1$, $\mu _2>0$ and for any scalar functions $\xi$ and for $R_1$, $R_2$ satisfying $0\le R_1<R_2 \le \infty$ (with an implicit constant depending on $\mu _1$ and $\mu _2$):

$$\begin{aligned}&\int \limits _{\{r=R_1\}} \frac{r^2 (1_{\{q\ge 0\}}(1+|q|)^{\mu _2}+1_{\{q< 0\}}(1+|q|)^{-1-\mu _1})\xi ^2}{(1+s)^\alpha } \sin \theta \,{\text {d}}\theta \,{\text {d}}\varphi \\&\qquad +\int _{\min \{R_1,t\}}^{\min \{R_2,t\}}\int _{{\mathbb {S}}^2} \frac{\xi ^2}{(1+|q|)^{2+\mu _1}}\frac{r^2 \sin \theta \,{\text {d}}\theta \,{\text {d}}\varphi \,{\text {d}}r}{(1+s)^\alpha }\\&\qquad +\int _{\max \{R_1,t\}}^{\max \{R_2,t\}}\int _{{\mathbb {S}}^2} \frac{\xi ^2}{(1+|q|)^{1-\mu _2}}\frac{r^2 \sin \theta \,{\text {d}}\theta \,{\text {d}}\varphi \,{\text {d}}r}{(1+s)^\alpha }\\&\quad \lesssim \int \limits _{\{r=R_2\}} \frac{r^2 (1_{\{q\ge 0\}}(1+|q|)^{\mu _2}+1_{\{q< 0\}}(1+|q|)^{-1-\mu _1})\xi ^2}{(1+s)^\alpha } \sin \theta \,{\text {d}}\theta \,{\text {d}}\varphi \\&\qquad +\int _{\min \{R_1,t\}}^{\min \{R_2,t\}} \int _{{\mathbb {S}}^2}\frac{|\partial _r\xi |^2}{(1+|q|)^{\mu _1}}\frac{r^2 \sin \theta \,{\text {d}}\theta \,{\text {d}}\varphi \,{\text {d}}r}{(1+s)^\alpha }\\&\qquad +\int _{\max \{R_1,t\}}^{\max \{R_2,t\}}\int _{{\mathbb {S}}^2} \frac{|\partial _r\xi |^2 (1+|q|)^{1+\mu _2} r^2 \sin \theta \,{\text {d}}\theta \,{\text {d}}\varphi \,{\text {d}}r}{(1+s)^\alpha }. \end{aligned}$$

Here, $1_{\{q<0\}}$ and $1_{\{q\ge 0\}}$ denote the indicator functions of the sets $\{q<0\}$ and $\{q\ge 0 \}$, respectively. Notice that one of the two integrals $\int _{\min \{R_1,t\}}^{\min \{R_2,t\}}$ and $\int _{\max \{R_1,t\}}^{\max \{R_2,t\}}$ can possibly be empty. Moreover, when $R_2=\infty$, we do not need the first integral on the right-hand side.

Proof

As in [46], we consider the weight function⁶⁰

$$\begin{aligned} n(q)={\left\{ \begin{array}{ll}(1+|q|)^{\mu _2} &{} \text{ if } q\ge 0\\ (1+|q|)^{-1-\mu _1} &{} \text{ if } q<0. \end{array}\right. } \end{aligned}$$

We then compute

$$\begin{aligned} n'(q)={\left\{ \begin{array}{ll}\mu _2(1+|q|)^{-1+\mu _2} &{} \text{ if } q> 0\\ (1+\mu _1)(1+|q|)^{-2-\mu _1} &{} \text{ if } q<0. \end{array}\right. } \end{aligned}$$

On the other hand, we have

$$\begin{aligned} \partial _r\left( \frac{r^2 n(q)}{(1+s)^\alpha }\right) =\left( \frac{2}{r}-\frac{\alpha }{1+s}+\frac{n'(q)}{n(q)}\right) \frac{r^2 n(q)}{(1+s)^\alpha }\ge \frac{r^2 n'(q)}{(1+s)^\alpha }, \end{aligned}$$

which implies

$$\begin{aligned} \partial _r\left( \frac{r^2 n(q)\xi ^2}{(1+s)^\alpha }\right) \ge \frac{r^2 n'(q)\xi ^2}{(1+s)^\alpha }+\frac{2r^2 n(q)\xi \partial _r\xi }{(1+s)^\alpha }. \end{aligned}$$

Integrating from $R_1$ to $R_2$ for every fixed $(\theta ,\varphi )$, we get

$$\begin{aligned} \begin{aligned}&\frac{r^2 n(q)\xi ^2}{(1+s)^\alpha } \restriction _{r=R_1}+\int _{R_1}^{R_2} \frac{r^2 n'(q)\xi ^2}{(1+s)^\alpha } \hbox {d}r\\&\quad \le \frac{r^2 n(q)\xi ^2}{(1+s)^\alpha } \restriction _{r=R_2}+\int _{R_1}^{R_2} \left| \frac{2r^2 n(q)\xi \partial _r\xi }{(1+s)^\alpha }\right| \hbox {d}r. \end{aligned} \end{aligned}$$

Applying the Cauchy–Schwarz inequality, the last term can be controlled by

$$\begin{aligned} \int _{R_1}^{R_2} \left| \frac{2r^2 n(q)\xi \partial _r\xi }{(1+s)^\alpha }\right| \hbox {d}r\le \int _{R_1}^{R_2} \frac{r^2 n'(q)\xi ^2}{(1+s)^\alpha } \hbox {d}r+\int _{R_1}^{R_2} \frac{r^2 n^2(q)|\partial _r\xi |^2}{n'(q)(1+s)^\alpha } \hbox {d}r. \end{aligned}$$

Notice that $|\frac{n(q)}{n'(q)}|\lesssim (1+|q|)$. Therefore, absorbing $\int _{R_1}^{R_2} \frac{r^2 n'(q)\xi ^2}{(1+s)^\alpha } dr$ to the left hand side and integrating over ${\mathbb {S}}^2$ with respect to $\sin \theta \,{\text {d}}\theta \,{\text {d}}\varphi$ yield the desired conclusion. $\square$

Remark 11.7

In the case $R_1=0$ and $R_2=\infty$, we recover the Hardy inequality in [46].

11.3 Klainerman–Sobolev Inequality

We record the following Klainerman–Sobolev inequality. Such global Sobolev inequalities first appeared in the work of Klainerman [33]. The precise weighted version that we use can be found in Proposition 14.1 in [46].

Proposition 11.8

There exists a universal constant C such that for any function⁶¹$\xi \in C^\infty _c({\mathbb {R}}^{3+1})$, the following estimate holds for $t\ge 0$:

$$\begin{aligned} \sup _{x}|\xi (t,x)|(1+s)(1+|q|)^{\frac{1}{2}} w(q)^{\frac{1}{2}}\le C\sum _{|I|\le 3}\Vert w^{\frac{1}{2}}(|\cdot |-t)\Gamma ^I\xi (t,\cdot ) \Vert _{L^2({\mathbb {R}}^3)} . \end{aligned}$$

11.4 Decay Estimates

While the Klainerman–Sobolev inequality gives pointwise decay of a function in terms of the weighted $L^2$ norms of its higher derivatives, in view of the fact that the bounds on the energies we obtain grow with time (see Propositions 15.2, 16.6, 17.2), it does not give the sharp pointwise decay near the wave zone. We thus need to complement this inequality with an ODE argument near the wave zone. This argument was first used in [40] for the constant coefficient wave equation and in [45, 46] for the variable coefficient wave equation. The proof of the following proposition is modified from [46]. Notice in particular that in the gauge used in this paper, we have integrable decay for $H_{LL}$, which results in a slightly stronger proposition.

First, we need a computation⁶² from [46]:

Proposition 11.9

(Lemma 5.2, [46]). Suppose $\xi$ and F are functions such that ${\widetilde{\Box }}_g\xi =F$. Then, at points such that H satisfies $|H|\le \frac{1}{4}$, there exists a function f(t, x, g) with $|f(t,x,g)|\lesssim |H|_{LL}$ such that the following estimate holds:

$$\begin{aligned} \begin{aligned} \left| \left( \partial _s +f\partial _q\right) \partial _q(r\xi )\right| \lesssim&\left( 1+\frac{r|H|_{L{\mathcal {T}}}}{1+|q|}+|H|\right) r^{-1}\\&\times \sum _{|I|\le 2}|\Gamma ^I\xi |+r^{-1}|H||\partial _q(r\xi )|+r|F|. \end{aligned} \end{aligned}$$

Using Proposition 11.9, we obtain the following decay estimates.

Proposition 11.10

Suppose ${\widetilde{\Box }}_g\xi =F$, where $\xi$ is either a scalar or a 2-tensor and g satisfies the bootstrap assumptions (6.2)–(6.6). Then, for $\varpi (q):=(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}$, the following decay estimate holds:

$$\begin{aligned} \begin{aligned}&\sup _x(1+s)\varpi (q)|\partial \xi (t,x)|\\&\quad \lesssim \sup _{0\le \tau \le t}\sum _{|I|\le 1}\Vert \varpi (|\cdot |-\tau )\Gamma ^I\xi (\tau ,\cdot )\Vert _{L^\infty (\Sigma _\tau )}\\&\qquad +\int _0^t \left( (1+\tau )\Vert \varpi (|\cdot |-\tau )F(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}\right. \\&\qquad \left. +\sum _{|I|\le 2}(1+\tau )^{-1}\Vert \varpi (|\cdot |-\tau )\Gamma ^I\xi (\tau ,\cdot )\Vert _{L^\infty (D_\tau )}\right) {\text {d}}\tau . \end{aligned} \end{aligned}$$

Here, $D_t$ is defined to be the region $D_t:=\{x:\frac{t}{2}\le |x|\le 2t\}$.

Proof

We will only prove the proposition where $\xi$ is a scalar—the case where $\xi$ is a 2-tensor can be proven analogously by considering separately every component with respect to the Minkowskian coordinates.

We now carry out some easy reductions. First, we can assume $t\ge T$ for any finite $T>0$, since as long as we allow the implicit constant to depend on T, the desired estimate when $t<T$ follows from Proposition 7.1. (In fact, the estimate holds even only with the first term on the right-hand side.) We can therefore choose T sufficiently large such that according to (7.1) and (6.5), $|H|\le \frac{1}{4}$ holds for $t\ge T$.

Second, by Proposition 7.1, we only need to prove the desired estimate in the region $\frac{t}{2}+\frac{1}{2} \le |x|\le 2t-1$, since in the complement of this region, we have $(1+|q|)^{-1}\lesssim (1+s)^{-1}$. (As in the $t<T$ case, the estimate holds even only with the first term on the right-hand side.)

By the choice of T above, if $t\ge T$, then $|H|\le \frac{1}{4}$ and we can apply Proposition 11.9, which implies

$$\begin{aligned} \begin{aligned}&\left| \left( \partial _s +f\partial _q\right) (\varpi (q)\partial _q(r\xi ))\right| \\&\quad \lesssim \left( 1+\frac{r|H|_{L{\mathcal {T}}}}{1+|q|}+|H|\right) r^{-1}\sum _{|I|\le 2}\varpi (q)|\Gamma ^I\xi |\\&\qquad +(r^{-1}|H|\varpi (q)+|H|_{LL}\varpi '(q))|\partial _q(r\xi )|+r\varpi (q)|F|. \end{aligned} \end{aligned}$$

(11.13)

Let (t, x) be such that $t\ge T$ and $\frac{t}{2}+\frac{1}{2} \le |x|\le 2t-1$. Consider the integral curves of the vector field $\partial _s+f\partial _q$ through the point (t, x) restricted to the region $\cup _{\tau \ge T} D_\tau$. Since $|f|\lesssim |H|_{LL}\lesssim \frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}}{(1+s)^{1+\frac{\gamma }{2}}w(q)^{\frac{1}{2}}}$ by (7.4), the integral curve intersects the boundary of $\cup _{\tau \ge T} D_\tau$ at a point with t-value comparable to t. Integrating (11.14) along such an integral curve, using the Grönwall’s inequality and noting that $\int _1^{\infty } \sup _{x\in D_t}(r^{-1}|H|+|H|_{LL}\frac{\varpi '(q)}{\varpi (q)})\, {\text {d}}t\lesssim \epsilon ^{\frac{1}{2}}$ (by (7.1), (7.5), (6.5) and (6.6)) thus give the desired conclusion. $\square$

As in [45, 46], we note that the estimate in Proposition 11.10 still holds after projecting to the vector fields in ${\mathcal {T}}$ and/or ${\mathcal {U}}$.

Proposition 11.11

Suppose ${\widetilde{\Box }}_g\xi =F$, where $\xi$ is a 2-tensor and g satisfies the bootstrap assumptions (6.2)–(6.6). Then, for $\varpi (q):=(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}$, the following decay estimate holds:

$$\begin{aligned} \begin{aligned}&\sup _x(1+s)\varpi (q)|\partial \xi (t,x)|_{{\mathcal {T}}{\mathcal {U}}}\\&\quad \lesssim \sup _{0\le \tau \le t}\sum _{|I|\le 1}\Vert \varpi (|\cdot |-\tau )\Gamma ^I\xi (\tau ,\cdot )\Vert _{L^\infty (\Sigma _\tau )}\\&\qquad +\int _0^t \left( (1+\tau )\Vert \varpi (|\cdot |-\tau )|F(\tau ,\cdot )|_{{\mathcal {T}}{\mathcal {U}}}\Vert _{L^\infty (D_\tau )}\right. \\&\qquad \left. +\sum _{|I|\le 2}(1+\tau )^{-1}\Vert \varpi (|\cdot |-\tau )\Gamma ^I\xi (\tau ,\cdot )\Vert _{L^\infty (D_\tau )}\right) {\text {d}}\tau . \end{aligned} \end{aligned}$$

As before, $D_t$ is defined to be the region $D_t:=\{x:\frac{t}{2}\le |x|\le 2t\}$.

Proof

After noting that $\partial _s$ and $\partial _q$ commute with the projection to vector fields in ${\mathcal {T}}$ and ${\mathcal {U}}$, the proof is completely analogous to that in Proposition 11.10 and will be omitted. $\square$

12 Definition of the Spacetime Regions

Starting from this section and until Sect. 17, our goal is to prove energy estimates for $\Gamma ^{I} h$ and $\Gamma ^{I} \beta$ for $\vert I\vert \le N$ under the bootstrap assumptions made in Sect. 6 (for the end result, see Theorem 17.3). Our argument depends crucially on the decomposition of the spacetime into the regions ${\mathcal {R}}_{1}, \ldots , {\mathcal {R}}_{4}$ introduced in Sect. 2, which we recall now: Given parameters $T > 0$, $U_{2} < 0$ and $U_{3} > 0$ to be fixed below, we define

$$\begin{aligned} {\mathcal {R}}_1&:= \{(t,x):t\le T\}, \\ {\mathcal {R}}_2&:=\left\{ (t,x):t\ge T,\,t-|x|-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U_2 \right\} ,\\ {\mathcal {R}}_3&:=\left\{ (t,x):t\ge T,\,U_2\le t-|x|-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\le U_3 \right\} ,\\ {\mathcal {R}}_4&:=\left\{ (t,x):t\ge T,\,t-|x|-\frac{1}{(1+t)^{\frac{\gamma }{4}}}\ge U_3 \right\} . \end{aligned}$$

Recall also the notation ${\mathcal {R}}_{j, \tau } := {\mathcal {R}}_{j} \cap \{t = \tau \}$ and ${\mathcal {B}}_{U} := \{(t,x): t - \vert x\vert - \frac{1}{(1+t)^{\frac{\gamma }{4}}} = U\}$. See Fig. 1.

Fig. 1

Decomposition of the spacetime employed in the proof. We have drawn the standard Penrose diagram with respect to the background Minkowski metric m, i.e., a fixed-$(\theta , \varphi )$ plane in the coordinates $({\tilde{U}} = \arctan (t-r), {\tilde{V}} = \arctan (t + r), \theta , \varphi )$, where the future-pointing null ${\tilde{U}}$- and ${\tilde{V}}$-axes are drawn at $45^{\circ }$ with respect to the vertical axis. For radial vectors, the causality properties read off from the diagram coincide with those with respect to m. Abusing the terminology a bit, we refer to the (dashed) idealized boundary curve $\{ {\tilde{V}} = \frac{\pi }{2} \}$ as null infinity, and its past and future endpoints as spacelike and timelike infinities, respectively. By Proposition 7.3, $\{t-r = U_{j}\}$ $(j=2, 3)$, which is evidently null with respect to m, is asymptotically null with respect to g as t increases. Accordingly, the hypersurface ${\mathcal {B}}_{U_{j}} \cap \{t \ge T\} = \{(t, x) : t - \vert x\vert + \frac{1}{(1+t)^{\frac{\gamma }{4}}} = U_{j}, \, t \ge T\}$, which asymptotes to $\{t-r=U_{j}\}$ as $t \rightarrow \infty$, is spacelike with respect to g for T large enough, as we have implicitly observed in Propositions 11.3–11.5

Energy estimates for h and $\beta$ are proved sequentially in the regions ${\mathcal {R}}_{1}$, ${\mathcal {R}}_{2}$, ${\mathcal {R}}_{3}$ and ${\mathcal {R}}_{4}$, in Sects. 13, 15, 16 and 17, respectively. The parameters $U_{2}$, $U_{3}$ and T are fixed at the end of Sect. 17; we refer to Remark 6.1 for the precise order of the choices of the parameters involved in the proof.

13 Cauchy Stability Up to Large Time

In this section, we prove the energy estimates in the region ${\mathcal {R}}_1$. This is a standard Cauchy stability argument, which we include for completeness. We begin with Lemma 13.1. The main estimate will be proven in Proposition 13.2.

Lemma 13.1

Suppose $\Box _g\xi =F$, where $\xi$ is a scalar function and g satisfies the bootstrap assumptions (6.2)–(6.6). Then, for every $T>0$, there exists ${{\tilde{\epsilon }}}_1>0$ such that for $\epsilon <{{\tilde{\epsilon }}}_1$, the following estimate holds for all $T'\le T$ with an implicit constant⁶³ depending on T (in addition to C, $\gamma$, N and $\delta _0$):

$$\begin{aligned} \begin{aligned} \sup _{\tau \in [0,T']}\int _{\Sigma _\tau } |\partial \xi |^2\,w(r-\tau )\, {\text {d}}x\lesssim _T&\int _{\Sigma _0} |\partial \xi |^2\,w(r)\, {\text {d}}x+\int _0^{T'}\int _{\Sigma _t} |\partial \xi ||F|\,w(q)\, {\text {d}}x\, {\text {d}}t. \end{aligned} \end{aligned}$$

Proof

Let $T>0$ be as in the statement of the lemma. In the proof of this lemma, we allow all implicit constants to depend on T (in addition to C, $\gamma$, N and $\delta _0$).

It is convenient to proceed in a more geometric fashion for which we need some notations. Introduce the stress–energy–momentum tensor⁶⁴

$$\begin{aligned} \mathbf{T}_{\mu \nu }=\partial _\mu \xi \partial _\nu \xi -\frac{1}{2} g_{\mu \nu }(g^{-1})^{\alpha \beta }\partial _\alpha \xi \partial _\beta \xi . \end{aligned}$$

Since $\Box _g\xi =F$, $\mathbf{T}_{\mu \nu }$ satisfies⁶⁵$D^\mu \mathbf{T}_{\mu \nu }=(\partial _\nu \xi )F$. Contracting this with $-(Dt)^{\mu }=-(g^{-1})^{\mu \nu }\partial _\mu t$, integrating this in the region $\{0\le t\le \tau \}$ (for $\tau \in [0,T]$) with respect to the volume form $w(q)\,dVol:=w(q)\,\sqrt{-\det g}\,{\text {d}}t\, {\text {d}}x^1 {\text {d}}x^2\,{\text {d}}x^3$, and applying the divergence theorem, we obtain

$$\begin{aligned} \begin{aligned}&-\int _{\Sigma _\tau } \mathbf{T}_{\mu \nu } \mathbf{N}^{\mu }(D t)^{\nu }w(r-\tau )\sqrt{\det {\hat{g}}}\, {\text {d}}x\\&\quad \lesssim -\int _{\Sigma _0} \mathbf{T}_{\mu \nu } \mathbf{N}^{\mu }(D t)^{\nu }w(r)\sqrt{\det {\hat{g}}} \, {\text {d}}x\\&\qquad +\int _0^{\tau }\int _{\Sigma _t} \left( |\partial \xi ||F|+\left( 1+|D^2 t|\right) |\partial \xi |^2\right) \,w(q)\, \hbox {d}Vol, \end{aligned} \end{aligned}$$

(11.14)

where $\mathbf{N}^\mu$ is the future directed unit normal to the constant t hypersurfaces. To derive (13.1), we have used the upper bounds for g and $g^{-1}$, which follow from (2) in Definition 3.1, the bootstrap assumption (6.5) and the estimate (7.1); and also $|\partial w|\lesssim w$.

We now show that the boundary term on the left-hand side of (13.1) controls the derivatives of $\xi$. Since $\mathbf{N}^\mu =-\frac{(g^{-1})^{\mu \nu }\partial _\nu t}{\sqrt{-(g^{-1})^{00}}}$, we apply⁶⁶ (3.2), (3.3) and the bootstrap assumption (6.5) to obtain

$$\begin{aligned}&-\int _{\Sigma _\tau } \mathbf{T}_{\mu \nu } \mathbf{N}^{\mu }(D t)^{\nu }\,w(r-\tau )\sqrt{\det {\hat{g}}}\, {\text {d}}x^1\,{\text {d}}x^2\,{\text {d}}x^3\\&\qquad > rsim \int _{\Sigma _\tau }\left( (\mathbf{N}\xi )^2+\sum _{i=1}^3(\partial _i\xi )^2\right) \,w(r-\tau )\, {\text {d}}x. \end{aligned}$$

Since we have⁶⁷$\mathbf{N}=\sqrt{-(g^{-1})^{00}}\partial _t-\frac{(g^{-1})^{0i}}{\sqrt{-(g^{-1})^{00}}}\partial _i$, this then implies

$$\begin{aligned} -\int _{\Sigma _\tau } \mathbf{T}_{\mu \nu } \mathbf{N}^{\mu }(D t)^{\nu }w(r-\tau )\sqrt{\det {\hat{g}}}\, {\text {d}}x^1\,{\text {d}}x^2\,{\text {d}}x^3 > rsim \int _{\Sigma _\tau }|\partial \xi |^2\,w(r-\tau )\, {\text {d}}x.\nonumber \\ \end{aligned}$$

(13.1)

On the other hand, by (3.2), (3.3) and (6.5), we have

$$\begin{aligned} -\int _{\Sigma _0} \mathbf{T}_{\mu \nu } \mathbf{N}^{\mu }(D t)^{\nu }w(r)\sqrt{\det {\hat{g}}} \, {\text {d}}x\lesssim \int _{\Sigma _0} |\partial \xi |^2 w(r) \, {\text {d}}x. \end{aligned}$$

(13.2)

To proceed, note that⁶⁸$(g^{-1})^{00}=\frac{\det {\hat{g}}}{\det g}$, which implies upper and lower bounds for $\det g$. Therefore, (13.1),(13.2) and (13.3) together imply

$$\begin{aligned} \begin{aligned} \int _{\Sigma _\tau } |\partial \xi |^2\, w(r-\tau )\, {\text {d}}x \lesssim&\int _{\Sigma _0} |\partial \xi |^2\,w(r) \, {\text {d}}x\\&+\int _0^{\tau }\int _{\Sigma _t} \left( |\partial \xi ||F|+\left( 1+|D^2 t|\right) |\partial \xi |^2\right) \,w(q)\, {\text {d}}x\, {\text {d}}t, \end{aligned} \end{aligned}$$

Finally, by (6.5) and (7.1), we have $|D^2 t|\lesssim 1$ and therefore the desired conclusion follows after an application of the Grönwall’s inequality. $\square$

We now apply Lemma 13.1 to obtain the following energy estimates in the region ${\mathcal {R}}_1$:

Proposition 13.2

There exists $\epsilon _1>0$ sufficiently small such that for every $T>0$, there exists a constant $C_T$ (depending on T in addition to C, $\gamma$, N and $\delta _0$) such that the following estimate holds in $[0,T]\times {\mathbb {R}}^3$:

$$\begin{aligned} \sup _{0 \le t\le T} \left( \sum _{|I|\le N}\int _{\Sigma _t}\left( |\partial \Gamma ^I h|^2+|\partial \Gamma ^I\beta |^2\right) w(q)\, {\text {d}}x\right) ^{\frac{1}{2}}\le C_T \epsilon \end{aligned}$$

whenever $\epsilon <\epsilon _1$.

Proof

For this argument in ${\mathcal {R}}_1$, we only need a much rougher form of the equation than that in Propositions 9.15 and 10.1. By Propositions 9.15 and 10.1 and the bootstrap assumptions (6.2) and (6.5), we easily obtain

$$\begin{aligned} \begin{aligned}&|{\widetilde{\Box }}_g \Gamma ^I h|+|{\widetilde{\Box }}_g \Gamma ^I \beta |\\&\quad \lesssim \frac{\epsilon \log ^2 (2+s)}{(1+s)^2(1+|q|)w(q)^{\frac{\gamma }{1+2\gamma }}}+\sum _{|J|\le |I|} \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |+(1+|q|)^{-1}|\Gamma ^J h|\right) .\nonumber \\ \end{aligned} \end{aligned}$$

(13.3)

By (10.4), (9.20) and (8) in Definition 3.1, we can replace the ${\widetilde{\Box }}_g$ in (13.4) by the scalar d’Alembertian $\Box _g$ for each component of h and $\beta$, while retaining the same bounds on the right-hand side. Therefore, by Lemma 13.1 (which is applicable if we choose $\epsilon _1<{\tilde{\epsilon }}_1$) and the Cauchy–Schwarz inequality, we have

$$\begin{aligned} \begin{aligned}&\sup _{0 \le t\le T'} \sum _{|I|\le k}\int _{\Sigma _t}\left( |\partial \Gamma ^I h|^2+|\partial \Gamma ^I\beta |^2\right) w(q)\, {\text {d}}x\\&\quad \lesssim _T \sum _{|I|\le k}\int _{\Sigma _0}\left( |\partial \Gamma ^I h|^2+|\partial \Gamma ^I\beta |^2\right) w(r)\, {\text {d}}x\\&\qquad +\sum _{|I|\le k}\int _0^{T'}\int _{\Sigma _t} \left( \frac{\epsilon ^2 \log ^4 (2+s)}{(1+s)^4(1+|q|)^2 w(q)^{\frac{2\gamma }{1+2\gamma }}}\right. \\&\qquad \left. +|\partial \Gamma ^I h|^2+|\partial \Gamma ^I\beta |^2+\frac{|\Gamma ^I h|^2}{(1+|q|)^2}\right) \,w(q)\, {\text {d}}x\, {\text {d}}t\\&\quad \lesssim _T \epsilon ^2+\sum _{|I|\le k}\int _0^{T'}\int _{\Sigma _t} \left( |\partial \Gamma ^I h|^2+|\partial \Gamma ^I\beta |^2\right) \,w(q)\, {\text {d}}x\, {\text {d}}t, \end{aligned} \end{aligned}$$

where in the last line we have used $\int _0^T\int _{\Sigma _t} \frac{\epsilon ^2 \log ^4 (2+s)}{(1+s)^4(1+|q|)^2 w(q)^{\frac{2\gamma }{1+2\gamma }}}\,w(q)\, {\text {d}}x\, {\text {d}}t\lesssim \epsilon ^2$ as well as the Hardy inequality in Proposition 11.6 with $\alpha =\mu _1=0$ and $\mu _2=2\gamma$. The conclusion thus follows from Grönwall’s inequality. $\square$

14 Estimates for the Error Terms Arising from the Energy Estimates

In this section and the next three sections, we prove energy estimates for the metric h and the scalar field $\beta$. We first show that most of the terms in the equation for ${\widetilde{\Box }}_g\Gamma h$ in Proposition 9.15 and all of the terms for ${\widetilde{\Box }}_g\Gamma ^I\beta$ in Proposition 10.1 can in fact be controlled by the energy itself with a smallness constant (and allowing some growth in the lower-order term). The only term in Proposition 9.15 that cannot be controlled in such a manner is what we called the “bad term,” i.e., the term ${\mathfrak {B}}_I$. Indeed, this ${\mathfrak {B}}_I$ term has to be dealt with differently in each of the regions ${\mathcal {R}}_2$, ${\mathcal {R}}_3$ and ${\mathcal {R}}_4$ and will be treated in Sects. 15–17.

In this section, we instead control all the other terms which are better behaved. The main results of this section are contained in Propositions 14.7 and 14.8. In order to show the estimates for all regions simultaneously, we introduce the following notation: We will use ${\mathcal {R}}$ to denote either the regions ${\mathcal {R}}_2$, ${\mathcal {R}}_3$ or ${\mathcal {R}}_4$. Also, ${\mathcal {R}}_\tau$ will denote the intersection of ${\mathcal {R}}$ and a constant $\{t=\tau \}$ hypersurface.

We first control the terms in $|\Box _g\Gamma ^I h|$ except for ${\mathfrak {B}}_I$. According to Proposition 9.15, we need to control the terms ${\mathfrak {I}}_I$, ${\mathfrak {G}}_I$, ${\mathfrak {T}}_I$, ${\mathfrak {L}}_I$, ${\mathfrak {W}}_I$ and ${\mathfrak {N}}_I$. As a first step, we use the bootstrap assumptions (6.2) and (6.5) to further estimate the ${\mathfrak {N}}_I$ term:

$$\begin{aligned} \begin{aligned}&{\mathfrak {N}}_I \lesssim \sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ \max \{|J_1|,|J_2|\}\le |I|-1 \end{array}}\left( |\partial \Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|+|\partial \Gamma ^{J_1}\beta ||\partial \Gamma ^{J_2}\beta |+\frac{|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|}{1+|q|}\right) \\&\qquad +\sum _{|J_2|\le |I|,\,|J_1|+(|J_2|-1)_+\le |I|}\frac{|\Gamma ^{J_1} h|_{LL}|\partial \Gamma ^{J_2} h|}{1+|q|}\\&\quad \lesssim \sum _{|J|\le |I|-1} \frac{\left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) }{(1+s)^{1-\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}}\\&\qquad +\sum _{|J|\le |I|-1} \frac{|\Gamma ^J h|}{(1+s)^{1-\delta _0}(1+|q|)^{\frac{3}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}}\\&\qquad +\sum _{|J|\le |I|} \frac{|\Gamma ^J h|_{LL}}{(1+s)^{1-\delta _0}(1+|q|)^{\frac{3}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}} \end{aligned} \end{aligned}$$

We will control the ${\mathfrak {N}}_I$ term together with the ${\mathfrak {L}}_I$, ${\mathfrak {G}}_I$ terms. More precisely, define

$$\begin{aligned} \tilde{{\mathfrak {L}}}_I:= \sum _{|J|\le |I|-1}\left( \frac{|\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |}{(1+s)^{1-\delta _0}}+\frac{|\Gamma ^J h|}{(1+s)^{1-\delta _0}(1+|q|)^{1+\gamma }}\right) , \end{aligned}$$

(14.1)

and

$$\begin{aligned} \tilde{{\mathfrak {G}}}_I := \sum _{|J|\le |I|}\frac{|\Gamma ^J h|_{LL}}{(1+s)^{1-\delta _0}(1+|q|)^{1+\gamma }}+\sum _{|J|\le |I|}\frac{|{\bar{\partial }}\Gamma ^J h|+|{\bar{\partial }}\Gamma ^J \beta |}{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}.\nonumber \\ \end{aligned}$$

(14.2)

It is easy to see that we have

Proposition 14.1

The following pointwise estimate holds everywhere in $[0,\infty )\times {\mathbb {R}}^3$:

$$\begin{aligned} {\mathfrak {G}}_I+{\mathfrak {L}}_I+{\mathfrak {N}}_I\lesssim \tilde{{\mathfrak {G}}}_I+\tilde{{\mathfrak {L}}}_I. \end{aligned}$$

We will therefore control the terms ${\mathfrak {I}}_I$, ${\mathfrak {T}}_I$, ${\mathfrak {W}}_I$, $\tilde{{\mathfrak {L}}}_I$, $\tilde{{\mathfrak {G}}}_I$ in the w(q)-weighted $L^1_tL^2_x$ space according to the energy estimates (Propositions 11.3, 11.4, 11.5). We note again that we do not bound the term ${\mathfrak {B}}_I$ in this section, but will estimate it in later sections.

Before we proceed, we introduce some more notations. In the following, we will frequently apply the Hardy inequality in Proposition 11.6 and will generate boundary terms on ${\mathcal {B}}_U$. To capture these boundary terms, we introduce the notation⁶⁹ that for every scalar function $\xi$, let

$$\begin{aligned} \Vert v(U)\xi \Vert _{L^2({\mathbb {S}}^2(U,\tau ))}^2:=v(U)\int _{\{t=\tau ,\,t-r-\frac{1}{(1+t)^{\frac{\gamma }{4}}}=U\}} |\xi |^2 r^2\sin \theta \,{\text {d}}\theta \,{\text {d}}\varphi ,\qquad \end{aligned}$$

(14.3)

where

$$\begin{aligned} v(U):={\left\{ \begin{array}{ll} (1+|U|)^{2\gamma } &{}\text{ if } U\le 0\\ (1+|U|)^{-1} &{}\text{ if } U\ge 0 \end{array}\right. }. \end{aligned}$$

Moreover, we define $U'({\mathcal {R}})$ to be the U value associated with the hypersurface ${\mathcal {B}}_{U'}$ to the past of the region ${\mathcal {R}}$ and $U({\mathcal {R}})$ to be the U value associated with the hypersurface ${\mathcal {B}}_U$ to the future of the region ${\mathcal {R}}$. More precisely, for the region ${\mathcal {R}}_2$, we have $U'({\mathcal {R}}_2)=-\infty$, $U({\mathcal {R}}_2)=U_2$; for the region ${\mathcal {R}}_3$, we have $U'({\mathcal {R}}_3)=U_2$, $U({\mathcal {R}}_3)=U_3$; and for the region ${\mathcal {R}}_4$, we have $U'({\mathcal {R}}_4)=U_3$, $U({\mathcal {R}}_4)=\infty$. We will also use the convention that in the case $U'({\mathcal {R}}_2)=-\infty$ and $U({\mathcal {R}}_4)=\infty$, the term in (14.3) is taken to be zero.

We will also introduce the following convention for the $L^2({\mathcal {R}}_\tau )$ norm. Given a function F in the spacetime variables (t, x), unless otherwise stated, the norm $\Vert F w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}$ will be understood such that F is evaluated at $(\tau ,x)$, while w is evaluated at $|x|-\tau$, i.e., 

$$\begin{aligned} \Vert F w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}:=\left( \int _{{\mathbb {R}}^3} |F|^2(\tau ,x) w(r-\tau )\, {\text {d}}x\right) ^{\frac{1}{2}}. \end{aligned}$$

We now turn to the estimates. First, we consider the term ${\mathfrak {I}}_I$.

Proposition 14.2

The following estimate holds for $|I|\le N$ and $t>T>0$:

$$\begin{aligned} \int _T^t \Vert {\mathfrak {I}}_I w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )} {\text {d}}\tau \lesssim \epsilon \log ^4(2+t). \end{aligned}$$

Proof

Recalling the definition of ${\mathfrak {I}}_I$ in Proposition 9.15, we get⁷⁰

$$\begin{aligned}&\int _T^t \Vert {\mathfrak {I}}_I w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )} {\text {d}}\tau \nonumber \\&\quad \lesssim \epsilon \int _T^t \left( \int _0^{\infty }\frac{\log ^4(2+\tau +r) w(r-\tau )^{1-\frac{2\gamma }{1+2\gamma }} r^2\,{\text {d}}r}{(1+\tau +r)^4(1+|r-\tau |)^2} \right) ^{\frac{1}{2}}\, {\text {d}}\tau \nonumber \\&\quad \lesssim \epsilon \int _T^t \left( \int _0^{\infty }\frac{\log ^4(2+\tau +r) \,{\text {d}}r}{(1+\tau +r)^2(1+|r-\tau |)} \right) ^{\frac{1}{2}}\, {\text {d}}\tau \nonumber \\&\quad \lesssim \epsilon \int _T^t \frac{\log ^3(2+\tau )}{1+\tau }\left( \int _{-\infty }^{\infty }\frac{\hbox {d}q}{(1+|q|)\log ^2(2+|q|)} \right) ^{\frac{1}{2}}\, {\text {d}}\tau \nonumber \\&\quad \lesssim \epsilon \int _T^t \frac{\log ^3(2+\tau )}{1+\tau } {\text {d}}\tau \lesssim \epsilon \log ^4(2+t). \end{aligned}$$

(14.4)

Notice that in line (14.4), we have used $\frac{r^2}{(1+\tau +r)^2}\lesssim 1$ and $\frac{w(q)^{1-\frac{2\gamma }{1+2\gamma }}}{1+|q|}\lesssim 1$. $\square$

We now estimate the ${\mathfrak {T}}_I$ term, which can be controlled easily using the $\frac{1}{(1+s)^{1+\frac{\gamma }{2}}}$ decay:

Proposition 14.3

The following estimate holds for $|I|\le N$ and $t>T>0$:

$$\begin{aligned} \int _T^t \Vert {\mathfrak {T}}_I w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )} {\text {d}}\tau \lesssim T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}. \end{aligned}$$

Proof

Recalling the definition of ${\mathfrak {T}}_I$ in Proposition 9.15, we get

$$\begin{aligned} \begin{aligned}&\sum _{|J|\le |I|}\int _T^t \left( \int _{{\mathcal {R}}_\tau } |{\mathfrak {T}}_I|^2 w(r-\tau ) {\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}\tau \\&\quad \lesssim \sum _{|J|\le |I|}\int _T^t \left( \int _{{\mathcal {R}}_\tau } \frac{\left( |\partial \Gamma ^J h|^2+|\partial \Gamma ^J \beta |^2\right) w(r-\tau )}{(1+\tau +r)^{2+\gamma }} {\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}\tau \\&\quad \lesssim \sum _{|J|\le |I|} \sup _{\tau \in [T,t]}\left( \int _{{\mathcal {R}}_\tau } \left( |\partial \Gamma ^J h|^2+|\partial \Gamma ^J \beta |^2\right) w(r-\tau ) {\text {d}}x\right) ^{\frac{1}{2}}\left( \int _T^t\frac{{\text {d}}\tau }{(1+\tau )^{1+\frac{\gamma }{2}}}\right) \\&\quad \lesssim T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}. \end{aligned} \end{aligned}$$

$\square$

We now bound the term ${\mathfrak {W}}_I$. These estimates require the use of the Hardy inequality in Proposition 11.6 and therefore have a boundary term⁷¹ on ${\mathcal {B}}_{U({\mathcal {R}})}$.

Proposition 14.4

The following estimate holds for $|I|\le N$ and $t>T>0$:

$$\begin{aligned}&\int _T^t \Vert {\mathfrak {W}}_I w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )} {\text {d}}\tau \\&\qquad \lesssim T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|} \sup _{\tau \in [T,t]}\left( \Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}+\Vert v(U'({\mathcal {R}}))|\Gamma ^J h|\Vert _{L^2({\mathbb {S}}^2(U'({\mathcal {R}}),\tau ))}\right) . \end{aligned}$$

Proof

Recalling the definition of ${\mathfrak {W}}_I$ in Proposition 9.15, we get

$$\begin{aligned}&\int _T^t \left( \int _{{\mathcal {R}}_\tau } |{\mathfrak {W}}_I|^2 w(r-\tau ) {\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}\tau \nonumber \\&\quad \lesssim \sum _{|J|\le |I|}\int _T^t \left( \int _{{\mathcal {R}}_\tau } \frac{\log ^2(2+\tau +r)|\Gamma ^J h|^2 w(r-\tau )}{(1+\tau +r)^{4-4\delta _0}(1+|r-\tau |)^{2\gamma +4\delta _0}} {\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}\tau \nonumber \\&\quad \lesssim \sum _{|J|\le |I|}\sup _{\tau \in [T,t]} \left( \int _{{\mathcal {R}}_\tau } \frac{|\Gamma ^J h|^2 w(r-\tau )}{(1+|r-\tau |)^2} {\text {d}}x\right) ^{\frac{1}{2}}\left( \int _T^t\frac{\log (2+\tau )\,{\text {d}}\tau }{(1+\tau )^{1+\gamma }}\right) \end{aligned}$$

(14.5)

$$\begin{aligned}&\quad \lesssim T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\sup _{\tau \in [T,t]} \left( \Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}+\Vert v(U'({\mathcal {R}}))|\Gamma ^J h|\Vert _{L^2({\mathbb {S}}^2(U'({\mathcal {R}}),\tau ))}\right) , \end{aligned}$$

(14.6)

where in (14.5), we used $\left( \frac{\log ^2(2+\tau +r)(1+|r-\tau |)^{2-2\gamma -4\delta _0}}{(1+\tau +r)^{4-4\delta _0}}\right) ^{\frac{1}{2}}\lesssim \frac{\log (2+\tau )}{(1+\tau )^{1+\gamma }};$ and in (14.6) we have used the Hardy inequality in Proposition 11.6 with $\alpha =0$, $\mu _1=0$ and $\mu _2=2\gamma$. $\square$

We now bound the $\tilde{{\mathfrak {L}}}_I$ term:

Proposition 14.5

The following estimate holds for $|I|\le N$ and $t>T>0$:

$$\begin{aligned} \begin{aligned}&\int _T^t \Vert \tilde{{\mathfrak {L}}}_I w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )} {\text {d}}\tau \\&\quad \lesssim (1+t)^{\delta _0}\sum _{|J|\le |I|-1} \sup _{\tau \in [T,t]}\left( \Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}\right. \\&\qquad \left. +\Vert v(U'({\mathcal {R}}))|\Gamma ^J h|\Vert _{L^2({\mathbb {S}}^2(U'({\mathcal {R}}),\tau ))}\right) . \end{aligned} \end{aligned}$$

Proof

Recalling the definition of $\tilde{{\mathfrak {L}}}_I$ in (14.1), we get

$$\begin{aligned}&\int _T^t \left( \int _{{\mathcal {R}}_\tau } |\tilde{{\mathfrak {L}}}_I|^2 w(r-\tau ) {\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}\tau \nonumber \\&\quad \lesssim \sum _{|J|\le |I|-1}\int _T^t \left( \int _{{\mathcal {R}}_\tau } \frac{\left( |\partial \Gamma ^J h|^2+|\partial \Gamma ^J \beta |^2\right) w(r-\tau )}{(1+\tau +r)^{2-2\delta _0}} {\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}\tau \nonumber \\&\qquad +\sum _{|J|\le |I|-1}\int _T^t \left( \int _{{\mathcal {R}}_\tau } \frac{|\Gamma ^J h|^2 w(q)}{(1+\tau +r)^{2-2\delta _0}(1+|r-\tau |)^{2+2\gamma }} {\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}\tau \nonumber \\&\quad \lesssim \sum _{|J|\le |I|-1}\sup _{\tau \in [T,t]} \left( \int _{{\mathcal {R}}_\tau }\left( |\partial \Gamma ^J h|^2+ |\partial \Gamma ^J \beta |^2\right) w(r-\tau ) {\text {d}}x\right) ^{\frac{1}{2}}\left( \int _T^t\frac{{\text {d}}\tau }{(1+\tau )^{1-\delta _0}}\right) \nonumber \\&\qquad +\sum _{|J|\le |I|-1}\sup _{\tau \in [T,t]} \left( \int _{{\mathcal {R}}_\tau } \frac{|\Gamma ^J h|^2 w(r-\tau )}{(1+|r-\tau |)^2} {\text {d}}x\right) ^{\frac{1}{2}}\left( \int _T^t\frac{{\text {d}}\tau }{(1+\tau )^{1-\delta _0}}\right) \nonumber \\&\quad \lesssim (1+t)^{\delta _0}\sum _{|J|\le |I|-1}\sup _{\tau \in [T,t]} \left( \Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}\right. \nonumber \\&\qquad \left. +\Vert v(U'({\mathcal {R}}))|\Gamma ^J h|\Vert _{L^2({\mathbb {S}}^2(U'({\mathcal {R}}),\tau ))}\right) , \end{aligned}$$

(14.7)

where in (14.7) we have used the Hardy inequality in Proposition 11.6 with $\alpha =0$, $\mu _1=0$ and $\mu _2=2\gamma$. $\square$

Finally, we move to the good term $\tilde{{\mathfrak {G}}}_I$.

Proposition 14.6

The following bound⁷² holds for $|I|\le N$ and $t>T>0$:

$$\begin{aligned} \begin{aligned}&\int _T^t \Vert \tilde{{\mathfrak {G}}}_I w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )} {\text {d}}\tau \\&\quad \lesssim \epsilon \log ^4(2+t)+T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\sup _{\tau \in [T,t]}\Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\left( \int _T^t \int _{ {\mathcal {R}}_\tau } \left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\\&\qquad +(1+t)^{\delta _0}\sum _{|J|\le |I|-1} \sup _{\tau \in [T,t]}\Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}\\&\qquad +\sum _{|J|\le |I|}\sup _{\tau \in [T,t]}(1+\tau )^{\delta _0}\Vert v(U'({\mathcal {R}}))|\Gamma ^J h|\Vert _{L^2({\mathbb {S}}^2(U'({\mathcal {R}}),\tau ))}. \end{aligned} \end{aligned}$$

Proof

In order to control $\tilde{{\mathfrak {G}}}_I$, we recall from (14.2) that

$$\begin{aligned} \tilde{{\mathfrak {G}}}_I\lesssim \underbrace{\sum _{|J|\le |I|}\frac{|\Gamma ^J h|_{LL}}{(1+s)^{1-\delta _0}(1+|q|)^{1+\gamma }}}_{=:\hbox {I}}+\underbrace{\sum _{|J|\le |I|}\frac{|{\bar{\partial }}\Gamma ^J h|+|{\bar{\partial }}\Gamma ^J\beta |}{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}}_{=:\hbox {II}}.\nonumber \\ \end{aligned}$$

(14.8)

We first control the term II, which has a good derivative. As we will see later, it will be convenient to derive a slightly better estimate in which we bound

$$\begin{aligned} \hbox {II}':=\sum _{|J|\le |I|}\frac{|{\bar{\partial }}\Gamma ^J h|+|{\bar{\partial }}\Gamma ^J\beta |}{(1+s)^{1-\delta _0}(1+|q|)^{\frac{7\gamma }{8}}} \end{aligned}$$

(14.9)

instead of II. As a consequence of Definition 5.1, $w'(q)$ is positive and in fact satisfies the lower bounds

$$\begin{aligned} w'(q) > rsim {\left\{ \begin{array}{ll} (1+|q|)^{2\gamma } &{}\text{ if } q\ge 0\\ (1+|q|)^{-1-\frac{\gamma }{2}} &{}\text{ if } q< 0. \end{array}\right. } \end{aligned}$$

Therefore, for $\delta _0$ satisfying (6.1), we can estimate $\hbox {II}'$ separately in the regions $r-\tau \ge 0$ and $r-\tau <0$ to obtain

$$\begin{aligned} \begin{aligned}&\sum _{|J|\le |I|}\int _T^t \left( \int _{{\mathcal {R}}_\tau } \frac{\left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) w(r-\tau )}{(1+s)^{2-2\delta _0}(1+|r-\tau |)^{\frac{7\gamma }{4}}} {\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}\tau \\&\quad \lesssim \sum _{|J|\le |I|} \left( \int _{\{\tau \in [T,t], r-\tau \ge 0\}\cap {\mathcal {R}}} \frac{\left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) (1+|r-\tau |)^{1+\frac{\gamma }{4}}}{(1+\tau +r)^{1-2\delta _0-\gamma }} {\text {d}}x\,{\text {d}}\tau \right) ^{\frac{1}{2}}\\&\qquad \left( \int _T^t \frac{{\text {d}}\tau }{(1+\tau )^{1+\gamma }}\right) ^{\frac{1}{2}}\\&\qquad +\sum _{|J|\le |I|} \left( \int _{\{\tau \in [T,t], r-\tau< 0\}\cap {\mathcal {R}}} \frac{\left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) }{(1+\tau +r)^{1-2\delta _0-\gamma }(1+|r-\tau |)^{\frac{7\gamma }{4}}} {\text {d}}x\,{\text {d}}\tau \right) ^{\frac{1}{2}}\\&\qquad \left( \int _T^t \frac{{\text {d}}\tau }{(1+\tau )^{1+\gamma }}\right) ^{\frac{1}{2}}\\&\quad \lesssim T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|} \left( \int _{\{\tau \in [T,t], r-\tau \ge 0\}\cap {\mathcal {R}}} \left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) (1+|r-\tau |)^{\frac{5\gamma }{4}+2\delta _0} {\text {d}}x\,{\text {d}}\tau \right) ^{\frac{1}{2}} \\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|} \left( \int _{\{\tau \in [T,t], r-\tau < 0\}\cap {\mathcal {R}}} \frac{|{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2 }{(1+|r-\tau |)^{1+\frac{3\gamma }{4}-2\delta _0}} {\text {d}}x\,{\text {d}}\tau \right) ^{\frac{1}{2}} \\&\quad \lesssim \sum _{|J|\le |I|}T^{-\frac{\gamma }{2}}\left( \int _T^t \int _{ {\mathcal {R}}_\tau } \left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}.\nonumber \end{aligned}\\ \end{aligned}$$

(14.10)

We now turn to term I in (14.8). Notice that $\partial _q$ commutes with the projection to L. Hence,

$$\begin{aligned} |\partial _r ((\Gamma ^J h)_{LL})|\lesssim |\partial \Gamma ^J h|_{LL}+|{\bar{\partial }}\Gamma ^J h|. \end{aligned}$$

Therefore, we can apply the Hardy inequality in Proposition 11.6 with $\alpha =2-2\delta _0$, $\mu _1=\frac{7\gamma }{4}$ and $\mu _2=\frac{\gamma }{4}$ to obtain

$$\begin{aligned}&\sum _{|J|\le |I|}\int _T^t \left( \int _{{\mathcal {R}}_\tau } \frac{|\Gamma ^J h|_{LL}^2 w(r-\tau )}{(1+\tau +r)^{2-2\delta _0}(1+|r-\tau |)^{2+2\gamma }} {\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}\tau \nonumber \\&\quad \lesssim \sum _{|J|\le |I|}\int _T^t \left( \int _{{\mathcal {R}}_\tau } \frac{|\Gamma ^J h|_{LL}^2 w(r-\tau )}{(1+\tau +r)^{2-2\delta _0}(1+|r-\tau |)^{2+\frac{7\gamma }{4}}} {\text {d}}x\right) ^{\frac{1}{2}}\,{\text {d}}\tau \nonumber \\&\quad \lesssim \sum _{|J|\le |I|}\int _T^t \frac{\Vert v(U'({\mathcal {R}}))|\Gamma ^J h|_{LL}\Vert _{L^2({\mathbb {S}}^2(U'({\mathcal {R}}),\tau ))}}{(1+\tau )^{1-\delta _0}}{\text {d}}\tau \nonumber \\&\qquad +\sum _{|J|\le |I|} \int _T^t \left( \int _{{\mathcal {R}}_\tau } \frac{(|\partial \Gamma ^J h|_{LL}^2+|{\bar{\partial }}\Gamma ^J h|^2)w(r-\tau )}{(1+\tau +r)^{2-2\delta _0}(1+|r-\tau |)^{\frac{7\gamma }{4}}} {\text {d}}x\right) ^{\frac{1}{2}}{\text {d}}\tau \nonumber \\&\quad \lesssim \sum _{|J|\le |I|}\sup _{\tau \in [T,t]}(1+\tau )^{\delta _0}\Vert v(U'({\mathcal {R}}))|\Gamma ^J h|_{LL}\Vert _{L^2({\mathbb {S}}^2(U'({\mathcal {R}}),\tau ))}\nonumber \\&\qquad +\sum _{|J|\le |I|} \int _T^t \left( \int _{{\mathcal {R}}_\tau } \frac{(|\partial \Gamma ^J h|_{LL}^2+|{\bar{\partial }}\Gamma ^J h|^2)w(r-\tau )}{(1+\tau +r)^{2-2\delta _0}(1+|r-\tau |)^{\frac{7\gamma }{4}}} {\text {d}}x\right) ^{\frac{1}{2}}{\text {d}}\tau . \end{aligned}$$

(14.11)

Notice that in the first inequality above, we simply discard the extra $\frac{1}{(1+|r-\tau |)^{\frac{\gamma }{4}}}$ decay. Similarly, in the second inequality, we discard the extra decay in $1+|r-\tau |$ in the boundary term.

Clearly, the terms with $|{\bar{\partial }}\Gamma ^J h|$ in the last line of (14.11) can be handled by the estimate⁷³ (14.10). The other term in (14.11), i.e., the term with $|\partial \Gamma ^I h|_{LL}$, can be handled using Proposition 8.3, which implies that

$$\begin{aligned} \begin{aligned}&|\partial \Gamma ^I h|_{LL}\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}+\frac{\log (2+s)}{(1+s)(1+|q|)^\gamma }\sum _{|J|\le |I|}|\Gamma ^J h|+\frac{\log (2+s)}{1+s}\sum _{|J|\le |I|}|\partial \Gamma ^J h|\\&\qquad +\sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|+\sum _{|J|\le |I|}|{\bar{\partial }}\Gamma ^J h|+\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}+\frac{\log (2+s)}{(1+s)^{1-\delta _0}(1+|q|)^{\gamma +\delta _0}}\sum _{|J|\le |I|}|\Gamma ^J h|\\&\qquad +\frac{\log (2+s)(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}}{(1+s)^{1-\delta _0}}\sum _{|J|\le |I|}|\partial \Gamma ^J h|+\sum _{|J|\le |I|}|{\bar{\partial }}\Gamma ^J h|+\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|, \end{aligned} \end{aligned}$$

where in the last line we have used the bootstrap assumptions (6.2) and (6.5). Therefore, for $\delta _0$ satisfying (6.1), we have⁷⁴

$$\begin{aligned} \begin{aligned}&\frac{|\partial \Gamma ^I h|_{LL}}{(1+s)^{1-\delta _0}(1+|q|)^{\frac{7\gamma }{8}}}\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^{3-\delta _0}(1+|q|)^{\frac{7\gamma }{8}}w(q)^{\frac{\gamma }{1+2\gamma }}}+\frac{\log (2+s)}{(1+s)^{2-2\delta _0}(1+|q|)^{\frac{15\gamma }{8}+\delta _0}}\sum _{|J|\le |I|}|\Gamma ^J h|\\&\qquad +\frac{1}{(1+s)^{1+\frac{\gamma }{2}}}\sum _{|J|\le |I|}|\partial \Gamma ^J h|+\frac{1}{(1+s)^{1-\delta _0}(1+|q|)^{\frac{7\gamma }{8}}}\sum _{|J|\le |I|}|{\bar{\partial }}\Gamma ^J h|\\&\qquad +\frac{1}{(1+s)^{1-\delta _0}(1+|q|)^{\frac{7\gamma }{8}}}\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|\\&\quad \lesssim {\mathfrak {I}}_I+{\mathfrak {W}}_I+{\mathfrak {T}}_I+\tilde{{\mathfrak {L}}}_I+\frac{1}{(1+s)^{1-\delta _0}(1+|q|)^{\frac{7\gamma }{8}}}\sum _{|J|\le |I|}|{\bar{\partial }}\Gamma ^J h|. \end{aligned} \end{aligned}$$

Note that the last term, which can be bounded above by (14.9), can be dealt with by (14.10). Therefore, using Propositions 14.2, 14.3, 14.4, 14.5 and (14.10), we have⁷⁵

$$\begin{aligned} \begin{aligned}&\sum _{|J|\le |I|} \int _T^t \left( \int _{{\mathcal {R}}_\tau } \frac{|{\partial }\Gamma ^J h|_{LL}^2 w(r-\tau )}{(1+\tau +r)^{2-2\delta _0}(1+|r-\tau |)^{\frac{7 \gamma }{4}}} {\text {d}}x\right) ^{\frac{1}{2}}{\text {d}}\tau \\&\quad \lesssim \epsilon \log ^4(2+t)+T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\sup _{\tau \in [T,t]}\left( \Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}\right. \\&\qquad \left. +\Vert v(U'({\mathcal {R}}))|\Gamma ^J h|\Vert _{L^2({\mathbb {S}}^2(U'({\mathcal {R}}),\tau ))}\right) \\&\qquad +(1+t)^{\delta _0}\sum _{|J|\le |I|-1} \sup _{\tau \in [T,t]}\left( \Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}\right. \\&\qquad \left. +\Vert v(U'({\mathcal {R}}))|\Gamma ^J h|\Vert _{L^2({\mathbb {S}}^2(U'({\mathcal {R}}),\tau ))}\right) \\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\left( \int _T^t \int _{ {\mathcal {R}}_\tau } |{\bar{\partial }}\Gamma ^J h|^2 w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

Combining this with (14.8), (14.10) and (14.11) gives the desired bounds. $\square$

We gather all the bounds derived so far in this section to obtain the following proposition:

Proposition 14.7

The following bounds hold for $|I|\le N$ and $t>T>0$:

$$\begin{aligned} \begin{aligned}&\int _T^t \Vert ({\mathfrak {I}}_I+{\mathfrak {G}}_I+{\mathfrak {T}}_I+{\mathfrak {L}}_I+{\mathfrak {W}}_I+{\mathfrak {N}}_I) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )} {\text {d}}\tau \\&\quad \lesssim \epsilon \log ^4(2+t)+(1+t)^{\delta _0}\sum _{|J|\le |I|-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\left( \int _T^t \int _{ {\mathcal {R}}_\tau } \left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\\&\qquad +\sum _{|J|\le |I|}\sup _{\tau \in [T,t]}(1+\tau )^{\delta _0}\Vert v(U'({\mathcal {R}}))|\Gamma ^J h|\Vert _{L^2({\mathbb {S}}^2(U'({\mathcal {R}}),\tau ))}. \end{aligned} \end{aligned}$$

We end this section by proving an analogue of Proposition 14.7 for terms in the equation ${\widetilde{\Box }}_g(\Gamma ^I \beta )$. Recall from Proposition 10.1 that all of the terms are analogous to those in Proposition 9.15 with the important exception that there are no analogue of ${\mathfrak {B}}_I$ in Proposition 10.1. As a consequence, using exactly the same argument as that which leads to Proposition 14.7, we have the following estimate for $|{\widetilde{\Box }}_g(\Gamma ^I \beta )|$.

Proposition 14.8

The following bounds hold for $|I|\le N$ and $t>T>0$:

$$\begin{aligned} \begin{aligned}&\int _T^t \Vert |{\widetilde{\Box }}_g(\Gamma ^I\beta )| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )} {\text {d}}\tau \\&\quad \lesssim \epsilon \log ^4(2+t)+(1+t)^{\delta _0}\sum _{|J|\le |I|-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_\tau )}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\left( \int _T^t \int _{ {\mathcal {R}}_\tau } \left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\\&\qquad +\sum _{|J|\le |I|}\sup _{\tau \in [T,t]}(1+\tau )^{\delta _0}\Vert v(U'({\mathcal {R}}))|\Gamma ^J h|\Vert _{L^2({\mathbb {S}}^2(U'({\mathcal {R}}),\tau ))}. \end{aligned} \end{aligned}$$

15 Region Near Spacelike Infinity

In this section, we prove the energy estimates in the region ${\mathcal {R}}_2$ near spacelike infinity (see Fig. 1); the main result of the section is Proposition 15.2. We first need to control the bad term ${\mathfrak {B}}_I$ in Proposition 9.15, which has not been estimated in Proposition 14.7. The key observation, as we discussed in the Introduction, is that we can obtain a smallness constant for $U_2$ sufficiently negative.

Proposition 15.1

In the region ${\mathcal {R}}_2$, for $U_2<0$, the following bounds for ${\mathfrak {B}}_I$ hold for $|I|\le N$ and $t>T>0$:

$$\begin{aligned} \begin{aligned} \int _T^t \Vert {\mathfrak {B}}_I w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })} {\text {d}}\tau \lesssim&\max \left\{ \epsilon ^{\frac{1}{2}},\frac{1}{(1+|U_2|)^{\gamma }}\right\} \\&\times \sum _{|J|= |I|}\int _T^t \frac{\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })}}{1+\tau } {\text {d}}\tau . \end{aligned} \end{aligned}$$

Proof

Recall from (9.15) that

$$\begin{aligned} {\mathfrak {B}}_I= |\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}|\partial h|_{{\mathcal {T}}{\mathcal {U}}}+|\partial \Gamma ^I\beta ||\partial \beta |+\frac{|\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}+|\partial \Gamma ^I\beta |}{(1+s)(1+|q|)^{\gamma }}. \end{aligned}$$

By the bootstrap assumptions (6.4) and (6.9), we have $|\partial h|_{{\mathcal {T}}{\mathcal {U}}}+|\partial \beta |\le \frac{2\epsilon ^\frac{1}{2}}{(1+s)}.$ Also, in the region ${\mathcal {R}}_2$, the bound $\frac{1}{(1+s)(1+|q|)^{\gamma }}\le \frac{1}{(1+s)(1+|U_2|)^{\gamma }}$ holds. The conclusion follows from directly plugging in these bounds. $\square$

Using the energy estimates in Proposition 11.3 and controlling the error terms using Propositions 14.7 and 15.1, we get

Proposition 15.2

Let $0\le k\le N$. There exists $\epsilon _2\in (0,\epsilon _1]$ sufficiently small, $U_2<0$ sufficiently negative and $T_2>0$ sufficiently large such that the following estimate⁷⁶ holds in the region ${\mathcal {R}}_2$:

$$\begin{aligned} \begin{aligned} \sum _{|I|\le k}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^I h|+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })} \lesssim&C_T\,\epsilon (1+t)^{(2k+2)\delta _0}, \end{aligned} \end{aligned}$$

for $\epsilon <\epsilon _2$ and $t>T>T_2$. Moreover, on the boundary ${\mathcal {B}}_{U_2}$, the following estimates are verified:

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\left( \int _{{\mathcal {B}}_{U_2}\cap \{T\le \tau \le t\}}\left( |{\bar{\partial }}\Gamma ^I h|^2+|{\bar{\partial }}\Gamma ^I \beta |^2+\frac{|\partial \Gamma ^I h|^2+|\partial \Gamma ^I \beta |^2}{(1+t)^{\frac{\gamma }{4}+1}}\right) w(r-\tau )\,{\text {d}}x\right) ^{\frac{1}{2}}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+2)\delta _0}\nonumber \end{aligned}\\ \end{aligned}$$

(15.1)

and

$$\begin{aligned} \sum _{|I|\le k}\Vert v(U_2)|\Gamma ^I h|\Vert _{L^2({\mathbb {S}}^2(U_2,t))}\lesssim C_T\,\epsilon (1+t)^{(2k+2)\delta _0}. \end{aligned}$$

(15.2)

Proof

By Propositions 11.3, 13.2 and 14.7, for every choice of $U_2$, there exists $T'_2(U_2)$ sufficiently large such that the following estimate holds for $T>T'_2(U_2)$ with implicit constants in $\lesssim$ in particular independent⁷⁷ of $U_2$, T and $T'_2(U_2)$:

$$\begin{aligned}&\sup _{\tau \in [T,t]}\left( \int _{{\mathcal {R}}_{2,\tau }} \left( |\partial \Gamma ^I h|^2+|\partial \Gamma ^I \beta |^2\right) w(r-\tau )\,{\text {d}}x\right) ^{\frac{1}{2}}\nonumber \\&\qquad +\left( \int _{T}^{t}\int _{{\mathcal {R}}_{2,\tau }}\left( |{\bar{\partial }}\Gamma ^I h|^2+|{\bar{\partial }}\Gamma ^I \beta |^2\right) w'(r-\tau )\,{\text {d}}x\,{\text {d}}\tau \right) ^{\frac{1}{2}}\nonumber \\&\qquad +\left( \int _{{\mathcal {B}}_{U_2}\cap \{T\le \tau \le t\}}(|{\bar{\partial }}\Gamma ^I h|^2+|{\bar{\partial }}\Gamma ^I \beta |^2+\frac{|\partial \Gamma ^I h|^2+|\partial \Gamma ^I \beta |^2}{(1+t)^{\frac{\gamma }{4}+1}}) w(r-\tau )\,{\text {d}}x\right) ^{\frac{1}{2}}\nonumber \\&\quad \lesssim \left( \int _{{\mathcal {R}}_{2,T}} \left( |\partial \Gamma ^I h|^2+|\partial \Gamma ^I \beta |^2\right) w(r-T)\,{\text {d}}x\right) ^{\frac{1}{2}}\nonumber \\&\qquad +\left( \int _{T}^{t}\Vert \left( |{\widetilde{\Box }}_g(\Gamma ^I h)|+|{\widetilde{\Box }}_g(\Gamma ^I \beta )|\right) w^{\frac{1}{2}}\Vert _{L^2({\mathcal {R}}_{2,\tau })}\,{\text {d}}\tau \right) ^{\frac{1}{2}}\nonumber \\&\quad \lesssim C_T\,\epsilon \log ^4(2+t)+T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })}\nonumber \\&\qquad +(1+t)^{\delta _0}\sum _{|J|\le |I|-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })}\nonumber \\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\left( \int _T^t \int _{{\mathcal {R}}_{2,\tau }} \left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\nonumber \\&\qquad +\max \left\{ \epsilon ^{\frac{1}{2}},\frac{1}{(1+|U_2|)^{\gamma }}\right\} \sum _{|J|= |I|}\int _T^t \frac{\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })}}{1+\tau } {\text {d}}\tau . \end{aligned}$$

(15.3)

Notice that we have applied Proposition 14.7 with $U'({\mathcal {R}}_2)=-\infty$, i.e., there are no boundary terms on ${\mathcal {B}}_{U'({\mathcal {R}}_2)}$ when applying Proposition 14.7. We now sum (15.3) over all $|I|\le k$. For every $U_2$, there exists a large $T''_2(U_2)>T'_2(U_2)$ such that for $T>T''_2(U_2)$, the second and fourth terms can be absorbed into the left-hand side to get

$$\begin{aligned}&\sum _{|I|\le k}\left( \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })}\right. \nonumber \\&\qquad \left. +\left( \int _{T}^{t}\int _{{\mathcal {R}}_{2,\tau }}\left( |{\bar{\partial }}\Gamma ^I h|^2+|{\bar{\partial }}\Gamma ^I \beta |^2\right) w'(r-\tau )\,{\text {d}}x\,{\text {d}}\tau \right) ^{\frac{1}{2}}\right) \nonumber \\&\qquad +\sum _{|I|\le k}\left( \int _{{\mathcal {B}}_{U_2}\cap \{T\le \tau \le t\}}\left( |{\bar{\partial }}\Gamma ^I h|^2+|{\bar{\partial }}\Gamma ^I \beta |^2+\frac{|\partial \Gamma ^I h|^2+|\partial \Gamma ^I \beta |^2}{(1+t)^{\frac{\gamma }{4}+1}}\right) w(r-\tau )\,{\text {d}}x\right) ^{\frac{1}{2}}\nonumber \\&\quad \lesssim C_T\,\epsilon \log ^{4}(2+t)+(1+t)^{\delta _0}\sum _{|J|\le k-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })}\nonumber \\&\qquad +\max \left\{ \epsilon ^{\frac{1}{2}},\frac{1}{(1+|U_2|)^{\gamma }}\right\} \sum _{|J|= k}\int _T^t \frac{\Vert \left( |\partial \Gamma ^J h|+\Vert |\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })}}{1+\tau } {\text {d}}\tau .\nonumber \!\!\!\!\!\!\\ \end{aligned}$$

(15.4)

We now proceed to show by induction that by choosing $U_2$ and $\epsilon _2$ appropriately, and then choosing $T_2>T''_2(U_2)$, we have

$$\begin{aligned} \sum _{|I|\le k} \sup _{\tau \in [T,t]} \Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })}\lesssim C_T\,\epsilon (1+t)^{2(k+1)\delta _0}\qquad \end{aligned}$$

(15.5)

for every $k\le N$. To begin with the base case, notice that when $k=0$, the second term in (15.4) is absent. Therefore, for $\epsilon$ sufficiently small and $U_2$ sufficiently negative, we have by the Grönwall’s inequality that⁷⁸

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\sup _{\tau \in [T,t]}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })}\\&\quad \lesssim C_T\,\epsilon \log ^4(2+t)\exp \left( C_2\max \left\{ \epsilon ^{\frac{1}{2}},\frac{1}{(1+|U_2|)^{\gamma }}\right\} \int _T^t \frac{{\text {d}}\tau }{1+\tau }\right) \\&\quad \lesssim C_T\,\epsilon (1+t)^{\delta _0}\log ^4(2+t)\lesssim C_T\,\epsilon (1+t)^{2\delta _0}. \end{aligned} \end{aligned}$$

We now continue with the induction step by assuming that (15.5) holds with $k\le k_0-1$ for some $1\le k_0\le N$. Then using (15.4) again we have

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k_0+1)\delta _0}\\&\qquad +\max \left\{ \epsilon ^{\frac{1}{2}},\frac{1}{(1+|U_2|)^{\gamma }}\right\} \sum _{|J|= k}\int _T^t \frac{\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })}}{1+\tau } {\text {d}}\tau . \end{aligned} \end{aligned}$$

By Grönwall’s inequality, we obtain that for $\epsilon$ sufficiently small and $U_2$ sufficiently negative

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{2,\tau })}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k_0+1)\delta _0}\exp \left( C_2\max \left\{ \epsilon ^{\frac{1}{2}},\frac{1}{(1+|U_2|)^{\gamma }}\right\} \int _T^t \frac{{\text {d}}\tau }{1+\tau }\right) \\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k_0+2)\delta _0}. \end{aligned} \end{aligned}$$

This concludes the proof of (15.5). Returning to (15.4), we also get (15.1). Finally, (15.2) follows from the estimate (15.5) together with an application of the Hardy inequality in Proposition 11.6 with $\alpha =0$, $\mu _2=2\gamma$, $R_1=t-\frac{1}{(1+t)^{\frac{\gamma }{4}}}-U_2$ and $R_2=\infty$. $\square$

This concludes the estimates in the region ${\mathcal {R}}_2$. We now fix the parameter $U_2$ according to Proposition15.2.

16 Region Near Null Infinity

In this section, we prove energy estimates in the region ${\mathcal {R}}_3$, which is the region near null infinity but away from spacelike and timelike infinities (see Fig. 1). In this region, the background quantities $|\partial \Gamma ^I h_B|$ and $|\partial \Gamma ^I\phi _B|$ are only of size $\frac{C}{1+t}$, without any additional smallness as⁷⁹ in the regions ${\mathcal {R}}_2$ and ${\mathcal {R}}_4$. The term $\frac{C}{1+t}$ is barely non-integrable in time, and if one were to estimate the corresponding error term naively using Grönwall’s inequality, the energy would grow as $(1+t)^C$ and one will not be able to recover the bootstrap assumptions.

In order to handle these terms, we need to capture the reductive structure of the system of equations when proving energy estimates. In other words, we need to first prove energy estimates for the components of $\partial \Gamma ^I h$ for which the right-hand side does not have the bad terms alluded to above. We then use these estimates that we have already obtained to control the remaining components of $\partial \Gamma ^I h$, so that the energy would still grow only with a slow rate. This is reminiscent of the reductive structure that was used in [45, 46], although in [45, 46] it was only used for the $L^\infty$ estimate. In order to reveal this reductive structure for the energy estimates (as opposed to $L^\infty$ estimates), we need to commute ${\widetilde{\Box }}_g$ with the projections to $\mathbf{E}^\mu$. One of the key observations is that the $\frac{1}{r}|\partial \Gamma ^I h|$ terms that we generate in this commutation in fact contain only good derivatives, i.e., they are of the form $\frac{1}{r} |{\bar{\partial }}\Gamma ^I h|$ (see Proposition 16.1). As a consequence, all such terms obey sufficiently strong estimates (Proposition 16.4). We can then use this and the reductive structure to prove the desired energy estimates (Propositions 16.5, 16.6).

We now turn to the details. First, we have the following proposition, which contains the crucial observation that the most slowly decaying terms in the commutation of ${\widetilde{\Box }}_g$ with the projection to $\mathbf{E}^\mu$ in fact have good ${\bar{\partial }}$ derivatives:

Proposition 16.1

Given $\mathbf{E}^{\mu },\mathbf{E}^{\nu }\in \{L,{\underline{L}},E^1,E^2,E^3\}$, we have for every $(t,x)\in [0,\infty )\times {\mathbb {R}}^3$ that

$$\begin{aligned} |({\widetilde{\Box }}_g \Gamma ^I h_{\mu \nu })\mathbf{E}^{\mu }{} \mathbf{E}^{\nu }-{\widetilde{\Box }}_g ((\Gamma ^I h)_{\mu \nu }{} \mathbf{E}^{\mu }{} \mathbf{E}^{\nu })|\lesssim&\frac{1}{r} |{\bar{\partial }}\Gamma ^I h|+\frac{1}{r^2}|\Gamma ^I h|\\&+\frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}}{r(1+s)^{1-\delta _0}}|\partial \Gamma ^I h|. \end{aligned}$$

Proof

A direct calculation shows that

$$\begin{aligned} \begin{aligned}&({\widetilde{\Box }}_g \Gamma ^I h_{\mu \nu })\mathbf{E}^{\mu }{} \mathbf{E}^{\nu }-{\widetilde{\Box }}_g (\Gamma ^I h_{\mu \nu }{} \mathbf{E}^{\mu }{} \mathbf{E}^{\nu })\\&\quad =-2(g^{-1})^{\alpha \beta }(\Gamma ^I h_{\mu \nu })(\partial _\alpha \mathbf{E}^\mu )(\partial _\beta \mathbf{E}^\nu )\\&\qquad -\underbrace{4(g^{-1})^{\alpha \beta }\partial _\alpha (\Gamma ^I h_{\mu \nu })(\partial _\beta \mathbf{E}^\mu ) \mathbf{E}^\nu }_{=:\hbox {main\,term}}-2(\Gamma ^I h_{\mu \nu })({\widetilde{\Box }}_g \mathbf{E}^\mu ) \mathbf{E}^\nu . \end{aligned} \end{aligned}$$

(16.1)

Expressing the $\mathbf{E}^\mu$ in terms of the coordinate vector fields $\partial _\alpha$, we notice that the coefficients are either constant or take the form $\frac{x^i}{r}$. Therefore, we have

$$\begin{aligned} |\mathbf{E}|\lesssim 1,\quad |\partial \mathbf{E}|\lesssim \frac{1}{r},\quad |{\widetilde{\Box }}_g \mathbf{E}|\lesssim \frac{1}{r^2}. \end{aligned}$$

Therefore,

$$\begin{aligned} |-2(g^{-1})^{\alpha \beta }(\Gamma ^I h_{\mu \nu })(\partial _\alpha \mathbf{E}^\mu )(\partial _\beta \mathbf{E}^\nu )-2(\Gamma ^I h_{\mu \nu })({\widetilde{\Box }}_g \mathbf{E}^\mu ) \mathbf{E}^\nu |\lesssim \frac{1}{r^2}|\Gamma ^I h|.\nonumber \\ \end{aligned}$$

(16.2)

It thus remains to control the main term in (16.1) above. We now write $(g^{-1})^{\alpha \beta }=m^{\alpha \beta }+H^{\alpha \beta }$ so that in the main term, there is a contribution from $m^{\alpha \beta }$ and one from $H^{\alpha \beta }$. Recall that $m^{\alpha \beta }=-L^{(\alpha }{\underline{L}}^{\beta )}+\sum _{A=1}^3 E^A E^A$ and notice that we have $\partial _s \mathbf{E}^\mu =\partial _q \mathbf{E}^\mu =0$ for any $\mathbf{E}^\mu$. Therefore, in the contribution from $m^{\alpha \beta }$, there are no $\frac{1}{r}|\partial _q \Gamma ^I h|$ terms! On the other hand, the contribution from $H^{\alpha \beta }$ has more decay. More precisely,

$$\begin{aligned} \begin{aligned}&|-4(g^{-1})^{\alpha \beta }\partial _\alpha (\Gamma ^I h_{\mu \nu })(\partial _\beta \mathbf{E}^\mu ) \mathbf{E}^\nu |\\&\quad =|-4m^{\alpha \beta }\partial _\alpha (\Gamma ^I h_{\mu \nu })(\partial _\beta \mathbf{E}^\mu ) \mathbf{E}^\nu -4H^{\alpha \beta }\partial _\alpha (\Gamma ^I h_{\mu \nu })(\partial _\beta \mathbf{E}^\mu ) \mathbf{E}^\nu |\\&\quad =|-2\sum _{i,j=1}^3\left( \frac{x^i}{r}\partial _j(\Gamma ^I h_{\mu \nu })-\frac{x^j}{r}\partial _i(\Gamma ^I h_{\mu \nu })\right) \left( \frac{x^i}{r}\partial _j\mathbf{E}^\mu -\frac{x^j}{r}\partial _i\mathbf{E}^\mu \right) \mathbf{E}^\nu \\&\qquad -4H^{\alpha \beta }\partial _\alpha (\Gamma ^I h_{\mu \nu })(\partial _\beta \mathbf{E}^\mu ) \mathbf{E}^\nu |\\&\quad \lesssim \frac{1}{r}|{\bar{\partial }}\Gamma ^I h|+\frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}}{r(1+s)^{1-\delta _0}}|\partial \Gamma ^I h|,\nonumber \end{aligned}\\ \end{aligned}$$

(16.3)

where in the last line we have also used the bounds for |H| in Proposition 7.3 together with bootstrap assumption (6.5). Combining (16.1), (16.2) and (16.3) gives the conclusion of the proposition. $\square$

Remark 16.2

While Proposition 16.1 shows that the commutation of ${\widetilde{\Box }}_g$ and the projection to the $\mathbf{E}^\mu$ is favorable in the sense that the $\frac{1}{r} |\partial \Gamma ^I h|$ terms are absent, it seems that this is only useful in the region under consideration, but not in the regions near spacelike infinity or timelike infinity. As we will see below, the crucial fact for $|{{\bar{\partial }}}\Gamma ^I\phi |$ that we will use is that it obeys an $L^2_tL^2_x$ estimate. On the other hand, it is also important that we are only dealing with a region with finite q range, as otherwise the |q|-weights in the $L^2_tL^2_x$ estimate will not be sufficient to control this term.

Our next goal is to show that all the error terms in Proposition 16.1 arising from commutation with the projection to $\mathbf{E}^\mu$ can be controlled. In Region ${\mathcal {R}}_3$, if $T>2U_3$, then we have $t\lesssim r$ and therefore the term $\frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}}{r(1+s)^{1-\delta _0}}|\partial \Gamma ^I h|$ behaves better than the ${\mathfrak {T}}_I$ term. It can therefore be treated in the same manner as in Proposition 14.3. Let us summarize this as follows:

Proposition 16.3

For every $U_3>0 > U_{2}$, if $T>2U_3$, then the following estimate holds for all $|I|\le N$ and $t>T$:

$$\begin{aligned} \begin{aligned} \int _T^t \left\| \frac{(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}}{r(1+s)^{1-\delta _0}}|\partial \Gamma ^I h|w^{\frac{1}{2}}\right\| _{L^2_x({\mathcal {R}}_{3,\tau })}\,{\text {d}}\tau \lesssim T^{-\frac{\gamma }{2}}\sup _{\tau \in [T,t]}\Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}. \end{aligned} \end{aligned}$$

Proof

This follows from noting that the term can be dominated by ${\mathfrak {T}}_I$ and using the estimates in Proposition 14.3. $\square$

On the other hand, the other two error terms in Proposition 16.1 are not as good as the terms estimated in Sect. 14 and we need to crucially use the fact that we are localized in a bounded q region⁸⁰. More precisely, we have the following bounds for those terms:

Proposition 16.4

For every $U_3>0 > U_2$, if $T>2U_3$, then the following estimate holds for all $|I|\le N$ and $t>T$:

$$\begin{aligned} \begin{aligned}&\int _T^t \left( \underbrace{\Vert \frac{1}{r} |{\bar{\partial }}\Gamma ^I h|w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}}_{=:\hbox {I}}+\underbrace{\Vert \frac{1}{r^2}|\Gamma ^I h|w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}}_{=:\hbox {II}}\right) \,{\text {d}}\tau \\&\quad \lesssim T^{-\frac{1}{2}}\max \{|U_2|^{\frac{1}{2}},|U_3|^{\frac{1}{2}+\frac{\gamma }{4}}\}\left( \int _T^t\int _{{\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^I h|^2 w'(r-\tau ) {\text {d}}x\,{\text {d}}\tau \right) ^{\frac{1}{2}}\\&\qquad +T^{-1}\max \{|U_2|,|U_3|\}\\&\qquad \times \sup _{\tau \in [T,t]} \left( \Vert |\partial \Gamma ^I h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}+\Vert v(U_2) |\Gamma ^I h|\Vert _{L^2_x({\mathbb {S}}^2(U_2,\tau ))}\right) . \end{aligned} \end{aligned}$$

Proof

In the following, we will frequently use the easy observation that if $T>2U_3$, then we have $1+s\lesssim r$ in region ${\mathcal {R}}_3$. We first control the term I, which involves a good derivative of $\Gamma ^I h$:

$$\begin{aligned} \begin{aligned}&\int _T^t \Vert \frac{1}{r} |{\bar{\partial }}\Gamma ^I h|w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}{\text {d}}\tau \\&\quad \lesssim \max \{|U_2|^{\frac{1}{2}},|U_3|^{\frac{1}{2}+\frac{\gamma }{4}}\}\left( \int _T^t \frac{{\text {d}}\tau }{(1+s)^2}\right) ^{\frac{1}{2}} \left( \int _T^t\int _{{\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^I h|^2 w'(r-\tau ) {\text {d}}x\,{\text {d}}\tau \right) ^{\frac{1}{2}}\\&\quad \lesssim T^{-\frac{1}{2}}\max \{|U_2|^{\frac{1}{2}},|U_3|^{\frac{1}{2}+\frac{\gamma }{4}}\}\left( \int _T^t\int _{{\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^I h|^2 w'(r-\tau ) {\text {d}}x\,{\text {d}}\tau \right) ^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

Here, we have used that fact that $\frac{w(q)}{w'(q)}\lesssim {\left\{ \begin{array}{ll} 1+|q|,\quad \text{ if } q\ge 0\\ (1+|q|)^{1+\frac{\gamma }{2}},\quad \text{ if } q< 0 \end{array}\right. }$.

The term II in the statement of the proposition can be controlled using the Hardy inequality (Proposition 11.6) after losing appropriate powers of $|U_2|$ and $|U_3|$. More precisely, we apply Proposition 11.6 with $\alpha =\mu _1=0$, $\mu _2=2\gamma$ to get

$$\begin{aligned}&\int _T^t \Vert \frac{1}{r^2} |\Gamma ^I h|w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}{\text {d}}\tau \\&\quad \lesssim \int _T^t \left( \int _{{\mathcal {R}}_{3,\tau }\cap \{r-\tau \ge 0\}} \frac{|\Gamma ^I h|^2 (1+|r-\tau |)^{1+2\gamma }}{(1+s)^4} {\text {d}}x\right) ^{\frac{1}{2}}{\text {d}}\tau \\&\qquad +\int _T^t \left( \int _{{\mathcal {R}}_{3,\tau }\cap \{r-\tau< 0\}} \frac{|\Gamma ^I h|^2}{(1+s)^4} {\text {d}}x\right) ^{\frac{1}{2}}{\text {d}}\tau \\&\quad \lesssim |U_2|\int _T^t \left( \int _{{\mathcal {R}}_{3,\tau }\cap \{r-\tau \ge 0\}} \frac{|\Gamma ^I h|^2 }{(1+s)^4(1+|r-\tau |)^{1-2\gamma }} {\text {d}}x\right) ^{\frac{1}{2}}{\text {d}}\tau \\&\qquad +|U_3|\int _T^t \left( \int _{{\mathcal {R}}_{3,\tau }\cap \{r-\tau < 0\}} \frac{|\Gamma ^I h|^2}{(1+s)^4(1+|r-\tau |)^{2}} {\text {d}}x\right) ^{\frac{1}{2}}{\text {d}}\tau \\&\quad \lesssim \max \{|U_2|,|U_3|\}\left( \sup _{\tau \in [T,t]} \left( \int _{{\mathcal {R}}_{3,\tau }} |\partial \Gamma ^I h|^2 w(r-\tau ) {\text {d}}x\right) ^{\frac{1}{2}}\right) \left( \int _T^t \frac{{\text {d}}\tau }{(1+\tau )^2}\right) \\&\qquad +\max \left\{ |U_2|,|U_3|\right\} \left( \sup _{\tau \in [T,t]}\Vert v(U_2) |\Gamma ^I h|\Vert _{L^2({\mathbb {S}}^2(U_2,\tau ))}\right) \left( \int _T^t \frac{{\text {d}}\tau }{(1+\tau )^2}\right) \\&\quad \lesssim T^{-1}\max \{|U_2|,|U_3|\}\sup _{\tau \in [T,t]} \left( \Vert |\partial \Gamma ^I h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}+\Vert v(U_2) |\Gamma ^I h|\Vert _{L^2({\mathbb {S}}^2(U_2,\tau ))}\right) . \end{aligned}$$

$\square$

We now proceed to obtaining the energy estimates for h in this region. We first derive the estimates for $|\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}$. Recall from Proposition 9.18 that the right-hand side of the $({\widetilde{\Box }}_g\Gamma ^I h)_{{\mathcal {T}}{\mathcal {U}}}$ does not contain the ${\mathfrak {B}}_I$ term. Therefore, we have the following estimate for $|\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}$ in region ${\mathcal {R}}_3$:

Proposition 16.5

For every $U_3> 0 >U_2$, there exists $\epsilon '_3\in (0,\epsilon _2]$, $T'_3> T_2$ such that if $\epsilon \le \epsilon '_3$, $t>T> T'_3$ and $k\le N$, we have

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +\sum _{|I|\le k}\left( \int _{{\mathcal {B}}_{U_3}\cap \{T\le \tau \le t\}}\left( |{\bar{\partial }}\Gamma ^I \beta |^2+\frac{|\partial \Gamma ^I \beta |^2}{(1+t)^{\frac{\gamma }{4}+1}}\right) w(r-\tau ) \,{\text {d}}x\right) ^{\frac{1}{2}}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+3)\delta _0}+(1+t)^{\delta _0}\sum _{|J|\le k-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le k}\left( \sup _{\tau \in [T,t]}\Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}+\left( \int _T^t \int _{ {\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^J h|^2 w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\right) . \end{aligned} \end{aligned}$$

Proof

We first bound $|\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}$. Take $\mathbf{E}_1^\alpha \in {\mathcal {T}}$ and $\mathbf{E}_2^\alpha \in {\mathcal {U}}$. We apply Proposition 11.4 to $h_{\mu \nu }{} \mathbf{E}_1^\mu \mathbf{E}_2^\nu$. By Proposition 13.2 and (15.1) in Proposition 15.2, we know that for $|I|\le k$, the “initial data” terms, i.e., the first two terms on the right-hand side in Proposition 11.4, can be controlled by $C_T\,\epsilon (1+t)^{(2k+2)\delta _0}$. Therefore, by Proposition 11.4, for $|I|\le k$, we have

$$\begin{aligned} \begin{aligned}&\sup _{\tau \in [T,t]}\Vert |\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}} w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\quad \lesssim C_T \epsilon (1+t)^{(2k+2)\delta _0}+\left( \int _{T}^{t}\Vert |{\widetilde{\Box }}_g \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\,{\text {d}}\tau \right) ^{\frac{1}{2}}\\&\qquad +\left( \int _{T}^{t}\Vert \left( ({\widetilde{\Box }}_g \Gamma ^I h_{\mu \nu })\mathbf{E}^{\mu }{} \mathbf{E}^{\nu }-{\widetilde{\Box }}_g (\Gamma ^I h_{\mu \nu }{} \mathbf{E}^{\mu }\mathbf{E}^{\nu })\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\,{\text {d}}\tau \right) ^{\frac{1}{2}}.\nonumber \end{aligned}\\ \end{aligned}$$

(16.4)

The main observation is that $|{\widetilde{\Box }}_g \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}$ does not contain the ${\mathfrak {B}}_I$ term (see Proposition 9.18) and therefore, we can apply Proposition 14.7 to control the $|{\widetilde{\Box }}_g \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}$ term. Using Proposition 14.7 together with the bound (15.2) in Proposition 15.2 for $\sum _{|J|\le |I|}\Vert v(U'({\mathcal {R}}_3))|\Gamma ^J h|\Vert _{L^2({\mathbb {S}}^2(U'({\mathcal {R}}_3)))}$, we get

$$\begin{aligned} \begin{aligned}&\left( \int _{T}^{t}\Vert |{\widetilde{\Box }}_g \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}} w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\,{\text {d}}\tau \right) ^{\frac{1}{2}}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+3)\delta _0}+(1+t)^{\delta _0}\\&\qquad \times \sum _{|J|\le |I|-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\left( \int _T^t \int _{ {\mathcal {R}}_{3,\tau }} \left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}.\nonumber \end{aligned}\\ \end{aligned}$$

(16.5)

The final term in (16.4) can be controlled by combining the estimates in Propositions 16.1, 16.3 and 16.4, i.e., 

$$\begin{aligned}&\left( \int _{T}^{t}\Vert \left( ({\widetilde{\Box }}_g \Gamma ^I h_{\mu \nu })\mathbf{E}^{\mu }{} \mathbf{E}^{\nu }-{\widetilde{\Box }}_g (\Gamma ^I h_{\mu \nu }{} \mathbf{E}^{\mu }{} \mathbf{E}^{\nu })\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\,{\text {d}}\tau \right) ^{\frac{1}{2}}\nonumber \\&\quad \lesssim T^{-\frac{1}{2}}\max \{|U_2|^{\frac{1}{2}},|U_3|^{\frac{1}{2}+\frac{\gamma }{4}}\}(\int _T^t\int _{{\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^I h|^2w'(q) {\text {d}}x\,{\text {d}}\tau )^{\frac{1}{2}}\nonumber \\&\qquad +T^{-1}\max \{|U_2|,|U_3|\}\nonumber \\&\qquad \sup _{\tau \in [T,t]} \left( \Vert |\partial \Gamma ^I h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}+\Vert v(U_2) |\Gamma ^I h|\Vert _{L^2({\mathbb {S}}^2(U_2,\tau ))}\right) \nonumber \\&\qquad +T^{-\frac{\gamma }{2}}\sup _{\tau \in [T,t]}\Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\nonumber \\&\quad \lesssim T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\left( \sup _{\tau \in [T,t]}\Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\right. \nonumber \\&\qquad \left. +\left( \int _T^t \int _{ {\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^J h|^2 w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\right) , \end{aligned}$$

(16.6)

where in the last line we have chosen $T'_3$ to be sufficiently large depending on $|U_2|$ and $|U_3|$ so that for $T> T_3'$, it holds that $T^{-\frac{1}{2}}\max \{|U_2|^{\frac{1}{2}},|U_3|^{\frac{1}{2}+\frac{\gamma }{4}}\}+T^{-1}\max \{|U_2|,|U_3|\}\le T^{-\frac{\gamma }{2}}$.

Next, we control the scalar field. Since there are no bad terms in the equation for ${\widetilde{\Box }}_g \Gamma ^I \beta$, we apply Propositions 11.4, 13.2, 15.2 and 14.8 to obtain the following bound for $|I|\le k$:

$$\begin{aligned}&\sup _{\tau \in [T,t]}\Vert |\partial \Gamma ^I \beta | w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{3,\tau })}+\left( \int _T^t \int _{ {\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^I \beta |^2 w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\nonumber \\&\qquad +\left( \int _{{\mathcal {B}}_{U_3}\cap \{T\le \tau \le t\}}(|{\bar{\partial }}\Gamma ^I \beta |^2+\frac{|\partial \Gamma ^I \beta |^2}{(1+t)^{\frac{\gamma }{4}+1}})w(r-\tau ) \,{\text {d}}x\right) ^{\frac{1}{2}}\nonumber \\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+3)\delta _0}+(1+t)^{\delta _0}\sum _{|J|\le |I|-1}\nonumber \\&\qquad \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\nonumber \\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\nonumber \\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le |I|}\left( \int _T^t \int _{ {\mathcal {R}}_{3,\tau }} \left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}. \end{aligned}$$

(16.7)

Combining (16.4), (16.5), (16.6) and (16.7) and summing over $|I|\le k$, we get

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +\sum _{|I|\le k}\left( \int _T^t \int _{ {\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^I \beta |^2 w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\\&\qquad +\sum _{|I|\le k}\left( \int _{{\mathcal {B}}_{U_3}\cap \{T\le \tau \le t\}}\left( |{\bar{\partial }}\Gamma ^I \beta |^2+\frac{|\partial \Gamma ^I \beta |^2}{(1+t)^{\frac{\gamma }{4}+1}}\right) w(r-\tau ) \,{\text {d}}x\right) ^{\frac{1}{2}}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+3)\delta _0}+(1+t)^{\delta _0}\sum _{|J|\le k-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le k}\sup _{\tau \in [T,t]}\left\| \left( |\partial \Gamma ^J h|+\underbrace{|\partial \Gamma ^J \beta |}_{=:\hbox {I}}\right) w^{\frac{1}{2}}\right\| _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le k}\left( \int _T^t \int _{ {\mathcal {R}}_{3,\tau }} \left( |{\bar{\partial }}\Gamma ^J h|^2+\underbrace{|{\bar{\partial }}\Gamma ^J \beta |^2}_{=:\hbox {II}}\right) w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

Choosing $T_3'> T_2$ to be sufficiently large, we can then absorb the terms I and II to the left-hand side for $T> T'_3$ and obtain the desired conclusion. $\square$

In region ${\mathcal {R}}_3$, we can only use the naive estimate to control the ${\mathfrak {B}}_I$ term. Nevertheless, we make use of the fact that the estimates for ${\mathfrak {B}}_I$ depends only on $|\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}$ but not general components $|\partial \Gamma ^I h|$. We then apply the estimates for $|\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}$ from Proposition 16.5 which give us a smallness constant to close the estimates.

Proposition 16.6

For every $U_3>U_2$, there exists $\epsilon _3\in (0,\epsilon _2]$, $T_3> T_2$ such that if $\epsilon \le \epsilon _3$, $t>T> T_3$ and $k\le N$, we have

$$\begin{aligned} \begin{aligned} \sum _{|I|\le k}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^I h|+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\lesssim C_T\,\epsilon (1+t)^{(2k+4)\delta _0}. \end{aligned} \end{aligned}$$

(16.8)

Moreover, on the boundary ${\mathcal {B}}_{U_3}$, the following estimates are verified:

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\left( \int _{{\mathcal {B}}_{U_3}\cap \{T\le \tau \le t\}}(|{\bar{\partial }}\Gamma ^I h|^2+|{\bar{\partial }}\Gamma ^I \beta |^2+\frac{|\partial \Gamma ^I h|^2+|\partial \Gamma ^I \beta |^2}{(1+t)^{\frac{\gamma }{4}+1}})w(r-\tau ) \,{\text {d}}x\right) ^{\frac{1}{2}}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+4)\delta _0}\nonumber \end{aligned}\\ \end{aligned}$$

(16.9)

and

$$\begin{aligned} \sum _{|I|\le k}\Vert v(U_3)|\Gamma ^I h|\Vert _{L^2({\mathbb {S}}^2(U_3,t))}\lesssim C_T\,\epsilon (1+t)^{(2k+4)\delta _0}. \end{aligned}$$

(16.10)

Proof

Using the bootstrap assumptions (6.4) and (6.9), we can bound ${\mathfrak {B}}_I$ as follows:

$$\begin{aligned} \begin{aligned} \int _T^t\Vert {\mathfrak {B}}_I w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}{\text {d}}\tau \lesssim \int _T^t\frac{\Vert \left( |\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}}{1+\tau }{\text {d}}\tau . \end{aligned} \end{aligned}$$

Applying Proposition 16.5, we then have, for $|I|\le k$,

$$\begin{aligned} \begin{aligned}&\int _T^t\Vert {\mathfrak {B}}_I w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}{\text {d}}\tau \\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+3)\delta _0}+(1+t)^{\delta _0}\sum _{|J|\le k-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\quad +T^{-\frac{\gamma }{2}}\sum _{|J|\le k}\int _T^t \frac{\left( \sup _{\tau \in [T,t']}\Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}+\left( \int _T^{t'} \int _{ {\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^J h|^2 w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\right) }{1+t'}\, {\text {d}}t'.\nonumber \end{aligned}\!\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(16.11)

By Proposition 11.4 and the bounds in Proposition 13.2 and (15.1) in Proposition 15.2, we have

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\left( \sup _{\tau \in [T,t]}\Vert |\partial \Gamma ^I h| w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{3,\tau })}+\left( \int _T^t \int _{ {\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^J h|^2 w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\right) \\&\qquad +\sum _{|I|\le k}\left( \int _{{\mathcal {B}}_{U_3}\cap \{T\le \tau \le t\}}\left( |{\bar{\partial }}\Gamma ^I h|^2+\frac{|\partial \Gamma ^I h|^2}{(1+t)^{\frac{\gamma }{4}+1}}\right) w(r-\tau ) \,{\text {d}}x\right) ^{\frac{1}{2}}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+3)\delta _0}+\sum _{|I|\le k}\left( \int _{T}^{t}\Vert |{\widetilde{\Box }}_g(\Gamma ^I h)|w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\,{\text {d}}\tau \right) ^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

Now $|{\widetilde{\Box }}_g(\Gamma ^I h)|$ contains the term ${\mathfrak {B}}_I$ together with the terms in Proposition 14.7. We bound the ${\mathfrak {B}}_I$ term by combining (16.11) and the bounds from Proposition 16.5. The remaining terms can be estimated using Proposition 14.7. Therefore, we have

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\left( \sup _{\tau \in [T,t]}\Vert |\partial \Gamma ^I h| w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{3,\tau })}+\left( \int _T^t \int _{ {\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^J h|^2 w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\right) \\&\qquad +\sum _{|I|\le k}\left( \int _{{\mathcal {B}}_{U_3}\cap \{T\le \tau \le t\}}\left( |{\bar{\partial }}\Gamma ^I h|^2+\frac{|\partial \Gamma ^I h|^2}{(1+t)^{\frac{\gamma }{4}+1}}\right) w(r-\tau ) \,{\text {d}}x\right) ^{\frac{1}{2}}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+3)\delta _0}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le k}\left( \sup _{\tau \in [T,t]}\Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}+\left( \int _T^t \int _{ {\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^J h|^2 w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\right) \\&\qquad +(1+t)^{\delta _0}\sum _{|J|\le k-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le k}\int _T^t \frac{\left( \sup _{\tau \in [T,t']}\Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}+\left( \int _T^{t'} \int _{ {\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^J h|^2 w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\right) }{1+t'}\, {\text {d}}t'\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+3)\delta _0}+(1+t)^{\delta _0}\sum _{|J|\le k-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +T^{-\frac{\gamma }{2}}\sum _{|J|\le k}\int _T^t \frac{\left( \sup _{\tau \in [T,t']}\Vert |\partial \Gamma ^J h| w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}+\left( \int _T^{t'} \int _{ {\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^J h|^2 w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\right) }{1+t'}\, {\text {d}}t',\nonumber \end{aligned}\!\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(16.12)

where the last step is achieved by choosing $T_3>T_2$ to be sufficiently large so that for $T>T_3$, we can absorb the terms to the left-hand side. Applying Grönwall’s inequality to (16.12) gives⁸¹

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\left( \sup _{\tau \in [T,t]}\Vert |\partial \Gamma ^I h| w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{3,\tau })}+\left( \int _T^t \int _{ {\mathcal {R}}_{3,\tau }} |{\bar{\partial }}\Gamma ^J h|^2 w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\right) \\&\qquad +\sum _{|I|\le k}\left( \int _{{\mathcal {B}}_{U_3}\cap \{T\le \tau \le t\}}\left( |{\bar{\partial }}\Gamma ^I h|^2+\frac{|\partial \Gamma ^I h|^2}{(1+t)^{\frac{\gamma }{4}+1}}\right) w(r-\tau ) \,{\text {d}}x\right) ^{\frac{1}{2}}\\&\quad \lesssim \left( C_T\,\epsilon (1+t)^{(2k+3)\delta _0}+(1+t)^{\delta _0}\sum _{|J|\le k-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\right) \\&\qquad \times \exp (C_3T^{-\frac{\gamma }{2}} \log (2+t))\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+4)\delta _0}+(1+t)^{2\delta _0}\sum _{|J|\le k-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })},\nonumber \end{aligned}\!\!\!\!\!\!\!\\ \end{aligned}$$

(16.13)

for $T_3>T_2$ chosen to be sufficiently large. Combining (16.13) with Proposition 16.5 gives

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^I h|+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +\sum _{|I|\le k}\left( \int _{{\mathcal {B}}_{U_3}\cap \{T\le \tau \le t\}}\left( |{\bar{\partial }}\Gamma ^I h|^2+\frac{|\partial \Gamma ^I h|^2}{(1+t)^{\frac{\gamma }{4}+1}}\right) w(r-\tau ) \,{\text {d}}x\right) ^{\frac{1}{2}}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+4)\delta _0}+(1+t)^{2\delta _0}\sum _{|J|\le k-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}, \end{aligned} \end{aligned}$$

A simple induction in k as⁸² in the proof of Proposition 15.2 then allows us to conclude that

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^I h|+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +\sum _{|I|\le k}\left( \int _{{\mathcal {B}}_{U_3}\cap \{T\le \tau \le t\}}\left( |{\bar{\partial }}\Gamma ^I h|^2+\frac{|\partial \Gamma ^I h|^2}{(1+t)^{\frac{\gamma }{4}+1}}\right) w(r-\tau ) \,{\text {d}}x\right) ^{\frac{1}{2}}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+4)\delta _0}.\nonumber \end{aligned}\\ \end{aligned}$$

(16.14)

This proves (16.8) and the estimates for $\sum _{|I|\le k}|\partial \Gamma ^I h|$ in (16.9). To obtain the estimates for $\sum _{|I|\le k}|\partial \Gamma ^I \beta |$ in (16.9), we combine the estimates from Proposition 16.5, (16.13) and (16.14). Finally, (16.10) follows from the estimate (16.14) together with the Hardy inequality in Proposition 11.6 with $\alpha =\mu _1=0$, $\mu _2=2\gamma$, $R_1=t-\frac{1}{(1+t)^{\frac{\gamma }{4}}}-U_3$ and $R_2=t-\frac{1}{(1+t)^{\frac{\gamma }{4}}}-U_2$. $\square$

This concludes the estimates in the region ${\mathcal {R}}_3$. Notice that the parameter $U_3$ that is used to define the region ${\mathcal {R}}_3$ is not yet chosen. This will be chosen in Sect. 17. In particular, it is important that Proposition 16.6 holds for every $U_3>U_2$.

17 Region Near Timelike Infinity

In this section, we prove the energy estimates for the region near timelike infinity, i.e., the region ${\mathcal {R}}_4$ in Fig. 1. This will then conclude the proof of the energy estimates in all regions of the spacetime. In fact, the region ${\mathcal {R}}_4$ is treated in a manner analogous to the region ${\mathcal {R}}_2$ (see Sect. 15), except that we now have to choose $U_3$ to be large and positive instead of negative and we pick up extra boundary terms from region ${\mathcal {R}}_3$.

As in Sect. 15, we begin with the estimate for ${\mathfrak {B}}_I$.

Proposition 17.1

In the region ${\mathcal {R}}_4$, for $U_3>0$, the following bounds for ${\mathfrak {B}}_I$ hold for $|I|\le N$ and for $t>T$:

$$\begin{aligned} \begin{aligned}&\int _T^t \Vert {\mathfrak {B}}_I w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{4,\tau })} {\text {d}}\tau \\&\quad \lesssim \max \left\{ \epsilon ^{\frac{1}{2}},\frac{1}{(1+|U_3|)^{\gamma }}\right\} \sum _{|J|= |I|}\int _T^t \frac{\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{4,\tau })}}{1+\tau } {\text {d}}\tau . \end{aligned} \end{aligned}$$

Proof

The proof is completely analogous to Proposition 15.1 except that we now use that we are in the region ${\mathcal {R}}_4$ and obtain smallness using the parameter $U_3$. $\square$

We then prove the energy estimates in the region ${\mathcal {R}}_4$ in an analogous manner as Proposition 15.2:

Proposition 17.2

There exists $U_3>0$ sufficiently large, $T_4>T_3$ and $\epsilon _4\in (0,\epsilon _3]$ such that

$$\begin{aligned} \begin{aligned} \sum _{|I|\le k}\sup _{\tau \in [T,t]} \Vert \left( |\partial \Gamma ^I h|+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{4,\tau })}\lesssim C_T\epsilon (1+t)^{(2k+6)\delta _0} \end{aligned} \end{aligned}$$

for $t> T> T_4$, $\epsilon \in (0,\epsilon _4]$ and $k\le N$.

Proof

We apply the energy estimates in Proposition 11.5. Using Proposition 13.2 and the bound (16.9), the first two terms on the right-hand side of Proposition 11.5 are bounded by $C_T\epsilon (1+t)^{(2k+4)\delta _0}$. Therefore, we have

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^I h|+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{4,\tau })}\\&\qquad +\sum _{|I|\le k}\left( \int _T^t \int _{ {\mathcal {R}}_{4,\tau }} \left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+4)\delta _0}+\sum _{|I|\le k}\left( \int _{T}^{t}\Vert |{\widetilde{\Box }}_g(\Gamma ^I h)|w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{4,\tau })}\,{\text {d}}\tau \right) ^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

To control $|{\widetilde{\Box }}_g(\Gamma ^I h)|$, we use Proposition 17.1 to bound the ${\mathfrak {B}}_I$ term and use Proposition 14.7 to estimate the remaining terms. More precisely, we have

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^I h|+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{4,\tau })}\\&\qquad +\sum _{|I|\le k}\left( \int _T^t \int _{ {\mathcal {R}}_{4,\tau }} \left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+5)\delta _0}+(1+t)^{\delta _0}\sum _{|J|\le k-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +\underbrace{T^{-\frac{\gamma }{2}}\sum _{|J|\le k}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}}_{=:\hbox {I}}\\&\qquad +\underbrace{T^{-\frac{\gamma }{2}}\sum _{|J|\le k}\left( \int _T^t \int _{ {\mathcal {R}}_{3,\tau }} \left( |{\bar{\partial }}\Gamma ^J h|^2+|{\bar{\partial }}\Gamma ^J \beta |^2\right) w'(r-\tau ) {\text {d}}x\, {\text {d}}\tau \right) ^{\frac{1}{2}}}_{=:\hbox {II}}\\&\qquad +\max \left\{ \epsilon ^{\frac{1}{2}},\frac{1}{(1+|U_3|)^{\gamma }}\right\} \sum _{|J|\le k}\int _T^t \frac{\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{4,\tau })}}{1+\tau } {\text {d}}\tau \\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k+5)\delta _0}+(1+t)^{\delta _0}\sum _{|J|\le k-1} \sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{3,\tau })}\\&\qquad +\max \left\{ \epsilon ^{\frac{1}{2}},\frac{1}{(1+|U_3|)^{\gamma }}\right\} \sum _{|J|\le k}\int _T^t \frac{\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{4,\tau })}}{1+\tau } {\text {d}}\tau ,\nonumber \end{aligned}\!\!\!\!\!\!\\ \end{aligned}$$

(17.1)

where in the last line we have used that we can choose $T_4'$ to be sufficiently large such that whenever $T> T_4'$, the terms I and II can be absorbed to the left-hand side. We now proceed to an induction argument in k to prove the proposition. First, for $k=0$, (17.1) gives⁸³

$$\begin{aligned} \begin{aligned}&\sup _{\tau \in [T,t]}\Vert \left( |\partial h|+|\partial \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{4,\tau })}\\&\quad \lesssim C_T\,\epsilon (1+t)^{5\delta _0}+\max \left\{ \epsilon ^{\frac{1}{2}},\frac{1}{(1+|U_3|)^{\gamma }}\right\} \int _T^t \frac{\Vert \left( |\partial h|+|\partial \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{4,\tau })}}{1+\tau } {\text {d}}\tau \\&\quad \lesssim C_T\,\epsilon (1+t)^{5\delta _0}\exp \left( C_4\max \left\{ \epsilon ^{\frac{1}{2}},\frac{1}{(1+|U_3|)^{\gamma }}\right\} \int _T^t \frac{{\text {d}}\tau }{1+\tau }\right) \lesssim \epsilon (1+t)^{6\delta _0}, \end{aligned} \end{aligned}$$

using Grönwall’s inequality, as long as $U_3$ is sufficiently large and $\epsilon _4$ is sufficiently small. Now assume that for some $k_0\ge 1$, we have

$$\begin{aligned} \sum _{|I|\le k_0-1}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^I h|+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{4,\tau })}\lesssim \epsilon (1+t)^{(2(k_0-1)+6)\delta _0}.\nonumber \\ \end{aligned}$$

(17.2)

Then, by (17.1) and (17.2), we have

$$\begin{aligned} \begin{aligned}&\sum _{|I|\le k_0}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^I h|+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{4,\tau })}\\&\quad \lesssim C_T\,\epsilon (1+t)^{(2k_0+5)\delta _0}\\&\qquad +\max \left\{ \epsilon ^{\frac{1}{2}},\frac{1}{(1+|U_3|)^{\gamma }}\right\} \sum _{|J|\le k_0}\int _T^t \frac{\Vert \left( |\partial \Gamma ^J h|+|\partial \Gamma ^J \beta |\right) w^{\frac{1}{2}}\Vert _{L^2_x({\mathcal {R}}_{4,\tau })}}{1+\tau } {\text {d}}\tau . \end{aligned} \end{aligned}$$

For $U_3$ sufficiently large and $\epsilon _4$ sufficiently small, Grönwall’s inequality implies

$$\begin{aligned} \sum _{|I|\le k_0}\sup _{\tau \in [T,t]}\Vert \left( |\partial \Gamma ^I h|+|\partial \Gamma ^I \beta |\right) w^{\frac{1}{2}} \Vert _{L^2_x({\mathcal {R}}_{4,\tau })}\lesssim C_T\,\epsilon (1+t)^{(2k_0+6)\delta _0}. \end{aligned}$$

This concludes the induction step. Once we have fixed $U_3$, we then choose $T_4> \max \{T_4', T_3\}$ sufficiently large. This then concludes the proof of the proposition. $\square$

This also concludes the proof of energy estimates in all regions of the spacetime. At this point, we fix $U_3$ and $T>T_4$ according to Proposition 17.2. Since T is fixed, from now on, we allow the implicit constant in $\lesssim$ to depend on T.

We end this section by summarizing the energy estimates that have been proven:

Theorem 17.3

For $\epsilon _4>0$ as in Proposition 17.2, the following estimate holds⁸⁴ for all $t\ge 0$ and for all $\epsilon \in (0,\epsilon _4]$:

$$\begin{aligned} \sum _{|I|\le N}\left( \sup _{\tau \in [0,t]}\int _{\Sigma _\tau } \left( |\partial \Gamma ^I h|^2+|\partial \Gamma ^I \beta |^2\right) (\tau ,x)\, w(q) \,{\text {d}}x\right) ^{\frac{1}{2}}\lesssim \epsilon (1+t)^{(2N+6)\delta _0},\nonumber \\ \end{aligned}$$

(17.3)

Proof

Combine the estimates in Propositions 13.2, 15.2, 16.6 and 17.2. $\square$

18 Recovering the Bootstrap Assumptions

Our main goal in this section is to show that the energy bound (17.3) implies decay estimates that in particular improve the bootstrap assumptions (6.2)–(6.6) and (6.7)–(6.9) (see Proposition 18.14).

As a preliminary step, we need a lemma which allows us to control in a pointwise fashion any function by its derivative via integrating along constant⁸⁵$(s,\omega )$ curves. We will repeatedly use this lemma below.

Lemma 18.1

Let f(q) be a positive function such that⁸⁶$f(q)\sim (1+|q|)^{\beta }$ for $\beta >1$ if $q\ge 0$ and $f(q)\sim (1+|q|)^\sigma$ for $\sigma < 1$ if $q<0$. Also let $\alpha >0$ and k(s) be a positive function of s such that $|k(s)|\le (1+s)^{\alpha }$. Then, for every sufficiently regular scalar function $\xi :[0,\infty )\times {\mathbb {R}}^3\rightarrow {\mathbb {R}}$ and for $t\ge 0$, we have

$$\begin{aligned} \begin{aligned}&\sup _{x}k(t+r)(1+|r-t|)^{-1}f(r-t)|\xi |(t,x)\\&\quad \lesssim \sup _x (1+r)^{-1+\alpha +\beta }|\xi |(0,x)+\sup _{\begin{array}{c} \tau \in [0, t]\\ x\in {\mathbb {R}}^3 \end{array}}k(\tau +r) f(r-\tau )|\partial _q \xi |(\tau ,x). \end{aligned} \end{aligned}$$

Proof

Since $\beta >1$, $f(q)^{-1}$ is integrable for $q\ge 0$ and moreover

$$\begin{aligned} \int _q^{\infty } f(q')^{-1}\,\hbox {d}q'\sim f(q)^{-1}(1+|q|). \end{aligned}$$

(18.1)

The lemma then follows from integrating $\partial _q \xi$ along curves with constant $(s,\omega )$ in the $-\partial _q$ direction, i.e., for every fixed (t, x), we have

$$\begin{aligned} \begin{aligned}&k(t+|x|)|\xi |(t,x)\\&\quad \le k(t+|x|)|\xi |(0,x+t\tfrac{x}{|x|}) \\&\qquad +k(t+|x|)\int _{|x|-t}^{\infty }\sup _{\begin{array}{c} \tau \in [0, t]\\ x'\in \{x'\in {\mathbb {R}}^3:\tau +|x'|=t+|x|,\,|x'|-\tau =q'\} \end{array}}|\partial _q \xi |(\tau ,x') \, \hbox {d}q' \\&\quad \le k(t+|x|)|\xi |\left( 0,x+t\tfrac{x}{|x|}\right) \\&\qquad +\sup _{\begin{array}{c} \tau \in [0, t]\\ x'\in \{x'\in {\mathbb {R}}^3:\tau +|x'|=t+|x|\} \end{array}}k(\tau +|x'|) f(|x'|-\tau )|\partial _q \xi |(\tau ,x')\int _{r-t}^{\infty }f(q')^{-1} \, \hbox {d}q' \end{aligned} \end{aligned}$$

and using (18.1). $\square$

We now begin the proof of the decay estimates. First, as an immediate consequence of (17.3) and the Klainerman–Sobolev inequality (Proposition 11.8), we have:

Proposition 18.2

The energy bound (17.3) implies that

$$\begin{aligned}&\sum _{|I|\le N-3}(1+s)^{1-(2N+6) \delta _0}(1+|q|)^{\frac{1}{2}}w(q)^{\frac{1}{2}}(|\partial \Gamma ^I h|+|\partial \Gamma ^I \beta |)(t,x)\lesssim \epsilon , \nonumber \\\end{aligned}$$

(18.2)

$$\begin{aligned}&\sum _{|I|\le N-3}(1+s)^{1-(2N+6) \delta _0}(1+|q|)^{-\frac{1}{2}}w(q)^{\frac{1}{2}}(|\Gamma ^I h|+|\Gamma ^I \beta |)(t,x)\lesssim \epsilon , \nonumber \\\end{aligned}$$

(18.3)

$$\begin{aligned}&\sum _{|I|\le N-4}(1+s)^{2-(2N+6) \delta _0}(1+|q|)^{-\frac{1}{2}}w(q)^{\frac{1}{2}}(|{{\bar{\partial }}}\Gamma ^I h|+|{{\bar{\partial }}}\Gamma ^I \beta |)(t,x)\lesssim \epsilon .\nonumber \\ \end{aligned}$$

(18.4)

Proof

(18.2) is a direct consequence of Proposition 11.8 and (17.3). (18.3) follows from applying Lemma 18.1 with $k(s)=(1+s)^{1-(2N+6)\delta _0}$ and $f(q)=(1+|q|)^{\frac{1}{2}}w(q)^{\frac{1}{2}}$. Notice in particular that the term on $\{t=0\}$ can be controlled thanks to Remark 5.4. Finally, (18.4) is a direct consequence of (18.3) and Proposition 7.1. $\square$

Observe that the decay estimates in Proposition 18.2 alone are insufficient to recover the bootstrap assumptions (6.2), (6.3), (6.5), (6.7), (6.8) and (6.9). We therefore need to combine them with Propositions 11.10 and 11.11 to prove stronger decay estimates.

Recall from Proposition 11.10 that $\varpi (q)$ is a weight function defined by⁸⁷

$$\begin{aligned} \varpi (q):=(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}. \end{aligned}$$

(18.5)

Define

$$\begin{aligned} \pi _k(t):=\sum _{|I|\le k}\sup _{\begin{array}{c} \tau \in [0, t]\\ x\in {\mathbb {R}}^3 \end{array}} (1+\tau +r)\varpi (r-\tau )\left( |\partial \Gamma ^I h|+|\partial \Gamma ^I \beta |\right) (\tau ,x). \end{aligned}$$

(18.6)

We will also use the notation that $\pi _{-k}=0$ if $-k<0$. Define also the notation $\sigma _k(t)$ in a similar way as $\pi _k(t)$, but keeps track only of the ${\mathcal {T}}{\mathcal {U}}$ components of $\Gamma ^I h$ and the derivative of the scalar field:

$$\begin{aligned} \sigma _k(t):=\sum _{|I|\le k}\sup _{\begin{array}{c} \tau \in [0, t]\\ x\in {\mathbb {R}}^3 \end{array}} (1+\tau +r)\varpi (r-\tau )\left( |\partial \Gamma ^I h|_{{\mathcal {T}}{\mathcal {U}}}+|\partial \Gamma ^I \beta |\right) (\tau ,x).\nonumber \\ \end{aligned}$$

(18.7)

We now proceed to control (18.6) and (18.7). We first need the following proposition, which combines Propositions 11.10 and 11.11 with the decay bounds we have obtained in Proposition 18.2.

Proposition 18.3

The following estimates hold for $|I|\le \lfloor \frac{N}{2}\rfloor +1$:

$$\begin{aligned} \begin{aligned} \sup _x(1+t)\varpi (q)|\partial \Gamma ^I h(t,x)| \lesssim&\epsilon +\int _0^t (1+\tau )\Vert \varpi (r-\tau )|{\widetilde{\Box }}_g (\Gamma ^I h)|(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \sup _x(1+t)\varpi (q)|\partial \Gamma ^I h(t,x)|_{{\mathcal {T}}{\mathcal {U}}} \lesssim&\epsilon +\int _0^t (1+\tau )\Vert \varpi (r-\tau )|{\widetilde{\Box }}_g (\Gamma ^I h)|_{{\mathcal {T}}{\mathcal {U}}}(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \sup _x(1+t)\varpi (q)|\partial \Gamma ^I \beta (t,x)| \lesssim&\epsilon +\int _0^t (1+\tau )\Vert \varpi (r-\tau )|{\widetilde{\Box }}_g (\Gamma ^I \beta )|(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau . \end{aligned} \end{aligned}$$

Proof

By Propositions 11.10 and 11.11, in order to show the desired estimates it suffices to show that

$$\begin{aligned} \sup _{0\le \tau \le \infty }\sum _{|J|\le |I|+1}\left( \Vert \varpi (r-\tau )\Gamma ^J h(\tau ,\cdot )\Vert _{L^\infty }+\Vert \varpi (r-\tau )\Gamma ^J \beta (\tau ,\cdot )\Vert _{L^\infty }\right) \lesssim \epsilon \nonumber \\ \end{aligned}$$

(18.8)

and

$$\begin{aligned}&\sum _{|J|\le |I|+2}\int _0^\infty (1+\tau )^{-1}\left( \Vert \varpi (r-\tau )\Gamma ^J h(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}\right. \nonumber \\&\qquad \left. +\Vert \varpi (r-\tau )\Gamma ^J \beta (\tau ,\cdot )\Vert _{L^\infty (D_\tau )}\right) {\text {d}}\tau \lesssim \epsilon .\nonumber \\ \end{aligned}$$

(18.9)

Since $N\ge 11$, we have $\lfloor \frac{N}{2}\rfloor +3\le N-3$. Therefore, by (18.3) in Proposition 18.2, (18.8) and (18.9) both hold, since $\delta _0$ satisfy (6.1). $\square$

Using Proposition 18.3, we can obtain the required pointwise bounds by estimating ${\widetilde{\Box }}_g \Gamma ^I h$ and ${\widetilde{\Box }}_g \Gamma ^I \beta$. We now control the contributions from each of the terms in Propositions 9.15 and 10.1. The bounds for ${\mathfrak {I}}_I$, ${\mathfrak {T}}_I$, ${\mathfrak {L}}_I$, ${\mathfrak {W}}_I$ and ${\mathfrak {B}}_I$ (and their $^{(\phi )}$-counterparts) are relatively straightforward, and we will begin with them, starting with the inhomogeneous terms ${\mathfrak {I}}_I$ and ${\mathfrak {I}}_I^{(\phi )}$:

Proposition 18.4

The following estimate holds for ${\mathfrak {I}}_I$ and ${\mathfrak {I}}_I^{(\phi )}$ for $|I|\le \lfloor \frac{N}{2}\rfloor +1$:

$$\begin{aligned} \begin{aligned} \int _0^t (1+\tau )\Vert \varpi (r-\tau )({\mathfrak {I}}_I+{\mathfrak {I}}_I^{(\phi )})(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \lesssim {\left\{ \begin{array}{ll} \epsilon &{} \text{ if } |I|=0\\ \epsilon \log ^3(2+t) &{}\text{ if } |I|\ge 1. \end{array}\right. } \end{aligned} \end{aligned}$$

Proof

For $|I|=0$ (recall the better bounds that we have for ${\mathfrak {I}}_0$ and ${\mathfrak {I}}_0^{(\phi )}$ in Propositions 9.15 and 10.1), we have

$$\begin{aligned} \begin{aligned}&\int _0^t (1+\tau )\Vert \varpi (r-\tau )({\mathfrak {I}}_0+{\mathfrak {I}}_0^{(\phi )})(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \\&\quad \lesssim \int _0^t (1+\tau )\sup _x\frac{\epsilon \varpi (r-\tau )\log ^2(2+\tau )}{(1+\tau )^{2+\frac{\gamma }{2}}(1+|r-\tau |)^{\frac{1}{2}-\frac{\gamma }{2}-\delta _0}w(r-\tau )^{\frac{1}{2}}}\, {\text {d}}\tau \\&\quad \lesssim \int _0^t \frac{\epsilon \log ^2(2+\tau )}{(1+\tau )^{1+\frac{\gamma }{2}-\frac{\gamma }{4}-\delta _0}}\, {\text {d}}\tau \lesssim \epsilon , \end{aligned} \end{aligned}$$

as long as $\delta _0<\frac{\gamma }{4}$.

For $|I|\ge 1$, we estimate the term ${\mathfrak {I}}_I$ as follows:

$$\begin{aligned} \begin{aligned} \int _0^t (1+\tau )\Vert \varpi (r-\tau )({\mathfrak {I}}_I+{\mathfrak {I}}_I^{(\phi )})(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \lesssim&\int _0^t \frac{\epsilon \log ^2 \tau }{1+\tau } {\text {d}}\tau \lesssim \epsilon \log ^3(2+t). \end{aligned} \end{aligned}$$

$\square$

We next bound the top order term ${\mathfrak {T}}_I$ and its ${ }^{(\phi )}$-counterpart. Since this is straightforward, we omit the proof.

Proposition 18.5

The following estimate holds for ${\mathfrak {T}}_I$ and ${\mathfrak {T}}_I^{(\phi )}$ for $|I|\le \lfloor \frac{N}{2}\rfloor +1$:

$$\begin{aligned} \begin{aligned} \int _0^t (1+\tau )\Vert \varpi (r-\tau )({\mathfrak {T}}_I+{\mathfrak {T}}_I^{(\phi )})(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \lesssim&\int _0^t \frac{\pi _{|I|}(\tau )}{(1+\tau )^{1+\frac{\gamma }{2}}} \,{\text {d}}\tau . \end{aligned} \end{aligned}$$

We now turn to the lower-order term ${\mathfrak {L}}_I$ and its ${ }^{(\phi )}$-counterpart.

Proposition 18.6

The following estimate holds for ${\mathfrak {L}}_I$ and ${\mathfrak {L}}_I^{(\phi )}$ for $|I|\le \lfloor \frac{N}{2}\rfloor +1$:

$$\begin{aligned} \begin{aligned} \int _0^t&(1+\tau )\Vert \varpi (r-\tau )({\mathfrak {L}}_I+{\mathfrak {L}}_I^{(\phi )})(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \lesssim \epsilon \log (2+t)\\&\quad + \int _0^t \frac{\log (2+\tau )\pi _{|I|-1}(\tau )}{(1+\tau )} \,{\text {d}}\tau . \end{aligned} \end{aligned}$$

Proof

We will only deal with the term $\sum _{|J|\le |I|-1}\frac{|\Gamma ^J h|}{(1+s)(1+|q|)^{1+\gamma }}$ for the other terms are trivial. For this, we note that

$$\begin{aligned} \begin{aligned}&\sum _{|J|\le |I|-1}\sup _{x\in D_\tau }(1+\tau )\varpi (r-\tau )\frac{|\Gamma ^J h|(\tau ,x)}{(1+\tau +r)(1+|r-\tau |)^{1+\gamma }}\\&\quad \lesssim \sum _{|J|\le |I|-1}\frac{1}{(1+\tau )}\sup _{x\in D_\tau }(1+\tau +r)\frac{\varpi (r-\tau )}{(1+|r-\tau |)}|\Gamma ^J h|(\tau ,x)\\&\quad \lesssim \frac{\epsilon }{1+\tau }+ \frac{\pi _{|I|-1}(\tau )}{1+\tau } , \end{aligned} \end{aligned}$$

where in the last line we have used Lemma 18.1 with $k(s)=(1+s)$, $f(q)=\varpi (q)$, noting that the term on $\{t=0\}$ can be controlled thanks to Remark 5.4 and gives rise to the term $\frac{\epsilon }{1+\tau }$. After integrating in $\tau$ over [0, t], the proposition follows. $\square$

To control the ${\mathfrak {W}}_I$ term, we have

Proposition 18.7

The following estimate holds for ${\mathfrak {W}}_I$ and ${\mathfrak {W}}_I^{(\phi )}$ for $|I|\le \lfloor \frac{N}{2}\rfloor +1$:

$$\begin{aligned} \begin{aligned} \int _0^t (1+\tau )\Vert \varpi (r-\tau )({\mathfrak {W}}_I+{\mathfrak {W}}_I^{(\phi )})(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau&\lesssim \epsilon + \int _0^t \frac{\log (2+\tau )\pi _{|I|}(\tau )}{(1+\tau )^{1+\gamma }}{\text {d}}\tau . \end{aligned} \end{aligned}$$

Proof

Using Lemma 18.1 with $k(s)=(1+s)$, $f(q)=\varpi (q)$ (and Remark 5.4 to bound the term on $\{t=0\}$), we have

$$\begin{aligned} \begin{aligned}&\sup _{x\in D_\tau }(1+\tau )\varpi (r-\tau )({\mathfrak {W}}_I+{\mathfrak {W}}_I^{(\phi )})(\tau ,x)\\&\quad \lesssim \sum _{|J|\le |I|}\sup _{x\in D_\tau }\frac{\log (2+\tau )}{(1+\tau )^{1-2\delta _0}}\frac{\varpi (r-\tau )}{(1+|r-\tau |)^{\gamma +2\delta _0}}|\Gamma ^J h|(\tau ,x)\\&\quad \lesssim \sum _{|J|\le |I|}\frac{\log (2+\tau )}{(1+\tau )^{1+\gamma }}\sup _{x\in D_\tau }(1+\tau +r)\frac{\varpi (r-\tau )}{(1+|r-\tau |)}|\Gamma ^J h|(\tau ,x)\\&\quad \lesssim \frac{\log (2+\tau )}{(1+\tau )^{1+\gamma }}\epsilon + \frac{\log (2+\tau )}{(1+\tau )^{1+\gamma }} \pi _{|I|}(\tau ). \end{aligned} \end{aligned}$$

Integrating thus gives the desired estimate. $\square$

The bad term ${\mathfrak {B}}_I$ can also be controlled easily. Let us emphasize again that this term is only present when ${\widetilde{\Box }}_g \Gamma ^I h$ is projected to ${\underline{L}}{\underline{L}}$, as this structure will be important later.

Proposition 18.8

The following estimate holds for ${\mathfrak {B}}_I$ for $|I|\le \lfloor \frac{N}{2}\rfloor +1$:

$$\begin{aligned} \begin{aligned} \int _0^t (1+\tau )\Vert \varpi (q)({\mathfrak {B}}_I)(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \lesssim&\int _0^t \frac{\sigma _{|I|}(\tau )}{1+\tau } \,{\text {d}}\tau . \end{aligned} \end{aligned}$$

Proof

This follows directly from the assumptions on $|\partial h_B|_{{\mathcal {T}}{\mathcal {U}}}$ and $|\partial \phi _B|$ in Definition 3.1 and bootstrap assumptions (6.4) and (6.9) for $|\partial h|_{{\mathcal {T}}{\mathcal {U}}}$ and $|\partial \beta |$. Notice that the estimates indeed depend only on $\sigma _{|I|}$ but not $\pi _{|I|}$. $\square$

Before we proceed to the nonlinear term ${\mathfrak {N}}_I$ and the the good term ${\mathfrak {G}}_I$. We need to estimate $|\Gamma ^J h|_{LL}$ using the generalized wave coordinate condition. More precisely, we have the following lemma:

Lemma 18.9

The following estimate for $|\Gamma ^J h|_{LL}$ holds for $|I|\le \lfloor \frac{N}{2}\rfloor +1$:

$$\begin{aligned} \sup _x(1+t)(1+|q|)^{-1}\varpi (q)|\Gamma ^I h|_{LL}(t,x)\lesssim \frac{\epsilon }{(1+t)^{\frac{\gamma }{8}}}+\pi _{|I|-2}(t). \end{aligned}$$

Proof

By Proposition 8.3,

$$\begin{aligned} \begin{aligned}&|\partial \Gamma ^I h|_{LL}\\&\quad \lesssim \frac{\epsilon \log (2+s)}{(1+s)^2 w(q)^{\frac{\gamma }{1+2\gamma }}}+\frac{\log (2+s)}{(1+s)(1+|q|)^\gamma }\sum _{|J|\le |I|}|\Gamma ^J h|\\&\qquad +\frac{\log (2+s)}{1+s}\sum _{|J|\le |I|}|\partial \Gamma ^J h|+\sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|+\sum _{|J|\le |I|}|{\bar{\partial }}\Gamma ^J h|\\&\qquad +\sum _{|J|\le |I|-2}|\partial \Gamma ^J h|. \end{aligned} \end{aligned}$$

Using the estimates from Proposition 18.2, we have

$$\begin{aligned}&\sum _{|J|\le |I|}|{{\bar{\partial }}} \Gamma ^J h|\lesssim \frac{\epsilon (1+|q|)^{\frac{1}{2}}}{(1+s)^{2-(2N+6) \delta _0} w(q)^{\frac{1}{2}}}, \\&\frac{\log (2+s)}{1+s}\sum _{|J|\le |I|}(|\Gamma ^J h|+|\partial \Gamma ^J h|)\lesssim \frac{\epsilon (1+|q|)^{\frac{1}{2}}\log (2+s)}{(1+s)^{2-(2N+6) \delta _0} w(q)^{\frac{1}{2}}}. \end{aligned}$$

and

$$\begin{aligned} \sum _{|J_1|+|J_2|\le |I|}|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|\lesssim \frac{\epsilon ^2}{(1+s)^{2-2(2N+6) \delta _0} w(q)}. \end{aligned}$$

By definition of $\pi _{|I|-2}$,

$$\begin{aligned} \sum _{|J|\le |I|-2}|\partial \Gamma ^J h|\lesssim \frac{\pi _{|I|-2}(t)}{(1+s)\varpi (q)}. \end{aligned}$$

Therefore, combining the estimates above, we obtain

$$\begin{aligned} |\partial \Gamma ^I h|_{LL}(t,x)\lesssim \frac{\epsilon (1+|q|)^{\frac{1}{2}}\log (2+s)}{(1+s)^{2-2(2N+6) \delta _0} w(q)^{\frac{1}{2}}}+\frac{\pi _{|I|-2}(t)}{(1+s)\varpi (q)}, \end{aligned}$$

which implies

$$\begin{aligned} (1+s)\varpi (q)|\partial \Gamma ^I h|_{LL}(t,x)\lesssim \frac{\epsilon }{(1+s)^{\frac{\gamma }{8}}}+\pi _{|I|-2}(t), \end{aligned}$$

by (18.5) since $\delta _0\le \frac{\gamma }{16(2N+6)}$ by (6.1). The conclusion then follows from Lemma 18.1 after noting that $\partial _q$ commutes with the projection to L. $\square$

We now turn to the nonlinear terms ${\mathfrak {N}}_I$ and its ${ }^{(\phi )}$-counterpart.

Proposition 18.10

The following estimate holds for ${\mathfrak {N}}_I+{\mathfrak {N}}_I^{(\phi )}$ for $|I|\le \lfloor \frac{N}{2}\rfloor +1$:

$$\begin{aligned} \begin{aligned}&\int _0^t (1+\tau )\Vert \varpi (r-\tau )({\mathfrak {N}}_I+{\mathfrak {N}}_I^{(\phi )})(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \\&\quad \lesssim \int _0^t \frac{\epsilon \pi _{|I|}(\tau )}{(1+\tau )^{1+\frac{\gamma }{8}}}\,{\text {d}}\tau +\int _0^t \frac{\pi _{|I|-1}(\tau )\pi _{|I|-1}(\tau )}{1+\tau } {\text {d}}\tau . \end{aligned} \end{aligned}$$

Proof

We will bound ${\mathfrak {N}}_I$ as ${\mathfrak {N}}_I^{(\phi )}$ can be controlled in a completely identical manner. We have three contributions:

$$\begin{aligned}&\sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ \max \{|J_1|,|J_2|\}\le |I|-1 \end{array}}|\partial \Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|, \end{aligned}$$

(18.10)

$$\begin{aligned}&\sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ \max \{|J_1|,|J_2|\}\le |I|-1 \end{array}}\frac{|\Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|}{1+|q|}, \end{aligned}$$

(18.11)

and

$$\begin{aligned} \sum _{|J_1|+|J_2|\le |I|}\frac{|\Gamma ^{J_1} h|_{LL}|\partial \Gamma ^{J_2} h|}{1+|q|}. \end{aligned}$$

(18.12)

We first consider (18.10).

$$\begin{aligned} \begin{aligned}&\sum _{\begin{array}{c} |J_1|+|J_2|\le |I|\\ \max \{|J_1|,|J_2|\}\le |I|-1 \end{array}}\int _0^t (1+\tau )\Vert \varpi (r-\tau )|\partial \Gamma ^{J_1}h||\partial \Gamma ^{J_2}h|(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \\&\quad \lesssim \sum _{\begin{array}{c} k_1+k_2\le |I|\\ \max \{k_1,k_2\}\le |I|-1 \end{array}}\int _0^t \frac{\pi _{k_1}(\tau )\pi _{k_2}(\tau )}{1+\tau }{\text {d}}\tau . \end{aligned} \end{aligned}$$

(18.13)

In view of Lemma 18.1, the term (18.11) can be estimated in an identical manner as (18.10). For the final term (18.12), we use Lemma 18.9 to bound $\frac{(1+\tau )\varpi (r-\tau )|\Gamma ^{J_1} h|_{LL}}{1+|q|}$ and obtain

$$\begin{aligned} \begin{aligned}&\sum _{|J_1|+|J_2|\le |I|}\int _0^t (1+\tau )\Vert \varpi (r-\tau )\frac{|\Gamma ^{J_1} h|_{LL}|\partial \Gamma ^{J_2} h|}{1+|r-\tau |}(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \\&\quad \lesssim \int _0^t \frac{\epsilon \pi _{|I|}(\tau )}{(1+\tau )^{1+\frac{\gamma }{8}}}\,{\text {d}}\tau +\sum _{k=0}^{|I|-2}\int _0^t \frac{\pi _k(\tau )\pi _{|I|-k-2}(\tau )}{1+\tau } {\text {d}}\tau . \end{aligned} \end{aligned}$$

(18.14)

Finally, notice that the terms (18.13) and (18.14) are both acceptable. This concludes the proof of the proposition. $\square$

Finally, we control the good term ${\mathfrak {G}}_I$ and its ${ }^{(\phi )}$-counterpart:

Proposition 18.11

The following estimate holds for ${\mathfrak {G}}_I+{\mathfrak {G}}_I^{(\phi )}$ for $|I|\le \lfloor \frac{N}{2}\rfloor +1$:

$$\begin{aligned} \begin{aligned}&\int _0^t (1+\tau )\Vert \varpi (r-\tau )({\mathfrak {G}}_I+{\mathfrak {G}}_I^{(\phi )})(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \lesssim \epsilon +\int _0^t \frac{\pi _{|I|-2}(\tau )\, {\text {d}}\tau }{1+\tau }. \end{aligned} \end{aligned}$$

Proof

We will only need to bound ${\mathfrak {G}}_I$, as ${\mathfrak {G}}_I^{(\phi )}$ contains a strict subset of terms. By Proposition 9.15, we have

$$\begin{aligned}&\int _0^t (1+\tau )\Vert \varpi (r-\tau )({\mathfrak {G}}_I)(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \nonumber \\&\quad \lesssim \int _0^t \sum _{|J|\le |I|}\sup _x\frac{\varpi (r-\tau )|\Gamma ^J h|_{LL}}{(1+|r-\tau |)^{1+\gamma }}(\tau ,x){\text {d}}\tau \nonumber \\&\qquad +\int _0^t(1+\tau )^{\delta _0}\sum _{|J|\le |I|}\sup _x \frac{\varpi (r-\tau )(|{{\bar{\partial }}}\Gamma ^J h|+|{{\bar{\partial }}}\Gamma ^J \beta |)(\tau ,x)}{(1+|r-\tau |)^{\gamma +\delta _0}} {\text {d}}\tau . \end{aligned}$$

(18.15)

To control the first term, we apply Lemma 18.9, which gives

$$\begin{aligned} \begin{aligned}&\int _0^t \sum _{|J|\le |I|}\sup _x\frac{\varpi (r-\tau )|\Gamma ^J h|_{LL}}{(1+|r-\tau |)^{1+\gamma }}(\tau ,x){\text {d}}\tau \\&\quad \lesssim \int _0^t \left( \frac{\epsilon }{(1+\tau )^{1+\frac{\gamma }{8}}}+\frac{\epsilon \pi _{|I|-2}(\tau )}{1+\tau }\right) {\text {d}}\tau \lesssim \epsilon +\int _0^t \frac{\epsilon \pi _{|I|-2}(\tau )}{1+\tau }\,{\text {d}}\tau . \end{aligned} \end{aligned}$$

For the second term in (18.15), we can use (18.4) in Proposition 18.2 to get

$$\begin{aligned} \begin{aligned}&\int _0^t(1+\tau )^{\delta _0}\sum _{|J|\le |I|}\sup _x \frac{\varpi (r-\tau )(|{{\bar{\partial }}}\Gamma ^J h|+|{{\bar{\partial }}}\Gamma ^J \beta |)(\tau ,x)}{(1+|r-\tau |)^{\gamma +\delta _0}} {\text {d}}\tau \\&\quad \lesssim \int _0^t \sup _x\frac{\epsilon (1+|r-\tau |)^{1-\frac{\gamma }{4}}}{(1+\tau +r)^{2-(2N+6)\delta _0}(1-|r-\tau |)^{\gamma +\delta _0}}{\text {d}}\tau \\&\quad \lesssim \int _0^t\epsilon (1+\tau )^{-1-\frac{3\gamma }{4}+(2N+6)\delta _0}{\text {d}}\tau \lesssim \epsilon , \end{aligned} \end{aligned}$$

since $\delta _0$ satisfy (6.1). Combining these estimates, we get the desired conclusion. $\square$

We have now estimated each of the error terms in ${\widetilde{\Box }}_g (\Gamma ^I h)$ and ${\widetilde{\Box }}_g (\Gamma ^I \beta )$. We are now ready to apply Proposition 18.3 to obtain the desired pointwise bounds. We start with the lowest-order estimates:

Proposition 18.12

The following estimates hold:

$$\begin{aligned} \sigma _0(t)\lesssim \epsilon ,\quad \pi _0(t)\lesssim \epsilon \log (2+t). \end{aligned}$$

Proof

By definition, the lower-order term ${\mathfrak {L}}_{I}$ is missing in ${\widetilde{\Box }}_{g} h$ for $|I|=0$. Moreover, recall from Proposition 9.18 that the bad term ${\mathfrak {B}}_I$ is absent when the inhomogeneous term is projected to ${\mathcal {T}}{\mathcal {U}}$. Therefore, using Proposition 18.3, we can combine the bounds in Propositions 18.4, 18.5, 18.7, 18.10 and 18.11 to obtain

$$\begin{aligned} \sigma _0(t)\lesssim \epsilon +\int _0^t \frac{\pi _0(\tau )}{(1+\tau )^{1+\frac{\gamma }{8}}} \,{\text {d}}\tau . \end{aligned}$$

(18.16)

On the other hand, for a general component, we also have the contribution from the ${\mathfrak {B}}_I$ term in Proposition 18.8. Therefore, we have

$$\begin{aligned} \begin{aligned} \pi _0(t)\lesssim&\epsilon +\int _0^t \frac{\sigma _0(\tau )}{(1+\tau )} \,{\text {d}}\tau +\int _0^t \frac{\pi _0(\tau )}{(1+\tau )^{1+\frac{\gamma }{8}}} \,{\text {d}}\tau . \end{aligned} \end{aligned}$$

Since $\frac{1}{(1+\tau )^{1+\frac{\gamma }{2}}}$ in integrable in $\tau$, it then follows from Grönwall’s inequality that

$$\begin{aligned} \pi _0(t)\lesssim \epsilon +\int _0^t \frac{\sigma _0(\tau )}{(1+\tau )} \,{\text {d}}\tau . \end{aligned}$$

(18.17)

A simple continuity argument shows that (18.16) and (18.17) together imply the desired conclusion. $\square$

Using the estimates we have obtained, we can show by induction the following pointwise bounds up to $\lfloor \frac{N}{2}\rfloor +1$ derivatives of h and $\beta$:

Proposition 18.13

Let $\delta >0$ be sufficiently small. For $1\le k\le \lfloor \frac{N}{2}\rfloor +1$, the following holds with an implicit constant depending on $\delta$ (in addition to C, $\gamma$ and $\delta _0$, but independent of $\epsilon$):

$$\begin{aligned} \pi _k(t)+\sigma _k(t)\lesssim \epsilon (1+\tau )^{2^k\delta }. \end{aligned}$$

Proof

By Proposition 18.3 together with the estimates in Propositions 18.4, 18.5, 18.6, 18.7, 18.8, 18.10 and 18.11, we have

$$\begin{aligned} \pi _k(t)&\lesssim \sum _{|I|\le k}\int _0^t (1+\tau )\Vert \varpi (q)(|{\widetilde{\Box }}_g (\Gamma ^I h)|+|{\widetilde{\Box }}_g (\Gamma ^I \beta )|)(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \nonumber \\&\lesssim \epsilon \log ^3(2+t)+\int _0^t \frac{ \pi _{k}(\tau )\, {\text {d}}\tau }{(1+\tau )^{1+\frac{\gamma }{8}}}+\int _0^t \frac{ \log (2+\tau )\pi _{k-1}(\tau )\, {\text {d}}\tau }{1+\tau } \nonumber \\&\quad +\int _0^t \frac{ \pi _{k-1}(\tau )\pi _{k-1}(\tau )\, {\text {d}}\tau }{1+\tau } +\int _0^t \frac{\sigma _{k}(\tau )}{1+\tau } \,{\text {d}}\tau . \end{aligned}$$

(18.18)

On the other hand, recall that the bad term is absent in $({\widetilde{\Box }}_g (\Gamma ^I h))_{{\mathcal {T}}{\mathcal {U}}}$, Therefore, by Propositions 18.3, 18.4, 18.5, 18.6, 18.7, 18.10 and 18.11, we have

$$\begin{aligned} \sigma _k(t)&\lesssim \sum _{|I|\le k}\int _0^t (1+\tau )\Vert \varpi (q)(|{\widetilde{\Box }}_g (\Gamma ^I h)|_{{\mathcal {T}}{\mathcal {U}}}+|{\widetilde{\Box }}_g (\Gamma ^I \beta )|)(\tau ,\cdot )\Vert _{L^\infty (D_\tau )}{\text {d}}\tau \nonumber \\&\lesssim \epsilon \log ^3(2+t)+\int _0^t \frac{ \pi _{k}(\tau )\, {\text {d}}\tau }{(1+\tau )^{1+\frac{\gamma }{8}}}+\int _0^t \frac{ \log (2+\tau )\pi _{k-1}(\tau )\, {\text {d}}\tau }{1+\tau } \nonumber \\&\quad +\int _0^t \frac{ \pi _{k-1}(\tau )\pi _{k-1}(\tau )\, {\text {d}}\tau }{1+\tau }. \end{aligned}$$

(18.19)

We claim that our desired estimates follow from (18.18) and (18.19). We prove this by induction in k. For the $k=1$ case, using the estimates in Proposition 18.12 and Grönwall’s inequality, (18.18) and (18.19) reduce to

$$\begin{aligned} \begin{aligned} \pi _1(t)&\lesssim \epsilon \log ^3(2+t) +\int _0^t \frac{\sigma _{1}(\tau )}{1+\tau } \,{\text {d}}\tau . \end{aligned} \end{aligned}$$

(18.20)

and

$$\begin{aligned} \sigma _1(t)\lesssim \epsilon \log ^3(2+t)+\int _0^t \frac{ \pi _{1}(\tau )\, {\text {d}}\tau }{(1+\tau )^{1+\frac{\gamma }{8}}}. \end{aligned}$$

(18.21)

Substituting (18.20) into (18.21) and using the monotonicity of $\sigma _1$, we get

$$\begin{aligned} \begin{aligned} \sigma _1(t)&\lesssim \epsilon \log ^3(2+t)+\int _0^t \frac{ \left( \epsilon \log ^3(2+\tau )+\int _0^\tau \frac{\sigma _{1}(\tau ')\,{\text {d}}\tau '}{1+\tau '}\right) \, {\text {d}}\tau }{(1+\tau )^{1+\frac{\gamma }{8}}}\\&\lesssim \epsilon \log ^3(2+t)+\int _0^t \frac{\log (2+\tau )\sigma _{1}(\tau ) \, {\text {d}}\tau }{(1+\tau )^{1+\frac{\gamma }{8}}}\lesssim \epsilon \log ^3(2+t), \end{aligned} \end{aligned}$$

where in the last step we have used Grönwall’s inequality. Plugging this estimate back to (18.20), we also obtain

$$\begin{aligned} \pi _1(t)\lesssim \epsilon \log ^4(2+t). \end{aligned}$$

We have thus proved the desired (and in fact much stronger) estimates for $\pi _1$ and $\sigma _1$. Now assume we have the desired estimate for $\pi _{k-1}$ and $\sigma _{k-1}$. Then, (18.18) and (18.19) reduce to

$$\begin{aligned} \begin{aligned} \pi _k(t)\lesssim&\epsilon (1+t)^{2^k\delta } +\int _0^t \frac{\sigma _{k}(\tau )}{1+\tau } \,{\text {d}}\tau . \end{aligned} \end{aligned}$$

(18.22)

and

$$\begin{aligned} \sigma _k(t)\lesssim \epsilon (1+t)^{2^k\delta }+\int _0^t \frac{ \pi _{k}(\tau )\, {\text {d}}\tau }{(1+\tau )^{1+\frac{\gamma }{8}}}. \end{aligned}$$

(18.23)

As long as $2^N \delta \ll \frac{\gamma }{8}$, we argue as before to substitute (18.22) into (18.23) to obtain

$$\begin{aligned} \sigma _k(t) \lesssim \epsilon (1+t)^{2^k\delta }, \end{aligned}$$

which then implies

$$\begin{aligned} \pi _k(t) \lesssim \epsilon (1+t)^{2^k\delta } \end{aligned}$$

after plugging the estimate for $\sigma _k(t)$ into (18.22). $\square$

Finally, we improve all the bootstrap assumptions:

Proposition 18.14

For $\delta >0$ sufficiently small such that $2^{\lfloor \frac{N}{2}\rfloor +1}\delta \ll \delta _0$, the following pointwise bounds hold:

$$\begin{aligned}&\sup _{t,x}\sum _{|I|\le \lfloor \frac{N}{2}\rfloor +1} (1+s)^{1-\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}|\partial \Gamma ^I h (t,x)|\lesssim \epsilon , \end{aligned}$$

(18.24)

$$\begin{aligned}&\sup _{t,x}\sum _{|I|\le \lfloor \frac{N}{2}\rfloor } (1+s)^{2-\delta _0}(1+|q|)^{-\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}|{{\bar{\partial }}} \Gamma ^I h (t,x)|\lesssim \epsilon , \end{aligned}$$

(18.25)

$$\begin{aligned}&\sup _{t,x}(1+s)|\partial h(t,x)|_{{\mathcal {T}}{\mathcal {U}}}\lesssim \epsilon , \end{aligned}$$

(18.26)

$$\begin{aligned}&\sup _{t,x}\sum _{|I|\le \lfloor \frac{N}{2}\rfloor +1} (1+s)^{1-\delta _0}(1+|q|)^{-\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}|\Gamma ^I h (t,x)| \lesssim \epsilon , \end{aligned}$$

(18.27)

$$\begin{aligned}&\sup _{t,x}(1+s)^{1+\frac{\gamma }{2}}(1+|q|)^{-\frac{1}{2}-\gamma }w(q)^{\frac{1}{2}}\big (|h (t,x)|_{L{\mathcal {T}}}+\sum _{|I|\le 1}|\Gamma ^I h(t,x)|_{LL}\big )\lesssim \epsilon , \nonumber \\\end{aligned}$$

(18.28)

$$\begin{aligned}&\sup _{t,x}\sum _{|I|\le \lfloor \frac{N}{2}+1\rfloor } (1+s)^{1-\delta _0}(1+|q|)^{\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}|\partial \Gamma ^I \beta (t,x)|\lesssim \epsilon , \end{aligned}$$

(18.29)

$$\begin{aligned}&\sup _{t,x}\sum _{|I|\le \lfloor \frac{N}{2}\rfloor } (1+s)^{2-\delta _0}(1+|q|)^{-\frac{1}{2}-\frac{\gamma }{4}}w(q)^{\frac{1}{2}}|{{\bar{\partial }}} \Gamma ^I \beta (t,x)|\lesssim \epsilon \end{aligned}$$

(18.30)

$$\begin{aligned}&\sup _{t,x}(1+s)|\partial \beta (t,x)|\lesssim \epsilon . \end{aligned}$$

(18.31)

In particular, there exists $\epsilon _0\in (0,\epsilon _4]$ sufficiently small such that if $\epsilon \in (0,\epsilon _0]$, we have improved the bootstrap assumptions (6.2)–(6.6), (6.7)–(6.9).

Proof

(18.24) follows directly from the estimate of $\pi _k$ in Propositions 18.12 and 18.13. (18.26) follows from the bound for $\sigma _0$ in Proposition 18.12. (18.27) follows from combining (18.24) and Lemma 18.1. (18.25) then follows from (18.27) and Proposition 7.1. Finally, it remains to prove (18.28). This requires the use of the generalized wave coordinate condition. More precisely, by Proposition 8.2 and the bounds (18.24), (18.25) and (18.27), we obtain the bound

$$\begin{aligned} |\partial h(t,x)|_{L{\mathcal {T}}}\lesssim \frac{\epsilon \log (2+s)(1+|q|)^{\frac{1}{2}+\frac{\gamma }{4}}}{w(q)^{\frac{1}{2}}(1+s)^{2-2\delta _0}}\lesssim \frac{\epsilon (1+|q|)^{\frac{7\gamma }{8}}}{w(q)^{\frac{1}{2}}(1+|q|)^{\frac{1}{2}}(1+s)^{1+\frac{5\gamma }{8}-2\delta _0}}. \end{aligned}$$

Similarly, by Proposition 8.2 and (18.24), (18.25) and (18.27), we have

$$\begin{aligned} \sum _{|I|\le 1}|\partial \Gamma ^I h(t,x)|_{LL}\lesssim \frac{\epsilon (1+|q|)^{\frac{7\gamma }{8}}}{w(q)^{\frac{1}{2}}(1+|q|)^{\frac{1}{2}}(1+s)^{1+\frac{5\gamma }{8}-2\delta _0}}. \end{aligned}$$

Notice that $\partial _q$ commutes with the projection to $\{L,{\underline{L}},E^1,E^2,E^3\}$. By (6.1), $\frac{5\gamma }{8}-2\delta _0\ge \frac{\gamma }{2}$. By Lemma 18.1 with $k(s)=(1+s)^{1+\frac{5\gamma }{8}-2\delta _0}$ and $f(q)=w(q)^{\frac{1}{2}}(1+|q|)^{\frac{1}{2}-\frac{7\gamma }{8}}$, we therefore obtain (18.28).

We now turn to the bounds for the scalar field: (18.29) and (18.31) follow from Propositions 18.12 and 18.13. (18.30) can be obtained in a similar manner as (18.25), i.e., first use (18.29) and Lemma 18.1 to obtain an estimate for $\sum _{|I|\le \lfloor \frac{N}{2}\rfloor +1}|\Gamma ^I\beta |$ and then apply Proposition 7.1.

This concludes the proof of the proposition. $\square$

These estimates easily allow us to conclude the proof of Theorem 5.2:

Proof of Theorem 5.2

For $\epsilon \in (0,\epsilon _0]$, where $\epsilon _0>0$ is as in Proposition 18.14, we have closed all the bootstrap assumptions. It is therefore standard to conclude that all the estimates that are proven indeed hold for g and $\phi$ satisfying the equations in Proposition 4.1. In particular, (17.3) holds. Standard results on local existence of solutions then imply that the solution is global in (t-)time.

Finally, the estimate (5.1) follows from (17.3) if $(2N+6)\delta _0\le \delta _1$. For every $\delta _1>0$, we can therefore choose $(2N+6)\delta _0\le \delta _1$ so that (5.1) holds for $\epsilon$ appropriately small (depending in particular on $\delta _1$). This concludes the proof of Theorem 5.2. $\square$