Abstract
I study a class of global, causal geodesically complete solutions to the spherically symmetric Einstein scalar field (SSESF) system . Extending results of Luk and Oh (Anal PDE 8(7):1603–1674, 2015), Luk et al. (Ann PDE 4(1):1–59, 2018), I provide new bounds controlling higher derivatives of both the metric components of the solution and the scalar field itself for large data solutions to SSESF. Moreover, by constructing a particular set of generalized wave coordinates, I show that, assuming sufficient regularity of the data, these solutions are globally non-linearly stable to non-spherically symmetric perturbations by recent results of Luk and Oh. In particular, I demonstrate the existence of a large collection of non-trivial examples of large data, globally nonlinearly stable, dispersive solutions to the Einstein scalar field system.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
I study the decay properties of a class of spherically symmetric solutions \((M,g,\phi )\) to the Einstein scalar field system, for M a \(3+1\)-dimensional manifold, g a Lorentzian metric, and \(\phi :M \rightarrow {\mathbb {R}}\) a real-valued scalar field:

Recently, Luk and Oh in [15] proved a large data stability criterion for solutions to (ESF); in this paper, I prove the following
Theorem 1.1
There exist large data solutions satisfying the stability criterion of [15].
From this, we obtain the immediate corollary:
Corollary 1.2
There exists an open set of large initial data for ESF which give rise to dispersive solutions.
This is the first such result in the large data case; previously there is no known existence result for global dispersive solutions to (ESF) outside of spherical symmetry [18], or the small data regime [7, 14] (note, however, the spectacular recent advances in the stability of the black hole problem, see [10, 12, 13]).
I build off the results of Luk–Oh–Yang in [18] in which a large class of large data spherically symmetric solutions to the Einstein scalar field system are constructed to the future of a coneFootnote 1, with decay estimates both toward null and timelike infinity up to second derivatives in a spherically symmetric double null coordinate system:
-
I begin by improving the estimates of Luk–Oh–Yang to all order of derivatives, since the stability result of Luk–Oh, [15], requires \(\ge 11\) derivatives. Given the basic control of the spacetime geometry that has been established in [16], these estimates follow from the methods of [18], with some additional care given to controlling terms near the axis of symmetry.
-
Next, I extend the Luk–Oh–Yang spacetime (originally only to the future of a cone) to a larger spacetime defined to the future of an asymptotically flat Cauchy hypersurface. This is realized by solving a “sideways” characteristic initial value problem toward spatial infinity. This builds upon the work of Dafermos in [9]. As before, I prove decay estimates for all higher order derivatives.
-
In this spherically symmetric spacetime, I then introduce a future-normalized spherically symmetric double-null gauge in which one obtains some slightly stronger decay estimates. It is at this point when one identifies the logarithmic terms arising from the contribution of the mass, which play an important role in the generalized wave coordinates that are later introduced.
-
Finally, I introduce a generalized wave coordinate system and show that the constructed spacetime satisfies the estimates required by Luk–Oh in [15], which are defined in terms of commuting vector fields in terms of the generalized wave coordinates. Here, one must take advantage of the null condition (manifested in the different decay estimates for the \(\partial _v\) and \(\partial _u\) derivatives) and also be careful about the regularity of the solution at the axis (since the function r is not smooth at the axis).
1.1 Prior Results
In the early 1990s, Christodoulou-Klainerman in [7] established the first global nonlinear stability results in the asymptotically flat setting, showing that Minkowski spacetime is globally non-linearly stable under the Einstein vacuum equations; see also [11]. In particular, they showed that for asymptotically flat initial data which are sufficiently close to Minkowski, the maximal globally hyperbolic development is causally geodesically complete and approaches Minkowski at large times. Lindblad-Rodnianski [14] later simplified the proof and extended the result to the Einstein scalar field system. These results both require explicit smallness of the data. Recently, Luk-Oh further extended the results and techniques of [14] in [15], to give a set of criteria for large data causally geodesically complete solutions to be globally non-linearly stable for the Einstein scalar field system. These criteria consist of decay conditions for high order derivatives of the geometry and scalar field, as well as the existence of a gauge in which the solution satisfies some specific asymptotic relations. This was the first such stability result for large data.
The spherically symmetric Einstein scalar field system has been studied extensively over the past four decades, being among the most accessible systems containing matter in the spherically symmetric class. Through the 1980s and 1990s, Christodoulou established a complete picture of the singularity structure of spherically symmetric solutions (cf [1,2,3,4,5,6]). In particular, he showed that generic (in BV) initial data give rise to a solution which is either dispersive, or contains a black hole region and a spacelike curvature singularity. This work established both a complete understanding of the singularity structure of the spherically symmetric Einstein scalar field and qualitative description of the long term dynamics of the system. Moreover, [1] gives quantitative control for small data. It remained to establish quantitative bounds in the large data case.
There has since been significant progress in this direction. In the black hole case, this was done by Dafermos-Rodnianski in [8], in which they established polynomial decay rates conjectured by Price [19]. Corresponding lower bounds have more recently been established in [17]. We will focus on the dispersive case, which was studied by Luk-Oh in [16]. They establish quantitative decay rates for \(\phi \) as well as the geometry of the system for up to \(C^2\) solutions, without (quantitative) restriction on the BV norm of the data. The new high-order decay established in this paper is an extension of these results to \(C^k\) data for arbitrary \(k \ge 2\) (controlling up to k derivatives of \(\phi \) and geometric terms).
The above references provide only an incomplete picture of the full development of the current understanding of the Einstein scalar field system. For a more complete collection, see [15].
1.2 Outline of the Paper
In Sect. 2, we will lay out the problem, establish our notations and conventions, and restate some prior results (from [9, 16]) which will be referenced later. In Sect. 3, we will provide precise statements of the primary results of the paper (cf. theorems 3.1 and 3.4).
The remainder of the paper is devoted to proving the results stated in Sect. 3. In Sects. 4 and 5, we have Theorem 3.1. In particular, Sect. 4 provides estimates at arbitrary differential order in a region with compact curves of constant u (respectively, v). In Sect. 5, I establish the estimates of Theorem 3.1 in a region away from the axis of symmetry. Together, these complete the proof of Theorem 3.1.
Finally, Sects. 6 and 7 are devoted to proving global nonlinear stability of the spacetimes considered in Theorem 3.1 (Theorem 3.4), from the results of Theorem 3.1. In Sect. 7, we show that our estimates in spherical symmetry extend nicely to the full, un-reduced spacetime, and in Sect. 6 we check that the class of solutions considered in Theorem 3.4 in fact satisfies the conditions of the main theorem of [15] and thus exhibits global nonlinear stability to (an open class of) non-spherically symmetric perturbations.
2 Preliminaries
In this section, we will go over the setup of the problem at hand, the form of the equations and coordinates we will use, some important terms and useful machinery, and prior results we will use throughout the paper.
2.1 The Einstein Scalar Field System
We begin with an overview of the deriving of the spherically symmetric Einstein scalar field system. We begin with the full Einstein scalar field system in 3+1 dimensions.
Solutions are described by a triple \(({\mathcal {M}},\mathbf{g }_{\mu \nu },\phi )\) where \(({\mathcal {M}},\mathbf{g }_{\mu \nu })\) is a \((3+1)\)-dimensional Lorentzian manifold, and \(\phi \) is a real-valued function on \({\mathcal {M}}\). The metric and scalar field satisfy the Einstein scalar field system:

where \(R_{\mu \nu }\) is the Ricci curvature of \(\mathbf{g }\), R is the scalar curvature, \(\nabla _{\mu }\) is the covariant derivative corresponding to the Levi-Civita connection on \(({\mathcal {M}},\mathbf{g })\), and \(T_{\mu \nu }\) is the energy–momentum tensor given by \(\phi \):
Assume that \(({\mathcal {M}},\mathbf{g },\phi )\) admits a smooth action of SO(3) by isometries on \(({\mathcal {M}},\mathbf{g })\) such that each orbit is either a point, or isometric to \(S^2\) with a round metric, and \(\phi \) is constant on each orbit. Such a solution is called spherically symmetric. These properties are all propagated by (ESF); thus, if \(({\mathcal {M}},\mathbf{g },\phi )\) is a Cauchy development of some initial data, it suffices to assume that the initial data are spherically symmetric to ensure spherical symmetry of the solution.
Under this assumption, we can take the quotient \({\mathcal {M}}/SO(3)\) which yields a \((1+1)\)-dimensional Lorentzian manifold with boundary which we will denote by (M, g). The boundary \(\Gamma \) is the set of fixed points of the SO(3) action.
In this setup, we can define the area radius function r on M by
with \(r = 0\) on \(\Gamma \). Note that each connected component of \(\Gamma \) is a timelike geodesic.
Henceforth, we will assume that \(\Gamma \) is non-empty and connected, and that there exists a system of global double null coordinates (u, v), in which the metric takes the form
for some \(\Omega > 0\). Both of these assumptions are certainly justified so long as \(({\mathcal {M}},\mathbf{g })\) is a Cauchy development of a spacelike hypersurface homeomorphic to \({\mathbb {R}}^3\).
We can recover the metric \(\mathbf{g }\) on \({\mathcal {M}}\) from \(\Omega \) and r:
where \(\mathrm{d}s^2_{S^2}\) is the line element for the unit sphere \(S^2 \subset {\mathbb {R}}^3\). From this, we can reformulate our inherited equations on (M, g) as the spherically symmetric Einstein scalar field system (SSESF) in terms of the triple \((\phi ,r,\Omega )\) as

with the boundary condition \(r = 0\) on \(\Gamma \).
We can reformulate this problem once more in terms of the Hawking mass m defined by
We also define the mass ratio:
and introduce some shorthand for important derivatives of r:
With this in mind, we see that we can reformulate (SSESF) in terms of the triple \((\phi ,r,m)\) in the following way:
We say that \((\phi ,r,m)\) is a solution to (SSESF) if the following relations hold:

and moreover, \(r = m = 0\) on \(\Gamma \).
Observe that we can equivalently write our equation for \(r\phi \) as:
2.2 Notation and Conventions
Here we will write down some notation and assumptions that will carry throughout the remainder of the paper.
We begin with a more concrete definition of the reduced space we work with.
Let \({\mathbb {R}}^{1+1}\) denote the \((1+1)\) dimensional Minkowski space with standard double null coordinates (u, v). Let M be a \((1+1)\) dimensional Lorentzian manifold conformally embedded in \({\mathbb {R}}^{1+1}\) with \(\mathrm{d}s^2_M = -\Omega ^2\mathrm{d}u\mathrm{d}v\). From r a non-negative function on M, define the set

Define \({\mathcal {M}} = M \times S^2/\sim \) where \(\sim \) is the equivalence
if and only if \((u,v) \in \Gamma , s,s' \in S^2\). This is the full \(3+1\)-dimensional space above M.
We assume that \(\Gamma \) is connected, the image of a future-directed timelike curve emanating from (1, 1). We also assume that \(C_R,{\underline{C}}_{R} \subset M\) for all \(R > 0\), where

Finally, define past and future null infinity (denoted by \({\mathcal {I}}^{-},{\mathcal {I}}^+\), respectively) to be the sets of “points” \((-\infty ,v)\), and \((u,\infty )\), respectively, s.t. \(\sup _{C_u}r = \sup _{{\underline{C}}_v}r = \infty \).
Combining this with the Hawking mass above, we define the Bondi mass as \(M_u = \lim _{v \rightarrow \infty }m(u,v)\). The final Bondi mass \(M_f = \lim _{u \rightarrow \infty } M_u\) and the initial Bondi mass \(M_i = \lim _{u \rightarrow -\infty } M_u\).
We also outline our convention for integrating over curves in M. When integrating over \(C_u\) or \({\underline{C}}_v\), we write

We define the domain of dependence of a line segment  (which we denote \({\mathcal {D}}(u_0,v_0)\)) to be the set of points \(p \in M\) such that all past-directed causal curves through p intersect
(which we denote \({\mathcal {D}}(u_0,v_0)\)) to be the set of points \(p \in M\) such that all past-directed causal curves through p intersect  along with the segment
along with the segment  .
.
2.3 Gauge Conditions
Observe that, to this point, the coordinates u, v are free to be reparametrized by transformations of the form
for any monotone increasing \({\tilde{u}}, {\tilde{v}}\). To fix these coordinates, we must prescribe some gauge condition.
In what follows, we will consider the following three different conditions:
-
(G1)
\(\lambda \equiv \frac{1}{2}\) on \(C_{1}\),
 .
. -
(G2)
\(\lim _{v \rightarrow \infty }\nu (u,v) = -\frac{1}{2}\) for all u, and
 .
. -
(G3)
\(\lambda \equiv \frac{1}{2}\) on \(C_1\) and \(\nu \equiv -\frac{1}{2}\) on \({\underline{C}}_R\) for some \(R \gg 1\)
Remark 2.1
The gauge (G2) can be obtained from (G1) by the following transformations:
where \({\bar{\nu }}(u) := \lim _{v \rightarrow \infty }\nu (u,v)\).
(G3) can be obtained via a similar transformation fixing \(v = R\) rather than taking this limit.
Remark 2.2
In both the gauges (G1) and (G2) for r, \(\phi \) \(C^k\)-smooth on M, the following hold
for all \(l \le k\).
Remark 2.3
Also under either of (G1) or (G2), the domain of dependence \({\mathcal {D}}(u_0,v_0)\) has the form

2.4 The Characteristic Initial Value Problem
We are now ready to pose the problem on which our analysis will focus throughout the first half of the paper. Of course, the equation we must satisfy is given by (SSESF’), but it remains to specify the precise notions of solution and specify the constraints on initial data that we will consider.
This initial data are quite constrained by (SSESF’). In fact, to obtain a solution in all of \({\mathbb {R}}^{1+1}_{x \ge 0}\) it suffices to pose data for \(\partial _v(r\phi )\) and \(\partial _u(r\phi )\) on the characteristic curves \(C_1\) and \({\underline{C}}_R\), respectively, as well as the values \(\phi (1,1),m(1,1)\) (which we will take to be 0), and a choice of gauge. The data on \(C_1\) then completely determine the solution in the region \({\mathcal {D}}_{C_1}\), because our gauge in combination with the equation determines data for m and r as well. Of course, on \({\underline{C}}_R\) we must check that our data in the region \(u \ge 1\) are compatible with that posed for \({\underline{C}}_{R}\). This is only a local constraint, in that we can prescribe whatever data we want for \(u < 1-\epsilon \) for any \(\epsilon > 0\), and (\(C^k\))-smoothly interpolate in the region \([1-\epsilon ,1]\).
Definition 2.4
(\(C^k\) solutions to (SSESF’) (in (G1))) A solution \((\phi ,r,m)\) to (SSESF’) is called a \(C^k\) solution on M if the following holds on every domain of dependence \({\mathcal {D}}(u_0,v_0)\):
-
(1)
\(\sup _{{\mathcal {D}}(u_0,v_0)}(-\nu ), \sup _{{\mathcal {D}}(u_0,v_0)}\lambda ^{-1} < \infty \).
-
(2)
\(\lambda , \nu \) are \(C^k\) on \({\mathcal {D}}(u_0,v_0)\).
-
(3)
For each \((u,u) \in \Gamma \)
$$\begin{aligned} \lim _{\epsilon \rightarrow 0^+}(\nu + \lambda )(u,u+\epsilon ) = \lim _{\epsilon \rightarrow 0^+}(\nu + \lambda )(u-\epsilon ,u) = 0. \end{aligned}$$ -
(4)
\(\partial _v(r\phi ), \partial _u(r\phi )\) are \(C^k\) on \({\mathcal {D}}(u_0,v_0)\).
-
(5)
For each \((u,u) \in \Gamma \)
$$\begin{aligned} \lim _{\epsilon \rightarrow 0^+}(\partial _v(r\phi ) + \partial _u(r\phi ))(u,u+\epsilon ) = \lim _{\epsilon \rightarrow 0^+}(\partial _v(r\phi ) + \partial _u(r\phi ))(u-\epsilon ,u) = 0. \end{aligned}$$
This initial value problem is well-posed for \(C^k\) (\(k \ge 1\)) initial data: For compatible \(C^k\) initial data posed on \(C_1\) and \({\underline{C}}_R\), there exists a unique \(C^k\) solution on some domain  where \({\bar{u}},{\bar{v}}\) depend only on R and the size of the initial data (in \(C^k\)). The proof is via standard iteration and not repeated here. For discussion of the compatibility of the two pieces of data, see [9].
where \({\bar{u}},{\bar{v}}\) depend only on R and the size of the initial data (in \(C^k\)). The proof is via standard iteration and not repeated here. For discussion of the compatibility of the two pieces of data, see [9].
Note that data which are \(C^k\) on \(C_1, {\underline{C}}_R\) will give rise to a \(C^k\) solution.
2.5 Definitions and Prior Results
Here we state some longer definitions of terms we will use throughout the paper.
It is essential to obtaining the desired decay that the prescribed initial data already verify such an estimate. As such, we make the following definition.
Definition 2.5
(Asymptotic Flatness of Order \(\omega ' \ge 0\) in \(C^k\)) An initial data set is said to be asymptotically flat of order \(\omega '\) in \(C^k\) toward \({\mathcal {I}}^+\) (resp. \({\mathcal {I}}^-\)) if \(\partial _v(r\phi )(1,\cdot ) \in C^k[1,\infty )\) (\(\partial _u(r\phi )(\cdot ,R) \in C^k(-\infty ,1]\)) and there exists \(A>0\) (\(A'\)) such that
for all \(l \le k\).
The solutions we consider will also be required to satisfy an additional constraint:
Definition 2.6
(Local Scattering) A \(C^k\) solution \((\phi ,r,m)\) on M is said to be locally scattering if the following holds:
-
(1)
The full \((3+1)\)-dimensional solution \(({\mathcal {M}},\mathbf{g },\phi )\) is future causally geodesically complete.
-
(2)
There exists \(r_0 > 0\) such that

as \(u \rightarrow \infty \).
Throughout what follows, we will frequently be writing down bounds for various quantities. We will not often write out explicit constants, as all will be taken to be the same in the end and depend on the same quantities. To this end, we will write \(\partial ^{\alpha }A \lesssim B\) to mean that A is bounded by B up to a constant depending on the constants \(A,A'\) above, the order of derivative \(\left|\alpha \right|\), the initial Bondi mass \(M_{-\infty }\), and some more complicated quantities depending on low-order behavior of solutionsFootnote 2. The important point is that our constants are global; in particular, they have no dependence on coordinates.
Here we will give some names to various spacetime regions we will be interested in. Let

Remark 2.7
The region \(\mathbb {I}\) corresponds to essentially to the future of the curve \(u+v = 0\) in this spacetime.
We will also be interested in decay of solutions along certain vector fields, in particular those generating the symmetries of Minkowski space. We introduce some shorthand for these (vector fields on \({\mathcal {M}}\)). In what follows in this section, let \((t,x^1,x^2,x^3)\) be coordinates on the manifold(-with-boundary) \([0,\infty ) \times {\mathbb {R}}^3\), \({\tilde{r}} = \sqrt{\sum _{i = 1}^3(x^i)^2}\). We will write latin indices  for spatial coordinates and greek indices
for spatial coordinates and greek indices  for spacetime coordinates (in what follows \(t = x^0\)).
for spacetime coordinates (in what follows \(t = x^0\)).
Definition 2.8
(Minkowski Commuting Vector Fields) The Minkowskian commuting vectors fields are the set of vector fields

We will henceforth use \(\Gamma \) to denote a general Minkowskian commuting vector field. For a multi-index \(I = (i_1,i_2,\dotsc ,i_{\left|I \right|})\), \(\Gamma ^I\) denotes a product of \(\left|I \right|\) Minkowksian vector fields.
We will also write in these coordinates \({\tilde{r}} = \sqrt{\sum (x^i)^2}\).
We also define the vector fields \(L,{\underline{L}},E^1,E^2,E^3\):
Definition 2.9
Let \(\partial _{{\tilde{r}}} = \sum _{i = 1}^3 \frac{x^i}{{\tilde{r}}}\partial _i\). Define
Define the vector fields

tangent to the coordinate 2-spheres of constant \({{\tilde{r}}},t\).
Later, we will use coordinates \((s,q,\theta ,\phi )\) where \((\theta ,\phi )\) the standard spherical coordinates, and (s, q) are given by
This leads us immediately to the vector fields
We introduce a little more notation before we are ready for our final definition. For a scalar function \(\xi \), we write

Next, for a 2-tensor p define
Define also for a first-order differential operator D, Dp to be D applied component-wise to p: \((Dp)_{\mu \nu } = D(p_{\mu \nu })\).
With this in mind, we make the following definition:
Definition 2.10
Let  ,
,  ,
,  . Then, for any two of these families \({\mathcal {V}},{\mathcal {W}}\) (allowing repeats), and a 2-tensor p define
. Then, for any two of these families \({\mathcal {V}},{\mathcal {W}}\) (allowing repeats), and a 2-tensor p define
Now we make the following definition as in [15].
Definition 2.11
(Dispersive Spacetime Solution of Size \((C,\gamma _0,N)\)) Let \(\gamma _0 > 0\) be a real number and \(N \ge 11\) be an integer. A spacetime \(({\mathcal {M}} = [0,\infty )\times {\mathbb {R}}^3,g)\) with scalar field \(\phi :{\mathcal {M}} \rightarrow {\mathbb {R}}\) is a dispersive spacetime solution of size \((C,\gamma _0,N)\) if
-
(D1)
The triple \(({\mathcal {M}},g,\phi )\) is a solution to the Einstein scalar field system.
-
(D2)
There exists a global system of coordinates \((t,x^1,x^2,x^3)\) such that with respect to this coordinate system the metric takes the form
$$\begin{aligned} g - m = h \end{aligned}$$where
$$\begin{aligned} m = -\mathrm{d}t^2 + \sum _{i = 1}^3 (\mathrm{d}x^i)^2 \end{aligned}$$is the Minkowski metric and h satisfies the bound
$$\begin{aligned} \left|\Gamma ^Ih \right| \le \frac{C\log (2+s)}{1+s} \end{aligned}$$for \(\left|I \right| \le N+1\) where I a multi-index, \(\Gamma \)’s are the Minkowski commuting vector fields defined above.
-
(D3)
For \(\left|I \right| \le N+1\), we have
$$\begin{aligned} \left|\partial \Gamma ^Ih \right| \le \frac{C}{(1+s)(1+\left|q \right|)^{\gamma _0}} \end{aligned}$$for any combination of Minkowski commuting vector fields \(\Gamma \).
-
(D4)
For \(\left|I \right| \le N+1\), we have
$$\begin{aligned} \left|{{\bar{\partial }}} \Gamma ^I h \right| \le \frac{C}{(1+s)^{1+\gamma _0}} \end{aligned}$$for any combination of Minkowskian commuting vector fields \(\Gamma \).
-
(D5)
For \(\left|I \right| \le 1\), the following components satisfy bounds:
$$\begin{aligned} \sum _{\left|I \right| \le 1} \left|\Gamma ^Ih \right|_{LL} + \left|h \right|_{L{\mathcal {T}}} \le \frac{C}{(1+s)^{1+\gamma _0}}. \end{aligned}$$ -
(D6)
For \(\left|I \right| \le N+1\), we have
$$\begin{aligned} \left|\partial \Gamma ^I\phi \right| \le \frac{C}{(1+s)(1+\left|q \right|)^{\gamma _0}},\quad \left|{{\bar{\partial }}}\Gamma ^I\phi \right| \le \frac{C}{(1+s)^{1+\gamma _0}}. \end{aligned}$$ -
(D7)
The metric g is everywhere Lorentzian with uniformly bounded inverse
$$\begin{aligned} \left|g^{-1} \right| \le C. \end{aligned}$$Let \(({\hat{g}})_{ij}\) be the restriction of the metric g on the tangent space to the constant t-hypersurfaces (\(i,j = 1,2,3\)). \(({\hat{g}})_{ij}\) satisfies the condition that for any \(\xi _i\),
$$\begin{aligned} C^{-1}\left|\xi \right|^2 \le \sum _{i,j = 1}^3 ({\hat{g}}^{-1})^{ij}\xi _i\xi _j \le C \left|\xi \right|^2 \end{aligned}$$where
$$\begin{aligned} \left|\xi \right|^2 = (\xi _1)^2 + (\xi _2)^2 + (\xi _3)^2. \end{aligned}$$Moreover, the spacetime gradient of t is timelike and satisfies
$$\begin{aligned} (g^{-1})^{00} = (g^{-1})^{\alpha \beta }\partial _\alpha t\partial _\beta t \le -C^{-1} < 0. \end{aligned}$$ -
(D8)
For \(\left|I \right| \le N+1\), the global coordinate functions satisfy the estimate
$$\begin{aligned} \left|\Gamma ^I(\Box _{g}x^{\mu }) \right| \le \frac{C\log (2+s)}{(1+s)^2} \end{aligned}$$where \(\Box _{\mathbf{g }}\) is the Laplace–Beltrami operator associated with g:
$$\begin{aligned} \Box _{\mathbf{g }} = \frac{1}{\sqrt{-\det g}}\partial _{\alpha }((g^{-1})^{\alpha \beta }\sqrt{-\det g}\partial _\beta ). \end{aligned}$$
Finally, we are ready to state the main theorem of [15]
Theorem
(Large Data Stability, Luk & Oh) Let \(N \ge 11\) and \(0 < \gamma ,\gamma _0 \le \frac{1}{8}\). For every-dispersive spacetime solution \({\mathcal {M}},g,\phi )\) of size \((C,\gamma _0,N)\) there exists \(\epsilon = \epsilon (C,\gamma ,\gamma _0,N) > 0\) such that for all \((\epsilon ,\gamma ,N)\)-admissible perturbationsFootnote 3 of \(({\mathcal {M}},g,\phi )\) the maximal globally hyperbolic future development is future causally geodesically complete and the spacetime remains close to \(({\mathcal {M}},g,\phi )\)Footnote 4.
This paper is devoted to finding a class of spherically symmetric solutions which satisfy the hypotheses of this theorem.
2.6 Averaging Operators
Some of the estimates near the axis will require some extra machinery to obtain. In particular, it will sometimes be useful to consider the averages of certain quantities over regions near the axis in order to obtain better control over them. To this end, following [18] we introduce the operators:
where as above \({\tilde{r}} := v-u\)
Similar to the u, v cases demonstrated in [18], we have for this r-averaging operator a differential formula:
Lemma 2.12
For \(s \ge 1\),
Proof
The procedure is identical to that presented in [18], but we will repeat it here in the new case for completeness. So let \(\rho = r^{s}\). Then \(s\rho ^{1 - \frac{1}{s}}\mathrm{d}r = \mathrm{d}\rho \) and \(s\rho ^{1-\frac{1}{s}}\partial _{\rho } = \partial _r\). Then, the LHS is
One then checks that, letting \(\sigma ' = \frac{\rho '}{\rho }\)
Thus,
So substituting we have
as claimed. \(\square \)
3 Main Results
In this section, I give precise formulations of the main results of this paper. The first two sections will focus on establishing decay for \(\phi \) and the geometry of solutions in the \(1+1\)-dimensional, spherically symmetric setting:
Theorem 3.1
Let \((\phi ,r,m)\) be a locally scattering solution to (SSESF’) with initial data asymptotically flat of order \(\omega ' \ge 2\) in \(C^k\) (\(k \ge 1\)) toward \({\mathcal {I}}^+\) and \({\mathcal {I}}^-\). Then, the following estimates hold in \(\mathbb {I}\) for all multi-indices \(\alpha ,\beta \) with \(\left|\alpha \right| \le k, \left|\beta \right| \le k+1\):










for \(l \le 2\).
Here, and throughout the remainder of this paper we will use the symbol \(\lesssim \) to indicate an inequality up to an unspecified constant depending only on the size of initial data (Bondi mass and \(\left|\phi \right|\)), \(\left|\alpha \right|\) and \(\left|\beta \right|\).
Remark 3.2
There exist locally scattering solutions with initial data of the above required asymptotic flatness. In particular, Luk, Oh and Yang show in [18] (see Theorem 1.5) that initial data \(\partial _v (r\phi )(1,v) = \Phi (v)\) asymptotically flat of order \(\omega ' > 1\) satisfying
for some \(\gamma ,\epsilon > 0\), and
gives rise to an equation satisfying the bounds:



Here \(\omega = \min {\omega ',3}\). In particular, for \(\omega ' \ge 2\), these three bounds imply that the solution corresponding to \(\Phi \) is locally scattering in \(C^k\) in the sense described above. In particular, any initial data which are asymptotically flat of the required order and satisfy these additional bounds give rise to a locally scattering solution of the type considered in Theorem 3.1.
Remark 3.3
In the proof of this theorem, we will not explicitly check that data of the type above gives rise to a global solution (i.e., one defined in the entire right half plane) of the form we wish to consider. This is, however, true, and we will assume as much. For discussion of this, see [9].
In fact, we will prove slightly stronger decay in \({\mathcal {Q}}\) en-route to this theorem; however, the above bounds suffice to prove our second result:
Theorem 3.4
Let \((\phi ,r,m)\) be as above, and suppose \(k \ge 11\). Let \(0 < \gamma \le \frac{1}{8}\). Then, the corresponding \((3+1)\)-dimensional solution to ESF \(({\mathcal {M}}, \mathbf{g }, {\tilde{\phi }})\) is a dispersive spacetime solution of size \((C,\gamma _0,k)\) (for some \(C > 0\) depending on the constants of Theorem 3.1) and is thus globally non-linearly stable to good non-spherically symmetric perturbations by Sect. 2.5.
4 Inductive Estimates in u, v in the Region \({\mathcal {Q}}\)
In this section, we prove that in \({\mathcal {Q}}\) all  satisfy estimates of the form
satisfy estimates of the form

to arbitrary differential order. We will work in the gauge (G1). Moreover, in this section we will only consider data posed on \(C_1\), rather than the full setting eventually required. This is all that’s required to address the region \({\mathcal {Q}}\), and is consistent by our compatibility assumption on the initial data.
We will, throughout this section, make use of several of the estimates in \({\mathcal {Q}}\) proved in [16]
Theorem
Let \((\phi ,r,m)\) be a locally scattering solution to (SSESF’) on \({\mathcal {Q}}\) with initial data asymptotically flat of order \(\omega '\) in \(C^k\) toward \({\mathcal {I}}^+\) for \(k \ge 1\). Then, the following bounds hold:









4.1 Outline of the Proof
The proof proceeds in three main parts. First we obtain the required control of mixed derivatives of r and \(r\phi \) which follow directly from the inductive hypothesis and our equation. We also obtain some initial improvements on decay for certain derivatives of \(m, \phi \) and \(\frac{m}{r^k}\) for \(k = 1,2\) in the same manner. Next we establish the required estimates for non-mixed (only u or v) derivatives of \(r\phi \). In v, these are obtained via a bootstrap argument, using the boundedness of the total variation in \(r\phi \), and the boundedness (resp. decay) of \(\phi \) and \(\frac{m}{r^2}\), combined with our high order asymptotic flatness assumption. In u, they are obtained by bootstrapping from the boundary condition. Finally, we use these estimates for u and v derivatives to obtain bounds for non-mixed derivatives of r and the required bounds for \(\phi ,m,\mu ,\) and \(\frac{m}{r^2}\) using the equation.
4.2 Inductive Framework
The goal in this section is to obtain bounds to arbitrary differential order in u, v via an inductive process. Our goal is the following inductive step:
Theorem 4.1
Let \((\phi ,r,m)\) be a locally scattering, asymptotically flat of order \(\omega ' \ge 2\) in \(C^q\) toward \({\mathcal {I}}^+\) solution to (SSESF’) in \({\mathcal {Q}}\), with data prescribed on some \(C_u\). Suppose that for all \(\alpha = (\alpha _u,\alpha _v),\beta \in {\mathbb {Z}}^2\) multindices with \(1 \le |\alpha | \le n < q\), \(|\beta | \le n+1\) (excluding \(\alpha ,\beta = (0,0)\)), we have the estimates










for \(k \le 2\), where in the region \({\mathcal {Q}}\), and we take \(\alpha _u,\beta _u > 0\) in (4.11), and (4.17), and \(\alpha _v, \beta _v > 0\) in (4.13) and (4.17), respectively. Then, in fact these bounds hold for \(\left|\alpha \right| = n+1, \left|\beta \right| = n+2\).
The remainder of this section will be devoted to the proof of this result and thus the closing of our first inductive bounds.
Before proceeding any further, it will be useful at times to exchange the order of (gauge invariant) derivatives without worry about changing the form of the resulting bounds. Moreover, we would like to know that the above bounds apply to more than just the specific orderings of derivatives written. To this end, we prove the following lemma:
Lemma 4.2
Suppose the bounds of Theorem 4.1 hold for \(\left|\alpha \right| \le n, \left|\beta \right| \le n+1\). Then, if any of the bounds (4.11), (4.13), (4.14), or (4.18) hold for some ordering of derivatives \(\left( \lambda ^{-1}\partial _v\right) ^{},\left( \nu ^{-1}\partial _u\right) ^{}\) at differential order \(n+1\), then in fact the same estimates hold for arbitrary reorderings of \(\left( \nu ^{-1}\partial _u\right) ^{},\left( \lambda ^{-1}\partial _v\right) ^{}\).
Moreover, if Eqs. (4.11) and (4.13) hold at order \(n+1\), then if (4.17) holds at order \(n+2\) for any ordering of \(\left( \lambda ^{-1}\partial _v\right) ^{},\left( \nu ^{-1}\partial _u\right) ^{}\), it holds for all orderings.
Proof
It suffices to check that the difference between two adjacent (i.e. differing by a single exchange of u and v derivatives) orderings always satisfies at least the same bound as the initial ordering.
We denote an ordering as a k-tuple of integers \(\mathbf {l}\) where the first entry represents the number of u derivatives acting at the far left of our differential expression, and subsequent entries give the number of derivative of the type different from that preceding it that occur before the next change. We will write an ordered gauge normalized differential with multi-index \(\gamma = (\gamma _u,\gamma _v)\) as \({\bar{\partial }}^{\gamma ,\mathbf {l}}\). For example, \({\bar{\partial }}^{(2,1),(1,1,1)}f = \left( \nu ^{-1}\partial _u\right) ^{}\left( \lambda ^{-1}\partial _v\right) ^{}\left( \nu ^{-1}\partial _u\right) ^{}f\).
We begin with the first part of our result. We also assume that Lemma 4.2 holds at all orders \(\le n\).
Then, let \(\left|\gamma \right| = n+1\), \(\mathbf {l},\mathbf {l}'\) be two orderings corresponding to \(\gamma \) that differ by one exchange. Then, for a function \(f = f(u,v)\) we can write
for \(\gamma _1,\gamma _2,\mathbf {l}_1,\mathbf {l}_2\) splitting \(\gamma ,\mathbf {l}\) around the two derivatives which are exchanged. Thus, we see that if
for all \(\gamma _3 + \gamma _3' = \gamma _1\) and appropriate sub-orderings given by the Leibniz rule, then the \(\mathbf {l}'\) ordering must satisfy the same estimate as the \(\mathbf {l}\) ordering. So in our first case, since all our bounds increase by no more than one power of r or u as a derivative is added, we need only check that

and the analogous statement for \(\lambda \). But each of these hold immediately since \(\left|\gamma \right|+1 \le n\) by construction, so by our hypotheses, these terms verify (4.13), (4.11), respectively. (There is a single exception to this, which is the case of a derivative of \(\lambda \) or \(\nu \) with only a single u or v derivative, respectively. In this case, the change in hypothesized order of decay from the mixed derivative to the non-mixed is slightly more; however, one checks that in fact the change is still covered, since it is given by exactly the extra term we obtain from the exchange). Thus, our first case is complete.
The second case is completely identical, requiring this extra order of derivative only because we work at one order higher (again there is some subtlety making the change from a mixed derivative of \(r\phi \) to a non-mixed derivative. Again one easily checks that this in fact a non-issue).
It remains to check that our assumption that Lemma 4.2 holds at all lower orders is justified. By induction, it suffices to check this for the case \(n = 0\). The only non-trivial case here is

which is better decay than that hypothesized for \(\left( \nu ^{-1}\partial _u\right) ^{}\left( \lambda ^{-1}\partial _v\right) ^{}(r\phi )\), so the exchange holds (note that this also checks the problematic portion of the second case above).
Thus, the proof is complete. \(\square \)
4.3 Decay for Mixed Derivatives of r
We begin with mixed derivatives of r, i.e., \(\partial ^\alpha r\) such that neither \(\alpha _u\) nor \(\alpha _v\) is 0.
Lemma 4.3
Under the hypothesis of Theorem 4.1, let \(\left|\alpha \right|,\left|\beta \right| = n+1\) and \(\alpha _u,\beta _v > 0\). Then, the following hold:


Proof
In each case, this is essentially completely computational. We start with (4.20). By our hypothesis and (SSESF’), we can rewrite the LHS as
Expanding this expression via the Leibniz rule, we have a general term:
where \(\alpha ^1+\alpha ^2+\alpha ^3 = (\alpha _u-1,\alpha _v)\). We may ignore the leading term as \(\mu < \frac{1}{2}\) by (4.1), so we only consider the differential terms. There are, in principle, many combinations to check; however, observing that by the form of our hypothesized estimates (in particular the uniform gains on certain terms) we only need to address the following cases:
-
(1)
\(\alpha ^1 = \alpha ^2 = 0\).
-
(2)
\(\alpha ^1 = \alpha ^3 = 0\).
-
(3)
\(\alpha ^2 = \alpha ^3 = 0\).
-
(4)
\(\alpha ^2 = 0\), \(\alpha ^1,\alpha ^4 \ne 0\).
All other terms are strictly better by our inductive hypothesis, since they gain more than one power of decay per derivative. In the first case, we have

by (4.9), (4.18). The second case is bounded (up to a constant) by

The third case has

Finally, in the fourth case we have

Thus, all our terms satisfy the desired decay.
The \(\nu \) case then amounts to the same bounds, except that we lose a power of v via (SSESF’) instead of u. Thus, we will not repeat the details of this proof. \(\square \)
This proposition leaves out exactly two cases, \(\partial ^{n+1}_u\nu ,\partial ^{n+1}_v\lambda \), which require slightly more careful treatment. We will return to these after closing some of the other bounds at order \(n+1\).
4.4 Decay for Mixed Derivatives of \(r\phi \)
We are now ready to work on derivatives of \(r\phi \) at order \(n+2\). The goal is as above:
Lemma 4.4
Under the hypotheses of Theorem 4.1 for \(\beta \) a multi-index with \(\left|\beta \right| = n+2\) and \(\beta _u,\beta _v \ne 0\), we have

Proof
The procedure here is roughly the same as that for mixed derivatives of \(\lambda \) and \(\nu \) above. We have by the wave equation for \(\phi \) that
Thus, we can rewrite our first expression as
Then, we can expand this term by term via the Leibniz rule with the general term being of the form (omitting terms of order 1)
with \(\sum _{i}\gamma _i = \alpha '\). As before, the terms with lowest order of decay occur when exactly one term is acted on by all derivatives. Thus, we have three cases to check:
-
(1)
\(\gamma ^1 = \gamma ^2 = 0\).
-
(2)
\(\gamma ^1 = \gamma ^3 = 0\).
-
(3)
\(\gamma ^2 = \gamma ^3 = 0\).
All other mixtures only improve by a constant order in r or u, so we need not consider these.
In the first case, we have

by (4.9), (4.14), (4.17), (4.15). In the second case, we have

by (4.9), (4.5), (4.2). The third case similarly gives us

by (4.2), (4.5), (4.18). So in each case the the desired bound holds, and we conclude that the first relation holds at order \(n+1\). \(\square \)
As above, it remains to deal with the cases \(\partial ^{n+1}_v(r\phi ),\partial ^{n+1}_u(r\phi )\).
4.5 Preliminary Estimates for \(\phi \), m and \(\frac{m}{r^k}\)
In this section, we will use our upgraded bounds for derivatives of r above to obtain some initial estimates for \(\phi \), m weightings at order \(n+1\). We will begin with an easy bound for \(\phi \).
Lemma 4.5
Suppose our inductive hypotheses hold at order n. Then, for \(\left|\alpha \right| = n+1\) we have the bounds

Proof
This follows by expanding \(\left|\left( \nu ^{-1}\partial _u\right) ^{\alpha _u}\left( \lambda ^{-1}\partial _v\right) ^{\alpha _v}(r\phi ) \right|\) to obtain

by (4.15), (4.16), (4.17), where \(\vartheta (n) = {\left\{ \begin{array}{ll} 1 &{} n \ge 1\\ 0 &{} \text {otherwise}\end{array}\right. }\). So then via the triangle inequality we can write

and thus

dividing through by the r and taking our most weakly decaying terms (those which lose a v derivative acting on \(\phi \)) on the RHS as our minimal order of decay to obtain our desired bound. \(\square \)
Observe that this bound then allows us to immediately obtain optimal next order control over m as well:
Corollary 4.6
With the estimate Lemma 4.5 we have, for \(\left|\alpha \right| = n+1, \alpha _v > 0\), we have

Proof
We begin with our first relation. Recall from (SSESF’) that we have
Then, the cases we need to consider here are:
-
i.
All derivatives act on \(r^2\) and \((\partial _v \phi )^2\).
-
ii.
All derivatives act on \((1-\mu )\) and \(r^2\).
In the first case, we have a general term:

for \(\left|\beta \right| \le 2\), where we have used the inductive hypothesis and the result of Lemma 4.5, as well as the fact that  to control each case, as we gain the same overall power of decay by taking a derivative of r, as we do by differentiating a copy of \(\left( \lambda ^{-1}\partial _v\right) ^{}\phi \). This gives us the desired order of decay.
to control each case, as we gain the same overall power of decay by taking a derivative of r, as we do by differentiating a copy of \(\left( \lambda ^{-1}\partial _v\right) ^{}\phi \). This gives us the desired order of decay.
In the second case, we have the term

using (4.7), (4.18) and the same strategy as above. Thus, we have our bound in the case \(\alpha _v > 0\).
It remains to address the case where \(\alpha _v = 0\). Now we must use our other equation for m:
As above, we have two distinct cases. The overall analysis is the same, differing only in the fact that we now lose our extra power of r decay from the additional \(\left( \lambda ^{-1}\partial _v\right) ^{}\phi \) term. As such we will arrive at a bound of the same overall form, with one less power of r decay than we would expect if we had a v derivative, and so arrive at a bound:
by the same computation as above. \(\square \)
With this control of m established, we now must concern ourselves with the weighted versions \(\mu ,\frac{m}{r^2}\). The following lemma will take care of this:
Lemma 4.7
Given the result of Corollary 4.6, we have the bounds

for \(k = 1,2\), \(\left|\alpha \right| = n+1\).
Proof
We will employ a similar technique as was used to gain our initial bound on \(\partial ^{\alpha }\phi \) above. In particular, observe that we have
So rearranging we find
This gives rise to the bound

where we bound the general term in the sum using that . Thus, the overall order of decay this obtains is
. Thus, the overall order of decay this obtains is

\(\square \)
Remark 4.8
The r decay obtained in this manner for \(\mu ,\frac{m}{r^2}\) is already as strong as we hope for.
4.6 Full Decay for Derivatives of \(r\phi \)
With this initial control, we find ourselves in a difficult position. The remaining terms to bound all suffer from a heavy \(r^{-1}\) weighting, which will prevent us from closing any further bounds through the standard manner of computation we have pursued thus far (and also excludes the use of averaging operators).
In order to proceed, it will be necessary to obtain some next order control near the axis as well. To do this, we will employ a bootstrapping approach centered around next order control of \(r\phi \). Before beginning this however, we will need a few preliminary estimates in order to check that the bootstrap closes:
Proposition 4.9
Suppose, under the hypotheses of Lemma 4.5, with associated constants at order \(\alpha = (\alpha _u,\alpha _v)\), \(C_{\alpha _u,\alpha _v}\), we, in addition, have the bound
For \(1 \le u < U\).
Then, the following hold on \(1 \le u < U\), for some \(C'\) depending only on n (in particular, we require only one constant on all of \({\mathcal {Q}}\))



Proof
To obtain (4.23), we simply employ our averaging operator:
and then applying our hypothesis (4.22) the RHS is bounded in absolute value by

where the first bound is obtained by dividing through by \(v^{-(n+2)}\) and pulling out the remaining copy of \(v^{-1}\), to yield a bounded integral with an additional u weight, and the second bound is obtained by using the simple supremum estimate to remove the v term and then integrating directly. The additional factor of \(\frac{3}{2}\) results from evaluating the integral in r thanks to our bound on \(\left|\lambda \right|\), (4.1). Since the derivatives acting on extra factors of \(\lambda \) are all well controlled, we ignore these terms without restriction.
Next, turning our attention to (4.24) we observe:
Note that by our hypotheses we can then simply ignore the terms with derivatives acting on the \(\lambda \)’s, as these cannot be worse than those in which only \(\frac{m}{r^3}\) is differentiated. We do not have enough a-priori control of either of these terms. Observe that, employing averaging operators, we have
In particular, we need only to bound the term \(\partial _v^n \frac{\partial _v m}{r^2}\) in order to control the derivative of \(\frac{m}{r^3}\). But this is exactly our first term, thus estimating this is sufficient. By our equation (SSESF’), the first term is
Observing that, by our hypotheses and the bound found above, all these terms gain either a power of r or of u decay for each derivative applied, we immediately have:

by our hypotheses and the above estimates (Thus, \(C_1\) depends only on constants controlling lower-order terms and C for the highest derivatives of \(\phi \)). This controls the first term we are interested in directly, and we use this to obtain

Splitting the integral into regions \(r^{n+4}(u,v') < u^{n+6},r^{n+4}(u,v') > u^{n+6}\) and applying the appropriate bounds to obtain the first bound, and simply using the uniform u bound to obtain the second, modifying the constant to \(C_2\) to account for various constants (all independent of C by our above bounds) that enter in this integration, the desired estimate (4.24) follows.
Finally, we will check (4.25). This is quite similar to (4.24) above, but now our term is:
The second term is already optimally controlled by our hypotheses, so we need only address the first. This is given by
Since we lose at most one derivative to removing this extra power of r, this is bounded by

Combining this with our bound for the second term, we obtain the desired bound (with an extra leading factor to observe the constant independent of C). \(\square \)
In order to do our bootstrapping, we must guarantee some smallness of the term dependent on the highest order constant C above. To this end, we prove the following proposition:
Proposition 4.10
Let \(\epsilon > 0\). There exists some \(v_0 > 1\) such that for all \(v > v_0\),
and
Proof
Since we need only find some \(v_0 > 1\), and r is monotone in v and unbounded, we may assume without restriction that \(r(1,v)> \frac{v}{6} > 1\). We begin with (4.26). We have by eq. (4.9) that

By monotonicity of r in u, we can thus bound (4.26) by
Now recall that \(\frac{1}{3}(v-u) \le r(u,v) \le \frac{1}{2}(v-u)\); thus, we conclude that
The first two terms can simply be evaluated directly. The last term can be rewritten
Then, evaluating each term above using these bounds, we conclude that we can bound (4.26) by
with \(C_1,C_2\) accounting for the necessary change of variable factors. Thus, we see that we can take  and this satisfies the required conditions.
and this satisfies the required conditions.
We will now address (4.27). In this case, we have by (4.2) that

Thus, (4.27) is bounded by
Integrating, and absorbing constants from changing variables into an overall factor \({\tilde{C}}''\), we can bound (4.27) by
with \(C_4\) absorbing any multiplicative factors in the logarithm (again from integration). Thus, we can find a \(v_0\) satisfying our requirements.
Finally, to obtain (4.28), we have

by simply integrating to \(u' = \frac{v}{2}\) in \(r^{-2}\) and the rest of the way using the u bound. We thus, again, find a suitable \(v_0\). Taking the largest of the three choices, we have our result. \(\square \)
Lemma 4.11
In fact, we have:
Proof
Recall from the asymptotic flatness and gauge conditions that we have (2.5):
Moreover, observe that we have the following bound for \(\frac{\partial _u}{\nu }\left( \frac{\partial _v}{\lambda }\right) ^{n+2}(r\phi )\):

using the results of corollary 4.6 and lemma 4.5, with our remainder term contributed by those terms in which some derivative acts on the \(\lambda ^{-1},\nu ^{-1}\) weights. In particular, for any \(C > 0\) there is an \(\epsilon _{C}\) such that
for all \(\delta \le \epsilon _{C}\). Thus, we are in the scenario of proposition 4.9, and we can conclude the results of proposition 4.9 for \(u \le 1+\epsilon _{C}\). Our goal is to bootstrap this bound for \(\left( \lambda ^{-1}\partial _v\right) ^{n+2}(r\phi )\), so in particular we would like to improve our control of the integral
Observe that by taking C large enough, we can ignore all the integral terms that do not themselves include a factor of C. By proposition 4.9 and our previous bounds, all terms immediately verify estimates with the proper u and v weights except those with all derivatives acting on one of \(\phi ,\mu \) and \(\frac{m}{r^2}\). We will check these explicitly. In the \(\phi \) case, we have

using proposition 4.9 and (4.26), so long as \(v > v_0\) corresponding to the required \(\epsilon \) (which depends only on n by construction). By (4.25) and our bounds on \(\phi \), the \(\mu \) case satisfies the same bound (in fact better, but the procedure is the same). It remains to check the \(\frac{m}{r^2}\) case. Here we have:

using proposition 4.9. We obtain the same result for the other \(\left( \lambda ^{-1}\partial _v\right) ^{n+1}\frac{m}{r^2}\) term, as a consequence of (4.28). Since we can suppress our leading constants as much as we like for \(v > v_0\), and the region  is compact, if we take our C large enough, we can improve our estimates to:
is compact, if we take our C large enough, we can improve our estimates to:
Using (4.26), and Gronwall’s lemma, we can deal with this last term to obtain
Taking \(\epsilon \) small enough, this represents a strict improvement on our initial bound.
Thus, we conclude by continuity, and our preliminary estimates, that the region on which \(\partial _v^{n+2}(r\phi )\) satisfies our bound is, in fact, strictly larger along each \(\underline{C_v}\). In particular, we conclude that the region on which (4.29) is closed (by continuity), open, and non-empty (by the above). Thus, it is our entire domain, so we have our required estimate. \(\square \)
With this established, we can also address the u derivative case.
Lemma 4.12
Suppose the following bound holds in a neighborhood \(Op(\Gamma )\) of the axis:
Then, we have the following bounds on a neighborhood of \(\Gamma \):



Proof
The approach for each term is essentially the same as above. In order to obtain (4.31), we again employ our averaging operators, now integrating in u rather than v. We have
So using the sup bound for our u term, and integrating in r, we find that
If we instead use the sup bound for r, and integrate in u, we also obtain
Together, these give our bound.
Now we can move to \(\frac{m}{r^2}\). We can employ the same technique as above, noting that
As above we will ignore terms in which \(\nu \) is differentiated, as these are no worse than those in which \(\frac{m}{r^3}\) is by hypothesis. Similar to the above, it suffices to control the expression
This verifies the bound

This controls our first term directly, so we need only address our \(\frac{m}{r^3}\) term. This time we obtain control by averaging in u:
Observe that, substituting our bounds in, this integral is the same as that used to bound (4.24) but with the roles of u and r interchanged. Thus, we obtain the following bound:

Finally, we can address (4.33). As above, we need only consider the term
Applying the same analysis as above, we conclude that

so taking \(C'\) sufficiently large we have our result. \(\square \)
Again in parallel to the case above, we must obtain some small quantities in order to close this second bootstrap.
Proposition 4.13
For any \(\epsilon > 0\) there is \(U > 1\) such that for all \(u > U\),
Proof
We begin with (4.34). By (4.9), we have the bound

So, integrating the second bound from \(r = 0\) to 1, and the first the rest of the way, we obtain
where \(C'\) absorbs any integration constants. Thus, we have our result, taking \(U > \frac{C_1C' + 1}{\epsilon }\). \(\square \)
Lemma 4.14
Similar to Lemma 4.11, we in fact have:
Proof
As above, we will ignore the extraneous factors of \(\lambda ,\nu \) introduced by our weighted derivatives, since these cannot contribute anything worse than our desired decay.
Recall that, by our initial data, we have that, on \(\Gamma \):
for all k. In particular, we obtain the bound:
from our bounds (4.29), and Lemma 4.4, for some \(C > 0\). Then, by continuity, there is a neighborhood \(N \supset \Gamma \) such that
for all \((u,v) \in {\overline{N}}\). We can also estimate \(\left( \nu ^{-1}\partial _u\right) ^{n+2}(r\phi )\) by
In turn, we can bound this by:
for \(C_1,{\tilde{C}}\) independent of our bootstrap constant C, in particular depending only on n, and bounds on low order derivatives of \(\lambda ,\nu \).
The only terms which can contribute constants proportional to C are those in which all derivatives act on \(\phi ,\mu \) or \(\frac{m}{r^2}\). In the first two cases, we find similar to the above that this constant can be suppressed as much as we like outside some region with bounded u, by (4.31), (4.33), (4.34). Thus, we are left only to address the \(\frac{m}{r^2}\) terms. First, we have

for \(C'\) dependent only on n. Splitting the integral in a manner similar to the above, we conclude that we can bound this term by
Thus, as above, this constant can be suppressed arbitrarily outside of some finite u region.
Finally, we have

So once again integrating, we obtain a bound
Thus, we conclude that there is some universal \(U > 1\) satisfying the conditions for (4.34) to hold with small enough \(\epsilon \) and moreover satisfying

In particular, this U does not depend on C or N. Then, taking C large enough to absorb lower order constants, we conclude that we strictly improve our estimate in the region \(u > U\). For \(u \le U\), we can simply take C large enough to make our bound hold everywhere in this region if it does not already, since for any finite u region we require only some constant bound, which holds immediately by continuity. Thus, we conclude that we can improve our estimate to
on N. Then, our initial bound is satisfied on some strictly larger neighborhood, and as above we conclude by connectedness and continuity that there is C such that
on all of \({\mathcal {Q}}\). \(\square \)
4.7 Full Decay for Derivatives of \(\lambda ,\nu \)
We are now ready to control non-mixed derivatives of r.
Lemma 4.15


Proof
As usual, we can safely ignore terms where some derivatives act on different copies of \(\lambda \) or \(\nu \), as there immediately satisfy our bounds as a consequence of our inductive hypothesis.
We’ll start with (4.36). To begin, we use our gauge condition to obtain:
The only term we must control on the RHS is

since all the other terms satisfy the required decay up to some constant C by our hypotheses, (4.24), (4.25), Lemma 4.3 and the split integration employed above. This can then be controlled by Gronwall’s lemma, and (4.26); thus, we conclude (4.36).
For (4.37), we gain initial control by the second half of our gauge condition:
on \(\Gamma \). As a result of this, (4.36) and Lemma 4.3, we conclude that
Thus, we have
As above, we can commute the v derivative past all the others, and then, we only need to control the term
By (4.33), (4.32), Lemma 4.3, and splitting the integral into the regions \(r<1\), \(r > 1\) we control all terms adequately except that in which all derivatives act on \(\nu \). In this case, we once again employ Gronwall and (4.34) and conclude the desired bound. \(\square \)
4.8 Full Decay for Derivatives of \(\phi \),\(\frac{m}{r^k}\)
Following the results of proposition 4.9, eqs. (4.29) and (4.35), and lemma 4.12, we can conclude optimal bounds for all the \(n+1\)st derivatives of \(\phi ,\mu \) and \(\frac{m}{r^2}\). To aid in this, we will need some auxiliary estimates:
Proposition 4.16
For \(\phi \) a solution to (SSESF’)
Proof
Observe that we have
By (SSESF’) \(\partial _u\partial _v(r\phi ) = \phi \partial _u\partial _v r\), so we are left with
Now consider
Expanding this last term, we see
Returning to our original equation, we find that
thus, substituting this in and rearranging we have
\(\square \)
We also note the following relation:
for \(k = 1,2\).
We begin with \(\phi \).
Lemma 4.17
The following holds for \(\left|\alpha \right| = n+1\).

Proof
The non-mixed cases have already been done, and moreover, the r weighted bounds follow immediately from (4.4), (4.29), (4.35) and our inductive hypothesis by the same method as Lemma 4.5. Thus, it remains only to address the non-r-weighted bounds. In order to do this we employ proposition 4.16, noting that, as a consequence, we can write for \(\left|\alpha \right| = n+1, \alpha _u,\alpha _v > 0\):
The left hand side can be rewritten
where \(R_0\) equal to the sum of remaining terms (those with some product of derivatives of at least two of \(\lambda ,\nu \) and \(\partial _u\partial _v\phi \)) all of which are controlled by hypothesis as each individual term is of lower total differential order. In particular, we have that
On the RHS, we will work term by term:
First, we have
where as above \(R_1\) collects terms with derivatives acting on at least two of \(\lambda ,\nu ,\phi \). This is similarly controlled by the hypotheses (4.14), (4.11), (4.10), (4.12), and (4.13) as each derivative is of total order smaller than \(n+1\), so we have
The next term is
with \(R_2\) defined similar to \(R_0,R_1\) above. But all of these terms are immediately bounded (up to overall constant) by \(u^{-(\left|\alpha \right|+4)}\) by (4.14), (4.11), (4.10), (4.12), and (4.13) since no single term receives more than n derivatives.
Finally, we consider
where \(R_3\) absorbs all terms with at least two derivatives acting on r. We can rewrite this further in terms of our gauge invariant derivatives as
where \(R_3'\) additionally absorbs the additional mixed derivative remainder terms from converting to gauge invariant derivatives excluding those from \(r\partial _u^{\alpha _u}\partial _v^{\alpha _v+1}\phi \) already included above. This term is controlled by (4.14), (4.3), (4.11), (4.10), (??), and (4.13) as no derivative of order greater than n acts on \(\phi \), and no term of order beyond \(n+1\) acts on \(\lambda ,\nu \). As such, this term satisfies
Combining all of this, we arrive at the following equation:
Observe that we have two terms proportional to \(\left( \nu ^{-1}\partial _u\right) ^{\alpha _u}\left( \lambda ^{-1}\partial _v\right) ^{\alpha _v}\phi \) on the RHS, so we can rearrange to obtain:
Then, recall that  , for some \(C > 0\); thus, outside of some compact region we have \((\alpha _v+1-\left( \lambda ^{-1}\partial _v\right) ^{}\lambda ) > 1\) for all \(\alpha _v \ge 1\). Since the region is compact, we need not be concerned with the behavior inside as this can be absorbed by a constant.
, for some \(C > 0\); thus, outside of some compact region we have \((\alpha _v+1-\left( \lambda ^{-1}\partial _v\right) ^{}\lambda ) > 1\) for all \(\alpha _v \ge 1\). Since the region is compact, we need not be concerned with the behavior inside as this can be absorbed by a constant.
Thus, it suffices to bound the RHS of (4.42) in order to control \(\left( \nu ^{-1}\partial _u\right) ^{\alpha _u}\left( \lambda ^{-1}\partial _v\right) ^{\alpha _v}\phi \). We will do this inductively, inducting on \(\alpha _u\). The base case \(\alpha _u = 0\) is already covered by our bootstrap, so suppose the bound (4.39) holds for \(\alpha _u< k < n\). So treating each term individually, we have by our inductive hypothesis (on \(\alpha _u\))

which is strictly better than required (the estimates agree near the axis, and the r estimate is strictly better at large r). Thus, we can move to our next term:
but there is nothing to do here, as all these terms are controlled by hypothesis and thus immediately verify the necessary bounds.
Next, we consider
This now is controlled by our inductive hypothesis, as we take one fewer derivatives in u and overall order \(n+1\). This leaves us
where we obtain this bound by the same mechanism as Lemma 4.5 at the next order. Finally, we have
again obtaining an \(r^{-1}\) weighted bound in the manner of Lemma 4.5 and using the \(u^{-3}\) bound for \(\left( \nu ^{-1}\partial _u\right) ^{}\lambda ,\left( \nu ^{-1}\partial _u\right) ^{}\nu \) of eq. (4.4), (4.11).
Putting this all together, we obtain
So by induction on \(\alpha _u\) we have our result. \(\square \)
It remains only to check that \(\mu ,\frac{m}{r^2}\) also verify the required estimates to complete our induction:
Lemma 4.18
For \(\left|\alpha \right| = n+1, \alpha _u,\alpha _v \ne 0\) we have

for \(k = 1,2\).
Proof
Recall that for \(\alpha _v = n+1,\alpha _u = n+1\) we already have our optimal bounds via the bootstrap. Moreover, optimal r-weighted bounds are achieved in general in Lemma 4.7, so we need only concern ourselves with bounds in terms of u only. We will proceed via induction in \(\alpha _u\) with base case 0 already done. To induct, suppose (4.43) already holds for all \(\alpha _u< l < n\). By Lemma 4.2, it suffices to control \(\left( \nu ^{-1}\partial _u\right) ^{l-1}\left( \lambda ^{-1}\partial _v\right) ^{n+1-l}\left( \nu ^{-1}\partial _u\right) ^{}\frac{m}{r^k}\) in order to proceed to the next level. Then, by Eq. (4.38) we have
Splitting this up term by term, we have

by our inductive hypothesis. Next we have
and
Observe that regardless of the derivative that acts on \(\phi \) these terms will satisfy the same order of u decay by our above results, so we will only prove this for the first of these terms.
When \(k = 2\), this is simply
by (4.14). When \(k=1\) we have
by (4.14), obtaining a term with an \(r^{-1}\) (in the case all derivatives act on the \(\left( \nu ^{-1}\partial _u\right) ^{}\phi \)’s) by the methods of Lemma 4.5.
Putting this together, we have our result by induction. \(\square \)
4.9 Closing Induction
Finally, we can close our induction checking that our bounds hold at order \(\left|\alpha \right| = 1\), which is immediate from the previous results of [16].
5 Extension to the First Quadrant
To prove Theorem 3.1, it remains to control solutions in the region \(\mathbb {I} \setminus {\mathcal {Q}}\). In order to do this, we will have to turn to our full data prescribed on both \(C_1\) and \({\underline{C}}_R\). In fact, we will establish estimates on all of the region \({\mathcal {O}}_R\), completing the proof of Theorem 3.1Footnote 5. The initial data considered in Sect. 4 are thus extended by any compatible prescription of \(\partial _u(r\phi ),\nu \) on \({\underline{C}}_{2R}\) (we modify our notation here slightly to ease things later). Note that this is a well-posed problem since we work in the spherically symmetrically reduced setting. This extension is studied at first order in [9], and one can check by a standard iteration argument that this is a well-posed initial value problem on the region between \(C_1\) and \({\underline{C}}_{2R}\) for sufficiently regular data, so long as one guarantees that the data agree at the intersection point \(C_1\cap {\underline{C}}_{2R}\).
In this section, we will consider data which are asymptotically flat of order \(\omega ' \ge 2\) in \(C^k\) toward both \({\mathcal {I}}^+\) and \({\mathcal {I}}^-\) and the gauge (G3).
As in Sect. 4, we will inductively establish the control that we need. The goal will be the following
Theorem 5.1
Let \((r,\phi ,m)\) a solution to (SSESF’) in the region \({\mathcal {O}}_{2R}\) with data asymptotically flat of order \(\omega ' \ge 2\) in \(C^k\) toward both \({\mathcal {I}}^+\) and \({\mathcal {I}}^-\). Then, the following bounds hold for all multi-indices \(\alpha ,\beta \) with \(\left|\alpha \right| \le k\), \(\left|\beta \right| \le k+1\):










where we take \(\alpha _u,\beta _u\) to be nonzero in eqs. (5.2) and (5.8), respectively, and \(\alpha _v,\beta _v\) nonzero in eqs. (5.4) and (5.8), respectively.
5.1 First Estimates for \(\lambda ,\nu ,r\phi \) and m
We will make use of the following result of [9] (cf. Proposition 5):
Proposition 5.2
There exists \(R_0 > 1\) (depending on the size of our data) such that for \(R > R_0\) the domain of the solution to (SSESF’) with data posed on \({\underline{C}}_{2R}\) (in the u, v coordinates) is \({\mathcal {O}} = [-\infty ,1] \times [2R,\infty ]\), and moreover, the following estimates hold on \({\mathcal {O}}\):
We’ll now obtain some additional low order bounds necessary to begin our bounding by induction on the order of derivatives.
Proposition 5.3
The following bounds hold on \({\mathcal {O}}\):
Proof
(5.19), (5.21), (5.28), and (5.29) can be read off directly from (SSESF’) and proposition 5.2.
From here, we will begin with (5.22), and (5.23). For (5.22), we have
So rearranging, we have by (5.16), and (5.11)
The same can be done for \(\left( \nu ^{-1}\partial _u\right) ^{}\phi \) using (5.15),and (5.11), and we obtain (5.23) as well.
Now we can move to our bounds for m (5.24) and (5.25). For (5.24), we have
using (5.22). We similarly obtain (5.25) using (5.23).
From this, (5.26) and (5.27) follow immediately via the Leibniz rule and (5.12), (5.13).
Next, for (5.18):
By our assumptions on R, and (5.19) \(\int _1^u \left|\partial _u\lambda (u',v) \right| \mathrm{d}u' \lesssim r^{-1}(1,v)\) for all \(v \ge 2R\), so we can apply Gronwall’s inequality to deal with our first term, and our decay will be determined by the second term. Applying (SSESF’), this can be bounded by
The \(\partial _v\lambda \) can be grouped with our other term containing this in our application of Gronwall (the coefficient decays like \(\frac{m}{r^2}\) and thus is integrable by (5.25)), so our decay is determined by the remaining terms, thus bounded by \(r^{-2}v^{-1}\) (with the term differentiating \(r^{-2}\) having the lowest order of decay), using (5.21), (5.24). Thus, integrating we obtain (5.18). Again repeating the same procedure for \(\left( \lambda ^{-1}\partial _v\right) ^{}\nu \) obtains the symmetric u bound (5.20).
Now, for (5.30) we have
This leading term is bounded by \(v^{-3}\), and the latter term can be written
The second term here can be controlled via Gronwall’s inequality since \(\partial _u \lambda \) is integrable by (5.19). The first term can be expanded:
As usual, we can absorb the \(\left( \lambda ^{-1}\partial _v\right) ^{2}(r\phi )\) term via Gronwall, so we are left with only the other terms. By the above results, we have that these are all bounded by \(r^{-2}v^{-2}\), so we obtain as an overall bound:
since our integral contributes a \(r^{-1}v^{-2}\) which is strictly smaller than \(v^{-3}\) on \({\mathcal {O}}\). One sees directly that (5.31) can be obtained in the same manner by exchanging the roles of u and v at each step and substituting the correct bounds from above. \(\square \)
5.2 Higher-Order Derivatives
The remainder of this section will be devoted to closing the following induction which completes the proof of Theorem 5.1:
Lemma 5.4
Let \(r,\phi ,m\) solve (SSESF’) in the region \({\mathcal {O}}\) with initial data smooth, asymptotically flat to order N, satisfying the assumptions of Proposition 5.2. Suppose the following bounds hold for multi-indices \(\left|\alpha \right| \le n, \left|\beta \right| \le n+1 < N\):










where we take \(\alpha _u\) to be nonzero in (5.33), respectively, and \(\alpha _v\) nonzero in (5.35) and \(\beta _u,\beta _v\) both nonzero in (5.39).
Then, in fact these estimates hold for \(\left|\alpha \right| \le n+1, \left|\beta \right| \le n+2\).
Before proving this, we must check, in the same vein as Lemma 4.2, that in fact suffices to control only one ordering of the above derivatives in order to obtain the listed order of decay for any rearrangement of them:
Proposition 5.5
Suppose the hypotheses of Lemma 5.4 hold for \(\left|\alpha \right| \le n, \left|\beta \right| \le n+1\), for some ordering of derivatives \(\left( \lambda ^{-1}\partial _v\right) ^{},\left( \nu ^{-1}\partial _u\right) ^{}\), then in fact the same estimates hold for arbitrary reorderings of \(\left( \nu ^{-1}\partial _u\right) ^{},\left( \lambda ^{-1}\partial _v\right) ^{}\).
Proof
The proof is identical to that given for Lemma 4.2 above and is not repeated. \(\square \)
Observe that the hypothesis above is immediately satisfied by proposition 5.3. Thus, proving Lemma 5.4 immediately gives us Theorem 5.1.
Proof of lemma 5.4
We begin with (5.36). In this case, we write
where \(\vartheta (x)\) is a step function, 0 for \(x < 0\), 1 for \(x \ge 0\). Thus, we obtain the desired bound
by simply multiplying our hypothesized bounds at these orders and using the fact that \(u,v \lesssim r\) in \({\mathcal {O}}\).
Next, we move to (5.39). By proposition 5.5, it suffices to check the following case:
By hypothesis, this is bounded by
so we have our required decay.
The bounds (5.33), and (5.35) follow similarly directly from (SSESF’) and our hypothesis.
Now for (5.37), we consider the terms
In each case, the term with minimal decay is when all derivatives act on some copy of \(\left( \lambda ^{-1}\partial _v\right) ^{}\phi \) or \(\left( \nu ^{-1}\partial _u\right) ^{}\phi \), respectively, and by (5.36) this is bounded by
and
But by proposition 5.5, the difference between these two terms is of order
so in fact each satisfies both bounds, and we can safely take the minimal value of these two bounds. Thus, we obtain (5.37). From this, (5.38) follows immediately by splitting the derivatives over m and \(r^{-k}\).
Next we can proceed to (5.32), and (5.34). The approach and bounds are completely symmetric by exchanging u for v, so we will only prove (5.32) in detail. So we write:
By the same procedure as used in the proof of proposition 5.5, this integrand can be bounded by
By our hypothesized bounds and the results above, all of the terms in the latter sum are bounded by \(r^{-1}v^{-\left|\alpha \right|}u^{-1}\), or by \(r^{-2}\left( \lambda ^{-1}\partial _v\right) ^{\left|\alpha \right|}\lambda \) and so can be controlled by Gronwall’s inequality. In either case, we have the necessary decay (since the former term integrates to \(v^{-(\left|\alpha \right| + 1)}\)), so we can safely ignore these. Thus, all that remains is
The term in which all derivatives act on \(\lambda \) can be controlled by Gronwall, since \(r^{-2}\) in globally integrable, and the remaining terms all satisfy decay like \(r^{-2}v^{-\left|\alpha \right|}\) with \(\left( \lambda ^{-1}\partial _v\right) ^{\left|\alpha \right|}r^{-2}\) being the term with the lowest power of decay. Thus, integrating, we obtain the bound
as desired.
Finally, we move to (5.40), (5.41). As with (5.32), and (5.34), the proof of (5.41) is the same as that for (5.40) with the roles of u and v interchanged, and so is not repeated. Thus, we have
By our constraints on the data, \(\left( \lambda ^{-1}\partial _v\right) ^{\left|\beta \right|}(r\phi )(1,v)\) is already good enough so we need to control the integral term. We can bound this integrand by
This second term already satisfies the necessary decay, so we are concerned only with the first. By our hypothesis and the bounds already checked above, we have that (expanding) each term in this derivative verifies decay bounded by at least
Thus, our integral is bounded overall by \(v^{-(\left|\beta \right| + 1)}\), so we have
The u case is similar. \(\square \)
This completes the proof of Lemma 5.4 and thus Theorem 5.1. In particular, we have our first main result: Theorem 3.1.
6 Stability to Non-symmetric Perturbations
It remains now to prove Theorem 3.4. We have established control in spherical symmetry through the proof of Theorem 3.1 above, but it remains to check that the lifts of these solutions to \((3+1)\)-dimensional solutions to (ESF) are in fact dispersive of order \((C,\gamma _0,N)\) for \(\gamma _0,N\) sufficiently large. To do this, we must (1) check that these bounds transfer nicely to the full \((3+1)\)-dimensional solution, and (2) construct a suitable gauge and coordinate system.
In this section, we address this second issue. In particular, we construct a gauge and coordinate system and check that in this setting (given a resolution for the first concern above) the conditions for our solution \(({\mathcal {M}},\mathbf{g },{\tilde{\phi }})\) to be dispersive of order \((C,\gamma _0,N)\) hold for the solutions considered in the hypotheses of Theorem 3.4.
6.1 Coordinates and Gauge
We must construct a set of coordinates and prescribe a gauge for our solutions to (ESF) on \({\mathcal {M}}\) before we can check the conditions of 2.11. Since we take our solution to project to a solution of (SSESF’) of the type considered in Theorem 3.1, we have immediately that our solution is spherically symmetric and admits a double-null-ruling by coordinates \(({\hat{u}},{\hat{v}},\theta ,\phi )\) in which the metric takes the form
as in Sect. 2. Recall also that these coordinates present our solution as a lift of the solution to (SSESF’) via the projection \(({\hat{u}},{\hat{v}},\theta ,\varphi ) \mapsto ({\hat{u}},{\hat{v}})\). Thus, as in the \((1+1)\)-dimensional reduced case, these \({\hat{u}},{\hat{v}}\) are free up to a choice of gauge. In what follows, we will impose the gauge condition (G2).
Then, define \(t = {\hat{u}} + {\hat{v}}\) and \({\hat{r}} = {\hat{v}} - {\hat{u}}\). From here, we obtain a coordinate system \((t,x^1,x^2,x^3)\) defined as
The remainder of this section will be devoted to showing that lifts of the solutions considered in Theorem 3.1 represented in this coordinate system and gauge satisfy the conditions of 2.11. We do this in two parts: First we check that changing from (G1) to (G2) preserves the decay properties shown in Theorem 3.1. Then, we check the remaining conditions of 2.11 using the results of Sect. 7.
6.2 Changing Gauge
Here we check that changing gauge from (G1) to (G2) (at least) preserves the decay found in Theorem 3.1. Observe that it suffices to do so in the \((1+1)\)-dimensional setting, since the null coordinates here induce an equivalent choice of null coordinates on \({\mathcal {M}}\) by construction.
The result is the following:
Lemma 6.1
Let \((r,\phi ,m)\) a solution to (SSESF’) verifying hypothesis of Theorem 3.1 in (G1). Then, the estimates eqs. (3.1)–(3.10) also hold exchanging the u, v of (G1) for \({\tilde{u}},{\tilde{v}}\) null coordinates for the gauge (G2).
Proof
Recall that we obtain the coordinates \({\tilde{u}},{\tilde{v}}\) from u, v by the transformation
where \({{\bar{\nu }}}(x) = \lim _{v \rightarrow \infty }\nu (x,v)\). It follows that
By the above,
Then, by the bounds eqs. (3.1) and (3.3), it follows immediately from Theorem 3.1 that any solution satisfying the hypotheses of Theorem 3.1 in (G1) verifies the same decay estimates in (G2) as well. \(\square \)
Remark 6.2
Essentially the same argument allows us to pass between (G3) and (G1) without concern as well, since our transformation is nearly identical.
Note that in (G2) we can augment the bounds of Theorem 3.1 slightly, as we obtain some new control of \(\partial _u^l \nu \). In particular, we have the following:
Lemma 6.3
Let \((r,\phi ,m)\) be as in Theorem 3.1, but presented in the gauge (G2). Then, we have

Proof
In (G2), we have \(\lim _{v \rightarrow \infty } \nu (u,v) \equiv -\frac{1}{2}\). In particular, we have \(\lim _{v\rightarrow \infty }\partial _u^l \nu (u,v) = 0\) for any u, \(l \le k\) (since the convergence to \(-\frac{1}{2}\) is uniform by construction). Thus, we can write
The desired bound then follows immediately from (3.4). \(\square \)
Finally, (G2) gives us control of the limiting values of \(\lambda \) at \({\mathcal {I}}^-\):
Proposition 6.4
In (G2) we have \(\lim _{v \rightarrow \infty }\lambda (u,v) = \frac{1}{2}\).
Proof
We have by (G2) that \(\lambda (u,u) = -\nu (u,u)\) for all \(u \ge 1\). Moreover, by Theorem 3.1 we have that  .
.
Integrating the intermediate bound \((1+\left|u \right|)^{-1}(1+v)^{-1}\), we conclude
Then, we have \((\partial _u + \partial _v) \nu \lesssim (1+ \left|u \right|)^{-2}\), and \(\lim _{t \rightarrow \infty }\nu (t,{\hat{r}}) = -\frac{1}{2}\) for any \({\hat{r}}\). Thus
so we conclude that
and thus, our limit holds. \(\square \)
From this bound, we have immediately the following corollary:
Corollary 6.5
6.3 Checking Dispersiveness
Finally we are ready to check the conditions of 2.11. Note that conditions (D1), (D7) follow immediately from Theorem 3.1 and our choice of coordinates. It remains to carefully check the remaining conditions of 2.11. We will do this in two parts: first when \(\left|I \right| = 0\) and then addressing separately the case \(\Gamma ^I\) acts on the term of interest.
Proposition 6.6
The bounds (D2)–(D8) hold for \(\left|I \right| = 0\).
Proof
We begin with the components of the metric \(h_B\). Recall that in null coordinates the metric has the form:
Thus, in our \((t,{\mathbf {x}})\) coordinates described above the metric has the following components:
where \(\Omega ^2 = \frac{-4\lambda \nu }{1-\mu }\), and \(\delta _{ij}\) is the Kronecker \(\delta \).
So the components of the background-subtracted metric \(h_B\) are:
We’ll begin with the necessary estimates near the axis (\({\hat{r}} \le 1\)).
There are three terms we must control:
We start with (6.1). Recall that \(\Omega ^2 = \frac{-4\lambda \nu }{1-\mu }\). By (4.9), we can write this as
and thus,
Then, by (4.9) \(\left|\mu ^n \right| \lesssim r^{3n-1}(1+\left|u \right|)^{-6n}\), so this latter term immediately satisfies the required decay for \(r \le 1\), since \(\lambda \nu \) is bounded, and \(t \le 2(\left|u \right|+1)\) in this region. It thus remains to control \(-4\lambda \nu - 1\). Observe that by our construction of the gauge (G2), we have that
Thus, \(\lim _{t\rightarrow \infty }\lambda \nu (t,0) = -\frac{1}{4}\). So we can write
Observe that since we are near \(\Gamma \), we are WLOG in the region \({\mathcal {Q}}\) upon projection. Thus, by the results of Sect. 4 we have that \(\partial _t(\lambda \nu ) \lesssim (1+\left|u \right|)^{-3} \lesssim t^{-3}\). We thus obtain
since \(t \sim v\) in the region \({\hat{r}} \le 1\). Moreover, by the results of Sects. 4 and 7 we have that
so we conclude that for all \(\left|x \right| \le 1\),
as well. Thus, we have the necessary control of (6.1).
Next we consider the term (6.2). Observe that we can write (reducing to 2-dimensions by spherical symmetry):
Let \(\lambda _0(t,x) = \lambda (t,0)\), and \(\nu _0(t,x) = \nu (t,0)\). Then, we can rewrite the above as:
and so we have:
Thus, similar to the above we must control the terms \((\lambda _0 - \nu _0)^2 - 1\) and \(\frac{1}{{\hat{r}}}\int _0^{\left|x \right|} (\lambda - \nu )(t,{\hat{r}}) - (\lambda _0 - \nu _0)(t,{\hat{r}})d{\hat{r}}\).
We begin with the former. By the above, we have that \(\lim _{t\rightarrow \infty } \lambda _0 = lim_{t\rightarrow \infty } -\nu _0 = \frac{1}{2}\). Thus, we have
By Sect. 4, \(\left|\partial _t(\lambda - \nu )(t,0) \right| \lesssim (1 + \left|u \right|)^{-3}\), and thus,
as required. We can thus move to our other term.
In this case, we have
by Theorem 3.1. By arguments of Sect. 7, we in fact have that \(\partial _{{\hat{r}}}(\lambda - \nu )\mid _{\Gamma } = 0\); thus, we can write
Substituting this in above, and using the bounds of Theorem 3.1 we have
satisfying the required bound for \(\left|x \right| \le 1\). This bounds (6.2).
Finally, we move to (6.3). We start with just \(\Omega ^2 - \frac{r^2}{{\hat{r}}^2}\). Now we can write:
Note that since \(\lambda = -\nu \) on \(\Gamma \) we have that \(-4\lambda _0\nu _0 = 4\lambda _0^2 = (2\lambda _0)^2 = (\lambda _0-\nu _0)^2\) so these constant terms vanish. By the above, it remains only to estimate
By the arguments presented in Sect. 7, it follows that
so we have
Putting this together, we see that
and thus satisfies the required bound.
This establishes the condition (D2) close to the axis, for \(\left|I \right| = 0\). In fact, with the strength of the estimates above, this also establishes (D5) under the same extra conditions. It remains to address (D3) and (D4).
In this case, since \(u \sim v\) in the finite \({\hat{r}}\) region we can address each term at the same time. As above, there are three distinct terms to deal with:
It suffices to control \(\partial _{\alpha }(h_B)_{\mu \nu }\) (as the angular terms in \({{\bar{\partial }}}\) can only act on the \(x_ix_j\) which does not affect the decay at all). In the first two cases, the result follows directly from the analysis of corollary 7.4. In the case (6.6), this instead follows from corollary 7.6, and the above work to show (D2).
With this completed, it remains to establish the required estimates in the region \({\hat{r}} > 1\). In this region, we need not worry about potential singularities in our metric components, since everything is uniformally bounded and smooth away from the axis. Once more we have three types of terms that we must bound:
where \(S_j(\theta ,\phi ) = \frac{x_i}{{\hat{r}}}\) is the completely angular part of \(x_i\) written in \((t,{\hat{r}},\theta ,\phi )\) coordinates. Note that
We first establish (D2) for each of these terms and then move on to each of (D3)–(D5)
We’ll begin with \(\Omega ^2 - 1\). Here we have
By proposition 6.4 and Theorem 3.1, we can write
where \(\left|E_\lambda \right| \lesssim \frac{1}{1+v} + \frac{\log (1+\left|u \right|)}{1+v}\), and \(\left|E_\nu \right| \lesssim \frac{1}{1+v}\). Thus, we can write:
By Theorem 3.1, terms with \(n \ge 1\) immediately satisfy the bounds of (D2) since the prefactor is uniformly bounded. The remaining term is
but then as above, each of these also satisfies the bounds of (D2), since \(\left|u \right| \lesssim \left|v \right|\) in \(\mathbb {I}\).
Next we move on to \(\frac{r^2}{{\hat{r}}^2} - 1\), so we begin by showing that this, in fact, vanishes for large \({\hat{r}}\). Note that we have
Then, as above we can write
so we have
By Theorem 3.1 and the arguments of proposition 6.4, we have that

and moreover, in \(\mathbb {I}\) we have \({\hat{r}} \le v, \left|u \right| \le {\hat{r}}\), so this is bounded by
so we can write
where \(\left|E_r \right| \lesssim \log (2+{\hat{r}})\). Thus, we conclude:
Above, we already showed that this term is bounded by \(\frac{{\hat{r}}^2}{(1+v)^3}\), so, applying this new bound in the region \(\mathbb {I} \setminus {\mathcal {Q}}\) we have the required control of this term.
Finally, we consider \(\left( \Omega ^2 - \frac{r^2}{{\hat{r}}^2} \right) S_iS_j\), but this is immediately controlled by combining our work above for \(\Omega ^2 - 1\) and \(\frac{r^2}{{\hat{r}}^2} - 1\), and the boundedness of the \(S_i\)’s.
Now we address (D3). Thus, we must establish the bound
for some \(\gamma _0 > 0\). In fact, we obtain this for any \(\gamma _0 < 1\). In the case of \(\partial _t\), all of the required bounds hold immediately by Theorem 3.1, and corollary 6.5. For \(\partial _i\), if we allow this to act on a \(\Omega ^2\), then this again immediately satisfies our bound by Theorem 3.1. If instead we allow this to act on some \(S_iS_j\) term, then this simply multiplies \(\left( \Omega ^2 - \frac{r^2}{{\hat{r}}^2} \right) \) by a term proportional to \(\frac{1}{{\hat{r}}}\). By our above work to prove (D2), this gives us the required bound as well.
Finally, we must deal with the case \(\partial _i\frac{r^2}{{\hat{r}}^2}\). In this case, we can expand:
It thus suffices to establish an estimate for \({\hat{r}}(\lambda - \nu ) - r\). Recalling what we’ve done above, we can write this as
so we are left with:
Thus, the overall term can be written as
By the results of Sect. 5 in the region \({\mathcal {Q}}\), \(E_{\lambda }\) and \(E_{\nu }\) are controlled by \(\frac{1}{t^2}\), so our term is immediately bounded by
On the other hand, using the universal bounds of Theorem 3.1 as we did above, we obtain the bound
Together, these give us the required bound in the region \({\hat{r}} > 1\), so we conclude that (D3) holds.
Next we consider (D4). Here we must bound  ; we will treat these terms separately, beginning with \(\partial _v h = (\partial _t + \partial _r)h\). We have by Theorem 3.1 that \(\partial _v \Omega ^2\) immediately satisfies the required estimates. In the case of \(\frac{r^2}{{\hat{r}}^2}\), we have
; we will treat these terms separately, beginning with \(\partial _v h = (\partial _t + \partial _r)h\). We have by Theorem 3.1 that \(\partial _v \Omega ^2\) immediately satisfies the required estimates. In the case of \(\frac{r^2}{{\hat{r}}^2}\), we have
Now similar to the above we must bound
and thus, the resulting term is
As above, this is bounded by \(\frac{1}{t^2{\hat{r}}}\), and \(\frac{\log (2+{\hat{r}})}{{\hat{r}}^2}\) which gives us the overall required bound.
Finally, \(\partial _v\) acts as 0 on the \(S_i\) as these are totally angular.
Thus, we are left to deal with  .
.  acts non-trivially only on non-spherically symmetric terms, so this can only affect the terms \(x_ix_j\) in our metric. On these terms, the operator acts as:
acts non-trivially only on non-spherically symmetric terms, so this can only affect the terms \(x_ix_j\) in our metric. On these terms, the operator acts as:

for \(j,k \ne i\). In particular, this serves to multiply by an additional factor of \(\frac{1}{{\hat{r}}}\). Thus, we can apply our work above for (D2) and immediately conclude (D4).
Finally, we must deal with (D5). All terms without a \(\Gamma \) are identically 0 in this case thanks to simple algebraic cancellations.
Now we move to \(\phi \) and (D6). Again we are interested only in the case where \(\left|I \right| = 0\). We begin near the axis. For both \(\left|\partial \phi \right|\) and \(\left|{{\bar{\partial }}}\phi \right|\), the required bounds of (D6) hold immediately by corollary 7.4, since \(u \sim v\). Away from the axis, we can directly apply the results of Theorem 3.1. In particular, \(\left|\partial \phi \right| \lesssim \left|\partial _u \phi \right|\), and \(\left|\bar{\partial \phi } \right| = \left|\partial _v \phi \right|\), since the \(\phi \) is spherically symmetric, so the angular portion of \({{\bar{\partial }}}\) vanishes. Thus, the desired estimates follow directly from Theorem 3.1.
Finally, we must deal with (D8). We must begin by computing \(\Box _{\mathbf{g }}\) in the first place. Using our computed metric components above, we see through a bit of algebra that
We can also compute the components of the inverse metric \((g^{-1})^{\alpha \beta }\):
Thus, we have
and there are four terms we must address:
for \(j = 1,2,3\). As above, we separate the near axis and large \({\hat{r}}\) estimates.
We begin with (6.10), near the axis (\({\hat{r}} < t/2\)). We can rewrite this as:
\(\Omega ^{-2}\) is uniformly bounded, so we must control \(\frac{\lambda +\nu }{r}\). By (G2) we have that \(\lambda + \nu \mid _{\Gamma } = 0\), we can write by our averaging operator:
We show in Sect. 7 that \(\frac{{\hat{r}}}{r}\) is bounded, so it suffices to control the averaged term. Then, by Theorem 3.1 we have
Thus, integrating, \(\Box _{\mathbf{g }}t\) satisfies the required bound.
Away from the axis (\({\hat{r}} \ge t/2\)), we must control \(\partial _t\frac{r^2}{{\hat{r}}^2}\), since once again the pre-factor is only uniformly bounded. This is:
By corollary 6.5, we have that \(\left|\lambda + \nu \right| \lesssim \frac{\log (2+\left|u \right|)}{(1+v)}\), so we immediately obtain an overall bound of
This is good enough outside of \({\mathcal {Q}}\), and moreover, using the better bounds which hold in \({\mathcal {Q}}\) by Theorem 3.1 in this region, we in fact have
which gives us the required bound everywhere.
Finally, we turn to (6.11), beginning near the axis. As before \(\Omega ^{-2}\frac{{\hat{r}}^2}{r^2}\) is uniformly bounded, so we are concerned only with the differential terms. In each case, we are thus left with
We have already obtained sufficient control of \(\frac{1}{{\hat{r}}^2}\left( \frac{r^2}{{\hat{r}}^2} - \Omega ^2 \right) x_j\) above, so we need only be concerned with \(\partial _i \Omega ^2\) and \(\partial _i\left( \frac{1}{{\hat{r}}^2}\left( \frac{r^2}{{\hat{r}}^2} - \Omega ^2 \right) \right) x_ix_j\). Each of these quantities is adequately controlled by Theorem 3.1 and Sect. 7, so again we can move to the case away from the axis.
Observe that in fact
Thus, we are left to control the terms:
and
But these two terms are already adequately bounded by our work to conclude (D2) and (D3) above, so there is nothing left to do. \(\square \)
Proposition 6.7
The bounds (D2)–(D8) hold for \(\left|I \right| \le k\).
Proof
The idea for each term, both near and far from the axis, is to be able to count the total number of derivatives acting, as well as the total powers of the accompanying weights, and then apply the results of Theorem 3.1 in order to obtain the required decay. To this end, we will write the most general operator which may act on a given term, and then examine this count of derivatives and weights.
We begin with the components of the metric \(h_B\) near the axis.
Here we have a general term:
where A, B, C are multi-indices specifying the particular \(\Gamma \) applied. We will work right to left to write the general term we must bound in a nicer way. To do this, we determine the form of the general term of the above operator acting on a spherically symmetric function f. Once we have done this, we will go back to modify our expression to account for the non-spherically symmetric parts of \(h_B\).
So we begin with \(S = t\partial _t + {\hat{r}}\partial _{{\hat{r}}}\). Observe that we can rewrite this in terms of the operator \({\hat{X}} := \frac{1}{{\hat{r}}}\partial _{{\hat{r}}}\):
Observe that \({\hat{X}}t = 0\), and \({\hat{X}}{\hat{r}}^2 = 2\), so \(t\partial _t\) and \({\hat{r}}^2{\hat{X}}\) commute, and we can write:
We can write a generic term in this sum (up to a multiplicative constant) as:
for \(n_1< n,n_2 < l-n\).
The next term that can act on our sum above is:
The multi-index C need not be ordered since these all commute with each other (up to differential terms with no weight, thus not contributing negatively to our final power counting). Now note that \(\partial _t {\hat{r}}^2 = 0, \partial _it = 0,\partial _i{\hat{r}}^2 = 2x^i\), and, since \({\hat{X}}^l\partial _t^sf\) is spherically symmetric for any l, s we have that
Finally, \(\partial _t\) and \(\partial _i\) commute for all i, so we need not be concerned with ordering these either. The generic operator this contributes is then:
For  the number of time derivatives acting on factors of t, and
the number of time derivatives acting on factors of t, and  similar. Finally, letting this act on our general term above, we have
similar. Finally, letting this act on our general term above, we have
Now we have the term \((x^i\partial _j - x^j\partial _i)^B\). Observe that this operator is completely angular, and thus acts as 0 on \(t,{\hat{r}}^2\) and derivatives of f, and only has the effect of exchanging a copy of \(x^i\) for one of \(x^j\) (possibly with a change of sign). We can ignore the sign here, since this is just a global multiplicative factor, so letting the multi-index \(B = (B_{12} + B_{21},B_{23} + B_{32},B_{31} + B_{13})\) we have the general term:
for \(j \ne i\), and \(B_{ij} \le C_i + B_{ji} - 2q_i\).
Finally, we have our derivatives \(\partial ^{A}\) for a multi-index \(A = (A_t,A_1,A_2,A_3)\). The resulting term letting \(\partial ^A\) act on the above expression is:
This gives the general term we will consider for our spherically symmetric functions near the axis.
In the case of the background-subtracted metric \(h_B\), the only non-spherically symmetric terms we must consider are of the form
composed of a spherically symmetric term
and some non-symmetric terms \(x_ix_j\). t derivatives act trivially on the \(x_i\), if a \({\hat{r}}^2{\hat{X}}\) operator acts on the non-spherically symmetric part we have
and finally we have
In particular, an indefinite number of \({\hat{r}}^2{\hat{X}}\) terms can be absorbed by the non-symmetric terms, and only at most two spatial directional derivatives (without weighting) can act on non-symmetric terms before they vanish, as with any spatial coordinate terms the angular derivatives can exchange an \(x_i\) for and \(x_j\). Thus, our generic operator above may be modified by reducing the powers of \({\hat{r}}^2\) and \({\hat{X}}\) in proportion to one another (i.e., reducing l and associated quantities)—recalling the order in which these terms appear—dropping exchanging pairs (i.e., decreasing the total order of \(\left|B \right|\)) and dropping at most two isolated spatial directional derivatives (reducing the \(A_i\) or the \(m_i\) contributing to differential terms).
Thus, the terms (acting on spherically symmetric parts) we must consider are:
as the number of \({\hat{r}}^2\) terms and \(x^i\) terms remain relative to the number of \({\hat{X}}\) factors, but up to two \(t\partial _i\) terms may lose their derivatives, leaving (at worst) an extra two factors of t. Then, Lemma 7.3 allows us to write these terms as acting as:
where \(s \le 2, s \le \left|m \right|\). From here the bounds (and corresponding order-on-order increases in decay) of Theorem 3.1, reduce this to a question of counting derivatives and the corresponding powers of weights. In this generic term, we find that we have
derivatives acting on a given term (we do not distinguish between \({\hat{r}}\) and t derivatives since we will work with bounds in terms of u and v, and each of these operators mix the two),
powers of t and
powers of \({\hat{r}}\). Since \({\hat{r}}\) is at worst comparable to t in the near axis region, we can combine these weights to get a total weight of
and so the net difference between the total number of derivatives and total power of weights is \(-2,-\left|m \right| \le \left|A \right| + A_t - s\). Observe also that this s only enters on our terms with some non-spherically symmetric part, and in this case, Lemma 7.5 also gives us two extra differential orders, so our difference is actually just \(\left|A \right| + A_t\), as we might expect. The required bounds now follow immediately by the work done in the previous proposition, and the u, v bounds given by Theorem 3.1.
Away from the axis (\({\hat{r}} > t/2\)), we must take a slightly different approach in order to obtain our proper decay. In particular, we observe that we can write our differential operators (when acting on spherically symmetric terms) in terms of u and v as follows:
and we also have that \((x^i\partial _j - x^j \partial _i)S^i = -S^j\). Since the only non-spherically symmetric terms we will work with are products of the \(x^i\) or \(S^i\) these relations, along with the definition of the \(\partial _i,\partial _t\) allows us to deal with all of our differential terms. In particular, we see that any auxiliary powers of v come along with an additional v derivative, and likewise for u. Thus, the bounds of Theorem 3.1, and Lemma 6.3 yield the required decay for (D2), (D3), and (D4).
The case is similar for \(\phi \), since this is spherically symmetric and satisfies similar (also sufficient) bounds by Theorem 3.1.
Finally, we must check (D8). This is much the same as what we have done above for (D2) but requires a bit more care.
We begin in the near axis region, \({\hat{r}} < t/2\), with our \(\Box _{\mathbf{g }} t\) term. This is completely spherically symmetric, so we are again in the case of our generic near axis operator above acting on
In the proof of corollary 7.4 below we establish the bounds
and control these derivatives of \(\Omega ^{-2}\) in terms of bounds for derivatives of \(\lambda \nu \) and \(\mu \). Moreover, in the previous proposition we have established behavior for non-differentiated terms, so this is simply a matter of applying our general form for the operator acting on spherically symmetric terms found above and counting worst-case order of decay. Doing this, we find that we have exactly one extra derivative in comparison to our counting above, so in particular our decay improves by a power of \(1+\left|u \right|\), which is comparable to \(1+v\) in the small \({\hat{r}}\) region we consider, and thus, our bounds will hold in this case.
Away from the axis again things are less subtle, and we can apply our simpler general operator found above, differentiating naïvely throughout and again count our decay. In this case, we act on the expression \(\Omega ^{-2}\frac{\lambda +\nu }{r} = \frac{(1-\mu )(\lambda +\nu )}{4r\lambda \nu }\). As previously, we have already controlled all these terms in their undifferentiated state in the previous proposition, so, by our power counting above we need only check that a \(\partial _u\) (resp. \(\partial _v\)) derivative acting on each term results in an improvement in decay of one power of u (resp. v). Comparing our bounds of the previous proposition with those of Theorem 3.1 and the improvements in Lemma 6.3, we find that this is the case, and thus, the required estimates hold here as well.
Next we must address our spatial coordinate terms, and again we must deal with some non-spherically symmetric pieces. Recall that we have
We can split this into three terms which we will deal with individually:
We begin with the near axis case. Here, (6.12) is immediately controlled sufficiently by the power counting above and theorem 3.1 and Lemma 6.3, since we gain an extra order of derivative immediately (\(\partial _i\) commutes with our other operators up to more strongly decaying terms), and this provides the extra order of decay required for (D8). Similarly, writing \(\partial _i = x^i{\hat{X}}\) we see that (6.13) gains the required decay by our power counting (losing up to three spatial derivatives now), and corollary 7.6, which gives us an extra two derivatives acting, and thus an extra two powers of decay, for a total of one additional power as required. (6.14) follows in the same manner (we lose our extra derivative and one potential lost differential order from (6.13)).
Finally, away from the axis we see that the required bound on (6.12) follows directly from our power counting and Theorem 3.1. Here it is easier to combine (6.13) and (6.14) and write them instead as
Then, using \({\hat{r}} \sim v\) in this region, and the estimates already considered above the required bound is direct from power counting and Theorem 3.1, Lemma 6.3.
With this, we establish all the conditions for 2.11, and so we obtain stability for our class of solutions. \(\square \)
7 Regularity Near the Axis
In this section, we prove several key results used above in the proof of Theorem 3.4. In particular, we show that the lift of our reduced spherically symmetric solution to (SSESF’) given above gives rise to a smooth solution to (ESF) with good decay in \((3+1)\) dimensions. Note that the only issue is due to the singularity of the (u, v) coordinates along the axis of symmetry, thus away from the axis there is already nothing left to do. However, in order to guarantee control of spatial (\(x^i\)) derivatives near the axis, we must control the differential operator \({\tilde{X}} := \frac{1}{{\hat{r}}}\partial _{{\hat{r}}}\) across the axis (observe that away from the axis this is immediately controlled).
In order to do this, we note that it suffices to establish estimates in \((1+1)\) dimensions for the operator \(X := \frac{1}{{\tilde{r}}}\partial _{{\tilde{r}}}\) near the axis of symmetry. Thus, we reduce again to the \((1+1)\) dimensional setting for the remainder of this section.
7.1 Preparations
Before beginning, we note a few essential facts:
Remark 7.1
Corresponding to \((r,\phi ,m)\) a solution to (SSESF’) in \((1+1)\), there is a spherically symmetric solution \(({\mathcal {M}},\phi ,\mathbf{g })\) to (ESF) in \((3+1)\) dimensions which reduces to \((r,\phi ,m)\). Moreover if the data are sufficiently smooth (\(C^{\infty }\) certainly suffices), then by persistence of regularity and Sobolev embedding the solution may be taken to be at least \(C^k\), so \(\phi \) and the components of the metric must be \(C^k\) smooth in the smooth structure \({\mathbb {R}}^{3+1}\). In particular, reducing to \((1+1)\) dimensions, this immediately implies that \(X^l\phi \) is well defined on \({\mathbb {R}}^{(1+1)}_{+}\), and bounded on the axis for \(l \le k\), and thus, \(\partial _{{\hat{r}}}^{2l+1}\phi \mid _{\Gamma } = 0\) for all \(l \le \lfloor \frac{k}{2} \rfloor -1\). This final fact will be essential to what follows.
We will also make use of the following elementary proposition:
Proposition 7.2
Let  , and let \(f:{\mathbb {R}}^{(1+1)}_+ \rightarrow {\mathbb {R}}\) be \(C^k\) up to the boundary. Suppose the extension \({\bar{f}}\) to all of \({\mathbb {R}}^{(1+1)}\) given by
, and let \(f:{\mathbb {R}}^{(1+1)}_+ \rightarrow {\mathbb {R}}\) be \(C^k\) up to the boundary. Suppose the extension \({\bar{f}}\) to all of \({\mathbb {R}}^{(1+1)}\) given by
is \(C^k\) as well. Then, \(\lim _{x \rightarrow 0^+}\partial ^{2l+1}_{x}f(x,t) = 0\) for all \(l \le \lfloor \frac{k}{2} \rfloor - 1\).
7.2 Estimates For \(\phi ,\mu ,\lambda - \nu \), and \(\lambda \nu \)
In order to establish the necessary control of \(\phi ,\mu , \lambda -\nu \) and \(\lambda \nu \), we will make use of the following lemma:
Lemma 7.3
Let \(f:{\mathbb {R}}^2_+ \rightarrow {\mathbb {R}}\) a \(C^{2k}\) function such that \(\partial _x^{2l-1}f\mid _{\Gamma } \equiv 0\) for all \(l \le k\). Then, for \(2l+s \le 2k\):
Proof
Observe that since odd order derivatives of f vanish on the axis, we can write

Since we have
and so applying our differentiation formula for averaging operators, and rewriting the integrand (multiplying and dividing by \(x'\) to obtain extra X operators and maintain the averaging operator form), we obtain the above expression.
Thus, integrating using the supremum bound for our f term we have
so it suffices to bound \(X^{l-1}\partial ^2_xf\) by \(\partial ^{2l}_xf\). But \(\partial ^2_xf\) satisfies the same assumptions as f with \(k' = k-1\). Proceeding inductively, we conclude by the same reasoning as above that
Thus, it follows that
for all \(l \le k\).
Now observe that, since odd order derivatives of f vanish on the axis, \(\partial _x,\partial _t\) commute, and the axis is an integral curve of \(\partial _t\), we in fact have that
for any \(2l-1+s\le k\). But then \(\partial _t^sf\) satisfies the assumptions of our lemma, so by the above argument we in fact have
\(\square \)
Corollary 7.4
Let \((r,\phi ,m)\) a locally scattering solution to (SSESF’) in \({\mathcal {Q}}\) with data asymptotically flat of order \(\omega ' \ge 2\) in \(C^{2k}\) toward \({\mathcal {I}}^+\). Then, the following bounds hold for all \(l \le k\):
Proof
Observe that (7.1) holds immediately by Lemma 7.3 and Theorem 3.1, since \(\phi \) lifts to a smooth function on \({\mathbb {R}}^{(3+1)}\), and thus has \(X^l\phi \) bounded for all \(l \le 2k\), thus immediately verifying the hypotheses of Lemma 7.3.
We turn next to (7.3), and (7.4). Observe that the function \({\bar{r}}(u,v) := {\left\{ \begin{array}{ll}r(u,v) &{} v \ge u\\ -r(v,u) &{} v \le u \end{array}\right. }\) is a smooth extension of r to all of \({\mathbb {R}}^{(1+1)}\) (one checks directly that the derivatives in u and v match up across the axis so long as they are well defined in \({\mathbb {R}}^{(1+1)}_{+}\)). Moreover this function is odd in the \({\hat{r}}\) coordinate (this is exactly the condition in u, v translated to these other coordinates), and thus, it follows immediately that \(\partial _{{\tilde{r}}}{\bar{r}} = \frac{1}{2}({\bar{\lambda }} - {\bar{\nu }})\) is even. Thus, \(\lambda - \nu \) immediately satisfies the hypotheses of Lemma 7.3, and thus, by Theorem 3.1 verifies (7.4).
In the case of \(\lambda \nu \), observe that \({\bar{\lambda }}{\bar{\nu }}\) is a smooth function on \({\mathbb {R}}^{(1+1)}\), and we have
by construction of \({\bar{r}}\). Thus, we have
So \({\bar{\lambda }}{\bar{\nu }}\) is an even function, \(C^{2k}\) extension of \(\lambda \nu \). As above, it follows by Lemma 7.3 and Theorem 3.1 that \(\lambda \nu \) satisfies (7.3).
We are left to deal with (7.2), which is rather more involved. Observe first that we can write:
We will deal with the terms \(\frac{{\tilde{r}}}{r}\) and \(\frac{1}{{\tilde{r}}}\int _{S_{u+v}(v-u)}\partial _{{\tilde{r}}}md{\tilde{r}}'\) separately, beginning with the latter.
Employing our averaging operators, we have
We also have
Recall that \(\partial _{{\tilde{r}}}^{2l-1}\phi \) vanishes on the axis. It follows that the extension \({\bar{\phi }}(u,v):= {\left\{ \begin{array}{ll} \phi (u,v)&{} v\ge u\\ \phi (v,u) &{} u \ge v \end{array}\right. }\) is a smooth, even extension of \(\phi \) to all of \({\mathbb {R}}^{(1+1)}\). Moreover, we have that
In particular, the function
is a smooth extension of \(\frac{1}{\lambda }(\partial _v\phi )^2 - \frac{1}{\nu }(\partial _u\phi )^2\), which is even, and thus has vanishing odd order \(\partial _{{\tilde{r}}}\) derivatives on the axis. Since r admits an odd extension, \(r^2\) is a smooth even extension and thus also has vanishing odd order derivatives. Thus, we conclude that, so long as \(\partial _{{\tilde{r}}}^{l-1}(1-\mu ) = \partial _{{\tilde{r}}}\mu \) vanishes along \(\Gamma \), so does
In particular, so long as \(\frac{{\tilde{r}}}{r}\) is well behaved, we can conclude by induction that \(\mu \) has vanishing odd order \({\tilde{r}}\) derivatives on the axis.
Now we must deal with \(\frac{{\tilde{r}}}{r}\), as above we wish to show that the odd order \({\tilde{r}}\) derivatives vanish on the axis. Observe that since \(\frac{{\tilde{r}}}{r}\) is bounded away from 0 (since \(\lambda ,\nu \) are bounded away from 0), it suffices to work with \(\frac{r}{{\tilde{r}}}\). This is advantageous, as we can write
Thus, we have
So by our analysis of \(\lambda -\nu \) above, we conclude that every odd-order derivative of \(\frac{{\tilde{r}}}{r}\) vanishes on the axis. Thus the same holds for \(\frac{r}{{\tilde{r}}}\). Moreover, we conclude by Theorem 3.1 that
counting powers in the bounds (3.2), (3.4).
Combining this with the above, we conclude inductively that \(\partial _{{\tilde{r}}}^{2l-1}\mu \) vanishes on \(\Gamma \) (since an odd number of derivatives must always act on one of the terms in our expression for \(\mu \)). Thus, (7.2) holds as well. \(\square \)
Finally, we would like to make use of the above bounds for the extended cases \(\frac{\mu }{{\tilde{r}}^2}, \frac{(\lambda - \nu )-(\lambda _0 - \nu _0)}{{\tilde{r}}^2}\), and \(\frac{\lambda \nu - \lambda _0\nu _0}{{\tilde{r}}^2}\) (where \(\lambda _0(t,{\tilde{r}}) = \lambda (t,0)\), \(\nu _0\) likewise). To this end, we have the following lemma:
Lemma 7.5
Suppose f is as in Lemma 7.3 and moreover satisfies \(f(t,0) = 0\). Then, \({\tilde{f}} := \frac{f}{{\tilde{r}}^2}\) also satisfies the assumptions of Lemma 7.3 and the bound:
Proof
We check that the even extension of \({\tilde{f}}\) (which we also denote by \({\tilde{f}}\)) is in fact differentiable across the axis by inductively controlling its derivatives in terms of those of f. First, we can write
since f and \(\partial _{{\tilde{r}}}f\) each vanish on the axis. We thus conclude that
and moreover (via the same argument with the value on the axis subtracted), if f is \(C^k\) for \(k \ge 2\) (resp. \(>2\)), then \({\tilde{f}}\) is differentiable (resp. continuously differentiable) across the axis.
Suppose now that we have that \(\left|\partial _{{\tilde{r}}}^{n-1}{\tilde{f}}(t,R) \right| \le \sup _{r < R}\left|\partial _{{\tilde{r}}}^{n+1}f \right|\) for all \(0 \le n-1 < k-2\). We show that such a bound holds for at order n as well. So we can write:
Observe that every term in this sum vanishes along the axis by assumptions on f, so we can differentiate each term and integrate to obtain
Combining terms with equal powers of r and differential order on f, we obtain
Once again every term in this sum vanishes on the axis so we can differentiate and integrate once more to obtain
Every term in this expression cancels except for the highest differential order, and we obtain:
From this expression, we immediately have the bound
and similar to the above we also conclude that f is differentiable at order \(n+1\) as well. Moreover, since odd-order derivatives of f vanish along the axis, the same is true of those of \({\tilde{f}}\), and thus, we are in the situation of Lemma 7.3, and we obtain the required bounds. \(\square \)
Corollary 7.6
Notes
In [18], Luk–Oh–Yang also construct global spacetimes by solving a scattering problem from past null infinity. For technical reasons, I do not directly control such global spacetimes, but instead start from the spacetimes defined to the future of a cone. It thus remains open whether there are future and past complete spacetimes satisfying the assumptions of Luk–Oh’s result [15] in both the future and past directions.
For details of these dependencies see [16].
For a definition of this term see [15] section 3.
In a sense defined precisely in Section 4 of [15].
In fact, this leaves a compact region of \(\mathbb {I}\) without explicit control. By standard persistence of regularity, the solution is still \(C^k\) smooth in this region (for some discussion cf. [9]), and thus, the decay can be realized simply by adjusting our constants.
References
Christodoulou, D.: The problem of a self-gravitating scalar field. Commun. Math. Phys. 105(3), 337–361 (1986)
Christodoulou, D.: A mathematical theory of gravitational collapse. Commun. Math. Phys. 109(4), 613–637 (1987)
Christodoulou, D.: The formation of black holes and singularities in spherically symmetric gravitational collapse. Commun. Pure Appl. Math. 44(3), 339–373 (1991)
Christodoulou, D.: Bounded variation solutions of the spherically symmetric Einstein-scalar field equations. Commun. Pure Appl. Math. 46(8), 1131–1220 (1993)
Christodoulou, D.: Examples of naked singularities in the gravitational collapse of a scalar field. Ann. Math. 140(3), 604–653 (1994)
Christodoulou, D.: The instability of naked singularity formation in the gravitational collapse of a scalar field. Ann. Math. 149(1), 183–217 (1999)
Christodoulou, D., Klainerman, S.: The Global Nonlinear Stability of the Minkowski Space. Princeton Mathematical Series, vol. 41 (1993)
Dafermos, M., Rodnianski, I.: A proof of Price’s law for the collapse of a self-gravitating scalar field. Invent. Math. 162(2), 381–457 (2005)
Dafermos, M.: Black hole formation from a complete regular past. Commun. Math. Phys. 289(2), 579–596 (2009)
Dafermos, M., Holzegel, G., Rodnianski, I., Taylor, M.: The non-linear stability of the Schwarzschild family of black holes. arXiv: 2103.08222 (2021)
Friedrich, H.: On the existence of n-geodesically complete or future complete solutions of Einstein’s field equations with smooth asymptotic structure. Commun. Math. Phys 107(4), 587–609 (1986)
Hintz, P., Vasy, A.: The global non-linear stability of the Kerr-de Sitter family of black holes. Acta Math. 220(1), 1–206 (2018)
Klainerman, S., Szeftel, J.: Global nonlinear stability of Schwarzschild spacetime under polarized perturbations. arXiv:gr-qc/1711.07597 (2018)
Lindblad, H., Rodnianski, I.: The global stability of Minkowski space-time in harmonic gauge. Ann. Math. 171(3), 1401–1477 (2010)
Luk, J., Oh, S.J.: Global nonlinear stability of large dispersive solutions to the Einstein equations, Currently Unpublished, Preprint
Luk, J., Oh, S.J.: Quantitative decay rates for dispersive solutions to the Einstein-scalar field system in spherical symmetry. Anal. PDE 8(7), 1603–1674 (2015)
Luk, J., Oh, S.J.: Strong cosmic censorship in spherical symmetry for two-ended asymptotically flat initial data I. The interior of the black hole region. arXiv:gr-qc/1702.05715 (2019)
Luk, J., Oh, S.J., Oh, Y.S.: Solutions to the Einstein-scalar-field system in spherical symmetry with large bounded variation norms. Ann. PDE 4(1), 1–59 (2018)
Price, R.H.: Nonspherical perturbations of relativistic gravitational collapse. I. Scalar and gravitational perturbations. Phys. Rev. D 5, 2419–2438 (1972)
Acknowledgements
Many thanks to Jonathan Luk for guidance, many helpful discussions, and providing numerous references. I would also like to thank the SURIM program for helping to support this work as part of my undergraduate thesis.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Mihalis Dafermos.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Kilgore, E. Global Non-linearly Stable Large Data Solutions to the Einstein Scalar Field System. Ann. Henri Poincaré 23, 3093–3157 (2022). https://doi.org/10.1007/s00023-022-01162-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-022-01162-4



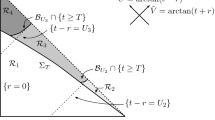

 .
. .
.