1 Introduction

As is well known, there are only four kinds of normed algebras over the real field. Following the old works of Hurwitz, the Cayley octonions, denoted by \({\mathbb {O}}\), form the largest normed division algebra over the real numbers and thus represent a very special important case. Recently, the eight-dimensional non-associative octonion algebra has attracted a lot of attentions of mathematicians and physicists. For example, there are many significant developments in the function theory [2, 12, 13], functional analysis [5, 6, 8, 9, 15] and quantum mechanics over octonions [3, 7, 20].

Central to these developments is the theory of octonionic spaces, or more precisely, octonionic modules. Hence, gaining a profound comprehension of the structure of octonionic modules is essential.

Due to the non-associativity, there are some new phenomena in the octonionic setting. Significantly different from other normed division algebras, the submodules generated by one element is involved. For example, the submodule generated by \(x=(e_1,e_2,e_3)\) in \({\mathbb {O}}^3\) is the entire space \({\mathbb {O}}^3\), instead of the form of

$$\begin{aligned} {\mathbb {O}}x:=\{px\mid p\in {\mathbb {O}}\}. \end{aligned}$$

Here \(e_0=1,e_1,\ldots ,e_7\) is a basis of \({\mathbb {O}}\). This phenomenon has been observed already in 1964 by Goldstine and Horwitz [5]. This starkly contrasts with classical cases, presenting a substantial challenge in the advancement of octonionic analysis.

In this article, we aim to characterize the submodules generated by one element on an octonionic bimodule. The key point is that we find a new relation between the commutators and associators. This helps us to establish the characterization of submodules generated by one element and leads to a deeper understanding on the \({\mathbb {O}}\)-bimodule structure. Ultimately, we obtain that the submodule generated by one element x is \({\mathbb {O}}^5x\) instead of \({\mathbb {O}}x\).

To obtain the key relation between the commutators and associators, it is essential to utilize the real part structure of \({\mathbb {O}}\)-bimodules. Similar as in quaternionic case [16], there also exists a real part structure on an octonionic bimodule which can be expressed as

$$\begin{aligned} Re \,x=\frac{5}{12}x-\frac{1}{12}\sum _{i=1}^7 e_ixe_i \end{aligned}$$

for any x in an \({\mathbb {O}}\)-bimodule M. Every element x can be decomposed as

$$\begin{aligned} x=\sum _{i=0}^7e_ix_i, \end{aligned}$$

where \(x_i\in Re \,M\) for \(i=0,\ldots ,7\). Utilizing this, we establish the key identity connecting the commutators and associators.

Theorem 1.1

Let M be an \({\mathbb {O}}\)-bimodule. For any \(x\in M\), we have

$$\begin{aligned} 4[e_i,x]=\sum _{j,k=1}^7 \epsilon _{ijk}[e_j,e_k,x],\quad i=1,\ldots ,7, \end{aligned}$$
(1.1)

where \(\epsilon _{ijk}\) are constants from the octonionic multiplication table:

$$\begin{aligned} e_ie_j=\epsilon _{ijk}e_k-\delta _{ij} \end{aligned}$$

for \(i,j=1,\ldots ,7\).

This shows that the right multiplication of an octonionic bimodule is uniquely determined by its left module structure. Hence the notion of left submodules coincides with the notion of sub-bimodules in an octonionic bimodule. Furthermore, it is obtained that the number of right \({\mathbb {O}}\)-scalar multiplications defined on a left \({\mathbb {O}}\)-module M such that M becomes an \({\mathbb {O}}\)-bimodule is 0 or 1.

As a contrast, we review the quaternionic setting. We confine ourselves to Hilbert spaces. Let H be a Hilbert right \({\mathbb {H}}\)-module with the quaternionic inner product \(\left\langle \cdot ,\cdot \right\rangle \). Here \({\mathbb {H}}\) denotes the algebra of quaternions. There always exist infinite left \({\mathbb {H}}\)-scalar multiplications such that H becomes a \({\mathbb {H}}\)-bimodule [4]. More precisely, pick out a Hilbert basis N of H and define the left scalar multiplication “\(\cdot \)” of H induced by N as the map

$$\begin{aligned} {\mathbb {H}}\times H\rightarrow & H\\ (q,u)\mapsto & q\cdot u:=\sum _{z\in N}zq\left\langle z,u\right\rangle . \end{aligned}$$

Moreover, H becomes a Hilbert \({\mathbb {H}}\)-bimodule with the initial right scalar multiplication and the above left scalar multiplication. This means that, every Hilbert right quaternionic module can be endowed with infinite many left scalar multiplications to make it become a Hilbert \({\mathbb {H}}\)-bimodule. However, as shown by identity (1.1), the number of compatible left scalar multiplications in a Hilbert right \({\mathbb {O}}\)-module is 1 at most. Thus the octonionic setting is completely different from the quaternionic case when considering Hilbert spaces.

From identity (1.1), we conclude a new expression of the real part and imaginary part of an element in an \({\mathbb {O}}\)-bimodule. For any x in an \({\mathbb {O}}\)-bimodule M, we have

$$\begin{aligned} Re \,x=x+\frac{1}{48}\sum _{i,j,k=1}^7\epsilon _{ijk}e_i[e_j,e_k,x]. \end{aligned}$$
(1.2)

And the imaginary part can be expressed in terms of associators

$$\begin{aligned} Im \, x=-\frac{1}{48}\sum _{i,j=1}^7[e_i,e_j,(e_ie_j)x]. \end{aligned}$$

The identity (1.2) plays a key role in discussing the submodule generated by one element. For any subset S of an \({\mathbb {O}}\)-bimodule, we denote by \({\mathbb {O}}S\) the set

$$\begin{aligned} \left\{ \sum _{i=1}^np_is_i\mid n\in {\mathbb {N}}, p_i\in {\mathbb {O}},s_i\in S\right\} . \end{aligned}$$

We simply denote that

$$\begin{aligned} {\mathbb {O}}^kx:={\mathbb {O}}({\mathbb {O}}^{k-1}x). \end{aligned}$$

Let \(\left<x\right>_{{\mathbb {O}}}\) denote the submodule generated by x. The submodule generated by one element in an \({\mathbb {O}}\)-bimodule can be characterized as follows.

Theorem 1.2

Let M be an \({\mathbb {O}}\)-bimodule. For any \(x=\sum _{i=0}^7e_ix_i\in M\), where \(x_i\in Re \,M\) for \(i=0,\ldots ,7\), we have

$$\begin{aligned} \left<x\right>_{{\mathbb {O}}}={\mathbb {O}}^5x. \end{aligned}$$
(1.3)

Let

$$\begin{aligned} \{x_{i_1},\ldots ,x_{i_l}\} \end{aligned}$$

be the maximal real linearly independent system of \(\{x_0,\ldots , x_7\}\). Then we have

$$\begin{aligned} \left<x\right>_{{\mathbb {O}}}=\bigoplus _{k=1}^l{\mathbb {O}}x_{i_k}. \end{aligned}$$
(1.4)

The structure of octonionic submodules shall play a pivotal role in the exploration of octonionic functional analysis. For instance, in employing the Hahn–Banach extension theorem, there often arises a necessity to devise a functional defined on a submodule that is generated by one element. The findings presented in this article empower us to construct such functionals. Furthermore, these results bear significant potential for application in the realm of octonionic function theory. This is because, as demonstrated in [2], the octonionic Hardy space can be regarded as an octonionic Hilbert space.

2 Preliminaries

In this section, we review some basic properties of the algebra \({\mathbb {O}}\) of the octonions and \({\mathbb {O}}\)-modules, and introduce some fundamental notations.

The algebra \({\mathbb {O}}\) is a non-associative, non-commutative, normed division algebra over the real algebra \({\mathbb {R}}\). Let \(e_1,\ldots ,e_7\) be its natural basis throughout this paper, i.e.,

$$\begin{aligned} e_ie_j+e_je_i=-2\delta _{ij},\quad i,j=1,\ldots ,7. \end{aligned}$$

For convenience, we denote \( e_0=1\).

In terms of the natural basis, an element in \({\mathbb {O}}\) can be written as

$$\begin{aligned} x=x_0+\sum _{i=1}^7x_ie_i,\quad x_i\in {\mathbb {R}}, \end{aligned}$$

The conjugate octonion of x is defined by \({\overline{x}}:=x_0-\sum _{i=1}^7x_ie_i\), and the norm of x equals \(|x|:=\sqrt{x{\overline{x}}}\in {\mathbb {R}}\), the real part of x is \( Re \,{x}:=x_0=\frac{1}{2}(x+{\overline{x}})\).

The associator of three octonions is defined as

$$\begin{aligned} {[}x,y,z]:=(xy)z-x(yz) \end{aligned}$$

for any \(x,y,z\in {\mathbb {O}}\), which is alternative in its arguments and has no real part. That is, \({\mathbb {O}}\) is an alternative algebra and hence it satisfies the so-called R. Moufang identities [18]:

$$\begin{aligned} (xyx)z=x(y(xz)),\ z(xyx)=((zx)y)x,\ x(yz)x=(xy)(zx). \end{aligned}$$

The commutator is defined as

$$\begin{aligned} [x,y]:=xy-yx. \end{aligned}$$

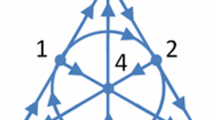
The full multiplication table is conveniently encoded in the 7-point projective plane, which is often called the Fano mnemonic graph. In the Fano mnemonic graph (see Fig. 1), the vertices are labeled by \(1, \ldots , 7\) instead of \(e_1,\ldots , e_7\). Each of the 7 oriented lines gives a quaternionic triple. The product of any two imaginary units is given by the third unit on the unique line connecting them, with the sign determined by the relative orientation.

Fig. 1
figure 1

Fano mnemonic graph

Full size image

It will be convenient to use an \(\epsilon \)-notation that will now be introduced (see [1]). This is the unique symbol that is skew-symmetric in either three or four indices.

One way to think of this symbol is:

$$\begin{aligned} e_ie_j&=\epsilon _{ijk}e_k-\delta _{ij}, \end{aligned}$$
(2.1)
$$\begin{aligned} {[}e_i,e_j,e_k]&=2\epsilon _{ijkl}e_l. \end{aligned}$$
(2.2)

The symbol \(\epsilon \) satisfies various useful identities. For example (using the summation convention),

$$\begin{aligned} \epsilon _{ijk}\epsilon _{ijl}&=6\delta _{kl}, \end{aligned}$$
(2.3)
$$\begin{aligned} \epsilon _{ijq}\epsilon _{ijkl}&=4\epsilon _{qkl}. \end{aligned}$$
(2.4)

We shall always use the Einstein summation convention when we compute in terms of \(\epsilon \)-notation.

We next recall the definition of \({\mathbb {O}}\)-modules. There are abundant results on octonionic bimodules, or more generally, alternative bimodules. Already in 1952, Schafer [17] gave the birepresentations of alternative algebras. Subsequently, Jacobson [11] determined the irreducible representations for finite dimensional semi-simple alternative algebras. A more general study for alternative bimodules is given in [19].

Definition 2.1

An \({\mathbb {R}}\)-vector space M is called a left \({\mathbb {O}}\)-module, if there is an \({\mathbb {R}}\)-linear map

$$\begin{aligned} L: {\mathbb {O}}\rightarrow & \text {End}_{{\mathbb {R}}}M\\ p\mapsto & L_p \end{aligned}$$

satisfying \(L_1=id_M\) and

$$\begin{aligned} {[}p,q,x]=-[q,p,x] \end{aligned}$$

for all \( p,q\in {\mathbb {O}}\) and \(x\in M\). Here

$$\begin{aligned} {[}p,q,x]:=(pq)x-p(qx)=L_{pq}(x)-L_pL_q(x), \end{aligned}$$

called the left associator of M. The definition of right \({\mathbb {O}}\)-module is similar.

A left \({\mathbb {O}}\)-module M is called an \({\mathbb {O}}\)-bimodule if it is equipped with a right \({\mathbb {O}}\)-scalar multiplication and the associator is alternative:

$$\begin{aligned} {[}p,q,m]=[m,p,q]=[q,m,p] \end{aligned}$$

\(\text { for all } p,q\in {\mathbb {O}}\text { and all }m\in M\). Here the middle associator [q, m, p] is defined by

$$\begin{aligned} {[}q,m,p]:=(qm)p-q(mp), \end{aligned}$$

and the right associator [p, q, m] is defined by

$$\begin{aligned} [p,q,m]:=(pq)m-p(qm). \end{aligned}$$

Remark 2.2

The definition of left, right and middle associators is actually of the same form. Formally, we can define

$$\begin{aligned} {[}x,y,z]:=(xy)z-x(yz), \end{aligned}$$

where two elements of x, y, z are in \({\mathbb {O}}\), the rest element is in M. It becomes evident that the notation for associators in \({\mathbb {O}}\) aligns precisely with the notation for associators in an octonionic bimodule, when considering \({\mathbb {O}}\) as an octonionic bimodule.

One useful identity which holds in any left \({\mathbb {O}}\)-module M is

$$\begin{aligned} {[}p,q,r]m+p[q,r,m]=[pq,r,m]-[p,qr,m]+[p,q,rm]. \end{aligned}$$
(2.5)

Here \(m\in M\) is an arbitrary element and \(p,q,r\in {\mathbb {O}}\) are arbitrary octonions. One can check this identity directly.

We shall denote by \({\mathscr {A}}(M) \) the set

$$\begin{aligned} {\mathscr {A}}(M):=\{m\in M\mid [p,q,m]=0\text { for all } p,q \in {\mathbb {O}}\}, \end{aligned}$$

whose elements are called associative elements. And denote by \({\mathscr {Z}}(M)\) the commutative center

$$\begin{aligned} {\mathscr {Z}}(M):=\{m\in M\mid pm=mp\text { for all } p\in {\mathbb {O}}\}. \end{aligned}$$

We denote by \(\text {Reg}\,{{\mathbb {O}}}\), or just \({\mathbb {O}}\) if there is no confusion, the regular bimodule with the multiplication given by the product in \({\mathbb {O}}\). Clearly, the \({\mathbb {O}}\)-bimodule \(\text {Reg}\,{{\mathbb {O}}}\) is irreducible. Moreover, it is the only irreducible \({\mathbb {O}}\)-bimodule; see the results by Schafer [17] and Jacobson [11]. We have

$$\begin{aligned} {\mathscr {A}}(M)={\mathscr {Z}}(M) \end{aligned}$$

for any \({\mathbb {O}}\)-bimodule M and

$$\begin{aligned} M=\bigoplus _{i=0}^7e_i{\mathscr {A}}(M). \end{aligned}$$

We define the real part operator as the projective operator [10]

$$\begin{aligned} Re \,: M\rightarrow {\mathscr {A}}(M). \end{aligned}$$

For any \(x\in M\), there is a decomposition

$$\begin{aligned} x=\sum _{i=0}^7e_ix_i. \end{aligned}$$

We have a concrete expression of the real part operator in terms of scalar multiplications [10]

$$\begin{aligned} Re \,x=\frac{5}{12}x-\frac{1}{12}\sum _{i=1}^7 e_ixe_i. \end{aligned}$$
(2.6)

3 The main results

Let M be an \({\mathbb {O}}\)-bimodule in this section. It turns out that there is a succinct relation between the commutators and associators.

Theorem 3.1

Let M be an \({\mathbb {O}}\)-bimodule. For any \(x\in M\), we have

$$\begin{aligned} 4[e_i,x]=\sum _{j,k=1}^7 \epsilon _{ijk}[e_j,e_k,x],\quad i=1,\ldots ,7. \end{aligned}$$
(3.1)

Proof

For any given \(x\in M\), let

$$\begin{aligned} x=\sum _{i=0}^7 e_jx_j, \end{aligned}$$

where \(x_j\in {\mathscr {A}}(M),\ j=0,1,\ldots , 7.\)

Using Einstein summation convention, we have

Note that \(x_j\in {\mathscr {A}}(M)={\mathscr {Z}}(M),\ j=0,1,\dots , 7.\) We thus have

$$\begin{aligned} 4[e_i,x]= & 4\left[ e_i,\sum _{m=0}^7e_mx_m\right] \\= & 4\sum _{m=1}^7\left( e_i(e_mx_m)-(e_mx_m)e_i\right) \\= & 4\sum _{m=1}^7\left( (e_ie_m)x_m-e_m(x_me_i)\right) \\= & 4\sum _{m=1}^7\left( e_ie_m-e_me_i\right) x_m \\= & 4(\epsilon _{imn}e_n-\epsilon _{min}e_n)x_m\\= & 8\epsilon _{imn}e_nx_m. \end{aligned}$$

This proves (3.1) as desired. \(\square \)

Remark 3.2

Identity (3.1) shows that the right multiplication of an octonionic bimodule is uniquely determined by its left module structure. More precisely, for any \(x\in M\), the right multiplication is given by

$$\begin{aligned} xe_i=e_ix-\dfrac{1}{4}\sum _{j,k=1}^7 \epsilon _{ijk}[e_j,e_k,x],\quad i=1,\ldots ,7. \end{aligned}$$
(3.2)

Hence the notion of left submodules of an octonionic bimodule coincides with the notion of its sub-bimodules, which means that it is closed under both left \({\mathbb {O}}\)-scalar multiplications and right \({\mathbb {O}}\)-scalar multiplications. The notion of left \({\mathbb {O}}\)-homomorphisms coincides with the notion of \({\mathbb {O}}\)-bihomomorphisms, which will be just referred to as \({\mathbb {O}}\)-homomorphisms or an \({\mathbb {O}}\)-linear maps in the sequel. And it is no need to consider these notions separately as in [14, 15].

We remark that this is a new phenomenon in contrast to the quaternionic case. Given a left Hilbert quaternionic module M, there always exist infinite right quaternionic scalars such that M becomes a quaternionic bimodule (see [4, section 3.1]).

We summarize the above discussion as the following corollary.

Corollary 3.3

Let M be a left \({\mathbb {O}}\)-module. The number of right \({\mathbb {O}}\)-scalar multiplications defined on M such that M becomes an \({\mathbb {O}}\)-bimodule is 0 or 1.

As a consequence, we express the real part of an element x into the left octonionic scalars of x.

Corollary 3.4

Let M be an \({\mathbb {O}}\)-bimodule. For any \(x\in M\), we have

$$\begin{aligned} Re \,x=x+\frac{1}{48}\sum _{i,j,k=1}^7\epsilon _{ijk}e_i[e_j,e_k,x]. \end{aligned}$$
(3.3)

Proof

In view of identities (2.6) and (3.2), we have

$$\begin{aligned} Re \,x= & \frac{5}{12}x-\frac{1}{12}\sum _{i=1}^7 e_ixe_i\\= & \frac{5}{12}x-\frac{1}{12}\sum _{i=1}^7 e_i\left( e_ix-\dfrac{1}{4}\sum _{j,k=1}^7 \epsilon _{ijk}[e_j,e_k,x]\right) \\= & x+\frac{1}{48}\sum _{i,j,k=1}^7\epsilon _{ijk}e_i[e_j,e_k,x]. \end{aligned}$$

This proves the formula (3.3). \(\square \)

We define the imaginary part of an element x as

$$\begin{aligned} Im \, x:=x- Re \,x. \end{aligned}$$

It turns out that the imaginary part of an element can be expressed in terms of the associators.

Corollary 3.5

Let M be an \({\mathbb {O}}\)-bimodule. For any \(x\in M\), we have

$$\begin{aligned} Im \, x=-\frac{1}{48}\sum _{i,j=1}^7[e_i,e_j,(e_ie_j)x]. \end{aligned}$$
(3.4)

Proof

In view of identity (3.3), we have

$$\begin{aligned} Im \, x= & x- Re \,x\nonumber \\= & -\frac{1}{48}\sum _{i,j,k=1}^7\epsilon _{ijk}e_i[e_j,e_k,x]. \end{aligned}$$
(3.5)

It suffices to show that

$$\begin{aligned} \sum _{i,j=1}^7[e_i,e_j,(e_ie_j)x]=\sum _{i,j,k=1}^7\epsilon _{ijk}e_i[e_j,e_k,x]. \end{aligned}$$

For any \(i\ne j\), it follows from (2.5) that

$$\begin{aligned} {[}e_i,e_j,(e_ie_j)x]= & [e_i,e_j,e_ie_j]x+e_i[e_j,e_ie_j,x]-[e_ie_j,e_ie_j,x]+[e_i,e_j(e_ie_j),x]\\= & \epsilon _{ijk}e_i[e_j,e_k,x]-[e_i,e_j(e_je_i),x]\\= & \epsilon _{ijk}e_i[e_j,e_k,x]. \end{aligned}$$

Note that

$$\begin{aligned} [e_i,e_j,(e_ie_j)x]=0 \end{aligned}$$

for \(i=j\). Hence we get

$$\begin{aligned} \sum _{i,j=1}^7[e_i,e_j,(e_ie_j)x]=\sum _{i,j,k=1}^7\epsilon _{ijk}e_i[e_j,e_k,x] \end{aligned}$$

as desired. \(\square \)

For any subset S of an \({\mathbb {O}}\)-bimodule M, we denote by \({\mathbb {O}}S\) the set

$$\begin{aligned} \left\{ \sum _{i=1}^np_is_i\mid n\in {\mathbb {N}}, p_i\in {\mathbb {O}},s_i\in S\right\} . \end{aligned}$$

We simply write

$$\begin{aligned} {\mathbb {O}}^kx:={\mathbb {O}}({\mathbb {O}}^{k-1}x). \end{aligned}$$

For example, we have

$$\begin{aligned} e_i[e_j,e_k,x]\in {\mathbb {O}}^3 x. \end{aligned}$$

Let \(\left<S\right>_{{\mathbb {O}}}\) denote the submodule generated by S, and simply denote by \(\left<x\right>_{{\mathbb {O}}}\) the submodule generated by x. We now come to characterize the submodules generated by one element in an \({\mathbb {O}}\)-bimodule.

Theorem 3.6

Let M be an \({\mathbb {O}}\)-bimodule. For any \(x=\sum _{i=0}^7e_ix_i\in M\), where \(x_i\in Re \,M\) for \(i=0,\ldots ,7\), we have

$$\begin{aligned} \left<x\right>_{{\mathbb {O}}}={\mathbb {O}}^5x. \end{aligned}$$
(3.6)

Let

$$\begin{aligned} \{x_{i_1},\ldots ,x_{i_l}\} \end{aligned}$$

be the maximal real linearly independent system of \(\{x_0,\ldots , x_7\}\). Then we have

$$\begin{aligned} \left<x\right>_{{\mathbb {O}}}=\bigoplus _{k=1}^l{\mathbb {O}}x_{i_k}. \end{aligned}$$
(3.7)

Proof

By induction, it is easy to show that

$$\begin{aligned} {\mathbb {O}}^kx\subseteq \left<x\right>_{{\mathbb {O}}} \end{aligned}$$

for any number k. Hence we have

$$\begin{aligned} {\mathbb {O}}^5x\subseteq \left<x\right>_{{\mathbb {O}}}. \end{aligned}$$
(3.8)

Conversely, note that for each \(i=0,\ldots ,7\),

$$\begin{aligned} x_i= Re \,(\overline{e_i}x). \end{aligned}$$

In view of (3.3), we obtain

$$\begin{aligned} x_i\in {\mathbb {O}}^4x \end{aligned}$$

for each \(i=0,\ldots ,7\). Thus

$$\begin{aligned} {\mathbb {O}}\{x_0,\ldots ,x_7\}\subseteq {\mathbb {O}}^5x. \end{aligned}$$

By definition, one can check that \({\mathbb {O}}\{x_0,\ldots ,x_7\}\) is an \({\mathbb {O}}\)-submodule and \(x\in {\mathbb {O}}\{x_0,\ldots ,x_7\}\). This implies that

$$\begin{aligned} \left<x\right>_{{\mathbb {O}}}\subseteq {\mathbb {O}}\{x_0,\ldots ,x_7\}\subseteq {\mathbb {O}}^5x. \end{aligned}$$

Combining with (3.8), we have

$$\begin{aligned} {\mathbb {O}}^5x\subseteq \left<x\right>_{{\mathbb {O}}}\subseteq {\mathbb {O}}^5x. \end{aligned}$$

This prove (3.6).

Next we prove (3.7). Since \(\{x_{i_1},\ldots ,x_{i_l}\}\) is the maximal linearly independent system of \(\{x_0,\ldots , x_7\}\), it follows that

$$\begin{aligned} x=\sum _{i=0}^7e_ix_i\in \bigoplus _{k=1}^l{\mathbb {O}}x_{i_k}. \end{aligned}$$

Clearly, \(\bigoplus _{k=1}^l{\mathbb {O}}x_{i_k}\) is an \({\mathbb {O}}\)-submodule. This implies that

$$\begin{aligned} \left<x\right>_{{\mathbb {O}}}\subseteq \bigoplus _{k=1}^l{\mathbb {O}}x_{i_k}. \end{aligned}$$

Conversely, since \(x_i= Re \,(\overline{e_i}x)\) for each \(i=0,\ldots ,7\), we conclude from (3.3) that \(x_i\in \left<x\right>_{{\mathbb {O}}}\). Hence we obtain

$$\begin{aligned} \bigoplus _{k=1}^l{\mathbb {O}}x_{i_k}\subseteq \left<x\right>_{{\mathbb {O}}}. \end{aligned}$$

This proves the theorem. \(\square \)

Remark 3.7

For any \(x=\sum _{i=0}^7e_ix_i\in M\), with \(x_i\in Re \,M\) for \(i=0,\ldots ,7\), let

$$\begin{aligned} \{x_{i_1},\ldots ,x_{i_l}\} \end{aligned}$$

be the maximal real linearly independent system of \(\{x_0,\ldots , x_7\}\) as above. We call l the length of x, denoted by \(l_x\). Then by Theorem 3.6, we have

$$\begin{aligned} \left<x\right>_{{\mathbb {O}}}\cong {\mathbb {O}}^{l_x}. \end{aligned}$$

The length of an element in an octonionic module is an invariant which reflects the complexity of the submodule generated by it.