Classification of Left Octonionic Modules

Abstract

In this article, we provide a complete classification of left octonionic modules (finite or infinite dimensions) in terms of new notions such as associative elements and conjugate associative elements. We give a simple approach to determine the irreducible left $\mathbb {O}$-modules by utilizing the Clifford algebra $C\ell _{7}$. We find that every left $\mathbb {O}$-module has a basis in some sense. This means that every left $\mathbb {O}$-module is a “free” module.

1 Introduction

The theory of quaternion Hilbert spaces brings the classical theory of functional analysis into the non-commutative realm (see [10, 16, 17, 19, 20]). It raises some new notions such as spherical spectrum, which has potential applications in quantum mechanics (see [4, 6]). All these theories are based on quaternion vector spaces, or more precisely, quaternion modules, and quaternion bimodules. A systematic study of quaternion modules is given by Ng [15]. It turns out that the category of (both one-sided and two-sided) quaternion vector spaces is equivalent to the category of real vector spaces.

It is a natural question to study the theory of octonionic spaces. Goldstine and Horwitz in 1964 [8] initiated the study of octonionic Hilbert spaces. More recently, Ludkovsky [12, 13] studied the algebras of operators in octonionic Banach spaces and spectral representations in octonionic Hilbert spaces. Although there are few results about the theory of octonionic Hilbert spaces, it is not full developed since it even lacks of coherent definition of octonionic Hilbert spaces.

We remark that Eilenberg [5] initiated the study of bimodules over non-associative rings. Later, Jacobson studied the structures of bimodules over a Jordan algebra or an alternative algebra [11]. One-sided modules over octonions were investigated in [8] for studying octonionic Hilbert spaces.

The purpose of this article is to characterize the structure of $\mathbb {O}$-modules completely. The modules considered in this paper are the left-alternative left-modules for the real algebra of octonions. Notice that these have been considered, in a much greater generality, by several mathematicians. In particular, the irreducible ones are known to be isomorphic to the regular or conjugate regular modules (see, for example, Chapter 11 of the monograph by Zhevlakov, Slinko, Shirshov, and Shestakov [22]). However, in the case of octonion algebra which is a normed algebra, we can give a much simpler way to determine the irreducible modules and give a complete description of left $\mathbb {O}$-modules. It turns out that left $\mathbb {O}$-modules are all free modules, looking much like the vector spaces over other normed algebras.

The set $\mathbb {O}$ admits two distinct $\mathbb {O}$-module structures. One is the canonical one, denoted by $\mathbb {O}$; the other is denoted by $\overline{\mathbb {O}}$ (see Example 3.5). To characterize any $\mathbb {O}$-module M, we need to introduce new notions, called associative elements and conjugate associative elements. Their collections are denoted by $\mathscr {A}(M)$ and $\mathscr {A}^{-}(M)$, respectively. The ordered pair of their dimensions as real vector spaces is called the type of M. These concepts are crucial in the classification of left $\mathbb {O}$-modules.

Our main result is about the characterization of the left $\mathbb {O}$-modules.

Theorem 1.1

Let M be a left $\mathbb {O}$-module. Then there is a natural $\mathbb {O}$-module isomorphism:

$$\begin{aligned} \mathbb {O}\otimes (\mathscr {A}(M)\oplus \mathscr {A}^{-}(M))\cong M. \end{aligned}$$

Its proof depends heavily on the isomorphism between the category $\mathbb {O}$-$\mathbf {Mod}$ and the category $C\ell _7$-$\mathbf {Mod}$. Since $C\ell _{7}$ is isomorphic to $M(8,\mathbb {R}) \oplus M(8,\mathbb {R})$, there are only two types of simple left $\mathbb {O}$-modules, namely, $\mathbb {O}$ and $\overline{\mathbb {O}}$ up to isomorphism. Let M be a left $\mathbb {O}$-module. Then

$$\begin{aligned} M=\oplus _{i\in \Lambda } M_i, \end{aligned}$$

where $M_i$ is a submodule isomorphic either to $\mathbb {O}$ or to $\overline{ \mathbb {O}}$ for each $i\in \Lambda$. With some elementary properties of $\mathscr {A}(M)$ and $\mathscr {A}^{-}(M)$, we can obtain a bijective map:

$$\begin{aligned} \mathbb {O}\otimes (\mathscr {A}(M)\oplus \mathscr {A}^{-}(M))\rightarrow M. \end{aligned}$$

We can show that this is an $\mathbb {O}$-module isomorphism with respect to a natural $\mathbb {O}$-module structure of $\mathbb {O}\otimes (\mathscr {A}(M)\oplus \mathscr {A}^{-}(M))$.

Finally, we discuss the free property of left $\mathbb {O}$-modules. It turns out that every left $\mathbb {O}$-module is “free” in some sense.

2 Preliminaries

In this section, we introduce some notations on octonions and some basic properties.

2.1 The Algebra of the Octonions $\mathbb {O}$

The algebra of the octonions $\mathbb {O}$ is a non-associative, non-commutative, normed division algebra over $\mathbb {R}$. Let $e_0,e_1,\ldots ,e_7$ be its natural basis throughout this paper, i.e.,

$$\begin{aligned} e_ie_j+e_je_i=-2\delta _{ij},\quad i,j=1,\ldots ,7. \end{aligned}$$

For convenience, we denote $e_0=1$.

In terms of the natural basis, every octonion can be written as

$$\begin{aligned} x=x_0+\sum _{i=1}^7x_ie_i,\quad x_i\in \mathbb {R}. \end{aligned}$$

The conjugate octonion of x is defined by

$$\begin{aligned} \overline{x}=x_0-\sum _{i=1}^7x_ie_i, \end{aligned}$$

and the norm of x equals $|x|=\sqrt{x\overline{x}}\in \mathbb {R}$, the real part of x is $\textit{Re}\,{x}=x_0=\frac{1}{2}(x+\overline{x})$.

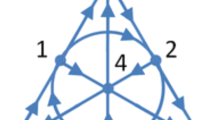
The full multiplication table is conveniently encoded in the Fano mne-mon-ic graph (see [2, 21]). In the Fano mnemonic graph, the vertices are labeled by $1, \ldots , 7$ instead of $e_1,\ldots , e_7$. Each of the seven oriented lines gives a quaternionic triple. The product of any two imaginary units is given by the third unit on the unique line connecting them, with the sign determined by the relative orientation.

Fig. 1

Fano mnemonic graph

The associator of three octonions is defined as

$$\begin{aligned}{}[x,y,z]=(xy)z-x(yz) \end{aligned}$$

for any $x,y,z\in \mathbb {O}$, which is alternating in its arguments and has no real part. That is, $\mathbb {O}$ is an alternative algebra and hence it satisfies the so-called R. Moufang identities [18]:

$$\begin{aligned} (xyx)z=x(y(xz)),\ z(xyx)=((zx)y)x,\ x(yz)x=(xy)(zx). \end{aligned}$$

The commutator is defined as

$$\begin{aligned}{}[x,y]=xy-yx. \end{aligned}$$

2.2 Clifford Algebra

We shall use the Clifford algebra $C\ell _7$ to study left $\mathbb {O}$-modules. In this subsection, we review some basic facts for Clifford algebras. The Clifford algebras were introduced by Clifford in 1882. For their recent development, we refer to [1, 7, 9, 14].

Definition 2.1

([9]) Given a Euclidean vector space $(V,\left<\cdot ,\cdot \right>)$ of signature $p,\ q$, the Clifford algebra $C\ell (V)$ is the quotient $\sum _{k=1}^{+\infty }\otimes ^k V/I(V)$, where I(V) is the two-sided ideal in $\sum _{k=1}^{+\infty }\otimes ^k V$ generated by all elements:

$$\begin{aligned} x\otimes x+\left<x,x\right> \end{aligned}$$

(2.1)

with $x\in V$.

We state the Fundamental Lemma for Clifford algebras.

Lemma 2.2

[9] Given a Euclidean vector space $(V,\left<\cdot ,\cdot \right>)$ and a linear map $\phi :V\rightarrow \mathbb {A}$ from V into $\mathbb {A}$, an associative algebra with unit. If

$$\begin{aligned} \phi (x)\phi (x)=-\left<x,x\right>,\quad \text { for all }x\in V, \end{aligned}$$

(2.2)

then $\phi$ has a unique “extension” (also denoted $\phi )$ to an algebra homomorphism of $C\ell (V)$ into $\mathbb {A}$:

Let $V=\mathbb {R}^n$ be equipped with the usual Euclidean inner product. Denote $C\ell (V)=C\ell _n$ and denote by $\iota : V\rightarrow C\ell _n$ the embedding map. We need some notations and conventions.

• $x=(x_1,\ldots ,x_n)\in \mathbb {R}^n,\ \left| x\right| ^2=\sum _{i=1}^{n}x_i^2$.

• Let $\{f_i\}_{i=1}^n$ be the canonical orthonormal basis of $\mathbb {R}^n$, i.e., $f_i=(0,\ldots ,0,1,0,\ldots ,0)$ with 1 in the i-th slot. Denote $g_i=\iota (f_i)\in C\ell _n$.

• Let $\mathcal {P}(n)$ be the set of all the subsets of $\{1,\ldots ,n\}$.

• For any $\alpha \in \mathcal {P}(n)$, if $\alpha \ne \emptyset$, we write $\alpha =\{\alpha _1,\ldots ,\alpha _k\}$ with $1\le \alpha _1<\cdots <\alpha _k\le n$ and we set $g_{\alpha }=g_{\alpha _1}\cdots g_{\alpha _k}$. Otherwise, we denote $g_{\emptyset }=1$.

The Clifford algebra $C\ell _n$ can be described alternatively with the above notations as

• (i) $C\ell _n$ is $\mathbb {R}$-linearly generated by $\{g_\alpha \mid \ \alpha \in \mathcal {P}(n)\}$;

• (ii) $g_ig_j+g_jg_i=-2\delta _{ij}$ for any $i,j=1,\ldots ,n$.

At the last of this subsection, we give the following algebra isomorphism of $C\ell _n$ (see for example [1]).

• $C\ell _{n+8}\cong C\ell _n\otimes M(16,\mathbb {R})\cong M(16,C\ell _n)$;

• for $n=0,\ldots ,7$ we have Table 1

Table 1 Isomorphism classes of $C \ell _n$

Here, we denote by $M(k, \mathbb F)$ the algebra of all $k\times k$ matrices with entries in the algebra $\mathbb F$.

3 $\mathbb {O}$-Modules

We set up in this section some preliminary definitions and results on left $\mathbb {O}$-modules.

Definition 3.1

A real vector space M is called a (left) $\mathbb {O}$-module if it is equipped with a multiplication $\mathbb {O}\times M\rightarrow M$, denoted by

$$\begin{aligned} (q,m)\mapsto qm, \end{aligned}$$

such that the following axioms hold for all $q,q_1,q_2\in \mathbb {O},\; \lambda \in \mathbb {R}$ and all $m,m_1,m_2\in M$:

• (i) $(\lambda q)m=\lambda (qm)=q(\lambda m)$;

• (ii) $(q_1+q_2)m=q_1m+q_2m, \ q(m_1+m_2)=qm_1+qm_2$;

• (iii) $[q_1,q_2,m]=-[q_2,q_1,m];$

• (iv) $1m=m.$

Here, the left associator is defined by

$$\begin{aligned}{}[q_1,q_2,m]:=(q_1q_2)m-q_1(q_2m). \end{aligned}$$

Note that this definition is equivalent to the definition given in [12, 13], wherein the axiom $(\mathrm {iii)}$ is replaced by

$$\begin{aligned} q^2m=q(qm),\quad \text { for all } q\in \mathbb {O},\;\; m\in M. \end{aligned}$$

The proof is trivial by polarizing the above relation. It also agrees with the definition given in [8] where M needs to satisfy an additional axiom: $p(p^{-1}x)=x$, which can be deduced from the equation $p(px)=p^2x$ directly.

Let $M,M'$ be left $\mathbb {O}$-modules. The definition of the words submodule, homomorphism, isomorphism, kernel of a homomorphism, which are familiar from the study of associative modules, do not involve associativity of multiplication and are thus immediately applicable to O-modules. Let $\text {Hom}_{\mathbb {O}}(M,M')$ denote the set of all $\mathbb {O}$-homomorphisms from M to $M'$ as usual. The notation JN means the subset of M spanned by all products rn with $r\in J$ and $n\in N$ (J being an arbitrary non-empty subset of $\mathbb {O}$ and N being an arbitrary nonempty subset of M). Namely,

$$\begin{aligned} JN:=\text {span}\{rn: r\in J\subset \mathbb {O}, \ n\in N \subset M\}. \end{aligned}$$

Here we must of course distinguish between $J_1(J_2N)$ and $(J_1J_2)N$. Let $\left\langle N\right\rangle _\mathbb {O}$ denote the the smallest submodule that contains N. An element $m\in M$ is said to be associative if

$$\begin{aligned}{}[p,q,m]=0\quad \text {for all } p,q\in \mathbb {O}. \end{aligned}$$

Denote by $\mathscr {A}(M)$ the set of all associative elements in M

$$\begin{aligned} \mathscr {A}(M):=\{m\in M\mid [p,q,m]=0\quad \text {for all } p,q \in \mathbb {O}\}. \end{aligned}$$

We call $\mathscr {A}(M)$ the nucleus of M. One useful identity which holds in any $\mathbb {O}$-module M is

$$\begin{aligned} {[}p,q,r]m+p[q,r,m]=[pq,r,m]-[p,qr,m]+[p,q,rm], \end{aligned}$$

(3.1)

where $p,q,r\in \mathbb {O},\ m\in M$. The proof is by straightforward calculations. In particular, it provides a useful identity for associative elements as follows.

Lemma 3.2

For all associative element $m\in \mathscr {A}(M)$, we have

$$\begin{aligned}{}[p,q,rm]=[p,q,r]m, \quad \text {for all } p,q,r \in \mathbb {O}. \end{aligned}$$

The following elementary property will be useful in the sequel. The proof is trivial and will be omitted here.

Proposition 3.3

If $f\in \text {Hom}_{\mathbb {O}}(M,N)$, then $f([p,q,x])=[p,q,f(x)]$ for all $p,q\in \mathbb {O},\ x\in M$. Therefore $f(\mathscr {A}(M))\subseteq \mathscr {A}(N)$. In particular, if $M\cong _\mathbb {O}N$, then

$$\begin{aligned} \mathscr {A}(M)\cong _\mathbb {R}\mathscr {A}(N). \end{aligned}$$

We give several examples of left $\mathbb {O}$-modules.

Example 3.4

It is easy to see that the real vector spaces $\mathbb {O},\; \mathbb {O}^n,\; M(n,\mathbb {O})$ with the obvious multiplication are all left $\mathbb {O}$-modules. Clearly, the nuclei on these modules are $\mathbb {R},\;\mathbb {R}^n,\;M(n,\mathbb {R})$ respectively.

We can define a different $\mathbb {O}$-module structure on the octonions $\mathbb {O}$ itself.

Example 3.5

($\overline{\mathbb {O}}$) Define:

$$\begin{aligned} p \, \hat{\cdot } \, x:=\overline{p}x,\quad \text {for all } p\in \mathbb {O},\;\; x\in \mathbb {O}. \end{aligned}$$

It is easy to check that this is a left $\mathbb {O}$-module. Indeed

$$\begin{aligned} p^2\,\hat{\cdot }\,x=\overline{p}^2x=p\,\hat{\cdot }\, (p\,\hat{\cdot }\, x). \end{aligned}$$

We shall denote this $\mathbb {O}$-module by $\overline{\mathbb {O}}$. By direct calculations, we obtain:

$$\begin{aligned}{}[p,q,x]_{\overline{\mathbb {O}}}=[p,q,x]+\overline{[p,q]}x. \end{aligned}$$

This implies that

$$\begin{aligned} \mathscr {A}(\overline{\mathbb {O}})=\{0\}. \end{aligned}$$

Note that Proposition 3.3 demonstrates that

$$\begin{aligned} \mathbb {O}\ncong \overline{\mathbb {O}}. \end{aligned}$$

However, the elements of $\mathbb {R}$ have a special property in $\overline{\mathbb {O}}$ which leads to the new concept of conjugate associative element.

Definition 3.6

An element $m\in M$ is said to be conjugate associative if

$$\begin{aligned} (pq)m=q(pm),\quad \text { for all } p,q\in \mathbb {O}. \end{aligned}$$

Denote by $\mathscr {A}^{-}(M)$ the set of all conjugate associative elements.

Lemma 3.7

$\mathscr {A}^{-}(\overline{\mathbb {O}})=\mathbb {R}.$

Proof

For any $x\in \mathscr {A}^{-}(\overline{\mathbb {O}})$ and any $p,q\in \mathbb {O}$, we have

$$\begin{aligned} 0=(pq){\,\hat{\cdot }\,}x-q{\hat{\cdot }}(p{\,\hat{\cdot }\,}x)= [\overline{q},\overline{p},x]. \end{aligned}$$

This implies that $x\in \mathbb {R}$. Clearly $\mathbb {R}\subseteq \mathscr {A}^{-}(\overline{\mathbb {O}})$ and we conclude $\mathscr {A}^{-}(\overline{\mathbb {O}})=\mathbb {R}.$ $\square$

Remark 3.8

Let M be a left $\mathbb {O}$-module. We have defined a different left $\mathbb {O}$-module structure on M:

$$\begin{aligned} p\,\hat{\cdot }\, x:=\overline{p}x,\quad \text {for all } p\in \mathbb {O},x\in M. \end{aligned}$$

We shall denote the set M with this new module structure by $M^{-}$. Then one can check that

$$\begin{aligned} \mathscr {A}(M^{-})=\mathscr {A}^{-}(M) \end{aligned}$$

(3.2)

Obviously, if we are interested in associative elements, this shows that we must also consider conjugate associative elements. It also shows that every statement involving $\mathscr {A}(M)$ automatically brings a statement involving $\mathscr {A}^{-}(M)$ without any extra-proof.

Lemma 3.9

For any left $\mathbb {O}$-module M, we have

$$\begin{aligned} \mathscr {A}(M)\cap \mathscr {A}^{-}(M)=\{0\}. \end{aligned}$$

Proof

Obviously, $0\in \mathscr {A}(M)\cap \mathscr {A}^{-}(M)$. If $x\in \mathscr {A}(M)\cap \mathscr {A}^{-}(M)$, then for any $p,q\in \mathbb {O}$,

$$\begin{aligned}{}[p,q]x=(pq)x-(qp)x=(pq)x-p(qx)=[p,q,x]=0. \end{aligned}$$

This implies $x=0$ since we can choose $p,q\in \mathbb {O}$ such that $[p,q]\ne 0$. This proves the lemma. $\square$

Remark 3.10

Clearly, both $\mathscr {A}(M)$ and $\mathscr {A}^{-}(M)$ are real vector spaces. If M is of finite dimension, we call the ordered pair

$$\begin{aligned} (\dim _{\mathbb {R}}\mathscr {A}(M), \ \dim _{\mathbb {R}}\mathscr {A}^{-}(M)) \end{aligned}$$

the type of M. We shall use this notion to describe the structure of left $\mathbb {O}$-modules. It turns out that the type is a complete invariant in the finite dimensional case.

Let M be a left $\mathbb {O}$-module. We shall now provide some properties of associative elements and conjugate associative elements which will be used in the sequel.

Lemma 3.11

Let $\{x_i\}_{i=1}^n$ be an $\mathbb {R}$-linearly independent set of associative elements of M. If

$$\begin{aligned} \sum _{i=1}^nr_ix_i=0 ,\ \ r_i\in \mathbb {O}\quad \text {for } \ \ i=1,\dots , n, \end{aligned}$$

then $r_i=0$ for $i=1,\dots , n.$

Proof

The proof is by induction on n. For the case $n=1$, we have $rx=0$. If $r\ne 0$, since $x\in \mathscr {A}(M),$ it follows that

$$\begin{aligned} 0=r^{-1}(rx)=(r^{-1}r)x=x, \end{aligned}$$

a contradiction with our assumption $x\ne 0$. Assume that the lemma holds for $n=k$, we will prove it for $k+1$. Suppose

$$\begin{aligned} \sum _{i=1}^{k+1}r_ix_i=0 \quad \text{ and } \quad r_{k+1}\ne 0. \end{aligned}$$

This can be rewritten as

$$\begin{aligned} x_{k+1}=\sum _{i=1}^k s_ix_i \end{aligned}$$

(3.3)

with $s_i:=-r_{k+1}^{-1}r_i.$ Since $x_{k+1}\in \mathscr {A}(M)$, for all $p,q,\in \mathbb {O}$ we have

$$\begin{aligned} 0=[p,q,x_{k+1}]=\sum _{i=1}^k[p,q,s_ix_i]=\sum _{i=1}^k[p,q,s_i]x_i, \end{aligned}$$

where we have used Lemma 3.2 in the last identity. Hence by induction hypothesis we have

$$\begin{aligned}{}[p,q,s_i]=0 \end{aligned}$$

for all $i\in \{1,\dots , k\}$ and all $p,q\in \mathbb {O}.$ This implies $s_i\in \mathbb {R}$. Due to (3.3), we conclude that $\{x_i\}_{i=1}^n$ is $\mathbb {R}$-linearly independent, a contradiction to our hypothesis. This completes the proof. $\square$

Notice that we have actually proved a somewhat stronger assertion:

Corollary 3.12

Let $S\subseteq \mathscr {A}(M)$. Then S is $\mathbb {O}$-linearly independent if and only if it is $\mathbb {R}$-linearly independent.

A similar statement also holds for conjugate elements.

Lemma 3.13

Let $S=\{x_i\}_{i=1}^n\subseteq \mathscr {A}^{-}(M)$ be an $\mathbb {R}$-linearly independent set. If

$$\begin{aligned} \sum _{i=1}^nr_ix_i=0 \end{aligned}$$

for any $r_i\in \mathbb {O}$ and $i=1,\dots , n$, then $r_i=0$ for every $i=1,\dots , n.$

Proof

This can also be proved similarly by induction on n. Here we would like to provide an alternative proof based on the relation between associative and conjugate associative elements in (3.2).

Assume that $\sum _{i=1}^nr_ix_i=0$. Since

$$\begin{aligned} S=\{x_i\}_{i=1}^n\subseteq \mathscr {A}^{-}(M)=\mathscr {A}(M^{-}) \end{aligned}$$

is an $\mathbb {R}$-linearly independent set, by Lemma 3.11, we conclude from

$$\begin{aligned} \sum _{i=1}^nr_ix_i=\sum _{i=1}^n\overline{ r_i}\;\hat{\cdot }\,x_i=0 \end{aligned}$$

that $r_i=0$ for all $i=1,\dots , n.$ $\square$

4 The Structure of Left $\mathbb {O}$-Moudles

In this section, we are in a position to describe the structure of any left $\mathbb {O}$-module.

It is well-known (for example, [2, 9]) that octonions have a very close relationship with spinors in seven and eight dimensions. In particular, multiplication by imaginary octonions is equivalent to Clifford multiplication on spinors in dimension seven. It turns out that the category of left $\mathbb {O}$-modules is isomorphic to the category of left $C\ell _{7}$-modules.

For any left $\mathbb {O}$-module M, since $[e_i,e_j,x]=-[e_j,e_i,x]$, the left multiplication operator L satisfies:

$$\begin{aligned} L_{e_i}L_{e_j}+L_{e_j}L_{e_i}=-2\delta _{ij}Id. \end{aligned}$$

Let $\mathbb {A}$ be the associative subalgebra of $\text {End}_{\mathbb {R}}M$ generated by $\{L_{e_i}\mid i=0,1,\ldots ,7 \}$. According to Lemma 2.2, there exist a ring homomorphism

$$\begin{aligned} C\ell _7\rightarrow \mathbb {A}\hookrightarrow \text {End}_{\mathbb {R}}M. \end{aligned}$$

This yields a $C\ell _{7}$-module structure on M. Denote this $C\ell _{7}$-module by ${}_{C\ell _{7}}M$, or just M, and the $C\ell _{7}$-scalar multiplication is given by

$$\begin{aligned} g_{\alpha }m: = e_{\alpha _1}(e_{\alpha _2}(\cdots (e_{\alpha _k}m))) \end{aligned}$$

for any $\alpha \in \mathcal {P}(n)$. Here,

$$\begin{aligned} g_{\alpha }=g_{\alpha _1}\cdots g_{\alpha _k}:=L_{e_{\alpha _1}}\cdots L_{e_{\alpha _k}}. \end{aligned}$$

Let $f\in \text {Hom}_\mathbb {O}(M,M')$ be a left $\mathbb {O}$-homomorphism, where $M,M'$ are two left $\mathbb {O}$-modules. Then

$$\begin{aligned} f(L_{e_i}x)=f(e_ix)=e_if(x)=L_{e_i}f(x). \end{aligned}$$

and hence $f(g_\alpha x)=g_\alpha f(x)$. This means $f\in \text {Hom}_{C\ell _{7}}(M,M')$.

Conversely, for any left $C\ell _{7}$-module M, let $\{g_i\}_{i=1}^7$ be a basis in $\mathbb {R}^7$. Define:

$$\begin{aligned} e_i\tilde{\cdot }x:=g_ix. \end{aligned}$$

Then

$$\begin{aligned} e_i\tilde{\cdot }(e_j\tilde{\cdot }x)=g_i(g_jx)=(g_ig_j)x=(-2\delta _{ij}-g_jg_i)x=-2\delta _{ij}x-e_j\tilde{\cdot }(e_i\tilde{\cdot }x) \end{aligned}$$

and by transposition of terms, we have

$$\begin{aligned} e_i\tilde{\cdot }(e_j\tilde{\cdot }x)+e_j\tilde{\cdot }(e_i\tilde{\cdot }x)=(e_ie_j+e_je_i)\tilde{\cdot }x \end{aligned}$$

so that

$$\begin{aligned}{}[e_i,e_j,x]=-[e_j,e_i,x]. \end{aligned}$$

This yields $[p,q,x]=-[q,p,x]$ for any $p,q\in \mathbb {O}$. Consequently M is a left $\mathbb {O}$-module. For any $f\in \text {Hom}_{C\ell _{7}}(M,M')$,

$$\begin{aligned} f(e_i\tilde{\cdot }x)=f(g_ix)=g_if(x)=e_i\tilde{\cdot }f(x) \end{aligned}$$

Therefore $f\in \text {Hom}_\mathbb {O}(M,M')$. In summary, we get the following key result:

Theorem 4.1

The category of left $\mathbb {O}$-module is isomorphic to the category of left $C\ell _{7}$-module. Moreover, the only two kinds of simple $\mathbb {O}$-module are $\mathbb {O}$ and $\overline{\mathbb {O}}$ up to isomorphism.

Proof

We have two natural categories $\mathbb {O}$-$\mathbf {Mod}$ and $C\ell _7$-$\mathbf {Mod}$. By the preceding construction, we have a bijection

$$\begin{aligned} T:\mathbb {O}\text {-}\mathbf {Mod}\longrightarrow & {} C\ell _7\text{- }\mathbf {Mod}{\tiny } \\ {}_{\mathbb {O}}M\mapsto & {} {}_{{C\ell _7}}M \end{aligned}$$

and for any morphism $\varphi \in \text {Hom}_\mathbb {O}(M,N)$, it maps $\varphi$ to $T(\varphi ):{}_{{C\ell _7}}M\rightarrow {}_{{C\ell _7}}N$, which is given by

$$\begin{aligned} T(\varphi ):m\mapsto \varphi (m). \end{aligned}$$

Clearly, this is an isomorphism by the above discussion. As is well known, $C\ell _{7}$ is a semi-simple algebra with the decomposition

$$\begin{aligned} C\ell _{7}\cong M(8,\mathbb {R}) \oplus M(8,\mathbb {R}), \end{aligned}$$

and the simple $C\ell _{7}$-modules are $(\mathbb {R}^8,0)$ and $(0,\mathbb {R}^8)$ up to isomorphism [7]. Hence there also exist only two types of simple $\mathbb {O}$-module. In view of Example 3.5, we thus conclude that $\mathbb {O}$ and $\overline{\mathbb {O}}$ are the only two different types of simple $\mathbb {O}$-modules. This completes the proof. $\square$

If R is a semi-simple associative and unital ring, every (left or right) R-module is a direct sum of simple R-modules (see, for instance, [3, Section I-4]); moreover, R is a finite direct sum of simple ideals, and the number of these ideals is the number of types of simple R-modules.

Corollary 4.2

If M is a left $\mathbb {O}$-module. Then

$$\begin{aligned} M=\oplus _{i\in \Lambda } M_i, \end{aligned}$$

where $M_i$ is a submodule isomorphic either to $\mathbb {O}$ or to $\overline{ \mathbb {O}}$ for each $i\in \Lambda$.

Let M be a left $\mathbb {O}$-module. Then $\left\langle m\right\rangle _\mathbb {O}$ is finite dimensional for any $m\in M$. More precisely, the dimension is at most 128, because the $\mathbb {O}$-submodule generated by m is also the $C\ell _{7}$-submodule generated by m. In fact, this property has already appeared in [8]. However, the proof can be greatly simplified in view of the relationship of left $\mathbb {O}$-modules and $C\ell _{7}$-modules. We shall use this property to characterize the structure of left $\mathbb {O}$-modules more precisely.

Theorem 4.3

Let M be a left $\mathbb {O}$-module. Then there is a natural $\mathbb {O}$-module isomorphism:

$$\begin{aligned} \mathbb {O}\otimes (\mathscr {A}(M)\oplus \mathscr {A}^{-}(M))\cong M. \end{aligned}$$

In particular,

$$\begin{aligned} \mathbb {O}(\mathscr {A}(M)\oplus \mathscr {A}^{-}(M))= M. \end{aligned}$$

Proof

We introduce the natural mapping

$$\begin{aligned} \phi : \quad \mathbb {O}\otimes \mathscr {A}(M)\oplus {\mathbb {O}}\otimes \mathscr {A}^{-}(M)\longrightarrow & {} M,\\ \left( \sum _{i=1}^nr_i\otimes x_i,\ \ \sum _{i=1}^{n'}p_i\otimes y_i\right)\mapsto & {} \sum _{i=1}^nr_i x_i+\sum _{i=1}^{n'}p_i y_i . \end{aligned}$$

We define the module structure of the tensor product as follows:

$$\begin{aligned} q\cdot \left( \sum _{i=1}^nr_i\otimes x_i,\ \ \sum _{i=1}^{n'}p_i\otimes y_i\right) := \left( \sum _{i=1}^nqr_i\otimes x_i,\ \ \sum _{i=1}^{n'}p_iq\otimes y_i\right) . \end{aligned}$$

Then $\phi$ is clearly an $\mathbb {O}$-module homomorphism by the definition of associative and conjugate associative elements.

We come to show that $\phi$ is injective. Assume that

$$\begin{aligned} \sum _{i=1}^nr_i x_i+\sum _{i=1}^{n'}p_i y_i =0 \end{aligned}$$

for some $x_i\in \mathscr {A}(M)$ and $y_i\in \mathscr {A}^{-}(M)$. Without loss of generality we can assume both $\{x_i\}_{i=1}^n$ and $\{y_i\}_{i=1}^{n'}$ are $\mathbb {R}$-linearly independent. It follows from Lemma 3.9 that

$$\begin{aligned} \sum _{i=1}^nr_i x_i=0,\quad \sum _{i=1}^{n'}p_i y_i =0. \end{aligned}$$

In view of Lemmas 3.11 and  3.13, we conclude that $r_i=0$ and $p_j=0$ for all i, j. This means that $\phi$ is injective.

To prove that $\phi$ is surjective, we let $m\in M$ be arbitrary. Since $\left\langle m\right\rangle _\mathbb {O}$ is finite dimensional, by Corollary 4.2, there are two non-negative integers n and $n'$, such that

$$\begin{aligned} \left\langle m\right\rangle _\mathbb {O}\cong \mathbb {O}^{n}\oplus \overline{ \mathbb {O}}^{n'}. \end{aligned}$$

We thus have an expression

$$\begin{aligned} m=\sum _{i=1}^nr_i x_i+\sum _{i=1}^{n'}p_i y_i \end{aligned}$$

for some $x_i\in \mathscr {A}(M)$ and $y_i\in \mathscr {A}^{-}(M)$. This means

$$\begin{aligned} m=\phi \left( \sum _{i=1}^n r_i \otimes x_i+\sum _{i=1}^{n'}p_i \otimes y_i\right) . \end{aligned}$$

Since

$$\begin{aligned} \mathbb {O}\otimes \mathscr {A}(M)\oplus {\mathbb {O}}\otimes \mathscr {A}^{-}(M)=\mathbb {O}\otimes (\mathscr {A}(M)\oplus \mathscr {A}^{-}(M)), \end{aligned}$$

we obtain the $\mathbb {O}$-module isomorphism as desired. Note that the image of $\phi$ is just $\mathbb {O}(\mathscr {A}(M)\oplus \mathscr {A}^{-}(M))$, it follows that $M=\mathbb {O}(\mathscr {A}(M)\oplus \mathscr {A}^{-}(M))$. $\square$

Remark 4.4

Following the definition of Jacobson [11], we call a left $\mathbb {O}$-module M to be an $\mathbb {O}$-bimodule if the associator is alternating. That is,

$$\begin{aligned} {[}p,q,m] =[q,m,p]=[m,p,q] \end{aligned}$$

(4.1)

for all $p,q\in \mathbb {O}$ and $m\in M$.

We point out that the $\mathbb {O}$-vector space studied by Ludkovsky [12] may not be an $\mathbb {O}$-bimodule in general. By his definition [12], an $\mathbb {O}$-vector space X is defined to be an additive group for which the multiplication of the vectors $v\in X$ on scalars $a, b\in \mathbb {O}$ from the left and the right satisfies the axioms of the alternativity and distributivity. Here the alternativity from the left means that $b(bv) = (b^2)v$ for each $b\in \mathbb {O}$ and $v\in X$, the alternativity from the right means that $(vb)b = v(b^2)$ for each $b\in \mathbb {O}$ and $v\in X$. From his definition, we find that an $\mathbb {O}$-vector space is actually referred to as a left $\mathbb {O}$-module equipped with an arbitrary right $\mathbb {O}$-module structure without the assumption of (4.1). This means that the left associator [p, q, m] and the right associator [m, p, q] in an $\mathbb {O}$-vector space are two independent and distinct notions.

We remark that if the right module structure of an $\mathbb {O}$-vector space M is incompatible with its left module structure in the sense of (4.1), then M may fail to have the decomposition

$$\begin{aligned} M=\mathscr {A}(M)\otimes \mathbb {O}. \end{aligned}$$

However, this decomposition was used directly in the proof of Hahn-Banach Theorem in [12, Theorem 2.4.1] and some other places. So there are some gaps in the study of octonionic Hilbert space and Banach space before in the literature.

Finally, we discuss the free property of left $\mathbb {O}$-modules. It turns out that every left $\mathbb {O}$-module is “free” in some sense. To this end, we need to introduce the notion of $\mathbb {O}$-basis of an $\mathbb {O}$-module.

Definition 4.5

Let M be a left $\mathbb {O}$-module. A subset $S\subseteq M$ is called a $\mathbb {O}$-basis if S is $\mathbb {O}$-linearly independent and $M=\mathbb {O}S$.

Theorem 4.6

Every left $\mathbb {O}$-module M has an $\mathbb {O}$-basis S. More precisely, we can choose S to be an $\mathbb {R}$-basis of the real vector space $\mathscr {A}(M)\oplus \mathscr {A}^{-}(M)$.

Proof

Let S be an $\mathbb {R}$-basis of the real vector space $\mathscr {A}(M)\oplus \mathscr {A}^{-}(M)$. In view of Lemmas 3.11 and 3.13, we know that S is also $\mathbb {O}$-linearly independent. Thanks to Theorem 4.3, we have

$$\begin{aligned} \mathbb {O}S=\mathbb {O}(\mathbb {R}S)=\mathbb {O}(\mathscr {A}(M)\oplus \mathscr {A}^{-}(M))=M. \end{aligned}$$

This completes the proof. $\square$

Remark 4.7

We have given the detail characterization of left $\mathbb {O}$-modules in terms of associative elements and conjugate associative elements. This will be very useful for our further discussion on the theory of $\mathbb {O}$-Hilbert space as well as the $\mathbb {O}$-Gelfand–Naimark theorem later.