Critical Sliding in Rolling Bearings under Hydrodynamic Friction Conditions

Abstract—

Conditions for seizing during hydrodynamic contact between parts under rolling friction have been studied. For this purpose, a known friction model based on the generalized Eyring equation and taking into account the phenomenon of oil film self-heating has been used. The fact that a correct description of friction curves using this model is possible has been confirmed by comparison with published experimental data. Conditions are revealed, under which in the thermal zone of friction curves, despite a decrease in the friction coefficient, an increase in friction power loss continues. It is shown that the bearing seizing hazard occurs when the bearings operate in a thermal zone of the friction curves. A concept of critical slide–roll ratio that represents a boundary of the thermal zone of friction curves has been introduced, and its dependence on the contact pressure and temperature has been studied for PAO1 grade polyalphaolefin oil in the temperature range of 40–100°C and for MN-7.5u grade oil in the range of 60−140°C. It is shown that the critical sliding-to-rolling ratio increases with decreasing contact pressure in the bearing, as well as with increasing oil temperature. It is concluded that the conditions of contact between the rollers and the inner ring promote an increase in friction power loss to a greater extent than the conditions of contact between the rollers and the outer ring. This indicates a higher seizing hazard in the case of the inner ring than in the case of the outer ring, which is confirmed by the statistics of rolling bearing failures. In order to prevent seizing in bearings, it is necessary to provide a margin with respect to critical sliding at the bearing design stage.

INTRODUCTION

One of the characteristics of hydrodynamic contact interaction between rolling bearings consists in their mutual slipping. Moderate slipping exerts a positive effect on the bearing operation, since less power is spent for driving the bearing, a decrease in the heat flux occurs, as well as the operating temperature of the bearing is reduced and the bearing service life increases. However, excessive slipping in the contact zones of rolling bodies and raceways often causes bearing failures. In this case, seizing can occur followed by an increase in the wear level of the working surfaces [1].

The immediate cause of seizing consists in significant self-heating of the contact oil layer caused by slipping and a decrease in the oil layer viscosity, which results in an unacceptable decrease in the thickness of the oil layer. Most of the rheological parameters of hydrodynamic models for contact friction are determined based on experimental friction curves, i.e., the coefficient of sliding friction depending on the ratio between the sliding velocity and the rolling velocity obtained with the use of a friction machine, which is called a slide–roll ratio. In the course of such testing, just as in the case of bearing operation, a gradual increase in the temperature of the contact oil film occurs owing to friction.

Nowadays, there are two main approaches to accounting for the self-heating of contact oil layers when determining the rheological characteristics of the oil. One of the approaches is based on constructing a contact friction model a part of which consists in the calculation of the heat release power in the oil film followed by taking into account the effect of an elevated temperature on the properties of the oil. For this purpose, thermophysical properties inherent in both lubricants and contacting parts are taken into account. Such a model has been proposed and experimentally verified, for example, by the authors of [2, 3]. In the scope of the second approach, it is proposed to determine the rheological oil characteristics based on reconstructed isothermal friction curves [4].

In order to do this, it is necessary to have a sufficient array of experimental friction curves obtained at different initial temperature values. The characteristics obtained by this method are considered reliable only in the case of a sufficiently low slide–roll ratio being less than 8% [5]. This approach complicates solving the practical problems of determining the conditions for contact interaction and self-heating, since in each specific case it requires solving an associated problem of contact friction and thermal conductivity both in the oil layer and in the areas of contacting parts adjacent to the contact zone.

There is no consensus on the issue of acceptable, seizing-free sliding in bearings. So, for example, some authors consider that a long-term decrease in the separator speed in roller bearings caused by sliding in the contact zone of rolling bodies and raceways less than 5% is quite acceptable, the others take the value amounting to 10% [6], whereas in the case of complete bearing lubrication and cooling they accept a slipping level amounting up to 30% [7]. The seizing criteria proposed by different authors considered according to a maximum contact pressure, according to the maximum oil film thickness [8] and others [9] have been developed based on limited experimental data and, when applied to different conditions, often show unrealistic results.

Objective—To determine the slide–roll ratio between the rolling elements and raceways of the bearing critical for the onset of seizing, in accordance with the features of the contact interaction hydrodynamics.

HYDRODYNAMIC FRICTION MODEL

The hydrodynamic friction model proposed by the authors of [2, 3] is based on the following generalized Eyring relationship:

$$\gamma = \frac{1}{G}\frac{{d\tau }}{{dt}} + \frac{{{{\tau }_{0}}}}{{{{\eta }_{{\text{N}}}}}}\sinh \frac{\tau }{{{{\tau }_{0}}}},$$

(1)

where the first and second terms on the right side of relationship (1) denote the elastic and viscous components of shear rate γ, respectively; G is the shear modulus; τ is the shear stress; η_N is the Newtonian viscosity; and τ₀ is the characteristic stress value corresponding to the onset of non-Newtonian fluid behavior.

The Newtonian viscosity is described by an exponential dependence on pressure p and temperature θ at a high pressure, as it follows:

$$\begin{gathered} {{\eta }_{{\text{N}}}} = {{\eta }_{{{\text{N}}{\text{,i}}}}}\exp \left\{ { - \left( {{{\beta }_{0}} + \gamma p} \right)\theta } \right\}, \\ {{\eta }_{{{\text{N}}{\text{,i}}}}} = {{\eta }_{{{\text{N}},0}}}\exp \left( {\bar {\alpha }p} \right),{{\;}} \\ \end{gathered} $$

(2)

where β₀ is the temperature coefficient of viscosity at an atmospheric pressure; γ is the coefficient of combined temperature and pressure effect on the oil viscosity; ${{\eta }_{{{\text{N}},0}}}$ is the atmospheric viscosity; ${{\eta }_{{{\text{N}}{\text{,i}}}}}$ is the isothermal Newtonian viscosity; and $\bar {\alpha }$ is the piezoviscosity coefficient.

For practical calculations of hydrodynamic friction coefficient ${{\mu }_{{{\text{hd}}}}}$, the authors of [2, 3] have obtained the following relationship:

$${{\mu }_{{{\text{hd}}}}} = \frac{{{{\tau }_{0}}}}{{\bar {p}}}S,$$

(3)

where $\bar {p}$ is the mean Hertzian pressure and S is the dimensionless shear stress.

The dimensionless shear stress can be determined according to the following relationship:

$$S = \frac{{\bar {\tau }}}{{{{\tau }_{0}}}}$$

(4)

and can be calculated using the following formula

$$S = \frac{{{{{\left\{ \begin{gathered} {{D}_{{\text{i}}}}\Phi \ln \left( {2{{\sigma }_{{\text{i}}}}} \right) - 2\left( {1 + \Phi {{\sigma }_{{\text{i}}}}} \right) \\ + \,\,2\left[ {{{{\left( {1 + \Phi {{\sigma }_{{\text{i}}}}} \right)}}^{2}} - {{D}_{{\text{i}}}}\Phi \ln \left( {2{{\sigma }_{{\text{i}}}}} \right)} \right] \\ \end{gathered} \right\}}}^{{\frac{1}{2}}}}}}{{{{D}_{{\text{i}}}}{{\Phi }^{2}}{{\sigma }_{{\text{i}}}}}},$$

(5)

where $\bar {\tau }$ is the average shear stress in the contact zone, Φ is the dimensionless temperature change, D_i is the isothermal Deborah number, and σ_i is the dimensionless isothermal shear rate.

In order to determine these parameters the following relationships are used:

$$\begin{gathered} {{\sigma }_{{\text{i}}}} = \frac{{{{\eta }_{{{\text{Ni}}}}}{v}}}{{{{\tau }_{0}}h}},\,\,\,\,{{D}_{{\text{i}}}} = {{\;}}\frac{{{{\eta }_{{{\text{Ni}}}}}u}}{{\Gamma b}},\,\,\,\,\Phi = \frac{{\left( {{{\beta }_{0}} + \gamma \bar {p}} \right)\varsigma \tau _{0}^{2}h}}{{{{\eta }_{{{\text{Ni}}}}}}}, \\ \varsigma = \frac{{0.97{{b}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{{\left( {\pi {{K}_{m}}{{\rho }_{m}}{{c}_{m}}u} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} + \frac{h}{{12{{K}_{f}}}}. \\ \end{gathered} $$

(6)

Here, ς is the ratio between the increase in oil film temperature and the shear work caused this increase; h is the thickness of the oil film; b is the half-width of the contact zone, Γ is the shear modulus of the liquid; u is the rolling velocity; K_f is the thermal conductivity of the oil; K_m is the thermal conductivity of the material composing the contacting parts; C_m is the specific heat capacity of the material of the contacting parts; and ρ_m is the material density of the contacting parts.

The friction curves determined using a friction machine are usually divided into three zones [2, 3, 10]. The zone of small slide–roll ratio is linear. In the second, nonlinear zone, the friction coefficient increases until it reaches its maximum value. In the third zone, the friction coefficient gradually decreases, since resulting from self-heating in the contact zone, the viscosity of the lubricant decreases and its structure changes [11]. This zone is called a thermal zone.

As an example, let us consider the application of this model to polyalphaolefin oil belonging to an ISO VG 320 viscosity group, the experimental friction curves of which have been reported by the authors of [5] under a designation of PAO1. These data have been obtained under rolling a ball with a diameter of 19 mm against a disk with a diameter of 100 mm, the ball and the disk being made of AISI 52 100 grade steel. Based on the results presented here, the following temperature dependences have been taken into account: kinematic viscosity $\nu = 2{\kern 1pt} 367{\kern 1pt} 473~{{T}^{{ - 2.4151}}}$ mm²/s; piezoviscosity coefficient $\bar {\alpha } = 15.666 - 0.0666~T$ GPa^–1; oil shear modulus $\Gamma = 7.444 + 0.0163~T - 0.002083~{{T}^{2}} +$ $0.0000121~{{T}^{3}}$ MPa; and characteristic stress ${{\tau }_{0}} = 8.46 - 0.054~T$ MPa, where T is the temperature in Celsius.

The other rheological parameters of the oil are K_f = 0.1304 W/(m K); γ = 1.2 × 10^–10 (K Pa)^–1; β₀ = 0.023 K^–1. For the contacting steel parts, K_m = 45.4 W/(m K); ρ_m = 830 kg/m³; and c_m = 520 J/(kg K).

The comparison of experimental [5] and calculated friction curves for PAO1 grade oil in the temperature range of 40–100°C, at maximum contact pressure of 1 GPa, and at a rolling velocity of 2.5 m/s, is shown in Fig. 1. The contact interaction parameters were calculated using Hertz formulas for a point contact.

Fig. 1.

Comparison of experimental and calculated friction curves for PAO1 grade oil at different temperature values, at a maximum contact pressure of 1 GPa and at a rolling velocity of 2.5 m/s. The dots correspond to experimental values [5], the lines corresponding to calculated values: (1, ▲) 40; (2, ◻) 50; (3, ⚪) 60; (4, ◇) 80; (5, △) 100°С.

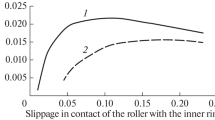
The effect of contact pressure on the friction curves of the same oil is presented in Fig. 2 by the example of contact between the inner ring and the roller of a cylindrical roller bearing for the case of a constant rotational frequency of the ring. The raceway diameter amounted to 180 mm, the roller diameter being 21 mm. The contact interaction parameters have been calculated using Hertz formulas for a linear contact.

Fig. 2.

Calculated friction curves for PAO1 grade oil in the contact zone between the inner ring and the roller of a cylindrical roller bearing at a ring rotational frequency of 530 rpm, at a temperature of 50°C and at maximum contact pressure values amounting to (1) 0.7; (2) 1.5; (3) 2; and (4) 2.5 GPa.

THERMAL ZONE OF FRICTION CURVES

The decrease in the friction coefficient with increasing slide–roll ratio in the thermal zone on the experimental friction curves is caused by an increase in the heat release power. This power can be calculated according to the following relationship:

$$N = {{\mu }_{{{\text{hd}}}}}Q{v},$$

(7)

where Q is the normal force; v is the sliding velocity amounting to the difference in the velocities of the contacting surfaces: v = v₁ – v₂, v₁ > v₂.

The experimental friction curves are usually plotted for a constant rolling velocity that can be determined according to relationship u = (v₁ + v₂)/2. Then, instead of (7), one can write

$$N = {{\mu }_{{{\text{hd}}}}}Qus,$$

(8)

where s is slide–roll ratio, s = v/u.

Since the decrease in the friction coefficient with increasing slide–roll ratio in the thermal zone of the experimental curves occurs slowly, then the product μ_hds increases and the heat release power exhibits an increase.

The condition for increasing heat release power written as

$$\frac{{dN}}{{ds}} = Qus{{\mu }_{{{\text{hd}}}}}\left( {\frac{1}{{{{\mu }_{{{\text{hd}}}}}}}\frac{{d{{\mu }_{{{\text{hd}}}}}}}{{ds}} + \frac{1}{s}} \right) > 0$$

(9)

for the case of the thermal zone can be represented in the following form

$$\left| {\frac{{d{{\mu }_{{{\text{hd}}}}}}}{{ds}}} \right| < \frac{{{{\mu }_{{{\text{hd}}}}}}}{s}.$$

(10)

Under the conditions of a fluid friction mode in the thermal zone, for known experimental friction curves, the left side of inequality (10) represents a monotonically increasing function of s, whereas the right side is a monotonically decreasing function. Taking into account inequality (10) at s < 1, it can be replaced by a more stringent one

$$\frac{1}{{{{\mu }_{{{\text{hd}}}}}}}\left| {\frac{{d{{\mu }_{{{\text{hd}}}}}}}{{ds}}} \right| < 1.$$

(11)

Next, let us consider the cases when one of the velocities of the contacting bodies is maintained constant. For the case of v₂ = const, one can write:

$${v} = \frac{{2s{{{v}}_{2}}}}{{\left( {2 - s} \right)}},\,\,\,\,\frac{{dN}}{{ds}} = Q{{{v}}_{2}}{{\mu }_{{{\text{hd}}}}}\left( {\frac{1}{{{{\mu }_{{{\text{hd}}}}}}}\frac{{d{{\mu }_{{{\text{hd}}}}}}}{{ds}} + \frac{4}{{{{{(2 - s)}}^{2}}}}} \right).$$

(12)

It is obvious that always

$$\frac{4}{{{{{(2 - s)}}^{2}}}} \geqslant 1.$$

(13)

For the case of v₁ = const

$${v} = \frac{{2s{{{v}}_{1}}}}{{\left( {2 + s} \right)}},\,\,\,\,\frac{{dN}}{{ds}} = Q{{{v}}_{1}}{{\mu }_{{{\text{hd}}}}}\left( {\frac{1}{{{{\mu }_{{{\text{hd}}}}}}}\frac{{d{{\mu }_{{{\text{hd}}}}}}}{{ds}} + \frac{4}{{{{{(2 + s)}}^{2}}}}} \right).$$

(14)

Here,

$$\frac{4}{{{{{(2 + s)}}^{2}}}} < 1.$$

(15)

Term $\frac{1}{{{{\mu }_{{{\text{hd}}}}}}}\frac{{d{{\mu }_{{{\text{hd}}}}}}}{{ds}}$ in the relationships written above reflects both the conditions under which the change in heat release power and the rheological properties of the oil are determined, whereas the second terms depend only on the kinematic conditions under consideration. Inequalities (13) and (15) show that the case of v₂ = const promotes increasing heat release power with an increase in slide–roll ratio to a greater extent than the case of v₁ = const.

The slide–roll ratio between the rolling elements and the raceways in bearings is considered for the case of a “stopped separator” [12]. In most practical cases, the rotational frequency of the bearing rings under operation are preset. However, since the rotational frequency of the separator depends on the slipping of the rolling elements, then in the case of a stopped separator, rotational frequencies of the rolling elements depend on slipping, too. As an example, let us consider a roller bearing having cylindrical rollers with a rotating inner ring and a fixed outer ring. It can be easily seen that changing heat release power in the contact zone between the inner ring and the roller can be described by the following relationship:

$$\begin{gathered} \frac{{d{{N}_{i}}}}{{d{{s}_{i}}}} = Q{{\mu }_{{{\text{hd}}}}}\frac{{2{{s}_{i}}\left[ {{{\omega }_{i}}{{R}_{i}}\left( {1 - \varphi } \right) + \varphi {{{v}}_{o}}} \right]}}{{2 + {{s}_{i}}\left( {1 - 2\varphi } \right)}} \\ \times \,\,\left\{ {\frac{1}{{{{\mu }_{{{\text{hd}}}}}}}\frac{{d{{\mu }_{{{\text{hd}}}}}}}{{d{{s}_{i}}}} + \frac{2}{{{{s}_{i}}\left[ {2 + {{s}_{i}}(1 - 2\varphi )} \right]}}} \right\}, \\ \end{gathered} $$

(16)

where v_o is the sliding velocity in the contact zone between the roller and the outer ring, s_i is the sliding-to-rolling ratio in the contact zone between the roller and the inner ring, ω_i is the angular velocity of the inner ring, parameter φ = R_i/(2R_m), R_i is the radius of the inner ring raceway, and R_m is the circle radius of roller centers.

For the bearing considered above, the condition of

$$\frac{2}{{{{s}_{i}}\left[ {2 + {{s}_{i}}(1 - 2\varphi )} \right]}} \geqslant 1$$

(17)

is satisfied at s_i ≤ 0.94.

The change in the heat release power in the contact zone between the outer ring and the roller can be described by the following relationship:

$$\begin{gathered} \frac{{d{{N}_{o}}}}{{d{{s}_{o}}}} = Q{{\mu }_{{{\text{hd}}}}}\frac{{2{{s}_{o}}\left( {1 - \varphi } \right)\left[ {{{\omega }_{i}}{{R}_{i}} - {{{v}}_{i}}} \right]}}{{2 + {{s}_{o}}\left( {1 - 2\varphi } \right)}} \\ \times \,\,\left\{ {\frac{1}{{{{\mu }_{{{\text{hd}}}}}}}\frac{{d{{\mu }_{{{\text{hd}}}}}}}{{d{{s}_{o}}}} + \frac{2}{{{{s}_{o}}\left[ {2 + {{s}_{o}}(1 - 2\varphi )} \right]}}} \right\}, \\ \end{gathered} $$

(18)

where v_i is the sliding velocity in the contact zone between the roller and the inner ring, s_o is the sliding-to-rolling ratio in the contact zone between the roller and the outer ring.

It is quite easy to verify that at the same values of the normal force, of the slide–roll ratio and of the friction coefficient in the contact zones of the roller with the inner and outer rings ${{d{{N}_{i}}} \mathord{\left/ {\vphantom {{d{{N}_{i}}} {d{{s}_{i}}}}} \right. \kern-0em} {d{{s}_{i}}}} > {{d{{N}_{o}}} \mathord{\left/ {\vphantom {{d{{N}_{o}}} {d{{s}_{o}}}}} \right. \kern-0em} {d{{s}_{o}}}}$.

Thus, the contact conditions between the rollers and the inner ring promote an increase in heat generation power to a greater extent than the contact conditions between the rollers and the outer ring. In addition, the results of experimental and theoretical studies show that when operating bearings with a rotating inner and fixed outer rings, the slide–roll ratio for the inner ring is to a considerable extent higher than that for the outer ring. Both of these circumstances indicate a significantly greater hazard of seizing for the case of the inner ring than is observed for the outer ring, which is confirmed by the statistics of rolling bearing failures [8, 13].

The operation of a bearing in the thermal zone is unacceptable, since decreasing friction coefficient with an increase in sliding under bearing operation, in turn, leads to a greater increase in the slide–roll ratio and, consequently, to a greater increase in heat generation. The process with such positive feedback is accompanied by a decrease in the thickness of the oil layer and, if not interrupted, inevitably leads to a boundary friction mode and to seizing. In order to exclude the operation of the bearing in the thermal zone, the slide–roll ratio in the bearing under operation should be lower than critical value s_cr so that the friction curve corresponds to the maximum value of the friction coefficient and the onset of the thermal zone. In this case, it is desirable to have a certain margin with respect to sliding, s_cr/s > 1.

The comparison of the experimental [5] and calculated critical slide–roll ratio values depending on temperature for PAO1 grade oil is shown in Fig. 3. By the example of the abovementioned contact between the inner ring and the roller of a roller bearing, Fig. 4 shows that the critical slide–roll ratio decreases with increasing maximum contact pressure at different temperature values.

Fig. 3.

Critical slide–roll ratio depending on temperature for PAO1 grade oil at a maximum contact pressure of 1 GPa and at a rolling velocity of 2.5 m/s: (1) experimental curve; (2) friction model.

Fig. 4.

Calculated critical slide–roll ratio depending on the maximum contact pressure in the contact zone between the inner ring and the roller of a cylindrical roller bearing at a ring rotational frequency of 530 rpm and at different PAO1 grade oil temperature values: (1) 40; (2) 60; (3) 80; and (4) 100°С.

Other oils exhibit similar properties. The calculated relationships for MN-7.5u grade oil are shown in Fig. 5 for the case of contact between the roller and the inner ring of a roller bearing whose inner raceway diameter and roller diameter amount to 165 mm and 15 mm, respectively. For the calculations, hydrodynamic oil parameters reported by the authors of [14] have been used.

Fig. 5.

Calculated critical slide–roll ratio for MN-7.5u grade oil depending on the normal contact force in the contact zone between the inner ring and the roller of a cylindrical roller bearing at a ring rotational frequency of 8000 rpm and at different oil temperature values: (1) 60; (2) 100; and (3) 140°С.

The friction model described in [2, 3] can be used in order to reconstruct isothermal friction curves. After the model parameters are determined from the experimental curves, it is sufficient to exclude accounting for the self-heating phenomenon from the model. The comparison of the PAO1 grade oil friction curves reconstructed according to different methods for a temperature of 40°C is shown in Fig. 6. From Fig. 6 one can see that the effect of self-heating on the friction curves is exhibited mainly in the thermal zone. The calculated value of the critical slide–roll ratio amounts to 0.16, the experimental value being 0.19.

Fig. 6.

Friction curves for PAO1 grade oil at 40°C, at a maximum contact pressure of 1 GPa and at a rolling velocity of 2.5 m/s: (1) experimental values [5]; (2) reconstructed isothermal curve [5]; (3) calculation according to a model presented in [2, 3]; and (4) calculation according to a model presented in [2, 3] with no self-heating taken into account.

Owing to the fact that the operation of a bearing in a thermal zone is undesirable, and the effect of self-heating is exhibited mainly in the thermal zone on friction curves, the issue of the reconstruction accuracy of isothermal friction curves with the use of different methods for the design of rolling bearings is not relevant.

CONCLUSIONS

Conditions required for the onset of seizing under hydrodynamic contact between parts in the course of rolling friction have been studied. To do this, a well-known friction model has been used making it possible to take into account the phenomenon of self-heating in the oil film [2, 3]. The fact that a correct description of friction curves using this model is quite possible has been confirmed via comparing the experimental data obtained by the authors of [5]. Relationships describing changes in the heat release power as the sliding-to-rolling ratio in the oil film increases under different conditions of interaction between the contacting bodies, as well as in the contact zones between the rollers and rings of bearings with cylindrical rollers. Conditions are obtained under which an increase in the heat release power continues in the thermal zone of friction curves despite a decrease in the friction coefficient. It is shown that the bearing seizing hazard occurs when the bearings operate in the thermal zone. A concept of critical slide–roll ratio that represents a boundary of the thermal zone of friction curves, has been introduced. The dependence of this quantity on the contact pressure and temperature has been studied. In order to prevent seizing in bearings, it is necessary to provide a margin with respect to critical sliding at the bearing design stage.

NOTATION

b is the half-width of the Hertz contact

C_m is the specific heat capacity of contacting parts

D_i is the isothermal Deborah number

G is the shear modulus

h is the film thickness

K_f is the thermal conductivity of oil

K_m is the thermal conductivity of contacting parts

N is the heat dissipation power

$\bar {p}$ is the mean Hertzian pressure

Q is the normal force

R_i is the inner ring raceway radius

R_m is the circle radius of roller centers

S is the dimensionless mean shear stress

s is the slide–roll ratio

s_cr is the critical slide–roll ratio

T is the temperature

u is the rolling velocity

v is the sliding velocity

v₁, v₂ are the velocities of contacting parts

$\bar {\alpha }$ is the effective piezoviscosity coefficient

β₀ is the viscosity–temperature coefficient at atmospheric pressure

Γ is the shear modulus of fluid

γ is the coefficient of cross term of viscosity–temperature–pressure relation

ς is the ratio between the increase in oil film temperature and the shear work caused this increase

η_N is the Newtonian viscosity

${{\eta }_{{{\text{N}},0}}}$ is the atmospheric viscosity

${{\eta }_{{{\text{N}}{\text{,i}}}}}$ is the isothermal Newtonian viscosity

μ_bd is the friction coefficient under boundary lubrication conditions

${{\mu }_{{{\text{hd}}}}}$ is the friction coefficient under hydrodynamic lubrication conditions

ρ_m is the material density of contacting parts

σ_i is the dimensionless isothermal shear rate

τ is the shear stress

τ₀ is the characteristic stress value corresponding to the onset of non-Newtonian fluid behavior

$\bar {\tau }$ is a mean shear stress

Φ is the dimensionless temperature change

φ is a parameter