INTRODUCTION

Contact hydrodynamic friction between bodies and raceways is one of the main factors determining the performance of rolling bearings. The correct choice of the contact friction model determines the correctness of the calculation of the dynamics of mutual motion and force interaction of bearing parts, including their relative slippage, wear, and seizure. To obtain sufficiently accurate solutions, models are used in which the friction coefficient depends on several pareameters. Models of both Newtonian and non-Newtonian fluids are used. Initially, these models described piezoviscous elastic, or elastic-hydrodynamic, contact interaction, and then piezoviscous rigid and viscoelastic models appeared [1]. More complex models based on the use of oil film parameters have also been proposed [2]. In this case, the friction coefficient consists of several coefficients that take into account both liquid and boundary friction [3]. Such models introduce a single dependence of the friction coefficient on the sliding speed, contact forces, and other factors for all rolling elements in the bearing.

As a result of the change in contact force, the coefficient of friction between the roller and the raceways changes even during one revolution of the rolling element. An appropriate recalculation of friction coefficients can be performed at each time step in the simulation of the roller bearing dynamics. However, due to the very long duration of the computer execution time, such a calculation is far from always realizable. Therefore, when calculating bearings, the model parameters, including the coefficient of friction, are usually taken to correspond to the maximum value of the contact load, which somewhat roughens the simulation results.

An important goal of dynamic calculation of a bearing is to determine slippage, which is the relative decrease in the speeds of rotation of the rollers and cage compared to their epicyclic values. Slippage can result in bearing wear and seizing. However, running a bearing in slip conditions without seizing has two advantages. First, less power is lost to drive the bearing; this reduces the heat flow, reduces the operating temperature of the bearing, and increases its durability. Secondly, the centrifugal forces of the rolling elements decrease, and, consequently, the stresses in their contacts with the outer ring raceway [4]. Therefore, in practice, slippage is allowed, but they try to limit it in order to avoid seizing. Seizure occurs with a significant decrease in the speed of the cage and, accordingly, the entire set of rolling elements. There is no consensus on the issue of allowable cage slippage. In some studies, long-term cage slippage in roller bearings is considered to be no more than 5%, in others, 10% [5], and with full lubrication and cooling of the bearing, slippage of up to 30% is allowed [4].

Objective—To develop an effective numerical procedure for determining the amount of slip in rolling bearings under hydrodynamic friction and estimating its allowable value.

Friction Model

The nature of friction is determined depending on the thickness of oil layer h by oil film parameter

$$\Lambda = \frac{h}{{1.25~\sqrt {R_{{{\text{a1}}}}^{2} + R_{{{\text{a2}}}}^{2}} }},$$
(1)

where Ra1 and Ra2 are the arithmetic mean roughness of the contacting surface profiles.

To describe all types of friction between bodies and raceways, the following relationship was proposed for the friction coefficient in [3], which combines two friction coefficients:

$$\mu = \left\{ {\begin{array}{*{20}{c}} {{{\mu }_{{bd}}}}&{{\text{at}}}&{\Lambda < {{\Lambda }_{{bd}}}} \\ {\frac{{{{\mu }_{{bd}}} - {{\mu }_{{hd}}}}}{{{{{\left( {{{\Lambda }_{{bd}}} - {{\Lambda }_{{hd}}}} \right)}}^{6}}}}{\kern 1pt} {{{(\Lambda {\kern 1pt} {\kern 1pt} - {\kern 1pt} {\kern 1pt} {{\Lambda }_{{hd}}})}}^{6}}{\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} {{\mu }_{{hd}}}}&{{\text{at}}}&{{{\Lambda }_{{bd}}}{\kern 1pt} {\kern 1pt} \leqslant {\kern 1pt} {\kern 1pt} \Lambda {\kern 1pt} {\kern 1pt} < {\kern 1pt} {\kern 1pt} {{\Lambda }_{{hd}}}} \\ {{{\mu }_{{hd}}}}&{{\text{at}}}&{{{\Lambda }_{{hd}}} \leqslant \Lambda ,} \end{array}} \right.$$
(2)

where μbd is the coefficient of friction at boundary friction, μhd is the coefficient of hydrodynamic friction, and Λbd, Λhd are constants.

To describe the boundary friction, we will use the Kragelsky formula [6]

$${{\mu }_{{bd}}} = \left( { - 0.1 + 22.28s} \right){\text{exp}}\left( { - 181.46s} \right) + 0.1.$$
(3)

Here, s is the slip coefficient, which is the ratio of sliding speed to rolling speed.

For small slips coefficients of hydrodynamic friction with increasing slippage first increases linearly, then its change gradually slows down and becomes non-linear. After reaching the maximum, the friction coefficient decreases, which is caused by the thermal effect of friction in the oil, self-heating of the oil film, which occurs at relatively high slip values. The corresponding portions of the dependence of the coefficient of friction on slip are designated as linear, non-linear, and thermal.

In order to explain this characteristic behavior of oils in hydrodynamic contact, several rheological models have been proposed in which oils are assumed to behave as non-Newtonian viscous liquids or elastic or plastic solids [2, 7, 8]. It has been recognized that oils are practically Newtonian fluids at low pressure or high temperature, but they behave like elastic solids at high pressure or low temperature and at low shear rates.

A complete viscoelastic model of oil, taking into account all the above features of its behavior in hydrodynamic contact, was proposed and experimentally confirmed in [7, 8]. It is based on the generalized Eyring dependence, which is presented by the author of these studies in form

$$\gamma = \frac{1}{\Gamma }\frac{{d\tau }}{{dt}} + \frac{{{{\tau }_{0}}}}{{{{\eta }_{N}}}}\sinh \frac{\tau }{{{{\tau }_{0}}~}},$$
(4)

where the first and second terms on the right side of the equation represent the elastic and viscous components of shear rate γ, respectively, Γ is the shear modulus, τ is the shear stress, ηN is the Newtonian viscosity, and τ0 is the characteristic stress corresponding to the beginning of the non-Newtonian behavior of the fluid.

In order to take into account the effect of thermal action on the Newtonian viscosity, it is assumed that heat is generated uniformly in the film and that an equal amount of heat is removed through two solid contact surfaces. Newtonian viscosity is described by an exponential dependence on pressure p and temperature θ at high pressure:

$$\begin{gathered} {{\eta }_{N}} = {{\eta }_{{N,i}}}\exp \left\{ { - \left( {{{\beta }_{0}} + \gamma p} \right)\theta } \right\}, \\ {{\eta }_{{N,i}}} = {{\eta }_{{N,0}}}\exp \left( {\bar {\alpha }p} \right),{{\;}} \\ \end{gathered} $$
(5)

where β0 is the temperature coefficient of viscosity at atmospheric pressure, γ is the coefficient of the combined effect of temperature and pressure on the viscosity of the oil, \({{\eta }_{{N,0}}}\) is the atmospheric viscosity, and \({{\eta }_{{N,i}}}\) is the isothermal Newtonian viscosity.

For practical calculations of the hydrodynamic coefficient of friction \({{\mu }_{{hd}}}\) in [7, 8], the following dependence was obtained:

$${{\mu }_{{hd}}} = \frac{{{{\tau }_{0}}}}{{\bar {p}}}S,$$
(6)

where \(\bar {p}\) is the average pressure of Hertz and S is the dimensionless shear stress.

When calculating the contact pressure between the bodies and the raceways, the Poiseuille flow is not taken into account and it is assumed that the contact pressure for hydrodynamic friction calculations can be determined by the average Hertzian pressure.

The dimensionless shear stress is determined by dependence

$$S = \frac{{\bar {\tau }}}{{{{\tau }_{0}}}},$$
(7)

which is calculated by formula

$$S = \frac{{{{D}_{i}}\Phi {\kern 1pt} \ln {\kern 1pt} \left( {2{{\sigma }_{i}}} \right){\kern 1pt} {\kern 1pt} - {\kern 1pt} {\kern 1pt} 2{\kern 1pt} \left( {1{\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} \Phi {{\sigma }_{i}}} \right) + 2{\kern 1pt} {{{\left[ {{{{\left( {1{\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} \Phi {{\sigma }_{i}}} \right)}}^{2}}{\kern 1pt} {\kern 1pt} - {\kern 1pt} {\kern 1pt} {{D}_{i}}{{\;}}{\kern 1pt} \Phi \ln {\kern 1pt} \left( {2{{\sigma }_{i}}} \right)} \right]}}^{{\frac{1}{2}}}}}}{{{{D}_{i}}^{2}{{\Phi }^{2}}{{\sigma }_{i}}}}{\kern 1pt} ,$$
(8)

where \(\bar {\tau }\) is the average shear stress in the contact, Φ is the dimensionless temperature change, Di is the isothermal Deborah number, and σi is the dimensionless isothermal shear rate.

The following dependences are used to determine these parameters:

$$\begin{gathered} {{\sigma }_{i}} = \frac{{{{\eta }_{{Ni}}}{v}}}{{{{\tau }_{0}}h}},\,\,\,\,{{D}_{i}} = {{\;}}\frac{{{{\eta }_{{Ni}}}u}}{{\Gamma b}},\,\,\,\,\Phi = \frac{{\left( {{{\beta }_{0}} + \gamma \bar {p}} \right)\varsigma \tau _{0}^{2}h}}{{{{\eta }_{{Ni}}}}}, \\ \varsigma = \frac{{0.97{{b}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{{\left( {\pi {{K}_{m}}{{\rho }_{m}}{{c}_{m}}u} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} + \frac{h}{{12{{K}_{f}}}}. \\ \end{gathered} $$
(9)

Here, ς is the ratio of the oil film temperature increase to the shear work that caused this increase, b is half the width of the contact area, u is the rolling speed, Kf is the thermal conductivity coefficient of oil, Km is the coefficient of thermal conductivity of the material of the contacting parts, Cm is the specific heat capacity of the material of contacting parts, and ρm is the density of the material of the contacting parts.

The calculation of the average contact stress and contact width is carried out according to the formulas [9]. To calculate the thickness of the oil layer, dependences are used that correspond to the friction mode occured in the bearing: rigid piezoviscous or elastic piezoviscous (elastic-hydrodynamic).

As an example, Fig. 1 shows the dependences of the hydrodynamic coefficient of friction on the sliding of the roller on the inner ring in a 1 032 930 roller bearing at 30°C, the rotational speed of the inner ring is 6371 rpm and two values of the normal contact force are 518 N and 300 N. The geometry parameters of this bearing used for the calculation are shown in Table 1. Lubrication was VNII NP 50-1-4U oil.

Fig. 1.
figure 1

Dependence of the coefficient of sliding friction on slippage in contact of the roller with the inner ring of a 1 032 930 bearing at 30°C and normal contact force values of 518 N (1) and 300 N (2).

Full size image
Table 1.   Basic geometry parameters of a 1 032 930 bearing
Full size table

Figure 1 shows that the slip at which the thermal section of the diagram begins depends on the magnitude of the contact force.

Effective Coefficient of Friction

Let us introduce two effective coefficients of friction: between the rollers, on the one hand, and the outer or inner raceways, on the other. These are the same average coefficients for all rolling elements, at which the total torque from the friction forces on a given track is equal to the total friction torque at the actual values of these coefficients. Averaging is performed for one revolution of the rotating ring for the given operating conditions of the bearing: temperature of the parts, rotational speed, external loads, working radial clearance, distortions [10], and other parameters.

The effective coefficient depends on the operating conditions of the bearing under which it was determined. The correctness of such averaging is due to the fact that in the operating range of bearing rotation speeds, the duration of one revolution of the rotating ring is one or two orders of magnitude less than the duration of the transient process of cage rotation, which occurs in the event of a change in torque. The torque acting on the cage is created by forces from the rolling elements.

The effective coefficients of friction of contacts with the inner and outer rings are calculated for a range of specified slip values. As a result, dependences of the effective coefficients of friction on slippage of both the separator and the rolling elements are obtained.

To calculate the effective coefficient of friction, first, a quasi-static calculation of the contact forces between the bodies and the raceways [9] is performed for several time points uniformly distributed within one revolution of the rotating bearing ring. Calculation of effective friction coefficients is performed by formula

$${{\mu }_{e}} = \frac{{\sum\limits_k {\sum\limits_m {({{\mu }_{{km}}}{{Q}_{{km}}})} } }}{{\sum\limits_k {\sum\limits_m {{{Q}_{{km}}}} } }},$$
(10)

where k is the rolling element number, m is the point in time number, and Qkm, μkm are the contact force and the coefficient of friction calculated by formulas (2)–(9) for the corresponding roller and moment of time. The summation in (10) is performed over all rolling elements and time points within one revolution of the rotating ring.

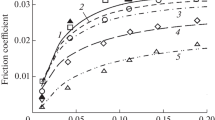
Figure 2 shows the results of the calculation: graphs of dependences of effective friction coefficients on slippage for roller bearing 1 032 930 at 70°C, the rotational speed of the inner ring is 6371 rpm and the radial load on the bearing is 3415 N. From these figures it can be seen that for the considered range of cage slippage, the thermal section of the diagrams is observed only on the inner ring. In the thermal section, an increase in cage slippage is accompanied by a decrease in the coefficient of hydrodynamic friction. A decrease in the coefficient of friction during operation of the bearing, in turn, leads to even greater slippage. A process with such a “positive feedback,” if not interrupted, leads to an increasing heating of the oil, a decrease in the thickness of the oil film and, as a result, to its rupture, the occurrence of boundary friction, intense wear, and seizure. The amount of cage slip that achieves the maximum effective friction coefficient on the inner ring is critical. Its value depends both on the properties of the oil and the internal geometry of the bearing, and on external influences on the bearing: forces, rotational speed, and temperature. In the considered example, the critical slip of the cage was 11%. The slip allowed during operation of the bearing must be determined taking into account the margin, which depends on the accuracy of the initial parameters, for example, the accepted properties of the oil.

Fig. 2.
figure 2

Dependences of the effective friction coefficients of rollers and raceways in a 1 032 930 roller bearing at 70°C, an inner ring speed of 6367 rpm, and a radial load on the bearing of 3415 N.

Full size image

Figure 3, as another illustration, shows the dependences of the coefficients of friction in the contacts of the rollers and the inner ring and the effective coefficient of friction on the inner ring of the bearing under consideration on cage slippage at 50°C, the rotational speed of the inner ring is 6371 rpm, and the radial force on the bearing is 1037 N. The dotted curves are plots of the coefficient of friction on individual rollers for different values of the normal forces. It can be seen from the figure that the effective friction coefficient is less than the coefficient of friction on the most loaded roller. This difference depends on the nature of the distribution of forces over all rollers. The critical value of cage slip in this case was 50%.

Fig. 3.
figure 3

Dependence of the friction coefficients and the effective friction coefficient in the contacts of the rollers and the inner ring of the 1 032 930 bearing on the cage slip at 50°C, the rotational speed of the inner ring of 6371 rpm, and the radial force on the bearing of 1037 N.

Full size image

The dependences of the effective friction coefficients on the slippage of rollers on the inner and outer rings are used in the dynamic calculation of bearings. Figure 4 compares the changes in the angular velocity of the cage and the bearing roller under the above conditions, obtained using conventional and effective coefficients of hydrodynamic friction. The calculations were performed using a multi-mass bearing dynamics model similar to that presented in [11]. The uneven distribution of contact forces along the length of the rollers and the profile of the rollers in this model are taken into account by dividing the rollers into short cylinders or slices.

Fig. 4.
figure 4

Change in the angular velocity of the cage (a) and roller (b) of a 1 032 930 bearing at 50°C, the rotational speed of the inner ring of 6371 rpm, and the radial force on the bearing of 1037 N, obtained in dynamic calculations using effective friction coefficients (—) and conventional friction coefficients (– – –).

Full size image

In calculations with different friction coefficients, the same initial values of the velocities of the cage and rollers were set. As can be seen from Fig. 4a, calculated by different methods, the values of the steady-state angular velocities of the cage, which are one of the main goals of the dynamic calculation, practically do not differ. There are no noticeable differences in the processes of convergence of the calculation results to the established solution. The speeds of the rollers are very close to each other (Fig. 4b).

The use of effective friction coefficients significantly reduces the computational time when simulating the dynamics of roller bearings compared to conventional coefficients. To recalculate the friction coefficient in one contact at the current step of the numerical solution, when using the effective friction coefficient, 3 operations are required, and when using conventional friction coefficients, 115 operations are required. For comparison, we note that when counting with a constant predetermined coefficient of friction, the number of such operations is equal to zero. The time spent on the preliminary calculation of the dependences of the effective friction coefficients on slippage on a personal computer of average performance takes several minutes, which is approximately an order of magnitude less than the time required to calculate the dynamic problem to obtain a steady-state solution.

CONCLUSIONS

The influence of contact hydrodynamic friction on the slippage of parts in roller bearings and on the conditions for the occurrence of seizing in them is considered. The concept of effective hydrodynamic coefficient of friction between the rollers and the raceway is introduced. The use of effective coefficients makes it possible to perform dynamic calculations of bearings taking into account the dependence of friction coefficients on cyclically changing contact forces without a noticeable increase in the calculation time compared to the simplest case of using constant friction coefficients. It is shown that seizing is a consequence of a decrease in the friction coefficient with increasing slip in the thermal section of the dependence between these parameters. The proposed approach makes it possible to determine the cage slip values that are critical from the point of view of seizing, depending on the specific operating conditions of the bearing.

NOTATION

b half width of Hertz contact

Cm specific heat of roller

Di isothermal Deborah number

h film thickness

Kf thermal conductivity of oil

Km thermal conductivity of contacting parts

k rolling element number

m time moment number

\(\bar {p}\) mean Hertzian pressure

Q normal force

Ra1, Ra2 arithmetic mean roughness of contacting surface profiles

S dimensionless mean shear stress

s slide-roll ratio

u mean rolling speed

β0 viscosity temperature coefficient at atmospheric pressure

Γ shear modulus of fluid

γ coefficient of cross term of viscosity-temperature-pressure relation

ς ratio of the increase in oil film temperature to the shear work that caused this increase

ηN Newtonian viscosity

\({{\eta }_{{N,0}}}\) atmospheric viscosity

\({{\eta }_{{N,i}}}\) isothermal Newtonian viscosity

Λ film parameter

Λbd, Λhd constants

μ friction coefficient

μbd friction coefficient under boundary lubrication

\({{\mu }_{{hd}}}\) friction coefficient under hydrodynamic lubrication

ρm density of contacting part material

σi dimensionless isothermal shear rate

τ shear stress

τ0 representative stress corresponding to the onset of non-Newtonian behavior of the fluid

\(\bar {\tau }\) mean shear stress

Φ dimensionless temperature rise