History, Origins and Prediction of Elastohydrodynamic Friction

Abstract

There is currently considerable debate concerning the most appropriate rheological model to describe the behaviour of lubricant films in rolling–sliding, elastohydrodynamic contacts. This is an important issue since an accurate model is required to predict friction in such contacts. This paper reviews the origins of this debate, which primarily concerns a divergence of views between researchers using high pressure, high shear rate viscometry and those concerned with the measurement and analysis of elastohydrodynamic friction; the former advocate a Carreau-based shear stress/strain rate model while the latter generally favour an Eyring-based one. The crucial importance of accounting for shear heating effects in analysing both viscometric and friction data is discussed. The main criticisms levied by advocates of a Carreau-based model against Eyring’s model are discussed in some detail. Finally, the ability of both types of rheological model to fit elastohydrodynamic friction measurements for a quite simple, well-defined base fluid is tested, using previously measured pressure–viscosity behaviour for the fluid. Both models appear to fit the experimental data over a wide temperature range quite well, though fit of the Eyring model appears slightly closer than that of the Carreau–Yasuda model. Friction data from a wider range of well-defined fluid types are needed to identify categorically the most appropriate model to describe elastohydrodynamic friction.

1 Introduction

An important challenge in mechanical engineering is to increase the efficiency of machine components and thereby reduce energy consumption and greenhouse gas emissions. One way to achieve this is to reduce friction losses between moving surfaces. In consequence, there is currently great interest in understanding the origins of friction in both lubricated and unlubricated components.

In lubricated machine components that are based on elements that both roll and slide together, including rolling bearings, gears, constant velocity joints and cam/follower systems, much of the friction loss originates in elastohydrodynamic (EHD) contacts. To roll, elements must be non-conforming, and this means that the contact region between them is very small and so at very high pressure. Hydrodynamic lubricant films can only form in such contacts because the pressure has two beneficial effects—of elastically flattening the surfaces to form a tiny, conforming contact region and of increasing locally the effective viscosity of lubricants in the inlet. The consequent regime of lubrication is known as piezoviscous-elastic or elastohydrodynamic lubrication [1].

Figure 1 shows optical interference images of EHD lubricating films within a rolling point (ball on flat) and part of a line (cylinder on flat) contact taken from [2]. The shapes of the EHD contacts are evident. There is a flattened region that corresponds closely to the Hertzian contact area within which, under most conditions, the film thickness is quite uniform except for a constriction, 20 to 40 % less thick, at the rear and sides of the contact. In both images in Fig. 1, the film thickness in the central region is about 400 nm, while the width of the contact is about 300 μm, both typical values for EHD contacts.

Fig. 1

Optical interference images of a point contact, b line contact

Figure 2 shows the film thickness profile across the midline of the contact taken from the point contact image in Fig. 1, displayed with identical vertical and horizontal scales. This shows clearly two separate regions, the converging inlet region to the left and the extremely thin central region. It helps explain one of the characteristic features of elastohydrodynamic lubrication, which is that EHD film thickness and EHD friction are largely decoupled. The quantity of lubricant entrained and thus the film thickness is determined primarily by the geometry and properties of the lubricant in the immediate inlet region that spans a zone from about distance b (the contact half-width or radius) in front of the inlet edge of the flat region to this inlet edge itself. In this region the pressure in the lubricant rises progressively from atmospheric pressure to about 150 MPa, while its viscosity increases correspondingly, to reach a value about ten times its atmospheric pressure value as the inlet edge is approached. The quantity of lubricant entrained depends on a composite value of the viscosity of the lubricant over this inlet region. The prevailing strain rate in the inlet is determined by recirculation of lubricant and is usually about 10⁶ s⁻¹, so a typical lubricant reaches a shear stress (viscosity × strain rate) of ca. 0.1 to 1 MPa on its approach to the inlet edge. Under these relatively low shear stress conditions, most base fluids are Newtonian (i.e, the shear stress is proportional to the shear strain rate), so film thickness depends on the piezoviscous but Newtonian properties of the lubricant. The EHD film is so thin that once within the contact, the lubricant has no option but to progress through to the exit i.e, there is negligible side leakage. This means that the film thickness does not depend on the properties of the lubricant film within the flat, central region of the contact.

Fig. 2

EHD film thickness profile across centreline of point contact from inlet to outlet

By contrast, in rolling–sliding contacts, EHD friction depends almost entirely on the properties of the lubricant film within the flat central contact region since this part of the film is highly pressurised and thus has high shear stress. The conditions in this region are extraordinarily severe; the pressure is typically greater than 1 GPa; the shear rate is typically 10⁵–10⁷ s⁻¹; oil film temperature can rise by more than 50 °C; the lubricant is pressurised and depressurised within a fraction of a millisecond. Under these conditions even the simplest organic liquids behave in a highly non-Newtonian fashion, exhibiting viscoelastic and extensive shear thinning behaviour, and the EHD friction is determined by this non-Newtonian response. Experimentally it is found that EHD friction depends strongly on molecular structure, in a fashion that indicates that properties such as bond flexibility and free volume are predominant. This suggests that friction depends on the ease with which layers of molecules are forced to slide past one another at very high pressure, in a fashion that is not mirrored at low pressure.

Our understanding of and ability to predict EHD film thickness are well developed. So long as inlet shear thinning does not occur, the composite piezoviscous response over the inlet region can be measured using high-pressure rheometry [3] or estimated directly from measurements of EHD film thickness [4, 5] and applied in regression-based film thickness equations [6]. For polymer solutions and some very high molecular weight base fluids, where inlet shear thinning does occur, its effect can also be taken into account [7, 8]. Unfortunately our understanding of EHD friction is much less complete. Although we have a reasonably clear overall picture of the general pattern of behaviour, there is still considerable debate as to the most appropriate rheological model to describe fluid behaviour within EHD contacts. This debate has caused general uncertainty in both academia and industry about how best to calculate EHD friction.

This paper will review the origins and content of this debate and, it is hoped, help clarify for the reader how to predict friction in EHD contacts. The development of our understanding of EHD friction will first be reviewed from an historical perspective, considering in turn EHD friction measurements, high shear stress viscometry, models of shear thinning and piezoviscosity. Then two important factors that contribute to the problem, shear heating, especially in high-stress rheometry, and the poorly defined nature of most lubricating base oils, will be discussed. The scene having been set, the main arguments for and against the two main proposed models of EHD rheology will then be considered and the predictions of the two models compared with measured EHD friction data. Finally, two possible developments that may help clarify our understanding of EHD friction in future are briefly outlined.

The paper will focus on experimental work since only this can ultimately validate models of EHD behaviour. It will examine EHD friction and not discuss the much more tractable issue of EHD film thickness. It should be noted that in the field of elastohydrodynamic lubrication, the term “EHD traction” is often used in place of “EHD friction.” In the current paper, the term “EHD friction” will be used throughout.

2 Two Main Approaches to EHD Rheology

In order to be able to predict friction in an EHD contact, we need a constitutive equation that describes the way that the shear stress of a fluid film in an EHD contact depends on pressure, temperature, strain rate and strain history. The sliding friction is then simply the integral of the shear stress over the contact area. Since EHD friction is known to depend on molecular structure, from the scientific viewpoint, it would also be desirable if this constitutive equation were based on a physically realistic model of underlying molecular behaviour, rather than to originate only from curve fitting.

There have been two main approaches to deriving such an equation. One is analysis of friction measurements taken from EHD contacts to extract the rheological expression that best explains these measurements. The key advantage of this approach is that the lubricant film is obviously subjected to conditions that are wholly realistic of actual EHD contacts. The key disadvantage is that the pressure, temperature and contact time, and consequently the rheological properties of the lubricant film, vary across the contact. The measured friction represents a single, integrated value of this locally varying shear stress, so rheological information has to be extracted from this integrated value.

The second approach is high-stress viscometry, where a pressurised sample of oil is sheared at high applied strain rate in a well-defined geometry. The key advantage of this method is, unlike the above, that it studies a sample of fluid that is all subject to the same, well-defined set of conditions, making direct connection of strain rate with shear stress relatively straightforward. Its main disadvantage is that it is very difficult to subject fluid samples in a viscometer to the levels of stress and strain rate experienced in EHD contacts, and, when this is achieved, it is impossible at present to avoid large rises in temperature that impact strongly on the rheological response.

The development of both of these approaches is outlined below.

3 Rheology from EHD Friction Measurements

3.1 Early Work

Ertel’s seminal solution of the EHD lubrication problem was first published in English in 1949 [9], and this led to a rapid growth in research interest in the field. The initial focus of experimental work was on film thickness [10–12], but by the end of the 1950s, disc machines started to be used to measure friction in controlled, mixed rolling–sliding conditions. It was soon realised that when the effect of the contact pressure on viscosity was taken into account, the friction in EHD contacts was much lower than that predicted based on Newtonian behaviour. This phenomenon was explored via the measurement of “traction curves” to show how friction varied with sliding speed at a fixed mean rolling, or “entrainment” speed and thus at a constant EHD film thickness [13, 14]. A typical example of an early traction curve is shown in Fig. 3 [15]. Such traction curves have played a crucial role in deriving lubricant rheology from friction measurements.

Fig. 3

EHD traction curves from a line contact form of friction per unit length versus sliding speed; (applied load decreases from a to c); from [15]

In early work, most authors interpreted their friction measurements in terms of a “mean effective viscosity,” calculated as the ratio of mean shear stress to strain rate across the EHD contact, i.e.,

$$ \bar{\eta }_{e} = \frac{{\bar{\tau }}}{{\dot{\gamma }}} = \frac{F/A}{{\Delta{u}/h}} $$

(1)

where τ is the shear stress, $\dot{\gamma },$ the strain rate, F the friction force, A the contact area, $\Delta{u}$ the sliding speed and h the central film thickness. The bars denote average values across the contact area. Research then sought to explain why this mean effective viscosity was lower than the mean Newtonian viscosity. Using a line contact disc machine, Crook found that at very low sliding speeds, the mean effective viscosity matched the Newtonian value quite closely but that it fell increasingly below it as the rolling speed increased, even when the sliding speed remained constant [15]. He concluded that the effective viscosity depended on the time of passage of the fluid through the contact and suggested that this represented a viscoelastic response of the oil, with the elastic strain within the fluid film accommodating a significant proportion of the total displacement during short transit times [15]. An alternative conjecture was that when the lubricant entered the contact, its viscosity took a finite time to reach its equilibrium, high pressure value [16]. At high sliding speeds, Crook found that the effective mean viscosity fell greatly below the Newtonian value, which he interpreted as being due to shear heating of the oil film.

Smith studied the elliptical contact between cylindrical and spherical rollers and obtained very small amounts of controlled sliding by skewing the axes of the two [14]. Again he found lower-than-expected friction at very low entrainment speeds, which he ascribed to elastic effects of the rollers. Smith proposed that levelling-out of friction at high sliding speeds resulted from the lubricant film yielding at a critical shear stress, coupled with shear heating.

In 1964, Bell and co-workers studied the EHD friction properties of a polyphenylether lubricant in a disc machine at low sliding speeds and noted a similar pattern of variation of friction with sliding speed to Crook [17]. The authors showed that the overall form of their friction versus strain rate curve could be explained if viscous shear thinning according to the Eyring viscosity model was assumed. They did not, however, provide a direct comparison between experiment values and predictions from this model.

Throughout the 1960s and 1970s, a series of increasingly accurate friction measurements were obtained using twin disc machines, in particular by the research groups of Johnson [18–25] and Hirst [26–31]. Traction curves were obtained over a range of entrainment speeds, contact pressures, temperatures, lubricant viscosities and lubricant types. By the mid-1970s, there was also a trend away from interpreting traction curves in terms of mean effective viscosity versus sliding speed, or slide–roll ratio (the ratio of sliding speed to mean rolling speed) and instead considering them in terms of mean shear stress, $\bar{\tau }$ versus strain rate, $\dot{\gamma }$.

In 1967, Johnson and co-workers measured EHD friction in a power-circulating twin disc machine that enabled very accurate control of sliding speed over a wide range of conditions [18, 19]. They deduced that it was not possible to explain the observed friction behaviour at high sliding speeds solely in terms of either shear heating, as suggested by Crook [15], or a shear rate-independent limiting shear stress, as proposed by other researchers [14, 32, 33]. In 1974, Hirst and Moore showed that the Eyring viscosity model originally proposed by Bell et al. fitted experimentally measured friction data accurately [27]. They also suggested that the friction at low sliding speeds could originate alternatively from a Newtonian response (at low pressure) or a viscoelastic one (at high pressure).

In an important study in 1974, Johnson and Roberts studied the impact on friction of skewing and tilting of one disc against the other in a crowned twin-disc machine so as deliberately to introduce spin and cross slip into the EHD film [20]. The friction behaviour they observed strongly supported the presence of a viscoelastic response of the fluid in the contact.

3.2 Viscoelastic and Eyring Model

In 1977, Johnson and Tevaarwerk proposed that EHD friction was controlled by a combination of behaviours which they described overall as “nonlinear Maxwell” [22]. Johnson and Tevaarwerk’s equation is shown in Eq. 2 and indicates that the strain rate originates from two components, the first viscoelastic and the second a viscous, Eyring shear thinning term;

$$ \dot{\gamma } = \frac{1}{{G_{\text{p}} }}\frac{{{\text{d}}\tau }}{{{\text{d}}t}} + \frac{{\tau_{e} }}{{\eta_{\text{p}} }}\sinh \left( {\frac{\tau }{{\tau_{e} }}} \right) $$

(2)

where G _p and η _p are the elastic shear modulus and low shear rate Newtonian dynamic viscosity of the lubricant, respectively, both at the pressure p, while τ _e is the “Eyring stress.” The latter is the threshold shear stress above which significant shear thinning occurs (formally at which the effective viscosity falls to a fraction 1/sinh(1) or about 85 % of its Newtonian value) and typically has a value between 5 and 10 MPa. In stress versus strain rate form, Eq. 2 rearranges to

$$ \tau = \tau_{e} \sinh^{ - 1} \left( {\frac{{\eta_{p} }}{{\tau_{e} }}\left( {\dot{\gamma } - \frac{1}{{G_{p} }}\frac{{{\text{d}}\tau }}{{{\text{d}}t}}} \right)} \right) $$

(3)

The latter shows clearly how the elastic term reduces the shear stress in the contact by accommodating some of the applied strain. For lubricants at high pressure, G _p is typically of order 10⁹ Pa, the shear stress in EHD contact rarely exceeds 10⁸ Pa, while the time for the oil to pass through the contact is of order 10⁻⁴ s. Inserting these values in the viscoelastic term of Eq. 3 indicates that viscoelastic term is only a significant proportion of the whole at strain rates less than ca. 10⁵ s⁻¹. In practice, this means that the elastic term is only important when transit times are short and where strain rates are modest, for example in rolling element bearings when slide–roll ratios are low. It is of less significance in high sliding contacts. Johnson and Tevaarwerk also suggested that viscoelasticity is only significant when the low shear rate viscosity of the fluid in the contact, η _p , exceeds 10⁵–10⁶ Pa.s.

When the elastic term is negligible compared to the viscous term, Eqs. 2 and 3 reduce to

$$ \dot{\gamma } = \frac{{\tau_{e} }}{{\eta_{p} }}\sinh \left( {\frac{\tau }{{\tau_{e} }}} \right) $$

(4)

and

$$ \tau = \tau_{e} \sinh^{ - 1} \left( {\frac{{\eta_{p} \dot{\gamma }}}{{\tau_{e} }}} \right) $$

(5)

The sinh(x) function has two important mathematical properties. One is that at low values of x it approaches the value x. This means that at low shear stress, when τ ≪ τ _e , Eq. 4 becomes $\dot{\gamma } = \tau /\eta_{p}$, i.e, the fluid becomes Newtonian. The second is that at values of x greater than about 1.5, sinh(x) approaches e^x/2, so that when the shear stress τ exceeds τ _e , Eq. 5 very quickly becomes

$$ \tau = \tau_{e} \log_{e} \left( {2\eta_{p} \dot{\gamma }/\tau_{e} } \right) $$

(6)

which expands to

$$ \tau = \tau_{e} \log_{e} \left( {\dot{\gamma }} \right) + \tau_{e} \log_{e} \left( {2\eta_{p} /\tau_{e} } \right) $$

(7)

Johnson and Tevaarwerk’s model thus suggests that at low strain rates, fluids behave in a Newtonian fashion if they have low viscosity or are at modest pressure, but that in high-pressure contacts, they show a viscoelastic response. At all contact pressures, as the strain rate and thus the shear stress is increased, fluid shear becomes dominated by Eyring shear thinning which ultimately leads to a linear mean shear stress versus log(strain rate) relationship at high sliding speeds, at least until contact heating prevails. This is shown in Fig. 4 from [22], where traction divided by contact area (mean shear stress) is plotted against log(slide–roll ratio), which, at constant entrainment speed, is proportional to strain rate.

Fig. 4

Mean shear stress versus slide–roll ratio traction curves for five different fluids; the nonlinear Maxwell-fitted equation predictions are shown as solid lines; from [22]

Equation 7 also shows that so long as τ > 1.5τ _e over most of the contact, values of the Eyring stress, τ _e , and mean low shear rate viscosity, $\bar{\eta }_{p}$, can be determined from a plot of $\bar{\tau }$ versus log_e($\dot{\gamma }$) at a fixed temperature and load.

If the contact is assumed to operate at a mean, constant pressure, $\bar{p}$, and the low shear rate viscosity is assumed to vary with pressure according to the Barus equation, $\eta_{p} = \eta_{o} e^{\alpha p}$, where α is the pressure–viscosity coefficient of the lubricant, a further simplification is possible in that Eq. 7 becomes [22];

$$ \bar{\tau } = \tau_{e} \log {}_{e}\left( {\dot{\gamma }} \right) + \tau_{e} \left( {\log_{e} \left( {\frac{{2\eta_{o} }}{{\tau_{e} }}} \right) + \alpha \bar{p}} \right) $$

(8)

This means that when $\bar{\tau }$ > 1.5τ _e , the Eyring stress and the pressure–viscosity coefficient can be calculated either from the plot of mean shear stress against strain rate at constant applied load, or from a plot of mean shear stress against pressure at constant strain rate. The validity of using the Barus piezoviscosity equation will be discussed later in this paper. This approach assumes, as a first approximation, that τ _e and α are independent of pressure. In practice, both may vary linearly with pressure, and the extent of this variation can be estimated by comparing friction results at different mean contact pressures.

Hirst and Moore derived essentially the same model as Johnson and Tevaarwerk and tested it on a much wider range of fluids and over a wider temperature range [30, 31]. They studied low molecular weight polymers and simple molecular fluids as well as mineral oils. This is important, since, as will be discussed later, in principle Eyring’s equation is only applicable to simple molecular liquids, and also because it means that some of their work can be reproduced today, which is not possible in the case of polymeric or mineral oil-based fluids.

Since 1980, Johnson and Tevaarwerk’s model has been accepted by many EHD researchers, and the main focus of further research has been on testing it and refining the fit between measurements and model, in particular by taking account of temperature rise in the contact and of the variation of pressure across the contact.

3.3 Temperature Correction

The combination of high shear rate and shear stress leads to large concentrations of heat being generated and thus to a significant temperature rise in the contact, and this greatly complicates the interpretation of EHD friction measurements. The equations governing temperature rise in an EHD contact were described by Archard [34]. There are two components, the “mean flash temperature rise,” $\Delta \bar{T}_{\text{surf}}$, of the solid surfaces in response to transient heat input as they traverse the contact, and an additional rise of mean oil film temperature above that of the bounding solid surfaces, $\Delta \bar{T}_{\text{oil}}$, due to the relatively low thermal conductivity of the oil.

The total mean temperature rise of the oil film above the inlet temperature is then given, for a point contact, by:

$$ \Delta \bar{T} =\Delta \bar{T}_{\text{surf}} +\Delta \bar{T}_{\text{oil}} = \frac{1}{{\left( {2\pi K_{s} \rho c} \right)^{0.5} }}\left( \frac{2b}{U} \right)^{0.5} \bar{\tau }\Delta u + \frac{h}{{8K_{\text{oil}} }}\bar{\tau }\Delta u $$

(9)

where the first term describes the mean flash temperature rise and the second the additional oil film temperature rise. In Eq. 9, b is the half-width of the contact, K _s , ρ and c the thermal conductivity, density and specific heat of the solid bodies, respectively, U the entrainment speed, h the film thickness and K _oil the thermal conductivity of the oil at the mean pressure of the contact. The ratio 2b/U represents the time taken for the surfaces to pass through the contact. The product of mean shear stress and sliding speed, $\bar{\tau }\Delta u$, is the heat generated per unit area in the contact. The flash temperature term in Eq. 9 assumes that both solids are of the same material and travel at approximately the same speed with respect to the contact, but it can quite easily be adjusted to accommodate different materials and speeds. In the second term, the value in the denominator 8 is debated and depends on where heat is generated in the oil film. Archard derived the value of 8 assuming that heat is generated evenly through the oil film thickness while a value of 4 was obtained if all the heat is generated at the mid-plane.

Equation 9 shows that at high values of mean shear stress and sliding speed, the mean oil film temperature can rise very significantly, especially when the film thickness, h, is large. For example, for a typical steel ball on flat sliding/rolling contact as described later in this paper and a film thickness of 500 nm, a value of $\bar{\tau }u_{s}$ = 10⁷ W/m² gives a mean oil film temperature rise of 50 °C. Shear stress falls typically 4 % for every 1 °C rise in temperature, so this temperature increase has a very strong effect on EHD friction at high strain rates and is primarily responsible for the levelling out and decrease in friction seen in traction curves at high sliding speeds, for example in Fig. 3. It also complicates the interpretation of traction curves since it must be accounted for before any model of rheology can be inferred. One approach is to confine any analysis of the traction data to results that are known, based on Eq. 9, to originate from films that have experienced a minimal temperature rise, e.g. $\Delta \bar{T}$ < 2 °C. However, as discussed by Hirst and Richmond, at high pressure this may leave only a small range strain rates between the viscoelastic region and the thermal region from which to derive a description of shear thinning behaviour [35].

Conroy et al. addressed this problem by obtaining traction curves at various temperatures [25]. Combination of the results, based on film temperatures calculated using Eq. 9, then enabled isothermal traction curves to be constructed even within the “thermal” region. Evans and Johnson used a similar approach in which they employed values of $\Delta \bar{T}$ calculated from Eq. 9 to adjust the bulk temperature and sliding speed during friction tests so as to obtain isothermal EHD friction data over a very wide range of conditions for three lubricants [36, 37]. Their results, shown in Fig. 5 for a mineral base oil, confirmed the nonlinear Maxwell model of Eq. 2 [36], but also identified, for two of the fluids tested, a limiting shear stress, τ _c , at which the shear stress levelled out at high strain rate, suggestive of plastic yield behaviour. Evans and Johnson found that τ _c increased linearly with mean pressure of the lubricant film. Incorporating this limiting shear stress into Johnson and Tevaarwerk’s model gives Eq. 10, where Λ _e describes the proportionality between τ _c and mean pressure.

$$ \tau = \hbox{min} \left[ {\tau_{e} \sinh^{ - 1} \left( {\frac{{\eta_{p} }}{{\tau_{e} }}\left( {\dot{\gamma } - \frac{1}{{G_{e} }}\frac{d\tau }{dt}} \right)} \right),\varLambda_{e} p} \right] $$

(10)

In this equation, G _e is a composite elastic shear modulus incorporating both the shear modulus of the lubricant film at high pressure and the elastic shear of the solid surfaces [37].

Fig. 5

Isothermal traction curves over a wide range of contact pressures for one mineral oil; from [36]

Hirst and Richmond discussed the thermal problem in some detail and applied a very accurate thermal correction procedure to EHD friction measurements. They found that isothermally corrected shear stress versus log(strain rate) curves only became precisely linear at high strain rates, as predicted by Eq. 7, if the values of lubricant thermal conductivity employed in the thermal correction were those measured at high pressure [35]. They noted that the thermal conductivities of lubricants at 1 GPa are generally about twice as large as the corresponding values at atmospheric pressure.

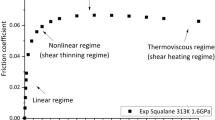
An alternative method of extending the thermal region was developed by LaFountain et al. who used a rolling–sliding ball on flat disc tribometer [38]. They conducted a series of Stribeck curve measurements (friction measured as a function of increasing entrainment speed and thus film thickness) at different, fixed slide–roll ratios. When converted to friction coefficient versus strain rate curves, this gave an extended isothermal region represented by the minima of the Stribeck curves, as shown in Fig. 6. In essence, this approach, by measuring Stribeck curves, identifies values of friction that are measured at the smallest possible film thickness to ensure full film conditions, and thus with lowest possible oil film temperature rise.

Fig. 6

Use of a series of Stribeck curves at different slide–roll ratios to obtain full film EHD friction data over a wide shear rate range; from [38]

3.4 Variation of Pressure Across the Contact

As already indicated, the main disadvantage of using EHD friction to determining fluid rheology is that the friction measured is a composite value of shear stress integrated over a wide range of conditions within the contact. Of particular concern is the variation of pressure, and thus low shear rate piezoviscosity η _p across the contact

One approach in analysing EHD friction data is to assume that the whole film is at the mean Hertz contact pressure. However, in practice, pressure varies greatly over an EHD contact and at high loads and low speeds can be approximated to the Hertz pressure distribution. Hirst and Richmond provide expressions to test when the assumption of a Hertz pressure distribution is valid [35].

The mean shear stress can be calculated by allowing η _p to vary with pressure over a contact, and for a point contact and Eyring shear thinning this gives:

$$ \bar{\tau } = \frac{F}{A} = \frac{{2\pi \tau_{e} }}{{\pi b^{2} }}\int\limits_{0}^{b} r \sinh^{ - 1} \left( {\frac{{\eta_{p} \dot{\gamma }}}{{\tau_{e} }}} \right){\text{d}}r.$$

(11)

For τ > 1.5τ _e this becomes;

$$ \bar{\tau } = \frac{F}{W} = \frac{{2\pi \tau_{e} }}{{\pi b^{2} }}\int\limits_{0}^{b} {r\log_{e} } \left( {\frac{{2\eta_{p} \dot{\gamma }}}{{\tau_{e} }}} \right){\text{d}}r.$$

(12)

For a circular, point contact, according to Hertz theory

$$ p = p_{\hbox{max} } \left( {1 - \frac{{r^{2} }}{{b^{2} }}} \right)^{1/2} $$

(13)

where b is the Hertz contact radius. Assuming this pressure distribution and the Barus viscosity–pressure equation

$$ \bar{\tau } = \frac{{2\tau_{e} }}{{b^{2} }}\int\limits_{0}^{b} r \log_{e} \left( {\frac{{\eta_{o} e^{{\alpha p_{\hbox{max} } \left( {1 - r^{2} /b^{2} )^{1/2} } \right)}} \dot{\gamma }}}{{\tau_{e} }}} \right){\text{d}}r.$$

(14)

Combination of the exponential and logarithmic terms means that when this equation is integrated, it yields the expression

$$ \bar{\tau } = \tau_{e} \left( {\log_{e} \left( {\dot{\gamma }} \right) + \log_{e} \left( {\frac{{2\eta_{o} }}{{\tau_{e} }}} \right) + \frac{{2\alpha p_{\hbox{max} } }}{3}} \right) $$

(15)

Since p _mean  = 2p _max /3, this is identical to the expression obtained using the mean Hertzian pressure in Eq. 8. A similar identity between the mean pressure and integrated pressure shear stress equations is also found for line contact. These identities show that as long as τ > 1.5τ _e over most of the contact and τ _e is taken to be pressure-independent, the mean pressure approach is wholly valid for the Barus equation. Analytical integration of the logarithmic form is also quite straightforward for many other exponential-based viscosity–pressure equations such as the polynomial and Paluch relationships described later in this paper. From Eq. 12, any form of viscosity–pressure equation will, of course, yield a linear shear stress versus log (strain rate) relationship so long as the strain rate is constant and τ > 1.5τ _e over most of the contact.

At lower shear stresses when $\dot{\gamma }\eta_{p} < 1.5\tau_{e}$, the logarithmic approximation is no longer appropriate, and integration of the sinh⁻¹() expression, or even one including the viscoelastic term over the varying pressure of the contact, has to be carried out [30, 39, 40]. This is particularly the case for low viscosity fluids, where the shear stress of a significant proportion of the film does not reach τ _e . Muraki and Dong have shown that in this case, it is possible to treat the contact as two separate regions, one assumed to be Newtonian and the other to obey the logarithmic relationship of Eq. 8. The two regions are separated, for circular contact, by the radius at which the sinh⁻¹ term, $(\eta_{p} \dot{\gamma }/\tau_{e} )$ is equal to unity [40].

Allowance of variation of pressure across the contact was taken further in 2000 by Fang et al., who assumed a line contact EHD film with a Hertzian pressure distribution, equations to describe how low shear rate viscosity varied with the pressure and temperature and the Eyring equation to describe shear thinning behaviour [41, 42]. They then repeatedly solved for temperature and shear stress distribution across the contact while systematically varying the constants τ _e and α until the predicted EHD friction fitted most closely with the measured values.

The above has described how analysis of EHD friction data since the 1960s has led EHD researchers to a rheological equation for lubricant behaviour based on a combination of viscoelasticity, the Eyring shear thinning equation and, at very high stresses, a limiting shear stress. Perhaps surprisingly there has been little systematic attempt to test the fit of friction data to other shear thinning equations, though it has been claimed that a linear relationship between shear stress and log(strain rate) can be predicted using other models [43, 44], or indeed, simply result from shear heating [45].

Full computational solutions of the EHD problem have been carried out by numerous researchers using a wide range of shear thinning equations and the results compared to friction measurements, e.g. [46–52]. All produce, as might be expected, the general shape of traction curves, with varying levels of quantitative match. However, in view of the complexity of full EHD solutions, the authors do not believe that this approach provides a robust way of validating shear thinning models.

4 Rheology from High-Stress Viscometers

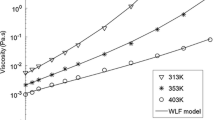
It became clear in the 1960s that progress in elastohydrodynamic lubrication required knowledge of the properties of lubricants at a combination of high pressure and high strain rate, and this led researchers at Georgia Institute of Technology to build a succession of high-pressure rheometers aimed at measuring liquid properties under these conditions. In 1968, Novak and Winer developed a capillary viscometer able to reach a pressure of 0.7 GPa with an applied shear stress of 0.1 MPa and employed this to study the viscosity of several lubricants [53]. For the polymer solutions tested, they found shear thinning behaviour, but all of the base oils tested showed Newtonian response at all test conditions. This approach was extended in 1975 by using shorter capillaries to reach shear stresses as high as 4 MPa, but again base oils behaved only in a Newtonian fashion once heating effects were taken into account [54].

These two studies failed to reach a sufficiently high shear stress for shear thinning of low MWt base oils to occur, but in 1979, Bair and Winer developed three new high-pressure rheometers based on shear of fluid between a moving piston and stator [55]. They used these to explore both the elastic (stress vs. strain) and viscous (stress vs. strain rate) behaviour of three base fluids. At high pressures and low temperatures up to about 50 °C above the glass transition temperature, all three lubricants behaved as elastic solids upon initial application of stress, with an apparent yield stress that increased with pressure and temperature. This yield stress also increased with strain rate. One of the three rheometers was able to reach a combination of high shear stress (up to 50 MPa) with quite high strain rate (up to 500 s⁻¹). This showed that at lower pressures and higher temperatures, all three fluids showed shear thinning behaviour above a shear stress of about 10 MPa, tending towards a limiting shear stress value, τ _L , that increased linearly with pressure and decreased with temperature. Bair and Winer proposed an equation based on an asymptotic shear thinning expression combined with a viscoelastic term [56];

$$ \dot{\gamma } = \frac{1}{{G_{p} }}\frac{{{\text{d}}\tau }}{{{\text{d}}t}} - \frac{{\tau_{L} }}{{\eta_{p} }}\log_{e} \left( {1 - \frac{\tau }{{\tau_{L} }}} \right) $$

(16)

This can be rearranged in terms of shear stress as;

$$ \tau = \tau_{L} \left( {1 - e^{{ - \frac{{\eta_{p} }}{{\tau_{L} }}\left( {\dot{\gamma } - \frac{1}{{G_{p} }}\frac{{{\text{d}}\tau }}{{{\text{d}}t}}} \right)}} } \right) $$

(17)

In 1982, Bair and Winer developed a new piston-based rheometer to address a problem of pressure drop during test measurement, and shear stress versus strain rate curves were measured for a range of lubricants, including polymer solutions, up to 1.1 GPa and a shear stress of 80 MPa [57]. Shear thinning occurred for both base fluids and polymer solutions and shear stress levelled out as strain rate increased, in a fashion consistent with Eq. 17.

A very different method for studying lubricant rheology at high shear stresses was developed by Ramesh and Clifton in 1987 [58]. They measured the compression and shear waves transmitted from the impact of two flat plates separated by a very thin film of lubricant and from these were able to monitor the shear stress and strain of the film over a time scale of less than a millisecond. The approach could not directly study the variation of shear stress with strain rate and applied only very small amounts of shear, but did show that the lubricants tested had an apparent limiting shear stress that increased linearly with pressure over the pressure range of 1–5 GPa.

In 1990, Bair and Winer developed a new high-pressure viscometer based on a rotating cylinder configuration in order to reach controlled, high strain rates [43]. A key barrier in such development is heating of the test fluid during shear and consequent reduction in effective viscosity. The new design addressed this by using a very short duration of shear to avoid unacceptable cylinder temperature increases, combined with a very narrow film gap down to almost one micron to minimise oil film temperature rise. This enabled combinations of shear stress and strain rate, up to 10 MPa and 10⁴ s⁻¹, respectively, to be reached without significant shear heating. Two fluids were studied, and the same pattern of shear stress versus strain rate behaviour was found as noted at higher pressures and lower strain rates, i.e, linear increase on a log/log plot at low strain rates followed by levelling out towards a limiting value as strain rate was increased. In a subsequent paper in 1992, Bair and Winer combined this data with some taken at very high pressures and low strain rates to suggest that the transition from Newtonian to plastic behaviour described by Eq. 17 broadened as pressure was increased [59]. They proposed a modification of this equation to accommodate this.

Further thermal analysis showed that there was a significant flash temperature effect in the cylinder walls even during short duration tests and this led Bair and Winer in 1993 to develop another, “isothermal” concentric cylinder viscometer with a shorter time of operation of 3 ms, so as to prevent significant temperature increase of the cylinders [60]. Again, as shown in Fig. 7, they found levelling-out of shear stress/strain rate curves at high strain rates, in support of the existence of a limiting shear stress, τ _L .

Fig. 7

Shear stress versus strain rate data for a 5-phenyl-4-ether (5P4E) showing “limiting shear stress” from two high-stress viscometers; from [60]

The high-pressure capability of this viscometer was increased by Bair to 600 MPa in 1995 [61] and to almost 1 GPa in 2002 [62]. In 1995, Bair also suggested the use of the reduced Carreau–Yasuda equation;

$$ \tau = \frac{{\eta_{p} \dot{\gamma }}}{{\left( {1 + \left( {\frac{{\eta_{p} \dot{\gamma }}}{{\tau_{o} }}} \right)^{a} } \right)^{{\left( {1 - n} \right)/a}} }} $$

(18)

where a and n are constants and n < 1 [61]. τ _o is a modulus or stress at which shear thinning becomes significant. Initially Bair used τ _L in place of τ _o but it is clear that τ _o does not represent a limiting shear stress. For a = 2 and n = 0.5, it is the stress at which the effective viscosity has fallen 21 % below its Newtonian value and it typically has a value between 4 to 10 MPa for simple molecular fluids, but a much smaller one for polymeric liquids. More recently, Bair has tended to use the term τ _C [44] or G [63], but in this review, τ _o is preferred to avoid confusion with the elastic shear modulus used in the viscoelastic term. In 2002, Bair added a pressure-dependent, limiting shear stress to the Carreau Yasuda model [44] to give, omitting the Maxwell viscoelastic term,

$$ \tau = \hbox{min} \left[ {\dot{\gamma }\eta_{p} \left[ {1 + \left( {\frac{{\eta_{p} \dot{\gamma }}}{{\tau_{o} }}} \right)^{a} } \right]^{{\left( {n - 1} \right)/a}} ,\varLambda_{c} p} \right] $$

(19)

Since 2002, there appears to have been relatively little further development of high shear stress viscometry. Bair and his colleagues at Georgia Institute of Technology remain the only group to construct and employ short duration, high-stress/high-strain viscometers, perhaps because of the formidable problems involved in their design, in particular to limit their response time. Bair has used the Carreau–Yasuda equation for modelling EHD lubrication, accompanied by criticism of the Eyring equation [44, 45, 64]. The relative suitability of these equations in EHD contact conditions will be discussed later in this paper, but first their origins are briefly outlined.

5 EHL Rheology Models

5.1 Eyring

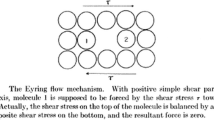
Eyring’s model of viscosity, introduced in 1936, treats liquid flow as a unimolecular, “chemical” reaction in which the elementary process is a molecule (or flow unit) passing from one equilibrium position to another over a potential energy barrier [65]. It was based on the newly developed partition state chemical reaction rate theory [66, 67]. Figures 8 and 9 show the process schematically. A molecule moves approximately one molecular distance, λ, into a neighbouring hole in the liquid. If no external force is applied, the number of times per second that molecules passes over the energy barrier and hence moves in either direction, i.e, their diffusion rate, is given by:

$$ k_{D} = Be^{{ - E_{a} /kT}} $$

(20)

where E _a is the activation energy for flow and B contains the ratio of the partition functions of the activated and initial state, which includes a free-volume term.

Fig. 8

Elementary flow process, a flow unit of area l ₁ l ₂ moves distance l into an available hole due to an applied shear force; from [68]

Fig. 9

Applied shear stress, f, decreases the activation energy for flow in the forward direction and increases it in the backward direction; from [66]

However, when a shear force is applied, this has the effect of reducing the activation energy for a flow process in the direction of applied force and increasing it in the reverse direction, as shown in Fig. 9. The activation energy is assumed to be raised and lowered by the value τλ ₂ λ ₃ λ/2, where τ is the applied shear force per unit area, λ ₂ is the length of the molecule in the direction of the applied force, λ ₃ is its length in the transverse direction (so τλ ₂ λ ₃ is the shear force on the individual molecule) and λ/2 the distance it has to move to reach the top of the energy barrier.

The specific flow rates in the forward and backward directions, k _f and k _b , are therefore given by:

$$ k_{f} = Be^{{ - \left( {E_{a} - \tau \lambda_{2} \lambda_{3} \lambda /2} \right)/kT}} = k_{D} e^{{\tau \lambda_{2} \lambda_{3} \lambda /2kT}} $$

(21)

$$ k_{b} = Be^{{ - \left( {E_{a} + \tau \lambda_{2} \lambda_{3} \lambda /2} \right)/kT}} = k_{D} e^{{ - \tau \lambda_{2} \lambda_{3} \lambda /2kT}} $$

(22)

Since each time a molecule passes over a potential barrier, it moves a distance λ, the rate of motion of the layer relative to its neighbour is given by:

$$ \Delta u = k_{D} \lambda \left( {k_{f} - k_{b} } \right) = k_{D} \lambda \left( {e^{{\tau \lambda_{2} \lambda_{3} \lambda /2kT}} - e^{{ - \tau \lambda_{2} \lambda_{3} \lambda /2kT}} } \right) $$

(23)

or, from the definition of the sinh() function,

$$ \Delta u = 2k_{D} \lambda \sinh \left( {\frac{{\tau \lambda_{2} \lambda_{3} \lambda }}{2kT}} \right).$$

(24)

The shear rate is given by the difference in velocity divided by the spacing between layers, λ ₁

$$ \dot{\gamma } = \frac{{\Delta u}}{{\lambda_{1} }} = \frac{{2k_{D} \lambda }}{{\lambda_{1} }}\sinh \left( {\frac{{\tau \lambda_{2} \lambda_{3} \lambda }}{2kT}} \right) $$

(25)

while the effective viscosity is the shear stress divided by the strain rate:

$$ \eta_{e} = \frac{\tau }{{\dot{\gamma }}} = \frac{{\tau \lambda_{1} }}{{2k_{D} \lambda \sinh \left( {\frac{{\tau \lambda_{2} \lambda_{3} \lambda }}{2kT}} \right)}}.$$

(26)

At low shear stresses when τ ≪ 2kT/λ ₂ λ ₃ λ, $\sinh \left( {\frac{{\tau \lambda_{2} \lambda_{3} \lambda }}{2kT}} \right) = \frac{{\tau \lambda_{2} \lambda_{3} \lambda }}{2kT}$, so under these conditions, the (Newtonian) viscosity is given by;

$$ \eta = \frac{{\tau \lambda_{1} }}{{2k_{D} \lambda \frac{{\tau \lambda_{2} \lambda_{3} \lambda }}{2kT}}} = \frac{{2kT\lambda_{1} }}{{2k_{D} \lambda_{2} \lambda_{3} \lambda^{2} }} $$

(27)

or

$$ k_{D} = \frac{{kT\lambda_{1} }}{{\eta \lambda_{2} \lambda_{3} \lambda^{2} }}. $$

(28)

Substituting Eq. 28 into Eq. 25 gives

$$ \dot{\gamma } = \frac{2kT}{{\eta \lambda_{2} \lambda_{3} \lambda }}\sinh \left( {\frac{{\tau \lambda_{2} \lambda_{3} \lambda }}{2kT}} \right) $$

(29)

If we set τ _e  = $2kT/\lambda_{2} \lambda_{3} \lambda$, this becomes Eq. 5, the Eyring equation adopted by many EHD researchers.

The product $\lambda_{2} \lambda_{3} \lambda$ is called the “activation volume.” Eyring found that for simple molecular liquids, Eq. 27 predicted the actual Newtonian viscosity when this activation volume was approximately the size of the molecule, but that for larger molecules, the activation volume required to predict the measured viscosity was less that the molecular size [68]. He suggested that this was because the flow unit was not the whole molecule but that the molecule moved in a segmental fashion.

In 1941, Eyring included the effect of applied pressure on activation energy to obtain a relationship between viscosity and pressure [69].

It should be noted that in 1936, Eyring’s goal was to develop a priori model of the viscosity of simple liquids which was able to explain how Newtonian viscosity varied with temperature, free-volume and molecular properties. The shear thinning equation via which this was derived was essentially a by-product, and he initially gave it little attention. However, other scientists working on shear thinning of polymer solutions and dispersions very soon started to apply Eyring’s equation to model their findings, with variable degrees of success.

In 1955, since the original model failed to model complex fluids and multiphase systems, Ree and Eyring extended Eyring’s model to allow for multiple flow units, for example of dispersed particles in a fluid medium [70, 71]. Their equation was

$$ \tau = \sum\limits_{i} {a_{i} x_{i} \sinh^{ - 1} \left( {\beta_{i} \dot{\gamma }} \right)} $$

(30)

where x _i is the fraction of a shearing layer occupied by flow unit type i, a _i  = $\left( {\frac{kT}{{\lambda_{2} \lambda_{3} \lambda }}} \right)_{i}$ is this unit’s τ _e and β _i  = $\left( {\frac{{\lambda_{i} }}{{2k_{D} \lambda }}} \right)$ is its relaxation time.

The complexity of Eq. 30 means that the Ree–Eyring model has not generally found favour, and it is unfortunate that the earliest EHD publications cited these later Ree and Eyring papers while actually used the original simpler Eyring equation [17, 72], with the result that Eyring’s model is often, incorrectly, termed the Ree–Eyring model in the EHD literature. Eyring’s model has also recently been referred to as the Prantl–Eyring model [73], since Prantl, in 1928, developed a similar thermally activated shear model to describe the plastic flow of solids and also dry friction [74, 75].

5.2 Carreau and Yasuda

By the 1960s, several shear thinning models had been developed specifically to describe complex fluids [76]. In 1965, Cross derived a viscosity model for polymer solutions and colloidal dispersions based on equilibrium between the formation and rupture of linkages between dispersed or dissolved particles [77]. This took the form:

$$ \eta {}_{e} = \eta_{\infty p} + \left( {\eta_{p} - \eta_{\infty p} } \right)\left( {\frac{1}{{1 + \left( {\alpha \dot{\gamma }} \right)^{2/3} }}} \right) $$

(31)

where α is a constant associated the rupture of linkages, η _p is the low shear rate Newtonian viscosity and η _∞p is its viscosity at infinite shear rate, i.e, when the fluid has shear thinned fully to reach a “second Newtonian.” Note that in the above and the following equations, the suffix p has been included to remind readers that these are limiting Newtonian values at the prevailing pressure. Although Cross derived the value 2/3 as the power of the strain rate term, nowadays, this is often generalised to become a constant m, with value less than 1.

This form of shear thinning equation, with limiting values of a first and second Newtonian, is appropriate to fluids where the shear thinning component is dispersed in a Newtonian continuous phase such as a polymer in solvent, and is widely used to describe shear thinning of lubricants containing viscosity modifier polymers. If η _∞p is set to zero, as might be appropriate for a polymer melt, or simply when it much lower than η _p and not reached in experiments [78], then the Cross equation becomes:

$$ \eta_{e} = \frac{{\eta_{p} }}{{1 + \left( {\alpha \dot{\gamma }} \right)^{2/3} }} $$

(32)

In principle, all shear thinning equations can include a second Newtonian, and Eyring and Powell extended the Eyring equation in this fashion in 1944 [79].

By the 1960s, a model of polymer rheology was taking shape based on molecular network theory in which randomly arranged polymer chains are linked together by temporary junctions which are lost and created as the liquid flows [80]. In 1972, Carreau showed that one mathematical solution to this type of model was

$$ \eta_{e} = \frac{{\eta_{p} }}{{\left( {1 + \left( {\lambda \dot{\gamma }} \right)^{2} } \right)^{{\frac{1 - n}{2}}} }} $$

(33)

where λ is a time constant and n < 1 [81]. He notes that this solution is not unique, stating “unfortunately the modified network theory does not shed any light on the actual forms of the functions f _p (II) and g _p (II). In this section, we select arbitrarily plausible forms which will permit good fit of the experimental data for various flow situations.”

At very high shear rates when $\lambda \dot{\gamma } \gg 1$, Carreau’s equation reduces to

$$ \eta_{e} = \eta_{p} \left( {\lambda \dot{\gamma }} \right)^{n - 1} $$

(34)

so that a plot of log(effective viscosity) versus log(shear rate) should give a straight line of gradient (n − 1).

In 1981, Yasuda carried out an extensive study of the shear thinning of polystyrene polymer solutions and suggested a modification to the Carreau equation to improve its fit in the transition region between Newtonian and strong shear thinning [82]. This has the form;

$$ \eta_{e} = \frac{{\eta_{p} }}{{\left( {1 + \left( {\lambda \dot{\gamma }} \right)^{a} } \right)^{{\frac{{\left( {1 - n} \right)}}{a}}} }} $$

(35)

where a and n are constants. a usually has a value close to 2, as in the Carreau equation. This equation has become known as the Carreau–Yasuda equation and widely used to describe polymer shear thinning, both in the above form and with a second Newtonian term;

$$ \eta_{e} = \eta_{\infty p} + \left( {\eta_{p} - \eta_{\infty p} } \right)\left( {\frac{1}{{\left( {1 + \left( {\lambda \dot{\gamma }} \right)^{a} } \right)^{{\left( {1 - n} \right)/a}} }}} \right) $$

(36)

Like the Carreau equation, Eq. 35 reduces to Eq. 34 at high strain rates. The Carreau and Carreau–Yasuda equations can be expressed in terms of shear stress simply by multiplying through by the strain rate, e.g.,

$$ \tau = \frac{{\eta_{p} \dot{\gamma }}}{{\left( {1 + \left( {\lambda \dot{\gamma }} \right)^{a} } \right)^{{\left( {1 - n} \right)/a}} }} $$

(37)

When the time constant, λ, is replaced by η _p /τ _o , this results in the form of the Carreau–Yasuda equation advocated by Bair and coworkers and shown in Eq. 18.

According to Bair, from thermodynamic arguments, τ _o can be equated to N _v kT where N _v is the number of molecules per unit volume [83]. Interestingly, this is very closely related to the expression for τ _e  = kT/λ ₁ λ ₂ λ in the Eyring equation, where λ ₁ λ ₂ λ is the activation volume. Indeed, if we set the volume of a molecule equal to the activation volume, τ _e and τ _o become identical. Bair estimated the value of τ _o for various liquids and found that for simple liquids, 1/N _v corresponds quite closely to the volume of a molecule but that for polymers, it becomes much smaller than this [83], just as was found by Kauzmann and Eyring for simple fluids versus ones with larger molecules [68].

6 Low Shear Rate Piezoviscosity

All the shear thinning equations described above reduce, at very low shear rate, to viscosity η _p , which is taken to be the Newtonian viscosity of the fluid at the prevailing pressure. Therefore, although not critical in choosing the form of shear thinning equation, when testing any such equation, it is essential to have an accurate description of the way that viscosity varies with pressure over the range of pressures of interest. Indeed, much of the debate about preferred shear thinning models has been confused by simultaneous concern about which pressure–viscosity equation to employ. This section therefore briefly reviews the development of our understanding of pressure–viscosity equations.

In 1884, Warburg and Sachs carried out viscosity measurements on three liquids and proposed a linear equation [84]:

$$ \eta_{p} = \eta_{o} \left( {1 + bp} \right) $$

(38)

Less than a decade later, Barus, who was able to reach higher pressures, found that viscosity increased much more rapidly than linearly with pressure and proposed his well-known exponential equation, which predicts that log(η _p) varies linearly with pressure [85];

$$ \eta_{p} = \eta_{o} e^{\alpha p} $$

(39)

Warburg’ and Barus’ equations are not contradictory since the exponential equation reduces to the linear form when p ≪ α.

Subsequent measurements over the next 50 years showed that Barus equation gave a good first approximation but was rarely obeyed accurately over a wide pressure range. Liquids generally show a gradient of logη versus p that progressively reduces with increasing pressure (concave to the pressure axis) at low-to-moderate pressures and a gradient that increases with pressure (convex to the pressure axis) at very high pressures, with the transition from concave to convex shape occurring at lower pressure as temperature is reduced, as shown schematically in Fig. 10 for the fluid di-ethylhexylphthalate. In 1953, an influential study sponsored by the ASME studied 56 lubricants having a wide range of structures and viscosities up to a pressure of 1 GPa [86]. This indicated that the majority of lubricating oils have concave-shaped curves up to 1 GPa in the temperature range 0 to 200 °C.

Fig. 10

Typical viscosity versus pressure for a liquid showing “concave”- and “concave/convex”-shaped behaviour

Using available data including the ASME report results, in 1966, Roelands developed two equations that gave good fit to viscosity–pressure behaviour for a wide range of fluids over the region where fluids showed concave-shaped curves [87]. The simpler of these is

$$ \eta_{p} = \eta_{R} e^{{\left( {\log_{e} \left( {\frac{{\eta_{o} }}{{\eta_{R} }}} \right)\left( {1 + \frac{p}{{p_{R} }}} \right)^{Z} } \right)}} $$

(40)

where η _R and p _R are universal constants having values of 6.31.10⁻⁵ Pas and 196 MPa, respectively. η _o is the low-pressure viscosity and Z has a value specific to the lubricant, typically around 0.6. If Z < 1, then Roelands’ equation fits concave-shaped curves, while if Z > 1, it fits convex-shaped behaviour [87]. Roelands’ equation, like that of Barus, has single fitting constant, while his equation expressing how viscosity varies with both pressure and temperature has two fitting constants.

Recently Paluch has suggested a two constant equation specifically to fit convex-shaped piezoviscous behaviour [88];

$$ \eta_{p} = \eta_{o} e^{{\left( {Cp/\left( {p_{\infty } - p} \right)} \right)}} $$

(41)

where C is a dimensionless constant, while $p_{\infty }$ is the pressure at which the viscosity becomes infinite.

To describe the whole viscosity–pressure behaviour where there is first a concave-shaped log(η _p) versus p curve at low pressures and a convex-shaped on at higher pressures, the third-order polynomial expression can be fitted;

$$ \eta_{p} = \eta_{o} e^{{\left( {a_{o} + a_{1} p + a_{2} p^{2} + a_{3} p^{3} } \right)}} $$

(42)

where a _o , a ₁ , a ₂ , a ₃ are constants.

A useful concept to explain origins of viscosity–pressure behaviour and from which to develop viscosity–pressure–temperature equations is that of free volume. Diffusion of molecules in a liquid is considered as a process in which the molecules move into neighbouring holes, so the diffusion rate depends on the availability of these holes, and thus on the free volume, i.e., volume of the liquid not occupied by molecules. In 1951, Doolittle found that the viscosity of several liquids depended on

$$ \eta_{p} = Ae^{{\left( {\frac{{V_{o} }}{{V - V_{o} }}} \right)}} $$

(43)

where V is the average volume of a molecule (volume of liquid divided by number of molecules) and V _o is the volume actually occupied by a molecule (its Van der Waal’s volume) [89]. (V−V _o ) is thus the free volume. Equation 43 was subsequently given a theoretical basis by Cohen and Turnbull in terms of the statistical availability of holes large enough to accommodate moving molecules [90].

Doolittle’s equation has resulted in a large number of viscosity–pressure–temperature equations based on different assumptions of the dependence of V _o and V on pressure and temperature. In general, it has been found that while V depends on both pressure and temperature, V _o depends only on temperature. Roelands has shown that his pressure–viscosity equation can be derived from free-volume theory by assuming a Weibull distribution of available holes, rather than the exponential one assumed by Cohen and Turnbull [87].

Yasutomi et al. have developed a liquid viscosity–pressure–temperature equation based on free-volume principles of the form [91];

$$ \eta_{p} = \eta_{g} e^{{\left( {\frac{{ - 2.3C_{1} (T - T_{g} )F}}{{C_{2} + (T - T_{g} )F}}} \right)}} $$

(44)

where T _g is the glass transition temperature, given by $T_{g} = T_{go} + A_{1} \log_{e} \left( {1 + A_{2} p} \right)$, $F = 1 - B_{1} \log_{e} \left( {1 + B_{2} p} \right)$ and A₁, A₂, B₁, B₂, C₁, C₂ are constants. Bair has reviewed pressure–viscosity relationships as used in EHD, with a particular focus on free volume-based models [92].

In EHD research, the most widely used pressure–viscosity equations have been the Barus and Roelands’ equations. These have the advantage of having just one disposable constant, while the Barus equation is also appealing due to its mathematic simplicity. It is generally accepted that the Barus equations is only an approximation and rarely holds over a wide pressure range. The Roelands’ equation is only applicable when the viscosity–pressure behaviour is monotonic and cannot capture a combination of concave- followed by convex-shaped behaviour. Fortunately, most modern EHD friction studies use temperatures above 50 °C, to be relevant to steady-state conditions in engines and transmissions. At and above this temperature, most lubricants show concave deviation from log/linear behaviour, at least up to 1 GPa. Unfortunately, while viscosity measurements up to 200 MPa are quite easy to acquire using commercial equipment, very few groups are currently able to make such measurements above 1 GPa, as needed for application in EHD shear thinning equations. In consequence, the Roelands’ and Barus equations are sometimes used inappropriately to extrapolate measured data to higher pressures.

7 Two Problem Areas

Before discussing the relative merits of the Eyring and Carreau–Yasuda models with respect to describing lubricant rheology in EHD conditions, two other aspects of the problem will be discussed, both of which have impacted the debate: the critical issue of shear heating and the problem of lubricant repeatability.

7.1 The Thermal Problem

A key issue, which is not always clear from the literature, is that for most practical lubricants, there is only marginal overlap between conditions over which high shear stress rheological data and EHD friction measurements can currently be acquired. This is because high-stress viscometers are more severely constrained by shear heating than EHD contacts. Equation 45 shows the EHD temperature rise presented earlier in Eq. 9, now expressed in terms of strain rate instead of sliding speed and with the ratio 2b/U replaced by its equivalent time, i.e, the time of transit of the surfaces across the contact, t _i .

$$ \Delta \bar{T} = \left( {\frac{1}{{\left( {2\pi K_{s} \rho c} \right)^{0.5} }}t_{i}^{0.5} h + \frac{1}{{8K_{\text{oil}} }}h^{2} } \right)\bar{\tau }\dot{\gamma } $$

(45)

If we apply this equation to an EHD contact and insert typical thermal properties of steel, K _s  = 47 J/msK, ρ = 7,850 kg/m³, c = 475 J/kgK, thermal conductivity of oil K _oil = 0.25 J/msK, (a typical value at 1 GPa [93] ), representative values of b of 0.15 mm, U = 3 m/s, t _i  = 0.1 ms, and h = 150 nm, Eq. 45 becomes

$$ \Delta T = \left( {6 + 1} \right) \times 10^{ - 14} \bar{\tau }\dot{\gamma } $$

(46)

This implies that, for the temperature rise not to exceed 1 °C, the product $\bar{\tau }\dot{\gamma }$ must be less than ~1.5.10¹³ W/m³. We can thus reliably measure a shear stress of 2.10⁷ Pa only up to a strain rate of ca. 10⁶ s⁻¹ without recourse to thermal correction.

Equation 45 can also be applied to estimate the temperature rise in short-duration, high-stress viscometers. To analyse oil film temperature rise in these, Bair has suggested the use of the Brinkman or Nahme-Griffith number, $Na = \beta \tau \dot{\gamma }h^{2} /K_{oil}$, where β is the temperature coefficient of viscosity [59]. Bair suggests a value for β of 0.05. It is evident that this non-dimensional group is very closely related to the second term in Eq. 45.

In a short duration, rotating cylinder viscometer, t _i , corresponds to the minimum time for the viscometer to stabilise at the required strain rate and for a stress to be measured. Bair and Winer refer to this as the response time and indicate that it is as low as 3 ms for their isothermal viscometer [60]. If this value, the thermal properties of Bair’s viscometer [94] and a gap size of h = 2 μm are inserted into Eq. 45 we obtain

$$ \Delta T = \left( {3 + 2} \right).10^{ - 12} \bar{\tau }\dot{\gamma } $$

(47)

This implies that, for a limit of ΔT = 1 °C, the product $\bar{\tau }\dot{\gamma }$ must be less than ~2.10¹¹ W/m³. We can thus reliably measure a shear stress of 2.10⁷ Pa only up to strain rate of 10⁴ s⁻¹. However, in the EHD contact, because of its short transit time, viscoelasticity influences shear stress below a strain rate of ~10⁵ s⁻¹. This means that direct comparison of shear stresses from an EHD contact and a high-stress rheometer is only possible over a very narrow shear rate range and for low shear stress conditions. Figure 11 compares the practical boundaries of shear stress and strain rate below which reasonably “isothermal” data, i.e, with ΔT < 2 °C, can be obtained based on the above film gaps, h, and response times, t _i , superimposed on a set of typical measured EHD shear stress versus strain rate curves.

Fig. 11

Representative EHD friction curves showing representative upper limits of high-stress viscometer measurements (dashed line) and EHD friction measurements (solid line) to ensure ΔT _oil < 2 °C

Equation 45 also indicates the importance, when presenting high-stress viscometer results, of providing information as to both response time and film gap, and for EHD friction of providing film thickness and entrainment velocity values, so that the possible impact of heating can be assessed by the reader.

7.2 Lubricant Repeatability Problem

In historical terms, a significant problem in EHD research in general, and in comparing EHD friction with high-stress viscometer data in particular, is that practically all liquid lubricant base fluids are poorly defined mixtures, so that it is usually impossible to repeat or extend any research conducted in the past. Base mineral oils are mixtures of hydrocarbon structures whose proportions vary with crude oil source and refining processes. Polymer base oils such silicones, polyglycols and their fluorinated analogues, perfluoropolyethers, also vary from batch to batch in terms of molecular weight distribution even when they have the same viscosity. The highly researched oligomer 5-pheny-4-ether (5P4E) is a mix of various isomers, which can cause a large variation in low-temperature viscometric properties from sample to sample. There are pitfalls even for apparently well-defined base fluids; for example Santotrac 40, which has one predominant molecular structure, is often compared with Santotrac 50, which includes a viscosity modifier and other additives. One group of base fluids that offers some possibility of reproducibility are the esters, which generally have defined molecular structures. Unfortunately, while it is possible to obtain esters in pure form, commercial ester base oils are always complex mixtures, with their name referring simply to their predominant component. Indeed, mixtures are almost always preferable to pure materials for use as lubricants, since when all the molecules have the same molecular structure, there is a greater tendency for the liquid to crystallise when cooled rather remain a viscous fluid.

All of the above means that most research measurements of high-pressure viscosity, EHD friction or high shear stress/strain rate behaviour made between the 1960s and 1990s cannot be confirmed or extended at the present day. This is one reason for a problem that has already been alluded to, which is that historically EHD researchers have rarely had available pressure–viscosity data for the specific lubricants they have studied over the range of pressures relevant to EHD friction. Instead, they have had to assume a form of the pressure–viscosity response—usually, for simplicity, Barus—and have tried to estimate both pressure–viscosity and shear thinning behaviour from the same experiments. This will be discussed in more detail later.

This issue has been recognised and a few liquids have been identified that can be purchased as almost pure compounds to form a basis of parallel study of both viscosity and shear thinning by different research groups now and in the future [95, 96]. These include the hydrocarbon squalane and some esters. Another ester that was initially favoured, di-isodecylphthalate, unfortunately turned out to be an isomeric blend whose properties varied with provenance [97].

8 Eyring versus Carreau–Yasuda

It is clear that there are differing views as to which constitutive equation most accurately describes the rheology of lubricants in EHD contact conditions. Whereas many EHD researchers have accepted and used the Eyring model, Bair and co-workers have argued for the Carreau–Yasuda model together with a limiting shear stress, based on high-stress viscometry.

This is an important issue since an appropriate model of EHD rheology is needed for EHD simulations aimed at predicting EHD friction, and the two models predict quite different shear stress behaviour when applied over a wide range of strain rates.

The Eyring equation is remarkable in that it describes the relationship between shear stress and strain rate using only one disposable parameter, τ _e . It is thus particularly easy to seek a fit to experimental data. This convenience, the fact that it appears to fit EHD friction data closely and also that it is based on a fundamental molecular model, albeit one that originated in 1936, has made it the equation of choice for most EHD researchers. Not surprisingly, the latter have proved quite reluctant to replace it by the Carreau–Yasuda model, which has at least three disposable constants and, as will be shown, appears to be no better at fitting EHD friction data than the Eyring equation.

This reluctance has led Bair and co-workers to publish a series of papers in support of the Carreau–Yasuda and against the Eyring equation. Broadly speaking their advocacy of Carreau–Yasuda is based on the following four arguments.

• 1. Shear stress versus strain rate behaviour in high-stress viscometers does not obey the Eyring equation but does fit the Carreau–Yasuda equation

• 2. The Carreau–Yasuda equation provides observed EHD friction behaviour, in particular the observation that mean EHD shear stress varies linearly with log(strain rate).

• 3. Use of the Eyring equation predicts unrealistic piezoviscous behaviour.

• 4. The Eyring equation is “wrong.”

These arguments are discussed in turn below.

• 1. Fit of Carreau–Yasuda and Eyring equations to high-stress viscometer data

Over the last twelve years, Bair and co-workers have studied the shear thinning properties of a wide range of fluids using short duration, high-stress viscometry and fitted the results with the Carreau and Carreau–Yasuda equations. Many of these fluids have been formulated lubricating oils of unknown composition or complex mixtures of hydrocarbons, but a few are well defined. Of particular interest is a study of several pure liquids [62]. Figure 12 shows Bair’s data values for the pure hydrocarbon squalane at three pressures, together with dashed lines showing his derived Carreau parameters. The test temperature is 20 °C. Also on this figure are solid lines showing predictions using the Eyring equation, based on τ _e  = 5.5 MPa and the low shear rate viscosity at the appropriate pressure. It can be seen that the Eyring equation provides excellent fit—to the extent that the lines largely obscure the Carreau lines.

Fig. 12

High-stress viscometer data for squalane measured at 20 °C from [62]; solid lines are Eyring shear thinning equation fits while the dashed lines (often obscured) are the Carreau fits from [62]

Similar close fit between the Eyring equation and shear stress/shear rate measurements was found by the authors for all of the well-defined fluids described in [62]. This similarity of fit between the Carreau and Eyring equations at relatively low strain rates is not surprising since the Carreau and Eyring equations are remarkably similar in form. Thus, if we expand the two equations in a Taylor series, we find, assuming n = 0.5 in the Carreau equation,

$$ \tau = \tau_{e} \sinh^{ - 1} \left( {\frac{{\eta_{p} \dot{\gamma }}}{{\tau_{e} }}} \right) = \eta_{p} \dot{\gamma }\left[ {1 - \frac{1}{6}\left( {\frac{{\eta_{p} \dot{\gamma }}}{{\tau_{e} }}} \right)^{2} + \frac{3}{40}\left( {\frac{{\eta_{p} \dot{\gamma }}}{{\tau_{e} }}} \right)^{4} - \frac{5}{112}\left( {\frac{{\eta_{p} \dot{\gamma }}}{{\tau_{e} }}} \right)^{6} .\,\,.\,\,.} \right] $$

(48)

$$ \tau_{(n = 0.5)} = \eta_{p} \dot{\gamma }\left( {1 + \left( {\frac{{\eta_{p} \dot{\gamma }}}{{\tau_{o} }}} \right)^{2} } \right)^{{\frac{0.5 - 1}{2}}} = \eta_{p} \dot{\gamma }\left[ {1 - \frac{1}{4}\left( {\frac{{\eta_{p} \dot{\gamma }}}{{\tau_{o} }}} \right)^{2} + \frac{5}{32}\left( {\frac{{\eta_{p} \dot{\gamma }}}{{\tau_{o} }}} \right)^{4} - \frac{15}{158}\left( {\frac{{\eta_{p} \dot{\gamma }}}{{\tau_{o} }}} \right)^{6} .\,\,.\,\,.} \right] $$

(49)

With appropriate choices for τ _e and τ _o , the sums of the two series only diverge markedly when the inner bracketed term becomes greater than unity.

Figure 13 shows a comparison of high-stress viscosity data with predictions from the Carreau–Yasuda and Eyring equations using data for a commercial polybutene taken from [98] showing that the Eyring equation can also fit polymer melt shear thinning behaviour.

Fig. 13

High-stress viscometer data for polybutene measured at 345 MPa from [98]; solid lines are Eyring shear thinning equation fits while the dashed lines (partially obscured) are the Carreau–Yasuda fits from [98]

This close fit does not, however, mean that either equation will necessarily correctly describe shear thinning in EHD contacts, where strain rates are generally at least an order of magnitude greater. Figure 14 extrapolates the predictions of both the Carreau with Eyring equations for squalane to higher strain rates, more relevant to EHD contacts, but not yet attainable in high-stress viscometers. Plots are shown in the log/log form favoured by polymer rheologists, the linear/log form used by most EHD researchers and the linear/linear form used to display traction curves. It can be seen that the two equations predict very different behaviours at strain rates above 10⁴ s⁻¹.

Fig. 14

Shear thinning data for squalane from Fig. 12 showing divergence of Carreau and Eyring predictions at high strain rate; curves shown in log/log, linear/log and linear/linear shear stress versus strain rate forms

For some fluids tested in high-stress viscometry, the shear stress appears to level out at a limiting value at high strain rate, when plotted in log/log form. Early observations of this effect may be tainted by thermal effects, but similar behaviour has been seen in more recent work after the thermal problem was fully recognised [44, 59–61, 83]. Unfortunately such data are not always accompanied by information as to the film gap and the viscometer response time, so it is not possible to verify that the effect is wholly rheological or in part due to a surface temperature rise.

• 2. The logarithmic traction curve

A characteristic feature of EHD friction measurements, as can be seen in Figs. 4, 5 and 6, is that they invariably show linear mean shear stress versus log(strain rate) behaviour at high strain rates, until thermal effects ensue. Furthermore, application of thermal correction results in this linearity being preserved to even higher strain rates [35]. This behaviour is anticipated from the Eyring model for shear thinning although this does not appear to have played a role in the initial choice of the Eyring equation to describe EHD friction [17, 27].

Considerable effort has been expended by researchers using high-stress viscometry to show that the shear thinning equations developed from their data also predict this characteristic mean shear stress/strain rate behaviour. This requires these equations to be integrated over the contact area to obtain mean shear stress, e.g., for point contact,

$$ \bar{\tau } = \frac{F}{A} = \frac{2}{{b^{2} }}\int\limits_{o}^{b} {r.{\text{f}}\left( {\eta_{p} \dot{\gamma }} \right)} dr $$

(50)

where τ = ${\text{f}}\left( {\eta_{p} \dot{\gamma }} \right)$ is the preferred shear thinning model. The pressure is assumed to vary according to the Hertz equation, $p = p_{o} \left( {1 - r^{2} /b^{2} } \right)^{0.5}$.

When integrated in Eq. 50, the Carreau–Yasuda equation still fails to predict linear mean shear stress versus log(strain rate) behaviour at high strain rates. To achieve the latter, a limiting shear stress has to be imposed to curtail the rise in shear stress at high strain rates. In 1990, Bair and Winer thus proposed that a combination of Newtonian viscosity with Barus piezoviscous response in regions of the contact below a critical pressure and having a limiting shear stress in regions above it, i.e. $\tau = \hbox{min} \left[ {\eta_{o} e^{\alpha p} ,\varLambda p} \right]$, was able to give the required linear/log response [43]. Unfortunately, as noted in a Discussion to this paper, their mathematical analysis was flawed [99].

To test whether the various suggested shear thinning equations give linear/log behaviour, Eq. 50 below has been solved for one fluid using four different shear thinning equations; (1) Newtonian, (2) asymptotic as in Eq. 17, but without a viscoelastic term, (3) Carreau–Yasuda and (4) Eyring.

$$ \bar{\tau } = \frac{F}{A} = \frac{2\pi }{{\pi b^{2} }}\int\limits_{o}^{b} {r.\hbox{min} \left[ {{\text{f}}\left( {\eta_{p} \dot{\gamma }} \right),\varLambda_c p} \right]} dr $$

(51)

The properties of the lubricant chosen were again those of squalane at 20 °C, with the shear thinning properties; Eyring stress τ _e  = 5.5 MPa; Carreau–Yasuda parameters τ _o  = 6.6 MPa, a = 2, n = 0.46; Λ _c  = 0.075. The Carreau–Yasuda values were taken from [62] while the value of Λ _c was arbitrary. The contact conditions were p _o  = 0.9 GPa, a = 0.1 mm. The lubricant had η _o  = 0.039 Pas, while its pressure–viscosity response was described by a third-order polynomial as Eq. 42, determined by best-fitting viscosity data in [95].

The predictions are shown in Fig. 15, where the dashed lines are from Eq. 50, i.e, with no limiting shear stress, while the solid lines are from Eq. 51 with a limiting shear stress. In the absence of a limiting shear stress, the Newtonian and Carreau–Yasuda equations predict very high mean shear stress at high strain rate, while the Eyring response is linear/log above a mean shear stress of about 20 MPa. When the limiting shear stress Λ _c is imposed, the Eyring equation still shows linear/log behaviour until it levels out quite sharply at the limiting stress, as also noted for experimental EHD friction results by Evans and Johnson [36]. None of the other equations yield a significant linear region with the data used. This is further discussed when the Carreau–Yasuda equation is fitted to experimental EHD friction data later in this paper.

Fig. 15

Mean shear stress versus strain rate curves for squalane in an EHD contact predicted by four rheological models based on integrating shear stress across a Hertzian contact using measured pressure–viscosity data; dashed lines show Newtonian and Carreau response without an assumed limiting shear stress

• 3. Eyring equation predicts unrealistic piezoviscous behaviour

One criticism levelled at the Eyring equation is that when applied to EHD friction data in the form of Eq. 8 to extract both the Eyring stress, τ _o , and also the pressure–viscosity coefficient, α, the values of the latter are often different from those determined using high-pressure viscometry [100]. This is probably because Eq. 8 assumes that the fluid obeys the Barus viscosity–pressure equation, which is generally not accurate over a large pressure range. It is possible to assume other viscosity–pressure data and extract best-fit constants to these from EHD friction data, but a much better approach is, of course, to determine viscosity–pressure response using a high-pressure viscometer and employ this when fitting shear thinning equations to friction measurements. This will be illustrated later in this paper.

• 4. The Eyring equation is “wrong”

A theme of criticism of the Eyring model by advocates of the Carreau–Yasuda and related shear thinning equations is that the Eyring equation is “wrong”—primarily that it has been disproved by other researchers, and that Eyring himself has disowned it.

It has been repeatedly suggested by Bair and co-workers that Eyring eventually “rejected” his original viscosity model, e.g. [45, 64, 73, 100–102]. This is based on a paper in 1958 [71] in which Ree, Ree and Eyring state that Eyring’s original equation did not adequately describe the shear thinning of complex fluids to which other researchers were applying it, and provided an extended model based on multiple flow units to apply to such materials. This was not a disavowal of the original model. Indeed, in another paper the same year, Eyring and coauthors outlined three separate but related models, his original one for simple liquids, the Ree–Eyring model for polymer solutions and a third for high MWt polymer melts [103]. They wrote of Eyring’s original model that “it gives a very satisfactory account of the viscosity of simple liquids.”

It should be appreciated that when it was introduced in 1936, the Eyring viscosity model was one of very few liquid shear thinning models, and the only one with a theoretical basis. As such, it was widely applied by researchers concerned with shear thinning phenomena. Unfortunately, the only liquids that showed shear thinning at attainable strain rates in high shear conditions at that time were (and to a large extent remain) complex fluids such as polymer solutions and melts and dispersions of solid particles in liquids. Thus, the Eyring model was applied to diverse materials including polymer solutions, cordite and masticated rubber, to which, since the model is based on there being one predominant flow unit, it was inappropriate. Indeed, until the development of EHD and high-stress rheometers, the only liquids that showed any shear thinning at attainable strain rates in high shear conditions were complex fluids. These are very different from the simple molecular liquids for which Eyring’s model was developed, so was hardly surprising that his model did not find general favour until a sufficiently severe application arose—EHD lubrication—to make even low molecular weight liquids shear thin.

The majority of lubricants used today, including the mineral oils, PAOs and esters, are low viscosity, small molecule-based blends with average MWt rarely greater than 400. As such they correspond quite closely the type of fluids for which the Eyring model was intended.

As a corollary, it is perhaps relevant to query the suitability of the Carreau–Yasuda or Carreau rheological models to describe shear thinning of simple molecular liquids. The Carreau model was developed to describe polymer shear thinning, based on the formation and breakdown of networks, while the Yasuda’s variant simply introduced an extra variable to improve fit to shear thinning measurements on polystyrene solutions. There is no reason to suppose that such a model is appropriate to describe the shear thinning behaviour of non-polymeric liquids such as low MWt base oils. Polymer shear thinning is generally considered to involve polymer molecule alignment, while in EHD contacts, shear thinning with characteristic linear/log shear stress versus strain rate response is seen even for simple, spherical type molecules, such as cyclohexane, where alignment is very unlikely, although the molecular mechanism of shear thinning remains obscure.

8.1 Fitting of Eyring and Carreau–Yasuda Equations to EHD Friction Curves

As indicated earlier in this paper, many studies have fitted the Eyring-based, Johnson-Tevaarwerk model to EHD friction data, especially during the 1970s and 1980s. However, there have been relatively few systematic attempts to fit other shear thinning models to such friction curves. This may reflect the dichotomy between, on the one hand, researchers with access to EHD friction-measuring facilities, who have tended to focus on Eyring, and on the other, rheologists, with a greater interest in models such as Carreau–Yasuda but limited access to raw EHD friction measurements.

There have also been very few studies in which Eyring-based or other models have been fitted to friction curves using measured low strain rate, high-pressure viscosity data. Presumably, this is because such data were not generally available for the specific lubricants being tested. Instead, it was generally assumed that viscosity varied with pressure according to the Barus equation and plots of mean shear stress versus log (strain rate) or mean pressure were used to extract both Eyring stress and pressure viscosity coefficient, as described earlier. One notable advance on this approach is a study by Muraki and Konishi who compared the fit of various shear thinning models for the pure ester lubricant, di-ethylhexyl-phthalate to EHD friction curves using pressure–viscosity data of this fluid from [86] fitted to Roelands’ equation [104]. They found that the Eyring equation fitted better than other models tested, but did not test the Carreau–Yasuda equation.

A comparison of both the Carreau–Yasuda and Eyring models with EHD friction measurements for a range of well-defined fluids has recently been made by the authors and will be published in a separate paper. A single example is included in this review. Figure 16 shows EHD friction data in the form of mean shear stress versus strain rate for the fluid di-2-ethylhexyl-phthalate (DEHP).

Fig. 16

Measured mean shear stress versus strain rate curves for di-2-ethylhexyl-phthalate at seven test temperatures. Applied load is 20 N, corresponding to a maximum Hertz pressure of 0.83 GPa, entrainment speed = 2.5 m/s; dashed lines are isothermally corrected values

This was chosen because it is a well-defined fluid (99.5 % Aldrich), has available pressure–viscosity data up to 1 GPa from two independent sources [86, 100] and is also one of the few where a detailed fit of EHD friction measurements with shear thinning models, although not the Carreau–Yasuda model, has already been attempted [104]. The test rig used was a minitraction machine (MTM) which has a rolling–sliding ball on disc configuration. The applied load was 20 N, corresponding to a maximum Hertz pressure of 0.83 GPa. This relatively low load was chosen both to minimise viscoelastic effects and to ensure that the maximum contact pressure was within the pressure range for which viscosity–pressure data are available. The shear rate values were determined from EHD film thickness measurements using optical interferometry at the same temperatures and load, with a small correction to allow for the different elastic moduli of glass and steel in the EHD film thickness and MTM friction tests, respectively. Tests were carried out at 10 °C intervals between 30 and 110 °C, and this allowed accurate correction of the effect of temperature rise to be made, as carried out by previous researchers [35]. The dashed lines in Fig. 16 show the EHD friction data with an applied temperature correction to bring them to isothermal conditions. It can be seen that the levelling-out of friction observed at high speed originates wholly from thermal effects at this applied load. It is important to note that the temperature correction involves no assumptions as to the rheology of the lubricant and is based simply on determining the variation of shear stress with temperature at each strain rate.

The measurements in Fig. 16 were regression-fitted using both the Carreau–Yasuda and Eyring models by comparing the measured mean shear stress with the one calculated using Eq. 50, with viscosity varying with pressure according to the Yasutomi model constants for DEHP given in [100]. Fitting was made only to the data at strain rates greater than 2.5 × 10⁵ s⁻¹, to avoid the viscoelastic region.

For the Carreau–Yasuda equation, the four values τ _o , n, a and Λ _c were allowed to vary, τ _o between 2 and 50 MPa, n between 0.1 and 0.5, a between 1 and 2 and Λ _c between 0.04 and 1. For the Eyring equation, two types of fit were made. One assumed that τ _e was independent of pressure and within the range 2 to 50 MPa, while the second, following previous workers [22, 104], introduced a second variable parameter by allowing τ _e to vary linearly with pressure with respect to a reference pressure p _R , according to Eq. 52, where k ₁ was between ± 3.10⁻⁸ Pa⁻¹.

$$ \tau_{e} = \tau_{eR} \left( {1 + k_{1} \left( {p - p_{R} } \right)} \right) $$

(52)

Figure 17 shows the Carreau–Yasuda best fits.

Fig. 17

Comparison of Carreau–Yasuda equation predictions with isothermally corrected EHD mean shear stress versus strain rate curves for di-ethylhexyl-phthalate; solid lines are Carreau–Yasuda fits; dashed line is fit to 30 °C data without an assumed limiting shear stress

In this figure and the two following ones, the isothermally corrected experimental values are shown as their individual data points for clarity, while the best-fit predictions are shown as solid lines. It can be seen that at test temperatures of 70 °C and above, there is good fit over the whole strain rate range. At a combination of low temperature and low strain rate, measured shear stress falls below predicted values due to an elastic component. The latter was not taken account of in this analysis in which curve fitting was confined to data at strain rates greater than 2.5 × 10⁵ s⁻¹. At low temperatures and high shear stresses, in the Carreau–Yasuda equation, there is a small discrepancy between measured data and best-fit curves. Table 1 lists the best-fit constants used in this graph. In practice, with four disposable constants, several combinations of constants τ _o, a and n gave similar quality fits, and the ones listed are simply those with the lowest variance. The values of n, 0.15–0.3, were considerably lower than the value of 0.41 suggested from high-stress viscometer measurements [55], indicating more a severe mode of shear thinning in EHD contacts than found using viscometry.

Table 1 Carreau–Yasuda equation best-fit constants

Figure 18 shows best fits using the simple Eyring equation, where τ _e is taken as independent of pressure (though dependent on temperature). As with the Carreau Yasuda equation, the measured mean shear stresses fall below the predicted values at low strain rates due to an elastic component. However, at all other conditions, the fit is remarkably close considering that for each temperature there is only one disposable constant, τ _e . At lower temperatures, the predicted shear stresses are just slightly higher than the measured values. This small divergence can be resolved by allowing τ _e to vary linearly with pressure as shown in Fig. 19. Figures 18 and 19 are indeed very similar and the only difference that can be clearly seen is at 60 °C, where the predicted shear stresses using the simple Eyring equation are very slightly higher than the measured values. Table 2 lists the constants used for the Eyring fits shown in Figs. 18 and 19.

Fig. 18

Comparison of Eyring equation predictions with isothermally corrected EHD mean shear stress versus strain rate curves for di-2-ethylhexyl-phthalate; solid lines are Eyring fits

Fig. 19

Comparison of pressure-dependent Eyring equation predictions with isothermally corrected EHD mean shear stress versus strain rate curves for di-2-ethylhexyl-phthalate; solid lines are Eyring fits

Table 2 Eyring equation best-fit constants

It is important to note that the limiting shear stress ratio, Λ _c, added to the Carreau–Yasuda equation by Bair (Eq. 19), is quite different from the value Λ _e introduced into the Maxwell-Eyring equation by Evans and Johnson (Eq. 10). The latter is considered to represent the ratio of shear strength to pressure of an organic solid [36], has a value of greater than 0.1 that is broadly independent of temperature and is only reached for fluids with high EHD friction such as traction fluids. In Figs. 16 to 19, it might be expected to produce a levelling-out of shear stress when this reaches ca. 60 MPa, at considerably above 10⁸ s⁻¹. By contrast, to fit EHD friction data, Λ _c must have a much lower value to provide levelling-out of friction at about 40 MPa.

The above comparison of EHD friction measurements with predictions of the Carreau–Yasuda and Eyring shear stress/strain rate models using actual pressure–viscosity data for the fluid indicates that both equations give reasonably close fit to experimental data. However, the Eyring equation matches low-temperature data somewhat better, especially when a second disposable constant is introduced via pressure dependence of τ _e . The Carreau–Yasuda equation can be made to fit friction-derived shear stress data by assuming low values of the Carreau constants n and a, lower than determined from high-stress viscometry. It is important to note, however, that only one lubricant is shown here, and this is a relatively simple molecular fluid for which the Eyring model was designed. Further comparisons to include a wider range of fluids, including polymeric fluids, are needed to determine the suitability, or otherwise, of the two rheological equations, and indeed others, to predict EHD friction of the various lubricant types.

9 Current and Future Developments

The above comparison of the suitability of the Eyring and Carreau–Yasuda equations to describe the rheology of lubricant films in EHD contact conditions show quite clearly the problems involved in high-stress viscometry of reaching the EHD contact conditions and in EHD friction of deconvoluting film rheology from a single-friction measurement obtained over a range of contact conditions. Clearly what is needed is a wholly new approach which avoids these problems entirely. Such a “philosophers stone” is sadly not yet available but two techniques, one experimental the other computational, have potential in the future for resolving, at least in part, the debate about EHD rheology.

9.1 Probing the Velocity Profile in EHD Contact

An underlying assumption when modelling EHD and also when interpreting friction data in terms of shear thinning equations is that, at least in the absence of thermal effects or until a critical shear stress is reached, the rheological properties of the lubricant do not vary through its thickness. This is implicit in applying models such as the Eyring and Carreau–Yasuda equations to predict friction since they assume that in the absence of a pressure gradient, the strain rate is given by Δ _u /h, i.e, that the film is subject to Couette shear. To go further than this, we need to be able to measure the velocity profile across the thickness of the EHD contact.

In 1993, Bair and Winer studied velocity profiles by tracking micro-sized dispersed particles in three lubricants sheared between two flat surfaces at high shear stress [105]. The lubricant films were observed from the side, which meant that their thickness, of 150 μm, was much greater than a normal EHD film. The applied pressure was up to 0.3 GPa, the shear stress 25 MPa and the strain rate 10 s⁻¹, and low temperatures were used to ensure high viscosity and thus high shear stress conditions. Linear flow profiles were observed, but at conditions at which shear thinning should occur, localised slip bands, evident by local variations in refractive index, were seen, aligned at an angle to the walls. It is not clear, however, whether similar behaviour would occur within a film of EHD dimensions and pressure.

Recently, a very promising new experimental method for obtaining velocity profiles through EHD films has been described [106]. An EHD contact is established between two glass surfaces using a lubricant containing dissolved fluorescent dye. A small column of lubricant within this contact is bleached using a narrow laser beam, and the movement of this column is observed over time by mapping the fluorescence intensity. Typical distributions of intensity during sliding are shown in Fig. 20. From these distributions, velocity profiles across EHD films of ca 100 nm thickness were obtained. It was found that low MWt polybutenes give Couette shear in low-pressure EHD contacts, but form a velocity profile suggestive of plug flow at higher pressures [106]. When a hydrophobic coating was applied to one surface, slip at this surface was observed [107].

Fig. 20

Through thickness velocity profiles of an EHD film of polybutene in sliding contact (film thickness = 630 nm); from [106]

To date, this method has only been applied to viscous lubricants and to pure sliding conditions, but it holds the potential for greatly extending our understanding of the rheology of EHD films in the future. Clearly, if it is shown that flow is not based on Couette shear over a significant range of operating conditions, this will profoundly change our approach to modelling EHD friction.

9.2 Molecular Dynamics Simulation (MDS)

In molecular dynamics computer simulation, a large ensemble of molecules is placed in an imaginary box with appropriate attractive and repulsive forces between all the individual atoms present. The boundaries are then subject to shear (by displacing molecules at the top and bottom of the box), and the motion of all the molecules is tracked over a large number of tiny time steps. From the resulting forces and motion, the shear stress and velocity profile can be obtained. In principle, this approach can determine precisely how liquids flow under shear at a molecular level, and there have been many studies aimed at this [108]. These have provided support to many different models of shear thinning, including both the Eyring and Carreau equations, e.g. [109–114]. There are still a number of major problems to the approach, however. Because very short time steps have to be used, the computational time to model low shear rates is very large and currently it is only possible to directly simulate shear rates greater than about 10⁸ s⁻¹, higher than that can be reached in experimental work. There are various mathematical ways of addressing this problem [108, 115]. Another issue is how to take account of the heat generated at very large rates of shear in realistic fashion.

However, the main problem with respect to predicting EHD friction is to determine the correct interaction forces and, in particular, the forces that hinder rotation and bending within individual molecules. It is known that EHD friction is very critically dependent on molecular flexibility, so such forces must be defined very precisely. The MDS approach holds great promise in future for establishing the nature of and the impact of molecular structure on shear thinning of liquids at high stresses. However, much further validation, ideally using experimental data at higher shear rates than currently attainable, is needed before it can become a reliable predictive tool.

10 Conclusions

This paper has reviewed the history of research on elastohydrodynamic friction and the existing controversy concerning the most appropriate rheological model to use for predicting this type of friction.

Measurement of EHD friction over a wide range of conditions by many authors has found that friction is controlled by three main types of rheological behaviour, a viscoelastic response at low slide–roll ratios, a shear thinning response at intermediate to high sliding speeds and thus strain rates, and possibly, though the evidence is more limited, a pressure-dependent limiting shear stress at very high sliding speeds and pressures. Shear thinning becomes significant for simple molecular lubricants such as most ester and low MWt hydrocarbon oils above a shear stress of between 5 and 10 MPa. However, for lubricants based on polymer melts, the onset of shear thinning can occur at lower shear stresses.

There is disagreement concerning the most appropriate relationship between shear stress and strain rate to describe shear thinning in EHD contacts. Practitioners of high-stress viscometry advocate the use of the Carreau or Carreau–Yasuda equation coupled with a limiting shear stress (Eq. 19),while many EHD researchers prefer the Eyring equation (Eq. 5). A problem that is not always recognised is that high-stress viscometry measurement is critically limited by the problem of temperature rise of both the lubricant film and the bounding solid surfaces due to shear heating. This means that high-stress viscometry is incapable of reaching the combinations of high strain rate and high stress relevant to most EHD friction studies. It also makes it crucial when interpreting EHD friction data to account for the oil film temperature rise.

This paper has examined the relative merits of the Eyring and Carreau–Yasuda model as applied to EHD friction, in particular considering some of the arguments used against the Eyring model by advocates of Carreau–Yasuda. Most of these arguments appear spurious. It has been noted that both the Eyring and Carreau equations can be arranged to give very similar predictions and fit high-stress viscometer data equally well up to maximum shear stresses attainable in high-stress viscometry. However, at stresses more representative of those present in EHD contacts, the predictions of Eyring and Carreau–Yasuda equation diverge quite markedly.

A complication that has confused the choice of shear thinning model is that both models require knowledge of the pressure–viscosity behaviour of the lubricant of interest up to the high pressures present within EHD contacts. Such data is rarely available for commercial lubricants. This perhaps explains why there appear to have been surprisingly few systematic attempts, with one notable exception [104], to test the fits of Eyring, Carreau–Yasuda or, indeed, other rheological models, to experimental EHD friction data using fluids of known pressure–viscosity behaviour.

To address this issue, recent work by the authors is described, which tests the ability of the Carreau–Yasuda and Eyring equations to fit EHD friction data for a well-defined ester, di-ethylhexyl-phthalate, of known pressure–viscosity properties. This finds that both equations can predict EHD friction data well at high temperatures and thus low shear stresses, but the Carreau–Yasuda equation is slightly less able to predict friction accurately at high stresses, even when a quite low limiting shear stress is assumed. The Eyring shear thinning equation provides close fit to experimental, isothermal friction data over the whole range of shear stresses reached.