Explicit impacts of harvesting on a fractional-order delayed predator–prey model

Abstract

We propose a fractional-order prey-predator model with delay and harvesting. Comparatively, only a few analyses are made to explore the impact of harvesting on population fluctuation due to time delay and fractional order. Thus, our focus is whether harvesting effort can stabilize or destabilize the system by varying the fractional order or keeping it fixed. We have observed that fractional order influences the delayed system and the number of stability switching differently in the case of either predator or prey harvesting. Both fractional order and predator harvesting have a destabilizing effect, whereas prey harvesting has a stabilizing effect on the system. In addition, we observed stability switching induced by predator harvesting while keeping the delay fixed. Moreover, in the case of predator harvesting, when the carrying capacity of prey exceeds a certain threshold, the number of switching regions increases significantly. For yield maximization, we observe that maximum sustainable yield (MSY) exists for predator harvesting only; however, yield at MSY produces stable stock only when the time delay is minimal.

1 Introduction

Time delay plays a significant role in investigating the dynamic relationship between predator–prey interaction. Delay arises in different forms, such as temporal delay, maturation delay, gestation delay, dispersal delay, etc. But maturation and gestation delays are common and unavoidable in a predator–prey interaction (Kar and Matsuda [19], Chakraborty et al. [8], Dubey et al [11]). Gourley and Kuang [13] reported that delay is the cause of oscillation in a stage-structured prey-predator model. Rihan et al. [33] discussed a delayed model of two prey and one common predator with the Allee effect at prey growth rate. They showed that at the primary stage with low population density, the small change in the Allee threshold makes the system highly sensitive, and this sensitivity decreases with time.

In general, predators react differently to variations in prey density. The rate of prey intake per predator as a function of prey density is a functional response, and it plays an essential role in the ecological system. Two kinds of functional responses, prey-dependent and predator-dependent, are common in the ecological literature. The prey-dependent functional response is the intake rate of a single predator to the prey species (see in [15]). While the predator-dependent functional response is the intake rate of a single predator depending on prey and predator density (see in [28]). The latter type of functional response is also called ratio-dependent functional response because it has the ratio of prey species to the predator species [3, 21]. Alsakaji et al. [2] have discussed a prey-predator model with Monod-Haldane and Holling type II functional response.

Many researchers have been interested in fractional-order dynamical systems, particularly in science and engineering. Beyond the traditional integer-order dynamical systems, the fundamental difference with the fractional-order systems is that it consists of a non-local and weakly singular kernel [1, 43]. Thus, the system has infinite memory, more degrees of freedom, and long-range interactivity in space and time [4, 5, 34, 37]. In ecology, problems have memory and spatial interaction in the long run. Humans utilize their memory with the experiences of the past. Biological organisms also follow the same. Therefore, fractional dynamics happen due to carrying memory in most biological organisms and their inheritance. The carrying memory is a process where the biological component for the current and future development of the population dynamics carries out the history. These are the main reason behind the importance of fractional order dynamics rather than the integer order. Incorporating fractional order in dynamics makes the system much more realistic and complex, which can improve the biological system [9]. The flexibility of the fractional order system in stability analysis is high rather that of the integer order system [20, 32]. Caputo and Atangana-Baleanu fractional derivative operators are used in fractional order prey-predator models with Holling type-II functional response and Lotka-Volterra response function in different tropic levels (see [30, 31]). Recently, few researchers have incorporated fractional order in the prey-predator model with delay [9, 35, 40], and without delay, [26, 29, 38], which improves the dynamics into a large number of results. Sekerci [39] observed that climate change affects the dynamics of the fractional-order prey-predator model. The fractional order contributes to ecology and epidemiology [24, 25] and eco-epidemiology [14, 36].

Harvesting has a substantial impact on the dynamic evolution of a population. Depending on the nature of the applied harvesting strategy, the long-run stationary density of the population may be significantly smaller than the long-run static density of a population in the absence of harvesting. Harvesting can also lead to incorporating a positive extinction probability and, therefore, to potential extinction in finite time. Thus, harvesting strongly influences the evolution of the dynamic system. Moreover, it is a user-dependent property since we can regulate the dynamics externally. Mainly two kinds of harvesting are studied constant-yield harvesting and constant-effort harvesting. Some authors like Kar [17], Martin and Ruan [27], and Barman and Ghosh [6] studied the delayed prey-predator model with harvesting. They showed that harvesting has a substantial impact on delayed prey-predator dynamics. Ho and Ou discuss the stability switching on the Lotka-Volterra type predator–prey model [14]. Barman and Ghosh [6] depicted the effect of explicit harvesting on the delayed dynamical system with the Holling type-II response function. Moreover, the impact of harvesting on fractional order prey-predator models without delay is studied by [16, 26, 38, 41, 42]. But from the above literature survey, we observe that the impact of harvesting in a delayed fractional-order prey-predator model is studied only by Song et al. [40]. They have taken the prey-predator model with the linear functional response and showed the impact of harvesting and the static balance. Also, we found that no one explicitly discussed the effect of harvesting on fractional order delay prey-predator model with Holling type-II intake rate by the predator.

Due to the over-exploitation of marine species, many management tools are now being used to face this challenge. Among these, maximum sustainable yield (MSY) is used frequently, allowing harvesting to be carried on sustainably. Many researchers have studied the significance of MSY on single and multi-species systems [12, 18, 22]. Few have also assessed the shortcomings of MSY as it does not involve environmental fluctuations or economic factors, and conservation biologists regard it as unsafe and misused.

Thus, from the above literature study, we observe that fewer studies were made on harvesting in a delayed fractional-order dynamical system. No one explicitly discussed the impact of fractional order and harvesting on time delay and the number of switching for the Holling type-II response function. Also, MSY is an important policy that is measured for the future survival of the population. No such attempts are studied on the delayed fractional-order prey-predator model with harvesting. This motivates us to construct and analyze a delayed fractional order model with Holling type-II response function and harvesting. Most researchers used the time delay as a control parameter to analyze the prey-predator dynamics. But, the time delay is an internal property and is a slow process compared to harvesting. Hence corresponding to invariant time delay harvesting can vary and be controlled.

Thus in our paper, we intend to study the following important issues:

• (i) whether the time delay and stability-switching of the prey-predator model are affected by fractional order and harvesting.

• (ii) whether harvesting effort or fractional order or both have any effect of stabilizing or destabilizing the system.

• (iii) whether prey or predator harvesting always gives the stable, steady state at MSY level.

This paper is organized as follows: In Sect. 2, we formulate a delayed prey-predator model and analyze the model dynamics for both the unharvested and harvested system and Hopf-bifurcation. In Sect. 3, we discuss the numerical simulation with the aid of delay and a number of switching changes for fractional order unharvested system, individual harvesting, and harvesting of both the tropic levels. The simultaneous effect of fractional order and individual harvesting is discussed. Also, we focus on the MSY policy elaborately. Section 4 provides some discussion and concluding remarks.

2 The model

We consider a predator–prey model with Holling type-II trophic function for the issues raised in the introductory portion. The time delay induced in the logistic growth term of prey species. Harvesting is used as a control parameter for a delayed system.

$$\begin{aligned} \begin{aligned} D^\theta x(t)&=rx(t)\left( 1-\frac{x(t-\tau )}{k}\right) -\frac{p x(t) y(t)}{1+qx(t)}-E_1 x(t),\\ D^\theta y(t)&= \frac{s p x(t) y(t)}{1+qx(t)}-s_0 y(t)-E_2 y(t), \end{aligned} \end{aligned}$$

(2.1)

where $D^{\theta },0<\theta \le 1$ is the Caputo fractional derivative, $\tau$ is the measure of maturation time-delay of prey species with the initial conditions $x(t)=\phi (t)>0$ and $y(t)=\psi (t)>0$ for $t\in [-\tau ,0]$, r is the growth rate of prey species, k is the carrying capacity, p is the consumption rate of the predator, q is the half-saturation constant of prey species, s is the conversion rate of the predator, $s_0$ is the death rate of the predator, $E_1$ and $E_2$ are the harvesting efforts of prey and predator species respectively.

Primary tools:

Definition 1

[20] The Riemann-Liouville (R-L) fractional integral operator of order $\theta$ of a continuous function $g\in L^1 \mathbb {(R^+)}$ is defined as

$$\begin{aligned} I^\theta g(t)=\frac{1}{\Gamma (\theta )}\int _0^{t}(t-\eta )^{(\theta -1)}~g(\eta )~d\eta , \end{aligned}$$

where $\Gamma (.)$ is the Gamma function for, $\theta >0$.

Definition 2

[20] The Caputo fractional derivative of order $\theta >0$, $m-1<\theta <m, m\in \mathbb {N}$ is defined as

$$\begin{aligned} D^{\theta }g(t)=&\frac{1}{\Gamma (m-\theta )}\int _0^{t}\frac{g^m(\eta )}{(t-\eta )^{(\theta +1-m)}}~d\eta\\ =&I^{(m-\theta )}g^m(t). \end{aligned}$$

Lemma 2.1

[23] Consider the following fractional differential system with Caputo derivative

$$\begin{aligned} D^\theta Y=AY,~~~~~Y(0)=Y_0 \end{aligned}$$

with $\theta \in (0,1], Y\in \mathbb {R}^m$ and $A\in \mathbb {R}^{m\times m}$. The characteristic equation of the system is $\det (\lambda ^{\theta } I-A)=0$. If all of the roots of the characteristic equation have negative real parts, then the zero solution of the system is asymptotically stable.

Lemma 2.2

[10] Considering the fractional delayed differential system with Caputo derivative,

$$\begin{aligned}& D^\theta Y(t)=AY(t)+BY(t-\tau ),\\ &Y(t)=\phi (t), ~t\in [-\tau ,0] \end{aligned}$$

with $\theta \in (0,1], Y\in \mathbb {R}^m$ and $A,B\in \mathbb {R}^{m\times m}$ and $\tau \in \mathbb {R}^{+(m\times m)}$. If all of the roots of the characteristic equation have negative real parts, then the zero solution of the system is asymptotically stable.

2.1 Fractional order delayed predator–prey model without harvesting

In this section, we describe and analyze the stability of the fractional order delayed predator–prey system without harvesting. For this purpose we consider $E_1=0,~E_2=0$ in equation (2.1) and obtain,

$$\begin{aligned} \begin{aligned} D^\theta x(t)&= rx(t)\left( 1-\frac{x(t-\tau )}{k}\right) -\frac{p x(t) y(t)}{1+qx(t)},\\ D^\theta y(t)&= \frac{s p x(t) y(t)}{1+qx(t)}-s_0 y(t). \end{aligned} \end{aligned}$$

(2.2)

The equilibrium point of the above system is (0, 0),  (k, 0),  and $(x^*,y^*)$, where $x^{*}=\frac{s_0}{ps-qs_0}$ and $y^{*}=\frac{r}{p}(1+qx^*)(1-\frac{x^*}{k})$. Hence for both the species to co-exist, $ps-qs_0>0,$ and $~x^*<k$.

To find the local stability of the co-existing equilibrium, we perturb the system about the interior equilibrium $(x^*,y^*)$. The transformation $u(t)=x(t)-x^*$ and $v(t)=y(t)-y^*$ in equation (2.2), we obtain the linearized system as,

$$\begin{aligned} \begin{aligned} D^\theta u(t)&= -\frac{px^{*}}{1+qx^{*}}v(t)-\frac{rx^{*}}{k}u(t-\tau ),\\ D^\theta v(t)&= \frac{psy^{*}}{(1+qx^{*})^2}u(t). \end{aligned} \end{aligned}$$

(2.3)

The associate characteristic equation of the above-linearized system is given by

$$\begin{aligned} \lambda ^{2\theta }+a_1\lambda ^{\theta }e^{-\lambda \tau }+a_2=0, \end{aligned}$$

(2.4)

where $a_1=\frac{rx^{*}}{k}>0$ and $a_2=\frac{p^{2}sx^{*}y^{*}}{(1+qx^{*})^{3}}>0$.

Lemma 2.3

When $\tau =0$, the interior equilibrium point $(x^*,y^*)$ of the system (2.2) is locally asymptotically stable.

Proof

When $\tau =0$, the associate characteristic equation (2.4) takes the form,

$$\begin{aligned} \lambda ^{2\theta }+a_1\lambda ^{\theta }+a_2=0. \end{aligned}$$

(2.5)

From Lemma 2.1, if all of the roots consist of negative real parts, i.e., $\Re (\lambda )<0$, then the interior equilibrium $(x^*,y^*)$ of system (2.2) with $\tau =0$ is locally asymptotically stable.

Now, we consider $z=\lambda ^{\theta }$, then the system (2.5) turns to

$$\begin{aligned} z^2+a_1 z+a_2=0. \end{aligned}$$

(2.6)

From notion of complex analysis, we obtain that the condition $\Re (\lambda )<0$, in the characteristic equation (2.5) can be transformed to $|\arg (z)|>\frac{\theta \pi }{2}$ in Eq. (2.6). Since $a_1>0$ and $a_2>0$, both the roots $z_1$ and $z_2$ of equation (2.6) has negative real part satisfying the condition $|\arg (z)|>\frac{\theta \pi }{2}$. Hence this completes the proof. $\hfill\square$

Now we will discuss the stability nature of the system for $\tau >0$. We want to find the value of positive $\omega$ such that $\lambda =\pm i \omega$ satisfies. Putting $\lambda =i \omega$ in the characteristic Eq. (2.4) and separating real and imaginary parts, we get

$$\begin{aligned} \begin{array}{lll} \omega ^{2\theta }\cos {(\theta \pi )}+a_2=-a_1\omega ^{\theta }\cos {(\omega \tau -\frac{\theta \pi }{2})},\\ \omega ^{2\theta }\sin {(\theta \pi )}=a_1\omega ^{\theta }\sin {(\omega \tau -\frac{\theta \pi }{2})}. \end{array} \end{aligned}$$

(2.7)

Squaring and adding the above two equations in (2.7), we get

$$\begin{aligned} \begin{array}{lll} \omega ^{4\theta }-(a_1^{2}-2a_2\cos {(\theta \pi )})\omega ^{2\theta }+a_2^{2}=0. \end{array} \end{aligned}$$

(2.8)

Considering $w=\omega ^{2\theta }$ in Eq. (2.8), we can rewrite the form as

$$\begin{aligned} \begin{array}{lll} w^{2}-(a_1^{2}-2a_2\cos {(\theta \pi )})w+a_2^{2}=0. \end{array} \end{aligned}$$

(2.9)

Now we consider a few conditions as follows.

P1.   $(a_1^{2}-2a_2\cos {(\theta \pi )})\le 0$,   P2.   $(a_1^{2}-2a_2\cos {(\theta \pi )})>0$,   P3.   $0<(a_1^{2}-2a_2\cos {(\theta \pi )})<2a_2$,   P4.   $(a_1^{2}-2a_2\cos {(\theta \pi )})>2a_2$,   P5.   $(a_1^{2}-2a_2\cos {(\theta \pi )})^2-4a_2^{2}<0$,   P6.   $(a_1^{2}-2a_2\cos {(\theta \pi )})^2-4a_2^{2}>0$.

Theorem 2.4

If P3 holds, then the co-existing equilibrium $(x^*,y^*)$ of system (2.2) is locally asymptotically stable for each $\tau \ge 0$, i.e., both predator and prey will eventually be stable.

Proof

From Lemma 2.3, we obtain that all of the roots of equation (2.4) consist of negative real parts for $\tau =0$. The main objective is to find the nature when $\tau >0$. It is obvious that $\lambda =0$ cannot be the root of the equation (2.4). For this purpose we will put $\lambda =\pm i\omega (\omega >0)$ in (2.4) and after few steps we get Eq. (2.9).

If condition P1 holds, then no positive roots will occur for equation  (2.9). If condition P3 holds, then P2 and P5 are satisfied and the Eq. (2.9) has no positive roots. Thus, when P3 is satisfied, the equation (2.8) has no positive roots. This indicates that each root of characteristic Eq. (2.4) has negative real parts for $\tau >0$. With the help of Lemma 2.2, we can say that the existence of co-existing equilibrium point $(x^*,y^*)$ is locally asymptotically stable for each $\tau \ge {0}$. $\hfill\square$

If P4 hold, then the other two inequality P2 and P6 are both satisfied. Hence, the equation (2.9) has two unique positive roots. After solving the above quadratic Eq. (2.9) and replacing $\omega ^{2\theta }$ in place of w, we obtain

$$\begin{aligned} \omega _{\pm }=\left( {\frac{(a_1^{2}-2a_2\cos {(\theta \pi )})\pm \sqrt{(a_1^{2}-2a_2\cos {(\theta \pi )})^2-4a_2^2}}{2}}\right) ^{\frac{1}{2\theta }}. \end{aligned}$$

(2.10)

The Eq. (2.7) gives the values of $\tau _n^{\pm }~(n=0,1,2,...)$ for each $\omega _{\pm }$ as

$$\begin{aligned} \tau _n^{\pm }=&\frac{1}{\omega _{\pm }}\left[ \arccos \left( \frac{\omega _\pm ^{2\theta }\cos {\theta \pi }+a_2}{-a_1\omega _\pm ^{\theta }}\right) +\frac{\theta \pi }{2}+2n\pi \right] ,\\ &\qquad \qquad n=0,1,2,... \end{aligned}$$

(2.11)

The above analysis shows that one or more pair of eigenvalues has real parts zero at $\tau =\tau _n^{\pm }$. Now we will check whether the real part of each eigenvalue changes or not near $\tau _n^{\pm }$ and how they change. We use the transversality condition that specifies the rate of change of the real part of eigenvalues.

Now,

$$\begin{aligned} &\left( \frac{d(Re\lambda )}{d\tau }\right) ^{-1}\bigg |_{\lambda =i\omega ,\tau = \tau _n^\pm }\\ &\qquad=\frac{\theta ~(\omega ^{4\theta }-a_2^2)}{\omega ^2\{(a_2+\omega ^{2\theta }\cos {\theta \pi })^2+\omega ^{4\theta }\sin ^2{\theta \pi }\}} \end{aligned}$$

(2.12)

and

$$\begin{aligned} \begin{aligned} sign\left( \frac{d(Re\lambda )}{d\tau }\right) ^{-1}\bigg |_{\lambda =i\omega ,\tau = \tau _n^\pm }&=sign(\omega ^{4\theta }-a_2^2)\\&=sign(\omega ^{2\theta }-a_2). \end{aligned} \end{aligned}$$

(2.13)

Therefore,

$$\begin{aligned} \begin{aligned}&\left( \frac{d(Re\lambda )}{d\tau }\right)^{-1}\bigg |_{\lambda =i\omega _{+},\tau = \tau_n^{+}}>0,\\&\left( \frac{d(Re\lambda )}{d\tau }\right)^{-1}\bigg |_{\lambda =i\omega_{-},\tau = \tau_n^{-}}<0. \end{aligned} \end{aligned}$$

(2.14)

The above two conditions in (2.14) say that the real part of each eigenvalue is zero at $\tau _n^{\pm }$. But, the rate of change of the real part of eigenvalues becomes positive or negative accordingly $\tau$ passes through $\tau _n^{+}$ and $\tau _n^{-}$. Thus, Hopf-bifurcation occurs at $\tau _n^{\pm }$.

Now, we can use the following lemma for finding the number of eigenvalues when $\lambda$ crosses the imaginary axis.

Lemma 2.5

The characteristic equation $F(\lambda ,\tau )=\lambda ^{2\theta }+a_1\lambda ^{\theta }e^{-\lambda \tau }+a_2=0$, where $a_1>0,a_2>0$ provides simple roots on the imaginary axis.

Proof

If possible, let us consider $\lambda =i\omega$ is the root of $F(\lambda ,\tau )=0$ are not simple. Now putting $\lambda ^\theta =h$ for changing the domain from fractional order to integer order in $F(\lambda ,\tau )=0$, we get $G(h,\tau )=h^{2}+a_1 h e^{- h^{\frac{1}{\theta }}\tau }+a_2=0$. Now, $\frac{\partial G}{\partial h}=0$ implies that $G_1(h,\tau )=2\,h +a_1 e^{- h^{\frac{1}{\theta }}\tau }[1-\frac{\tau }{\theta } h^{\frac{1}{\theta }}]=0$. From $G(h,\tau )=0$ we obtain $a_1 e^{- h^{\frac{1}{\theta }}\tau }=-\frac{(h^2+a_2)}{h}$ and replacing in $G_1(h,\tau )=0$ we get $h^2-a_2+\frac{\tau }{\theta }(h^2+a_2) h^{\frac{1}{\theta }}=0$. Then by putting $h=(i \omega )^\theta$ and equating the real part zero, we get $a_2=\omega ^2 \cos {\theta \pi }$. But, $|\cos {\theta \pi }|\le 1, \forall \theta \in [0,1)$. Thus $a_2$ is not always positive, which contradicts our assumption. This completes the proof. $\hfill\square$

Remark

Since $\omega _{-}<\omega _{+}$, $\tau _{n+1}^{+}-\tau _{n}^{+}=\frac{2\pi }{\omega _{+}}<\frac{2\pi }{\omega _{-}}=\tau _{n+1}^{-}-\tau _{n}^{-}$ for $n=0,1,2,...$

This condition expresses that the distance between two consecutive $\tau _n^-$ is greater than the distance between two consecutive $\tau _n^+.$ Hence it implies that two consecutive members of {$\tau _n^+\}_{n=0}^\infty$ must lie between two consecutive member of {$\tau _n^-\}_{n=0}^\infty$ (see [7]).

Now we will establish theorems on stability for the increasing delay.

Theorem 2.6

When $\tau _n^{\pm }$’s are in order $\tau _0^{+}<\tau _1^{+}<\tau _0^{-}$, then system will be stable in $[0,\tau _0^{+})$. Hopf-bifurcation occurs at $\tau =\tau _0^{+}$, and the system will always be unstable for $\tau >\tau _0^{+}$.

Proof

Consider $\tau _0^{+}<\tau _1^{+}<\tau _0^{-}$. At $\tau =0$, the system exhibits stable behavior (see Lemma 2.3). But when $\tau >0$, then corresponding to each $\tau _0^{+}$ there exists a simple root $\lambda =i \omega _{+}$ (from Lemma 2.5). Since the complex conjugate of the eigenvalue is pairwise, $\lambda =\pm i \omega _{+}$ is the eigenvalue corresponding to $\tau _0^{+}$.

The first condition of (2.14) implies that at $\tau =\tau _0^{+}$ the eigenvalues cross the imaginary axis from the left to the right plane (positive real part) for increasing delay and near to $\tau _0^{+}$. Thus the system becomes unstable. As the delay is further increased, at $\tau =\tau _1^{+}$ yet another pair of eigenvalues of the form $\lambda =\pm i \omega _{+}$ is present. From a similar transversality condition of (2.14), the system is unstable.

Now at $\tau =\tau _0^-$, the corresponding eigenvalues are $\lambda =\pm i \omega _{-}$. Thus the second condition of (2.14) tells us that the said pair cross the imaginary axis giving a negative real part of the eigenvalue. But there are still positive real parts of the eigenvalue when $\tau$ passes through $\tau _1^{+}$, and hence the system remains unstable.

For every $\tau _n^{\pm }$, only one pair of eigenvalues crosses the imaginary axis, and consecutive eigenvalue can not appear for $\tau _n^{-}$ (see Remark). Hence instability occurs for every $\tau >\tau _0^{+}$. $\hfill\square$

Another important theorem we can define regarding stability-switching of the system (2.2) as follows.

Theorem 2.7

If $0<\tau _0^{+}<\tau _0^{-}<\tau _1^{+}<\tau _1^{-}<...<\tau _{\bar{k}}^{+}<\tau _{\bar{k}+1}^{+}<\tau _{\bar{k}}^{-}<...$ where ${\bar{k}}$ is an positive integer. Then ${\bar{k}}$ number of switching occurs from stable to unstable and back to stable, and finally, for $\tau =\tau _{\bar{k}}^{+}$ system becomes unstable. Further, at $\tau =\tau _n^{\pm }$ Hopf-bifurcation occur.

Proof

We consider first three order of given inequality $\tau _0^{+}<\tau _0^{-}<\tau _1^{+}$, where $\tau _0^{+},\tau _0^{-},\tau _1^{+}$ are the time delays exhibits as Hopf-bifurcation points. The system shows stable behavior at $\tau =0$ (from Lemma (2.3)). When delay is increasing at $\tau =\tau _0^{+}$, a pair of eigenvalues $\lambda =\pm i \omega _{+}$ of (2.4) will appear on the purely imaginary axis. The transversality condition at $\tau =\tau _0^{+}$ says that the real part of the eigenvalue will be positive when $\tau$ passes through $\tau _0^{+}$. Thus the system will no longer persist in a stable state.

Again, if we increase the delay, there corresponds to an eigenvalue $\lambda =\pm i \omega _{-}$ of $\tau _0^{-}$, the transversality condition at $\tau =\tau _0^{-}$ implies the real part of the eigenvalue is negative when $\tau$ passes through $\tau _0^{-}$. Thus the system becomes stable. So stability-switching occurs (i.e., stable to unstable and back to a stable state) at the positive equilibrium of system (2.2) with increasing delay.

Similarly, for other $\tau \le \tau _{\bar{k}}^{-}$ the stability switching will be continued till $\tau <\tau _{\bar{k}}^{+}$ (${\bar{k}}$=number of switching), occur. If the delay parameter satisfying $\tau _{\bar{k}}^{+}<\tau _{{\bar{k}}+1}^{+}<\tau _{\bar{k}}^{-}$, the Theorem 2.6 tells that the system is always unstable for $\tau >\tau _{\bar{k}}^{+}$. $\hfill\square$

2.2 Fractional order delayed predator–prey model with harvesting

In this section, we discuss the case $E_1\ne 0$ and $E_2\ne 0$ of Eq. (2.1). This system has a co-existing equilibrium $({\bar{x}}^*,{\bar{y}}^*)$, where ${\bar{x}}^*=\frac{s_0+E_2}{ps-q(s_0+E_2)}$ and ${\bar{y}}^*=\frac{1+q{\bar{x}}^*}{p} \left[ r(1-\frac{{\bar{x}}^*}{k})-E_1 \right]$. For feasibility of the equilibrium point, $0< E_1 <r\left( 1-\frac{\bar{x}^{*}}{k}\right)$ and $0< E_2< \frac{ps}{q}-s_0$. Now we perturbed the system (2.1) around the unique equilibrium $({\bar{x}}^*,{\bar{y}}^*)$. By using transformation $u(t)=x(t)-{\bar{x}}^*$, $v(t)=y(t)-{\bar{y}}^*$, we get the linear form as

$$\begin{aligned} \begin{aligned} D^\theta u(t)&=-\frac{p{\bar{x}}^*}{1+q{\bar{x}}^*}v(t)-\frac{r{\bar{x}}^*}{k}u(t-\tau ),\\ D^\theta v(t)&=\frac{ps{\bar{y}}^*}{(1+q{\bar{x}}^*)^2}u(t),\\ \end{aligned} \end{aligned}$$

(2.15)

which gives the characteristic equation as

$$\begin{aligned} \begin{array}{lll} \lambda ^{2\theta }+\bar{a_1}\lambda ^{\theta }e^{-\lambda \tau }+\bar{a_2}=0, \end{array} \end{aligned}$$

(2.16)

where $\bar{a_1}=\frac{r{\bar{x}}^*}{k}>0$ and $\bar{a_2}=\frac{p^2s{\bar{x}}^*{\bar{y}}^*}{(1+q{\bar{x}}^*)^3}>0$.

For $\tau =0$, we follow the same procedure as discussed in the unharvested system in Lemma 2.3. This implies that all the roots of Eq. (2.16) have negative real parts when $\tau =0$.

Again when $\tau \ne 0$, from Eq. (2.16) we observe that $\lambda =0$ cannot be the root of (2.16). Let $\lambda =i \omega (\omega >0)$, be the roots of Eq. (2.16). Then,

$$\begin{aligned} \begin{array}{lll} \omega ^{2\theta }e^{i \theta \pi }+\bar{a_1}\omega ^{\theta }e^{-i (\omega \tau -\frac{\theta \pi }{2})}+\bar{a_2}=0. \end{array} \end{aligned}$$

(2.17)

Separating real and imaginary parts we get,

$$\begin{aligned} \begin{aligned} \omega ^{2\theta }\cos {(\theta \pi )}+\bar{a_2}&=-\bar{a_1}\omega ^{\theta }\cos {(\omega \tau -\frac{\theta \pi }{2})},\\ \omega ^{2\theta }\sin {(\theta \pi )}&=\bar{a_1}\omega ^{\theta }\sin {(\omega \tau -\frac{\theta \pi }{2})}. \end{aligned} \end{aligned}$$

(2.18)

The above equation leads to a polynomial in $\omega$ as,

$$\begin{aligned} \begin{array}{lll} \omega ^{4\theta }-(\bar{a_1}^{2}-2\bar{a_2}\cos {(\theta \pi )})\omega ^{2\theta }+\bar{a_2}^{2}=0. \end{array} \end{aligned}$$

(2.19)

We consider two conditions as, P7.   $\bar{a_1}^{2}-2\bar{a_2}\cos {(\theta \pi )}<2\bar{a_2}$,   P8.   $\bar{a_1}^{2}-2\bar{a_2}\cos {(\theta \pi )}>2\bar{a_2}$. If P7 holds, then equation (2.19) has no positive roots.

Again if P8 holds, then also two inequalities $\bar{a_1}^{2}-2\bar{a_2}\cos {(\theta \pi )}>0$ and $(\bar{a_1}^{2}-2\bar{a_2}\cos {(\theta \pi )})^2-4\bar{a_2}^{2}>0$ satisfied. Therefore, Eq. (2.19) has two positive roots as follows

$$\begin{aligned} \omega _{\pm }=\left( {\frac{(\bar{a_1}^{2}-2\bar{a_2}\cos {(\theta \pi )})\pm \sqrt{(\bar{a_1}^{2}-2\bar{a_2}\cos {(\theta \pi )})^2-4\bar{a_2}^2}}{2}}\right) ^{\frac{1}{2\theta }}. \end{aligned}$$

(2.20)

From the first equation of (2.18) we can rearrange it as,

$$\begin{aligned} \tau _n^{\pm }=&\frac{1}{\omega _{\pm }}\left[ \arccos \left( \frac{\omega _\pm ^{2\theta }\cos {(\theta \pi )}+\bar{a_2}}{-\bar{a_1}\omega _\pm ^{\theta }}\right) +\frac{\theta \pi }{2}+2n\pi \right] ,\\ &\qquad\qquad n=0,1,2,... \end{aligned}$$

(2.21)

Similar analysis as section 2.1 leads to few conclusions if P8 satisfied. These are

• (i) $\lambda =i \omega (\omega >0)$ is a simple root of (2.16),

• (ii) the transversality condition hold $(\frac{d(Re\lambda )}{d\tau })^{-1}|_{\lambda =i\omega _{+},\tau = \tau _n^{+}}>0$ and $(\frac{d(Re\lambda )}{d\tau })^{-1}|_{\lambda =i\omega _{-},\tau = \tau _n^{-}}<0$,

• (iii) since $\omega _{-}<\omega _{+}$, $\tau _{n+1}^{+}-\tau _{n}^{+}=\frac{2\pi }{\omega _{+}}<\frac{2\pi }{\omega _{-}}=\tau _{n+1}^{-}-\tau _{n}^{-}$ for $n=0,1,2,...$, there exists a positive integer $\bar{k}$ which makes the following inequality in group formed: $0<\tau _0^{+}<\tau _0^{-}<\tau _1^{+}<\tau _1^{-}<...<\tau _{\bar{k}}^{+}<\tau _{\bar{k}+1}^{+}<\tau _{\bar{k}}^{-}$.

Thus, two sets $T^{+}=[0,\tau _0^{+})\cup (\tau _0^{-},\tau _1^{+})...\cup (\tau _{\bar{k}-1}^{-},\tau _{\bar{k}}^{+})$ and $T^{-}=(\tau _0^{+},\tau _0^{-})\cup (\tau _1^{+},\tau _1^{-})...\cup (\tau _{\bar{k}-1}^{+},\tau _{\bar{k}-1}^{-})\cup (\tau _{\bar{k}}^{+},+\infty )$ are respectively determined for the stable and unstable state of the system. For $\tau \in T^{+}$, all the roots of the characteristic Eq. (2.16) have negative real parts. While for $\tau \in T^{-}$, the Eq. (2.16) has at least one root with a positive real part.

From the above content, we can conclude the results as follows.

Theorem 2.8

The following statements are true for system (2.1):

• 1. If P7 hold, then coexisting equilibrium of system (2.1) is locally asymptotically stable for $\tau \ge 0$.

• 2. If P8 hold, then there exists positive integer $\bar{k}$ such that the coexisting equilibrium point $({\bar{x}}^*,{\bar{y}}^*)$ switches $\bar{k}$ times from stability to instability and back to stability, i.e., $({\bar{x}}^*,{\bar{y}}^*)$ is locally asymptotically stable for $\tau \in T^{+}$ and unstable for $\tau \in T^{-}$.

2.3 The impacts of harvesting

This section is devoted to discussing the impacts of harvesting on system (2.1). Here, the condition of existence of the coexisting equilibrium $0< E_1 <r\left( 1-\frac{\bar{x}^{*}}{k}\right)$ and $0< E_2< \frac{ps}{q}-s_0$ must hold. We shall describe the change of equilibrium component with respect to an individual or both harvesting as follows.

Predator harvesting: For this case $E_1=0$ leads the positive equilibrium point of system (2.1) as $({\bar{x}}^*,{\bar{y}}^*)$, where ${\bar{x}}^*=\frac{s_0+E_2}{ps-q(s_0+E_2)}$ and ${\bar{y}}^*=\frac{1+q{\bar{x}}^*}{p} \left[ r(1-\frac{{\bar{x}}^*}{k}) \right]$. It is observed that both ${\bar{x}}^*$ and ${\bar{y}}^*$ are continuously differentiable function of $E_2$. Then, we get

$$\begin{aligned}{} & {} \frac{d{\bar{x}}^*}{dE_2}=\frac{ps}{\{ps-q(s_0+E_2)\}^2}>0, \\[5pt] & {} \quad \frac{d{\bar{y}}^*}{dE_2}=\frac{r}{p}\left( q-\frac{1+2{\bar{x}}^*q}{k}\right) \frac{d{\bar{x}}^*}{dE_2} >or<0 \end{aligned}$$

according as $k-\frac{1}{q}>$or$<2{\bar{x}}^*$.

Therefore, when $E_2$ increases ${\bar{x}}^*$ monotonically increases. But, ${\bar{y}}^*$ monotonically increases or decreases according as $k-\frac{1}{q}>$or$<2{\bar{x}}^*$. If we increase the effort of harvesting, prey biomass will increase, whereas predator biomass will conditionally increase or decrease. Predator biomass will increase or decrease when the difference between carrying capacity and the inverse of the half-saturation constant of prey species is greater or less than double of equilibrium component ${\bar{x}}^*$.

Prey harvesting: For $E_2=0$, the coexisting equilibrium point of the system (2.1) is given by $({\bar{x}}^*,{\bar{y}}^*)$, where ${\bar{x}}^*=\frac{s_0}{ps-qs_0}$ and ${\bar{y}}^*=\frac{1+q{\bar{x}}^*}{p} \left[ r(1-\frac{{\bar{x}}^*}{k})-E_1 \right]$. It is obvious that ${\bar{x}}^*$ and ${\bar{y}}^*$ are continuously differentiable with respect to $E_1$. Then we obtain

$$\begin{aligned} \frac{d{\bar{x}}^*}{dE_1}=0,~~~\frac{d{\bar{y}}^*}{dE_1}=-\frac{1+q{\bar{x}}^*}{p}<0. \end{aligned}$$

Hence, when $E_2$ increase then ${\bar{x}}^*$ remains unchanged while ${\bar{y}}^*$ decreases. Thus when prey harvesting increases, the density of prey remains unchanged, whereas the predator density will decrease.

Both prey and predator harvesting: When both $E_1E_2\ne 0$, then both ${\bar{x}}^*$ and ${\bar{y}}^*$ are continuously differentiable function of $E_1$ and $E_2$. By partial differentiation, we get

$$\begin{aligned}{} & {} \frac{\partial {\bar{x}}^*}{ \partial E_1}=0,\frac{\partial {\bar{y}}^*}{ \partial E_1}=-\frac{1+q{\bar{x}}^*}{p}<0 \\{} & {} \frac{\partial {\bar{x}}^*}{ \partial E_2}=\frac{ps}{\{ps-q(s_0+E_2)\}^2}>0,\\ &\frac{\partial {\bar{y}}^*}{ \partial E_2}=\frac{r}{p}\left( q-\frac{1+2{\bar{x}}^*q}{k}\right) \frac{\partial {\bar{x}}^*}{\partial E_2} >or<0 \end{aligned}$$

according as $k-\frac{1}{q}>$or$<2{\bar{x}}^*$.

Thus prey density remains unchanged, and predator density goes towards extinction when effort $E_1$ increases. Again, when $E_2$ increases, prey density increases, but predator density will increase or decrease according to the difference in carrying capacity and inverse of half-saturation of prey species greater or less than double of equilibrium component ${\bar{x}}^*$.

3 Numerical simulation

All simulations on analytical results are done with the help of MATLAB. Also, the predictor-corrector scheme is used to plot time series.

3.1 Without harvesting

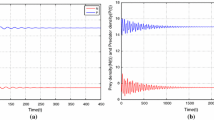
In this section, we will describe the dynamics of the unharvested system (2.2). First, we focus on the dynamical nature of the system (2.2) for $\theta =1$. We consider the initial condition $x(t)=1,y(t)=3,t\in [-\tau ,0)$. For the parameter set $r=2,k=15,p=0.5,q=0.01,s=0.5,$and $s_0=0.8$ the equilibrium point $E^*$ is unstable when $\theta =1$ (Fig. 1(i)) and asymptotically stable when $\theta =0.9$ (Fig. 1(ii)).

Fig. 1

Effect of fractional order in unexploited dynamics (2.2) for the parameter set $r=2,k=15,p=0.5,q=0.01,s=0.5,s_0=0.8, \tau =1.3$, becomes (i) unstable for $\theta =1$, and (ii) locally asymptotically stable for $\theta =0.9$

Moreover, the delay is also affected by $\theta$. Also for same parameter set we observe that, for $\tau \in [0,\tau _0^{+})\cup (\tau _0^{-},\tau _1^{+})=[0,1.17)\cup (5.23,5.86)$ system is asymptotically stable and unstable for $\tau >5.86$. Thus, one stability switching occur. We observe from Table  1 that switching numbers varies as $\theta$ changes. These are also shown in Fig. 2. The colored region is the region of stability concerning fractional order $\theta$. The region is decreasing with $\theta$.

Fig. 2

Time delays $\tau _n^{\pm }$ and number of stability switching is effected by the fractional order $\theta$ for the parameter set $r=2,k=15,p=0.5,q=0.01,s=0.5,s_0=0.8, E_1=0, E_2=0, \theta \in [0.88,1]$

Table 1 The delay parameter value $\tau _n^{\pm }$ corresponding to different $\theta$ of system (2.2) is listed. The corresponding parameter set is $r=2,k=15,p=0.5,q=0.01,s=0.5,s_0=0.8, E_1=0, E_2=0, \theta \in [0.88,1]$

Again in Fig. 2, if delay $\tau$ start from $[\tau _0^{+}(1),\tau _0^{+}(0)]=[1.17,2.31]$ on the $\tau _n^{\pm }-$axis and we increase the fractional order $(\theta )$ then stable region enters into the unstable region after crossing critical fractional order (at which order changes stable to unstable). Thus, we show fractional order has a destabilizing effect. From an ecological point of view, when fractional order $\theta$ increases, the carrying memory of the prey-predator will decrease in the neighbourhood of $\theta =1$. There is no carrying memory for $\theta =1$. When $\theta =0.88$, prey species carry a fear of the predator’s attacking place and time as a memory. Similarly, predators also wait for prey species’ movement, which they observed before. Both prey and predator awareness are very high when fractional order quantity is less in numeric value. Thus, the stability region is high for less fractional order where both the species consist of highly carrying memory. Hence, the time delay $\tau$ and the number of switching is affected by fractional order $\theta$. As per example, we are considering the population of zebra and lion, then the survival of the zebra depends on the carrying memory of both species. But, when the carrying memory of both species decreases, then the survival rate of zebra decreases. Thus, the numerical simulation is consistent with the real-life phenomenon.

3.2 With harvesting

Any ecological system of interacting species is strongly impacted by harvesting. The coexisting population’s long-term stationary biomass may be unstable and, eventually, become extinct depending on the trophic level at which harvesting is carried on. However, most ecological models of species interacting over time are examined using delay as a control parameter. We should consider harvesting effort as a control parameter to regulate the system because time delay is an inherent feature and varies on a very slow time scale, especially for harvested systems. With this motivation, we will examine the effects of harvesting on the delayed fractional order system.

3.2.1 Predator harvesting

Using numerical simulation, we validate the findings in this section for predator harvesting only (i.e., $E_1=0$). We can take the parameter set as $r=2,k=30,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9,E_1=0,E_2\in [0,0.38]$, where $k-\frac{1}{q}>2{\bar{x}}^*$. The effects of $E_2$ on the positive equilibrium point and time delay are depicted in Figs. 3 and 4, respectively. In Fig. 4, the stable region shrinks as $E_2$ rises, particularly given that one switch for $E_2=0.38$ and eight switching for $E_2=0$. Thus, we can say that the parameter $E_2$ impacts the stability switching times. The values of $\tau _n^{\pm }$ with $E_2=0$ and $E_2=0.38$ are shown in Table 2 for the convenience of discussion. Moreover, we note that the simulations are happening for fixed carrying memory $\theta =0.9$. It is implied that when the predator equilibrium increases with harvesting effort for a fixed memory, the stability region of the static balance will decrease with such effort. Again in Fig. 4, if delay $\tau$ start from $[\tau _0^{+}(0.38),\tau _0^{+}(0)]=[1.67,2.83]$ on the $\tau _n^{\pm }-$ axis and we increase the harvesting effort, the equilibrium point shifts from a stable to an unstable region after crossing the critical effort. Thus, harvesting effort has a destabilizing effect.

Table 2 The delay parameter value $\tau _n^{\pm }$ corresponding to different predator harvesting effort $E_2$ of system (2.1) are listed for the set $r=2,k=30,p=0.5,q=0.1,s=0.5, s_0=0.8,\theta =0.9,E_1=0$

Fig. 3

Equilibrium component ${\bar{x}}^*$ and ${\bar{y}}^*$ are effected by the harvesting effort $E_2$ for the parameter set $r=2,k=30,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9,E_1=0,E_2\in [0,0.38],k-\frac{1}{q}>2{\bar{x}}^*$

Fig. 4

Time delays $\tau _n^{\pm }$ and number of stability switching is affected by the predator harvesting effort $E_2$ for the parameter set $r=2,k=30,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9, E_1=0, E_2\in [0,0.38],k-\frac{1}{q}>2{\bar{x}}^*$

For another parameter set $r=2,k=15,p=0.5,q=0.01,s=0.5,s_0=0.8,\theta =0.9,E_1=0,E_2\in [0,1.8]$, we can discuss the impact of harvesting effort $E_2$ also. But, where the condition $k-\frac{1}{q}<2{\bar{x}}^*$ satisfied, which is discussed elaborately in the section 2.3. Figures 5 and 6 showed the impact of harvesting effort $E_2$ on the coexisting equilibrium point and time delay, respectively. It is noticed that in Fig. 5, the predator equilibrium decreases, and in Fig. 6, the stable region decreases with the increasing harvesting effort $E_2$. There exists two switching for $E_2=0$ and no switching for $E_2=1.8$. Thus, we can say that number of stability switching is affected by the harvesting effort $E_2$. In Fig. 6, if we take the delay parameter $\tau$ within the range $[\tau _0^{+}(1.8),\tau _0^{+}(0)]=[0.83,1.94]$ on the $\tau _n^{\pm }-$axis and increases the harvesting effort $E_2$, then the stable region enters into the unstable region after crossing a critical effort. The system again shows a destabilizing effect for predator harvesting.

Fig. 5

Equilibrium component ${\bar{x}}^*$ and ${\bar{y}}^*$ are effected by the harvesting effort $E_2$ for the parameter set $r=2,k=15,p=0.5,q=0.01,s=0.5,s_0=0.8,E_1=0,E_2\in [0,1.8],k-\frac{1}{q}<2{\bar{x}}^*$

Fig. 6

Time delays $\tau _n^{\pm }$ and number of stability switching is affected by the predator harvesting effort $E_2$ for the parameter set $r=2,k=15,p=0.5,q=0.01,s=0.5,s_0=0.8,\theta =0.9, E_1=0, E_2\in [0,1.8],k-\frac{1}{q}<2{\bar{x}}^*$

From Fig. 4 and Fig. 6, we conclude that switching is comparatively greater in the first than the second. In the first case, $k-\frac{1}{q}>2{\bar{x}}^*$ is satisfied while $k-\frac{1}{q}<2{\bar{x}}^*$ is satisfied for the latter. The carrying memory is fixed as $\theta =0.9$ in both cases. In Fig. 7, we take the parameter set, which is the same as in Fig. 6, but here $\theta \in [0.9,0.99]$ is varied. We show the simultaneous effect of harvesting effort $E_2$ and fractional order $\theta$ on the delay surface $\tau =\tau _n^{\pm }(E_2,\theta )$. In Fig. 2, we got the stable region corresponding to $\theta =1$. But if we give a small harvesting effort, $E_2$ cannot find a feasible delay surface. Thus, the delay surface in Fig. 7 will be found in the neighbourhood of $\theta =1$. The cross-section corresponding to $\theta =0.9$ and $\theta =0.93$ gives Figs. 6 and 8, respectively. These two figures show that the number of switching regions decreases in Fig. 7 whenever fractional order $\theta$ tends to 0.99. As an example, we may consider small fish and piranha populations. If both small fish and piranha carry a specific memory, the small fish is afraid of attacking the situation of piranha, and the piranha waits to catch the small fish. When the piranha are captured from their biomass system, and the memory of both species loses, the survival rate of small fish decreases. The numerical simulations accurately reflect reality. As a result, we can conclude that system (2.1) can achieve a stable status by appropriately adjusting the harvesting effort $E_2$.

Fig. 7

Surface of time delays $\tau =\tau _n^{\pm }$ and number of stability switching is affected by the predator harvesting effort $E_2$ and fractional order $\theta$ for the parameter set $r=2,k=15,p=0.5,q=0.01,s=0.5,s_0=0.8,\theta \in [0.9,0.99], E_1=0, E_2\in [0,1.8],k-\frac{1}{q}<2{\bar{x}}^*$

Fig. 8

Time delays $\tau _n^{\pm }$ and number of stability switching is affected by the predator harvesting effort $E_2$ for the parameter set $r=2,k=15,p=0.5,q=0.01,s=0.5,s_0=0.8,\theta =0.93, E_1=0, E_2\in [0,1.8],k-\frac{1}{q}<2{\bar{x}}^*$

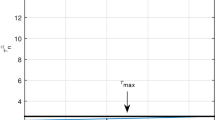
Again, we consider another parameter set $r=0.5,k=10,p=0.5,q=0.01,s=0.5,s_0=0.8,\theta =0.93,E_1=0,E_2\in [0,1.4]$. Figure 9 reflects the corresponding numerical simulation. The region between two red lines $\tau _{min}=2.88$ and $\tau _{max}=3.28$ shows the harvesting-induced switching in the presence of fixed memory $\theta =0.93$. The region between $E_2-$axis and the curve $\tau =\tau _0^{+}(E_2)$ is the region of stability. Thus, the region enclosed by $\tau _{min}=2.88$, $\tau =\tau _0^{+}(E_2)$, $\tau _{max}=3.28$ and $\tau _n^{\pm }-$ axis is stable region. If the delay $\tau$ starts from $[\tau _{min},\tau _{max}]=[2.88,3.28]$ on the $\tau _n^{\pm }-$axis, then the stable state of the system moves to an unstable region after crossing the critical effort and further increase of effort fall into a stable state. Now, ecologically we can interpret that when a stable system moves to an unstable state, the appropriate harvesting of predator species leads the system back to a stable state in the presence of fixed carrying memory.

Fig. 9

The harvesting induced stability switching is depicted for parameter set $r=0.5,k=10,p=0.5,q=0.01,s=0.5,s_0=0.8,\theta =0.93, E_1=0,E_2\in [0,1.4]$

3.2.2 Prey harvesting

In this section, we will discuss the dynamical nature of the system (2.1) when prey species is harvested (i.e. $E_2=0$). For validating the above theoretical results, take a parameter set as $r=2,k=30,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9, E_2=0$ and $E_1\in [0,1.6]$. In Figs. 10 and 11, we show that the prey harvesting effort affects the equilibrium point and delay. It is implied from Fig. 10 that for a fixed carrying memory $\theta =0.9$, the prey equilibrium component is constant, whereas the predator equilibrium component decreases with increasing harvesting effort $E_1$. In Fig. 11, we observe all the curves $\tau =\tau _n^{\pm }(E_1)$ increases with the increase of $E_1$. The coloured region between $E_1-$axis and $\tau =\tau _0^{+}(E_1)$ is the stability region that increases with increasing effort $E_1$, and other coloured regions decrease with the effort $E_1$. The values $\tau _n^{\pm }$ with $E_1=0$ and $E_1=1.6$ are shown in Table 3 for convenience of discussion. We notice that eight switchings occur for $E_1=0$ and no switching occurs for $E_1=1.6$. These discussions are made only for the carrying memory $\theta =0.9$. Thus, for fixed memory, prey harvesting affects the stability switching of the system (2.1).

Fig. 10

Equilibrium component ${\bar{x}}^*$ and ${\bar{y}}^*$ are effected by the harvesting effort $E_1$ for the parameter set $r=2,k=30,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9,E_1\in [0,1.6],E_2=0$

Fig. 11

Time delays $\tau _n^{\pm }$ and number of stability switching is affected by the predator harvesting effort $E_1$ for the parameter set $r=2,k=30,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9, E_1\in [0,1.6], E_2=0$

Again in Fig. 11, if delay $\tau$ start from $[\tau _0^{+}(0),\tau _0^{-}(0)]=[2.83,3.81]$ on the $\tau _n^{\pm }-$axis and we increase the harvesting effort, then the system shifts from the unstable region to the stable region after crossing the critical effort (at which effort changes unstable to stable). Thus, we show prey harvesting effort has a stabilizing effect. From an ecological point of view, the stable region between $E_1-$axis and $\tau =\tau _0^{+}(E_1)$ can express as when the matured time of prey species is very short, then for fixed memory of both prey and predator species stability region increases with the appropriate effort of prey harvesting. But when the matured time duration of prey species is high, for the fixed carrying memory of both species, then the region of stability decreases. For example, the striped bass is among the main predators of African killifish. Killifish grows fast; hence they have a short maturation time. If killifish and striped bass have a fixed carrying memory, then appropriate harvesting of killifish increases the stable region. In order to, we may consider the population of rabbits and foxes as prey and predator, respectively. But, the maturation delay of prey species is comparatively higher from the above example. When rabbits and foxes utilize the fixed carrying memory, suitable prey harvesting decreases the region of the static balance of both rabbit-fox systems.

Fig. 12

Surface of time delays $\tau =\tau _n^{\pm }$ and the number of stability switching is affected by the predator harvesting effort $E_1$ and fractional order $\theta$ for the parameter set $r=2,k=30,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta \in [0.9,0.99], E_1\in [0,1.6], E_2=0$

Fig. 13

Time delays $\tau _n^{\pm }$ and number of stability switching is affected by the predator harvesting effort $E_1$ for the parameter set $r=2,k=30,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.93, E_1\in [0,1.6], E_2=0$

In Fig. 12, we take the same parameter set, as in Fig. 11, but only one parameter $\theta \in [0.9,0.99]$ is added and varied. Here, we have taken the delay surface $\tau =\tau _n^{\pm }(E_1,\theta )$, which consists of the simultaneous effect of both prey harvesting effort $E_1$ and fractional order $\theta$. We observe from Fig. 12, that when both the species are not carrying any memory (i.e., $\theta =1$), the system (2.1) does not give any feasible delay surface for the small change of effort. Thus, we have depicted our figure in the neighbourhood of $\theta =1$. The cross-section is taken in the Figs. 11 and 13 corresponding to $\theta =0.9$ and $\theta =0.93$, respectively. Figures 11 and 13 shows that the number of stability switching regions decreases with the decreasing carrying memory $\theta$ when the prey harvesting is still effective. As an example, we may consider the tuna and shark fish populations. Large shark fish highly predate tuna fish. Tuna fish accounted for the attacking behavior of large shark fish carrying in their memory. Similarly, large shark fish are aware of the current position of tuna fish with the help of carrying memory observed before. If we harvest the tuna fish and if gradually both fish lose their carrying memory, their stability switching region will decrease. Thus, we can conclude that appropriately harvesting prey species makes the system less sensitive when they put the memory information outside.

Table 3 The delay parameter value $\tau _n^{\pm }$ corresponding to different prey harvesting effort $E_1$ of system (2.1) are listed for the set $r=2,k=30,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9, E_1\in [0,1.6], E_2=0$

Fig. 14

Planer equilibrium component ${\bar{x}}^*$ and ${\bar{y}}^*$ are effected by the both harvesting effort $E_1$ and $E_2$ for the parameter set $r=2,k=15,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9,E_1\in [0,0.9],E_2\in [0,0.52]$

Fig. 15

Surface of time delays $\tau =\tau _n^{\pm }$ and number of stability switching is affected by the predator harvesting effort $E_1$ and prey harvesting effort $E_2$ for the parameter set $r=2,k=15,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9, E_1\in [0,0.9], E_2\in [0,0.52]$

Fig. 16

Change of static balance for different simultaneous harvesting efforts are shown for the parameter set $r=2,k=15,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9,\tau =1.2,$ (a) $E_1=0.1, E_2=0.6$, (b) $E_1=0.5, E_2=0.2$

Fig. 17

For fixed memory, the stable and unstable regions are shown for both prey-predator harvesting efforts. Corresponding parameter set is $r=2,k=15,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9,\tau =1.2, E_1\in [0,0.6], E_2\in [0,1]$

3.2.3 Simultaneous harvesting

In this portion, we will emphasize the dynamical change of the system (2.1) with both prey and predator effort (i.e., $E_1\ne 0, E_2\ne 0$). We can take the parameter set as $r=2,k=15,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9,E_1\in [0,0.9],E_2\in [0,0.52]$. It is observed that the simultaneous effects of $E_1$ and $E_2$ exist on the surface of the component of equilibrium $({\bar{x}}^*,{\bar{y}}^*)$ and on the delay surface and on delay surface which is depicted in Figs. 14 and 15 respectively. From Fig. 14, we show that the surface ${\bar{x}}^*$ incline and the surface ${\bar{y}}^*$ decline in the normal direction of $(E_1,E_2)$ plane for simultaneous effort. The Fig. 15 depicts that all delay surface $\tau =\tau _n^{\pm }(E_1,E_2)$ corresponds to a fixed fractional order $\theta =0.9$.

Again, we consider the parameter set $r=2,k=15,p=0.5,q=0.1,s=0.5,s_0=0.8,\theta =0.9,$ and $\tau =1.2$. We are taking the initial condition $x(t)=1,y(t)=3,t\in [-\tau ,0)$. For showing the impact of harvesting, the effort $E_1=0.1, E_2=0.6$ gives the unstable static balance, which is depicted in Fig. 16(i). We obtain locally asymptotically stable behavior for another effort, $E_1=0.5, E_2=0.2$ in Fig. 16(ii).

Figure 17 shows that for delay $\tau =1.2$ and the range of harvesting $(E_1,E_2)$ the system (2.1)is locally asymptotically stable. Based on Figs. 16 and 17, we know that the proper harvesting of prey and predator species makes the system (2.1) stable. From the above discussion, we can conclude that harvesting has an important role in surviving prey and predator species.

3.3 Maximum sustainable yield

The interior equilibrium point is invariant of the fractional operator. For predator harvesting it is given by $({\bar{x}}^*,{\bar{y}}^*)=\left( \frac{s_0+E_2}{p s-q(s_0+E_2)},\frac{ s r [(s_0+E_2)(1+k q)-k p s]}{k [p s - q (s_0+E_2)]^2 }\right)$.

The yield at this equilibrium point is given by

$$\begin{aligned} Y(E_2)&=E_2 {\bar{y}}^*\end{aligned}$$

(3.1)

$$\begin{aligned}&=\frac{ E_2 s r [(s_0+E_2)(1+k q)-k p s]}{k [p s - q (s_0+E_2)]^2}. \end{aligned}$$

(3.2)

Correspondingly, the maximum yield is attained at,

$$\begin{aligned} E_2^{MSY}=\frac{(p s - q s_0) (k p s - s_0 - k q s_0)}{2 p s + k p q s - q s_0 - k q^2 s_0}. \end{aligned}$$

In Fig. 18, the species coexist for the effort range $E_2\in$ (0,1.4). Here $E^{MSY}_2=0.76$ is shown in the vertical black line, and we assume that it cuts the $\tau _0^+(E_2)$ curve at $(E_2^{MSY},\tau ^*)$. Referring to the same figure, we see that

• (i) for $\tau <\tau ^*$, the unexploited system is stable. Moreover, harvesting at MSY produces a stable stock.

• (ii) for $\tau \in (\tau ^*,\tau _0^+(0))$ the coexisting equilibrium for the unharvested system is stable, but harvesting at MSY yields an unstable stock.

• (iii) For any further increase in delay ($\tau >\tau _0^+(0)$), in an unharvested state, the coexisting equilibrium is unstable. Furthermore, harvesting at MSY cannot yield a stable stock.

Although $E_2^{MSY}$ is invariant of the fractional order ($\theta$), but $\tau _n^\pm$ is not. However, change in the fractional order gives similar dynamics to the above three observations. So yield at MSY cannot guarantee stable stock when the unharvested system is stable. However, it is possible if the delay is small. For large delay values harvesting at MSY can never produce a stable stock.

Fig. 18

MSY corresponding to the parameter set $r=0.5,k=10,p=0.5,q=0.01,s=0.5,s_0=0.8,\theta =0.93,E_1=0,E_2\in [0,1.4]$

4 Discussion and conclusion

This paper describes a delayed fractional-order prey-predator model with Holling type-II functional response and harvesting. The main analysis is carried on by varying the fractional order, time delay, and harvesting as the control parameter. First, we discuss the unexploited dynamics of the fractional order prey-predator model with delay, mainly the system (2.2). We observe that fractional order affects the time delay and the number of stability switching of the system (2.2). The theoretical results and analysis are discussed without harvesting, with harvesting and the impact of harvesting in Sections 2.1, 2.2, and 2.3, respectively.

Javidi and Nyamoradi [16], have investigated a fractional-order prey-predator model with harvesting. But they have not emphasized much on the dynamics of the system as harvesting effort is varied. Mandal et al. [26], also conducted various numerical simulations on the fractional-order system and demonstrated that increasing fractional order produces a stable limit cycle. However, both of these studies have not associated time delay. The impact of varying delays on the fractional-order system has been inspected by many researchers [9, 35, 43]. To our knowledge, Song et al. [40] is the first to incorporate harvesting into such a delayed system. Their analysis shows that decreasing fractional order($\theta$) or increasing harvesting effort can stabilize the system.

Next, we discuss the delayed fractional-order prey-predator model with harvesting, mainly the system (2.1). We have yet to focus much on local stability. Since the maturation time of different species is variable, a discussion is needed to generalize the time delay. Few are described in terms of local stability for the validation. But the central perspective of our simulation result is how the maturation time is affected by fractional-order, individual harvesting, or simultaneous harvesting. In Sect. 3.1, we observe that fractional order affects the static balance of the equilibrium point, time delay, and the number of stability switches. Again, for the fixed delay, it has a destabilizing effect when the carrying memory decreases, i.e., fractional-order $\theta$ increases. As for the impact of harvesting on prey and predator, we get the following consequences in Sect. 3.2. In two cases, capturing predator species only induces fixed and variable carrying memory. For the first case, the stable state becomes stable(unstable) for a small(large) time delay by controlling the harvesting effort $E_2$. The harvesting effort $E_2$ has a destabilizing effect. Also, the predator harvesting effort causes the transformation of a stable to a stable state via an unstable state for a fixed memory. This implies that predator harvesting induces stability switching. But, the second case shows that a fixed delay, with the change of carrying memory, affects the number of switching regions when predator harvesting effort induces. An important observation is made for predator-induced harvesting that when the carrying capacity is greater(or less) from a critical value, then the number of switching regions increases(or decreases) for fixed carrying memory (see Figs. 4, 6). Again, the capturing of prey species only described corresponds to fixed and variable carrying memory in two ways. The first shows that for the small time delay, the stable status on the unharvested system remains stable with increased prey capture only. But the larger time delay on the unharvested system with unstable mode becomes stable for inducing the harvesting effort. Thus, prey harvesting has a stabilizing effect. But, the second case shows that a fixed delay with a fixed carrying memory affects the number of switching regions when prey harvesting effort induces. While prey and predator are harvested, the system can move into a stable(unstable) from an unstable(stable) state with the control of appropriate harvesting effort $E_1$ and $E_2$. In addition, the harvesting effort $E_1$ and $E_2$ impact the number of stability switches. The concept of MSY is also implemented for predator harvesting. We observe that harvesting at MSY can produce a stable stock only for a small delay. Moreover, whether the unexploited system is stable cannot guarantee the stock to be stable at MSY. All of the results have profoundly affected surviving prey and predator. The simulated result follows a real-life phenomenon and may help to develop ecological theories relating to the predator–prey system.