Introduction

Prey-predator models are very useful for acquiring the knowledge of dynamics of interacting populations of prey-predators and hence the prey-predator model acts a key role in both theoretical as well as experimental ecology and mathematical ecology. This type of ecological model will go forward as one of the key ideas due to its importance and simplicity (see Kar and Jana 2012; Fussmann et al. 2005; Chakraborty et al. 2012a; Mishra et al. 2016; Sahoo et al. 2016; Shaikh et al. 2018; Foutayeni et al. 2020; Khatua et al. 2020; Thakur et al. 2020). In the last few decades, these prey-predator theory have progressed very much but still there are lots of mathematical and ecological problems that can be studied through this tool. The dynamics of a prey-predator model are influenced by many constituents, e.g., the densities of prey and predators, harvesting of preys or predators or both etc. But the proposed model should be possible easiest biologically applicable form, even if the dynamics of the model may suggest difficult behaviour, e.g., stationary oscillations of the sizes of population, or suggest the dependency on some parameters, e.g., the “paradox of enrichment” (see for details Rosenzweig 1971) which indicates that increasing in the carrying capacity of the prey population conducts either to increase in size of the predator but not size of prey population or perniciously very much increase of predator population which is responsible for the extinction of prey populations. The kind of discussion observed in the articles [see (Berryman 1992; Jensen et al. 2005)] and in the book Arditi et al. 2012 renders rich inspiration for the study of the mathematical modelling on which common ecological models are constructed through the ordinary differential equations.

The functional response in pry-predator model is commonly defined as the number of preys that are predated by an individual predator in unit time. Functional response of a predator population acts a significant role in ecology (Berryman 1992). Usually two types of functional responses considered in mathematical ecology: prey-dependent and predator-dependent functional responses. In the case of prey-dependent functional response, we accept that the number of prey eaten by a single predator in unit time depends on the number of preys or density of the prey only, for example, Holling Types I–III (see Holling 1959). Therefore, this type of functional response is the function of prey density only. The predator-dependent functional response assumes the number of preys eaten by a single predator in unit time which depends on the density of prey and predator both, e.g., DeAngelis functional response (Mesterton 1996). Therefore, this type of functional response is the function of both the prey and predator populations. In this type of functional response, it is often called ratio-dependent because of it is the function of ratio of the prey population to the predator population (Arditi et al. 2012; Berryman 1992; Kumar et al. 2018),

Food is necessary to survive animals in the universe. Harvesting is nothing but the away of collecting or consuming food. But, we cannot continue to harvest fishes from the river or sea quicker than the unexhausted fishes can substitute their removed companions. If we do so then the sustainable of fish will damage and we will not get fish in the future. Similarly, we cannot keep harvesting farming crops if the quality and quantity of soil fatigues or sources of water become inadequate. In addition, we cannot preserve the diversity of the nature if we continue to drive species to extinction. To maintain sustainable food we should harvest scientifically. We commonly considered three types of harvesting in mathematical ecology: constant rate harvesting (Chakraborty et al. 2012b; Huang et al. 2013), proportional harvesting (Leard et al. 2008; Lenzini et al. 2010; Israel et al. 2015), and nonlinear harvesting (Clark 1979; Das et al. 2009; Jana et al. 2015; Agmour et al. 2020).

System of ordinary differential equations models for the interactions between species (e.g., prey-predator) is one of the classical approaches of mathematical ecology. In recent, researchers are interested in formulating mathematical models with the help of fractional-order differential equations as it is a magnificent tool for description of hereditary properties and also memory of several biological elements and it has very close relations to the fractals. These are the principal benefit of a mathematical model by fractional-order derivatives in analogy with models based on the classical ordinary-order derivatives in which such special properties are neglected. Therefore fractional-order differentiation is more realistic than ordinary differentiation. The fractional-order models have earned popularity after some famous books on fractional-order differential equations (Podlubny 1999; Miller et al. 1993; Hilfer 2000; Diethelm et al. 2003; Kilbas et al. 2006; Petras 2011). Fractional-order differential equations can be defined several ways. The most useful and popular definitions are in the sense of Riemann-Liouville, Grüunwald-Letnikov and the Caputo definitions. The Caputo definition is most popular and operable definition in mathematical ecology as in this definition the initial conditions are uttered in a similar fashion as we use for integer-order differentiations. There are limited theories for the mathematical model through fractional-order derivatives to analyze their dynamical behaviors (Delavai et al. 2012; Deshpande et al. 2017; Guo 2014; Hong Li et al. 2016; Liang et al. 2015; Li et al. 2010; Omar 2019a, b; Omar et al. 2019). In recent days, the linearization method, Lyapunov method and Lyapunov direct method (due to Lyapunov function) have proved to examine the stability of different stationary points of systems through fractional calculus.

Model formulation

We construct the following model in our present work:

$$\begin{aligned} \begin{aligned} \frac{dx}{dt}&= r \left( 1-\frac{x}{k}\right) x-\frac{axy}{1+bx}-q_1Ex \\ \frac{dy}{dt}&= \frac{maxy}{1+bx}-dy-\eta yz-q_2Ey \end{aligned} \end{aligned}$$
(2.1)

Here, x and y describe the biomass densities of prey and the predator population at the time t respectively. Here all the parameters used in the model (2.1), \(r,~k,~a,~b,~m,~d,~\eta ,~q_1,~q_2\), and E are taken as positive. In the proposed model, r symbolizes intrinsic growth rate of the prey; the environmental carrying capacity of the prey is denoted by k; the natural death rate of the predator is referred by d; a/b denotes the maximum number of the prey eaten by each individual predator in unit time and 1/b be the necessary density of prey population inhabited in environment to attain one half of that rate; m be conversion rate of biomass of the prey to the predator population referring the total number of newly born predators for each of prey captured by the predator. The term \(\frac{ax}{1+bx}\) refers to the Holling type II functional response (see Holling 1959) of the predator. Here, we consider harvesting on both the prey and predator populations. In this regard, it is considered that \(q_1\) and \(q_2\) be the catchability coefficients of prey and the predator respectively; the combined harvesting effort to yield both these populations be E. Natural enemies of predators (i.e. super-predator) are being eradicated from an ecosystem because of predation by a higher trophic levels (e.g. eagle is a super-predator for the population of rats in grassland) or human activities, viz, usage of pesticides, hunting, etc. In this paper, we assume that the predators takes away from the ecosystem owing to predation by the super-predators (the natural enemy of a predator) ( Mbava et al. (2016). For the simplicity of the model, we do not look at the super-predator as a separate state variable, instead we consider the population of super-predator exhibit in the ecosystem at constant density (z) and assume the predation rate of super-predator (to the natural enemy, predator, y) as \(\eta\). Note that \(q_1E\) and \(q_2E\) are the harvesting mortality rate of the prey and the predator respectively.

Fractional-order form of our proposed model (2.1) is followed by

$$\begin{aligned} \begin{aligned} {}_{t_0}D_t^{\alpha _1}x(t)&={\tilde{r}} x \left( 1-\frac{x}{{\tilde{k}}}\right) -\frac{{\tilde{a}}xy}{1+{\tilde{b}}x}-\tilde{q_1}{\tilde{E}}x, ~~x(t_0)=x_0>0 \\ {}_{t_0}D_t^{\alpha _2}y(t)&= \frac{{\tilde{m}}{\tilde{a}}xy}{1+{\tilde{b}}x}-{\tilde{d}}y-{\tilde{\eta }}zy-\tilde{q_2}{\tilde{E}}y,~~ y(t_0)=y_0>0 \end{aligned} \end{aligned}$$
(2.2)

Here, for \(i=1, 2\), \(\alpha _i\in (0,1)\), \({}_{t_0}D_t^{\alpha _i}\) are the fractional order derivatives in the sense of Caputo ( Podlubny 1999; Petras 2011). Here, we consider different fractional differentiations \(\alpha _1\) and \(\alpha _2\) for prey and the predators respectively as the memory of several species are different in general. Since the left-hand dimension of first and second equations of (2.2) are \({\text{time}}^{-\alpha _1}\), \({time}^{-\alpha _2}\), respectively, and the right-hand dimension is \({\text{time}}^{-1}\), we correct the dimensions of the system as

$$\begin{aligned} \begin{aligned} {}_{t_0}D_t^{\alpha _1}x(t)&={\tilde{r}}^{\alpha _1} x \left( 1-\frac{x}{{\tilde{k}}}\right) -\frac{{\tilde{a}}^{\alpha _1}xy}{1+{\tilde{b}}x}-\tilde{q_1}^{\alpha _1}{\tilde{E}}x, ~~x(t_0)=x_0>0 \\ {}_{t_0}D_t^{\alpha _2}y(t)&= \frac{{\tilde{m}}^{\alpha _2}{\tilde{a}}^{\alpha _1}xy}{1+{\tilde{b}}x}-{\tilde{d}}^{\alpha _2}y-{\tilde{\eta }}^{\alpha _2}zy-\tilde{q_2}^{\alpha _2}{\tilde{E}}y,~~ y(t_0)=y_0>0 \end{aligned} \end{aligned}$$
(2.3)

For simplicity in representing (2.3), we substitute \(r={\tilde{r}}^{\alpha _1}\), \(k={\tilde{k}}\), \(a={\tilde{a}}^{\alpha _1}\), \(b={\tilde{b}}\), \(q_1=\tilde{q_1}^{\alpha _1}\), \(E={\tilde{E}}\), \(m={\tilde{m}}^{\alpha _2}\), \(d={\tilde{d}}^{\alpha _2}\), \(\eta ={\tilde{\eta }}^{\alpha _2}\), \(q_2=\tilde{q_2}^{\alpha _2}\) and then the system (2.3) reduces as

$$\begin{aligned} \begin{aligned} {}_{t_0}D_t^{\alpha _1}x(t)&= r x \left( 1-\frac{x}{k}\right) -\frac{axy}{1+bx}-q_1Ex, ~~x(t_0)=x_0>0 \\ {}_{t_0}D_t^{\alpha _2}y(t)&= \frac{maxy}{1+bx}-dy-\eta yz-q_2Ey,~~y(t_0)=y_0>0 \end{aligned} \end{aligned}$$
(2.4)

The system (2.5) for different fractional differentiation is known as an incommensurate fractional-order system and if \(\alpha _1=\alpha _2=\alpha \in (0,1)\), then this type of fractional differentiation is known as a commensurate fractional-order system which is followed by

$$\begin{aligned} \begin{aligned} {}_{t_0}D_t^{\alpha }x(t)&= r x \left( 1-\frac{x}{k}\right) -\frac{axy}{1+bx}-q_1Ex ,~~x(t_0)=x_0>0 \\ {}_{t_0}D_t^{\alpha }y(t)&= \frac{maxy}{1+bx}-dy-\eta yz-q_2Ey,~~~~~y(t_0)=y_0>0 \end{aligned} \end{aligned}$$
(2.5)

The rest portion of the present work is prepared as follows: in “Some preliminaries”, we remember few important lemmas and theorems that help us to analyze our system. In “Dynamical behaviour of fractional order system”, we work out several equilibria of (2.5) and then by using these lemmas and theorem, we establish the non-negativity and boundedness of the solutions for our model system (2.5). The local and also global stability analysis of several equilibria are also discussed in “Dynamical behaviour of fractional order system”. Some numerical simulation works to confirm our analytical results are performed in the “Numerical simulations”. Finally, a brief discussion and conclusion are presented in “Conclusion and discussion”.

Some preliminaries

Here, we state some necessary definition, useful lemmas, and theorems for both types of commensurate and incommensurate fractional-order systems which help us to study the analytical results of our model.

Definition 3.1

(Petras 2011) The Caputo type fractional order derivative of \(\alpha >0\) order for the function \(f : { {C}}^n[t_0,\infty )\rightarrow {\mathbb {R}}\) may be defined and denoted by

$$\begin{aligned} {}_{t_0}D_t^{\alpha }f(t)=\frac{1}{\Gamma (n-\alpha )} \int _{t_0}^{t}\frac{f^{(n)}(\zeta )}{(t-\zeta )^{\alpha -n+1}}d\zeta \end{aligned}$$

where \({ {C}}^n[t_0,\infty )\) is a space of n times continuously differentiable functions on \([t_0,\infty )\), \(t> t_0\) and \(\Gamma (\cdot )\) be the Gamma function with \(n\in {\mathbb {Z}}^+\) (the set of all positive integers) such that \(n-1<\alpha <n\). Particularly, if \(0<\alpha <1\), the definition becomes

$$\begin{aligned} {}_{t_0}D_t^{\alpha }f(t)=\frac{1}{\Gamma (1-\alpha )} \int _{t_0}^{t}\frac{f'(\zeta )}{(t-\zeta )^{\alpha }}d\zeta \end{aligned}$$

Lemma 3.1

(Odibat et al. 2007) Let us assume that \(\alpha \in (0,1]\) and both the functions f(t) and its fractional derivative \({}_{t_0}D_t^{\alpha }f(t)\) be elements of the metric space C[a, b]. If for all, \(t \in [a,b]\), \({}_{t_0}D_t^{\alpha }f(t)\ge 0\) then the function f(t) is a monotone increasing, but the function is monotone decreasing if \({}_{t_0}D_t^{\alpha }f(t)\le0\) for all \(t\in [a,b]\).

Lemma 3.2

(Hong Li et al. 2016) Let us consider that \(x:[t_0,\infty )\rightarrow {\mathbb {R}}\) be continuous function and satisfies the following:

$$\begin{aligned} {}_{t_0}D_t^{\alpha }x(t)+\mu x(t)\le \nu ,~x(t_0)=x_0,~t_0\ge 0,~\mu , \nu \in {\mathbb {R}},~\mu \ne 0,~\text{ and }~\alpha \in (0,1) \end{aligned}$$

Then, we have the inequality:

$$\begin{aligned} x(t)\le \left( x_0-\frac{\nu }{\mu }\right) E_{\alpha }[-\mu (t-t_0)^{\alpha }]+\frac{\nu }{\mu } \end{aligned}$$

for all \(t\ge t_0\). Here \(E_{\alpha}\) is the Mittag-Lefflar function of one parameter.

Lemma 3.3

(Petras 2011) Assume the following fractional order system of the order \(\alpha \in (0,1]\)

$$\begin{aligned} {}_{t_0}D_t^{\alpha }x(t)=Mx,~~x(t_0)=x_0>0. \end{aligned}$$

where \(x\in {\mathbb {R}}^n\) and \(M\in {\mathbb {R}}^{n\times n}\). The system is said to be stable asymptotically iff \(|\arg (\lambda )|>\frac{\alpha \pi }{2}\) satisfy for each of the eigenvalues \(\lambda\) of the matrix M and the system is said to be stable only iff \(|\arg (\lambda )|\ge \frac{\alpha \pi }{2}\) for each of the eigenvalues of the matrix M with the eigenvalues satisfying the critical condition \(|\arg (\lambda )|=\frac{\alpha \pi }{2}\) must have geometric multiplicity one.

Lemma 3.4

(Petras 2011) Let us assume the fractional order system of the order \(\alpha \in (0,1]\)

$$\begin{aligned} {}_{t_0}D_t^{\alpha }x(t)=f(x),~~x(t_0)=x_0>0 \end{aligned}$$

where \(x\in {\mathbb {R}}^n\). A stationary point of the system is called to be locally asymptotically stable iff \(|\arg (\lambda _k)|>\frac{\alpha \pi }{2}\) for all eigenvalues \(\lambda _k~(k=1,2\ldots n)\) of Jacobian matrix \(J =\frac{\partial f}{\partial x}\) calculated at the corresponding stationary point.

Dynamical behaviour of fractional order system

Here, first we assume commensurate fractional-order system (2.5) by considering \(\alpha _1=\alpha _2=\alpha \in (0,1]\) in the incommensurate system (2.4).

Equilibria

We study the existence of the non-negative equilibria of the system (2.5). The system (2.5) possesses three possible equilibria which are (1) trivial equilibrium point \(E^0(0,0)\), (2) predator-free equilibrium point \(E^1(x^1,0)\) and (3) the interior equilibrium point \(E^*(x^*,y^*)\), where \(x^1=k(1-\frac{Eq_1}{r}),~ x^*=\frac{e}{a m-b e}\) and \(y^*=\frac{mrx^*(x^1-x^*)}{ke}\) with \(e=d+E q_2+\eta z\).

Predator free equilibrium point \(E^1\) exists if \(Eq_1<r\) and the interior equilibrium \(E^*\) exists if \(am>be\) and \(r> \frac{kq_1E(am-be)}{k(am-be)-e}\).

Existence and uniqueness of solutions

In this stage, we state and prove following lemma with the help of Li et al. (2010).

Lemma 4.1

Let us assume the following fractional order differential equation of the order of differentiation \(\alpha \in (0,1]\):

$$\begin{aligned} {}_{t_0}D_t^{\alpha }x(t)= f(t,x),~~x(t_0)=x_0>0 \end{aligned}$$
(4.1)

where \(f:[t_0,\infty )\times {\mathfrak {D}}\rightarrow {\mathbb {R}}^n, {\mathfrak {D}}\subset {\mathbb {R}}^n\) is a function. If the Lipschitz condition is satisfied by the function f(t, x) with respect to x in \([t_0,\infty )\times {\mathfrak {D}}\), then \(\exists\) a unique solution to the system (4.1) on \([t_0,\infty )\times {\mathfrak {D}}\).

Proof

To prove this lemma, we assume the following region \([t_0,A]\times {\mathfrak {D}}\) where \({\mathfrak {D}}=\{(x,y)\in {\mathbb {R}}^2: \max \{|x|,|y|\}\le B\}\), and A and B be two finite positive real numbers. Assume \({\tilde{x}}=(x,y)\) and \(\tilde{x_1}=(x_1,y_1)\) be two points in \({\mathfrak {D}}\) and define the mapping \(I:{\mathfrak {D}}\rightarrow {\mathbb {R}}^2\) by \(I({\tilde{x}})=(I_1({\tilde{x}}),I_2({\tilde{x}}))\), where

$$\begin{aligned} I_1({\tilde{x}})= & {} r \left( 1-\frac{x}{k}\right) x-\frac{axy}{1+bx}-q_1Ex ~~~~~~~~~~~~~~~ \\ I_2({\tilde{x}})= & {} \frac{maxy}{1+bx}-dy-\eta yz-q_2Ey=\frac{maxy}{1+bx}-ey \end{aligned}$$

Let \({\tilde{x}}, \tilde{x_1}\in {\mathfrak {D}}\) be arbitrary. Then

$$\begin{aligned} \begin{aligned} ||I({\tilde{x}})-I(\tilde{x_1})||&=|I_1({\tilde{x}})-I_1(\tilde{x_1})|+|I_2({\tilde{x}})-I_2(\tilde{x_1})|\\&=|r x \left( 1-\frac{x}{k}\right) -\frac{axy}{1+bx}-q_1Ex-r x_1 \left( 1-\frac{x_1}{k}\right) +\frac{ax_1y_1}{1+bx_1}+q_1Ex_1|\\&\quad +|\frac{maxy}{1+bx}-ey-\frac{max_1y_1}{1+bx_1}+ey_1|\\&\le |r(x-x_1)-\frac{r}{k}(x^2-x_1^2)-q_1E(x-x_1)-\frac{a\{(xy-x_1y_1)+bxx_1(y-y_1)\}}{(1+bx)(1+bx_1)}| \\&\quad +|\frac{ma\{(xy-x_1y_1)+bxx_1(y-y_1)\}}{(1+bx)(1+bx_1)}-e(y-y_1)|\\&\le |x-x_1|\left( r+\frac{2rB}{k}+q_1E\right) +a\{B|x-x_1|+B(1+bB)|y-y_1|\}\\&\quad +ma\{B(1+bB)|y-y_1|+B|x-x_1|\}+e|y-y_1|\\&=\left[ r+\left( \frac{2r}{k}+a(1+m)\right) B+q_1E\right] |x-x_1|+[aB(1+bB)(1+m)+e]|y-y_1|\\&\le N||{\tilde{x}}-\tilde{x_1}||,\\&\quad \text{ where }~ N =\max \left\{ r+\frac{2rB}{k}+q_1E+a(1+m)B,aB(1+bB)(1+m)+e\right\} \end{aligned} \end{aligned}$$

Hence the function I(x) satisfies Lipschitz’s condition corresponding to the variable \({\tilde{x}}=(x,y)\in {\mathfrak {D}}\). Therefore by using the Lemma (4.1), we may draw the conclusion that the system (2.5) possesses a unique solution \({\tilde{x}}\in {\mathfrak {D}}\) with respect to initial condition \(\tilde{x_{t_0}}=(x_{t_0} , y_{t_0} )\in {\mathfrak {D}}\). Therefore, using this lemma, we can prove the next theorem:

Theorem 4.2

For every initial point \({\tilde{x}}_{t_0}=(x_{t_0} , y_{t_0} )\in {\mathfrak {D}}\) \(\exists\) a unique solution \(\tilde{x_t}=(x(t) , y(t) )\in {\mathfrak {D}}\) of the model system (2.5) for any time \(t>t_0\).

Nonnegativity and boundedness of solutions

The nonnegative and bounded solutions of a system are the most important and useful solutions in the context of mathematical ecology. Let us assume \({\mathfrak {D}}^+=\{(x,y)\in {\mathfrak {D}}: x,y\in {\mathbb {R}}^+\}\), where \({\mathbb {R}}^+=\{x\in {\mathbb {R}}: x\ge 0\}\).

Theorem 4.3

All the solutions of the model system ( 2.5 ) starting in \({\mathbb {R}}{^+}^2\) are all nonnegative and bounded uniformly.

Proof

(Non-negativity): Assume that \({\tilde{x}}_{t_0}=(x_{t_0} , y_{t_0} )\in {\mathfrak {D}}^+\) be an initial solution of the system(2.5). We prove that any solution \(x(t)\in {\mathbb {R}}^+\) is non-negative. Suppose T be a real number satisfying \(t_0\le t<T\) and

$$\begin{aligned} x(t)= {\left\{ \begin{array}{ll} &{}~0, ~~ t_0\le t<T\\ &{} ~0,~~ t=T\\ &{}<0, ~~ t=T^+\\ \end{array}\right. } \end{aligned}$$

With the help of first equation of the sysytem (2.5), we get \({}_{t_0}D_t^{\alpha }x(t)|_{x(T)}=0\). By the Lemma 3.1, we get \(x(T^+) = 0,\) which is a contradiction to the assumption \(x(T^+) < 0\). Therefore, for every \(t\in [t_0, \infty )\), we get \(x(t)\ge 0\). By the application of the same procedure, for all \(t\in [t_0, \infty )\), we get \(y(t)\ge 0\). \(\square\)

(Uniform boundedness): To prove the uniform boundedness of solutions, let us formulate the following function:

$$\begin{aligned} G(t)=x(t)+\frac{y(t)}{m}. \end{aligned}$$

Then, we have

$$\begin{aligned} \begin{aligned} {}_{t_0}D_t^{\alpha }G(t)+eG(t)&=r \left( 1-\frac{x}{k}\right) x-\frac{axy}{1+bx}-q_1Ex+\frac{axy}{1+bx}-\frac{e}{m}y+ex+\frac{e}{m}y\\&\le -x^2\frac{r}{k}+(r+e)x ~~\text{ since }~ x(t)>0\\&= -x^2\frac{r}{k}+ex ~~\text{ since } ~x(t)>0\\&= -\frac{r}{k}\left( x-\frac{k(e+r)}{2r}\right) ^2+\frac{k^2(e+r)^2}{4r^2}\\&\le \frac{k^2(r+e)^2}{4r^2} \end{aligned} \end{aligned}$$

With the help of the Lemma 3.2, we get

$$\begin{aligned} G(t)\le \left( G(t_0)- \frac{k^2(r+e)^2}{4r^2e}\right) E_{\alpha }[-e(t-t_0)^{\alpha }]+\frac{k^2(r+e)^2}{4r^2e}\rightarrow \frac{k^2(r+e)^2}{4r^2e}~ \text {as}~ t\rightarrow \infty . \end{aligned}$$

Therefore, all solutions of the model system (2.5) starting in the region \({\mathfrak {D}}^+\) are lying in the region \(\Phi =\left\{ (x,y)\in {\mathfrak {D}}^+ :x+\frac{y}{m}\le \frac{k^2(r+e)^2}{4r^2e}+\alpha , ~\alpha >0\right\}\).

Dynamical behavior

The local stability analysis can be done by using the linearization technique around each equilibrium points. The jacobian matrix J of the given system (2.5) at any point (x, y) is followed by

$$\begin{aligned} J(x,y)= & {} \left( \begin{array}{cc} a_{11} &{} a_{12} \\ a_{21} &{} a_{22} \\ \end{array} \right) \hbox { , where} \\ a_{11}= & {} r-Eq_1-\frac{a y}{(1+b x)^2}-\frac{2 r x}{k}, \\ a_{12}= & {} -\frac{a x}{1+b x}, \\ a_{21}= & {} \frac{a m y}{(1+b x)^2},~~ a_{22}=\frac{a m x}{1+b x}-e \end{aligned}$$

The Jacobian matrix at the trivial equilibrium point \(E^0(0,0)\) is given by: \(J(0,0)=\left( \begin{array}{cc} r-Eq_1 &{} 0 \\ 0 &{} -e \\ \end{array} \right)\)

Hence eigenvalues at \(E^0(0,0)\) of the model (2.5) are \(\lambda _1= r-Eq_1\) and \(\lambda _2=-e\). See that \(|\arg (\lambda _1)|=\pi >\frac{\alpha \pi }{2}\) if \(r-Eq_1<0\) i.e. \(E>r/q_1\), otherwise \(|\arg (\lambda _1)|=0<\frac{\alpha \pi }{2}\), where \(\alpha \in (0,1)\) and \(|\arg (\lambda _2)|=\pi >\frac{\alpha \pi }{2}\), \(\alpha \in (0,1)\). Therefore, by using the Lemma 3.3, we can conclude that the system is asymptotically stable locally around the trivial equilibrium if and only if \(E>r/q_1\). We are in a situation to state next theorem regarding the local asymptotic stability at \(E^0(0,0)\).

Theorem 4.4

\(E^0(0,0)\), the trivial equilibrium point of the system (2.5) is asymptotically stable locally if and only if \(E>r/q_1\).

At the predator-free equilibrium point \(E^1(x^1,0)\), the Jacobian matrix J of the model (2.5) is followed by:

$$\begin{aligned} J(x^1,0)=\left( \begin{array}{cc} -(r-Eq_1) &{} -\frac{a k (r-Eq_1)}{r+bk(r-Eq_1)} \\ 0 &{} \frac{a km (r-Eq_1)}{r+bk(r-Eq_1)}-e \\ \end{array} \right) \end{aligned}$$

The eigenvalues of the system (2.5) at \(E^1(x^1,0)\) are \(\lambda _1= -(r-Eq_1)\) and \(\lambda _2=\frac{a km (r-Eq_1)}{r+bk(r-Eq_1)}-e\).

Theorem 4.5

\(E^1(x^1,0)\), the predator-free equilibrium point of the system (2.5) is asymptotically stable locally if and only if \(Eq_1<r<Eq_1+\frac{rx^*}{k}\).

Proof

Since \(\alpha \in (0,1)\) notice that \(|\arg (\lambda _1)|=\pi >\frac{\alpha \pi }{2}\) if \(r-Eq_1>0\) i.e. \(r>Eq_1\), otherwise \(|\arg (\lambda _1)|=0<\frac{\alpha \pi }{2}\) and \(|\arg (\lambda _2)|=\pi >\frac{\alpha \pi }{2}\) if \(\frac{a km (r-Eq_1)}{r+bk(r-Eq_1)}-e<0\) i.e. \(r<Eq_1+\frac{rx^*}{k}\) otherwise \(|\arg (\lambda _2)|=0<\frac{\alpha \pi }{2}\), where \(\alpha \in (0,1)\). Therefore, by the Lemma 3.4 the system is asymptotically stable locally at \(E^1(x^1,0)\), the predator-free equilibrium point if and only if \(Eq_1<r<Eq_1+\frac{rx^*}{k}\).

Hence the \(E^1\) is stable whenever \(E^0\) is unstable. Hence, the proof. \(\square\)

Next, our aim is to analyze the local asymptotic stability behavior at \(E^*(x^*,y^*)\), interior equilibrium point. J, the Jacobian matrix of the model (2.5) at \(E^*(x^*,y^*)\) is presented by \(J(x^*,y^*)=\left( \begin{array}{cc} b_{11} &{} b_{12}\\ b_{21} &{} b_{22}\\ \end{array} \right)\), where

$$\begin{aligned} b_{11}= & {} -(r-Eq_1)-\frac{2er}{k(am-be)}-\frac{k}{am}[k(r-Eq_1)(am-be)-er],~~~~ \\ b_{12}= & {} -\frac{e}{m}, \\ b_{21}= & {} \frac{k}{a}[k(r-Eq_1)(am-be)-er], ~~~~~ b_{22}=0 \end{aligned}$$

The characteristic equation of the matrix \(J(x^*,y^*)\) is \(\lambda ^2-b_{11}\lambda +b_{12}b_{21}=0\). Let \(\lambda _1\) and \(\lambda _2\) be the eigenvalues. Then \(\lambda _1 +\lambda _2=b_{11}\) and \(\lambda _1\lambda _2=b_{12}b_{21}\). Now, \(b_{11}\) will be negative if

$$\begin{aligned} r>\frac{q_1Ek^3(am-be)^2}{k(am-be)[(am-ke)+(am-be)k^2]+2ame}=r^*,~say \end{aligned}$$
(4.2)

The eigenvalues are

$$\begin{aligned} \lambda _{1,2}=\frac{b_{11}}{2}\pm \frac{\sqrt{b_{11}^2-4b_{12}b_{21}}}{2} \end{aligned}$$

The different values of \(\lambda _1\) and \(\lambda _2\) are depending on the coefficients \(b_{11}, b_{12}\) and \(b_{21}\).

  1. (i)

    If \(b_{11}^2\ge 4b_{12}b_{21}\) and \(b_{11} < 0\), then both the eigenvalues \(\lambda _1\), \(\lambda _2\) are negative. Therefore, \(|\arg (\lambda _{1,2})|=\pi >\frac{\alpha \pi }{2}\), \(\alpha \in (0,1)\) and hence by Lemma 3.3 and 3.4 we can draw the conclusion that \(E^*(x^*,y^*)\) is asymptotically stable.

  2. (ii)

    If \(b_{11}^2\ge 4b_{12}b_{21}\) and \(b_{11} \ge 0\), then one of the eigenvalues \(\lambda _1\) or \(\lambda _2\) will be nonnegative. Therefore \(|\arg (\lambda _{i})|=0<\frac{\alpha \pi }{2}\) for \(i=1\) or 2, where \(\alpha \in (0,1)\) and hence by Lemma 3.3 and 3.4 , the interior equilibrium is unstable.

  3. (iii)

    If \(b_{11}^2< 4b_{12}b_{21}\) and \(b_{11} > 0\), then both the eigenvalues \(\lambda _1\) and \(\lambda _2\) will be complex conjugate:

$$\begin{aligned} \lambda _{1,2}=\frac{b_{11}}{2}\pm i\frac{\sqrt{4b_{12}b_{21}-b_{11}^2}}{2}, \end{aligned}$$

where \(i=\sqrt{-1}\), imaginary unit. Therefore \(|\arg (\lambda _{1,2})|=\tan ^{-1} | \frac{\sqrt{4b_{12}b_{21}-b_{11}^2}}{b_{11}} |\). Then \(E^*\) will be stable asymptotically if \(\tan ^{-1} | \frac{\sqrt{4b_{12}b_{21}-b_{11}^2}}{b_{11}} |>\frac{\alpha \pi }{2}\). In this case we find an interval of differentiation of \(\alpha\) as \(0<\alpha <\frac{2}{\pi }\tan ^{-1} | \frac{\sqrt{4b_{12}b_{21}-b_{11}^2}}{b_{11}}|\) and the interior equilibrium point is asymptotically stable in this interval.

  1. (iv)

    If \(b_{11}^2< 4b_{12}b_{21}\) and \(b_{11} < 0\), then \(|\arg (\lambda _{1,2})|=\pi -\tan ^{-1} | \frac{\sqrt{4b_{12}b_{21}-b_{11}^2}}{b_{11}} |\). Then \(E^*\) will be stable asymptotically if \(\pi -\tan ^{-1} | \frac{\sqrt{4b_{12}b_{21}-b_{11}^2}}{b_{11}} |>\frac{\alpha \pi }{2}\). The interval of differentiation for \(\alpha\) is \(0<\alpha <2-\frac{2}{\pi }\tan ^{-1} | \frac{\sqrt{4b_{12}b_{21}-b_{11}^2}}{b_{11}}|\), where the interior equilibrium \(E^*\) is asymptotically stable.

  2. (v)

    If \(b_{11}^2< 4b_{12}b_{21}\) and \(b_{11} = 0\), then \(|\arg (\lambda _{1,2})|=\frac{\pi }{2}>\frac{\alpha \pi }{2}\). Therefore, \(E^*\) is asymptotically stable.

Existence criteria of Hopf Bifurcation

We rewrite our proposed model system (2.5) as

$$\begin{aligned} {}_{t_0}D_t^{\alpha }{\tilde{x}}(t)= g(r,{\tilde{x}}),~t_0>0,~{\tilde{x}}=(x,y)\in {\mathbb {R}}^2 ~\text{ and }~{\tilde{x}}(t_0)=(x_0,y_0)~\text{ with }~ x_0>0,~y_0>0 \end{aligned}$$
(4.3)

where \(\alpha \in (0,1]\) and \(g(r,{\tilde{x}})=g(x,y)=\left( r x \left( 1-\frac{x}{k}\right) -\frac{axy}{1+bx}-q_1Ex , \frac{maxy}{1+bx}-dy-\eta yz-q_2Ey\right)\), is a function from \([t_0,\infty )\times {\mathfrak {D}}\) to \({\mathbb {R}}^2\) with \({\mathfrak {D}}\subset {\mathbb {R}}^2\) with parameter \(r\in {\mathbb {R}}\). For \(E^*\), the interior equilibrium of the system (4.3), suppose \(\lambda _1(r)\) and \(\lambda _2(r)\) are complex conjugate eigenvalues of Jacobian matrix J of model system (4.3) at \(E^*\) (which exists by the above discussion of case (iii) with \(b_{11}=0\)). The system(4.3) undergoes a Hopf bifurcation for the critical value \(r=r^*\) [by (4.2)] such that following singularity condition[(i)] and transversality condition [(ii)] are satisfied (see Deshpande et al. 2017).

$$\begin{aligned} \begin{aligned}&(i)~ |\arg (\lambda _{i}(r^*))|=\frac{\alpha \pi }{2} ~for~ i=1 ~and~ 2.\\&(ii) ~ \frac{d}{dr}|\arg (\lambda _{i}(r))|\ne 0 ~at~ r=r^*~ for~ i=1 ~and~ 2.\\ \end{aligned} \end{aligned}$$

Global Stability of equilibrium points

In this portion, we state only some necessary lemma to check the criterion for the global asymptotic stability at predator-free \(E^1\) and also interior equilibrium point \(E^*\).

Lemma 4.6

( Li et al. 2010) Let \(\psi :{\mathbb {R}}\rightarrow {\mathbb {R}}^+\) be a fractional continuously differentiable function of the order \(\alpha \in (0,1).\)Then the following result hold for any time \(t>t_0\) and \(\sigma \in \mathbb {R^+}:\)

$$\begin{aligned} {}_{t_0}D_t^{\alpha }\left( \psi (t)-\sigma -\sigma \log \frac{\psi (t)}{\sigma }\right) \le \left( 1-\frac{\sigma }{\psi (t)}\right) {}_{t_0}D_t^{\alpha }. \end{aligned}$$

Now, we state and prove the following two theorems in connection with global asymptotic stability criterion for predator-free and interior equilibrium points respectively.

Theorem 4.7

If \(E>\max \left\{ \frac{2r}{q_1},\frac{mak-(d+\eta z)}{q_2}\right\}\), then \(E^1(x^1,0)\), the predator-free equilibrium of the our suggested model system (2.5) is asymptotically stable globally.

Proof

To prove this theorem, we formulate the following positive definite Lyapunov function:

$$\begin{aligned} L(x,y)=x-k(1+\log \frac{x}{k})+\frac{y}{m} \end{aligned}$$

By applying the Lemma 4.6, we get

$$\begin{aligned} \begin{aligned} {}_{t_0}D_t^{\alpha }L(x,y)&\le \left( 1-\frac{k}{x}\right) {}_{t_0}D_t^{\alpha }x(t)+\frac{1}{m} {}_{t_0}D_t^{\alpha }y(t)\\&=(x-k)\left[ r(1-\frac{x}{k})-\frac{ay}{1+bx}-q_1E\right] +\left[ \frac{axy}{1+bx}-\frac{ey}{m}\right] \\&=-\frac{r}{k}(x-k)^2-q_1E(x-k)+\frac{aky}{1+bx}-\frac{ey}{m}\\&\le -\frac{r}{k}(x-k)^2-q_1E(x-k)+(ak-\frac{e}{m})y\\&=-\frac{r}{k}x^2+(2r-q_1E)x+(ak-\frac{e}{m})y+(q_1E-r)k\\ \end{aligned} \end{aligned}$$

Since \(q_1E-r<0\) for the existence of \(E^1\), \({}_{t_0}D_t^{\alpha }L(x,y)\le 0\) if \(2r-q_1E<0\) and \(ak-\frac{e}{m}<0\). As \(e=d+\eta z+q_2E\), \({}_{t_0}D_t^{\alpha }L(x,y)\le 0\) if \(E>\max \left\{ \frac{2r}{q_1},\frac{mak-(d+\eta z)}{q_2}\right\}\). Hence the theorem.

Notice that the combined harvesting effort E plays an important role in the global stability of predator-free equilibrium \(E^1\). Theorem 4.7 shows that if the harvesting mortality rate for prey i.e. \(q_1E\) is larger than twice of intrinsic growth rate r of prey population, then \(E^1\) will be asymptotically stable globally. \(\square\)

Theorem 4.8

If \(E<\frac{D_2-\sqrt{D_2^2+4D_1D_3}}{2D_1}\) then \(E^*(x^*,y^*)\), interior equilibrium of the model (2.5) is asymptotically stable globally, where \(D_1, D_2, D_3\) are given in the proof.

Proof

We formulate the following positive definite Lyapunov function to prove the theorem:

$$\begin{aligned} L(x,y)=\frac{P}{m}(y-y^*(1+\log \frac{y}{y^*}))+x-x^*(1+\log \frac{x}{x^*}) \end{aligned}$$

where P is a constant determine later. We have the following two equations as \(E^*(x^*,y^*)\) be an equilibrium of the model (2.5),

$$\begin{aligned} \begin{aligned} r x^* \left( 1-\frac{x^*}{k}\right) -\frac{ax^*y^*}{1+bx^*}-q_1Ex^*&=0 ~~\\ \frac{max^*y^*}{1+bx^*}-ey^*&=0\\ \end{aligned} \end{aligned}$$
(4.4)

The Lemma 4.6 implies that

$$\begin{aligned} \begin{aligned} {}_{t_0}D_t^{\alpha }L(x,y)&\le \frac{x-x^*}{x}{}_{t_0}D_t^{\alpha }x(t)+\frac{P(y-y^*)}{my} {}_{t_0}D_t^{\alpha }y(t)\\&=P(y-y^*)\left[ \frac{ax}{1+bx}-\frac{e}{m}\right] +(x-x^*)\left[ r(1-\frac{x}{k})-\frac{ay}{1+bx}-q_1E\right] \\&= (x-x^*)\left[ r(1-\frac{x}{k})-\frac{ay}{1+bx}-r(1-\frac{x^*}{k})+\frac{ay^*}{1+bx^*}\right] +P(y-y^*)\left[ \frac{ax}{1+bx}-\frac{ax^*}{1+bx^*}\right] ,~\text{by}~\text{using}~(4.4)\\&\le -\frac{abx^*(x-x^*)(y-y^*)}{(1+bx)(1+bx^*)}-\frac{r}{k}(x-x^*)^2-\frac{a(x-x^*)(y-y^*)}{(1+bx)(1+bx^*)}+\frac{aby^*(x-x^*)^2}{(1+bx)(1+bx^*)}\\&\quad +\frac{Pa(x-x^*)(y-y^*)}{(1+bx)(1+bx^*)}\\&=-\frac{r}{k}\left[ 1-\frac{kaby^*}{r(bx+1)(bx^*+1)}\right] (x-x^*)^2+\frac{a(x-x^*)(y-y^*)}{(1+bx)(1+bx^*)}\left[ P-1-bx^*\right] \\ \end{aligned} \end{aligned}$$

Let us take P such that \(P-1-bx^*=0\) which implies \(P=\frac{am}{am-be}\). Putting the values of P and \(y^*\) in the above equation, we get

$$\begin{aligned} \begin{aligned} {}_{t_0}D_t^{\alpha }L(x,y)&\le -\frac{r}{k}\left[ 1-\frac{mabx^*(x^1-x^*)}{e(1+bx)(1+bx^*)}\right] (x-x^*)^2\\&\le \frac{r}{k}\frac{mab(x^1-x^*)}{e(1+bx^*)}(x-x^*)^2,~~\text {since}~x(t)>0\\&\le \frac{mab}{e}(x^1-x^*)\frac{r}{k}(x-x^*)^2,~~\text {since}~x^*>0\\&=\frac{mab}{e}\left[ k-\frac{kEq_1}{r}-\frac{e}{am-be}\right] \frac{r}{k}(x-x^*)^2\\ \end{aligned} \end{aligned}$$

Therefore \({}_{t_0}D_t^{\alpha }L(x,y)\le 0\) if \(k-\frac{kEq_1}{r}-\frac{e}{am-be}<0\) which imply \(D_1E^2-D_2E-D_3<0\), where \(D_1=bkq_1q_2\), \(D_2=r(1+bk)q_2+amkq_1-bk(d+\eta z)q_1\) and \(D_3=r(d+\eta z)(1+bk)-amrk\) and if hence \(E<\frac{D_2-\sqrt{D_2^2+4D_1D_3}}{2D_1}\), then \(E^*\) is asymptotically stable globally. This completes the proof. \(\square\)

Incommensurate fractional-order system

In this stage, we analyze the incommensurate fractional-order system (2.4). Here \(\alpha _i\in (0,1]\) for \(i=1,2\) and consider \(\beta =\frac{1}{A}\) where \(A=lcm(q_1,q_2)\) and for \(i=1,2\), \(\alpha _i=\frac{p_i}{q_i}\) with \(p_i\) and \(q_i\) are relatively primes. At the any equilibrium point E(x, y) of the given model is asymptotically stable locally if and only if \(|\arg (\lambda )|>\frac{\beta \pi }{2}\) for all the eigenvalues \(\lambda 's\) of the difference of the matrix \(M=diag(\lambda ^{A\alpha _1},\lambda ^{A\alpha _2})\) and Jacobian matrix \(J =\frac{\partial f}{\partial x}\) calculated at that point E(x, y) (Saka et al. 2019).

Numerical simulations

In this section, we check the validity of the analytical results of our formulated model by numerical techniques in MATLAB with help of the algorithm modified predictor-corrector (MPC) method ( Diethelm et al. 2003). We mainly emphasize the effect of the parameters: r, intrinsic growth rate, harvesting effort E, biomass conversion rate of the prey to the predator i.e. m, half saturation constant 1/b and the order \(\alpha\) of fractional differentiation in our model system (2.5) as these are the most important parameters from the view point of ecological sense. \(E^*(x^*,y^*)\), the interior equilibrium point will be asymptotically stable locally if

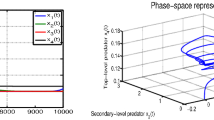
$$\begin{aligned} r> \frac{kq_1E(am-be)}{k(am-be)-e} ~\text {and} ~r>\frac{q_1Ek^3(am-be)^2}{k(am-be)[(am-ke)+(am-be)k^2]+2ame}~ \text {for}~ b_{11}<0 \end{aligned}$$

. Now we choose a parameter set \(P_1= \{r, k, a, b, d, q_1, q_2, \eta , m, E, z \}\) as \(\{1.5, 110, 0.56,0.018, 0.04, 0.15, 0.05, 0.5, 0.03, 0.85, 0.25 \}\), then \(\frac{kq_1E(am-be)}{k(am-be)-e}=0.965195\)   and \(\frac{q_1Ek^3(am-be)^2}{k(am-be)[(am-ke)+(am-be)k^2]+2ame}=0.960725\). So the intrinsic growth rate r plays a significant role in stability of \(E^*\). When r exceeds 0.96 all the trajectories are pulled towards the interior equilibrium point. As r tends to 0.96 we will see limit cycles are formed around \(E^*\) for a particular order of differentiation \(\alpha\). For another set of parameters, we may also observe stable limit cycles and hence the interior equilibrium loses its stability. For the parameter set \(P_1\) along with \(\alpha =0.85\) and the initial point (9, 7), Fig. 1 verifies that the solution converges to \(E^*=(15.721,2.652)\).

Fig. 1
figure 1

Left: time series plot Right: phase plane plot of (2.5) corresponding to the parameter set \(P_1\) and \(\alpha =0.85\)

Full size image

Let us choose another set of parameters \(P_2\) as \(P_1\bigcup \{\alpha =0.95\}\), Fig. 2 confirm that solution asymptotically converges to \(E^*=(15.721,2.652)\).

Fig. 2
figure 2

Left: time series plot Right: phase plane plot of (2.5) corresponding to the parameter set \(P_2\)

Full size image

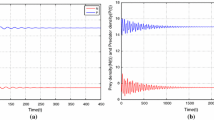
For the parameter set \(P_3=P_1\bigcup \{\alpha =0.99\}\), Fig. 3 show that there are stable limit cycles .

Fig. 3
figure 3

Left: time series plot Right: phase plane plot of (2.5) corresponding to the parameter set \(P_3\)

Full size image

Keeping all the parameters of \(P_1\) remain same, we change \(r=1.5\) to \(r=0.98\) only i.e. we choose the following parameter set

\(P_4=\{r, k, a, b, d, q_1, q_2, \eta , m, E, z, \alpha \}=\{0.98, 110,0.56, 0.018, 0.04, 0.15, 0.05, 0.5,0.03, 0.85,0.25, 0.99\}\). Fig. 4 verifies that there exist a limit cycle of system (2.5) around \(E^*\), interior equilibrium point.

Fig. 4
figure 4

Left: time series plot Right: phase plane plot of (2.5) corresponding to the parameter set \(P_4\)

Full size image

Again we change only the parameter \(r=0.98\) to \(r=3.85\) and let \(P_5=\{r, k, a, b, d, q_1, q_2, \eta , m, E, z \}=\{3.85, 110, 0.56, 0.018, 0.04, 0.15,0.05,0.5,0.03,0.85,0.25 \}\). Fig. 5 depicts that solution of the model system (2.5) converges asymptotically to interior equilibrium \(E^*=(15.88,7.271)\) for the parameter set \(P_5\) with \(\alpha =0.9\).

Fig. 5
figure 5

Left: time series plot Right: phase plane plot of (2.5) corresponding to the parameter set \(P_5\) with \(\alpha =0.9\)

Full size image

Let us choose \(P_6\) as \(P_5\bigcup \{\alpha =0.91,\alpha =0.93\}\) and \(P_{7}=P_7\bigcup \{\alpha =0.97\}\). The parameter set \(P_6\) confirms that the solutions asymptotically converges to the \(E^*=(15.88,7.271)\) (Fig. 6).

Fig. 6
figure 6

Left: time series plot for prey Middle: time series plot for predator Right: phase plane plot of (2.5) corresponding to the parameter set \(P_6\)

Full size image

The parameter set \(P_7\) shows that there is a stable limit cycle which is given in Fig. 7.

Fig. 7
figure 7

Left: time series plot for prey Middle: time series plot for predator Right: phase plane plot of (2.5) corresponding to the parameter set \(P_{7}\)

Full size image

Let us vary the parameters \(r=0.98\) to \(r=3.85\) and \(E=0.85\) to \(E=1\) and consider \(P_8=\{r, k, a, b, d, q_1, q_2, \eta , m, E, z,\alpha \}=\{1.85, 110, 0.56, 0.018, 0.04, 0.15,0.05,0.5,0.03, 1, 0.25,0.99 \}\). For the parameter set \(P_8\), Fig.8 confirm that there are stable limit cycles.

Fig. 8
figure 8

Left: time series plot for prey Middle: time series plot for predator Right: phase plane plot of (2.5) corresponding to the parameter set \(P_{8}\) with the initial conditions (9,7) and (25,3.5)

Full size image

Let us choose \(P_{9}\) as \(P_9=\{r, k, a, b, d, q_1, q_2, \eta , E, z,\alpha \}\bigcup \{m\}=\) \(\{1.85, 110,0.56, 0.018,0.04,0.15, 0.05,0.5,0.85,0.25,0.95\}\bigcup \{00,0.01,0.02,0.03\}\). Fig. 9 depicts for the parameter set\(P_{9}\).

Fig. 9
figure 9

Left: time series plot for prey Middle: time series plot for predator Right: phase plane plot of (2.5) corresponding to the parameter set \(P_{9}\)

Full size image

Again consider \(P_{10}\) as \(P_{10}=\{r, k, a, b, d, q_1, q_2, \eta , m, E, z \}\bigcup \{\alpha \}=\) \(\{1.85,110, 0.56,0.018,0.04,0.15,0.05,0.5,0.03,0.85,0.25 \}\bigcup \{0.85,0.9,0.95,0.99\}\). Fig.10 depicts for the parameter set \(P_{10}\).

Fig. 10
figure 10

Left: time series plot for prey Middle: time series plot for predator Right: phase plane plot of (2.5) corresponding to the parameter set \(P_{10}\)

Full size image

Let us assume \(P_{11}\) as \(P_{11}=\{r, k, a, d, q_1, q_2, \eta , m, E, z,\alpha \}\bigcup \{b\}= \{1.85, 110,0.56,0.04,0.15, 0.05, 0.5,0.03, 0.85, 0.25,0.95 \} \bigcup \{0.01,0.02,0.03,0.04\}\). We solve the model (2.5) with the help of the parameter set \(P_{11}\). The Fig.11 presents these solutions.

Fig. 11
figure 11

Left: time series plot for prey Middle: time series plot for predator Right: phase plane plot of (2.5) corresponding to the parameter set \(P_{11}\)

Full size image

Lastly, choose the parameter set \(P_{12}\) as \(P_{12}=\{r, k, a, b, d, q_1, q_2, \eta , m, E, z,\alpha \}\bigcup \{E\}= \{1.85, 110, 0.56, 0.018,0.04, 0.15,0.05, \eta =0.5, 0.03, 0.25,0.95 \} \bigcup \{0.9,1.4,1.9,2.4,2.8,3.5)\}\). Fig. 12 depicts for the parameter set \(P_{12}\).

Fig. 12
figure 12

Left: time series plot for prey Middle: time series plot for predator Right: phase plane plot of (2.5) corresponding to the parameter set \(P_{12}\)

Full size image

For the incommensurate fractional-order system (2.4), first we use the parameter set \(P_1\) and consider \(\alpha _1=0.8\), \(\alpha _2=0.9\) and then \(\frac{\beta \pi }{2}=0.1570<\min |arg(\lambda )|=0.3396\). Hence the system (2.4) is asymptotically stable. Fig. 13 verifies this. Now we consider the parameter set \(P_1\) and take \(\alpha _1=0.97\), \(\alpha _2=0.98\) and then \(\frac{\beta \pi }{2}=0.01570>\min |arg(\lambda )|=0.012548\). Hence the system (2.4) is not stable. Fig. 14 asserts this.

Fig. 13
figure 13

Left: time series plot Right: phase plane plot of (2.4) corresponding to the parameter set \(P_{1}\) with \(\alpha _1=0.8\) and \(\alpha _2=0.9\)

Full size image
Fig. 14
figure 14

Left: time series plot Right: phase plane plot of (2.4) corresponding to the parameter set \(P_{1}\) with \(\alpha _1=0.97\) and \(\alpha _2=0.98\)

Full size image

Conclusion and discussion

In our present paper, we have formulated and examined a fractional order model for the interactions of prey and predator populations in the presence of harvesting and also the Holling type-II functional response. Harvesting of combined prey and predators make our model more realistic. The fractional-order system is more realistic and it causes more impacts than the ordinary system or integer-order system of differential equations. The quality of many real problems (or systems) ensures that they possibly more exactly modeled with a fractional-order system of differential equations, for example, the anomalous diffusion equation is modeled with it. A higher-order system can be also modeled to a lower order model by using fractional-order which is one of the key advantages of the fractional calculus. In the case of control theory, the model system by fractional-order differential equations produces a much better effect than the ordinary or integer-order system of differential equations.

We resolve the problem of time dimension of the commensurate model system (2.3). Also, we rebuilt the system to the commensurate system (2.5) and incommensurate system (2.4). Again, we observed that the time dimension is not an issue for the stability of several equilibria. Next, we derived the conditions for the existence and uniqueness of various equilibria of our system in several fractional-order cases. Then we tested the conditions for non-negativity of solutions and also uniform boundedness of that solutions. Furthermore, we established some criterion to verify the asymptotic stability globally of predator free \(E^1\) and the interior \(E^*\) equilibrium point of our model (2.5) by formulating desirable Lyapunov functions. The theoretical results are asserting by some numerical simulations. Our numerical works also demonstrate the influence of intrinsic growth rate r of prey, harvesting effort E, biomass conversion rate m, half saturation constant 1/b and the fixed order \(\alpha\) or various orders \(\alpha _1\), \(\alpha _2\) of fractional differentiation on each population density (biomass).

From the numerical simulations we observed that it is possible to control the populations of prey and also predator by controlling the following parameters: r, intrinsic growth rate (Figs. 1, 2, 3, 4), biomass conversion rate m (Fig. 9), half saturation constant 1/b (Fig. 11) and harvesting effort E (Fig. 12).

In these numerical simulations, we have applied the Predictor-Corrector \(P(EC)^mE\) (Predict, multi-term(Evaluate, Correct), Evaluate) method ( Diethelm et al. 2002, 2003; Garrappa 2010) with the help of MATLAB software. Here we use the solver function as implicit fractional linear multistep methods (FLMMs) for the fractional order differential equations and we have described the corresponding phase portrait of our model system with the help of the solutions by the solver. Notice that \(P(EC)^mE\) is a modified iteration formula of the method PECE (Predict, Evaluate, Correct, Evaluate) and the Adams-Moulton algorithm. Several numerical techniques for the fractional-order systems are a extremely progressive. Various numerical methods like the Taylor series approximations method, Homotopy perturbation method, Diethelma’s method, and Adomian decomposition method, etc. are widely applied method in connections with numerical computations of a fractional order system. In our future works, we will study several fractional-order systems with the help of various numerical methods to obtain more effective results.