Introduction

Since pest species are harmful to plants and their control has become a challenge for us. Pest population is responsible for severe environmental and realistic problems [11, 26]. Also, many authors have discussed the models based on chemical pesticides, which are less harmful to humanity and environment [5, 9, 16, 17, 27]. For productive use of biological or natural methods to manage pest populations, without any adverse effects, it is important to understand the biology of beneficial species or natural enemy and pests [8]. Our most important aim is to control negative impacts of agriculture pests, for both humanity and agriculture, which harms the environment and generating different types of pollution. The irrigation and emissions from the paddy field were the most environmentally burdening stages across all major impact categories [10]. Moreover, they have shown that the manufacture of fertilizer and pesticide also play a significant role in putting environmental load. Researchers must have to produce, the natural systems to control pests by taking into account the communications between solid Allee effect in pests with natural methods: alternative food support for the natural enemy, introduction of infected pests to control healthy pests [7, 18] The interactions between pests and natural enemies in the same biological environment is an ample exciting area of research as per Lotka and Volterra. Natural enemies are more vulnerable to the infected pest since infectious pest population is weak and less active. Therefore natural enemy efficiently harvests pests. Due to the interaction between infected pests and natural enemy, the natural enemies must be infected. Hence natural enemy populations may live on other food resources for their growth and survival. Also, the species do not grow instantaneously; some time is taken by the species to give a new generation, called gestation lag period [20]. Functional responses play an important role to develop a predator-prey system in population dynamics. Various factors like hiding technique of pests from the natural enemy, shooting ability of the predator to harvest insect, etc., have a large influence on functional responses. Functional responses are of different types: for example, Holling type I–III, etc. A mathematical model has studied and analyzed to study the effect of toxicant in a three-species food-chain system incorporating delay in toxicant uptake process by prey population [14]. They formulated the model using the system of nonlinear ordinary differential equations. Also, people are more conscious and choose, the modern methods to manage agricultural pests, for example, less harmful chemical pesticides and natural techniques [2, 6, 21, 28, 29], whereas biological techniques are simple and safer to control pests than pesticide practices. Also time lag factors are of great significance to produce population models and used by numerous authors [1, 3, 4, 12, 13, 15, 19, 23,24,25]. According to many authors, models with continuous lag factors are practical [15] than instant delays [13].

Keeping in mind the recent literature, in the present study, the dynamics of a food chain model with the gestation delay for both pest the natural enemy is proposed and analyzed. This paper is organized as follows: Sect. 1, consists of an introduction. The proposed modeling approach and the mathematical system is presented, in Sects. 2 and 3 respectively. In Sect. 4, the boundedness of the system has been given and discussed. Equilibrium points and their stability analysis is carried out for possible steady states, in Sect. 5. The sensitivity analysis of the system at interior equilibrium point for system parameters is presented, in Sect. 6. In Sect. 7, numerical simulations are presented to support our analytic results. Finally, the results have been concluded in the last section.

Modelling approach

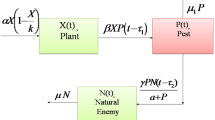
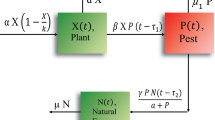
In this paper, we propose a food chain dynamics of plant–pest–natural enemies, keeping in view that the natural systems to control pests. The biological dynamics is shown in Fig. 1. We will use the compartmental modeling approach considering three compartments of the population, namely, plant, pest, and natural enemy.

Fig. 1
figure 1

Biological dynamics

Full size image

Further, in the absence of pest, the particular type of plant grows logistically, and the pest has alternative food for survival, details modeling assumptions are stated in the next section.

The proposed mathematical system

The assumptions of the proposed model are as follows:

  1. (1)

    In a particular habitat, there are three types of populations, namely, plant X(t), pest P(t) and natural enemy N(t).

  2. (2)

    Plants grow logistically with \(\alpha\) as intrinsic growth rate and k being carrying capacity. Thus, per capita growth rate for plants is \(\alpha X \left( 1-\frac{X}{k}\right)\), when system is free from pest species.

  3. (3)

    Also, the pest species grow logistically with \(\alpha _1\) as intrinsic growth rate and \(k_1\) being carrying capacity. Thus, per capita growth rate for pests is \(\alpha _1 P \left( 1-\frac{P}{k_1}\right)\).

  4. (4)

    Plants are harvested by pests with Holling type-I, response function.

  5. (5)

    Pests can hide from the natural enemy, hence the natural enemy harvesting pests with Holling type-II response function.

  6. (6)

    Let \(\beta\) be the predation rate of the plant by pest; \(\beta _1\) is the conversion rate for pest; \(\gamma\) is the harvesting rate of pests by the natural enemy. Let a be the half-saturation constant. Let \(\gamma _1\) be the conversion rate for the natural enemy; \(\mu\) be the natural death rate of natural enemy.

  7. (7)

    Finally, \(\tau _1\) and \(\tau _2\) are the gestation delays for the pest and the natural enemy.

Keeping in view the assumptions and interactions, the schematic flow of the proposed dynamics shown in Fig. 2. Hence our proposed dynamics can express as a system of equations of the form:

$$\begin{aligned} \frac{dX}{dt} = \alpha X\left( 1-\frac{X}{k}\right) -\beta X P(t-\tau _1) ,\end{aligned}$$
(1)
$$\begin{aligned} \frac{dP}{dt} = \alpha _1 P \left( 1-\frac{P}{k_1}\right) +\beta _1 X P-\frac{\gamma P N(t-\tau _2)}{a+P} ,\end{aligned}$$
(2)
$$\begin{aligned} \frac{dN}{dt} = \frac{\gamma _1 P N}{a+P}-\mu N, \end{aligned}$$
(3)

with initial conditions: \(X(0)>0\), \(P(0)>0\) and \(N(0)>0\).

Fig. 2
figure 2

Schematic diagram

Full size image

Boundedness

Here, the boundedness of solution of the system (1)–(3) is discussed below:

Lemma 1

The solution of proposed model (1)–(3) is uniformly bounded in \(\Omega\), where

$$\begin{aligned} \Omega = \left\{ (X,P,N):0 \le X(t)+P(t)+N(t)\le W_0\right\} , \end{aligned}$$

\(\mu '=min\{\mu ,-\alpha ,-\alpha _1 \}, \ \gamma _1<<\gamma , \ \beta _1<<\beta , \ W_0= e^{-\mu 't+c}\).

Proof

Let \(W(t)=X(t)+P(t)+N(t)\). Now, differentiating W(t) w.r.t. t, we have

$$\begin{aligned} \frac{dW(t)}{dt} =\alpha X\left( 1-\frac{X}{k}\right) -\beta X P+\alpha _1 P\left( 1-\frac{P}{k_1}\right) +\beta _1 X P-\frac{\gamma P N}{a+P}+\frac{\gamma _1 P N}{a+P}-\mu N. \end{aligned}$$

Since \(\mu '=min\{\mu ,-\alpha ,-\alpha _1 \}, \ \beta _1<<\beta , \ \gamma _1<<\gamma\), we have

$$\begin{aligned}&\frac{dW(t)}{dt} \le - \mu ' W-\frac{\alpha X^2}{k}-\frac{\alpha _1 P^2}{k_1} \\&\frac{dW(t)}{dt} + \mu ' W \le 0. \end{aligned}$$

Therefore, \(W=W_0= e^{-\mu 't+c}\) Hence, W(t) is bounded, i.e., the proposed system is bounded. \(\square\)

Equilibria and their stability analysis

The system of Eqs. (1)–(3) have four feasible equilibrium points:

  1. (1)

    The equilibrium point \(E_0(0,0,0)\) always exists.

  2. (2)

    The equilibrium point \(E_1(k,0,0)\) exists.

  3. (3)

    The natural enemy free equilibrium \(E_2(X_2,P_2,0)\) exists only when

    \((H_1):= \alpha>\beta k_1\) holds, where \(X_2=\frac{k(\alpha -\beta k_1)\alpha _1}{\alpha \alpha _1+k k_1 \beta \beta _1}, P_2=\frac{k_1 \alpha (\alpha _1+ k \beta _1)}{\alpha \alpha _1+k k_1 \beta \beta _1}\).

  4. (4)

    Interior equilibrium \(E^*(X^*,P^*,N^*)\) exists, when

    $$\begin{aligned} \gamma _1>max\left\{ \mu , \frac{\mu (\alpha +a\beta )}{\alpha },\frac{\alpha \alpha _1 \mu (a+k)+(\alpha +a\beta )(k k_1 \beta _1)}{\alpha k(\alpha _1+k_1 \beta _1)}\right\} , \end{aligned}$$

    where \(X^*,P^*,N^*\) are given by

    $$\begin{aligned} \left\{ \begin{array}{l} X^*=k+\frac{a k\beta \mu }{\alpha (\mu -\gamma _1)}, \\ P^*=\frac{a\mu }{\gamma _1-\mu },\\ N^*=-\frac{a\gamma _1(\alpha \alpha _1(a\mu +k_1(\mu -\gamma _1))+k k_1\beta _1((\alpha +a\beta )\mu -\alpha \gamma _1)}{\alpha \gamma k_1(\mu -\gamma _1)^2}. \end{array} \right. \end{aligned}$$
    (4)

Theorem 1

The local behavior of different equilibrium points of the system (1)–(3) is as follows:

  1. (i)

    The equilibrium point \(E_0(0,0,0)\) is always exist and unstable.

  2. (ii)

    The equilibrium point \(E_1(k,0,0)\) exists and unstable.

Proof

  1. (i)

    The characteristic equation for \(E_0(0,0,0)\) is

    $$\begin{aligned} (-\lambda +\alpha )(-\lambda +\alpha _1)(-\lambda -\mu )=0. \end{aligned}$$
    (5)

    Here, the characteristic roots are \(\lambda =\alpha\), \(\lambda =\alpha _1\), \(\lambda =-\mu\). The equilibrium \(E_0(0,0,0)\) is always unstable, since two of the characteristic roots, i.e., \(\lambda =\alpha\) and \(\lambda =\alpha _1\) of (5) are positive.

  2. (ii)

    The characteristic equation for \(E_1(k,0,0)\) is

    $$\begin{aligned} (-\lambda -\alpha )(-\lambda +(k\beta _1+\alpha _1))(-\lambda -\mu )=0. \end{aligned}$$
    (6)

    The characteristic roots are \(\lambda =-\alpha\), \(\lambda =k\beta _1+\alpha _1\), \(\lambda =-\mu\). Hence, the equilibrium point \(E_1(k,0,0)\) is unstable because one of the eigen value, i.e., \(\lambda =k\beta _1+\alpha _1\) of Eq. (6) is positive.

\(\square\)

Now, we state a lemma as similar to [22]:

Lemma 2

For the polynomial of the form, \(z^3+pz^2+qz+r=0\),

  1. (i)

    If \(r<0\) , then the equation has at least one non negative root;

  2. (ii)

    If \(r\ge 0\) and \(\triangle ={p}^2-3q\le 0,\) the equation has no non-negative value;

  3. (iii)

    If \(r\ge 0\) and \(\triangle ={p}^2-3q>0,\) the equation has non-negative roots if and only if \(z_1^*=\frac{-p+\sqrt{\triangle }}{3}\) and \(h(z_1^*)\le 0,\) where \(h(z)=z^3+pz^2+qz+r\).

Theorem 2

Let (\(H_2\)) holds. For the system (1)–(3),

  1. (i)

    The natural enemy free equilibrium \(E_2(X_2,P_2,0)\) is locally asymptotically stable for all \(\tau _1\in [0,\tau _{10}^+)\).

  2. (ii)

    If \(\tau _1\ge \tau _{10}^+\), then the equilibrium \(E_2(X_2,P_2,0)\) is unstable and undergoes Hopf bifurcation.

Proof

The characteristic equation of the jacobian matrix at \(E_2\) can be written as:

$$\begin{aligned} (\lambda ^3+A\lambda ^2+B\lambda +C)+(E\lambda +D)e^{-\lambda \tau _1}=0, \end{aligned}$$
(7)

where \(A=-a_1-a_4-a_6\), \(B= a_6(a_1+a_4)+a_1 a_4\), \(C=-a_1 a_4 a_6\), \(E=-a_2 a_3\), \(D=a_2 a_3 a_6\) and \(a_1=-\frac{2X_2\alpha }{k}+\alpha -P_2 \beta\), \(a_2=-X_2 \beta\), \(a_3=P_2 \beta _1\), \(a_4=\alpha _1-\frac{2 P_2 \alpha _1}{k_1}+X_2 \beta _1\), \(a_5=-\frac{P_2 \gamma }{a+P_2}\), \(a_6=-\mu +\frac{P_2\gamma _1}{a+P_2}\).

In the absence of delay (\(\tau _1=0\)), the transcendental Eq. (7) reduces to

$$\begin{aligned} \lambda ^3+A\lambda ^2+(B+E)\lambda +(C+D)=0, \end{aligned}$$
(8)

where \(A=-a_1-a_4-a_6\), \(B+E=a_6(a_1+a_4)+a_1 a_4-a_2 a_3\), \(C+D=-a_1 a_4 a_6+a_2 a_3 a_6\). By Routh–Hurwitz criterion, all the roots of Eq. (8) have negative real parts and the equilibrium \(E_2\) is locally asymptotically stable if \((H_2)\): A, \((B+E)\), \(C+D>0\) and \(A(B+E)-(C+D)>0\) holds. Assume that \(\lambda =iw\) is root of (7), therefore we have

$$\begin{aligned} {(iw) }^3+ & {} A(iw)^2+B(iw)+C+((E(iw) +D)e^{-iw \tau _1}=0. \end{aligned}$$
(9)

Equating real and imaginary parts from (9), it can be obtained

$$\begin{aligned} Ew\sin {w\tau _1}+D\cos {w\tau _1}= & {} A w^2-C, \end{aligned}$$
(10)
$$\begin{aligned} E w\cos {w\tau _1}- D\sin {w\tau _1}= & {} w^3-B w. \end{aligned}$$
(11)

Solving (10) and (11), we get

$$\begin{aligned} w^6+pw^4+qw^2+r=0, \end{aligned}$$
(12)

where

$$\begin{aligned} \begin{array}{ll} p=A^2-2B,\\ q=B^2-2(A C)-E^2,\\ r=C^2-D^2. \end{array} \end{aligned}$$

By substituting \(w^2=z\) in Eq. (12), we define

$$\begin{aligned} F(z)=z^3+pz^2+qz+r. \end{aligned}$$

By Lemma 2, there exists at least one positive root \(w=w_0\) of Eq. (12) satisfying (10) and (11), which implies that Eq. (7) has a pair of purely imaginary roots \(\pm iw_0\). Solving (10) and (11) for \(\tau _1\) and substituting the value of \(w=w_0\), the corresponding \(\tau _{1k}>0\) is given by

$$\begin{aligned} \tau _{1k}^+=\frac{1}{w_0}\left[ \cos ^{-1}\left( \frac{E w_0^4+(A D-B E)w_0^2-C D }{E^2w_0^2+D^2)^2}\right) + 2k\pi \right] , \end{aligned}$$

where, k is a positive integer. Since the existence of Hopf bifurcation at \(\tau _{10}^+,\) it is required that the transversality condition \(Re\left[ \left( \frac{d\lambda }{d\tau _1}\right) ^{-1}\right] _{\tau _1=\tau _{10}^+}\ne 0\) should hold, therefore taking the derivative of \(\lambda\) with respect to \(\tau _1\) in (7), we get

$$\begin{aligned} \left( \frac{d\lambda }{d\tau _1}\right) ^{-1}=\frac{(3\lambda ^2+2A\lambda +B)e^{\lambda \tau _1}+E}{\lambda (E \lambda +D)}-\frac{\tau _1}{\lambda }. \end{aligned}$$

At \(\lambda =iw_0\) and \(\tau _1=\tau _{10}^+\), we have

$$\begin{aligned} Re \left[ \left( \frac{d\lambda }{d\tau _1}\right) ^{-1}\right] =\frac{MQ-NR}{w_0(L^2+M^2)}, \end{aligned}$$

where \(K=-3w_0^2+B\), \(L=2A w_0\), \(M=D\), \(N=E w_0\), \(Q=K \sin w_0 \tau _{10}+L \cos w_0 \tau _{10}\) and \(R=K \cos w_0 \tau _{10}-L \sin w_0 \tau _{10}+E\).

Now, we have,

$$\begin{aligned} Re\left[ \left( \frac{d\lambda }{d\tau _1}\right) ^{-1}\right] _{\tau _1=\tau _{10}^+}\ne 0, \ if \ MQ\ne NR. \end{aligned}$$

\(\square\)

Theorem 3

Let (\(H_3\)) holds. For the system (1)–(3),

  1. (i)

    The interior equilibrium \(E^*(X^*,P^*,N^*)\) is locally asymptotically stable for all \(\tau _1\in [0,\tau _{10}^+)\).

  2. (ii)

    If \(\tau _1\ge \tau _{10}^+\), then the equilibrium \(E^*(X^*,P^*,N^*)\) is unstable and undergoes Hopf bifurcation.

Proof

The characteristic equation of the jacobian matrix at \(E^*\) can be written as:

$$\begin{aligned} (\lambda ^3+A_2\lambda ^2+A_1\lambda +A_0)+(B_1\lambda +B_0)e^{-\lambda \tau _1}+(C_1\lambda +C_0)e^{-\lambda \tau _2}=0, \end{aligned}$$
(13)

where \(A_2=-(b_1+b_4+b_7)\), \(A_1= b_1 b_4+b_1 b_7+b_4 b_7\), \(A_0=- b_1 b_4 b_7\), \(B_1=-b_2 b_3\), \(B_0=b_2 b_3 b_7\), \(C_1=-b_5 b_6\), \(C_0=b_1 b_5 b_6\)

and

\(b_1=-\frac{X^*\alpha }{k}+(1-\frac{X^*}{k})\alpha -P^* \beta\), \(b_2=-X^* \beta\), \(b_3=P^* \beta _1\), \(b_4=\frac{P^* N^* \gamma }{(a+P^*)^2}-\frac{N^* \gamma }{a+P^*}+(1-\frac{P^*}{k_1})\alpha _1-\frac{P^* \alpha _1}{k_1} +X^* \beta _1\), \(b_5=-\frac{P^* \gamma }{a+P^*}\), \(b_6=-\frac{P^* N^* \gamma _1}{(a+P^*)^2}+\frac{N^* \gamma _1}{a+P^*}\), \(b_7=-\mu +\frac{P^*\gamma _1}{a+P^*}\).

In the absence of delay \(\tau _1=0\) and \(\tau _2=0\), the transcendental Eq. (13) reduces to

$$\begin{aligned} \lambda ^3+A_2\lambda ^2+(A_1+B_1+C_1)\lambda +(A_0+B_0+C_0)=0, \end{aligned}$$
(14)

By Routh–Hurwitz criterion, we know that if \((H_3):A_0+B_0+C_0>0\), \(A_2(A_1+B_1+C_1)>A_0+B_0+C_0\) holds, then all the roots of Eq. (14) have negative real parts and the equilibrium \(E^*\) is locally asymptotically stable. Obviously, \(iv(\tau _1)\) \(v>0\) is a root of Eq. (13) with \(\tau _2=0\) if and only if \(-iv^3-A_2 v^2+(A_1+C_1)vi +A_0+C_0+(iB_1v+B_0)(\cos v \tau _1-i \sin v \tau _1)=0\) [30]. On separating real and imaginary parts from above equation, we have

$$\begin{aligned} \left\{ \begin{array}{l} -v^3+(A_1+C_1)v=B_0 \sin v \tau _1-B_1 v \cos v\tau _1, \\ A_2v-(A_0+C_0)=B_0 \cos v\tau _1+B_1 v \sin v \tau _1, \end{array} \right. \end{aligned}$$
(15)

which gives us

$$\begin{aligned} v^6+p_1 v^4+q_1 v^2+r_1=0, \end{aligned}$$
(16)

where

$$\begin{aligned} \begin{array}{ll} p_1=A_2^2-2(A_1+C_1),\\ q_1=(A_1+C_1)^2-2A_2(A_0+C_0)-B_1^2,\\ r_1=(A_0+C_0)^2-B_0^2. \end{array} \end{aligned}$$

Let \(v^2=y\), then Eq. (16) becomes,

$$\begin{aligned} F(z)=y^3+p_1 y^2+q_1 y+r_1=0. \end{aligned}$$

By using Lemma 2 and proceeding like above Theorem (2), i.e., to avoid the repetition of mathematical calculations, we get the required existence condition of Hopf bifurcation for equilibrium point \(E^*\) at \(\tau _{10}^+\). we see that if \(\tau _1\ge \tau _{10}^+\), then the equilibrium \(E^*(X^*,P^*,N^*)\) is unstable and undergoes Hopf bifurcation. \(\square\)

Sensitivity analysis

In this section, the sensitivity analysis of the system (1)–(3) at the interior equilibrium point is carried out. The respective sensitive parameters of the state variables of the system at interior equilibrium point are given in the Table 1, using the values of parameters: \(\alpha =1.1\); \(k=2\); \(\beta =0.05\); \(\alpha _1=1.6\); \(k_1=3\); \(\beta _1=0.01\); \(\gamma =0.5\); \(a=1\); \(\gamma _1=0.3\); \(\mu =0.2\). It is clear that \(\alpha\), k, \(\gamma _1\) have a positive impact on \(X^*\). Also, the impact of \(\beta\), a, \(\mu\) is negative on \(X^*\), whereas the impact of remaining parameters on \(X^*\) is zero. The parameter k is more sensitive to \(X^*\). Also a, \(\mu\) have a positive impact on \(P^*\). The impact of parameter \(\gamma _1\) on \(P^*\) is negative; the remaining parameters have zero impact on \(P^*\). The more sensitive parameters to \(P^*\) are \(\gamma _1\) and \(\mu\). Again, the impact of \(\alpha\), k, \(\alpha _1\), \(k_1\), \(\beta _1\), \(\gamma _1\) on \(N^*\) is positive. The impact of \(\beta\), \(\gamma\), a, \(\mu\) is negative on \(N^*\). Clearly, \(\gamma _1\) and \(\mu\) are more sensitive parameters to \(N^*\).

Table 1 The sensitive indices \(\gamma _{y_u}^{x_v}=\frac{\partial x_v}{\partial y_u}\times \frac{y_u}{x_v}\) of the model (1)–(3) to the parameters \(y_u\) for the parameter values: \(\alpha =1.1\); \(k=2\); \(\beta =0.05\); \(\alpha _1=1.6\); \(k_1=3\); \(\beta _1=0.01\); \(\gamma =0.5\); \(a=1\); \(\gamma _1=0.3\); \(\mu =0.2\)
Full size table

Numerical simulations

Numerical simulations of the system (1)–(3) are performed to support our analytic findings with the help of MATLAB. The natural enemy free equilibrium \(E_2(1.24,2.44,0)\) is stable for parameter values: \(\alpha =4.5\); \(k=2\); \(\beta =0.7\); \(\alpha _1=0.6\); \(k_1=1.2\); \(\beta _1=0.5\); \(\gamma =0.05\); \(a=1\); \(\gamma _1=0.044\); \(\mu =0.05\) and result is shown in Fig. 3. Moreover, the natural enemy free equilibrium \(E_2(2.26,7.81,0)\) is stable for the parametric values: \(\alpha =1.8\); \(k=17\); \(\beta =0.2\); \(\alpha _1=0.3\); \(k_1=6\); \(\beta _1=0.04\); \(\gamma =0.6\); \(a=0.05\); \(\gamma _1=0.3\); \(\mu =0.001\); \(\tau _1=8.3<\tau _{10}^+=9.25\), see Fig. 4. The natural enemy free equilibrium \(E_2(2.26,7.81,0)\) is unstable and Hopf bifurcation appears for the parametric values: \(\alpha =1.8\); \(k=17\); \(\beta =0.2\); \(\alpha _1=0.3\); \(k_1=6\); \(\beta _1=0.04\); \(\gamma =0.6\); \(a=0.05\); \(\gamma _1=0.3\); \(\mu =0.001\); \(\tau _1=10.25>\tau _{10}^+=9.25\) and result is shown in Fig. 5. The interior equilibrium \(E^{*}(1.82,2,3.31)\) is stable for parametric values: \(\alpha =1.1\); \(k=2\); \(\beta =0.05\); \(\alpha _1=1.6\); \(k_1=3\); \(\beta _1=0.01\); \(\gamma =0.5\); \(a=1\); \(\gamma _1=0.3\); \(\mu =0.2\), see Fig. 6. It is clear from Fig. 7 that the interior equilibrium \(E^{*}(1.88,0.25,1.23)\) is stable for parametric values: \(\alpha =0.2\); \(k=5\); \(\beta =0.5\); \(\alpha _1=0.32\); \(k_1=2\); \(\beta _1=0.1\); \(\gamma =0.2\); \(a=1\); \(\gamma _1=0.01\); \(\mu =0.002\); \(\tau _1=0.6<\tau _{10}^+=1\). It is obvious from Fig. 8 that the interior equilibrium \(E^{*}(1.88,0.25,1.23)\) is unstable and Hopf bifurcation appears for the parametric values: \(\alpha =0.2\); \(k=5\); \(\beta =0.5\); \(\alpha _1=0.32\); \(k_1=2\); \(\beta _1=0.1\); \(\gamma =0.2\); \(a=1\); \(\gamma _1=0.01\); \(\mu =0.002\); \(\tau _1=1.5>\tau _{10}^+=1\).

Fig. 3
figure 3

The natural enemy free equilibrium \(E_2(1.24,2.44,0)\) is stable for parameter values: \(\alpha =4.5\); \(k=2\); \(\beta =0.7\); \(\alpha _1=0.6\); \(k_1=1.2\); \(\beta _1=0.5\); \(\gamma =0.05\); \(a=1\); \(\gamma _1=0.044\); \(\mu =0.05\)

Full size image
Fig. 4
figure 4

The natural enemy free equilibrium \(E_2(2.26,7.81,0)\) is stable for the parametric values: \(\alpha =1.8\); \(k=17\); \(\beta =0.2\); \(\alpha _1=0.3\); \(k_1=6\); \(\beta _1=0.04\); \(\gamma =0.6\); \(a=0.05\); \(\gamma _1=0.3\); \(\mu =0.001\); \(\tau _1=8.3<\tau _{10}^+=9.25\)

Full size image
Fig. 5
figure 5

The natural enemy free equilibrium \(E_2(2.26,7.81,0)\) is unstable and Hopf bifurcation appears for the parametric values: \(\alpha =1.8\); \(k=17\); \(\beta =0.2\); \(\alpha _1=0.3\); \(k_1=6\); \(\beta _1=0.04\); \(\gamma =0.6\); \(a=0.05\); \(\gamma _1=0.3\); \(\mu =0.001\); \(\tau _1=10.25>\tau _{10}^+=9.25\)

Full size image
Fig. 6
figure 6

The interior equilibrium \(E^{*}(1.82,2,3.31)\) is stable for parametric values: \(\alpha =1.1\); \(k=2\); \(\beta =0.05\); \(\alpha _1=1.6\); \(k_1=3\); \(\beta _1=0.01\); \(\gamma =0.5\); \(a=1\); \(\gamma _1=0.3\); \(\mu =0.2\)

Full size image
Fig. 7
figure 7

The interior equilibrium \(E^{*}(1.88,0.25,1.23)\) is stable for parametric values: \(\alpha =0.2\); \(k=5\); \(\beta =0.5\); \(\alpha _1=0.32\); \(k_1=2\); \(\beta _1=0.1\); \(\gamma =0.2\); \(a=1\); \(\gamma _1=0.01\); \(\mu =0.002\); \(\tau _1=0.6<\tau _{10}^+=1\)

Full size image
Fig. 8
figure 8

The interior equilibrium \(E^{*}(1.88,0.25,1.23)\) is unstable and Hopf bifurcation appears for the parametric values: \(\alpha =0.2\); \(k=5\); \(\beta =0.5\); \(\alpha _1=0.32\); \(k_1=2\); \(\beta _1=0.1\); \(\gamma =0.2\); \(a=1\); \(\gamma _1=0.01\); \(\mu =0.002\); \(\tau _1=1.5>\tau _{10}^+=1\)

Full size image

Conclusion

Here, a food chain: a plant–pest–natural enemy system with the gestation delay for pest and the natural enemy is proposed. There are four feasible equilibrium points, and asymptotic stability of the system is studied and analyzed for all equilibria. The steady states \(E_0(0,0,0)\) and \(E_0(K,0,0)\) are always unstable. The existence of Hopf bifurcation at the natural enemy free as well as interior equilibrium point is explored and determined the critical limits for gestation delay, \(\tau _1\). It is observed that the natural enemy free steady state is stable if the gestation delay for pest (\(\tau _1\)) is below a certain threshold otherwise system observed oscillating behavior. A similar oscillating solution exists for the interior steady state. It is studied that the natural enemy free and interior equilibrium are asymptotically stable under certain conditions. Also, the sensitivity analysis is performed at interior equilibrium point for the system parameters. Numerical simulations of the system are carried out with a particular set of parameter values to verify our analytic results.