Electrokinetic energy conversion of two immiscible Newtonian fluids with pressure-dependent viscosities in the microchannel

Abstract

By perturbation method, this article presents asymptotic analytical solutions for streaming potential and electrokinetic energy conversion (EKEC) efficiency of two immiscible fluids between microparallel plates. The results show that the EKEC efficiency can be enhanced obviously by the permittivity and viscosity ratios, the maximum efficiency is about 67% and 28%, respectively, but shows a decreasing trend with the interface electric potential difference, the maximum efficiency is about 44%. This indicates that the permittivity and viscosity ratios can improve the energy conversion efficiency. Furthermore, we company the EKEC efficiency in two-layer and single-layer fluid. It is found that the conversion efficiency of two-layer fluid systems can be higher than that of single-layer fluid systems by up to 50%. This work adds a quantitative dimension to the understanding of the interplay between physical parameters, and manipulation of interfaces can effectively facilitate the separation of biological samples and direct the flow direction of fluids in flow-switching devices.

1 Introduction

Microfluidic has drawn millions of interests from scientists all over the world and will strictly run on, where microfluidic structures and materials are a considerable research area in the field of microfluidic, which may still boost the application of microfluidic devices in plentiful scientific fields. On the other hand, microfluidic furnishes a formidable and elastic platform for material manufacturing. The design and development of productive microfluidic equipment is a hurried demand for the further development of technology. The latest research on microfluidics involves drug screening, and drug delivery, single-cell analysis, 3D printed microfluidics for bioanalysis, and nucleic acid detection with microfluidic chip [1,2,3,4]. Bhattacharya et al. [5] discuss the mixing performance of micromixers by improving the passive T-shaped micromixer with a sinusoidal wavy wall. Gayen et al. [6] tried to use electrodynamic effects (such as electroosmotic flow) to improve the mixing efficiency of two fluids of different concentrations in a micromixer. They explored the combined effect of electroosmotic flow and rigid baffles. Kumar et al. [7] reported the design of a new electroosmotic micromixer, which uses a square SSAR structure and microelectrodes. The effects of airflow (inlet velocity) and electric field (electrode potential arrangement, voltage, AC frequency, and phase difference) parameters on the mixing performance of the new microchannel mixer were studied in depth. Customarily, tiny fluids can be accurately coped with and manipulated by microfluidics technology using pressure gradients, electric fields, magnetic fields, or suitable combinations [8,9,10]. Such as, Chu and Jian [11] took the conjunct impact on the two kinds of forced time cyclical electric fields and the outer perpendicular magnetic fields into account, and achieved the magnetohydrodynamic electroosmotic flow for Maxwell fluid via both microparallel plates with patterned charged surfaces. Qi et al. [12] performed a comprehensive theoretical exploration of the electromagnetic fluid flow through rectangular microchannels with the composite action of exterior electric and magnetic fields. The heat transfer attribute of incompressible magnetohydrodynamic flow via two-dimensional rectangular microchannels was theoretically investigated by Yang et al. [13], who added a transverse electric field and a perpendicular magnetic field to the existing axial electric field, taking into account the electromagnetic effect under the combined action of electrodynamics.

Theoretically, most substances' hand surface charges have been brought into contact with the water medium. The re-disposition of charges both on the solid surface and in the liquid contributes to the composition of an electric double layer (EDL), which mostly pushes to a nanometer thickness. Considering the pressure-driven transmission is triggered in the micro/nanochannels, the electric charge of EDL is transferred downstream, resulting in the build-up of downstream charged particles. Thus, the potential difference generated between upstream and downstream is called the SP. The above research on SP mainly concentrates on the transport of electrolyte solutions with surface charge and electric potential [14,15,16]. The SP of the microparallel channel considering the rotation effect under the low potential approximation is discussed by Chen et al. [17]. The results show that the SP decreases along with the increase of the electrokinetic width. Zhang et al. [18] computed and compared the SP under different period functions, which produced a result that the square waveform can effectively heighten the SP. In addition, besides SP, the emergence of mechanical energy via pressure driving and the chemical energy generated by EDL will be transformed into electric energy. This transformation is called electrokinetic energy conversion (EKEC) in academia. In some research articles, it is generally represented quantitatively by EKEC efficiency. In some effective engineering problems, the magnitude of EKEC efficiency is specifically significant, thus this kind of problem has been widely considered by scholars [19,20,21]. Xie and Jian [22] deliberated the EKEC of power-law fluids in slit nanochannels. The results express that the transformation efficiency of pseudoplastic fluid is topmost compared with that of dilatant fluid and Newtonian fluid under the same physical parameters. Gao et al. [23] theoretically analyzed and compared the EKEC efficiency of viscoelastic fluid using Maxwell as a model in a circular microchannel driven by a periodic pressure gradient. The results declare that the EKEC efficiency of square wave periodic pressure gradient is the most significant in both low and high frequencies. Ding et al. [24] researched the influence of curvature on EKEC in curved microtubules using perturbation solutions. Research has found that the bent channel shape may be conducive to elevating the utmost efficiency of EKEC.

Evidence from early literature suggests that the viscosity of various liquids is a strong index of pressure, thus the linear correlation between viscosity and pressure is also to be supposed to consider in the process of micro-electro-mechanical-systems (MEMS) design. Experimental data on liquid flow in high-pressure (1-30Mpa)-driven microtubes suggest that the pressure gradient is changeable, which is the result of the pressure dependence of viscosity [25]. The correlation-dependence of fluid viscosity respecting pressure has been studied in several relevant research fields, such as metallic glasses, the development of heavy crudes, and the measurement of ionic liquid [26,27,28]. Fluids of viscosity depending on the pressure at high-pressure techniques have received increasing attention over the past few decades result of the mounting awareness in high-pressure engineering applications and techniques [29,30,31]. Chen et al. [32] discussed flow driven by pressure in slippery nanochannels of an incompressible viscoelastic fluid, where related to exponential pressure-dependent viscosity and relaxation time. The outcomes imply that in pace with the growth of the pressure relaxation coefficient, the SP of the fluid reduces, and the fluid viscosity increases. When the slip length increases, the viscosity of viscoelastic fluid weakens. Fetecau et al. [33] built an accurate and simple representation of the permanent solution corresponding to the two oscillating motions of impressible convection Maxwell fluid for exponential viscosity and pressure among parallel plates. Jian [34] has used the asymptotic solution to predict the EKEC efficiency well when the velocity and pressure are unknown. Research has shown that pressure-dependent viscosity could slightly heighten the SP and EKEC efficiency. It was implied by added output that electric energy could be utilized for external loads.

According to the above, the theoretical, numerical, and experimental research on the SP and the EKEC efficiency in single-layer flow systems have been extensively studied. Two or more layers of unmixing liquid flow systems are the central issue respecting research fields for manufacturing, mining process, and biochemical analysis. Based on the prosperous application of a monolayer electroosmosis pump, the electroosmosis driving mechanism has been automatically expanded in double- or multilayer fluid systems. Generally speaking, at two or more layers of unmixing liquids hand mutually, a laminar fluid interface is created, so precise control of the fluid interface is required. On account of the triumphant application of the classical driving mechanism in the monolayer flow system, the driving mechanism is straight copied in a doublelayer or multilayer flow system [35,36,37]. The entropy-produced analytical research of dual-fluid drawing systems is discussed by Xie et al. [38]. In the case where the bottom fluid is assumed to be an electrolyte solution affected by the magnetic field, and the upper fluid is assumed to be a nonconductive viscoelastic Phan-Thien-Tanner fluid, the consequences demonstrate that the magnetic field could promote local entropy yield, while the viscoelastic physical parameters could suppress local entropy yield. Under the stack effect of EDL, imposed electric field and pressure in the vicinity of the solid interface and both liquid interface, Deng et al. [39] studied the electric osmosis and pressure-driven two-layer combined flow of power-law fluid in the circular channel. Xie and Jian [40] analyzed the entropy generation of the two-layer MHD electroosmotic flow via channel. The affection of the ratio of fluid physical parameters concerning the velocity and temperature distribution of the two layers of fluid is discussed. The consequences reveal that the entropy production of fluid forcefully counts on the velocity field and temperature field, and the local entropy production of both bottom fluid and upper fluid shows a diminishing trend from the microchannel wall to the fluid interface.

Inspired by the abovementioned investigations, the SP and EKEC efficiency of two immiscible liquid layers of Newtonian fluid with pressure-dependent viscosity via a microparallel channel will be studied. In addition, as far as authors know, meticulous considerations have not been appreciated on the microfluidic flow mechanism of two immiscible liquid layers applied pressure gradient. In this paper, interface electric potential difference, the ratio of the permittivity, the ratio of fluid viscosity, and dimensionless electrokinetic width are considered, respectively. Meanwhile, many scholars [41, 42] used the PM to study the influence of the abovementioned related parameters on the efficiency of EKEC, which shows that the asymptotic solution has become a usable method to develop fluid flow in more complex situations. At the same time, the manipulation of the interface can effectively promote the separation of biological samples, which effectively promotes the development of biomedicine and bioanalysis. Eventually, we provide an intuitive comparison between the EKEC efficiency in two-layer fluid and that of single-layer fluid. The research shows that the EKEC efficiency of the two-layer fluidic system emerges as a visible enhancement compared with the single-layer fluidic system. Our findings hope to provide feasible and valuable theoretical guidance for considering two immiscible Newtonian fluids to improve the efficiency of EKEC.

2 Theoretical derivation

2.1 Mathematical model

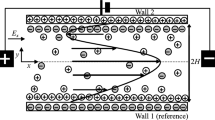
Figure 1 describes the physical model of the electrokinetic flow behavior of two immiscible liquid layers with Newtonian fluid possessing the characteristic of pressure-dependent viscosity through the microparallel plate channel in the process of imposed pressure gradient. In a parallel plate channel of length $l$, width $W$, height of the upper fluid $H_{1}$, the height of the bottom fluid $H_{2}$, and the overall height of the microchannel ${\text{H}}$, that is, $H = H_{1} + H_{2}$. Assuming that the length is much greater than the height, that is, $l$»$H$. Besides, the interface between the two immiscible fluids is a plane. The Cartesian coordinate system is founded at the fluid interface.

Fig. 1

Schematic diagram of in two-layer Newtonian fluids through a parallel microchannel

2.2 EDL potential distribution

Due to the electrochemical interaction between the Newtonian fluid and the channel wall, the EDL appeared near the channel wall. The relationship between local volumetric net charge density and the electrical potential of the first and second layers could be portrayed by the subsequent Poisson-Boltzmann equation:

$$ \frac{{d^{2} \psi_{i} }}{{dy^{2} }} = - \frac{{\rho_{{e_{i} }} }}{{\varepsilon_{i} }}\;\;\;i = 1,\;2 $$

(1)

where $\psi_{{\text{i}}}$ is the electric potential and ${\text{i}}$ denotes the upper or bottom fluid layer. $\rho_{{e_{i} }}$ is the local volumetric net charge density for layer I and layer II respectively and $\varepsilon_{i}$ is the permittivity of the electrolyte liquid for layer I and layer II, respectively. Assuming that the ions are point charges, the variation of local volumetric net charge density follows Boltzmann distribution, as follow:

$$ \rho_{{e_{i} }} = - 2n_{0} ez\sinh \left( {\frac{{ez\psi_{i} }}{{k_{B} T_{av} }}} \right)\;\;\;i = 1,\;2 $$

(2)

where ${\text{n}}_{0}$ is ion density of bulk solution, ${\text{e}}$ is the elementary charge and ${\text{z}}$ is the ion valence, as well as ${\text{k}}_{{\text{B}}}$ is the Boltzmann constant and ${\text{T}}_{{{\text{av}}}}$ is the absolute temperature. Combining Eqs. (1) and (2), we obtained:

$$ \frac{{d^{2} \psi_{i} }}{{dy^{2} }} = \frac{{2n_{0} ez}}{{\varepsilon_{i} }}\sinh \left( {\frac{{ez\psi_{i} }}{{k_{B} T_{av} }}} \right)\;\;\;i = 1,\;2 $$

(3)

For smaller value of electrical potential, the Debye–Hückel linearization principle for the sine hyperbolic function at the right side of Eq. (3) can be used, namely, $\sinh \left( {\frac{{ez\psi_{i} }}{{k_{B} T_{av} }}} \right) \approx \frac{{ez\psi_{i} }}{{k_{B} T_{av} }}$ yields,

$$ \frac{{d^{2} \psi_{1} }}{{dy^{2} }} = \kappa_{1}^{2} \psi_{1} \;\;\;0 \le y \le H_{1} $$

(4)

$$ \frac{{d^{2} \psi_{2} }}{{dy^{2} }} = \kappa_{2}^{2} \psi_{2} \;\;\; - H_{2} \le y \le 0 $$

(5)

where $\kappa_{i} = \left( {{{2e^{2} z^{2} n_{0} } \mathord{\left/ {\vphantom {{2e^{2} z^{2} n_{0} } {\varepsilon_{i} k_{B} T_{av} }}} \right. \kern-0pt} {\varepsilon_{i} k_{B} T_{av} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$ is the Debye-Hückel parameter and ${1 \mathord{\left/ {\vphantom {1 {\kappa_{{\text{i}}} }}} \right. \kern-0pt} {\kappa_{{\text{i}}} }}$ indicates the characteristic thickness of the EDL.

Suppose the microchannel surface supports a zeta potential $\zeta_{1}$ at the upper wall and $\zeta_{2}$ at the bottom wall, respectively. We introduce Gauss’s law into the electrical displacement and the zeta potential difference at the interface (y = 0) between layer I and layer II [37], [43]. Thus, the boundary conditions can be simplified to:

$$ \psi_{1} \left| {_{{y = H_{1} }} = \zeta_{1} } \right.,\;\psi_{2} \left| {_{{y = - H_{2} }} = \zeta_{2} } \right.,\;\left( {\psi_{1} - \psi_{2} } \right)\left| {_{y = 0} } \right. = \Delta \psi ,\;\left( {\varepsilon_{1} \frac{{d\psi_{1} }}{dy} - \varepsilon_{2} \frac{{d\psi_{2} }}{dy}} \right)\left| {_{y = 0} } \right. = - q_{s} $$

(6)

Next, we introduce some nondimensional variables.

$$ \overline{y} = \frac{y}{H},\;\left[ {\overline{\psi }_{1} ,\overline{\psi }_{2} ,\overline{\zeta }_{1} ,\overline{\zeta }_{2} ,\Delta \overline{\psi }} \right] = \frac{ez}{{k_{B} T_{av} }}\left[ {\psi_{1} ,\psi_{2} ,\zeta_{1} ,\zeta_{2} ,\Delta \psi } \right] $$

(7)

Substituting in the above nondimensional variables into Eqs. (4)–(6), the governing equation and boundary conditions turn into,

$$ \frac{{d^{2} \overline{\psi }_{1} }}{{d\overline{y}^{2} }} = K_{1}^{2} \overline{\psi }_{1} \;\;\;0 \le \overline{y} \le h_{1} $$

(8)

$$ \frac{{d^{2} \overline{\psi }_{2} }}{{d\overline{y}^{2} }} = K_{2}^{2} \overline{\psi }_{2} \;\;\; - h_{2} \le \overline{y} \le 0 $$

(9)

$$ \overline{\psi }_{1} \left| {_{{\overline{y} = h_{1} }} = \overline{\zeta }_{1} } \right.,\;\overline{\psi }_{2} \left| {_{{\overline{y} = - h_{2} }} = \overline{\zeta }_{2} } \right.,\;\left( {\overline{\psi }_{1} - \overline{\psi }_{2} } \right)\left| {_{{\overline{y} = 0}} } \right. = \Delta \overline{\psi },\;\left( {\varepsilon^{ * } \frac{{d\overline{\psi }_{1} }}{{d\overline{y}}} - \frac{{d\overline{\psi }_{2} }}{{d\overline{y}}}} \right)\left| {_{{\overline{y} = 0}} } \right. = - Q $$

(10)

where $h_{i} = {{H_{i} } \mathord{\left/ {\vphantom {{H_{i} } H}} \right. \kern-0pt} H}$, $K_{i} = \kappa_{i} H$, $\varepsilon^{ * } = {{\varepsilon_{1} } \mathord{\left/ {\vphantom {{\varepsilon_{1} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}$, $Q = {{\left( {q_{s} ezH} \right)} \mathord{\left/ {\vphantom {{\left( {q_{s} ezH} \right)} {\left( {\varepsilon_{2} k_{B} T_{av} } \right)}}} \right. \kern-0pt} {\left( {\varepsilon_{2} k_{B} T_{av} } \right)}}$. Significantly, the electrokinetic width ${\text{K}}_{{\text{i}}}$ of the two layers of fluid is identical in the current study, namely $K_{1} = K_{2} = K$. $\varepsilon^{ * }$ is the ratio of the permittivity. Equations (8) and (9) have general solutions below,

$$ \overline{\psi }_{1} = A_{1} \cosh \left( {K_{1} \overline{y}} \right) + B_{1} \sinh \left( {K_{1} \overline{y}} \right) $$

(11)

$$ \overline{\psi }_{2} = A_{2} \cosh \left( {K_{2} \overline{y}} \right) + B_{2} \sinh \left( {K_{2} \overline{y}} \right) $$

(12)

Operating the boundary condition (10) will get ${\text{A}}_{1}$, ${\text{B}}_{1}$, ${\text{A}}_{2}$ and ${\text{B}}_{2}$, where,

$$ \begin{gathered} B_{2} = \frac{{\overline{\zeta }_{1} \varepsilon^{ * } K_{1} \cosh \left( {K_{2} h_{2} } \right) + Q\sinh \left( {K_{1} h_{1} } \right)\cosh \left( {K_{2} h_{2} } \right) - \left( {\overline{\zeta }_{2} \varepsilon^{ * } K_{1} + \Delta \overline{\psi }\varepsilon^{ * } K_{1} \cosh \left( {K_{2} h_{2} } \right)} \right)\cosh \left( {K_{1} h_{1} } \right)}}{{\varepsilon^{ * } K_{1} \cosh \left( {K_{2} h_{2} } \right)}} \\ \frac{{\varepsilon^{ * } K_{1} }}{{K_{2} \sinh \left( {K_{1} h_{1} } \right) - \varepsilon^{ * } K_{1} \tanh \left( {K_{2} h_{2} } \right)\cosh \left( {K_{1} h_{1} } \right)}} \\ \end{gathered} $$

$$ B_{1} = \frac{{B_{2} K_{2} - Q}}{{\varepsilon^{ * } K_{1} }} $$

$$ A_{2} = \frac{{\overline{\zeta }_{2} + B_{2} \sinh \left( {K_{2} h_{2} } \right)}}{{\cosh \left( {K_{2} h_{2} } \right)}} $$

$$ A_{1} = A_{2} + \Delta \overline{\psi } $$

2.3 Two-layer fluid velocity distribution

Consider a pressure-driven electrokinetic flow in a two-layer incompressible Newtonian fluid with pressure dependence on viscosity. The corresponding equation in continuity and Navier–Stokes equation [34] are as follows:

$$ \nabla u_{j} = 0 $$

(13)

$$ \rho_{i} \left[ {\frac{{\partial u_{j} }}{\partial t} + \left( {u_{j} \cdot \nabla } \right)u_{j} } \right] = - \nabla P_{j} + \nabla \tau_{i} + \rho_{{e_{i} }} E_{s} ,\;\;\;j = {\rm I},\Pi $$

(14)

where $\rho_{i}$ is the fluid density, $u_{j}$ is the flow velocity, ${\text{P}}$ is the pressure, $\vec{E}_{s} = \left( {E_{s} ,0,0} \right)$ is the induced electric field vector due to the SP, and $\nabla \tau_{i}$ is the Cauchy stress tensor. ${\text{j}}$ stands for upper or bottom fluid velocity and pressure symbol. Here, suppose dynamic viscosity $\eta$ has a linear relationship with pressure ${\text{P}}$, as follows:

$$ \eta \left( P \right) = \eta_{0} \left( {1 + \beta P} \right) $$

(15)

here, $\eta_{0}$ is the viscosity at the reference pressure ${\text{P}} = 0$, β is the constant pressure-viscosity coefficient. Hence, the momentum equation for Newtonian fluids in the two-layer fluids could change into,

$$ - \frac{{\partial P_{\rm I} }}{\partial x} + \eta_{0} \left( {1 + \beta P_{\rm I} } \right)\frac{{d^{2} u_{\rm I} }}{{dy^{2} }} + \eta_{0}^{2} \beta^{2} \frac{{\partial P_{\rm I} }}{\partial x}\left( {\frac{{du_{\rm I} }}{dy}} \right)^{2} + \rho_{{e_{1} }} E_{s} = 0 $$

(16)

$$ - \frac{{\partial P_{\Pi } }}{\partial x} + \eta_{0} \left( {1 + \beta P_{\Pi } } \right)\frac{{d^{2} u_{\Pi } }}{{dy^{2} }} + \eta_{0}^{2} \beta^{2} \frac{{\partial P_{\Pi } }}{\partial x}\left( {\frac{{du_{\Pi } }}{dy}} \right)^{2} + \rho_{{e_{2} }} E_{s} = 0 $$

(17)

To resolve the reduced governing equations, it is necessary to give appropriate boundary conditions. Firstly, the no-slip boundary condition requests that the velocity must disappear at the microchannel wall. Secondly, the velocity is assured of continuity at the interface of two immiscible fluids. Eventually, the balance condition of total stress is deployed at the fluid interface analog to the understanding in Ref. [40]. Moreover, different from the invariant pressure gradient-driven flow, the pressure in the immediate problem is an unidentified function that depends on ${\text{x}}$ and ${\text{y}}$ , and must be bound to dispose contemporaneously with the flow velocity. Therefore, set the pressure at the outlet of the parallel plate and specify a constant volume flow in advance. At the interface, the velocities of the two fluids should be the same and the total stress between the two layers should be the same. Different from the traditional pressure-driven mechanism, when considering the pressure-related electroviscous effect, the pressure is an unknown quantity, so it is necessary to solve the pressure and velocity simultaneously under given boundary conditions. These boundary conditions could be portrayed mathematically,

$$ u_{\rm I} \left| {_{{y = H_{1} }} } \right. = 0,\;u_{\Pi } \left| {_{{y = - H_{2} }} } \right. = 0,\;u_{\rm I} \left| {_{y = 0} } \right. = u_{\Pi } \left| {_{y = 0} } \right.,\;\mu_{1} \frac{{du_{\rm I} }}{dy}\left| {_{y = 0} } \right. = \mu_{2} \frac{{du_{\Pi } }}{dy}\left| {_{y = 0} } \right. $$

$$ P_{\rm I} \left( {l,0} \right) = 0,\;P_{\Pi } \left( {l,0} \right) = 0,\;\int_{0}^{{H_{1} }} {u_{\rm I} } dy = \frac{{Q_{1} }}{W},\;\int_{{ - H_{2} }}^{0} {u_{\Pi } } dy = \frac{{Q_{2} }}{W} $$

(18)

where $\mu_{i}$ is the fluid viscosity, $Q_{i}$ is a constant volumetric flow rate. Dimensionless variables and parameters are regulated below,

$$ \begin{gathered} \overline{x} = \frac{x}{l},\overline{u}_{j} = \frac{{u_{j} }}{{U_{i} }},U_{i} = \frac{{Q_{i} }}{HW},\overline{P}_{j} = \frac{P}{{P_{i}^{ * } }},P_{i}^{ * } = \frac{{12\eta_{0} lU_{i} }}{{H^{2} }},\overline{E}_{s} = \frac{{E_{s} }}{{E_{0} }},\varepsilon_{j} = \beta P_{i}^{ * } , \hfill \\ u_{r} = - \frac{{\varepsilon_{1} \psi_{0} E_{0} }}{{\eta_{0} U_{1} }},\alpha = \frac{H}{l},\psi_{0} = \frac{{k_{B} T_{av} }}{ez},U^{ * } = \frac{{U_{1} }}{{U_{2} }},\mu = \frac{{\mu_{1} }}{{\mu_{2} }}. \hfill \\ \end{gathered} $$

(19)

where ${\text{l}}$ is the length of the microplate, $U_{i}$ is the characteristic velocity, and $P_{i}^{ * }$ is the characteristic pressure. $E_{0}$ is the characteristic electric field, and $\varepsilon_{j}$ is the normalized pressure-viscosity coefficient. Fundamentally, ${\text{u}}_{{\text{r}}}$ stands for the ratio of electroosmotic velocity to the average velocity at the exit plane of the upper fluid. $\alpha$ is the geometrical aspect ratio. ${\text{U}}^{ * }$ is the ratio of the characteristic velocity of the upper fluid and the bottom fluid, which is set as 1 and $\mu$ is the ratio of fluid viscosity.

Substitute the mentioned dimensionless variables into Eqs. (16) and (17), the dimensionless governing equations and related boundary conditions become,

$$ - 12\frac{{\partial \overline{P}_{\rm I} }}{{\partial \overline{x}}} + \left( {1 + \varepsilon_{\rm I} \overline{P}_{\rm I} } \right)\frac{{d^{2} \overline{u}_{\rm I} }}{{d\overline{y}^{2} }} + \frac{{\varepsilon_{\rm I}^{2} \alpha^{2} }}{12}\frac{{\partial \overline{P}_{\rm I} }}{{\partial \overline{x}^{2} }}\left( {\frac{{d\overline{u}_{\rm I} }}{{d\overline{y}}}} \right)^{2} + u_{r} K_{1}^{2} \overline{\psi }_{1} \overline{E}_{s} = 0 $$

(20)

$$ - 12\frac{{\partial \overline{P}_{\Pi } }}{{\partial \overline{x}}} + \left( {1 + \varepsilon_{\Pi } \overline{P}_{\Pi } } \right)\frac{{d^{2} \overline{u}_{\Pi } }}{{d\overline{y}^{2} }} + \frac{{\varepsilon_{\Pi }^{2} \alpha^{2} }}{12}\frac{{\partial \overline{P}_{\Pi } }}{{\partial \overline{x}^{2} }}\left( {\frac{{d\overline{u}_{\Pi } }}{{d\overline{y}}}} \right)^{2} + \frac{{u_{r} K_{2}^{2} \overline{\psi }_{2} \overline{E}_{s} U^{ * } }}{{\varepsilon^{ * } }} = 0 $$

(21)

$$\overline{u}_{{\text{I}}} \left| {_{{\overline{y} = h_{1} }} } \right. = 0,\;\overline{u}_{\Pi } \left| {_{{\overline{y} = - h_{2} }} } \right. = 0,\;\overline{u}_{{\text{I}}} \left| {_{{\overline{y} = 0}} } \right. = \overline{u}_{\Pi } \left| {_{{\overline{y} = 0}} } \right.,\;\mu \frac{{d\overline{u}_{{\text{I}}} }}{{d\overline{y}}}\left| {_{{\overline{y} = 0}} } \right. = \frac{{d\overline{u}_{\Pi } }}{{d\overline{y}}}\left| {_{{\overline{y} = 0}} } \right.$$

$$ \overline{P}_{\rm I} \left( {1,0} \right) = 0,\;\overline{P}_{\Pi } \left( {1,0} \right) = 0,\;\int_{0}^{{h_{1} }} {\overline{u}_{\rm I} } d\overline{y} = 1,\;\int_{{ - h_{2} }}^{0} {\overline{u}_{\Pi } } d\overline{y} = 1 $$

(22)

The nonlinear control equation has now been reduced to a partial differential equation, but Eqs. (20) and (21) still contain two unknowns, respectively; (namely, the pressure $\overline{P}_{j}$ and the velocity $\overline{u}_{j}$). To obtain the distribution of velocity and pressure, the perturbation method is utilized and the dimensionless pressure-viscosity coefficient $\varepsilon_{j}$ is the perturbation parameter. In performing the present analyses, the typical flow parameters will be specified as follows: half-height and length of the channels are ${{\text{H}} \mathord{\left/ {\vphantom {{\text{H}} 2}} \right. \kern-0pt} 2} = 10 - 100{\text{nm}}$ and $l = 10 - 100\mu {\text{m}}$, individually. Fluid density $\rho_{i} = 10^{3} {\text{kgm}}^{ - 3}$, dynamic viscosity $\eta_{0} = 10^{ - 3} - 10^{ - 2} {\text{kg}}\left( {{\text{ms}}} \right)^{ - 1}$, pressure-viscosity coefficient $\beta = 10 - 70\;{\text{GPa}}^{ - 1}$, average velocity at the exit plane $U_{i} = 10^{ - 3} {\text{ms}}^{ - 1}$. Consequently, the extent of the parameter $\varepsilon_{{\text{j}}}$ in Eqs. (20) and (21) turn from 0.001 to 0.2. Developing the axial velocity ${\overline{\text{u}}}_{{\text{j}}}$ and pressure ${\overline{\text{P}}}_{{\text{j}}}$ treat as a perturbation series with $\varepsilon_{{\text{j}}}$ as little parameter,

$$ \overline{u}_{\rm I} \left( {\overline{y}} \right) = \overline{u}_{0} \left( {\overline{y}} \right) + \varepsilon_{\rm I} \overline{u}_{1} \left( {\overline{y}} \right) + \varepsilon_{\rm I}^{2} \overline{u}_{2} \left( {\overline{y}} \right) + \cdots $$

(23)

$$ \overline{P}_{\rm I} \left( {\overline{x},\overline{y}} \right) = \overline{P}_{0} \left( {\overline{x},\overline{y}} \right) + \varepsilon_{\rm I} \overline{P}_{1} \left( {\overline{x},\overline{y}} \right) + \varepsilon_{\rm I}^{2} \overline{P}_{2} \left( {\overline{x},\overline{y}} \right) + \cdots $$

(24)

$$ \overline{u}_{\Pi } \left( {\overline{y}} \right) = \overline{u}_{3} \left( {\overline{y}} \right) + \varepsilon_{\Pi } \overline{u}_{4} \left( {\overline{y}} \right) + \varepsilon_{\Pi }^{2} \overline{u}_{5} \left( {\overline{y}} \right) + \cdots $$

(25)

$$ \overline{P}_{\Pi } \left( {\overline{x},\overline{y}} \right) = \overline{P}_{3} \left( {\overline{x},\overline{y}} \right) + \varepsilon_{\Pi } \overline{P}_{4} \left( {\overline{x},\overline{y}} \right) + \varepsilon_{\Pi }^{2} \overline{P}_{5} \left( {\overline{x},\overline{y}} \right) + \cdots $$

(26)

The above series expansion is substituted into Eqs. (20) and (21), and the coefficients of the same power of $\varepsilon_{j}$ on both sides are equal to acquire the zero-order, first-order, and second-order control equations and relevant boundary conditions.

2.3.1 Zero-order solution

To start with, zero-order governing equation and boundary conditions are acquired by calculation, which reads,

$$ 12\frac{{\partial \overline{P}_{0} }}{{\partial \overline{x}}} = \frac{{d^{2} \overline{u}_{0} }}{{d\overline{y}^{2} }} + u_{r} K_{1}^{2} \overline{\psi }_{1} \overline{E}_{s} $$

(27)

$$ 12\frac{{\partial \overline{P}_{3} }}{{\partial \overline{x}}} = \frac{{d^{2} \overline{u}_{3} }}{{d\overline{y}^{2} }} + \frac{{u_{r} K_{2}^{2} \overline{\psi }_{2} \overline{E}_{s} U^{ * } }}{{\varepsilon^{ * } }} $$

(28)

$$\overline{u}_{0} \left| {_{{\overline{y} = h_{1} }} } \right. = 0,\;\overline{u}_{3} \left| {_{{\overline{y} = - h_{2} }} } \right. = 0,\;\overline{u}_{0} \left| {_{{\overline{y} = 0}} } \right. = \overline{u}_{3} \left| {_{{\overline{y} = 0}} } \right.,\;\mu \frac{{d\overline{u}_{0} }}{{d\overline{y}}}\left| {_{{\overline{y} = 0}} } \right. = \frac{{d\overline{u}_{3} }}{{d\overline{y}}}\left| {_{{\overline{y} = 0}} } \right.$$

$$ \overline{P}_{0} \left( {1,0} \right) = 0,\;\overline{P}_{3} \left( {1,0} \right) = 0,\;\int_{0}^{{h_{1} }} {\overline{u}_{0} } d\overline{y} = 1,\;\int_{{ - h_{2} }}^{0} {\overline{u}_{3} } d\overline{y} = 1 $$

(29)

Obviously, on the left of Eqs. (27) and (28) is a function of $\overline{x}$ and $\overline{y}$, and on the right is a function decided by ${\overline{\text{y}}}$. Hence, if Eqs. (27) and (28) have solutions, both sides are equal to the same constant value. Let this constant value be $C_{0}$ and $D_{0}$ to give,

$$ 12\frac{{\partial \overline{P}_{0} }}{{\partial \overline{x}}} = C_{0} $$

(30)

$$ \frac{{d^{2} \overline{u}_{0} }}{{d\overline{y}^{2} }} + u_{r} K_{1}^{2} \overline{\psi }_{1} \overline{E}_{s} = C_{0} $$

(31)

$$ 12\frac{{\partial \overline{P}_{3} }}{{\partial \overline{x}}} = D_{0} $$

(32)

$$ \frac{{d^{2} \overline{u}_{3} }}{{d\overline{y}^{2} }} + \frac{{u_{r} K_{2}^{2} \overline{\psi }_{2} \overline{E}_{s} U^{ * } }}{{\varepsilon^{ * } }} = D_{0} $$

(33)

Integrating twice Eqs. (31) and (33) about $\overline{y}$, the general solution of zero-order velocity reads,

$$ \overline{u}_{0} \left( {\overline{y}} \right) = - u_{r} \overline{E}_{s} \overline{\psi }_{1} + \frac{1}{2}C_{0} \overline{y}^{2} + a_{1} \overline{y} + a_{2} $$

(34)

$$ \overline{u}_{3} \left( {\overline{y}} \right) = - \frac{{u_{r} \overline{E}_{s} \overline{\psi }_{2} U^{ * } }}{{\varepsilon^{ * } }} + \frac{1}{2}D_{0} \overline{y}^{2} + b_{1} \overline{y} + b_{2} $$

(35)

Substituting the first four boundary conditions in Eq. (29), we can get,

$$ \begin{aligned} b_{1} = & \quad - \frac{{\mu u_{r} \bar{E}_{s} A_{1} }}{{\left( {\mu h_{2} + h_{1} } \right)}} + \frac{{u_{r} \bar{E}_{s} \mu \left( {A_{1} \cosh \left( {K_{1} h_{1} } \right) + B_{1} \sinh \left( {K_{1} h_{1} } \right)} \right)}}{{\left( {\mu h_{2} + h_{1} } \right)}} - \frac{{C_{0} h_{1}^{2} \mu }}{{2\left( {\mu h_{2} + h_{1} } \right)}} + \frac{{u_{r} \bar{E}_{s} U^{*} B_{2} K_{2} h_{1} }}{{\varepsilon ^{*} \left( {\mu h_{2} + h_{1} } \right)}} \\ & \quad\; - \frac{{u_{r} \bar{E}_{s} B_{1} K_{1} h_{1} \mu }}{{\left( {\mu h_{2} + h_{1} } \right)}} + \frac{{u_{r} \bar{E}_{s} A_{2} U^{*} \mu }}{{\varepsilon ^{*} \left( {\mu h_{2} + h_{1} } \right)}} - \frac{{u_{r} \bar{E}_{s} U^{*} \mu \left( {A_{2} \cosh \left( {K_{2} h_{2} } \right) - B_{2} \sinh \left( {K_{2} h_{2} } \right)} \right)}}{{\varepsilon ^{*} \left( {\mu h_{2} + h_{1} } \right)}} + \frac{{D_{0} h_{2}^{2} \mu }}{{2\left( {\mu h_{2} + h_{1} } \right)}} \\ \end{aligned} $$

(36)

$$ a_{1} = - \frac{{u_{r} \overline{E}_{s} U^{ * } B_{2} K_{2} }}{{\varepsilon^{ * } \mu }} + \frac{{b_{1} }}{\mu } + u_{r} \overline{E}_{s} B_{1} K_{1} $$

(37)

$$ a_{2} = u_{r} \overline{E}_{s} \left( {A_{1} \cosh \left( {K_{1} h_{1} } \right) + B_{1} \sinh \left( {K_{1} h_{1} } \right)} \right) - \frac{1}{2}C_{0} h_{1}^{2} - a_{1} h_{1} $$

(38)

$$ b_{2} = \frac{{u_{r} \overline{E}_{s} A_{2} U^{ * } }}{{\varepsilon^{ * } }} - u_{r} \overline{E}_{s} A_{1} + a_{2} $$

(39)

Make use of the last two kings of flow rate condition of Eq. (29), the constant $C_{0}$ and $D_{0}$ could be identified by,

$$ C_{0} = \frac{{6u_{r} \overline{E}_{s} }}{{h_{1}^{3} }}\left( {\frac{{A_{1} \sinh \left( {K_{1} h_{1} } \right)}}{{K_{1} }} + \frac{{B_{1} \cosh \left( {K_{1} h_{1} } \right)}}{{K_{1} }}} \right) - \frac{{3a_{1} }}{{h_{1} }} - \frac{{6a_{2} }}{{h_{1}^{2} }} - \frac{{6u_{r} \overline{E}_{s} B_{1} }}{{h_{1}^{3} K_{1} }} + \frac{6}{{h_{1}^{3} }} $$

(40)

$$ D_{0} = - \frac{{6u_{r} \overline{E}_{s} U^{ * } }}{{h_{2}^{3} \varepsilon^{ * } }}\left( {\frac{{B_{2} \cosh \left( {K_{2} h_{2} } \right)}}{{K_{2} }} - \frac{{A_{2} \sinh \left( {K_{2} h_{2} } \right)}}{{K_{2} }}} \right) + \frac{{3b_{1} }}{{h_{2} }} - \frac{{6b_{2} }}{{h_{2}^{2} }} + \frac{{6u_{r} \overline{E}_{s} B_{2} U^{ * } }}{{h_{2}^{3} K_{2} \varepsilon^{ * } }} + \frac{6}{{h_{2}^{3} }} $$

(41)

Afterward, the zero-order pressure field $\overline{P}_{0}$ and $\overline{P}_{3}$ could be achieved by integrating Eqs. (30) and (32),

$$ \overline{P}_{0} \left( {\overline{x},\overline{y}} \right) = \frac{1}{12}C_{0} \overline{x} + G_{0} \left( {\overline{y}} \right) $$

(42)

$$ \overline{P}_{3} \left( {\overline{x},\overline{y}} \right) = \frac{1}{12}D_{0} \overline{x} + G_{3} \left( {\overline{y}} \right) $$

(43)

where $G_{0} \left( {\overline{y}} \right)$ and $G_{3} \left( {\overline{y}} \right)$ are a function of ${\overline{\text{y}}}$ and supposing it is a constant. Take advantage of the condition involving exit edge pressure in Eq. (29), we discover the zero-order pressure turns into,

$$ \overline{P}_{0} \left( {\overline{x},\overline{y}} \right) = \frac{1}{12}C_{0} \left( {\overline{x} - 1} \right) $$

(44)

$$ \overline{P}_{3} \left( {\overline{x},\overline{y}} \right) = \frac{1}{12}D_{0} \left( {\overline{x} - 1} \right) $$

(45)

2.3.2 First-order solution

Since, the first-order governing equation and boundary conditions are,

$$ 12\frac{{\partial \overline{P}_{1} }}{{\partial \overline{x}}} - \overline{P}_{0} \frac{{d^{2} \overline{u}_{0} }}{{d\overline{y}^{2} }} = \frac{{d^{2} \overline{u}_{1} }}{{d\overline{y}^{2} }} $$

(46)

$$ 12\frac{{\partial \overline{P}_{4} }}{{\partial \overline{x}}} - \overline{P}_{3} \frac{{d^{2} \overline{u}_{3} }}{{d\overline{y}^{2} }} = \frac{{d^{2} \overline{u}_{4} }}{{d\overline{y}^{2} }} $$

(47)

$$\overline{u}_{1} \left| {_{{\overline{y} = h_{1} }} } \right. = 0,\;\overline{u}_{4} \left| {_{{\overline{y} = - h_{2} }} } \right. = 0,\;\overline{u}_{1} \left| {_{{\overline{y} = 0}} } \right. = \overline{u}_{4} \left| {_{{\overline{y} = 0}} } \right.,\;\mu \frac{{d\overline{u}_{1} }}{{d\overline{y}}}\left| {_{{\overline{y} = 0}} } \right. = \frac{{d\overline{u}_{4} }}{{d\overline{y}}}\left| {_{{\overline{y} = 0}} } \right.$$

$$ \overline{P}_{1} \left( {1,0} \right) = 0,\;\overline{P}_{4} \left( {1,0} \right) = 0,\;\int_{0}^{{h_{1} }} {\overline{u}_{1} } d\overline{y} = 0,\;\int_{{ - h_{2} }}^{0} {\overline{u}_{4} } d\overline{y} = 0 $$

(48)

Analog to the zero-order issue, placing both sides of Eqs. (46) and (47) to be the equivalent constant $C_{1}$ and $D_{1}$, written by,

$$ 12\frac{{\partial \overline{P}_{1} }}{{\partial \overline{x}}} - \overline{P}_{0} \frac{{d^{2} \overline{u}_{0} }}{{d\overline{y}^{2} }} = C_{1} $$

(49)

$$ \frac{{d^{2} \overline{u}_{1} }}{{d\overline{y}^{2} }} = C_{1} $$

(50)

$$ 12\frac{{\partial \overline{P}_{4} }}{{\partial \overline{x}}} - \overline{P}_{3} \frac{{d^{2} \overline{u}_{3} }}{{d\overline{y}^{2} }} = D_{1} $$

(51)

$$ \frac{{d^{2} \overline{u}_{4} }}{{d\overline{y}^{2} }} = D_{1} $$

(52)

Integrating twice of Eqs. (50) and (52) concerning $\overline{y}$, the solution of first-order velocity $\overline{u}_{1} \left( {\overline{y}} \right)$ and $\overline{u}_{4} \left( {\overline{y}} \right)$ yield,

$$ \overline{u}_{1} \left( {\overline{y}} \right) = \frac{1}{2}C_{1} \overline{y}^{2} + d_{1} \overline{y} + d_{2} $$

(53)

$$ \overline{u}_{4} \left( {\overline{y}} \right) = \frac{1}{2}D_{1} \overline{y}^{2} + e_{1} \overline{y} + e_{2} $$

(54)

Substituting the first four boundary conditions in Eq. (48), we can get,

$$ d_{1} = \frac{{D_{1} h_{2}^{2} - C_{1} h_{1}^{2} }}{{2\left( {\mu h_{2} + h_{1} } \right)}} $$

(55)

$$ e_{1} = \mu d_{1} $$

(56)

$$ d_{2} = e_{2} = \frac{{\mu h_{2} \left( {D_{1} h_{2}^{2} - C_{1} h_{1}^{2} } \right)}}{{2\left( {\mu h_{2} + h_{1} } \right)}} - \frac{1}{2}D_{1} h_{2}^{2} $$

(57)

Reusing the last two flow rate conditions of Eq. (48), we realize $C_{1} = D_{1} = 0$,$d_{1} ,d_{2} ,e_{1} ,e_{2} = 0$, and so $\overline{u}_{1} \left( {\overline{y}} \right) = \overline{u}_{4} \left( {\overline{y}} \right) = 0$. Integrating Eqs. (49) and (51) on $\overline{x}$ change,

$$\overline{P}_{1} \left( {\overline{x},\overline{y}} \right) = \frac{{C_{0} }}{144}\left( {\frac{1}{2}\overline{x}^{2} - \overline{x}} \right)\left( {C_{0} - {{u_{r} K_{1}^{2} \overline{\psi }_{1} \overline{E}_{s} }}{{}}} \right) + G_{1} \left( {\overline{y}} \right)$$

(58)

$$ \overline{P}_{4} \left( {\overline{x},\overline{y}} \right) = \frac{{D_{0} }}{144}\left( {\frac{1}{2}\overline{x}^{2} - \overline{x}} \right)\left( {D_{0} - \frac{{u_{r} K_{2}^{2} \overline{\psi }_{2} \overline{E}_{s} U^{ * } }}{{\varepsilon^{ * } }}} \right) + G_{4} \left( {\overline{y}} \right) $$

(59)

where $G_{1} \left( {\overline{y}} \right)$ and $G_{4} \left( {\overline{y}} \right)$ are the function of $\overline{y}$ and supposing it is a constant. Taking $C_{1} = 0$ and $D_{1} = 0$ into account and substituting the boundary condition of Eq. (48), the first-order pressure field is calculated as,

$$ \overline{P}_{1} \left( {\overline{x},\overline{y}} \right) = \frac{{C_{0}^{2} }}{288}\left( {\overline{x} - 1} \right)^{2} - \frac{{C_{0} u_{r} K_{1}^{2} \overline{E}_{s} }}{288}\left[ {\left( {\overline{x}^{2} - 2\overline{x}} \right)\overline{\psi }_{1} + A_{1} } \right] $$

(60)

$$ \overline{P}_{4} \left( {\overline{x},\overline{y}} \right) = \frac{{D_{0}^{2} }}{288}\left( {\overline{x} - 1} \right)^{2} - \frac{{D_{0} u_{r} K_{2}^{2} \overline{E}_{s} U^{ * } }}{{288\varepsilon^{ * } }}\left[ {\left( {\overline{x}^{2} - 2\overline{x}} \right)\overline{\psi }_{2} + A_{2} } \right] $$

(61)

2.3.3 Second-order solution

Finally, the second-order governing equation and boundary conditions are,

$$ 12\frac{{\partial \overline{P}_{2} }}{{\partial \overline{x}}} - \overline{P}_{0} \frac{{d^{2} \overline{u}_{1} }}{{d\overline{y}^{2} }} - \overline{P}_{1} \frac{{d^{2} \overline{u}_{0} }}{{d\overline{y}^{2} }} = \frac{{d^{2} \overline{u}_{2} }}{{d\overline{y}^{2} }} + \frac{{\alpha^{2} }}{12}\frac{{\partial \overline{P}_{0} }}{{\partial \overline{x}}}\left( {\frac{{d\overline{u}_{0} }}{{d\overline{y}}}} \right)^{2} $$

(62)

$$ 12\frac{{\partial \overline{P}_{5} }}{{\partial \overline{x}}} - \overline{P}_{3} \frac{{d^{2} \overline{u}_{4} }}{{d\overline{y}^{2} }} - \overline{P}_{4} \frac{{d^{2} \overline{u}_{3} }}{{d\overline{y}^{2} }} = \frac{{d^{2} \overline{u}_{5} }}{{d\overline{y}^{2} }} + \frac{{\alpha^{2} }}{12}\frac{{\partial \overline{P}_{3} }}{{\partial \overline{x}}}\left( {\frac{{d\overline{u}_{3} }}{{d\overline{y}}}} \right)^{2} $$

(63)

$$\overline{u}_{2} \left| {_{{\overline{y} = h_{1} }} } \right. = 0,\;\overline{u}_{5} \left| {_{{\overline{y} = - h_{2} }} } \right. = 0,\;\overline{u}_{2} \left| {_{{\overline{y} = 0}} } \right. = \overline{u}_{5} \left| {_{{\overline{y} = 0}} } \right.,\;\mu \frac{{d\overline{u}_{2} }}{{d\overline{y}}}\left| {_{{\overline{y} = 0}} } \right. = \frac{{d\overline{u}_{5} }}{{d\overline{y}}}\left| {_{{\overline{y} = 0}} } \right.$$

$$ \overline{P}_{2} \left( {1,0} \right) = 0,\;\overline{P}_{5} \left( {1,0} \right) = 0,\;\int_{0}^{{h_{1} }} {\overline{u}_{2} } d\overline{y} = 0,\;\int_{{ - h_{2} }}^{0} {\overline{u}_{5} } d\overline{y} = 0 $$

(64)

Similarly, setting both sides of Eqs. (62) and (63) to be the same constant $C_{2}$ and $D_{2}$, we get,

$$ 12\frac{{\partial \overline{P}_{2} }}{{\partial \overline{x}}} - \overline{P}_{0} \frac{{d^{2} \overline{u}_{1} }}{{d\overline{y}^{2} }} - \overline{P}_{1} \frac{{d^{2} \overline{u}_{0} }}{{d\overline{y}^{2} }} = C_{2} $$

(65)

$$ \frac{{d^{2} \overline{u}_{2} }}{{d\overline{y}^{2} }} + \frac{{\alpha^{2} }}{12}\frac{{\partial \overline{P}_{0} }}{{\partial \overline{x}}}\left( {\frac{{d\overline{u}_{0} }}{{d\overline{y}}}} \right)^{2} = C_{2} $$

(66)

$$ 12\frac{{\partial \overline{P}_{5} }}{{\partial \overline{x}}} - \overline{P}_{3} \frac{{d^{2} \overline{u}_{4} }}{{d\overline{y}^{2} }} - \overline{P}_{4} \frac{{d^{2} \overline{u}_{3} }}{{d\overline{y}^{2} }} = D_{2} $$

(67)

$$ \frac{{d^{2} \overline{u}_{5} }}{{d\overline{y}^{2} }} + \frac{{\alpha^{2} }}{12}\frac{{\partial \overline{P}_{3} }}{{\partial \overline{x}}}\left( {\frac{{d\overline{u}_{3} }}{{d\overline{y}}}} \right)^{2} = D_{2} $$

(68)

Integrating twice of Eqs. (66) and (68) concerning $\overline{y}$, the solution of second-order velocity $\overline{u}_{2} \left( {\overline{y}} \right)$ and $\overline{u}_{5} \left( {\overline{y}} \right)$ response as,

$$\begin{aligned}{{\bar u}_2}\left( {\bar y} \right) &= \frac{1}{2}{C_2}{y^2} + {m_1}\bar y + {m_2} - \frac{{{\alpha ^2}{C_0}}}{{144}}\left\{ {\begin{array}{*{20}{c}} {}\\ {} \end{array}} \right.\frac{{C_0^2}}{{12}}{{\bar y}^4} + \frac{{a_1^2}}{2}{{\bar y}^2} + \frac{{{C_0}{a_1}}}{3}{{\bar y}^3} - 2{a_1}{u_r}{{\bar E}_s}\left( {\frac{{{A_1}\sinh \left( {{K_1}\bar y} \right)}}{{{K_1}}} + \frac{{{B_1}\cosh \left( {{K_1}\bar y} \right)}}{{{K_1}}}} \right)\\ &\quad + \frac{{u_r^2\bar E_s^2\left[ {A_1^2K_1^2\left( {{e^{2{K_1}\bar y}} - 4K_1^2{{\bar y}^2} + {e^{ - 2{K_1}\bar y}}} \right) + 4{A_1}{B_1}K_1^2\sinh \left( {2{K_1}\bar y} \right) + B_1^2K_1^2\left( {{e^{2{K_1}\bar y}} + 4K_1^2{{\bar y}^2} + {e^{ - 2{K_1}\bar y}}} \right)} \right]}}{{16K_1^2}}\\ & \quad- \frac{{2{C_0}{u_r}{K_1}{{\bar E}_s}\left[ {{A_1}\left( {{K_1}\bar y\left( {{e^{{K_1}\bar y}} - {e^{ - {K_1}\bar y}}} \right) - 2{e^{{K_1}\bar y}} - 2{e^{ - {K_1}\bar y}}} \right) + {B_1}\left( {{K_1}\bar y\left( {{e^{{K_1}\bar y}} + {e^{ - {K_1}\bar y}}} \right) - 2{e^{{K_1}\bar y}} + 2{e^{ - {K_1}\bar y}}} \right)} \right]}}{{2K_1^3}}\left. {\begin{array}{*{20}{c}} {}\\ {} \end{array}} \right\} \end{aligned}$$

(69)

$$ \begin{aligned} {{\bar u}_5}\left( {\bar y} \right) & = \frac{1}{2}{D_2}{y^2} + {n_1}\bar y + {n_2} - \frac{{{\alpha ^2}{D_0}}}{{144}}\left\{ {\begin{array}{*{20}{c}} {}\\ {} \end{array}} \right.\frac{{D_0^2}}{{12}}{{\bar y}^4} + \frac{{b_1^2}}{2}{{\bar y}^2} + \frac{{{D_0}{b_1}}}{3}{{\bar y}^3} - \frac{{2{b_1}{u_r}{{\bar E}_s}{U^ * }}}{{{\varepsilon ^ * }}}\left( {\frac{{{A_2}\sinh \left( {{K_2}\bar y} \right)}}{{{K_2}}} + \frac{{{B_2}\cosh \left( {{K_2}\bar y} \right)}}{{{K_2}}}} \right)\\ &\quad + \frac{{u_r^2\bar E_s^2{U^{{ * ^2}}}\left[ {A_2^2K_2^2\left( {{e^{2{K_2}\bar y}} - 4K_2^2{{\bar y}^2} + {e^{ - 2{K_2}\bar y}}} \right) + 4{A_2}{B_2}K_2^2\sinh \left( {2{K_2}\bar y} \right) + B_2^2K_2^2\left( {{e^{2{K_2}\bar y}} + 4K_2^2{{\bar y}^2} + {e^{ - 2{K_2}\bar y}}} \right)} \right]}}{{16{\varepsilon ^{{ * ^2}}}K_2^2}}\\ &\quad - \frac{{2{u_r}{{\bar E}_s}{U^ * }{D_0}{K_2}}}{{{\varepsilon ^ * }}}\frac{{\left[ {{A_2}\left( {{K_2}\bar y\left( {{e^{{K_2}\bar y}} - {e^{ - {K_2}\bar y}}} \right) - 2{e^{{K_2}\bar y}} - 2{e^{ - {K_2}\bar y}}} \right) + {B_2}\left( {{K_2}\bar y\left( {{e^{{K_2}\bar y}} + {e^{ - {K_2}\bar y}}} \right) - 2{e^{{K_2}\bar y}} + 2{e^{ - {K_2}\bar y}}} \right)} \right]}}{{2K_2^3}}\left. {\begin{array}{*{20}{c}} {}\\ {} \end{array}} \right\} \end{aligned} $$

(70)

The process of solving is similar to that of solving the zero-order solution, and the corresponding parameters $m_{1}$, $m_{2}$, $n_{1}$, $n_{2}$, $C_{2}$ and $D_{2}$ are given in Appendix A. Regarding the second-order pressure field, integrating Eqs. (65) and (67) to read,

$$ \overline{P}_{2} \left( {\overline{x},\overline{y}} \right) = \frac{{C_{0} - u_{r} K_{1}^{2} \overline{\psi }_{1} \overline{E}_{s} }}{12}\left\{ {\frac{{C_{0}^{2} }}{864}\left( {\overline{x} - 1} \right)^{3} - \frac{{C_{0} u_{r} K_{1}^{2} \overline{E}_{s} }}{288}\left[ {\left( {\frac{1}{3}\overline{x}^{3} - \overline{x}^{2} } \right)\overline{\psi }_{1} + A_{1} \overline{x}} \right]} \right\} + \frac{{C_{2} }}{12}\overline{x} + G_{2} \left( {\overline{y}} \right) $$

(71)

$$ \overline{P}_{5} \left( {\overline{x},\overline{y}} \right) = \frac{{D_{0} \varepsilon^{ * } - u_{r} K_{2}^{2} \overline{\psi }_{2} \overline{E}_{s} U^{ * } }}{{12\varepsilon^{ * } }}\left\{ {\frac{{D_{0}^{2} }}{864}\left( {\overline{x} - 1} \right)^{3} - \frac{{D_{0} u_{r} K_{2}^{2} \overline{E}_{s} U^{ * } }}{{288\varepsilon^{ * } }}\left[ {\left( {\frac{1}{3}\overline{x}^{3} - \overline{x}^{2} } \right)\overline{\psi }_{2} + A_{2} \overline{x}} \right]} \right\} + \frac{{D_{2} }}{12}\overline{x} + G_{5} \left( {\overline{y}} \right) $$

(72)

The boundary condition of Eq. (64) is used, and $\overline{P}_{2} \left( {\overline{x},\overline{y}} \right)$ and $\overline{P}_{5} \left( {\overline{x},\overline{y}} \right)$ can be finally given as

$$ \begin{aligned} \bar{P}_{2} \left( {\bar{x},\bar{y}} \right) & = \frac{{C_{0} - u_{r} K_{1}^{2} \bar{\psi }_{1} \bar{E}_{s} }}{{12}}\left\{ {\frac{{C_{0}^{2} }}{{864}}\left( {\bar{x} - 1} \right)^{3} - \frac{{C_{0} u_{r} K_{1}^{2} \bar{E}_{s} }}{{288}}\left[ {\left( {\frac{1}{3}\bar{x}^{3} - \bar{x}^{2} } \right)\bar{\psi }_{1} + A_{1} \bar{x}} \right]} \right\} + \frac{{C_{2} }}{{12}}\left( {\bar{x} - 1} \right) \\ & \quad + \frac{{C_{0} - u_{r} K_{1}^{2} A_{1} \bar{E}_{s} }}{{12}}\left( {\frac{{C_{0} u_{r} K_{1}^{2} \bar{E}_{s} A_{1} }}{{864}}} \right) \\ \end{aligned} $$

(73)

$$ \begin{aligned} \bar{P}_{5} \left( {\bar{x},\bar{y}} \right) & = \frac{{D_{0} \varepsilon ^{*} - u_{r} K_{2}^{2} \bar{\psi }_{2} \bar{E}_{s} U^{*} }}{{12\varepsilon ^{*} }}\left\{ {\frac{{D_{0}^{2} }}{{864}}\left( {\bar{x} - 1} \right)^{3} - \frac{{D_{0} u_{r} K_{2}^{2} \bar{E}_{s} U^{*} }}{{288\varepsilon ^{*} }}\left[ {\left( {\frac{1}{3}\bar{x}^{3} - \bar{x}^{2} } \right)\bar{\psi }_{2} + A_{2} \bar{x}} \right]} \right\} + \frac{{D_{2} }}{{12}}\left( {\bar{x} - 1} \right) \\ & \quad + \frac{{D_{0} \varepsilon ^{*} - u_{r} K_{2}^{2} A_{2} \bar{E}_{s} U^{*} }}{{12\varepsilon ^{*} }}\left( {\frac{{D_{0} u_{r} K_{2}^{2} U^{*} \bar{E}_{s} A_{2} }}{{864\varepsilon ^{*} }}} \right) \\ \end{aligned} $$

(74)

So far, up to second-order velocity and pressure distributions have been received, but the SP${\overline{\text{E}}}_{{\text{s}}}$ in the velocity and pressure fields is unidentified. Next, it could be obtained by installing the neutral condition in the subsequent section.

2.4 Streaming potential

To calculate the SP $\overline{E} _{s}$, the electro-neutrality condition is put to use, which can be written mathematically by,

$$ I = 2ez\int_{{ - H_{2} }}^{{H_{1} }} {\left( {n_{ + } u_{ + } - n_{ - } u_{ - } } \right)dy} = 0 $$

(75)

where

$$ u_{ \pm } = u \pm \frac{{ezE_{s} }}{f} $$

(76)

above $u$ is the advection velocity, $\pm {{ezE_{s} } \mathord{\left/ {\vphantom {{ezE_{s} } f}} \right. \kern-0pt} f}$ is the electromigration velocity, and $f$ is the ionic friction coefficient.

Exercising linearized Boltzmann distribution $n_{ \pm } = n_{0} \exp \left[ { \mp {{\left( {ez\psi_{i} } \right)} \mathord{\left/ {\vphantom {{\left( {ez\psi_{i} } \right)} {\left( {k_{B} T_{av} } \right)}}} \right. \kern-0pt} {\left( {k_{B} T_{av} } \right)}}} \right] \approx n_{0} \left[ {1 \mp {{\left( {ez\psi_{i} } \right)} \mathord{\left/ {\vphantom {{\left( {ez\psi_{i} } \right)} {\left( {k_{B} T_{av} } \right)}}} \right. \kern-0pt} {\left( {k_{B} T_{av} } \right)}}} \right]$ and Eq. (76), the net ionic current Eq. (75) could be reduced as

$$ U_{1} \int_{0}^{{h_{1} }} {\overline{\psi }_{1} } \overline{u}_{\rm I} d\overline{y} + U_{2} \int_{{ - h_{2} }}^{0} {\overline{\psi }_{2} \overline{u}_{\Pi } d\overline{y} = \frac{{ez\overline{E}_{s} E_{0} \left( {h_{1} + h_{2} } \right)}}{f}} $$

(77)

Bedding the zero-, first-, second-order velocities and electrical potential into Eq. (77), the analytical expression of the cubic equation about the SP $\overline{E}_{s}^{3}$ is written by

$$ T_{0} + T_{1} \overline{E}_{s} + T_{2} \overline{E}_{s}^{2} + T_{3} \overline{E}_{s}^{3} = 0 $$

(78)

here, $T_{0}$, $T_{1}$, $T_{2}$, and $T_{3}$ are constants.

Moreover, Eq. (78) has a real root and a pair of imaginary roots. The real root is picked for the SP $\overline{E}_{s}$

$$ \begin{gathered} \overline{E}_{s} = - \frac{{T_{2} }}{{3T_{3} }} - \frac{{2^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} \left( { - T_{2}^{2} + 3T_{3} T_{1} } \right)}}{{3T_{3} \left( { - 2T_{2}^{3} + 9T_{3} T_{2} T_{1} - 27T_{3}^{2} T_{2}^{2} + \sqrt {4\left( { - T_{2}^{2} + 3T_{3} T_{1} } \right)^{3} + \left( { - 2T_{2}^{3} + 9T_{3} T_{2} T_{1} - 27T_{3}^{2} T_{2}^{2} } \right)^{2} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} }} \\ + \frac{{\left( { - 2T_{2}^{3} + 9T_{3} T_{2} T_{1} - 27T_{3}^{2} T_{0} + \sqrt {4\left( { - T_{2}^{2} + 3T_{3} T_{1} } \right)^{3} + \left( { - 2T_{2}^{3} + 9T_{3} T_{2} T_{1} - 27T_{3}^{2} T_{2}^{2} } \right)^{2} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} }}{{32^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} T_{3} }} \\ \end{gathered} $$

(79)

2.5 Electric energy conversion efficiency

The mechanical energy yielded in time of pressure driving and the chemical energy produced by EDL would transform into electrical energy in time of fluid flow. This proceeding is called EKEC. Taking account of the pressure-dependent viscosity, the SP plays a significant role in examining the efficiency of EKEC. Therefore, the expression of EKEC efficiency is defined as

$$ \xi = \frac{{P_{out} }}{{P_{in} }} $$

(80)

where $P_{in}$ and $P_{out}$ in several denote the input and output powers, which have the form

$$ P_{in} = \left| {\left( { - \frac{dP}{{dx}}} \right)_{m} Q_{in} } \right| $$

(81)

$$ P_{out} = \frac{{\left| {I_{s} E_{s} } \right|}}{4} $$

(82)

where $\left( { - \frac{dP}{{dx}}} \right)_{m}$ stands for pure average pressure gradient in ${\text{x}}$ axial direction a lack of the effect of SP $E_{s}$. Given by

$$ \left( { - \frac{dP}{{dx}}} \right)_{m} = \frac{1}{l}\int_{0}^{l} { - \frac{dP}{{dx}}\left| {_{{E_{s} = 0}} } \right.} dx $$

(83)

Additionally, the input volume flow rate $Q_{in}$, such that

$$ Q_{in} = \int_{{ - H_{2} }}^{{H_{1} }} {u_{p} dy} = \int_{{ - H_{2} }}^{{H_{1} }} {u\left| {_{{E_{s} = 0}} dy} \right.} = U_{1} H\int_{0}^{{h_{1} }} {\overline{u}_{\rm I} } \left| {_{{\overline{E}_{s} = 0}} d\overline{y} + U_{2} H\int_{{ - h_{2} }}^{0} {\overline{u}_{\Pi } \left| {_{{\overline{E}_{s} = 0}} d\overline{y}} \right.} } \right. $$

(84)

which ought to be calculated employing purely pressure-driven flow velocity ${\text{u}}_{{\text{p}}}$ when the SP is equivalent to zero, i.e.$u_{p} = u\left| {_{{E_{s} = 0}} } \right.$. The streaming current turns into

$$ I_{s} = 2ez\int_{{ - H_{2} }}^{{H_{1} }} {u\left( {n_{ + } - n_{ - } } \right)dy} $$

(85)

In reality, electro-neutrality conditions of Eqs. (75) and (76) have that

$$ I = 2ez\int_{{ - H_{2} }}^{{H_{1} }} {u\left( {n_{ + } - n_{ - } } \right)dy} + \frac{{2e^{2} z^{2} E_{s} }}{f}\int_{{ - H_{2} }}^{{H_{1} }} {\left( {n_{ + } + n_{ - } } \right)dy = I_{s} } + I_{c} = 0 $$

(86)

Thus, we get $\xi$ from Eqs. (80) to (86) as

$$ \xi = \frac{{e^{2} z^{2} n_{0} \overline{E}_{s}^{2} E_{0}^{2} H\left( {h_{1} + h_{2} } \right)}}{{\left| {\left\{ {\frac{{12\eta_{0} U_{1} }}{{ - H_{1} }}\left( {\frac{{F_{2} }}{12} - \varepsilon_{\rm I} \frac{{F_{2}^{2} }}{288} + \varepsilon_{\rm I}^{2} \left( {\frac{{F_{8} }}{12} + \frac{{F_{2}^{3} }}{10368}} \right)} \right) + \frac{{12\eta_{0} U_{2} }}{{ - H_{2} }}\left( {\frac{{F_{4} }}{12} - \varepsilon_{\Pi } \frac{{F_{4}^{2} }}{288} + \varepsilon_{\Pi }^{2} \left( {\frac{{F_{12} }}{12} + \frac{{F_{4}^{3} }}{10368}} \right)} \right)} \right\}Q_{in} } \right|}} $$

(87)

where $F_{2}$, $F_{4}$, $F_{8}$, and $F_{12}$ are constants and expressions are shown in Appendix B.

3 Results and discussion

In the prior sections, the asymptotic solutions of dimensionless velocity and pressure of two immiscible Newtonian fluids with viscosity depending on pressure in parallel microchannels by PM have been derived. On this basis, the SP and EKEC are further come by computation. Before analyzing the characteristics of electrodynamic flow, it is necessary to discuss the allowable range of relational flow parameters as well as the ratio of physical parameters of the upper fluid to the lower fluid. Absolute temperature $T_{av} = 298{\text{K}}$, Boltzmann constant $k_{B} = 1.381 \times 10^{ - 23} {\text{J}} \cdot {\text{K}}^{ - 1}$, Electronic charge $e = 1.6 \times 10^{ - 19} {\text{C}}$, the ion valence $z = 1$, ion density of the bulk solution $n_{0} = 10^{ - 5} {\text{m}}^{ - 3}$, induced electric field $E_{0} = 0 - 10^{5} {{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{m}}}} \right. \kern-0pt} {\text{m}}}$, the bottom layer liquid viscosity is $\mu_{2} = 10^{ - 3} {{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {\left( {{\text{ms}}} \right)}}} \right. \kern-0pt} {\left( {{\text{ms}}} \right)}}$. $\psi_{0} = - 0.025{\text{V}}$, the value of $10^{ - 12} {\text{N}} \cdot {\text{s}} \cdot {\text{m}}^{ - 1}$ is suggested on $f$. Additionally, the ratio of electroosmotic velocity to the average velocity at the exit plane ($u_{r}$) is hardened to 1. In addition, we pick the extent of $K$ transforms from 1 to 5 by reason of $K = \kappa H$. Other parameters are set into $h_{1} = h_{2} = 0.5$, $\overline{\zeta }_{1} = \overline{\zeta }_{2} = 1$, $Q = 0.001 - 0.05$.

In order to validate the applicability of the present model, we compare the prediction of EKEC efficiency with the result of Xie et al. [44], who investigated the EKEC efficiency of two immiscible fluids in a nanochannel. When the pressure-viscosity coefficient is ignored, the present model can be viewed as that of Xie et al. [44]. Figure 2 shows an excellent agreement, implying that the performance of our model is satisfactory.

Fig. 2

Comparisons of the EKEC efficiency between the present result and that of Xie et al. [44] when the pressure-viscosity coefficient approaches zero

Figure 3 shows the variation of SP with electrokinetic width for various interface electric potential differences values through two-layer immiscible Newtonian fluids. It is seen that the SP increases with the electrokinetic width and decreases with the interface electric potential difference. This implies that such interface electric potential differences should be selected to obtain more SP from the present two-layer fluid system for other given flow parameters. Moreover, it reveals that the interface electric potential differences promote the potential to arrest the velocity gradient in the fluid–fluid interfacial region. The velocity encourages the transport of mobile ions in the EDL. The reasons for this phenomenon include the following two aspects. Firstly, with the enhancement of the positive value of interface potential difference, the upper fluid potential is greater than the bottom fluid potential at the liquid–liquid interface. In other words, the electric potential of the upper fluid is greater than that of the lower fluid in $\overline{y} = 0$. Thus, the upper fluid velocity is greater than the bottom fluid. The SP is equivalent to the reverse electric field of the entire two-layer fluid system of immiscibility, which has an inhibited effect on the flow velocity of the system’s entirety. Therefore, the larger the electric potential difference is, the weaker the ion transport capacity will be, leading to a reduction in the SP.

Fig. 3

The variations of SP with electrokinetic width $K$ for different the interface electric potential difference $\Delta \overline{\psi }$, when $\varepsilon^{ * }$ = 0.008, $\mu$ = 2.0. a two-dimensional graph, b contour plot

Figure 4 shows the variation of SP with electrokinetic width for various ratios of fluid viscosity values through two-layer immiscible Newtonian fluids. Figure 4a shows that K = 3 is the cut-off point of SP change, where the two sides show different trends with the rising viscosity ratio. It is seen that SP decreases with fluid viscosity ratio initially, after attaining the median, and then increases gradually. A high viscosity ratio produces a high flow resistance for the moving liquid, resulting in a smaller velocity amplitude. This is because the SP determined by the electrical potential is mainly concentrated at the EDL. On the one hand, when the viscosity of the lower fluid remains unchanged, as the viscosity ratio increases, the viscosity of the upper fluid increases. The increase in fluid viscosity hinders the movement of excess ions in the electrolyte solution, that is, the resistance generated by the fluid viscosity increases, and fewer excess ions gather downstream, causing a smaller SP (K<3); when K>3, the opposite is true.

Fig. 4

The variations of SP with electrokinetic width $K$ for different the ratio of fluid viscosity $\mu$ at $\Delta \overline{\psi }$ = 1, $\varepsilon^{ * }$ = 0.05. a two-dimensional graph, b contour plot

Figure 5 represents the variation of EKEC efficiency for different values of the interface electric potential difference $\Delta \overline{\psi }$ in a two-layer immiscible Newtonian fluid. It can be observed that the magnitude of EKEC efficiency shows a decreasing trend with the increase of interface electric potential difference. It is well known that the EKEC efficiency is the ratio of output power to input power. This implies that the mechanical energy generated by the pressure drive and the chemical energy generated by the EDL are greater than the generated electrical energy (here considered as SP). The electrokinetic width affects the electrical potential distribution of EDL, which in turn affects the distribution of electroosmotic force and, in turn, the flow. Therefore, it is clear that less energy is produced in the microchannel by the interface electric potential difference.

Fig. 5

The variations of EKEC efficiency with electrokinetic width $K$ for different the interface electric potential difference $\Delta \overline{\psi }$, when $\varepsilon^{ * }$ = 0.9, $\mu$ = 1.1

Figure 6 exhibits the EKEC efficiency for different ratios of permittivity, which tend to increase the EKEC efficiency in the microchannel. The increase of the EKEC efficiency for the effect of the permittivity ratio is significant. When the permitting ratio increases, the permittivity of upper fluid can be increased, resulting in the enhancement of upper fluid conductivity. This will cause the enhancement of electroosmotic force. Thus, the velocity of the upper fluid can be enhanced, resulting in a large EKEC efficiency. On the other hand, the increase in the permitting ratio will lead to improved free ion transport, resulting in a larger SP. Therefore, the EKEC efficiency is also improved accordingly, which can be obtained from Eq. (87).

Fig. 6

The variations of EKEC efficiency with electrokinetic width $K$ for different the ratio of the permittivity $\varepsilon^{ * }$, when $\Delta \overline{\psi }$ = 0.5, $\mu$ = 1. a Two-dimensional graph, b contour plot

Figure 7 depicts the result of EKEC efficiency as a function of the electrokinetic width for different viscosity ratios. It can be observed that the magnitude of EKEC efficiency shows an increasing trend with the increase of electrokinetic width. A high viscosity ratio will result in a greater flow resistance of the liquid, resulting in a decrease in velocity, which further leads to an increase in EKEC efficiency. This is because the SP is mainly concentrated at the EDL, where we find a significant increase in the SP. Likewise, the favorable pressure gradient provides a necessary driving force for EOF. This result indicates that it is feasible to improve the efficiency of EKEC by increasing the viscosity ratio.

Fig. 7

The variations of EKEC efficiency with electrokinetic width $K$ for different the ratio of fluid viscosity $\mu$ at $\Delta \overline{\psi }$ = 0.5, $\varepsilon^{ * }$ = 1.0. a Two-dimensional graph, b contour plot

Figure 8 compares the EKEC efficiency in two-layer and that of single-layer fluid with normalized pressure-viscosity coefficient changes. Compared to the single-layer fluid, the efficiency in a two-layer fluid is increased by up to 50% within the current range of physical parameters when the normalized pressure-viscosity coefficient equals 0.001, as well as the EKEC efficiency decreases in pace with the enhancement of K. Besides, with the increase of pressure-viscosity coefficient, the EKEC efficiency gap between two-layer fluid and single-layer fluid is narrowing. Similarly, along with the multiplication of the pressure-viscosity coefficient, the EKEC efficiency of both single and two layers shows a downward trend, which could keep pace with the research consequences of Ref. [38]. This result indicates a possibility, where the EKEC can increase by using two immiscible fluid layers.

Fig. 8

Comparisons of EKEC efficiency between two-layer fluid and that of single-layer fluid at the normalized pressure-viscosity coefficient changes, where two-layer fluid: $\Delta \overline{\psi }$ = 0.001, $\varepsilon^{ * }$ = 0.5, $\mu$ = 0.5, $Q$ = 0.001; single-layer fluid: $\Delta \overline{\psi }$ = 0, $\varepsilon^{ * }$ = 1.0, $\mu$ = 1.0, $Q$ = 0

4 Conclusions

A theoretical model has been established in this study, which is driven by the pressure gradient, in two immiscible fluid layers confined with parallel plate microchannels. The streaming potential and EKEC efficiency in the two fluid layers have been obtained analytically, under pressure-dependent viscosities conditions. It has been verified that the asymptotic analytical solutions agree excellently with the result of Xie et al. [44]. Results show that the EKEC efficiency can be enhanced obviously by the permittivity and viscosity ratios, the maximum efficiency is about 67% and 28%, respectively, but shows a decreasing trend with the interface electric potential difference, the maximum efficiency is about 44%. This implies that more electrokinetic power output can be obtained by altering the permittivity and viscosity. Furthermore, we company the EKEC efficiency in two-layer and that of single-layer fluid. It is found that, for given flow parameters, the conversion efficiency of two-layer fluid systems can be higher than that of single-layer fluid systems by up to 50%. Besides, the optimal ratios can also be obtained in the two-layer fluid system and the conversion efficiency attains the maximum at these optimal ratios. Finally, to enhance the energy conversion efficiency, the pressure-viscosity coefficient may be considered. The present theoretical result can be viewed as an efficiency validation for complex electrokinetic flow in a two-layer fluid system. The optimal parameters can be used to design an electrokinetic energy conversion device with high conversion efficiency.

Appendices

Appendix A

$$\begin{aligned} {n_1} = & - \frac{{\mu {C_2}h_1^2}}{{2\left( {\mu {h_2} + {h_1}} \right)}} + \frac{{{\alpha ^2}{C_0}\mu }}{{144\left( {\mu {h_2} + {h_1}} \right)}}\left\{ {\begin{array}{*{20}{l}} {}\\ {} \end{array}} \right.\frac{{C_0^2}}{{12}}h_1^4 + \frac{{a_1^2}}{2}h_1^2 + \frac{{{C_0}{a_1}}}{3}h_1^3 - 2{a_1}{u_r}{{\bar E}_s}\left( {\frac{{{A_1}\sinh \left( {{K_1}{h_1}} \right)}}{{{K_1}}} + \frac{{{B_1}\cosh \left( {{K_1}{h_1}} \right)}}{{{K_1}}}} \right)\\ & + \frac{{u_r^2\bar E_s^2\left[ {A_1^2K_1^2\left( {{e^{2{K_1}{h_1}}} - 4K_1^2h_1^2 + {e^{ - 2{K_1}{h_1}}}} \right) + 4{A_1}{B_1}K_1^2\sinh \left( {2{K_1}{h_1}} \right) + B_1^2K_1^2\left( {{e^{2{K_1}{h_1}}} + 4K_1^2h_1^2 + {e^{ - 2{K_1}{h_1}}}} \right)} \right]}}{{16K_1^2}}\\ &- \frac{{2{C_0}{u_r}{K_1}{{\bar E}_s}\left[ {{A_1}\left( {{K_1}{h_1}\left( {{e^{{K_1}{h_1}}} - {e^{ - {K_1}{h_1}}}} \right) - 2{e^{{K_1}{h_1}}} - 2{e^{ - {K_1}{h_1}}}} \right) + {B_1}\left( {{K_1}{h_1}\left( {{e^{{K_1}{h_1}}} + {e^{ - {K_1}{h_1}}}} \right) - 2{e^{{K_1}{h_1}}} + 2{e^{{K_1}{h_1}}}} \right)} \right]}}{{2K_1^3}}\left. {\begin{array}{*{20}{l}} {}\\ {} \end{array}} \right\}\\ &+ \frac{{{\alpha ^2}{D_0}{h_1}}}{{144\left( {\mu {h_2} + {h_1}} \right)}}\left( {\frac{{u_r^2\bar E_s^2{U^{{ * ^2}}}{A_2}{B_2}{K_2}}}{{2{\varepsilon ^{{ * ^2}}}}} + \frac{{4{u_r}{{\bar E}_s}{U^ * }{D_0}{B_2}}}{{{\varepsilon ^ * }{K_2}}} - \frac{{2{b_1}{u_r}{{\bar E}_s}{U^ * }{A_2}}}{{{\varepsilon ^ * }}}} \right) - \frac{{{\alpha ^2}{C_0}{h_1}\mu }}{{144\left( {\mu {h_2} + {h_1}} \right)}}\left( {\begin{array}{*{20}{l}} {}\\ {} \end{array}} \right.\frac{{u_r^2\bar E_s^2{A_1}{B_1}{K_1}}}{2}\\ & + \frac{{4{C_0}{u_r}{{\bar E}_s}{B_1}}}{{{K_1}}} - 2{\alpha _1}{u_r}{{\bar E}_s}{A_1}\left. {\begin{array}{*{20}{l}} {}\\ {} \end{array}} \right) - \frac{{{\alpha ^2}{C_0}\mu }}{{144\left( {\mu {h_2} + {h_1}} \right)}}\left( {\frac{{u_r^2\bar E_s^2\left( {A_1^2 + B_1^2} \right)}}{8} + \frac{{4{C_0}{u_r}{{\bar E}_s}{A_1}}}{{K_1^2}} - \frac{{2{a_1}{u_r}{{\bar E}_s}{B_1}}}{{{K_1}}}} \right) + \frac{{{D_2}h_2^2\mu }}{{2\left( {\mu {h_2} + {h_1}} \right)}}\\ & - \frac{{{\alpha ^2}{D_0}\mu }}{{144\left( {\mu {h_2} + {h_1}} \right)}}\left\{ {\begin{array}{*{20}{l}} {}\\ {} \end{array}} \right.\frac{{D_0^2}}{{12}}h_2^4 + \frac{1}{2}b_1^2h_2^2 - \frac{{{D_0}{b_1}}}{3}h_2^3 - \frac{{2{b_1}{u_r}{{\bar E}_s}{U^ * }}}{{{\varepsilon ^ * }}}\left( {\frac{{{B_2}\cosh \left( {{K_2}{h_2}} \right)}}{{{K_2}}} - \frac{{{A_2}\sinh \left( {{K_2}{h_2}} \right)}}{{{K_2}}}} \right)\\ &+ \frac{{u_r^2\bar E_s^2{U^{{ * ^2}}}\left[ {A_2^2K_2^2\left( {{e^{ - 2{K_2}{h_2}}} - 4K_2^2h_2^2 + {e^{2{K_2}{h_2}}}} \right) - 4{A_2}{B_2}K_2^2\sinh \left( {2{K_2}{h_2}} \right) + B_2^2K_2^2\left( {{e^{ - 2{K_2}{h_2}}} + 4K_2^2h_2^2 + {e^{2{K_2}{h_2}}}} \right)} \right]}}{{16{\varepsilon ^{{ * ^2}}}K_2^2}}\\ & - \frac{{2{u_r}{{\bar E}_s}{U^ * }{D_0}{K_2}}}{{{\varepsilon ^ * }}}\left( {\frac{{{A_2}\left( {{K_2}{h_2}\left( {{e^{{K_2}{h_2}}} - {e^{ - {K_2}{h_2}}}} \right) - 2{e^{ - {K_2}{h_2}}} - 2{e^{{K_2}{h_2}}}} \right) - {B_2}\left( {{K_2}{h_2}\left( {{e^{ - {K_2}{h_2}}} + {e^{{K_2}{h_2}}}} \right) + 2{e^{ - {K_2}{h_2}}} - 2{e^{{K_2}{h_2}}}} \right)}}{{2K_2^3}}} \right)\left. {\begin{array}{*{20}{l}} {}\\ {} \end{array}} \right\}\\ & + \frac{{{\alpha ^2}{D_0}\mu }}{{144\left( {\mu {h_2} + {h_1}} \right)}}\left( {\frac{{u_r^2\bar E_s^2{U^{{ * ^2}}}\left( {A_2^2 + B_2^2} \right)}}{{8{\varepsilon ^{{ * ^2}}}}} + \frac{{4{u_r}{{\bar E}_s}{U^ * }{D_0}{A_2}}}{{K_2^2}} - \frac{{2{b_1}{u_r}{{\bar E}_s}{U^ * }{B_2}}}{{{\varepsilon ^ * }{K_2}}}} \right) \end{aligned} $$

(88)

$$ \begin{aligned} m_{1} = &\frac{{n_{1} }}{\mu } - \frac{{\alpha^{2} D_{0} }}{144\mu }\left( {\frac{{u_{r}^{2} \overline{E}_{s}^{2} U^{{ *^{2} }} A_{2} B_{2} K_{2} }}{{2\varepsilon^{{ *^{2} }} }} + \frac{{2u_{r} \overline{E}_{s} U^{ * } D_{0} B_{2} }}{{\varepsilon^{ * } K_{2} }} - \frac{{2b_{1} u_{r} \overline{E}_{s} U^{ * } A_{2} }}{{\varepsilon^{ * } }}} \right) \\ &+ \frac{{\alpha^{2} C_{0} }}{144}\left( {\frac{{u_{r}^{2} \overline{E}_{s}^{2} A_{1} B_{1} K_{1} }}{2} + \frac{{2C_{0} u_{r} \overline{E}_{s} B_{1} }}{{K_{1} }} - 2a_{1} u_{r} \overline{E}_{s} A_{1} } \right) \\ \end{aligned} $$

(89)

$$ \begin{aligned} m_{2} = &- \frac{1}{2}C_{2} h_{1}^{2} - m_{1} h_{1} + \frac{{\alpha^{2} C_{0} }}{144}\left\{ {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \right.\frac{{C_{0}^{2} }}{12}h_{1}^{4} + \frac{{a_{1}^{2} }}{2}h_{1}^{2} + \frac{{C_{0} a_{1} }}{3}h_{1}^{3} - 2a_{1} u_{r} \overline{E}_{s} \left( {\frac{{A_{1} \sinh \left( {K_{1} h_{1} } \right)}}{{K_{1} }} + \frac{{B_{1} \cosh \left( {K_{1} h_{1} } \right)}}{{K_{1} }}} \right) \\ &+ \frac{{u_{r}^{2} \overline{E}_{s}^{2} \left[ {A_{1}^{2} K_{1}^{2} \left( {e^{{2K_{1} h_{1} }} - 4K_{1}^{2} h_{1}^{2} + e^{{ - 2K_{1} h_{1} }} } \right) + 4A_{1} B_{1} K_{1}^{2} \sinh \left( {2K_{1} h_{1} } \right) + B_{1}^{2} K_{1}^{2} \left( {e^{{2K_{1} h_{1} }} + 4K_{1}^{2} h_{1}^{2} + e^{{ - 2K_{1} h_{1} }} } \right)} \right]}}{{16K_{1}^{2} }} \\ &- \frac{{2C_{0} u_{r} K_{1} \overline{E}_{s} \left[ {A_{1} \left( {K_{1} h_{1} \left( {e^{{K_{1} h_{1} }} - e^{{ - K_{1} h_{1} }} } \right) - 2e^{{K_{1} h_{1} }} - 2e^{{ - K_{1} h_{1} }} } \right) + B_{1} \left( {K_{1} h_{1} \left( {e^{{K_{1} h_{1} }} + e^{{ - K_{1} h_{1} }} } \right) - 2e^{{K_{1} h_{1} }} + 2e^{{ - K_{1} h_{1} }} } \right)} \right]}}{{2K_{1}^{3} }}\left. {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \right\} \\ \end{aligned} $$

(90)

$$ \begin{aligned} n_{2} = & m_{2} + \frac{{\alpha^{2} D_{0} }}{144\mu }\left( {\frac{{u_{r}^{2} \overline{E}_{s}^{2} U^{{ *^{2} }} \left( {A_{2}^{2} + B_{2}^{2} } \right)}}{{8\varepsilon^{{ *^{2} }} }} + \frac{{4u_{r} \overline{E}_{s} U^{ * } D_{0} A_{2} }}{{K_{2}^{2} }} - \frac{{2b_{1} u_{r} \overline{E}_{s} U^{ * } B_{2} }}{{\varepsilon^{ * } K_{2} }}} \right) \\ &- \frac{{\alpha^{2} C_{0} }}{144}\left( {\frac{{u_{r}^{2} \overline{E}_{s}^{2} \left( {A_{1}^{2} + B_{1}^{2} } \right)}}{8} + \frac{{4C_{0} u_{r} \overline{E}_{s} A_{1} }}{{K_{1}^{2} }} - \frac{{2a_{1} u_{r} \overline{E}_{s} B_{1} }}{{K_{1} }}} \right) \\ \end{aligned} $$

(91)

$$ \begin{aligned} C_{2} = &\frac{{3m_{1} }}{{ - h_{1} }} + \frac{{6m_{2} }}{{ - h_{1}^{2} }} + \frac{{\alpha^{2} C_{0} }}{{24h_{1}^{3} }}\left\{ {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \right.\frac{{C_{0}^{2} }}{60}h_{1}^{5} + \frac{{a_{1}^{2} }}{6}h_{1}^{3} + \frac{{C_{0} a_{1} }}{12}h_{1}^{4} - 2a_{1} u_{r} \overline{E}_{s} \left( {\frac{{A_{1} \cosh \left( {K_{1} h_{1} } \right) + B_{1} \sinh \left( {K_{1} h_{1} } \right)}}{{K_{1}^{2} }}} \right) \\ & + \frac{{u_{r}^{2} \overline{E}_{s}^{2} \left[ {A_{1}^{2} K_{1}^{2} \left( {\frac{{e^{{2K_{1} h_{1} }} - e^{{ - 2K_{1} h_{1} }} }}{{2K_{1} }} - \frac{{4K_{1}^{2} h_{1}^{3} }}{3}} \right) + 2A_{1} B_{1} K_{1} \cosh \left( {2K_{1} h_{1} } \right) + B_{1}^{2} K_{1}^{2} \left( {\frac{{e^{{2K_{1} h_{1} }} - e^{{ - 2K_{1} h_{1} }} }}{{2K_{1} }} + \frac{{4K_{1}^{2} h_{1}^{3} }}{3}} \right)} \right]}}{{16K_{1}^{2} }} \\ &- \frac{{2C_{0} u_{r} K_{1} \overline{E}_{s} \left[ {A_{1} \left( {e^{{K_{1} h_{1} }} \left( {K_{1} h_{1} - 1} \right) + e^{{ - K_{1} h_{1} }} \left( {K_{1} h_{1} + 1} \right) - 2e^{{K_{1} h_{1} }} + 2e^{{ - K_{1} h_{1} }} } \right)} \right]}}{{2K_{1}^{4} }} \\ &- \frac{{2C_{0} u_{r} K_{1} \overline{E}_{s} \left[ {B_{1} \left( {e^{{K_{1} h_{1} }} \left( {K_{1} h_{1} - 1} \right) - e^{{ - K_{1} h_{1} }} \left( {K_{1} h_{1} + 1} \right) - 2e^{{K_{1} h_{1} }} - 2e^{{ - K_{1} h_{1} }} } \right)} \right]}}{{2K_{1}^{4} }}\left. {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \right\} \\ &- \frac{{\alpha^{2} C_{0} }}{{24h_{1}^{3} }}\left( {\frac{{u_{r}^{2} \overline{E}_{s}^{2} A_{1} B_{1} K_{1} }}{{8K_{1}^{2} }} + \frac{{6C_{0} u_{r} \overline{E}_{s} B_{1} }}{{K_{1}^{3} }} - \frac{{2a_{1} u_{r} \overline{E}_{s} A_{1} }}{{K_{1}^{2} }}} \right) \\ \end{aligned} $$

(92)

$$ \begin{aligned} D_{2} = &\frac{{3n_{1} }}{{h_{2} }} - \frac{{6n_{2} }}{{h_{2}^{2} }} - \frac{{\alpha^{2} D_{0} }}{{24h_{2}^{3} }}\left\{ {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \right.\frac{{D_{0}^{2} }}{ - 60}h_{2}^{5} - \frac{{b_{1}^{2} }}{6}h_{2}^{3} + \frac{{D_{0} b_{1} }}{12}h_{2}^{4} + \frac{{2b_{1} u_{r} \overline{E}_{s} U^{ * } }}{{\varepsilon^{ * } }}\left( {\frac{{B_{2} \sinh \left( {K_{2} h_{2} } \right) - A_{2} \cosh \left( {K_{2} h_{2} } \right)}}{{K_{2}^{2} }}} \right) \\ & + \frac{{u_{r}^{2} \overline{E}_{s}^{2} U^{{ *^{2} }} \left[ {A_{2}^{2} K_{2}^{2} \left( {3e^{{ - 2K_{2} h_{2} }} + 8K_{2}^{2} h_{2}^{3} - 3e^{{K_{2} h_{2} }} } \right) + 12A_{2} B_{2} K_{2} \cosh \left( {2K_{2} h_{2} } \right) + B_{2}^{2} K_{2}^{2} \left( {3e^{{ - 2K_{2} h_{2} }} - 8K_{2}^{2} h_{2}^{3} - 3e^{{2K_{2} h_{2} }} } \right)} \right]}}{{96\varepsilon^{{ *^{2} }} K_{2}^{3} }} \\ &- \frac{{2D_{0} u_{r} K_{2} \overline{E}_{s} U^{ * } \left[ {A_{2} \left( {e^{{ - K_{2} h_{2} }} \left( { - K_{2} h_{2} - 1} \right) - e^{{K_{2} h_{2} }} \left( {K_{2} h_{2} - 1} \right) - 2e^{{ - K_{2} h_{2} }} + 2e^{{K_{2} h_{2} }} } \right)} \right]}}{{2\varepsilon^{ * } K_{2}^{4} }} \\ &- \frac{{2D_{0} u_{r} K_{2} \overline{E}_{s} U^{ * } \left[ {B_{2} \left( {e^{{ - K_{2} h_{2} }} \left( { - K_{2} h_{2} - 1} \right) + e^{{K_{2} h_{2} }} \left( {K_{2} h_{2} - 1} \right) - 2e^{{ - K_{2} h_{2} }} - 2e^{{K_{2} h_{2} }} } \right)} \right]}}{{2\varepsilon^{ * } K_{2}^{4} }}\left. {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \right\} \\ &+ \frac{{\alpha^{2} D_{0} }}{{24h_{2}^{3} }}\left( {\frac{{u_{r}^{2} \overline{E}_{s}^{2} U^{{ *^{2} }} A_{2} B_{2} }}{{8\varepsilon^{{ *^{2} }} K_{2} }} + \frac{{6D_{0} u_{r} \overline{E}_{s} B_{2} U^{ * } }}{{\varepsilon^{ * } K_{2}^{3} }} - \frac{{2b_{1} u_{r} \overline{E}_{s} U^{ * } A_{2} }}{{\varepsilon^{ * } K_{2}^{2} }}} \right) \\ \end{aligned} $$

(93)

Appendix B:

$$ F_{2} = \frac{{Q_{2} Q_{4} + Q_{5} Q_{4} }}{{Q_{1} Q_{5} - Q_{2} Q_{6} }} $$

(94)

$$ F_{4} = \frac{{Q_{6} Q_{4} + Q_{1} Q_{4} }}{{Q_{1} Q_{5} - Q_{2} Q_{6} }} $$

(95)

$$ F_{8} = \frac{{Q_{13} Q_{23} + Q_{17} Q_{18} }}{{Q_{12} Q_{18} - Q_{13} Q_{19} }} $$

(96)

$$ F_{12} = \frac{{Q_{17} Q_{19} + Q_{12} Q_{23} }}{{Q_{12} Q_{18} - Q_{13} Q_{19} }} $$

(97)

$$ Q_{1} = \frac{{h_{1}^{4} }}{{4\left( {\mu h_{2} + h_{1} } \right)}} - \frac{{h_{1}^{3} }}{3} $$

(98)

$$ Q_{2} = \frac{{h_{1}^{2} h_{2}^{2} }}{{4\left( {\mu h_{2} + h_{1} } \right)}} $$

(99)

$$ Q_{4} = 1 $$

(100)

$$ Q_{5} = \frac{{\mu h_{2}^{4} }}{{4\left( {\mu h_{2} + h_{1} } \right)}} - \frac{{h_{2}^{3} }}{3} $$

(101)

$$ Q_{6} = \frac{{\mu h_{1}^{2} h_{2}^{2} }}{{4\left( {\mu h_{2} + h_{1} } \right)}} $$

(102)

$$ Q_{12} = \frac{{h_{1}^{4} }}{{4\left( {\mu h_{2} + h_{1} } \right)}} - \frac{{h_{1}^{3} }}{3} $$

(103)

$$ Q_{13} = \frac{{h_{1}^{2} h_{2}^{2} }}{{4\left( {\mu h_{2} + h_{1} } \right)}} $$

(104)

$$ \begin{aligned} Q_{17} =& \left( {\frac{{\alpha^{2} F_{2} h_{1}^{2} }}{{288\left( {\mu h_{2} + h_{1} } \right)}} - \frac{{\alpha^{2} F_{2} h_{1} }}{144}} \right)\left( {\frac{{F_{2}^{2} h_{1}^{4} }}{12} + \frac{{L_{2}^{2} h_{1}^{2} }}{2} + \frac{{F_{2} L_{2} h_{1}^{3} }}{3}} \right) + \frac{{\alpha^{2} F_{2} }}{144}\left( {\frac{{F_{2}^{2} h_{1}^{5} }}{60} + \frac{{L_{2}^{2} h_{1}^{3} }}{6} + \frac{{F_{2} L_{2} h_{1}^{4} }}{12}} \right) \\ &- \frac{{\alpha^{2} F_{4} h_{1}^{2} }}{{288\left( {\mu h_{2} + h_{1} } \right)}}\left( {\frac{{F_{4}^{2} h_{2}^{4} }}{12} + \frac{{L_{6}^{2} h_{2}^{2} }}{2} - \frac{{L_{6} F_{4} h_{2}^{3} }}{3}} \right) \\ \end{aligned} $$

(105)

$$ Q_{18} = \frac{{\mu h_{2}^{4} }}{{4\left( {\mu h_{2} + h_{1} } \right)}} - \frac{{h_{2}^{3} }}{3} $$

(106)

$$ Q_{19} = \frac{{\mu h_{1}^{2} h_{2}^{2} }}{{4\left( {\mu h_{2} + h_{1} } \right)}} $$

(107)