The effect of asymmetric zeta potentials on the electro-osmotic flow of a generalized Phan–Thien–Tanner fluid

Abstract

Electrokinetic flows driven by electro-osmotic forces are especially relevant in micro and nano-devices, presenting specific applications in medicine, biochemistry, and miniaturized industrial processes. In this work, we integrate analytical solutions with numerical methodologies to explore the fluid dynamics of viscoelastic electro-osmotic/pressure-driven fluid flows (described by the generalized Phan–Thien–Tanner (gPTT) constitutive equation) in a microchannel under asymmetric zeta potential conditions. The constitutive equation incorporates the Mittag–Leffler function with two parameters ($\alpha$ and $\beta$), which regulate the rate of destruction of junctions in a network model. We analyze the impact of the various model parameters on the velocity profile and observe that our newly proposed model provides a more comprehensive depiction of flow behavior compared to traditional models, rendering it suitable for modeling complex viscoelastic flows.

1 Introduction

Electro-osmosis is a flow-forcing method with particular applicability in medicine, biochemistry, and miniaturized industrial processes, quite suitable for flows in micro and nano-devices. In this type of flow, an external potential difference between the inlet and outlet of the channel induces the flow of an electrolyte. This potential difference acts on the ions near the wall region, which are not balanced because of the interaction between the dielectric channel walls and the fluid. Since these fluid layers have a higher concentration of counter-ions (ions with the opposite charge of the wall), this fluid will move by the action of the applied electric field, which then drags by viscous forces, the electrically neutral core as a solid body [1]. This behavior has been extensively described in the literature, first for Newtonian fluids [2,3,4,5,6,7,8,9] and more recently for some non-Newtonian fluids [10,11,12,13,14,15,16,17,18,19].

This study focuses on the electro-osmotic (EO) flow of viscoelastic fluids, described by more advanced models and particularly under the influence of asymmetric zeta potentials at the channel walls. Asymmetric zeta potentials may arise in various manufacturing techniques due to the use of different materials with differing dielectric properties at distinct walls [20]. For instance, in soft lithography, microchannels are often made of polydimethylsiloxane (PDMS), while the top wall is typically constructed from glass for optical access or another material for a different purpose [20].

Given the significance of this topic, it is crucial to review the relevant recent literature on the influence of asymmetric zeta potentials, and particularly for fluids of complex rheology.

For instance, Afonso et al. [20] provided insightful analytical solutions for combined EO and pressure-driven flows of viscoelastic fluids under asymmetric zeta potentials at the channel walls. The viscoelastic fluids analyzed were described by the linear Phan-Thien–Tanner (PTT) model and by the finite extensible nonlinear elastic model with Peterlin’s approximation (FENE-P). Escandon et al. [21] presented both analytical and numerical solutions for transient EO flows in microchannels. Their study encompassed symmetric and asymmetric uniform zeta potentials, but was concerned with Maxwell fluids which are devoid of a variable viscosity that is important near the walls, where shear rates are high.

Sadek and Pinho [22] contributed with analytical solutions for the small amplitude oscillatory shear flow (SAOS) of viscoelastic fluids induced by EO forcing. They specifically explored the case of a straight microchannel with asymmetric wall zeta potentials for the purpose of measuring linear viscoelastic fluid properties, hence their rheological model was the multi-mode upper-convected Maxwell model. Their analysis investigated the impact of relevant dimensionless parameters on normalized velocity profiles and in the linear response of relevance in SAOS when an external potential field was applied.

Sanchez et al. [23] obtained analytical solutions for an electrokinetic battery comprising parallel plates, driven by osmotic flow. Their work involved the use of the Debye–Hückel approximation to calculate the electric double layer (EDL) potential coupled with asymmetric hydrodynamic slip. The authors explicitly addressed asymmetries both in the Navier slip lengths and zeta potentials, providing insights into the interplay of these boundary conditions.

In our current investigation, the focus is on the application of a more advanced rheological constitutive equation, the gPTT model, incorporating the Mittag-Leffler function as a function of the trace of the stress tensor. This model introduces two additional fitting constants, enhancing its capability to describe the rheological properties of viscoelastic fluids [24]. Initially explored in Couette and pressure-driven flows, as well as combined EO/pressure-driven and annular flows (refer to [18, 25,26,27]), the gPTT model has been recently scrutinized in studies addressing EO flow.

Herrera-Valencia et al. [28] introduced an advanced rheological model called the generalized exponential thixotropic-elasto-viscoplastic-banded model. It effectively predicts several non-Newtonian and complex fluid behaviors, including shear-thinning/shear-thickening, yield stress, thixotropy/rheopexy, and shear banding flow. This is achieved through a combination of a nonlinear generalization of the Burgers model with a structured exponential equation, to account for structural changes of the material induced by the flow. The authors conducted an analytical investigation of the EO flow of a viscoelastic fluid in microchannels, and found that their new model successfully captures the essential physics needed to describe the enhancement and conversion of both linear and nonlinear electrokinetic rheological flows.

Teodoro et al. [29] derived an approximate and a numerical solution for laminar viscoelastic fluid flow through a parallel flat plate microchannel driven by EO and external pressure forces considering the gPTT rheological model. Their approach incorporates a nonlinear Navier slip law at the wall, depicting a power-law behavior on shear stress. The Debye–Hückel approximation for the electric potential in the EDL is applied, assuming symmetric zeta potentials at the wall. Additionally, Hernandez et al. [30] investigated numerically the EO flow in a microchannel with a viscoelastic fluid, using the gPTT model as a constitutive equation to explore the thermodiffusion effect, comparing results with those obtained through the linear PTT model [31].

In this study, we develop a new semi-analytical solution for the EO microchannel flow of viscoelastic fluids (described by gPTT constitutive equation), under asymmetric wall zeta potentials. Our investigation explores the influence of both pure EO and the combined effects of EO and pressure gradient forces in the fluid flow, taking into account the fluid rheology, the EDL thickness, and the ratio of wall zeta potentials. These findings, together with the developed analytical solutions, provide valuable insights for industries involved in this field. Furthermore, the obtained results can be used as effective tools for validating Computational Fluid Dynamics (CFD) codes. We are not aware of experimental data for polymer solutions in this flow or in fully developed duct flows of large aspect ratio, but the fluids used by [32,33,34,35] are adequate for fitting by the gPTT constitutive equation.

The remainder of this paper is organized as follows: the next section presents the governing equations, followed by the new semi-analytical solution in Sect. 3, the discussion of the results in Sect. 4, and the closure of the paper in Sect. 5.

2 Governing equations

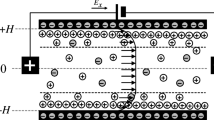
The EO flow in a microchannel under asymmetric zeta potentials of a viscoelastic gPTT fluid is shown schematically in Fig. 1, where x and y represent the streamwise and transverse directions, respectively, and the channel width is 2H. EO flows typically have velocities of the order of $\sim 0.1$ mm/s and consequently we are dealing here with a very low Reynolds number flow, also called creeping flow, which typically develops very quickly, hence in most of the microchannel the flow has conditions of fully developed flow. The flow is driven by the applied external electric field in the streamwise direction ($E_x$) and the electric charge density, $\rho _e$, is associated with the spontaneously formed EDLs, that in here are assumed not to be affected by the imposed electric field (this is the case for weak electric fields).

Fig. 1

Schematic of the flow in a parallel plate microchannel

The electric field is related to a potential, $\Phi$, by ${\textbf{E}}=-\nabla \Phi$, with $\Phi =\psi + \phi$, where $\phi$ is the applied streamwise potential and $\psi$ is the equilibrium induced potential at the channel walls, that is associated with the interaction between the ions of the fluid and the dielectric properties of the wall. The induced potential $\psi$ can be assumed independent of the applied potential $\phi$ provided the latter is not too strong [12].

The assumptions used here are all consistent with the so-called standard electrokinetic model where local EO velocities are small, EDLs are thin, and applied electric potentials are weak, so that the effect of the flow on the charge distribution and electric fields is negligible.

In this study, we have also excluded the effects of finite ionic size and volume. The impact of the former in the symmetric case was previously examined in [18].

At the walls, the no-slip condition is applied and also asymmetric zeta potentials are considered. Since the flow is fully developed, the velocity and stress fields only depend on the transverse coordinate y [20].

The flow due to combined EO/pressure gradient forcings can easily occur, as observed in experimental works [36,37,38,39] in microchannels. The mixed EO and pressure-driven flows can be imposed by using the electrodes to apply the external electric field along the channel, while the pressure gradient is formed by creating a pressure head difference between the inlet and exit reservoirs (calculation can be used to account for entrance and exit losses but often these are negligible in comparison with the fully developed channel loss). For this numerical study, we considered combined EO/pressure gradient forcings.

The equations governing the flow of an isothermal incompressible fluid are the continuity equation

$$\begin{aligned} \nabla \cdot \textbf{u}=0, \end{aligned}$$

(1)

and the linear momentum equation

$$\begin{aligned} \rho \frac{\textrm{D} \textbf{u}}{\textrm{D}t}=-\nabla p + \nabla \cdot \varvec{\tau } + \rho _e \textbf{E} \end{aligned}$$

(2)

where ${\textbf{u}}$ is the velocity vector, $\frac{\textrm{D}}{\textrm{D}t}$ is the material derivative, p is the pressure, t is the time, $\rho$ is the fluid density, $\varvec{\tau }$ is the extra-stress tensor, ${\textbf{E}}$ is the electric field, and $\rho _{e}$ is the electric charge density in the fluid.

2.1 Constitutive equation

To obtain a closed system of equations, a constitutive equation for the extra-stress tensor, $\varvec{\tau }$, must be defined. In 2019, Ferrás et al. [24] proposed a new differential rheological model based on the Phan–Thien–Tanner constitutive equation (PTT model [40, 41]), derived from the Lodge–Yamamoto type of network theory for polymeric fluids. The new model considers a more general function for the rate of destruction of junctions, the Mittag–Leffler function, where two fitting coefficients are included, in order to achieve additional fitting flexibility [24].

The Mittag–Leffler function is given by,

$$\begin{aligned} E_{\alpha ,\beta }\left( z\right) =\sum _{j=0}^{\infty }\frac{z^j}{\Gamma \left( \alpha j+\beta \right) }, \end{aligned}$$

(3)

with the Gamma function ($\Gamma \left( \right)$) defined by $\Gamma \left( t\right) = \int _{0}^{\infty } x^{t-1} e^{-x} dx$, where we consider $\alpha$ and $\beta$ to be positive real numbers and $z \in \mathbb {C}$, with $\mathbb {C}$ the set of complex numbers. When $\alpha =\beta =1$, the Mittag–Leffler function reduces to the exponential function, and when $\beta =1$ the original one-parameter Mittag-Leffler function, $E_\alpha$ is obtained [42].

The gPTT constitutive equation is given by

$$\begin{aligned} K(\tau _{kk})\varvec{\tau } +\lambda \overset{\triangledown }{{\varvec{\tau }}}= 2\eta _p{\textbf{D}}, \end{aligned}$$

(4)

where $\tau _{kk}$ is the trace of the extra-stress tensor, $\lambda$ is the relaxation time, $\eta _p$ is the polymeric viscosity coefficient, ${\textbf{D}}$ is the rate of deformation tensor, and the function $K(\tau _{kk})$ is given by

$$\begin{aligned} K(\tau _{kk})=\Gamma \left( \beta \right) E_{\alpha ,\beta }\left( \frac{\varepsilon \lambda }{\eta _p}\tau _{kk}\right) . \end{aligned}$$

(5)

The normalization $\Gamma \left( \beta \right)$ is used to ensure that $K(0)=1$ (for all choices of $\beta$) and $\varepsilon$ represents the extensibility parameter. $\overset{\triangledown }{{\varvec{\tau }}}$ represents the upper-convected derivative, defined as

$$\begin{aligned} \overset{\triangledown }{{\varvec{\tau }}}=\frac{\partial \varvec{\tau }}{\partial t} + {\textbf{u}}\cdot \nabla \varvec{\tau }-\left( \nabla {\textbf{u}}\right) ^T\cdot \varvec{\tau }-\varvec{\tau } \cdot \left( \nabla {\textbf{u}}\right) , \end{aligned}$$

(6)

where $\nabla {\textbf{u}}$ is the velocity gradient.

The influence of parameters $\alpha$ and $\beta$ on fluid rheology is quite elaborate. Ferrás and Afonso [43] showed that increasing $\alpha$ and $\varepsilon$ results in a response similar to increasing the number of arms q of a branched molecule in the extended PTT (PTT-X) model (a simplified version of the extended pom-pom (XPP) model [44]), leading to an increase in shear-thinning behavior. It should be noted that for steady shear flows with an imposed pressure gradient, a decrease in $\alpha$ (with $\varepsilon$ kept constant) leads to higher Weissenberg number [24]. Although we expect an increase in elasticity with increasing $\alpha$, since in the original XPP model [44], more arms generally lead to higher elasticity due to increased entanglement. The true physical meaning of the $\beta$ parameter is more complex, as it is used in both the Mittag-Leffler function and the normalization of the gPTT kernel.

Further details on the model, including its material functions and the procedures required to quantify all the model coefficients from data obtained in classical rheological flows, can be found in [24, 25, 43].

2.2 Electric potential

When a liquid comes into contact with a dielectric surface, the interactions between the ions and the wall lead to a spontaneous charge distribution within both the fluid and the wall. The wall becomes charged, attracting counter-ions from the fluid while repelling co-ions. Consequently, an electrically charged layer forms in the fluid in close proximity to the wall, known as the electric double layer (EDL). For more details, see [1]. The induced potential field within the EDL can be given by a Poisson equation:

$$\begin{aligned} \nabla ^2 \psi =-\frac{\rho _e}{\epsilon }, \end{aligned}$$

(7)

where $\psi$ denotes the EDL potential and $\epsilon$ is the dielectric constant of the solution. For fully developed flow, this simplifies to

$$\begin{aligned} \frac{\textrm{d}^2\psi }{\textrm{d}y^2}=-\frac{\rho _e}{\epsilon }. \end{aligned}$$

(8)

The net electric charge density in the fluid, $\rho _e$, can be given by the Boltzmann distribution:

$$\begin{aligned} \rho _e=-2n_{0}ez\sinh \left( \frac{ez}{k_{B}T}\psi \right) , \end{aligned}$$

(9)

where $n_0$ is the ion density, e the elementary charge, z the valence of the ions, T the absolute temperature, and $k_B$ the Boltzmann constant. Combining this with Eq. (8) for the induced potential equation leads to the Poisson-Boltzmann equation:

$$\begin{aligned} \frac{\textrm{d}^2\psi }{\textrm{d}y^2}=\frac{2n_{0}ez}{\epsilon }\sinh \left( \frac{ez}{k_{B}T}\psi \right) . \end{aligned}$$

(10)

Assuming the Debye–Hückel linearization principle, a valid approximation for small values of $\psi$ [11, 14, 18, 20] and of the remaining ratio in the argument of $\textrm{sinh}$, then $\textrm{sinh}\; x \approx x$ in Eq. (10). The assumption of small $ez\xi /k_{B}T$, where $\xi$ is the maximum value of $\psi$ at the wall, is equivalent to a small ratio of electrical to thermal energies, so the temperature effect on the potential distribution is negligible. For instance, for an electrolyte in water at ambient temperature, this implies a zeta potential of less than about 26 mV leading to $\frac{ez\xi }{k_{B}T} \sim 1$ [14]. Under these conditions, the Poisson-Boltzmann equation (Eq. (10)) for the 2D channel flow simplifies to

$$\begin{aligned} \frac{\textrm{d}^2\psi }{\textrm{d}y^2}=\kappa ^2\psi , \end{aligned}$$

(11)

where $\kappa ^2=2n_{0}e^2z^2/\epsilon k_B T$ is the Debye–Hückel parameter, which is related to the thickness of the Debye layer, $\lambda _D=1/\kappa$, also called the EDL thickness.

Integrating Eq. (11) together with the boundary conditions for different zeta potential at the walls, specifically $\psi \left( y=-H\right) =\xi _1$ and $\psi \left( y=H\right) =\xi _2$, leads to the following induced electric field, $\psi$:

$$\begin{aligned} \psi \left( y\right) =\xi _1\left( \Psi _1\textrm{e}^{\kappa y} - \Psi _2\textrm{e}^{-\kappa y}\right) \end{aligned}$$

(12)

with $\Psi _1 = \frac{R_\xi \textrm{e}^{\kappa H}- \textrm{e}^{-\kappa H}}{2 \mathrm {\sinh }\left( 2\kappa H\right) }$ and $\Psi _2 = \frac{R_\xi \textrm{e}^{-\kappa H}- \textrm{e}^{\kappa H}}{2 \mathrm {\sinh }\left( 2\kappa H\right) }$, where $R_\xi =\frac{\xi _2}{\xi _1}$ denotes the ratio of zeta potentials of the two walls. This equation is valid for $-H \le y \le H$, and when $R_\xi =1$, the symmetric potential profile is recovered [11, 18].

With the induced potential, the electric charge density, $\rho _e$ (Eq. (9) with the Debye-Hückel linearization principle) becomes

$$\begin{aligned} \rho _e=-\epsilon \kappa ^2 \xi _1 \left( \Psi _1\textrm{e}^{\kappa y} - \Psi _2\textrm{e}^{-\kappa y}\right) = -\epsilon \kappa ^2 \xi _1 \Omega ^{-}\left( y\right) \end{aligned}$$

(13)

where the operator $\Omega ^{\pm }\left( y\right) = \Psi _{1} \textrm{e}^{\kappa y} \pm \Psi _{2} \textrm{e}^{-\kappa y}$ is a hyperbolic function of the transverse variable y which depends on the ratio of zeta potentials and on the thickness of the Debye layer.

3 Semi-analytical solution for the EO flow of a gPTT fluid under asymmetric zeta potentials

We derive the analytical solution considering a fully developed flow for EO of a gPTT fluid under asymmetric zeta potentials (cf. Figure 1). The momentum equation, Eq. (2), simplifies to

$$\begin{aligned} \frac{\textrm{d}\tau _{xy}}{\textrm{d}y}=P_x - \rho _e E_x, \end{aligned}$$

(14)

where $P_x \equiv \frac{\textrm{d}p}{\textrm{d}x}$ is a constant streamwise pressure gradient, $\tau _{xy}$ the shear stress, and $E_x \equiv -\frac{\textrm{d}\phi }{\textrm{d}x}$ is the imposed constant streamwise gradient of electric potential. This equation is valid regardless of the rheological constitutive equation considered.

For this flow, the constitutive equation for the gPTT model (Sect. 2.1) can be further simplified, leading to

$$\begin{aligned} K(\tau _{kk})\tau _{xx}=2\lambda \dot{\gamma }\tau _{xy}, \end{aligned}$$

(15)

$$\begin{aligned} K(\tau _{kk})\tau _{yy}=0, \end{aligned}$$

(16)

$$\begin{aligned} K(\tau _{kk})\tau _{xy}=\eta _p\dot{\gamma }, \end{aligned}$$

(17)

where the velocity gradient $\dot{\gamma }$ is a function of y ($\dot{\gamma }(y)\equiv \frac{\textrm{d}u}{\textrm{d}y}$) and $\tau _{kk}=\tau _{xx}+\tau _{yy}+\tau _{zz}$ is the trace of the extra- stress tensor. Under fully developed flow conditions, $\tau _{zz}=0$, thus the trace of the extra-stress tensor becomes $\tau _{kk}=\tau _{xx}$.

Using Eq. (13), we can now integrate Eq. (14) resulting in the following shear stress distribution:

$$\begin{aligned} \tau _{xy}=\epsilon \kappa \xi _1 E_x \Omega ^+\left( y\right) + P_x y + c_1, \end{aligned}$$

(18)

where $c_1$ is a shear stress integration constant, obtained later from the boundary conditions.

Dividing Eq. (15) by Eq. (17), $K(\tau _{xx})$ cancels out, and an explicit relationship between the streamwise normal stress and the shear stress is found:

$$\begin{aligned} \tau _{xx}=2\frac{\lambda }{\eta _p}\tau _{xy}^2. \end{aligned}$$

(19)

Now combining Eqs. (17), (18), and (5), the following velocity gradient profile is obtained,

$$\begin{aligned} & \!\!\!\!\!\!\dot{\gamma }(y)=\frac{\Gamma (\beta )}{\eta _p} E_{\alpha ,\beta } \nonumber \\ & \left( \frac{2\varepsilon \lambda ^2}{\eta _p^2}\left( \epsilon \kappa \xi _1 E_x \Omega ^+\left( y\right) + P_x y + c_1\right) ^2 \right) \left( \epsilon \kappa \xi _1 E_x \Omega ^+\left( y\right) + P_x y + c_1\right) , \end{aligned}$$

(20)

which can be rewritten in dimensionless form as

$$\begin{aligned} \frac{\textrm{d}\overline{u}}{\textrm{d}\overline{y}}=\Gamma (\beta ) E_{\alpha ,\beta }\left( \frac{2\varepsilon Wi^2}{\overline{\kappa }^2}\left( \Upsilon \overline{y} -\overline{\kappa } \overline{\Omega }^+\left( \overline{y}\right) + \overline{\tau }_1 \right) ^2 \right) \left( \Upsilon \overline{y} -\overline{\kappa } \overline{\Omega }^+\left( \overline{y}\right) + \overline{\tau }_1 \right) ,\qquad \end{aligned}$$

(21)

where $Wi=\lambda \kappa u_{sh}$ is the Weissenberg number and $u_{sh}$ is the Helmholtz-Smoluchowski EO velocity, defined as $u_{sh}=-\frac{\epsilon \xi _1 E_x}{\eta _p}$, $\overline{u}=\frac{u}{u_{sh}}$, $\overline{y}=\frac{y}{H}$, $\overline{\kappa }=\kappa H$, and $\overline{\tau }_1 = \frac{c_1 H}{\eta _p u_{sh}}$. The non-dimensional parameter $\Upsilon = -\frac{H^2 P_x}{\epsilon \xi _1 E_x}$ represents the ratio of pressure to EO driving forces and $\overline{\Omega }^{+}\left( \overline{y}\right) =\overline{\Psi }_{1} \textrm{e}^{\overline{\kappa }\, \overline{y}} +\overline{\Psi }_{2} \textrm{e}^{-\overline{\kappa }\, \overline{y}}$, with $\overline{\Psi }_1 = \frac{R_\xi \textrm{e}^{\overline{\kappa }}- \textrm{e}^{-\overline{\kappa }}}{2 \mathrm {\sinh }\left( 2\overline{\kappa }\right) }$ and $\overline{\Psi }_2 = \frac{R_\xi \textrm{e}^{-\overline{\kappa }}- \textrm{e}^{\overline{\kappa }}}{2 \mathrm {\sinh }\left( 2\overline{\kappa }\right) }$. For simplicity, the dimensionless quantities were based on the zeta potential at the bottom wall.

For pure EO flow $\Upsilon =0$, the velocity profile can be obtained by integrating the velocity gradient profile (Eq. (21)), subject to the no-slip boundary condition at the top (+) or bottom (-) walls, $\overline{u}\left( \overline{y} = -1 \right) =\overline{u}\left( \overline{y} = 1 \right) = 0$. Simplifying Eq. (21) we obtain,

$$\begin{aligned} \overline{u}\left( \overline{y}\right) = \Gamma (\beta ) \sum _{j=0}^{\infty }\left( \frac{2\varepsilon Wi^2}{{\overline{\kappa }^2}}\right) ^j \frac{1}{\Gamma \left( \alpha j +\beta \right) } \left( \int _{-1}^{\overline{y}} \left( -\overline{\kappa } \overline{\Omega }^+\left( \overline{z}\right) + \overline{\tau }_1 \right) ^{2j+1} \textrm{d}\overline{z} \right) ,\nonumber \\ \end{aligned}$$

(22)

with $\overline{z}$ a dummy variable.

Following some algebraic manipulations, Eq. (22) can be further simplified, resulting in the following nested sum expression for the velocity profile,

$$\begin{aligned}&\overline{u}\left( \overline{y}\right) =\Gamma (\beta ) \Biggl (\displaystyle \sum _{j=0}^{\infty } \frac{2\varepsilon Wi^2}{\overline{\kappa }^2\left( \Gamma (\alpha j +\beta )\right) }\nonumber \\&\left[ \displaystyle \sum _{m=0}^{2j+1} {2j+1 \atopwithdelims ()m} \left( {\overline{\tau }_1}^m\right) \right. \nonumber \\&\left. \Biggl \{\displaystyle \sum _{i=0}^{2j+1-m} {2j+1-m \atopwithdelims ()i} \frac{\left( -\overline{\kappa } \overline{\Psi }_1 \right) ^{2j-m-i+1} \left( -\overline{\kappa } \overline{\Psi }_2\right) ^{i}}{\overline{\kappa }\left( 2j-2i-m+1\right) } \textrm{e}^{\left( 2j-2i-m+1\right) \overline{\kappa }\,\overline{y}} \Biggl \} \right] \Biggl ) + c_2, \end{aligned}$$

(23)

with $c_2$ obtained using $\overline{u}\left( 1 \right) = 0$, and given by,

$$\begin{aligned}&c_2 =-\Gamma (\beta ) \Biggl (\displaystyle \sum _{j=0}^{\infty } \frac{2\varepsilon Wi^2}{\overline{\kappa }^2\left( \Gamma (\alpha j +\beta )\right) }\nonumber \\&\quad \left[ \displaystyle \sum _{m=0}^{2j+1} {2j+1 \atopwithdelims ()m} \left( {\overline{\tau }_1}^m\right) \right. \nonumber \\&\quad \left. \Biggl \{\displaystyle \sum _{i=0}^{2j+1-m} {2j+1-m \atopwithdelims ()i} \frac{\left( -\overline{\kappa } \overline{\Psi }_1 \right) ^{2j-m-i+1} \left( -\overline{\kappa } \overline{\Psi }_2\right) ^{i}}{\overline{\kappa }\left( 2j-2i-m+1\right) } \textrm{e}^{\left( 2j-2i-m+1\right) \overline{\kappa }} \Biggl \} \right] \Biggl ). \end{aligned}$$

(24)

$\overline{\tau }_1$ is obtained by solving numerically $\overline{u}\left( -1 \right) = 0$.

4 Results and discussion

4.1 Assessment of the series solution

In this section, we compare the velocity profile given by Eq. (22) (obtained by a numerical quadrature rule, and referred to as numerical solution) with the analytical solution given by Eq. (23). The numerical results were obtained using the Mathematica software.

For the numerical solution, we first obtain $\overline{\tau }_1$ using the secant method to find the root of,

$$\begin{aligned} \Gamma (\beta ) \sum _{j=0}^{\infty }\left( \frac{2\varepsilon Wi^2}{{\overline{\kappa }^2}}\right) ^j \frac{1}{\Gamma \left( \alpha j +\beta \right) } \left( \int _{-1}^{1} \left( -\overline{\kappa } \overline{\Omega }^+\left( \overline{z}\right) + \overline{\tau }_1 \right) ^{2j+1} \textrm{d}\overline{z} \right) =0. \end{aligned}$$

(25)

The $\overline{\tau }_1$ value obtained is then substituted in Eq. (22), and the numerical velocity profile is finally obtained.

The analytical solution given by Eq. (23) is composed by an infinite series. Therefore, we need to assess the number of terms required in the series to achieve a precise and accurate solution. To do this, we used as a reference the numerical solution.

The new truncated solution is obtained from Eq. (23), truncating the sum with $j+1$ terms. To validate the solution a reference “exact” case with 201 equidistant mesh points across the channel height (2H) was considered and the error measured as the root mean squared error (RMSE) obtained at these points by

$$\begin{aligned} RMSE = \sqrt{\frac{1}{n} \displaystyle \sum _{i=1}^{n} \left( {\overline{u}}(\overline{y})_{num}-u(\overline{y})_{t}\right) ^2}, \end{aligned}$$

where ${\overline{u}}(\overline{y})_{num}$ is the reference numerical value of the velocity and ${\overline{u}}(\overline{y})_{t}$ is the velocity value for the truncated series. Three different values of $\varepsilon Wi^2$ were considered: 0.5, 1, and 2 and two different values for $R_\xi$: $-1$ and 0.5. We set $\beta =1$ and tested two different values of $\alpha$, 0.5 and 1.5. We only change the values of $\alpha$, because this parameter is the most sensitive to changes in the series.

Table 1 RMSE for $\varepsilon Wi^2=0.5$ and $\alpha = 0.5$

Table 2 RMSE for $\varepsilon Wi^2=1$ and $\alpha = 0.5$

Table 3 RMSE for $\varepsilon Wi^2=2$ and $\alpha = 0.5$

Tables 1, 2, and 3 show the RMSE for $\varepsilon Wi^2=0.5$, 1, and 2, respectively, and considering $\alpha =0.5$, $R_\xi =0.5$, and $-1$. As the number of terms in the series (Eq. (23)) increases, the error decreases as expected. This parametric study provides insights into the behavior of the truncated solution. For instance, as $\varepsilon Wi^2$ increases (refer to Table 2 and 3), and with $R_\xi =0.5$, the series solution exhibits slower convergence. On the other hand, for lower $\varepsilon Wi^2$ values, the series solution converges very rapidly. Table 4 shows the RMSE for $\varepsilon Wi^2=2$, $\alpha =1.5$, and considering $R_\xi =0.5$ and $-1$. Notably, as $\alpha$ increases, the error decreases more rapidly with an increase in the number of terms in the series (even for high values of $\varepsilon Wi^2$). We experimented with a higher number of terms in the series for cases with high $\varepsilon Wi^2$ and low $\alpha$, and found that a favorable balance between computation time, simplicity, and solution accuracy could be achieved for $j=20$.

Table 4 RMSE for $\varepsilon Wi^2=2$ and $\alpha = 1.5$

The velocity profiles obtained by the numerical solution of Eq. (22) and the analytical solution obtained by Eq. (23) for different j are shown in Figs. 2 and 3, where $u/u_{sh}$ is the normalized velocity profile. These particular results indicate that the velocity profile converges to the correct profile as the number of terms in the series increases, and that this convergence is slower for lower values of $\alpha$.

Fig. 2

Velocity profiles for $\beta =1$, $R_\xi =0.5$ and $\bar{\kappa }=20$. (a) $\alpha =0.5$, $\varepsilon Wi^2=1$; (b) $\alpha =1.5$, $\varepsilon Wi^2=2$

Fig. 3

Velocity profiles for $\beta =1$, $R_\xi =-1$ and $\bar{\kappa }=20$. (a) $\alpha =0.5$, $\varepsilon Wi^2=1$; (b) $\alpha =1.5$, $\varepsilon Wi^2=2$

4.2 Discussion

4.2.1 Pure EO and asymmetric zeta potentials

In this section, we explore the impact of the Mittag-Leffler function parameters, $\alpha$ and $\beta$, on the distribution of the velocity profile under pure EO driving forces (across the channel). We consider different values of $\varepsilon Wi^2$ and $R_{\xi }$, allowing for a comparison of results with those obtained for the exponential PTT model.

Figure 4 compares the velocity profiles obtained for EO flow under asymmetric zeta potentials considering two different $\varepsilon Wi^2$ values and different values of $\alpha$ (Fig. 4a) and $\beta$ (Fig. 4b) for $\overline{\kappa }=20$ and $R_{\xi }=0.5$.

In Fig. 4a ($\beta =1$), we observe that for increasing $\varepsilon Wi^2$ and decreasing $\alpha$ the flow rate increases, leading to an increase of the skewed pluglike profile. In Fig. 4b ($\alpha =1$), a similar qualitative behavior is obtained, i.e., increasing $\varepsilon Wi^2$ and decreasing $\beta$, the flow rate increases. However, there are quantitative differences with the effect of $\alpha$ being stronger than the effect of $\beta$. These variations are consistent with enhanced shear-thinning leading to lower viscosities in the wall region.

Fig. 4

Velocity profiles for $R_\xi =0.5$, $\overline{\kappa }=20$ and $\varepsilon Wi^2=0.5$ and 1 a $\beta =1$, $\alpha =0.5,~1$ and  1.5; b $\alpha =1$, $\beta =0.5,~1$ and 1.5

Figure 5 compares the velocity profiles obtained for EO flow under asymmetric zeta potentials considering two different $\varepsilon Wi^2$ values and different values of $\alpha$ (Fig. 5a) and $\beta$ (Fig. 5b) at $\overline{\kappa }=20$ and $R_{\xi }=-1$.

Fig. 5

Velocity profiles for $R_\xi =-1$, $\overline{\kappa }=20$ and $\varepsilon Wi^2=0.5$ and  1 a $\beta =1$, $\alpha =0.5,~1$ and  1.5; b $\alpha =1$, $\beta =0.5,~1$ and  1.5

In Fig. 5a ($\beta =1$), we observe that for increasing $\varepsilon Wi^2$ and decreasing $\alpha$, the flow rate increases, leading to an increase of an anti-symmetric pluglike profile. In Fig. 5b ($\alpha =1$), a similar qualitative behavior is obtained, i.e., increasing $\varepsilon Wi^2$ and decreasing $\beta$, the flow rate increases. However, there are quantitative differences with the effect of $\alpha$ being stronger than the effect of $\beta$. The pronounced flow with the increasing of $\varepsilon Wi^2$ is associated with the shear-thinning behavior of the fluid. It is also clear from the plots of Figs. 4, 5, 6 that the two EDL are thin, typically not exceeding $10 \%$ of the channel half-width, as required by the assumptions invoked.

Fig. 6

Variation of $\overline{\tau }_1$, for purely EO viscoelastic flow, as a function of the ratio of zeta potentials, $R_{\xi }$ considering $\overline{\kappa }=20$, $\beta =1$ and $\alpha =1$ and 1.5

Figure 6 shows the variation of coefficient $\overline{\tau }_1$, for a purely EO viscoelastic flow, as a function of the ratio of zeta potentials, $R_{\xi }$. We consider $\alpha =\beta =1$ (which corresponds to the exponential PTT model) and $\alpha =1.5$ and $\beta =1$. By looking at the results, we see that for $R_\xi =1$, we have $\overline{\tau }_1=0$, in agreement with the results obtained for the symmetric case studied by Afonso et al. [11, 20]. For $R_\xi <1$, $\overline{\tau }_1$ is always negative, its value decreases but its magnitude increases with the increase of $\varepsilon Wi^2$, indicating that the shear stress in real value, is also decreasing as $\varepsilon Wi^2$ increases. For $R_\xi >1$, $\overline{\tau }_1$ is always positive and increases with $\varepsilon Wi^2$, which indicates that the shear stress is higher as we increase the shear-thinning behavior of the fluid. The case $\alpha < 1$ was not considered, due to convergence problems at high values of $\varepsilon Wi^2$.

Since one of the goals of this work is to provide a tool for validating future numerical implementations of this model in general numerical codes, the Mathematica numerical codes used to obtain the solution are provided as supplementary material.

4.2.2 Mixed driving forces and asymmetric zeta potentials

For combined EO and pressure-driven flows, Eq. (21) has to be integrated numerically if $\Upsilon \ne 0$. The influence of the new model on the velocity profile was assessed considering $\Upsilon =2.5$ and $R_{\xi }=0.5$ and $\Upsilon =-2$ and $R_{\xi }=-1$. We also considered different values for $\alpha$ and $\beta$.

Figure 7 presents the velocity profiles obtained for combined EO/pressure gradient forcings under asymmetric zeta potentials. We consider two different $\varepsilon Wi^2$ values and different values of $\alpha$ (Fig. 7a) and $\beta$ (Fig. 7b) for $\overline{\kappa }=20$, $R_{\xi }=0.5$ and $\Upsilon =2.5$ (adverse pressure gradient).

Fig. 7

Velocity profiles for $R_\xi =0.5$, $\Upsilon =2.5$, $\overline{\kappa }=20$ and $\varepsilon Wi^2=0.5$ and  1 a $\beta =1$, $\alpha =0.5,~1$ and 1.5; b $\alpha =1$, $\beta =0.5,~1$ and 1.5

In Fig. 7a ($\beta =1$) and b ($\alpha =1$), the velocity profiles show a double peak due to the retarding action of the pressure gradient. We observe a consistent pattern, related to what was found in Fig. 4, where an increase in $\varepsilon Wi^2$ and a decrease in $\alpha$ correspond to an increase in the flow rate because the shear-thinning led to lower wall viscosities. Notably, the impact of $\alpha$ on the flow rate is more pronounced compared to the effect of $\beta$.

In Fig. 8, we keep the parameters consistent with those in Fig. 7, except for the updated values of $R_{\xi }=-1$ and $\Upsilon =-2$ (indicating a favorable pressure gradient).

Fig. 8

Velocity profiles for $R_\xi =-1$, $\Upsilon =-2$, $\overline{\kappa }=20$ and $\varepsilon Wi^2=0.5$ and 1 a $\beta =1$, $\alpha =0.5,~1$ and 1.5; b $\alpha =1$, $\beta =0.5, 1$ and  1.5

In Fig. 8, (a) with varying $\alpha$ and setting $\beta =1$, and (b) with varying $\beta$ and setting $\alpha =1$, the velocity profiles exhibit an increase with the increase of $\varepsilon Wi^2$ and a decrease in $\alpha$. Again this is attributed to shear-thinning effects, resulting in higher shear rates near the walls.

Remark

The diverse array of flow behaviors observed, stemming from the variation in different model parameters and flow conditions, offers valuable insights for understanding and predicting the flow patterns of rheologically characterized viscoelastic fluids. While the analysis presented here provides insights into such behavior, it does not comprehensively cover all possible flows of interest, given the limited number of parameter values considered. To facilitate more targeted studies, we share the codes used in this research in the supplementary material section, enabling the industrial sector and academia to replicate and further develop these results.

5 Conclusions

We have developed an analytical solution expressing the velocity profile in a series form for the EO flow of a gPTT fluid. This solution was used to illustrate how various model parameters impact the velocity profiles. As anticipated, a decrease in $\alpha$ and $\beta$ for the same $\varepsilon Wi^2$ leads to an increase in flow velocity. Consequently, when $R_{\xi }>0$, a more pronounced skewed pluglike profile is observed, whereas $R_{\xi }<0$ results in a more pronounced anti-symmetric pluglike profile.

The influence of $\beta$ is less evident due to its dual role in affecting the rate of destruction of junctions. It serves as a parameter in the Mittag-Leffler function and also functions as a normalization factor. This dual impact contributes to the subtlety of its influence. Our newly proposed model offers a broader description of flow behavior compared to traditional models, making it applicable in the modeling of complex viscoelastic flows.

These analytical and semi-analytical solutions not only serve as valuable tools for validating CFD codes but also enhance our comprehension of the behavior of the model in simple shear flows. This expanded understanding facilitates more accurate modeling of complex viscoelastic flows.