Enhanced joint remote state preparation under correlated amplitude damping decoherence by weak measurement and quantum measurement reversal

Abstract

A joint remote state preparation (JRSP) scheme is put forward to prepare an arbitrary single-qubit state. Specifically, the GHZ-state of three qubits as a resource successively passes through the correlated amplitude damping (CAD) noisy channel. Then, an analytical expressions quantifying the average fidelity of JRSP is obtained under the CAD noisy channel. Comparing with the results of uncorrelated amplitude damping (AD) noise, we find that the correlated effects enable to improve the average fidelity of JRSP in the CAD noisy channel. Furthermore, by introducing the weak measurement (WM) and quantum measurement reversal (QMR), and we calculate the average fidelity as a function of the decoherence strength, memory parameter, measurement strength of WM and measurement strength of QMR for an arbitrary quantum state to be prepared. These results demonstrate that the combination of WM and QMR can significantly improve the average fidelity in both uncorrelated and correlated AD noise. Our results may extend the capabilities of WM as a technique in various quantum information processing which are affected by correlated noise.

1 Introduction

One of the key tasks of quantum information [1,2,3,4] is the use of entangled states to transmit information in quantum systems. The striking characteristic of entanglement [5,6,7] enables communication methods completely different from classical ones. As the most well-known example of quantum communication, quantum teleportation (QT) was first proposed by Bennet et al. [8], which allows one to convey an arbitrary single quantum state from the sender to a distant receiver via consuming one ebit and two cbits. In order to reduce the classical resources required in QT, the first remote state preparation (RSP) scheme was first put forward by Pati [9] in 2000, where the sender and the receiver share one ebit of entanglement in advance, and the sender holds all the classical information of the target state. This RSP is completed probabilistically after the sender’s single-qubit von Neumann measurement and the receiver’s recovery operation. After Pati’s pioneering work, much attention is focused on RSP in both theoretical [10,11,12,13,14,15] and experimental [16,17,18] aspects. In the RSP scheme, the information transmitted remotely is assigned to only one sender, which may lead to information disclosure when the sender is dishonest.

In order to address this deficiency, JRSP was proposed by increasing the number of senders [19, 20]. In the process of JRSP, the teleported information is broken up into several parts, all of the senders must cooperate to aid the receiver to restore the target state. It means that neither a single sender nor part of the senders can help the receiver to reconstruct the target state, thus the JRSP can improve the communication security. Due to the remarkable advantage, JRSP has attracted great interest since its first appearance, and different entangled states, like Bell, GHZ, W, cluster and Brown states, are used as shared resource in JRSP [21,22,23,24,25,26,27,28]. The JRSP containing some special quantum states, such as four-dimensional GHZ-type state [29], cluster-type [30, 31], W-type [32], equatorial two-qudit state [33, 34] and more, are investigated. In 2012, Luo et al. [18] proposed the experimental architecture of JRSP using GHZ state. Nguyen et al. [35] presented the quantum circuit of JRSP by using POVM measurement. Yu et al. [36] designed the schemes for JRSP of arbitrary two- and three-photon states with linear-optical elements. It is easy to find that all of the JRSP schemes above are considered in an ideal environment. However, quantum noise is an unavoidable phenomenon in realistic environment. Noise can decohere a quantum entangled state, in which case the output state received is inconsistent with the prepared state. In other words, the entanglement is fragile and easily broken via environmental noise. Therefore, it is meaningful to study the influence of noise on JRSP.

Each physical process, as we all know, can be viewed as a quantum channel, which maps the initial state of the system to the final state [8, 37]. For multipartite quantum systems or consecutive uses of the same channel, these channels can be divided into correlated or uncorrelated channel. The effect of the uncorrelated noise on JRSP has been widely studied by a number of researchers [38,39,40,41,42,43,44,45,46]. Nevertheless, the correlated channel is more practical in physical process, especially, in the case of high transmission rate [47,48,49]. Unlike the uncorrelated AD channel in which each qubit independently experiences the noise, the qubits may suffer relaxation simultaneously in the CAD channel [50]. As shown in Ref. [51], the correlation effects help to avoid entanglement sudden death. However, to the best of our knowledge, few detailed investigations involving the influence of CAD on JRSP are available at the present. On the other hand, to overcome the impact of decoherence on quantum entanglement, several types of decoherence suppression methods have been proposed, including dynamical decoupling [52], quantum entanglement purification [53], quantum error coding [54], and decoherence-free subspace [55].

As an important quantum technology, weak measurement (WM) has attracted extensive attention in the past few years [51, 56,57,58,59,60]. Different from the traditional von Neumann orthogonal projection measurement, WM can not completely collapse the measured quantum system, and it is more gentle in extracting information from the system. Thus, we can use quantum measurement reversal (QMR) to restore the initial state with a certain probability. Recently, some researchers have found the ability of WM and QMR to protect entanglement from AD noise [57, 59, 61,62,63,64,65,66,67,68,69]. To be specific, it needs repeatedly measurement to gain an unknown state information with a finite probability. The probability of success decreases with increasing strength of the measurement. Meanwhile, the action that accompanies the weak measurement is the quantum measurement reversal (QMR), which utilized to erasure the influence of the first measurement [65]. In 2008, Katz et al. [66] discussed the relationship between the fidelity and the strength of the measurement in the system of superconducting qubit. Then, Kim et al. [67] utilized the form of operator to describe the process of weak measurement and recover measurement in 2009. They also researched the feasibility of utilizing weak measurement method in the system of photonic qubit. Whereafter, in 2011, Kim et al. [68] proposed the weak measurement method can resist the decoherence phenomenon of single (two)-qubit entangled state in AD channel, and Lee et al. [69] demonstrated it in experimental. However, no systematic study devoted to the application of WM and QMR with CAD noise on JRSP protocol has been reported yet. This motivates us to utilize WM and QMR to study the JRSP under CAD noise. More importantly, we also need to know whether WM and QMR can suppress the influence of CAD noise on JSRP protocol.

In this paper, we firstly consider the influence of CAD noise on JRSP, and then propose a scheme to improve the average fidelity with the help of WM and QMR. We find that the average fidelity of JRSP under CAD noise is better than that under AD noise. In addition, we also show that the combined WM and QMR can greatly improve the average fidelity in both AD and CAD noise. In particular, for the completely uncorrelated AD and fully correlated amplitude damping (FCAD), the average fidelity may be close to 1.

The rest of this paper is organized as follows. In Sect. 2, the JRSP via three-qubit entangled GHZ-state as quantum channel under CAD noise is investigated in detail. Then in Sect. 3, we show that how to use WM and QMR to improve average fidelity of JRSP. Finally, some conclusions are drawn in Sect. 4.

2 JRSP under CAD

In this section, we investigate JRSP under CAD for an unknown single-qubit state. The scheme involves totally three parties located in different places: two observers Alice and Bob, and a receiver Charlie. Suppose that two senders Alice and Bob would like to help the receiver Charlie prepare an arbitrary unknown single-qubit state $|\xi \rangle$, which can be given by

$$\begin{aligned} |\xi \rangle =\cos \frac{\theta }{2}|0\rangle +\sin \frac{\theta }{2}e^{i\phi }|1\rangle , \end{aligned}$$

(1)

where $\theta$ and $\phi$ are the polar and the phase parameters, respectively, and satisfy $\theta \in [0,\pi ]$ and $\phi \in [0,2\pi ]$. Alice and Bob own the information of amplitude and phase factor, respectively. Assumed that Alice holds a quantum resource generator in her laboratory and she generates the three-qubit entangled GHZ-state, such that

$$\begin{aligned} |{\mathcal {G}}\rangle _{ABC}=\frac{1}{\sqrt{2}}(|000\rangle +|111\rangle )_{ABC}, \end{aligned}$$

(2)

and sends qubit B and C to Bob and Charlie through channel with CAD noise successively, respectively. Due to the consecutive uses of the noisy channel, the correlated effect should be considered. Therefore, the entangled state $|{\mathcal {G}}\rangle _{ABC}$ has suffered CAD noise during the distribution. The dynamics of an entangled state subject to CAD nose is described by the quantum super-operation $\varepsilon$ acting on the initial state [60].

$$\begin{aligned} \varepsilon _{CAD}(\rho )=(1-\mu )\sum ^1_{i,j=0}(I\otimes E_{ij})\rho (I\otimes E_{ij})^{\dagger } +\mu \sum ^1_{k=0}(I\otimes A_k)\rho (I\otimes A_k)^{\dagger }, \end{aligned}$$

(3)

where I is a second-order identity matrix, $\mu$ is the correlated parameter (memory parameter) with $0\le \mu \le 1$, and

$$\begin{aligned} \rho =|{\mathcal {G}}\rangle _{ABC}\langle {\mathcal {G}}|=\frac{1}{2}(|000\rangle +|111\rangle )_{ABC}(\langle 000|+\langle 111|). \end{aligned}$$

(4)

Obviously, we can obtain the uncorrelated AD channel by $\mu =0$ and get the FCAD channel when $\mu =1$. $E_{ij}= E_i\otimes E_j$ is the tensor product for Kraus operators of AD noise. The corresponding Kraus operators are

$$\begin{aligned} E_0=\left( \begin{array}{cc} 1 &\quad{} 0 \\ 0 &\quad{} \sqrt{1-\gamma } \\ \end{array} \right) ,~~ E_1=\left( \begin{array}{cc} 0 &\quad{} \sqrt{\gamma } \\ 0 &\quad{} 0 \\ \end{array} \right) , \end{aligned}$$

(5)

the parameter $\gamma$ is the decoherence strength of the AD channel and $0\le \gamma \le 1$. $A_k$ has been solved by studying the correlated Lindblad equation [61], which gives the following formalism

$$\begin{aligned} A_0= \left( \begin{array}{cccc} 1 &\quad{} 0 &\quad{} 0 &\quad{} 0 \\ 0 &\quad{} 1 &\quad{} 0 &\quad{} 0 \\ 0 &\quad{} 0 &\quad{} 1 &\quad{} 0 \\ 0 &\quad{} 0 &\quad{} 0 &\quad{} \sqrt{1-\gamma } \\ \end{array} \right) ,~~ A_1= \left( \begin{array}{cccc} 0 &\quad{} 0 &\quad{} 0 &\quad{} \sqrt{\gamma } \\ 0 &\quad{} 0 &\quad{} 0 &\quad{} 0 \\ 0 &\quad{} 0 &\quad{} 0 &\quad{} 0 \\ 0 &\quad{} 0 &\quad{} 0 &\quad{} 0 \\ \end{array} \right) . \end{aligned}$$

(6)

The evolution of the initially shared state in Eq. (2) under the CAD noise can be obtained from Eqs. (3–5), which is expressed as

$$\begin{aligned} \begin{aligned} \varepsilon _{CAD}(\rho )&=\frac{1}{2}[|000\rangle \langle 000|+(\overline{\mu }\overline{\gamma }+\mu \sqrt{\overline{\gamma }})(|000\rangle \langle 111|+|111\rangle \langle 000|)&\\&\quad +(\overline{\mu }\overline{\gamma }^2+\mu \overline{\gamma })|111\rangle \langle 111|+\overline{\mu }\overline{\gamma }\gamma (|110\rangle \langle 110|+|101\rangle \langle 101|)&\\&\quad +(\overline{\mu }\gamma ^2+\mu \gamma )|100\rangle \langle 100|]_{ABC},&\end{aligned} \end{aligned}$$

(7)

where $\overline{\mu }=1-\mu$ and $\overline{\gamma }=1-\gamma$. Our scheme includes the following three steps:

Step 1. Alice implements a single qubit von Neumann measurement with the basis $\mathcal{M}\mathcal{A}=\{\mathcal{M}\mathcal{A}_0$, $\mathcal{M}\mathcal{A}_1\}$ on qubit A, where

$$\begin{aligned} \mathcal{M}\mathcal{A}_0=\left(\cos \frac{\theta }{2}|0\rangle +\sin \frac{\theta }{2}|1\rangle )(\cos \frac{\theta }{2}\langle 0|+\sin \frac{\theta }{2}\langle 1| \right) \end{aligned}$$

(8)

and

$$\begin{aligned} \mathcal{M}\mathcal{A}_1= \left(\sin \frac{\theta }{2}|0\rangle -\cos \frac{\theta }{2}|1\rangle )(\sin \frac{\theta }{2}\langle 0|-\cos \frac{\theta }{2}\langle 1|\right). \end{aligned}$$

(9)

After the measurement, Alice encodes the result in classical bit m and sends it to Bob and Charlie via the classical channel. The system state after Alice’s measurement is

$$\begin{aligned} \rho _m=\textrm{tr}_A \left[\frac{\mathcal{M}\mathcal{A}_m\varepsilon _{CAD}(\rho )(\mathcal{M}\mathcal{A}_m)^{\dagger }}{\textrm{tr}(\mathcal{M}\mathcal{A}_m\varepsilon (\rho )(\mathcal{M}\mathcal{A}_m)^{\dagger }} \right], ~~~\textrm{with}~~~ m\in \{0,1\}. \end{aligned}$$

(10)

Step 2. Bob performs a single qubit von Neumann measurement with the basis $\mathcal{M}\mathcal{B}_m=\{\mathcal{M}\mathcal{B}^0_m$, $\mathcal{M}\mathcal{B}^1_m\}$ on qubit B according to Alice’s result m, where $\mathcal{M}\mathcal{B}^0_m=|O^0_m\rangle \langle O^0_m|$ and $\mathcal{M}\mathcal{B}^1_m=|O^1_m\rangle \langle O^1_m|$, and $\{|O^n_m\rangle : n\in \{0,1\}\}$ are in the form

$$\begin{aligned} \left( \begin{array}{c} |O^0_m\rangle \\ |O^1_m\rangle \rangle \\ \end{array} \right) =V_m \left( \begin{array}{c} |0\rangle \\ |1\rangle \\ \end{array} \right) \end{aligned}$$

(11)

with

$$\begin{aligned} V_0=\frac{1}{\sqrt{2}} \left( \begin{array}{cc} 1 &{} e^{-i\phi } \\ 1 &{} -e^{-i\phi } \\ \end{array} \right) ~~~\textrm{and}~~~ V_1=\frac{1}{\sqrt{2}} \left( \begin{array}{cc} e^{-i\phi } &{} 1 \\ -e^{-i\phi } &{} 1 \\ \end{array} \right) . \end{aligned}$$

(12)

Then, he informs Charlie his measurement result n. The system state after Bob’s measurement result is

$$\begin{aligned} \rho ^n_m=\textrm{tr}_B \left[\frac{\mathcal{M}\mathcal{B}^n_m\rho _m(\mathcal{M}\mathcal{B}^n_m)^{\dagger }}{\textrm{tr}(\mathcal{M}\mathcal{B}^n_m\rho _m (\mathcal{M}\mathcal{B}^n_m)^{\dagger })} \right],~~~\textrm{with}~~~m,n\in \{0,1\}. \end{aligned}$$

(13)

Step 3. According to Alice’s and Bob’s measurement results, Charlie can construct the state $|\xi \rangle$ by performing the recovery operator $R^n_m$, where $R^0_0=|0\rangle \langle 0|+|1\rangle \langle 1|$, $R^1_0= |0\rangle \langle 0|-|1\rangle \langle 1|$, $R^0_1=|0\rangle \langle 1|-|1\rangle \langle 0|$ and $R^1_1= |0\rangle \langle 1|+|1\rangle \langle 0|$.

After the above three steps, Charlie finally obtains the output state $\rho _m^n(out)=R^n_m\rho _m^n(R^n_m)^{\dagger }$, which can be given by

$$\begin{aligned} \begin{aligned} \rho ^0_0(out)=\rho ^1_0(out)&=\left(\cos ^2\frac{\theta }{2}+\gamma \sin ^2\frac{\theta }{2} \right)|0\rangle \langle 0| +\overline{\gamma }\sin ^2\frac{\theta }{2}|1\rangle \langle 1|&\\&\quad +(\overline{\mu }\overline{\gamma }+\mu \sqrt{\overline{\gamma }}) \sin \frac{\theta }{2}\cos \frac{\theta }{2}(e^{-i\phi }|0\rangle \langle 1|+e^{i\phi }|1\rangle \langle 0|),&\\ \rho ^0_1(out)=\rho ^1_2(out)&=\left(\sin ^2\frac{\theta }{2}+\gamma \cos ^2\frac{\theta }{2}\right)|1\rangle \langle 1| +\overline{\gamma }\cos ^2\frac{\theta }{2}|0\rangle \langle 0|&\\&\quad +(\overline{\mu }\overline{\gamma }+\mu \sqrt{\overline{\gamma }}) \sin \frac{\theta }{2}\cos \frac{\theta }{2}(e^{-i\phi }|0\rangle \langle 1|+e^{i\phi }|1\rangle \langle 0|).&\end{aligned} \end{aligned}$$

(14)

In the JRSP scheme, the credibility of quantum teleportation through CAD noise is usually quantified by the fidelity which measures the overlap between the initial $|\xi \rangle$ and the finally teleported state $\rho _m^n(out)$,

$$\begin{aligned} F^n_m=\langle \xi |\rho ^n_m(out)|\xi \rangle ,~~~\textrm{with}~~~m,n\in \{0,1\}. \end{aligned}$$

(15)

Considering the fact that the output state may come up with certain probability, we invoke the average fidelity

$$\begin{aligned} F_{av}=\sum ^1_{m,n=0}q_{mn}F^n_m, \end{aligned}$$

(16)

where $\{q_{mn}\}$ is the probability that the state $\rho ^n_m$ occurs. Through calculation, $q_{mn}$ equals to $\frac{1}{4}$ for any $m,n\in \{0,1\}$ in this section. Note that this average fidelity depends on the target state, so we call it the state dependent average fidelity.

From Eqs. (1), (14), (15) and (16), it follows that the fidelity is explicitly expressed

$$\begin{aligned} F_{av}= \frac{1}{2} \left[1+\overline{\mu }\overline{\gamma }+\mu \sqrt{\overline{\gamma }}(\sqrt{\overline{\gamma }}cos^2\theta +sin^2\theta ) \right]. \end{aligned}$$

(17)

In general, the average fidelity is determined by the target state $|\xi \rangle$ and the corresponding noise channel. Therefore, it is natural to average over all of the target state to obtain a state independent effect of the corresponding noise channel, the formula of the average fidelity is as following

$$\begin{aligned} \langle \overline{F}\rangle =\frac{1}{4\pi }\int ^\pi _0\sin \theta \textrm{d}\theta \int ^{2\pi }_0\textrm{d}\phi \cdot F_{av}, \end{aligned}$$

(18)

this average fidelity is over all of the qubit states, thus we call it the state independent average fidelity.

By substituting Eqs. (17) and (18), we can obtain the formula of the average fidelity

$$\begin{aligned} \langle \overline{F}\rangle =1+\frac{\mu }{3}(\sqrt{\overline{\gamma }}-\overline{\gamma })-\frac{1}{2}\gamma . \end{aligned}$$

(19)

The behaviors of average fidelity as a function of the parameter $\gamma$ and $\mu$ are shown in Fig. 1.

Fig. 1

The relationship among the average fidelity, the parameters $\gamma$ and $\mu$

As one might expect, in the uncorrelated circumstance (i.e., $\mu =0$), the average fidelity ranges from 1 to 1/2 when the decoherence strength $\gamma$ increases from 0 to 1. Specifically, in the case of $\mu =1$, the second use has full correlation of the first use, the average fidelity $\langle \overline{F}\rangle$ is $(3+\overline{\gamma } +2\sqrt{\overline{\gamma }})/6$, which attains its maximum 1 at $\gamma =0$ and minimum 1/2 at $\gamma =1$. The partial derivative of $\langle \overline{F}\rangle$ with respect to the correlated parameter $\mu$ is

$$\begin{aligned} \frac{\partial \langle \overline{F}\rangle }{\partial \mu }=\frac{1}{3}\sqrt{\overline{\gamma }}(1-\sqrt{\overline{\gamma }})\ge 0. \end{aligned}$$

(20)

That is to say that the average fidelity $\langle \overline{F}\rangle$ is increasing with the correlated parameter $\mu$ regardless of the noise parameter $\gamma$. The average fidelity of our JRSP scheme is increased by $\mu \sqrt{\overline{\gamma }}(1-\sqrt{\overline{\gamma }})/3$ in CAD noise channel. This result means that the correlated effect enables to enhance the average fidelity of JRSP which is subject to AD noise.

3 Protecting JRSP by WM and QWR

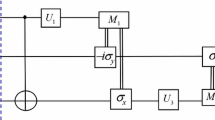
In Sect. 2, we have studied the influence of CAD noise on JRSP. We find that even though the correlated effect could potentially improve the fidelity, the unfavorable effects of uncorrelated AD noise still remain. In this section, we turn to introduce the technique of WM and QMR to remove the adverse effects in both uncorrelated AD and CAD noises. As mentioned earlier, the state $|{\mathcal {G}}\rangle _{ABC}$ shared by Alice, Bob and Charlie is subject to a prior WM (carried by Alice) before the qubits suffer the CAD noise; after that a post-QMR is performed by Alice and Bob, respectively. This of operations can be expressed as

$$\begin{aligned} \rho _{\textrm{QMR}}=M_{\textrm{QMR}}[\varepsilon _{\textrm{CAD}}(M_{\textrm{WM}}\rho M^{\dagger }_{\textrm{WM}})]M^{\dagger }_{\textrm{QMR}}, \end{aligned}$$

(21)

where $M_{\textrm{WM}}$ and $M_{\textrm{QMR}}$ are non-unitary quantum operations, which are described as follows

$$\begin{aligned} \begin{aligned}&M_{\textrm{WM}}=\left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} \sqrt{1-p} \\ \end{array} \right) _A\otimes \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} \sqrt{1-p} \\ \end{array} \right) _B,&\\&M_{\textrm{QWR}}=\left( \begin{array}{cc} \sqrt{1-q} &{} 0 \\ 0 &{} 1 \\ \end{array} \right) _A\otimes \left( \begin{array}{cc} \sqrt{1-q} &{} 0 \\ 0 &{} 1 \\ \end{array} \right) _B.&\end{aligned} \end{aligned}$$

(22)

Here p, q are the measurement strengths of WM and QMR, respectively, and $0\le p, q\le 1$. For $0<p<1$, it represents the WM does not completely collapse the state to $|00\rangle$, while $0<q<1$ indicates that the measured state is still recoverable. Note that both WM and QMR are local operators, and thus it does not require Alice and Bob in the same place. It is also interesting to find that the QMR could be rewritten as

$$\begin{aligned} \left( \begin{array}{cc} \sqrt{1-q} &{} 0 \\ 0 &{} 1 \\ \end{array} \right) =\frac{1}{\sqrt{1-q}}X \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} \sqrt{1-q} \\ \end{array} \right) X, \end{aligned}$$

(23)

where $X=|0\rangle \langle 1|+|1\rangle \langle 0|$ is bit-flip operation. Equation. (23) means that the QMR is constructed by three local operations: a bit-flip operation, a WM and a second bit-flip operation. The implementation of WM has been achieved in both photonic qubits [1, 2] and superconducting qubits [3]. For instance, as shown in Refs. [1, 2], the WM is implemented with a Brewster angle glass plate (BAGP) for the photon polarization qubit. The BAGP reflects vertical polarization with a certain probability and completely transmits horizontal polarization, which exactly functions as the WM.

From Eqs. (4) and (21), the final state of entangled state can be written as

$$\begin{aligned} \begin{aligned} \rho _{\mathrm {\textrm{QMR}}}&=\frac{1}{N}[\overline{q}^2|000\rangle \langle 000|+V|111\rangle \langle 111|+\overline{q}^2W|100\rangle \langle 100|&\\&\quad +\overline{q}X(|000\rangle \langle 111|+|111\rangle \langle 000|)+\overline{q}Y(|110\rangle \langle 110|+|101\rangle \langle 101|)],&\end{aligned} \end{aligned}$$

(24)

where $V=\overline{p}^2(\overline{\mu }\overline{\gamma }^2+\mu \overline{\gamma })$, $W=\overline{p}^2(\overline{\mu }\gamma ^2+\mu \gamma )$, $X=\overline{p}(\overline{\mu }\overline{\gamma }+\mu \sqrt{\overline{\gamma }})$, $Y=\overline{p}^2\overline{\mu }\overline{\gamma }\gamma$. $N=\overline{q}^2(1+W)+V+2\overline{q}Y$ is the normalization factor.

Through the standard procedure of JRSP, the state held by Charlie is one of the following four states:

$$ \begin{aligned} \dot{\rho }_{0}^{0} (out) = \dot{\rho }_{0}^{1} (out) = & \frac{2}{{\sigma _{1} }}\left\{ {\left[ {\bar{q}^{2} \cos ^{2} \frac{\theta }{2} + (\bar{q}^{2} W + \bar{q}Y)\sin ^{2} \frac{\theta }{2}} \right]|0\rangle \langle 0| + (V + \bar{q}Y)\sin ^{2} \frac{\theta }{2}|1\rangle \langle 1|} \right. \\ & \left. { + \bar{q}X\sin \frac{\theta }{2}\cos \frac{\theta }{2}(e^{{ - i\phi }} |0\rangle \langle 1| + e^{{i\phi }} |1\rangle \langle 0|)} \right\} \\ \dot{\rho }_{1}^{0} (out) = & \dot{\rho }_{1}^{1} (out) = \frac{2}{{\sigma _{2} }}\left\{ {2\left[ {\bar{q}^{2} \sin ^{2} \frac{\theta }{2} + (\bar{q}^{2} W + \bar{q}Y)\cos ^{2} \frac{\theta }{2}} \right]|1\rangle \langle 1| + 2(V + \bar{q}Y)\cos ^{2} \frac{\theta }{2}|0\rangle \langle 0|} \right. \\ & \left. { + \bar{q}X\sin \frac{\theta }{2}\cos \frac{\theta }{2}(e^{{ - i\phi }} |0\rangle \langle 1| + e^{{i\phi }} |1\rangle \langle 0|)} \right\} \\ \end{aligned} $$

(25)

where $\sigma _1 = (2\overline{q}^2-N)\cos \theta +N,\,\sigma _2 = (N-2\overline{q}^2)\cos \theta + N$.

From Eqs. (1), (15), (16) and (25), the state-dependent average fidelity can be obtained as

$$\begin{aligned} \dot{F}_{av}=\frac{1}{2N}[2(\overline{q}^2+V+\overline{q}Y)+(\overline{q}^2W+2\overline{q}X-\overline{q}^2-V)\sin ^2\theta ]. \end{aligned}$$

(26)

Similarly, we can get the state independent average fidelity

$$\begin{aligned} \langle \bar{\dot{F}}\rangle =\frac{(2+W)\overline{q}^2+(2X+3Y)\overline{q}+2V}{3[(1+W)\overline{q}^2+2Y\overline{q}+V]}. \end{aligned}$$

(27)

Now, let us make a detailed analysis of the average fidelity $\langle \bar{\dot{F}}\rangle$. Firstly, in order to achieve the maximal value of $\langle \bar{\dot{F}}\rangle$, we need to choose the optimal QMR strength q. It can be obtained by calculating the following conditions: $\partial \langle \bar{\dot{F}}\rangle /\partial q=0$ and $\partial ^2\langle \bar{\dot{F}}\rangle /(\partial q)^2<0$. Specifically, the following equation holds on here,

$$\begin{aligned} \partial \langle \bar{\dot{F}}\rangle /\partial q = \frac{1}{3N}[2\overline{q}(W+2)+2X+3Y] - \frac{2\sigma _3}{3N^2}[\overline{q}(W+1)+Y]=0, \end{aligned}$$

(28)

where $\sigma _3 =\overline{q}^2(2+W) + \overline{q}(2X+3Y)+2V)$. Then, from the condition $\partial ^2\langle \bar{\dot{F}}\rangle /(\partial q)^2<0$, the result turns out to be

$$\begin{aligned} q = 1 + \frac{VW-\sqrt{\sigma _4}}{2X(W+1)+Y(W-1)}, \end{aligned}$$

(29)

where $\sigma _4 = V(VW^2+4X^2(W+1)-Y^2(W-1)-4XY)$. Therefore, the maximally teleported average fidelity can be expressed as

$$\begin{aligned} F_{av}^{opt} = \frac{1}{6}\cdot \frac{4+2W+\sigma _5/ \sqrt{\sigma _4}}{1+W+\sigma _6/\sqrt{\sigma _4}}, \end{aligned}$$

(30)

where $\sigma _5 = 4X^2(W+1)+3Y^2(W-1)+4XY(2W+1)-2VW(W+2),\,\sigma _6 = Y^2(W-1)+(2XY-VW)(W+1)$. Obviously, the teleported average fidelity is equal to 1 when $\gamma =0$.

Figure 2 shows the result of an average fidelity as a function of decoherence under CAD noise with the assistance of WM and QMR. It is straightforward to note that the average fidelity rapidly decreases with the increase in $\gamma$ if neither WM nor QWR is executed.

Fig. 2

Average fidelity $F_{av}^{opt}$ as a function of decoherence strength $\gamma$ for different measurement strengths p of WM with $\mu =0$

Each line of this figure can be seen as follows.

$$\begin{aligned} F(p=0) = -\frac{\left( \gamma -1\right) \,\left( 4\,\gamma \,A_{21}-32\,\gamma +4\,A_{21}-3\,\gamma ^2\,A_{21} +8\,\gamma ^3\,A_{21}+\gamma ^4\,A_{21}+44\,\gamma ^2-36\,\gamma ^3+18\,\gamma ^4-10\,\gamma ^5+16\right) }{3\,\left( {\left( \gamma -1\right) }^2+\frac{\left( \gamma ^2+1\right) \,{\left( A_{21}-\gamma ^2+\gamma ^3\right) }^2}{{\left( \gamma ^3+2\,\gamma ^2-\gamma +2\right) }^2}-\frac{2\,\gamma \,\left( \gamma -1\right) \,\left( A_{21} -\gamma ^2+\gamma ^3\right) }{\gamma ^3+2\,\gamma ^2-\gamma +2}\right) \,{\left( \gamma ^3+2\,\gamma ^2-\gamma +2\right) }^2} \end{aligned}$$

(31)

where $A_{21} = \sqrt{{\left( \gamma -1\right) }^2\,\left( 5\,\gamma ^2-4\,\gamma +4\right) }.$

$$\begin{aligned} F(p=0.4) = \frac{500\,\sqrt{5}\,A_{22}-16000\,\gamma +12300\,\gamma ^2-7380\,\gamma ^3+1890\,\gamma ^4-810\,\gamma ^5+300\,\sqrt{5}\, \gamma \,A_{22}-135\,\sqrt{5}\,\gamma ^2\,A_{22}+216\,\sqrt{5}\,\gamma ^3\,A_{22}+\frac{81\,\sqrt{5}\,\gamma ^4\,A_{22}}{5} +10000}{21150\,\gamma ^2-24000\,\gamma -15390\,\gamma ^3+5670\,\gamma ^4-2430\,\gamma ^5+900\,\sqrt{5}\,\gamma \,A_{22} -540\,\sqrt{5}\,\gamma ^2\,A_{22}+324\,\sqrt{5}\,\gamma ^3\,A_{22}+15000} \end{aligned}$$

(32)

where $A_{22} = \sqrt{{\left( \gamma -1\right) }^2\,\left( 9\,\gamma ^2-12\,\gamma +20\right) }.$

$$\begin{aligned} F(p=0.8) = \frac{500\,\sqrt{5}\,A_{23}-12000\,\gamma +2700\,\gamma ^2-740\,\gamma ^3+50\,\gamma ^4-10\,\gamma ^5 +100\,\sqrt{5}\,\gamma \,A_{23}-15\,\sqrt{5}\,\gamma ^2\,A_{23}+8\,\sqrt{5}\,\gamma ^3\,A_{23} +\frac{\sqrt{5}\,\gamma ^4\,A_{23}}{5}+10000}{4350\,\gamma ^2-18000\,\gamma -1470\,\gamma ^3+150\,\gamma ^4-30\,\gamma ^5 +300\,\sqrt{5}\,\gamma \,A_{23}-60\,\sqrt{5}\,\gamma ^2\,A_{23}+12\,\sqrt{5}\,\gamma ^3\,A_{23}+15000} \end{aligned}$$

(33)

where $A_{23} = \sqrt{{\left( \gamma -1\right) }^2\,\left( \gamma ^2-4\,\gamma +20\right) }.$

$$\begin{aligned} F(p=0,q=0) = 1-\frac{\gamma }{2}. \end{aligned}$$

(34)

However, the average fidelity, when the WM and QMR are introduced, could be enhanced. Particularly, we find the larger the measurement strength of WM is, the larger the average fidelity would be. A more clearer description of the role of p is shown in Fig. 3,

Fig. 3

Average fidelity $F_{av}^{opt}$ as a function of measurement strength p of WM for different memory parameters $\mu$ with $\gamma =0.5$

where the plot of $F_{av}^{opt}$ is shown as a function of measurement strength p of WM for different memory parameters $\mu$ with $\gamma =0.5$. Each line of this figure can be expressed as:

$$\begin{aligned} F(\mu = 0) = \frac{B_{31}^{(0)}}{B_{{31}}^{(1)}};\; F(\mu = 0.4) = \frac{B_{32}^{(0)}}{B_{{32}}^{(1)}};\; F(\mu = 0.8) = \frac{B_{{33}}^{(0)}}{B_{{33}}^{(1)}};\; F(\mu = 1) = \frac{B_{{34}}^{(0)}}{B_{{34}}^{(1)}} \end{aligned}$$

(35)

where $B_{3i}^{(k)}\;(i=1,2,3,4;k=0,1)$ can be seen in “Appendix”.

The participation of WM and QMR enables us to improve the average fidelity on the basis of correlate noise. The maximally achievable fidelity always approaches 1 without regard to $\gamma$ when $\mu =0,1$. However, for the intermediate cases $0<\mu <1$, the maximal value of $F_{av}^{opt}$ is less than 1. The explanation of this phenomenon could be understood as follows. From Eq.(3), we note that in both uncorrelated AD and FCAD channels, only one dissipative channel is formulated in the decoherence process, i.e., $|11\rangle \rightarrow (|10\rangle , |01\rangle )\rightarrow |00\rangle$ for uncorrelated AD noise and $|11\rangle \rightarrow |00\rangle$ for FCAD noise. The above features ensure the operation of QMR could recover the initial information before the decoherence. However, for the general CAD channel ($0<\mu <1$), the QMR can not exactly distinguish such two dissipative channels, and hence the fidelity cannot achieve 1. To illustrate this phenomenon more clearly, we plot Fig. 4 to show the dependency between the maximal achievable fidelity and the correlated parameter $\mu$. It is obvious that the fidelity is no longer a monotonic function of $\mu$ with the given $\gamma$ and $p>0$.

Fig. 4

The relation of $\gamma ,\mu$ and $F_{av}^{opt}$ when $p=0$ in (a), $p=0.5$ in (b), $p=0.8$ in (c), $p=0.99$ in (d)

Each expression is

$$\begin{aligned} F(p=0) = -\frac{B_{{41}}^{(0)}}{B_{{41}}^{(1)}};\; F(p=0.5) = -\frac{B_{{42}}^{(0)}}{B_{{42}}^{(1)}};\; F(p=0.8) = -\frac{B_{43}^{(0)}}{B_{43}^{(1)}};\; F(p=0.99) = -\frac{B_{44}^{(0)}}{B_{44}^{(1)}}, \end{aligned}$$

(36)

where $B_{4j}^{(k)}$ can be seen in “Appendix”.

Moreover, when no weak measurement operation is implemented from Fig. 4a, it can be concluded that (i) the average fidelity of fully correlated channel ($\mu =1$) is always greater than general correlated channel ($0<\mu <1$), and (ii) the average fidelity of general correlated channel ($0<\mu <1$) is always greater than that of uncorrelated channel ($\mu =0$). However, as long as the measurement strengths of WM, p, is larger than 0, the phenomenon (ii) is not valid. It can be seen from any graph in Fig. 4b–d that when the decoherence strength $\gamma$ is close to 1, the average fidelity decreases sharply with the small increase in the correlated parameter $\mu$. In combination with Fig. 4b–d, we find that the measurement strength p of WM has an impact on this downward trend, that is, the larger the measurement strength P of WM, the larger the base amount of the average fidelity to be reduced.

Figure 5 shows the average fidelity as a monotonically increasing function of the memory parameter $\mu$ with $\gamma =0.5$, whether WM and QMR are involved or not. Further, we find that for any given memory parameter $\mu$, the greater the measurement strength p of WM is, the greater the average fidelity would be. That is, on the basis of memory enhancing the average fidelity on AD noise, the participation of WM and QWR can further improve the average fidelity of JRSP.

Fig. 5

Average fidelity $F_{av}^{opt}$ as a function of memory parameter $\mu$ for different measurement strength p of WM with $\gamma =0.5$

Each expression can be seen as:

$$\begin{aligned} F(p = 0) = \frac{B_{51}^{(0)}}{B_{51}^{(1)}};\; F(p = 0.3) = \frac{B_{52}^{(0)}}{B_{52}^{(1)}};\; F(p = 0.5) = \frac{B_{53}^{(0)}}{B_{53}^{(1)}};\; F(p = 0.8) = \frac{B_{54}^{(0)}}{B_{54}^{(1)}}, \end{aligned}$$

(37)

where $B_{5j}^{(k)}(j=1,2,3,4;k=0,1)$ can be seen in “Appendix”.

Obviously, the total probability of success can be obtained by adding each probability that corresponding to $\dot{\rho }^i_j (out)$ ($i,j=0,1$)

$$\begin{aligned} p_{total}=\sum ^1_{i,j=0}p_{ij}=\frac{V+W+2Y-2q-2Wq-2Yq+Wq^2+q^2+1}{N}. \end{aligned}$$

(38)

where $p_{ij}$ comes from the standard procedure of JRSP. After replacing V, W, Y, N with $p,q,\mu ,\gamma$, the total probability of success can be simplified to 1. Therefore, our scheme is perfect although it suffers noise channel.

4 Conclusion

In summary, by using three-qubit entangled GHZ-state as the quantum channel, we study the influence of correlated AD noise on the scheme of JRSP for arbitrary single-qubit state. Letting the qubits of a sender and the receiver pass through the channel with AD noise, we get results for the JRSP scheme as following: (A) The analytical formulas of the output state in the JRSP scheme under correlated AD nosy channel is presented. Based on these formulae of the output state, the state dependent and independent average fidelities of the target and output states are calculated. Consequently, the expression of the partial derivative of the state independent average fidelity with respect to the correlated parameter $\mu$ is obtained. The partial derivative is positive for any value of the decoherence parameter $\gamma$, which means that the correlated parameter can increase the fidelity in JRSP in correlated AD noise environment. (B) The state independent average fidelity as a function of the decoherence parameter and the correlated parameter is plotted, and its increment caused by the correlated parameter is given.

Subsequently, utilizing WM and QMR to the uncorrelated and correlated AD noisy channel, we obtain the formulae of the output state in JRSP scheme under AD and CAD noise environments, and calculate the state dependent and independent average fidelities of the target and output states. By making relevant graphics of the state independent average fidelity in JRSP scheme under AD and CAD noise environments, we find that the combined action of WM and QMR can almost completely suppress the AD and CAD decoherence if the careful optimization of the strengths of WM and QMR is carried out. That is, the combination of WM and QMR in both AD and CAD channels can greatly improve the efficiency of JRSP. Our result may be applied to enhance the communication efficiency of experimental realization of JRSP scheme under AD and CAD noise environments.

Appendix

This section, we demonstrate the concrete expressions for each line in Figs. 3, 4 and 5.

1.1 Explicit expressions for $B_{3j}^{(k)}$

In Fig. 3, the expressions for each $B_{3j}^{(k)}$ can be seen as follows.

$$\begin{aligned} B_{21}^{(0)}= &\, {} 2\,{\left( p-1\right) }^2\,\left( 101\,A_{31}-60\,p\,A_{31}-176\,p+248\,p^2-48\,p^3+20\,p^4+42\,p^2\,A_{31}-20\,p^3\,A_{31}\right. \nonumber \\{} & {} \left. +p^4\,A_{31}+468\right) \end{aligned}$$

(39)

$$\begin{aligned} B_{21}^{(1)}= & {} \left( 3\,{\left( p-1\right) }^2+\frac{48\,{\left( p-1\right) }^3\,\left( \frac{p}{4}+\frac{A_{31}}{4} -\frac{p^2}{8}-\frac{1}{8}\right) }{p^3-7\,p^2+7\,p-17}\right. \nonumber \\{} & {} \left. +\frac{12\,{\left( p-1\right) }^2\,\left( \frac{p^2}{4} -\frac{p}{2}+\frac{5}{4}\right) \,{\left( 2\,p+2\,A_{31}-p^2-1\right) }^2}{{\left( p^3-7\,p^2+7\,p-17\right) }^2}\right) \,{\left( p^3-7\,p^2+7\,p-17\right) }^2 \end{aligned}$$

(40)

$$\begin{aligned} B_{{32}}^{(0)}= & {} 2\,{\left( p-1\right) }^2\,\Big (4835\,\sqrt{7}\,A_{32}-982464\,\sqrt{2}\,p-1889664\,p+6816\,\sqrt{14}\,A_{32} +1389696\,\sqrt{2}\nonumber \\{} & {} +818496\,\sqrt{2}\,p^2-216384\,\sqrt{2}\,p^3+65856\,\sqrt{2}\,p^4+1927296\,p^2-925904\,p^3+386316\,p^4\nonumber \\{} & {} -82320\,p^5+13720\,p^6-2514\,\sqrt{7}\,p^2\,A_{32}+980\,\sqrt{7}\,p^3\,A_{32}-497\,\sqrt{7}\,p^4\,A_{32}\nonumber \\{} & {} +3360\,\sqrt{14}\,p^2\,A_{32}-672\,\sqrt{14}\,p^3\,A_{32}+2636\,\sqrt{7}\,p\,A_{32}-5664\,\sqrt{14}\,p\,A_{32}+2093756\Big ); \end{aligned}$$

(41)

$$\begin{aligned} B_{{32}}^{(1)}= & {} \left( 21\,{\left( p-1\right) }^2-\frac{3600\,{\left( p-1\right) }^3\,\left( \frac{49\,p}{100}+\frac{\sqrt{7}\,A_{32}}{100}-\frac{49\,p^2}{200}-\frac{49}{200}\right) }{216\,\sqrt{2}-112\,\sqrt{2}\,p-171\,p+56\,\sqrt{2}\,p^2+147\,p^2-21\,p^3+285}\right. \nonumber \\{} & {} \left. +\frac{60\,{\left( p-1\right) }^2\,\left( \frac{7\,p^2}{20}-\frac{7\,p}{10}+\frac{27}{20}\right) \,{\left( 98\,p+2\,\sqrt{7}\,A_{32}-49\,p^2-49\right) }^2}{{\left( 216\,\sqrt{2}-112\,\sqrt{2}\,p-171\,p+56\,\sqrt{2}\,p^2+147\,p^2-21\,p^3+285\right) }^2}\right) \,\left( 123120\,\sqrt{2}-137712\,\sqrt{2}\,p\right. \nonumber \\{} & {} \left. -194238\,p+133728\,\sqrt{2}\,p^2-61152\,\sqrt{2}\,p^3+21168\,\sqrt{2}\,p^4-2352\,\sqrt{2}\,p^5+186503\,p^2-87332\,p^3\right. \nonumber \\{} & {} \left. +35063\,p^4-6174\,p^5+441\,p^6+174537\right) \end{aligned}$$

(42)

where $A_{32} = \sqrt{1056\,\sqrt{2}-432\,\sqrt{2}\,p-962\,p+336\,\sqrt{2}\,p^2+941\,p^2-280\,p^3+70\,p^4+1591}.$

$$\begin{aligned} B_{{33}}^{(0)}= & {} 2\,{\left( p-1\right) }^2\,\left( 14784\,\sqrt{2}\,\sqrt{A_{33}}-1231488\,\sqrt{2}\,p-7982928\,p\right. \nonumber \\{} & {} \left. +1354752\,\sqrt{2}+26124\,p\,\sqrt{A_{33}}+1026432\,\sqrt{2}\,p^2-321408\,\sqrt{2}\,p^3+93312\,\sqrt{2}\,p^4+22935\,\sqrt{A_{33}}\right. \nonumber \\{} & {} \left. -29826\,p^2\,\sqrt{A_{33}}+16740\,p^3\,\sqrt{A_{33}}-4293\,p^4\,\sqrt{A_{33}}+7283592\,p^2-3736368\,p^3+1520532\,p^4\right. \nonumber \\{} & {} \left. -349920\,p^5+58320\,p^6+8640\,\sqrt{2}\,p^2\,\sqrt{A_{33}}-1728\,\sqrt{2}\,p^3\,\sqrt{A_{33}}-14016\,\sqrt{2}\,p\,\sqrt{A_{33}}+7008372\right) \end{aligned}$$

(43)

$$\begin{aligned} B_{{33}}^{(1)}= & {} \left( 27\,{\left( p-1\right) }^2-\frac{1200\,{\left( p-1\right) }^3\,\left( \frac{81\,p}{100} +\frac{3\,\sqrt{A_{33}}}{100}-\frac{81\,p^2}{200}-\frac{81}{200}\right) }{464\,\sqrt{2}-288\,\sqrt{2}\,p-79\,p+144\,\sqrt{2}\,p^2 +63\,p^2-9\,p^3+105}\right. \nonumber \\{} & {} \left. +\frac{540\,{\left( p-1\right) }^2\,\left( \frac{9\,p^2}{20}-\frac{9\,p}{10}+\frac{29}{20}\right) \,{\left( 54\,p+2\,\sqrt{A_{33}}-27\,p^2-27\right) }^2}{{\left( 464\,\sqrt{2}-288\,\sqrt{2}\,p-79\,p +144\,\sqrt{2}\,p^2+63\,p^2-9\,p^3+105\right) }^2}\right) \,\left( 97440\,\sqrt{2}-133792\,\sqrt{2}\,p\right. \nonumber \\{} & {} \left. -551118\,p+134208\,\sqrt{2}\,p^2-67392\,\sqrt{2}\,p^3+23328\,\sqrt{2}\,p^4-2592\,\sqrt{2}\,p^5+452623\,p^2-177732\,p^3 \right. \nonumber \\{} & {} \left. +46863\,p^4-1134\,p^5+81\,p^6+441617\right) \end{aligned}$$

(44)

where $A_{33} = 768\,\sqrt{2}-416\,\sqrt{2}\,p-3066\,p+288\,\sqrt{2}\,p^2+2273\,p^2-720\,p^3+180\,p^4+3973.$

$$\begin{aligned} B_{{34}}^{(0)}= & {} 6\,p\,{\left( {A_{34}}\right) }^{3}-750\,p\,{A_{34}}-13280\,p+250\,{A_{34}}+14\,{\left( {A_{34}}\right) }^{3} +16496\,p^2-13056\,p^3+7648\,p^4\nonumber \\{} & {} -3168\,p^5+976\,p^6-192\,p^7+24\,p^8+955\,p^2\,{A_{34}}-748\,p^3\,{A_{34}}-7\,p^2\, {\left( {A_{34}}\right) }^{3}+413\,p^4\,{A_{34}}\nonumber \\{} & {} +4\,p^3\,{\left( {A_{34}}\right) }^{3}-158\,p^5\,{A_{34}} -p^4\,{\left( {A_{34}}\right) }^{3}+45\,p^6\,{A_{34}}-8\,p^7\,{A_{34}}+p^8\,{A_{34}}+6600 \end{aligned}$$

(45)

$$\begin{aligned} B_{{34}}^{(1)}= & {} 48\,{\left( p^2-2\,p+3\right) }^2\,{A_{34}}^2 \end{aligned}$$

(46)

where $A_{34} = \left( p^2-2\,p+5\right)$

1.2 Explicit expressions for $B_{4j}^{(k)}$

In Fig. 4, the expressions for each $B_{4j}^{(k)}$ can be seen as follows. In the upper left figure,

$$\begin{aligned} B_{{41}}^{(0)}= & {} 2 \mu +2 \gamma +\left( 2 \gamma -2\right) \left( \mu \gamma -\gamma +1\right) -2 \mu \gamma -2 \mu \sqrt{1-\gamma }-\gamma \left( \mu +\gamma -\mu \gamma \right) \nonumber \\{} & {} +\frac{B_{{41}}^{(00)}}{B_{{41}}^{(11)}}-\frac{B_{{41}}^{(01)}}{B_{{41}}^{(11)}} +\frac{B_{{41}}^{(02)}}{B_{{41}}^{(11)}}-3 \gamma \left( \mu -1\right) \left( \gamma -1\right) +\frac{B_{{41}}^{(03)}}{B_{{41}}^{(11)}}-\frac{B_{{41}}^{(04)}}{B_{{41}}^{(11)}} +\frac{B_{{41}}^{(05)}}{B_{{41}}^{(11)}}-4 \end{aligned}$$

(47)

$$\begin{aligned} B_{{41}}^{(1)}= & {} \frac{3 \left( \gamma \left( \mu +\gamma -\mu \gamma \right) +1\right) {\left( \gamma -1\right) }^2 {B_{{41}}^{(10)}}^2}{{\left( B_{{41}}^{(11)}\right) }^2} -3 \left( \gamma -1\right) \left( \mu \gamma -\gamma +1\right) +\frac{6 \gamma \left( \mu -1\right) {\left( \gamma -1\right) }^2B_{{41}}^{(10)}}{B_{{41}}^{(11)}} \end{aligned}$$

(48)

where

$$\begin{aligned} B_{{41}}^{(00)}= & {} 16 \mu ^2 \gamma ^2-12 \gamma -8 \mu -8 \mu ^2 \gamma ^3+4 \gamma \sqrt{A_{{41}}^{(0)}}+24 \mu \gamma -4 \sqrt{A_{{41}}^{(0)}}+8 \mu \sqrt{1-\gamma }-36 \mu \gamma ^2\nonumber \\{} & {} -8 \mu ^2 \gamma +20 \mu \gamma ^3+16 \gamma ^2-12 \gamma ^3+8 \mu \gamma ^2 \sqrt{1-\gamma }+8 \mu ^2 \gamma \sqrt{1-\gamma }-8 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+8 \end{aligned}$$

(49)

$$\begin{aligned} B_{{41}}^{(01)}= & {} 2 \left( A_{{41}}^{(1)}\right) ^2 \end{aligned}$$

(50)

$$\begin{aligned} B_{{41}}^{(02)}= & {} \left( 2 \mu \gamma -2 \gamma -2 \mu +2 \mu \sqrt{1-\gamma }+2\right) \left( A_{{41}}^{(1)}\right) \end{aligned}$$

(51)

$$\begin{aligned} B_{{41}}^{(03)}= & {} 2 \gamma \left( \mu +\gamma -\mu \gamma \right) \left( A_{{41}}^{(1)}\right) \end{aligned}$$

(52)

$$\begin{aligned} B_{{41}}^{(04)}= & {} \gamma \left( \mu +\gamma -\mu \gamma \right) \left( A_{{41}}^{(1)}\right) ^2 \end{aligned}$$

(53)

$$\begin{aligned} B_{{41}}^{(05)}= & {} 3 \gamma \left( \mu -1\right) \left( \gamma -1\right) \left( A_{{41}}^{(1)}\right) \end{aligned}$$

(54)

$$\begin{aligned} B_{{41}}^{(10)}= & {} \left( \mu ^2 \gamma ^2-\mu ^2 \gamma ^3+\mu \gamma -A_{41}^{(\frac{1}{2})}-2 \mu \gamma ^2+2 \mu \gamma ^3+\gamma ^2-\gamma ^3\right) \end{aligned}$$

(55)

$$\begin{aligned} B_{{41}}^{(11)}= & {} 3 \mu ^2 \gamma ^2-3 \gamma -2 \mu -\mu ^2 \gamma ^4+5 \mu \gamma +2 \mu \sqrt{1-\gamma }-6 \mu \gamma ^2-2 \mu ^2 \gamma +\mu \gamma ^3+2 \mu \gamma ^4\nonumber \\{} & {} +3 \gamma ^2-\gamma ^3-\gamma ^4+2 \mu \gamma ^2 \sqrt{1-\gamma }+2 \mu ^2 \gamma \sqrt{1-\gamma }-2 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+2 \end{aligned}$$

(56)

$$\begin{aligned} A_{{41}}^{(0)}= & {} \left( \mu \gamma -\gamma +1\right) \left( 30 \mu ^2 \gamma ^2-8 \gamma -8 \mu -14 \mu ^2 \gamma ^3-12 \mu ^3 \gamma ^2+4 \mu ^3 \gamma ^3+20 \mu \gamma +8 \mu \sqrt{1-\gamma }-26 \mu \gamma ^2\right. \nonumber \\{} & {} \left. -16\mu ^2 \gamma +15 \mu \gamma ^3+8 \mu ^3 \gamma -8 \mu ^2 \sqrt{1-\gamma }+8 \mu ^2+9 \gamma ^2-5 \gamma ^3+8 \mu \gamma ^2 \sqrt{1-\gamma }+12 \mu ^2 \gamma \sqrt{1-\gamma }\right. \nonumber \\{} & {} \left. -8 \mu ^3 \gamma \sqrt{1-\gamma }-16 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+8 \mu ^3 \gamma ^2 \sqrt{1-\gamma }-4 \mu \gamma \sqrt{1-\gamma }+4\right) \end{aligned}$$

(57)

$$\begin{aligned} A_{{41}}^{(1)}= & {} 4 \mu ^2 \gamma ^2-3 \gamma -2 \mu -2 \mu ^2 \gamma ^3+\gamma \sqrt{A_{{41}}^{(0)}}+6 \mu \gamma -\sqrt{A_{{41}}^{(0)}}+2 \mu \sqrt{1-\gamma }-9 \mu \gamma ^2\nonumber \\{} & {} -2\mu ^2 \gamma +5 \mu \gamma ^3+4 \gamma ^2-3 \gamma ^3+2 \mu \gamma ^2 \sqrt{1-\gamma }+2 \mu ^2 \gamma \sqrt{1-\gamma }-2 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+2 \end{aligned}$$

(58)

In the upper right figure,

$$\begin{aligned} B_{{42}}^{(0)}= & {} \frac{B_{42}^{(00)}}{B_{42}^{(11)}}-4 \gamma -4 \mu +4 \mu \gamma +4 \mu \sqrt{1-\gamma }+\gamma \left( \mu +\gamma -\mu \gamma \right) +\frac{B_{42}^{(01)}}{{\left( B_{42}^{(11)}\right) }^2}\nonumber \\{} & {} -2 \left( \gamma -1\right) \left( \mu \gamma -\gamma +1\right) +3 \gamma \left( \mu -1\right) \left( \gamma -1\right) +\frac{B_{42}^{(02)}}{B_{42}^{(11)}} +\frac{B_{42}^{(03)}}{B_{42}^{(11)}}+\frac{B_{42}^{(04)}}{{\left( B_{42}^{(11)}\right) }^2} +\frac{B_{42}^{(05)}}{B_{42}^{(11)}}+12 \end{aligned}$$

(59)

$$\begin{aligned} B_{{42}}^{(1)}= & {} 3 \left( \gamma -1\right) \left( \mu \gamma -\gamma +1\right) -\frac{12 {\left( \gamma -1\right) }^2 \left( \frac{\mu \gamma }{4}-\frac{\mu \gamma ^2}{4}+\frac{\gamma ^2}{4}+1\right) \left( {B_{42}^{(10)}}\right) ^2}{{\left( B_{42}^{(11)}\right) }^2}+\frac{6 \gamma \left( \mu -1\right) {\left( \gamma -1\right) }^2 B_{42}^{(10)}}{B_{42}^{(11)}} \end{aligned}$$

(60)

where

$$\begin{aligned} B_{42}^{(00)}= & {} 4 \left( 32 \mu ^2 \gamma ^2-80 \gamma -64 \mu -16 \mu ^2 \gamma ^3+4 \gamma \sqrt{A_{42}^{(0)}}+100 \mu \gamma -4 \sqrt{A_{42}^{(0)}}+64 \mu \sqrt{1-\gamma }-72 \mu \gamma ^2-16 \mu ^2 \gamma \right. \nonumber \\{} & {} \left. +36 \mu \gamma ^3+36 \gamma ^2-20 \gamma ^3+16 \mu \gamma ^2 \sqrt{1-\gamma }+16 \mu ^2 \gamma \sqrt{1-\gamma }-16 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+64\right) \end{aligned}$$

(61)

$$\begin{aligned} B_{42}^{(01)}= & {} 8 \left( 8 \mu ^2 \gamma ^2-20 \gamma -16 \mu -4 \mu ^2 \gamma ^3+\gamma \sqrt{A_{42}^{(0)}}+25 \mu \gamma -\sqrt{A_{42}^{(0)}}+16 \mu \sqrt{1-\gamma }-18 \mu \gamma ^2-4 \mu ^2 \gamma \right. \nonumber \\{} & {} \left. +9 \mu \gamma ^3+9 \gamma ^2-5 \gamma ^3+4 \mu \gamma ^2 \sqrt{1-\gamma }+4 \mu ^2 \gamma \sqrt{1-\gamma }-4 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+16\right) ^2 \end{aligned}$$

(62)

$$\begin{aligned} B_{42}^{(02)}= & {} 4 \left( 8 \mu \gamma -8 \gamma -8 \mu +8 \mu \sqrt{1-\gamma }+8\right) \left( A_{42}^{(1)}\right) \end{aligned}$$

(63)

$$\begin{aligned} B_{42}^{(03)}= & {} 16 \gamma \left( \mu +\gamma -\mu \gamma \right) \left( A_{42}^{(1)}\right) \end{aligned}$$

(64)

$$\begin{aligned} B_{42}^{(04)}= & {} \gamma \left( \mu +\gamma -\mu \gamma \right) \left( 8 \mu ^2 \gamma ^2-20 \gamma -16 \mu -4 \mu ^2 \gamma ^3+\gamma \sqrt{A_{42}^{(0)}}+25 \mu \gamma -\sqrt{A_{42}^{(0)}}+16 \mu \sqrt{1-\gamma }-18 \mu \gamma ^2\right. \nonumber \\{} & {} \left. -4 \mu ^2 \gamma +9 \mu \gamma ^3+9 \gamma ^2-5 \gamma ^3+4 \mu \gamma ^2 \sqrt{1-\gamma }+4 \mu ^2 \gamma \sqrt{1-\gamma }-4 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+16\right) ^2 \end{aligned}$$

(65)

$$\begin{aligned} B_{42}^{(05)}= & {} 24 \gamma \left( \mu -1\right) \left( \gamma -1\right) \left( A_{42}^{(1)}\right) \end{aligned}$$

(66)

$$\begin{aligned} B_{42}^{(10)}= & {} \left( \mu ^2 \gamma ^2-\mu ^2 \gamma ^3+\mu \gamma -\sqrt{A_{42}^{(0)}}-2 \mu \gamma ^2+2 \mu \gamma ^3+\gamma ^2-\gamma ^3\right) \end{aligned}$$

(67)

$$\begin{aligned} B_{42}^{(11)}= & {} 16 \mu +20 \gamma -7 \mu ^2 \gamma ^2+2 \mu ^2 \gamma ^3+\mu ^2 \gamma ^4-24 \mu \gamma -16 \mu \sqrt{1-\gamma }+15 \mu \gamma ^2+4 \mu ^2 \gamma -5 \mu \gamma ^3\nonumber \\{} & {} -2 \mu \gamma ^4-8 \gamma ^2+3 \gamma ^3+\gamma ^4-4 \mu \gamma ^2 \sqrt{1-\gamma }-4 \mu ^2 \gamma \sqrt{1-\gamma }+4 \mu ^2 \gamma ^2 \sqrt{1-\gamma }-16 \end{aligned}$$

(68)

$$\begin{aligned} A_{42}^{(0)}= & {} \left( \mu \gamma -\gamma +1\right) \left( 133 \mu ^2 \gamma ^2-96 \gamma -128 \mu -53 \mu ^2 \gamma ^3-48 \mu ^3 \gamma ^2+16 \mu ^3 \gamma ^3+208 \mu \gamma +128 \mu \sqrt{1-\gamma }-136 \mu \gamma ^2\right. \nonumber \\{} & {} \left. -128 \mu ^2 \gamma +57 \mu \gamma ^3+32 \mu ^3 \gamma -128 \mu ^2 \sqrt{1-\gamma }+128 \mu ^2+52 \gamma ^2-20 \gamma ^3+32 \mu \gamma ^2 \sqrt{1-\gamma }\right. \nonumber \\{} & {} \left. +64 \mu ^2 \gamma \sqrt{1-\gamma }-32 \mu ^3 \gamma \sqrt{1-\gamma }-64 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+32 \mu ^3 \gamma ^2 \sqrt{1-\gamma }-32 \mu \gamma \sqrt{1-\gamma }+64\right) \end{aligned}$$

(69)

$$\begin{aligned} A_{42}^{(1)}= & {} \mu ^2 \gamma ^2-\frac{5 \gamma }{2}-2 \mu -\frac{\mu ^2 \gamma ^3}{2}+\frac{\gamma \sqrt{A_{42}^{(0)}}}{8}+\frac{25 \mu \gamma }{8}-\frac{\sqrt{A_{42}^{(0)}}}{8}+2 \mu \sqrt{1-\gamma }-\frac{9 \mu \gamma ^2}{4}\nonumber \\{} & {} -\frac{\mu ^2 \gamma }{2}+\frac{9 \mu \gamma ^3}{8}+\frac{9 \gamma ^2}{8}-\frac{5 \gamma ^3}{8}+\frac{\mu \gamma ^2 \sqrt{1-\gamma }}{2}+\frac{\mu ^2 \gamma \sqrt{1-\gamma }}{2}-\frac{\mu ^2 \gamma ^2 \sqrt{1-\gamma }}{2}+2 \end{aligned}$$

(70)

In the bottom left figure,

$$\begin{aligned} B_{43}^{(0)}= & {} \frac{B_{43}^{(00)}}{B_{43}^{(11)}}-10 \gamma -\left( 2 \gamma -2\right) \left( \mu \gamma -\gamma +1\right) -10 \mu +10 \mu \gamma +10 \mu \sqrt{1-\gamma }+\gamma \left( \mu +\gamma -\mu \gamma \right) \nonumber \\{} & {} +\frac{2 B_{43}^{(00)}}{{\left( B_{43}^{(11)}\right) }^2}+3 \gamma \left( \mu -1\right) \left( \gamma -1\right) +\frac{B_{43}^{(01)}}{B_{43}^{(11)}}+\frac{B_{43}^{(02)}}{B_{43}^{(11)}} +\frac{B_{43}^{(03)}}{{\left( B_{43}^{(11)}\right) }^2}+\frac{B_{43}^{(04)}}{B_{43}^{(11)}}+60 \end{aligned}$$

(71)

$$\begin{aligned} B_{43}^{(1)}= & {} 3 \left( \gamma -1\right) \left( \mu \gamma -\gamma +1\right) -\frac{75 {\left( \gamma -1\right) }^2 \left( \frac{\mu \gamma }{25}-\frac{\mu \gamma ^2}{25}+\frac{\gamma ^2}{25}+1\right) \left( B_{43}^{(10)}\right) ^2}{{\left( B_{43}^{(11)}\right) }^2}+\frac{6 \gamma \left( \mu -1\right) {\left( \gamma -1\right) }^2 B_{43}^{(10)}}{B_{43}^{(11)}} \end{aligned}$$

(72)

$$\begin{aligned} B_{43}^{(00)}= & {} 25 \left( 20 \mu ^2 \gamma ^2-275 \gamma -250 \mu -10 \mu ^2 \gamma ^3+\gamma \sqrt{A_{43}^{(0)}}+286 \mu \gamma -\sqrt{A_{43}^{(0)}}+250 \mu \sqrt{1-\gamma }-57 \mu \gamma ^2\right. \nonumber \\{} & {} \left. -10 \mu ^2 \gamma +21 \mu \gamma ^3+36 \gamma ^2-11 \gamma ^3+10 \mu \gamma ^2 \sqrt{1-\gamma }+10 \mu ^2 \gamma \sqrt{1-\gamma }-10 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+250\right) ^2 \end{aligned}$$

(73)

$$\begin{aligned} B_{43}^{(01)}= & {} 25 \left( 50 \mu \gamma -50 \gamma -50 \mu +50 \mu \sqrt{1-\gamma }+50\right) \left( A_{43}^{(1)}\right) \end{aligned}$$

(74)

$$\begin{aligned} B_{43}^{(02)}= & {} 250 \gamma \left( \mu +\gamma -\mu \gamma \right) \left( A_{43}^{(1)}\right) \end{aligned}$$

(75)

$$\begin{aligned} B_{43}^{(03)}= & {} \gamma \left( \mu +\gamma -\mu \gamma \right) \left( 20 \mu ^2 \gamma ^2-275 \gamma -250 \mu -10 \mu ^2 \gamma ^3+\gamma \sqrt{A_{43}^{(0)}}+286 \mu \gamma -\sqrt{A_{43}^{(0)}}+250 \mu \sqrt{1-\gamma }-57 \mu \gamma ^2\right. \nonumber \\{} & {} \left. -10 \mu ^2 \gamma +21 \mu \gamma ^3+36 \gamma ^2-11 \gamma ^3+10 \mu \gamma ^2 \sqrt{1-\gamma }+10 \mu ^2 \gamma \sqrt{1-\gamma }-10 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+250\right) ^2 \end{aligned}$$

(76)

$$\begin{aligned} B_{43}^{(04)}= & {} 375 \gamma \left( \mu -1\right) \left( \gamma -1\right) \left( A_{43}^{(1)}\right) \end{aligned}$$

(77)

$$\begin{aligned} B_{43}^{(10)}= & {} \left( \mu ^2 \gamma ^2-\mu ^2 \gamma ^3+\mu \gamma -\sqrt{A_{43}^{(0)}}-2 \mu \gamma ^2+2 \mu \gamma ^3+\gamma ^2-\gamma ^3\right) \end{aligned}$$

(78)

$$\begin{aligned} B_{43}^{(11)}= & {} 250 \mu +275 \gamma -19 \mu ^2 \gamma ^2+8 \mu ^2 \gamma ^3+\mu ^2 \gamma ^4-285 \mu \gamma -250 \mu \sqrt{1-\gamma }+54 \mu \gamma ^2+10 \mu ^2 \gamma -17 \mu \gamma ^3\nonumber \\{} & {} -2 \mu \gamma ^4-35 \gamma ^2+9 \gamma ^3+\gamma ^4-10 \mu \gamma ^2 \sqrt{1-\gamma }-10 \mu ^2 \gamma \sqrt{1-\gamma }+10 \mu ^2 \gamma ^2 \sqrt{1-\gamma }-250 \end{aligned}$$

(79)

$$\begin{aligned} A_{43}^{(0)}= & {} \left( \mu \gamma -\gamma +1\right) \left( 1126 \mu ^2 \gamma ^2-3000 \gamma -5000 \mu -326 \mu ^2 \gamma ^3-300 \mu ^3 \gamma ^2+100 \mu ^3 \gamma ^3+6100 \mu \gamma \right. \nonumber \\{} & {} \left. +5000 \mu \sqrt{1-\gamma }-1450 \mu \gamma ^2-3200 \mu ^2 \gamma +351 \mu \gamma ^3+200 \mu ^3 \gamma -5000 \mu ^2 \sqrt{1-\gamma }+5000 \mu ^2+625 \gamma ^2\right. \nonumber \\{} & {} \left. -125 \gamma ^3+200 \mu \gamma ^2 \sqrt{1-\gamma }+700 \mu ^2 \gamma \sqrt{1-\gamma }-200 \mu ^3 \gamma \sqrt{1-\gamma }-400 \mu ^2 \gamma ^2 \sqrt{1-\gamma }\right. \nonumber \\{} & {} \left. +200 \mu ^3 \gamma ^2 \sqrt{1-\gamma }-500 \mu \gamma \sqrt{1-\gamma }+2500\right) \end{aligned}$$

(80)

$$\begin{aligned} A_{43}^{(1)}= & {} \frac{4 \mu ^2 \gamma ^2}{25}-\frac{11 \gamma }{5}-2 \mu -\frac{2 \mu ^2 \gamma ^3}{25}+\frac{\gamma \sqrt{A_{43}^{(0)}}}{125}+\frac{286 \mu \gamma }{125}-\frac{\sqrt{A_{43}^{(0)}}}{125}+2 \mu \sqrt{1-\gamma }-\frac{57 \mu \gamma ^2}{125}\nonumber \\{} & {} -\frac{2 \mu ^2 \gamma }{25}+\frac{21 \mu \gamma ^3}{125}+\frac{36 \gamma ^2}{125}-\frac{11 \gamma ^3}{125}+\frac{2 \mu \gamma ^2 \sqrt{1-\gamma }}{25}+\frac{2 \mu ^2 \gamma \sqrt{1-\gamma }}{25}-\frac{2 \mu ^2 \gamma ^2 \sqrt{1-\gamma }}{25}+2 \end{aligned}$$

(81)

In the bottom right figure,

$$\begin{aligned} B_{44}^{(0)}= & {} \frac{B_{44}^{(00)}}{{\left( B_{44}^{(11)}\right) }^2}-200 \gamma -200 \mu +200 \mu \gamma +200 \mu \sqrt{1-\gamma }+\gamma \left( \mu +\gamma -\mu \gamma \right) +\frac{2 B_{44}^{(00)}}{B_{44}^{(11)}}\nonumber \\{} & {} -2 \left( \gamma -1\right) \left( \mu \gamma -\gamma +1\right) +\frac{B_{44}^{(01)}}{B_{44}^{(11)}}+3 \gamma \left( \mu -1\right) \left( \gamma -1\right) +\frac{B_{44}^{(02)}}{{\left( B_{44}^{(11)}\right) }^2} +\frac{B_{44}^{(03)}}{B_{44}^{(11)}}+\frac{B_{44}^{(04)}}{B_{44}^{(11)}}+20200 \end{aligned}$$

(82)

$$\begin{aligned} B_{44}^{1}= & {} 3 \left( \gamma -1\right) \left( \mu \gamma -\gamma +1\right) -\frac{3 {\left( \gamma -1\right) }^2 \left( \mu \gamma -\mu \gamma ^2+\gamma ^2+10000\right) \left( B_{44}^{(10)}\right) ^2}{{\left( B_{44}^{(11)}\right) }^2}+\frac{6 \gamma \left( \mu -1\right) {\left( \gamma -1\right) }^2 B_{44}^{(10)}}{B_{44}^{(11)}} \end{aligned}$$

(83)

$$\begin{aligned} B_{44}^{(00)}= & {} 20000 \left( 400 \mu ^2 \gamma ^2-2010000 \gamma -2000000 \mu -200 \mu ^2 \gamma ^3+2010201 \mu \gamma +\gamma \sqrt{\left( \mu \gamma -\gamma +1\right) \left( A_{44}^{(0)}\right) }\right. \nonumber \\{} & {} \left. +2000000 \mu \sqrt{1-\gamma }-\sqrt{\left( \mu \gamma -\gamma +1\right) \left( A_{44}^{(0)}\right) }-10602 \mu \gamma ^2-200 \mu ^2 \gamma +401 \mu \gamma ^3+10201 \gamma ^2\right. \nonumber \\{} & {} \left. -201 \gamma ^3+200 \mu \gamma ^2 \sqrt{1-\gamma }+200 \mu ^2 \gamma \sqrt{1-\gamma }-200 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+2000000\right) ^2 \end{aligned}$$

(84)

$$\begin{aligned} B_{44}^{(01)}= & {} 10000 \left( 20000 \mu \gamma -20000 \gamma -20000 \mu +20000 \mu \sqrt{1-\gamma }+20000\right) \left( A_{44}^{(1)}\right) \end{aligned}$$

(85)

$$\begin{aligned} B_{44}^{(02)}= & {} \gamma \left( \mu +\gamma -\mu \gamma \right) \left( 400 \mu ^2 \gamma ^2-2010000 \gamma -2000000 \mu -200 \mu ^2 \gamma ^3+2010201 \mu \gamma +\gamma \sqrt{\left( \mu \gamma -\gamma +1\right) \left( A_{44}^{(0)}\right) }\right. \nonumber \\{} & {} \left. +2000000 \mu \sqrt{1-\gamma }-\sqrt{\left( \mu \gamma -\gamma +1\right) \left( A_{44}^{(0)}\right) }-10602 \mu \gamma ^2-200 \mu ^2 \gamma +401 \mu \gamma ^3+10201 \gamma ^2\right. \nonumber \\{} & {} \left. -201 \gamma ^3+200 \mu \gamma ^2 \sqrt{1-\gamma }+200 \mu ^2 \gamma \sqrt{1-\gamma }-200 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+2000000\right) ^2 \end{aligned}$$

(86)

$$\begin{aligned} B_{44}^{(03)}= & {} 2000000 \gamma \left( \mu +\gamma -\mu \gamma \right) \left( A_{44}^{(1)}\right) \end{aligned}$$

(87)

$$\begin{aligned} B_{44}^{(04)}= & {} 3000000 \gamma \left( \mu -1\right) \left( \gamma -1\right) \left( A_{44}^{(1)}\right) \end{aligned}$$

(88)

$$\begin{aligned} B_{44}^{(10)}= & {} \left( \mu ^2 \gamma ^2-\mu ^2 \gamma ^3+\mu \gamma -\sqrt{\left( \mu \gamma -\gamma +1\right) \left( A_{44}^{(0)}\right) }-2 \mu \gamma ^2+2 \mu \gamma ^3+\gamma ^2-\gamma ^3\right) \end{aligned}$$

(89)

$$\begin{aligned} B_{44}^{(11)}= & {} 2000000 \mu +2010000 \gamma -399 \mu ^2 \gamma ^2+198 \mu ^2 \gamma ^3+\mu ^2 \gamma ^4-2010200 \mu \gamma \nonumber \\{} & {} -2000000 \mu \sqrt{1-\gamma }+10599 \mu \gamma ^2+200 \mu ^2 \gamma -397 \mu \gamma ^3-2 \mu \gamma ^4-10200 \gamma ^2\nonumber \\{} & {} +199 \gamma ^3+\gamma ^4-200 \mu \gamma ^2 \sqrt{1-\gamma }-200 \mu ^2 \gamma \sqrt{1-\gamma }+200 \mu ^2 \gamma ^2 \sqrt{1-\gamma }-2000000 \end{aligned}$$

(90)

$$\begin{aligned} A_{44}^{(0)}= & {} 4250001 \mu ^2 \gamma ^2-404000000 \gamma -800000000 \mu -130001 \mu ^2 \gamma ^3-120000 \mu ^3 \gamma ^2\nonumber \\{} & {} +40000 \mu ^3 \gamma ^3+808040000 \mu \gamma +800000000 \mu \sqrt{1-\gamma }-8180000 \mu \gamma ^2-404080000 \mu ^2 \gamma \nonumber \\{} & {} +140001 \mu \gamma ^3+80000 \mu ^3 \gamma -800000000 \mu ^2 \sqrt{1-\gamma }+800000000 \mu ^2+4050000 \gamma ^2\nonumber \\{} & {} -50000 \gamma ^3+80000 \mu \gamma ^2 \sqrt{1-\gamma }+4080000 \mu ^2 \gamma \sqrt{1-\gamma }-80000 \mu ^3 \gamma \sqrt{1-\gamma }\nonumber \\{} & {} -160000 \mu ^2 \gamma ^2 \sqrt{1-\gamma }+80000 \mu ^3 \gamma ^2 \sqrt{1-\gamma }-4000000 \mu \gamma \sqrt{1-\gamma }+400000000 \end{aligned}$$

(91)

$$\begin{aligned} A_{44}^{(1)}= & {} \frac{\mu ^2 \gamma ^2}{2500}-\frac{201 \gamma }{100}-2 \mu -\frac{\mu ^2 \gamma ^3}{5000}+\frac{2010201 \mu \gamma }{1000000}+\frac{\gamma \sqrt{\left( \mu \gamma -\gamma +1\right) \left( A_{44}^{(0)}\right) }}{1000000}\nonumber \\{} & {} +2 \mu \sqrt{1-\gamma }-\frac{\sqrt{\left( \mu \gamma -\gamma +1\right) \left( A_{44}^{(0)}\right) }}{1000000}-\frac{5301 \mu \gamma ^2}{500000}-\frac{\mu ^2 \gamma }{5000}+\frac{401 \mu \gamma ^3}{1000000}\nonumber \\{} & {} +\frac{10201 \gamma ^2}{1000000}-\frac{201 \gamma ^3}{1000000}+\frac{\mu \gamma ^2 \sqrt{1-\gamma }}{5000}+\frac{\mu ^2 \gamma \sqrt{1-\gamma }}{5000}-\frac{\mu ^2 \gamma ^2 \sqrt{1-\gamma }}{5000}+2 \end{aligned}$$

(92)

1.3 Explicit expressions for $B_{5j}^{(k)}$

In Fig. 5, the expressions for each $B_{5j}^{(k)}$ can be seen as follows.

$$\begin{aligned} B_{51}^{(0)}= & {} 2304\,\sqrt{2}\,\mu -472\,\mu -482\,\mu \,A_{51}+202\,A_{51}+832\,\sqrt{2}\,\mu ^2-2240\,\sqrt{2}\,\mu ^3\nonumber \\{} & {} -832\,\sqrt{2}\,\mu ^4-64\,\sqrt{2}\,\mu ^5+374\,\mu ^2\,A_{51}+130\,\mu ^3\,A_{51}+1736\,\mu ^2+4376\,\mu ^3\nonumber \\{} & {} +1328\,\mu ^4+96\,\mu ^5-320\,\sqrt{2}\,\mu ^2\,A_{51}-96\,\sqrt{2}\,\mu ^3\,A_{51}+416\,\sqrt{2}\,\mu \,A_{51}+936 \end{aligned}$$

(93)

$$\begin{aligned} B_{51}^{(1)}= & {} \left( 3\,\mu +\frac{3\,\left( \mu +5\right) \,{\left( 2\,\mu -2\,A_{51}+\mu ^2+1\right) }^2}{{\left( 20\,\sqrt{2}\,\mu -12\,\mu +4\,\sqrt{2}\,\mu ^2-5\,\mu ^2+17\right) }^2}+\frac{3\,\left( 16\,\mu -16\right) \,\left( \frac{\mu }{4}-\frac{A_{51}}{4}+\frac{\mu ^2}{8}+\frac{1}{8}\right) }{20\,\sqrt{2}\,\mu -12\,\mu +4\,\sqrt{2}\,\mu ^2-5\,\mu ^2+17}\right. \nonumber \\{} & {} \left. +3\right) \,\left( 680\,\sqrt{2}\,\mu -408\,\mu -344\,\sqrt{2}\,\mu ^2-296\,\sqrt{2}\,\mu ^3-40\,\sqrt{2}\,\mu ^4+774\,\mu ^2+440\,\mu ^3+57\,\mu ^4+289\right) \end{aligned}$$

(94)

where $A_{51} = \sqrt{\left( \mu +1\right) \,\left( 32\,\sqrt{2}\,\mu -21\,\mu -24\,\sqrt{2}\,\mu ^2-8\,\sqrt{2}\,\mu ^3+46\,\mu ^2+12\,\mu ^3+13\right) }$.

$$\begin{aligned} B_{52}^{(0)}= & {} 100907385600\,\sqrt{2}\,\mu -32975491192\,\mu -188364722\,\mu \,\sqrt{\left( \mu +1\right) \,A_{52}}+84523138\, \sqrt{\left( \mu +1\right) \,A_{52}}\nonumber \\{} & {} +18869939200\,\sqrt{2}\,\mu ^2-100154432000\,\sqrt{2}\,\mu ^3-18869939200\,\sqrt{2}\,\mu ^4-752953600\,\sqrt{2}\, \mu ^5\nonumber \\{} & {} +196853678\,\mu ^2\,\sqrt{\left( \mu +1\right) \,A_{52}}+28663138\,\mu ^3\,\sqrt{\left( \mu +1\right) \,A_{52}}+69808280024\, \mu ^2\nonumber \\{} & {} +173779616024\,\mu ^3+29359447208\,\mu ^4+1129430400\,\mu ^5-147392000\,\sqrt{2}\,\mu ^2\,\sqrt{\left( \mu +1\right) \,A_{52}}\nonumber \\{} & {} -20744640\,\sqrt{2}\,\mu ^3\,\sqrt{\left( \mu +1\right) \,A_{52}}+168136640\,\sqrt{2}\,\mu \,\sqrt{\left( \mu +1\right) \,A_{52}}+42765828000 \end{aligned}$$

(95)

$$\begin{aligned} B_{52}^{(1)}= & {} \left( 147\,\mu +3\,\left( 548800\,\mu -548800\right) \,\left( \frac{49\,\mu }{400} -\frac{\sqrt{\left( \mu +1\right) \,A_{52}}}{400}+\frac{49\,\mu ^2}{800}+\frac{49}{800}\right) \frac{1}{B_{52}^{(10)}}\right. \nonumber \\{} & {} \left. +3\,\left( 2401\,\mu +22001\right) \,{\left( 98\,\mu -2\,\sqrt{\left( \mu +1\right) \,A_{52}}+49\,\mu ^2+49\right) }^2\frac{1}{{\left( B_{52}^{(10)}\right) }^2}\right. \nonumber \\{} & {} \left. +147\right) \,\left( 556867760\,\sqrt{2}\,\mu -409279200\,\mu -413372240\,\sqrt{2}\,\mu ^2-134467760\, \sqrt{2}\,\mu ^3\right. \nonumber \\{} & {} \left. -9027760\,\sqrt{2}\,\mu ^4+747956382\,\mu ^2+201605600\,\mu ^3+12987009\,\mu ^4+240343009\right) \end{aligned}$$

(96)

$$\begin{aligned} B_{52}^{(10)}= & {} 17960\,\sqrt{2}\,\mu -13200\,\mu +1960\,\sqrt{2}\,\mu ^2-2303\,\mu ^2+15503 \end{aligned}$$

(97)

where $A_{52} = \left( 303200\,\sqrt{2}\,\mu -234999\,\mu -264000\,\sqrt{2}\,\mu ^2-39200\,\sqrt{2}\,\mu ^3+450901\,\mu ^2+58800\,\mu ^3+128500\right) .$

$$\begin{aligned} B_{53}^{(0)}= & {} \frac{4447014038798929\,\mu }{34359738368}+\frac{1731999573283827\,\mu \,A_{53}}{1099511627776}+2530\,A_{53} -256\,\sqrt{2}\,\mu ^5\nonumber \\{} & {} -\frac{42546806858567\,\mu ^2\,A_{53}}{1099511627776}+450\,\mu ^3\,A_{53} +\frac{13712264631662189\,\mu ^2}{137438953472}\nonumber \\{} & {} +\frac{954132002979149\,\mu ^3}{34359738368} +\frac{203154529470867\,\mu ^4}{137438953472}+384\,\mu ^5-320\,\sqrt{2}\,\mu ^3\,A_{53}+55968 \end{aligned}$$

(98)

$$\begin{aligned} B_{53}^{(1)}= & {} \left( 3\,\mu +\frac{3\,\left( 64\,\mu -64\right) \,\left( \frac{\mu }{16}-\frac{A_{53}}{16}+\frac{\mu ^2}{32} +\frac{1}{32}\right) }{B_{53}^{(10)}}+\frac{3\,\left( \mu +17\right) \,{\left( 2\,\mu -2\,A_{53}+\mu ^2+1\right) }^2}{{\left( B_{53}^{(10)}\right) }^2}\right. \nonumber \\{} & {} \left. +3\right) \,\left( \frac{166993454639279\,\mu }{8589934592}-144\,\sqrt{2}\,\mu ^4 +\frac{60243921354669\,\mu ^2}{8589934592}+\frac{408726400289561\,\mu ^3}{1099511627776}+209\,\mu ^4+14641\right) \end{aligned}$$

(99)

$$\begin{aligned} B_{53}^{(10)}= & {} 136\,\sqrt{2}\,\mu -112\,\mu +8\,\sqrt{2}\,\mu ^2-9\,\mu ^2+121 \end{aligned}$$

(100)

where $A_{53} = \sqrt{\left( \mu +1\right) \,\left( \frac{149436005184641\,\mu }{549755813888}-32\,\sqrt{2}\,\mu ^3+\frac{804247227640749\,\mu ^2}{8796093022208}+48\,\mu ^3+212\right) }.$

$$\begin{aligned} B_{54}^{(0)}= & {} \frac{1961207684361405\,\mu }{67108864}+\frac{538579401443961\,\mu \,A_{54}}{8589934592}+87562\,A_{54}\nonumber \\{} & {} +\frac{165512947439037\,\mu ^2\,A_{54}}{17179869184}+\frac{40123449911847\,\mu ^3\,A_{54}}{549755813888}+\frac{39193419728658571\,\mu ^2}{2147483648}\nonumber \\{} & {} +\frac{125668827204021\,\mu ^3}{33554432}+\frac{98298304814965\,\mu ^4}{2147483648}+\frac{37729274270505\,\mu ^5}{274877906944}+14673000 \end{aligned}$$

(101)

$$\begin{aligned} B_{54}^{(1)}= & {} \left( 3\,\mu +\frac{3\,\left( 400\,\mu -400\right) \,\left( \frac{\mu }{100}-\frac{A_{54}}{100} +\frac{\mu ^2}{200}+\frac{1}{200}\right) }{B_{54}^{(10)}}+\frac{3\,\left( \mu +101\right) \, {\left( 2\,\mu -2\,A_{54}+\mu ^2+1\right) }^2}{{\left( B_{54}^{(10)}\right) }^2}\right. \nonumber \\{} & {} \left. +3\right) \,\left( \frac{116681510080633\,\mu ^4}{2199023255552}+\frac{239451137688417\,\mu ^3}{17179869184} +\frac{126605283049529\,\mu ^2}{134217728}\right. \nonumber \\{} & {} \left. +\frac{493342114160233\,\mu }{134217728}+3690241\right) \end{aligned}$$

(102)

$$\begin{aligned} B_{54}^{(10)}= & {} \frac{525957652160415\,\mu }{549755813888}+20\,\sqrt{2}\,\mu ^2-21\,\mu ^2+1921 \end{aligned}$$

(103)

where $A_{54} = \sqrt{\left( \mu +1\right) \,\left( \frac{618743323903621\,\mu }{68719476736}-200\,\sqrt{2}\,\mu ^3+\frac{620108701709191\,\mu ^2}{274877906944}+300\,\mu ^3+9125\right) }.$