1 Introduction

Soliton theory was developed in the 1840s, and has become an important means to study nonlinear science [1]. Soliton is a quasi-particle that is morphologically stable and excited by a nonlinear field with non-dispersive energy. Soliton possesses all the properties of particles, including energy, momentum, and mass, and so on. They also adhere to all the laws of nature [2, 3]. It can describe some physical phenomena, and is widely used to explain water wave propagation in rivers and oceans, signal transmission in optical fiber communication, and some special phenomena in the field of plasma physics [4,5,6]. Some eloquent developments in nonlinear physics have been made [7,8,9]. The discovery of soliton phenomena can be traced back to 1844, when British scientist Scott Russell [10] accidentally discovered a strange phenomenon of water waves while walking in the river. Since then, the concept of soliton waves entered everyone’s vision. Subsequently, in 1895, Korteweg and Vries introduced the signature KdV equation for isolated waves [11], and since then, the existence of solitary waves has been widely recognized by the academic community. In 1965, Zabusky and Kruskal used numerical methods to study the interaction process of solitary waves in plasma, and confirmed that the waveforms do not change after the interaction of solitary waves, and were named soliton [12]. The development of soliton is of great significance to mathematics and other scientific fields [13,14,15,16,17]. At present, soliton theory seems to have shown its vigorous vitality, and has become a new science, and its research will undoubtedly promote the development of modern mathematical physics and applied engineering [18,19,20,21,22].

There are many famous methods to derive the soliton solution of the nonlinear equation, such as inverse scattering method [23], Bäckloud transformation method [24], Lie group method [25], Darboux transformation method [26] and Hirota bilinear method [27]. In addition, there are various methods to derive soliton solutions of the nonlinear equation [28]. The Hirota bilinear method applied in this paper is proposed by Hirota in 1971 [29]. It is a powerful tool to construct analytical solutions [30,31,32]. Moreover, somenew works find new properties of PDEs by using bilinear method [33,34,35]. We apply the bilinear method in this work, which has the advantages of simplicity and directness. It does not require that the nonlinear partial differential equations under study have Lax pairs, i.e., regardless of the existence of Lax pairs in equations, the equations can be solved directly by transforming them into bilinear type by means of bilinear transformations.

In addition, solitons with different structures have also been studied, such as the dark solitons [36], anti-dark solitons [37], W-type solitons [38] as well as multi-solitons [39, 40]. The concept of rogue wave [41] was proposed by the British writer Darp, which is a peak value structure with limitations in space and time, and it is also known as the wave of “coming without shadow, going without trace”. Breathers are nonlinear waves that are periodic in both time and space, and can be divided into Akhmediev breathers [42] and Kuznetsov-Ma breathers [43]. Akhmediev breathers are periodic and completely localized in the direction of evolution, while Kuznetsov-Ma breathers are periodic and localized in the direction of evolution. Many mathematical models can describe these nonlinear waves, such as the Korteweg-de Vries (KdV) equation [11] and the nonlinear Schrödinger (NLS) equation [44], as well as their various deformations.

The breather is a local wave that exhibits periodic oscillation behavior in a certain direction [45]. Recent studies have shown that breather solutions exist for many nonlinear equations, including sine-Gordon equation [46], Kudryashov-Sinelshchikov equation [47], (4+1)-dimensional Fokas equation [48], Korteweg-de Vries (KdV) equation [49]. Lump is derived from breather degradation (period is infinite), that is, a limiting structure of breather [50]. Under certain conditions, breathers and rogue waves can be converted into other types of nonlinear waves, referred as the state transformation of waves [51, 52].

In nonlinear systems, higher-order effects and coupling effects have significant effects on the state transformation of nonlinear waves. In this case, the breather can be seen as a single pulse composed of a nonlinear superposition of a solitary wave component and a periodic wave component with their own velocities \(V_s\) and \(V_p\). In general, the velocity difference between the two components is not zero, that is, \(V_s\ne V_p\). Conversely, if \(V_s=V_p\), the breather can be transformed into other nonlinear waves, such as antidark solitons (\(\eta _s\ne 0,\eta _p=0\)), M-type or W-type solitons (\(\eta _s\approx \eta _p\)), multi-peak solitons (\(\eta _s<\eta _p\)), periodic wave (\(\eta _s=0,\eta _p\ne 0\)), where \(\eta _s,\eta _p\) represents the wave number of the solitary wave component and the periodic wave component, respectively. Moreover, in recent years, some rich nonlinear wave structures have been discovered in the plane wave background in the higher-order nonlinear equations. [53] proved that the breathers in the higher-order NLS equation can be converted into non-pulsed solitons. The conservation between rogue waves and W-type solitons in the Hirota equation has been discovered, which is influenced by higher-order effects [54]. Breather-to-soliton transitions, nonlinear wave interactions, and modulational instability have been found in a higher-order generalized nonlinear Schrödinger equation [55]. In addition, the (2+1)-dimensional KdV equation and the state transition between lump wave and breather have been studied in [56].

In view of previous studies, the transformation mechanism for the (2+1)-dimensional sine-Gordon equation and (2+1)-dimensional modified Boussinesq equation has not yet been studied. Motivated by these, we investigate nonlinear wave state transitions for the (2+1)-dimensional sine-Gordon equation [57] and the (2+1)-dimensional modified Boussinesq equation [59].

The (2+1)-dimensional sine-Gordon equation is given as follows:

$$\begin{aligned} u_{xx}+u_{yy}-u_{tt}=\sin {u}. \end{aligned}$$
(1.1)

Equation (1.1) is the classical wave equation with a nonlinear sine source term. The sine-Gordon partial differential equations can be used to simulate the dynamic mechanism of base motion during DNA transcription and remaking. The equations are widely used in research because of their adaptability, nonlinearity and increasing dispersion accuracy. [58] derived localized dynamical behavior in the (2+1)-dimensional sine-Gordon equation. [60] studied new kink-shaped solutions and periodic wave solutions for the (2+1)-dimensional sine-Gordon equation. New class of running-wave solutions of the (2+1)-dimensional sine-Gordon equation have also been given in [61].

Here we take

$$\begin{aligned} u=2i\ln \left( \frac{f^*}{f} \right) , \end{aligned}$$
(1.2)

where f is any complex function, \(*\) denotes the complex conjugate, and \(i=\sqrt{-1}\) Then we get the bilinear form of the (2+1)-dimensional sine-Gordon equation:

$$\begin{aligned} (D_x^2+D_y^2-D_t^2)(f \cdot f)=\frac{1}{2}(f^2-(f^*)^2), \end{aligned}$$
(1.3)

where \(D_x,D_y\) and \(D_t\) are bilinear operators. They are defined by

$$\begin{aligned} D_t^m\ D_x^n\ D_y^p (f\cdot g)= & {} (\partial _t-\partial _{t'})^m (\partial _x-\partial _{x'})^n (\partial _y-\partial _{y'})^p\nonumber \\{} & {} {}[f(t,x,y)g(t',x',y')] |_{t'=t,x'=x,y'=y}. \end{aligned}$$
(1.4)

The (2+1)-dimensional modified Boussinesq equation is given as follow:

$$\begin{aligned} u_{tt}-u_{xx}-u_{yy}-3\left( u^2 \right) _{xx}-u_{xxxx}=0. \end{aligned}$$
(1.5)

The standard Boussinesq equation is often used to describe the propagation and change of nonlinear shallow water waves, including shallow water deformation, reflection, diffraction, refraction, wave breaking and dissipation, wave current interaction, and tidal current phenomenon caused by waves [62, 63]. Solutions and conservation laws of a (2+1)-dimensional Boussinesq equation have been given [64]. The decomposition method for solving (2+1)-dimensional Boussinesq equation have also been studied in [65]. [66] researched on lump solution of (2+1)-dimensional Boussinesq equation. This paper is evolved from the generalized (2+1)-dimensional Boussinesq equation, which is shown as follows:

$$\begin{aligned} u_{tt}+\alpha u_{xx}-u_{yy}+\beta \left( u^2 \right) _{xx}+\gamma u_{xxxx}=0. \end{aligned}$$

When \(\alpha =-1,\beta =-3,\gamma =-1\), it is the (2+1)-dimensional modified Boussinesq equation.

In order to obtain the bilinear form of equation (1.5), first we let

$$\begin{aligned} u=2(\ln f)_{xx}. \end{aligned}$$
(1.6)

Substituting Eq. (1.6) into Eq. (1.5) , we get:

$$\begin{aligned} (D_t^{2}-D_x^{2}-D_y^{2}-D_x^{4} )(f\cdot f)=0. \end{aligned}$$
(1.7)

The main purpose of this work is to study the state transition of nonlinear waves and various properties of transformed waves via nonlinear superposition, characteristic lines and phase shift analysis of the (2+1)-dimensional sine-Gordon equation and the (2+1)-dimensional modified Boussinesq equation. Thus, following problems need to be further considered:

  • What is the nonlinear superposition mechanism of the breathers of these two equations?

  • Do state transition conditions exist for breathers?

  • How does time change affect nonlinear waves?

In addition, compared with previous studies, we also have some innovations, which are as follows:

  • According to the Hirota method, we derive the breather solutions and some conversion waves of the two equations for the first time.

  • We also present a certain nonlinear superposition mechanism of some breathers. The breathers and transformed waves are the nonlinear superpositions of solitary and periodic waves. Those results help us understand some structures of the transformed solutions.

  • The characteristic lines of the transformed waves are parallel, and the distance between them is a function of the time t. As the time changes, the geometry of the characteristic lines also changes, thus having the evolution of the other transformed waves. It is helpful for finding various types of solutions with position and range requirements.

1.1 Main Results

Theorem 1.1

The transformed wave solution \(\widetilde{u}_2\) of the breather for the (2+1)-dimensional sine-Gordon equation can be expressed as:

$$\begin{aligned} \widetilde{u}_2=2i\ln (\frac{(2\sqrt{\lambda _2}\cosh ({\theta _1+\ln {\sqrt{\lambda _2}}})+\lambda _3\cos {\Lambda _1})^*}{2\sqrt{\lambda _2}\cosh {\theta _1+\ln {\sqrt{\lambda _2}}}+\lambda _3\cos {\Lambda _1}}), \end{aligned}$$
(1.8)

where parameters \(a_1,b_1\) are arbitrary constant, \(\theta _1,\lambda _2,\lambda _3,\Lambda \) are defined in Eq. (2.23). The relationship between various types of transformed waves and parameters is shown in Table 1.

Table 1 Various types of transformed waves and corresponding wave parameters
Full size table

Remark 1

The constants \(a_1,b_1\) in Eq. (2.23) control the locality and oscillation of the transformed wave respectively. The larger the value of \(a_1(b_1)\), the stronger locality (oscillation) the wave is.

Remark 2

Equation (1.8) is composed of hyperbolic and trigonometric functions, so the transformed waves are nonlinear superpositions of solitary and periodic waves.

Remark 3

\(\beta _1 (\theta _1+\ln \sqrt{\lambda _2}=0)\) and \(\beta _2(\Lambda _1=0)\) are the characteristic lines of the transformed waves. The two characteristic lines are parallel, and the distance between them is a function of the time t. As the time changes, the geometry of the characteristic lines also changes, thus having the evolution of the other transformed waves.

Theorem 1.2

The transformed wave solution \(\widetilde{u}_2\) of the (2+1)-dimensional modified Boussinesq equation can be expressed as:

$$\begin{aligned} \begin{aligned} \widetilde{u}_2&=2[\ln (2\sqrt{\lambda }_2\cosh (\theta _1+\ln \sqrt{\lambda }_2))+\lambda _1\cos \Lambda _1]_{xx} \\&=\frac{8a_1^2 \lambda _2-2b_1^2 \lambda _1^2+4(a_1^2-b_1^2 ) \lambda _1 \sqrt{\lambda }_2\cosh (\theta _2+\ln \sqrt{\lambda }_2)\cos (\Lambda _2)}{(2\sqrt{\lambda }_2\cosh (\theta _2+\ln \lambda _2 )+\lambda _1\cos (\Lambda _2))^2} \\ {}&\quad +\frac{8a_1 b_1 \lambda _1 \sqrt{\lambda }_2 \sinh (\theta _2+\ln \sqrt{\lambda }_2 )\sin (\Lambda _2 )}{(2\sqrt{\lambda }_2\cosh (\theta _2+\ln \sqrt{\lambda }_2 )+\lambda _1\cos (\Lambda _2 ))^2}, \end{aligned} \end{aligned}$$
(1.9)

where parameters \(a_1,b_1\) are arbitrary constant, \(\theta _1,\lambda _1,\lambda _2\) are defined in Eq. (3.14). The relationship between various types of transformed waves and parameters is shown in Table 2.

Table 2 Various types of transformed waves and corresponding wave parameters
Full size table

Remark 4

\(a_1\) is always smaller than \(b_1\), periodicity of transformed waves is stronger when \(a_1\) is much smaller than \(b_1\).

Remark 5

Equation (1.9) is composed of hyperbolic and trigonometric functions, so the transformed waves are nonlinear superpositions of solitary and periodic waves.

Remark 6

\(\beta _1 (\theta _1+\ln \sqrt{\lambda _2}=0)\) and \(\beta _2(\Lambda _1=0)\) are the characteristic lines of the transformed wave. At the point the two characteristic lines are parallel, and the distance between these characteristic lines is a function of the time t. As the time changes, the geometry of the characteristic lines also changes, thus having the evolution of the other transformed waves.

1.2 Plan of Proof

In this paper, the state transformation of nonlinear equations is studied. In order to study this problem, we must first obtain the soliton solution of the equation, the breather solution. So the structure of this paper is as follows:

In Sect. 2, we derive single soliton solution and double soliton solution of the (2+1)-dimensional sine-Gordon equation, and we prove Theorem 1.1 in subsection 2.2 and 2.3 of this chapter.

In Sect. 3, N-soliton solution and breather solution of the (2+1) dimensional modified Boussinesq equation are derived. Then the state transition problem of the equation is studied by the characteristic line analysis, Theorem 1.2 is proved here.

In Sect. 4, we summarize the previous work.

In Sect. 5, we say the future recommendations.

2 Breather Transition and Its Mechanism of (2+1)-Dimensional Sine-Gordon Equation

The (2+1)-dimensional sine-Gordon equation is given in the previous section. In this chapter, we mainly learn about the characteristic line of its solution.

2.1 Soliton Solution of (2+1)-Dimensional Sine-Gordon Equation

Let f be expanded in series according to the parameter \(\varepsilon \) as:

$$\begin{aligned} f=1+f^{(1)}\varepsilon +f^{(2)}\varepsilon ^2+\cdots +f^{(n)}\varepsilon ^n+ \cdots \cdots \end{aligned}$$
(2.1)

Then we substitute Eq. (2.1) into Eq. (1.2), and collect the coefficients of the same degree \(\varepsilon \) to obtain the following equation:

$$\begin{aligned}{} & {} \varepsilon :f_{xx}^{(1)}+f_{yy}^{(1)}-f_{tt}^{(1)}=\frac{1}{2}(f^{(1)}-(f^{(1)})^*), \end{aligned}$$
(2.2)
$$\begin{aligned}{} & {} \varepsilon ^2:2(f_{xx}^{(2)}+f_{yy}^{(2)}-f_{tt}^{(2)})+(D_x^2+D_y^2-D_t^2)(f^{(1)}\cdot f^{(1)})\nonumber \\{} & {} \quad =\frac{1}{2}((f^{(1)})^2-((f^{(1)})^*)^2)+f^{(2)}-(f^{(2)})^*, \end{aligned}$$
(2.3)
$$\begin{aligned}{} & {} \varepsilon ^3:(f_{xx}^{(3)}+f_{yy}^{(3)}-f_{tt}^{(3)})+(D_x^2+D_y^2-D_t^2)(f^{(1)}\cdot f^{(2)})\nonumber \\{} & {} \quad =\frac{1}{2}(f^{(3)}-(f^{(3)})^*+f^{(1)}f^{(2)}-(f^{(1)})^*(f^{(2)})^*).\nonumber \\{} & {} \quad \cdots \cdots \end{aligned}$$
(2.4)

2.1.1 Single Soliton Solution

Since f is any complex function here, let’s set

$$\begin{aligned} f^{(1)}=e^{\xi _1}\cdot e^{\frac{i\pi }{2}},\xi _1=k_1x+l_1y+w_1t+\gamma _1, \end{aligned}$$
(2.5)

where \(k_1,l_1,w_1,\gamma _1\) are all real numbers, substituting Eq. (2.5) into Eq. (2.2), we get

$$\begin{aligned} k_1^2+l_1^2-w_1^2=1. \end{aligned}$$
(2.6)

Then we substitute the Eq. (2.5) into (2.3),

$$\begin{aligned} f_{xx}^{(2)}+f_{yy}^{(2)}-f_{tt}^{(2)}=\frac{1}{2}(f^{(2)}-(f^{(2)})^*). \end{aligned}$$
(2.7)

The same as Eq. (2.1), so let \(f^{(2)}=0\), we get

$$\begin{aligned} f_{xx}^{(3)}+f_{yy}^{(3)}-f_{tt}^{(3)}=\frac{1}{2}(f^{(3)}-(f^{(3)})^*). \end{aligned}$$
(2.8)

Here we take \(f^{(3)}= 0\), in turn, we can get \(f^{(4)} = f^{(5)}= \cdots = 0\). So if we set \(\varepsilon =1\), then

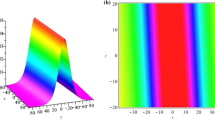
$$\begin{aligned} f_1=1+f^{(1)}=1+e^{\xi _1}\cdot e^{\frac{i\pi }{2}}. \end{aligned}$$
(2.9)

By substituting the above equation into Eq. (1.5), we obtain the single soliton solution of this equation.

$$\begin{aligned} u_1=2i\ln \frac{f_1^*}{f_1} =2i\ln \frac{1-ie^{\xi _1}}{1+ie^{\xi _1}}=4\arctan (e^{\xi _1}). \end{aligned}$$
(2.10)

Thus, we can get the three-dimensional diagram of its soliton solution at time \(t=-7,0,7\).

Fig. 1
figure 1

Structure of Single Soliton Solutions as t changes. a \(t=-7\). b \(t=0\). c \(t=7\). Parameters \(k_1=3, l_1=5, \gamma _1=0, w_1=\sqrt{k_1^2+l_1^2-1}=\sqrt{33}\)

Full size image

2.1.2 Double Soliton Solution

In order to find a double soliton solution to the equation, let’s set

$$\begin{aligned} f^{(1)}=(e^{\xi _1}+e^{\xi _2}) \cdot e^{\frac{i\pi }{2}},\xi _j=k_j x+l_j y+w_j t+\gamma _j,j=1,2,k_{j}^{2}+l_{j}^{2}-w_{j}^{2}=1.\nonumber \\ \end{aligned}$$
(2.11)

By plugging in Eq. (2.3) and setting \(f^{(2)}= e^{\xi _1+\xi _2+A_{12} }\cdot e^{i\pi }\), among them the first index of the last item for soliton interactions, so we can get

$$\begin{aligned} e^{A_{12}}=\frac{(k_1-k_2)^2+(l_1-l_2)^2-(w_1-w_2)^2}{(k_1+k_2)^2+(l_1+l_2)^2-(w_1+w_2)^2}, \end{aligned}$$

then

$$\begin{aligned} f_2=1+f^{(1)}+f^{(2)}=1+(e^{\xi _1}+e^{\xi _2})\cdot e^{\frac{i\pi }{2}}+e^{\xi _1+\xi _2+A_{12}}\cdot e^{i\pi }. \end{aligned}$$
(2.12)

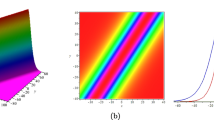
By substituting the above equation into (1.2), we derive the double soliton solution of the equation

$$\begin{aligned} u_2=2i\ln \left( \frac{f^*}{f} \right) =4\arctan \left( \frac{e^{\xi _1}+e^{\xi _2}}{1-e^{\xi _1+\xi _2+A_{12}}}\right) . \end{aligned}$$
(2.13)

We use mathematical software again to draw a three-dimensional diagram of the double soliton solution at time \(t=-1,0,1\) as shown in Fig. 2.

Fig. 2
figure 2

Structure of Double Soliton Solutions as t changes. a \(t=-1\). b \(t=0\). c \(t=1\). Parameters \(k_1=3,l_1=5,k_2=2,l_2=2,\gamma _1=\gamma _2=0,w_1=\sqrt{k_1^2+l_1^2-1}=\sqrt{33},w_2=\sqrt{k_2^2+l_2^2-1}=\sqrt{7}\)

Full size image

2.2 The Breather Solution and Characteristic Line Analysis of (2+1)-Dimensional Sine-Gordon Equation

In order to obtain the breather solution of the (2+1)-dimensional sine-Gordon equation, we pluralize the wave number of the double soliton solution \(u_2\), i.e., Eq. (2.13). Let’s set

$$\begin{aligned} k_1=k_2^*=a_1+ib_1,l_1=l_2^*=p_1+iq_1,\gamma _1=\gamma _2^*=\ln \frac{\lambda _1}{2}+\delta _1+\eta _1, \end{aligned}$$
(2.14)

where \(a_1,b_1,p_1,q_1,\lambda _1,\delta _1,\eta _1\) are real numbers, we plug in (2.12)

$$\begin{aligned} \begin{aligned} f_2&=1+e^{\frac{i\pi }{2}}(e^{\theta _1+i\Lambda _1+\ln \frac{\lambda _1}{2}}+e^{\theta _1-i\Lambda _1+\ln \frac{\lambda _1}{2}})+e^{2\theta _1+2\ln \frac{\lambda _1}{2}+A_{12}+i\pi }\\&=1+\lambda _1 e^{\theta _1+\frac{i\pi }{2}}\cos (\Lambda _1)+\frac{\lambda _1^{2}H}{4}e^{2\theta _1+i\pi }, \end{aligned} \end{aligned}$$
(2.15)

where

$$\begin{aligned} \theta _1= & {} a_1x+p_1y+\sqrt{\rho }\cos \frac{\alpha _1}{2}t+\delta _1, \nonumber \\ \Lambda _1= & {} b_1 x+q_1y+\sqrt{\rho }\sin \frac{\alpha _1}{2}t+\eta _1, \nonumber \\ H= & {} e^{A_12}=\frac{(k_1-k_2 )^2+(l_1-l_2 )^2-(w_1-w_2 )^2}{(k_1+k_2 )^2+(l_1+l_2 )^2-(w_1+w_2 )^2} \nonumber \\= & {} \frac{-4b_1^2-4q_1^2-((a_1+ib_1 )^2+(p_1+iq_1 )^2-(a_1-ib_1 )^2-(p_1-iq_1 )^2)^2}{4b_1^2+4q_1^2-((a_1+ib_1 )^2+(p_1+iq_1 )^2-2+(a_1-ib_1 )^2+(p_1-iq_1 )^2)^2}, \nonumber \\ \rho \cos {\alpha _1}= & {} a_1^2+p_1^2-b_1^2-q_1^2-1, \nonumber \\ \rho \sin {\alpha _1}= & {} 2a_1b_1+2p_1q_1, \end{aligned}$$
(2.16)

then we take

$$\begin{aligned} \lambda _2=\frac{\lambda _1^{2}H}{4}e^{i\pi },\lambda _3=\lambda _1e^{\frac{i\pi }{2}}. \end{aligned}$$

In order to better reflect the characteristics of breather, we will be on both sides of Eq. (2.15) at the same time divided by \(e^{\theta _1}\), the resulting

$$\begin{aligned} \begin{aligned} \frac{f_2}{e^{\theta _1}}&=e^{-\theta _1}+\lambda _3\cos (\Lambda _1 )+\lambda _2 e^{\theta _1} \\&=2\sqrt{\lambda _2}\frac{\sqrt{\lambda _2}e^{\theta _1}+\frac{e^{\theta _1}}{\sqrt{\lambda _2}}}{2}+\lambda _3\cos (\Lambda _1)\\&=2\sqrt{\lambda }_2\cosh (\theta _1+\ln \sqrt{\lambda }_2)+\lambda _3\cos (\Lambda _1). \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} f_2\sim 2\sqrt{\lambda _2}\cosh (\theta _1+\ln \sqrt{\lambda }_2)+\lambda _3\cos (\Lambda _1). \end{aligned}$$
(2.17)

Therefore, we get its breather solution by substituting Eq. (2.17) into (1.5), i.e.,

$$\begin{aligned} u_2=2i\ln \left( \frac{f^*}{f} \right) =2i\ln \left( \frac{(2\sqrt{\lambda _2}\cosh ({\theta _1+\ln {\sqrt{\lambda _2}}})+\lambda _3\cos {\Lambda _1})^*}{2\sqrt{\lambda _2}\cosh {\theta _1+\ln {\sqrt{\lambda _2}}}+\lambda _3\cos {\Lambda _1}}\right) .\nonumber \\ \end{aligned}$$
(2.18)

If \(f_2\) is converted to Eq. (2.17), It can be seen that the breather solution \(u_2\) is localized and periodic, where the hyperbolic function \((\cosh ,\sinh )\) determines its localization and the hyperbolic function \((\cos ,\sin )\) determines its periodicity. Therefore, the breather structure can be considered as a family of solitary wave and periodic wave components. In order to better understand the wave state of the breather, we need to analyze the characteristic lines of the solitary wave and the periodic wave. According to the derivation process, we get two characteristic lines \(\beta _1 (\theta _1+\ln \sqrt{\lambda _2}=0)\) and \(\beta _2(\Lambda _1=0)\) of the breather. Notice that the solitary wave component is traveling at \(\frac{\sqrt{\rho } \cos \frac{\alpha _1}{2}}{a_1}\) velocity on the x-axis, and \(\frac{\sqrt{\rho }\cos \frac{\alpha _1}{2}}{p_1}\) on the y-axis. The propagation velocity of the periodic wave in the x-axis is \(\frac{\sqrt{\rho }\cos \frac{\alpha _1}{2}}{b_1}\), and the propagation velocity in the y-axis is \(\frac{\sqrt{\rho }\cos \frac{\alpha _1}{2}}{q_1}\).

Figure 3 is the three-dimensional diagram of breather at \(t=0\), the contour diagram and the characteristic diagram at \(t=0,1\).

Fig. 3
figure 3

a Spatial structure of the breather solution at \(t = 0\). b The contour figure of a. L1 and L2 represent the characteristic lines. c The characteristic lines of a in the (x, y)-plane at \(t = 0\) and \(t = 1\). Parameters \(a_1=0.1,b_1=2,p_1=1,q_1=1,\lambda _1=2,\delta _1=0,\eta _1=0\). \(L1=0.1x + y + 0.5230469914t - 1.723950496\), \(L2=2x + y + 2.294248931t.\)

Full size image

From Fig. 3, we can see that the angle between the two characteristic lines does not change with time. So we cannot help but ask under what conditions are the two feature lines parallel? What happens to its wave state in this case? This is what we are going to study next in the equation breather state transition problem.

2.3 State Transition of Breather in (2+1)-Dimensional Sine-Gordon Equation

Through the previous analysis, we know that the two characteristic lines of the breather are:

$$\begin{aligned}&\beta _1:a_1 x+p_1 y+\sqrt{\rho }\cos \frac{\alpha _1}{2}t+\delta _1+ \ln \sqrt{\lambda _2}=0, \end{aligned}$$
(2.19)
$$\begin{aligned}&\beta _2:b_1 x+q_1 y+\sqrt{\rho }\cos \frac{\alpha _1}{2}t+\eta _1=0. \end{aligned}$$
(2.20)

Then the condition that the two characteristic lines are parallel is:

$$\begin{aligned} \left| \begin{array}{cc} a_1 &{} \quad p_1 \\ b_1 &{}\quad q_1 \\ \end{array} \right| =0. \end{aligned}$$

Then we get a relation: \(a_1q_1-b_1p_1=0\), further we can know

$$\begin{aligned} \frac{b_1}{a_1}=\frac{q_1}{p_1} =l, \end{aligned}$$
(2.21)

where l is a constant, then we can analyze how the breather changes under the condition of parallel characteristic lines according to this relation, that is, how its wave state changes.

From (2.21), we can get \(b_1=la_1,q_1=lp_1\). Then we obtain the breather solutions in the new form,

$$\begin{aligned} f_2\sim 2\sqrt{\lambda _2}\cosh (\theta _1+\ln {\sqrt{\lambda _2}})+\lambda _3\cos (\Lambda _1), \end{aligned}$$
(2.22)

where

$$\begin{aligned} \theta _1= & {} a_1x+p_1y+\sqrt{\rho }\cos \frac{\alpha _1}{2}t+\delta _1, \nonumber \\ \Lambda _1= & {} la_1 x+lp_1y+\sqrt{\rho }\sin \frac{\alpha _1}{2}t+\eta _1, \nonumber \\ H= & {} e^{A_{12}}=\frac{(k_1-k_2 )^2+(l_1-l_2 )^2-(w_1-w_2 )^2}{(k_1+k_2 )^2+(l_1+l_2 )^2-(w_1+w_2 )^2}\nonumber \\= & {} \frac{-4b_1^2-4q_1^2-((a_1+ib_1 )^2+(p_1+iq_1 )^2-(a_1-ib_1 )^2-(p_1-iq_1)^2)^2}{4b_1^2+4q_1^2-((a_1+ib_1 )^2+(p_1+iq_1 )^2-2+(a_1-ib_1 )^2+(p_1-iq_1 )^2)^2}\nonumber \\= & {} \frac{-4(la_1)^2-4(lp_1)^2-((a_1+ila_1 )^2+(p_1+ilq_1 )^2-(a_1-ila_1 )^2-(p_1-ilp_1 )^2)^2}{4(la_1)^2+4(lp_1)^2-((a_1+ila_1 )^2+(p_1+ilp_1 )^2-2+(a_1-ila_1 )^2+(p_1-ilp_1 )^2)^2},\nonumber \\ \lambda _2= & {} \frac{\lambda _1^2H}{4}e^{i\pi },\lambda _3=\lambda _1e^{\frac{i\pi }{2}}. \end{aligned}$$
(2.23)

By substituting in (1.5), we get

$$\begin{aligned} \widetilde{u}_2=2i \ln \frac{f_2^*}{f_2} =2i\ln \left( \frac{(2\sqrt{\lambda _2}\cosh (\theta _1+\ln {\sqrt{\lambda _2}})+\lambda _3\cos (\Lambda _1))^*}{2\sqrt{\lambda _2}\cosh (\theta _1+\ln {\sqrt{\lambda _2}})+\lambda _3\cos (\Lambda _1)}\right) .\nonumber \\ \end{aligned}$$
(2.24)

From the perspective of form alone, Eq. (2.24) and (2.18) have no difference, but they are different in essence. The solitary wave and periodic wave of Eq. (2.24) solution are superimposed in the same direction, and the characteristic direction is the same, that is to say

$$\begin{aligned} \theta _2=\kappa _1 \Lambda _2+\kappa _2. \end{aligned}$$
(2.25)

So we use the characteristic line expression to define the characteristic direction angle,

$$\begin{aligned} \varphi =\arctan \left( \frac{p_1}{a_1}\right) , \end{aligned}$$

where \(\varphi \) is the positive angle between the characteristic line and the y-axis, which needs to be distinguished from the general definition.

Since f is a complex function, so \(\frac{f_2^*}{f}\) can be written in exponential form, then \(\ln (\frac{f_2^*}{f})\) can be converted, then we have to consider the conditions required in the function f, according to Eq. (2.22) we can know that \(\lambda _2\ne 0\), then \(H\ne 0\). According to equation (2.21), the breather can be converted into other waves under the condition that the characteristic lines are parallel. Then we get three-dimensional maps of the other nonlinear waves by using mathematical software.

Fig. 4
figure 4

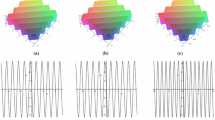
Spatial structure of the transformed nonlinear wave solution at \(t = 0\). a Quasi-anti-dark soliton. Parameters \(l=\frac{1}{3},a_1=3,b_1=1,p_1=3,q_1=1\). b M-type soliton. Parameters \(l=1,a_1=1,b_1=1,p_1=1,q_1=1\). c Oscillating M-type soliton. Parameters \(l=2,a_1=1,b_1=2,p_1=1,q_1=2\) d Multi-peak soliton. \(l=5,a_1=1,b_1=5,p_1=1,q_1=5\). e Quasi-sine-wave. Parameters \(l=1000,a_1=0.001,b_1=1,p_1=0.001,q_1=1\). f Quasi-periodic anti-dark soliton. Parameters \(l=3000,a_1=0.001,b_1=3,p_1=0.001,q_1=3, l=\frac{b_1}{a_1}\). Other parameters \(\lambda _1=2,\delta _1=0,\eta _1=0\)

Full size image

Figure 4 is based on the change of wave-number ratio l. In Fig. 4, it can be found that when \(l=\frac{1}{3}\), the breather transforms into a quasi-anti-dark soliton with only one extreme line and is symmetric about the characteristic direction. When \(l=1\), the breather transforms into an M-type soliton with three extreme lines, one crest and two troughs. When \(l=2\), the breather again becomes an oscillating M-type soliton. When \(l=5\), the breather is transformed into multi-peak soliton, \(l=1000\), is transformed into quasi-sine wave, and \(l=3000\), is transformed into quasi-periodic anti-dark soliton. In this case, there is almost no localization in other directions, and the localization of waves is almost only shown in the characteristic direction. It can be seen that with the increase of the parameter l, the transformation of the breather into other waves follows the following rules: quasi-anti-dark soliton \(\rightarrow \) M-type soliton \(\rightarrow \) oscillating M-type soliton \(\rightarrow \) multi-peak soliton \(\rightarrow \) quasi-sine wave \(\rightarrow \) quasi-periodic anti-dark soliton.

From Fig. 4, we find that parameter condition \(a_1>b_1\) represents waves with strongly solitary states and weakly periodic states, while \(a_1<b_1\) represents waves with weakly solitary states and strongly periodic states. So when \(a_1\) increase, nonlinear wave solitons sexual enhancement, \(b_1\) increases, the nonlinear wave periodic enhancement. We can verify this conclusion with images.

Since the above results are obtained by fixing the time \(t=0\), what effect does the time change have on the transformed waves? Next, we continue to study the effect of time change on the transformed waves.

We can get from the previous work that the characteristic line of the transformed waves are:

$$\begin{aligned}&\beta _3: a_1 x+p_1 y+\sqrt{\rho }\cos \frac{\alpha _1}{2}t+\delta _1+ \ln \sqrt{\lambda _2}=0, \end{aligned}$$
(2.26)
$$\begin{aligned}&\beta _4: la_1 x+lp_1 y+\sqrt{\rho }\cos \frac{\alpha _1}{2}t+\eta _1=0. \end{aligned}$$
(2.27)

The direction of the two characteristic lines is the same, but the velocity is different. For its solitary wave component, its velocity on the x-axis and y-axis are respectively:

$$\begin{aligned} V_{1,x}&=\frac{\sqrt{\rho } \cos \frac{\alpha _1}{2}}{a_1},\\ V_{1,y}&=\frac{\sqrt{\rho } \cos \frac{\alpha _1}{2}}{p_1}. \end{aligned}$$

For the periodic wave component, its velocity on the x-axis and y-axis are:

$$\begin{aligned} V_{2,x}&=\frac{\sqrt{\rho } \cos \frac{\alpha _1}{2}}{la_1},\\ V_{2,y}&=\frac{\sqrt{\rho } \cos \frac{\alpha _1}{2}}{lp_1}. \end{aligned}$$

So the two characteristic line with change with the change of time, set the distance of two characteristic line is \(d_1\), we have

$$\begin{aligned} d_1=\frac{|(\frac{\sqrt{\rho } \sin \frac{\alpha _1}{2}}{l}-\sqrt{\rho }\cos \frac{\alpha _1}{2})t+\frac{\eta _1}{l}-\delta _1-\ln \sqrt{\lambda _2}|}{\sqrt{a_1^2+p_1^2}}. \end{aligned}$$

It can be seen that with the change of time, the distance between the two characteristic lines also changes, and the shape of the transformed waves also changes.

The following is an analysis of the different transformed waves. The first is the quasi-anti-dark soliton at different times, whose three-dimensional maps are drawn by Maple software.

Fig. 5
figure 5

Structure of the quasi-anti-dark soliton as t changes. a \(t=-1\). b \(t=0\). c \(t=1\). Parameters \(l=\frac{1}{3},a_1=3,b_1=1,p_1=3,q_1=1,\lambda _1=2,\delta _1=0,\eta _1=0\)

Full size image

As shown in Fig. 5, the time change does not have much effect on quasi-anti-dark soliton.

Next is a three-dimensional diagram of M-type soliton at different times.

Fig. 6
figure 6

Structure of M-type soliton as t changes. a \(t=-1\). b \(t=0\). c \(t=1\). Parameters \(l=1,a_1=1,b_1=1,p_1=1,q_1=1,\lambda _1=2,\delta _1=0,\eta _1=0\)

Full size image

It is found from the Fig. 6 that time change has a great influence on M-type soliton.

3 Breather Transition and Its Mechanism of the (2+1)-Dimensional Modified Boussinesq Equation

This chapter we continue to study the N-soiton solution of the (2+1)-dimensional modified Boussinesq equation by using the Hirota bilinear method, and construct the breather solution by wave number pluralization, and study the state transition of the equation.

The (2+1)-dimensional modified Boussinesq equation to be studied in this chapter is given in the previous section.

3.1 Soliton Solution of the (2+1)-Dimensional Modified Boussinesq Equation

Based on the Hirota bilinear method, we get the N-soliton solution of Eq. (1.5):

$$\begin{aligned} u_N=2(\ln f_{N})_{xx}, f_N=\sum _{\mu =0,1}\exp \left( \sum _{j=1}^{N}\mu _{j}\xi _{j}+\sum _{1\le j<l}^{N}\mu _j \mu _l A_{jl}\right) , \end{aligned}$$
(3.1)

where

$$\begin{aligned} e^{A_{jl}}&=-\frac{(k_j w_j-k_l w_l)^2-(k_j-k_l)^2- (k_j p_j-k_l p_l)^2-(k_j-k_l)^4}{(k_j w_j+k_l w_l)^2- (k_j+k_l)^2- (k_j p_j+k_l p_l)^2-(k_j+k_l)^4},\\ \xi _i&=k_i(x+p_i y+w_it)+\gamma _i,w_i^2=1+k_i^2+p_i^2,i=1,2. \end{aligned}$$

3.1.1 Single Soliton Solution

When \(N=1\), we can get the single soliton solution of this equation:

$$\begin{aligned} u_1=2(\ln f_1 )_{xx}=2(\ln (1+e^{\xi _1}))_{xx}=\frac{k_1^2}{2}\left( {{\,\textrm{sech}\,}}\frac{\xi _1}{2}\right) ^2. \end{aligned}$$
(3.2)

By using mathematical software, we can get the three-dimensional diagram of its soliton solution at time \(t=-2,0,2\) as shown in Fig. 7.

Fig. 7
figure 7

Structure of Single Soliton Solutions as t changes. a \(t=-2\). b \(t=0\). c \(t=2\). Parameters \(k_1=1,p_1=1,w_1=\sqrt{1+k_1^2+p_1^2} =\sqrt{3},\gamma _1=0\)

Full size image

3.1.2 Double Soliton Solution

\(f_2\) is represented as follows:

$$\begin{aligned} f_2=1+e^{\xi _1}+e^{\xi _2}+e^{\xi _1+\xi _2+A_{12}}, \end{aligned}$$
(3.3)

where \(e^{A_{12}}=-\frac{(k_1 w_1-k_2 w_2)^2- (k_1-k_2)^2- (k_1 p_1-k_2 p_2)^2-(k_1-k_2)^4}{(k_1 w_1+k_2 w_2)^2- (k_1+k_2)^2- (k_1 p_1+k_2 p_2)^2-(k_1+k_2)^4}.\) So, we get the double soliton solution of the equation

$$\begin{aligned} u_2=2(\ln f_2)_{xx}=2(\ln (1+e^{\xi _1} +e^{\xi _2}+e^{\xi _1+\xi _2+A_{12}}))_{xx}. \end{aligned}$$
(3.4)

We use mathematical software again to draw a three-dimensional diagram of the double soliton solution at time \(t=-1,0,1\). As shown in Fig. 8.

Fig. 8
figure 8

Structure of Double Soliton Solutions as t changes. a \(t=-1\). b \(t=0\). c \(t=1\). Parameters \(k_1=6,p_1=1,k_2=4,p_2=4,\gamma _1=\gamma _2=0,w_1=\sqrt{k_1^2+p+1}=\sqrt{38},w_2=\sqrt{k_2^2+p_2^2+1}=\sqrt{33}\)

Full size image

3.2 The Breather Solution and Characteristic Line Analysis of the (2+1)-Dimensional Modified Boussinesq Equation

We use the double soliton solution in Sect. 2 of this chapter to pluralize the wave number of Eq. (3.4). Let

$$\begin{aligned} k_1=k_2^{*}=a_1+ib_1,p_1=p_2^{*}=c_1+id_1,\gamma _1=\gamma _2^{*}=\ln \frac{\lambda _1}{2}+\delta _1+i\eta _1, \end{aligned}$$
(3.5)

where \(a_1,b_1,c_1,d_1,\lambda _1,\delta _1,\eta _1\) are real numbers, we plug in (3.3),

$$\begin{aligned} \begin{aligned} f_2&=1+e^{\theta _1+i\Lambda _1+\ln \frac{\lambda _1}{2}}+e^{\theta _1-i\Lambda _1+\ln \frac{\lambda _1}{2}}+e^{2\theta _1+2\ln \frac{\lambda _1}{2}+A_{12}}\\&=1+\lambda _1 e^{\theta _1}\cos (\Lambda _1)+\frac{\lambda _1^2H}{4}e^{2\theta _1}, \end{aligned} \end{aligned}$$
(3.6)

where

$$\begin{aligned} \begin{aligned} \theta _1&=a_1x+(a_1 c_1-b_1 d_1)y+\sqrt{\rho }(a_1\cos \frac{\alpha _1}{2}-b_1\sin \frac{\alpha _1}{2})t+\delta _1, \\ \Lambda _1&=b_1 x+(a_1 d_1+b_1 c_1)y+\sqrt{\rho }(a_1\sin \frac{\alpha _1}{2}+b_1\cos \frac{\alpha _1}{2})t+\eta _1, \\ H&=e^{A_{12}}=-\frac{(k_1 w_1-k_2 w_2)^2- (k_1-k_2)^2- (k_1 p_1-k_2 p_2)^2-(k_1-k_2)^4}{(k_1 w_1+k_2 w_2)^2- (k_1+k_2)^2-(k_1 p_1+k_2 p_2)^2-(k_1+k_2)^4}, \\ \rho \cos {\alpha _1}&=a_1^{2}+c_1^{2}-b_1^{2}-d_1^{2}+1,\\ \rho \sin {\alpha _1}&=2a_1b_1+2c_1d_1. \end{aligned}\nonumber \\ \end{aligned}$$
(3.7)

Let’s set

$$\begin{aligned} \lambda _2=\frac{\lambda _1^2H}{4}. \end{aligned}$$

In order to better reflect the characteristics of the breather, we will be on both sides of Eq. (3.6) at the same time divided by \(e^{\theta _1}\), the resulting is

$$\begin{aligned} \begin{aligned} \frac{f_2}{e^{\theta _1}}&=e^{-\theta _1} +\lambda _1\cos (\Lambda _1 )+\lambda _2 e^{\theta _1} \\&=2\sqrt{\lambda _2}\frac{\sqrt{\lambda _2}e^{\theta _1}+\frac{e^{\theta _1}}{\sqrt{\lambda _2}}}{2}+\lambda _1\cos (\Lambda _1)\\&=2\sqrt{\lambda }_2\cosh (\theta _1+\ln \sqrt{\lambda }_2)+\lambda _1\cos (\Lambda _1), \end{aligned} \end{aligned}$$

thus,

$$\begin{aligned} f_2\sim 2\sqrt{\lambda }_2\cosh (\theta _1+\ln \sqrt{\lambda }_2)+\lambda _1\cos ( \Lambda _1). \end{aligned}$$
(3.8)

Then we get its breather solution by substituting the equation (3.8) into (1.6).

$$\begin{aligned} \begin{aligned} u_2&=2(\ln f_2)_{xx} =2[\ln 2\sqrt{\lambda }_2\cosh (\theta _1+\ln \sqrt{\lambda }_2)+\lambda _1\cos \Lambda _1]_{xx} \\&=\frac{8a_1^2 \lambda _2-2b_1^2 \lambda _1^2+4(a_1^2-b_1^2 ) \lambda _1 \sqrt{\lambda _2}\cosh (\theta _1+\ln \sqrt{\lambda _2})\cos (\Lambda _1 )}{2\sqrt{\lambda _2} \cosh (\theta _1+\ln \sqrt{\lambda _2})+\lambda _1 \cos (\Lambda _1))^2}\\&\quad +\frac{8a_1 b_1 \lambda _1 \sqrt{\lambda _2} \sinh (\theta _1+\ln \sqrt{\lambda _2})\sin {\Lambda _1}}{(2\sqrt{\lambda _2}\cosh (\theta _1+\ln \sqrt{\lambda _2 })+\lambda _1 \cos (\Lambda _1))^{2}}. \end{aligned} \end{aligned}$$
(3.9)

As a result of \(f_2>0\), and \(2\cosh (\theta _1+\ln \sqrt{\lambda _2})+\lambda _1\cos (\Lambda _1))\) has the minimum value of \(2\sqrt{\lambda _2}-|\lambda _1|\), so when \(\lambda _2>\frac{\lambda _1^2}{4}\), i.e.\(H>1\), there is a non-singular solution to Eq. (3.9).

If \(f_2\) is converted to Eq. (3.8), it can be seen that the breather solution \(u_2\) is local and periodic, in which the hyperbolic function \((\cosh ,\sinh )\) determines its locality, and the hyperbolic function \((\cos ,\sin )\) determines its periodicity. This kind of breather is a combination of the two components of solitary wave and periodic wave. In order to better understand the wave state of the breather, we need to analyze the characteristic lines of the solitary wave component and the periodic wave component. According to the derivation process, we get two characteristic lines \(\beta _1 (\theta _1+\ln \sqrt{\lambda _2}=0)\) and \(\beta _2(\Lambda _1=0)\) of the breather.

We can see from the characteristic lines that the propagation velocity of the solitary wave in the x-axis is \(\frac{\sqrt{\rho }(a_1\cos \frac{\alpha _1}{2}-b_1\sin \frac{\alpha _1}{2})}{a_1}\) and in the y-axis is \(\frac{\sqrt{\rho }(a_1\cos \frac{\alpha _1}{2}-b_1\sin \frac{\alpha _1}{2})}{a_1 c_1-b_1 d_1}\). the periodic wave component is traveling at \(\frac{a_1\sin \frac{\alpha _1}{2}+b_1\cos \frac{\alpha _1}{2}}{b_1}\) velocity on the x-axis, and \(\frac{a_1\sin \frac{\alpha _1}{2}+b_1\cos \frac{\alpha _1}{2}}{a_1 d_1+b_1 c_1}\) on the y-axis. Observing the expression of the characteristic lines, we can see that the angle (or parallel) between the two characteristic lines does not change with time, from a physical point of view, which shows that the shape and amplitude of the breather do not change with time, only the phase changes with time.

Figure 9 is the three-dimensional diagram of breather at \(t=0\),the contour diagram and the characteristic diagram at \(t=0,1\).

Fig. 9
figure 9

a Spatial structure of the breather solution at \(t = 0\). b The contour figure of a. L1 and L2 represent the characteristic lines. c The characteristic lines of a in the (x, y)-plane at \(t = 0\) and \(t = 1\). Parameters \(a_1=0.1,b_1=1,c_1=1,d_1=1,\lambda _1=2,\delta _1=\eta _1=0\). \(L1=0.1x - 0.9y - 0.9311534897t + 1.931492390\), \(L2=x + 1.1y + 1.164034421t\)

Full size image

As shown in Fig. 9, under the above parameters, two characteristic lines intersect and the angle does not change with time, then we will also have a question, under what conditions will two characteristic lines be parallel? What happens to the breather in this case? If it changes, will it change in the same way as in the previous chapter? This is the state transition problem of this nonlinear wave that we want to study.

3.3 State Transition of Breather for (2+1)-Dimensional Modified Boussinesq Equation

Through the previous analysis, we know that the two characteristic lines of breather are:

$$\begin{aligned}&\beta _1: a_1 x+(a_1 c_1-b_1 d_1)y+\sqrt{\rho }\left( a_1\cos \frac{\alpha _1}{2}-b_1\sin \frac{\alpha _1}{2}\right) t+\delta _1+\ln \sqrt{\lambda }_2=0, \end{aligned}$$
(3.10)
$$\begin{aligned}&\beta _2:b_1 x+(a_1 d_1+b_1 c_1)y+\sqrt{\rho }\left( a_1\cos \frac{\alpha _1}{2}-b_1\sin \frac{\alpha _1}{2}\right) t+\eta _1=0. \end{aligned}$$
(3.11)

Then the condition that the two characteristic lines are parallel is that the following determinant is zero.

$$\begin{aligned} \left| \begin{array}{cc} a_1 &{} a_1c_1-b_1d_1 \\ b_1 &{} a_1d_1+b_1c_1 \\ \end{array} \right| =0. \end{aligned}$$

Then we get a relation: \((a_1^2-b_1^2)d_1=0\), so when \(a_1^2-b_1^2\ne 0\), \(d_1=0\), so at this time

$$\begin{aligned} H=\frac{\sqrt{-b_1^2-2ia_1 b_1+a_1^2+c_1^2+1}\cdot \sqrt{-b_1^2+2ia_1 b_1+a_1^2+c_1^2+1}-a_1^2+7b_1^2-c_1^2-1}{\sqrt{-b_1^2-2ia_1 b_1+a_1^2+c_1^2+1}\cdot \sqrt{-b_1^2+2ia_1 b_1+a_1^2+c_1^2+1}-7a_1^2+b_1^2-c_1^2-1}.\nonumber \\ \end{aligned}$$
(3.12)

When \(a_1=0.5,b_1=2,c_1=1\),\(H=9.77\), this satisfies nonsingular conditions, and in this case the characteristic lines are parallel. All the transformed waves in the following paper satisfy the non-singular condition.

Next we’ll let \(d_1=0\) in breather solutions in the equation of a new form:

$$\begin{aligned} f_2\sim 2\sqrt{\lambda }_2\cosh (\theta _1+\ln \sqrt{\lambda }_2)+\lambda _1\cos (\Lambda _2), \end{aligned}$$
(3.13)

where

$$\begin{aligned}{} & {} \theta _2 =a_1 x+a_1 c_1 y+\sqrt{\rho }(a_1\cos \frac{\alpha _1}{2}-b_1\sin \frac{\alpha _1}{2})t+\delta _1, \nonumber \\{} & {} \Lambda _2 =b_1 x+b_1 c_1 y+\sqrt{\rho }(a_1\sin \frac{\alpha _1}{2}+b_1\cos \frac{\alpha _1}{2})t+\eta _1,\nonumber \\{} & {} H=\frac{\sqrt{-b_1^2-2ia_1 b_1+a_1^2+c_1^2+1}\cdot \sqrt{-b_1^2+2ia_1 b_1+a_1^2+c_1^2+1}-a_1^2+7b_1^2-c_1^2-1}{\sqrt{-b_1^2-2ia_1 b_1+a_1^2+c_1^2+1}\cdot \sqrt{-b_1^2+2ia_1 b_1+a_1^2+c_1^2+1}-7a_1^2+b_1^2-c_1^2-1}, \nonumber \\{} & {} \lambda _2 =\frac{\lambda _1^2H}{4}. \end{aligned}$$
(3.14)

By substituting in (3.4), we get

$$\begin{aligned} \widetilde{u}_2=2(\ln f_2)_{xx}= & {} 2[\ln (2\sqrt{\lambda }_2\cosh (\theta _1+\ln \sqrt{\lambda }_2))+\lambda _1\cos \Lambda _1]_{xx} \nonumber \\= & {} \frac{8a_1^2 \lambda _2-2b_1^2 \lambda _1^2+4(a_1^2-b_1^2 ) \lambda _1 \sqrt{\lambda }_2\cosh (\theta _2+\ln \sqrt{\lambda }_2)\cos (\Lambda _2)}{(2\sqrt{\lambda }_2\cosh (\theta _2+\ln \lambda _2 )+\lambda _1\cos (\Lambda _2))^2} \nonumber \\{} & {} +\frac{8a_1 b_1 \lambda _1 \sqrt{\lambda }_2 \sinh (\theta _2+\ln \sqrt{\lambda }_2 )\sin (\Lambda _2 )}{(2\sqrt{\lambda }_2\cosh (\theta _2+\ln \sqrt{\lambda }_2 )+\lambda _1\cos (\Lambda _2 ))^2}. \end{aligned}$$
(3.15)

From the perspective of form alone, Eqs. (3.15) and (3.9) have no difference, but they are different in essence. The solitary wave and periodic wave of Eq. (3.15) solution are superimposed in the same direction, and the characteristic direction is the same, that is to say,

$$\begin{aligned} \theta _2=\kappa _1 \Lambda _2+\kappa _2. \end{aligned}$$
(3.16)

So we use the characteristic line expression to define the characteristic direction angle,

$$\begin{aligned} \varphi =\arctan c_1, \end{aligned}$$

where \(\varphi \) is the positive angle between the characteristic line and the y-axis, which needs to be distinguished from the general definition.

In other words, when we fixed \(c_1\), under the condition of characteristic line parallel of the characteristics of nonlinear wave direction does not change, and when \(H>1\), the equation has a non-singular solution, then the breather can be converted into various other types of waves, such as quasi-antidark solitons, M-type solitons, oscillating M-type solitons, multimodal solitons, quasi-sine waves, and quasi-periodic waves.

Figure 10 is a 3D diagram of the conversion of the breather into other types of waves under different conditions at \(t=0\) time.

Fig. 10
figure 10

Spatial structure of the transformed nonlinear wave solution at \(t = 0\). a Quasi-anti-dark soliton. Parameters \(l=2,a_1=1,b_1=2\) b Oscillating M-type soliton. Parameters \(l=2,a_1=0.5,b_1=2\) c Multi-peak soliton. \(l=10,a_1=0.5,b_1=5\) d Quasi-sine wave. Parameters \(l=124,a_1=0.01,b_1=1.24\) e Quasi-periodic anti-dark soliton. Parameters \(l=300,a_1=0.01,b_1=3. l=\frac{b_1}{a_1}\). Other parameters \(c_1=1,\lambda _1=2,\delta _1=0,\eta _1=0\)

Full size image

Same as the analysis in the previous chapter, we can find that the transformed waves also change with the change of the wave-number ratio \(l=\frac{b_1}{a_1}\). When the wave-number ratio increases, the transformed waves change as follows: quasi-anti-dark soliton \(\rightarrow \) oscillating M-type soliton \(\rightarrow \) multi-peak soliton \(\rightarrow \) quasi-sine wave \(\rightarrow \) quasi-periodic anti-dark soliton.

At the same time we find in the process \(a_1\) is always smaller than \(b_1\), and when the \(a_1\) is far less than \(b_1\), periodicity of the transformed waves is stronger.

Since the above results are obtained by fixing the time \(t=0\), what effect does the time change have on the transformed waves? Next, we continue to study the effect of time change on transformed waves.

We know from the previous work that the characteristic line of the conversion wave is:

$$\begin{aligned} \beta _3:&a_1 x+a_1 c_1 y+\sqrt{\rho }\left( a_1\cos \frac{\alpha _1}{2}-b_1\sin \frac{\alpha _1}{2}\right) t+\delta _1+ \ln \sqrt{\lambda _2}=0, \end{aligned}$$
(3.17)
$$\begin{aligned} \beta _4:&b_1 x+b_1 c_1 y+\sqrt{\rho }\left( a_1\sin \frac{\alpha _1}{2}+b_1\cos \frac{\alpha _1}{2}\right) t+\eta _1=0. \end{aligned}$$
(3.18)

The direction of the two characteristic lines is the same, but the propagation velocity is different. For its solitary wave component, its propagation velocity on the x-axis and y-axis are respectively:

$$\begin{aligned}&V_{1,x}=\frac{\sqrt{\rho }(a_1\cos \frac{\alpha _1}{2}-b_1\sin \frac{\alpha _1}{2})}{a_1},\\&V_{1,y}=\frac{\sqrt{\rho }(a_1\cos \frac{\alpha _1}{2}-b_1\sin \frac{\alpha _1}{2})}{a_1 c_1}. \end{aligned}$$

For the periodic wave component, its propagation velocity on the x-axis and y-axis are:

$$\begin{aligned}&V_{2,x}=\frac{\sqrt{\rho }(a_1\sin \frac{\alpha _1}{2}+b_1\cos \frac{\alpha _1}{2})}{b_1},\\&V_{2,y}=\frac{\sqrt{\rho }(a_1\sin \frac{\alpha _1}{2}+b_1\cos \frac{\alpha _1}{2})}{b_1 c_1}. \end{aligned}$$

So the two characteristic line with change with the change of time, set the distance of two characteristic line is \(d_2\), then

$$\begin{aligned} d_2=\frac{|\frac{a_1^2+b_1^2}{a_1 b_1}\sqrt{\rho }\sin \frac{\alpha _1}{2}t+\frac{\eta _1}{b_1} -\frac{\delta _1}{a_1}-\frac{\ln \sqrt{\lambda _2 }}{a_1}|}{\sqrt{1+c_1^2}}. \end{aligned}$$

It can be seen that with the change of time, the distance between the two characteristic lines also changes, and the shape of the transformed waves also changes.

The following is an analysis of the different transformed waves. Since we have analyzed quasi-antidark solitons in the previous chapter, we would hazard a guess that time change has no effect on it, and we can verify this conclusion by plotting. So next we study the oscillating M-type solitons, the following is the change of the transformed wave at different times.

The following Fig. 11 shows the oscillating M-type soliton at \(t=-2,0,4\).

Fig. 11
figure 11

Structure of the oscillating M-type soliton as t changes. a \(t=-2\). b \(t=0\). c \(t=4\). Parameters \(l=4,a_1=0.5,b_1=2,c_1=1,\lambda _1=2,\delta _1=0,\eta _1=0\)

Full size image

Through observation, we can find that the change of time has a certain effect on the transformed waves such as oscillating M-type soliton.

4 Conclusions

In this paper, bilinear forms of two (2+1)-dimensional equations are studied and their breather solutions are obtained, and we derive the state transition problem by using their breather solutions. The results are as follows:

  1. 1.

    We get the soliton solution and breather solution of the (2+1)-dimensional Sine-Goedon equation via Hirota bilinear method, and derive the conversion conditions of the breather into other waves. We also analyze the influence of wave number ratio on solitary wave and periodic wave, and learn obout the influence of time change on transformed waves.

  2. 2.

    Similarly, we use the same method to obtain N-soliton solution of the (2+1)-dimensional modified Boussinesq equation, and then obtain its breather solution by wave number pluralization. And when the two characteristic lines are parallel, that is to say, \(H>1\), the breather can be converted into other types of nonlinear waves. In addition, we find that the difference in wave-number ratio also affects the solitary and periodic waves.

  3. 3.

    Through the analysis of the above two equations, we find that both breathers and transformed waves are formed by the nonlinear superposition of solitary waves and periodic waves, the difference is the characteristic direction of the solitary waves and periodic waves, and the conversion conditions of the breather into other waves of the two equations are different, but the difference in wave number ratio has an impact on both solitary waves and periodic waves. And the change of time also has an effect on some transformed waves.

Through the analysis in this paper, we can know that the breathers and other nonlinear waves are formed by the nonlinear superposition of solitary waves and periodic waves. In addition, we try to investigate the dynamics process of nonlinear transformed waves over time. And from the perspective of the change of the geometric structure of the characteristic lines, the principle behind it is analyzed. In the future work, we will focus on studying the conversion mechanisms of higher-dimensional equations, including not only the problem of converting the states of the equation breather, but also the conversion mechanism of the equation lump wave, and so on. This work will be beneficial for the study of nonlinear physics, fluid dynamics, solitons, and other related fields.

5 Future Recommendations

The (2+1)-dimensional sine-Gordon equation has significant applications in studying the motion of charged particles in nonlinear fields, field coupling in quantum field theory, and other related problems. The (2+1)-dimensional modified Boussinesq equation is a widely applicable tool for describing the propagation of nonlinear waves in various fields of study, including water wave theory. They are particularly useful for describing phenomena such as ocean waves, optical waves, and fluctuations in solid materials. Therefore, in the future we can explore more analytical and numerical solutions of these two equations to deepen our understanding of them. Further mechanisms of nonlinear wave transitions can also be investigated and attempts can be made to apply these mechanisms to other nonlinear dynamical systems to explore their generalisability and application. We can also extend the research results to other fields, such as biomedical engineering and seismology, to explore the significance and potential applications of breather conversion in different fields.