1 Introduction

Modern cosmological observations indicate the accelerating expansion of our universe [1,2,3]. To check the late-time cosmic acceleration, a number of observations have been made toward its explanation. Although general relativity (GR) is a fairly successful theory and it is worth noticing that this success is valid observationally below the solar system scale and theoretically far away from the Planck scale. We can roughly say that GR has some observational shortcomings at IR and theoretical shortcomings at UV scale. The enormous efforts have been done in recent times to modify gravity [4,5,6] to solve the problem of non-renormalizability [7, 8] in (GR). The theoretical explanations for cosmic acceleration are usually described in two ways: The first approach suggests modification in the energy budget of the cosmos, presenting a dark energy (DE) region that is inspired either by a canonical scalar field, a phantom field, or the combination of both fields in a unified model, and leading toward more complicated developments [9, 10]. The second is focused on the modification of gravitational sector [11,12,13]. One may change it as a whole or partly from one way to another by keeping the physical interpretations in mind, but the number of extra degrees of freedom is definitely an essential feature [14]. So one can also use any of the forms mentioned above in accordance with the gravitational and non-gravitational sector.

The reason of modification in gravitational theories is the generalization of Einstein–Hilbert (EH) action, which is the one that may derive with gravity-curvature interpretation in GR. Some promising modified gravitational theories (MGT) such as Gauss–Bonnet (GB) theory and its extended versions [15,16,17], f(R) theory (R is the Ricci scalar) [18, 19] and its generalizations with minimal/non-minimal interactions among various fields (higher-order curvature correction terms, matter and scalar fields as well as torsion scalar) like f(R, T) [20,21,22,23] and f(R, T, Q) theories [24,25,26,27], scalar-tensor theories and its generalized versions [28, 29] and the famous teleparallel theory of gravity with its modifications [30,31,32,33].

The teleparallel approach to modify gravity is considerably interesting due to second-order partial differential equations, consequently we get rid of higher-order equation problem that exists in other MGT. The f(T) gravity is the most common and the best studied model, where the generalized Lagrangian is presumed to be an arbitrary function of the torsion scalar [34, 35]. In teleparallel gravity, the Weitzenböck connection (WBC) is being used instead of torsion-free Levi-Civita metric connection (LMC) on a Riemann–Cartan space-time. In GR, the gravitational field intensity is verbalized by the torsion-less LMC so that the gravitational field intensity is determined by curvature [36,37,38].

A recent modification in f(T) gravity is known as \( f(T,\mathcal {T}) \) gravity [39,40,41], which is inspired by \(f(R,\mathcal {T})\) theory of gravity [42], where rather combining the Ricci scalar with the trace of EMT, one couples it with the torsion scalar. The dependence of \(\mathcal {T}\) may be introduced by exotic imperfect fluids or quantum effects (conformal anomaly). In \(f(R,\mathcal {T})\) gravity, as a result of coupling between matter and geometry, motion of test particles is non-geodesic and an extra acceleration is always present. In this gravity, cosmic acceleration may result not only due to geometrical contribution to the total cosmic energy density but it also depends on matter contents. Based on \(f(R,\mathcal {T})\) gravity, the resulting \(f(T,\mathcal {T})\) theory is a new modification of gravity theory, since it is different from all the existing torsion or curvature-based constructions. It also yields an interesting cosmological phenomenology as it encompasses a unified description of the expansion history with an initial inflationary phase, a subsequent non-accelerated, matter-dominated expansion and a final late-time accelerating phase [43]. A detailed study of the scalar perturbations at the linear level revealed that the resulting \(f(T,\mathcal {T})\) cosmology can be free of ghosts and instabilities for a wide class of ansatz and model parameters.

In astrophysics, the exact solutions of Einstein field equations (EFEs) provide information about fluid distribution inside stellar objects. Schwarzschild [44] calculated the spherical solution for vacuum taking perfect fluid distribution in the exterior region. Several exact solutions for perfect fluid have been computed by Tolman [45] including cosmological constant, and junction conditions have been investigated. Lemaitre [46] suggested some possible ways for the existence of anisotropic effects inside stellar objects, which may be due to “phase transition, rotational motion, presence of magnetic field or mixture of bi-fluids”, etc. To examine the salient properties of anisotropic distribution of fluid, a large number of feasible solutions were obtained in relativistic gravity theories [47,48,49,50,51,52,53]. To get exact solutions for interior geometry of a star taking anisotropic fluid distribution is a challenge because of the nonlinear term in the evolution equations.

Generally, as a simplest case, perfect fluid (isotropic fluid) is assumed inside the stellar object to study its interior structure and evolution. However, present observation shows that the fluid pressure of the highly compact astrophysical objects becomes anisotropic in nature, which means the pressure can be resolved into two components namely radial pressure and the transverse pressure. So to examine the anisotropy effects a parameter \(\Delta =p_t-p_r\) has been introduced known as the anisotropic factor. The anisotropy may arise for the different cases such as the existence of solid core, in presence of type P superfluid, phase transition, rotation, magnetic field, mixture of two fluids, and existence of external field. Paul and Dep [54] have discovered suitable anisotropic solutions for compact objects. Sah and Deb [55] studied the anisotropic interior solutions of quintessence strange stars in f(T) gravity using MCG model. In f(R, T) theory of gravity, Zubair et al. [56] investigated the spherical solutions admitting conformal killing vector field for both perfect and imperfect fluid distribution. Some researchers worked in \(f(T,\mathcal {T})\) gravity to drive exact solutions of collapsing compact objects [57, 58]. In this context, Saleem et. al [59] found the interior isotropic solutions of compact stars in \(f(T,\mathcal {T})\) theory for KB metric using non-diagonal tetrad under Karmarkar condition. Abbas et al. [60] discussed the solutions of anisotropic strange stars that correspond to quintessence model via an EoS \(p=\alpha \rho ,~0<\alpha \le 1\) (p is pressure and \(\rho \) be the density of fluid).

The electromagnetic field plays an important role in structure formation and equilibrium of collapsing bodies. The electromagnetic forces are the main cause to generate the repulsive effects that counterbalance the attractive gravitational force. Lobo and Arellano [61] constructed various gravastar models with nonlinear electrodynamics and studied their solutions as well as some basic physical characteristics. Using MIT bag model, the effect of electromagnetic fields on anisotropic strange stars was investigated by different authors [62, 63]. Horvat et al. [64] extended the gravastar built by anisotropic inhomogeneous fluid with a particular behavior of radial pressure in the presence of an electrically charged component. They solved Einstein–Maxwell field equations in asymptotically de Sitter interior, where a source of electric field is coupled to the fluid’s energy density. Under charge, they evaluated EoS, the speed of sound and the surface redshift for considered models.

In this paper, our target is to evaluate the exact spherical solutions taking anisotropic fluid distribution with charge in the interior of strange stars within the background of \(f(T,\mathcal {T})\) theory. To this end, we utilize an EoS for MCG model. In Sect. 2, we briefly describe the mathematical development of \(f(T,\mathcal {T})\) theory. In Sect. 3, we formulate the field equations for KB metric taking anisotropic fluid distribution. Further, we solve the equations analytically to derive the exact solutions choosing \(f(T,\mathcal {T})=\alpha _{1}T^{n}(r)+\beta \mathcal {T}(r)+\phi \) (\(\alpha _{1},~\beta \) are arbitrary real constants, \(\phi =2.036\times 10^{-35}\) is the cosmological constant and \(n>1\)) along with MCG model. Section 4 is devoted to analyze the physical characteristics of the obtained results via energy bounds, stability, mass function, compactness and surface redshift. By smooth matching of considered interior metric with exterior Schwarzschild metric, we calculate the unknown constants, which are further constraint for four different strange stars. The results are interpreted graphically. The outcomes are discussed in Sect. 5.

2 Fundamentals of \( f(T,\mathcal {T}) \) theory of gravity

Since torsion-trace gravity is an extended form of f(T) theory, therefore based on the geometry of WBC [65]. The torsion tensor can be given as [65, 66]

$$\begin{aligned} {T^{\eta }}_{\mu \nu }=\Gamma ^{\eta }_{\mu \nu }-\Gamma ^{\eta }_{\nu \mu }=e^{\eta }_{i}\big (\partial _{\mu }e^{i}_{\nu }-\partial _{\nu }e^{i}_{\mu }\big ), \end{aligned}$$
(1)

here Greek letters denote spacetime indices. While Latin indices i, j, k, ... represent the tangent Minkowski spaces. The contorsion tensor is defined as

$$\begin{aligned} {K^{\mu \nu }}_\sigma =-\frac{1}{2}\big ({T^{\nu \mu }}_\sigma -{T_\sigma }^{\mu \nu } -{T_{\sigma }}^{\mu \nu }\big ). \end{aligned}$$
(2)

The components of superpotential tensor, \({S_\sigma }^{\mu \nu }\) are defined as

(3)

The torsion scalar can be derived from the product of torsion and contorsion tensors as follows

$$\begin{aligned} T={S_{\sigma }}^{\mu \nu }{ T^{\sigma }}_{\mu \nu }. \end{aligned}$$
(4)

One can extend f(T) to \(f(T,\mathcal {T})\) gravity by defining the following action [39,40,41]

$$\begin{aligned} S=\frac{1}{2\kappa ^{2}}\int d^4{xe}[f(T,\mathcal {T})+\mathcal {L}_{(Matter)}(\phi _{A})], \end{aligned}$$
(5)

where \(e=det(e^\alpha _{i})=\sqrt{-g},~\kappa ^{2}=\frac{8\pi G}{c^2}=1\) (G is well-known gravitational constant and c is the speed of light), \(\mathcal {L}_{(Matter)}\) is the matter Lagrangian density, and \(f(T,\mathcal {T})\) be any arbitrary function of T and \(\mathcal {T}=\delta ^\nu _\mu \mathcal {T}^\mu _\nu \). By varying the action defined in Eq. (5) with respect to tetrad, we get following set of field equations

$$\begin{aligned}&-\frac{{e^\nu }_i}{4}f+{\omega ^i}_{\eta \nu } {S_i}^{\nu \mu }f_T+ {e^\mu }_i{T^\eta }_{\mu \kappa } {S_\eta }^{\nu \kappa }f_T+ e^{-1}\partial _\mu ({e}{e^\sigma }_i {S_\sigma }^{\mu \nu })f_T+{e^\sigma }_i {S_\sigma }^{\mu \nu }\partial _\mu Tf_{TT} \nonumber \\&\quad -\frac{f_\mathcal {T}}{2}\big ({e^{\eta }}_i \mathcal {T}^{\nu }_{\eta }+ p_{r}{e^{\nu }}_i\big )+{e^{\sigma }}_i {S_{\sigma }}^{\mu \nu }\mathcal {T}f_{T\mathcal {T}}=-4\pi {e^\eta }_i \mathcal {T}^\nu _\eta , \end{aligned}$$
(6)

where \(f_\mathcal {T}=\frac{\partial f}{\partial \mathcal {T}},~f_{T\mathcal {T}}=\frac{\partial ^2 f}{\partial T \partial \mathcal {T}},~f_{T}=\frac{\partial f}{\partial T}\) and \(f_{TT}=\frac{\partial ^{2}f}{\partial T^{2}}\), and spin connection, \(\omega ^i_{\eta \nu }=0\). The EMT for anisotropic fluid can be written as

$$\begin{aligned} T_{\mu \nu }=\big (\rho +p_{t}\big )u_{\mu }u_{\nu }-p_{t}g_{\mu \nu }+\big (p_{r}-p_{t}\big )v_{\mu }v_{\nu }, \end{aligned}$$
(7)

where \(u_{\mu }=e^{\frac{\xi }{2}}\delta ^{0}_{\mu }\) is the four velocity, \(v_{\mu }=e^{\frac{\xi }{2}}\delta ^{1}_{\mu }\) is the radial four vectors, \(\rho \) is the energy density, \(p_{r},~p_{t}\) are the radial and tangential pressure components. The electromagnetic field is described by EMT given under

$$\begin{aligned} E^{\nu }_{\mu }=\frac{1}{4\pi }\bigg (g^{\delta \omega }F_{\mu \delta }F^{\nu }_{\omega }-\frac{1}{4}g^{\nu }_{\mu } F_{\delta \omega }F^{\delta \omega }\bigg ), \end{aligned}$$
(8)

where \(F_{\mu \nu }\) is the Maxwell field tensor, which can be defined as

$$\begin{aligned} F_{\mu \nu }=\phi _{\mu ,\nu }-\phi _{\nu ,\mu }, \end{aligned}$$

and \(\phi _{\mu }\) is the four potential.

3 Exact solutions of the field equations in \(f(T,\mathcal {T})\) gravity

Here, we take KB metric [67] representing the interior geometry of a strange star

$$\begin{aligned} ds^{2}=e^{a(r)}dt^{2}-e^{b(r)}dr^{2}-r^{2}d\theta ^{2}-r^{2}\sin ^{2}\theta d\phi ^{2}, \end{aligned}$$
(9)

where a(r) and b(r) are the metric potentials. We consider the non-diagonal tetrad given as follows [59]

$$\begin{aligned} e^i_\mu =\left( \begin{array}{cccc} \text {e}^{\frac{a(r)}{2}} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \text {e}^{\frac{b(r)}{2}}\sin \theta \cos \phi &{}\quad \text {e}^{\frac{b(r)}{2}}\sin \theta \sin \phi &{}\quad \text {e}^{\frac{b(r)}{2}}\cos \theta \\ 0 &{}\quad -r\cos \theta \cos \phi &{}\quad -r\cos \theta \sin \phi &{}\quad r\sin \theta \\ 0 &{}\quad r \sin \theta \sin \phi &{}\quad -\sin \theta \cos \phi &{}\quad 0 \\ \end{array} \right) \end{aligned}$$
(10)

where \(e=\det e^{i}_{\mu }=r^{2}e^{\frac{a(r)+b(r)}{2}}\sin \theta \). substituting this vierbein into Eq. (4), we found the torsion scalar T(r) and its derivative \(T^{\prime }(r)\) with respect to radial coordinate r, serving as the basis of the theory, are given by

$$\begin{aligned} T(r)= & {} \frac{2{e}^{-b(r)}}{r^2} \big (r a'(r)-{e}^{\frac{b(r)}{2}}+1\big )\big (1-{e}^{\frac{b(r)}{2}}\big ),\nonumber \\ T'= & {} \frac{\big (e^{\frac{b(r)}{2}}-ra'(r)-1\big )}{r^2}\bigg (-\frac{4e^{-b(r)}\big (e^{\frac{b(r)}{2}}-1\big )}{r} -2e^{-b(r)}\big (e^{\frac{b(r)}{2}}-1\big )b'(r) \end{aligned}$$
(11)
$$\begin{aligned}&+ e^{\frac{-b(r)}{2}}b'(r)\bigg ) +\frac{2{e}^{-b(r)}\big (e^{\frac{b(r)}{2}}-1\big )}{r^{2}}\big (\frac{e^{\frac{b(r)}{2}}}{2}b'(r)-ra''(r)-a'(r)\big ). \end{aligned}$$
(12)

The corresponding field equations in \(f(T,\mathcal {T})\) theory are obtained through Eqs. (6), (8) and (10) as

$$\begin{aligned} 4\pi \rho -2E^{2}= & {} -e^{\frac{-b(r)}{2}}\bigg (e^{\frac{-b(r)}{2}}-1 \bigg )\bigg (\frac{ f_{T\mathcal {T}} \mathcal {T}^{\prime }(r)+ f_{TT} T'(r)}{r}\bigg )-\frac{f_{T}}{2}\bigg ( \frac{T}{2} -\frac{1}{r^{2}} \bigg )\nonumber \\&-\frac{f_{T}}{2}\bigg (\frac{e^{-b(r)}\big (1-rb^{\prime }(r) \big )}{r^{2}}\bigg )+\frac{f}{4}+\frac{ f_{\mathcal {T}} }{2}\big ({\rho }+p_{t}\big ), \end{aligned}$$
(13)
$$\begin{aligned} 4\pi p_{r}+2E^{2}= & {} \bigg (\frac{e^{-b(r)}\big (ra^{\prime }(r)+1\big )}{r^{2}}-\frac{1}{r^{2}}+\frac{T}{2} \bigg )\frac{f_{T}}{2}-\frac{f_{\mathcal {T}}}{2}\big (p_{t}-p_{r}\big )-\frac{f}{4}, \nonumber \\ 4\pi p_{t}+2E^{2}= & {} \frac{1}{2}e^{-b(r)}\bigg (\frac{e^\frac{{-b(r)}}{2}}{r}+\frac{a^{\prime }(r)}{2}+\frac{1}{r}\bigg ) \big ( f_{T\mathcal {T}} \mathcal {T}^{\prime }(r)+ f_{TT} T^{\prime }(r)\big )-\frac{f}{4} \end{aligned}$$
(14)
$$\begin{aligned}&+\bigg (e^{-b(r)}\bigg (\bigg (\frac{a^{\prime }}{4}+\frac{1}{2r}\bigg )\big (a^{\prime }(r)-b^{\prime }(r)\big ) +\frac{a^{\prime \prime }}{2}\bigg )+\frac{T}{2}\bigg )\frac{f_{T}}{2}. \end{aligned}$$
(15)

We use a viable model of \(f(T,\mathcal {T})\) theory given as \(f(T,\mathcal {T})=\alpha _{1} T^{n}(r)+\beta \mathcal {T}(r)+\phi \). Teleparallel gravity is being recovered for \(\alpha _{1}=n=1,~\beta =\phi =0\). Harko et al. [39] constructed cosmological solutions for a model \(f(T,\mathcal {T})\)=\(\alpha _{1} T^{2}(r)+\beta \mathcal {T}(r)\). The trace of EMT is defined as \(\mathcal {T}=\rho -p_{r}-2p_{t}\). In order to obtain the exact solutions of Eqs. (13)–(15), the metric functions are considered to be

$$\begin{aligned} a(r)=Br^{2}+Cr^{3}, \quad b(r)=Ar^{3}, \end{aligned}$$
(16)

along with an EoS for MCG model [68]

$$\begin{aligned} p_{r}=\xi \rho -\frac{\zeta }{\rho ^{\alpha }}, \end{aligned}$$
(17)

where \(\xi ,~\alpha \) and \(\zeta \) are free model parameters. The MCG EoS has two parts, the first term gives an ordinary fluid obeying a linear barotropic EoS and second term relates pressure to some power of the inverse of energy density. However, it is possible to consider barotropic fluid with quadratic EoS or even with higher-order EoS. Therefore, it is interesting to extend MCG EoS, which recovers at least barotropic fluid with quadratic EoS. From Eqs. (13)–(15) and taking \(\alpha =1\), we obtain exact solutions of \(\rho ,~p_{r},~p_{t}\) and \(E^{2}\), respectively, as

$$\begin{aligned} \rho= & {} \frac{1}{2}\left( \frac{1}{(1+\xi )(8\pi -\beta )} \left( \frac{f_{1}n(n-1)\alpha _{1}}{r}\left( \left( f_{1}f_{2}\right) ^{n-2} \left( f_{2}\left( -\frac{2f_{1}}{r}\right. \right. \right. \right. \right. \nonumber \\&\left. \left. \left. +3Ar^{2}\left( e^\frac{{-Ar^{3}}}{2}-f_{1}\right) \right) \right) +\frac{f_{1}}{r^{2}} \left( \frac{3Ar^{2}e^\frac{{Ar^{3}}}{2}}{2}-4Br-9Cr^{2}\right) \right) +\frac{e^{-Ar^{3}}n\alpha _{1}}{r^{2}}\nonumber \\&\left. \times \left( \left( f_{1}f_{2}\right) ^{n-1}r^{2}\left( 3Ar+2B+3Cr\right) \right) \right) + \left( \left( \left( \frac{1}{(1+\xi )(8\pi -\beta )}\left( \frac{f_{1}}{r}\right. \right. \right. \right. \nonumber \\&\times n\alpha _{1}(n-1)\left( \left( f_{1}f_{2}\right) ^{n-2} \left( f_{2}\left( \frac{-2f_{1}}{r}+3Ar^{2}\left( e^{\frac{-Ar^{3}}{2}}-f_{1}\right) \right) \right) \right. \nonumber \\&\left. +\frac{f_{1}}{r^{2}}\left( \frac{3Ar^{2}e^{\frac{Ar^{3}}{2}}}{2} -4Br-9Cr^{2}\right) \right) +\frac{e^{-Ar^{3}}n\alpha _{1}}{r^{2}} \left( \left( f_{1}f_{2}\right) ^{n-1}r^{2}\left( 3Ar\right. \right. \nonumber \\&\left. \left. \left. \left. \left. \left. \left. +2B+3Cr\right) \right) \right) \right) ^{2} +\frac{4\zeta }{1+\xi }\right) \right) ^{\frac{1}{2}}\right) , \end{aligned}$$
(18)
$$\begin{aligned} p_{r}= & {} \frac{\xi }{2}\left( \frac{1}{(1+\xi )(8\pi -\beta )}\left( \frac{f_{1}n(n-1) \alpha _{1}}{r}\left( \left( f_{1}f_{2}\right) ^{n-2} \left( f_{2}\left( -\frac{2f_{1}}{r}\right. \right. \right. \right. \right. \nonumber \\&\left. \left. \left. +3Ar^{2}\left( e^\frac{-{Ar^{3}}}{2}-f_{1}\right) \right) \right) +\frac{f_{1}}{r^{2}} \left( \frac{3Ar^{2}e^\frac{{Ar^{3}}}{2}}{2}-4Br-9Cr^{2}\right) \right) +\frac{e^{-Ar^{3}}n\alpha _{1}}{r^{2}} \nonumber \\&\left. \times \left( \left( f_{1}f_{2}\right) ^{n-1}r^{2}\left( 3Ar+2B+3Cr\right) \right) \right) +\left( \left( \left( \frac{1}{(1+\xi )(8\pi -\beta )}\left( \frac{f_{1}}{r}\right. \right. \right. \right. \nonumber \\&\times n\alpha _{1}(n-1)\left( \left( f_{1}f_{2}\right) ^{n-2} \left( f_{2}\left( -\frac{2f_{1}}{r}+3Ar^{2}\left( e^\frac{{-Ar^{3}}}{2}-f_{1}\right) \right) \right) \right. \nonumber \\&\left. +\frac{f_{1}}{r^{2}}\left( \frac{3Ar^{2}e^\frac{{Ar^{3}}}{2}}{2}-4Br-9Cr^{2}\right) \right) +\frac{e^{-Ar^{3}}n\alpha _{1}}{r^{2}}\left( \left( f_{1}f_{2}\right) ^{n-1}r^{2}\right. \nonumber \\&\left. \left. \left. \left. \left. \left. \times \left( 3Ar+2B+3Cr\right) \right) \right) \right) ^{2} +\frac{4\zeta }{1+\xi }\right) \right) ^{\frac{1}{2}}\right) - \zeta \left( \frac{1}{2}\left( \frac{1}{(1+\xi )(8\pi -\beta )}\right. \right. \nonumber \\&\times \left( \frac{f_{1}n(n-1)\alpha _{1}}{r} \left( \left( f_{1}f_{2}\right) ^{n-2} \left( f_{2}\left( \frac{-2f_{1}}{r}+3Ar^{2}\left( e^\frac{{-Ar^{3}}}{2}-f_{1}\right) \right) \right) +\frac{f_{1}}{r^{2}}\right. \right. \nonumber \\&\left. \times \left( \frac{3Ar^{2} e^\frac{{Ar^{3}}}{2}}{2}-4Br-9Cr^{2}\right) \right) +\frac{e^{-Ar^{3}}n\alpha _{1}}{r^{2}}\left( \left( f_{1}f_{2}\right) ^{n-1}r^{2}\left( 3Ar\right. \right. \nonumber \\&\left. \left. \left. + 2B+3Cr\right) \right) \right) + \left( \left( \left( \frac{1}{(1+\xi )(8\pi -\beta )}\left( \frac{f_{1}n(n-1)\alpha _{1}}{r}\left( \left( f_{1}\right. \right. \right. \right. \right. \right. \nonumber \\&\left. \times f_{2}\right) ^{n-2}\left( f_{2}\left( \frac{-2f_{1}}{r}+3Ar^{2} \left( e^\frac{{-Ar^{3}}}{2}-f_{1}\right) \right) \right) +\frac{f_{1}}{r^{2}}\left( \frac{3Ar^{2}e^\frac{{Ar^{3}}}{2}}{2}\right. \nonumber \\&\left. \left. \left. \left. - 4Br-9Cr^{2}\right) \right) +\frac{e^{-Ar^{3}}n\alpha _{1}}{r^{2}}\left( \left( f_{1}f_{2}\right) ^{n-1} r^{2}\left( 3Ar+2B+3Cr\right) \right) \right) \right) ^{2} \nonumber \\&\left. \left. \left. \left. +\frac{4\zeta }{1+\xi }\right) \right) ^{\frac{1}{2}}\right) \right) ^{-1}, \end{aligned}$$
(19)
$$\begin{aligned} p_{t}= & {} \frac{2}{8\pi -\beta }\left( \frac{e^{-Ar^{3}}\alpha _{1}n(n-1)}{2} \left( \left( \frac{-e^{\frac{Ar^{3}}{2}}}{r} +\frac{2Br+3Cr^{2}}{2}+\frac{1}{r}\right) \right. \right. \nonumber \\&\times \left( \left( f_{1}f_{2}\right) ^{n-2}\right) \left( f_{2} \left( \frac{-2f_{1}}{r}+3Ar^{2}\left( e^{\frac{-Ar^{3}}{2}}-f_{1}\right) \right) \right) \nonumber \\&\left. +\frac{f_{1}}{r^{2}}\left( \frac{e^{\frac{-Ar^{3}}{2}}3Ar^{2}}{2}-4Br-9Cr^{2}\right) \right) + \frac{\alpha _{1}n\left( f_{1}f_{2}\right) ^{n-1}}{2}\left( e^{-Ar^{3}}\right. \nonumber \\&\times \left( \left( \frac{2Br+3Cr^{2}}{4}+ \frac{1}{2r}\right) \left( 2Br+3Cr^{2}-3Ar^{2}\right) +\frac{2B+6Cr}{2}\right) \nonumber \\&\left. \left. +\frac{f_{1}f_{2}}{2}\right) -\frac{\alpha _{1}\left( f_{1}f_{2}\right) ^{n}}{4}-\frac{\beta }{4} \left( \rho -p_{r}\right) -\frac{\phi }{4}-2E^{2}\right) , \end{aligned}$$
(20)
$$\begin{aligned} E^{2}= & {} n\alpha _{1}\left( f_{1}f_{2}\right) ^{n-1}\left( \frac{e^{-Ar^{3}}\left( 2Br^{2}+3Cr^{3}+1\right) }{r^{2}}-\frac{1}{r^{2}} +\frac{f_{1}f_{2}}{2}\right) -\frac{\alpha _{1}\left( f_{1}f_{2}\right) ^{n}}{2} \nonumber \\&-\frac{\phi }{2}-\frac{\beta }{2}\rho +\left( \frac{3\beta -16\pi }{2}\right) p_{r}, \end{aligned}$$
(21)

where

$$\begin{aligned} f_{1}=2e^{-Ar^{3}}(e^{\frac{Ar^{3}}{2}}-1),\quad f_{2}=\frac{e^{\frac{Ar^{3}}{2}}-2Br^{2}-3Cr^{3}-1}{r^{2}}. \end{aligned}$$

The quantity q(r) shows an effective charge in a spherical system, defined as

$$\begin{aligned} q(r)=\frac{4\pi }{r}\int _{0}^{r}r^{2}\chi (r)e^{\frac{b(r)}{2}}dr, \quad E(r)=\frac{q(r)}{r^{2}}, \end{aligned}$$
(22)

here \(\chi \) and E represent the surface charge density and electric field intensity, respectively. So the net amount of charge inside a sphere is calculated by

$$\begin{aligned} q(r)= & {} r^{2}\bigg (n\alpha _{1}\big (f_{1}f_{2}\big )^{n-1}\bigg (\frac{e^{-Ar^{3}} \big (2Br^{2}+3Cr^{3}+1\big )}{r^{2}}-\frac{1}{r^{2}}+\frac{f_{1}f_{2}}{2}\bigg ) \nonumber \\&-\frac{\alpha _{1}\big (f_{1}f_{2}\big )^{n}}{2}-\frac{\phi }{2} -\frac{\beta }{2}\rho +\big (\frac{3\beta -16\pi }{2}\big )p_{r}\bigg )^{\frac{1}{2}}. \end{aligned}$$
(23)

4 Physical analysis

In this section, we will examine structural properties of the obtained anisotropic solutions, i.e., behavior of density and pressure, anisotropic stress, charge, energy conditions, mass function, compactness and surface redshift.

4.1 Behavior of density and components of pressure

To illustrate physical nature of above-mentioned physical quantities of anisotropic stellar objects, we assign different numeric values to free involved model parameters.

Fig. 1
figure 1

\(\rho \) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 2
figure 2

\(p_{r}\) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 3
figure 3

\(p_{t}\) versus r for different stars by varying \(\beta \) and n

Full size image

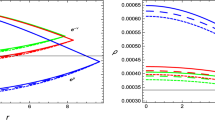
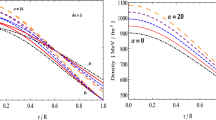
Energy density distribution given in Eq. (18) is plotted in Fig. 1 for different values of the involved parameters exhibiting positive decaying behavior with respect to radius r (km). It is maximum at \(r=0\) and goes on decreasing as we move away from the center. It can be seen from Fig. 1 that the model’s energy density is sensitive for all the involved parameters.

Fig. 4
figure 4

\(\frac{d\rho }{dr}\) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 5
figure 5

\(\frac{dp_{r}}{dr}\) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 6
figure 6

\(\frac{d^{2}\rho }{dr^{2}}\) versus r for different stars by varying \(\beta \) and n

Full size image

The graphical description of radial pressure, which is obtained in Eq. (19) has been shown in Fig. 2. We can see that the trajectories of \(p_{r}-r\) lies in the negative region and attain the peak value at the center and start to decrease toward the boundary of stellar object. Figure 3 is showing the behavior of tangential pressure with respect to r. It falls in positive region throughout the stellar configuration and admits maximum values at the center then rolls down toward the boundary of star. It is noticed that \(p_{r}\) vanishes at \(r=R\) whereas \(p_{t}\) stays in positive region.

Evolution of energy density is presented in Fig. 4, which fulfills the physical restriction, \(\frac{d\rho }{dr}<0\) at specific values of the model parameters. The evolution of \(p_r\) is plotted in Fig. 5 while second-order derivative of density with respect to r has been shown in Fig. 6. It is clear from the figure that \(\frac{dp_{r}}{dr}<0\), which means that DE has large negative pressure and \(\frac{d^{2}\rho }{dr^{2}}<0\), which implies decaying behavior of energy density. The second derivative of \(p_{r}\) with respect to r has been plotted in Fig. 7, which lies in negative region and monotonically decreasing function of radius. It has been checked that the quantities \(\frac{d^{2}\rho }{dr^{2}}\) and \(\frac{d^{2}p_r}{dr^{2}}\) exhibit the same physical behavior for different values of \(\xi \) and \(\zeta \).

Fig. 7
figure 7

\(\frac{d^{2}p_{r}}{dr^{2}}\) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 8
figure 8

Anisotropic parameter versus r for different stars by varying \(\beta \) and n

Full size image

The anisotropic stress (\(\Delta =p_{t}-p_{r}\) is shown in Fig. 8 for different values of \(\beta \) and n) has extreme value in the interval [0.77, 0.81]. It is worthwhile to mention that \(\Delta >0\) if \(p_{t}>p_{r}\) is an outward directed repulsive gravitational force, which counterbalance the gradients, and if \(\Delta <0\), then anisotropic stress shows an attractive gravitational force. At the central point, \(\Delta \) shows neither repulsive nor attractive forces because at this point, the components \(p_{r}\) and \(p_{t}\) are stable. But as we approached to boundary of the star, these quantities float independently and hence \(\Delta \) adopts the increasing behavior.

Fig. 9
figure 9

\(E^{2}\) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 10
figure 10

\(\rho +\frac{E^{2}}{8\pi }\) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 11
figure 11

\(\rho +p_{r}\) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 12
figure 12

\(\rho +3p_{r}\) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 13
figure 13

\(\rho +p_{t}+\frac{E^{2}}{4\pi }\) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 14
figure 14

\(\rho +p_{r}+2p_{t}+\frac{E^{2}}{4\pi }\) versus r for different stars by varying \(\beta \) and n

Full size image

4.2 Energy conditions

The existence of the ordinary matter within stellar geometry is guaranteed by some energy constraints. The obtained solutions must satisfy these constraints for the physical permissibility of our models. These energy conditions are classified into, null energy condition (NEC), weak energy condition (WEC), strong energy condition (SEC) and dominant energy condition (DEC). At any interior point of the charged fluid sphere, the following inequalities must be satisfied simultaneously:

$$\begin{aligned} \begin{aligned} NEC&:\quad \rho +\frac{E^{2}}{8\pi }\ge 0, \\ WEC&:\quad \rho +p_{r}\ge 0, \quad \rho +p_{t}+\frac{E^{2}}{4\pi }\ge 0,\\ SEC&:\quad \rho +p_{r}+2p_{t}+\frac{E^{2}}{4\pi }\ge 0. \end{aligned} \end{aligned}$$
(24)

Figure 9 shows that effect of electric charge goes on decreasing with the increment in radius. It is clear from the graphs plotted in Figs. 10, 11, 12, 13 and 14 that all of the energy conditions are fully satisfied. It is worth noticing from Figs. 1 and 12 that \(\rho +3p_{r}<0\), so we observed that EoS parameter lies in the interval \(-1<\omega <-\frac{1}{3}\), hence it lies in quintessence phase, which belongs to corresponding model.

4.3 Calculation of unknown metric potentials by smooth matching conditions

In order to match the exterior solution with the interior one, several authors [59,60,61,62,63,64,65,66,67,68,69] have focused on the matching conditions. The line element of Schwarzchild metric is given by

$$\begin{aligned} ds^{2}=-\bigg (1-\frac{2M}{r}\bigg )dt^{2}+{\bigg (1-\frac{2M}{r}\bigg )}^{-1}dr^{2}+r^{2} \big (d\theta ^{2}+\sin \theta ^{2}d\phi ^{2}\big ). \end{aligned}$$
(25)

At the boundary \(r=R\), the continuity of metric components yields

$$\begin{aligned} \mathrm {g}_{tt}^-=\mathrm {g}_{tt}^+,\quad \mathrm {g}_{rr}^-=\mathrm {g}_{rr}^+,\quad \frac{\partial \mathrm {g}_{tt}^-}{\partial r}=\frac{\partial \mathrm {g}_{tt}^+}{\partial r}, \end{aligned}$$
(26)

where −ve and +ve sign indicate the interior and exterior solutions. Now using Eq.(26) and the metrics (9) and (25), we get the unknowns as follows

$$\begin{aligned} A= & {} -\frac{1}{R^{3}}\ln \bigg (1-\frac{2M}{R}\bigg ),\nonumber \\ B= & {} \frac{3}{R^{2}}\ln \bigg (1-\frac{2M}{R}\bigg )-\frac{2M}{R^{3}}\bigg (1-\frac{2M}{R}\bigg )^{-1},\nonumber \\ C= & {} \frac{2M}{R^{4}}\bigg (1-\frac{2M}{R}\bigg )^{-1}-\frac{2}{R^{3}}\ln \bigg (1-\frac{2M}{R}\bigg ). \end{aligned}$$
(27)

The parameter \(\alpha _{1}\) can be evaluated considering \(\rho =0\) in Eq. (18) and turn out to be

$$\begin{aligned} \alpha _{1}= & {} \left( 4\zeta \bigg (\bigg (\big (1+\xi \big )\bigg (\frac{1}{(1+\xi )(8\pi -\beta )}\bigg (\frac{f_{1}n(n-1)}{r} \bigg (\big (f_{1}f_{2}\big )^{n-2}\right. \nonumber \\&\times \left( f_{2} \left( -\frac{2f_{1}}{r}+3Ar^{2}\left( e^\frac{-{Ar^{3}}}{2}-f_{1}\right) \right) \right) +\frac{f_{1}}{r^{2}}\left( \frac{3Ar^{2}e^\frac{{Ar^{3}}}{2}}{2}-4Br\nonumber \right. \\&\left. \left. - 9Cr^{2}\right) \right) +\frac{e^{-Ar^{3}}n}{r^{2}}\bigg (\big (f_{1}f_{2}\big )^{n-1}r^{2}\big (3Ar+2B+3Cr\big )\bigg )\bigg )\bigg )^{2}\bigg ) \nonumber \\&-\bigg (\frac{1}{(1+\xi )(8\pi -\beta )}\bigg (\frac{f_{1}n(n-1)}{r}\bigg (\big (f_{1}f_{2}\big )^{n-2} \big (f_{2}\big (-\frac{2f_{1}}{r}\nonumber \\&+ 3Ar^{2}\big (e^\frac{-{Ar^{3}}}{2}-f_{1}\big )\big )\big )+\frac{f_{1}}{r^{2}}\big (\frac{3Ar^{2}e^\frac{{Ar^{3}}}{2}}{2}-4Br-9Cr^{2}\big )\bigg ) +\frac{e^{-Ar^{3}}n}{r^{2}}\nonumber \\&\times \bigg (\big (f_{1}f_{2}\big )^{n-1}r^{2}\big (3Ar+2B+3Cr\big )\bigg )\bigg )\bigg ) ^{2}\bigg )^{-1}\bigg )^{\frac{1}{2}}. \end{aligned}$$
(28)
Fig. 15
figure 15

\(v^{2}_{sr}\) versus r for different stars by varying \(\beta \) and n

Full size image

4.4 Stability criteria

Here the radial and transversal components of a physical quantity, i.e., square speed of sound have been calculated. Herrera [70] proposed an important “cracking” concept to check the stability of a stellar system having anisotropic fluid distribution. According to this technique, the stability can be achieved if the speed of radial sound would be greater than the speed of transversal sound otherwise the system will be unstable. The square speed of sound in both directions must satisfy the given inequalities to attain stable strange stars, these are \(0<v^{2}_{sr}\le 1\) and \(0<v^{2}_{st}\le 1\), where \(v^{2}_{sr}=\frac{dp_r}{d\rho }, ~v^{2}_{st}=\frac{dP_t}{d\rho }\) represent radial and transversal components of speed of sound, respectively.

Fig. 16
figure 16

\(v^{2}_{st}\) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 17
figure 17

\(v^{2}_{st}-v^{2}_{sr}\) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 18
figure 18

\(|v^{2}_{st}-v^{2}_{sr}|\) versus r for different stars by varying \(\beta \) and n

Full size image

From Figs. 15 and 16, it is clear that our obtained solutions fulfill the stability requirements as \(v^{2}_{sr}\) and \(v^{2}_{st}\) always lie in the positive region and below unity within stellar objects. Their difference shows that radial sound speed is greater than the transversal sound speed. Also Fig. 18 is in good agreement with the stability criteria, \(|v^{2}_{st}-v^{2}_{sr}|\le 1\) [54]. Hence, our developed strange star model with the help of MCG in \(f(T,\mathcal {T})\) gravity is potentially stable.

5 Mass function, compactness factor and surface redshift

The mass and radius of anisotropic stellar objects are related to each other such that the mass vanishes at \(r=0\) [54]. It can be seen that the mass function is regular at origin and monotonically increasing with respect to radius. It is evaluated as

$$\begin{aligned} m(r)= & {} \int _{0}^r 4\pi r^{2}\rho dr,\nonumber \\= & {} \int _{0}^r \left( 2\pi r^{2}\left( \frac{1}{(1+\xi )(8\pi -\beta )}\left( \frac{f_{1}n(n-1)\alpha _{1}}{r} \left( \left( f_{1}f_{2}(r)\right) ^{n-2} \Bigg (f_{2}\Bigg .\right. \right. \right. \right. \nonumber \\&\left. \left. \times \left( -\frac{2f_{1}}{r}+3Ar^{2}\left( e^\frac{-{Ar^{3}}}{2}-f_{1}\right) \right) \right) +\frac{f_{1}}{r^{2}} \left( \frac{3Ar^{2}e^\frac{{Ar^{3}}}{2}}{2}-4Br-9Cr^{2}\right) \right) \nonumber \\&\left. +\frac{e^{-Ar^{3}}n\alpha _{1}}{r^{2}}\left( \left( f_{1}f_{2} \right) ^{n-1}r^{2}\left( 3Ar+2B+3Cr\right) \right) \right) +\left( \left( \left( \frac{1}{(1+\xi )(8\pi -\beta )}\right. \right. \right. \nonumber \\&\times \left( \frac{f_{1}n(n-1)\alpha _{1}}{r}\left( \left( f_{1}f_{2}\right) ^{n-2} \left( f_{2}\left( \frac{-2f_{1}}{r}+3Ar^{2}\left( e^{\frac{-Ar^{3}}{2}}-f_{1}\right) \right) \right) \right. \right. \nonumber \\&\left. +\frac{f_{1}}{r^{2}}\left( \frac{3Ar^{2}e^{\frac{Ar^{3}}{2}}}{2}-4Br-9Cr^{2}\right) \right) +\frac{e^{-Ar^{3}}n\alpha _{1}}{r^{2}}\left( \left( f_{1}f_{2}\right) ^{n-1}r^{2}\left( 3Ar\right. \right. \nonumber \\&\left. \left. \left. \left. \left. \left. \left. \left. +2B+3Cr\right) \right) \right) \right) ^{2} +\frac{4\zeta }{1+\xi }\right) \right) ^{\frac{1}{2}}\right) \right) dr. \end{aligned}$$
(29)
Fig. 19
figure 19

m(r) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 20
figure 20

u(r) versus r for different stars by varying \(\beta \) and n

Full size image
Fig. 21
figure 21

\(z_{s}\) versus r for different stars by varying \(\beta \) and n

Full size image

The compactness of a star is defined by \(u(r)=\frac{m(r)}{r}\), where corresponding m(r) is given in Eq.(29). The redshift function is given by

$$\begin{aligned} z_{s}+1=(1-2u(r))^{\frac{-1}{2}}, \end{aligned}$$

where u(r) can be evaluated from above expression. Figures 19 and 20 show that \(\frac{m(r)}{r}\) is a significant tool to observe the compactness factor of the stellar objects. For static spherically symmetric star under anisotropic fluid distribution, the mass–radius ratio for u(r) should not exceed from a numeric value \(\frac{4}{9}\), i.e., \(u(r)=\frac{m}{r}<\frac{4}{9}\); (\(c=G=1\)) [71]. In anisotropic fluid distribution, the maximum value of possible gravitational redshift function is \(z_{s}\le 5\) shown in Fig. 21.

6 Final outcomes

This work can be an important contribution in studying the exact stellar solutions of EFEs using EoS of DE for anisotropic fluid distribution within \(f(T,\mathcal {T})\) gravity. For investigation, we have considered the accessible data from current literature of four compact stars PSRJ 1614-2230 and SAXJ 1808.4-3658 while the graphical analysis of 4U 1820-30, Vela X-12 is added in “Appendix.” In order to find the solutions of solar system constraints that cannot be interpreted in the presence of diagonal tetrad field in f(T) gravity, we use off-diagonal tetrad field in \(f(T,\mathcal {T})\) theory. For better configuration of obtained results, we use the arbitrary function \(f(T,\mathcal {T})=\alpha _{1}T^{n}(r)+\beta \mathcal {T}(r)+\phi \), physically acceptable function in \(f(T,\mathcal {T})\) theory along with an EoS for MCG. By applying the exterior and interior matching conditions, we calculate the numeric values of unknowns involved in the chosen metric potentials, i.e., \(a(r)=Br^{2}+Cr^{3},~b(r)=Ar^{3}\), are shown in Table 1. We derived analytical solutions and addressed their stability and different physical features of compact objects under anisotropic fluid distribution in \(f(T,\mathcal {T})\) theory.

Table 1 Numerical values of the obtained constants A,  B,  C and \(\alpha _{1}\) for some strange stars fixing \(\beta =n=3,~\zeta =2,~\xi =3\)
Full size table
Table 2 Measurement of \(\alpha _{1}\) for different values of \(\beta \) and n and fixing \(\xi =\zeta =1\) for some strange stars. In the similar manner, we can evaluate \(\alpha _{1}\) for others values of the parameters
Full size table

  • Figures 1, 2 and 3 ensure that energy density and components of pressure fulfill the physical criteria that both are monotonically decreasing as we approach toward boundary (Table 2).

  • The gradients of \(\rho ,~p_r\) are showing negative trend in the interior of stars as shown in Figs. 4, 5, 6 and 7. We have also checked that the EoS parameter \(\omega \) lies in the quintessence region.

  • Figure 8 depicts that \(\Delta >0\), which shows expansion. It means that there exists repulsive gravitational force, which is the attestation to escape the compact stellar objects from gravitational collapse to a singularity. From Fig. 9, it is clear that the effect of electric field in stellar objects is decreasing as we move toward the boundary.

  • Figures 10, 11, 12, 13 and 14 verified that all the energy conditions are fully satisfied. The energy density remains positive and attains maximum value at the center and declined toward boundary of stellar object.

  • Figures 15, 16, 17 and 18 advocate the physical stability of attained solutions as they satisfy the casuality conditions \((0<v^2_{sr},~v^2_{st}<1)\) and Abrue Conditions \((0<|v^2_{sr}-v^2_{st}|<1)\).

  • The corresponding mass function is regular as shown in Fig. 19. It vanishes for vanishing radius, then monotonically increasing to attain physical mass range. Compactness factor also satisfies the Buchdahl condition (\(\frac{m}{r}<\frac{4}{9}\)) for our model (Fig. 20). The gravitational redshift factor also admits the proposed range \(z_{s}\le 5\) (Fig. 21).

It is worthy to mention here that for \(\alpha _1=n=1,~\beta =0\), the results reduced to [55]. Also, this work is an extension of our previous work [59] in which we found the interior isotropic solutions of compact stars in \(f(T,\mathcal {T})\) theory under Karmarkar condition. This work has more complex analysis due to anisotropic distribution of the fluid along with more general metric potentials as compared to [59]. Generally, we conclude that the stellar solutions evaluated in this manuscript are physically viable and graphically stable.