Relativistic solutions of anisotropic compact objects

Abstract

We present a class of new relativistic solutions with anisotropic fluid for compact stars in hydrostatic equilibrium. The interior space-time geometry considered here for compact objects are described by parameters namely, λ, k, A, R and n. The values of the geometrical parameters are determined here for obtaining a class of physically viable stellar models. The energy-density, radial pressure and tangential pressure are finite and positive inside the anisotropic stars. Considering some stars of known mass we present stellar models which describe compact astrophysical objects with nuclear density.

1 Introduction

The precision astronomical observations in the last couple of decades predicted the existence of massive compact objects. A number of compact objects with very high densities are discovered in the recent times (Lattimer 2010). To describe such compact objects general theory of relativity is most useful. The theoretical investigation of such compact astrophysical objects has been a key issue in relativistic astrophysics over a couple of decades. Astrophysical objects with perfect fluid necessarily requires the pressure inside is isotropic (Ivanov 2002). In general, a polytropic equation of state (EOS) is used widely to describe a white dwarf or a less compact star (Shapiro and Teukolosky 1983). However, theoretical understanding in the last couple of decades made it clear that there is a deviation from local isotropy in the interior pressure. At very high enough densities with smaller radial size the anisotropic pressure plays an important role in determining stellar properties (Ruderman 1972; Canuto 1974; Patel et al. 1997). The physical situations where anisotropic pressure may be relevant are very diverse for a compact stellar object (Ruderman 1972; Canuto 1974; Maharaj and Maartens 1989; Bower and Liang 1974). By anisotropic pressure we mean the radial component of the pressure (p _r ) different from that of the tangential pressure (p _t ). After the seminal work of Bower and Liang (1974), a number of literature appeared considering an anisotropic spherically symmetric static general relativistic object. Ruderman (1972) and Canuto (1974) theoretically investigated compact objects and observed that a star with matter density (ρ>10¹⁵ gm/cc), where the nuclear interaction become relativistic in nature, are likely to be anisotropic. It is further noted that anisotropy in fluid pressure in a star may originate due to number of processes e.g., the existence of a solid core, the presence of type 3A super fluid etc. (Kippenhahm and Weigert 1990). Recently, Mak and Harko (2004) determined the maximum mass and mass to radius ratio of a compact isotropic relativistic star. Maharaj and Maartens (1989), Bower and Liang (1974), Bayin (1982) examined spherical distribution of anisotropic matter in the framework of general relativity and derived a number of solutions to understand the interior of such stars. A handful number of exact interior solutions in general relativity for both the isotropic and the anisotropic compact objects have been reported in the literature (Delgaty and Lake 1998). Delgaty and Lake (1998) analysed 127 published solutions out of which they found that only 16 of the published results satisfy all the conditions for a physically viable stellar model. In the case of a compact stellar object it is essential to satisfy all the conditions outlined by Delgaty and Lake as the EOS of the fluid of the compact dense object is not known.

The discovery of compact stellar objects, such as X-ray pulsars, namely Her X1, millisecond pulsar SAX J1808.43658, X-ray sources, 4U 1820-30 and 4U 1728-34 are important and interesting as these are considered to be probable strange star candidates. The existence of such characteristics compact objects led to critical studies of stellar configurations (Dey et al. 1999; Li et al. 1999; Knutsen 1988; Maharaj and Leach 1996; Mukherjee et al. 1997; Negi and Durgapal 1999; Bombaci 1997; Tikekar and Thomas 1998; Tikekar 1990; Gupta and Jassim 2000; Jotania and Tikekar 2006; Tikekar and Jotania 2005; Finch and Skea 1989). However, the equation of state (EOS) of matter inside a superdense strange star at present is not known. In this context Vaidya and Tikekar (1982) and Tikekar (1990) have shown that in the absence of definite information about the EOS of matter content of stellar configuration, an alternative approach of prescribing a suitable ansatz for the geometry of the interior physical 3-space of the configuration leads to simple easily accessible physically viable models of such stars. Relativistic models of superdense stars based on different solutions of Einstein’s field equations obtained by Vaidya-Tikekar approach of assigning different geometries with physical 3-spaces of such objects are reported in the literature (Knutsen 1988; Mukherjee et al. 1997; Tikekar and Thomas 1998; Jotania and Tikekar 2006; Tikekar and Jotania 2005). Pant and Sah (1985) obtained a class of relativistic static non-singular analytic solutions in isotropic form with a spherically symmetric distribution of matter in a static space time. Pant and Sah solution is found to lead to a physically viable causal model of neutron star with a maximum mass of 4M_⊙. Recently, Deb et al. (2012) obtained a class of compact stellar models using Pant and Sah solution in the case of spherically symmetric space time. In this paper we obtain a class of new relativistic solutions which accommodate anisotropic stars possessing mass relevant for neutron stars. Usually a stellar model is obtained using Einstein field equation for a known EOS and then the geometry of the space-time is determined. In this paper we follow an alternative approach (Synge approach) by first making an ad hoc choice of the geometry and then explore the EOS for matter. A class of new relativistic solutions are discussed here which accommodate anisotropic star in hydrostatic equilibrium having mass and radius relevant for neutron stars (Steiner et al. 2010).

The paper is organised as follows: In Sect. 2, we set up the relevant field equations and its solutions. In Sect. 3, physical properties of anisotropic star is presented. In Sect. 4, we present physical analysis of stellar models with the observational stellar mass for different model parameters. Finally in Sect. 5, we give a brief discussion.

2 Field equation and solutions

The Einstein’s field equation is

$$ R_{\mu\nu} -\frac{1}{2} g_{\mu\nu} R = 8 \pi G \; T_{\mu\nu} $$

(1)

where g _μν , R, R _μν and T _μν are the metric tensor, Ricci scalar, Ricci tensor and energy momentum tensor respectively.

We use spherically symmetric space time metric given by

$$ ds^2= e^{\nu(r)}dr^2-e^{\mu(r)} \bigl(dr^2+r^2d\varOmega^2\bigr) $$

(2)

where ν(r) and μ(r) are unknown metric functions and dΩ²=dθ²+sin² θ  dϕ². We assume an anisotropic pressure distribution for the fluid content of the star. The energy momentum tensor for such fluid in equilibrium is given by

$$ T^{\mu}_{\mu} = \operatorname {diag}(\rho, - p_r,- p_t, - p_t) $$

(3)

where ρ is the energy-density, p _r is the radial pressure, p _t is the tangential pressure and Δ=p _t −p _r is the measure of pressure anisotropy (Steiner et al. 2010). Using the space time metric given by Eq. (2), the Einstein’s field equation (1) reduces to the following equations:

$$\begin{aligned} &\rho=-e^{-\mu} \biggl(\mu''+\frac{\mu^{\prime\,2}}{4}+ \frac{2\mu'}{r} \biggr), \end{aligned}$$

(4)

$$\begin{aligned} &p_r=e^{-\mu} \biggl(\frac{\mu^{\prime\,2}}{4}+\frac{\mu'}{r}+ \frac{\mu'\nu'}{2}+\frac{\nu'}{r} \biggr), \end{aligned}$$

(5)

$$\begin{aligned} & p_t=e^{-\mu} \biggl(\frac{\mu''}{2}+\frac{\nu''}{2}+ \frac{\nu^{\prime\,2}}{4}+\frac{\mu'}{2r}+\frac{\nu'}{2r} \biggr). \end{aligned}$$

(6)

Using Eqs. (5) and (6) along with the definition of anisotropy of fluid we obtain

$$ \biggl(\frac{\mu''}{2}+\frac{\nu''}{2}+\frac{\nu^{\prime\,2}}{4}-\frac{\mu^{\prime\,2}}{4}- \frac{\mu'}{2r}-\frac{\nu'}{2r}-\frac{\mu'\nu'}{2} \biggr)=\Delta e^{\mu}. $$

(7)

Equation (7) is a second-order differential equation which admits a class of new solution with anisotropic fluid distribution given by

$$ e^{\frac{\nu}{2}}=A \biggl(\frac{1-k\alpha+n\frac{r^2}{R^2}}{1+k\alpha } \biggr),\qquad e^{\frac{\mu}{2}}=\frac{(1+k\alpha)^2}{1+\frac{r^2}{R^2}} $$

(8)

where

$$ \alpha(r)=\sqrt{\frac{1+\frac{r^2}{R^2}}{1+ \lambda\frac{ r^2}{R^2}}} $$

(9)

with R, λ, k, A and n are arbitrary constants. It may be pointed out here that n=0 corresponds to a solution for isotropic stellar model obtained by Pant and Sah (1985). We consider here non-zero n to obtain an anisotropic stellar model in hydrostatic equilibrium. Equation (8) permits a relation amongst the parameters which is useful for obtaining stellar models. The allowed values of the parameters are determined using the physical conditions imposed on the stellar solution for a viable stellar model. The geometry of the 3-space in the above metric is given by

$$ d\sigma^2=\frac{dr^2+r^2(d\theta^2+\sin^2\theta d\phi^2)}{1+\frac{r^2}{R^2}}. $$

(10)

It corresponds to a 3 sphere immersed in a 4-dimensional Euclidean space. Accordingly the geometry of physical space obtained at the t=constant section of the space time is given by

$$\begin{aligned} ds^2&=A^2 \biggl(\frac{1-k\alpha+n\frac{r^2}{R^2}}{1+k\alpha} \biggr)^2 dt^2 \\ &\quad -\frac{(1+k\alpha)^4}{(1+\frac{r^2}{R^2})^2} \bigl[dr^2+r^2\bigl(d \theta^2+\sin^2\theta d\phi^2\bigr) \bigr]. \end{aligned}$$

(11)

The pressure anisotropy term becomes

$$ \Delta= \frac{ n \alpha\frac{r^2}{R^2} (8 \alpha(1+ \lambda\frac {r^2}{R^2} )^3 + k^2 \alpha X + Y ) }{ (1+\lambda\frac{r^2}{R^2})^2 (1+k \alpha)^6 (1 + n \frac{r^2}{R^2} - k \alpha) } $$

(12)

where $X= 8 \lambda^{2} \frac{r^{6}}{R^{6}} + 4 \lambda(1+5 \lambda) \frac {r^{4}}{R^{4}}+12 \lambda-4$, $Y=(15 \lambda^{2}+10 \lambda-1) \frac{r^{2}}{R^{2}} +k(4+12 \lambda+16 \lambda^{2}) \frac{r^{6}}{R^{6}} + 4 \lambda(5+ 7 \lambda) \frac{r^{4}}{R^{4}} +(15 \lambda^{2}+26 \lambda+7)\frac{r^{2}}{R^{2}}$. The geometry of 3-space obtained at t=constant section of the space time metric (11) given above incorporates a deviation in a spherical 3 space, k is a geometrical parameter measuring inhomogeneity of the physical space and n is related to the anisotropy. For k=0 and n=0, the space time metric (11) degenerates into that of Einstein’s static universe which is filled with matter of uniform density. The solution obtained by Pant and Sah corresponds to the case when n=0 and k≠0 (Pant and Sah 1985). It reduces to a generalization of the Buchdahl solution, the physical 3-space associated with which has the same feature. However, for λ>0, the solution corresponds to finite boundary models. In this paper we study physical properties of compact objects filled with anisotropic fluid (n≠0) and determine the values of R, λ, k and A for a viable stellar model as permitted by the field equation. The exterior Schwarzschild line element is given by

$$\begin{aligned} ds^2&= \biggl( 1 - \frac{2m}{r_o} \biggr) dt^2 - \biggl( 1 - \frac{2m}{r_o} \biggr)^{-1} dr^2 \\ &\quad - r_o^2 \bigl(d\theta^2 + \sin^2 \theta d\phi^2\bigr) \end{aligned}$$

(13)

where m represents the mass of spherical object. The above metric can be expressed in an isotropic metric form (Narlikar 2010)

$$ ds^2= \biggl(\frac{1-\frac{m}{2r}}{1+\frac{m}{2r}} \biggr)^2dt^2- \biggl(1+\frac{m}{2r} \biggr)^4\bigl(dr^2+r^2d \varOmega^2\bigr) $$

(14)

using the transformation $r_{o}= r (1+ \frac{m}{2r} )^{2}$ where r _o is the radius of the compact object. This form of the Schwarzschild metric will be used here to match at the boundary with the interior metric given by Eq. (11) at the boundary.

3 Physical properties of anisotropic compact star

The solution given by Eq. (8) is useful to study physical features of compact objects with anisotropy in a general way which are outlined as follows:

• (1) In this model, a positive central density ρ is obtained for $\lambda<\frac{4}{k}+1$.

• (2) At the boundary of the star (r=b), the interior solution should be matched with the isotropic form of Schwarzschild exterior solution, i.e.,

  $$ e^{\frac{\nu}{2}}|_{r=b}= \biggl( \frac{1-\frac{m}{2b}}{1+\frac{m}{2b}} \biggr);\qquad e^{\frac{\mu}{2}}|_{r=b}= \biggl(1+\frac{m}{2b} \biggr)^2 $$

  (15)

• (3) The physical radius of a star (r _o ), is determined knowing the radial distance where the pressure at the boundary vanishes (i.e., p(r)=0 at r=b). The physical radius is related to the radial distance (r=b) through the relation $r_{o}= b (1+ \frac{m}{2b} )^{2}$ (Narlikar 2010).

• (4) The ratio $\frac{m}{b}$ is determined using Eqs. (8) and (14), which is given by

  $$ \frac{m}{b} = 2 \pm2A \biggl( \frac{1-k\alpha+n y^2}{\sqrt{1+y^2}} \biggr) $$

  (16)

  where $y=\frac{b}{R}$. In the above we consider only negative sign as it corresponds to a physically viable stellar model.

• (5) The density inside the star should be positive i.e., ρ>0.

• (6) Inside the star the stellar model should satisfy the condition, $\frac{dp}{d\rho}<1$ for the sound propagation to be causal.

The usual boundary conditions are that the first and second fundamental forms required to be continuous across the boundary r=b. We determine n, k, λ and A which satisfy the criteria for a viable stellar model outlined above. As the field equations are highly non-linear and intractable to obtain a known functional relation between pressure and density we adopt numerical technique. Imposing the condition that the pressure at the boundary vanishes, we determine y from Eq. (5). The square of the acoustic speed $\frac{dp}{d\rho}$ becomes:

$$ \frac{dp}{d\rho}=-\frac{\sqrt{\alpha}(1+k\sqrt{\alpha})(A+\frac{B}{\sqrt {\alpha}}+C+D)}{E} $$

(17)

where

$$\begin{aligned} A &= -4 \bigl(-1+n+n^2+2n^2r^2+nr^4 \bigr) \bigl(1+r^2\lambda \bigr)^5 \\ &\quad +2k^4\bigl(1+r^2\bigr)^4\lambda \bigl(-1+3\bigl(3+2r^2\bigr)\lambda\bigr) \\ B&=2k^3 \bigl(1+r^2 \bigr)^3\bigl( \bigl(1+r^2 \bigr) (\lambda-1)\lambda \\ &\quad + n\bigl(1+\bigl(1+4r^2+2r^4\bigr) \lambda-r^4\lambda^2\\ &\quad +r^4\bigl(3+4r^2+2r^4 \bigr)^3\lambda\bigr)\bigr), \\ C&=k\sqrt{\alpha} \bigl(1+r^2\lambda \bigr)^3\bigl(-2 \bigl(-1+ \lambda-r^2\lambda+r^2\lambda^2 \bigr) \\ &\quad -n\bigl(-6+10\lambda+8r^6\lambda+4r^8 \lambda^2\\ &\quad +r^2\bigl(-21 +34\lambda-5\lambda^2 \bigr) +r^4\bigl(-5+12\lambda+\lambda^2\bigr) \bigr)\\ &\quad +n^2\bigl(-8+4r^8(\lambda -1)\lambda-2r^2(9+7 \lambda)\\ &\quad +r^6\bigl(5-26 \lambda+5\lambda^2 +r^4 \bigl(3-52\lambda+9\lambda^2\bigr)\bigr)\bigr)\bigr), \\ D&=k^2 \bigl(1+r^2 \bigr) \bigl(1+r^2\lambda \bigr) \bigl(-2\bigl(5+ \bigl(4r^2-7-4r^4 \bigr)\lambda \\ &\quad +\bigl(6+8r^2+19r^4+2r^6\bigr) \lambda^2 +r^4\bigl(-3+2r^2\bigr) \lambda^3\bigr)\\ &\quad +n^2\bigl(1+r^2\bigr) \bigl(4r^8(\lambda-1)\lambda ^2-4-2r^2(3+5 \lambda) \\ &\quad +r^6\lambda\bigl(3\lambda^2-5-6\lambda \bigr)-r^4\bigl(1+16\lambda+3\lambda ^2\bigr)\bigr)\\ &\quad +n \bigl(12-8\lambda+12r^8\lambda^3+4r^10 \lambda^3\\ &\quad +r^2 \bigl(42\lambda-1-29\lambda^2 \bigr) +r^6\lambda\bigl(5+2\lambda+9\lambda ^2 \bigr)\\ &\quad +r^4\bigl(25\lambda-3+3\lambda^2-9 \lambda^3\bigr)\bigr)\bigr), \\ E&=6 \bigl(1+nr^2-k\sqrt{\alpha} \bigr)^2\bigl(2\sqrt{ \alpha} \bigl(1+r^2\lambda \bigr)^5 \\ &\quad +k^3\bigl(1+r^2\bigr)^4\lambda \bigl(-1+\bigl(3+2r^2\bigr)\lambda\bigr)\\ &\quad +2k^2 \bigl(1+r^2\bigr)\sqrt{\alpha }\bigl(2+\bigl(3r^2-3-2r^4 \bigr)\lambda \\ &\quad +\bigl(4+5r^2+13r^4\bigr)\lambda ^2+r^2\bigl(4+7r^2+13r^4+2r^6 \bigr)\lambda^3\\ &\quad +r^6\bigl(r^2-1\bigr)\lambda ^4\bigr)\\ &\quad +k\bigl(1+r^2\bigr) \bigl(6+\bigl(-5+16r^2-3r^4 \bigr)\lambda\\ &\quad +\bigl(5+3r^2+33r^4-r^6\bigr) \lambda ^2\\ &\quad +r^2\bigl(5+6r^2+27r^4+2r^6 \bigr)\lambda^3\\ &\quad +\bigl(4r^8-2r^6\bigr) \lambda^4\bigr)\bigr). \end{aligned}$$

We study the physical properties of anisotropic compact objects numerically and follow the following steps. For given values of λ and k, the size of the star is estimated from the condition that pressure vanishes at the boundary which follows from Eq. (5). The mass to radius $\frac{m}{b}$ of a star is determined from Eqs. (8) and (14), which in turn determines the physical size of the compact star (r _o ). For a given set of values of the parameters λ, A, k, n, and the mass (m), the radius of an anisotropic compact object is obtained in terms of the model parameter R. Thus for a known mass of a compact star R is determined which in turn determines the corresponding radius.

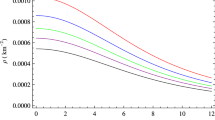
The radial variation of pressure and density of anisotropic compact objects for different parameters are plotted in Figs. 1–4. In Figs. 1 and 2, variation of radial pressure is plotted for a given set of values of A, n and λ for different k. It is noted that the pressure increases with an increase in k whereas the density decreases. The central density also found to increases with decrease in the value of k. The radial variation of pressure with n is plotted in Fig. 3. It is evident that although the pressure inside the star decreases with an increase in n, the density remains invariant. The radial variation of density with λ is plotted in Fig. 4. Both the density and the pressure are found to increase with an increase in λ value showing an increase in corresponding central density. But the difference between central density with that of surface density reduces with increase in λ. It is noted that both the pressure and the density are independent on A. The radial variation of pressure for different λ is shown in Fig. 5, it is evident that the decrease in radial pressure near the boundary is sharp for higher values of λ. The variation of both radial and transverse pressure are plotted in Fig. 6, it is noted that the value of transverse pressure at the boundary is more than that of radial pressure although they begin with same central pressure at the centre. Figure 7 is a plot of squared speed of sound i.e., $\frac{dp}{d\rho}$ with different n values. It is found that $\frac{dp}{d\rho}$ is positive inside the star and obeys causality condition. It shows stability of the stellar models. To check the strong energy condition we plot the radial variation of (ρ−3p) for different values of n, λ and k values in Figs. 8–12. In Figs. 8 and 9 it is observed the SEC is obeyed. But from Figs. 10, 11 and 12, it is noted that there exist a region near the center of the star where SEC is not obeyed. It is further noted that the radius of that region increases with an increase in the parameter values n, k and λ. This is interesting as two distinct regions are found to exist in the compact objects corresponding to the solution obtained here which may be useful for constructing a core-envelope model of the star. The radial variation of anisotropy inside the star for different n values are plotted in Fig. 13. It is evident that the anisotropy of a star increases with increase in value of the parameter n.

Fig. 1

Radial variation of pressure for different k with n=0.60, λ=1.9999 and A=2. Red line for k=0.55, blue line for k=0.5 and dashed line for k=0.4

Fig. 2

Radial variation of density for different k with n=0.60, λ=2 and A=2. Blue line for k=0.40, dashed line for k=0.50 and red line for k=0.55

Fig. 3

Radial variation of pressure for different n with k=0.31, λ=2 and A=2. Blue line for n=1.22, dashed line for n=0.95 and red line for n=0.8

Fig. 4

Radial variation of density for different λ with k=0.641, n=0.60 and A=2. Blue line for λ=1.9999, and red line for λ=1.1

Fig. 5

Variation of radial pressure for different λ with k=0.641, n=0.60 and A=2. Blue line for λ=1.0, dashed line for λ=1.5 and thick line for λ=1.9999

Fig. 6

Radial variation of transverse and radial pressure with λ=10, n=0.8, A=2 and k=0.31. Blue line for radial pressure and red line for transverse pressure

Fig. 7

Radial variation of $\frac{dp}{d\rho}$ with different n for k=0.61669, λ=2, A=2. Red line for n=0.4, dashed line for n=0.3 and blue line for n=0.2

Fig. 8

Variations of parameter n with radial distant r (in km) for SEC (ρ−3p). Blue line for n=0.7 and red line for n=1

Fig. 9

Variations of parameter k with radial distance r (in km) for SEC (ρ−3p). Blue line for k=0.4 and red line for k=0.50

Fig. 10

Radial variations of SEC i.e., (ρ−3p) with different n for k=0.641, λ=2 and A=2. Dashed line for n=0.8, red line for n=0.7 and thick line for n=0.67

Fig. 11

Radial variations of SEC i.e., (ρ−3p) with different λ for k=0.641, n=0.65 and A=5. Dashed line for λ=2, blue line for λ=1.8 and thick line for λ=1.7

Fig. 12

Radial variations of SEC i.e., (ρ−3p) with different k for n=0.65, λ=1.8 and A=5. Blue line for k=0.641 and thick line for k=0.6

Fig. 13

Radial variations of anisotropic parameter Δ for different n. Blue line for n=0.7 and red line for n=1

The reduced size of a star ($\tilde{b}=\frac{b}{R}$) is tabulated for different n and λ values in Table 1. It is evident that for a given λ if one increases n the reduced size of a star increases. On the other hand for a isotropic star as λ increases for a given n the reduced size increases but in the case of an anisotropic star the reduced size decreases in this case as one increases λ. In Table 2 reduced size of a star is tabulated for different k and λ values. It is evident that for a given λ as we increase k the reduced size increases. However for a given k on increasing λ the reduced size of the compact object decreases.

Table 1 Variation of $\tilde{b}=\frac{b}{R}$ for given n=0,0.55,0.58,0.60 with different λ

Table 2 Variation of reduced size $\tilde{b}=\frac{b}{R}$ with λ for different k

4 Physical analysis

For a given mass of a compact star, it is possible to estimate the corresponding radius in terms of the geometric parameter R. To obtain stellar models we consider compact objects with observed mass (Lattimer 2010) which determines the radius of the star for different values of R with given set of values of n, A, k and λ. It is known that the radius of a neutron star is ≤(11–14) km (Steiner et al. 2010), therefore, to obtain a viable stellar model for compact object the upper bound of the size is fixed accordingly. In the next section we consider three stars whose masses (Dey et al. 1999; Li et al. 1999; Lattimer 2010) are known from observations to explore suitability of the solutions considered here.

Model 1

For X-ray pulsar Her X-1 (Lattimer 2010; Dey et al. 1999; Sharma and Maharaj 2007) characterized by mass m=1.47M_⊙, where M_⊙=the solar mass we obtain a stellar configuration with radius r _o =8.31106 km, for R=8.169 km. The compactness of the star in this case is $u=\frac{m}{r_{o}} = 0.30$. The ratio of density at the boundary to that at the centre for the star is 0.128 which is satisfied for the parameters λ=1.9999, k=0.641, A=2 and n=0.697. It is found that compactness factor u=0.2 accommodates a star of radius r _o =11.925 km. However, stellar models with different size and compactness factor with the above mass permitted here are tabulated in Table 3. It is also observed that as the compactness factor increases size of the star decreases. It is evident from the second column of Table 4 that increase in λ value which is related to geometry lead to a decrease in the density profile of the compact object.

Table 3 Variation of size of a star with $\frac{m}{b}$ for k=0.641, n=0.697, λ=1.9999 and A=2

Table 4 Density profile $\frac{\rho(b)}{\rho(0)}$ of compact objects

Model 2

For X-ray pulsar J1518+4904 (Lattimer 2010; Dey et al. 1999; Sharma and Maharaj 2007) characterized by mass m=0.72 M_⊙, where M_⊙=the solar mass it is noted that it permits a star with radius r _o =4.071 km, for R=8.169 km. The compactness of the star in this case is $u=\frac{m}{r_{o}} = 0.30$. The ratio of its density at the boundary to that at the centre is 0.142 which is obtained for values of the parameters λ=1.1, k=0.641, A=2 and n=0.60. It is noted that a star of radius r _o =12.332 km. results with same mass having lower compactness factor u=0.09. It is evident from Table 5 that in this case also as the compactness increases radius of the star decreases. The variation of density profile with λ is tabulated in the 3rd column of Table 4. It is found that the density profile decreases as λ increases.

Table 5 Variation of size of a star with $\frac{m}{b}$ for k=0.63, n=0.60, λ=1.1 and A=2

Model 3

In this case we consider a compact object B1855+09(g) (Lattimer 2010; Dey et al. 1999; Sharma and Maharaj 2007) characterized by mass m=1.6M_⊙, where M_⊙=the solar mass, it is noted that its radius is r _o =9.047 km, for R=8.169 km with compactness factor $u=\frac{m}{r_{o}} = 0.30$. The ratio of density at the boundary to that at the centre for the star is 0.187 which is found for the values of the parameters λ=1, k=0.52, A=2 and n=0.50. It is noted that a star of compactness factor u=0.22 accommodates a star with radius r _o =11.907 km. For the same mass considered here it is possible to obtain a class of stellar models with different size and compactness which are tabulated in Table 6. We note that size of the star decreases with the increase in compactness. The variation of density profile with λ is displayed in 4th column of Table 4. It is evident the density profile decreases as λ increases.

Table 6 Variation of size of a star with $\frac{m}{b}$ for k=0.63, n=0.60, λ=1.1 and A=2

5 Discussion

In this paper, we present a class of new general relativistic solutions for a class of compact stars which are in hydrostatic equilibrium considering an anisotropic interior fluid distribution. The radial pressure and the tangential pressure are different, variations of the pressures are determined. As the EOS of the fluid inside a neutron star is not known so we adopt here numerical technique to determine a suitable EOS of the matter content inside the star for a given space-time geometry. The interior space-time geometry considered here is characterized by five geometrical parameters namely, λ, R, k, A and n which are used to obtain different stellar models. For n=0, the relativistic solution reduces to that considered in by Pant and Sah (1985) and Deb et al. (2012). The permitted values of the unknown parameters are determined from the following conditions: (a) metric matching at the boundary, (b) $\frac{dp}{d\rho}<1$, (c) pressure at the boundary is zero i.e., p=0 and (d) the positivity of density.

We note the following: (i) In Figs. 1 and 2, the radial variation of pressure and density are plotted for different k for a given set of values of λ, A, n and k. The radial pressure increase with an increase in k but the density is found to decrease. The central density of the compact object increases if k decreases. (ii) In Fig. 3, variation of radial pressure inside the star is plotted for different n. We note that pressure decreases as n increases, however, density does not change. (iii) In Figs. 4 and 5, radial variation of density and pressure are plotted for different λ. We note that both the pressure and the density increases with an increase in λ. The central density is found to increase with an increase in λ in this case. The radial variation of pressure for different λ is shown in Fig. 5. It is noted that the radial pressure near the boundary decreases sharply for higher values of λ.

(iv) It is evident from Figs. 8 and 9 that SEC is obeyed inside the stars for the configurations considered in the two cases. In Figs. 10–12 we obtain an interesting result where SEC is violated. The size of the region near the centre is further increases with an increase in the value of one of the parameters, n, k and λ keeping the other parameters unchanged. Thus the solution obtained here may be useful to construct a core-envelope model of a compact star which will be discussed elsewhere. (v) In Fig. 13, the radial variation of anisotropy inside the star for different n values are plotted. The increase in value of n is related to increase in anisotropy of the fluid pressure. (vi) For a given λ as we increase n the reduced size of star increases. However for n=0 the size of a star increases with an increase in λ which is tabulated in Table 1. It is noted that for non-zero values of n the size of the star however found to decrease.

(vii) For a given λ the size of the star increases as k increases, but for a given k the size of the star decreases as λ increases which is shown in Table 2. (viii) Considering observed masses of the compact objects namely, HER X-1, J1518+4904 and B1855+09(g) we explore the interior of the star. A class of compact stellar models with anisotropic pressure distribution are permitted with the new solution discussed here. In the models stars of different compactness factor which are shown in Tables 3, 5 and 6 for different geometric parameters. The density profile of the models are also tabulated in Tables 4. The density profile inside the star is found to decrease as λ increases. (ix) We obtain functional relation of the radial pressure with the density for the models considered here which is presented in Table 7. It is noted that a viable stellar model may be obtained here with a polynomial EOS. In the table we have displayed linear and a quadratic EOS only, it may be mentioned here that similar EOS are considered recently in Maharaj and Takisa (2012) and Chattopadhyay et al. (2012) to obtain relativistic stellar models. We note that though a stellar configuration in our case permits a linear EOS, it does not accommodate a star satisfying MIT bag model (Chattopadhyay et al. 2012). It is also noted that the stellar models obtained here allows neutron stars with mass less than 2M_⊙ for an anisotropic fluid distribution. The observed maximum mass of a neutron star is 2M_⊙, therefore the stellar models obtained here may be relevant for compact objects with nuclear density. A physically realistic stellar model up to radius ∼(11–14) km may be permitted here with the relativistic solutions accommodating less compactness (Steiner et al. 2010). (x) We plot radial variation of the anisotropy measurement in pressure i.e., Δ in Fig. 14 with n. It is evident from the 3D plot that Δ→0 when n→0 which leads to isotropic pressure case. For n>0, the difference in tangential pressure to radial pressure initially increases which however attains a constant value for large n. It is also noted from Eq. (12) that Δ=0 when r=0 i.e., in the stellar model both the tangential and radial pressure are equal at the center.

Fig. 14

Plot of Δ with positive n and radial distance with λ=2 and k=0.4

Table 7 Variation of radial pressure with density for different stellar models