Natural frequency calculation of open laminated conical and cylindrical shells by a meshless method

Abstract

In this paper, a new and an efficient solution method based on local gradient smoothing method has been applied to free vibration problem of open composite laminated cylindrical and conical shells with elastic boundary conditions. The theoretical model is formulated by the first-order shear deformation theory, and the motion equation is obtained by the Hamilton’s principle. The motion equation is discretized by meshless shape function; in this process, the derivatives of the shape function are approximated by local gradient smoothing method. The accuracy, applicability and efficiency of this method are demonstrated for free vibrations of open composite laminated cylindrical and conical shells with different geometric, material parameters and boundary condition. The numerical results show good convergence characteristics and good agreement between the present method and the existing literature. And through several numerical examples, some useful results for free vibration results of open composite laminated cylindrical and conical shells are obtained, which may serve as a benchmark solutions for researchers to check their analytical and numerical methods.

1 Introduction

As the rapid development of science and technology, new processes for manufacturing composite materials are used in variety of engineering fields such as aerospace, high-speed train and ship engineering and are developing rapidly. With the development of new composite materials manufacturing processes, the cost of materials has reduced and application fields of composite materials are extending more widely. The study on free vibration of shells, one of the structural elements widely used in engineering, has attracted of attention many researchers.

So far, for analyzing the dynamic characteristics of shell, classical shell theory (CST) [1,2,3,4,5], first-order shear deformation theory (FSDT) [6,7,8,9] and HSDT (higher-order shear deformation theory) [10,11,12,13,14,15] have been developed and used. Since transverse normal and shear deformations are neglected in the CST, the FSDT was developed to correct these defects. HSDT is a theory developed to avoid the use of shear correction coefficient introduced in FSDT and to predict more accurate vibration behavior.

However, as pointed out by Qu et al. [7], somewhat complex formulas and boundary terms are introduced in the HSDT, which are much more computationally complex than the FSDT. Therefore, it is very important to carefully select rational shell theory for free vibration analysis of composite laminated shells. In the existing literature, it can be seen that FSDTs with appropriate shear correction factors are suitable for predicting the vibration behavior of composite laminated shells. Francesco [16,17,18,19] has used FSDT to perform static and dynamic analyses of various types of laminate shells and panels on the Winkler–Pasternak elastic foundation, achieving very good results.

From these results, FSDT is just applied for presented method. Based on various shell theories (e.g., CST, FSDT and HSDT), a number of methods have been proposed, such as the Rayleigh–Ritz method, the Haar wavelet discretization method (HWDM), the Galerkin method and the finite element method (FEM), to deal with the vibration problems of the laminated composite shell.

Many researchers have made efforts to analyze the vibration behavior of laminated composite shell by using approach analytical and numerical techniques, such as Fourier–Ritz method [20,21,22,23,24,25,26], Jacobi–Ritz method [27,28,29,30,31], differential quadrature method (DQM) [2, 4, 9, 32, 33], discrete singular convolution method (DSCM) [5, 6], a general domain decomposition method [7, 34], Haar wavelet discretization method (HWDM) [35, 36], meshless method [13, 37, 38], spline method [8, 39] and FEM [40]. Some researchers have applied differential geometry within the generalized differential quadrature (GDQ) method while performing static and dynamic analysis of functionally graded (FGM) and laminated shells and panels resting on linear and nonlinear elastic foundations [18, 19].

From the review of previous literature, it can be seen that although there are many methods for vibration analysis of laminated composite shell, finding a reliable and efficient approach to laminated composite shells with different boundary conditions is still a big challenge. Therefore, the purpose of this work is to introduce a simple and effective method to deal with the vibration behavior of the structures. The solution is obtained by using the numerical technique termed the meshless collocation method, which leads to a generalized eigenvalue problem. The mathematical basis and recent developments of this method and its application in engineering are described in detail below.

The meshfree method is a numerical method used to establish a system algebraic equation for the entire problem domain without using a predefined mesh for domain discretization [41]. Over the last few decades, the meshfree methods have been rapidly developed and successfully applied in many fields such as the plate and shell analysis [42,43,44,45], nonlinear dynamic analysis [46, 47], large deformation simulation [48], fluid analysis [49,50,51,52,53,54], and impact and fragmentation simulation [55].

Recently, the detailed investigations have been conducted on various types of meshfree method and their properties [56, 57]. Compared to the weak-form method, the meshless collocation method is very simple and is considered a true meshless method because it doesn’t even need a background cell for numerical integration [58]. On the other hand, the Galerkin meshfree method requires special treatment to apply Dirichlet boundary condition due to the non-interpolatory property of the meshfree shape function, but in the meshless collocation method it can be applied directly without any other treatment. In the past, many researchers have conducted studies on the strong-form meshfree method and its application, and interesting arrangement methods have been proposed such as least-squares radial point collocation method [59], isogeometric collocation method [60], finite point method [61], strong-form meshless implementation of Taylor series method [62], etc. However, in the methods mentioned above, higher-order derivatives of the shape function are required, which is one of the causes of the instability and the inaccuracy of the solution. Wang et al. have approximated the derivatives of meshfree shape function by using the gradient smoothing method (GSM) in the strong form of the given problem [63]. The first-order smoothing gradient of meshfree shape function is obtained by the meshfree interpolation of its standard derivatives, and the second-order smoothing gradients are calculated by directly differentiating the first-order smoothing gradients. Liu et al. used GSM instead of the generalized finite difference method (FDM) to successfully approximate the first- and second-order derivatives of the field function in the solid mechanics problems [64].

GSM is a kind of systematic technique for approximating the derivatives of a function by using the smoothing operation expressed in integral form. Compared to the conventional finite difference and the generalized finite difference methods, GSM has the advantage of being easily applied to arbitrary irregular meshes for complex geometry. In GSM, a well-designed smoothing domain is generated around the node of interest, and the derivative of the field function at that node is approximated by the integration of the field function along the smoothing domain boundary. At this time, the sum of the areas of the smoothing domains for all nodes is equal to the area of the entire problem domain [58, 64]. However, a fixed smoothing mesh domain which is time-consuming to create in the problem domain is required in GSM.

In this paper, a local gradient smoothing method (LGSM) is proposed to approximate the derivatives of the meshfree shape function in the local smoothing domain. In this method, the local smoothing domains corresponding to the nodes are independent of each other and therefore spacing may occur between them. In other words, the sum of the areas of the local smoothing domains according to all the nodes may not be equal to the area of the problem domain. The proposed method makes it possible to reduce the effort of making the smoothing domains. The integration of field function in the smoothing domains is calculated by using the numerical integration methods such as Gauss quadrature rule. In this paper, the derivatives of the meshfree shape function approximated by the proposed method are applied to the vibration motion equations of the considered shell structures, in which shell structures selected the open laminated composite cylindrical and conical shell, in order to depict a generalized shell structure. Several numerical examples to some benchmark problems are provided to model the free vibration of open composite laminated cylindrical and conical shells with classical, elastic and combined boundary conditions. The proposed numerical example shows that the current methods can obtain solutions with high accuracy.

2 Theoretical formulations

2.1 Local gradient smoothing method

In the paper, the derivatives of the meshless shape function are approximated by using the local gradient smoothing method. According to the local gradient smoothing method, the first-order smoothing gradients of the meshless shape function at node $i$ can be expressed as:

$$ \varvec{\varPhi}_{,\zeta } (\varvec{x}_{i} ) = \int\limits_{{\varOmega_{i} }} {\varvec{\varPhi}_{,\zeta } (\varvec{x})}\varvec{\varPsi}\left( {\varvec{x} - \varvec{x}_{i} } \right){\text{d}}\varOmega $$

(1)

where $\zeta = (1,2)$ denote the $x$ and $\theta$ directions, $\varvec{\varPsi}$ is the smoothing function, $\varOmega_{i}$ is the local smoothing domain and $\left( {} \right)_{,\zeta }$ represent $\frac{\partial }{\partial \zeta }$. The comparison of the smoothing domains in the traditional GSM with that in the proposed method is shown in Fig. 1. As shown in Fig. 1a, GSM is a global method that uses a fixed smoothing domain according to the node distribution of the problem area. In contrast, the local smoothing domains corresponding to the nodes are independent of each other. Since the smoothing domains may be overlapped or spaced, the sum of smoothing domain areas cannot be equal to the area of problem domain. These features of the local smoothing domain make its generation process very simple.

Fig. 1

The smoothing domains of traditional GSM (a) and local gradient smoothing method (b)

A weighted Shepard function is used as the smoothing function:

$$ \varvec{\varPsi}\left( {\varvec{x} - \varvec{x}_{i} } \right) = \frac{{\psi \left( {\varvec{x} - \varvec{x}_{i} } \right)}}{{\sum\nolimits_{j = 1}^{N} {\psi \left( {\varvec{x} - \varvec{x}_{j} } \right)A_{j} } }} $$

(2)

where $N$ is the number of nodes distributed in the problem domain and $A_{j}$ is the local smoothing domain area corresponding to the $j$ th node. The following piecewise constant function is used in this paper:

$$ \psi \left( {\varvec{x} - \varvec{x}_{i} } \right) = \left\{ {\begin{array}{*{20}l} 1 & \quad {\varvec{x} \in \varOmega_{i} } \\ 0 & \quad {\varvec{x} \notin \varOmega_{i} } \\ \end{array} } \right. $$

(3)

Substituting Eq. (3) into Eq. (2), the smoothing function is

$$ \varvec{\varPsi}\left( {\varvec{x} - \varvec{x}_{i} } \right) = \left\{ {\begin{array}{*{20}l} {\frac{1}{{\sum\nolimits_{k = 1}^{{n_{i} }} {A_{k} } }}} & \quad {\varvec{x} \in \varOmega_{i} } \\ 0 & \quad {\varvec{x} \notin \varOmega_{i} } \\ \end{array} } \right. $$

(4)

where $n_{i}$ is the number of nodes in the local smoothing domain of node $i$. In this paper, the local smoothing domain of node $i$ is made small enough to not contain any nodes other than node $i$. That is, Eq. (4) is simplified as

$$ \varvec{\varPsi}\left( {\varvec{x} - \varvec{x}_{i} } \right) = \left\{ {\begin{array}{*{20}l} {1/A{}_{i}} & \quad {\varvec{x} \in \varOmega_{i} } \\ 0 \quad & {\varvec{x} \notin \varOmega_{i} } \\ \end{array} } \right. $$

(5)

Integrating by parts Eq. (2) is

$$ \varvec{\varPhi}_{,\zeta } (\varvec{x}_{i} ) = \int\limits_{{\varGamma_{i} }} {\varvec{\varPhi}(\varvec{x})} \varvec{n}_{\zeta } \left( \varvec{x} \right)\varvec{\varPsi}\left( {\varvec{x} - \varvec{x}_{i} } \right){\text{d}}\varGamma - \int\limits_{{\varOmega_{i} }} {\varvec{\varPhi}(\varvec{x})}\varvec{\varPsi}_{,\zeta } \left( {\varvec{x} - \varvec{x}_{i} } \right){\text{d}}\varOmega $$

(6)

where $\varvec{n}_{\zeta } \left( \varvec{x} \right)$ is the $\zeta$ direction unit outward normal vector on the local smoothing domain boundary. Since the smoothing function is chosen as a constant, the second term of the right-hand side of Eq. (6) is eliminated:

$$ \varvec{\varPhi}_{,\zeta } (\varvec{x}_{i} ) = \int\limits_{{\varGamma_{i} }} {\varvec{\varPhi}(\varvec{x})} \varvec{n}_{\zeta } \left( \varvec{x} \right)\varvec{\varPsi}\left( {\varvec{x} - \varvec{x}_{i} } \right){\text{d}}\varGamma = \frac{1}{{A_{i} }}\int\limits_{{\varGamma_{i} }} {\varvec{\varPhi}(\varvec{x})} \varvec{n}_{\zeta } \left( \varvec{x} \right){\text{d}}\varGamma $$

(7)

As a result, the first-order derivative of the shape function becomes the line integration along the boundary of the local smoothing area.

In the paper, the integrals of Eq. (7) are obtained by using Gauss quadrature:

$$ \varvec{\varPhi}_{,\zeta } (\varvec{x}_{i} ) = \frac{1}{{A_{i} }}\sum\limits_{k = 1}^{{n_{q} }} {w_{k} }\varvec{\varPhi}(\varvec{x}_{Qk} )\varvec{n}_{\zeta } \left( {\varvec{x}_{Qk} } \right)\left| {\varvec{J}_{i} } \right| $$

(8)

where $n_{q}$ is the number of Gauss points placed on the boundary of the local smoothing domain, $w_{k}$ the Gauss weighting factor of Gauss point $\varvec{x}_{Qk}$ and $\varvec{J}_{i}$ Jacobian matrix for the curve integration in the boundary $\varGamma_{i}$. Similarly, according to the procedure described in Eqs. (1)–(8), the second-order gradient of the shape function is approximated as:

$$ \varvec{\varPhi}_{,\zeta \eta } (\varvec{x}_{i} ) = \frac{1}{{A_{i} }}\sum\limits_{k = 1}^{{n_{q} }} {w_{k} }\varvec{\varPhi}_{,\zeta } (\varvec{x}_{Qk} )\varvec{n}_{\eta } \left( {\varvec{x}_{Qk} } \right)\left| {\varvec{J}_{i} } \right| $$

(9)

where $\zeta ,\eta = (1,2)$ denote the $x$ and $\theta$ directions. Substituting Eq. (8) into Eq. (9), the second-order gradient of the shape function can be rewritten as:

$$ \varvec{\varPhi}_{,\zeta \eta } (\varvec{x}_{i} ) = \frac{1}{{A_{i} }}\sum\limits_{k = 1}^{{n_{q} }} {w_{k} } \left[ {\frac{1}{{A_{Qk} }}\sum\limits_{m = 1}^{{n_{Q} }} {w_{m} }\varvec{\varPhi}(\varvec{x}_{Qm} )\varvec{n}_{\zeta } \left( {\varvec{x}_{Qm} } \right)\left| {\varvec{J}_{Qk} } \right|} \right]\varvec{n}_{\eta } \left( {\varvec{x}_{Qk} } \right)\left| {\varvec{J}_{i} } \right| $$

(10)

where $A_{Qk}$ and $n_{Q}$ are the area of the local smoothing domain $\varOmega_{Qk}$ generated around the Gauss point $\varvec{x}_{Qk}$ and the number of Gauss points placed on the boundary of $\varOmega_{Qk}$, respectively, $w_{k}$ is the Gauss weighting factor for Gauss point $\varvec{x}_{Qm}$ and $\varvec{J}_{Qk}$ is the Jacobian matrix for the curve integration of the boundary $\varGamma_{Qk}$.

As shown in Fig. 2, the local smoothing domains of the second-order gradient are generated around the Gauss points placed on the boundary of the local smoothing domain of the first-order gradient. The first- and second-order gradients according to $\alpha_{q}$ when using the rectangular local smoothing domain in a two-dimensional problem are shown in Figs. 3 and 4. In the figure, $\alpha_{q}$ is a coefficient related to the size of the local smoothing domain:

$$ \alpha_{q} = \frac{{d_{L} }}{{d_{c} }} $$

(11)

where $d_{c}$ and $d_{L}$ are the average nodal spacing and the size of local smoothing domain, respectively. For example, in a two-dimensional domain, $\alpha_{q}$ is

$$ \alpha_{q} = \frac{{d_{Lx} }}{{d_{cx} }} = \frac{{d_{Ly} }}{{d_{cy} }} $$

(12)

where $d_{cx}$ and $d_{cy}$ are the average nodal spacings in the x and y directions and $d_{Lx}$ and $d_{Ly}$ are the length and width of the rectangular local domain.

Fig. 2

The local smoothing domain of the second-order gradient

Fig. 3

The first-order gradients according to $\alpha_{q}$ in the two-dimensional domain a $\alpha_{q} = 0.01$, b $\alpha_{q} = 0.1$, c $\alpha_{q} = 0.5$, d $\alpha_{q} = 1.0$

Fig. 4

The second-order gradients according to $\alpha_{q}$ in the two-dimensional domain a $\alpha_{q} = 0.01$, b $\alpha_{q} = 0.1$, c $\alpha_{q} = 0.5$, d $\alpha_{q} = 1.0$

2.2 Description of the model

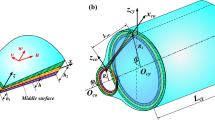
Open composite laminated cylindrical and conical shell with uniform thickness h selected as the analysis model is shown in Fig. 5.

Fig. 5

Geometry and definition of an open composite laminated shell: a coordinate system, b cylindrical, c conical

An orthogonal curvilinear coordinate system (α, β and z) in Fig. 5a is established in the middle surface of the open composite laminated shell. Rα and R_β denote the principal curvature radius in the middle surface along α and β axes, and Lα and L_β denote the lengths of open shell in α and β directions, respectively. In order to simulate the generalized boundary conditions, three groups of translational springs (ku, kv and kw) and two groups of rotational springs (kφ and k_θ) are introduced along the edges of the open shell. The boundary conditions can be generalized readily by assigning the proper values of spring stiffnesses. The geometry and notation of open composite laminated conical shell are shown in Fig. 5b. L and a denote the cone length and the cone semi-vertex angle of the conical shell, R₁ and R₂ are the radius of the cone at start and end edges of conical shell, respectively. The radius R which defined between R₁ and R₂ is a function along x-axis coordinate. If the semi-vertex angle is set to α = 0 in Fig. 5b, it can be considered open cylindrical shells (Fig. 5a) which is a special case of conical shells, and the formulation of conical shell can be reduced to formulation of cylindrical shells.

2.3 Governing equations

The displacement field for the shell based on FSDT assumptions takes the following form [31, 35, 36]:

$$ \begin{aligned} u\left( {x,\theta ,z,t} \right) & = u_{0} \left( {x,\theta ,t} \right) + z\chi_{x} \left( {x,\theta ,t} \right) \\ v\left( {x,\theta ,z,t} \right) & = v_{0} \left( {x,\theta ,t} \right) + z\chi_{\theta } \left( {x,\theta ,t} \right) \\ w\left( {x,\theta ,z,t} \right) & = w_{0} \left( {x,\theta ,t} \right) \\ \end{aligned} $$

(13)

u, v and w denote the generalized displacements, and u₀, v₀ and w₀ are displacements of a point on the reference surface (z = 0) along meridional, circumferential and normal directions, respectively.

$\chi_{x}$ and $\chi_{\theta }$ represent transverse normal rotations at middle surface (z = 0) with respect to β and α axis. t represents the time variable. The strain–displacement relations at any points lying of the conical shell space can be written in the following matrix form:

$$ \underbrace {{\left[ {\begin{array}{*{20}l} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\gamma_{x\theta } } \\ {\chi_{x} } \\ {\chi_{\theta } } \\ {\chi_{x\theta } } \\ {\gamma_{\theta z} } \\ {\gamma_{xz} } \\ \end{array} } \right]}}_{\varvec{\varepsilon}} = \left[ {\begin{array}{*{20}l} {\frac{\partial }{\partial x}} & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ {\frac{\sin \varphi }{R}} & \quad {\frac{1}{R}\frac{\partial }{\partial \theta }} & \quad {\frac{\cos \varphi }{R}} & \quad 0 & \quad 0 \\ {\frac{1}{R}\frac{\partial }{\partial \theta }} & \quad {\frac{\partial }{\partial x} - \frac{\sin \varphi }{R}} & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 \quad & {\frac{\partial }{\partial x}} & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad {\frac{\sin \varphi }{R}} & \quad {\frac{1}{R}\frac{\partial }{\partial \theta }} \\ 0 & \quad 0 & \quad 0 & \quad {\frac{1}{R}\frac{\partial }{\partial \theta }} & \quad {\frac{\partial }{\partial x} - \frac{\sin \varphi }{R}} \\ 0 & \quad { - \frac{\cos \varphi }{R}} & \quad {\frac{1}{R}\frac{\partial }{\partial \theta }} & \quad 0 & \quad 1 \\ 0 & \quad 0 \quad & {\frac{\partial }{\partial x}} & \quad 1 & \quad 0 \\ \end{array} } \right]\underbrace {{\left[ {\begin{array}{*{20}l} u \\ v \\ w \\ {\xi_{x} } \\ {\xi_{\theta } } \\ \end{array} } \right]}}_{\varvec{u}} $$

(14)

where $\varepsilon_{x}^{0}$, $\varepsilon_{\theta }^{0}$ and $\gamma_{x\theta }^{0}$ are the membrane strains on the reference surface, $\chi_{x}$, $\chi_{\theta }$ and $\chi_{x\theta }$ the curvature changes and $\gamma_{xz}$ and $\gamma_{\theta z}$ the transverse shearing strains.

Then, the constitutive equations are expressed in the matrix form as follows:

$$ \varvec{N} = \varvec{D\varepsilon } $$

(15)

where

$$ \varvec{N} = \left[ {\begin{array}{*{20}l} {N_{x} } & {N_{\theta } } & {N_{x\theta } } & {M_{x} } & {M_{\theta } } & {M_{x\theta } } & {Q_{\theta } } & {Q_{x} } \\ \end{array} } \right]^{T} $$

(16a)

$$ \varvec{\varepsilon}= \left[ {\begin{array}{*{20}l} {\varepsilon_{x} } & {\varepsilon_{\theta } } & {\gamma_{x\theta } } & {\chi_{x} } & {\chi_{\theta } } & {\chi_{x\theta } } & {\gamma_{\theta z} } & {\gamma_{xz} } \\ \end{array} } \right]^{T} $$

(16b)

$$ \varvec{D} = \left[ {\begin{array}{*{20}l} {A_{11} } & \quad {A_{12} } & \quad {A_{16} } & \quad {B_{11} } & \quad {B_{12} } & \quad {B_{16} } & \quad 0 & \quad 0 \\ {A_{12} } & \quad {A_{22} } & \quad {A_{26} } & \quad {B_{12} } & \quad {B_{22} } & \quad {B_{26} } & \quad 0 & \quad 0 \\ {A_{16} } & \quad {A_{26} } & \quad {A_{66} } & \quad {B_{16} } & \quad {B_{26} } & \quad {B_{66} } & \quad 0 & \quad 0 \\ {B_{11} } & \quad {B_{12} } & \quad {B_{16} } & \quad {D_{11} } & \quad {D_{12} } & \quad {D_{16} } & \quad 0 & \quad 0 \\ {B_{12} } & \quad {B_{22} } & \quad {B_{26} } & \quad {D_{12} } & \quad {D_{22} } & \quad {D_{26} } & \quad 0 & \quad 0 \\ {B_{16} } & \quad {B_{26} } & \quad {B_{66} } & \quad {D_{16} } & \quad {D_{26} } & \quad {D_{66} } & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad {A_{44} } & \quad {A_{45} } \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad {A_{45} } & \quad {A_{55} } \\ \end{array} } \right] $$

(16c)

The individual elements of the stiffness matrix D are expressed as:

$$ \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {A_{ij} = \sum\nolimits_{k = 1}^{{N_{L} }} {\bar{Q}_{ij}^{k} \left( {z_{k + 1} - z_{k} } \right)} } & \quad {i,j = 1,2,6} \\ \end{array} } \\ {\begin{array}{*{20}l} {A_{ij} = k_{c} \sum\nolimits_{k = 1}^{{N_{L} }} {\bar{Q}_{ij}^{k} \left( {z_{k + 1} - z_{k} } \right)} } & \quad {i,j = 4,5} \\ \end{array} } \\ {\begin{array}{*{20}l} {B_{ij} = \frac{1}{2}\sum\nolimits_{k = 1}^{{N_{L} }} {\bar{Q}_{ij}^{k} \left( {z_{k + 1}^{2} - z_{k}^{2} } \right)} } & \quad {i,j = 1,2,6} \\ \end{array} } \\ {\begin{array}{*{20}l} {D_{ij} = \frac{1}{3}\sum\nolimits_{k = 1}^{{N_{L} }} {\bar{Q}_{ij}^{k} \left( {z_{k + 1}^{3} - z_{k}^{3} } \right)} } & \quad {i,j = 1,2,6} \\ \end{array} } \\ \end{array} } \right. $$

(17)

where A_ij, B_ij and D_ij denote extensional stiffness, the extensional-bending coupling stiffness and the bending stiffness, respectively, and $\kappa_{c}$ is the shear correction factor. $\bar{Q}_{ij}^{k}$ are the elements of the dislocation stiffness matrix $\bar{\varvec{Q}}^{k}$ corresponding to the kth layer, expressed as following:

$$ \bar{\varvec{Q}}^{k} = \varvec{T}_{k} \varvec{Q}^{k} \varvec{T}_{k}^{T} $$

(18)

In Eq. (18), the transformation matrix $\varvec{T}_{k}$ and the reduced the stiffness matrix $\varvec{Q}^{k}$ for kth layer are defined as:

$$ \varvec{T}_{k} = \left[ {\begin{array}{*{20}l} {\cos^{2} \delta_{k} } & {\sin^{2} \delta_{k} } & 0 & 0 & { - 2\sin \delta_{k} \cos \delta_{k} } \\ {\sin^{2} \delta_{k} } & {\cos^{2} \delta_{k} } & 0 & 0 & {2\sin \delta_{k} \cos \delta_{k} } \\ 0 & 0 & {\cos \delta_{k} } & {\sin \delta_{k} } & 0 \\ 0 & 0 & { - \sin \delta_{k} } & {\cos \delta_{k} } & 0 \\ {\sin \delta_{k} \cos \delta_{k} } & { - \sin \delta_{k} \cos \delta_{k} } & 0 & 0 & {\cos^{2} \delta_{k} - \sin^{2} \delta_{k} } \\ \end{array} } \right] $$

(19)

where $\delta_{k}$ denotes fiber direction angle of kth layer:

$$ \varvec{Q}^{k} = \left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} {Q_{11}^{k} } & {Q_{12}^{k} } & 0 & 0 & 0 \\ {Q_{21}^{k} } & {Q_{22}^{k} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{44}^{k} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{55}^{k} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{66}^{k} } \\ \end{array} } \right] $$

(20)

The reduced stiffness $Q_{ij}^{k} (i,j = 1,2,4,5,6)$ of the orthotropic materials is defined as

$$ \begin{array}{*{20}l} {Q_{11}^{k} = \frac{{E_{11}^{k} }}{{1 - \mu_{12}^{k} \mu_{21}^{k} }},} \hfill & {Q_{12}^{k} = Q_{21}^{k} = \frac{{\mu_{12}^{k} E_{11}^{k} }}{{1 - \mu_{12}^{k} \mu_{21}^{k} }},} \hfill & {Q_{22}^{k} = \frac{{E_{22}^{k} }}{{1 - \mu_{12}^{k} \mu_{21}^{k} }}} \hfill \\ {Q_{44}^{k} = G_{23}^{k} ,} \hfill & {Q_{55}^{k} = G_{13}^{k} ,} \hfill & {Q_{66}^{k} = G_{12}^{k} } \hfill \\ \end{array} $$

(21)

where $E_{11}^{k} ,E_{22}^{k}$ are the Young’s modulus in the principal directions of the kth layer, $G_{12}^{k} ,G_{23}^{k}$ and $G_{13}^{k}$ are shear modulus, respectively. $\mu_{12}^{k} ,\mu_{21}^{k}$ are the Poisson’s ratios.

According to Hamilton’s principle, the governing equations of open composite laminated conical shell shown in Fig. 5 can be written as [6, 65]:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial N_{x} }}{\partial x} + \frac{1}{R}\frac{{\partial N_{x\theta } }}{\partial \theta } + (N_{x} - N_{\theta } )\frac{\sin \varphi }{R} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \xi_{x} }}{{\partial t^{2} }}} \hfill \\ {\frac{{\partial N_{x\theta } }}{\partial x} + \frac{1}{R}\frac{{\partial N_{\theta } }}{\partial \theta } + 2N_{x\theta } \frac{\sin \varphi }{R} + Q_{\theta } \frac{{co\text{s} \varphi }}{R} = I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \xi_{\theta } }}{{\partial t^{2} }}} \hfill \\ {\frac{{\partial Q_{x} }}{\partial x} + \frac{1}{R}\frac{{\partial Q_{\theta } }}{\partial \theta } + Q_{x} \frac{\sin \varphi }{R} - N_{\theta } \frac{{co\text{s} \varphi }}{R} = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \hfill \\ {\frac{{\partial M_{x} }}{\partial x} + \frac{1}{R}\frac{{\partial M_{x\theta } }}{\partial \theta } + (M_{x} - M_{\theta } )\frac{\sin \varphi }{R} - Q_{x} = I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \xi_{x} }}{{\partial t^{2} }}} \hfill \\ {\frac{{\partial M_{x\theta } }}{\partial x} + \frac{1}{R}\frac{{\partial M_{\theta } }}{\partial \theta } + 2M_{x\theta } \frac{\sin \varphi }{R} - Q_{\theta } = I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \xi_{\theta } }}{{\partial t^{2} }}} \hfill \\ \end{array} } \right. $$

(22)

$N_{x} ,N_{\theta }$ and $N_{x\theta }$ are the in-plane force per unit length of shell, $M_{x} ,M_{\theta }$ and $M_{x\theta }$ are the bending moment and twisting moment and $Q_{\theta }$ and $Q_{x}$ are the transverse shear force, respectively. And $R$ is the radius of curvature at a given point and is expressed as:

$$ R = R_{0} + x\sin \varphi $$

(23)

And the mass inertias term I₀, I₁ and I₂ can be expressed as Eq. (24), where $N_{L}$ and $\rho_{k}$ denote the number of layers in shell structure and the density of the kth layer per unit reference surface area, respectively:

$$ \left[ {I_{0} ,I_{1} ,I_{2} } \right] = \sum\limits_{k = 1}^{{N_{L} }} {\int\limits_{{z_{k} }}^{{z_{k + 1} }} {\rho_{k} \left[ {1,z,z^{2} } \right]} } {\text{d}}z $$

(24)

2.4 Solution procedure and implementation of LGSM

In the meshless collocation method, the discretized simultaneous system equations are obtained by directly discretizing the strong forms of the governing equations and boundary condition equations at the nodes. The advantages of meshless collocation method are that algorithm is simple and there are no meshes or cells in the problem domain.

Equation (22) in Sect. 2.3 can be expressed in the matrix form as follows:

$$ \varvec{I\ddot{u}} + \varvec{LN} = {\mathbf{0}} $$

(25)

Individual terms in Eq. (25) can be expressed as follows in detail; N is defined from Eq. (15):

$$ \varvec{I} = \left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} { - I_{0} } & 0 & 0 & { - I_{1} } & 0 \\ 0 & { - I_{0} } & 0 & 0 & { - I_{1} } \\ 0 & 0 & { - I_{0} } & 0 & 0 \\ { - I_{1} } & 0 & 0 & { - I_{2} } & 0 \\ 0 & { - I_{1} } & 0 & 0 & { - I_{2} } \\ \end{array} } \right] $$

(26a)

$$ \varvec{L} = \left[ {\begin{array}{*{20}l} {\frac{\partial }{\partial x} + \frac{\sin \varphi }{R}} & { - \frac{\sin \varphi }{R}} & {\frac{1}{R}\frac{\partial }{\partial \theta }} & 0 & 0 & 0 & 0 & 0 \\ 0 & {\frac{1}{R}\frac{\partial }{\partial \theta }} & {\frac{\partial }{\partial x} + 2\frac{\sin \varphi }{R}} & 0 & 0 & 0 & {\frac{\cos \varphi }{R}} & 0 \\ 0 & { - \frac{\cos \varphi }{R}} & 0 & 0 & 0 & 0 & {\frac{1}{R}\frac{\partial }{\partial \theta }} & {\frac{\partial }{\partial x} + \frac{\sin \varphi }{R}} \\ 0 & 0 & 0 & {\frac{\partial }{\partial x} + \frac{\sin \varphi }{R}} & { - \frac{\sin \varphi }{R}} & {\frac{1}{R}\frac{\partial }{\partial \theta }} & 0 & { - 1} \\ 0 & 0 & 0 & 0 & {\frac{1}{R}\frac{\partial }{\partial \theta }} & {\frac{\partial }{\partial x} + 2\frac{\sin \varphi }{R}} & { - 1} & 0 \\ \end{array} } \right] $$

(26b)

$$ \varvec{\ddot{u}} = \left[ {\begin{array}{*{20}l} {\frac{{\partial^{2} u}}{{\partial t^{2} }}} & {\frac{{\partial^{2} v}}{{\partial t^{2} }}} & {\frac{{\partial^{2} w}}{{\partial t^{2} }}} & {\frac{{\partial^{2} \xi_{x} }}{{\partial t^{2} }}} & {\frac{{\partial^{2} \xi_{\theta } }}{{\partial t^{2} }}} \\ \end{array} } \right]^{T} $$

(26c)

All of the displacements in the equilibrium equations of motion can be approximated as following form using a meshfree shape function:

$$ \underbrace {{\left[ {\begin{array}{*{20}l} u \\ v \\ w \\ {\xi_{x} } \\ {\xi_{\theta } } \\ \end{array} } \right]}}_{\varvec{u}} = \underbrace {{\left[ {\begin{array}{*{20}l} {\phi_{1} } & 0 & 0 & 0 & 0 & {\phi_{2} } & 0 & 0 & 0 & 0 & \cdots & {\phi_{n} } & 0 & 0 & 0 & 0 \\ 0 & {\phi_{1} } & 0 & 0 & 0 & 0 & {\phi_{2} } & 0 & 0 & 0 & \cdots & 0 & {\phi_{n} } & 0 & 0 & 0 \\ 0 & 0 & {\phi_{1} } & 0 & 0 & 0 & 0 & {\phi_{2} } & 0 & 0 & \cdots & 0 & 0 & {\phi_{n} } & 0 & 0 \\ 0 & 0 & 0 & {\phi_{1} } & 0 & 0 & 0 & 0 & {\phi_{2} } & 0 & \cdots & 0 & 0 & 0 & {\phi_{n} } & 0 \\ 0 & 0 & 0 & 0 & {\phi_{1} } & 0 & 0 & 0 & 0 & {\phi_{2} } & \cdots & 0 & 0 & 0 & 0 & {\phi_{n} } \\ \end{array} } \right]}}_{{\varvec{\varPhi}^{T} }}\underbrace {{\left[ {\begin{array}{*{20}l} {u_{1} } \\ {v_{1} } \\ {w_{1} } \\ {\xi_{x1} } \\ {\xi_{\theta 1} } \\ \vdots \\ {u_{n} } \\ {v_{n} } \\ {w_{n} } \\ {\xi_{xn} } \\ {\xi_{\theta n} } \\ \end{array} } \right]}}_{{\varvec{U}_{s} }} $$

(27)

where $n$ is the number of nodes in the support domain of the node being discussed, $\varvec{\varPhi}^{T}$ is the shape function matrix and $\varvec{U}_{s}$ is the node displacement matrix.

By substituting Eq. (27) into Eqs. (14), (14) can be rewritten as the matrix form:

$$ \varvec{\varepsilon = BU}_{s} $$

(28)

where $\varvec{B = }\left[ {\begin{array}{*{20}l} {\varvec{B}_{1} } & {\varvec{B}_{2} } & \cdots & {\varvec{B}_{i} } & \cdots & {\varvec{B}_{n} } \\ \end{array} } \right]$, B_i is expressed as follows:

$$ \varvec{B}_{i} = \left[ {\begin{array}{*{20}l} {\frac{{\partial \phi_{i} }}{\partial x}} & 0 & 0 & 0 & 0 \\ {\frac{\sin \varphi }{R}\phi_{i} } & {\frac{1}{R}\frac{{\partial \phi_{i} }}{\partial \theta }} & {\frac{\cos \varphi }{R}\phi_{i} } & 0 & 0 \\ {\frac{1}{R}\frac{{\partial \phi_{i} }}{\partial \theta }} & {\frac{{\partial \phi_{i} }}{\partial x} - \frac{\sin \varphi }{R}\phi_{i} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{{\partial \phi_{i} }}{\partial x}} & 0 \\ 0 & 0 & 0 & {\frac{\sin \varphi }{R}\phi_{i} } & {\frac{1}{R}\frac{{\partial \phi_{i} }}{\partial \theta }} \\ 0 & 0 & 0 & {\frac{1}{R}\frac{{\partial \phi_{i} }}{\partial \theta }} & {\frac{{\partial \phi_{i} }}{\partial x} - \frac{\sin \varphi }{R}\phi_{i} } \\ 0 & { - \frac{\cos \varphi }{R}\phi_{i} } & {\frac{1}{R}\frac{{\partial \phi_{i} }}{\partial \theta }} & 0 & {\phi_{i} } \\ 0 & 0 & {\frac{{\partial \phi_{i} }}{\partial x}} & {\phi_{i} } & 0 \\ \end{array} } \right] $$

(29)

By substituting Eqs. (15), (27) and (28) into Eq. (25), the discretized systematic equation can be obtained for any node I of the open composite laminated shell:

$$ \varvec{M}_{I} \varvec{\ddot{U}}_{s} + \varvec{K}_{I} \varvec{U}_{s} = {\mathbf{0}} $$

(30)

where the stiffness matrix $\varvec{K}_{I}$ and the mass matrix $\varvec{M}_{I}$ of the node I are expressed as follows:

$$ \varvec{K}_{I} = \varvec{L}_{5 \times 8} \varvec{D}_{8 \times 8} \varvec{B}_{8 \times 5n} = \left[ {\begin{array}{*{20}l} {\varvec{K}_{I1} } & {\varvec{K}_{I2} } & \cdots & {\varvec{K}_{Ii} } & \cdots & {\varvec{K}_{In} } \\ \end{array} } \right] $$

(31a)

$$ \varvec{M}_{I} = \left[ {\begin{array}{*{20}l} {\varvec{M}_{I1} } & {\varvec{M}_{I2} } & \cdots & {\varvec{M}_{Ii} } & \cdots & {\varvec{M}_{In} } \\ \end{array} } \right] $$

(31b)

Detailed expressions of individual elements of stiffness and mass matrix are presented in “Appendix.”

Finally, the total mass and the stiffness matrices corresponding to the all of the nodes distributed in the area considered can be obtained by arranging the individual mass matrices and the stiffness matrices corresponding to the node number in the row direction.

That is, the vibration equation of the total system discretized into the node number of $N$ is defined follows:

$$ \varvec{M\ddot{U}} + \varvec{KU} = {\mathbf{0}} $$

(32)

where $\varvec{U}$ is the total displacement matrix, K and M are the total stiffness matrices and total mass matrices of considered shell structure, respectively, and they are expressed as follows:

$$ \varvec{U} = \left[ {\begin{array}{*{20}l} {u_{1} } & {v_{1} } & {w_{1} } & {\xi_{x1} } & {\xi_{\theta 1} } & \cdots & {u_{N} } & {v_{N} } & {w_{N} } & {\xi_{xN} } & {\xi_{\theta N} } \\ \end{array} } \right]^{T} $$

(33a)

$$ \varvec{\ddot{U}} = \left[ {\begin{array}{*{20}l} {\frac{{\partial^{2} u_{1} }}{{\partial t^{2} }}} & {\frac{{\partial^{2} v_{1} }}{{\partial t^{2} }}} & {\frac{{\partial^{2} w_{1} }}{{\partial t^{2} }}} & {\frac{{\partial^{2} \xi_{x1} }}{{\partial t^{2} }}} & {\frac{{\partial^{2} \xi_{\theta 1} }}{{\partial t^{2} }}} & \cdots & {\frac{{\partial^{2} u_{N} }}{{\partial t^{2} }}} & {\frac{{\partial^{2} v_{N} }}{{\partial t^{2} }}} & {\frac{{\partial^{2} w_{N} }}{{\partial t^{2} }}} & {\frac{{\partial^{2} \xi_{xN} }}{{\partial t^{2} }}} & {\frac{{\partial^{2} \xi_{\theta N} }}{{\partial t^{2} }}} \\ \end{array} } \right]^{T} $$

(33b)

$$ \varvec{M}_{5N \times 5N} = \left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l} {\varvec{M}_{11} } & {\varvec{M}_{12} } & \cdots & {\varvec{M}_{1N} } \\ {\varvec{M}_{21} } & {\varvec{M}_{22} } & \cdots & {\varvec{M}_{2N} } \\ \vdots & \vdots & \ddots & \vdots \\ {\varvec{M}_{N1} } & {\varvec{M}_{N2} } & \cdots & {\varvec{M}_{NN} } \\ \end{array} } \right],\,\varvec{K}_{5N \times 5N} = \left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l} {\varvec{K}_{11} } & {\varvec{K}_{12} } & \cdots & {\varvec{K}_{1N} } \\ {\varvec{K}_{21} } & {\varvec{K}_{22} } & \cdots & {\varvec{K}_{2N} } \\ \vdots & \vdots & \ddots & \vdots \\ {\varvec{K}_{N1} } & {\varvec{K}_{N2} } & \cdots & {\varvec{K}_{NN} } \\ \end{array} } \right] $$

(33c)

The natural frequencies of the considered shell structures can be determined by solving the standard eigenvalue problem in Eq. (32).

It should be noted that the global matrix in Eq. (33c) contains a matrix corresponding to the boundary condition. In the meshless collocation method, the equations of motion are directly discretized about all of nodes including boundary nodes. Therefore, the boundary condition is reflected in the stiffness and the mass matrix of the whole system represented in Eq. (33c). Discretization of nodes on the boundary proceeds in the following order: The boundary condition equation generalized in the open composite laminated conical shell shown in Fig. 5 can be written as [65]:

$$ \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {N_{x} - k_{x0}^{u} u = 0} \hfill \\ {N_{x\theta } - k_{x0}^{v} v = 0} \hfill \\ {Q_{x} - k_{x0}^{w} w = 0} \hfill \\ \begin{aligned} M_{x} - k_{x0}^{x} \xi_{x} = 0 \hfill \\ M_{x\theta } - k_{x0}^{\theta } \xi_{\theta } = 0 \hfill \\ \end{aligned} \hfill \\ \end{array} } & {x = 0} \\ \end{array} } \right.,\,\left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {N_{x} + k_{x1}^{u} u = 0} \hfill \\ {N_{x\theta } + k_{x1}^{v} v = 0} \hfill \\ {Q_{x} + k_{x1}^{w} w = 0} \hfill \\ \begin{aligned} M_{x} + k_{x1}^{x} \xi_{x} = 0 \hfill \\ M_{x\theta } + k_{x1}^{\theta } \xi_{\theta } = 0 \hfill \\ \end{aligned} \hfill \\ \end{array} } & {x = L} \\ \end{array} } \right. , $$

(34a)

$$ \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {N_{x\theta } - k_{\theta 0}^{u} u = 0} \hfill \\ {N_{\theta } - k_{\theta 0}^{v} v = 0} \hfill \\ {Q_{\theta } - k_{\theta 0}^{w} w = 0} \hfill \\ \begin{aligned} M_{x\theta } - k_{\theta 0}^{x} \xi_{x} = 0 \hfill \\ M_{\theta } - k_{\theta 0}^{\theta } \xi_{\theta } = 0 \hfill \\ \end{aligned} \hfill \\ \end{array} } & {\theta = 0} \\ \end{array} } \right.,\,\left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {N_{x\theta } + k_{\theta 1}^{u} u = 0} \hfill \\ {N_{\theta } + k_{\theta 1}^{v} v = 0} \hfill \\ {Q_{\theta } + k_{\theta 1}^{w} w = 0} \hfill \\ \begin{aligned} M_{x\theta } + k_{\theta 1}^{x} \xi_{x} = 0 \hfill \\ M_{\theta } + k_{\theta 1}^{\theta } \xi_{\theta } = 0 \hfill \\ \end{aligned} \hfill \\ \end{array} } & {\theta = \theta_{0} } \\ \end{array} } \right. , $$

(34b)

where $k_{m}^{u} ,k_{m}^{v} ,k_{m}^{w} ,k_{m}^{x}$ and $k_{m}^{\theta }$$(m = x0,x1,\theta 0,\theta 1)$ are the spring coefficients of the boundary foundation, as shown in Fig. 5a.

In Eq. (34a), the boundary condition equation for x = 0 can be written as follows in the matrix form:

$$ \left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ \end{array} } \right]\varvec{N - }\left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} {k_{x0}^{u} } & 0 & 0 & 0 & 0 \\ 0 & {k_{x0}^{v} } & 0 & 0 & 0 \\ 0 & 0 & {k_{x0}^{w} } & 0 & 0 \\ 0 & 0 & 0 & {k_{x0}^{x} } & 0 \\ 0 & 0 & 0 & 0 & {k_{x0}^{\theta } } \\ \end{array} } \right]\varvec{u = }{\mathbf{0}} $$

(35)

Substituting Eqs. (15), (27) and (28) into Eq. (35), the discretized boundary condition equation for the nodes on the boundary of $x = 0$ is obtained as:

$$ \begin{array}{*{20}l} {\left( {\varvec{C}_{x} \varvec{DB} - \varvec{k}_{x0} } \right)\varvec{U}_{s} = {\mathbf{0}}} & {x = 0} \\ \end{array} $$

(36)

where

$$ \varvec{C}_{x} = \left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ \end{array} } \right] $$

(37a)

$$ \varvec{k}_{x0} = \left[ {\begin{array}{*{20}l} {k_{x0}^{u} \phi_{1} } & 0 & 0 & 0 & 0 & \cdots & {k_{x0}^{u} \phi_{n} } & 0 & 0 & 0 & 0 \\ 0 & {k_{x0}^{v} \phi_{1} } & 0 & 0 & 0 & \cdots & 0 & {k_{x0}^{v} \phi_{n} } & 0 & 0 & 0 \\ 0 & 0 & {k_{x0}^{w} \phi_{1} } & 0 & 0 & \cdots & 0 & 0 & {k_{x0}^{w} \phi_{n} } & 0 & 0 \\ 0 & 0 & 0 & {k_{x0}^{x} \phi_{1} } & 0 & \cdots & 0 & 0 & 0 & {k_{x0}^{x} \phi_{n} } & 0 \\ 0 & 0 & 0 & 0 & {k_{x0}^{\theta } \phi_{1} } & \cdots & 0 & 0 & 0 & 0 & {k_{x0}^{\theta } \phi_{n} } \\ \end{array} } \right] $$

(37b)

For other boundaries, discretized boundary condition equations can be obtained in the same way as above:

$$ \begin{array}{*{20}l} {\left( {\varvec{C}_{x} \varvec{DB} + \varvec{k}_{x1} } \right)\varvec{U}_{s} = {\mathbf{0}}} & {x = L} \\ \end{array} $$

(38)

$$ \begin{array}{*{20}l} {\left( {\varvec{C}_{\theta } \varvec{DB} - \varvec{k}_{\theta 0} } \right)\varvec{U}_{s} = {\mathbf{0}}} & {\theta = 0} \\ \end{array} $$

(39)

$$ \begin{array}{*{20}l} {\left( {\varvec{C}_{\theta } \varvec{DB} + \varvec{k}_{\theta 1} } \right)\varvec{U}_{s} = {\mathbf{0}}} & {\theta = \theta_{0} } \\ \end{array} $$

(40)

where

$$ \varvec{C}_{\theta } = \left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ \end{array} } \right] $$

(41a)

$$ \varvec{k}_{x1} = \left[ {\begin{array}{*{20}l} {k_{x1}^{u} \phi_{1} } & 0 & 0 & 0 & 0 & \cdots & {k_{x1}^{u} \phi_{n} } & 0 & 0 & 0 & 0 \\ 0 & {k_{x1}^{v} \phi_{1} } & 0 & 0 & 0 & \cdots & 0 & {k_{x1}^{v} \phi_{n} } & 0 & 0 & 0 \\ 0 & 0 & {k_{x1}^{w} \phi_{1} } & 0 & 0 & \cdots & 0 & 0 & {k_{x1}^{w} \phi_{n} } & 0 & 0 \\ 0 & 0 & 0 & {k_{x1}^{x} \phi_{1} } & 0 & \cdots & 0 & 0 & 0 & {k_{x1}^{x} \phi_{n} } & 0 \\ 0 & 0 & 0 & 0 & {k_{x1}^{\theta } \phi_{1} } & \cdots & 0 & 0 & 0 & 0 & {k_{x1}^{\theta } \phi_{n} } \\ \end{array} } \right] $$

(41b)

$$ \varvec{k}_{\theta 0} = \left[ {\begin{array}{*{20}l} {k_{\theta 0}^{u} \phi_{1} } & 0 & 0 & 0 & 0 & \cdots & {k_{\theta 0}^{u} \phi_{n} } & 0 & 0 & 0 & 0 \\ 0 & {k_{\theta 0}^{v} \phi_{1} } & 0 & 0 & 0 & \cdots & 0 & {k_{\theta 0}^{v} \phi_{n} } & 0 & 0 & 0 \\ 0 & 0 & {k_{\theta 0}^{w} \phi_{1} } & 0 & 0 & \cdots & 0 & 0 & {k_{\theta 0}^{w} \phi_{n} } & 0 & 0 \\ 0 & 0 & 0 & {k_{\theta 0}^{x} \phi_{1} } & 0 & \cdots & 0 & 0 & 0 & {k_{\theta 0}^{x} \phi_{n} } & 0 \\ 0 & 0 & 0 & 0 & {k_{\theta 0}^{\theta } \phi_{1} } & \cdots & 0 & 0 & 0 & 0 & {k_{\theta 0}^{\theta } \phi_{n} } \\ \end{array} } \right] $$

(41c)

$$ \varvec{k}_{\theta 1} = \left[ {\begin{array}{*{20}l} {k_{\theta 1}^{u} \phi_{1} } & 0 & 0 & 0 & 0 & \cdots & {k_{\theta 1}^{u} \phi_{n} } & 0 & 0 & 0 & 0 \\ 0 & {k_{\theta 1}^{v} \phi_{1} } & 0 & 0 & 0 & \cdots & 0 & {k_{\theta 1}^{v} \phi_{n} } & 0 & 0 & 0 \\ 0 & 0 & {k_{\theta 1}^{w} \phi_{1} } & 0 & 0 & \cdots & 0 & 0 & {k_{\theta 1}^{w} \phi_{n} } & 0 & 0 \\ 0 & 0 & 0 & {k_{\theta 1}^{x} \phi_{1} } & 0 & \cdots & 0 & 0 & 0 & {k_{\theta 1}^{x} \phi_{n} } & 0 \\ 0 & 0 & 0 & 0 & {k_{\theta 1}^{\theta } \phi_{1} } & \cdots & 0 & 0 & 0 & 0 & {k_{\theta 1}^{\theta } \phi_{n} } \\ \end{array} } \right] $$

(41d)

3 Numerical results and discussion

In this section, the computational efficiency and accuracy of the proposed method are verified through the comparison with the results of previous literature, and the several numerical examples for the free vibration analysis of the open composite laminated conical and cylindrical shell with different geometric dimension, material properties and boundary conditions are presented. In order to indicate boundary conditions simply, the clamped boundary is denoted by C, the free boundary is denoted by F, the simply supported boundary is denoted by S, and E¹, E² and E³ represent three types of elastic boundaries, respectively. Unless stated otherwise, non-dimensional frequencies are defined as $\varOmega = \omega L^{2} \sqrt {\rho h/D}$ in this paper, where $\rho$ is the material density, $L$ and $h$ are the shell length and thickness and D is the flexural stiffness of the shell, is defined as $D = E_{1} h^{3} /12\left( {1 - \mu_{12} \mu_{21} } \right)$. where $E_{1} ,\mu_{12} ,\mu_{21}$ are the Young’s modulus and Poisson’s ratio, respectively.

3.1 Convergence and verification study

In the numerical calculation by using current method, taking into account the calculation time of the numerical solution, the number of terms in the series should be truncated to the appropriate finite number. Therefore, to establish the number of terms that should be used to obtain accurate results, a convergence study is required. In addition, the boundary conditions in proposed method are decided by the boundary spring parameters. For example, to simulate the clamped boundary, it is necessary to set the boundary spring parameters to infinite in theory. However, this will make the matrix infinite, which will lead to ill-conditioned solution without real exact solution. Therefore, in order to select an appropriate value of the boundary spring parameters, it is also necessary to study the convergence of the boundary spring parameters.

Firstly, the convergence characteristics according to the change in the coefficient $\alpha_{q}$ related to the size of the local smoothing domain will be studied. The non-dimensional frequency convergence results of the open composite laminated cylindrical and conical shell along result of the reduction of the coefficient $\alpha_{q}$ are shown in Fig. 6. The boundary conditions of considered shells are defined as CCCC and SSSS, respectively. Geometric dimensions are defined as follows: both of cylindrical shell and conical shell, L = 1 m, h = 0.1 m, for cylindrical shell R = 1 m, for conical shell, R₀ = 1 m, and semi-vertex angle φ = π/4. The material properties for cylindrical shell and conical shell are defined as follows: ρ = 1500 kg/m³, E₁ = 150 GPa, E₂ = 10 GPa, μ₁₂ = 0.25, G₁₂ = G₁₃ = G₂₃ = 5 GPa, and fiber direction angle is $\delta_{k} = \left[ {0^{ \circ } /90^{ \circ } /0^{ \circ } } \right]$.

Fig. 6

Convergence of non-dimensional frequencies according to the decrease in coefficient $\alpha_{q}$. Cylindrical shell: a CCCC, b SSSS; conical shell: c CCCC, d SSSS

As can be seen from Fig. 6, the non-dimensional frequencies of shell converge gradually with coefficient $\alpha_{q}$ decreasing. Specially, it can be seen that when the coefficient $\alpha_{q}$ is less than 0.1, the dimensionless frequency tends to converge, and when the coefficient $\alpha_{q}$ is less than 0.01, they hardly changes. Thus, in all numerical examples, coefficient $\alpha_{q}$ is set to 0.01.

Next, the convergence of boundary spring parameters is studied. The geometric dimensions and material properties are same with those in Fig. 6. In order to study the influence of boundary spring parameters, the one end of open shells is set as an elastic boundary, and the other three ends are defined as a clamped boundary, and only one type of spring stiffness value is changed from 10³ to 10¹⁸, while the spring stiffness value of the other type is set to 10¹⁵. The convergence results of non-dimensional frequencies in the cylindrical and conical shell are shown in Figs. 7 and 8, respectively. As can be seen in Figs. 7 and 8, the non-dimensional frequencies rapidly increase as springs' stiffness values increase from 10⁵ to 10¹⁰ and beyond this range, the variation of the non-dimensional frequencies is little. Based on that, it is assumed that to simulate the clamped boundary condition, the boundary spring stiffness value is set as 10¹⁴, and for the elastic boundary condition, the spring stiffness value is set as 10⁸. The spring stiffness values corresponding to each boundary condition are summed up in Table 1.

Fig. 7

Convergence curve of non-dimensional frequencies on the boundary spring stiffness of the open composite laminated cylindrical shell: a mode 1, b mode 2, c mode 3, d mode 4

Fig. 8

Convergence curve of non-dimensional frequencies on the boundary spring stiffness of the open composite laminated conical shell: a mode 1, b mode 2, c mode 3, d mode 4

Table 1 The spring stiffness value corresponding to boundary conditions

In this subsection, finally, based on the convergence study, a comparative validation study of proposed method will be carried out.

The comparison of the first four non-dimensional frequencies for open composite laminated cylindrical and conical shells with CCCC and SSSS boundary condition is presented in Tables 2 and 3, respectively. The geometric dimensions and material properties are same with those in Fig. 6. Table 4 shows the errors of solutions obtained using traditional GSM and existing method (LGSM) for the above problems. The error evaluation indicator is as follows:

$$ e_{f} = \sqrt {\frac{{\sum\nolimits_{i} {(f_{i}^{\text{num}} - f_{i}^{\text{exact}} )^{2} } }}{{\sum\nolimits_{i} {(f_{i}^{\text{exact}} )^{2} } }}} \times 100 $$

(42)

where $f_{i}^{\text{exact}}$ and $f_{i}^{\text{num}}$ are $i$ th non-dimensional frequencies obtained by the Fourier–Ritz method and the numerical method (GSM or LGSM), respectively. From Tables 2, 3 and 4, it can be observed that the calculation results obtained by the current method are in good agreement with the results of the Fourier–Ritz method compared to traditional GSM.

Table 2 The comparison of the non-dimensional frequencies for open composite laminated cylindrical shells with CCCC and SSSS boundary condition

Table 3 The comparison of the non-dimensional frequencies for open composite laminated conical shells with CCCC and SSSS boundary condition

Table 4 The comparison of error $e_{f}$ for GSM and LGSM (%)

3.2 Numerical example

In this subsection, based on the convergence study and the verification results for the proposed method, to enrich the free vibration analysis data of open composite laminated cylindrical and conical shells, some examples of the considered shell with different boundary conditions are numerically provided. Also, through numerical example, the geometrical dimension, material properties and the effects of boundary conditions on the free vibration behavior of open composite laminated cylindrical and conical shells will be studied.

Tables 5 and 6 show the nature frequencies of four-layered open composite laminated cylindrical shells and conical shell, respectively, in which nature frequencies are investigated according to change in ratio of length L to radius R (R for cylindrical shell and R₀ for conical shell); the boundary conditions are set various classical boundaries and the elastic boundaries. The material properties are defined as: ρ = 1500 kg/m³, E₂ = 10 GPa, E₁ = 15E₂, μ₁₂ = 0.25, G₁₂ = G₁₃ = G₂₃ = 0.5E₂, the angle-ply in cylindrical shell is [0°/− 45°/0°/− 45°], and the angle-ply in conical shell is [0°/45°/0°/45°]. Geometric dimensions of shells are defined as: in cylindrical shell; R = 1 m, θ = π/4, h = 0.1 m, in conical shell; R₀ = 1 m, θ = π/4, h = 0.1 m and cone semi-vertex angle φ = π/6. It can be seen from Tables 5 and 6 that, for both shell types, the natural frequencies are decreased when the radius R is constant and the length L increases, regardless of the boundary conditions. In a similar way as above, when the radius R is constant and the thickness h increases, the change in natural frequencies in open composite laminated cylindrical and conical shell is presented in Tables 7 and 8. The geometric dimensions and material properties are same as above, except the length L = 2 m. From Tables 7 and 8, it is clear that the natural frequencies of open composite laminated cylindrical and conical shell increase as the length L and radius R are constant and the thickness h increases.

Table 5 The nature frequencies of the open composite laminated cylindrical shell for length parameter with various boundary conditions

Table 6 The nature frequencies of the open composite laminated conical shell for length parameter with various boundary conditions

Table 7 The nature frequencies of the open composite laminated cylindrical shell for thickness parameter with various boundary conditions

Table 8 The nature frequencies of the open composite laminated conical shell for thickness parameter with various boundary conditions

The first four non-dimensional frequencies of open composite laminated cylindrical and conical shell with different boundary conditions and fiber layers are shown in Tables 9 and 10. The material properties for both cylindrical shell and conical shell are defined as: ρ = 1700 kg/m³, E₁ = 60.7 GPa, E₂ = 24.8 GPa, μ₁₂ = 0.23, G₁₂ = G₁₃ = G₂₃ = 12 GPa, and the geometric dimensions of shells are defined as: in cylindrical shell; R = 1 m, θ = π/4, L = 2 m, h = 0.1 m, in conical shell; R₀ = 1 m, θ = π/4, L = 2 m, h = 0.1 m and cone semi-vertex angle φ = π/6. From Table 9, it can be seen that in all boundary conditions except CFCF boundary, the non-dimensional frequencies of open composite laminated cylindrical shell in which cross-ply type is [0°/90°/0°] are smaller than those of the other two cases. It can be seen from Table 10 that open composite laminated conical shells have the opposite trend as with open composite laminated cylindrical shell.

Table 9 Non-dimensional frequencies of open composite laminated cylindrical shell with different fiber layers

Table 10 Non-dimensional frequencies of open composite laminated conical shell with different fiber layers

Figure 9 shows the change in non-dimensional frequencies of three-layer [0°/α°/0°] open composite laminated cylindrical shell with CCCC and CSCS boundary conditions according to the change in fiber direction α. The geometric dimensions and material properties are same with those in Table 9. It can be seen from Fig. 9 that the frequency of open composite laminated cylindrical shell changes symmetrically with respect to the fiber direction angle 90°, regardless of the boundary conditions.

Fig. 9

Change in non-dimensional frequencies of open composite laminated cylindrical shell according to the change in fiber direction α a CCCC, b CSCS

In Fig. 10, the effect of Young’s modulus ratio E₁/E₂ on the vibration characteristics of open composite laminated conical shell is investigated. The boundary conditions of this example are set to CCCC and CSCS. The geometric dimensions and material properties are same with those in Table 10; only the number of layers and the angle of fiber direction are different from the above. In this example, four-layer [45°/− 45°/45°/− 45°] conical shell is considered. The range of Young’s modulus ratio ${{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }}$ is defined as 1 to 20. From Fig. 10, it is found that the non-dimensional frequencies of open composite laminated conical shell increase with the increase in Young’s modulus ratio.

Fig. 10

Change in non-dimensional frequencies of open composite laminated conical shell according to the increase in Young’s modulus ratio a CCCC, b CSCS

Table 11 shows non-dimensional frequencies of open composite laminated conical shell with increasing cone semi-vertex angle under different boundary conditions and fiber layers. The material properties and the geometric dimensions are same with those in Table 10. As shown in Table 11, the non-dimensional frequencies of open conical shell increase with increasing semi-vertex angle, regardless of the laminating structure and boundary conditions.

Table 11 The non-dimensional frequencies of open composite laminated conical shell with increasing cone semi-vertex angle

Finally, the change characteristics of the non-dimensional frequencies in the four-layered cross-ply [0°/90°/0°/90°] open composite laminated conical shell with CCCC boundary condition along the change in circumferential rotation angle θ and cone semi-vertex angle φ are investigated. The material properties are same with those in Fig. 6, and the geometric dimensions are defined as: R₀ = 1 m, L = 2 m, h = 0.1 m. The investigated results are shown in Fig. 11. From Fig. 11, it can be intuitively seen that as the circumferential rotation angle θ increases, the non-dimensional frequency of open composite laminated shell decreases regardless of the increase in the cone semi-vertex angle φ. In other words, it can be seen that under the same conditions, the increase in the circumferential rotation angle θ results in a decrease in frequencies.

Fig. 11

Change in the non-dimensional frequencies of open composite laminated conical shell along the circumferential rotation angle θ and cone semi-vertex angle φ

4 Conclusions

In this paper, a new and an efficient solution method has been applied to free vibration problem of open composite laminated cylindrical and conical shells with elastic boundary conditions. The theoretical model is formulated by FSDT, and the motion equation is obtained by the Hamilton’s principle. The motion equation is discretized by meshless shape function; in this process, a new local gradient smoothing method has been introduced. The accuracy, applicability and efficiency of this method are demonstrated for free vibrations of open composite laminated cylindrical and conical shells with different geometric, material parameters and boundary condition. The numerical results show good convergence characteristics and good agreement between the present method and the existing literature. And through several numerical examples, some useful results for free vibration of open composite laminated cylindrical and conical shells are obtained, which may serve as a benchmark solutions for researchers to check their analytical and numerical methods.

Appendix

$$ \varvec{K}_{Ii} = \left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} {L_{11} } & {L_{12} } & {L_{13} } & {L_{14} } & {L_{15} } \\ {L_{21} } & {L_{22} } & {L_{23} } & {L_{24} } & {L_{25} } \\ {L_{31} } & {L_{32} } & {L_{33} } & {L_{34} } & {L_{35} } \\ {L_{41} } & {L_{42} } & {L_{43} } & {L_{44} } & {L_{45} } \\ {L_{51} } & {L_{52} } & {L_{53} } & {L_{54} } & {L_{55} } \\ \end{array} } \right],\,\varvec{M}_{Ii} = \left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} { - I_{0} \phi_{i} } & 0 & 0 & { - I_{1} \phi_{i} } & 0 \\ 0 & { - I_{0} \phi_{i} } & 0 & 0 & 0 \\ 0 & 0 & { - I_{0} \phi_{i} } & 0 & 0 \\ { - I_{1} \phi_{i} } & 0 & 0 & { - I_{2} \phi_{i} } & 0 \\ 0 & { - I_{1} \phi_{i} } & 0 & 0 & { - I_{2} \phi_{i} } \\ \end{array} } \right] $$

Detailed expressions of differential operators $L_{ij}$:

$$ L_{11} = A_{11} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2A_{16} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{A_{66} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + A_{11} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - A_{22} \frac{{\sin^{2} \varphi }}{{R^{2} }}\phi_{i} $$

$$ \begin{aligned} L_{12} & = A_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(A_{12} + A_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{A_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (A_{16} - A_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & - (A_{22} + A_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + A_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }}\phi_{i} \\ \end{aligned} $$

$$ L_{13} = A_{12} \frac{\cos \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} + A_{26} \frac{\cos \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } - A_{22} \frac{\sin \varphi \cos \varphi }{{R^{2} }}\phi_{i} $$

$$ L_{14} = B_{11} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2B_{16} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{B_{66} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + B_{11} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - B_{22} \frac{{\sin^{2} \varphi }}{{R^{2} }}\phi_{i} $$

$$ \begin{aligned} L_{15} & = B_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(B_{12} + B_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{B_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (B_{16} - B_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & - (B_{22} + B_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + B_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }}\phi_{i} \\ \end{aligned} $$

$$ \begin{aligned} L_{21} & = A_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(A_{12} + A_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{A_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (2A_{16} + A_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & + (A_{22} + A_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + A_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }}\phi_{i} \\ \end{aligned} $$

$$ \begin{aligned} L_{22} & = A_{66} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2A_{26} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{A_{22} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + A_{66} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & - (A_{66} \frac{{\sin^{2} \varphi }}{{R^{2} }} + A_{44} \frac{{\cos^{2} \varphi }}{{R^{2} }})\phi_{i} \\ \end{aligned} $$

$$ L_{23} = (A_{26} + A_{45} )\frac{\cos \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} + (A_{22} + A_{44} )\frac{\cos \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + A_{26} \frac{\sin \varphi \cos \varphi }{{R^{2} }}\phi_{i} $$

$$ \begin{aligned} L_{24} & = B_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(B_{12} + B_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{B_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (2B_{16} + B_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & + (B_{22} + B_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + \left( {B_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }} + A_{45} \frac{\cos \varphi }{R}} \right)\phi_{i} \\ \end{aligned} $$

$$ \begin{aligned} L_{25} & = B_{66} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2B_{26} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{B_{22} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + B_{66} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & - \left( {B_{66} \frac{{\sin^{2} \varphi }}{{R^{2} }} - A_{44} \frac{\cos \varphi }{R}} \right)\phi_{i} \\ \end{aligned} $$

$$ L_{31} = - A_{12} \frac{\cos \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - A_{26} \frac{\cos \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } - A_{22} \frac{\sin \varphi \cos \varphi }{{R^{2} }}\phi_{i} $$

$$ L_{32} = - (A_{26} + A_{45} )\frac{\cos \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - (A_{22} + A_{44} )\frac{\cos \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + A_{26} \frac{\sin \varphi \cos \varphi }{{R^{2} }}\phi_{i} $$

$$ L_{33} = A_{55} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2A_{45} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{A_{44} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + A_{55} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - A_{22} \frac{{\cos^{2} \varphi }}{{R^{2} }}\phi_{i} $$

$$ L_{34} = \left( {A_{55} - B_{12} \frac{\cos \varphi }{R}} \right)\frac{{\partial \phi_{i} }}{\partial x} + \left( {\frac{{A_{45} }}{R} - B_{26} \frac{\cos \varphi }{{R^{2} }}} \right)\frac{{\partial \phi_{i} }}{\partial \theta } + \left( {A_{55} \frac{\sin \varphi }{R} - B_{22} \frac{\sin \varphi \cos \varphi }{{R^{2} }}} \right)\phi_{i} $$

$$ L_{35} = \left( {A_{45} - B_{26} \frac{\cos \varphi }{R}} \right)\frac{{\partial \phi_{i} }}{\partial x} + \left( {\frac{{A_{44} }}{R} - B_{22} \frac{\cos \varphi }{{R^{2} }}} \right)\frac{{\partial \phi_{i} }}{\partial \theta } + \left( {A_{45} \frac{\sin \varphi }{R} + B_{26} \frac{\sin \varphi \cos \varphi }{{R^{2} }}} \right)\phi_{i} $$

$$ L_{41} = L_{14} $$

$$ \begin{aligned} L_{42} & = B_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(B_{12} + B_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{B_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (B_{16} - B_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & - (B_{22} + B_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + \left( {B_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }} + A_{45} \frac{\cos \varphi }{R}} \right)\phi_{i} \\ \end{aligned} $$

$$ L_{43} = \left( {B_{12} \frac{\cos \varphi }{R} - A_{55} } \right)\frac{{\partial \phi_{i} }}{\partial x} + \left( {B_{26} \frac{\cos \varphi }{{R^{2} }} - \frac{{A_{45} }}{R}} \right)\frac{{\partial \phi_{i} }}{\partial \theta } + (B_{12} - B_{22} )\frac{\sin \varphi \cos \varphi }{{R^{2} }}\phi_{i} $$

$$ L_{44} = D_{11} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2D_{16} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{D_{66} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + D_{11} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - \left( {D_{22} \frac{{\sin^{2} \varphi }}{{R^{2} }} + A_{55} } \right)\phi_{i} $$

$$ \begin{aligned} L_{45} & = D_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(D_{12} + D_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{D_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (D_{16} - D_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & - (D_{22} + D_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + \left( {D_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }} - A_{45} } \right)\phi_{i} \\ \end{aligned} $$

$$ \begin{aligned} L_{51} & = B_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(B_{12} + B_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{B_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (2B_{16} + B_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & + (B_{22} + B_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + B_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }}\phi_{i} \\ \end{aligned} $$

$$ L_{52} = L_{25} $$

$$ L_{53} = \left( {B_{26} \frac{\cos \varphi }{R} - A_{45} } \right)\frac{{\partial \phi_{i} }}{\partial x} + \left( {B_{22} \frac{\cos \varphi }{{R^{2} }} - \frac{{A_{44} }}{R}} \right)\frac{{\partial \phi_{i} }}{\partial \theta } + B_{26} \frac{\sin \varphi \cos \varphi }{{R^{2} }}\phi_{i} $$

$$ \begin{aligned} L_{54} & = D_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(D_{12} + D_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{D_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (2D_{16} + D_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & + (D_{22} + D_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + \left( {D_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }} - A_{45} } \right)\phi_{i} \\ \end{aligned} $$

$$ L_{55} = D_{66} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2D_{26} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{D_{22} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + D_{66} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - \left( {D_{66} \frac{{\sin^{2} \varphi }}{{R^{2} }} + A_{44} } \right)\phi_{i} $$