Free vibration analysis of combined composite laminated conical–cylindrical shells with varying thickness using the Haar wavelet method

Abstract

This paper presents the free vibration analysis of combined composite laminated conical–cylindrical shells with varying thickness using the Haar wavelet method (HWM). The displacement field of the combined shell is set based on the first-order shear deformation theory (FSDT), the displacement components, and rotation of individual shells including boundary conditions that are expanded by the Haar wavelet and Fourier series in the meridional and the circumferential direction. By solving the vibration characteristic equation discretized by the Haar wavelet, the vibrational results of combined shells are obtained. Then, the results of the proposed method are compared with those of published literature and finite element analysis (FEA). The results show that HWM has high convergence and high accuracy for the free vibration analysis of the combined composite laminated conical–cylindrical shells with varying thickness. Also, the effects of the parameters such as thickness variation parameters, material properties, geometrical dimensions, and different boundary conditions, on the vibrational behavior of the combined shells are investigated. Finally, new numerical results are provided to illustrate the free vibration behavior of the combined composite laminated conical–cylindrical shells with varying thickness.

1 Introduction

As is well known, shell structures such as conical shells and cylindrical shells are widely used in aerospace, marine, civil, chemical industry, and mechanical engineering as important elements of structures. In addition, with the development of science and technology, composite materials are actively used for these structural elements. In actual processes, the combined conical–cylindrical structures are often applied, and many studies on these combined structures are in progress.

Irie et al. [1] applied the transfer matrix method to investigate the vibration characteristics of coupled cylindrical–conical shells. By using the multi-segmental numerical integration technique, Hu and Raney [2] carried out vibration analyses of a coupled cylindrical–conical shell and confirmed the accuracy of the analytical results by experiments. Benjeddou [3] proposed the local–global B-spline finite element method for the modal analysis of the coupled shell structure. Caresta and Kessissoglou [4] studied the vibration characteristics of the coupled isotropic cylindrical–conical shell using the classical approach. In order to obtain the total governing equation of a coupled shell, the wave solution has been adopted for the cylindrical shell, and the power series solution has been adopted. Then, these two solutions are coupled by the continuity condition at the interface of two shells. EI Damatty et al. [5] used the three-dimensional finite element method for the numerical analysis of the dynamic behavior of the coupled cylindrical–conical shell. Qu et al. [6,7,8,9,10] analyzed the dynamic behaviors of the different coupled shells such as the ring-stiffened conical–cylindrical shell, cylindrical–conical–spherical shell, and spherical–cylindrical–spherical shell using a modified variational approach. Based on the modified Fourier–Ritz method, Ma et al. [11, 12] analyzed the vibrational characteristics of a coupled isotropic conical–cylindrical shell with general boundary conditions. Bagheri et al. investigated the free vibration characteristics of a coupled conical–cylindrical–conical shell [13] and conical–conical shell [14] made of isotropic material using the generalized differential quadrature (GDQ) method. Su et al. [15] analyzed the vibration characteristics of a coupled conical–cylindrical–spherical shell with general boundary conditions using the Fourier spectrum element method (FSEM). Cheng et al. [16] applied the variation method to investigate the vibration characteristics of a coupled conical–cylindrical shell. Chen et al. [17] proposed an analytic method to analyze free and forced vibration characteristics of ring-stiffened combined conical–cylindrical shells with arbitrary boundary conditions. By using a power series solution, Efraim and Eisenberger [18] investigated the free vibration characteristics of segmented axisymmetric shells and obtained relatively accurate natural frequencies.

Although many studies have been performed for free vibration analysis of conical–cylindrical coupling shells, it can be seen that most of them relate to coupled shell structures with uniform thickness. Kang [19] performed an analysis of the free vibration of a combined conical–cylindrical shell structure in which a conical shell with varying thickness and a cylindrical shell are combined. However, in this study, the coupled shell structure is made of an isotropic material. As can be seen from the literature review, there are few studies on the free vibration of the composite laminated combined conical–cylindrical shell structure of varying thickness. Therefore, this study focuses on the free vibration analysis of combined composite laminated conical–cylindrical shells of varying thicknesses.

Recently, the Carrera unified formulation (CUF) [20], proposed in 1995 by Italian scientist Carrera, has attracted the attention of scientists who are trying to solve the vibration problems of structural elements. Carrera et al. [21,22,23,24,25] made a great contribution to the static and dynamic analysis of structural elements such as beams, plates, and shells using CUF. The CUF is a technique that permits one to handle a large variety of shell models in a unified manner. The FSDT shell theories can also be obtained as particular cases of CUF. Therefore, in this study, the FSDT is introduced as a theoretical model for the analysis of free vibration of the combined composite laminated conical–cylindrical shells with varying thicknesses. HWM is applied to solve the equation of motion of the combined conical–cylindrical shell. It has already been verified that HWM is an efficient and accurate solution method not only for the free vibration analysis of cylindrical shells [26,27,28,29], conical shells [28, 30, 31], and doubly curved shells of revolution [32], but also for free vibration analysis of coupled shell structures [33]. All displacements and their derivatives in the motion equation are expressed by the Haar wavelet and their integrals in the axis direction and by Fourier series in the circumferential direction. The integral constant is determined by the boundary condition. New results to verify the accuracy and reliability of this method are performed by parametric studies and numerical examples.

2 Theoretical formulations

2.1 Description of the model

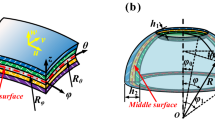
Figure 1 shows the geometric structure of a combined composite laminated conical–cylindrical shell with the semi-vertex angle φ of the cone, length L_co and the small radius R_co of the conical shell, and the radius R_cy and length L_cy of the cylindrical shell. The thickness h_cy of the cylindrical shell is constant while the thickness h_co of the conical shell varies according to a constant rule in the x-axis direction.

Fig. 1

Coordinate system and geometric relations of a combined composite laminated conical–cylindrical shell: a cross section and boundary condition, b geometric relations of the combined shell

The conical shell is defined by the coordinate system (x_co, θ_co, z_co), in which x_co and θ_co are the coordinates of axial and circumferential direction, and z_co is the coordinate in the direction perpendicular to the middle surface, respectively. The displacements of the conical shell in the x_co, θ_co, and z_co directions are denoted by u_co, v_co, w_co.

The radius at any point of the conical shell can be written as R_co(x_co) = R_0,co + x_co sinφ. The cylindrical shell is represented by the x_cy, θ_cy, z_cy coordinate system, in which x_cy, θ_cy, and z_cy mean axial, circumferential and radial directions, respectively. The displacements of the cylindrical shell in the x_cy, θ_cy, and z_cy directions are denoted by u_c, v_c, and w_c respectively. In all expressions of this work, the subscripts co and cy denote the conical and cylindrical shell, respectively.

The thicknesses at origin and end of the conical shell are represented by h_0,co and h_1,co, respectively, and the generalized equation of thickness depends on the following as:

$$h_{co} (x_{co} ) = h_{0,co} \left[ {1 - \alpha \left( {\frac{{x_{co} }}{{L_{co} }}} \right)^{\beta } } \right]$$

(1)

where α and β are thickness variation parameters.

2.2 Kinematic relations

FSDT is employed to represent the motion equations of the shell, and the displacement field for the shell based on the FSDT is expressed as follows [11, 29, 32, 33]:

$$\begin{gathered} u_{\zeta } (x,\theta ,z,t) = u_{\zeta }^{0} (x,\theta ,t) + z\psi_{x,\zeta } (x,\theta ,t), \hfill \\ v_{\zeta } (x,\theta ,z,t) = v_{\zeta }^{0} (x,\theta ,t) + z\psi_{\theta ,\zeta } (x,\theta ,t), \hfill \\ w_{\zeta } (x,\theta ,z,t) = w_{\zeta }^{0} (x,\theta ,t) \hfill \\ \end{gathered}$$

(2)

where the subscript ζ (= co, cy) denotes the conical and cylindrical shell, respectively, u, v, and w are the displacements in x, θ, and z directions, and ψ_x and ψ_θ represent the rotations of transverse normal with respect to the θ- and x-axis.

The strain–displacement relations at the middle surface can be written as follows:

Conical shell:

$$\begin{gathered} \varepsilon_{x,co}^{0} = \frac{{\partial u_{co}^{0} }}{{\partial x_{co} }},\;\;\;\varepsilon_{\theta ,co}^{0} = \frac{{\partial v_{co}^{0} }}{{R_{co} \partial \theta_{co} }} + \frac{{u_{co}^{0} }}{{R_{co} }}\cos \varphi + \frac{{w_{co}^{0} }}{{R_{co} }}\sin \varphi , \hfill \\ \gamma_{x\theta ,co}^{0} = \frac{{\partial v_{co}^{0} }}{{\partial x_{co} }} + \frac{{\partial u_{co}^{0} }}{{R_{co} \partial \theta_{co} }} - \frac{{v_{co}^{0} }}{{R_{co} }}\cos \varphi ,\,\,\,\,\,\chi_{x,co} = \frac{{\partial \psi_{x,c0} }}{{\partial x_{co} }}, \hfill \\ \chi_{\theta ,co} = \frac{{\partial \psi_{\theta ,c0} }}{{R_{co} \partial \theta_{co} }} + \frac{{\psi_{x,c0} }}{{R_{co} }}\cos \varphi ,\,\,\,\,\,\chi_{x\theta ,co} = \frac{{\partial \psi_{x,c0} }}{{R_{co} \partial \theta_{co} }} + \frac{{\partial \psi_{\theta ,c0} }}{{\partial x_{co} }} - \frac{{\psi_{\theta ,c0} }}{{R_{co} }}\cos \varphi , \hfill \\ \gamma_{xz,co} = \frac{{\partial w_{co}^{0} }}{{\partial x_{co} }} + \psi_{x,c0} ,\;\;\;\;\;\gamma_{\theta z,co} = \frac{{\partial w_{co}^{0} }}{{R_{co} \partial \theta_{co} }} - \frac{{v_{co}^{0} }}{{R_{co} }} + \psi_{\theta ,c0}; \hfill \\ \end{gathered}$$

(3)

Cylindrical shell:

$$\begin{gathered} \varepsilon_{x,cy}^{0} = \frac{{\partial u_{cy}^{0} }}{{\partial x_{cy} }},\;\;\;\varepsilon_{\theta ,cy}^{0} = \frac{{\partial v_{cy}^{0} }}{{R_{cy} \partial \theta_{cy} }} + \frac{{w_{cy}^{0} }}{{R_{cy} }},\,\,\,\,\,\,\,\gamma_{x\theta ,cy}^{0} = \frac{{\partial v_{cy}^{0} }}{{\partial x_{cy} }} + \frac{{\partial u_{cy}^{0} }}{{R_{cy} \partial \theta_{cy} }}, \hfill \\ \,\chi_{x,cy} = \frac{{\partial \psi_{x,cy} }}{{\partial x_{cy} }},\,\,\chi_{\theta ,cy} = \frac{{\partial \psi_{\theta ,cy} }}{{R_{cy} \partial \theta_{cy} }},\,\,\,\,\,\chi_{x\theta ,cy} = \frac{{\partial \psi_{\theta ,cy} }}{{\partial x_{cy} }} + \frac{{\partial \psi_{x,cy} }}{{R_{cy} \partial \theta_{cy} }}, \hfill \\ \gamma_{xz,cy}^{0} = \frac{{\partial w_{cy}^{0} }}{{\partial x_{cy} }} + \psi_{x,cy} ,\;\;\;\;\;\gamma_{\theta z,cy}^{0} = \frac{{\partial w_{cy}^{0} }}{{R_{cy} \partial \theta_{cy} }} - \frac{{v_{cy}^{0} }}{{R_{cy} }} + \psi_{\theta ,cy} \hfill \\ \end{gathered}$$

(4)

where $\varepsilon_{x,\zeta }^{0} ,\,\varepsilon_{\theta ,\zeta }^{0} ,\,\gamma_{x\theta ,\zeta }^{0}$ represent the normal and shear strains in the middle surface, $\,\chi_{x,\zeta } ,\,\,\chi_{\theta ,\zeta }$, and $\chi_{x\theta ,\zeta }$ are curvature and twist changes, and $\gamma_{xz,\zeta } ,\;\;\gamma_{\theta z,\zeta }$ are transverse shear strains [11, 32, 37].

The relations between the force and moment resultants with the strain and curvature changes of the middle surface are expressed in matrix form as follows:

$$\begin{gathered} \left\{ \begin{gathered} N_{{x,\zeta }} \hfill \\ N_{{\theta ,\zeta }} \hfill \\ N_{{x\theta ,\zeta }} \hfill \\ M_{{x,\zeta }} \hfill \\ M_{{\theta ,\zeta }} \hfill \\ M_{{x\theta ,\zeta }} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{{11,\zeta }} } & {A_{{12,\zeta }} } & {A_{{16,\zeta }} } \\ {A_{{12,\zeta }} } & {A_{{22,\zeta }} } & {A_{{26,\zeta }} } \\ {A_{{16,\zeta }} } & {A_{{26,\zeta }} } & {A_{{66,\zeta }} } \\ \end{array} } & {\begin{array}{*{20}c} {B_{{11,\zeta }} } & {B_{{12,\zeta }} } & {B_{{16,\zeta }} } \\ {B_{{12,\zeta }} } & {B_{{22,\zeta }} } & {B_{{26,\zeta }} } \\ {B_{{16,\zeta }} } & {B_{{26,\zeta }} } & {B_{{66,\zeta }} } \\ \end{array} } \\ {\begin{array}{*{20}c} {B_{{11,\zeta }} } & {B_{{12,\zeta }} } & {B_{{16,\zeta }} } \\ {B_{{12,\zeta }} } & {B_{{22,\zeta }} } & {B_{{26,\zeta }} } \\ {B_{{16,\zeta }} } & {B_{{26,\zeta }} } & {B_{{66,\zeta }} } \\ \end{array} } & {\begin{array}{*{20}c} {D_{{11,\zeta }} } & {D_{{12,\zeta }} } & {D_{{16,\zeta }} } \\ {D_{{12,\zeta }} } & {D_{{22,\zeta }} } & {D_{{26,\zeta }} } \\ {D_{{16,\zeta }} } & {D_{{26,\zeta }} } & {D_{{66,\zeta }} } \\ \end{array} } \\ \end{array} } \right]\left\{ \begin{gathered} \varepsilon _{{x,\zeta }}^{0} \hfill \\ \varepsilon _{{\theta ,\zeta }}^{0} \hfill \\ \gamma _{{x\theta ,\zeta }}^{0} \hfill \\ k_{{x,\zeta }} \hfill \\ k_{{\theta ,\zeta }} \hfill \\ k_{{x\theta ,\zeta }} \hfill \\ \end{gathered} \right\}, \hfill \\ \left\{ \begin{gathered} Q_{{x,\zeta }} \hfill \\ Q_{{\theta ,\zeta }} \hfill \\ \end{gathered} \right\} = \kappa \left[ {\begin{array}{*{20}c} {A_{{55,\zeta }} } & {A_{{45,\zeta }} } \\ {A_{{45,\zeta }} } & {A_{{44,\zeta }} } \\ \end{array} } \right]\left\{ \begin{gathered} \gamma _{{xz,\zeta }} \hfill \\ \gamma _{{\theta z,\zeta }} \hfill \\ \end{gathered} \right\} \hfill \\ \end{gathered}$$

(5)

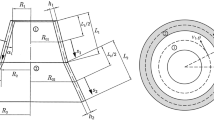
where N_x,ζ, N_θ,ζ, N_xθ,ζ, Q_θ,ζ, Q_x,ζ and M_x,ζ, M_θ,ζ, M_xθ,ζ are the in-plane force and twisting moment resultants. In Eq. (5), κ denotes the shear coefficient and is given as 5/6 in this paper. A_ij,ζ, B_ij,ζ, and D_ij,ζ represent extensional, extensional–bending, and bending stiffness, respectively, and they are expressed as:

$$\begin{gathered} A_{ij,\zeta } = \sum\limits_{k = 1}^{{N_{k} }} {\overline{Q}_{ij,\zeta }^{k} \left( {Z_{k + 1,\zeta } - Z_{k,\zeta } } \right)} ,\,\,\,\,\left( {i,j = 1,2,6} \right), \hfill \\ A_{ij,\zeta } = \kappa \sum\limits_{k = 1}^{{N_{k} }} {\overline{Q}_{ij,\zeta }^{k} \left( {Z_{k + 1,\zeta } - Z_{k,\zeta } } \right)} ,\,\,\,\,\left( {i,j = 4,5} \right), \hfill \\ B_{ij,\zeta } = \frac{1}{2}\sum\limits_{k = 1}^{{N_{k} }} {\overline{Q}_{ij,\zeta }^{k} \left( {Z_{k + 1,\zeta }^{2} - Z_{k,\zeta }^{2} } \right)} ,\,\,\,\,\left( {i,j = 1,2,6} \right), \hfill \\ D_{ij,\zeta } = \frac{1}{3}\sum\limits_{k = 1}^{{N_{k} }} {\overline{Q}_{ij,\zeta }^{k} \left( {Z_{k + 1,\zeta }^{3} - Z_{k,\zeta }^{3} } \right)} ,\,\,\,\,\left( {i,j = 1,2,6} \right) \hfill \\ \end{gathered}$$

(6)

where N_k denotes the number of total layers of the laminated shell, and Z_k and Z_k+1 are the distances between the kth or k + 1th layer and the middle surface. The coordinate Z_k of the bottom surface of the kth layer is expressed as a function of x,

$$z_{k} (x) = \left( { - \frac{1}{2} + \frac{k - 1}{{N_{k} }}} \right)h(x).$$

(7)

$\overline{Q}_{ij,\zeta }^{k} (i,j = 1,2,4,5,6)$ are transformed elastic coefficients of k^th layers and are defined as [11, 28, 33]:

$$\begin{gathered} \overline{Q}_{11,\zeta }^{k} = Q_{11,\zeta }^{k} \cos^{4} \phi_{fiber}^{k} + 2\left( {Q_{12,\zeta }^{k} + 2Q_{66,\zeta }^{k} } \right)\cos^{2} \phi_{fiber}^{k} \sin^{2} \phi_{fiber}^{k} + Q_{22,\zeta }^{k} \sin^{4} \phi_{fiber}^{k} , \hfill \\ \overline{Q}_{12,\zeta }^{k} = \left( {Q_{11,\zeta }^{k} + Q_{22,\zeta }^{k} - 4Q_{66,\zeta }^{k} } \right)\cos^{2} \phi_{fiber}^{k} \sin^{2} \phi_{fiber}^{k} + Q_{12,\zeta }^{k} \left( {\cos^{4} \phi_{fiber}^{k} + \sin^{4} \phi_{fiber}^{k} } \right), \hfill \\ \overline{Q}_{22,\zeta }^{k} = Q_{11,\zeta }^{k} \sin^{4} \phi_{fiber}^{k} + 2\left( {Q_{12,\zeta }^{k} + 2Q_{66,\zeta }^{k} } \right)\cos^{2} \phi_{fiber}^{k} \sin^{2} \phi_{fiber}^{k} + Q_{22,\zeta }^{k} \cos^{4} \phi_{fiber}^{k} , \hfill \\ \overline{Q}_{16,\zeta }^{k} = \left( {Q_{11,\zeta }^{k} - Q_{12,\zeta }^{k} - 2Q_{66,\zeta }^{k} } \right)\cos^{3} \phi_{fiber}^{k} \sin \phi_{fiber}^{k} + \left( {Q_{12,\zeta }^{k} - Q_{22,\zeta }^{k} + 2Q_{66,\zeta }^{k} } \right)\cos \phi_{fiber}^{k} \sin^{3} \phi_{fiber}^{k} , \hfill \\ \overline{Q}_{26,\zeta }^{k} = \left( {Q_{11,\zeta }^{k} - Q_{12,\zeta }^{k} - 2Q_{66,\zeta }^{k} } \right)\cos \phi_{fiber}^{k} \sin^{3} \phi_{fiber}^{k} + \left( {Q_{12,\zeta }^{k} - Q_{22,\zeta }^{k} + 2Q_{66,\zeta }^{k} } \right)\cos^{3} \phi_{fiber}^{k} \sin \phi_{fiber}^{k} , \hfill \\ \overline{Q}_{66,\zeta }^{k} = \left( {Q_{11,\zeta }^{k} + Q_{22,\zeta }^{k} - 2Q_{12,\zeta }^{k} - 2Q_{66,\zeta }^{k} } \right)\cos^{2} \phi_{fiber}^{k} \sin^{2} \phi_{fiber}^{k} + Q_{66,\zeta }^{k} \left( {\cos^{4} \phi_{fiber}^{k} + \sin^{4} \phi_{fiber}^{k} } \right), \hfill \\ \overline{Q}_{44,\zeta }^{k} = Q_{44,\zeta }^{k} \cos^{2} \phi_{fiber}^{k} + Q_{55,\zeta }^{k} \sin^{2} \phi_{fiber}^{k} , \hfill \\ \overline{Q}_{45,\zeta }^{k} = \left( {Q_{55,\zeta }^{k} - Q_{44,\zeta }^{k} } \right)\cos \phi_{fiber}^{k} \sin \phi_{fiber}^{k} , \hfill \\ \overline{Q}_{55,\zeta }^{k} = Q_{55,\zeta }^{k} \cos^{2} \phi_{fiber}^{k} + Q_{44,\zeta }^{k} \sin^{2} \phi_{fiber}^{k} \hfill \\ \end{gathered}$$

(8)

where $\phi_{fiber}^{k}$ indicates the angle between the principal material directions and the x-axis in the k^th layer. $Q_{ij,\zeta }^{k}$ are the reduced elasticity coefficient at the k^th layer and expressed as follows [11, 28, 33]:

$$\begin{gathered} Q_{11,\zeta }^{k} = \frac{{E_{1,\zeta }^{k} }}{{1 - \mu_{12,\zeta }^{k} \mu_{21,\zeta }^{k} }},\,\,Q_{22,\zeta }^{k} = \frac{{E_{2,\zeta }^{k} }}{{1 - \mu_{12,\zeta }^{k} \mu_{21,\zeta }^{k} }},\,\,\,Q_{12,\zeta }^{k} = \frac{{\mu_{12,\zeta }^{k} E_{2,\zeta }^{k} }}{{1 - \mu_{12,\zeta }^{k} \mu_{21,\zeta }^{k} }} \hfill \\ Q_{44,\zeta }^{k} = G_{23,\zeta }^{k} ,\,\,\,Q_{55,\zeta }^{k} = G_{13,\zeta }^{k} ,\,\,\,\,Q_{66,\zeta }^{k} = G_{12,\zeta }^{k} \hfill \\ \end{gathered}$$

(9)

where $E_{1,\zeta }^{k}$ and $E_{2,\zeta }^{k}$ represent Young’s moduli, and $G_{12,\zeta }^{k} ,G_{13,\zeta }^{k}$, and $G_{23,\zeta }^{k}$ are the shear moduli. $\mu_{12,\zeta }^{k}$, and $\mu_{21,\zeta }^{k}$ are Poisson’s ratios.

Since the thickness of the conical shell is changed in the x_co-axis direction, the stiffness coefficients A_ij,co, B_ij,co, and D_ij,co are functions of x_co, therefore, partial derivatives of the stiffness coefficients are appearing, and can be written as follows:

$$\left\{ \begin{gathered} \frac{{\partial A_{ij,co} }}{{\partial x_{co} }} = \sum\limits_{k = 1}^{{N_{k} }} {Q_{ij,co}^{k} \left( {\frac{{\partial z_{k + 1,co} }}{{\partial x_{co} }} - \frac{{\partial z_{k,co} }}{{\partial x_{co} }}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i,j = 1,2,6\,}, \hfill \\ \frac{{\partial A_{ij,co} }}{{\partial x_{co} }} = \kappa \sum\limits_{k = 1}^{{N_{k} }} {Q_{ij,co}^{k} \left( {\frac{{\partial z_{k + 1,co} }}{{\partial x_{co} }} - \frac{{\partial z_{k,co} }}{{\partial x_{co} }}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i,j = 4,5}, \hfill \\ \frac{{\partial B_{ij,co} }}{{\partial x_{co} }} = \sum\limits_{k = 1}^{{N_{k} }} {Q_{ij,co}^{k} \left( {z_{k + 1,co} \frac{{\partial z_{k + 1,co} }}{{\partial x_{co} }} - z_{k,co} \frac{{\partial z_{k,co} }}{{\partial x_{co} }}} \right)\,\,\,\,\,\,\,i,j = 1,2,6}, \hfill \\ \frac{{\partial D_{ij,c0} }}{{\partial x_{co} }} = \sum\limits_{k = 1}^{{N_{k} }} {Q_{ij,co}^{k} \left( {z_{k + 1,co}^{2} \frac{{\partial z_{k + 1,co} }}{{\partial x_{co} }} - z_{k,co}^{2} \frac{{\partial z_{k,co} }}{{\partial x_{co} }}} \right)\,\,\,\,\,i,j = 1,2,6}. \hfill \\ \end{gathered} \right.$$

(10)

From Eq. (6),

$$\frac{{\partial z_{k,co} }}{{\partial x_{co} }} = \left( { - 0.5 + \frac{k - 1}{{N_{k} }}} \right)\frac{{\partial h_{co} }}{{\partial x_{co} }},$$

(11)

where ${{\partial h} \mathord{\left/ {\vphantom {{\partial h} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}$ can be obtained from Eq. (1),

$$\frac{{\partial h_{co} }}{{\partial x_{co} }} = - \frac{{h_{1,co} \alpha \lambda }}{{x_{co} }}\left( {\frac{{x_{co} }}{{L_{co} }}} \right)^{\beta - 1}.$$

(12)

2.3 Governing equations, boundary and connecting condition

In the current study, Hamilton’s principle is applied for obtaining the equilibrium equations of motion of the laminated composite conical shell with varying thickness and of the cylindrical shell. The equations of motion of the laminated composite conical shell with varying thickness and the cylindrical shell for free vibration analysis of coupled structure can be written as follows:

For the conical shell:

$$\begin{gathered} \frac{{\partial N_{x,co} }}{{\partial x_{co} }} + \frac{1}{{R_{co} }}\frac{{\partial N_{x\theta ,co} }}{{\partial \theta_{co} }} + \left( {N_{x,co} - N_{\theta ,co} } \right)\frac{\cos \varphi }{{R_{co} }} = I_{0,co} \frac{{\partial^{2} u_{co}^{0} }}{{\partial t^{2} }} + I_{1,co} \frac{{\partial^{2} \psi_{x,co} }}{{\partial t^{2} }}, \hfill \\ \frac{{\partial N_{x\theta ,co} }}{{\partial x_{co} }} + \frac{1}{{R_{co} }}\frac{{\partial N_{\theta ,co} }}{{\partial \theta_{co} }} + Q_{\theta ,co} \frac{\sin \varphi }{{R_{co} }} + 2N_{x\theta ,co} \frac{\cos \varphi }{{R_{co} }} = I_{0,co} \frac{{\partial^{2} v_{co}^{0} }}{{\partial t^{2} }} + I_{1,co} \frac{{\partial^{2} \psi_{\theta ,co} }}{{\partial t^{2} }}, \hfill \\ \frac{{\partial M_{x,co} }}{{\partial x_{co} }} + \frac{1}{{R_{co} }}\frac{{\partial M_{x\theta ,co} }}{{\partial \theta_{co} }} + \left( {M_{x,co} - M_{\theta ,co} } \right)\frac{\cos \varphi }{{R_{co} }} - Q_{x,co} = I_{1,co} \frac{{\partial^{2} u_{co}^{0} }}{{\partial t^{2} }} + I_{2,co} \frac{{\partial^{2} \psi_{x,co} }}{{\partial t^{2} }}, \hfill \\ \frac{{\partial M_{x\theta ,co} }}{{\partial x_{co} }} + \frac{1}{{R_{co} }}\frac{{\partial M_{\theta ,co} }}{{\partial \theta_{co} }} + 2M_{x\theta ,co} \frac{\cos \varphi }{{R_{co} }} - Q_{\theta ,co} = I_{1,co} \frac{{\partial^{2} v_{co}^{0} }}{{\partial t^{2} }} + I_{2,co} \frac{{\partial^{2} \psi_{\theta ,co} }}{{\partial t^{2} }}. \hfill \\ \end{gathered}$$

(13)

For the cylindrical shell:

$$\begin{gathered} \frac{{\partial N_{x,cy} }}{{\partial x_{cy} }} + \frac{1}{{R_{cy} }}\frac{{\partial N_{x\theta ,cy} }}{{\partial \theta_{cy} }} = I_{0,cy} \frac{{\partial^{2} u_{cy}^{0} }}{{\partial t^{2} }} + I_{1,cy} \frac{{\partial^{2} \psi_{x,cy} }}{{\partial t^{2} }}, \hfill \\ \frac{{\partial N_{x\theta ,cy} }}{{\partial x_{cy} }} + \frac{1}{{R_{cy} }}\frac{{\partial N_{\theta ,cy} }}{{\partial \theta_{cy} }} + \frac{{Q_{\theta ,cy} }}{{R_{cy} }} = I_{0,cy} \frac{{\partial^{2} v_{cy}^{0} }}{{\partial t^{2} }} + I_{1,cy} \frac{{\partial^{2} \psi_{\theta ,cy} }}{{\partial t^{2} }}, \hfill \\ - \frac{{N_{\theta ,cy} }}{{R_{cy} }} + \frac{{\partial Q_{x,cy} }}{{\partial x_{cy} }} + \frac{1}{{R_{cy} }}\frac{{\partial Q_{\theta ,cy} }}{{\partial \theta_{cy} }} = I_{0,cy} \frac{{\partial^{2} w_{cy}^{0} }}{{\partial t^{2} }}, \hfill \\ \frac{{\partial M_{x,cy} }}{{\partial x_{cy} }} + \frac{1}{{R_{cy} }}\frac{{\partial M_{x\theta ,cy} }}{{\partial \theta_{cy} }} - Q_{x,cy} = I_{1,cy} \frac{{\partial^{2} u_{cy}^{0} }}{{\partial t^{2} }} + I_{2,cy} \frac{{\partial^{2} \psi_{x,cy} }}{{\partial t^{2} }}, \hfill \\ \frac{{\partial M_{x\theta ,cy} }}{{\partial x_{cy} }} + \frac{1}{{R_{cy} }}\frac{{\partial M_{\theta ,cy} }}{{\partial \theta_{cy} }} - Q_{\theta ,cy} = I_{1,cy} \frac{{\partial^{2} v_{cy}^{0} }}{{\partial t^{2} }} + I_{2,cy} \frac{{\partial^{2} \psi_{\theta ,cy} }}{{\partial t^{2} }} \hfill \\ \end{gathered}$$

(14)

where I_0,ζ, I_1,ζ, I_2,ζ are the inertia terms and defined as follows:

$$\left( {I_{0,\zeta } ,I_{1,\zeta } ,I_{2,\zeta } } \right) = \sum\limits_{k = 1}^{{N_{k} }} {\int\limits_{{z_{k} }}^{{z_{k + 1} }} {\rho^{k} \left( {1,\,z_{\zeta } ,\,z_{\zeta }^{2} } \right)} } dz.$$

(15)

ρ^k is the mass of the kth layer per unit middle surface area.

By substituting Eqs. (4)–(6) into Eqs. (13) and (14), the equations of motion of the individual shells (i.e., conical shell with varying thickness and cylindrical shell) are written in matrix form as follows:

$$\left[ \begin{gathered} L_{{11,\zeta }} \;L_{{12,\zeta }} \,L_{{13,\zeta }} \,L_{{14,\zeta }} \,L_{{15,\zeta }} \hfill \\ L_{{21,\zeta }} \;L_{{22,\zeta }} \,L_{{23,\zeta }} \,L_{{24,\zeta }} \,L_{{25,\zeta }} \hfill \\ L_{{31,\zeta }} \;L_{{32,\zeta }} \,L_{{33,\zeta }} \,L_{{34,\zeta }} \,L_{{35,\zeta }} \hfill \\ L_{{41,\zeta }} \;L_{{42,\zeta }} \,L_{{43,\zeta }} \,L_{{44,\zeta }} \,L_{{45,\zeta }} \hfill \\ L_{{51,\zeta }} \;L_{{52,\zeta }} \,L_{{53,\zeta }} \,L_{{54,\zeta }} \,L_{{55,\zeta }} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} u \hfill \\ v \hfill \\ w \hfill \\ \phi _{\alpha } \hfill \\ \phi _{\beta } \hfill \\ \end{gathered} \right] = 0$$

(16)

where the detailed expression formulas of the coefficients L_ij,ζ can be found in Appendix 1.

Choosing reasonable boundary conditions in vibration problems has always been one of the most important issues. Therefore, a consistent and useful approach is specified for handling boundary conditions. One of the advantages of this method is its good compatibility with boundary condition equations. In this paper, we simulated boundary conditions using artificial springs. Therefore, generalized elastic boundary conditions are well modeled using three kinds of linear springs (ku, kv, kw) and two kinds of rotational springs (kϕ, kθ). In other words, arbitrary boundary conditions can be modeled by selecting the appropriate stiffness values of these springs. For simplicity of representation, we denote fully clamped, free, simply supported, and shear diaphragm boundary conditions as C, F, SS, SD, respectively. In addition, in this study, three kinds of elastic boundary conditions, expressed as E₁, E₂, and E₃, are investigated. Then, the simulated boundary condition equations at the start edge of the conical shell and the end edge of the cylindrical shell can be expressed as

$$\begin{gathered} x_{{co}} = 0 \Rightarrow \,\,\,\,\,\left\{ \begin{gathered} k_{{ub}}^{{co}} u_{{co}} = N_{{x,co}} ,\,\,\,k_{{vb}}^{{co}} v_{{co}} = N_{{x\theta ,co}} ,\,\,k_{{wb}}^{{co}} w_{{co}} = Q_{{x,co}}, \hfill \\ k_{{xb,0}}^{{co}} \psi _{{x,co}} = M_{{x,co}} ,\,\,k_{{\theta b}}^{{co}} \psi _{{\theta ,co}} = M_{{x\theta ,co}}, \hfill \\ \end{gathered} \right. \hfill \\ x_{{cy}} = L_{{cy}} \Rightarrow \left\{ \begin{gathered} k_{{ub}}^{{cy}} u_{{cy}} = - N_{{x,cy}} ,\,\,\,k_{{vb}}^{{cy}} v_{{cy}} = - N_{{x\theta ,cy}} ,\,\,k_{{wb}}^{{cy}} w_{{cy}} = - Q_{{x,cy}}, \hfill \\ k_{{xb}}^{{cy}} \psi _{{x,cy}} = - M_{{x,cy}} ,\,\,k_{{\theta b}}^{{cy}} \psi _{{\theta ,cy}} = - M_{{x\theta ,cy}}. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$

(17)

The boundary conditions considered along with the corresponding values of spring stiffness are given in Table 1.

Table 1 Corresponding values of the spring stiffness for general boundary conditions

Taking into account the change in curvature, the coupling conditions at the interface between the conical shell and the cylindrical shell can be given as [11]

$$\begin{gathered} u_{co} = u_{cy} \cos \varphi - u_{co} \sin \varphi ,\,\,\,\,v_{co} = v_{cy}, \hfill \\ w_{co} = u_{cy} \sin \varphi + w_{co} \cos \varphi ,\,\,\,\psi_{x,co} = \psi_{x,cy} ,\,\,\psi_{\theta ,co} = \psi_{\theta ,cy} \,; \hfill \\ N_{x,co} = N_{cy} \cos \varphi - Q_{x,cy} \sin \varphi ,\,\,\,\,N_{x\theta ,co} = N_{x\theta ,cy} , \hfill \\ Q_{x,co} = N_{x,cy} \sin \varphi + Q_{x,cy} \cos \varphi ,\,\,\,M_{x,co} = M_{x,cy} ,\,\,\,M_{x\theta ,co} = M_{x\theta ,cy} \hfill \\ \end{gathered}$$

(18)

where φ is the angle of difference between conical shell and cylindrical shell in the meridian direction. Since different coordinate directions are used on both sides of the coupling interface, the transformation relationship in Eq. (18) ensures continuity of displacements, forces, and moments. The force and moment resultants at the junction of a combined conical–cylindrical shell are given in accordance with the sign convention shown in Fig. 2.

Fig. 2

Force and moment resultants at interface of the combined composite laminated conical–cylindrical shell

As shown in Eqs. (13) and (14), since the equations of motion of the conical shell and the cylindrical shell are partial differential equations, it is necessary to convert them into a set of ordinary differential equations. Considering that the shell discussed in this paper is a perfectly rotating shell, if we proceed with variable separation using the Haar wavelet series in the meridian direction and the Fourier series in the circumferential direction, the displacement and rotation components can be written as follows:

$$\begin{gathered} u_{\zeta }^{0} (x,\theta ,t) = U_{\zeta } (x)\cos (n\theta )\;e^{i\omega t} , \hfill \\ v_{\zeta }^{0} (x,\theta ,t) = V_{\zeta } (x)\sin (n\theta )\;e^{i\omega t} , \hfill \\ w_{\zeta }^{0} (x,\theta ,t) = W_{\zeta } (x)\cos (n\theta )\;e^{i\omega t} , \hfill \\ \psi_{x,\zeta } (x,\theta ,t) = \Phi_{\zeta } (x)\cos (n\theta )\;e^{i\omega t} , \hfill \\ \psi_{\theta ,\zeta } (x,\theta ,t) = \Theta_{\zeta } (x)\sin (n\theta )\;e^{i\omega t} \hfill \\ \end{gathered}$$

(19)

where ω is the angular frequency, and the nonnegative integer n is the number of waves of the corresponding mode. U(x), V(x), W(x), Φ(x), and Θ(x) are unknown functions to be determined. Substituting Eq. (19) into Eq. (16) and carrying out several algebraic operations, the governing equations of the individual shells can be written in the following unified form:

$$\begin{gathered} L_{{11,\zeta }}^{0} U_{\zeta } + L_{{11,\zeta }}^{1} \frac{{dU_{\zeta } }}{{dx_{\zeta } }} + L_{{11,\zeta }}^{2} \frac{{d^{2} U_{\zeta } }}{{dx_{\zeta }^{2} }} + L_{{12,\zeta }}^{0} V_{\zeta } + L_{{12,\zeta }}^{1} \frac{{dV_{\zeta } }}{{dx_{\zeta } }} + L_{{13,\zeta }}^{0} W_{\zeta } + L_{{13,\zeta }}^{1} \frac{{dW_{\zeta } }}{{dx_{\zeta } }} \hfill \\ \,\, + L_{{14,\zeta }}^{0} \Phi _{\zeta } + L_{{14,\zeta }}^{1} \frac{{d\Phi _{\zeta } }}{{dx_{\zeta } }} + L_{{14,\zeta }}^{2} \frac{{d^{2} \Phi _{\zeta } }}{{d\alpha ^{2} }} + L_{{15,\zeta }}^{0} \Theta _{\zeta } + L_{{15,\zeta }}^{1} \frac{{d\Theta _{\zeta } }}{{dx_{\zeta } }} + I_{{0,\zeta }} \omega ^{2} R_{\zeta }^{2} U_{\zeta } + I_{{1,\zeta }} \omega ^{2} R_{\zeta }^{2} \Phi _{\zeta } = 0, \hfill \\ \end{gathered}$$

(20.1)

$$\begin{gathered} L_{{31,\zeta }}^{0} U_{\zeta } + L_{{31,\zeta }}^{1} \frac{{dU_{\zeta } }}{{dx_{\zeta } }} + L_{{32,\zeta }}^{0} V_{\zeta } + L_{{33,\zeta }}^{0} W_{\zeta } + L_{{33,\zeta }}^{1} \frac{{dW_{\zeta } }}{{dx_{\zeta } }} + L_{{33,\zeta }}^{2} \frac{{d^{2} W_{\zeta } }}{{dx_{\zeta }^{2} }} \hfill \\ \,\, + L_{{34,\zeta }}^{0} \Phi _{\zeta } + L_{{34,\zeta }}^{1} \frac{{d\Phi _{\zeta } }}{{dx_{\zeta } }} + L_{{35,\zeta }}^{0} \Theta _{\zeta } + I_{{0,\zeta }} \omega ^{2} R_{\zeta }^{2} W_{\zeta } = 0, \hfill \\ \end{gathered}$$

(20.2)

$$\begin{gathered} L_{{31,\zeta }}^{0} U_{\zeta } + L_{{31,\zeta }}^{1} \frac{{dU_{\zeta } }}{{dx_{\zeta } }} + L_{{32,\zeta }}^{0} V_{\zeta } + L_{{33,\zeta }}^{0} W_{\zeta } + L_{{33,\zeta }}^{1} \frac{{dW_{\zeta } }}{{dx_{\zeta } }} + L_{{33,\zeta }}^{2} \frac{{d^{2} W_{\zeta } }}{{dx_{\zeta }^{2} }} \hfill \\ \,\, + L_{{34,\zeta }}^{0} \Phi _{\zeta } + L_{{34,\zeta }}^{1} \frac{{d\Phi _{\zeta } }}{{dx_{\zeta } }} + L_{{35,\zeta }}^{0} \Theta _{\zeta } + I_{{0,\zeta }} \omega ^{2} R_{\zeta }^{2} W_{\zeta } = 0, \hfill \\ \end{gathered}$$

(20.3)

$$\begin{gathered} L_{{41,\zeta }}^{0} U_{\zeta } + L_{{41,\zeta }}^{1} \frac{{dU_{\zeta } }}{{dx_{\zeta } }} + L_{{41,\zeta }}^{2} \frac{{d^{2} U_{\zeta } }}{{dx_{\zeta }^{2} }} + L_{{42,\zeta }}^{0} V_{\zeta } + L_{{42,\zeta }}^{1} \frac{{dV_{\zeta } }}{{dx_{\zeta } }} + L_{{43,\zeta }}^{0} W_{\zeta } + L_{{43,\zeta }}^{1} \frac{{dW_{\zeta } }}{{dx_{\zeta } }} \hfill \\ \,\, + L_{{44,\zeta }}^{0} \Phi _{\zeta } + L_{{44,\zeta }}^{1} \frac{{d\Phi _{\zeta } }}{{dx_{\zeta } }} + L_{{44,\zeta }}^{2} \frac{{d^{2} \Phi _{\zeta } }}{{dx_{\zeta }^{2} }} + L_{{45,\zeta }}^{0} \Theta _{\zeta } + L_{{45,\zeta }}^{1} \frac{{d\Theta _{\zeta } }}{{dx_{\zeta } }} + I_{{1,\zeta }} \omega ^{2} R_{\zeta }^{2} U_{\zeta } + I_{{2,\zeta }} \omega ^{2} R_{\zeta }^{2} \Phi _{\zeta } = 0, \hfill \\ \end{gathered}$$

(20.4)

$$\begin{gathered} L_{{51,\zeta }}^{0} U_{\zeta } + L_{{51,\zeta }}^{1} \frac{{dU_{\zeta } }}{{dx_{\zeta } }} + L_{{52,\zeta }}^{0} V_{\zeta } + L_{{52,\zeta }}^{1} \frac{{dV_{\zeta } }}{{dx_{\zeta } }} + L_{{52,\zeta }}^{2} \frac{{d^{2} V_{\zeta } }}{{dx_{\zeta }^{2} }} + L_{{53,\zeta }}^{0} W_{\zeta } \hfill \\ \,\, + L_{{54,\zeta }}^{0} \Phi _{\zeta } + L_{{54,\zeta }}^{1} \frac{{d\Phi _{\zeta } }}{{dx_{\zeta } }} + L_{{55,\zeta }}^{0} \Theta _{\zeta } + L_{{55,\zeta }}^{1} \frac{{d\Theta _{\zeta } }}{{dx_{\zeta } }} + L_{{55,\zeta }}^{2} \frac{{d^{2} \Theta _{\zeta } }}{{dx_{\zeta }^{2} }} + I_{{1,\zeta }} \omega ^{2} R_{\zeta }^{2} V_{\zeta } + I_{{2,\zeta }} \omega ^{2} R_{\zeta }^{2} \Theta _{\zeta } = 0 \hfill \\ \end{gathered}$$

(20.5)

where the detailed expressions of the coefficients $L_{ij,\zeta }^{k}$ can be found in Appendix 2.

The boundary condition equations can be obtained in a similar way to Eq. (20) and can be written as follows.

At the left boundary:

$$\left\{ \begin{gathered} A_{{11,co}} R_{{co}} \frac{{dU_{{co}} }}{{dx_{{co}} }} + \left( {A_{{12,co}} \sin \varphi - k_{{ub}}^{{co}} R_{{co}} } \right)U_{{co}} + A_{{12,co}} nV_{{co}} + A_{{12,co}} \cos \varphi W_{{co}} \hfill \\ \,\, + B_{{11,co}} R_{{co}} \frac{{d\Phi _{c} }}{{dx_{{co}} }} + B_{{12,co}} \sin \varphi \Phi _{{co}} + B_{{12,co}} \Theta _{{co}} = 0, \hfill \\ \,\, - A_{{66,co}} nU_{{co}} + A_{{66,co}} R_{{co}} \frac{{dV_{{co}} }}{{dx_{{co}} }} - \left( {A_{{66,co}} \sin \varphi + k_{{vb}}^{{co}} R_{{co}} } \right)V_{{co}} \hfill \\ \,\, - B_{{66,co}} n\Phi _{{co}} + B_{{66,co}} R_{{co}} \frac{{d\Theta _{{co}} }}{{dx_{{co}} }} - B_{{66,co}} \sin \varphi \Theta _{{co}} = 0, \hfill \\ \kappa A_{{55,co}} R_{{co}} \frac{{dW_{{co}} }}{{dx_{{co}} }} - k_{{wb}}^{{co}} R_{{co}} W_{{co}} + \kappa A_{{55,co}} R_{{co}} \Phi _{{co}} = 0, \hfill \\ B_{{11,co}} R_{{co}} \frac{{dU_{{co}} }}{{dx_{{co}} }} + B_{{12,co}} \sin \varphi U_{{co}} + B_{{12,co}} nV_{{co}} + B_{{12,co}} \cos \varphi W_{{co}} \hfill \\ \,\, + D_{{11,co}} R_{{co}} \frac{{d\Phi _{{co}} }}{{dx_{{co}} }} + \left( {D_{{12,co}} \sin \varphi - k_{{xb}}^{{co}} R_{{co}} } \right)\Phi _{{co}} + D_{{12,co}} n\Theta _{{co}} = 0, \hfill \\ \,\, - B_{{66,co}} nU_{{co}} + B_{{66,co}} R_{{co}} \frac{{dV_{{co}} }}{{dx_{{co}} }} - B_{{66,co}} \sin \varphi V_{{co}} - D_{{66,co}} n\Phi _{{co}} \hfill \\ \,\, + D_{{66,co}} R_{{co}} \frac{{d\Theta _{c} }}{{dx_{{co}} }} - \left( {D_{{66,co}} \sin \varphi + k_{{\theta b}}^{{co}} R_{c} } \right)\Theta _{{co}} = 0; \hfill \\ \end{gathered} \right.$$

(21.1)

At the right boundary:

$$\left\{ \begin{gathered} A_{11,cy} R_{cy} \frac{{dU_{cy} }}{{dx_{cy} }} + k_{ub}^{cy} R_{cy} U_{cy} + A_{12,cy} nV_{cy} + A_{12,cy} W_{cy} + B_{11,cy} R_{cy} \frac{{d\Phi_{l} }}{{dx_{cy} }} + B_{12,cy} n\Theta_{cy} = 0 \hfill \\ - A_{66,cy} nU_{cy} + A_{66,cy} R_{cy} \frac{{dV_{cy} }}{{dx_{cy} }} + k_{vb}^{cy} R_{cy} V_{cy} - B_{66,cy} n\Phi_{cy} + B_{66,cy} R_{cy} \Theta_{cy} = 0, \hfill \\ \kappa A_{55,cy} R_{cy} \frac{{dW_{cy} }}{{dx_{cy} }} + k_{wb}^{cy} R_{cy} W_{cy} + \kappa A_{55,cy} R_{cy} \Phi_{cy} = 0, \hfill \\ B_{11,cy} R_{cy} \frac{{dU_{cy} }}{{dx_{cy} }} + B_{12,cy} nV_{cy} + B_{12,cy} W_{cy} + D_{11,cy} R_{cy} \frac{{d\Phi_{cy} }}{{dx_{cy} }} + k_{xb}^{cy} R_{cy} \Phi_{cy} + D_{12,cy} n\Theta_{cy} = 0, \hfill \\ - B_{66,cy} nU_{cy} + B_{66,cy} R_{cy} \frac{{dV_{cy} }}{{dx_{cy} }} - D_{66,cy} n\Phi_{cy} + D_{66,cy} R_{cy} \frac{{d\Theta_{cy} }}{{dx_{cy} }} + k_{\theta b}^{cy} R_{cy} \Theta_{cy} = 0. \hfill \\ \end{gathered} \right.$$

(21.2)

2.4 Haar wavelet series and discretization

The Haar wavelet function h_i(x) for x ∈ [0, 1] is defined as [26, 27, 32, 33]

$$h_{i} (x) = \left\{ \begin{gathered} 1\,\,\,\,\,\,\,\,x \in \left[ {x_{1} ,x_{2} } \right] \hfill \\ - 1\,\,\,\,x \in \left[ {x_{2} ,x_{3} } \right] \hfill \\ 0\,\,\,\,\,\,\,{\text{elsewhere}} \hfill \\ \end{gathered} \right.$$

(22)

In Eq. (22), notations x₁ = k/m, and x₂ = (k + 0.5)/m, x₃ = (k + 1)/m are introduced, in which the integer m = 2j (j = 0, 1,…,J) is the scale factor, and the maximal level of resolution determined by the integer J; k = 0, 1,…, m-1 is the delay factor.

Any function f(x), which is square integrable in the interval [0, 1], can be expanded into Haar wavelet series of infinite terms. If f(x) is piecewise constant by itself, or may be approximated as piecewise constant during each subinterval, then f(x) will be truncated with finite terms, that is,

$$f(x) = \sum\limits_{i = 1}^{2M} {a_{i} h_{i} \left( x \right)}$$

(23)

where a_i(i = 1, 2, …, 2 M) is the unknown wavelet coefficient. The interval [0, 1] is divided into 2 M subintervals of equal length ∆x = 1/2 M; the collocation points are given as:

$$x_{l} = \frac{{\left( {l - 0.5} \right)}}{2M},\,\,\,l = 1,2,...,2M.$$

(24)

In order to solve an nth-order PDE, the integrals of the wavelets

$$p_{n,i} \left( x \right) = \underbrace {{\int_{0}^{x} {\int_{0}^{x} { \cdots \int_{0}^{x} {h_{i} \left( t \right)dt^{n} } } } }}_{n - times} = \frac{1}{{\left( {n - 1} \right)!}}\int_{0}^{x} {\left( {x - t} \right)^{n - 1} h_{i} \left( t \right)dt}$$

(25)

are required. In Eq. (25), i = 1,2,…,2 M. The case n = 0 corresponds to function h_i(t). These integrals can be calculated analytically. In case of i = 1, the integral of the wavelet is p_n,1(x) = xⁿ/n!, and in case i > 1 it is

$$p_{{n,i}} \left( x \right) = \left\{ \begin{gathered} 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x < x_{1}, \hfill \\ \frac{1}{{n!}}\left( {x - x_{1} } \right)^{n} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x_{1} < x < x_{2}, \hfill \\ \frac{1}{{n!}}\left[ {\left( {x - x_{1} } \right)^{n} - 2\left( {x - x_{2} } \right)^{n} } \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x_{2} < x < x_{3}, \hfill \\ \frac{1}{{n!}}\left[ {\left( {x - x_{1} } \right)^{n} - 2\left( {x - x_{2} } \right)^{n} + \left( {x - x_{3} } \right)^{n} } \right]\,\,\,\,\,x > x_{3}. \hfill \\ \end{gathered} \right.$$

(26)

For solving boundary value problems, the values p_n,i(0) and p_n,i(1) should be calculated in order to satisfy the boundary conditions. Substituting the collocation points in Eq. (24) into Eq. (26) yields

$${\varvec{p}}^{\left( n \right)} \left( {i,l} \right) = p_{n,i} \left( x \right)$$

(27)

where P⁽ⁿ⁾ is a 2 M × 2 M matrix. It should be noted that calculations of the matrices H(i, l) and P⁽ⁿ⁾(i, l) must be carried out only once.

The Haar wavelet series is defined in the interval [0, 1]; therefore, to apply the HWM, the linear transformation statute is used for the coordinate conversion from length interval [0, L] of the shell to the interval [0, 1] of the Haar wavelet series, that is,

$$\xi = \frac{x}{L}.$$

(28)

In the HWM, the highest order derivatives of the displacements are expressed using the Haar wavelet series, and the lower-order derivatives can be obtained by integrating the Haar wavelet series. The highest order derivative of the displacements in the governing equations of motion and boundary condition expressions is second order, which can be obtained by means of the Haar wavelet series as follows:

$$\begin{gathered} \frac{{d^{2} U(\xi )}}{{d\xi^{2} }} = \sum\limits_{i = 1}^{2M} {a_{i} h_{i} \left( \xi \right)} ,\;\;\,\,\,\,\,\,\frac{{d^{2} V(\xi )}}{{d\xi^{2} }} = \sum\limits_{i = 1}^{2M} {b_{i} h_{i} \left( \xi \right)} ,\;\,\,\,\,\,\,\,\,\,\frac{{d^{2} W(\xi )}}{{d\xi^{2} }} = \sum\limits_{i = 1}^{2M} {c_{i} h_{i} \left( \xi \right),} \hfill \\ \frac{{d^{2} \Phi (\xi )}}{{d\xi^{2} }} = \sum\limits_{i = 1}^{2M} {d_{i} h_{i} \left( \xi \right)} ,\,\,\,\,\,\,\,\,\frac{{d^{2} \Theta (\xi )}}{{d\xi^{2} }} = \sum\limits_{i = 1}^{2M} {e_{i} h_{i} \left( \xi \right)} ,\; \hfill \\ \end{gathered}$$

(29)

where a_i, b_i, c_i, and d_i are unknown coefficients of the Haar wavelets. The first-order derivatives of displacements are obtained by integrating Eq. (29), and the displacements and rotations can be calculated by integrating the above result again. The first-order derivatives of displacements and rotations are written as follows:

$$\begin{gathered} \frac{dU(\xi )}{{d\xi }} = \sum\limits_{i = 1}^{2M} {a_{i} P_{1,i} \left( \xi \right)} + \frac{dU(0)}{{d\xi }},\;\;\;\,\,\,\,\,U(\xi ) = \sum\limits_{i = 1}^{2M} {a_{i} P_{2,i} \left( \xi \right)} + \xi \frac{dU(0)}{{d\xi }} + U(0), \hfill \\ \frac{dV(\xi )}{{d\xi }} = \sum\limits_{i = 1}^{2M} {a_{i} P_{1,i} \left( \xi \right)} + \frac{dV(0)}{{d\xi }},\;\;\;\,\,\,\,\,V(\xi ) = \sum\limits_{i = 1}^{2M} {b_{i} P_{2,i} \left( \xi \right)} + \xi \frac{dV(0)}{{d\xi }} + V(0), \hfill \\ \frac{dW(\xi )}{{d\xi }} = \sum\limits_{i = 1}^{2M} {c_{i} P_{1,i} \left( \xi \right)} + \frac{dW(0)}{{d\xi }},\;\;\;\,\,\,\,W(\xi ) = \sum\limits_{i = 1}^{2M} {c_{i} P_{2,i} \left( \xi \right)} + \xi \frac{dW(0)}{{d\xi }} + W(0), \hfill \\ \frac{d\Phi (\xi )}{{d\xi }} = \sum\limits_{i = 1}^{2M} {d_{i} P_{1,i} \left( \xi \right)} + \frac{d\Phi (0)}{{d\xi }},\;\;\;\,\,\,\Phi (\xi ) = \sum\limits_{i = 1}^{2M} {d_{i} P_{2,i} \left( \xi \right)} + \xi \frac{d\Phi (0)}{{d\xi }} + \Phi (0), \hfill \\ \frac{d\Theta (\xi )}{{d\xi }} = \sum\limits_{i = 1}^{2M} {e_{i} P_{1,i} \left( \xi \right)} + \frac{d\Theta (0)}{{d\xi }},\;\;\;\,\,\,\,\Theta (\xi ) = \sum\limits_{i = 1}^{2M} {e_{i} P_{2,i} \left( \xi \right)} + \xi \frac{d\Theta (0)}{{d\xi }} + \Theta (0). \hfill \\ \end{gathered}$$

(30)

Equations (29) and (30) can be expressed in the discretized matrix form as follows:

$$\begin{array}{*{20}c} {\frac{{d^{2} \user2{U}}}{{d\xi ^{2} }} = \user2{Ha} + \user2{H}_{{11}} \user2{f},} & {\frac{{d\user2{U}}}{{d\xi }} = \user2{P}_{1} \user2{a} + \user2{P}_{{11}} \user2{f},} & {\user2{U} = \user2{P}_{2} \user2{a} + \user2{P}_{{22}} \user2{f},} \\ {\frac{{d^{2} \user2{V}}}{{d\xi ^{2} }} = \;\user2{Hb} + \user2{H}_{{11}} \user2{g},} & {\frac{{d\user2{V}}}{{d\xi }} = \;\user2{P}_{1} \user2{b} + \user2{P}_{{11}} \user2{g},} & {\user2{V} = \user2{P}_{2} \user2{b} + \user2{P}_{{22}} \user2{g},} \\ {\frac{{d^{2} \user2{W}}}{{d\xi ^{2} }} = \user2{Hc} + \user2{H}_{{11}} \user2{h},} & {\frac{{d\user2{W}}}{{d\xi }} = \user2{P}_{1} \user2{c} + \user2{P}_{{11}} \user2{h},} & {\user2{W} = \user2{P}_{2} \user2{c} + \user2{P}_{{22}} \user2{h},} \\ {\frac{{d^{2} {\mathbf{\Phi }}}}{{d\xi ^{2} }} = \user2{Hd} + \user2{H}_{{11}} \user2{k},} & {\frac{{d{\mathbf{\Phi }}}}{{d\xi }} = \user2{P}_{1} \user2{d} + \user2{P}_{{11}} \user2{k},} & {{\mathbf{\Phi }} = \user2{P}_{2} \user2{d} + \user2{P}_{{22}} \user2{k},} \\ {\frac{{d^{2} {\mathbf{\Theta }}}}{{d\xi ^{2} }} = \user2{He} + \user2{H}_{{11}} \user2{l},} & {\frac{{d{\mathbf{\Theta }}}}{{d\xi }} = \user2{P}_{1} \user2{e} + \user2{P}_{{11}} \user2{l},} & {{\mathbf{\Theta }} = \user2{P}_{2} \user2{e} + \user2{P}_{{22}} \user2{l},} \\ \end{array}$$

(31)

where H and P₁, P₂ are the Haar wavelet and its integrals, and are defined as

$${\varvec{H}}_{1} = \left[ {\begin{array}{*{20}c} {h_{1} (\xi_{1} )} & {h_{2} (\xi_{1} )} & \cdots & {h_{n} (\xi_{1} )} \\ {h_{1} (\xi_{2} )} & {\;h_{2} (\xi_{2} )} & \cdots & {h_{n} (\xi_{2} )} \\ { \vdots \;} & { \vdots \;} & \ddots & { \vdots \;} \\ {h_{1} (\xi_{n} )} & {h_{2} (\xi_{n} )} & \cdots & {h_{n} (\xi_{n} )} \\ \end{array} } \right],\,\,\,\,\,\,\,\,\,\,\,\,{\varvec{H}}_{11} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ { \vdots \;} & { \vdots \;} \\ 0 & 0 \\ \end{array} } \right],$$

(32)

$$\user2{P}_{1} = \left[ {\begin{array}{*{20}c} {P_{{1,1}} (\xi _{1} )} & {P_{{1,2}} (\xi _{1} )} & \cdots & {P_{{1,n}} (\xi _{1} )} \\ {P_{{1,1}} (\xi _{2} )} & {\;P_{{1,2}} (\xi _{2} )} & \cdots & {P_{{1,n}} (\xi _{2} )} \\ { \vdots \;} & { \vdots \;} & \ddots & { \vdots \;} \\ {P_{{1,1}} (\xi _{n} )} & {P_{{1,2}} (\xi _{n} )} & \cdots & {P_{{1,n}} (\xi _{n} )} \\ \end{array} } \right],\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\user2{P}_{{11}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 1 & 0 \\ { \vdots \;} & { \vdots \;} \\ 1 & 0 \\ \end{array} } \right],$$

(33)

$$\user2{P}_{2} = \left[ {\begin{array}{*{20}c} {P_{{2,1}} (\xi _{1} )} & {P_{{2,2}} (\xi _{1} )} & \cdots & {P_{{2,n}} (\xi _{1} )} \\ {P_{{2,1}} (\xi _{2} )} & {\;P_{{2,2}} (\xi _{2} )} & \cdots & {P_{{2,n}} (\xi _{2} )} \\ { \vdots \;} & { \vdots \;} & \ddots & { \vdots \;} \\ {P_{{2,1}} (\xi _{n} )} & {P_{{2,2}} (\xi _{n} )} & \cdots & {P_{{2,n}} (\xi _{n} )} \\ \end{array} } \right],\,\,\,\,\,\,\,\,\,\,\,\,\user2{P}_{{22}} = \left[ {\begin{array}{*{20}c} {\xi _{1} } & 1 \\ {\xi _{2} } & 1 \\ { \vdots \;} & { \vdots \;} \\ {\xi _{n} } & 1 \\ \end{array} } \right],$$

(34)

and the notations are defined as follows:

$$\begin{gathered} {\varvec{U}} = \left[ {U(\xi_{1} ),U(\xi_{2} ), \ldots ,U(\xi_{n} )} \right]^{T} ,\;\;\;\;\;\;\;\;{\varvec{a}} = \left[ {a_{1} ,a_{2} , \ldots ,a_{n} } \right]^{T} ,\;\;\;\;\;{\varvec{f}} = \left[ {\frac{{dU(\xi_{0} )}}{d\xi },U(\xi_{0} )} \right]^{T}, \hfill \\ {\varvec{V}} = \left[ {V(\xi_{1} ),V(\xi_{2} ), \cdots ,V(\xi_{n} )} \right]^{T} ,\;\;\;\;\;\;\;\;\;\;{\varvec{b}} = \left[ {b_{1} ,b_{2} , \cdots ,b_{n} } \right]^{T} ,\;\;\;\;\;\;{\varvec{g}} = \left[ {\frac{{dV(\xi_{0} )}}{d\xi },V(\xi_{0} )} \right]^{T}, \hfill \\ {\varvec{W}} = \left[ {W(\xi_{1} ),W(\xi_{2} ), \cdots ,W(\xi_{n} )} \right]^{T} ,\;\;\;\;\;\;\;{\varvec{c}} = \left[ {c_{1} ,c_{2} , \cdots ,c_{n} } \right]^{T} ,\;\;\;\;\;{\varvec{h}} = \left[ {\frac{{dW(\xi_{0} )}}{d\xi },W(\xi_{0} )} \right]^{T}, \hfill \\ {{\varvec{\Phi}}} = \left[ {\Phi (\xi_{1} ),\Phi (\xi_{2} ), \cdots ,\Phi (\xi_{n} )} \right]^{T} ,\;\;\;\,\,\,\,\,\,\,\,{\varvec{d}} = \left[ {d_{1} ,d_{2} , \cdots ,d_{n} } \right]^{T} ,\;\;\;\;{\varvec{k}} = \left[ {\frac{{d\Phi (\xi_{0} )}}{d\xi },\Phi (\xi_{0} )} \right]^{T}, \hfill \\ {{\varvec{\Theta}}} = \left[ {\Theta (\xi_{1} ),\Theta (\xi_{2} ), \cdots ,\Theta (\xi_{n} )} \right]^{T} ,\;\;\;\,\,\,\,\,\,\,\,{\varvec{e}} = \left[ {e_{1} ,e_{2} , \cdots ,e_{n} } \right]^{T} ,\;\;\;\;\;\,\,{\varvec{l}} = \left[ {\frac{{d\Theta (\xi_{0} )}}{d\xi },\Theta (\xi_{0} )} \right]^{T} \hfill \\ \end{gathered}$$

(35)

where f, g, h, k, and l indicate the integral constants, which can be obtained by applying the boundary condition. The highest order of the displacements of the boundary condition equations is first order, and the first-order derivatives and displacements in Eq. (30) are calculated when ξ = 0 and ξ = 1. The discretization of the boundary condition equation can be manipulated in the same way as that of the displacement, and it can be written in the matrix form as follows:

$$\begin{gathered} \frac{{d{\varvec{U}}_{{\mathbf{b}}} }}{d\xi } = {\mathbf{P}}_{{{\mathbf{bc1}}}} {\varvec{a}} + {\mathbf{P}}_{{{\mathbf{bc11}}}} \user2{f,}\;\;\frac{{d{\varvec{V}}_{{\mathbf{b}}} }}{d\xi } = {\mathbf{P}}_{{{\mathbf{bc1}}}} {\varvec{b}} + {\mathbf{P}}_{{{\mathbf{bc11}}}} \user2{g,}\;\;\;\frac{{d{\varvec{W}}_{{\mathbf{b}}} }}{d\xi } = {\mathbf{P}}_{{{\mathbf{bc1}}}} {\varvec{c}} + {\mathbf{P}}_{{{\mathbf{bc11}}}} \user2{h,}\; \hfill \\ \frac{{d{{\varvec{\Phi}}}_{{\mathbf{b}}} }}{d\xi } = {\mathbf{P}}_{{{\mathbf{bc1}}}} {\varvec{d}} + {\mathbf{P}}_{{{\mathbf{bc11}}}} \user2{k, }\,\,\frac{{d{{\varvec{\Theta}}}_{{\mathbf{b}}} }}{d\xi } = {\varvec{P}}_{{{\mathbf{bc1}}}} {\varvec{e}} + {\varvec{P}}_{{{\mathbf{bc11}}}} {\varvec{l}}, \hfill \\ \end{gathered}$$

(36)

$$\begin{gathered} \;{\varvec{U}}_{{\mathbf{b}}} = {\varvec{P}}_{{{\mathbf{bc2}}}} {\varvec{a}} + {\varvec{P}}_{{{\mathbf{bc22}}}} \user2{f,}\;\,\,\,\,\,\,\,\,{\varvec{V}}_{{\mathbf{b}}} = {\varvec{P}}_{{{\mathbf{bc2}}}} {\varvec{b}} + {\varvec{P}}_{{{\mathbf{bc22}}}} \user2{g,}\,\,\,\,\,\,\,\,\;{\varvec{W}}_{{\mathbf{b}}} = {\varvec{P}}_{{{\mathbf{bc2}}}} {\varvec{c}} + {\varvec{P}}_{{{\mathbf{bc22}}}} {\varvec{h}},\,\,\,\,\, \hfill \\ \,{{\varvec{\Phi}}}_{{\mathbf{b}}} = {\varvec{P}}_{{{\mathbf{bc2}}}} {\varvec{d}} + {\varvec{P}}_{{{\mathbf{bc22}}}} {\varvec{k}},\,\,\,\,\,\,\,\,\,\,\,{{\varvec{\Theta}}}_{{\mathbf{b}}} = {\varvec{P}}_{{{\mathbf{bc2}}}} {\varvec{e}} + {\varvec{P}}_{{{\mathbf{bc22}}}} {\varvec{l}} \hfill \\ \end{gathered}$$

(37)

where

Left boundary:

$$\begin{gathered} {\mathbf{P}}_{{{\mathbf{bc1}}}} = \left[ {\begin{array}{*{20}c} {p_{{1,1}} (0)} & {p_{{1,2}} (0)} & \cdots & {p_{{1,n}} (0)} \\ \end{array} } \right],\;\;\;\;\;\;\;{\mathbf{P}}_{{{\mathbf{bc11}}}} = \left[ {\begin{array}{*{20}c} 1 & 1 \\ \end{array} } \right], \hfill \\ {\mathbf{P}}_{{{\mathbf{bc2}}}} = \left[ {\begin{array}{*{20}c} {p_{{2,1}} (0)} & {p_{{2,2}} (0)} & \cdots & {p_{{2,n}} (0)} \\ \end{array} } \right],\;\;\;\;\;\;{\mathbf{P}}_{{{\mathbf{bc22}}}} = \left[ {\begin{array}{*{20}c} {\xi (0)} & 1 \\ \end{array} } \right]; \hfill \\ \end{gathered}$$

(38)

Right boundary:

$$\begin{gathered} {\mathbf{P}}_{{{\mathbf{bc1}}}} = \left[ {\begin{array}{*{20}c} {p_{{1,1}} (1)} & {p_{{1,2}} (1)} & \cdots & {p_{{1,n}} (1)} \\ \end{array} } \right],\;\;\;\;\;\;\;{\mathbf{P}}_{{{\mathbf{bc11}}}} = \left[ {\begin{array}{*{20}c} 1 & 1 \\ \end{array} } \right], \hfill \\ {\mathbf{P}}_{{{\mathbf{bc2}}}} = \left[ {\begin{array}{*{20}c} {p_{{2,1}} (1)} & {p_{{2,2}} (1)} & \cdots & {p_{{2,n}} (1)} \\ \end{array} } \right],\;\;\;\;\;\;{\mathbf{P}}_{{{\mathbf{bc22}}}} = \left[ {\begin{array}{*{20}c} {\xi (1)} & 1 \\ \end{array} } \right]. \hfill \\ \end{gathered}$$

(39)

With respect to the continuity condition, the equations can be expressed in a similar way as the boundary condition. Therefore, the entire systems of the combined composite laminated conical–cylindrical shell including boundary conditions are discretized using the HWM, and the entire governing equations can be expressed in matrix form as follows:

$$\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{dd} } & {{\mathbf{K}}_{db} } \\ {{\mathbf{K}}_{bb} } & {{\mathbf{K}}_{bd} } \\ \end{array} } \right]\left[ \begin{gathered} {\varvec{A}}_{d} \hfill \\ {\varvec{A}}_{b} \hfill \\ \end{gathered} \right] - \omega^{2} \left[ {\;\;\begin{array}{*{20}c} {{\mathbf{M}}_{dd} } & {{\mathbf{M}}_{db} } \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]\left[ \begin{gathered} {\varvec{A}}_{d} \hfill \\ {\varvec{A}}_{b} \hfill \\ \end{gathered} \right] = 0,$$

(40)

$${\mathbf{A}}_{d} = \left[ {{\varvec{a}},\;{\varvec{b}},\;{\varvec{c}},\;{\varvec{d}},\;{\varvec{e}},\;} \right]^{T} ,{\mathbf{A}}_{b} = \left[ {{\varvec{f}},\;{\varvec{g}},\;{\varvec{h}},\;{\varvec{k}},\;{\varvec{l}},\;} \right]^{T}.$$

(41)

A_b at both sides of Eq. (40) can be eliminated by performing some algebraic manipulations, and the standard characteristic equation is expressed as follows:

$$\left[ {{\mathbf{K}}_{dd} - {\mathbf{K}}_{db} {\mathbf{K}}_{bd}^{ - 1} {\mathbf{K}}_{bb} } \right]\user2{\rm A}_{d} = \omega^{2} \left[ {{\mathbf{M}}_{dd} - {\mathbf{M}}_{db} {\mathbf{K}}_{bd}^{ - 1} {\mathbf{K}}_{bb} } \right]\user2{\rm A}_{d}.$$

(42)

By the further simplification of the above equation, the following matrix expressions can be obtained:

$$\left( {{\mathbf{K}} - \omega^{2} {\mathbf{M}}} \right)\user2{\rm A}_{d} = 0$$

(43)

where ${\mathbf{K}} = \left[ {{\mathbf{K}}_{dd} - {\mathbf{K}}_{db} {\mathbf{K}}_{bd}^{ - 1} {\mathbf{K}}_{bb} } \right]$ and ${\mathbf{M}} = \left[ {{\mathbf{M}}_{dd} - {\mathbf{M}}_{db} {\mathbf{M}}_{bd}^{ - 1} {\mathbf{M}}_{bb} } \right]$ are stiffness and mass matrices of the structure, respectively.

3 Numerical results and discussions

In this Section, the convergence, accuracy, and reliability of the proposed HWM for the free vibration analysis of a combined composite laminated conical–cylindrical shell with a varying thickness are presented by numerical examples. First, the convergence and verification study of the presented method is performed. Then, the parametric studies including the thickness variation parameters, material properties, geometrical dimensions, and different boundary conditions are carried out. In order to express the boundary conditions, expressions such as C–SS are used, which denotes that both end boundaries of the combined shell are clamped and simply supported, respectively. Also, it is assumed that the conical and the cylindrical shell are made of the same laminated composite material, and unless otherwise stated, the material properties in the numerical examples below are as follows: E₂ = 10Gpa, E₁/E₂ = open, μ₁₂ = 0.25, G₁₂ = G₁₃ = 0.6E₂₂, G₂₃ = 0.5E₂₂, ρ = 1500 kg/m³.

In addition, the natural frequency of the combined composite laminated conical–cylindrical shell is expressed with the frequency parameter $\Omega = \omega R_{cy} \sqrt {\rho (1 - \mu_{12}^{2} )/E_{2} }$.

3.1 Convergence and verification study

As given in Sect. 2.4, theoretically, the Haar wavelet series can be extended to infinity. However, for the actual numerical calculation, it should be truncated into appropriate finite number terms in consideration of the accuracy of the solution and the calculation cost. Therefore, a convergence study is required to determine the appropriate number of series terms. Figure 3 shows the change of the frequency parameter of the composite laminated conical–cylindrical shell laminated with 3 layers [0°/90°/0°] according to the increase in the maximal level of resolution J. The geometric dimensions of the combined shell are as follows: h_co = 0.05 m, L_co = 2 m, R_0,co = 1 m, φ = 30°, L_cy = 5 m. In addition, the thickness variation parameters are α = − 1, β = 1, and the C–C boundary condition, which is completely clamped at both ends of the combined shell, is considered. As shown in Fig. 3, as the maximal level of resolution J increases, the frequency parameters of the combined shell are converged to a constant value regardless of the circumferential wave number and mode sequence. In particular, when J is less than 5, the frequency parameters are decreased rapidly, and when J is larger than 7, it converges to a constant value with little change. Based on the convergence results, it can be concluded that a relatively accurate solution for the free vibration of the combined shell can be obtained when J is 7 or more. In this paper, considering the calculation cost, J = 8 is set in all numerical examples.

Fig. 3

Convergence of frequency parameters for a combined composite laminated conical–cylindrical shell with varying thickness according to the maximal level of resolution J: a-mode1; b-mode2; c-mode3

Then, the verification studies are performed to verify whether an accurate solution can be obtained for the vibration analysis of combined composite laminated conical–cylindrical shells of varying thickness using HWM. First, the frequency parameters of a combined conical–cylindrical coupling of uniform thickness by the proposed method are compared with the results of the previous literature. Table 2 shows the frequency parameters of the combined isotropic conical–cylindrical shell according to different shell theories in comparison with the results of the proposed method. As shown in Table 2, the frequency parameters of the combined isotropic conical–cylindrical shell with uniform thickness by HWM are in good agreement with the results of the previous literature.

Table 2 Comparison of frequency parameters Ω for an isotropic combined conical–cylindrical shell with uniform thickness

Since this study is about the free vibration analysis of combined composite laminated conical–cylindrical shells with varying thickness, the accuracy of the proposed method for the structure to be considered should be verified.

Due to the lack of published literature on the free vibration analysis of this structure, in this verification study, the accuracy of HWM is verified by comparison with the FEA results. For the FEA, the finite element analysis software ABAQUS is used. The material properties and thickness variation parameters of the combined shell considered in this comparison study are the same as in the case of Fig. 3, and the geometric dimensions are as follows: h_co = 0.03 m, L_co = 2 m, R_0,co = 1 m, φ = 30°, L_cy = 3 m. For FEA, the element type S4R is selected. The calculation accuracy and efficiency of the proposed method in Table 3 are compared with the results of FEA.

Table 3 Calculation accuracy and efficiency of the proposed method for the free vibration analysis of a combined shell with varying thickness

As shown in Table 3, when the number of elements is 41224, it is the most similar to the result of the proposed method, and at this time, the required calculation time is about 30 s, although there is a slight difference depending on the boundary conditions. In the case of the proposed method, the calculation time is about 0.6 s (in the case of J = 8), and it can be seen that the calculation time is much shorter than that of the FEA. Thus, by the verification studies, it is confirmed that the proposed method is an efficient and accurate method for free vibration analysis of combined composite laminated conical–cylindrical shells with varying thicknesses.

3.2 Parametric studies and new results

In this Subsection, the influence of parameters such as thickness variation parameters, material properties, geometric dimensions, and various boundary conditions on the natural frequencies of combined composite laminated conical–cylindrical shells with varying thicknesses is reported by numerical examples.

As mentioned in the previous Section, one of the advantages of the proposed method is to model arbitrary boundary conditions with the introduction of the artificial spring technique. That is, the boundary conditions are changed according to the change of the stiffness values of the artificial spring, and consequently, the frequencies of combined shells are changed. Therefore, the effect of artificial spring stiffness on the free vibration of the combined shell is investigated. The variation of the first frequency parameters of the combined composite laminated conical–cylindrical shell according to different artificial springs (i.e., k_u, k_v, k_w, k_φ, k_θ) is shown in Fig. 5. The material properties and geometrical dimensions are the same as in Fig. 3. To investigate the effect of ku, the spring stiffness values are changed from 10⁴ to 10¹⁶. At this time, the other spring stiffness values (k_v, k_w, k_φ, k_θ) are set to infinite values (10²⁰). In the same way, the influences of different spring stiffness values on the frequency parameters of the combined shell are investigated. As shown in Fig. 4, the effect of individual spring stiffness values on the frequency parameters is different depending on the circumferential wave number and the mode sequence. However, the common point is that, in all cases, when the spring stiffness values are less than 10⁵, the frequency parameters hardly change, but when it exceeds 10⁵, the frequency parameters are increased rapidly. In addition, when the spring stiffness value is 10¹³ or more, the frequency parameters are hardly changed.

Fig. 4

Variation of frequency parameters of a combined composite laminated conical–cylindrical coupled shell with varying thickness according to the increase in the boundary spring stiffness

The change characteristics of the frequency parameters (n = 1, m = 1) of the combined shells with different boundary conditions for different thickness variation parameters are investigated by Fig. 5. The individual shells are laminated in three layers [90°/0°/90°], and the geometric dimensions of the combined shells are as follows: h_co = 0.05 m, L_co = 1 m, R_0,co = 1 m, φ = 30°, L_cy = 1 m. As shown in Fig. 5, the thickness variation parameters have a great influence on the frequency parameters of the combined shell. In particular, in the case of α = 1, the frequency parameters are changed very severely, unlike other cases.

Fig. 5

Variation of frequency parameters of the combined composite laminated conical–cylindrical shells with varying thickness as thickness variation parameters changes

Also, Fig. 5 shows that the boundary conditions have a very significant effect on the same thickness variation parameters.

The effects of the fiber angle on the frequency parameters (n = 1) of combined shells with different lamination schemes ([0°/ϕ°], [ϕ°/0°], [0°/ϕ°/0°], [ϕ°/0°/ϕ°]) are investigated. The geometric dimensions of the combined shell are: h_co = 0.05 m, L_co = 2 m, R_0,co = 1 m, φ = 30°, L_cy = 3 m, and the thickness variation parameters are α = − 1, β = 1. In addition, the fiber angle ϕ changes from 0° to 180° by setting the calculation interval equal to 5°.

As shown in Fig. 6, the frequency parameters are symmetrical with respect to ϕ = 90°, and the frequency parameter of the combined shell about the fiber angle is varied with the lamination schemes and mode sequence.

Fig. 6

First six frequency parameters of a combined composite laminated conical–cylindrical shell with varying thickness according to lamination schemes

Figure 7 shows the variations of the frequency parameters for a [0°/90°]_k combined shell with several thickness variation parameters against the number of layers k. Except for the length of the cylindrical shell L_cy = 1 m, other geometrical dimensions are the same as in Fig. 6. As clearly shown in Fig. 7, the frequency parameters of the combined shell increase rapidly with increasing layers and may reach their crest around k = 5 (i.e. the number of layers is 10), and beyond this range, the frequency parameters are hardly changed.

Fig. 7

Frequency parameters of a [0°/90°]_k combined shell with different thickness variation parameters: a n = 1, m = 1, b n = 2, m = 2, c n = 3, m = 3

Figure 8 shows the frequency parameters of the four-layered [0°/90°/0°/90°] combined shell according to the E₁/E₂ ratio. The geometric dimensions are: h_co = 0.05 m, L_co = 2 m, R_0,co = 1 m, φ = 30°, L_cy = 3 m, and thickness variation parameter β = 1. Figure 8 shows that as the ratio of E₁/E₂ increases, the frequency parameter of the combined shell increases for all boundary conditions and for different thickness variation parameters.

Fig. 8

Variation of the frequency parameters of the combined composite laminated conical–cylindrical shells with different elastic modulus ratios

Next, the effect of geometrical parameters on the frequencies of the combined composite laminated conical–cylindrical shell with varying thickness is presented with the new numerical results. Table 4 shows the frequency parameters of the combined shell for different thicknesses h_co of the conical shell according to the boundary conditions. The combined shell has been laminated in 4 layers [30°/− 30°/30°/− 30°], the geometric dimensions are: L_co = 2 m, R_0,co = 1 m, φ = 30°, L_cy = 1 m, and the thickness variation parameters are α = − 1, β = 1. As shown in Table 4, as the thickness h_co of the conical shell increases, the frequency parameters are increased for all boundary conditions except for the C–F boundary condition. Also, under the C–F boundary condition, the frequency parameters are varied irregularly when the thickness of the conical shell increases.

Table 4 Frequency parameters of a combined composite laminated conical–cylindrical shell with different thicknesses h_co (n = 2)

Table 5 presents the frequency parameters of the combined shell for the different semi-vertex angles of the conical shell. The combined shell has been laminated in 4 layers [30°/60°/30°/60°], and the geometric dimensions and thickness variation parameters are the same as in Table 4 except h_co = 0.05 m. Table 5 shows that the frequency parameters of the combined shell increase as the semi-vertex angle of the conical shell increases when other geometric dimensions are the same.

Table 5 Frequency parameters of a combined composite laminated conical–cylindrical shell with different semi-vertex angles φ (n = 2)

The frequency parameters of the combined shell according to the increase in the length L_cy of the cylindrical shell are presented in Table 6 for various boundary conditions. The combined shell has been laminated in 4 layers [15°/− 15°/15°/− 15°], and the geometric dimensions and thickness variation parameters are the same as in Table 4. As the length of the cylindrical shell increases, the frequency parameters of the combined shell decrease for all boundary conditions. This is related to a decrease in the stiffness of the combined shell as the length increases.

Table 6 Frequency parameters of a combined composite laminated conical–cylindrical shell with different lengths L_cy of the cylindrical shell (n = 2)

As the last numerical example of this study, Table 7 shows the change of the frequency parameters of the combined shell for different circumferential wave numbers. The combined shell has been laminated in 4 layers [45°/− 45°/45°/− 45°], and the geometric dimensions and thickness variation parameters are the same as in Table 4. As shown in Table 7, the frequency parameters of the combined shell vary depending on the circumferential wave number and the mode sequence.

Table 7 Frequency parameters of a combined composite laminated conical–cylindrical shell with different circumferential wave numbers

In order to help the reader understand the free vibration of the combined composite laminated shell with varying thickness, Figs. 8, 9, 10 show the mode shapes of the combined shell with the classical boundary conditions (C–C and C–F of Figs. 9 and 10) and the elastic boundary condition (Fig. 11). The combined shell has been laminated in 3 layers [0°/90°/0°], and the geometric dimensions of the combined shell are as follows: h_co = 0.05 m, L_co = 2 m, R_0,co = 1 m, φ = 30°, L_cy = 2 m. In addition, the thickness variation parameters are β = 1, the circumferential wave number is n = 3. As shown in Figs. 8, 9, 10, it can be intuitively seen that the mode shapes in the case where the thickness does not change (α = 0) for all boundary conditions are different from the mode shapes in the case where the thickness changes.

Fig. 9

Mode shapes of the combined composite laminated conical–cylindrical shell with varying thickness and C–C boundary condition, a: α = − 0.5, b: α = 0, c: α = 0.5

Fig. 10

Mode shapes of the combined composite laminated conical–cylindrical shell with varying thickness and C–F boundary condition, a: α = − 0.5, b: α = 0, c: α = 0.5

Fig. 11

Mode shapes of the combined composite laminated conical–cylindrical shell with varying thickness and E1–E1 boundary condition, a: α = − 0.5, b: α = 0, c: α = 0.5

4 Conclusions

This paper presents an effective solution method based on the Haar wavelet for the free vibration analysis of combined composite laminated conical–cylindrical shells with varying thickness. The FSDT is employed to formulate the theoretical model of combined shells, and the HWM is applied to discretize the governing equation of the combined shell. That is, displacement and rotation components of the combined shell are extended by the Haar wavelet series in the axis direction and by the Fourier series in the circumferential direction. The integral constant is satisfied by the boundary condition. The boundary conditions are generalized by using the artificial spring technique. The efficiency, reliability, and accuracy of this method are verified in the free vibration analysis of the combined shell with varying thickness by convergence, verification, and parametric studies. The advantages of the present method are its simplicity, fast convergence, and good accuracy. Several new results on the combined composite laminated conical–cylindrical shell with varying thickness which can be used as benchmark materials in this field are presented.

Appendices

Appendix 1

For the conical shell:

$$\begin{aligned} & L_{{11,co}} = A_{{11,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{2A_{{16,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{A_{{66,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} + \frac{{A_{{11,co}} \sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} - A_{{22,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{\partial A_{{11,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} + \frac{1}{{R_{{co}} }}\frac{{\partial A_{{16,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} + \frac{{\partial A_{{12,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }} - I_{{0,co}} \frac{{\partial ^{2} }}{{\partial t^{2} }}, \\ \end{aligned}$$

$$\begin{aligned} & L_{{12,co}} = A_{{16,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{A_{{12,co}} + A_{{66,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{A_{{26,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} - \frac{{A_{{26,co}} \sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} - \left( {A_{{22,co}} + A_{{66_{{co}} }} } \right)\frac{{\sin \varphi }}{{R_{{co}}^{2} }}\frac{\partial }{{\partial \theta _{{co}} }} \\ & \quad\quad\quad\,\,\, + A_{{26,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }}\, + \frac{{\partial A_{{16,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} + \frac{1}{{R_{{co}} }}\frac{{\partial A_{{12,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} - \frac{{\partial A_{{16,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }}, \\ \end{aligned}$$

$$L_{13,co} = A_{12,co} \frac{\cos \varphi }{{R_{co} }}\frac{\partial }{{\partial x_{co} }} + A_{26,co} \frac{\cos \varphi }{{R_{co}^{2} }}\frac{\partial }{{\partial \theta_{co} }} - A_{22,co} \frac{\sin \varphi \cos \varphi }{{R_{co}^{2} }} + \frac{{\partial A_{12,co} }}{{\partial x_{co} }}\frac{\cos \varphi }{{R_{co} }},$$

$$\begin{aligned} & L_{{14,co}} = B_{{11,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{2B_{{16}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{B_{{66}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} + B_{{11,co}} \frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} - B_{{22,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }} + \frac{{\partial B_{{11,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} \\ & \quad\quad\quad\,\,\, + \frac{1}{{R_{{co}} }}\frac{{\partial B_{{16,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} + \frac{{\partial B_{{12,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }} - I_{{1,co}} \frac{{\partial ^{2} }}{{\partial t^{2} }}, \\ \end{aligned}$$

$$\begin{aligned} & L_{{15,co}} = B_{{16,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{B_{{12,co}} + B_{{66,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{B_{{26,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} - B_{{26,co}} \frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} - \left( {B_{{22,co}} + B_{{66,co}} } \right)\frac{{\sin \varphi }}{{R_{{co}}^{2} }}\frac{\partial }{{\partial \theta _{{co}} }} \\ & \quad\quad\quad\,\,\, + B_{{26,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }}\, + \frac{{\partial B_{{16,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} + \frac{1}{{R_{{co}} }}\frac{{\partial B_{{12,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} - \frac{{\partial B_{{16,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }}, \\ \end{aligned}$$

$$\begin{aligned} & L_{{21,co}} = A_{{16,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{A_{{12,co}} + A_{{66,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{A_{{26,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} + \left( {A_{{26,co}} + 2A_{{16,co}} } \right)\frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} \\ & \quad\quad\quad\,\,\, + \left( {A_{{22,co}} + A_{{66,co}} } \right)\frac{{\sin \varphi }}{{R_{{co}}^{2} }}\frac{\partial }{{\partial \theta _{{co}} }}\, + A_{{26,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }}\, + \frac{{\partial A_{{16,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} + \frac{1}{{R_{{co}} }}\frac{{\partial A_{{66,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} + \frac{{\partial A_{{26,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }} \\ \end{aligned}$$

$$\begin{aligned} & L_{{22,co}} = A_{{66,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{2A_{{26,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + A_{{22,co}} \frac{1}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} + A_{{66,co}} \frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} \\ & \quad\quad\quad\,\,\, - \left( {A_{{66,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }} - A_{{44,co}} \frac{{\cos ^{2} \varphi }}{{R_{{co}}^{2} }}} \right) \\ & \quad\quad\quad\,\,\, + \frac{{\partial A_{{26,co}} }}{{\partial x_{{co}} }}\frac{1}{{R_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} + \frac{{\partial A_{{66,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} - \frac{{\partial A_{{66,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }} - I_{{0,co}} \frac{{\partial ^{2} }}{{\partial t^{2} }}, \\ \end{aligned}$$

$$L_{23,co} = \left( {A_{26,co} + A_{45,co} } \right)\frac{\cos \varphi }{{R_{co} }}\frac{\partial }{{\partial x_{co} }} + \left( {A_{22,co} + A_{44,co} } \right)\frac{\cos \varphi }{{R_{co}^{2} }}\frac{\partial }{{\partial \theta_{co} }} + A_{26,co} \frac{\sin \varphi \cos \varphi }{{R_{co}^{2} }} + \frac{{\partial A_{26,co} }}{{\partial x_{co} }}\frac{\cos \varphi }{{R_{co} }},$$

$$\begin{gathered} L_{{24,co}} = B_{{16,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{B_{{12,co}} + B_{{66,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{B_{{26,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} + \left( {B_{{26,co}} + 2B_{{16,co}} } \right)\frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} \hfill \\ \quad\quad \,\,\,\,\,\,\,\,\,\, + \left( {B_{{22,co}} + B_{{66,co}} } \right)\frac{{\sin \varphi }}{{R_{{co}}^{2} }}\frac{\partial }{{\partial \theta _{{co}} }}\, + \left( {B_{{26,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }} + A_{{45,co}} \frac{{\cos \varphi }}{{R_{{co}} }}} \right)\, \hfill \\ \quad\quad \,\,\,\,\,\,\,\,\,\, + \frac{{\partial B_{{16,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} + \frac{{\partial B_{{66,co}} }}{{\partial x_{{co}} }}\frac{1}{{R_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} + \frac{{B_{{26,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }}, \hfill \\ \end{gathered}$$

$$\begin{aligned} & L_{{25,co}} = B_{{66,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{2B_{{26,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{B_{{22,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} + B_{{66,co}} \frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} - \left( {B_{{66,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }} - A_{{44,co}} \frac{{\cos \varphi }}{{R_{{co}} }}} \right) \\ &\quad\quad\quad\,\,\, \, + \frac{{B_{{66,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} + \frac{{\partial B_{{26,co}} }}{{\partial x_{{co}} }}\frac{1}{{R_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} - \frac{{\partial B_{{66,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }} - I_{{1,co}} \frac{{\partial ^{2} }}{{\partial t^{2} }} \\ \end{aligned}$$

$$L_{31,co} = - A_{12,co} \frac{\cos \varphi }{{R_{co} }}\frac{\partial }{{\partial x_{co} }} - A_{26,co} \frac{\cos \varphi }{{R_{co}^{2} }}\frac{\partial }{{\partial \theta_{co} }} - A_{22,co} \frac{\sin \varphi \cos \varphi }{{R_{co}^{2} }},$$

$$L_{32,co} = - \left( {A_{26,co} + A_{45,co} } \right)\frac{\cos \varphi }{{R_{co} }}\frac{\partial }{{\partial x_{co} }} - \left( {A_{22,co} + A_{44,co} } \right)\frac{\cos \varphi }{{R_{co}^{2} }}\frac{\partial }{{\partial \theta_{co} }} + A_{26,co} \frac{\sin \varphi \cos \varphi }{{R_{co}^{2} }} - \frac{{\partial A_{45,co} }}{{\partial x_{co} }}\frac{\cos \varphi }{{R_{co} }},$$

$$\begin{aligned} & L_{{33,co}} = A_{{55,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{2A_{{45,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{A_{{44,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} + A_{{55,co}} \frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} \\ & \quad\quad\quad\,\, \, - A_{{22,co}} \frac{{\cos ^{2} \varphi }}{{R_{{co}}^{2} }} + \frac{{\partial A_{{55,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} + \frac{1}{{R_{{co}} }}\frac{{\partial A_{{45,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} - I_{{0,co}} \frac{{\partial ^{2} }}{{\partial t^{2} }}, \\ \end{aligned}$$

$$\begin{aligned} & L_{{34,co}} = \left( {A_{{55,co}} - B_{{12,co}} \frac{{\cos \varphi }}{{R_{{co}} }}} \right)\frac{\partial }{{\partial x_{{co}} }} + \left( {\frac{{A_{{45,co}} }}{{R_{{co}} }} - B_{{26,co}} \frac{{\cos \varphi }}{{R_{{co}}^{2} }}} \right)\frac{\partial }{{\partial \theta _{{co}} }} \\ & \quad\quad\quad\,\,\, + \left( {A_{{55,co}} \frac{{\sin \varphi }}{{R_{{co}} }} - B_{{22,co}} \frac{{\sin \varphi \cos \varphi }}{{R_{{co}}^{2} }}} \right) + \frac{{\partial A_{{55,co}} }}{{\partial x_{{co}} }}, \\ \end{aligned}$$

$$\begin{aligned} & L_{{35,co}} = \left( {A_{{45,co}} - B_{{26,co}} \frac{{\cos \varphi }}{{R_{{co}} }}} \right)\frac{\partial }{{\partial x_{{co}} }} + \left( {\frac{{A_{{44,co}} }}{{R_{{co}} }} - B_{{22,co}} \frac{{\cos \varphi }}{{R_{{co}}^{2} }}} \right)\frac{\partial }{{\partial \theta _{{co}} }} \\ & \quad\quad\quad\,\,\, + \left( {A_{{45,co}} \frac{{\sin \varphi }}{{R_{{co}} }} + B_{{26,co}} \frac{{\sin \varphi \cos \varphi }}{{R_{{co}}^{2} }}} \right) + \frac{{\partial A_{{45,co}} }}{{\partial x_{{co}} }}, \\ \end{aligned}$$

$$\begin{gathered} L_{41,co} = B_{11,co} \frac{{\partial^{2} }}{{\partial x_{co}^{2} }} + \frac{{2B_{16,co} }}{{R_{co} }}\frac{{\partial^{2} }}{{\partial x_{co} \partial \theta_{co} }} + B_{66,co} \frac{1}{{R_{co}^{2} }}\frac{{\partial^{2} }}{{\partial \theta_{co}^{2} }} + B_{11,co} \frac{\sin \varphi }{{R_{co} }}\frac{\partial }{{\partial x_{co} }} - B_{22,co} \frac{{\sin^{2} \varphi }}{{R_{co}^{2} }} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, + \frac{{B_{11,co} }}{{\partial x_{co} }}\frac{\partial }{{\partial x_{co} }} + \frac{1}{{R_{co} }}\frac{{B_{16,co} }}{{\partial x_{co} }}\frac{\partial }{{\partial \theta_{co} }} + \frac{{B_{12,co} }}{{\partial x_{co} }}\frac{\sin \varphi }{{R_{co} }} - I_{1,co} \frac{{\partial^{2} }}{{\partial t^{2} }}, \hfill \\ \end{gathered}$$

$$\begin{aligned} & L_{{42,co}} = B_{{16,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{B_{{12,co}} + B_{{66,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{B_{{26,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} v}}{{\partial \theta _{{co}}^{2} }} \\ &\quad\quad\quad\,\,\, - B_{{26,co}} \frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} - \left( {B_{{22,co}} + B_{{66,co}} } \right)\frac{{\sin \varphi }}{{R_{{co}}^{2} }}\frac{\partial }{{\partial \theta _{{co}} }} \\ &\quad\quad\quad\,\,\, \, + \left( {B_{{26,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }} + A_{{45,co}} \frac{{\cos \varphi }}{{R_{{co}} }}} \right)\, + \frac{1}{{R_{{co}} }}\frac{{B_{{12,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} + \frac{{B_{{16,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} - \frac{{B_{{16,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }}, \\ \end{aligned}$$

$$L_{43,co} = \left( {B_{12,co} \frac{\cos \varphi }{{R_{co} }} - A_{55,co} } \right)\frac{\partial }{{\partial x_{co} }} + \left( {B_{26,co} \frac{\cos \varphi }{{R_{co}^{2} }} - A_{45,co} \frac{1}{{R_{co} }}} \right)\frac{\partial }{{\partial \theta_{co} }} - B_{22,co} \frac{\sin \varphi \cos \varphi }{{R_{co}^{2} }} + \frac{{B_{12,co} }}{{\partial x_{co} }}\frac{\cos \varphi }{{R_{co} }},$$

$$\begin{aligned} & L_{{44,co}} = D_{{11,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{2D_{{16,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x\partial \theta }} + \frac{{D_{{66,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} + D_{{11,co}} \frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} - \left( {D_{{22,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }} + A_{{55,co}} } \right) \\ &\quad\quad\quad\,\,\, + \frac{{D_{{11,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} + \frac{{D_{{12,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }} + \frac{1}{{R_{{co}} }}\frac{{D_{{16,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} - I_{{2,co}} \frac{{\partial ^{2} }}{{\partial t^{2} }}, \\ \end{aligned}$$

$$\begin{aligned} & L_{{45,co}} = D_{{16,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{D_{{12,co}} + D_{{66,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{D_{{26,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} - D_{{26,co}} \frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} \\ &\quad\quad\quad\,\,\, - \left( {D_{{22,co}} + D_{{66,co}} } \right)\frac{{\sin \varphi }}{{R_{{co}}^{2} }}\frac{\partial }{{\partial \theta _{{co}} }} + \left( {D_{{26,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }} - A_{{45,co}} } \right) \\ & \quad\quad\quad\,\,\, + \frac{{D_{{12,co}} }}{{\partial x_{{co}} }}\frac{1}{{R_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} + \frac{{D_{{16,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} - \frac{{D_{{16,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }}, \\ \end{aligned}$$

$$\begin{aligned} & L_{{51,co}} = B_{{16,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{B_{{12,co}} + B_{{66,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{B_{{26,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} + \left( {2B_{{16,co}} + B_{{26,co}} } \right)\frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} \\ & \quad\quad\quad\,\,\, + \left( {B_{{22,co}} + B_{{66,co}} } \right)\frac{{\sin \varphi }}{{R_{{co}}^{2} }}\frac{\partial }{{\partial \theta _{{co}} }} + B_{{26,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }}\, + \frac{{B_{{16,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} + \frac{{B_{{66,co}} }}{{\partial x_{{co}} }}\frac{1}{{R_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} + \frac{{B_{{26,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }} ,\\ \end{aligned}$$

$$\begin{aligned} & L_{{52,co}} = B_{{66,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{2B_{{26,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{B_{{22,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} + B_{{66,co}} \frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} + \left( {A_{{44,co}} \frac{{\cos \varphi }}{{R_{{co}} }} - B_{{66,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }}} \right) \\ & \quad\quad\quad\,\,\, + \frac{{B_{{66,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} + \frac{{B_{{26,co}} }}{{\partial x_{{co}} }}\frac{1}{{R_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} - \frac{{B_{{66,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }} - I_{{1,co}} \frac{{\partial ^{2} }}{{\partial t^{2} }}, \\ \end{aligned}$$

$$L_{53,co} = \left( {B_{26,co} \frac{\cos \varphi }{{R_{co} }} - A_{45,co} } \right)\frac{\partial }{{\partial x_{co} }} + \left( {B_{22,co} \frac{\cos \varphi }{{R_{co}^{2} }} - A_{44,co} \frac{1}{{R_{co} }}} \right)\frac{\partial }{{\partial \theta_{co} }} + B_{26,co} \frac{\sin \varphi \cos \varphi }{{R_{co}^{2} }} + \frac{{B_{26,co} }}{{\partial x_{co} }}\frac{\cos \varphi }{{R_{co} }},$$

$$\begin{aligned} & L_{{54,co}} = D_{{16,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{D_{{12,co}} + D_{{66,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x_{{co}} \partial \theta _{{co}} }} + \frac{{D_{{26,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} + \left( {2D_{{16,co}} + D_{{26,co}} } \right)\frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} \\ & \quad\quad\quad\,\,\, + \left( {D_{{22,co}} + D_{{66,co}} } \right)\frac{{\sin \varphi }}{{R_{{co}}^{2} }}\frac{\partial }{{\partial \theta _{{co}} }} + \left( {D_{{26,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }} - A_{{45,co}} } \right) \\ & \quad\quad\quad\,\,\, + \frac{{D_{{16,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} + \frac{1}{{R_{{co}} }}\frac{{D_{{66,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} + \frac{{D_{{26,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }}, \\ \end{aligned}$$

$$\begin{aligned} & L_{{55,co}} = D_{{66,co}} \frac{{\partial ^{2} }}{{\partial x_{{co}}^{2} }} + \frac{{2D_{{26,co}} }}{{R_{{co}} }}\frac{{\partial ^{2} }}{{\partial x\partial \theta }} + \frac{{D_{{22,co}} }}{{R_{{co}}^{2} }}\frac{{\partial ^{2} }}{{\partial \theta _{{co}}^{2} }} + D_{{66,co}} \frac{{\sin \varphi }}{{R_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} - \left( {D_{{66,co}} \frac{{\sin ^{2} \varphi }}{{R_{{co}}^{2} }} - A_{{44,co}} } \right) \\ & \quad\quad\quad\,\,\, + \frac{{D_{{26,co}} }}{{\partial x_{{co}} }}\frac{1}{{R_{{co}} }}\frac{\partial }{{\partial \theta _{{co}} }} + \frac{{D_{{66,co}} }}{{\partial x_{{co}} }}\frac{\partial }{{\partial x_{{co}} }} - \frac{{D_{{66,co}} }}{{\partial x_{{co}} }}\frac{{\sin \varphi }}{{R_{{co}} }}, \\ \end{aligned}$$

For the cylindrical shell:

$$\begin{gathered} L_{11,cy} = A_{11,cy} \frac{{\partial^{2} }}{{\partial x_{cy}^{2} }} + \frac{{2A_{16,cy} }}{{R_{cy} }}\frac{{\partial^{2} }}{{\partial x_{cy} \partial \theta_{cy} }} + \frac{{A_{66,cy} }}{{R_{cy}^{2} }}\frac{{\partial^{2} }}{{\partial \theta_{cy}^{2} }} - I_{0,cy} \frac{{\partial^{2} }}{{\partial t^{2} }}\;,\; \hfill \\ L_{12,cy} = A_{16,cy} \frac{{\partial^{2} }}{{\partial x_{cy}^{2} }} + \left( {\frac{{A_{12,cy} }}{{R_{cy} }} + \frac{{A_{66,cy} }}{{R_{cy} }}} \right)\frac{{\partial^{2} }}{{\partial x_{cy} \partial \theta_{cy} }} + \frac{{A_{26,cy} }}{{R_{cy}^{2} }}\frac{{\partial^{2} }}{{\partial \theta_{cy}^{2} }},L_{13,cy} = \left( {\frac{{A_{12,cy} }}{{R_{cy} }}\frac{\partial }{{\partial x_{cy} }} + \frac{{A_{26,cy} }}{{R_{cy}^{2} }}\frac{\partial }{{\partial \theta_{cy} }}} \right), \hfill \\ L_{14,cy} = B_{11,cy} \frac{{\partial^{2} }}{{\partial x_{cy}^{2} }} + \frac{{2B_{16,cy} }}{{R_{cy} }}\frac{{\partial^{2} }}{{\partial x_{cy} \partial \theta_{cy} }} + \frac{{B_{66,cy} }}{{R_{cy}^{2} }}\frac{{\partial^{2} }}{{\partial \theta_{cy}^{2} }} - I_{1,cy} \frac{{\partial^{2} }}{{\partial t^{2} }}, \hfill \\ L_{15,cy} = B_{16,cy} \frac{{\partial^{2} }}{{\partial x_{cy}^{2} }} + \left( {\frac{{B_{12,cy} }}{{R_{cy} }} + \frac{{B_{66,cy} }}{{R_{cy} }}} \right)\frac{{\partial^{2} }}{{\partial x_{cy} \partial \theta_{cy} }} + \frac{{B_{26,cy} }}{{R_{cy}^{2} }}\frac{{\partial^{2} }}{{\partial \theta_{cy}^{2} }}, \hfill \\ \end{gathered}$$

$$\begin{gathered} L_{21,cy} = L_{12,cy} ,\;\;\;\;L_{22,cy} = A_{66,cy} \frac{{\partial^{2} }}{{\partial x_{cy}^{2} }} + \frac{{2A_{26,cy} }}{{R_{cy} }}\frac{{\partial^{2} }}{{\partial x_{cy} \partial \theta_{cy} }} + \frac{{A_{22,cy} }}{{R_{cy}^{2} }}\frac{{\partial^{2} }}{{\partial \theta_{cy}^{2} }} - \frac{{\kappa A_{44,cy} }}{{R_{cy}^{2} }} - I_{0,cy} \frac{{\partial^{2} }}{{\partial t^{2} }},\;\; \hfill \\ L_{23,cy} = \left( {\frac{{A_{26,cy} }}{{R_{cy} }} + \frac{{\kappa A_{45,cy} }}{{R_{cy} }}} \right)\frac{\partial }{{\partial x_{cy} }} + \left( {\frac{{A_{22} }}{{R_{cy}^{2} }} + \frac{{\kappa A_{44,cy} }}{{R_{cy}^{2} }}} \right)\frac{\partial }{{\partial \theta_{cy} }}, \hfill \\ L_{24,cy} = B_{16} \frac{{\partial^{2} }}{{\partial x_{cy}^{2} }} + \left( {\frac{{B_{12,cy} }}{{R_{cy} }} + \frac{{B_{66,cy} }}{{R_{cy} }}} \right)\frac{{\partial^{2} }}{{\partial x_{cy} \partial \theta_{cy} }} + \frac{{B_{26,cy} }}{{R_{cy}^{2} }}\frac{{\partial^{2} }}{{\partial \theta_{cy}^{2} }} + \frac{{\kappa A_{45} }}{{R_{cy} }},\; \hfill \\ L_{25,cy} = B_{66,cy} \frac{{\partial^{2} }}{{\partial x_{cy}^{2} }} + \frac{{2B_{26,cy} }}{R}\frac{{\partial^{2} }}{\partial x\partial \theta } + \frac{{B_{22,cy} }}{{R_{cy}^{2} }}\frac{{\partial^{2} }}{{\partial \theta_{cy}^{2} }} + \frac{{\kappa A_{44,cy} }}{R} - I_{1,cy} \frac{{\partial^{2} }}{{\partial t^{2} }}, \hfill \\ \end{gathered}$$

$$\begin{gathered} L_{31,cy} = L_{13,cy} ,\;\;L_{32,cy} = L_{23,cy} , \hfill \\ L_{33,cy} = \frac{{A_{22,cy} }}{{R_{cy}^{2} }} - \left( {\kappa A_{55,cy} \frac{{\partial^{2} }}{{\partial x_{cy}^{2} }} + \frac{{2\kappa A_{45,cy} }}{{R_{cy} }}\frac{{\partial^{2} }}{{\partial x_{cy} \partial \theta_{cy} }} + \frac{{\kappa A_{44,cy} }}{{R_{cy}^{2} }}\frac{{\partial^{2} }}{{\partial \theta_{cy}^{2} }}} \right) - I_{0,cy} \frac{{\partial^{2} }}{{\partial t^{2} }}, \hfill \\ L_{34,cy} = \left( {\frac{{B_{12,cy} }}{{R_{cy} }} - \kappa A_{55,cy} } \right)\frac{\partial }{{\partial x_{cy} }} + \left( {\frac{{B_{26,cy} }}{{R_{cy}^{2} }} - \frac{{\kappa A_{45,cy} }}{{R_{cy} }}} \right)\frac{\partial }{{\partial \theta_{cy} }},\;\; \hfill \\ L_{35,cy} = \left( {\frac{{B_{26,cy} }}{{R_{cy} }} - \kappa A_{45,cy} } \right)\frac{\partial }{{\partial x_{cy} }} + \left( {\frac{{B_{22,cy} }}{{R_{cy}^{2} }} - \frac{{\kappa A_{44,cy} }}{R}} \right)\frac{\partial }{{\partial \theta_{cy} }}, \hfill \\ \end{gathered}$$

$$\begin{gathered} L_{41,cy} = L_{14,cy} ,\;\;\;L_{42,cy} = L_{24,cy} ,\;\;\;L_{43,cy} = L_{34,cy} ,\;\,\, \hfill \\ L_{44,cy} = D_{11,cy} \frac{{\partial^{2} }}{{\partial x_{cy}^{2} }} + \frac{{2D_{16,cy} }}{{R_{cy} }}\frac{{\partial^{2} }}{{\partial x_{cy} \partial \theta_{cy} }} + \frac{{D_{66,cy} }}{{R_{cy}^{2} }}\frac{{\partial^{2} }}{{\partial \theta_{cy}^{2} }} - \kappa A_{55,cy} - I_{2,cy} \frac{{\partial^{2} }}{{\partial t^{2} }}, \hfill \\ L_{45,cy} = D_{16,cy} \frac{{\partial^{2} }}{{\partial x_{cy}^{2} }} + \left( {\frac{{D_{12,cy} }}{{R_{cy} }} + \frac{{D_{66,cy} }}{{R_{cy} }}} \right)\frac{{\partial^{2} }}{{\partial x_{cy} \partial \theta_{cy} }} + \frac{{D_{26,cy} }}{{R_{cy}^{2} }}\frac{{\partial^{2} }}{{\partial \theta_{cy}^{2} }} - \kappa A_{45,cy}, \hfill \\ \end{gathered}$$

$$\begin{gathered} L_{51,cy} = L_{15,cy} ,\;\;\,\,\,\,L_{52,cy} = L_{25,cy} ,\;\;\,\,\,\,L_{53,cy} = L_{35,cy} ,\;\;\,\,\,L_{54,cy} = L_{45,cy} ,\;\;\;\; \hfill \\ L_{55,cy} = D_{66,cy} \frac{{\partial^{2} }}{{\partial x_{cy}^{2} }} + \frac{{2D_{26,cy} }}{{R_{cy} }}\frac{{\partial^{2} }}{{\partial x_{cy} \partial \theta_{cy} }} + \frac{{D_{22,cy} }}{{R_{cy}^{2} }}\frac{{\partial^{2} }}{{\partial \theta_{cy}^{2} }} - \kappa A_{44,cy} - I_{2,cy} \frac{{\partial^{2} }}{{\partial t^{2} }}. \hfill \\ \end{gathered}$$

Appendix 2

Conical shell:

$$\begin{gathered} L_{11,co}^{0} = - A_{22,co} \sin^{2} \varphi - A_{66,co} n^{2} ,\,\,\,\,\,\,\,\,\,\,L_{11,co}^{1} = A_{11,co} R_{co} \sin \varphi ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,L_{11,co}^{2} = A_{11,co} R_{co}^{2} ,\, \hfill \\ L_{12,co}^{0} = - \left( {A_{66,co} + A_{22,co} } \right)n\sin \varphi ,\,\,\,\,\,\,\,L_{12,co}^{1} = \left( {A_{12,co} + A_{66,co} } \right)nR_{co} ,\,\,\, \hfill \\ L_{13,co}^{0} = - A_{22,co} \cos \varphi \sin \varphi ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,L_{13,co}^{1} = A_{12,co} R_{cy} \cos \varphi, \hfill \\ L_{14,co}^{0} = - B_{22,co} \sin^{2} \varphi - B_{66,co} n^{2} ,\,\,\,\,\,\,\,\,L_{14,co}^{1} = B_{11,co} R_{co} \sin \varphi ,\,\,\,\,\,\,\,\,\,\,\,\,L_{14,co}^{2} = B_{11,co} R_{co}^{2} ,\,\, \hfill \\ L_{15,co}^{0} = - \left( {B_{22,co} + B_{66,co} } \right)n\sin \varphi ,\,\,\,\,\,\,\,\,L_{15,co}^{1} = \left( {B_{12,co} + B_{66,co} } \right)nR_{co}, \hfill \\ \end{gathered}$$

$$\begin{gathered} L_{21,co}^{0} = - \left( {A_{22,co} + A_{66,co} } \right)n\sin \varphi ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,L_{21,co}^{1} = - \left( {A_{12,co} + A_{66,co} } \right)nR_{co} ,\, \hfill \\ L_{22,co}^{0} = - A_{22,co} n^{2} - A_{66,co} \sin^{2} \varphi - \kappa A_{44,co} \cos^{2} \varphi ,\,\,\,\,L_{22,co}^{1} = A_{66,co} R_{co} \sin \varphi ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,L_{22,co}^{2} = A_{66} R_{co}^{2}, \hfill \\ L_{23,co}^{0} = - A_{22,co} n\cos \varphi - \kappa A_{44,co} n\cos \varphi, \hfill \\ L_{24,co}^{0} = - \left( {B_{22,co} + B_{66,co} } \right)n\sin \varphi ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,L_{24,co}^{1} = - \left( {B_{12,co} + B_{66,co} } \right)nR_{co}, \hfill \\ L_{25,co}^{0} = \kappa A_{55,co} nR_{co} \cos \varphi - B_{66,co} \sin \varphi - B_{22,co} n^{2} ,\,\,\,\,\,L_{25,co}^{1} = B_{66,co} R_{co} \sin \varphi ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,L_{25,co}^{2} = B_{66,co} R_{co}^{2}, \hfill \\ \end{gathered}$$

$$\begin{gathered} L_{31,co}^{0} = - A_{22,co} \sin \varphi \cos \varphi ,\,\,\,\,\,\,\,\,\,\,\,L_{31,co}^{1} = - A_{12,co} R_{co} \cos \varphi ,\,\,\,\,\,\,\,\,\,\,L_{32,co}^{0} = - \left( {A_{22,co} + \kappa A_{44,co} } \right)n\cos \varphi, \hfill \\ L_{33,co}^{0} = - \kappa A_{44,co} n^{2} - A_{22,co} \cos^{2} \varphi ,\,\,\,\,\,\,\,L_{33,co}^{1} = \kappa A_{55,co} R_{co} \sin \varphi ,\,\,\,\,\,\,\,L_{33,co}^{2} = \kappa A_{55,co} R_{co}^{2} , \hfill \\ L_{34,co}^{0} = \kappa A_{55,co} R_{co} \sin \varphi - B_{22,co} \sin \varphi \cos \varphi ,\,\,\,\,\,\,\,\,L_{34,co}^{1} = \kappa A_{55,co} R_{co}^{2} - B_{12,co} \cos \varphi ,\, \hfill \\ \,L_{35,co}^{0} = \kappa A_{44,co} R_{co} - B_{22,co} n\cos \varphi, \hfill \\ \end{gathered}$$

$$\begin{gathered} L_{41,co}^{0} = - B_{22,co} \sin^{2} \varphi - B_{66,co} n^{2} ,\,\,\,\,\,\,\,\,L_{41,co}^{1} = B_{11,co} R_{co} \sin \varphi ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,L_{41,co}^{2} = B_{11,co} R_{co}^{2}, \hfill \\ L_{42,co}^{0} = - \left( {B_{22,co} + B_{66,co} } \right)n\sin \varphi ,\,\,\,\,\,\,\,L_{42,co}^{1} = \left( {B_{12,co} + B_{66,co} } \right)nR_{co}, \hfill \\ L_{43,co}^{0} = - B_{22,co} \sin \varphi \cos \varphi ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,L_{43,co}^{1} = B_{12,co} R_{co} \cos \varphi - \kappa A_{55,co} R_{co}^{2}, \hfill \\ L_{44,co}^{0} = - D_{22,co} \sin^{2} \varphi - D_{66,co} n^{2} - \kappa A_{55,co} R_{co}^{2} ,\,\,\,\,\,\,L_{44,co}^{1} = D_{11,co} R_{co} \sin \varphi ,\,\,\,\,\,\,L_{44,co}^{2} = D_{11,co} R_{co}^{2}, \hfill \\ L_{45,co}^{0} = - \left( {D_{22,co} + D_{66,co} } \right)n\sin \varphi ,\,\,\,\,\,\,\,L_{45,co}^{1} = \left( {D_{12,co} + D_{66,co} } \right)nR_{co}, \hfill \\ \end{gathered}$$

$$\begin{gathered} L_{51,co}^{0} = - \left( {B_{22,co} + B_{66,co} } \right)n\sin \varphi ,\,\,\,\,\,\,\,\,\,\,\,\,L_{51,co}^{1} = - \left( {B_{12,co} + B_{66,co} } \right)nR_{co} ,\,\,\,\, \hfill \\ L_{52,co}^{0} = \kappa A_{44,co} R_{co} \cos \varphi - B_{22,co} n^{2} - 2B_{66,co} \sin^{2} \varphi ,\,\,\,\,\,\,\,L_{52,co}^{1} = B_{66,co} R_{co} \sin \varphi ,\,\,\,\,\,L_{52,co}^{2} = B_{66,co} R_{co}^{2} , \hfill \\ L_{53,co}^{0} = \kappa A_{44,co} nR_{co} - B_{22,co} n\cos \varphi ,\,\,\,\,\,\,\,\,L_{54,co}^{0} = - \left( {D_{22,co} + D_{66,co} } \right)n\sin \varphi ,\, \hfill \\ L_{54,co}^{1} = - \left( {D_{12,co} + D_{66,co} } \right)nR_{co} ,\,\,\,\,L_{55,co}^{0} = - D_{66,co} \sin^{2} \varphi - \kappa A_{44,co} R_{co}^{2} - D_{22,co} n^{2} , \hfill \\ L_{55,co}^{1} = D_{66,co} R_{co} \sin \varphi ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,L_{55,co}^{2} = D_{66,co} R_{co}^{2}. \hfill \\ \end{gathered}$$

Cylindrical shell:

$$\begin{gathered} L_{11,cy}^{0} = - A_{66,cy} n^{2} ,\,\,\,\,\,\,\,L_{11,,cy}^{2} = A_{11,cy} R_{cy}^{2} ,\,\,\,\,\,\,L_{12,,cy}^{1} = \left( {A_{12,cy} + A_{66,cy} } \right)nR_{cy} ,\,\,\,\,\,L_{13,,cy}^{1} = A_{12,cy} R_{cy}, \, \hfill \\ L_{14,,cy}^{0} = - B_{66,cy} n^{2} ,\,\,\,\,\,\,\,\,L_{14,,cy}^{2} = B_{11} R_{cy}^{2} ,\,\,\,\,\,\,L_{15,cy}^{1} = \left( {B_{12,cy} + B_{66,cy} } \right)nR_{cy}, \hfill \\ \end{gathered}$$

$$\begin{gathered} L_{21,cy}^{1} = - \left( {A_{12,cy} + A_{66,cy} } \right)nR_{cy} ,\,\,\,\,\,\,\,L_{22,cy}^{0} = - A_{22,cy} n^{2} - \kappa A_{44,cy} ,\,\,\,\,\,\,\,\,\,L_{22,cy}^{2} = A_{66,cy} R_{cy}^{2}, \hfill \\ L_{23,cy}^{0} = - A_{22,cy} n - \kappa A_{44,cy} n,\,\,\,\,\,\,\,\,\,\,\,\,\,L_{24,cy}^{1} = - \left( {B_{12,cy} + B_{66,cy} } \right)nR_{cy}, \hfill \\ L_{25,cy}^{0} = \kappa A_{44,cy} nR_{cy} - B_{22,cy} n^{2} ,\,\,\,\,\,\,\,\,\,L_{25,cy}^{2} = B_{66,cy} R_{cy}^{2}, \hfill \\ \end{gathered}$$

$$\begin{gathered} L_{31,cy}^{1} = - A_{12,cy} R_{l} ,\,\,\,\,\,\,\,\,\,\,\,\,L_{32,cy}^{0} = \left( {A_{22,cy} + \kappa A_{44,cy} } \right)n,\,\,\,\,\,\,\,\,L_{33,cy}^{0} = \kappa A_{44,cy} n^{2} - A_{22,cy} ,\,\,\,\,\,\,\,\,\,\, \hfill \\ \,L_{33,cy}^{2} = - \kappa A_{55,cy} R_{cy}^{2} ,\,\,\,\,\,\,L_{34,cy}^{1} = B_{12} R_{cy} - \kappa A_{55,cy} R_{cy}^{2} ,\,\,\,\,\,\,L_{35,cy}^{0} = B_{22,cy} n - \kappa A_{44,cy} nR_{cy}, \hfill \\ \end{gathered}$$

$$\begin{gathered} L_{41,cy}^{0} = - B_{66,cy} n^{2} ,L_{41,cy}^{2} = B_{11,cy} R_{cy}^{2} ,L_{42,cy}^{1} = \left( {B_{12,cy} + B_{66,cy} } \right)nR_{cy} ,L_{43,cy}^{1} = B_{12,cy} R_{cy} - \kappa A_{55,cy} R_{cy}^{2} ,\,\,\,\,\, \hfill \\ L_{44,cy}^{0} = - D_{66,cy} n^{2} - \kappa A_{55,cy} R_{cy}^{2} ,\,\,\,\,\,\,\,\,\,L_{44,cy}^{2} = D_{11,cy} R_{cy}^{2} ,\,\,\,\,\,\,\,\,L_{45,cy}^{1} = \left( {D_{12,cy} + D_{66,cy} } \right)nR_{cy}, \hfill \\ \end{gathered}$$

$$\begin{gathered} L_{51,cy}^{1} = - \left( {B_{12,cy} + B_{66,cy} } \right)nR_{cy} ,\,\,\,\,\,L_{52,cy}^{0} = \kappa A_{44,cy} R_{cy} - B_{22,cy} n^{2} ,\,\,\,\,\,L_{52,cy}^{2} = B_{66,cy} R_{cy}^{2} ,\\ L_{53,cy}^{0} = \kappa A_{44,cy} nR_{cy} - B_{22,cy} n,\,\,\,\,\,\,\,\,\, \hfill \\ L_{54,cy}^{1} = - \left( {D_{12,cy} + D_{66,cy} } \right)nR_{cy} ,\,\,\,\,L_{55,cy}^{0} = - \kappa A_{44,cy} R_{cy}^{2} - D_{22,cy} n^{2} ,\,\,\,L_{55,cy}^{2} = D_{66,cy} R_{cy}^{2}. \hfill \\ \end{gathered}$$