Sensitivity on the non-continuous supported laminated cylindrical shell to boundary conditions and lamination schemes

Abstract

In this paper, the free vibration of laminated composited cylindrical shells with two kinds of non-continuous supported boundary condition are investigated. The artificial springs are used to simulate the arcs supported and points supported boundary condition. The equations of motion are derived by using the Chebyshev polynomials and the Lagrange equation, and Donnell’s shell theory is employed in this process. The accuracy of the present method compared with that of literature, and convergence analysis is carried out at the same time. Then, the influences of spring stiffness, the number of supported point, and the lamination schemes of non-continuous supported laminated composite cylindrical shells on frequency parameter are studied. The results show that the method can accurately deal with the free vibration of laminated shells with arbitrary non-continuous boundary and arbitrary lamination schemes.

1 Introduction

Free vibration analysis of laminated composite cylindrical shells has been a topic of major interest to many researchers due to the application in various branches of engineering, such as aerospace, petrochemical, mechanical engineering, energy and other fields. The study of free vibration behavior of laminated cylindrical shells has been carried out by many investigators. As a systematic summary of the study of shell structure analysis methods, Leissa [1] introduced a number of theories and solution techniques for various boundary conditions. Qatu made some review of research advances on the dynamic analysis of composite shells in [2, 3]. He presented that the research on the lamination material, sequence and fiber orientation is helpful for engineers to design superior structures. In the past, many studies have been made on laminated cylindrical shells with classical boundaries and elastic boundary conditions in literatures. Sun et al. [4] investigated the free vibration of the hard-coating cantilever cylindrical shell. At present, the analysis of laminated cylindrical shells focuses on the shells with continuous elastic boundary conditions. Jin et al. [5] studied the free vibration of moderately thick laminated shells with arbitrary boundary conditions and lamination schemes by using a new analytical method based on the first-order shear deformation theory. Jin et al. [6] presented a method of the vibration analysis of laminated cylindrical shells with arbitrary boundaries and lamination schemes by using a modified Fourier series. Xie et al. [7] investigated the free vibration of laminated cylindrical shell by using the Haar wavelet method. Ye and Jin [8] studied the free vibrations of laminated deep open shells with arbitrary boundary. Song et al. [9] analyzed the free vibrations of the symmetrically laminated composite cylindrical shells with arbitrary boundaries by employing a set of artificial springs based on the Donnell’s shells theory, orthogonal polynomials and Rayleigh-Ritz method. Later, Song et al. [10] investigated the free vibration of rotating cross-ply shells by using the Donnell’s shell theory and Rayleigh-Ritz method. Brischetto et al. [11] used the numerous methods to solve the shell vibration problems. Ma et al. [12] presented a unified method for coupled cylindrical shell with general coupling conditions.

In the past, the studying of vibration analysis of laminated cylindrical shells with non-continuous boundaries is rare. However, there may be more complicated boundary conditions in the actual project, such as, the shells and plates are joined at a few points through the screw bolt, the spot weld or riveting. The research of vibration analysis of laminated cylindrical shells with non-continuous boundaries is intensely indispensable and meaningful. Kandasamy and Singh [13] presented numerical studies of the free vibration analysis of open skewed circular cylindrical shells supported only on selected segments of the straight edges. Recently, Chen et al. [14] investigated the free vibration of a cylindrical shell with non-uniform elastic boundary constraints by using improved Fourier series method and Rayleigh–Ritz procedure. The points supported and arcs supported boundaries were considered. Xie et al. [15] used the wave-based method (WBM) to investigate the free and forced vibrations of points and arcs supported cylindrical shells. Tang [16] studied modeling and dynamic analysis of bolted joined cylindrical shell. The bolted joined were considered as points supported. From papers, the most of the existing researches of non-continuous boundary condition are limited to circular cylindrical shells. The research of non-continuous boundary laminated cylindrical shells is rare. The study of this paper is indispensable and meaningful.

Many comparisons of different theories were made by Lam [17], et al. Lam and Loy [17] made an analysis of natural frequencies of rotating laminated cylindrical shells with Donnell’s, Flügge’s, Love’s and Sanders’ shell theories, namely. The results indicated that Donnell’s shell theory is accurate for shells with small L / R ratios or when the circumferential wavenumber n is small, and Donnell’s theory is the most simplified. Because the content of this study is a short shell, Donnell’s shells theory is used in this paper. The widely used approximate functions in the axial direction are beam functions [17], Fourier series [18], orthogonal polynomials [19], Chebyshev polynomials [8], wave functions [20] and so on. Qin et al. [21] made a comparison study of free vibrations of cylindrical shells by three different sets of formulations, namely the modified Fourier series, the Orthogonal polynomials, and the Chebyshev polynomials. The Chebyshev polynomials show higher computational efficiency and convergence rate.

In this paper, the model of laminated composited cylindrical shells with points supported and arcs supported are established. The Donnell’s shells theory, Chebyshev polynomials and Lagrange equation are used in the established process of the governing equation. Then, the influence of spring stiffness, the number of supported point, and the lamination schemes on the frequency parameter of non-continuous supported laminated composite cylindrical shells are studied.

2 Theoretical formulations

2.1 Description of laminated cylindrical shells mode

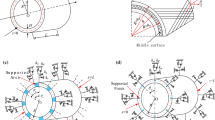
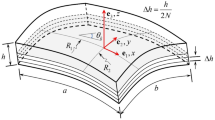
Consider a laminated composite cylindrical shell with non-continuous elastic boundary conditions as shown in Fig. 1a. The laminated cylindrical shell is assumed to have a length L, thickness H, radius R. The length x is replaced by a dimensionless length $\xi$ defined by $\xi =x$/L. x, $\theta$ and z are coordinates along the axial, circumferential, and radial directions, respectively. The displacements of a point on the middle surface are indicated byu,v and w, in the x, y, z directions. The angular orientation of fibers is defined by $\beta$ in Fig. 1b. The distance from the reference surface to the bottom of the pth layer is defined by $h_{p}$.

A schematic diagram of laminated cylindrical shells with arcs supported boundary condition or points supported boundary condition is illustrated in Fig. 1c, d, respectively. The boundary conditions of the shell are represented by introducing three sets of translational spring and one set of rotational spring of each end of the shell. For the laminated composite cylindrical shells with arcs supported boundary condition, the stiffness of the spring per unit arc length at the two ends of the shell, $x = 0$ and $x = L$, are denoted by $k_u^0 ,k_v^0 ,k_w^0 ,k_\theta ^0$ and $k_u^1 ,k_v^1 ,k_w^1 ,k_\theta ^1$ (N/$\hbox {m}^{2})$. $\theta _{1}$ is the location of starting radian and $\theta _{2}$ is the location of ending radian. For the points supported laminated cylindrical shells, the stiffness restraining axial displacement, circumferential displacement, radial displacement and rotations of supported points are denoted by ${k}_u^{'0} , {k}_v^{'0}, {k}_w^{'0} ,{k}_\theta ^{'0}$ and ${k}_u^{'1}, {k}_v^{'1} ,{k}_w^{'1} ,{k}_\theta ^{'1}$ (N/m). There are NA evenly distributed points at each end of the shell, and the location of first points are expressed by $\theta _{1}$. Suppose 1000 points on the circumference are whole circumference constraints.

Fig. 1

Model of a laminated composite cylindrical shell with non-continuous elastic boundary conditions: a coordinate system and geometry of the shell; b partial cross-sectional view of the shell; c The arcs supported shell; d The points supported shell

2.2 Expressions of laminated cylindrical shell’s energy

The kinetic energy T and the strain energy $U_{\upvarepsilon }$ of the laminated composite cylindrical shells can be calculated as follow

$$\begin{aligned} T= & {} \frac{\rho HL}{2}\int _0^{2\uppi } {\int _0^1 {({\dot{\varvec{u}}}^{2}+{\dot{\varvec{v}}}^{2}+{\dot{\varvec{w}}}^{2})} } Rd\xi \hbox {d}\theta \end{aligned}$$

(1)

$$\begin{aligned} U_\upvarepsilon= & {} \frac{L}{2}\int _0^1 {\int _0^{2\uppi } {{\varvec{\varepsilon }}^{T}} } [\varvec{S}]{\varvec{\varepsilon }} R\hbox {d}\theta \mathrm{d}\xi \end{aligned}$$

(2)

where $\rho$ is the density of the shell. The strain victor ${\varvec{\varepsilon }}^{\mathbf{T}}$ are defined as

$$\begin{aligned} {\varvec{\varepsilon }}^{\mathrm{T}}=\left\{ {{\begin{array}{cccccc} {\varepsilon _{\mathrm{x}} }&{} {\varepsilon _\theta }&{} \gamma _{\theta {\mathrm{x}}}&{} {\kappa _x }&{} {\kappa _\theta }&{} {\chi _{x\theta } } \\ \end{array} }} \right\} \end{aligned}$$

(3)

The strains of a point in pth layer of the shell are given by as follows

$$\begin{aligned} \left( {\begin{array}{l} \varepsilon _x \\ \varepsilon _\theta \\ \gamma _{x\theta } \\ \end{array}} \right) =\left( {\begin{array}{l} \varepsilon _x \\ \varepsilon _\theta \\ \gamma _{x\theta } \\ \end{array}} \right) _{(0)} +z\left( {\begin{array}{l} {\varvec{\kappa }} _x \\ {\varvec{\kappa }}_\theta \\ {\varvec{\kappa }}_{x\theta } \\ \end{array}} \right) \end{aligned}$$

(4)

where the subscript (0) denotes the middle surface of the different layer, $h_p \le z\le h_{p+1}$. The strain and the curvature of the middle surface of the shell can be defined as

$$\begin{aligned} \varepsilon _{x\left( 0 \right) }= & {} \frac{\partial u}{L\partial \xi },\,\,\,\varepsilon _{\theta \left( 0 \right) } =\frac{1}{R}\frac{\partial v}{\partial \theta }+\frac{w}{R},\,\,\,\gamma _{x\theta \left( 0 \right) } =\frac{1}{R}\frac{\partial u}{\partial \theta }+\frac{\partial v}{L\partial \xi },\,\,\, \nonumber \\ \kappa _x= & {} -\frac{\partial ^{2}w}{L^{2}\partial \xi ^{2}},\,\,\,\kappa _\theta =\frac{1}{R^{2}}\frac{\partial v}{\partial \theta }-\frac{1}{R^{2}}\frac{\partial ^{2}w}{\partial \theta ^{2}},\,\,\,\kappa _{x\theta } =\frac{1}{RL}\frac{\partial v}{\partial \xi }-\frac{2}{RL}\frac{\partial ^{2}w}{\partial \xi \partial \theta } \end{aligned}$$

(5)

The stress matrix S for laminated cylindrical shells are defined as follows

$$\begin{aligned}{}[{\varvec{S}}]=\left[ {\begin{array}{cccccc} {A_{11} }&{} {A_{12} }&{} {A_{16} } &{} {B_{11} }&{} {B_{12} }&{} {B_{16} } \\ {A_{12} }&{} {A_{22} }&{} {A_{26} } &{} {B_{12} }&{} {B_{22} }&{} {B_{26} } \\ {A_{16} }&{} {A_{26} }&{} {A_{66} } &{} {B_{16} }&{} {B_{26} }&{} {B_{66} } \\ {B_{11} }&{} {B_{12} }&{} {B_{16} } &{} {D_{11}} &{} {D_{12} }&{} {D_{16} } \\ {B_{12} }&{} {B_{22} }&{} {B_{26} } &{} {D_{12}} &{} {D_{22} }&{} {D_{26} } \\ {B_{16} }&{} {B_{26} }&{} {B_{66} } &{} {D_{16}} &{} {D_{26} }&{} {D_{66} } \\ \end{array}} \right] \end{aligned}$$

(6)

where $A_{ij}$, $B_{ij}$ and $D_{ij}$ is the stretching, coupling, and bending stiffness matrices, respectively.

$$\begin{aligned} A_{ij}= & {} \sum _{p=1}^P {{\overline{Q}} _{ij}^p } (h_{p+1} -h_p ) \nonumber \\ B_{ij}= & {} \frac{1}{2}\sum _{p=1}^P {{\overline{Q}} _{ij}^p } (h_{p+1}^2 -h_p^2 ) \nonumber \\ D_{ij}= & {} \frac{1}{3}\sum _{p=1}^P {{\overline{Q}} _{ij}^p } (h_{p+1}^3 -h_p^3 ) \end{aligned}$$

(7)

where p is the pth layer of the shell and P is the amount of the lamina. In addition, all the $B_{ij}$ terms become zero for cylindrical shells laminated symmetrically concerning their middle surfaces. ${\overline{{\varvec{Q}}}}$ is the transformation stiffness matrix, and it can be defined as follows

$$\begin{aligned} {\bar{Q}}_{11}= & {} Q_{11} \cos ^{4}\beta +2(Q_{12} +2Q_{66} )\sin ^{2}\beta \cos ^{2}\beta +Q_{22} \sin ^{4}\beta \nonumber \\ {\bar{Q}}_{12}= & {} (Q_{11} +Q_{22} -4Q_{66} )\sin ^{2}\beta \cos ^{2}\beta +Q_{12} (\sin ^{4}\beta +\cos ^{4}\beta ) \nonumber \\ {\bar{Q}}_{22}= & {} Q_{11} \sin ^{4}\beta +2(Q_{12} +2Q_{66} )\sin ^{2}\beta \cos ^{2}\beta +Q_{22} \cos ^{4}\beta \nonumber \\ {\bar{Q}}_{16}= & {} (Q_{11} -Q_{12} -2Q_{66} )\sin \beta \cos ^{3}\beta +(Q_{12} -Q_{22} +2Q_{66} )\sin ^{3}\beta \cos \beta \nonumber \\ {\bar{Q}}_{26}= & {} (Q_{11} -Q_{12} -2Q_{66} )\sin ^{3}\beta \cos \beta +(Q_{12} -Q_{22} +2Q_{66} )\sin \beta \cos ^{3}\beta \nonumber \\ {\bar{Q}}_{66}= & {} (Q_{11} +Q_{22} -2Q_{12} -2Q_{66} )\sin ^{2}\beta \cos ^{2}\beta +Q_{66} (\sin ^{4}\beta +\cos ^{4}\beta ) \end{aligned}$$

(8)

where the plane stress–strain matrix Q can be defined as follows

$$\begin{aligned} Q_{11} =\frac{E_{11} }{1-\mu _{12} \mu _{21} },Q_{12} =\frac{\mu _{12} E_{11} }{1-\mu _{12} \mu _{21} },Q_{22} =\frac{E_{22} }{1-\mu _{12} \mu _{21} },Q_{66} =G_{12} \end{aligned}$$

(9)

where $E_{1}$ and $E_{2}$ are Young’s moduli in the principal directions. $\mu _{12}$ and $\mu _{21}$ are the corresponding Poisson’s ratios, and the relationship between them can be calculated by using $E_{11} \mu _{21} =E_{22} \mu _{21}$. $G_{12}$ is moduli of rigidity.

2.3 The potential energy of the boundary springs

The points supported and arcs supported shell are shown in Fig. 1c, d. Artificial spring implemented at two ends of the shell are used to simulate arbitrary boundary conditions. The potential energy $U_{\mathrm{springs}}$ introduced by the elastic spring can be calculated as follows

(1) The potential energy $U_{\mathrm{springs}}^{\mathrm{arcs}}$ stored by the boundary spring of arcs supported laminated shells is given by

$$\begin{aligned} U_{\mathrm{springs}}^{\mathrm{arcs}}= & {} \frac{1}{2}\int _{\theta _1 }^{\theta _2 } \left\{ k_u^0 [u(0,\theta ,t)]^{2}+k_v^0 [v(0,\theta ,t)]^{2}\right. \nonumber \\&\quad \left. +\,k_w^0 [w(0,\theta ,t)]^{2}+k_\theta ^0 \left[ {\frac{\partial w(0,\theta ,t)}{L\partial \xi }} \right] ^{2} \right\} R\mathrm{d}\theta \nonumber \\&\quad +\,\frac{1}{2}\int _{\theta _1 }^{\theta _2 } \left\{ k_u^1 [u(1,\theta ,t)]^{2}+k_v^1 [v(1,\theta ,t)]^{2}+k_w^1 [w(1,\theta ,t)]^{2}\right. \nonumber \\&\left. \quad +\,k_\theta ^1 \left[ {\frac{\partial w(1,\theta ,t)}{L\partial \xi }} \right] ^{2} \right\} R\mathrm{d}\theta \end{aligned}$$

(10a)

Here $\theta _1$ and $\theta _2$ are the starting and ending radian, $k_{u,s}^0 \,$, $\,\,k_{v,s}^0 \,$, $k_{w,s}^0$, $k_{\theta ,s}^0$ and $k_{u,s}^1$, $k_{v,s}^1$, $k_{w,s}^1$, $k_{\theta ,s}^1$ are the stiffness of the spring per unit arc length of four groups of boundary spring at $x_{s}=0$ and $x_{s}=L$, respectively.

(2) The potential energy $U_{\mathrm{springs}}^{\mathrm{points}}$ stored by the boundary spring of points supported laminated shells is given by

$$\begin{aligned} U_{\mathrm{springs}}^{\mathrm{points}}= & {} \frac{1}{2}\sum _{\alpha =1}^{\mathrm{NA}} \left\{ {k'}_{u,\alpha }^0 [u(0,\theta _\alpha ,t)]^{2}+{k'}_{v,\alpha }^0 [v(0,\theta _\alpha ,t)]^{2}+{k'}_{w,\alpha }^0 [w(0,\theta _\alpha ,t)]^{2}\right. \nonumber \\&\left. +\,{k'}_{\theta ,\alpha }^0 \left[ {\frac{\partial w(0,\theta _\alpha ,t)}{L\partial \xi }} \right] ^{2} \right\} \nonumber \\&+\,\frac{1}{2}\sum _{\alpha =1}^{\mathrm{NA}} \left\{ {k'}_{u,\alpha }^1 [u(1,\theta _\alpha ,t)]^{2}+{k'}_{v,\alpha }^1 [v(1,\theta _\alpha ,t)]^{2}+{k'}_{w,\alpha }^1 [w(1,\theta _\alpha ,t)]^{2}\right. \nonumber \\&\left. +\,{k'}_{\theta ,\alpha }^1 \left[ {\frac{\partial w(1,\theta _\alpha ,t)}{L\partial \xi }} \right] ^{2} \right\} \end{aligned}$$

(10b)

where NA is the number of restrained points (In the paper, $NA\le 1000)$. $(x_{\alpha }, \theta _{\alpha })$ is used to represent the coordinates of the sth point. ${k'}_{u,\alpha }^0$, ${k'}_{v,\alpha }^0$, ${k'}_{w,\alpha }^0$ and ${k'}_{\theta ,\alpha }^0$ are the stiffness of four groups of boundary spring at the $\alpha$th point at $x_{\alpha } = 0$. Similarly, ${k'}_{u,\alpha }^1$, ${k'}_{v,\alpha }^1$, ${k'}_{w,\alpha }^1$ and ${k'}_{\theta ,\alpha }^1$ denote the stiffness of corresponding boundary spring.

2.4 Admissible displacement functions

According to Qin’s study [21], the modified Fourier series, the Orthogonal polynomials, and the Chebyshev polynomials show excellent accuracy, and the convergence rate and the computational efficiency of the Orthogonal polynomials and Chebyshev polynomials are higher, but the Chebyshev polynomials show the highest computational efficiency. Finally, the Chebyshev polynomials are used as admissible displacement functions in this paper.

The admissible displacement functions of the laminated composite cylindrical can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{l} u\left( {\xi ,\theta ,t} \right) \,=\sum \limits _{n=1}^N {\sum \limits _{m=0}^{\mathrm{NT}} {a_m T_m^*} \left( \xi \right) \left( {\cos n\theta +\sin n\theta } \right) } \mathrm{e}^{-j\omega t}={\bar{{\varvec{U}}}}^{T}{\varvec{q}}_{\varvec{u}} \\ v\left( {\xi ,\theta ,t} \right) \,=\sum \limits _{n=1}^N {\sum \limits _{m=0}^{\mathrm{NT}} {b_m T_m^*} \left( \xi \right) \left( {\sin n\theta +\cos n\theta } \right) } \mathrm{e}^{-j\omega t}={\bar{{\varvec{V}}}}^{T}{\varvec{q}}_{\varvec{v}} \\ w\left( {\xi ,\theta ,t} \right) =\sum \limits _{n=1}^N {\sum \limits _{m=0}^{\mathrm{NT}} {c_m T_m^*} \left( \xi \right) \left( {\cos n\theta +\sin n\theta } \right) } \mathrm{e}^{-j\omega t}={\bar{{\varvec{W}}}}^{T}{\varvec{q}}_{\varvec{w}} \\ \end{array}} \right. \end{aligned}$$

(11)

where $a_{m}$, $b_{m}$ and $c_{m}$ are the unknown corresponding coefficients.$T_m^*\left( \xi \right)$ are appropriate admissible displacement functions,NT is the number of terms in calculation. $\omega$ is the natural frequency of the shell. ${{\varvec{q}}}_{{\varvec{u}}}, {{\varvec{q}}}_{{\varvec{v}}}$ and ${{\varvec{q}}}_{{\varvec{w}}}$ are generalized coordinates.n is the circumferential wave number. ${\bar{{\varvec{U}}}}$, ${\bar{{\varvec{V}}}}$ and ${\bar{{\varvec{W}}}}$ are mode vector satisfying a boundary condition as the following expressions

$$\begin{aligned} {\bar{{\varvec{U}}}}^{T}= & {} \left[ T_m^*\left( \xi \right) \cos \theta \quad T_m^*\left( \xi \right) \,\,\,\,\sin \theta \quad \cdots \quad T_m^*\left( \xi \right) \cos n\theta \quad T_m^*\left( \xi \right) \,\,\,\sin n\theta \quad \cdots \quad T_m^*\left( \xi \right) \cos N\theta \quad T_m^*\left( \xi \right) \,\,\,\sin N\theta \right] \nonumber \\ {\bar{{\varvec{V}}}}^{T}= & {} \left[ T_m^*\left( \xi \right) \,\,\,\,\sin \theta \quad T_m^*\left( \xi \right) \cos \theta \quad \cdots \quad T_m^*\left( \xi \right) \,\,\,\sin n\theta \quad T_m^*\left( \xi \right) \cos n\theta \quad \cdots \quad T_m^*\left( \xi \right) \,\,\,\sin N\theta \quad T_m^*\left( \xi \right) \cos N\theta \right] \nonumber \\ {\bar{{\varvec{W}}}}^{T}= & {} \left[ T_m^*\left( \xi \right) \cos \theta \quad T_m^*\left( \xi \right) \,\,\,\,\sin \theta \quad \cdots \quad T_m^*\left( \xi \right) \cos n\theta \quad T_m^*\left( \xi \right) \,\,\,\sin n\theta \quad \cdots \quad T_m^*\left( \xi \right) \cos N\theta \quad T_m^*\left( \xi \right) \,\,\,\sin N\theta \right] \end{aligned}$$

(12)

$T_m^*\left( \xi \right)$ is a Chebyshev polynomial of displacement components, $T_m^*\left( \xi \right) =T_m \left( {2\xi -1} \right)$, $T_m \left( \cdot \right)$ is the Chebyshev polynomials of the first kind, of which the recurrence expressions are given by

$$\begin{aligned} T_0 \left( \xi \right) =1,T_1 \left( \xi \right) =\xi ,T_{m+1} \left( \xi \right) =2\xi T_m \left( \xi \right) -T_{m-1} \left( \xi \right) ,\left( {m\ge 2} \right) \end{aligned}$$

(13)

In the process of constructing Chebyshev polynomials, the polynomials are defined in the interval [−1, 1], while $\xi \in \left[ {0, 1} \right]$, and the transformation of coordinates from $\xi$ to 2$\xi$$-$ 1 is necessary.

2.5 Energy expressions and the solution procedure

Substituting Eq. (11) into Eqs. (1), (2) and (10), can obtain the kinetic energy, the strain energy, and the potential energy. T, $U_{\varepsilon }$ and $U_{spring}$ are written as

$$\begin{aligned} T= & {} \frac{1}{2}{\dot{{\varvec{q}}}}_u^T {\varvec{M}}^{uu}{\dot{{\varvec{q}}}}_u +\frac{1}{2}{\dot{{\varvec{q}}}}_v^T {\varvec{M}}^{vv}{\dot{{\varvec{q}}}}_v +\frac{1}{2}{\dot{{\varvec{q}}}}_w^T {\varvec{M}}^{ww}{\dot{{\varvec{q}}}}_w \end{aligned}$$

(14)

$$\begin{aligned} U_\varepsilon= & {} \frac{1}{2}{\varvec{q}}_u^T {\varvec{K}}^{uu}{\varvec{q}}_u +\frac{1}{2}{\varvec{q}}_u^T {\varvec{K}}^{uv}{\varvec{q}}_v +\frac{1}{2}{\varvec{q}}_u^T {\varvec{K}}^{uw}{\varvec{q}}_w +\frac{1}{2}{\varvec{q}}_v^T {\varvec{K}}^{vv}{\varvec{q}}_v +\frac{1}{2}{\varvec{q}}_v^T {\varvec{K}}^{vw}{\varvec{q}}_w +\frac{1}{2}{\varvec{q}}_w^T {\varvec{K}}^{ww}{\varvec{q}}_w \end{aligned}$$

(15)

$$\begin{aligned} U_{\mathrm{spr}}= & {} \frac{1}{2}{\varvec{q}}_u^T {\varvec{K}}_{spr}^{uu} {\varvec{q}}_u +\frac{1}{2}{\varvec{q}}_v^T {\varvec{K}}_{spr}^{vv} {\varvec{q}}_v +\frac{1}{2}{\varvec{q}}_w^T {\varvec{K}}_{spr}^{ww} {\varvec{q}}_w \end{aligned}$$

(16)

where ${{\varvec{M}}}^{uu}$, ${{\varvec{M}}}^{v}$ and ${{\varvec{M}}}^{ww}$ are the modal mass matrix of laminated cylindrical shells, which are given in “Appendix A”. ${{\varvec{K}}}^{uu}$, ${{\varvec{K}}}^{uv}$, ${{\varvec{K}}}^{uw}$, ${{\varvec{K}}}^{vv}$, ${{\varvec{K}}}^{vw }$ and ${{\varvec{K}}}^{ww}$ are the modal stiffness matrix, which are given in “Appendix B”. ${\varvec{K}}_{\mathrm{spr}}^{uu}$, ${\varvec{K}}_{\mathrm{spr}}^{vv}$ and ${\varvec{K}}_{\mathrm{spr}}^{ww}$ are the modal spring stiffness matrix, which are given in “Appendix C”.

The Lagrange equation of the vibration system can be given

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\left( {\frac{\partial T}{\partial {\dot{{\varvec{q}}}}}} \right) -\frac{\partial T}{\partial {\varvec{q}}}+\frac{\partial \left( {U_\upvarepsilon +U_{\mathrm{spring}} } \right) }{\partial {\varvec{q}}}=0 \end{aligned}$$

(17)

where q is the vector of generalized coordinates.

The kinetic energy and strain energy are brought into the Lagrange equation to obtain the differential equations of motion of laminated cylindrical shells

$$\begin{aligned} {\varvec{M}}\ddot{{\varvec{q}}}+\left( {{\varvec{K}}_{spr} +{\varvec{K}}} \right) {\varvec{q}}=0 \end{aligned}$$

(18)

where M, K and ${{\varvec{K}}}_{spr}$ are the generalized mass matrix, stiffness matrix, spring stiffness matrix vector.

$$\begin{aligned} {\varvec{M}}=\left[ {{\begin{array}{ccc} {{\varvec{M}}^{uu}}&{} &{} \\ &{} {{\varvec{M}}^{vv}}&{} \\ &{} &{} {{\varvec{M}}^{ww}} \\ \end{array} }} \right] , {\varvec{K}}=\left[ {{\begin{array}{ccc} {{\varvec{K}}^{uu}}&{} {\frac{1}{2}{\varvec{K}}^{uv}}&{} {\frac{1}{2}{\varvec{K}}^{uw}} \\ {\frac{1}{2}{\varvec{K}}^{uv}}&{} {{\varvec{K}}^{vv}}&{} {\frac{1}{2}{\varvec{K}}^{vw}} \\ {\frac{1}{2}{\varvec{K}}^{uw}}&{} {\frac{1}{2}{\varvec{K}}^{vw}}&{} {{\varvec{K}}^{ww}} \\ \end{array} }} \right] ,{\varvec{K}}_{\mathrm{spr}} =\left[ {{\begin{array}{ccc} {{\varvec{K}}_{\mathrm{spr}}^{uu} }&{} &{} \\ &{} {{\varvec{K}}_{\mathrm{spr}}^{vv}} &{} \\ &{} &{} {{\varvec{K}}_{\mathrm{spr}}^{ww}} \\ \end{array} }} \right] \end{aligned}$$

(19)

The non-dimensional frequency parameters $\omega ^*$ is used, of which the expression is denoted by

$$\begin{aligned} \omega ^*=\omega R\sqrt{\rho /{E_2 }} \end{aligned}$$

(20)

3 Validation and comparison

To illustrate the convergence and the accuracy of the current solution, some numerical results are provided in this part compared with the results of classic literature.

The boundary of laminated composite cylindrical shells with non-continuous elastic boundary conditions can be considered as a continuous whole-circle distribution if the length of supported arcs $\alpha =\sum {\left( {\theta _s -\theta ^{\prime }_s } \right) }$ is $2\uppi$ or the number of supported points NA is 1000. A three-layered, cross-ply $[0^{\circ }/90^{\circ }/0^{\circ }]$ cylindrical shell is used as an example by Lam [17]. The layer thickness and material parameters of the laminated composite cylindrical shells are listed in Tables 1 and 2.

Table 1 Properties of laminated cylindrical shells

Table 2 Corresponding stiffness for different types of classical boundaries [9, 14]

3.1 The accuracy of the current solution

The non-dimensional frequency parameters $\omega ^*$ for the same shell with S–S and C–C boundary conditions are given in Table 3. The comparisons are presented for the length–radius ratios $L/R = 1, 5$ and radius–thickness ratio $H/R = 0.002$, respectively. It can be observed that the present method has a small error between the studies [6, 17] dealing with free vibration of laminated cylindrical shells with classical boundary condition. The accuracy of the present mode is high, and it can be generalized to the calculation of the natural characteristics of the laminated cylindrical shells under any condition of spring stiffness.

Table 3 Frequency parameters $\omega ^*=\omega R\sqrt{\rho /{E_2 }}$ for a three-layer, cross-ply $[0^{\circ }/90^{\circ }/0^{\circ }]$ cylindrical shell with S–S and C–C boundary condition: ($H/R=0.002$, NT = 8)

3.2 Convergence of the current solution

The convergence of the frequency parameters of laminated cylindrical shells is discussed. The geometric parameters of laminated cylindrical shells are as below: cross-ply $[0^{\circ }/90^{\circ }/0^{\circ }]$, length–radius ratios $L/R=1$, radius–thickness ratio $H/R=0.002$ and circumferential wave number $N=6$, $m=1$. Five types of boundary conditions, that is, S–S, F–F, C–C, C–F, and C–S, are considered. For generality and convenience, the relative tolerance of the frequency is defined

$$\begin{aligned} \frac{\left| {\omega ^*_{\mathrm{NT}} -\omega ^*_{\mathrm{exact}}} \right| }{\omega *_{\mathrm{exact}}}\times 100\% \end{aligned}$$

(21)

where $\omega ^*_{NT}$ is the non-dimensional frequency parameters with respect to NT terms of admission functions. $\omega ^*_{exact}$ is the favorable result of the frequency. As the number of terms NT of admissible functions increases, the frequency parameter calculated in this paper is close to the exact result. The accuracy of the frequency parameters is not affected after NT is a larger number. Therefore, the frequency parameter of 25 terms of admissible functions is taken as the exact value in this section.

It can be observed from Fig. 2 that the relative tolerances decrease gradually with increase in the number of polynomials NT at first, then decrease slightly. The relative tolerance with 8 truncation terms are closed to 0%. The number of polynomial terms NT is chosen as 8 for simplified calculation, which means that the present method has excellent convergence.

Fig. 2

Variation of relative tolerance of the non-dimensional frequency parameters with respect to the number of terms of admission functions (NT): a arcs supported boundary conditions; b point supported boundary conditions ($m=1$, $N=6$)

4 Results and discussion

The convergence and the accuracy of the current solution have been verified by Sect. 3. Free vibration analysis of laminated cylindrical shells with arcs supported and points supported boundary condition are investigated in this section. The geometric parameters of laminated cylindrical shells are select in this section, as below: cross-ply $[0^{\circ }/90^{\circ }/0^{\circ }]$, length–radius ratios $L/R=1$, radius–thickness ratio $H/R=0.005$, the circumferential wave number n=1–6.

4.1 Shell with arcs supported boundary condition

For the form of welding that may occur in actual engineering, the arcs supported boundary condition is used for simulation. It is indispensable to study the natural frequency of arcs supported laminated cylindrical shell. The effects of the stiffness of the spring per unit arc length, lamination schemes combined elastic boundaries arcs on frequency parameters for laminated cylindrical shells with arcs supported boundary condition were studied.

4.1.1 The range of supported arcs

The effects of the range of constraint arcs on the frequency parameters and mode shapes of arcs supported laminated shells are analyzed in Figs. 3, 4, and 5, in which the shell is whole-circle clamped supported boundary condition in one edge while the other edge restrained by changing clamped supported arcs. The first three-order frequency parameters of the laminated shell with an increasing range of supported arcs are plotted in Fig. 3. It can be seen from the figure that the natural frequency of the laminated shell increases as the supported arcs range increases when the range is less than $\pi$, and the frequency remain unchanged after the range is greater than $\pi$. The boundary converges to the uniformly constrained clamped support boundary. The variation of the mode shape of the laminated cylindrical shell under different constraint range are plotted in Figs. 4 and 5. When the constraint range is small, the vibration amplitude of the shell is only small in the constraint region. When the constraint range is larger than $\pi$, the entire circumference of the boundary has a small amplitude of vibration. It can be seen from Fig. 5b that the shell has only a small amplitude in the constraint region, resulting in a small overall constraint amplitude.

As seen the phenomenon from Figs. 3, 4 and 5, we can explain from Eqs. (10a). With the increase in the supported arcs range, the integral range in the formula increases and the integrand is positive. So, the boundary stiffness is closer to the whole circumference constraint stiffness. When the constraint range is large, the constraint on the boundary can be approximated as a whole circumference constraint, so the frequency remains almost unchanged and the amplitude of the mode is almost zero.

Fig. 3

Effect of the range of supported arcs on the frequency parameter

Fig. 4

Comparison of 3D modes shapes for arcs supported shell with different constrained range: a$\alpha =0$; b$\alpha =\uppi$/5; c$\alpha =2\uppi$/5; d$\alpha =3\uppi$/5; e$\alpha =4\uppi$/5; f$\alpha =\uppi$; g$\alpha =6\uppi$/5; h$\alpha =2\uppi$

Fig. 5

Comparison of constraint end modes shapes for the arcs supported end with different constrained range: a relative free end maximum amplitude; b actual amplitude

Fig. 6

Variation of the frequency parameters with respect to elastic supports: $k_u^0 =k_v^0 =k_w^0 =k_\theta ^0 =10^{12}$a$\alpha =2\pi$; b$\alpha =\pi$; c$\alpha =\pi$/2

4.1.2 Spring stiffness

In the past studies, most of the research directions focused on the influence of single spring stiffness on the natural frequency of laminated shell, but less on the influence of multiple spring combinations on the natural frequency. In Fig. 6, the frequency parameters of laminated cylindrical shells with combined elastic boundary conditions are calculated. The boundary in one edge is clamped supports of whole circumference $(k_u^1 =k_v^1 =k_w^1 =k_\theta ^1 =10^{12}\hbox {N/m}^{2}(\hbox {N/rad}^{2}))$ while the other edge restrained by two sets of changing stiffness arcs supported spring $k_i^0 =10^{0}\sim 10^{12}\hbox {N/m}^{2}(\hbox {N/rad}^{2}),k_j^0 =10^{0}\sim 10^{12}\hbox {N/m}^{2}(\hbox {N/rad}^{2})\left( {i,j=u,\theta \hbox { and }v,\hbox {w}} \right)$, and other direction stiffness is 0 N/$\hbox {m}^{2}$(N/$\hbox {rad}^{2})$. In Fig. 6a, with increase in the stiffness of axial, circumferential, radial, and rotational directions, the frequency parameters remain unchanged first, then increase rapidly, and finally remain unchanged. And the value of one direction stiffness affects the influence of spring stiffness on the frequency parameter in the other direction. When $k_{w}$ is less than $10^{4}$, as $k_{v}$ increases from $10^{0}$ to $10^{12}$, the frequency parameter increases from 0.13 to 0.33. However, when $k_{w}$ is greater than $10^{4}$, the effect of $k_{v}$ on the frequency parameters becomes smaller. Especially when $k_{w}$ is greater than $10^{7}$, as $k_{v}$ increases from $10^{0}$ to $10^{12}$, the frequency parameter increases from 0.28 to 0.33. In different directions, the degree of mutual influence of stiffness in the two directions is different. For example, when $k_{w}$ is greater than $10^{9}$, the frequency parameter remains unchanged as $k_{w}$ increases. Figure 6b, c respectively, calculate the constraint range $\alpha$ as $\pi$ and $\pi$/2, and it can be seen that the effect of the stiffness change on the natural frequency is similar to Fig. 6a. Therefore, when the influence of spring stiffness on the natural frequency are analyzed, the stiffness in multiple directions should be considered at the same time. When the constraint range is small, the curve becomes nonsmooth and the range of sensitive intervals becomes larger, and this should be avoided in the project.

The stiffness has an important effect on mode shapes. The mode shapes of $\pi$/2 laminated cylindrical shell with different stiffness spring arcs supports are shown in Figs. 7 and 8. One end of the spring is clamped support of the whole circumference, and the other end is elastic support ($k_{w}=10^{5}\sim 10^{8 }\hbox {N}/\hbox {m}^{2}$, other direction stiffness is $0 \hbox {N}/\hbox {m}^{2})$. When $k_{w} <10^{5} \hbox {N}/\hbox {m}^{2}$, the boundary approximates the free boundary, and the constrained spring has small influence on the vibration mode; when the value of spring stiffness is in the sensitive interval, as the spring stiffness increases, the vibration amplitude in the constraint range gradually decreases; when the spring stiffness is greater than $10^{8} \hbox {N}/\hbox {m}^{2}$, the restraining area is a clamped support and the vibration amplitude is close to zero. It is proved that the boundary spring has a great influence on the vibration amplitude of the shell.

As seen the phenomenon from Figs. 6, 7 and 8, we can explain from Eqs. (10a) and (18). With the increase in the spring stiffness k in the potential energy of the boundary spring (Eq. (10a)), the spring stiffness matrix increase in Eq. (18). The boundary is close to the free boundary condition at the beginning of the stiffness being increased from $10^{0}$ to $10^{12}$, therefore, the frequency change slightly. Within the sensitive range, the spring stiffness matrix increases rapidly with increase in stiffness. The boundary can seem as the clamped boundary condition when the stiffness’s value is greater than the sensitive interval, and the frequency parameters of the laminated cylindrical shells remain unchanged.

Fig. 7

Comparison of 3D modes shapes for arcs supported shell with different spring stiffness (with the arcs radian from 0 to $\pi$/2): a$k_{w}=10^{5}$, b$k_{w}=10^{6}$, c$k_{w}=10^{7}$, d$k_{w}=10^{8}$

Fig. 8

Comparison of constraint end modes shapes for the arcs supported end with different spring stiffness: a relative free end maximum amplitude; b actual amplitude

4.1.3 Lamination schemes

Compared with the previous study [6, 22] focusing on the free vibration of the laminated shell with the determining boundary and lamination schemes, this paper discusses the free vibration of a three-layer arc supported laminated cylindrical shell with the continuously varying spring stiffness and lamination schemes. The effect of spring stiffness and lamination schemes on frequency parameters of the laminated cylindrical shell are a discussion in Fig. 9. To verify with Sect. 4.1.2, $\alpha$ is selected as $\pi$. The boundary in one edge is clamped supports of whole circumference ($k_u^1 =k_v^1 =k_w^1 =k_\theta ^1 =10^{12}\hbox {N/m}^{2}(\hbox {N/rad}^{2}))$ while the other edge of the arcs radian from 0 to $\pi$/2 restrained by one set of changing stiffness arcs supported spring $k_i^0 =10^{0}\sim 10^{12}\hbox {N/m}^{2}(\hbox {N/rad}^{2})\left( {i=u,\theta \,,\,\,v,w} \right)$, and other direction stiffness is 0 N/$\hbox {m}^{2}$(N/$\hbox {rad}^{2})$. The angular orientation $\beta$ of fibers of the middle layer continuously change from 0 to $\pi$, and the angular orientation of inner layer and outer layer keep unchanged. In Fig. 9a–d, when the spring stiffness is small, as the angular orientation of fibers of the middle layer increases from 0 to $\pi$, the frequency parameter decreases first, reaches a minimum at $\theta =\pi$/2, and then increases again. When the spring stiffness is greater than the sensitive interval, as the angular orientation increases from 0 to $\pi$/2, the frequency parameter first increases, and then decreases again, reaches a minimum at $\uptheta =\pi$/2. There is the same tendency compared with the layup angle from 0 to $\pi$/2 with the layup angle from $\pi$ to $\pi$/2. The angle $\theta$ at which the frequency reaches the maximum are $\pi$/6, 2$\pi$/9, $\pi$/3 and $\pi$ /18, respectively. Therefore, the spring stiffness in different directions has different effects on the frequency parameters of laminated shells with different laminated angles. In engineering design, the required natural frequency can be obtained by adjusting the boundary spring stiffness and the layup angle.

As seen the phenomenon from Fig. 9, we can explain from Eq. (8). When the angular orientation of fibers $\beta$ of the middle layer change from 0 to $\pi$, the transformation stiffness matrix ${\bar{Q}}$ is the sine and cosine about $\beta$ , and they show a cyclical change.

Fig. 9

Influence of the boundary condition stiffness and lamination schemes for a three-layered, cross-ply [0, $\theta$, 0] shell with clamped boundary conditions in one edge while the other edge only restrained by elastic spring: ($\alpha =\pi )$a$k_{u}$; b$k_{v}$; c$k_{w}$; d$k_{\theta }$

4.2 Shell with points supported boundary condition

The study on the natural frequency of point supported laminated shells provide theoretical reference for bolting in engineering. Then, the effects of the number of supported points, spring stiffness, and lamination schemes combined elastic boundaries on frequency parameters and mode shape of laminated cylindrical shells with points supported boundary condition were studied.

Fig. 10

Effect of the number of supported points on the frequency parameter

Fig. 11

Comparison of modes shapes for points supported shell: a NA = 1; b NA = 2; c NA = 3; d NA = 4; e NA = 5; f NA = 6; g NA = 7; hNA = 8

Fig. 12

Comparison of modes shapes for the points supported end: a relative free end maximum amplitude; b actual amplitude

Fig. 13

Variation of the frequency parameters with respect to elastic supports: $k_u^0 =k_v^0 =k_w^0 =k_\theta ^0 =10^{12}$a NA = 1000; b NA = 16; c NA = 8

Fig. 14

Comparison of 3D modes shapes for points supported shell with different spring stiffness (NA=8): a$k_{w}=10^{4}$, b$k_{w}=10^{5}$, c$k_{w}=10^{6}$, d$k_{w}=10^{7}$

4.2.1 Number of supported points

The effects of the number of constraint points on the frequency parameters and mode shapes of points supported laminated shells are analyzed in Figs. 10, 11, and 12, in which the shell is whole-circle clamped supported boundary condition in one edge while the other edge restrained by changing supported points. The first three-order frequency parameters of the laminated shell with changing number of supported points are plotted in Fig. 10. It can be seen from the figure that the natural frequency of the laminated shell increases as the number of point increases when the number of points is less than 13. When the number of points is greater than 13, the frequency parameter of the laminated shell remains stable as the number of point increases, that is, as the number of point increases, the boundary converges to the uniformly constrained fixed support boundary. The variation of the mode shape of the laminated cylindrical shell under different constraint points are plotted in Figs. 11 and 12. It can be seen that when the number of constraint points is small, the mode shape of the laminated shell only has an amplitude of 0 at the constraint point. When the number of points is increased to more than 6, the laminated shell has a little amplitude of vibration over the entire circumference. Through the above analysis, it can be considered that when the number of constraint points is large than 13, the boundary is approximately a clamped support for the entire circumference. As seen the phenomenon from Figs. 10, 11 and 12, we can explain from Eq. (10b). With increase in the number of points, the $U_{\mathrm {spring}}^{\mathrm {points}}$ is increasing and gradually approaching the value of the whole circumference constraint. When NA is large enough, the frequency will converge to the uniformly clamp supported condition.

4.2.2 Spring stiffness

The laminated cylindrical shells with clamped supported in one edge $({k}_u^{'1} ={k}_v^{'1} ={k}_w^{'1} ={k}_\theta ^{'1} =10^{9}\,\,N/\hbox {m}(N/\hbox {rad)})$ while the other edge restrained by two sets of changing stiffness spring is discussed in Figs. 13, 14, and 15. In this section, NA is selected as 1000 16 and 8 for having a clear distinction. In the figure, as the spring stiffness increases, the natural frequency first remains unchanged, rapidly increases in the sensitive interval, and finally remains unchanged. Take Fig. 13a as an example, when the radial spring stiffness ${k'}_w$ is less than $10^{0}$, the natural frequency of the laminated shell increases from 0.12 to 0.32 with increase in the circumferential spring stiffness; when the radial spring stiffness ${k'}_w$ is more than $10^{5}$, it increases from 0.28 to 0.32. It can be seen clearly that the effect of spring stiffness on the natural frequency in one direction is affected by the spring stiffness values in other directions. In Figs. 13b, c, the natural frequencies of NA=64 and 16 are studied, respectively. The sensitivity interval is also different under the number of different constraint points. In Fig. 13c, when the radial stiffness increases to $10^{6}$, the first-order natural frequency has a mutation. From Figs. 14 and  15, when the stiffness increases from $10^{6}$ to $10^{7}$, the circumferential wavenumber of the first-order frequency changes from 6 to 4, causing a sudden change in frequency. The effect of stiffness on frequency parameters of the points supported shells are consistent with those effect indicated from Fig. 3. The reason for the appearance of Fig. 13 is the same as Fig. 6, which is not discussion.

Fig. 15

Comparison of constraint end modes shapes for the points supported end with different spring stiffness: a relative free end maximum amplitude; b actual amplitude

4.2.3 Lamination schemes

In practical engineering, the cross-ply angle is an extremely important design parameter, so it is indispensable to study the influence of the cross-ply angle on the natural frequency of the laminated shell. The effect of the lamination schemes and spring stiffness on the natural frequency of the points supported laminated shell is analyzed in Fig. 16. To verify with Sect. 4.2.2, NA is selected as 16. A three-layered cross-ply [0, $\theta$, 0] $(\theta =0\sim \pi )$ laminated shell with whole cycle clamped supported in one edge (${k}_u^{'1} ={k}_v^{'1} ={k}_w^{'1} ={k}_\theta ^{'1} =10^{9}\,\,\hbox {N/m(N/rad)}$) while the other edge restrained by one set of changing stiffness spring $({k'}_i^0 =10^{-3}\sim 10^{9}\hbox {N/m(N/rad)}\left( {i=u,v,w,\theta } \right) )$ is discussed. In Figs. 16a–d, when the spring stiffness is small, as the middle layer angle increases from 0 to $\pi$, the frequency parameter decreases first and then increases, and the minimum value is obtained at $\pi$/2. And the curve is symmetric about $\pi$/2. When the spring stiffness is large, as the middle layer angle increases from 0 to $\pi$/2, the laminated shell frequency parameter increases first, and the maximum value is obtained around $\pi$/6, 2$\pi$/9, $\pi$/3 and $\pi$ /18, respectively, then decrease, taking the minimum at $\pi$/2; when the ply angle increases from $\pi$ to $\pi$/2, the frequency parameter change also increases first and then decreases, and the maximum value is obtained at 5$\pi$/6, 7$\pi$/9, 2$\pi$/3 and 17$\pi$ /18, respectively. According to the above analysis, the ply angle has a greater influence on the frequency parameters. Therefore, the required frequency parameters can be obtained by changing the layup angle of the middle layer during the engineering design process. The reason for this phenomenon is similar to Fig. 9 and will not be discussed here.

Fig. 16

Influence of the boundary condition stiffness and lamination schemes for a three-layered, cross-ply [0, $\theta$, 0] shell with clamped boundary conditions in one edge, while the other edge only restrained by elastic spring (NA = 16)

5 Conclusions

In this paper, the models of laminated composite cylindrical shells with non-continuous elastic boundary conditions are established and the natural character are investigated. By comparing the calculation results with the classic literature, the convergence and accuracy of the model are verified. In results and discussion, the effects of some parameters on free vibrations of non-continuous supported shells are studied and the conclusions are as follows.

• (1) With the increase in spring stiffness, the frequency remains unchanged at first, then increasing rapidly in sensitive interval finally almost keep a constant. The constant and sensitive interval also change with the change of the constraint range.

• (2) Compared with rotational spring stiffness, the change of spring stiffness in axial, radial and circumferential directions have a more significant effect on natural frequency. When the stiffness in two directions is considered, the effect on frequency will affect each other.

• (3) As the constraint range increases, the shell boundary approximates the entire circumference constraint.

• (4) The natural frequency changes periodically with the change of the lamination schemes of the middle layer. When $\beta$ is $\pi$/2, the frequency is the smallest.

Appendices

Appendix A. Expressions for the mass matrix M

$$\begin{aligned} {\varvec{M}}^{uu}= & {} \rho HLR\int _0^1 {\int _0^{2\pi } {[{\bar{\varvec{U}}}{\bar{\varvec{U}}}^{T}]}} \,\,d\theta d\xi \hbox { Equation Chapter 2 Section 1 } \end{aligned}$$

(A.1)

$$\begin{aligned} {\varvec{M}}^{vv}= & {} \rho HLR\int _0^1 {\int _0^{2\pi } {[{\bar{\varvec{V}}}{\bar{\varvec{V}}}^{T}]}} \,\,d\theta d\xi \end{aligned}$$

(A.2)

$$\begin{aligned} {\varvec{M}}^{ww}= & {} \rho HLR\int _0^1 {\int _0^{2\pi } {[{\bar{\varvec{W}}}{\bar{\varvec{W}}}^{T}]\,\,} } d\theta d\xi \end{aligned}$$

(A.3)

Appendix B. Expressions of the stiffness matrix K

$$\begin{aligned} {\varvec{K}}^{u}= & {} \frac{L}{R}\int _0^1 {\int _0^{2\pi } {\left( {A_{66} \frac{\partial {\bar{\varvec{U}}}}{\partial \theta }\frac{\partial {\bar{\varvec{U}}}^{T}}{\partial \theta }+\frac{R^{2}A_{11} }{L^{2}}\frac{\partial {\bar{\varvec{U}}}}{\partial \xi }\frac{\partial {\bar{\varvec{U}}}^{T}}{\partial \xi }+\frac{2RA_{16} }{L}\frac{\partial {\bar{\varvec{U}}}}{\partial \xi }\frac{\partial {\bar{\varvec{U}}}^{T}}{\partial \theta }} \right) } \,} \hbox {d}\theta \hbox {d}\xi \end{aligned}$$

(B.4)

$$\begin{aligned} {\varvec{K}}^{uv}= & {} \frac{L}{R}\int _0^1 \int _0^{2\pi } \left( \frac{2RA_{12} }{L}\frac{\partial {\bar{\varvec{U}}}}{\partial \xi }\frac{\partial {\bar{\varvec{V}}}^{T}}{\partial \theta }+\frac{2RA_{66} }{L}\frac{\partial {\bar{\varvec{U}}}}{\partial \theta }\frac{\partial {\bar{\varvec{V}}}^{T}}{\partial \xi }\right. \nonumber \\&\left. +\frac{2R^{2}A_{16} }{L^{2}}\frac{\partial {\bar{\varvec{U}}}}{\partial \xi }\frac{\partial {\bar{\varvec{V}}}^{T}}{\partial \xi }+2A_{26} \frac{\partial {\bar{\varvec{U}}}}{\partial \theta }\frac{\partial {\bar{\varvec{V}}}^{T}}{\partial \theta } \right) \, \hbox {d}\theta \hbox {d}\xi \end{aligned}$$

(B.5)

$$\begin{aligned} {\varvec{K}}^{uw}= & {} \frac{L}{R}\int _0^1 {\int _0^{2\pi } {\left( {\left. {\frac{2RA_{12} }{L}\frac{\partial {\bar{\varvec{U}}}}{\partial \xi }{\bar{\varvec{W}}}^{T}+2A_{26} \frac{\partial {\bar{\varvec{U}}}}{\partial \theta }{\bar{\varvec{W}}}^{T}} \right) } \right. } \hbox {d}\theta \hbox {d}\xi } \end{aligned}$$

(B.6)

$$\begin{aligned} {\varvec{K}}^{vv}= & {} \frac{L}{R}\int _0^1 \int _0^{2\pi } \left\{ \left( {A_{22} +\frac{D_{22} }{R^{2}}} \right) \frac{\partial {\bar{\varvec{V}}}}{\partial \theta }\frac{\partial {\bar{\varvec{V}}}^{T}}{\partial \theta }+\left( {\frac{R^{2}A_{66} }{L^{2}}+\frac{RD_{66} }{L^{2}}} \right) \frac{\partial {\bar{\varvec{V}}}}{\partial \xi }\frac{\partial {\bar{\varvec{V}}}^{T}}{\partial \xi }\right. \nonumber \\&\left. +\left( {\frac{2RA_{26} }{L}+\frac{2D_{26} }{LR}} \right) \frac{\partial {\bar{\varvec{V}}}}{\partial \xi }\frac{\partial {\bar{\varvec{V}}}^{T}}{\partial \theta } \right\} \, \hbox {d}\theta \hbox {d}\xi \end{aligned}$$

(B.7)

$$\begin{aligned} {\varvec{K}}^{vw}= & {} \frac{L}{R}\int _0^1 {\int _0^{2\pi } {\left( {\begin{array}{l} 2A_{22} \frac{\partial {\bar{\varvec{V}}}}{\partial \theta }{\bar{\varvec{W}}}^{T}-\frac{2D_{22} }{R^{2}}\frac{\partial {\bar{\varvec{V}}}}{\partial \theta }\frac{\partial ^{2}{\bar{\varvec{W}}}^{T}}{\partial \theta ^{2}}-\frac{4RD_{66} }{L^{2}}\frac{\partial {\bar{\varvec{V}}}}{\partial \xi }\frac{\partial ^{2}{\bar{\varvec{W}}}^{T}}{\partial \xi \partial \theta }-\frac{2D_{12} }{L^{2}}\frac{\partial {\bar{\varvec{V}}}}{\partial \theta }\frac{\partial ^{2}{\bar{\varvec{W}}}^{T}}{\partial \xi ^{2}} \\ +\frac{2RA_{26} }{L}\frac{\partial {\bar{\varvec{V}}}}{\partial \xi }{\bar{\varvec{W}}}^{T}-\frac{2RD_{16} }{L^{3}}\frac{\partial {\bar{\varvec{V}}}}{\partial \xi }\frac{\partial ^{2}{\bar{\varvec{W}}}^{T}}{\partial \xi ^{2}}-\frac{2D_{26} }{RL}\frac{\partial {\bar{\varvec{V}}}}{\partial \xi }\frac{\partial ^{2}{\bar{\varvec{W}}}^{T}}{\partial \theta ^{2}} \\ -\frac{4D_{26} }{RL}\frac{\partial {\bar{\varvec{V}}}}{\partial \theta }\frac{\partial ^{2}{\bar{\varvec{W}}}^{T}}{\partial \xi \partial \theta } \\ \end{array}} \right) } \,} \,\hbox {d}\theta \hbox {d}\xi \end{aligned}$$

(B.8)

$$\begin{aligned} {\varvec{K}}^{ww}= & {} \frac{L}{R}\int _0^1 {\int _0^{2\pi } {\left( {\begin{array}{l} \frac{D_{22} }{R^{2}}\frac{\partial ^{2}{\bar{\varvec{W}}}}{\partial \theta ^{2}}\frac{\partial ^{2}{\bar{\varvec{W}}}^{T}}{\partial \theta ^{2}}+A_{22} {\bar{\varvec{W}}}{\bar{\varvec{W}}}^{T}+\frac{4RD_{66} }{L^{2}}\frac{\partial ^{2}{\bar{\varvec{W}}}}{\partial \xi \partial \theta }\frac{\partial ^{2}{\bar{\varvec{W}}}^{T}}{\partial \xi \partial \theta }+\frac{R^{2}D_{11} }{L^{4}}\frac{\partial ^{2}{\bar{\varvec{W}}}}{\partial \xi ^{2}}\frac{\partial ^{2}{\bar{\varvec{W}}}^{T}}{\partial \xi ^{2}} \\ +\frac{2D_{12} }{L^{2}}\frac{\partial ^{2}{\bar{\varvec{W}}}}{\partial \xi ^{2}}\frac{\partial ^{2}{\bar{\varvec{W}}}^{T}}{\partial \theta ^{2}}+\frac{4RD_{16} }{L^{3}}\frac{\partial ^{2}{\bar{\varvec{W}}}}{\partial \xi ^{2}}\frac{\partial ^{2}{\bar{\varvec{W}}}^{T}}{\partial \xi \partial \theta }+\frac{4D_{26} }{RL}\frac{\partial ^{2}{\bar{\varvec{W}}}}{\partial \xi \partial \theta }\frac{\partial ^{2}{\bar{\varvec{W}}}^{T}}{\partial \theta ^{2}} \\ \end{array}} \right) } } \hbox {d}\theta \hbox {d}\xi \end{aligned}$$

(B.9)

Appendix C. Expressions of the spring stiffness matrix $K_{\mathrm{spr}}$

(a) The spring stiffness matrix ${{\varvec{K}}}_{\mathrm{spr}}$ of the arcs supported boundary condition

$$\begin{aligned} {\varvec{K}}_{\mathrm{spr}}^{uu}= & {} \int _{\theta _1 }^{\theta _2 } {\left( {k_u^0 {\bar{\varvec{U}}}\left( 0 \right) {\bar{\varvec{U}}}^{T}\left( 0 \right) +k_u^1 {\bar{\varvec{U}}}\left( 1 \right) {\bar{\varvec{U}}}^{T}\left( 1 \right) } \right) R} \hbox {d}\theta \end{aligned}$$

(C.10)

$$\begin{aligned} {\varvec{K}}_{\mathrm{spr}}^{vv}= & {} \int _{\theta _1 }^{\theta _2 } {\left( {k_v^0 {\bar{\varvec{V}}}\left( 0 \right) {\bar{\varvec{V}}}^{T}\left( 0 \right) +k_v^1 {\bar{\varvec{V}}}\left( 1 \right) {\bar{\varvec{V}}}^{T}\left( 1 \right) } \right) R} \hbox {d}\theta \end{aligned}$$

(C.11)

$$\begin{aligned} {\varvec{K}}_{\mathrm{spr}}^{ww}= & {} \int _{\theta _1 }^{\theta _2 } {\left( {k_w^0 {\bar{\varvec{W}}}\left( 0 \right) {\bar{\varvec{W}}}^{T}\left( 0 \right) +\frac{k_\theta ^0 }{L^{2}}\frac{\partial {\bar{\varvec{W}}}\left( 0 \right) }{\partial \xi }\frac{\partial {\bar{\varvec{W}}}^{T}\left( 0 \right) }{\partial \xi }} \right. } +k_w^1 {\bar{\varvec{W}}}\left( 1 \right) {\bar{\varvec{W}}}^{T}\left( 1 \right) \left. {+\frac{k_\theta ^1 }{L^{2}}\frac{\partial {\bar{\varvec{W}}}\left( 1 \right) }{\partial \xi }\frac{\partial {\bar{\varvec{W}}}\left( 1 \right) ^{T}}{\partial \xi }} \right) \nonumber \\&R\hbox {d}\theta \end{aligned}$$

(C.12)

(b) The spring stiffness matrix ${{\varvec{K}}}_{\mathrm{spr}}$ of the points supported boundary condition

$$\begin{aligned} {\varvec{K}}_{\mathrm{spr}}^{uu}= & {} \sum _{p=1}^{\mathrm{NA}} {\left( {{k'}_{u,p}^o {\bar{\varvec{U}}}\left( {0,\theta _p } \right) {\bar{\varvec{U}}}^{T}\left( {0,\theta _p } \right) +{k'}_{u,p}^1 {\bar{\varvec{U}}}\left( {0,\theta _p } \right) {\bar{\varvec{U}}}^{T}\left( {0,\theta _p } \right) } \right) } \end{aligned}$$

(C.13)

$$\begin{aligned} {\varvec{K}}_{\mathrm{spr}}^{vv}= & {} \sum _{p=1}^{\mathrm{NA}} {\left( {{k'}_{v,p}^0 {\bar{\varvec{V}}}\left( {0,\theta _p } \right) {\bar{\varvec{V}}}^{T}\left( {0,\theta _p } \right) +{k'}_{v,p}^1 {\bar{\varvec{V}}}\left( {1,\theta _p } \right) {\bar{\varvec{V}}}^{T}\left( {1,\theta _p } \right) } \right) } \end{aligned}$$

(C.14)

$$\begin{aligned} {\varvec{K}}_{\mathrm{spr}}^{ww}= & {} \sum _{p=1}^{\mathrm{NA}} {\left( {\begin{array}{l} {k'}_{w,p}^0 {\bar{\varvec{W}}}\left( {0,\theta _p } \right) {\bar{\varvec{W}}}^{T}\left( {0,\theta _p } \right) \\ +\frac{{k'}_{\theta ,s}^0 }{L^{2}}\frac{\partial {\bar{\varvec{W}}}\left( {0,\theta _p } \right) }{\partial \xi }\frac{\partial {\bar{\varvec{W}}}\left( {0,\theta _p } \right) ^{T}}{\partial \xi }+{k'}_{w,p}^1 {\bar{\varvec{W}}}\left( {1,\theta _p } \right) {\bar{\varvec{W}}}^{T}\left( {1,\theta _p } \right) +\frac{{k'}_{\theta ,p}^1 }{L^{2}}\frac{\partial {\bar{\varvec{W}}}\left( {1,\theta _p } \right) }{\partial \xi }\frac{\partial {\bar{\varvec{W}}}\left( {1,\theta _p } \right) ^{T}}{\partial \xi } \\ \end{array}} \right) } \qquad \qquad \end{aligned}$$

(C.15)