1 Introduction

In nonlinear sciences, the Kadomtsev–Petviashvili (KP) equation I

$$\begin{aligned} (u_t + 6uu_x + u_{xxx})_x -u_{yy }= 0, \end{aligned}$$
(1.1)

is a completely integrable system that describes the motion of two-dimensional solitary waves. For all integrable soliton equations, there exist soliton solutions, analytic and exponentially localized in certain directions [1]. In contrast to soliton solutions, lump solutions are a class of nonsingular rational solutions which decay to zero in all directions in the space [2,3,4,5,6,7]. There are various discussions on lump solutions to integrable equations such as the KPI Eq. (1.1) [2, 4], the B-type Kadomtsev–Petviashvili (BKP) equation [8, 9] and the Davey-Stewartson (DS) equation [10, 11]. It is known that long wave limits of the N-soliton solutions can generate multi-lump solutions of envelope hole type [2]. In particular, upon taking long wave limits on the two-soliton solutions, the KPI Eq. (1.1) has the following special lump solution [2, 12]:

$$\begin{aligned} u=4\frac{-\left[ x + ay + \left( a^2- b^2\right) t\right] ^2 + b^2\left( y + 2at\right) ^2 + 3/b^2}{\left\{ \left[ x + ay + (a^2 - b^2)t\right] ^2 + b^2(y + 2at)^2 + 3/b^2\right\} ^2 }, \end{aligned}$$
(1.2)

where a and b are real free parameters. Moreover, through symbolic computations with Maple, the KPI Eq. (1.1) possesses a class of lump solutions [4]:

$$\begin{aligned} u= & {} 2(\ln f )_{xx}, f=\Big ( a_1x+a_2y+\frac{a_1a_2^2-a_1a_6^2+2a_2a_5a_6}{a_1^2+a_5^2}t+a_4 \Big )^2\nonumber \\&+\Big (a_5x+a_6y+\frac{2a_1a_2a_6-a_2^2a_5+a_5a_6^2}{a_1^2+a_5^2}t+a_8 \Big )^2+\frac{3\left( a_1^2+a_5^2\right) ^3}{\left( a_1a_6-a_2a_5\right) ^2}, \end{aligned}$$
(1.3)

where the involved parameters \(a_i\)’s are arbitrary but \(a_1a_6- a_2a_5 \ne 0\). This contains the lump solution (1.2) presented earlier [2, 12].

Recently, there has been a growing interesting in lump or lump-type solutions, rationally localized in almost all directions in the space [13, 14]. By applying Maple symbolic computations, Ma et al. developed a direct and efficient way to construct generic one-lump or lump-type waves to nonlinear and linear partial differential equations [4, 15,16,17,18,19]. Aiming at multi-lump solutions, the long wave limit approach [2, 9, 20, 21], the bilinear transformation method [10, 11] and the nonlinear superposition formula [22, 23] articulate particular multi-lump wave solutions. In the above-mentioned methods, Hirota bilinear forms play a crucial role in constructing lump or lump-type solutions.

In this letter, let us consider the generalized Kadomtsev–Petviashvili (gKP) equations in (N + 1)-dimensions [3]:

$$\begin{aligned} (u_t + 6uu_{x_{1}} + u_{x_{1}x_{1}x_{1}})_{x_1}+\sum _{j=2}^{N}a_{jj}u_{x_jx_j}=0, \end{aligned}$$
(1.4)

where \(N\ge 2\) and \(a_{jj}, j\ge 2,\) are arbitrary non-zero real constants. When \(a_{jj} =-\,1, j=2,\ldots , N\), it is called the gKPI equation, and when \(a_{jj} =1, j=2,\ldots , N\), the gKPII equation. Under the dependent variable transformation

$$\begin{aligned} u=2(\ln f)_{x_1x_1}, \end{aligned}$$
(1.5)

a direct computation shows that (1.4) can be expressed as

$$\begin{aligned} \left( D_{x_1}^4+D_{x_1}D_{t}+\sum _{j=2}^{N}a_{jj}D_{x_j}^2\right) f\cdot f=0, \end{aligned}$$
(1.6)

where \(D_{x_1},D_{t}\) and \(D_{x_j}, j=2,\ldots , N\), are Hirota bilinear differential operators [1]. By taking \(N=2\) and \(a_{22} =-\,1\), note that (1.4) reduces to the \((2+1)\)-dimensional KPI Eq. (1.1), which possesses abundant lump solutions. However, in (\(N+ 1)\)-dimensions with \(N \ge 3\), the gKP Eq. (1.4) has no lump solutions generated from quadratic functions under the transformation \(u = 2(\ln f)_{x_1x_1}\) [3].

The main purpose of this study is to construct lump or lump-type solutions by taking a long wave limit of the corresponding soliton solutions to the \((N + 1)\)-dimensional gKP Eq. (1.4). The construction procedure for presenting rational solutions will be improved. The framework of this paper is as follows. In Sect. 2, for the \((2+1)\)-dimensional gKP equation, we will extend the technique of long wave limits to obtain a general class of one-lump solutions from the corresponding two solitons. Besides, multi-lump solutions will also be given by performing a limit procedure on the N-soliton solutions. In Sect. 3, we will formulate lump-type solutions to the above gKP equations in \((N+1)\)-dimensions with \(N \ge 3\). Finally, our conclusions and remarks will be given at the end of the paper.

2 Lump solutions to (1.4) with \(N=2\)

Let us first consider the simplest case: \(N = 2\). This yields the \((2+1)\)-dimensional gKP equation:

$$\begin{aligned} (u_t + 6uu_{x } + u_{x x x })_{x }+a_{22}u_{yy}=0, \end{aligned}$$
(2.1)

where setting \(x_1 = x\), \(x_2 = y\) and \(a_{22}\ne 0\). By the typical transformation \(u = 2(\ln f )_{xx}\), the corresponding Hirota bilinear form reads

$$\begin{aligned} \left( D_{x}^4+D_{x}D_{t}+ a_{22}D_{y}^2\right) f\cdot f=0. \end{aligned}$$
(2.2)

2.1 One-lump solutions

To get general one-lump solutions, now we introduce new variables

$$\begin{aligned} \eta _i=k_i(p_{i1}x+p_{i2}y+\omega _i t+\alpha _i)+\eta _i^{(0)}, \quad i\ge 1, \end{aligned}$$
(2.3)

with the dispersion relation being satisfied:

$$\begin{aligned} \omega _i=-\frac{k_i^2p_{i1}^4+a_{22}p_{i2}^2}{p_{i1}}. \end{aligned}$$
(2.4)

Obviously, the two-soliton solution to the bilinear Eq. (2.2) has the form

$$\begin{aligned} f_2=1+\hbox {e}^{\eta _1}+\hbox {e}^{\eta _2}+\hbox {e}^{\eta _1+\eta _2+A_{12}}, \end{aligned}$$
(2.5)

where

$$\begin{aligned} \hbox {e}^{A_{12}}=\frac{3\left( k_1p_{11}^2p_{21}-k_2p_{11}p_{21}^2 \right) ^2-a_{22}\left( p_{11}p_{22}-p_{12}p_{21}\right) ^2}{3\left( k_1p_{11}^2p_{21}+k_2p_{11}p_{21}^2\right) ^2-a_{22} \left( p_{11}p_{22}-p_{12}p_{21}\right) ^2}. \end{aligned}$$

For the two-soliton (2.5), if we set \(\hbox {e}^{\eta _i^{(0)}}=-\,1\) and \(k_i\rightarrow 0\) for \(i=1,2\) with \(k_1/k_2=O(1), p_{i1}=O(1)\) and \(p_{i2}=O(1)\), then we have

$$\begin{aligned} \hbox {e}^{A_{12}}=1+\frac{12k_1k_2p_{11}^3p_{21}^3}{a_{22} \left( p_{11}p_{22}-p_{12}p_{21}\right) ^2}+O(k^3), \end{aligned}$$
(2.6)

and

$$\begin{aligned} f_2=k_1k_2\left[ \theta _1\theta _2+\frac{12p_{11}^3p_{21}^3}{a_{22} \left( p_{11}p_{22}-p_{12}p_{21}\right) ^2}+O(k)\right] , \end{aligned}$$
(2.7)

with

$$\begin{aligned} \theta _i= p_{i1}x+p_{i2}y-\frac{a_{22}p_{i2}^2}{p_{i1}} t+\alpha _i, \quad i=1,2. \end{aligned}$$
(2.8)

Since u is given by the transformation \(u=2(\ln f_{2})_{xx}\), \(f_2\) is equivalent to \(\theta _1\theta _2+B_{12}\), where

$$\begin{aligned} B_{12}=\frac{12p_{11}^3p_{21}^3}{a_{22}(p_{11}p_{22}-p_{12}p_{21})^2}. \end{aligned}$$
(2.9)

We still denote \(\theta _1\theta _2+B_{12}\) as \(f_2\), then the corresponding rational solution to (2.1) can be written as

$$\begin{aligned} u=2(\ln f_{2} )_{xx},\quad f_{2} = \theta _1\theta _2+B_{12}, \end{aligned}$$
(2.10)

where \(\theta _1, \theta _2\) and \(B_{12}\) are defined by (2.8) and (2.9), respectively. Moreover, the selection of the parameters:

$$\begin{aligned} p_{11}= & {} c_{11}+\mathrm {I} d_{11}, \quad p_{12}=c_{12}+\mathrm {I} d_{12},\quad \alpha _1=l_1+\mathrm {I} m_1, \quad p_{21}=p_{11}^*,\nonumber \\ p_{22}= & {} p_{12}^*, \quad \alpha _2=\alpha _1^*,\quad c_{1j} ,d_{1j}, l_1,m_1 \in \mathbb R, \quad j=1,2, \,\mathrm {I} =\sqrt{-1}, \end{aligned}$$
(2.11)

yields \(\theta _2=\theta _1 ^*\). Here the asterisk denotes the complex conjugate. Substituting (2.11) into (2.9) and (2.10), we have

$$\begin{aligned} f_{2}= & {} \Big [c_{11}x+c_{12}y-\frac{a_{22}(c_{11}c_{12}^2-c_{11}d_{12}^2+2c_{12}d_{11}d_{12})}{c_{11}^2+d_{11}^2}t+l_1\Big ]^2\nonumber \\&+\Big [d_{11}x+d_{12}y-\frac{a_{22}(2c_{11}c_{12}d_{12}-c_{12}^2d_{11}+d_{11}d_{12}^2)}{c_{11}^2+d_{11}^2}t+m_1\Big ]^2\nonumber \\&-\frac{3(c_{11}^2+d_{11}^2)^3}{a_{22}(c_{11} d_{12}-c_{12}d_{11})^2}, \end{aligned}$$
(2.12)

where the involved six real parameters \(c_{11}, c_{12}, d_{11}, d_{12}, l_1, m_1\) are arbitrary but \(c_{11}d_{12}-c_{12}d_{11}\ne 0 \). It is easy to observe that \( f_{2}\) is a class of positive quadratic function solutions to the bilinear gKP Eq. (2.2) if the coefficient \(a_{22}<0\), and thus, a class of one-lump solutions to the \((2+1)\)-dimensional gKP Eq. (2.1) can be obtained through the transformation \(u=2(\ln f_{2})_{xx}\). But Eq. (2.1) has pole singularity in the (x, y)-plane at any time if the coefficient \(a_{22}>0\). Note that this result with \(a_{22}=-\,1\) is the same as the solutions (1.3) presented by Ma [4].

2.2 Multi-lump solutions

Following the preceding literature [2, 24], the \((2+1)\)-dimensional gKP Eq. (2.1) is completely integrable and in particular exists the three-soliton solution. By employing Hirota’s method, the N-soliton solution of (2.1) may be expressed as follows:

$$\begin{aligned} u=2(\ln f)_{xx}, f\equiv f_N=\sum _{\mu =0,1}\hbox {e}^{\sum \limits _{1\le i<j}^{N}\mu _i\mu _jA_{ij}+\sum \limits _{i=1}^{N}\mu _i\eta _i}, \end{aligned}$$
(2.13)

with

$$\begin{aligned} \eta _i= & {} k_i\Big (p_{i1}x+p_{i2}y-\frac{k_i^2p_{i1}^4+a_{22}p_{i2}^2}{p_{i1}} t+\alpha _i\Big )+\eta _i^{(0)},\\ \hbox {e}^{A_{ij}}= & {} \frac{3(k_ip_{i1}^2p_{j1}-k_jp_{i1}p_{j1}^2)^2-a_{22}(p_{i1}p_{j2}-p_{i2}p_{j1})^2}{3(k_ip_{i1}^2p_{j1}+k_jp_{i1}p_{j1}^2)^2-a_{22}(p_{i1}p_{j2}-p_{i2}p_{j1})^2}. \end{aligned}$$

The \(\sum _{\mu =0,1}\) denotes the summation over all possible combinations of \(\mu _1=0,1,\mu _2=0,1, \ldots , \mu _N=0,1\); the \(\sum _{1\le i<j}^{N}\) summation is over all possible combinations of the N elements with the specific condition \(1\le i<j\).

By virtue of the result discussed by Satsuma and Ablowitz [2], a solution of (2.2) given as a long wave limit of the N-soliton solution may be written as

$$\begin{aligned} f_N= & {} \prod \limits _{i=1}^{N}\theta _i+\frac{1}{2}\sum \limits _{1\le i<j}^{N}B_{ij}\prod \limits _{l\ne i,j}^{N}\theta _l+\cdots +\frac{1}{M!2^M}\nonumber \\&\times \sum \limits _{i,j,\ldots ,m,n}^{N}\overbrace{B_{ij}B_{kl}\cdots B_{mn}}^{M}\prod \limits _{q\ne i,j,\ldots ,m,n}^{N}\theta _q+\cdots , \end{aligned}$$
(2.14)

where

$$\begin{aligned} \theta _i= & {} p_{i1}x+p_{i2}y-\frac{a_{22}p_{i2}^2}{p_{i1}} t+\alpha _i,\\ B_{ij}= & {} \frac{12p_{i1}^3p_{j1}^3}{a_{22}(p_{i1}p_{j2}-p_{i2}p_{j1})^2}, \end{aligned}$$

and \(\sum _{i,j,\ldots ,m,n}^{N}\) denotes the summation over all possible combinations of \(i,j,\ldots ,m,n\) which are taken from \(1,2,\ldots ,N\). The first four in (2.14) can be expressed as

$$\begin{aligned} f_1= & {} \theta _1, \end{aligned}$$
(2.15a)
$$\begin{aligned} f_2= & {} \theta _1\theta _2+B_{12}, \end{aligned}$$
(2.15b)
$$\begin{aligned} f_3= & {} \theta _1\theta _2\theta _3+B_{12}\theta _3+B_{31}\theta _2+B_{23}\theta _1,\end{aligned}$$
(2.15c)
$$\begin{aligned} f_4= & {} \theta _1\theta _2\theta _3\theta _4+B_{12}\theta _3\theta _4+B_{13}\theta _2\theta _4+B_{14}\theta _2\theta _3+B_{23}\theta _1\theta _4\nonumber \\&+B_{24}\theta _1\theta _3+B_{34}\theta _1\theta _2+B_{12}B_{34}+B_{13}B_{24}+B_{14}B_{23}. \end{aligned}$$
(2.15d)

Furthermore, choosing \(a_{22}<0\), \(p_{M+i,1}=p_{i,1}^*, p_{M+i,2}=p_{i,2}^*,\) and \(\alpha _{M+i}=\alpha _{i}^*,i=1,2,\ldots ,M\) for \(N=2M\) in (2.14), the solution \(f_{N}\) of (2.2) can be presented in the following determinant form:

$$\begin{aligned} f_{2M}=\left| \begin{array}{cc} C &{}\quad A \\ -A^* &{} \quad C^{*T} \end{array} \right| , \end{aligned}$$
(2.16)

where T means the transpose of a matrix, A and C are \(M\times M\) matrices defined by

$$\begin{aligned} C= & {} \left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \theta _1 &{} \frac{2\sqrt{3p_{11}^3p_{21}^3}\;\mathrm {I}}{\sqrt{|a_{22}|}(p_{11}p_{22}-p_{12}p_{21})}&{} \cdots &{} \frac{2\sqrt{3p_{11}^3p_{M1 }^3}\;\mathrm {I}}{\sqrt{|a_{22}|}(p_{11}p_{M2}-p_{12}p_{M1})}\\ -\frac{2\sqrt{3p_{11}^3p_{21}^3}\;\mathrm {I}}{\sqrt{|a_{22}|}(p_{11}p_{22}-p_{12}p_{21})}&{} \theta _2&{}\cdots &{}\frac{2\sqrt{3p_{21}^3p_{M1 }^3}\;\mathrm {I}}{\sqrt{|a_{22}|}(p_{21}p_{M2}-p_{22}p_{M1})}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ -\frac{2\sqrt{3p_{11}^3p_{M1 }^3}\;\mathrm {I}}{\sqrt{|a_{22}|}(p_{11}p_{M2}-p_{12}p_{M1})}&{} -\frac{2\sqrt{3p_{21}^3p_{M1 }^3}\;\mathrm {I}}{\sqrt{|a_{22}|}(p_{21}p_{M2}-p_{22}p_{M1})} &{}\cdots &{}\theta _M \end{array} \right| , \nonumber \\\end{aligned}$$
(2.17)
$$\begin{aligned} A= & {} \left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \frac{2\sqrt{3p_{11}^3p_{11}^{*3}}\;\mathrm {I}}{{\sqrt{|a_{22}|}(p_{11}p_{12}^*-p_{12}p_{11}^*)}}&{} \frac{2\sqrt{3p_{11}^3p_{21}^{*3}}\;\mathrm {I}}{{\sqrt{|a_{22}|}(p_{11}p_{22}^*-p_{12}p_{21}^*)}}&{}\cdots &{}\frac{2\sqrt{3p_{11}^3p_{M1}^{*3}}\;\mathrm {I}}{{\sqrt{|a_{22}|}(p_{11}p_{M2}^*-p_{12}p_{M1}^*)}}\\ \frac{2\sqrt{3p_{21}^3p_{11}^{*3}}\;\mathrm {I}}{{\sqrt{|a_{22}|}(p_{21}p_{12}^*-p_{22}p_{11}^*)}}&{} \frac{2\sqrt{3p_{21}^3p_{21}^{*3}}\;\mathrm {I}}{{\sqrt{|a_{22}|}(p_{21}p_{22}^*-p_{22}p_{21}^*)}}&{}\cdots &{}\frac{2\sqrt{3p_{21}^3p_{M1}^{*3}}\;\mathrm {I}}{{\sqrt{|a_{22}|}(p_{21}p_{M2}^*-p_{22}p_{M1}^*)}}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ \frac{2\sqrt{3p_{M1}^3p_{11}^{*3}}\;\mathrm {I}}{{\sqrt{|a_{22}|}(p_{M1}p_{12}^*-p_{M2}p_{11}^*)}}&{} \frac{2\sqrt{3p_{M1}^3p_{21}^{*3}}\;\mathrm {I}}{{\sqrt{|a_{22}|}(p_{M1}p_{22}^*-p_{M2}p_{21}^*)}}&{}\cdots &{}\frac{2\sqrt{3p_{M1}^3p_{M1}^{*3}}\;\mathrm {I}}{{\sqrt{|a_{22}|}(p_{M1}p_{M2}^*-p_{M2}p_{M1}^*)}} \end{array} \right| . \end{aligned}$$
(2.18)

Owing to the determinant

$$\begin{aligned} f_{2M}=\left| \begin{array}{c@{\quad }c} C &{}A \\ -A^* &{} C^{*T} \end{array} \right| \end{aligned}$$

with A, C given by (2.17) and (2.18) is always positive, we may obtain a class of nonsingular rational solutions under the transformation \(u=2(\ln f_{2M})_{xx}\), which can describe a multiple collision of M lumps.

In the following, we present a two-lump solution with specific values of the parameters for the \((2+1)\)-dimensional KPI Eq. (1.1). The selection of the parameters:

$$\begin{aligned} M= & {} 2, \quad p_{11}=1+\mathrm {I}, \quad p_{12}=1+2\mathrm {I},\quad p_{21}=3-\mathrm {I},\nonumber \\ p_{22}= & {} 2+\mathrm {I},\quad p_{31}=p_{11}^*, \quad p_{32}=p_{12}^*,\quad p_{41}=p_{21}^*, \quad p_{42}=p_{22}^*,\nonumber \\ \alpha _1= & {} 1+\mathrm {I}, \quad \alpha _2=2+2\mathrm {I},\quad \alpha _3= \alpha _1* ,\quad \alpha _4= \alpha _2*, \end{aligned}$$
(2.19)

leads to

$$\begin{aligned} f_4= & {} 20x^4+25y^4+\frac{125}{4} t^4+240 y t x^2 +220y^2tx+180yt^2x+80xy^3 \nonumber \\&+120x^2y^2+80x^3y+80x^3t+130x^2t^2+100y^3t+150y^{2}t^2+20t^{3}x\nonumber \\&100t^3y+56x^3+90y^3+120t^3+172 x^2 y+160 x^2 t+192 x y^2\nonumber \\&+174 x t^2+290 y^2 t+325 y t^2+364 x y t+68 x^2+482 y^2+1849 t^2\nonumber \\&+164 x y+400 x t+1954 y t-144x+1064t+384y+6544, \end{aligned}$$
(2.20)

and so a special two-lump solution is give by

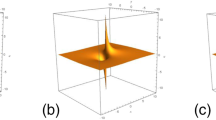
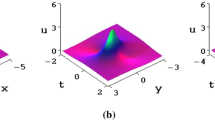
$$\begin{aligned} u=\frac{2f_{4,xx}}{f_4}-\frac{2f_{4,x}^2}{f_4^2}. \end{aligned}$$
(2.21)

Figure 1 depicts the interaction of the two-lump solution (2.21) at several time steps. The contour plots of moving process and curves of two-lump waves are shown in Figs. 2 and 3, respectively. It is seen that the two-lump solution has two distinct peaks and algebraically decays in all space directions.

Fig. 1
figure 1

The propagation of the solution (2.21) at: a\( t = -\,8\), b\( t =0\), c\( t =8\)

Full size image
Fig. 2
figure 2

Contour plots of the solution (2.21) at: a\( t = -\,8\), b\( t =0\), c\( t =8\)

Full size image
Fig. 3
figure 3

Profiles of the solution (2.21) with \(t=0\): ax-curves, by-curves

Full size image

3 Lump-type solutions to (1.4) with \(N\ge 3 \)

As we know, the above gKP equations in \((N+1)\)-dimensions with \(N \ge 3\) have no lump solutions generated from quadratic functions. This result has been proven by Ma and Zhou in [3]. In the following, we would like to present lump-type solutions to the \((N+1)\)-dimensional gKP Eq. (1.4) with \(N \ge 3\) by taking a long wave limit.

We begin with two-wave functions:

$$\begin{aligned} f_2=1+\hbox {e}^{\eta _1}+\hbox {e}^{\eta _2}+\hbox {e}^{\eta _1+\eta _2+A_{12}}, \end{aligned}$$
(3.1)

where

$$\begin{aligned} \eta _i= k_i\left( \sum \limits _{j=1}^{N}p_{ij}x_j+\omega _i t+\alpha _i\right) +\eta _i^{(0)},\quad i=1,2. \end{aligned}$$

Applying the Hirota’s bilinear method leads to

$$\begin{aligned} \omega _i=-\frac{k_i^2p_{i1}^4+\sum \nolimits _{j=2}^{N}a_{jj}p_{ij}^2}{p_{i1}},\quad i=1,2, \end{aligned}$$
(3.2)

and

$$\begin{aligned} \hbox {e}^{A_{12}}=\frac{3\left( k_1p_{11}^2p_{21}-k_2p_{11}p_{21}^2\right) ^2-\sum \nolimits _{j=2}^{N}a_{jj}\left( p_{11}p_{2j}-p_{1j}p_{21}\right) ^2}{3\left( k_1p_{11}^2p_{21}+k_2p_{11}p_{21}^2\right) ^2-\sum \nolimits _{j=2}^{N}a_{jj}\left( p_{11}p_{2j}-p_{1j}p_{21}\right) ^2}. \end{aligned}$$
(3.3)

Using the same limiting procedure presented in Sect. 2, we have

$$\begin{aligned} f_2=\theta _1\theta _2+B_{12}, \end{aligned}$$
(3.4)

where

$$\begin{aligned} \theta _i= & {} \sum \limits _{j=1}^{N}p_{ij}x_j- \frac{\sum \nolimits _{j=2}^{N}a_{jj}p_{ij}^2}{p_{i1}}t+\alpha _{i},\quad i=1,2, \end{aligned}$$
(3.5)
$$\begin{aligned} B_{12}= & {} \frac{12p_{11}^3p_{21}^3}{\sum \nolimits _{j=2}^{N}a_{jj}(p_{11}p_{2j}-p_{1j}p_{21})^2}. \end{aligned}$$
(3.6)

Additionally, taking the choices

$$\begin{aligned} p_{11}= & {} c_{11}+\mathrm {I} d_{11}, \quad p_{1j}=c_{1j}+\mathrm {I} d_{1j}, \quad \alpha _1=l_1+\mathrm {I} m_1,\nonumber \\ p_{21}= & {} p_{11}^*, \quad p_{2j}=p_{1j}^*, \quad \alpha _2=\alpha _1^*,\quad c_{1j} ,d_{1j}, l_1,m_1 \in \mathbb {R},\quad j=1,2,3,\ldots ,N,\qquad \end{aligned}$$
(3.7)

and substituting (3.7) into (3.4), a class of quadratic function solutions to (1.6) is given by

$$\begin{aligned} f_2= & {} \left[ \sum \limits _{j=1}^{N}c_{1j}x_j-\frac{\sum \nolimits _{j=2}^{N}a_{jj}(c_{11}c_{1j}^2+2d_{11}c_{1j}d_{1j}-c_{11}d_{1j}^2)}{c_{11}^2+d_{11}^2}t+l_1\right] ^2\nonumber \\&+\left[ \sum \limits _{j=1}^{N}d_{1j}x_j-\frac{\sum \nolimits _{j=2}^{N}a_{jj}(d_{11}d_{1j}^2+2c_{11}c_{1j}d_{1j}-d_{11}c_{1j}^2)}{c_{11}^2+d_{11}^2}t+m_1\right] ^2\nonumber \\&-\frac{3\left( c_{11}^2+d_{11}^2\right) ^3}{\sum \nolimits _{j=2}^{N}a_{jj}\left( c_{11} d_{1j}-c_{1j}d_{11}\right) ^2}, \end{aligned}$$
(3.8)

where the involved real parameters \(c_{1j}, d_{1j}, l_1, m_1, 1\le j\le N \), are arbitrary but \((c_{11}^2+d_{11}^2)\big [{\sum _{j=2}^{N}a_{jj}(c_{11} d_{1j}-c_{1j}d_{11})^2}\big ]\ne 0 \). Therefore, besides \(c_{11}^2+d_{11}^2\ne 0\), the condition for guaranteeing lump-type solutions is

$$\begin{aligned} \sum _{j=2}^{N}a_{jj}(c_{11} d_{1j}-c_{1j}d_{11})^2<0, \end{aligned}$$
(3.9)

which guarantees that \(f_2\) defined in (3.8) is positive.

It is easy to see that the condition (3.9) holds if we take

$$\begin{aligned} a_{jj}<0,\;\; \sum _{j=2}^{N} (c_{11} d_{1j}- c_{1j}d_{11})^2\ne 0 ,\quad j=2,\ldots , N, \end{aligned}$$
(3.10)

then the class of solutions (3.8) yields a kind of positive quadratic functions to (1.6). In turn, a class of lump-type solutions can be given for the \((N+1)\)-dimensional gKP Eq. (1.4) through the transformation \(u = 2(\ln f)_{x_1x_1}\). This shows that the \((N+1)\)-dimensional gKPI equations \((a_{jj} = -\,1, j=2,\ldots , N)\) with \(N\ge 3\) possess the discussed lump-type solutions whereas the \((N+1)\)-dimensional gKPII equations \((a_{jj} = 1, j=2,\ldots , N)\) with \(N\ge 3\) do not. Note that the condition (3.9) for guaranteeing lump-type solutions reduces to

$$\begin{aligned} \sum _{j=2}^{N_1}(c_{11} d_{1j}-c_{1j}d_{11})^2<\sum _{j=N_{1}+1}^{N} (c_{11} d_{1j}-c_{1j}d_{11})^2, \end{aligned}$$
(3.11)

upon taking

$$\begin{aligned} a_{jj} = 1 , j = 2,\ldots ,N_{1},\quad a_{jj} = -\,1, j = N_{1}+1,\ldots ,N. \end{aligned}$$
(3.12)

It is then shown that there exist positive quadratic function solutions to (1.6) with generic situations.

Below we consider the following \((3+1)\)-dimensional gKP equation:

$$\begin{aligned} (u_t + 6uu_x + u_{xxx})_x +\sigma u_{yy}-u_{zz} = 0, \quad \sigma =\mp 1, \end{aligned}$$
(3.13)

to shed light on lump-type solutions of (1.4). Through the dependent variable transformation \( u = 2(\ln f )_{xx},\) the corresponding \((3+1)\)-dimensional bilinear equation can be written as

$$\begin{aligned} \left( D_{x}^4 +D_{x}D_{t}+\sigma D_{y}^2-D_{z}^2\right) f\cdot f=0, \end{aligned}$$
(3.14)

which is identified as the bilinear KPI equation in \((3+1)\)-dimensions when \(\sigma =-\,1\). By the above result in (3.8), the resulting quadratic function solutions read

$$\begin{aligned} f= & {} \Big [c_{11}x + c_{12}y+c_{13}z-\frac{\sigma \mu _2- \mu _3}{c_{11}^2+d_{11}^2}t+l_1\Big ]^2\nonumber \\&+\Big [d_{11}x + d_{12}y+d_{13}z-\frac{\sigma \nu _2-\nu _3}{c_{11}^2+d_{11}^2}t+m_1\Big ]^2\nonumber \\&-\frac{3(c_{11}^2+d_{11}^2)^3}{\sigma (c_{11} d_{12}-c_{12}d_{11})^2-(c_{11} d_{13}-c_{13}d_{11})^2}, \end{aligned}$$
(3.15)

with

$$\begin{aligned} \mu _j=c_{11}c_{1j}^2+2d_{11}c_{1j}d_{1j} -c_{11}d_{1j}^2,\quad \nu _j=d_{11}d_{1j}^2+2c_{11}c_{1j}d_{1j}-d_{11}c_{1j}^2,\quad j=2,3, \end{aligned}$$

where all involved parameters are arbitrary provided that the expressions make sense. Therefore, for the \((3+1)\)-dimensional KPI equation, the conditions for guaranteeing lump-type solutions are

$$\begin{aligned} c_{11}^2+d_{11}^2\ne 0, (c_{11} d_{12}-c_{12}d_{11})^2+(c_{11} d_{13}-c_{13}d_{11})^2\ne 0, \end{aligned}$$
(3.16)

which guarantee that the quadratic function f defined by (3.15) is positive. If we take \(c_{11}=1\), then the resulting class of lump-type solutions is exactly the one in ref. [3]. In addition, when \(\sigma = 1\), the conditions are

$$\begin{aligned} c_{11}^2+d_{11}^2\ne 0,\quad (c_{11} d_{12}-c_{12}d_{11})^2<(c_{11} d_{13}-c_{13}d_{11})^2, \end{aligned}$$
(3.17)

which guarantee that the quadratic function f defined by (3.15) is positive.

Associated with

$$\begin{aligned} \sigma = 1, \quad c_{11}=1,\quad c_{12}=-\,2,\quad c_{13}=3,l_1=5,\quad d_{11}=0,\quad d_{12}=1,\quad d_{13}=4, m_1=8,\nonumber \\ \end{aligned}$$
(3.18)

the transformation \( u = 2(\ln f )_{xx}\) with (3.15) provides a lump-type solution to the \((3+1)\)-dimensional gKP Eq. (3.14):

$$\begin{aligned} u=\frac{4f-8(x-2y+3z-10t+5)^2}{f^2}, \end{aligned}$$
(3.19)

with

$$\begin{aligned} f=(x-2y+3z-10t+5)^2+(y+4z+28t+8)^2+\frac{1}{5}. \end{aligned}$$

4 Conclusion and remarks

To conclude, by using the long wave limit approach, we have presented lump or lump-type solutions to the generalized KP equations in \((N + 1)\)-dimensions. The construction procedure for presenting lump or lump-type solutions is improved by extending the involved parameters to the complex field. The resulting one-lump solutions are same as the solutions (1.3) generated by Maple symbolic computations for the \((2+1)\)-dimensional KPI equation. Particularly, a general class of nonsingular rational solutions with a determinant form has been given, which can describe a multiple collision of M lumps. And finally, a kind of lump-type solutions to (1.4) with \(N \ge 3\) was deduced by means of the improved limit technique of long waves. The \((3+1)\)-dimensional gKP equation as an application example was given, thereby presenting its particular lump-type solutions.

We remark that the improved long wave limit procedure can also be applied to construct generic lump or lump-type solutions for many other higher-dimensional equations such as the \((2+1)\)-dimensional to equation [25, 26], the \((3+1)\)-dimensional generalized BKP equation [27, 28] and the Jimbo–Miwa equation [29,30,31]. Future research problems for us include how to achieve interaction solutions between lumps and other kinds of exact solutions for nonlinear evolution equations by taking the long wave limit approach, and how to understand integrable characteristics of nonlinear multidimensional systems in mathematical physics [32,33,34,35,36,37].