Multi-Lump Structures in the Kadomtsev–Petviashvili Equation

Abstract

The lumps are specific types of solitary waves completely localised in the two-dimensional space. They represent exact solutions of the Kadomtsev–Petviashvili equation with the positive dispersion. A summary of up-to-date knowledge on lump solutions is presented. It is shown that they can form stationary bound states, and their interaction is very nontrivial.

1 Introduction

The spectrum of interests of Mikhail Rabinovich (MIR) is very broad, he is interested in many subjects and changed his fields of research many times. In his student years he published his own first scientific article “Process automation on the overhead thrust assembly line” in the prestigious Russian journal “Automation in Production”. Then he contributed to the theory of relaxing oscillations, mode competition in nonlinear systems, development of the asymptotic theory of oscillations, chaotic behaviour of simple systems,¹ strange attractors,² theory of turbulence,³ etc. Nowadays his scientific interest is in the development of the theory of cognitive systems and consciousness. One of his former interests was in the pattern formation in complex systems. In particular, he has demonstrated jointly with his colleagues that nontrivial three-dimensional patterns can exist within the framework of Ginzburg–Landau, Swift–Hohenberg and other equations; several interesting examples of single patterns and their couplings were presented in journal papers and reviews [7, 8, 12, 36].

In 2008 MIR visited Australia where he was an invited speaker of the International conference on cognitive systems. One day we undertook a trip to one of the most picturesque places in Australia, Blue Mountains, near Sydney. MIR admired looking at the rocks called “Three Sisters” (see Fig. 19.1) and as a follow-up of our discussion on multi-dimensional patterns said: “Yurah, do you know any exact solution of nonlinear equations which resembles such beautiful patterns like this “Three Sisters” rock?”. I answered: “Yes, such solutions and even more complex ones do exist within the framework of Kadomtsev–Petviashvili equation”. I did not have a computer at that moment to show the pictures and details of relevant solutions and promised to demonstrate them some time later. But the days to follow were very busy for both of us and we did not have time to come back to that issue. Now it is a good time to fulfill my promise. This chapter is devoted to the exact solutions of the Kadomtsev–Petviashvili equation in the form of lumps and their bound states.

Fig. 19.1

M.I. Rabinovich with the author against the background of the “Three Sisters” rock (Blue Mountains, Australia, 14 June 2008)

2 The Kadomtsev–Petviashvili Equation

In 1970 B.B. Kadomtsev and V.I. Petviashvili published a seminal paper [17] in which they derived a two-dimensional generalisation of the Korteweg–de Vries equation now known as the KP equation:

$$\displaystyle{ \frac{\partial } {\partial x}\left (\frac{\partial u} {\partial t} + c\frac{\partial u} {\partial x} +\alpha u\frac{\partial u} {\partial x} +\beta \frac{\partial ^{3}u} {\partial x^{3}}\right ) = -\frac{c} {2} \frac{\partial ^{2}u} {\partial y^{2}}, }$$

(19.1)

where c is the speed of long linear waves, α is the coefficient of nonlinearity, and β is the dispersion coefficient.

In that paper the authors investigated the stability of plane waves propagating along the x-axis and showed that for negative β plane waves with slightly modulated fronts are unstable with respect to self-focusing, whereas in the case of positive β the waves are stable against this phenomenon. That finding was later confirmed by Zakharov [42] who derived an exact formula for the growth rate of instability. Thus, in those and subsequent papers by many authors it was discovered that the properties of solutions of the KP equation essentially depend on the dispersive parameter β, therefore it is reasonable to distinguish two versions of this equation—KP1 equation for negative β and KP2 equation for positive β. Both versions of the KP equation are feasible in the physical context and can describe wave processes in different media.

Some time later Petviashvili discovered [33] numerically that the KP1 equation has solutions in the form of two-dimensional solitons called lumps and suggested an original numerical method for constructing stationary solutions of a certain class of nonlinear equations.⁴ Then an analytical solution was found for the lumps [1, 26] and it was shown that after the interaction with each other their initial parameters completely restore even without a phase shift which usually appears when the plane solitons interact (see, e.g., [2, 16]).

3 Lump Solutions of the Kadomtsev–Petviashvili Equation

Consider stationary solutions of the KP equation (19.1) which describe wave propagation at some angle with respect to the x-axis with velocity V = (V _x , V _y ). Let us represent Eq. (19.1) in dimensionless form bearing in mind that β < 0:

$$\displaystyle\begin{array}{rcl} \frac{\partial ^{2}\upsilon } {\partial X^{2}} + \frac{\partial ^{2}\upsilon } {\partial Y ^{2}} -\nu \frac{\partial ^{2}\upsilon } {\partial X\partial Y } = \frac{\partial ^{2}} {\partial X^{2}}\left (\upsilon ^{2} + \frac{\partial ^{2}\upsilon } {\partial X^{2}}\right ),& &{}\end{array}$$

(19.2)

$$\displaystyle\begin{array}{rcl} \mbox{ where}\quad \upsilon = \frac{\alpha u} {2(V _{x} - c)},\quad \nu = V _{y}\sqrt{ \frac{2} {c(c - V _{x})}},& &{}\end{array}$$

(19.3)

$$\displaystyle\begin{array}{rcl} X = \left [x - V _{x}\,t + \frac{V _{y}} {c} (y - V _{y}\,t)\right ]\sqrt{\frac{V _{x } - c} {\beta }},\quad Y = (y - V _{y}\,t)(c - V _{x})\sqrt{ \frac{2} {-\beta c}}.& &{}\end{array}$$

(19.4)

In the simplest case of a lump propagating along the x-axis (V _y  = 0, ν = 0), it is described by the formula derived for the first time in [26]:

$$\displaystyle{ u(X,Y ) = 12 \frac{3 + Y ^{2} - X^{2}} {\left (3 + Y ^{2} + X^{2}\right )^{2}}. }$$

(19.5)

Lump solutions play a fundamental role in the theory of KP1 equation. They describe nonlinear patterns in plasma [2, 16, 18, 34], on the surface of shallow water with dominating surface tension [4, 9, 18], in nonlinear optic media [32], in the Bose–Einstein condensate [27], in solids with inner microstructure [39], in thin elastic plates [35], etc. Due to the lump stability with respect to external perturbations [21], they can play a role of elementary wave excitations, and their ensembles with the nontrivial internal interaction between them (see below) may be regarded as a model of a strong wave turbulence.

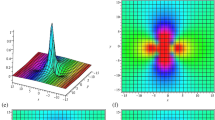
The solution (19.5) in dimensionless variables is shown in Fig. 19.2.

Fig. 19.2

3D profile of conventional KP1 lump as per Eq. (19.5)

For the lump propagating at an angle to the x-axis the generalised formula was actually derived in [26], but it was not analysed there in detail. Later the obliquely propagating lumps were rediscovered independently in [24, 25, 40] and were analysed in [37]. The solution is:

$$\displaystyle{ u(X,Y ) = 12(4 -\nu ^{2}) \frac{12 + (4 -\nu ^{2})\left [(4 -\nu ^{2})Y ^{2}/4 -\left (X +\nu Y/2\right )^{2}\right ]} {\left \{12 + (4 -\nu ^{2})\left [(4 -\nu ^{2})Y ^{2}/4 + \left (X +\nu Y/2\right )^{2}\right ]\right \}^{2}}, }$$

(19.6)

where − 2 < ν < 2. An example of the lump solution for ν = 1. 5 is shown in Fig. 19.3.

Fig. 19.3

3D profile of a skew lump as per Eq. (19.5) with ν = 1. 5

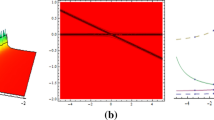
The restriction for the parameter ν (see above) imposes the restriction on possible velocity components in dimensional variables:

$$\displaystyle{ V _{x} = c -\frac{V _{y}^{2}} {2c}. }$$

(19.7)

The domain of possible velocity components of a single lump is shown in Fig. 19.4.

Fig. 19.4

The domain of possible velocity components (shaded) of a single lump as per Eq. (19.7)

Obliquely propagating lumps have asymmetrical skew shapes; their structure depends on the parameter ν. Figure 19.5 shows the contour plots of skew lumps for a few values of ν.

Fig. 19.5

Contour plots of lumps for different values of ν. (a ) ν = 0. 5; (b ) ν = 1. 0; (c ) ν = 1. 5; and (d ) ν = 1. 9. Arrows show maximum values, zero isolines are also indicated

4 Multi-Lump Solutions of the Kadomtsev–Petviashvili Equation

The wave field of a lump is non-monotonic in space, it contains two minima. Because of that two closely located lumps can form a bound state—a stationary moving bi-lump. Such a solution was obtained for the first time numerically [3], and then the analytical formulae were found for the bi-lumps propagating along the x-axis [29] and at the angle to the x-axis [37, 40]. The analytical formula for a bi-lump contains two free parameters, a and b, and can be written in the form:

$$\displaystyle{ \upsilon (X,Y ) = 6\frac{\partial ^{2}f(X,Y )} {\partial X^{2}},\quad \mbox{ where} }$$

(19.8)

$$\displaystyle\begin{array}{rcl} f(X,Y )& =& \left (X^{2} + Y ^{2}\right )^{3} + \frac{100} {4 -\nu ^{2}}X^{4} + 4\frac{17 + 14\nu ^{2} - 3\nu ^{4}} {4 -\nu ^{2}} Y ^{4} + bX^{3} + aY ^{3} +\nu ^{3}X^{3}Y ^{3} \\ & & - \frac{2000} {(4 -\nu ^{2})^{2}}X^{2} + 400 \frac{19 - 6\nu ^{2}} {(4 -\nu ^{2})^{2}}Y ^{2} - \frac{4b} {4 -\nu ^{2}}X - 4 \frac{5a + 8b\nu - 3b\nu ^{3}} {(4 -\nu ^{2})(1 -\nu ^{2})}Y \\ & & - \frac{2000\nu } {(4 -\nu ^{2})^{2}}XY + 60\frac{6 +\nu ^{2}} {4 -\nu ^{2}}X^{2}Y ^{2} + 3\nu XY \bigg[\left (X^{2} + Y ^{2}\right )^{2} +\nu XY \left (X^{2} + Y ^{2}\right ) \\ & & +\frac{40} {3} \frac{5X^{2} + \left (9 -\nu ^{2}\right )Y ^{2}} {4 -\nu ^{2}} -\frac{(a + b\nu )X + (b + a\nu )Y } {\nu (1 -\nu ^{2})} \,\bigg] \\ & & +\frac{ab\nu (3 -\nu ^{2}) + a^{2} + b^{2}} {(1 -\nu ^{2})^{2}(4 -\nu ^{2})} + \frac{120000} {(4 -\nu ^{2})^{3}}. {}\end{array}$$

(19.9)

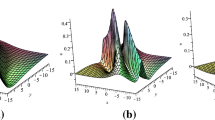
Depending on the parameters a, b and ν, this solution can represent either a bi-lump or even a triple-lump as shown in Figs. 19.6 and 19.7.

Fig. 19.6

Bi-lump solutions as per Eqs. (19.8) and (19.9) with a = b = 0. Panel (a ) ν = 0, panel (b ) ν = 1, panel (c ) ν = 1. 9

Fig. 19.7

Triple-lump solutions as per Eqs. (19.8) and (19.9) with a = 10, b = 0 and ν = 0. 99

In general, when ν approaches ± 2, the solution reduces to a very wide bi-lump of a small amplitude (see Fig. 19.6c), which completely vanishes in the limit | ν | = 2.

As was shown in [29], the KP1 equation possesses a countable number of stationary multi-lump solutions which can be presented in terms of Eq. (19.8), where f(X, Y ) is a polynomial on X and Y of degree p = m(m + 1), where m is an integer. For m = 1 (p = 2) we obtain a single lump solution; for m = 2 (p = 6)—bi-lump solutions (19.9); for m = 3 (p = 12)—triple-lump solutions; etc. The formulae become more and more complex when the degree of polynomial increases (the general problem of rational nonsingular solutions of the KP1 equation was considered in [20]). For simplicity we present only the next polynomial of degree 12 which describes a symmetrical triple-lump solution with ν = 0:

$$\displaystyle\begin{array}{rcl} f(X,Y )& =& \left (X^{2} + Y ^{2}\right )^{6} + 2\left (X^{2} + Y ^{2}\right )^{3}\left (49X^{4} + 198X^{2}Y ^{2} + 29Y ^{4}\right ) + 5\left (147X^{8}\right. \\ & & +\left.3724X^{6}Y ^{2} + 7490X^{4}Y ^{4} + 7084X^{2}Y ^{6} + 867Y ^{8}\right ) + \frac{140} {3} \left (539X^{6}\right. \\ & & +\left.4725X^{4}Y ^{2} - 315X^{2}Y ^{4} + 5707Y ^{6}\right ) + \frac{1225} {9} \left (391314X^{2}\right. \\ & & -\left.12705X^{4} + 4158X^{2}Y ^{2} + 40143Y ^{4} + 736890Y ^{2} + 717409\right ). {}\end{array}$$

(19.10)

The 3D plot of this exact analytical solution shown in Fig. 19.8 resembles the “Three Sisters” rock in Fig. 19.1.

Fig. 19.8

Triple-lump solution as per Eqs. (19.8) and (19.10) —“Three Sisters”

The stationary multi-lump structures can be interpreted within the theory of solitons as classical particles [13, 28]. According to that theory, solitons (and lumps, as the particular case) can be thought of as point particles with anisotropic masses $\hat{M}$ and described by the Newton equation:

$$\displaystyle{ \hat{M}\frac{d^{2}\mathbf{r}} {dt^{2}} = -\nabla U(\mathbf{r}),\quad \mbox{ where}\quad \hat{M} = \left (\begin{array}{cc} 1& 0\\ 0 & -1\\ \end{array} \right ), }$$

(19.11)

where r = X i + Y j.

The effective potential U(r) is determined by external fields. In particular, when two lumps interact, the potential for one lump is determined by the field of the other lump:

$$\displaystyle{ U(\mathbf{r}) = \frac{1} {24\pi }\int \!\!\!\int \upsilon ^{2}(\mathbf{r}^{{\prime}})\upsilon (\mathbf{r}^{{\prime}} + \mathbf{r})\,d\mathbf{r}^{{\prime}}, }$$

(19.12)

where υ is determined by Eq. (19.5), and integrals are taken over the entire X, Y -plane. The typical cross-sections of a lump are shown in Fig. 19.9.

Fig. 19.9

The longitudinal (line 1) and transverse (line 2) cross-sections of a lump as per Eq. (19.5)

The local extrema of solitons give rise to bound states which can be stable or unstable with respect to small perturbations. The theory provides good qualitative and even quantitative agreement with the exact solutions, which allows us to interpret formal mathematical results in physical terms. Non-stationary dynamics of lumps is briefly outlined in the next section.

5 Normal and Anomalous Lump Scattering

Lump interactions were briefly studied in the papers [1, 26] (see also [2]) where lump solutions were constructed for the first time. Investigation of the multisoliton formulae describing the scattering of lumps obtained in those papers reveals a striking property of such formation. Lumps not only retain their shapes and initial parameters (amplitudes, velocities, sizes) on collisions, but even their phase shifts also turn out to be equal to zero. This does not mean, however, that the interaction of lumps is as trivial as the interaction of linear pulses in non-dispersive media. Detailed studies [15] have shown that the interaction even between two lumps by no means reduces to the superposition of their fields, and can lead to unexpected effects which are characterised by an infinite rather than zero phase shift.

In the particular case when two lumps of different amplitudes move one after another along the x-axis (the larger one initially moving behind the smaller one), their interaction looks as follows. The smaller lump splits into two which move at some angle to the x-axis absorbing energy from the larger lump. The latter one decreases and eventually vanishes, transferring its energy into the two newly created lumps. These new lumps separate first at a certain distance, but then draw together and line up again along the x-axis such that the larger lump becomes leading and the smaller one following behind it. Eventually the lumps completely restore their shapes and all other parameters. This is normal scattering. Figure 19.10 illustrates the variations of relative distances, Δ X and Δ Y, between the lump maxima. The solid lines pertain to the exact analytical solution, and the dashed lines to the asymptotic theory of lumps as point classical particles described by Eq. (19.11).

Fig. 19.10

Relative distances between lump maxima as per exact solution (solid lines) and within the framework of the asymptotic theory (dashed lines). Panel (a ) shows two lumps with initial relative velocity Δ V = (0. 5, 0) (only the lower part of the figure is shown, whereas the figure is mirror symmetric with respect to the dashed horizontal line); panel (b ) shows two lumps with initial relative velocity Δ V = (0. 5, 0. 1)

When two lumps moving along the x-axis have initially equal amplitudes and speeds, they start attracting each other, because their effective potentials are negative (see line 1 in Fig. 19.9). Then, as in the previous case, the first lump splits into two moving at an angle with respect to the x-axis and absorbing energy from the lump following behind. The latter decreases and eventually vanishes completely transferring its energy into the two newly created lumps. These new lumps of equal amplitudes continue separating and eventually move parallel to each other and the x-axis. Parameters of these new lumps are the same as the parameters of the initial lumps, whereas eventually they move side by side at the infinite distance between them. To a certain extent the phase shift in this case is infinite because the lumps never return to the initial x-axis; therefore, such interaction was called anomalous scattering [15]. On the other hand, the anomalous scattering can be treated as a particular case of normal scattering when the time of returning of the secondary lumps to the x-axis goes to infinity.

A detailed study of normal lump interaction was undertaken in [24, 40]. It was discovered that the process of interaction depends on the lump velocities and amplitudes. Figure 19.11 shows an example of oblique interaction when y-components of lump velocities have opposite signs.

Fig. 19.11

Contour-plots of two lumps in the oblique interaction (case 1). Left (from top to bottom): t = 1,  2,  …,  5; right (from top to bottom): t = 6,  7,  …,  10

According to the exact solution illustrated by Fig. 19.11, two lumps are moving from opposite y-directions to the horizontal x-axis along their original paths without noticing each other until they collide. This is true even when the two lumps have different amplitudes and speeds. However, when they interact they are far from being just a linear superposition of two independent lumps.

Another type of lump interaction occurs when two lumps initially located at the same side of the x-axis travel to the other side of this axis with different velocities so that their trajectories intersect at some point. The numerical results obtained in [24] are shown in Fig. 19.12. One can see that, when the lumps approach each other from the same side and have relatively small difference in their amplitudes, the larger one gradually reduces its amplitude and velocity, while the smaller one increases its amplitude and velocity. At some moment the lumps become of the same size at a certain nonzero minimum distance apart. After that, the lumps interchange their positions experiencing an abrupt phase change. Due to the nonlinear interaction, the front lump becomes taller until it recovers its initial amplitude, while the rear lump decreases and gradually recovers its original state. Before the collision the lumps attract each other and after the collision they repel.

Fig. 19.12

Contour-plot of two lumps in the oblique interaction with relatively small amplitude difference (case 2). Left (from top to bottom): t = 1,  2,  3, and 4; right (from top to bottom): t = 5,  6,  7, and 8

Lump interaction is different when their relative amplitude difference is large enough. Two lumps can merge in this case and then separate and move along their own original paths. Figure 19.13 from [24] illustrates such interaction on the basis of the exact solution. Thus the interaction between two lumps strongly depends on their relative amplitude difference similarly to the KdV solitons. Strongly nonlinear overlapping interactions can occur when this difference becomes larger than a critical value which is not determined thus far. For the KdV equation it is known that the exchange-type interaction occurs when the soliton amplitude ratio A ₁∕A ₂ < 2. 62, and the overlapping-type interaction occurs when the soliton amplitude ratio A ₁∕A ₂ > 3. 0, whereas in the intermediate range, 2. 62 < A ₁∕A ₂ < 3, a more complex interaction occurs [23].

Fig. 19.13

Oblique interaction of two lumps with relatively big amplitude difference (case 2). From top to bottom: t = 1,  3,  5,  7,  9. In the middle frame, at t = 5, one can see overlapping of two lumps

6 Conclusion

In this brief review we presented interesting features of two dimensional nonlinear formations described by the Kadomtsev–Petviashvili equation. This remarkable equation plays a specific role in the physics of nonlinear phenomena. It is completely integrable and possesses a reach class of solutions fully localised in space. Moreover, this equation is not just a mathematical toy, it is applicable to description of real physical phenomena in different media, as mentioned in the Introduction. It is worth noting that similar and even more complex multi-lump formations can exist not only within the framework of the integrable KP equation, but within many other model equations (see, e.g., [4–6, 9, 14, 38, 41]).

The goal of this review was to attract the attention of young researchers to the physics of multidimensional patterns and to remind mature researchers about many unsolved problems in this area. Among such unsolved problems one can mention the stability of multidimensional formations, their possible role in the description of strong turbulence where lumps can represent elementary nonlinear excitations and form a gas of quasi-particles. As has been shown in [30] (see also [16] and the references therein), a chain of KP lumps can be formed in the course of instability of plane waves but the chain of lumps, in its turn, is unstable with respect to small modulations and can produce other chains of lumps, which are also unstable with respect to small modulations and so on. Therefore one can expect eventual stochastisation of lumps and formation of a random ensemble of nonlinear interacting quasi-particles. Such phenomena were in the range of MIR’s former interests (see, e.g., [7, 8, 12, 36]). I hope that someone of his numerous former or current students will advert to this intriguing problem.

In the conclusion I am wishing MIR many years of fruitful and productive work, as well as inexhaustible cheerfulness and health, which was always his distinctive feature, as one can see in Fig. 19.14.

Fig. 19.14

The “Three Brothers rock”: M.I. Rabinovich (centre) with Anatoly Fabrikant (left) and the author (right). The photo from the Workshop on Plasma Turbulence, Sochi, Russia, May, 1986