1 Introduction

The scattering of deuterons by complex nuclei is of particular interest from the point of view of studying the structure and interaction of the simplest composite nucleus with other nuclei. The peculiarity of deuteron scattering from nuclei is determined by the features of its bound state. Since the deuteron spin is equal to unity, the corresponding spin matrices are three-row, so their complete set can be represented by five independent components [1]. Hence it follows that dA-scattering will be characterized by a variety of polarization observables. The next feature of the deuteron is the non-sphericity of its spatial shape, which manifests itself in the presence of a D-state to its wave function. Finally, the deuteron is a weakly bound system that is reflected in the long tail of its density distribution, and this feature clearly manifests itself, for example, in direct nuclear reactions involving deuterons  [2, 3]. Since polarization effects are mainly peripheral, the asymptotic behavior of the deuteron wave function also becomes crucial for correct calculations.

The modern approach to describing collisions of light ions with atomic nuclei reflects the intention to create a unified theory that includes both a realistic model of target nuclei and the microscopic optical potential of nucleus-nucleus interaction [4]. For this purpose, the folding model is most often used (see, e.g., [5,6,7]), as well as its various variants developed within the framework of the Glauber-type eikonal approximation ([8,9,10,11] and references therein). In [12], the formula for the eikonal phase was generalized for using of realistic nuclear density distributions, that were expanded in the full Gaussoid basis. Together with the Gaussian expansions of the wave functions under the integral sign in the expression for the reaction amplitude, this made it possible to perform analytical integration and obtain general expressions for reaction observables in the form of multiple sums with elementary functions. This approach is due to the fact that the general formulas for the cross section and polarization in the problems of diffraction dA-scattering are quite inconvenient for direct numerical calculations, therefore, for practical purposes, they are usually modified by introducing additional simplifications and restrictions (e.g., the nucleus is opaque and non-diffuse; the deuteron radius is much smaller than the target one; and so on). Notice that, in diffraction approximation, the reaction density matrix is a five-fold integral only formally, because the profile functions, which the density matrix depends on, are also expressed in terms of multiple integrals. Therefore, generally speaking, we have rather a complicated computational problem. Nevertheless, the final formulas for the cross section and analyzing powers can be reduced to algebraic expressions if the integrands are expanded into a series of the form

$$\begin{aligned} \Psi (x)=\sum _{j=1}^{N}a_{j}|\psi _{j}\rangle = \sum _{j=1}^{N}a_{j}\exp {(-b_{j}x^2)}. \end{aligned}$$
(1)

Since the basis \(|\psi _{j}\rangle \) is complete, any square-integrable function in some region can be expanded in the same region with an arbitrary degree of accuracy. It should be noted that a similar approach is used often enough: in the variational method for obtaining the energy levels of a bound system [13,14,15], for the parametrization of nuclear charge densities in the ground state of nucleus [16, 17], in problems dealing with scattering [18], deuteron stripping [12, 19, 20], and fragmentation of light nuclei [21, 22].

The structure of the paper is as follows. Section 2 is devoted to the description of formalism applied while calculating the dA-scattering observables. In Sect. 3, the results of numerical calculations for the differential cross sections and analyzing powers are discussed and compared with the corresponding experimental data. Section 4 contains conclusions. The most important auxiliary formulas used to simplify the formalism description are given in appendices.

2 Formalism

All of the calculations that follow were made in the center-of-mass system using the system of units \(\hbar =c=1\), the Coulomb interaction was not taken into account. To describe the observables, we will use the formalism of the density matrix. Let us expand the density matrix of the system \(\rho \) in terms of the complete orthogonal set of spin tensors \(T_{IM}\) [1]

$$\begin{aligned} \rho =\frac{1}{3}\sum _{I=0}^{2}\sum _{M=-I}^{I}\langle {T_{IM}^{\dagger }}\rangle T_{IM}, \end{aligned}$$
(2)

where \(T_{IM}\) values are expressed in terms of the components of the deuteron spin operator \(\textbf{S}\) in the Cartesian coordinate system as follows [23]

$$\begin{aligned} T_{00}= & {} 1,\quad T_{10}=\sqrt{\frac{3}{2}}\,S_{z},\quad T_{11}=-\frac{\sqrt{3}}{2}\,(S_{x}+iS_{y}),\nonumber \\ T_{20}= & {} \frac{1}{\sqrt{2}}\,(3S_{z}^{2}-2),\nonumber \\ T_{21}= & {} -\frac{\sqrt{3}}{2}\,[(S_{x}+iS_{y})S_{z}+S_{z}(S_{x}+iS_{y})],\nonumber \\ T_{22}= & {} \frac{\sqrt{3}}{2}\,(S_{x}+iS_{y})^{2},\quad T_{i-j}=(-1)^{j}T_{ij}^{\dagger }. \end{aligned}$$
(3)

The polarization state of the scattered deuteron is completely described by the average values of the spin tensors

$$\begin{aligned} \langle {T_{IM}}\rangle =\frac{\text {Tr}\,(\rho \,T_{IM})}{\text {Tr}\,{\rho }}, \end{aligned}$$
(4)

where \(\rho =F_{d}F_{d}^{\dagger }\) is the density matrix, \(F_{d}\) is the deuteron-nucleus scattering amplitude.

In the Cartesian coordinate system, the z-axis of which coincides with the quantization axis (field direction), the polarization of the incident deuteron beam is described by two non-zero quantities [24]: \(p_{z}\) and \(p_{zz}\). Let \(N_{0}\), \(N_{+}\), \(N_{-}\) are the numbers of deuterons with zero, up, and down spin projections, respectively. Then the beam polarization asymmetry along the direction of the quantization axis is called the vector polarization and is described as

$$\begin{aligned} p_{z}=\frac{N_{+}-N_{-}}{N_{+}+N_{-}+N_{0}}. \end{aligned}$$
(5)

The beam polarization asymmetry in the plane perpendicular to the quantization axis is called the tensor polarization and is defined as follows

$$\begin{aligned} p_{zz}=\frac{N_{+}+N_{-}-2N_{0}}{N_{+}+N_{-}+N_{0}}. \end{aligned}$$
(6)

In a spherical coordinate system, the vector and tensor polarizations are related to the quantities (5), (6) by the formulas

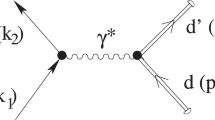
$$\begin{aligned} t_{10}=\sqrt{\frac{3}{2}}\,p_{z},\quad t_{20}=\frac{1}{\sqrt{2}}\,p_{zz}. \end{aligned}$$
(7)

According to the Madison convention [25], measured polarization is defined in the right-handed frame of references with the z-axis in the direction of the incident momentum \(\textbf{k}\) and the y-axis in the direction of \(\textbf{k}\times \textbf{k}'\), where \(\textbf{k}'\) is the momentum of the scattered particles (Fig. 1).

Transition to a new coordinate system whose quantization axis \(\textbf{P}\) is determined by the rotation angles \(\beta \) and \(\phi \), somewhat complicates the expression for the cross section, which will also depend on these angles. Using the polarization components (7), the differential cross section can be written as [24]

$$\begin{aligned}{} & {} \sigma (\theta ,\phi )=\sigma _{0}(\theta )(1+G_{11}+G_{20}+G_{21}+G_{22}),\nonumber \\{} & {} G_{11}=\sqrt{2}\sin {\beta }\cos {\phi }\,\langle {iT_{11}}\rangle \,t_{10},\nonumber \\{} & {} G_{20}=(3\cos {\beta }^{2}-1)/2\,\langle {T_{20}}\rangle \,t_{20},\nonumber \\{} & {} G_{21}=\sqrt{3/2}\sin {2\beta }\cos {\phi }\,\langle {T_{21}}\rangle \,t_{20},\nonumber \\{} & {} G_{22}=-\sqrt{3/2}\sin {\beta }^{2}\cos {2\phi }\,\langle {T_{22}}\rangle \,t_{20}, \end{aligned}$$
(8)

where \(\sigma _{0}(\theta )\) is the scattering cross section for unpolarized particles, and \(\langle {iT_{11}}\rangle \), \(\langle {T_{20}}\rangle \), \(\langle {T_{21}}\rangle \), \(\langle {T_{22}}\rangle \) are quantities (4).

Formulas (8) are general. Usually, the experiment geometry is chosen in such a way that \(\beta =\pi /2\), \(\phi =0\) (see, for example, [26, 27]), then

$$\begin{aligned} \sigma (\theta )=&\sigma _{0}(\theta ) \left[ 1+\sqrt{2}\,\langle {iT_{11}}\rangle \,t_{10} -\frac{1}{2}\,\langle {T_{20}}\rangle \,t_{20}\right. \nonumber \\&\qquad \qquad \left. -\sqrt{\frac{3}{2}}\,\langle {T_{22}}\rangle \,t_{20}\right] . \end{aligned}$$
(9)

Introducing

$$\begin{aligned} A_{y}=\frac{2}{\sqrt{3}}\langle {iT_{11}}\rangle ,\quad A_{yy}=-\frac{1}{\sqrt{2}}\langle {T_{20}}\rangle -\sqrt{3}\langle {T_{22}}\rangle , \end{aligned}$$
(10)

where \(A_{y}=A_{y}(\theta )\), \(A_{yy}=A_{yy}(\theta )\) are the polarizations (the analyzing powers) of outgoing particles, expression (9) can be written as

$$\begin{aligned} \sigma (\theta )=\sigma _{0}(\theta ) \left[ 1+\sqrt{\frac{3}{2}}\,A_{y}(\theta )\,t_{10}+\frac{1}{\sqrt{2}}\,A_{yy}(\theta )\,t_{20}\right] . \end{aligned}$$
(11)

Thus, the scattering cross section depends on the analyzing powers of the reaction and on the polarizations of the incident beam, which are specified by the experimental conditions.

Fig. 1
figure 1

The quantization axis \(\textbf{P}\) and the right-handed coordinate system as defined by the Madison convention [25]

Full size image

In the Glauber approximation, the amplitude of dA-scattering defined as [28]

$$\begin{aligned} F_{d}(\textbf{q})&=\frac{ik}{2\pi }\int d\textbf{b}\exp (i\textbf{qb}) \nonumber \\&\quad \int d{\textbf{r}}\, \varphi _{0}^{\dagger }(\textbf{r}) (\Omega _{1}+\Omega _{2}-\Omega _{1}\Omega _{2}) \varphi _{0}(\textbf{r}), \end{aligned}$$
(12)

where \(\textbf{q}\) is the momentum transfer, \(\textbf{b}\) is the impact parameter of deuteron center of mass, \(\varphi _{0}\) is the wave function of deuteron ground state, \(\Omega _{n}\) are the neutron-nucleus \((n=1)\) and proton-nucleus \((n=2)\) profile functions, which are operators

$$\begin{aligned} {\Omega }_{n}(\textbf{r}_{n}) = \omega _{n}(b_{n})\{1 + \gamma _{n}\exp (i\delta _{n}) {\varvec{\sigma }}_{n}((\textbf{k}/2)\!\times \!\nabla _{n})\}. \end{aligned}$$
(13)

The quantities \(\gamma _{n}\) and \(\delta _{n}\) in (13) are the parameters of the spin-orbit interaction, \({\varvec{\sigma }}_{n}\) are the Pauli matrices, \(\nabla _{n}\equiv \partial /\partial \textbf{r}_{n}\).

As \(\varphi _{0}(\textbf{r})\) in (12), we use the deuteron wave function [1]

$$\begin{aligned} \varphi _{0}(\textbf{r})=\varphi _{\text {S}}(r)+\varphi _{\text {D}}(r) \textbf{S}_{12}(\textbf{r},\textbf{S}), \end{aligned}$$
(14)

where \(\varphi _{\text {S}}\), \(\varphi _{\text {D}}\) are the radial components that describe the S- and D-states of the deuteron, \(\textbf{S}_{12}=6(\textbf{S}\textbf{r})^2/r^2-2{\textbf{S}}^2\) is the nucleon-nucleon spin operator, \(\textbf{S}=({\varvec{\sigma }}_{1}+{\varvec{\sigma }}_{2})/2\) is the deuteron total spin.

The amplitude (12) and the average values of the spin-tensor components (4) can be calculated using the microscopic approach described in [12]. As the radial components of \(\varphi _{0}(\textbf{r})\), we use their tabulated values for Nijmegen potentials [29], which we expand in series of Gaussoid basis functions

$$\begin{aligned} \varphi _{0}(\textbf{r})=\sum _{j=1}^{N}g_{j}\exp (-\lambda _{j}r^2)+ h_{j}r^{2}\exp (-\mu _{j}r^2)\textbf{S}_{12}(\textbf{r},\textbf{S}).\nonumber \\ \end{aligned}$$
(15)

We calculate \(\omega _{n}\) in (13) using the eikonal approximation (see Appendix A) and also expand them in the same way as in (15):

$$\begin{aligned} \omega _{n}(b_{n})=\sum _{j=1}^{N}\alpha _{nj}\exp (-b_{j}^{2}/d_{nj}),\quad d_{nj}=R_{\text {rms}}^{2}/j,\nonumber \\ \end{aligned}$$
(16)

where \(R_{\text {rms}}\) is the root-mean-square radius of the target nucleus.

The integral (12) with the functions (15), (16) is calculated analytically, so that the final result (the cross section \(\sigma _{0}\) and the values of \(\langle {T_{IM}}\rangle \)) can be presented as multiple sums.

Now, substituting (13), (15), (16) into (12), we obtain (see also [1]):

$$\begin{aligned}&\sigma _{0}=\frac{1}{3}\,\text {Tr}(F_{d}F_{d}^{\dagger })= |A|^2+\frac{2}{3}\,|B|^2+\frac{2}{9}\,|C|^2+\frac{2}{3}\,|D|^2, \end{aligned}$$
(17)
$$\begin{aligned}&\langle {T_{10}}\rangle =\frac{1}{3}\,\text {Tr}(F_{d}F_{d}^{\dagger }\,{T_{10}})=0, \end{aligned}$$
(18)
$$\begin{aligned}&\langle {iT_{11}}\rangle =\frac{1}{3}\,\text {Tr}(F_{d}F_{d}^{\dagger }\,{iT_{11}})= \frac{\sqrt{2}}{3\sigma _{0}}\,\text {Re}\Bigl (A-\frac{1}{3}\,C\Bigr )B^{*}, \end{aligned}$$
(19)
$$\begin{aligned}&\langle {T_{20}}\rangle =\frac{1}{3}\,\text {Tr}(F_{d}F_{d}^{\dagger }\,{T_{20}}) \nonumber \\&=\frac{\sqrt{2}}{3\sigma _{0}}\,\Bigl \{\text {Re}\,A(C-3D)^{*}+\text {Re}\,CD^{*}\nonumber \\&-\frac{1}{2}\,|B|^{2}-\frac{1}{6}\,|C|^{2}+\frac{1}{2}\,|D|^{2} \Bigr \},\end{aligned}$$
(20)
$$\begin{aligned}&\langle {T_{21}}\rangle =\frac{1}{3}\,\text {Tr}(F_{d}F_{d}^{\dagger }\,{T_{21}})= \frac{\sqrt{2}}{3\sigma _{0}}\,\text {Im}\,BD^{*},\end{aligned}$$
(21)
$$\begin{aligned}&\langle {T_{22}}\rangle =\frac{1}{3}\,\text {Tr}(F_{d}F_{d}^{\dagger }\,{T_{22}}) \nonumber \\&=\frac{1}{\sqrt{3}\sigma _{0}}\,\left\{ \text {Re}\,A(C+D)^{*}-\frac{1}{3}\,\text {Re}\,CD^{*}\right. \nonumber \\&\left. -\frac{1}{2}\,|B|^{2}+\frac{1}{6}\,|C|^{2}-\frac{1}{2}\,|D|^{2}\right\} . \end{aligned}$$
(22)

The values of A, B, C, and D are the result of integration in (12) and are defined as follows:

$$\begin{aligned} A&=\frac{ik\pi ^{3/2}}{2}\,\Bigl \{A_{1}-4A_{2}+2A_{3}- 64A_{4}+3q^{2}A_{5} \nonumber \\&\quad -384[\gamma _{1}\exp (i\delta _{1})+\gamma _{2}\exp (i\delta _{2})]A_{6}\Bigr \}, \end{aligned}$$
(23)
$$\begin{aligned} B&=\frac{qk^{2}\pi ^{3/2}}{4}\,\Bigl \{B_{1}-B_{2}+\sqrt{2}q^{2}B_{3} \nonumber \\&\quad -2[\gamma _{1}\exp (i\delta _{1})+\gamma _{2}\exp (i\delta _{2})]\bigl ( B_{4}-8B_{5}-\sqrt{8}B_{6}\bigr )\Bigr \}, \end{aligned}$$
(24)
$$\begin{aligned} C&=\frac{3iqk^{2}\pi ^{3/2}}{16}\,\Bigl \{C_{1}-12C_{2} -16\sqrt{2}\bigl (C_{3}-6C_{4}\bigr )\Bigr \}, \end{aligned}$$
(25)
$$\begin{aligned} D&=12ik\pi ^{3/2}\,\Bigl \{D_{1}-\sqrt{8}D_{2} \nonumber \\&\quad +[\gamma _{1}\exp (i\delta _{1})+\gamma _{2}\exp (i\delta _{2})]\bigl ( 6D_{3}+3\sqrt{8}D_{4}\bigr )\Bigr \}. \end{aligned}$$
(26)

Thus, the complete set of observables (17)–(22) is defined by 20 functions in the expressions (23)–(26) (see Appendix B).

3 Calculation results and discussion

The formalism described in the previous section was applied to analyze experimental data obtained for the polarized deuteron scattering from the \(^{16}\text {O}\) and \(^{40}\text {Ca}\) nuclei at projectile energy of 700 MeV in the laboratory frame [27, 30]. Description of the experimental setup is given in [26], according to which the polarizations (7) were defined as

$$\begin{aligned} t_{10}=\frac{1}{\sqrt{6}}\,P_{V},\quad t_{20}=\frac{1}{\sqrt{2}}\,P_{T}, \end{aligned}$$
(27)

where \(P_{V}\), \(P_{T}\) are the degrees of vector and tensor polarization of a polarized deuteron beam, the numerical values of which are given in [27, 30].

The spin-orbit interaction parameters in (13) were approximately determined from the experiments [31,32,33] on measuring the polarization of protons acquired by them upon scattering from \(^{16}\text {O}\) and \(^{40}\text {Ca}\) nuclei. As is known [34], the angular dependence of the nucleon polarization \(P(\theta )\) at intermediate energies is described by the Fermi formula, from which it follows that \(\delta =\text {arcsin}\,P(\theta _{\text {max}})\), where \(\theta _{\text {max}}\) is the scattering angle of maximum polarization; \(\gamma =(kq_{\text {max}})^{-1}\), where k is the nucleon momentum, \(q_{\text {max}}\) is the momentum transfer at \(\theta =\theta _{\text {max}}\). From the data of works [31,32,33], it follows that the parameters \(\delta =\delta _{1,2}\) and \(\gamma =\gamma _{1,2}\) are equal to 0.77 and 0.31\(\text {fm}^{2}\), respectively, for the \(^{16}\text {O}\) target nucleus, and to 0.64 and 0.34\(\text {fm}^{2}\), respectively, for \(^{40}\text {Ca}\).

Figure 2 shows the calculation results of the observables in the reaction of polarized deuteron scattering from \(^{16}\text {O}\) and \(^{40}\text {Ca}\) nuclei at 700 MeV.

Fig. 2
figure 2

Cross sections \(\sigma =\sigma (\theta )\), relative to Rutherford one \(\sigma _{R}=\sigma _{R}(\theta )\), and analyzing powers \(A_{y}(\theta )\), \(A_{yy}(\theta )\) in scattering reaction of polarized deuterons by \(^{16}\text {O}\) (a,c,e) and \(^{40}\text {Ca}\) (b,d,f) nuclei at 700 MeV in the laboratory frame. Experimental data were taken from [27, 30]. See text for details

Full size image

When expanding the wave function \(\varphi _{0}(\textbf{r})\) in series (15), tabulated data [29] for the S- and D-component of deuteron wave function obtained with the help of realistic NN-potentials Nijm I, Nijm II, Nijm 93, and Reid 93 were used. The curves corresponding to these potentials lie inside the dark gray bands (see Fig. 2). The profile functions \(\omega _{n}(b_{n})\) in (13), before a series expansion (16), were first calculated in the eikonal approximation making use of the tabulated nuclear density distributions for the \(^{16}\text {O}\) and \(^{40}\text {Ca}\) nuclei taken from [16]. The number of expansion terms in (15), (16) was \(N=12\).

Analysis of the behavior of the curves presented in Fig. 2 leads to the conclusion that the strong absorption model with one parameter \(N_{W}\) (see Appendix A) is capable of describing cross sections only in the first diffraction maximum (at scattering angles \(\theta <6^{\circ }\)). At that, the polarization data are satisfactorily described for \(\theta <16^{\circ }\). Therefore, to improve the description of experiments, a semi-microscopic approach [5] was used. The real part of the nucleon-nucleus potential was added to the expression for the eikonal phase (A.2) in the form

$$\begin{aligned} V(r)=V_{0}\Bigl [1+\exp \Bigl (\frac{r-R_{V}}{a_{V}}\Bigr )\Bigr ]^{-1}. \end{aligned}$$
(28)

The depth of potential (28) was given by the relation \(V_{0}=\bar{\alpha }_{NN}W_{0}\), where \(\bar{\alpha }_{NN}\) is the nuclear isospin-averaged ratio of the real to the imaginary part of the amplitude for nucleon-nucleon scattering at zero angle. The values of \(\bar{\alpha }_{NN}\) were taken from [35], the numerical values of \((r_{V}; a_{V})\) were equal to (0.98; 0.15) for the \(^{16}\text {O}\) target nucleus, and (1.08; 0.15) for \(^{40}\text {Ca}\). The corresponding results of calculating observables [27, 30] for the eikonal phase with the addition of potential (28) are presented in Fig. 3.

As follows from Fig. 3, for both target nuclei:

  1. (i)

    experimental differential cross sections are satisfactorily described in the first three maxima and minima;

  2. (ii)

    experimental values of \(A_{y}\) are satisfactorily described in the first two maxima;

  3. (iii)

    experimental values of \(A_{yy}\) are described both qualitatively and quantitatively.

Fig. 3
figure 3

The same as in Fig. 2, but for the eikonal phase with the addition of potential (28). Solid black curves are the results of theoretical calculations performed in [27, 36]

Full size image

For comparison, in Fig. 3 shows the results of works by other authors, where experiments [27, 30] were also analyzed (solid black curves). In particular, to describe the scattering of deuterons by \(^{16}\text {O}\) nuclei [27], an optical model with nine parameters was used, and for \(^{40}\text {Ca}\), a relativistic folding model with a phenomenological parametrization of the NN-interaction [36] was used.

From the analysis of the calculation results presented in Fig. 3, it follows that:

  1. (i)

    the optical model [27] provides the best description of the experiment; in our opinion, this is achieved by increasing the number of parameters of the optical model;

  2. (ii)

    the semi-microscopic formalism presented in this paper and Dirac’s microscopic formalism [36] lead to qualitatively identical results; it should be noted that agreement with experiment in [36] improved significantly only when the multiple scattering effects were taking into account.

4 Conclusions

The paper describes spin-dependent observables in the reaction of polarized deuteron scattering by spin-zero target nuclei at intermediate energies. Within the framework of the Glauber model, general analytical expressions are obtained for the reaction cross section and average values of the spin-tensor components.

The calculations used a semi-microscopic approach, in which neither the deuteron wave function nor the nucleon-nucleus profile functions were modeled. This made it possible to minimize the set of fitting parameters and establish, firstly, that:

  1. (i)

    the diffraction model of strong absorption allows to describe the experimental cross sections only in small range of scattering angles \(\theta <{6}^{\circ }\);

  2. (ii)

    introducing the real part of the nucleon-nucleus potential in Woods-Saxon form (28) into the expression for the eikonal phase (A.2) slightly expands the model applicability up to \(\theta <{{{15}^{\circ }}\div {{20}^{\circ }}}\), where the cross sections and tensor analysing powers can be described; on the other hand, the vector analysing powers were described qualitatively, except the region \(\theta <{10}^{\circ }\); agreement with these experiments could be improved by using model profile functions with additional parameters: this is usually done in an optical model, where the spin-orbit part of the potential differs from the central one.

Secondly, the diffraction model itself and the limits of its applicability to the kinematics of the reactions concerned were verified. The validity of the formula (12) is determined by the conditions \(q\ll {k}\) (or \(kR\gg 1\), where R is the radius of the deuteron-nucleus interaction). If we take for R, for example, the root-mean-square radius of the \(^{16}\text {O}\) nucleus, which is equal to 2.711 fm [16], then for deuteron energy of 700 MeV the inequality \(kR\gg 1\) undoubtedly satisfied. The inequality \(q\ll {k}\) gives the estimate \(\theta <\theta _{\text {max}}\simeq {10}^{\circ }\), which is confirmed by calculations for the diffraction model of strong absorption. As follows from the results obtained above, the refraction model extends the applicability domain of (12) up to \(\theta _{\text {max}}\simeq {20}^{\circ }\).