Reaction Mechanisms in Deuteron-Proton Elastic Scattering at Intermediate Energies

Abstract

Deuteron-proton elastic scattering is considered in the relativistic multiple scattering expansion framework. The four reaction mechanisms are included into consideration: one-nucleon exchange, single scattering, double scattering, and the term corresponding to the delta excitation in the intermediate state. The theoretical results are compared with the experimental data.

1 Introduction

Elastic deuteron-proton scattering is the simplest example of the hadron nucleus collision. Nowadays, a significant amount of the experimental data has been accumulated in a wide energy range both with unpolarised and polarised beams. However, we do not have any theory to describe the data for the energies above a few hundred MeV, especially, at backward scattering angles.

A good theoretical description of the deuteron-nucleon process was obtained at low energies, where the multiple scattering formalism based on the solution of the Faddeev equations, has been applied to this problem [1]. However, at the nucleon energies above 130 MeV there is some discrepancy between the experimental data and theoretical predictions in the minimum of the differential cross section [2].

The Glauber theory taking into account both single and double nucleon-nucleon interaction successfully describes the differential cross sections of the dp-elastic scattering at small angles [3, 4]. But it does not properly work at larger scattering angles.

We have previously proposed to use a model based on the multiple expansion of the reaction amplitude in powers of the nucleon-nucleon t-matrix [5,6,7]. We consider a multiple-scattering series up to the second-order terms of the NN t-matrix. Also $\varDelta$-isobar excitation in the intermediate state is included into consideration.

2 General Formalism

According to the three-body collision theory, the amplitude of the deuteron-proton elastic scattering $\mathcal J$ is defined by the matrix element of the transition operator $U_{11}$:

$$\begin{aligned} U_{dp\rightarrow dp}= & {} \delta (E_d+E_p-E^\prime _d-E^\prime _p) \mathcal{J}= \nonumber \\&<1(23)|[1-P_{12}-P_{13}]U_{11}|1(23)>. \end{aligned}$$

(72.1)

Here, the state $|1(23)>$ corresponds to the configuration, when nucleons 2 and 3 form the deuteron state and nucleon 1 is free. The permutation operators for two nucleons $P_{ij}$ reflects the fact that the initial and final states are antisymmetric due to the two particles exchange.

The transition operators for rearrangement scattering are defined by the Alt–Grassberger–Sandhas equations:

$$\begin{aligned} U_{11}= & {} ~~~~~~~~t_2g_0U_{21}+t_3g_0U_{31}, \nonumber \\ U_{21}= & {} g_0^{-1}+t_1g_0U_{11}+t_3g_0U_{31}, \\ U_{31}= & {} g_0^{-1}+t_1g_0U_{11}+t_2g_0U_{21}, \nonumber \end{aligned}$$

(72.2)

where $t_1=t(2,3)$, etc., is the t-matrix of the two-nucleon interaction and $g_0$ is the free three-particle propagator. The indices ij for the transition operators $U_{ij}$ denote free particles i and j in the final and initial states, respectively.

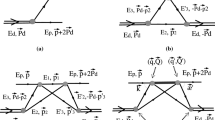
Iterating these equations up to the $t_i$-second-order terms, we can present the reaction amplitude as a sum of the four contributions:

$$\begin{aligned} \mathcal{J}_{dp\rightarrow dp}= & {} \mathcal{J}_\mathrm{ONE}+\mathcal{J}_\mathrm{SS}+\mathcal{J}_\mathrm{DS}+\mathcal{J}_{\varDelta }, \end{aligned}$$

(72.3)

one-nucleon exchange, single scattering, double scattering, and rescattering with $\varDelta$ -excitation in the intermediate state.

Fig. 72.1

The data are taken from [8] ($\bullet$), and [10] ($\blacktriangle$)

The differential cross section at the deuteron kinetic energy of 880 MeV as a function of the c.m. scattering angle.

3 Discussion and Conclusion

The results of the calculations for the differential cross sections at deuteron energies of 880 and 1200 MeV are presented in Figs. 72.1 and 72.2. Three different theoretical curves in the figures correspond to calculations taking into account only one-nucleon-exchange (ONE) and single-scattering (SS) terms (green), ONE+SS and double-scattering (DS) terms (blue), and ONE+SS+DS and $\varDelta$- isobar excitation in an intermediate state (red). All these curves practically coincide up to the scattering angles of about 60$^\circ$. It shows that the main contribution in this angular range gives SS term. We can get a good description of the differential cross sections at $\varTheta ^*\le 60^{\circ }$ taking into account only ONE+SS mechanisms. But at larger angles difference between the experimental data and ONE+SS-curve is significant and increases with the energy. Adding DS-term lets improve the agreement between the data and theory in the angular range about 60$^\circ$–140$^\circ$. Inclusion of $\varDelta$- isobar term helps to describe a rise of the differential cross sections at backward angles.

The model gives rather good agreement between the experimental data and theoretical predictions at energies where Faddeev calculations do not work. However, the data in some angular ranges cannot be properly described in the framework without further improvement of the model. The expansion of knowledge about nucleon- nucleon interactions is very important for it, especially for higher energies. The approach deals with reaction amplitudes what gives the opportunity to get both differential cross sections and polarisation observables.

Fig. 72.2

The data are taken from [9] ($\bullet$), and [10] ($\circ$)

The differential cross section at the deuteron kinetic energy of 1200 MeV as a function of the c.m. scattering angle.