1 Introduction

Elastic lepton scattering on nuclei provides a very powerful tool to investigate the internal structure of hadrons and obtain valuable information about the structure of nucleons and nuclei. This reaction provides useful information on the spin and the electromagnetic structures of the neutron and proton. Therefore, the investigation of spin observables in elastic scattering of leptons on nucleons and nuclei is one of the interesting topics in nuclear physics. This topic is still motivating and fascinating for researchers and deserves more investigations.

The study of light nuclei is one of the important points of interest in hadronic physics during the past decades [1,2,3,4]. For instance, the determination of the radii of light nuclei in elastic muon scattering on light nuclei is one of the main goals of the muon-proton scattering experiment (MUSE) [5,6,7,8,9,10,11]. Of particular interest is the experimental study on a few-nucleon scattering system, which is an attractive probe. This system plays a substantial role since the wave function of the few-nucleon system can be calculated without approximation by adapting a realistic nucleon–nucleon (NN) potential [12, 13]. In particular, the lepton-deuteron elastic scattering process provides us with abundant information on the internal deuteron structure and hence on the NN potential.

Polarization observables in elastic lepton scattering on light nuclei have been the subject of many theoretical studies [14,15,16,17,18,19]. For instance, the elastic lepton-deuteron scattering with a polarized lepton beam and polarized deuteron target in the one-photon-exchange Born approximation (OPEA) was studied in Ref. [14]. The authors of Ref. [15] have reanalyzed the existing, at that time, experimental data on the charge asymmetry of the lepton in both the elastic and the inelastic scattering of lepton on the nucleon and nuclei. The unpolarized and polarized cross sections for elastic scattering of leptons on the deuteron were performed in Refs. [16, 17]. Numerical estimations for spin correlation coefficients in the zero lepton mass limit were evaluated in Ref. [18] using the Reid-93 NN potential [20]. Numerical estimations for the spin correlation coefficients in elastic lepton-deuteron scattering due to the polarizations of lepton beam and vector deuteron target in the OPEA were given in Ref. [19]. The sensitivity of the obtained results to the realistic NN potential employed for the deuteron wave function was investigated, and a considerable dependence was found at incident beam energies greater than 2 fm\(^{-1}\) and backward scattering angles.

We would like to emphasize that none of the works in Refs. [14,15,16,17,18,19] investigate the sensitivity of tensor target spin asymmetries in elastic scattering of leptons on the deuteron to the choice of the realistic NN potential employed for the deuteron wave function. Indeed, the tensor spin asymmetries were chosen as a good tool for investigating the NN interaction at short distances [21,22,23]. This makes it possible to choose among different models of the NN interaction.

Therefore, we focus our attention in the present work on tensor target asymmetries in elastic lepton-deuteron scattering in the OPEA neglecting the lepton mass. We also discuss the sensitivity of the obtained results for tensor spin asymmetries to the realistic NN potential employed for the deuteron wave function. For this purpose, we consider in the present work the realistic and high-precision Nijmegen-II [20], Argonne v18 [24], CD-Bonn [25], and Bonn-Q [26] NN potentials. These NN potentials are exceedingly used for numerical estimations of electromagnetic processes on the deuteron, give a precise characterization of the NN scattering data and phase shifts, and used to characterize the range of the NN interaction. The standard dipole parameterization for the electromagnetic nucleon form factors from Ref. [27] is used in this work.

This paper is organized as follows: in the next section we briefly describe the formalism for the elastic scattering of leptons on the deuteron in the OPEA with neglecting lepton mass. The unpolarized and polarized differential cross sections as well as the explicit formulas for the tensor spin asymmetries in elastic lepton-deuteron scattering are given in this section. The numerical estimations of the tensor spin asymmetries are presented and discussed in Sect. 3. Last Sect. 4 is devoted to conclusions and outlook.

2 Formalism

Here, we briefly summarize the formalism for elastic scattering of leptons on the deuteron in the OPEA neglecting the lepton mass. This process can be written as

$$\begin{aligned} \ell (k_1) + d(p_1) \rightarrow \ell (k_2) + d(p_2)\,, \quad \ell =e,~\mu ,~\tau , \end{aligned}$$
(1)

where \(k_1\) (\(p_1\)) and \(k_2\) (\(p_2\)) are the four momenta of the lepton (deuteron) in the initial and final states, respectively. The Feynman diagram for this process is shown in Fig. 1. In the present work, we perform our analysis in the laboratory frame. In this frame, the components of the four momenta of the lepton and deuteron in the initial and final states are given as follows

$$\begin{aligned} k_1&=(\varepsilon _1, \vec{k}_1)\,, \qquad k_2=(\varepsilon _2, \vec{k}_2)\,,\\ p_1&=(M_d,0)\,, \qquad p_2=(E_2, \vec{p}_2)\,, \end{aligned}$$
(2)

where \(\varepsilon _1\) (\(\varepsilon _2\)) denotes the incident (scattered) lepton energy, \(E_2\) is the energy of the final deuteron, and \(M_d\) is the deuteron mass. The energy \(\varepsilon _2\) of the lepton in the final state is given in the zero lepton mass approximation by

$$\begin{aligned} \varepsilon _2 = \varepsilon _1 \left( 1+\frac{2\varepsilon _1}{M_d} \sin ^2(\frac{\theta }{2})\right) ^{-1}\,, \end{aligned}$$
(3)

where \(\theta\) is the scattering angle between the initial (\(k_1\)) and final (\(k_2\)) lepton momenta in the laboratory system. The relation between the virtual photon four-momentum squared \(Q^2\) and \(\varepsilon _1\) is given by

$$\begin{aligned} Q^2=-q^2=4\varepsilon _1^2\sin ^2(\frac{\theta }{2}) \left( 1+\frac{2\varepsilon _1}{M_d}\sin ^2(\frac{\theta }{2})\right) ^{-1}\,. \end{aligned}$$
(4)
Fig. 1
figure 1

Feynman diagram for elastic lepton-deuteron scattering in the one-photon-exchange Born approximation

Full size image

Thus, the incident lepton energy \(\varepsilon _1\) is given by

$$\begin{aligned} \varepsilon _1 = \frac{1}{4M_d}\left[ q^2 + \csc ^2(\frac{\theta }{2}) \sqrt{q^4\sin ^4(\frac{\theta }{2}) + 4q^2\sin ^2(\frac{\theta }{2}) M_d^2 }\right] \,. \end{aligned}$$
(5)

In the OPEA, the scattering matrix elements of elastic scattering of leptons on the deuteron are given by

$$\begin{aligned} \mathcal{M}=\frac{e^2}{Q^2}j_{\mu }J_{\mu }, \quad j_{\mu }=\bar{u}(k_2) \gamma _{\mu }u(k_1)\,. \end{aligned}$$
(6)

Following Refs. [16, 17], the general form of the electromagnetic current for the spin-1 deuteron satisfies the Lorentz invariance, current conservation, parity, and time-reversal invariance. It is completely described by three form factors and can be written as

$$\begin{aligned} \begin{aligned} J_{\mu }=&\ (p_1+p_2)_{\mu }\Big [-G_1(Q^2)\,U_1\cdot U_2^*\\&\ + \frac{G_3(Q^2)}{M_d^2} (U_1\cdot q\, U_2^*\cdot q-\frac{q^2}{2}U_1\cdot U_2^*)\Big ] \\&\ + G_2(Q^2)(U_{1\mu }U_2^*\cdot q-U_{2\mu }^*U_1\cdot q)\,, \end{aligned} \end{aligned}$$
(7)

where \(q=k_1-k_2=p_2-p_1\), \(U_{1\mu }\) denotes the polarization four vector for the deuteron in the initial state, and \(U_{2\mu }\) is the polarization four vector for the deuteron in the final state. The functions \(G_1(Q^2)\), \(G_2(Q^2)\), and \(G_3(Q^2)\) denote the deuteron electromagnetic form factors which are connected to the standard deuteron charge monopole \(G_C\), charge quadrupole \(G_Q\), and magnetic dipole \(G_M\) form factors by

$$\begin{aligned} \begin{aligned} G_C&=\frac{2}{3}\tau (G_2-G_3)+ (1+\frac{2}{3}\tau )G_1\,, \\ G_Q&=G_1+G_2+2G_3\,, \\ G_M&=-G_2, \end{aligned} \end{aligned}$$
(8)

with \(\tau =Q^2/(4M_d^2)\).

To calculate the unpolarized cross sections and polarization observables, one needs information about the deuteron form factors. In the present work, we use the parameterization from Refs. [28, 29] which reproduces well the experimental data. In this parameterization, the deuteron form factors \(G_C\), \(G_Q\), and \(G_M\) are given by

$$\begin{aligned} \begin{aligned} G_C&= G_E^S\,C_E\,, \\ G_Q&= G_E^S\,C_Q\,, \\ G_M&= 2G_M^S\,C_S + G_E^S\,C_L\,, \end{aligned} \end{aligned}$$
(9)

where \(G_E^S=G_E^p+G_E^n\) (\(G_M^S=G_M^p+G_M^n\)) gives the charge (magnetic) isoscalar nucleon form factor and \(G_{E,M}^{p,n}\) denotes the electric and magnetic form factors of the proton and the neutron. The nonrelativistic formulas for the structure functions \(C_E\), \(C_Q\), \(C_S\), and \(C_L\), are calculated using the \(^3S_1\)- and \(^3D_1\)-state deuteron wave functions, u(r) and w(r), respectively

$$\begin{aligned} C_E= & {} \int _0^\infty dr ~j_0\Big (\frac{qr}{2}\Big ) \Big [u^2(r) + w^2(r)\Big ]\,, \end{aligned}$$
(10)
$$\begin{aligned} C_Q= & {} \frac{3}{\sqrt{2}\tau }\int _0^\infty dr~ j_2\Big (\frac{qr}{2} \Big ) \Big [u(r) - \frac{w(r)}{\sqrt{8}}\Big ]w(r), \end{aligned}$$
(11)
$$\begin{aligned} \begin{aligned} C_S =&\ \int _0^\infty dr \Big \{\Big [u^2(r) - \frac{1}{2}w^2(r)\Big ] j_0\Big (\frac{qr}{2}\Big ) \\&\ +\frac{1}{2}\Big [\sqrt{2}u(r)w(r)+w^2(r)\Big ]j_2\Big (\frac{qr}{2}\Big )\Big \}, \end{aligned} \end{aligned}$$
(12)
$$\begin{aligned} C_L = \frac{3}{2}\int _0^\infty dr ~w^2(r)\Big [j_0\Big (\frac{qr}{2}\Big ) + j_2 \Big (\frac{qr}{2}\Big )\Big ], \end{aligned}$$
(13)

with \(\int _0^\infty dr \, [u^2(r)+w^2(r)] = 1\) and \(j_0(x)\) (\(j_2(x)\)) denotes the spherical Bessel function or order zero (two). For the calculation of the structure functions \(C_E\), \(C_Q\), \(C_S\), and \(C_L\), we adapt the realistic and high-precision Nijmegen-II [20], Argonne v18 [24], CD-Bonn [25], and Bonn-Q [26] NN potentials for the deuteron wave functions.

At \(Q^2=0\), the standard deuteron form factors are given by

$$\begin{aligned} \begin{aligned} G_C(Q^2=0)&=1\,, \\ G_Q(Q^2=0)&=M_d^2Q_d\,, \\ G_M(Q^2=0)&=(M_d/M_N)\mu _d\,, \end{aligned} \end{aligned}$$
(14)

where \(M_N\) is the nucleon mass and \(\mu _d\) (\(Q_d\)) is the static deuteron magnetic dipole (charge quadrupole) moments.

In the OPEA for the description of lepton-deuteron elastic scattering, the lepton interacts with each nucleon in the deuteron through a virtual photon and the form factors of the active nucleon are considered to be the same as those for a free nucleon. There exist several models for the nucleon structure [27, 30,31,32,33,34,35,36,37,38,39,40,41]. For the proton and neutron form factors \(G_{E,M}^{p,n}\), we use the standard dipole fit (DFF) [27]. It is given by

$$\begin{aligned} G_D = \left( 1+ \frac{Q^2}{\Lambda ^2}\right) ^{-2}\,, \end{aligned}$$
(15)

where \(\Lambda ^2=0.71\) (GeV/c)\(^2\). The electric form factors of the proton (neutron) are given by \(G_E^p=G_D\) (\(G_E^n=0\)), whereas the magnetic form factors of the proton (neutron) are given by the dipole parameterizations \(G_M^p=\mu _p\,G_E^p\) (\(G_M^n=\mu _n\,G_E^p\)), with \(\mu _p\) = 2.7928 and \(\mu _n\) = −1.9130.

The unpolarized differential cross section of elastic lepton-deuteron scattering in the OPEA neglecting the lepton mass is given in the laboratory frame by

$$\begin{aligned} \frac{d\sigma _{0}}{d\Omega }=\left( \frac{d\sigma }{d\Omega }\right) _{Mott}\mathcal{S}\,, \end{aligned}$$
(16)

where

$$\begin{aligned} \mathcal{S} = A(Q^2)+B(Q^2)\tan ^2(\frac{\theta }{2})\,. \end{aligned}$$
(17)

The Mott cross section is given by

$$\begin{aligned} \left( \frac{d\sigma }{d\Omega }\right) _{Mott}=\frac{\alpha ^2 \cos ^2(\frac{\theta }{2})}{4\varepsilon _1^2\sin ^4(\frac{\theta }{2})} \left( 1+2\frac{\varepsilon _1}{M_d}\sin ^2(\frac{\theta }{2}) \right) ^{-1}\,, \end{aligned}$$
(18)

where \(\alpha \simeq 1/137\). The structure functions \(A(Q^2)\) and \(B(Q^2)\) are given by

$$\begin{aligned} \begin{aligned} A(Q^2)&=G_C^2(Q^2)+\frac{8}{9}\tau ^2G_Q^2(Q^2)+\frac{2}{3} \tau G_M^2(Q^2)\,, \\ B(Q^2)&=\frac{4}{3}\tau (1+\tau )G_M^2(Q^2)\,. \end{aligned} \end{aligned}$$
(19)

By neglecting the lepton mass, \(A(Q^2)\) and \(B(Q^2)\) can be determined by measuring the unpolarized differential cross section at various values of \(\theta\) and the same value of \(Q^2\). Thus, one can calculate the magnetic form factor \(G_M(Q^2)\) and the set \(G_C^2(Q^2)+8\tau ^2G_Q^2(Q^2)/9\) of the charge and quadrupole form factors. To separate the charge \(G_C\) and quadrupole \(G_Q\) form factors, the measurement of another observable is required. This observable must be a polarization observable. The determination of polarization observables seeks us to choose a specific system of coordinate. As in Ref. [17], we consider in the present work the laboratory frame in which the z-axis is directed along the initial lepton beam momentum \(\vec{k}_1\). In this frame, the x-axis is chosen in order to form a left-handed coordinate system and the y-axis is directed along the vector \(\vec{k}_1 \times \vec{k}_2\). Thus, the xz plane represents the reaction plane.

The present work focuses on the spin asymmetries which are caused by tensor polarized deuteron target. In this case, the general structure of the spin-dependent tensor \(H_{\mu \nu }\) which describes the tensor-polarized initial deuteron and unpolarized final deuteron can be written in terms of five real structure functions as follows [17]

$$\begin{aligned} \begin{aligned} H_{\mu \nu }=&\ V_1(Q^2)\bar{Q}\tilde{g}_{\mu \nu }+V_2(Q^2)\frac{\bar{Q}}{M^2} \tilde{p}_{1\mu }\tilde{p}_{1\nu }\\&\ +V_3(Q^2)(\tilde{p}_{1\mu }\widetilde{Q}_{\nu }+\tilde{p}_{1\nu }\widetilde{Q}_{\mu }) +V_4(Q^2)\widetilde{Q}_{\mu \nu }\\&\ +iV_5(Q^2)(\tilde{p}_{1\mu }\widetilde{Q}_{\nu }-\tilde{p}_{1\nu }\widetilde{Q}_{\mu })\,, \end{aligned} \end{aligned}$$
(20)

where we introduce the following notations

$$\begin{aligned} \begin{aligned} \bar{Q}&=Q_{\alpha \beta }q_{\alpha }q_{\beta }.\quad \widetilde{Q}_{\mu }=Q_{\mu \nu }q_{\nu }-\frac{q_{\mu }}{q^2}\bar{Q}\,, \\ \widetilde{Q}_{\mu }q_{\mu }&=0\, \quad \widetilde{Q}_{\mu \nu }q_{\nu } = 0\,, \\ \widetilde{Q}_{\mu \nu }&= Q_{\mu \nu }+\frac{q_{\mu }q_{\nu }}{q^4}\bar{Q}-\frac{q_{\nu }q_{\alpha }}{q^2}Q_{\mu \alpha }-\frac{q_{\mu }q_{\alpha }}{q^2}Q_{\nu \alpha }\,. \end{aligned} \end{aligned}$$
(21)

The structure functions \(V_i(Q^2) \ (i=1-5)\), which describe the part of the hadronic tensor due to the tensor polarization of the deuteron target, have the following form in terms of the deuteron form factors

$$\begin{aligned} \begin{aligned} V_1(Q^2)&=-G_M^2\,,\\ V_2(Q^2)&=G_M^2+\frac{4}{1+\tau }(G_C+\frac{\tau }{3}G_Q +\tau G_M)G_Q\,, \\ V_3(Q^2)&=-2\tau [G_M^2+2G_QG_M]\,, \\ V_4(Q^2)&=4M_d^2\tau (1+\tau )G_M^2\,, \\ V_5(Q^2)&=0\,. \end{aligned} \end{aligned}$$
(22)

The fifth structure function \(V_5(Q^2)\) vanishes since the deuteron form factors are real functions for elastic scattering in the kinematical region considered. In the time-like region of momentum transfers, where the form factors are complex functions due to unitarity and analyticity, this structure function is not zero and is determined by the imaginary part of the form factors \(G_Q\) and \(G_M\). It is given in this case by \(V_5(Q^2)=-4\tau \,\mathfrak {I}m\, G_Q\,G_M^*\).

The differential cross section describing the elastic scattering of an unpolarized lepton beam on a tensor polarized deuteron target can be written as [17]

$$\begin{aligned} \begin{aligned} \frac{d\sigma }{d\Omega }=&\frac{d\sigma _{0}}{d\Omega }\Big [1+A^{(0)}_{xx}(Q_{xx}-Q_{yy}) \\&\ +A^{(0)}_{xz}Q_{xz}+A^{(0)}_{zz}Q_{zz}\Big ]\, \end{aligned} \end{aligned}$$
(23)

where \(A^{(0)}_{ij}\) are the tensor spin asymmetries. In the general case, the initial deuteron polarization state is described by the spin-density matrix. The general expression for the deuteron spin-density matrix in the coordinate representation is [42]

$$\begin{aligned} \begin{aligned} \rho _{\alpha \beta }^i=&\ -\frac{1}{3} \left( g_{\alpha \beta }-\frac{p_{1\alpha }p_{1\beta }}{M_d^2} \right) \\&\ +\frac{i}{2M_d}<\alpha \beta sp_1>+Q_{\alpha \beta }, \end{aligned} \end{aligned}$$
(24)

where \(g_{\mu \nu }\) is the symmetric tensor: \(g_{\mu \nu }=(\gamma _\mu \gamma _\nu +\gamma _\nu \gamma _\mu )/2\), \(<\mu \nu ab>=\varepsilon _{\mu \nu \rho \sigma }a^{\rho }b^{\sigma }\), \(s_{\mu }\) is the polarization four vector describing the vector polarization of the deuteron target \((p_1\cdot s=0,~ s^2=-1)\), and \(Q_{\mu \nu }\) is the tensor which describes the quadrupole polarization of the initial deuteron and satisfies the following conditions: \(Q_{\mu \nu }=Q_{\nu \mu }\), \(Q_{\mu \mu }=0\), \(p_{1\mu }Q_{\mu \nu }=0\). In the laboratory system, all time components of the tensor \(Q_{\mu \nu }\) are zero and the tensor polarization of the deuteron target is described by five independent space components

$$\begin{aligned} Q_{ij}=Q_{ji}, \ Q_{ii}=0, \quad i,j=x,y,z\,. \end{aligned}$$
(25)

As in Ref. [17], we considered that the tensor \(Q_{ij}\) is symmetrical and traceless, i.e., \(Q_{xx}+Q_{yy}+Q_{zz}=0\).

Neglecting the lepton mass, \(A^{(0)}_{ij}\) has the following form as functions of the deuteron form factors

$$\begin{aligned} \begin{aligned} A^{(0)}_{xx}=&\ \frac{\tau }{2{\mathcal {S}}}\Bigl \{\left( 1+\frac{\tau M_d^2}{\varepsilon ^2_1}\right) G^2_M\\&\ +\frac{4G_Q}{1+\tau }\Bigl [\tau \left( 1+\frac{M_d}{\varepsilon _1}\right) \left( 1-\tau \frac{M_d}{\varepsilon _1}\right) G_M \\&\ +\left( 1-\frac{\tau M_d^2}{\varepsilon ^2_1}-\frac{2\tau M_d}{\varepsilon _1}\right) \left( G_C+\frac{\tau }{3}G_Q\right) \Bigr ]\Bigr \}, \end{aligned} \end{aligned}$$
(26)
$$\begin{aligned} \begin{aligned} A^{(0)}_{xz}=&\frac{-1}{\mathcal {S}}\frac{\varepsilon _2}{M_d}\frac{\tau \sin \theta }{1+\tau }\Bigr \{ \left( 4+\frac{4M_d}{\varepsilon _1}\right) \left( G_CG_Q+\frac{\tau }{3}G^2_Q\right) \\&\ +(1+\tau )\left( 1+\frac{M_d}{\varepsilon _1}\right) \tan ^2(\frac{\theta }{2})G^2_M\\&\ +2\left( 1-\tau \frac{M_d}{\varepsilon _1}\right) \Bigr [-1-\tau +2\sin ^2(\frac{\theta }{2})\left( 1+\frac{\varepsilon _1}{M_d} \right. \\&\ \left. +\frac{\varepsilon ^2_1}{M_d^2}-\tau \frac{\varepsilon _1}{M_d}\right) \Bigr ] \left( 1+\tan ^2(\frac{\theta }{2})\right) G_MG_Q \Bigr \}\,, \end{aligned} \end{aligned}$$
(27)
$$\begin{aligned} \begin{aligned} A^{(0)}_{zz}=&\ \frac{-\tau }{2{\mathcal {S}}} \left\{ \left[ \frac{6\tau }{1+\tau }\frac{\varepsilon _1+\varepsilon _2}{\varepsilon _1}\left( 1+\frac{M_d}{\varepsilon _1}\right) G_Q-G_M\right] G_M \right. \\&\ \left. + \tan ^2(\frac{\theta }{2})\left[ 1-2\tau -6\tau \frac{M_d}{\varepsilon _1}\left( 1+\frac{M_d}{2\varepsilon _1}\right) \right] \right. \\&\ \times \,\left. \left[ G^2_M+\frac{4}{1+\tau }\cot ^2(\frac{\theta }{2})G_Q\left( G_C+\frac{\tau }{3}G_Q\right) \right] \right\} \,. \end{aligned} \end{aligned}$$
(28)

The terms \(A^{(0)}_{xx}\), \(A^{(0)}_{xz}\), and \(A^{(0)}_{zz}\) are the asymmetries in the OPEA, and they coincide with the corresponding results of Ref. [43].

The relations between the asymmetries \(A^{(0)}_{ij}\) (ij = xx, xz, zz) and the tensor asymmetries \(t_{mn}\) (mn = 20, 21, 22) more often used in the literature are the following [44]

$$\begin{aligned} \begin{aligned} t_{20}=&-\frac{\sqrt{2}}{3} \,A^{(0)}_{zz}\,,\\ t_{21}=&\frac{1}{2\sqrt{3}} \,A^{(0)}_{xz}\,, \\ t_{22}=&-\frac{1}{\sqrt{3}} \,A^{(0)}_{xx}\,. \end{aligned} \end{aligned}$$
(29)

We consider in the present work three tensor spin asymmetries in lepton-deuteron elastic scattering. These are the \(A^{(0)}_{xx}\), \(A^{(0)}_{xz}\), and \(A^{(0)}_{zz}\) asymmetries which are due to an unpolarized lepton beam and a tensor polarized deuteron target. The explicit expressions for these tensor target asymmetries are given in terms of the deuteron form factors in Eqs. (26), (27), and (28).

3 Results and Discussion

Now, we give numerical estimations for the tensor spin asymmetries \(A^{(0)}_{xx}\), \(A^{(0)}_{xz}\), and \(A^{(0)}_{zz}\) in the elastic scattering of leptons on the deuteron ignoring the lepton mass. We present results for these asymmetries as functions of the lepton beam energy \(\epsilon _1\) and the lepton scattering angle \(\theta\) using the standard dipole fit for nucleon form factors [27]. To explore the sensitivity of the obtained results for these spin asymmetries to the deuteron wave function, the realistic Nijmegen-II [20], Argonne v18 [24], CD-Bonn [25], and Bonn-Q [26] NN potentials are considered. We present the results for the tensor spin asymmetries \(A^{(0)}_{xx}\) (see Eq. (22) for its definition), \(A^{(0)}_{xz}\) (see Eq. (23) for its definition), and \(A^{(0)}_{zz}\) (see Eq. (24) for its definition) in the laboratory frame where the z-axis is in the direction of the momentum of incident lepton. As an application, we show the case of muon-deuteron elastic scattering.

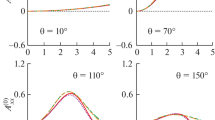
Figure 2 shows the results for \(A^{(0)}_{xx}\) as a function of the muon beam energy \(\epsilon _1\) for muon scattering angles \(\theta\) = 10\(^\circ\), 70\(^\circ\), 110\(^\circ\), and 150\(^\circ\). The solid, dotted, dashed, and dash-double-dotted curves display the results for \(A^{(0)}_{xx}\) using the Argonne v18, CD-Bonn, Nijmegen-II, and Bonn-Q NN potentials, respectively. We see that the results for \(A^{(0)}_{xx}\) vanish at zero muon scattering angle and small values of muon beam energy. When the muon scattering angle and the incident muon energy increase, \(A^{(0)}_{xx}\) becomes sizable. It begins with zero at \(\epsilon _1\) = 0 fm\(^{-1}\) and increases with increasing \(\epsilon _1\) until it reaches a maximum value at \(\epsilon _1\simeq\) 3 fm\(^{-1}\). Then, it decreases with increasing \(\epsilon _1\). The maximum value of \(A^{(0)}_{xx}\) is shifted toward lower muon beam energy with increasing the muon scattering angle. At extremely forward muon scattering angles, the maximum value is not seen and \(A^{(0)}_{xx}\) increases with increasing \(\epsilon _1\).

Fig. 2
figure 2

(Color online) Sensitivity of the tensor spin asymmetry \(A^{(0)}_{xx}\) in elastic muon-deuteron scattering as a function of the muon beam energy \(\epsilon _1\) at various fixed values of the muon scattering angle \(\theta\) to realistic deuteron wave functions using the standard dipole fit for nucleon form factors. The solid, dotted, dashed, and dash-double-dotted curves show the results for \(A^{(0)}_{xx}\) using the realistic and high-precision Argonne v18, CD-Bonn, Nijmegen-II, and Bonn-Q NN potentials, respectively

Full size image

From Fig. 2 it appears also that the sensitivity of the obtained results for \(A^{(0)}_{xx}\) to the NN potential used for the deuteron wave function is obvious at large muon scattering angles, in particular at muon beam energies higher than 3 fm\(^{-1}\). At extreme forward muon scattering angles, it is obvious that the results obtained for \(A^{(0)}_{xx}\) using various realistic NN potentials are indistinguishable (see the top left panel in Fig. 2). Similarly, at muon beam energies smaller than 3 fm\(^{-1}\), one can see that the results for \(A^{(0)}_{xx}\) obtained using various NN potentials are very close to each others. By increasing the muon scattering angle and beam energy, it is obvious that the estimations of \(A^{(0)}_{xx}\) using various NN potentials differ from one another.

In Fig. 3 we display the results for \(A^{(0)}_{xx}\) in a three-dimensional plot as a function of \(\epsilon _1\) and \(\theta\) using the DFF nucleon form factors. The left and right parts in Fig. 3 show the results for \(A^{(0)}_{xx}\)(\(\epsilon _1\), \(\theta\)) using the Argonne v18 and Bonn-Q NN potentials for the deuteron wave function, respectively. We see that the \(A^{(0)}_{xx}\) asymmetry vanishes at \(\theta\) = 0\(^\circ\) and at small muon beam energies. When the muon scattering angle and muon beam energy increase, \(A^{(0)}_{xx}\) exhibits a peak near \(\epsilon _1\) = 3 fm\(^{-1}\). The difference between the left and right parts in Fig. 3, which highlights the sensitivity of the results to the deuteron wave function, can be seen by comparing the solid (Argonne v18) and the dash-double-dotted (Bonn-Q) curves in Fig. 2. It is also clear that the sensitivity of \(A^{(0)}_{xx}\) to the deuteron wave function is very clear at muon scattering angles greater than 30\(^\circ\) and at \(\epsilon _1>\) 3 fm\(^{-1}\).

Fig. 3
figure 3

(Color online) A three-dimensional plot for the tensor spin asymmetry \(A^{(0)}_{xx}\) in elastic muon-deuteron scattering as a function of \(\epsilon _1\) and \(\theta\) using the DFF nucleon form factors. The left and right parts show the results for \(A^{(0)}_{xx}(\epsilon _1,\theta )\) using the Argonne v18 and Bonn-Q NN potentials for the deuteron wave functions, respectively

Full size image

The results for \(A^{(0)}_{xz}\) asymmetry as a function of \(\epsilon _1\) at the same values of \(\theta\) as in the case of \(A^{(0)}_{xx}\) asymmetry are shown in Fig. 4. We see that the \(A^{(0)}_{xz}\) asymmetry also vanishes at \(\theta\) = 0\(^\circ\) and small values of \(\epsilon _1\). By increasing \(\epsilon _1\) and \(\theta\), the asymmetry \(A^{(0)}_{xz}\) becomes sizable and its absolute values are large compared with the ones for \(A^{(0)}_{xx}\) with opposite behavior. It vanishes at \(\epsilon _1\) = 0 fm\(^{-1}\) and decreases with increasing \(\epsilon _1\) until it reaches a minimum value at \(\epsilon _1\simeq\) 3 fm\(^{-1}\). Then, it increases with increasing \(\epsilon _1\) until it reaches a maximum value at \(\epsilon _1\simeq\) 5 fm\(^{-1}\) and backward scattering angles and then decreases again. Figure 4 shows also that the sensitivity of the obtained results for \(A^{(0)}_{xz}\) to the NN potential used for the deuteron wave function is more sizable at backward muon scattering angles and large values of \(\epsilon _1\). As in the case of \(A^{(0)}_{xx}\) asymmetry, one can see at extreme forward muon scattering angles that the results obtained for \(A^{(0)}_{xz}\) using various realistic NN potentials are very close to each others (see the top left panel in Fig. 4). When \(\epsilon _1<\) 2 fm\(^{-1}\), we see that the values for \(A^{(0)}_{xz}\) obtained using various NN potentials are also very close to each others. By increasing \(\epsilon _1\) and \(\theta\), differences between the estimations of \(A^{(0)}_{xz}\) using various NN potentials are obtained.

Fig. 4
figure 4

(Color online) Same as in Fig. 2 but for the tensor spin asymmetry \(A^{(0)}_{xz}\). Results at \(\theta\) = 10\(^\circ\) are multiplied by the factor in the parentheses

Full size image

Figure 5 displays the results for \(A^{(0)}_{xz}\)(\(\epsilon _1\), \(\theta\)) in a three-dimensional plot as a function of \(\epsilon _1\) and \(\theta\) using the Argonne v18 (left part) and Bonn-Q (right part) NN potentials for the deuteron wave function. It is obvious that the \(A^{(0)}_{xz}\) asymmetry exhibits a minimum value near \(\epsilon _1\) = 3 fm\(^{-1}\) at muon scattering angles greater than 30\(^\circ\).

Fig. 5
figure 5

(Color online) Same as in Fig. 3 but for the tensor spin asymmetry \(A^{(0)}_{xz}\)(\(\epsilon _1\),\(\theta\))

Full size image

The results for \(A^{(0)}_{zz}\) as a function of \(\epsilon _1\) at the same values of the muon scattering angle as in the case of \(A^{(0)}_{xx}\) and \(A^{(0)}_{xz}\) asymmetries are displayed in Fig. 6. The \(A^{(0)}_{zz}\) asymmetry exhibits a different behavior compared with \(A^{(0)}_{xx}\) and \(A^{(0)}_{xz}\) asymmetries. It vanishes at zero muon scattering angle and small values of muon beam energy. At forward scattering angles, \(A^{(0)}_{zz}\) begins with zero at \(\epsilon _1\) = 0 fm\(^{-1}\) and decreases with increasing \(\epsilon _1\) until it reaches a minimum value at \(\epsilon _1\simeq\) 5 fm\(^{-1}\). Then, it increases with increasing \(\epsilon _1\). At extreme forward scattering angles, the minimum value is not seen (see the top left panel in Fig. 6). At backward scattering angles, we see that \(A^{(0)}_{zz}\) starts with zero and increases with increasing \(\epsilon _1\) until it reaches a maximum value at \(\epsilon _1\simeq\) 2 fm\(^{-1}\) and then rapidly decreases until it reaches a minimum value at \(\epsilon _1\simeq\) 5 fm\(^{-1}\) and increases again.

Fig. 6
figure 6

(Color online) Same as in Fig. 2 but for the tensor spin asymmetry \(A^{(0)}_{zz}\)

Full size image

With respect to the sensitivity of \(A^{(0)}_{zz}\) asymmetry to the deuteron wave function, we see from Fig. 6 that the results obtained for \(A^{(0)}_{zz}\) using various realistic NN potentials are indistinguishable at extreme forward angles and at \(\epsilon _1<\)2 fm\(^{-1}\). At higher muon beam energy and \(\theta>\)30\(^\circ\), we obtain differences between the estimations of \(A^{(0)}_{zz}\) using various NN potentials. A three-dimensional plot for the results of \(A^{(0)}_{zz}\)(\(\epsilon _1\), \(\theta\)) is displayed in Fig. 7 using the Argonne v18 (left part) and Bonn-Q (right part) NN potentials for the deuteron wave function. It is obvious that the \(A^{(0)}_{zz}\) asymmetry exhibits a minimum value at forward scattering angles and large beam energy, whereas a maximum value near \(\epsilon _1\) = 2 fm\(^{-1}\) is obtained.

Fig. 7
figure 7

(Color online) Same as in Fig. 3 but for the tensor spin asymmetry \(A^{(0)}_{zz}\)(\(\epsilon _1\),\(\theta\))

Full size image

The origin of the differences obtained using various realistic deuteron wave functions may be due to the tensor force between two nucleons. The authors of Refs. [45, 46] were expressed the measure of the tensor force strength in terms of the D-state probability \(P_D\) obtained for the deuteron. The \(P_D\) values for the realistic NN potentials used in the present work are 5.64% for Nijmegen-II, 5.76% for Argonne v18, 4.85% for CD-Bonn, and 4.38% for Bonn-Q. The dependence of the \(\gamma d\rightarrow \pi ^0 d\) and \(ed\rightarrow e'd'\) observables on the D-state component of the deuteron wave function was investigated in Refs. [47] and [48], respectively. It was found that the D-wave contribution becomes visible at backward scattering angles.

We would like to point out that similar characterizations for \(A^{(0)}_{xx}\), \(A^{(0)}_{xz}\), and \(A^{(0)}_{zz}\) are observed in Ref. [17]. The present estimations agree well with the calculations of tensor spin asymmetries in the same kinematical range. From the figures presented in the present work it appears that the sensitivity of the estimated tensor spin asymmetries to realistic deuteron wave function is large at muon scattering angles greater than 30\(^\circ\), in particular at muon beam energies greater than 3 fm\(^{-1}\). Unfortunately, measurements for these tensor spin asymmetries are not available in the literature. Thus, it would be very desirable to have experimental data for polarization observables in lepton-deuteron elastic scattering in the relevant kinematical region.

4 Conclusions and Outlook

We reported theoretical estimations for tensor spin asymmetries in the elastic scattering of leptons on the deuteron ignoring the lepton mass. Numerical results for the spin asymmetries \(A^{(0)}_{xx}\), \(A^{(0)}_{xz}\), and \(A^{(0)}_{zz}\) with unpolarized lepton beam and tensor deuteron target in two- and three-dimensional plots are given. As an application, the elastic scattering of muon on the deuteron in the laboratory system is shown. The sensitivity of the estimated results for tensor spin asymmetries to the realistic deuteron wave function of modern NN potential is studied. In our estimations, we used four realistic NN potentials, which are the Nijmegen-II [20], Argonne v18 [24], CD-Bonn [25], and Bonn-Q [26] potentials. For the proton and neutron form factors, the standard dipole fit [27] is used.

We found that the tensor spin asymmetries \(A^{(0)}_{xx}\), \(A^{(0)}_{xz}\), and \(A^{(0)}_{zz}\) vanish at zero muon scattering angle and small values of muon beam energy. By increasing the scattering angle and the incident energy of the muon, the tensor spin asymmetries become sizable. It is also shown that the results for the spin asymmetries obtained using various realistic deuteron wave functions are comparable at extreme forward muon scattering angles and muon beam energies less than 3 fm\(^{-1}\). When the energy of the muon beam and the scattering angle of the muon increase, theoretical discrepancies among the results for \(A^{(0)}_{xx}\), \(A^{(0)}_{xz}\), and \(A^{(0)}_{zz}\) using various realistic deuteron wave functions are obtained, which may be due to the tensor force between two nucleons.

More theoretical and experimental investigation on spin observables in the elastic scattering of leptons on the deuteron is needed. For instance, numerical estimations of physical observables in the elastic scattering of leptons on the deuteron with and without the lepton mass are useful and promising. This makes it possible to compare between the results for physical observables with and without the lepton mass. For instance, relevant deviations of the results for tensor spin asymmetries are expected when the mass of muons is considered in the theory, in particular in the lower range of muon energy. It has been shown in Ref. [14] that the effect of the muon mass on the incident beam energy is sizable at low beam energies and the relative effect of the muon mass is of about 10% on \(A_{xx}\) and \(A_{xz}\) and can reach 50% on \(A_{zz}\). Therefore, one can expect that the contributions of tensor spin asymmetries should have a large effect at low incident beam energies and backward scattering angles in presence of muon mass. When the muon beam energy is low and the muon mass is large, these contributions become important and the muon mass should be explicitly considered.

This subject is also relevant for the proton–antiproton annihilation experiment PANDA at GSI facility in Darmstadt [49] (see also Ref. [50] for a theoretical overview). On the experimental point of view, measurements for spin observables in lepton-deuteron elastic scattering in the relevant kinematical region are needed.