On the basis of the relationship between the model of large elastoplastic deformations [1, 2], it is proposed in [3] to divide the irreversible deformations acquired by the solid into deformations of creep and plastic flow by the mechanism of their production. Then the equation of variation of irreversible deformations is proved to be common for the deformations of creep and plasticity. The source of irreversible deformations is set in it differently. In the first case, it is the rates of creep strains during the deformation, which precedes the plastic flow or, during unloading in the second case, the rates of plastic deformations under the conditions of matching the stress states of the loading surface. The elastoplastic boundaries prove to be surfaces where the mechanism of accumulation of irreversible deformations changes from viscous (creep) to plastic and vice versa. The laws of creep and plastic flow should be coordinated in such a way that continuous growth of irreversible deformations was implemented on such surfaces, which is achieved by an appropriate choice of the conditions of plasticity and creep laws. In [4, 5] by the example of solving the boundary-value problems in the theory of large deformations, different approaches are indicated for this consistent choice using the generalization of the Tresca−Saint-Venant plasticity conditions for the case of viscous resistance to plastic flow. Here, we show such a match in the Norton creep law [6] and the Mises condition for ideal plasticity [7] by the example of solving the deformation problem under uniform compression of a hollow sphere providing both active loading and unloading including the possibility of repeated plastic flow.

1. We consider the one-dimensional problem of the loading and unloading of a spherical viscoelastoplastic layer bounded by the surfaces \(r = {{r}_{0}}\) and \(r = R\)\(\left( {{{r}_{0}} < R} \right)\) loaded by the pressure on its outer surface:

$$\begin{gathered} {{\sigma }_{{rr}}}\left( R \right) = - p(t),\quad {{\sigma }_{{rr}}}({{r}_{0}}) = 0. \\ \end{gathered} $$
((1))

In relations (1), \(p(t)\) is a set function and \({{\sigma }_{{rr}}}\) is the radial component of the stress tensor in the spherical coordinate system \(r,\theta ,\varphi \). For the components \(u = {{u}_{r}}\) of the displacement vector, the tensors of the small complete \({{d}_{{ij}}}\), reversible \({{e}_{{ij}}}\), irreversible \({{p}_{{ij}}}\) deformations, and the stresses \({{\sigma }_{{ij}}}\), we have

$$\begin{gathered} {{d}_{{rr}}} = {{e}_{{rr}}} + {{p}_{{rr}}} = \frac{{\partial u}}{{\partial r}},\quad {{d}_{{\theta \theta }}} = {{d}_{{\varphi \varphi }}} = {{e}_{{\varphi \varphi }}} + {{p}_{{\varphi \varphi }}} = \frac{u}{r}, \\ {{\sigma }_{{rr}}} = \left( {\lambda + 2\mu } \right){{e}_{{rr}}} + 2\lambda {{e}_{{\varphi \varphi }}}, \\ {{\sigma }_{{\theta \theta }}} = {{\sigma }_{{\varphi \varphi }}} = \lambda {{e}_{{rr}}} + 2\left( {\lambda + \mu } \right){{e}_{{\varphi \varphi }}}. \\ \end{gathered} $$
((2))

The dissipative mechanism of deformation is related to the viscous and plastic properties of the material. The irreversible deformations are accumulated from the onset of the deformation process and can be deformations of both creep and plasticity. In the regions where the stressed state has not yet achieved the yield surface or where the plastic flow proceeded but stopped, we assume the rates \({{\gamma }_{{ij}}}\) of irreversible deformations in the Norton creep power law [6] to be equal to the creep-strain rates \(\varepsilon _{{ij}}^{\nu }\):

$$\begin{array}{*{20}{c}} \begin{gathered} V({{\sigma }_{{ij}}}) = B{{\Sigma }^{n}}\left( {{{\sigma }_{1}},{{\sigma }_{2}},{{\sigma }_{3}}} \right), \\ \Sigma = \sqrt {3{\text{/}}2} {{({{({{\sigma }_{1}} - \sigma )}^{2}} + {{({{\sigma }_{2}} - \sigma )}^{2}} + {{({{\sigma }_{3}} - \sigma )}^{2}})}^{{1/2}}}, \\ \end{gathered} \\ {\sigma = \frac{{{{\sigma }_{{ii}}}}}{3} = \frac{{{{\sigma }_{1}} + {{\sigma }_{2}} + {{\sigma }_{3}}}}{3},\quad {{\gamma }_{{ij}}} = \varepsilon _{{ij}}^{\nu } = \frac{{\partial V}}{{\partial {{\sigma }_{{ij}}}}}.} \end{array}$$
((3))

Here \({{\sigma }_{i}}\) are the principal stress-tensor values and the constants B and n are the creep parameters of the material.

When achieving the stressed state of the yield surface, the dissipative mechanism is changed—plastic flow begins. Such a surface is set by the Mises plasticity condition [7]

$$\begin{gathered} f({{\sigma }_{{ij}}}) = {{s}_{{ij}}}{{s}_{{ji}}} - 8{{k}^{2}}{\text{/}}3,\quad {{s}_{{ij}}} = {{\sigma }_{{ij}}} - \sigma {{\delta }_{{ij}}}. \\ \end{gathered} $$
((4))

Without separating the irreversible deformations, we assume that the creep strains accumulated at the onset of the plastic flow are the initial values for their further growth in the flow region.

2. We consider the deformation of the material before the onset of plastic flow. For potential (3) and the creep-strain rates, we obtain

$$\begin{gathered} \begin{gathered} V({{\sigma }_{{ij}}}){{ = 2}^{{ - n/2}}}B({{({{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}})}^{2}} \\ \, + {{({{\sigma }_{{rr}}} - {{\sigma }_{{\theta \theta }}})}^{2}} + {{({{\sigma }_{{\varphi \varphi }}} - {{\sigma }_{{\theta \theta }}})}^{2}}{{)}^{{n/2}}}, \\ \end{gathered} \\ \varepsilon _{{rr}}^{\nu } = \frac{{\partial {{p}_{{rr}}}}}{{\partial t}} = - 2\varepsilon _{{\varphi \varphi }}^{\nu } = - 2\frac{{\partial {{p}_{{\varphi \varphi }}}}}{{\partial t}} = Bn{{({{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}})}^{{n - 1}}}, \\ \varepsilon _{{rr}}^{\nu } + 2\varepsilon _{{\varphi \varphi }}^{\nu } = 0,\quad {{p}_{{rr}}} + 2{{p}_{{\varphi \varphi }}} = 0. \\ \end{gathered} $$
((5))

Using dependences (2), (5), and the equilibrium equation

$$\begin{gathered} \frac{{\partial {{\sigma }_{{rr}}}}}{{\partial r}} + 2\frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}}}{r} = 0 \\ \end{gathered} ,$$
((6))

we obtain a relation valid within the entire deformation process independently of the type of accumulated irreversible deformation:

$${{p}_{{rr}}} = - \frac{{\lambda + 2\mu }}{{\mu (3\lambda + 2\mu )}}({{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}) - \frac{{2c(t)}}{{{{r}^{3}}(3\lambda + 2\mu )}}.$$
((7))

From equilibrium Eq. (6) with taking into account Eq. (7) and boundary conditions (1), we find the stress \({{\sigma }_{{rr}}}(r,t)\):

$$\begin{gathered} {{\sigma }_{{rr}}} = \frac{{2\mu (3\lambda + 2\mu )}}{{\lambda + 2\mu }}\int\limits_{{{r}_{0}}}^r {\frac{{{{p}_{{rr}}}}}{r}dr} + \frac{{4\mu c(t)}}{{3(\lambda + 2\mu )}}\left( {\frac{1}{{r_{0}^{3}}} - \frac{1}{{{{r}^{3}}}}} \right), \\ c(t)\, = - \frac{{3r_{0}^{3}{{R}^{3}}}}{{2({{R}^{3}} - r_{0}^{3})}}\left( {\frac{{\lambda + 2\mu }}{{2\mu }}p(t)\, + \,(3\lambda + 2\mu )\int\limits_{{{r}_{0}}}^R {\frac{{{{p}_{{rr}}}}}{r}dr} } \right). \\ \end{gathered} $$
((8))

Using Eqs. (5) and (7), we obtain the integro-differential equation for the component \({{p}_{{rr}}}(r,t) = - 2{{p}_{{\varphi \varphi }}}\) of irreversible deformations:

$$\begin{gathered} \frac{{\partial {{p}_{{rr}}}}}{{\partial t}} = Bn{{\left( { - \frac{\mu }{{\lambda + 2\mu }}\left( {\left( {3\lambda + 2\mu } \right){{p}_{{rr}}} + \frac{{2c(t)}}{{{{r}^{3}}}}} \right)} \right)}^{{n - 1}}} \\ \end{gathered} .$$
((9))

The solution of integro-differential Eq. (9) under the initial condition \({{p}_{{rr}}}(r,0) = 0\) was obtained by the method of finite differences. From the known values of stresses (7) and (8) from expressions (2), we obtain the components of elastic strains and the distribution of displacements along the spherical layer.

With a further increase in the function \(p(t)\) at the instant of time \(t = {{t}_{0}}\), plasticity condition (4) in the form \(\begin{gathered} {{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}} = 2k \\ \end{gathered} \) is fulfilled on the inner spherical surface. From this instant of time, the plastic-flow region \({{r}_{0}} \leqslant r \leqslant m(t)\) develops from the surface \(r = {{r}_{0}}\) and the region \(m(t) \leqslant r \leqslant R\) remains the region with the strains of elasticity and creep. The boundary r = \(m(t)\) is a movable boundary of the plastic-flow region.

Taking into account conditions (4) and (1) from the equilibrium equation in the region of plastic flow, we find the stress components

$${{\sigma }_{{rr}}} = - 4k\ln\frac{r}{{{{r}_{0}}}},\quad {{\sigma }_{{\varphi \varphi }}} = - 2k\left( {2\ln\frac{r}{{{{r}_{0}}}} + 1} \right).$$
((10))

The expression for the stress \({{\sigma }_{{rr}}}\) in the region of \(m(t) \leqslant r \leqslant R\) follows from dependences (6), (7), and the first condition on Eq. (1)

$$\begin{gathered} {{\sigma }_{{rr}}} = - \frac{{2\mu (3\lambda + 2\mu )}}{{\lambda + 2\mu }}\int\limits_r^R \frac{{{{p}_{{rr}}}}}{r}dr \\ \, - \frac{{4\mu c(t)}}{{3(\lambda + 2\mu )}}\left( {\frac{1}{{{{r}^{3}}}} - \frac{1}{{{{R}^{3}}}}} \right) - p(t). \\ \end{gathered} $$
((11))

In the region of \(m(t) \leqslant r \leqslant R\), as previously, integro-differential Eq. (9) is fulfilled taking into account the equality of stress components (10) and (11) on the elasto-plastic boundary \(r = m(t)\)

$$\begin{gathered} c(t) = - \frac{{3{{m}^{3}}{{R}^{3}}}}{{2({{R}^{3}} - {{m}^{3}})}} \\ \times \left( {\frac{{\lambda + 2\mu }}{{2\mu }}p(t)\, - \,\frac{{2k(\lambda + 2\mu )}}{\mu }\ln\frac{m}{{{{r}_{0}}}}\, + \,(3\lambda \, + \,2\mu )\int\limits_m^R \frac{{{{p}_{{rr}}}}}{r}dr} \right). \\ \end{gathered} $$
((12))

The relation for \({{p}_{{rr}}}\) in the region of \({{r}_{0}} \leqslant r \leqslant m(t)\) follows from Eq. (7) and plastic-flow condition (4):

$$\begin{gathered} {{p}_{{rr}}} = - \frac{2}{{3\lambda + 2\mu }}\left( {\frac{{c(t)}}{{{{r}^{3}}}} + \frac{{k\left( {\lambda + 2\mu } \right)}}{\mu }} \right). \\ \end{gathered} $$
((13))

Equations (13) in which \(r = m(t)\) and (9) form a set with respect to unknown functions \({{p}_{{rr}}}(r,t)\) in the region of \(m(t) \leqslant r \leqslant R\) and m(t). This set was also solved by the finite-difference method.

3. From the moment of time \(t = {{t}_{1}} > {{t}_{0}}\), the pressure p(t) is assumed constant, the discharge starts in the region of \({{m}_{1}}(t) \leqslant r \leqslant m({{t}_{1}})\), the plastic flow continues in the region \({{r}_{0}} \leqslant r \leqslant {{m}_{1}}(t)\), and the viscoelastic deformation continues as before in the region of \(m({{t}_{1}}) \leqslant r \leqslant R\). The new boundary \(r = {{m}_{1}}(t)\) separates the reduced plastic-flow region from the region in which irreversible deformations now are accumulated due to the creep process. It should be noted that the rate of displacement of the boundary \(r = {{m}_{1}}(t)\) along the medium is close to zero.

In the regions of \(m({{t}_{1}}) \leqslant r \leqslant R\) and \({{m}_{1}}(t)\, \leqslant \,r\, \leqslant \,m({{t}_{1}})\), we have integro-differential Eq. (9) with the function

$$\begin{gathered} c(t) = - \frac{{3m_{1}^{3}{{R}^{3}}}}{{2({{R}^{3}} - m_{1}^{3})}} \\ \times \left( {\frac{{\lambda \, + \,2\mu }}{{2\mu }}p(t)\, - \,\frac{{2k(\lambda \, + \,2\mu )}}{\mu }\ln\frac{{{{m}_{1}}}}{{{{r}_{0}}}}\, + \,(3\lambda \, + \,2\mu )\int\limits_{{{m}_{1}}}^R \frac{{{{p}_{{rr}}}}}{r}dr} \right). \\ \end{gathered} $$
((14))

The component of irreversible deformations prr in the region r0 ≤ r < m1(t) is calculated from relation (13). As before, system of equations (13), where r = m1(t) and (9) with respect to unknown functions m1(t) and prr(r, t) in domains m1(t) ≤ r ≤ m(t1), m(t1) ≤ r ≤ R is solved by the finite-difference method.

From the moment of time \(t = {{t}_{2}} > {{t}_{1}}\), the pressure p(t) is reduced, which leads to unloading the spherical layer. Thus, from the moment of time \(t = {{t}_{2}}\), the plastic flow ceases within the entire layer and the increment of irreversible deformations in the regions \({{r}_{0}} \leqslant r \leqslant {{m}_{1}}({{t}_{2}})\), \({{m}_{1}}({{t}_{2}}) \leqslant r \leqslant m({{t}_{1}})\), and \(m({{t}_{1}}) \leqslant r \leqslant R\) is associated only with the creep process. Equation (9) for irreversible deformations \({{p}_{{rr}}}\) is now fulfilled in the entire spherical layer in which the function c(t) and the stress components are determined from Eqs. (7) and (8).

The stress difference at the inner boundary of the layer \(r = {{r}_{0}}\) decreases, vanishes at the instant of time \(t = {{t}_{3}} > {{t}_{2}}\), and then increases in magnitude remaining negative. The spherical layer is divided into two regions with different signs of the stress difference. Therefore, according to Eq. (5), we have

$$\varepsilon _{{rr}}^{\nu } = \frac{{\partial {{p}_{{rr}}}}}{{\partial t}} = - 2\varepsilon _{{\varphi \varphi }}^{\nu } = Bn{{\left| {{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}} \right|}^{{n - 2}}}({{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}).$$
((15))

With taking into account Eq. (15), Eq. (9) for \({{p}_{{rr}}}\) is rewritten as follows:

$$\begin{gathered} \frac{{\partial {{p}_{{rr}}}}}{{\partial t}} = - \frac{{Bn{{\mu }^{{n - 1}}}}}{{{{{(\lambda + 2\mu )}}^{{n - 1}}}}} \\ \, \times \left( {(3\lambda + 2\mu ){{p}_{{rr}}}\, + \,\frac{{2c(t)}}{{{{r}^{3}}}}} \right){{\left| {(3\lambda + 2\mu ){{p}_{{rr}}}\, + \,\frac{{2c(t)}}{{{{r}^{3}}}}} \right|}^{{n - 2}}}. \\ \end{gathered} $$
((16))

During unloading, the stress state can again achieve the loading surface \(\begin{gathered} {{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}} = - 2k \\ \end{gathered} \) for \(r = {{r}_{0}}\) at the instant of time \(t = {{t}_{4}} > {{t}_{3}}\). With a further decrease in \(p(t)\) from the boundary \(r = {{r}_{0}}\), the region \({{r}_{0}} \leqslant r \leqslant {{m}_{2}}(t)\) of repeated plastic flow is developed. In the regions of \({{m}_{2}}(t) \leqslant r \leqslant {{m}_{1}}({{t}_{2}})\), \({{m}_{1}}({{t}_{2}}) \leqslant r \leqslant m({{t}_{1}})\), and \(m({{t}_{1}}) \leqslant r \leqslant R\), the material is deformed viscoelastically, where \(r = {{m}_{2}}(t)\) is the moving boundary of the region of repeated plastic flow.

Taking into account that, in the whole region of \({{r}_{0}} \leqslant r \leqslant {{m}_{2}}(t)\), the condition \(\begin{gathered} {{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}} = - 2k \\ \end{gathered} \) is satisfied, we find the stress components and the irreversible deformation by integrating the equilibrium equation with the second boundary condition from set (1)

$$\begin{gathered} {{\sigma }_{{rr}}} = 4k\ln\frac{r}{{{{r}_{0}}}},\quad {{\sigma }_{{\varphi \varphi }}} = 2k\left( {2\ln\frac{r}{{{{r}_{0}}}} + 1} \right), \\ \begin{gathered} {{p}_{{rr}}} = - \frac{2}{{3\lambda + 2\mu }}\left( {\frac{{c(t)}}{{{{r}^{3}}}} - \frac{{k\left( {\lambda + 2\mu } \right)}}{\mu }} \right). \\ \end{gathered} \\ \end{gathered} $$
((17))

In the region of \({{m}_{2}}(t) \leqslant r \leqslant {{m}_{1}}({{t}_{2}})\), \({{m}_{1}}({{t}_{2}})\, \leqslant \,r\, \leqslant \,m({{t}_{1}})\), and \(m({{t}_{1}}) \leqslant r \leqslant R\), integro-differential Eq. (16) continues to be fulfilled in which

$$\begin{gathered} c(t) = - \frac{{3m_{2}^{3}{{R}^{3}}}}{{2({{R}^{3}} - m_{2}^{3})}} \\ \times \left( {\frac{{\lambda \, + \,2\mu }}{{2\mu }}p(t)\, + \,\frac{{2k(\lambda \, + \,2\mu )}}{\mu }\ln\frac{{{{m}_{2}}}}{{{{r}_{0}}}}\, + \,(3\lambda \, + \,2\mu )\int\limits_{{{m}_{2}}}^R \frac{{{{p}_{{rr}}}}}{r}dr} \right). \\ \end{gathered} $$
((18))

The set of Eqs. (16) and (17), where \(r = {{m}_{2}}(t)\), is the set with respect to unknown functions \({{m}_{2}}(t)\) and \({{p}_{{rr}}}(r,t)\) in the regions of \({{m}_{2}}(t)\, \leqslant \,r\, \leqslant \,{{m}_{1}}({{t}_{2}}),\)\({{m}_{1}}({{t}_{2}})\, \leqslant \,r\, \leqslant \,m({{t}_{1}})\), and \(m({{t}_{1}}) \leqslant r \leqslant R\). The position of the elastoplastic boundary \(r = {{m}_{2}}(t)\) is unambiguously related to the decreasing external pressure. Under complete unloading (the external pressure \(p(t) = 0\) at \(t = {{t}_{k}}\)) in the relations setting the residual stresses and strains, \(c(t)\) takes the form

$$\begin{gathered} c(t) = - \frac{{3m_{2}^{3}{{R}^{3}}}}{{2({{R}^{3}} - m_{2}^{3})}} \\ \times \left( {\frac{{2k\left( {\lambda + 2\mu } \right)}}{\mu }\ln\frac{{{{m}_{2}}}}{{{{r}_{0}}}} + \left( {3\lambda + 2\mu } \right)\int\limits_{{{m}_{2}}}^R \frac{{{{p}_{{rr}}}}}{r}dr} \right). \\ \end{gathered} $$

From the moment of time \(t = {{t}_{k}}\), the plastic flow ceases and further change in the irreversible deformations is associated with the creep process within the entire layer.

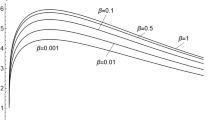
The dependence of the elastoplastic boundaries \(\tilde {m} = {m \mathord{\left/ {\vphantom {m R}} \right. \kern-0em} R}\) on the time \(\tau = \alpha t{\text{/}}\mu \) is shown in Fig. 1. The components of the residual stresses \({{{{\sigma }_{{rr}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{rr}}}} \mu }} \right. \kern-0em} \mu }\) and \({{{{\sigma }_{{\varphi \varphi }}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{\varphi \varphi }}}} \mu }} \right. \kern-0em} \mu }\) during their relaxation after removing the loading forces from \({{\tau }_{k}} = 0.08\) (solid lines) to \(\tau = 100\) (dashed lines) are shown in Fig. 2.

Fig. 1.
figure 1

Modification of elastoplastic boundaries.

Full size image
Fig. 2.
figure 2

Distributions of stress components.

Full size image

During the calculations, the linear function of pressure was used

$$p(t) = \left\{ \begin{gathered} \alpha t,\quad 0 \leqslant t < {{t}_{1}}, \hfill \\ \alpha {{t}_{1}},\quad {{t}_{1}} \leqslant t < {{t}_{2}}, \hfill \\ \alpha {{t}_{1}} - \beta (t - {{t}_{2}}),\quad {{t}_{2}} \leqslant t \leqslant {{t}_{k}} = \alpha {{t}_{1}}{\text{/}}\beta + {{t}_{2}} \hfill \\ \end{gathered} \right.$$

as well as the following values of the constants: n = 3, \(Bn{{\mu }^{3}}{\text{/}}\alpha = 3.5\), \(\lambda {\text{/}}\mu = 3.9\), \({{r}_{0}}{\text{/}}R\) = 0.1, \(k{\text{/}}\mu = 0.0026\), and \({\beta \mathord{\left/ {\vphantom {\beta {\alpha = 0.5}}} \right. \kern-0em} {\alpha = 0.5}}\).

ACKNOWLEDGMENTS

This work was supported in part by the Russian Foundation for Basic Research, project nos. 18-01-00038 and 16-31-60017 mol_a_dk.