1 Introduction

The expansion/contraction of a hollow sphere is one of the classical problems of plasticity. The brief literature review below is restricted to solutions at large strains. The first solution is derived in [1], where an elastic perfectly plastic model has been adopted. Elastic compressibility has been taken into account. This solution has been extended to strain-hardening materials in [2]. No restriction is imposed on the strain hardening law. Another solution for strain hardening materials is proposed in [3]. In contrast to [2], the model is rigid/plastic, and the material is incompressible. Using the solution found at the micro-level, the authors of [3] have calculated theoretical pressure–relative density curves in the process of compaction of metal powders. The solution provided in [4] is for power-law creep. The elastic portion of strain is neglected. Therefore, the material is incompressible. The solution is used at the micro-level for evaluating the contribution of creep to the final stage of densification in sintering processes. The importance of closed-form solutions for hollow spheres subjected to external pressure for micromechanical modeling of hot isostatic pressing of powder materials is emphasized in [5]. Closed-form solutions for hollow spheres under external pressure are found in [6], adopting the Mohr–Coulomb and Drucker–Prager yield criteria. The plastic flow rule associated with these criteria is used. Therefore, the material is compressible even though the elastic portion of strain is neglected. No hardening law is adopted. The solution is used to evaluate a Gurson-type yield criterion.

The description of material behavior under certain conditions requires constitutive equations that account for the dependence of the yield stress on both the equivalent strain (or the plastic work) and the equivalent strain rate. One of the most widely used models of this type has been proposed in [7]. This model postulates that the von Mises flow stress is the product of three specific functions. Each function depends on a single argument: the equivalent plastic strain or the equivalent plastic strain rate or temperature. The parameters involved in these functions have been identified for several materials [7,8,9]. Many generalizations of the model [7] are available in the literature. Paper [10] has combined the functions responsible for the strain rate and temperature effects in [7] and a new function of the equivalent strain. Experimental data have been presented for the Ti–6Al–4V alloy. An extension of the model [7] to anisotropic materials is proposed in [11]. It has been assumed that the constitutive equation proposed in [7] is valid along a selected direction. Experimental data have been presented for the Zn–Cu–Ti alloy. The models proposed in [12, 13] suppose that the flow stress is a function of the equivalent strain, the equivalent strain rate, and temperature. Then, experimental data are used to determine this function for different steels.

Under certain conditions, the temperature effect is negligible. In this case, the model [7] simplifies. In particular, the flow stress depends on two functions responsible for the equivalent strain and equivalent strain rate effects in the original model. Reference [14] has included the stress triaxiality in the model, and reference [15] the stress triaxiality and the cubic stress invariant. Also, these papers have adopted the function of the equivalent strain rate proposed in [16] instead of the original function involved in the model [7]. Paper [17] has developed a general model in which the flow stress is a function of the equivalent strain and the equivalent strain rate. A particular choice of this function reduces this model to that in [7] and other available models. Besides the model [7], the representation of the flow stress as the product of a power function of the equivalent plastic strain and a power function of the equivalent plastic strain rate is widely used in the literature (see, for example, [18]). A theory of elastic-viscoplastic strain hardening materials in which the plastic work is considered as a state variable is proposed in [19]. The theory has been verified for commercially pure titanium.

Paper [5] has analyzed strain-hardening viscoplastic thick-walled sphere and cylinder under external pressure. The elastic portion of strain is neglected, and the material is incompressible. The flow stress is the product of the Palm–Voce strain-hardening function and a power function of the equivalent strain rate. This constitutive equation is often used in conjunction with sequential limit analysis [20,21,22]. The present paper generalizes the solution for a sphere given in [5]. In particular, no restriction is imposed on the dependence of the equivalent stress on the equivalent strain and the equivalent strain rate. This feature of the solution is of special importance for micromechanical modeling since it is difficult to determine accurate constitutive equations at this level. Therefore, many calculations with different constitutive equations at the micro-level may be required to achieve sufficient accuracy at the macro-level. In [5], the constitutive equations have been intentionally simplified to obtain the analytic solution.

The solution below is facilitated by using the equivalent strain as one of the independent variables. Similar approaches have been used in [2, 23,24,25]. The radial coordinate of a spherical coordinate system has been replaced with the equivalent stress in [2] to analyze a thick-walled sphere loaded by internal and external pressure. The radial coordinate of a cylindrical coordinate system has been replaced with the equivalent strain in [23] to analyze the pure plane strain bending of a sheet. These two papers deal with large strains. Paper [24] concerns the expansion/contraction of a sphere at small strains. The radial coordinate of a spherical coordinate system has been replaced with the equivalent strain. Thermo-mechanical loading of a sphere assuming temperature-dependent material properties has been investigated in [25]. The temperature has been used as an independent variable in place of the radial coordinate of a spherical coordinate system. A common feature of the constitutive equations adopted in [2, 23,24,25] is that the equivalent stress depends on one quantity. Then, it becomes advantageous to replace the natural space coordinate with this quantity. An essential difference of the constitutive equations considered in the present paper is that the equivalent stress depends on two quantities. Therefore, the approach developed in [2, 23,24,25] should be generalized.

The method developed to derive the analytic solution applies to a class of boundary value problems. Among these problems are the expansion/contraction of a hollow cylinder under plane strain conditions, compression of a thin layer between parallel plates using conventional approximations (see, for example, [26, 27]), and compression of plastic material between rotating plates [28]. All these problems are of practical importance.

The solution found can be used as a benchmark problem for verifying numerical codes for quite a general model of plasticity accounting for strain- and rate-hardening, which is a necessary step before using such codes [29, 30].

2 Statement of the problem

Consider a hollow sphere whose initial inner and outer radii are \(a_{0}\) and \(b_{0}\), respectively. The current radii are denoted as a and b. It is natural to use the spherical coordinate system \(\left( {r,\;\theta ,\;\varphi } \right) \) with its origin at the center of the sphere. Let \(\sigma _{r} \), \(\sigma _{\theta } \), and \(\sigma _{\varphi }\) be the normal stresses referred to this coordinate system. These stresses are the principal stresses. By virtue of the symmetry,

$$\begin{aligned} \sigma _{\theta } =\sigma _{\varphi } . \end{aligned}$$
(1)

Any pressure-independent yield criterion is represented as

$$\begin{aligned} \left| {\sigma _{\theta } -\sigma _{r} } \right| =\sigma _{Y} . \end{aligned}$$
(2)

Here, \(\sigma _{Y} \) is the yield stress in tension. The plastic flow rule associated with the yield criterion (2) results in the equation of incompressibility and the condition that the plastic work rate is positive. Let \(\xi _{r} \), \(\xi _{\theta } \), and \(\xi _{\varphi } \) be the normal strain rates referred to the spherical coordinate system. Then, the equation of incompressibility can be written as

$$\begin{aligned} \xi _{r} +\xi _{\theta } +\xi _{\varphi } =0. \end{aligned}$$
(3)

It is assumed that the yield stress depends on both the equivalent strain rate, \(\xi _{\mathrm{eq}} \), and the equivalent strain, \(\varepsilon _{\mathrm{eq}} \). In the case under consideration, the equivalent strain rate and the equivalent strain are defined as

$$\begin{aligned} \xi _{\mathrm{eq}} =\sqrt{\frac{2}{3}} \sqrt{\xi _{r}^{2} +\xi _{\theta }^{2} +\xi _{\varphi }^{2} } \end{aligned}$$
(4)

and

$$\begin{aligned} \frac{\mathrm{d}\varepsilon _{\mathrm{eq}} }{\mathrm{d}t}=\xi _{\mathrm{eq}} . \end{aligned}$$
(5)

Here, t is the time and \(\mathrm{d}/{\mathrm{d}t}\) denotes the convected derivative. The yield criterion (2) can be rewritten as

$$\begin{aligned} \sigma _{\theta } -\sigma _{r} =m\sigma _{0} \Phi \left( {\varepsilon _{\mathrm{eq}} ,\;\xi _{\mathrm{eq}} } \right) \end{aligned}$$
(6)

where \(\sigma _{0} \) is a reference stress and \(\Phi \left( {\varepsilon _{\mathrm{eq}} ,\;\xi _{\mathrm{eq}} } \right) \) is an arbitrary function of its arguments. Moreover, here and in what follows, \(m=1\) in the case of expansion and \(m=-1\) in the case of contraction. The only stress equilibrium equation which is not identically satisfied in the spherical coordinate system is

$$\begin{aligned} \frac{\partial \sigma _{r} }{\partial r}+\frac{2\left( {\sigma _{r} -\sigma _{\theta } } \right) }{r}=0. \end{aligned}$$
(7)

The only nonzero velocity component is the radial velocity u. Then,

$$\begin{aligned} \xi _{r} =\frac{\partial u}{\partial r},\quad \xi _{\theta } =\xi _{\varphi } =\frac{u}{r}. \end{aligned}$$
(8)

The velocity boundary condition is

$$\begin{aligned} u=mU \end{aligned}$$
(9)

for \(r=a\). Here, \(U>0\). The stress boundary condition is

$$\begin{aligned} \sigma _{r} =0 \end{aligned}$$
(10)

for \(r=b\). Since the yield criterion is pressure-independent, the solution for the sphere loaded by uniform pressure over its outer or inner radius can be generated from the solution satisfying (10) by simply adding an appropriate uniform hydrostatic tension or compression.

3 General solution

Equations (3) and (8) combine to give \({\partial u}/{\partial r}+{2u}/r=0\). The solution of this equation satisfying the boundary condition (9) is

$$\begin{aligned} u=mU\left( {\frac{a}{r}} \right) ^{2}. \end{aligned}$$
(11)

By definition, \({\partial r} / {\partial t}=u\) and \({\partial a} / {\partial t}=mU\). Using these equations and (11), one gets

$$\begin{aligned} \frac{\partial r}{\partial a}=\left( {\frac{a}{r}} \right) ^{2}. \end{aligned}$$
(12)

Let R be the Lagrangian coordinate such that \(r=R\) at the initial instant. The solution of equation (12) satisfying this condition is

$$\begin{aligned} r^{3}=a^{3}+R^{3}-a_{0}^{3} . \end{aligned}$$
(13)

This equation can be solved for R:

$$\begin{aligned} R^{3}=r^{3}-a^{3}+a_{0}^{3} . \end{aligned}$$
(14)

Using (4), (8), (11), and (13), one finds the equivalent strain rate as

$$\begin{aligned} \xi _{\mathrm{eq}} =\frac{2Ua^{2}}{\left( {a^{3}+R^{3}-a_{0}^{3} } \right) }. \end{aligned}$$
(15)

Substituting (15) into (5) and taking into account that \({\partial a} / {\partial t}=mU\) yield

$$\begin{aligned} \frac{\partial \varepsilon _{\mathrm{eq}} }{\partial a}=m\frac{2a^{2}}{\left( {a^{3}+R^{3}-a_{0}^{3} } \right) }. \end{aligned}$$
(16)

The initial condition to this equation is \(\varepsilon _{\mathrm{eq}} =0\) at \(a=a_{0} \). The solution of equation (16) satisfying this condition is

$$\begin{aligned} \varepsilon _{\mathrm{eq}} =m\frac{2}{3}\ln \left( {\frac{a^{3}+R^{3}-a_{0}^{3} }{R^{3}}} \right) . \end{aligned}$$
(17)

Using (14), one rewrites this solution as

$$\begin{aligned} \varepsilon _{\mathrm{eq}} =m\frac{2}{3}\ln \left( {\frac{r^{3}}{r^{3}-a^{3}+a_{0}^{3} }} \right) . \end{aligned}$$
(18)

Solving this equation for \(r^{3}\) gives

$$\begin{aligned} r^{3}=\frac{\left( {a^{3}-a_{0}^{3} } \right) \exp \left( {\frac{3m}{2}\varepsilon _{\mathrm{eq}} } \right) }{\exp \left( {\frac{3m}{2}\varepsilon _{\mathrm{eq}} } \right) -1}. \end{aligned}$$
(19)

Replace the independent variable r with \(\varepsilon _{\mathrm{eq}} \). In this case,

$$\begin{aligned} \frac{\partial \sigma _{r} }{\partial r}=\frac{\partial \sigma _{r} }{\partial \varepsilon _{\mathrm{eq}} }\frac{\partial \varepsilon _{\mathrm{eq}} }{\partial r}. \end{aligned}$$
(20)

The derivative \({\partial \varepsilon _{\mathrm{eq}} } / {\partial r}\) is readily determined from (18). Then, substituting (20) into (7) and using (6) yields

$$\begin{aligned} \frac{\partial \sigma _{r} }{\sigma _{0} \partial \varepsilon _{\mathrm{eq}} }=\frac{\left( {r^{3}-a^{3}+a_{0}^{3} } \right) }{\left( {a_{0}^{3} -a^{3}} \right) }\Phi \left( {\varepsilon _{\mathrm{eq}} ,\;\xi _{\mathrm{eq}} } \right) . \end{aligned}$$
(21)

One can eliminate r in this equation using (19). As a result,

$$\begin{aligned} \frac{\partial \sigma _{r} }{\sigma _{0} \partial \varepsilon _{\mathrm{eq}} }=\frac{\Phi \left( {\varepsilon _{\mathrm{eq}} ,\;\xi _{\mathrm{eq}} } \right) }{1-\exp \left( {\frac{3m}{2}\varepsilon _{\mathrm{eq}} } \right) }. \end{aligned}$$
(22)

Using (13) and (19), one transforms Eq. (15) to

$$\begin{aligned} \xi _{\mathrm{eq}} =\frac{2Ua^{2}\left[ {\exp \left( {\frac{3m}{2}\varepsilon _{\mathrm{eq}} } \right) -1} \right] }{\left( {a^{3}-a_{0}^{3} } \right) \exp \left( {\frac{3m}{2}\varepsilon _{\mathrm{eq}} } \right) }. \end{aligned}$$
(23)

Then, the function \(\Phi \left( {\varepsilon _{\mathrm{eq}} ,\;\xi _{\mathrm{eq}} } \right) \) can be represented as

$$\begin{aligned} \Phi \left( {\varepsilon _{\mathrm{eq}} ,\;\xi _{\mathrm{eq}} } \right) =\Lambda \left( {\varepsilon _{\mathrm{eq}} ,\;a} \right) . \end{aligned}$$
(24)

The function \(\Lambda \left( {\varepsilon _{\mathrm{eq}} ,\;a} \right) \) is readily determined if the function \(\Phi \left( {\varepsilon _{\mathrm{eq}} ,\;\xi _{\mathrm{eq}} } \right) \) is prescribed. Equation (22) becomes

$$\begin{aligned} \frac{\partial \sigma _{r} }{\sigma _{0} \partial \varepsilon _{\mathrm{eq}} }=\frac{\Lambda \left( {\varepsilon _{\mathrm{eq}} ,\;a} \right) }{1-\exp \left( {\frac{3m}{2}\varepsilon _{\mathrm{eq}} } \right) }. \end{aligned}$$
(25)

This equation can be integrated at any value of a except \(a=a_{0} \). At \(a=a_{0} \), replacing r with \(\varepsilon _{\mathrm{eq}} \) is not justified since \(\varepsilon _{\mathrm{eq}} =0\) at the initial instant. However, the radial stress distribution at the initial instant is readily found from the original equations, which will be demonstrated below.

The solution of Eq. (25) should satisfy the boundary condition (10). It follows from (13) and (18) that

$$\begin{aligned} \varepsilon _{b} =m\frac{2}{3}\ln \left( {\frac{b^{3}}{b^{3}-a^{3}+a_{0}^{3} }} \right) =m\frac{2}{3}\ln \left( {\frac{a^{3}+b_{0}^{3} -a_{0}^{3} }{b_{0}^{3} }} \right) . \end{aligned}$$
(26)

Here, \(\varepsilon _{b} \) is the value of \(\varepsilon _{\mathrm{eq}} \) at \(r=b\) (or \(R=b_{0} )\). Therefore, the boundary condition (10) is equivalent to the condition \(\sigma _{r} =0\) for \(\varepsilon _{\mathrm{eq}} =\varepsilon _{b} \). Then, the solution of Eq. (25) can be represented as

$$\begin{aligned} \frac{\sigma _{r} }{\sigma _{0} }=\int \limits _{\varepsilon _{b} }^{\varepsilon _{\mathrm{eq}} } {\frac{\Lambda \left( {\chi ,\;a} \right) }{\left[ {1-\exp \left( {\frac{3m}{2}\chi } \right) } \right] }\mathrm{d}\chi } . \end{aligned}$$
(27)

The dependence of the radial stress on r is determined from (19) and (27) in parametric form, with \(\varepsilon _{\mathrm{eq}} \) being the parameter. Having found the radial stress, one can immediately determine the circumferential stress from (6). The pressure over the inner radius of the sphere is determined as \(P=-\sigma _{r} \) where \(\sigma _{r} \) is understood to be calculated at \(r=a\). Then, it follows from (27) that

$$\begin{aligned} p=\frac{P}{\sigma _{0} }=\int \limits _{\varepsilon _{a} }^{\varepsilon _{b} } {\frac{\Lambda \left( {\chi ,\;a} \right) }{\left[ {1-\exp \left( {\frac{3m}{2}\chi } \right) } \right] }\mathrm{d}\chi } . \end{aligned}$$
(28)

Here, \(\varepsilon _{a} \) is the value of \(\varepsilon _{\mathrm{eq}} \) at \(r=a\). It follows from (18) that

$$\begin{aligned} \varepsilon _{a} =2m\ln \left( {\frac{a}{a_{0} }} \right) . \end{aligned}$$
(29)

As it has been noted above, the general solution is not valid at the initial instant. The solution at the initial instant is derived below. Since the equivalent strain vanishes everywhere at the initial instant, Eq. (6) becomes

$$\begin{aligned} \sigma _{\theta } -\sigma _{r} =m\sigma _{0} \Phi \left( {0,\;\xi _{\mathrm{eq}} } \right) . \end{aligned}$$
(30)

Substituting this equation into (7) results in

$$\begin{aligned} \frac{\partial \sigma _{r} }{\partial r}=\frac{2m\sigma _{0} \Phi \left( {0,\,\xi _{\mathrm{eq}} } \right) }{r}. \end{aligned}$$
(31)

Equation (15) at the initial instant becomes

$$\begin{aligned} \xi _{\mathrm{eq}} =\frac{2Ua_{0}^{2} }{r^{3}}. \end{aligned}$$
(32)

Equation (31) can be rewritten as

$$\begin{aligned} \frac{\partial \sigma _{r} }{\partial \xi _{\mathrm{eq}} }\frac{\partial \xi _{\mathrm{eq}} }{\partial r}=\frac{2m\sigma _{0} \Phi \left( {0,\,\xi _{\mathrm{eq}} } \right) }{r}. \end{aligned}$$
(33)

The derivative \({\partial \xi _{\mathrm{eq}} } / {\partial r}\) is readily determined from (32) as

$$\begin{aligned} \frac{\partial \xi _{\mathrm{eq}} }{\partial r}=-\frac{6Ua_{0}^{2} }{r^{4}}. \end{aligned}$$
(34)

Substituting (34) into (33) and eliminating r by means of (32) yield

$$\begin{aligned} \frac{\partial \sigma _{r} }{\sigma _{0} \partial \xi _{\mathrm{eq}} }=-\frac{2m\Phi \left( {0,\,\xi _{\mathrm{eq}} } \right) }{3\xi _{\mathrm{eq}} }. \end{aligned}$$
(35)

The boundary condition (10) becomes

$$\begin{aligned} \sigma _{r} =0 \end{aligned}$$
(36)

for \(\xi _{\mathrm{eq}} =\xi _{b} \). Here \(\xi _{b} \) is the value of \(\xi _{\mathrm{eq}} \) at \(r=b_{0} \). It follows from (32) that

$$\begin{aligned} \xi _{b} =\frac{2Ua_{0}^{2} }{b_{0}^{3} }. \end{aligned}$$
(37)

Then, the solution of Eq. (35) can be written as

$$\begin{aligned} \frac{\sigma _{r} }{\sigma _{0} }=-\frac{2m}{3}\int \limits _{\xi _{b} }^{\xi _{\mathrm{eq}} } {\frac{\Phi \left( {0,\,\chi } \right) }{\chi }\mathrm{d}\chi } . \end{aligned}$$
(38)

The circumferential stress is determined from (30) and (38) as

$$\begin{aligned} \frac{\sigma _{\theta } }{\sigma _{0} }=-\frac{2m}{3}\int \limits _{\xi _{b} }^{\xi _{\mathrm{eq}} } {\frac{\Phi \left( {0,\,\chi } \right) }{\chi }\mathrm{d}\chi } +m\Phi \left( {0,\;\xi _{\mathrm{eq}} } \right) . \end{aligned}$$
(39)

The radial distribution of the radial and circumferential stresses follows from (38) and (39) where \(\xi _{\mathrm{eq}} \) should be eliminated using (32). The pressure over the inner radius of the sphere is found from (38) as

$$\begin{aligned} p=\frac{2m}{3}\int \limits _{\xi _{a} }^{\xi _{b} } {\frac{\Phi \left( {0,\,\chi } \right) }{\chi }\mathrm{d}\chi } . \end{aligned}$$
(40)

Here, \(\xi _{a} \) is the value of \(\xi _{\mathrm{eq}} \) at \(r=a_{0} \). It follows from (32) that

$$\begin{aligned} \xi _{a} =\frac{2U}{a_{0} }. \end{aligned}$$
(41)

4 Illustrative example

Comprehensive overviews of strain-hardening viscoplastic constitutive equations have been provided in [12, 17]. At a constant temperature, one of the widely used equations reads

$$\begin{aligned} \sigma _{Y} =\sigma _{0} \left( {1+\mu \varepsilon _{\mathrm{eq}}^{n} } \right) \left[ {1+\lambda \ln \left( {\frac{\xi _{\mathrm{eq}} }{\xi _{0} }} \right) } \right] . \end{aligned}$$
(42)

Here, \(\mu \), \(\lambda \), \(\xi _{0} \), and n are constitutive parameters. For mild steels, \(\mu =8.38\), \(\lambda =0.0362\), \(\xi _{0} =0.001\), and \(n=0.316\). This set of parameters is used in the subsequent calculations. Comparing the right-hand side of (6) and (42) shows that

$$\begin{aligned} \Phi \left( {\varepsilon _{\mathrm{eq}} ,\;\xi _{\mathrm{eq}} } \right) =\left( {1+\mu \varepsilon _{\mathrm{eq}}^{n} } \right) \left[ {1+\lambda \ln \left( {\frac{\xi _{\mathrm{eq}} }{\xi _{0} }} \right) } \right] . \end{aligned}$$
(43)

Equations (23) and (43) combine to give

$$\begin{aligned} \Lambda \left( {\varepsilon _{\mathrm{eq}} ,\;a} \right) =\left( {1+\mu \varepsilon _{\mathrm{eq}}^{n} } \right) \left\langle {1+\lambda \ln \left\{ {\frac{2Ua^{2}\left[ {\exp \left( {\frac{3m}{2}\varepsilon _{\mathrm{eq}} } \right) -1} \right] }{\xi _{0} \left( {a^{3}-a_{0}^{3} } \right) \exp \left( {\frac{3m}{2}\varepsilon _{\mathrm{eq}} } \right) }} \right\} } \right\rangle . \end{aligned}$$
(44)

It is convenient to introduce the dimensionless quantities:

$$\begin{aligned} \beta =\frac{2U}{\xi _{0} b_{0} }, \quad \alpha =\frac{a}{b_{0} }, \quad \rho =\frac{r}{b_{0} }, \hbox { and } c_{0} =\frac{a_{0} }{b_{0} }. \end{aligned}$$
(45)

Then, Eqs. (44), (26), (29), and (19) become

$$\begin{aligned} \Lambda \left( {\varepsilon _{\mathrm{eq}} ,\;a} \right)= & {} \left( {1+\mu \varepsilon _{\mathrm{eq}}^{n} } \right) \left\langle {1+\lambda \ln \left\{ {\frac{\beta \alpha ^{2}\left[ {\exp \left( {\frac{3m}{2}\varepsilon _{\mathrm{eq}} } \right) -1} \right] }{\left( {\alpha ^{3}-c_{0}^{3} } \right) \exp \left( {\frac{3m}{2}\varepsilon _{\mathrm{eq}} } \right) }} \right\} } \right\rangle , \end{aligned}$$
(46)
$$\begin{aligned} \varepsilon _{b}= & {} m\frac{2}{3}\ln \left( {\alpha ^{3}+1-c_{0}^{3} } \right) , \end{aligned}$$
(47)
$$\begin{aligned} \varepsilon _{a}= & {} 2m\ln \left( {\frac{\alpha }{c_{0} }} \right) , \end{aligned}$$
(48)

and

$$\begin{aligned} \rho ^{3}=\frac{\left( {\alpha ^{3}-c_{0}^{3} } \right) \exp \left( {\frac{3m}{2}\varepsilon _{\mathrm{eq}} } \right) }{\exp \left( {\frac{3m}{2}\varepsilon _{\mathrm{eq}} } \right) -1}, \end{aligned}$$
(49)

respectively. Substituting (46), (47), and (48) into (27) and (28), one can evaluate the integrals numerically. Then, Eq. (49) is used for finding the dependence of the radial and circumferential stresses on the dimensionless radial coordinate.

At the initial instant, it follows from (38), (39), and (43) that

$$\begin{aligned} \frac{\sigma _{r} }{\sigma _{0} }= & {} -\frac{2m}{3}\int \limits _{\xi _{b} }^{\xi _{\mathrm{eq}} } {\frac{1}{\chi }\left[ {1+\lambda \ln \left( {\frac{\chi }{\xi _{0} }} \right) } \right] \mathrm{d}\chi } =-\frac{2m}{3}\ln \left( {\frac{\xi _{\mathrm{eq}} }{\xi _{b} }} \right) -\frac{m\lambda }{3}\left[ {\ln ^{2}\left( {\frac{\xi _{\mathrm{eq}} }{\xi _{0} }} \right) -\ln ^{2}\left( {\frac{\xi _{b} }{\xi _{0} }} \right) } \right] , \nonumber \\ \frac{\sigma _{\theta } }{\sigma _{0} }= & {} -\frac{2m}{3}\ln \left( {\frac{\xi _{\mathrm{eq}} }{\xi _{b} }} \right) -\frac{m\lambda }{3}\left[ {\ln ^{2}\left( {\frac{\xi _{\mathrm{eq}} }{\xi _{0} }} \right) -\ln ^{2}\left( {\frac{\xi _{b} }{\xi _{0} }} \right) } \right] +m\left[ {1+\lambda \ln \left( {\frac{\xi _{\mathrm{eq}} }{\xi _{0} }} \right) } \right] . \end{aligned}$$
(50)

Equations (32), (37), (41), and (45) result in

$$\begin{aligned} \frac{\xi _{\mathrm{eq}} }{\xi _{0} }=\frac{\beta c_{0}^{2} }{\rho ^{3}},\quad \frac{\xi _{b} }{\xi _{0} }=\beta c_{0}^{2} ,\quad \frac{\xi _{a} }{\xi _{0} }=\frac{\beta }{c_{0} }. \end{aligned}$$
(51)

Equations (50) and (51) supply the dependence of the radial and circumferential stresses on the dimensionless radial coordinate. The pressure over the inner radius of the sphere is determined from (50) as

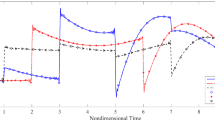
$$\begin{aligned} p=\frac{2m}{3}\ln \left( {\frac{\xi _{a} }{\xi _{b} }} \right) +\frac{2m\lambda }{3}\left\{ {\frac{\xi _{0}^{2} }{\xi _{a}^{2} }\left[ {1-\ln \left( {\frac{\xi _{a} }{\xi _{0} }} \right) } \right] -\frac{\xi _{0}^{2} }{\xi _{b}^{2} }\left[ {1-\ln \left( {\frac{\xi _{b} }{\xi _{0} }} \right) } \right] } \right\} . \end{aligned}$$
(52)

Figure 1 depicts the variation of the pressure required to expand a sphere whose initial inner dimensionless radius is \(c_{0} =1 / 2\) with \(\alpha \) for several \(\beta -\) values. The gradient of p is very high at the beginning of the process. The pressure attains a local maximum as a result of geometric changes. As expected, higher values of \(\beta \) lead to larger pressures. Figures 2 and 3 show the radial distribution of the radial and circumferential stresses at several stages of the process for \(\beta =0.1\). Monotonic functions of the dimensionless radius represent the distributions of the radial stress. The circumferential stress attains a local minimum if the value of \(\alpha \) is large enough.

Fig. 1
figure 1

Dependence of the inner pressure required to expand a sphere on \(\alpha \) at several values of \(\beta \). The initial dimensionless inner radius of the sphere is \(c_{0} =1 / 2\)

Full size image
Fig. 2
figure 2

Radial distribution of the radial stress in an expanding sphere at several values of \(\alpha \). The initial dimensionless inner radius of the sphere is \(c_{0} =1 /2\)

Full size image
Fig. 3
figure 3

Radial distribution of the circumferential stress in an expanding sphere at several values of \(\alpha \). The initial dimensionless inner radius of the sphere is \(c_{0} =1 /2\)

Full size image
Fig. 4
figure 4

Dependence of the outer pressure required to contract a sphere on \(\alpha \) at several values of \(\beta \). The initial dimensionless inner radius of the sphere is \(c_{0} =1 /2\)

Full size image
Fig. 5
figure 5

Radial distribution of the radial stress in a contracting sphere at several values of \(\alpha \). The initial dimensionless inner radius of the sphere is \(c_{0} =1/2\)

Full size image
Fig. 6
figure 6

Radial distribution of the circumferential stress in a contracting sphere at several values of \(\alpha \). The initial dimensionless inner radius of the sphere is \(c_{0} =1/2\)

Full size image

The method described at the end of Sect. 2 has been used for solving the problem for a sphere contracted by external pressure. In this case, the boundary condition (10) is replaced with the boundary condition:

$$\begin{aligned} \sigma _{r} =0 \end{aligned}$$
(53)

for \(\rho =\alpha \). Therefore, the stress solution is obtained by adding p shown in Fig. 1 to the stress components derived in Sect. 3. The dimensionless pressure applied to the external surface is \(p_{b} =-{\sigma _{r} } / {\sigma _{0} }\) where \(\sigma _{r} \) is understood to be calculated at \(r=b\). Figure 4 depicts the variation of this pressure for a sphere whose initial inner dimensionless radius is \(c_{0} =1 /2\) with \(\alpha \) for several \(\beta -\) values. The gradient of p is very high at the beginning of the process. Both the constitutive equations and geometric changes contribute to the increase in \(p_{b} \). Therefore, in contrast to the previous case, monotonic functions represent the variation of \(p_{b} \) with \(\alpha \). As in the previous case, higher values of \(\beta \) lead to larger pressures. Figures 5 and 6 show the radial distribution of the radial and circumferential stresses at several stages of the process for \(\beta =0.1\). Monotonic functions of the dimensionless radius represent the distributions of both stresses.

5 Conclusions

The present paper has extended the existing solution for the boundary value problem of thick-walled spheres subjected to internal and external pressures. The yield stress depends on both the equivalent strain and the equivalent strain rate, and no restriction is imposed on this dependence. The solution is practically analytic. A numerical treatment is only necessary to evaluate ordinary integrals. The solution is ready for use in conjunction with the available approaches for micromechanical modeling of the constitutive behavior of porous materials. It also can be used for testing numerical procedures for quite a general model of strain-hardening, viscoplastic materials.

The solution has been facilitated by using Lagrangian coordinates and the equivalent strain as an independent variable instead of the natural space coordinate. The reasoning adopted in deriving this solution suggests that the approach developed will successfully extend the solutions given in [26,27,28] to the constitutive equations used in the present paper.

The illustrative example has adopted a widely used model of viscoplastic hardening materials. The predictions are in agreement with physical expectations. In particular, the pressure required to deform an expanding sphere attains a maximum at a certain stage of the process (Fig. 1). This feature is a consequence of thinning the wall. In contrast, the pressure required to deform a contracting sphere is a monotonic function of the current inner radius of the sphere. It is evident that the wall is thickening in this process. The expansion/contraction speed effect is controlled by the parameter \(\beta \) introduced in (45). It is seen from Figs. 1 and 4 that this effect is more pronounced at smaller \(\beta -\) values. In the case of expanding spheres, the circumferential stress attains a minimum at a certain radius after a certain amount of expansion (Fig. 3).

The solution is rigid/plastic. Therefore, the distributions of residual stresses and strains cannot be found strictly speaking. Using the method proposed in [31], one can determine these distributions with high accuracy. However, it is impossible to apply this method in the case of the constitutive equation adopted in Sect. 4. It is seen from (42) that \(\sigma _{Y} \rightarrow \infty \) as \(\xi _{\mathrm{eq}} \rightarrow 0\). Therefore, this equation is not adequate at small \(\xi _{\mathrm{eq}} \) and has no sense at \(\xi _{\mathrm{eq}} =0\).