Keywords

1 Introduction

The issues of plasticity and elastic plasticity are described in many fundamental studies, including [1,2,3,4,5], etc. Publications are devoted to the statement of problems and calculations of axisymmetric and centrally symmetric elastoplastic bodies, of which the works [6,7,8], etc. can be noted. Calculations of inhomogeneous bodies constitute a special area of mechanics. Taking into account the dependence of mechanical characteristics on coordinates, it is rather difficult to solve such problems by analytical methods, and the development of this direction began with the emergence and development of computer technology and numerical methods. Some of the initiators of the development of the mechanics of inhomogeneous bodies were G. B. Kolchin, N. A. Rostovtsev, V. A. Lomakin, W. Olszak [9,10,11,12,13] and other scientists. The reasons for the continuous inhomogeneity of bodies are various fields or phenomena (high or low temperature, radiation, humidity, explosive effect [14,15,16,17,18,19,20,21,22,23], etc.).

The article deals with a one-dimensional problem of elastic and ideal-plasticity, in which the modulus of elasticity and the yield point of the material can vary in a wide range, which is the novelty of the work.

2 Statement of the Problem

Just as when considering the elastic problem for an inhomogeneous ball [13], when solving an elastoplastic problem for this body, the equation describing its behavior, solution methods and results are largely similar. A hollow thick-walled hollow ball with inner and outer radii \(a\) and \(b,\) loaded from inside and outside by uniform pressures \(p_{a}\) and \(p_{b}\) proportional to one parameter, is considered. The material is considered to be ideally plastic, while the modulus of elasticity \(E\) and yield stress \(\sigma _{T}\) are generally arbitrary functions of the radius. In addition, the material is considered to be incompressible in both the plastic and elastic zones. For the first time the formulation of such problems was given in [9, 20]. There are also solutions for the simplest dependencies and, represented by power functions of the form \(Ar^{k}\). This article provides a solution for the more general Young’s modulus and yield strength versus radius, allowing for some practical calculations.

The problem of calculating the ball is solved in a centrally symmetric setting. Thus, all functions depend on one coordinate the radius.

3 Derivation of Resolving Equations

In the presence of central symmetry, from the equilibrium equations in spherical coordinates, only the first remains, which, taking into account \(\frac{\partial }{{\partial \uptheta }} = \frac{\partial }{{\partial \phi }} = 0\) and \(\sigma _{\phi } = \sigma _{\uptheta }\), and the absence of volume forces and forced deformations, takes the form:

$$\frac{{d\sigma _{r} }}{{dr}} + \frac{2}{r}(\sigma _{r} - \sigma _{\uptheta } ) = 0.$$
(1)

The Cauchy relations taking into account \(v = w = 0\) are simplified, as a result we get:

$$\upvarepsilon _{r} = \frac{{du}}{{dr}};\upvarepsilon _{\uptheta } = \upvarepsilon _{\upvarphi } = \frac{u}{r},$$
(2)
$$\frac{{d\upvarepsilon _{\uptheta } }}{{dr}} + \frac{{\upvarepsilon _{\uptheta } - \upvarepsilon _{r} }}{r} = 0.$$
(3)

The angular deformations are identically zero. Hooke's law in spherical coordinates takes the form:

$$\upvarepsilon _{r} = \frac{1}{E}\left( {\sigma _{r} - 2\nu \sigma _{\uptheta } } \right);\quad \upvarepsilon _{\uptheta } = \upvarepsilon _{\upvarphi } = \frac{1}{E}\left[ {\left( {1 - \nu } \right)\sigma _{\uptheta } - \nu \sigma _{r} } \right].$$
(4)

Expressing \(\sigma _{\uptheta }\) from (1) through \(\sigma _{r}\), substituting \(\sigma _{\uptheta }\) into (4), differentiating \(\upvarepsilon _{\uptheta }\) with respect to and using (3) we can come to the resolving equation

$$\sigma ^{\prime\prime}_{r} + \frac{1}{r}\left( {4 - r\frac{{E^{\prime}}}{E} - \frac{{\nu ^{\prime}r}}{{1 - \nu }}} \right)\sigma ^{\prime}_{r} - \frac{1}{r}\left( {2\frac{{1 - 2\nu }}{{1 - \nu }} \cdot \frac{{E^{\prime}}}{E} + \frac{{4\nu ^{\prime}}}{{1 - \nu }}} \right)\sigma _{r} = 0.$$
(5)

In the elastic zone, the resolving Eq. (4) with allowance for \(\nu _{0} = 0.5\) can be written in the form:

$$r\sigma ^{\prime\prime}_{{re}} + \left( {4 - r\frac{{E^{\prime}}}{E}} \right)\sigma ^{\prime}_{{re}} = 0,$$
(6)

where the index e denotes the solution for the elastic zone (in what follows, the index \(p\) will be used for the plastic zone).

If we use the Huber-Mises plasticity criterion.

$$\sigma _{\uptheta } - \sigma _{r} = \chi \sigma _{T} \left( r \right),\chi = \pm 1.$$
(7)

The Treska–Saint–Venant plasticity condition gives the same equality.

Then using the equilibrium Eq. (1), it is possible to obtain the resolving equation for the plastic zone:

$$\frac{{d\sigma _{{rp}} }}{{dr}} = 2\chi \frac{{\sigma _{T} \left( r \right)}}{r}.$$
(8)

The integrals of Eqs. (6) and (8) essentially depend on the form of the functions \(E(r) {\text{and}} \sigma _{T} (r)\). Below is the calculation method for power functions \(E(r)\) and \(\sigma _{T} (r)\), which allow approximating a very wide class of real dependences:

$$E(r) = E_{0} + \left[ {1 + (k_{E} - 1)\left( {\frac{a}{r}} \right)^{{m_{E} }} } \right];$$
(9)
$$\sigma _{T} (r) = \sigma _{{T0}} \left[ {1 + \left( {k_{\sigma } - 1} \right)\left( {\frac{a}{r}} \right)^{{m_{\sigma } }} } \right]\,.$$
(10)

Substituting (9) and (10) in (6) and (8) and integrating these equations, one can obtain the general form of the solution in the elastic and plastic zones.

$$\left. \begin{aligned} \sigma _{{re}} = C_{2} + C_{1} \left[ { - \frac{{a^{3} }}{{3r^{3} }} - \frac{{k_{E} - 1}}{{m_{E} + 3}}\left( {\frac{a}{r}} \right)^{{m_{E} + 3}} } \right]; \hfill \\ \sigma _{{\uptheta e}} = C_{2} + C_{1} \left[ {\frac{{a^{3} }}{{6r^{3} }} + \frac{{\left( {k_{E} - 1} \right)\left( {m_{E} + 1} \right)}}{{2\left( {m_{E} + 3} \right)}}\left( {\frac{a}{r}} \right)^{{m_{E} + 3}} } \right]\,. \hfill \\ \end{aligned} \right\}$$
(11)
$$\,\left. \begin{gathered} \,\,\,\,\,\,\,\,\,\,\,\,\,\sigma _{{rp}} = D + 2\chi \sigma _{{T0}} \left[ {\ln \frac{r}{a} - \frac{{k_{T} - 1}}{{m_{\sigma } }}\left( {\frac{a}{r}} \right)^{{m_{\sigma } }} } \right]\,;\,\,\, \hfill \\ \sigma _{{\uptheta p}} = D + 2\chi \sigma _{{T0}} \left[ {\ln \frac{r}{a} + \frac{1}{2} + \frac{{\left( {k_{T} - 1} \right)\left( {m_{\sigma } - 2} \right)}}{{2m_{\sigma } }}\left( {\frac{a}{r}} \right)^{{m_{\sigma } }} } \right]\,.\, \hfill \\ \end{gathered} \right\}$$
(12)

Before proceeding to the definition of arbitrary C1, C2 constants and D, it is necessary to find the boundaries separating the zones of elastic and plastic deformations. Calculating from (11) the difference between the principal stresses and satisfying condition (7), we arrive at the equality

$$\Phi \left( r \right) = \frac{{C_{1} }}{{2\chi \sigma _{{T0}} }}\left( {\frac{a}{r}} \right)^{3} \frac{{1 + \left( {k_{E} - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a r}} \right. \kern-\nulldelimiterspace} r}} \right)^{{m_{E} }} }}{{1 + \left( {k_{\sigma } - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a r}} \right. \kern-\nulldelimiterspace} r}} \right)^{{m_{\sigma } }} }} = 1\,.$$
(13)

Now it is easy to find an equation for determining the radius \(r_{T}\), where the first plastic deformations occur. From the condition for the maximum of the function \(\Phi \left( r \right)\), we arrive at the equation

$$\begin{gathered} 3 + \left( {3 - m_{\sigma } } \right)\left( {k_{\sigma } - 1} \right)\left( {\frac{a}{{r_{T} }}} \right)^{{m_{\sigma } }} + \left( {3 + m_{E} } \right)\left( {k_{E} - 1} \right)\left( {\frac{a}{{r_{T} }}} \right)^{{m_{E} }} \hfill \\ + \left( {3 + m_{E} + m_{\sigma }^{{}} } \right)\left( {k_{\sigma } - 1} \right)\left( {k_{E} - 1} \right)\left( {\frac{a}{{r_{T} }}} \right)^{{m_{E} + m_{\sigma } }} = 0. \hfill \\ \end{gathered}$$
(14)

Depending on the values \(k_{E} ,\;\,k_{\sigma } ,\;\,m_{E}\) and \(m_{\sigma }\) behavior of the function \(\Phi \left( r \right)\) can be significantly different.

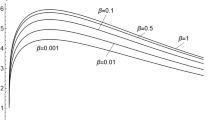
Figure 1 shows several options for the behavior of the functional part \(\Phi \left( r \right)\).

Fig. 1
figure 1

Change in the nature of the function \(\Phi \left( r \right)\) for different values of the parameters of inhomogeneity

Full size image

The dotted line shows the boundaries of the body, and note that if \(b \to \infty\), then \(k_{2} = {a \mathord{\left/ {\vphantom {a b}} \right. \kern-\nulldelimiterspace} b} \to 0\). It can be seen from the four graphs that \(\Phi \left( r \right)\) may not have a maximum (curve 1), and in the case of an extreme point, it can lie both within the interval \(\left( {a,b} \right)\) (curve 3) and outside it (curves 2 and 4). In the last two cases, obviously, plastic deformations occur either on the inner or outer surface of the body. In the absence of a maximum (curve 1), the highest value of \(\Phi \left( r \right)\) at \(r = a\) should be determined. Functions with a minimum are also possible, for example, when \(m_{E} < - \left( {m_{\sigma } + 2} \right)\). In this case, plastic deformations can occur sequentially on the surfaces of the body and close with increasing loads.

To determine the pressure difference at which plastic deformations appear for the first time, one should find a constant for a completely elastic solution, after which, from condition (14), we obtain

$$\begin{aligned} p_{T} = \left( {p_{a} - p_{b} } \right)_{T} &= \left[ {\frac{{1 - k_{2}^{3} }}{3} + \frac{{k_{E} - 1}}{{m_{E} + 3}}\left( {1 - k_{2}^{{m_{E} + 3}} } \right)} \right] \hfill \\ & \quad \cdot \frac{{2\chi \sigma _{{T0}} \left[ {1 + \left( {k_{\sigma } - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a {r_{T} }}} \right. \kern-\nulldelimiterspace} {r_{T} }}} \right)^{{m_{\sigma } }} } \right]}}{{\left[ {1 + \left( {k_{E} - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a {r_{T} }}} \right. \kern-\nulldelimiterspace} {r_{T} }}} \right)^{{m_{E} }} } \right]\left( {{a \mathord{\left/ {\vphantom {a {r_{T} }}} \right. \kern-\nulldelimiterspace} {r_{T} }}} \right)^{3} }}\,. \end{aligned}$$
(15)

From the last equality, you can also determine \(\chi\), since the sign of the expression in the first square brackets, given \(k_{E} ,\;\,m_{E}\) and \(k_{2}\) is known. So, for example, when \(m_{E} > 0,\,\,\chi = sign\left( {p_{a} - p_{b} } \right).\)

Depending on the place where plastic deformations occur, the further course of the solution will be different. Two cases are considered below: \(r_{T} = a\) and \(a < r_{T} < b\). The rest of the cases will not differ significantly from those considered.

Before proceeding to the study of the development of plastic deformations, it is necessary to write out the boundary conditions that must be satisfied by solutions (11) and (12) for a ball. At the boundaries of the body, the stresses are:

$$r = a,\;\sigma _{r} = - p_{a} ;\quad r = b,\;\sigma _{r} = - p_{b} .$$
(16)

In addition, at the boundaries \((r = r_{{T,i}} )\) separating the elastic and plastic zones (there can be one or two such boundaries), the following conditions must be met:

$$r = r_{{T,i}} \quad \left\{ {\begin{array}{*{20}l} {\sigma _{{re}} = \sigma _{{rp}} ;} \\ {\sigma _{{\uptheta e}} - \sigma _{{re}} = \chi \sigma _{T} ;} \\ {u_{e} = u_{p} \;.} \\ \end{array} } \right.$$
(17)

Here the second equality means the condition for the transition of the material from an elastic state to a plastic one, and \(u\)– radial displacement.

4 The Appearance of Plastic Deformations on the Inner Ball Surface \(\left( {r_{T} = a} \right)\)

In this case, with an increase in the pressure difference \(p = \left( {p_{a} - p_{b} } \right)\), the plastic zone extends into the depth of the ball wall. Let us denote the so far unknown radius of the sphere separating the elastic and plastic zones through \(r_{0}\)(Fig. 2). Substituting solutions (11) and (12) into (16) and into the first two equalities (17), one can obtain four relations for determining the constants \(C_{1} ,C_{2} ,D\) and \(r_{0}\), one of which will be transcendental:

$$\begin{gathered} \frac{p}{{2\chi \sigma _{{T0}} }} = \ln \frac{{r_{0} }}{a} + \frac{{k_{\sigma } - 1}}{{m_{\sigma } }}\left[ {1 - \left( {\frac{a}{{r_{0} }}} \right)^{{m_{\sigma } }} } \right] + \left\{ {\frac{1}{3}\left[ {\left( {\frac{a}{{r_{0} }}} \right)^{3} - k_{2}^{3} } \right]} \right. + \hfill \\ \quad \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left. {\frac{{k_{E} - 1}}{{m_{E} + 3}}\left[ {\left( {\frac{a}{{r_{0} }}} \right)^{{m_{E} + 3}} - k_{2}^{{m_{E} + 3}} } \right]} \right\}\frac{{r_{0}^{3} \left[ {1 + \left( {k_{\sigma } - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a {r_{0} }}} \right. \kern-\nulldelimiterspace} {r_{0} }}} \right)^{{m_{\sigma } }} } \right]}}{{a^{3} \left[ {1 + \left( {k_{E} - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a {r_{0} }}} \right. \kern-\nulldelimiterspace} {r_{0} }}} \right)^{{m_{E} }} } \right]}}\,. \hfill \\ \end{gathered}$$
(18)
Fig. 2
figure 2

Layer radii

Full size image

Since Eq. (18) is resolved with respect to \(p = p_{a} - p_{b}\), then, setting different values \(r_{0}\) on the interval \((a,b)\), it is possible to construct a dependence \(p(r_{0} )\) from which the required radius \(r_{0}\) is determined for any value. After that, the constants are easily found \(C_{1} ,C_{2} \,\,{\text{and}}\,\,D\):

$$\begin{aligned} &C_{1} = \frac{{2\chi \sigma _{{T0}} \left( {{{r_{0} } \mathord{\left/ {\vphantom {{r_{0} } a}} \right. \kern-\nulldelimiterspace} a}} \right)^{3} \left[ {1 + \left( {k_{\sigma } - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a {r_{0} }}} \right. \kern-\nulldelimiterspace} {r_{0} }}} \right)^{{m_{\sigma } }} } \right]}}{{1 + \left( {k_{E} - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a {r_{0} }}} \right. \kern-\nulldelimiterspace} {r_{0} }}} \right)^{{m_{E} }} }};\hfill \\ & C_{2} = - p_{b} + C_{1} \left( {\frac{{k_{2}^{3} }}{3} + \frac{{k_{E} - 1}}{{m_{E} + 3}}k_{2}^{{m_{E} + 3}} } \right); \end{aligned}$$
$$D = - p_{a} + 2\chi \sigma _{{T0}} \frac{{k_{\sigma } - 1}}{{m_{\sigma } }}.$$

Thus, the stressed elastic–plastic state of a thick-walled cylinder and a ball in the considered case (\(r_{T} = a\)) can be determined without using the third boundary condition from (17). It is necessary when determining the displacements, which are equal \(u_{e} = r\upvarepsilon _{{\uptheta e}}\) in the elastic zone, and \(\upvarepsilon _{{\uptheta e}}\) is determined from Hooke's law. Having done the appropriate calculations, we get:

$$u_{e} = \frac{{C_{1} a^{3} }}{{4E_{0} r^{2} }}.$$

In the plastic zone, integrating the material incompressibility condition \(2\frac{{du}}{{dr}} + \frac{u}{r} = 0,\) find displacement: \(u_{p} = B/r^{2} .\) The integration constant B is determined from the third boundary condition (17):

$$B = \frac{{C_{1} a^{3} }}{{4E_{0} }},$$
(19)

which allows you to write a unified formula for displacements in elastic and plastic zones.

5 The Appearance of Plastic Deformation Inside the Ball \(\left( {a < r_{T} < b} \right)\)

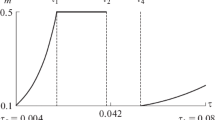
With the formation of plastic deformations inside the wall, a further increase in the pressure difference p leads to an expansion of the plastic zone in both directions, until one of the boundaries of this zone coincides with one of the surfaces of the body, and then until the body is completely transformed into the plastic state Denoting a smaller radius of the plastic zone \(r_{1}\), and a larger one \(r_{2}\), (Fig. 3) and satisfying the boundary conditions (16) and (17),one can find eight relations for determining the unknowns \(C_{1} - C_{4} ,D,B,\) \(r_{1}\) and \(r_{2}\) d where \(C_{3} \,{\text{and}}\,C_{4}\) are the constants of the solution of the type (11) for the outer elastic zone. It should be noted that, in contrast to the previous case, it is not possible to find stresses here without considering displacements, since otherwise for seven unknowns (excluding \(B\)) there will be only six boundary conditions. The solution of a system of eight equations is somewhat more complicated than in the case considered above, since, along with one transcendental equation, another nonlinear relation appears that connects \(r_{1}\) and \(r_{2}\):

$$\left( {\frac{{r_{1} }}{{r_{2} }}} \right)^{3} \frac{{1 + \left( {k_{\sigma } - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a {r_{1} }}} \right. \kern-\nulldelimiterspace} {r_{1} }}} \right)^{{m_{\sigma } }} }}{{1 + \left( {k_{\sigma } - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a {r_{2} }}} \right. \kern-\nulldelimiterspace} {r_{2} }}} \right)^{{m_{\sigma } }} }} = \frac{{1 + \left( {k_{E} - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a {r_{1} }}} \right. \kern-\nulldelimiterspace} {r_{1} }}} \right)^{{m_{E} }} }}{{1 + \left( {k_{E} - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a {r_{2} }}} \right. \kern-\nulldelimiterspace} {r_{2} }}} \right)^{{m_{E} }} }}\,.$$
Fig. 3
figure 3

Layer radii

Full size image

Obviously, this equation is satisfied at \(r_{1}\) = \(r_{2} ,\) which corresponds to the moment when plastic deformations appear (\(r = r_{T}\)). In addition, this equation must also have solutions for \(a \le r_{1} \le r_{T}\) and \(r_{T} \le r_{2} \le b\). By setting different values \(r_{1}\) on the interval (\(a,r_{T}\)) (the value \(r_{T}\) is determined in advance from (14)), the corresponding value \(r_{2}\) can be numerically determined. If in this case the plastic zone reaches the outer surface earlier, then \(r_{1}\) should be determined by value \(r_{2}\).

Each pair of values \(r_{1} ,\,\,r_{2}\) corresponds to a pressure difference \(p\), which is determined by the formula

$$\begin{aligned} \frac{p}{{2\chi \sigma _{{T0}} }} &= \ln \frac{{r_{2} }}{{r_{1} }} + \frac{{k_{\sigma } - 1}}{{m_{\sigma } }}\left[ {\left( {\frac{a}{{r_{1} }}} \right)^{{m_{\sigma } }} - \left( {\frac{a}{{r_{2} }}} \right)^{{m_{\sigma } }} } \right] + \left\{ {\frac{1}{3}\left[ {1 - \left( {\frac{a}{{r_{1} }}} \right)^{3} + \left( {\frac{a}{{r_{2} }}} \right)^{3} - k_{2}^{3} } \right] } \right. \hfill \\& \quad + \frac{{k_{E} - 1}}{{m_{E} + 3}}\left[ {1 - \left( {\frac{a}{{r_{1} }}} \right)^{{m_{E} + 3}} + \left( {\frac{a}{{r_{2} }}} \right)^{{m_{E} + 3}} - k_{2}^{{m_{E} + 3}} } \right]\\&\quad\left. { \times \frac{{r_{2}^{3} \left[ {1 + \left( {k_{\sigma } - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a {r_{2} }}} \right. \kern-\nulldelimiterspace} {r_{2} }}} \right)^{{m_{\sigma } }} } \right]}}{{a^{3} \left[ {1 + \left( {k_{E} - 1} \right)\left( {{a \mathord{\left/ {\vphantom {a {r_{2} }}} \right. \kern-\nulldelimiterspace} {r_{2} }}} \right)^{{m_{E} }} } \right]}}} \right\}\,. \hfill \\ \end{aligned}$$

Having built the dependence \(p\left( {r_{1} ,r_{2} } \right)\), it is possible, knowingly \(p_{a} {\text{and}} p_{b}\), to determine the boundaries of the plastic zone. After that, the rest of the constants are determined:

$$C_{1} = C_{3} = \frac{{2\chi \sigma _{{T0}} \left( {{{r_{1} } \mathord{\left/ {\vphantom {{r_{1} } a}} \right. \kern-\nulldelimiterspace} a}} \right)^{3} \left[ {1 + \left( {k_{\sigma } - 1} \right)\left( {a/r_{1} } \right)^{{m_{\sigma } }} } \right]}}{{1 + \left( {k_{E} - 1} \right)\left( {a/r_{1} } \right)^{{m_{E} }} }};$$
$$C_{2} = - p_{a} + C_{1} \left( {\frac{1}{3} + \frac{{k_{E} - 1}}{{m_{E} + 3}}} \right);C_{4} = - p_{b} + C_{3} \left( {\frac{{k_{2}^{3} }}{3} + \frac{{k_{E} - 1}}{{m_{E} + 3}}k_{2}^{{m_{E} + 3}} } \right);$$
$$\begin{aligned} D &= C_{2} + C_{1} \left[ { - \frac{1}{3}\left( {\frac{a}{{r_{1} }}} \right)^{3} - \frac{{k_{E} - 1}}{{m_{E} + 3}}\left( {\frac{a}{{r_{1} }}} \right)^{{m_{E} + 3}} } \right] \\ & \quad- 2\chi \sigma _{{T0}} \left[ {\ln \frac{{r_{1} }}{a} - \frac{{k_{\sigma } - 1}}{{m_{\sigma } }}\left( {\frac{a}{{r_{1} }}} \right)^{{m_{\sigma } }} } \right]\,. \end{aligned}$$

The constant B is found from relations (19).

6 Results

Below are some of the results of calculations performed according to the above method for various values of the ratio \(k_{2} = {a \mathord{\left/ {\vphantom {a b}} \right. \kern-\nulldelimiterspace} b}\) and parameters of inhomogeneity \(m_{E} = \,m_{\sigma } = 2.\) Figure 4 shows the graphs of the dependence on \(k_{E}\) the place of formation of the plastic zone in the ball for several values \(k_{\sigma }\) at \(m_{E} = \,m_{\sigma } = 2\). With an increase \(k_{\sigma }\) at a constant value \(k_{E}\), the place of formation of the plastic zone shifts from the inner surface of the ball into the depth of the wall. An increase \(k_{E}\), on the contrary, leads to a decrease in the radius \(r_{T}\). These two facts become clear from Fig. 5, which schematically shows the moment of the onset of the formation of plastic deformations in accordance with condition (7).

Fig. 4
figure 4

Dependence of the place of formation of the plastic zone on \(k_{E}\) and \(k_{\sigma }\) in the ball

Full size image
Fig. 5
figure 5

A qualitative representation of the conditions for the appearance of plastic deformations: —\(\chi \sigma _{T} (r)\), —\(\sigma _{\uptheta } - \sigma _{r}\)

Full size image
Fig. 6
figure 6

Dependence the parameters of elastic inhomogeneity: a in a thick-walled ball, b in an infinite array with a spherical cavity, \(\circ \,\, - \,k_{E} = k_{E}^{ * }\)- (formula 20)

Full size image

For a plastically homogeneous and elastically inhomogeneous body, the condition for the formation of plastic deformations on the inner surface of a cylinder or ball can be expressed by the elementary relation:

$$k_{E} \ge k_{E}^{*} = \frac{{m_{E} }}{{m_{\sigma } + 3}}.$$
(20)

In Fig. 6 shows the dependences of the pressure difference \(p_{T} = (p_{a} - p_{b} )_{T}\) corresponding to the moment of appearance of plastic deformations on the parameters of elastic inhomogeneity for a thick-walled ball and for an infinite array with a spherical cavity. It can be noted that the influence of the parameter \(m_{E}\) is ambiguous. At values of \(k_{E}\) close to zero, an increase in \(m_{E}\) can lead to a decrease in \(p_{T}\), and at higher \(k_{E} < 1\) values the opposite is true. In addition, in the region of small values of \(k_{E}\), an increase in this parameter leads to a slight increase in \(p_{T}\). It is also seen that, at \(k_{E} < 1\), the pressure at which plastic deformations arise can be significantly higher than in the homogeneous case (at \(k_{E} > 1\), the opposite the opposite picture is observed).

In Fig. 7 shows graphs that determine the change in the dimensions of the plastic zone in the ball from the load, at \(k_{\sigma } = 1;\) \(m_{E} = 2;\) \(k_{2} = {a \mathord{\left/ {\vphantom {a b}} \right. \kern-\nulldelimiterspace} b} = 0.5\) and \(k_{E} = 0.1\). Using this curve for a hollow sphere as an example, a method for determining the boundaries of the plastic zone (radii \(r_{1}\) and \(r_{2}\)) at a known load \(p^{ * }\) is shown.

Fig. 7
figure 7

Dependence of the size of the plastic zone on the load

Full size image

In elastic–plastic problems, displacements are of considerable interest. Figure 8 shows the dependence on the pressure difference \(p = p_{a} - p_{b}\) of the dimensionless displacement of the points of the inner contour of a thick-walled ball at \(k_{2} = 0,5\);\(k_{\sigma } = 1\);\(m_{E} = 2\) for different values of \(k_{E}\) that determine the degree of elastic inhomogeneity of the material. With an increase in the pressure difference, all the graphs merge, and the vertical asymptote corresponds to the complete transition of the cylinder to the plastic state.

Fig. 8
figure 8

Dependence of the displacements of the inner contour of the ball on pressure 1 \(k_{E} = 0.5;\) 2 \(k_{E} = 0.3;\) 3 \(k_{E} = 0.1\)

Full size image

Figure 9 shows the dependences of the displacements of the points of the contour of a spherical cavity in an infinite array loaded with external pressure \(p\). The calculations took into account both elastic and plastic inhomogeneity of the massif material.

Fig. 9
figure 9

Dependence of displacements spherical cavity contourin the array from pressure: 1 -\(k_{E}\) = 0.5, \(k_{\sigma }\) = 0.5; 2 -\(k_{E}\) = 0.1; \(k_{\sigma }\) = 1; 3 -\(k_{E}\) = 0.4, \(k_{\sigma }\) = 1; 4 -\(k_{E}\) = 0.6, \(k_{\sigma }\) = 1; 5 -\(k_{E}\) = 1; \(k_{\sigma }\) = 1; 6 -\(k_{E}\) = 0.5, \(k_{\sigma }\) = 2

Full size image

It can be noted that for a plastically homogeneous material (\(k_{\sigma } = 1\)) with an increase in pressure, the influence of elastic inhomogeneity, as in the case of a thick-walled cylinder, decreases. This is explained by the fact that more and more of the massif is involved in the work, and the relative fraction of the zone of elastic heterogeneity, which are local, decreases.

In turn, plastic inhomogeneity has a more significant effect on displacement, which is especially noticeable at high pressures. This fact is due to the fact that displacements are highly dependent on the size of the plastic zone, i.e. on the radius \(r_{0}\), and the latter essentially depends on the values of the parameters of the plastic inhomogeneity \(k_{\sigma }\) and \(m_{\sigma } .\)

7 Conclusions

In conclusion, one should pay attention to the fact that the solution of elastoplastic problems for elastically and plastically inhomogeneous bodies, or rather, the analysis of the occurrence of plastic deformations in such bodies, is largely similar to the solution of strength problems. Since the plasticity criteria of Tresk—Saint–Venant and Huber–Mises are equivalent to two widespread theories of strength, respectively, the theory of maximum tangential stresses and the energy theory, determining the place of occurrence of the first plastic deformations and the corresponding loads allows solving the strength problem at variable values of ultimate stresses.