Dedicated to Academician Viktor Pavlovich Maslov and the art of asymptotics that he developed in his work

1. Introduction

The second-order nonlinear difference equation

$$ \begin{array}{ll} {\rm dPII} & \displaystyle x_{n+1}+x_{n-1}=\frac{n x_n}{\nu (x_n^2-1)}\,,\qquad n \in {\mathbb N}, \end{array}$$
(1.1)

is called the discrete Painlevé equation of second type (see [1]–[3]).

It is easy to show [3] that this equation goes over into the Painlevé II differential equation in the limit \(\nu\to\infty\). Indeed, introducing a continuous variable \(t\) and a function \(u(t)\), we perform the scaling

$$ t=(n-2\nu)\,\nu^{-1/3}, \qquad x_n=(-1)^n\nu^{-1/3}u(t).$$
(1.2)

Then

$$\begin{aligned} \, x_{n\pm1}&=(-1)^{n+1}\nu^{-1/3} \biggl(u(t)\pm\nu^{-1/3}u'(t)+ \frac{1}{2} \nu^{-2/3} u''(t)+O(\nu^{-1})\biggr), \\ \frac{n x_n}{\nu(x_n^2-1)}&=(-1)^{n+1}\biggl(2+\nu^{-2/3}t+ \frac{1}{2}\nu^{-1}\biggr)\nu^{-1/3}u(t)\biggl(1+\nu^{-2/3}u^2(t)+ O(\nu^{-4/3})\biggr) \\& =(-1)^{n+1}\biggl(2\nu^{-1/3}u(t)+ \nu^{-1}(tu(t)+2u^3(t))+O(\nu^{-4/3})\biggr). \end{aligned}$$

Substituting this into (1.1) and passing to the limit \(\nu\to\infty\), we obtain

$$u''(t)=tu(t)+2u^3(t),$$

which is a special case of the classical Painlevé equation II [4].

Asymptotic solutions of equation dPII as \(n\to\infty\) are usually studied in the above limit [3]. Nonetheless, asymptotics for large \(n\) and finite \(\nu\) are of considerable interest in connection with various applications. For example, such solutions are used in the theory of matrix models in physics [5], [6], in calculations of zero-probabilities of eigenvalues of random matrices [7], and in symmetric group representations [8].

We will consider the Cauchy problem for equation (1.1) with initial conditions

$$ x_0=a, \qquad x_1=b.$$
(1.3)

The existence and uniqueness of the solution of problem (1.1), (1.3) are obvious, because equation dPII can be regarded as an iteration of the mappings of the plane into itself. Indeed, denoting \(y_n=x_n-x_{n-1}\), we write this mapping in the following form:

$$\mathcal{S}: \mathbb{R}^2 \to \mathbb{R}^2,$$

where

$$ {\left( {\begin{matrix} {x_{n+1} } \\ {y_{n+1}} \end{matrix} } \right) = \mathcal{S} \left( {\begin{matrix} x_{n} \\ y_{n} \end{matrix} } \right) } , \qquad { \mathcal{S}= \left( {\begin{matrix} {\dfrac{n}{\nu(x_n^2-1)}-1} & 1 \\[3mm] {\dfrac{n}{\nu(x_n^2-1)}-2} & 1 \end{matrix} } \right). } $$
(1.4)

In the case of real \(x_n\), the mapping \(\mathcal{S}\) is exponentially unstable, i.e., is ether an extension or a contracting, depending on the sign of the quantity \(n/\nu(x_n^2-1)\). The Julia set of the mapping \(\mathcal{S}\), i.e., the closure of the set of unstable periodic points [9], constitutes the domain bounded by the straight lines \(x=0\), \(x=y\), and the hyperbole \(y=x-1/x\). Therefore, a priori one would expect the chaotic behavior of the point \((x_n,y_n)\) for large \(n\) [10]. However, in this case, the mapping (1.4) possesses conservation laws, and equation dPII is completely integrable. In [8], it was integrated by the method of isomonodromic deformations and the corresponding Riemann problem was presented, which, in this case, is also discrete. Thus, in this case, there always exists a regular asymptotics of the solution.

In Secs. 2 and 3, we calculate the formal asymptotics of solutions of dPII for real and complex initial conditions. In Sec. 4, we consider the class of real initial conditions providing an exponentially decreasing asymptotics as \(n\to\infty\). It turns out that these solutions describe the distribution function of permutations of a symmetric group. This property can be used to justify the asymptotics and single out the transition domain from oscillations to an exponential decrease.

Just as other discrete integrable equations, dPII can be regarded as a chain of Bäcklund transformations of solutions of certain differential equations. In Sec. 5, we consider these equations as special cases of classical Painlevé equations of third and fifth type. The latter equation is used to justify the passage to the limit of the solution of dPII to the Hastings–McLeod solution of the Painlevé equation of second type.

2. Asymptotics of Real Solutions

In this section, we will consider the initial conditions (1.3) and the coefficient \(\nu\) to be real. Replacing the dependent variable \(x_n\):

$$ x_n=\sqrt{\frac{n}{\nu}}\,u_n,$$
(2.1)

we rewrite equation (1.1) as

$$ \sqrt{\frac{n+1}{n}}\,u_{n+1}+\sqrt{\frac{n-1}{n}}\,u_{n-1}= \frac{u_n}{u_n^2-\nu/n}\,.$$
(2.2)

As \(n\to\infty\), equation (2.2) in the leading order takes the form

$$ u_{n+1}+u_{n-1}=\frac{1}{u_n}\,.$$
(2.3)

The mapping (1.4) in this limit lets any initial condition \(u_0=a\), \(u_0=b\) tend to zero and to infinity. Indeed, the terms of the sequence \(u_n\) are of the form

$$u_{2n}=b\frac{(ab)^{n-1}}{(1-ab)^{n-1}}\,, \qquad u_{2n+1}=a\frac{(1-ab)^{n}}{(ab)^{n}}\,,$$

so that \(u_{2n} \to\infty\) and \(u_{2n+1} \to 0\) for \(ab > 1/2\). To these limits corresponds the one-parameter family of solutions of equation (2.3)

$$ u_n=\frac{(-1)^n}{\sqrt{2}} \tan\biggl(\frac{\pi n}{2}+\phi\biggr), \qquad \phi=\operatorname{const}.$$
(2.4)

as \(\phi \to \pi/2\) and \(\phi \to 0\).

The choice of the leading term of a real asymptotics of the form (2.4) is discussed below in Sec. 5, remark 1.

By analogy with the asymptotics of the classical Painlevé II equation [4, Chap. 6], we will search for corrections to the main term in the form

$$ u_n=\frac{(-1)^n}{\sqrt{2}}\biggl(1+\frac{\varkappa}{n}\biggr) \tan\biggl(\frac{\pi n}{2}+\alpha\sqrt{n}+\beta\ln(n)+\gamma\biggr).$$
(2.5)

Denote the phase of the tangent by

$$\phi_n=\frac{\pi n}2+\alpha\sqrt{n}+\beta\ln(n)+\gamma$$

and calculate the left-hand side of (2.2) up to \(O(n^{-3/2})\). We have

$$\begin{aligned} \, &\sqrt{\frac{n+1}{n}}\,u_{n+1}+\sqrt{\frac{n-1}{n}}\,u_{n-1} \\&\qquad =\frac{(-1)^n}{\sqrt{2}}\biggl(2\cot\phi_n+ \frac{4\varkappa+\alpha^2}{2n}\cot\phi_n+ \frac{\alpha^2}{2n}\cot^3 \phi_n\biggr)+O(n^{-3/2}). \end{aligned}$$

Compare this expression with the right-hand side of (2.2), obtaining

$$\frac{u_n}{u_n^2-\nu/n}=\frac{1}{u_n}+\frac{\nu}{n u_n^3}+ O(n^{-2})=\frac{(-1)^n}{\sqrt{2}} \biggl(2\cot\phi_n+\frac{2\nu}{n}\cot\phi_n+ \frac{4\nu}{n}\cot^3\phi_n\biggr)+O(n^{-2}).$$

This expression yields the following formulas for the first corrections for the amplitude and phase:

$$\varkappa=-\nu, \qquad \alpha=\sqrt{8\nu}\,.$$

The phase correction \(\beta\) for the logarithm in (2.5) is defined together with the following lower terms of the asymptotics:

$$ \begin{aligned} \, u_n&=\frac{(-1)^n}{\sqrt{2}}\biggl(1+\frac{\varkappa}{n}+ \frac{\epsilon}{n^{3/2}}\biggr)\biggl(\tan\phi_n+ \frac{\eta}{n^{3/2}}\tan^2\phi_n+\frac{\zeta}{n^{3/2}}\biggr), \\ \phi_n&=\frac{\pi n}{2}+\alpha\sqrt{n}+\beta\ln(n)+\gamma+ \frac{\delta}{\sqrt{n}}\,. \end{aligned}$$
(2.6)

Then the asymptotic term of order \(O(n^{-3/2})\) on the left-hand side of equation (2.2) is of the form

$$\frac{n^{-3/2}}{4\sqrt2}(8\eta-\alpha+8\alpha\beta(\cot\phi_n+ \cot^3\phi_n)+(8\eta-\alpha)\cot\phi_n).$$

Since there exist no terms of this order on the right-hand side of equation (2.2), the term indicated above must be set to zero. Then we obtain

$$\beta=0, \qquad \eta=\frac{\alpha}{8}=\sqrt{\frac{\nu}{8}}\,.$$

The remaining coefficients in the asymptotics (2.6) are obtained by comparing the terms of order \(O(n^{-2})\):

$$\zeta=\sqrt{\frac{\nu}{8}}\,, \qquad \epsilon=0, \qquad \delta=-\frac{2}{3}\,\nu^{3/2}.$$

Note that the final phase shift \(\gamma\) cannot be found from equation (1.1). Since the constant \(\phi\) in formula (2.4) for the exact solution of equation (2.2) is arbitrary, it follows that the formal asymptotics (2.5) is invariant under the shift \(\gamma\). Just as in the case of the classical Painlevé II equation, this shift must be determined from the initial condition (1.3) or from the conservation laws (integrals of motion) of a given solution. To calculate such shifts, one must apply the method of isomonodromic deformations, which is beyond the scope of this paper.

This proves the following theorem.

Theorem 1.

For real solutions of equation (1.1) with initial conditions (1.3) in the case of general position, the following formal asymptotics as \(n\to\infty\) holds:

$$ u_n=\frac{(-1)^n}{\sqrt{2}}\sqrt{\frac{n}{\nu}} \biggl(1-\frac{\nu}{n}+O(n^{-2})\biggr) \biggl(\tan\phi_n+n^{-3/2}\sqrt{\frac{\nu}{8}}\tan^2\phi_n+ n^{-3/2}\sqrt{\frac{\nu}{8}}\,\biggr),$$
(2.7)

where

$$\phi_n=\frac{\pi n}{2}+\sqrt{8\nu n}+\gamma- \frac{2}{3\sqrt{n}}\nu^{3/2},$$

and the constant \(\gamma\) is determined from the initial condition (1.3).

The case of special initial conditions leading to a different asymptotics than (2.7) is discussed below in Sec. 5.

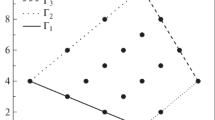
The solution of equation (1.1) with its asymptotics (2.7) is compared in Fig. 1.

Fig. 1.
figure 1

The real solution of dPII for \(\nu=1.5\) corresponding to the initial conditions \(x_0=-1\), \(x_1=2\) (small dots) and the asymptotics (2.7) (large dots).

Full size image

3. Asymptotics of Complex Solutions

In the case of the complex initial data (1.3), one can expect that the denominator of the right-hand side of the equation dPII does not vanish, and hence there will not be infinitely many poles, as in the real case.

To construct the asymptotics of the solution of dPII with complex initial conditions, again replacing the variable \(x_n\) (2.1), we pass to equation (2.2). Now we will search the solution of the equation in the leading order (2.3) in the form

$$ u_n=\frac{i}{\sqrt{2k'}}\operatorname{dn}(n(K+2iK')+\phi \mid k),$$
(3.1)

where \(\operatorname{dn}(x\mid k)\) is the Jacobi elliptic function of the modulus of \(k\) with primitive periods \(2K\) and \(4iK'\), where

$$K=\int_0^{\pi/2}\frac{d\varphi}{\sqrt{1-k^2\sin \varphi}}\,, \qquad K'=\int_0^{\pi/2}\sqrt{1-k^2\sin\varphi}\,d\varphi, \qquad k'=\sqrt{1-k^2}\,.$$

Equation (2.3) \(u_{n+1}+u_{n-1}=u_n^{-1}\) holds for the elliptic function (3.1) due to the periodicity relations [11, Chap. 13, Table 7]

$$\operatorname{dn}(nK+\phi \mid k)= \frac{k'}{\operatorname{dn}(\phi \mid k)}\,,\quad \operatorname{dn}(n K+2imK'+\phi\mid k)= -\frac{k'}{\operatorname{dn}(\phi \mid k)}\,, \qquad n,m \in \mathbb{Z}.$$

We will search for the asymptotic solution in the form similar to (2.6):

$$\begin{aligned} \, \nonumber u_n&=\frac{i}{\sqrt{2k'}}\biggl(1+\frac{\varkappa}{n}+ \frac{\varepsilon}{n^{2}}\biggr) \phi_n \mid k) \\ &\qquad\times \biggl(\operatorname{dn}(n(K+2iK')+\frac{\eta}{n^{3/2}}\operatorname{sn}(nK+\phi_n \mid k) \operatorname{cn}(nK+\phi_n \mid k)+\frac{\zeta}{n^{3/2}}\biggr), \\ \nonumber \phi_n&=\alpha\sqrt{n}+\beta\ln n+\chi+\frac{\gamma}{\sqrt{n}}\,, \end{aligned}$$
(3.2)

where \(\alpha\), \(\beta\), \(\gamma\), \(\varepsilon\), \(\chi\) are constants and \(\operatorname{sn}\), \(\operatorname{cn}\) are Jacobi elliptic sine and cosine. For brevity, in these functions, we will omit the modulus of \(k\) and the index \(n\) in the argument, \(\operatorname{dn}(\phi)=\operatorname{dn}(\phi_n \mid k)\). Substituting the asymptotic ansatz (3.2) into equation (2.2) and expanding in a Taylor series as \(n\to\infty\), we obtain the remainders of order \(O(n^{-1})\) on the right-hand side:

$$n^{-1}\bigl\{16\varkappa\operatorname{dn}^2(\phi)+ \alpha^2 k^2\operatorname{cn}^2(\phi)+ \alpha^2(k^2-1)k^2\operatorname{sn}^2(\phi)-16\sqrt{1-k^2}\,\nu\bigr\}.$$

Equating this expression to zero, we use the well-known relations for the Jacobi functions

$$\operatorname{sn}^2(\phi)+\operatorname{cn}^2(\phi)=1 \qquad\text{and}\qquad k^2\operatorname{sn}^2(\phi)+\operatorname{dn}^2(\phi)=1.$$

Then

$$ \alpha=\frac{\sqrt{8\nu}}{\sqrt[4]{1-k^2}}\,, \qquad \varkappa=-\frac{(k^2-2)\nu}{2\sqrt{1-k^2}}\,.$$
(3.3)

Equating to zero the next correction term of order \(O(n^{-3/2})\), we can write

$$\begin{aligned} \, &8\zeta(\sqrt{1-k^2}-1)+4\alpha\beta k^2\sqrt{1-k^2}\,\frac{\operatorname{cn}^2(\phi)+(k^2-1)\operatorname{sn}^2(\phi)} {\operatorname{dn}(\phi)} \\&\qquad +\sqrt{1-k^2}(\alpha k^2+16\eta) \operatorname{cn}(\phi)\operatorname{sn}(\phi)=0, \end{aligned}$$

whence we obtain the expressions for the following coefficients (3.2):

$$ \eta=-\frac{\alpha k^2}{16}, \qquad \zeta=0, \qquad \beta=0.$$
(3.4)

Finally, we write out terms of order \(O(n^{-2})\). We have

$$\begin{aligned} \, \nonumber n^{-2}\bigl\{&(k^2\operatorname{cn}^2(\phi)(\alpha(\alpha\varkappa+ 4\gamma)+4\beta^2)+(k^2-1)k^2\operatorname{sn}^2(\phi) (\alpha(\alpha\varkappa+4\gamma)+4\beta^2)+8\varepsilon-1) \\ &\qquad +4\beta k^2\operatorname{cn}^2(\phi)\operatorname{sn}^2(\phi) -8(\delta^2-\varepsilon)\operatorname{dn}^2(\phi)+ 48\varkappa\sqrt{1-k^2}\,\nu\bigr\}. \end{aligned}$$
(3.5)

Substitute here the values of \(\alpha\), \(\beta\), and \(\varkappa\) already found in (3.3) and (3.4). Then (3.5) simplifies to the form

$$\begin{aligned} \, n^{-2}\bigl\{&-8\sqrt{k^2-1}\,\epsilon+16\sqrt{2}(1-k^2)^{5/4} \gamma\sqrt{\nu}+\sqrt{k^2-1}\,(1+32(k^2-2)\nu^2) \\&\qquad +2\bigl(4(k^2-1)^{3/2}\varepsilon+(k^2-2) \sqrt{\nu}\,(4\sqrt{2}\,(1-k^2)^{5/4}\gamma \\&\qquad\qquad\hphantom{+2\bigl(} +3(k^2-2)\sqrt{k^2-1}\,\nu^{3/2})\bigr) \operatorname{dn}^2(\phi)\bigr\}. \end{aligned}$$

Again equating this expression to zero, we obtain the following formulas for \(\gamma\) and \(\varepsilon\):

$$ \gamma=\frac{k^2+88\nu^2-120k^2\nu^2+38k^4\nu^2-1} {8\sqrt{2}\,(1-k^2)^{3/4}(3k^2-4)\sqrt{\nu}}\,,\qquad \varepsilon=\frac{(k^2-2)(1+20(k^2-2)\nu^2)}{8(3k^2-4)}\,.$$
(3.6)

Note that, just as above, in the real case, the constant \(\chi\) in the phase remains undefined. The modulus of the elliptic function \(k\) also remains indefinite. These complex parameters correspond to the choice of a specific solution. of the equation dPII and are calculated from the initial condition or the invariants of the solution.

This proves the following theorem.

Theorem 2.

For the complex solutions of equation (1.1) with initial conditions (1.3), the formal asymptotics (3.2) as \(n\to\infty\) holds.

The solution of equation (1.1) is compared with its asymptotics (3.2) in Fig. 2 and Fig. 3. The points \(x_{2n}\) are connected sequentially by segments, and the odd points \(x_{2n+1}\) are not shown; they form \(n\) graphs symmetric with respect to the axis, because \(x_{2n+1} \sim -x_{2n}\).

Fig. 2.
figure 2

The complex solution of dPII for \(\nu=1.5\) corresponding to the initial conditions \(x_0=1\), \(x_1=0.3+0.3i\). The real part of the solution (solid line) and its asymptotics (dotted line) corresponds to \(k=0.50\), \(\chi=5.4+4.6i\).

Full size image
Fig. 3.
figure 3

The complex solution of dPII for \(\nu=1.5\) corresponding to the initial conditions \(x_0=1\), \(x_1=0.3+0.3i\). The pure imaginary part of the solution (solid line) and its asymptotics (dotted line) corresponds to \(k=0.50\), \(\chi=5.4+4.6i\).

Full size image

4. Exponentially Decreasing Solutions. Symmetric Group Representation

Equation dPII has an identically zero solution \(x_n \equiv 0\). Accordingly, the mapping \(\mathcal S\) (1.4) of the plane \(\mathbb R^2\) has the origin \((x,y)=(0,0)\) as a stationary point, and, for \(|x_n|<1\), this mapping is contractive. Therefore, one can expect that there exist solutions tending to the limit \(x_n\to 0\) as \(n\to\infty\).

It turns out that such solutions arise in applications of the equation dPII related to the calculation of the null probabilities of the distribution of eigenvalues of random matrices [12] and to symmetric group representations [7]. Let us briefly present these results and derive formulas for the exponentially decreasing solutions of (1.1).

Let \(S_n\) be a symmetric group of degree \(n\), i.e., the permutation group of a set of \(n\) elements, denoted usually by the natural numbers \(1, 2,\dots,n\). Denote by \(l_n(\sigma)\) the length of the largest increasing sequence of the substitution \(\sigma\in S_n\) and through \(|\,\cdot\,|\) is the number of elements in the set. Let us put

$$p_k^{n}=\frac{1}{n!}|\{\sigma\in S_n\mid l_n(\sigma)\le k\}|$$

and introduce the generating function

$$p_k(\nu)=e^{-\nu^2}\sum_{n=0}^\infty\frac{\nu^{2n}}{n!}\,p_k^n,$$

where \(\nu\) is a complex parameter. Another equivalent definition follows from the Robinson–Schoensted algorithm [13]. Take all partitions of the permutation

$$\lambda=(\lambda_1,\lambda_2,\dots,\lambda_l)\in S_{|\lambda|}$$

such that \(|\lambda_1|\ge\cdots\ge |\lambda_l|>0\), \(|\lambda_1|\le k\) and \(|\lambda|= |\lambda_1|+\cdots+|\lambda_l|\). Denote by \(\dim\lambda\) the dimension of the irreducible representation symmetric group \(S_{|\lambda|}\); then

$$p_k(\nu)=e^{-\nu^2}\sum_{|\lambda_1|\le k} {\biggl(\frac{\dim\lambda}{|\lambda|!}\,\nu^{|\lambda|}\biggr)}^2,$$

where the summation is taken over all such partitions of \(\lambda\).

Calculating the function \(p_k(\nu)\) is an important problem in the theory of symmetric group representations. It was proved in [14] that this function can be expressed in terms of the Toeplitz determinant:

$$ p_k(\nu)=e^{-\nu^2}\det[f_{i-j}]_{i,j=1}^k\,,\qquad \sum_{m=-\infty}^{+\infty}f_m\zeta^m=e^{\nu(\zeta+\zeta^{-1})}.$$
(4.1)

The connection between the function \(p_k(\nu)\) and the solution of equation dPII was first established in [12]. Define a sequence \(\{x_n\}_{n=0}^\infty\) by the initial conditions

$$ x_{0}=\mp 1, \qquad x_1=\pm \frac{f_1}{f_0}$$
(4.2)

with \(f_i\) from (4.1) and the recurrence relation

$$x_{n+1}+x_{n-1}=\frac{nx_n}{\nu(x_n^2-1)}\,, \qquad n\ge 1.$$

Then, for any \(k\ge 1\) and \(\nu\), in general position, the following recursive relations are valid:

$$ \frac{p_{k+1}(\nu)p_{k-1}(\nu)}{p_{k}^2(\nu)}=1-x_k^2.$$
(4.3)

Here the words “in general position” mean that \(\nu\) does not belong to the set of poles of the meromorphic function \(x_k=x_k(\nu)\).

Another derivation of this result using a discrete Riemann problem was given later in [7].

Equality (4.3) can be used to estimate the solution \(x_n\) with initial conditions (4.2). Let us note in passing that \(f_0=I_0(2\nu)\) and \(f_1=I_1(2\nu)\) in view of the well-known decomposition [11]

$$e^{\nu(\zeta+\zeta^{-1})}=\sum_{m=-\infty}^{+\infty} I_m(2\nu)\zeta^m,$$

where the \(I_m\) are the modified Bessel functions of the first kind.

For Toeplitz determinants (4.1), Szegö’s limit theorem s \(k\to\infty\) holds [15]:

$$\lim_{k\to\infty}\det[I_{i-j}(2\nu)]_{i,j=1}^k=e^{\nu^2}.$$

Thus, \(p_k(\nu) \to 1\) and \(x_k\to 0\) as \(k\to\infty\). From a probabilistic point of view, the asymptotics as \(p_k(\nu) \to 1\) corresponds to the total probability that an increasing subsequence \(l_n\) of the permutation \(\sigma \in S_n\) is of length at most \(n\).

To estimate the decay rate of the solution, we use the corresponding result from [16], where the quantity \(p_{k+1}(\nu)/p_k(\nu)\) was esimated. Let \(\gamma=2\nu/(n-1)\), and let \(\gamma <1\). Then there exist positive constants \(c\) and \(C\) depending on \(\gamma\) and such that

$$\biggl|\frac{p_{n+1}(\nu)}{p_n(\nu)}-1\biggr| < C e^{-cn},\qquad n > 2\nu +1.$$

It follows that the solution \(x_n\) is exponentially small in the domain \(n > 2\nu\). Figure 4 illustrates the behavior of the functions \(x_n\) also \(p_n\) for \(\nu=15\) and \(n\le 60\).

Fig. 4.
figure 4

The special the solution of dPII corresponding to \(\nu=15\) and the initial conditions (4.2) (small dots) and the values of the Toeplitz determinant \(p_n(\nu)\) (large dots).

Full size image

Thus, the following theorem holds.

Theorem 3.

Equation (1.1) with initial conditions (4.2)

$$x_0=\mp 1, \qquad x_1=\pm \frac{I_1(2\nu)}{I_0(2\nu)}$$

has exponentially decreasing solutions such that

$$|x_n|=o(e^{-cn}), \qquad n > 2\nu+1, \quad n\to\infty.$$

5. Equation dPII and Other Painlevé Equations

Equation dPII can be regarded as the Bäcklund transformation, connecting various solutions \(x_n(\nu)\) of some nonlinear differential equations with respect to the variable \(\nu\). This approach, which is common in the theory of solitons, can also be used to calculate the asymptotics of the solutions of equation dPII itself. It turns out that the nonlinear equations with respect to \(\nu\), to which dPII corresponds, are the classical Painlevé equations of third (PIII) and fifth (PV). type. Let us briefly summarize this conclusion following the paper [12] and then prove the validity of the scaling (1.2) mentioned in the Introduction as \(n,\nu \to\infty\).

Let use the following notation for the derivative with respect to \(\nu\): \(f'=df/d\nu\). The derivatives of \(x_n\) with respect to \(\nu\) from equation (1.1) are expressed as follows:

$$x_n' =\frac{n}{\nu}\,x_n+2x_{n+1}(1-x_n^2),$$
(5.1)
$$x_n' =\frac{n}{\nu}\,x_n-2x_{n-1}(1-x_n^2).$$
(5.2)

Obviously, equalities (5.1) and (5.2) are consistent with equation (1.1).

We find \(x_{n+1}\) from equality (5.1) and substitute it into (5.2), replacing \(n\) by \(n+1\). Then we obtain the following second-order equation for the function \(v_n=1-x_n^2\):

$$ v_n''=\frac{1}{2}\biggl(\frac{1}{v_n-1}+ \frac{1}{v_n}\biggr)(v_n')^2-\frac{v_n'}{\nu}- 8v_n(v_n-1)+2\frac{n^2}{\nu^2}\frac{v_n-1}{v_n}\,.$$
(5.3)

Equation (5.3) becomes the classical equation PV [4] if we replace \(\nu=t^2\) and \(v_n \mapsto v/v-1\) with coefficients \(\alpha=0\), \(\beta=-n^2/2\), \(\gamma=2\), and \(\delta=0\).

The third Painlevé equation is also derived from relations (5.1) and (5.2). Putting \(w_n=x_n/x_{n-1}\), we express the derivative of \(w_n\) from (5.1), replacing \(n\) by \(n-1\):

$$ w_n'=-\frac{2n-1}{\nu}\,w_n-2+4x_n^2-2w_n^2.$$
(5.4)

Further, using (5.2), we finally obtain

$$ w_n''=\frac{1}{w_n}(w_n')^2-\frac{1}{\nu}\,w_n'+ 4\frac{n-1}{\nu}\,w_n^2-\frac{4n}{\nu}+4w_n^3-\frac{4}{w_n}\,,$$
(5.5)

which coincides with equation PIII with coefficients \(\alpha=4(n-1)\), \(\beta=-4n\), \(\gamma=4\), and \(\delta=-4\) [4].

Let the real solution in equation (5.3) tend to to \(1\) at infinity with respect to \(\nu\). We also put \(n \gg 1\) and consider the behavior of the solution in a neighborhood of the point \(\nu=n/2\). Let us introduce the new variables

$$t=(n-2\nu)n^{-1/3}, \qquad v_n=1-n^{-2/3} u^2(t);$$

then equation (5.3) expands in powers of the small parameter \(n^{-1/3}\). At the highest power \(n^{-2/3}\), we will have the identity \(8u^2=8u^2\), and, at the next power \(n^{-4/3}\), we will have the following equation for the function \(u(t)\):

$$ u_{tt}=tu +2u^3.$$
(5.6)

Recalling the replacement \(v_n=1-x_n^2\), we conclude that, in the leading order, for large \(n\), the solution of dPII is the same up to sign with the solution of equation PII (5.6).

The choice of the solution of equation (5.6) is dictated here by the asymptotics of the real solution \(x_n\) decreasing for \(n>2\nu\). Theorem 3 implies that such a solution decreases exponentially, so that \(u(t)=o(e^{-ct})\) as \(t\to+\infty\). It is known that this solution of equation PII exists and is unique [4, Chap. 10]. This is the Hastings–McLeod solution, for large negative \(t\) with the asymptotics

$$u(t)=\sqrt{-\frac t2}+O((-t)^{-1/4}).$$

Thus, the passage to the limit (1.2) is valid only in the transition domain \(n \sim 2\nu\), where does the oscillating mode of \(x_n\) is sewn to the exponentially decreasing mode (see Fig. 4). In this case, the square \(x_n^2\) does not contain the multiplier \((-1)^n\) and is a smooth function of \(u^2(t)\).

Remark 1.

The real solutions of equation (5.6) in the case of general position have simple poles on the real axis. Their distribution as \(t\to +\infty\) is described by the asymptotics

$$ u(t)=\pm\sqrt{2t}\,\tan\biggl(\frac{\sqrt2}{3}\,t^{3/2}+ \frac{1}{2}\,c_1\ln t+c_2\biggr)+O(t^{-3/2}),$$
(5.7)

where the constants \(c_1\) and \(c_2\) are explicitly expressed in terms of the monodromy data of the Painlevé II equation (5.6) [4, Chap. 10, Theorem 10.1]. The asymptotics (5.7), in turn, is consistent with the representation of the solution \(u_n\) of dPII (2.7) for \(t=(n-2\nu)n^{-1/3} \gg 1\). This fact explains the choice of the leading term of the real asymptotics of \(u_n\) in the form of a tangent, but not as another solution of the discrete equation (2.3).