Asymptotic Expansions of Solutions to the Second Term of the Fourth Painlevé Hierarchy

Abstract

Asymptotic behavior and asymptotic expansions of solutions to the second term of the fourth Painlevé hierarchy are constructed using power geometry methods [1]. Only results for the case of general position—for the equation parameters $\beta ,\delta \ne 0$—are provided. For constructing asymptotic expansions, a code written in a computer algebra system is used.

1 INTRODUCTION

The aim of this paper is to investigate asymptotic expansions of the second term of the fourth Painlevé hierarchy [1, 2]. The Painlevé transcendents are used in statistical physics, quantum field theory, geometry of minimal surfaces, number theory, and other fields.

2 POWER GEOMETRY METHODS

Asymptotic expansions can be constructed using power geometry methods [3]. We now describe some steps of these methods.

We consider a differential equation in the form of a differential sum, i.e., its left-hand side is a polynomial in an independent variable, a dependent variable, and its derivatives—a sum of differential monomials. For this equation, we construct the Newton polygon on the coordinate plane (${{q}_{1}}$, ${{q}_{2}}$), which is the convex hull of the available points (see [3]). Each point of the Newton polygon is associated with one or more monomials. All generalized faces (vertices and edges) of this polygon are considered one by one. The monomials corresponding to the generalized face are summed to obtain the truncated sum function $\hat {f}_{j}^{{(d)}}(X) = \sum {{{a}_{i}}(X)}$ over $Q({{a}_{i}}) \in S_{j}^{{(d)}}$.

Then, outward normals the general form of the coordinates of which is $\lambda \omega (1,r)$, where $\lambda > 0$, are constructed for each edge. If $x \to 0$, then $\omega < 0$; and if $x \to \infty$, then $\omega > 0$. The coordinates of the normals determine the degree of the first term in the asymptotic expansion of the solution to the equation for which the asymptotic form y(x) is constructed; for an edge with the outward normal $\omega (1,r)$, the general asymptotic form is $y = c{{x}^{r}}$. For vertices, normal cones are defined as the parts of the plane lying between the rays spanned by the vectors of outward normal to the edges adjacent to the vertices.

3 CONSTRUCTION OF THE NEWTON POLYGON FOR THE SECOND TERM OF THE FOURTH PAINLEVÉ HIERARCHY

Write the second term of the fourth Painlevé hierarchy [3]. Note that this equation is represented by the differential sum

$$\begin{gathered} ({{y}_{{xx}}} - 2xy - 2{{y}^{3}} - \beta ){{y}^{2}}{{y}_{{xxxx}}} - \frac{1}{2}{{y}^{2}}y_{{xxx}}^{2} \\ + \;(2{{y}^{2}} + 8{{y}^{3}}{{y}_{x}} + 4y{{y}_{x}}x - {{y}_{x}}{{y}_{{xx}}} + \beta {{y}_{x}})y{{y}_{{xxx}}} \\ - \;\frac{4}{3}yy_{{xx}}^{3} + \left( {3x{{y}^{2}} + 3\beta y - \frac{3}{2}{{y}^{4}} + \frac{3}{2}y_{x}^{2}} \right)y_{{xx}}^{2} \\ + \;(\beta {{y}^{4}} - 2{{y}_{x}}{{y}^{2}} - 12y_{x}^{2}{{y}^{3}} - 2{{\beta }^{2}}y + 10x{{y}^{5}} \\ - \;3\beta y_{x}^{2} + 10{{y}^{7}} - 4xyy_{x}^{2} - 4\beta x{{y}^{2}}){{y}_{{xx}}} \\ + \;2(\beta \, - \,4{{y}^{3}}){{y}^{2}}{{y}_{x}}\, + \,\left( {4\beta xy\, + \,8x{{y}^{4}}\, + \,\frac{3}{2}{{\beta }^{2}}\, + \,12\beta {{y}^{3}}} \right)y_{x}^{2} \\ - \frac{{10}}{3}{{y}^{{10}}} - 8x{{y}^{8}} - 2\beta {{y}^{7}} - 6{{x}^{2}}{{y}^{6}} - 2x\beta {{y}^{5}} \\ + \;\left( {\frac{1}{2}{{\beta }^{2}} - 2 + 9\delta - \frac{4}{3}{{x}^{3}}} \right){{y}^{4}} + x{{\beta }^{2}}{{y}^{2}} + \frac{1}{3}{{\beta }^{3}}y = 0. \\ \end{gathered} $$

(3.1)

Here x is the independent complex variable, y is the dependent complex variable, and $\beta$ and $\delta$ are complex’ parameters. Below, we assume that both these parameters are nonzero.

The differential monomials in Eq. (3.1) have the following 18 exponents: $( - 4;\;3)$, $( - 6;\;4)$, $( - 3;\;4)$, (–4; 6), $( - 2;\;5)$, $( - 2;\;2)$, $( - 1;\;6)$, $( - 2;\;8)$, $( - 1;\;3)$, $(0;\;10)$, (1; 8), (0; 7), (2; 6), (–1; 5), (0; 4), (3; 4), (1; 2), and (0; 1).

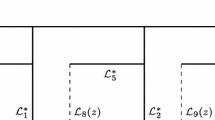
We put them onto the coordinate plane (${{q}_{1}}$, ${{q}_{2}}$) and construct the Newton polygon as their convex hull (see Fig. 1).

Fig. 1.

This polygon can be constructed using the code in Listing 1 (the left-hand side of Eq. (3.1) should be substituted for the ellipsis in the command Expand).

(*Original equation *)

equation = Expand [ . . . ] ;

order = 4 ; v a r i a b l e = x ;

function = y [ x ] ;

(*Calculation of vector exponents of monomials*)

d = Coefficient Rules [equation,

  Join [{variable, function},

  Table [D[function, {variable, i}],

  {i, 1, order}]]]/.Rule => List

vectorDegree [degrees_ ] :=

  {degrees [[1]], degrees[[2]]} +

  Total [Table[{=( i = 2), 1}

  degrees [[i]], {i, 3,

  Length [degrees]}]]

points = Sort [DeleteDuplicates [ Map [

vectorDegree, (#[[1]]) & /@d]]]

(*Construction of the Newton polygon *)

convexHull = ConvexHullMesh [points,

  PlotTheme => “Detailed”];

convexHull Points =

  MeshCoordinates [convexHull];

Show [convexHull, ListPlot [points,

  PlotStyle => {Red,

  PointSize [Large]}]]

Listing 1. Construction of the Newton polygon.

To each edge and vertex of the Newton polygon shown in Fig. 1, we assign the points ${{Q}_{i}}$ belonging to it and make up truncated sums. This can be done using the computer algebra code presented in Listing 2.

(*Points of the Newton polygon vertices *)

gamma0 = (#[[1]]) & /@

  Rationalize [ MeshPrimitives[

Region ‘ Mesh ‘ MergeCells [convexHull], 0]]

lines = Rationalize [ MeshPrimitives [

Region ‘Mesh‘ MergeCells [convexHull], 1]];

(*Points of the Newton polygon edges *)

gamma1 = Table [ Select [points,

  RegionMember[lines[[i]], #] &], {i,

  1, Length [lines]}]

(*Truncated equations for vertices *)

f0 = Table [FromCoefficientRules [ Map [

Rule [#[[1]], #[[2]]]&, Select [d,

vectorDegree [#[[1]]] == gamma0 [[i]]

&]], Join [{variable, function},

Table [ D [function, {variable, i}],

{ i, 1, order}]]], {i, 1,

Length [gamma0]}]

(*Truncated equations for edges *)

f1 = Table [FromCoefficientRules [ Map [

Rule [#[[1]], #[[2]]] &,

  Flatten [Table [Select[d,

  vectorDegree [#[[1]]] ==

  gamma1 [[i]] [[j]] &], {j, 1,

  Length [gamma1 [[i]]]}], 1]],

  Join [{variable, function},

  Table [D[function, {variable, i}],

  {i, 1, order}]]], {i, 1,

  Length [gamma1]}]

Listing 2. Calculation of truncated equations.

Now, we consider the edges of the resulting polygon one by one and then consider its vertices and find the asymptotic forms and asymptotic expansions corresponding to them.

4 EDGE ${{\Gamma }_{1}}$

The edge ${{\Gamma }_{1}}$ is associated with the outward normal ${{N}_{1}} = ( - 1; - {\kern 1pt} 2)$ and the truncated equation

$$\begin{gathered} {{y}_{{xx}}}{{y}^{2}}{{y}_{{xxxx}}} - \beta {{y}^{2}}{{y}_{{xxxx}}} - \frac{1}{2}{{y}^{2}}y_{{xxx}}^{2} - y{{y}_{x}}{{y}_{{xx}}}{{y}_{{xxx}}} \\ + \;\beta y{{y}_{x}}{{y}_{{xxx}}} - \frac{4}{3}yy_{{xx}}^{3} + 3\beta yy_{{xx}}^{2} + \frac{3}{2}y_{x}^{2}y_{{xx}}^{2} \\ - \,2{{\beta }^{2}}y{{y}_{{xx}}} - 3\beta y_{x}^{2}{{y}_{{xx}}} + \frac{3}{2}{{\beta }^{2}}y_{x}^{2} + c13{{\beta }^{3}}y = 0. \\ \end{gathered} $$

(4.1)

This edge is associated with the asymptotic form y = $c{{x}^{2}}$ as $x \to 0$. The values of c are found from the equation

$$\frac{1}{3}{{\beta }^{3}}c + 2{{\beta }^{2}}{{c}^{2}} - 12\beta {{c}^{3}} + \frac{{40}}{3}{{c}^{4}} = 0,$$

the nonzero roots of which are ${{c}_{1}} = - 0.1\beta$ (simple) and ${{c}_{2}} = 0.5\beta$ (of multiplicity two).

Let us check if there are critical numbers. We have the linear operator

$$\begin{gathered} {{y}_{{xx}}}{{y}^{2}}\frac{{{{d}^{4}}}}{{d{{x}^{4}}}} - \beta {{y}^{2}}\frac{{{{d}^{4}}}}{{d{{x}^{4}}}} - y{{y}_{x}}{{y}_{{xx}}}\frac{{{{d}^{3}}}}{{d{{x}^{3}}}} + \beta y{{y}_{x}}\frac{{{{d}^{3}}}}{{d{{x}^{3}}}} \\ - \;\frac{4}{3}y_{{xx}}^{3} - 4yy_{{xx}}^{2}\frac{{{{d}^{2}}}}{{d{{x}^{2}}}} + 3\beta y_{{xx}}^{2} + 6\beta y{{y}_{{xx}}}\frac{{{{d}^{2}}}}{{d{{x}^{2}}}} \\ + \;3y_{x}^{2}{{y}_{{xx}}}\frac{{{{d}^{2}}}}{{d{{x}^{2}}}} + 3{{y}_{x}}y_{{xx}}^{2}\frac{d}{{dx}} - 2{{\beta }^{2}}y\frac{{{{d}^{2}}}}{{d{{x}^{2}}}} - 2{{\beta }^{2}}{{y}_{{xx}}} \\ - \;6\beta {{y}_{x}}{{y}_{{xx}}}\frac{d}{{dx}} - - 3\beta y_{x}^{2}\frac{{{{d}^{2}}}}{{d{{x}^{2}}}} + 3{{\beta }^{2}}{{y}_{x}}\frac{d}{{dx}} + \frac{1}{3}{{\beta }^{3}}. \\ \end{gathered} $$

(4.2)

By substituting $y = - \tfrac{\beta }{{10}}{{x}^{2}}$ into (4.2), we obtain the operator

$$\begin{gathered} \varkappa = \frac{{108{{\beta }^{3}}}}{{125}} - \frac{{108{{\beta }^{3}}}}{{125}}x\frac{d}{{dx}} + \frac{{24{{\beta }^{3}}}}{{125}}{{x}^{2}}\frac{{{{d}^{2}}}}{{d{{x}^{2}}}} \\ + \;\frac{{3{{\beta }^{3}}}}{{125}}{{x}^{3}}\frac{{{{d}^{3}}}}{{d{{x}^{3}}}} - \frac{{3{{\beta }^{3}}}}{{250}}{{x}^{4}}\frac{{{{d}^{4}}}}{{d{{x}^{4}}}}. \\ \end{gathered} $$

Apply the operator $\varkappa$ to x^k and reduce the result by ${{x}^{k}}{{\beta }^{3}}$ to obtain the characteristic polynomial

$$\nu (k) = \frac{{108}}{{125}} - \frac{{117}}{{125}}k - \frac{3}{{250}}{{k}^{2}} + \frac{{12}}{{125}}{{k}^{3}} - \frac{3}{{250}}{{k}^{4}}$$

with the roots ${{k}_{1}} = - 3$, ${{k}_{2}} = 1$, ${{k}_{3}} = 4$, and ${{k}_{4}} = 6$. Taking into account the appropriate values of k, namely, k = 4 and $k = 6$, we write the set of exponents involved in the expansion that continues the asymptotic form under consideration and write the corresponding family of power expansions of solutions as $x \to 0$

$${{W}_{1}} = \left\{ {y = - \frac{{\beta {{x}^{2}}}}{{10}} + {{c}_{4}}{{x}^{4}} + \frac{\beta }{{80}}{{x}^{5}} + {{c}_{6}}{{x}^{6}} + \sum\limits_{k = 7}^\infty {{{c}_{k}}} {{x}^{k}}} \right\},$$

where ${{c}_{4}},{{c}_{6}} \in \mathbb{C}$ are arbitrary constants and the other coefficients ${{c}_{k}}$ for $k > 6$ are uniquely expressed in terms of these constants.

The substitution $y = \tfrac{\beta }{2}{{x}^{2}}$ gives a zero operator because the corresponding root is multiple. Make the change $y = \tfrac{\beta }{2}{{x}^{2}} + w$ in Eq. (3.1) and carry out calculations for the resulting equation. Then we obtain two versions for the next term of the expansion: w_{1, 2} = $\left( {\tfrac{\beta }{{20}} \pm \tfrac{{3\beta \sqrt {2\delta } }}{{250}}} \right){{x}^{5}}$. By applying the first variation of the truncated equation corresponding to the edge of the Newton polygon with the dependent variable $w$ (calculated on the solutions ${{w}_{{1,2}}}$) to x^k, we obtain the characteristic polynomial the roots of which are k₁ = 0, ${{k}_{2}} = 1$, ${{k}_{3}} = 4$, and ${{k}_{4}} = 6$. Again, only the values four and six are suitable. Thus, by continuing the asymptotic form $y = \tfrac{\beta }{2}{{x}^{2}}$ in the form of power asymptotic expansions, we obtain two families of expansions of the solutions as $x \to 0$:

$$\begin{gathered} {{W}_{{2,3}}} = \left\{ {y = \frac{{\beta {{x}^{2}}}}{2}} \right. + {{c}_{4}}{{x}^{4}} \\ + \;\left( {\frac{\beta }{{20}} \pm \frac{{3\beta \sqrt {2\delta } }}{{250}}} \right){{x}^{5}} + {{c}_{6}}{{x}^{6}} + \left. {\sum\limits_{k = 7}^\infty {{{c}_{k}}} {{x}^{k}}} \right\}, \\ \end{gathered} $$

where ${{c}_{4}},{{c}_{6}} \in \mathbb{C}$ are arbitrary constants, and ${{c}_{k}}$ for $k > 6$ are uniquely represented in terms of these constants.

5 EDGE ${{\Gamma }_{2}}$

This edge is associated with the outward normal ${{N}_{2}} = ( - 1;\;1)$ and the truncated equation

$$\begin{gathered} {{y}_{{xx}}}{{y}^{2}}{{y}_{{xxxx}}} - 2{{y}^{5}}{{y}_{{xxxx}}} - \frac{1}{2}{{y}^{2}}y_{{xxx}}^{2} + 8{{y}^{4}}{{y}_{x}}{{y}_{{xxx}}} \\ - \;{{y}_{x}}{{y}_{{xx}}}y{{y}_{{xxx}}} - \frac{4}{3}yy_{{xx}}^{3} - \frac{3}{2}{{y}^{4}}y_{{xx}}^{2} \\ \frac{3}{2}y_{x}^{2}y_{{xx}}^{2} - 12y_{x}^{2}{{y}^{3}}{{y}_{{xx}}} + 10{{y}^{7}}{{y}_{{xx}}} - \frac{{10}}{3}{{y}^{{10}}} = 0, \\ \end{gathered} $$

(5.1)

which yields the asymptotic form $y = \tfrac{c}{x}$ as $x \to 0$. The values of c are found from the equation

$${{c}^{4}}({{c}^{6}} - 6{{c}^{4}} + 9{{c}^{2}} - 4) = 0,$$

the nonzero roots of which are ${{c}_{1}} = 2$, ${{c}_{2}} = - 2$ (simple) and ${{c}_{3}} = 1$, ${{c}_{4}} = - 1$ (of multiplicity two each).

For the roots $c = \pm 2$, we conclude that the roots k of the characteristic polynomial are such that $k \in$ {–3, –2, 3, 4}, which affects the structure of the exponents involved in the power expansion. For continuing these asymptotic forms as $x \to 0$, we have the following families of expansions:

$${{W}_{4}} = \left\{ {y = \frac{2}{x} + \left( {\frac{{\beta - 2}}{{20}}} \right){{x}^{2}} + {{c}_{3}}{{c}^{3}} + {{c}_{4}}{{x}^{4}} + \sum\limits_{k = 5}^\infty {{{c}_{k}}} {{x}^{k}}} \right\};$$

$${{W}_{5}} = \left\{ {y = - \frac{2}{x} + \left( {\frac{{\beta + 2}}{{20}}} \right){{x}^{2}} + {{c}_{3}}{{c}^{3}} + {{c}_{4}}{{x}^{4}} + \sum\limits_{k = 5}^\infty {{{c}_{k}}} {{x}^{k}}} \right\},$$

here ${{c}_{3}},{{c}_{4}} \in \mathbb{C}$ are arbitrary constants, and the other coefficients ${{c}_{k}}$ for $k > 4$ are uniquely expressed in terms of these constants.

To analyze the expansions corresponding to the multiple roots $c = \pm 1$, we change the variables $y = \pm \tfrac{1}{x}$ + w in Eq. (5.1) while seeking the next asymptotic term for the new equation and its Newton polygon. For example, the next term is ${{w}_{{6,7}}} = \pm \tfrac{{\sqrt {9\delta - 8 - 8\beta - 2{{\beta }^{2}}} }}{{4\sqrt 2 }}{{x}^{2}}$ for $y = \tfrac{1}{x}$, and ${{w}_{{8,9}}} = \pm \tfrac{{\sqrt { - 9\delta + 8 - 8\beta + 2{{\beta }^{2}}} }}{{4\sqrt 2 }}{{x}^{2}}$ for $y = - \tfrac{1}{x}$ (here indexing is in accordance with indexing in the corresponding expansions). Next, we find the characteristic polynomial. Its roots are ${{k}_{1}} = - 2$, ${{k}_{2}} = 0$, ${{k}_{3}} = 3$, and ${{k}_{4}} = 4$. The critical numbers are ${{k}_{3}}$ and ${{k}_{4}}$ because $\operatorname{Re} {{k}_{i}} > 2$ for them. We have the following four families of asymptotic expansions as $x \to 0$:

$$\begin{gathered} {{W}_{{6,7}}} = \left\{ {y = \frac{1}{x} \pm \frac{{\sqrt {9\delta - 8 - 8\beta - 2{{\beta }^{2}}} }}{{4\sqrt 2 }}} \right.{{x}^{2}} \\ + \;{{c}_{3}}{{x}^{3}} + {{c}_{4}}{{x}^{4}} + \left. {\sum\limits_{k = 5}^\infty {{{c}_{k}}} {{x}^{k}}} \right\}; \\ \end{gathered} $$

$$\begin{gathered} {{W}_{{8,9}}} = \left\{ {y = - \frac{1}{x} \pm \frac{{\sqrt { - 9\delta + 8 - 8\beta + 2{{\beta }^{2}}} }}{{4\sqrt 2 }}} \right.{{x}^{2}} \\ + \;{{c}_{3}}{{x}^{3}} + {{c}_{4}}{{x}^{4}} + \left. {\sum\limits_{k = 5}^\infty {{{c}_{k}}} {{x}^{k}}} \right\}; \\ \end{gathered} $$

again, ${{c}_{3}},{{c}_{4}} \in \mathbb{C}$ are arbitrary constants, and the other constants c_k for $k > 4$ are uniquely determined in terms of the two first constants.

6 EDGE ${{\Gamma }_{3}}$

The edge ${{\Gamma }_{3}}$ is associated with the outward normal ${{N}_{3}} = (1;\;1{\text{/}}2)$ and the truncated equation

$$ - \frac{{10}}{3}{{y}^{{10}}} - 8x{{y}^{8}} - 6{{x}^{2}}{{y}^{6}} - \frac{4}{3}{{x}^{3}}{{y}^{4}} = 0.$$

(6.1)

Note that the truncated equation (6.1) is algebraic, and there are no critical points. On the basis of the form of the outward normal, we seek the power asymptotic form of the corresponding solution in the form $y = c{{x}^{{1/2}}}$ by substituting this expression into Eq. (6.1). Then, we obtain the equation

$$ - \frac{{10}}{3}{{c}^{{10}}}{{x}^{5}} - 8x{{c}^{8}}{{x}^{4}} - 6{{x}^{2}}{{c}^{6}}{{x}^{3}} - \frac{4}{3}{{x}^{3}}{{c}^{4}}{{x}^{2}} = 0,$$

whence we find the nonzero values of $c$: ${{c}_{{1,2}}} = \pm i$ of multiplicity two and simple roots ${{c}_{{3,4}}} = \pm i\sqrt {\tfrac{2}{5}}$. By continuing the asymptotic form $y = {{c}_{k}}{{x}^{{1/2}}}$ in the form of power asymptotic expansions, we obtain six expansions of the solutions as $x \to \infty$:

$$\begin{gathered} {{W}_{{10,11}}} \\ = \left\{ {y = i\sqrt x + \frac{{\beta \pm \sqrt {\beta - ({{\beta }^{2}} - 18\delta )} }}{{4x}} + \sum\limits_{k = 1}^\infty {{{c}_{k}}} {{x}^{{ - 1 - \frac{3}{2}k}}}} \right\}; \\ \end{gathered} $$

$$\begin{gathered} {{W}_{{12,13}}} \\ = \left\{ {y = - i\sqrt x + \frac{{\beta \pm \sqrt {\beta + ({{\beta }^{2}} - 18\delta )} }}{{4x}} + \sum\limits_{k = 1}^\infty {{{c}_{k}}} {{x}^{{ - 1 - \frac{3}{2}k}}}} \right\}; \\ \end{gathered} $$

$${{W}_{{14,15}}} = \left\{ {y = \pm \sqrt {\frac{2}{5}} i\sqrt x - \frac{\beta }{{2x}} + \sum\limits_{k = 1}^\infty {{{c}_{k}}} {{x}^{{ - 1 - \frac{3}{2}k}}}} \right\}.$$

7 EDGE ${{\Gamma }_{4}}$

The truncated equation for the edge ${{\Gamma }_{4}}$ is

$$ - \frac{4}{3}{{x}^{3}}{{y}^{4}} + x{{\beta }^{2}}{{y}^{2}} + \frac{1}{3}{{\beta }^{3}}y = 0,$$

and the outward normal is ${{N}_{4}} = (1;\; - 1)$; again, this edge is associated with asymptotic forms of solutions as $x \to \infty$—these are the asymptotic forms $y = c{{x}^{{ - 1}}}$. The truncated equation is again algebraic and gives no critical points. To find the values of $c$, we have the equation

$$ - \frac{4}{3}{{c}^{4}} + {{\beta }^{2}}{{c}^{2}} + \frac{1}{3}{{\beta }^{3}}c = 0,$$

whence we find the nonzero values of c: ${{c}_{1}} = \beta$ of multiplicity one and ${{c}_{2}} = - \tfrac{\beta }{2}$ of multiplicity two. By continuing the asymptotic form $y = {{c}_{k}}{{x}^{{1/2}}}$ in the form of power asymptotic expansions, we obtain three more expansions of the solutions as $x \to \infty$:

$${{W}_{{16}}} = \left\{ {y = \frac{\beta }{x} + \frac{{6\beta \delta - 7\beta - 5{{\beta }^{3}}}}{{2{{x}^{4}}}} + \sum\limits_{k = 2}^\infty {{{c}_{k}}} {{x}^{{ - 1 - 3k}}}} \right\};$$

$${{W}_{{17,18}}} = \left\{ {y = - \frac{\beta }{{2x}} \pm \frac{{3\beta \sqrt \delta }}{{4{{x}^{4}}}} + \sum\limits_{k = 2}^\infty {{{c}_{k}}} {{x}^{{ - 1 - 3k}}}} \right\}.$$

8 ASYMPTOTIC EXPANSIONS FOR VERTICES

Consider the truncated equations corresponding to the vertices.

The vertices (0, 1), (3, 4), and (0, 10) are associated with the algebraic monomials $1{\text{/}}3{{\beta }^{3}}y$, $- 4{\text{/}}3{{x}^{3}}{{y}^{4}}$, and $- 10{\text{/}}3{{y}^{{10}}}$; however, they do not give asymptotic forms of solutions to the equations according to [1]. The vertex $( - 6,\;4)$ is associated with the normal cone ${\text{\{ }}({{p}_{1}},{{p}_{2}}):({{p}_{1}},{{p}_{2}})$ = ${{\lambda }_{1}}( - 1;\; - {\kern 1pt} 2) + {{\lambda }_{2}}( - 1;\;1),$ ${{\lambda }_{1}},{{\lambda }_{2}} \in \mathbb{R},$ ${{\lambda }_{1}} > 0,{{\lambda }_{2}} > 0{\text{\} }}$, which gives constraints on the exponent: ${\text{\{ }}r: - 1 < \operatorname{Re} r < 2,\;r \ne - 1,\;r \ne 2{\text{\} }}$. Furthermore, this vertex is associated with the truncated equation

$${{y}^{2}}{{y}_{{xx}}}{{y}_{{xxxx}}} - \frac{{{{y}^{2}}y_{{xxx}}^{2}}}{2} - \frac{4}{3}yy_{{xx}}^{3} + \frac{3}{2}y_{x}^{2}y_{{xx}}^{2} - y{{y}_{x}}{{y}_{{xx}}}{{y}_{{xxx}}} = 0.$$

Substitute $y = c{{x}^{r}}$ into it, equate the result to zero, and solve the equation for r; this gives the possible values of $r$: $r = - 3,$ $r = 0,$ $r = 1,$ and $r = 4$.

Only r = 0 and $r = 1$ are in the normal cone corresponding to the vertex under examination; hence, we can easily calculate the additional one-parameter families of asymptotic forms of solutions of the second term of the fourth Painlevé hierarchy as $x \to 0$; more precisely, there are the asymptotic forms $y = c$ and $y = cx$, where $c \in \mathbb{C}{{\backslash \{ }}0{\text{\} }}$ is an arbitrary constant. In this paper, we continue only the second asymptotic form as an asymptotic expansion.

The standard method for calculating the expansion structure does not give an immediate result: linearization of the truncated equation corresponding to the vertex (–6, 4) on the solution $y = cx$ gives a zero operator. Therefore, we continue the calculations by making the shift $y = cx + w$. For the new solution, we obtain the Newton polygon depicted in Fig. 2.

Fig. 2.

We are interested only in its vertices and edges the normal cones to which can yield asymptotic forms corresponding to the cone of the problem $\mathcal{K} = {\text{\{ }}k:\operatorname{Re} k \geqslant 1$, $k \ne 1{\text{\} }}$. This condition agrees only with the vertices (0, 0) and (–4, 2) and with the edge connecting them. Consider them one by one.

The vertex (0, 0) is associated with a truncated algebraic equation that gives no asymptotic forms.

The vertex (–4, 2) is associated with the equation

$$\frac{3}{2}{{c}^{2}}w_{{xx}}^{2} - \frac{1}{2}{{c}^{2}}{{x}^{2}}w_{{xxx}}^{2} + {{c}^{2}}{{x}^{2}}{{w}_{{xx}}}{{w}_{{xxxx}}} - {{c}^{2}}x{{w}_{{xx}}}{{w}_{{xxx}}} = 0;$$

we substitute $w = {{c}_{1}}{{x}^{{{{r}_{1}}}}}$ into it and find that ${{r}_{1}} = 3$ or ${{r}_{1}} = 5$. None of the exponents is suitable because the vector $( - 1$, –r₁) does not lie within the vertex normal cone.

We assign to the edge connecting these vertices the truncated equation

$$\begin{gathered} \frac{3}{2}{{c}^{2}}w_{{xx}}^{2} - \frac{1}{2}{{c}^{2}}{{x}^{2}}w_{{xxx}}^{2} + {{c}^{2}}{{x}^{2}}{{w}_{{xx}}}{{w}_{{xxxx}}} - {{c}^{2}}xy{{w}_{{xx}}}{{w}_{{xxx}}} \\ - \;\beta {{c}^{2}}{{x}^{2}}{{w}_{{xxxx}}} + \beta {{c}^{2}}x{{w}_{{xxx}}} - 3\beta {{c}^{2}}{{w}_{{xx}}} + \frac{3}{2}{{\beta }^{2}}{{c}^{2}} = 0 \\ \end{gathered} $$

and the outward normal (–1, –2); therefore, we seek the solution to this equation in the form $w = A{{x}^{2}}$. After the substitution, we obtain

$$6{{A}^{2}} - 6\beta A + \frac{3}{2}{{\beta }^{2}} = 0,$$

whence $A = \tfrac{\beta }{2}$ is the root of multiplicity two. Therefore, we continue the calculations by making the shift $y = cx + \frac{\beta }{2}{{x}^{2}} + {{y}_{2}}$ to achieve nonzero values of linearization of the truncated equation on the solution. After the substitution, we obtain an equation with the Newton polygon in which the vertex (–4, 2), which gives the next term of the asymptotic form ${{c}_{3}}{{x}^{3}}$, the critical number 4, and the edge connecting the vertices (–4, 2) and (0, 4) of this polygon (the critical number 5).

As a result, we obtain the following families of power asymptotic expansions that continue the asymptotic form of the solution $y = cx$ as $x \to 0$:

$${{W}_{{19}}} = \left\{ {y = cx + \frac{\beta }{2}{{x}^{2}} + {{c}_{3}}{{x}^{3}} + {{c}_{4}}{{x}^{4}} + \sum\limits_{k = 5}^\infty {{{a}_{k}}} {{x}^{k}}} \right\};$$

$$\begin{gathered} {{W}_{{20,21}}} = \left\{ {y = cx + \frac{\beta }{2}{{x}^{2}} + \frac{{c(2 \pm 3\sqrt {2\delta } )}}{{12}}{{x}^{4}}} \right. \\ + \;{{c}_{5}}{{x}^{5}} + \left. {\sum\limits_{k = 6}^\infty {{{b}_{k}}} {{x}^{k}}} \right\}, \\ \end{gathered} $$

where c, ${{c}_{3}} \in \mathbb{C}{{\backslash \{ }}0{\text{\} }}$, ${{c}_{4}},$ ${{c}_{5}} \in \mathbb{C}$ are arbitrary constants, and the coefficients a_k and b_k are uniquely represented in terms of them.