On the $D(2)$-Vertex Distinguishing Total Coloring of Graphs with $\Delta=3$

Abstract

A $D(2)$-vertex-distinguishing total coloring of a graph $G$ is a proper total coloring such that no pair of vertices, within distance two, has the same set of colors, and the minimum number of colors required for such a coloring is called $D(2)$-vertex-distinguishing total chromatic number of $G$, and denoted by $\chi_{2vt}(G)$. In this paper, we prove that $\chi_{2vt}(G)\leq11$ for any graph $G$ with $\Delta(G)=3$.

1. Introduction

All graphs considered in this paper are simple, finite, and undirected. Let $G=(V(G), E(G))$ be a graph with vertex set $V(G)$ and edge set $E(G)$. Let $d_{G}(x)$ (denote by $d(x)$ for short) be the degree of a vertex $x$ in $G$, and $\Delta(G)=\max\{d(x)|x\in V(G)\}$ the maximum degree of $G$. Let $P_{n}$ and $C_{n}$$(n\ge 3)$ be the path and the cycle of order $n$, respectively, and $K_{m, n}$ be a complete bipartite graph with bipartition $(X, Y)$, where $|X|=m$ and $|Y|=n$. We call a path $P_{n+1}=u_{0}u_{1}\cdots u_{n}$ an internal path of $G$ if $d(u_{0})\geq3$, $d(u_{n})\geq3$, and $d(u_{i})=2$, $i=1, 2, \cdots, n-1$. Let $G-\{v\}$ be the subgraph of $G$ obtained by deleting the vertex $v$ and its incident edges. Let $G-\{uv\}$ and $G+\{uv\}$ be the graphs obtained from $G$ by deleting the edge $uv$ and by adding a new edge $uv$, respectively. A cut edge of $G$ is an edge $uv$ such that $\omega(G-\{uv\})>\omega(G)$, where $\omega(G)$ refers to the number of components in $G$. The disjoint union $G_{1} \dot{\cup} G_{2}$ of $G_{1}$ and $G_{2}$ is the graph with vertex set $V(G_{1})\cup V(G_{2})$ and edge set $E(G_{1})\cup E(G_{2})$. A vertex of degree one is called a pendent vertex. The distance between two vertices $u$ and $v$ in $G$, denoted by $d_{G}(u, v)$, is the length of a shortest $(u, v)$-path in $G$. A graph $G$ is $r$-regular if $d(u)=r$ for all $u\in V(G)$. Especially, if a graph $G$ has a $1$-regular spanning subgraph, then the spanning subgraph is called a perfect matching of $G$. The square $G^{2}$ of a graph $G$ can be obtained from $G$ by adding all edges between two vertices of distance two in $G$. For two sets $A$ and $B$, $A\backslash B$ represents the difference set of $A$ and $B$. The terminologies and notations used but undefined in this paper can be found in [1].

A proper $k$-total coloring of $G$ is a mapping $f: V(G)\cup E(G)\rightarrow\{1,\;2,\; \cdots,\;k\}$ such that any two adjacent or incident elements in $V(G)\cup E(G)$ receive different colors. We use

$$S_{f}(x)=\{f(x)\}\cup\{f(xy)|xy\in E(G)\}$$

to denote the set of colors assigned to a vertex $x$ and those edges incident with $x$. A proper $k$-total coloring $f$ of $G$ is said to be a $k$-$D(\beta)$-vertex distinguishing total coloring [2] (write as $k$-$D(\beta)$-VDTC for short) if $S_{f}(u)\not=S_{f}(v)$ for any two vertices $u, v\in V(G)$ with $d(u, v)\leq\beta$, and denote by $\chi_{\beta vt}(G)=\min\Big\{k|G \text{ has a } k-D(\beta)-\mathrm{VDTC}\Big\}$ the $D(\beta)$-vertex distinguishing total chromatic number of $G$. Especially, if $\beta=1$, then a $D(1)$-vertex distinguishing total coloring is just the adjacent vertex distinguishing total coloring of $G$ (see [3]); if $\beta=2$, then $D(\beta)$-vertex distinguishing total coloring is also called $D(2)$-vertex distinguishing total coloring of $G$, and the corresponding chromatic number is written as $\chi_{2vt}(G)$. Besides, let $f$ be a total coloring of $G$. If any two vertices $u, v\in V(G)$ with $d(u, v)\leq2$ satisfy $S_{f}(u)\not=S_{f}(v)$, then we call that $u$ and $v$ are $D(2)$-vertex distinguishable.

Graph coloring has always been classic topic in graph theory, and it’s widely applied in practice (see [1]). In recent decades, many scholars have conducted a series of researches around it [4]–[7]. The adjacent vertex distinguishing total coloring of graphs was first introduced by Zhang et al. in [3]. They conjectured that the adjacent vertex distinguishing total chromatic number $\chi_{at}(G)$ of any graph $G$, with order at least $2$, satisfies $\chi_{at}(G)\leq\Delta(G)+3$, and further showed that the conjecture holds for complete graph, complete bipartite graph, tree, and so on. After then, scholars have carried out a lot of research to the conjecture. Wang [8] and Chen [9] independently proved that if $G$ is a graph with maximum degree $\Delta(G)=3$, then $\chi_{at}(G)\leq6$. Cheng et al. [10] showed that for a planar graph $G$ with $\Delta(G)\geq10$, $\chi_{at}(G)\leq\Delta(G)+3$. Huang et al. [11] verified that $\chi_{at}(G)\leq2\Delta(G)$ for any graph $G$ with $\Delta(G)\geq3$. Later, B. Vučković [12] improved this bound, and got that $\chi_{at}(G)\leq2\Delta(G)-1$ if $\Delta(G)\geq4$.

In 2006, Zhang et al. [2] proposed the concept entitled $D(\beta)$-vertex distinguishing total coloring of graphs, and got the $D(\beta)$-vertex distinguishing total chromatic number of some simple graphs such as path, cycle, and complete graph for $\beta\geq2$. Based on the above, they presented the conjecture given below:

Conjecture 1 (see [2]).

Let $G$ be a connected graph on $n\geq2$ vertices. Then

$$\chi_{\beta vt}(G)\leq \mu_{\beta}(G)+1.$$

where $\mu_{\beta}(G)=\min\Big\{\theta:\;{\theta\choose i+1}\geq n_{i},\;\delta\leq i\leq\Delta\Big\}$ , $n_{i}=\max\Big\{|S|:\;S\subseteq V(G)\Big\}$ , and $S$ is composed of the vertices with degree $i$ and their distance is no more than $\beta$ .

From conjecture 1, if $\beta=2$, then we see that the following conjecture.

Conjecture 2 (see [2]).

Let $G$ be a connected graph on $n\geq2$ vertices. Then

$$\chi_{2vt}(G)\leq \mu_{2}(G)+1.$$

Meanwhile, Zhang et al.[2] also showed that the conjecture holds for some simple graphs. In this paper, we aim at Conjecture 2 to consider the $D(2)$-vertex distinguishing total coloring of a graph $G$, and prove that $\chi_{2vt}(G)\le11$ for any graph $G$ with maximum degree $\Delta(G)=3$.

2. Preliminaries

Lemma 1 (see [2, Theorem 2.2]).

Let $G$ be a graph with $n$ components, i.e., $G=G_{1}\cup G_{2}\cup\cdots\cup G_{n}$ . Then $\chi_{2vt}(G)=\max\big\{\chi_{2vt}(G_{i})|i=1,\;2,\;\cdots,\;n\big\}.$

Lemma 2 (see [2, Theorem 2.4]).

For a path $P_{n}$ with order $n\geq2$ , $\chi_{2vt}(P_{n})\leq4$ .

Lemma 3 (see [2, Theorems 2.7, 2.8, 2.9]).

Let $C_{n}$ be a cycle on $n\geq3$ vertices. Then $\chi_{2vt}(C_{n})\leq5$ .

Lemma 4 (see [13, pp.243], [14, Lemma 2.4.6]).

For a $3$ -regular graph $G$ , if $G$ contains no perfect matching, then $G$ has at least $3$ cut edges.

A list assignment of $G$ is a function $L$ which assigns to each vertex $x\in V(G)$ a list $L(x)$ of colors. A list coloring of $G$ with list assignment $L$ is a mapping $f: V(G)\rightarrow \bigcup_{x\in V(G)}L(x)$ such that $f(x)\in L(x)$ for all $x\in V(G)$ and $f(u)\not=f(v)$ for any adjacent vertices $u$ and $v$, and we say that $G$ is $L$-colorable. A graph is called $k$-choosable if $G$ is $L$-colorable whenever all lists have size $k$. The list chromatic number $\chi_{l}(G)$ is the minimum $k$ such that $G$ is $k$-choosable. In [15], the list chromatic number of the square $G^{2}$ of a graph $G$ with $\Delta(G)\leq3$ is given in the following.

Lemma 5 (see [15, Theorem 1]).

For a graph $G$ with $\Delta(G)\leq3$ , if $G$ is not isomorphic to the Petersen graph, then $\chi_{l}(G^{2})\leq8$ .

A proper vertex coloring of $G$ is a mapping $f: V(G)\rightarrow \{1,\;2,\;\cdots,\;k\}$ such that for any two adjacent vertices $u$ and $v$, $f(u)\not=f(v)$, and denote by $\chi(G)$ the proper vertex chromatic number of $G$. By the definition of list-coloring of $G$, we can see that a list-coloring of $G$ is also a proper vertex coloring of the graph, and $\chi(G)\leq\chi_{l}(G)$. A $2$-distance coloring of a graph $G$ is a proper vertex coloring such that no two vertices, within distance $2$ in $G$, are assigned the same color, and we denote by $\chi_{2}(G)$ the $2$-distance chromatic number of $G$. It is obvious that for any a simple graph $G$ and its square graph $G^{2}$, $\chi_{2}(G)=\chi(G^{2})$. Hence, we can deduce that $\chi_{2}(G)=\chi(G^{2})\leq\chi_{l}(G^{2})$. Furthermore, the following corollary can be deduced by Lemma 5.

Corollary 1.

If $G$ is a graph with $\Delta(G)\leq3$ , but not isomorphic to the Petersen graph, then

$$\chi_{2}(G)\leq8.$$

Lemma 6.

If $G$ is the Petersen graph, then $\chi_{2vt}(G)=6$ .

Proof.

Suppose that $G$ has vertex-set $V(G)=\{u_{1},\;u_{2},\;u_{3},\;u_{4},\;u_{5},\;v_{1},\; v_{2},\;v_{3},\;v_{4},\;v_{5}\}$ and edge-set $E(G)=\{u_{i}u_{i+1},\;u_{i}v_{i},\; v_{i}v_{i+2}\}$, where $i=1, 2, \cdots, 5$. According to the definition of $D(2)$-VDTC, $\chi_{2vt}(G)\geq6$ due to ${6\choose4}=15>10$ and ${5\choose4}=5<10$. Let $f: V(G)\cup E(G)\rightarrow\{1,\;2,\;\cdots,\;6\}$ be a total coloring of $G$. Suppose $f(u_{i}v_{i})=6$ for $i=1, 2, 3, 4, 5$. Then we color the vertices $u_{1}$, $u_{2}$, $u_{3}$, $u_{4}$, and $u_{5}$ with $1, 2, 3, 4$, and $5$ respectively, and color the vertices $v_{1}$, $v_{2}$, $v_{3}$, $v_{4}$, and $v_{5}$ with $5, 1, 2, 3$, and $4$ respectively. Meanwhile, the edges $u_{1}u_{2}$, $u_{2}u_{3}$, $u_{3}u_{4}$, $u_{4}u_{5}$, and $u_{5}u_{1}$ are colored by $3, 4, 5, 1,$ and $2$ respectively. After that, the edges $v_{1}v_{3}$, $v_{2}v_{4}$, $v_{3}v_{5}$, $v_{4}v_{1}$, and $v_{5}v_{2}$ are colored by $3, 4, 5, 1$, and $2$ respectively. Clearly, $f$ is a proper total coloring of $G$, and it is easy to see that

$$\begin{aligned} \, S(u_{1})&=\{1,\;2,\;3,\;6\}, & S(u_{2})&=\{2,\;3,\;4,\;6\}, & S(u_{3})&=\{3,\;4,\;5,\; 6\},\\ S(u_{4})&=\{1,\;4,\;5,\;6\}, & S(u_{5})&=\{1,\;2,\;5,\;6\}, & S(v_{1})&=\{1,\;3,\;5,\; 6\}, \\ S(v_{2})&=\{1,\;2,\;4,\;6\}, & S(v_{3})&=\{2,\;3,\;5,\;6\}, & S(v_{4})&=\{1,\;3,\;4,\; 6\}, \ \mbox{and} \\ S(v_{5})&=\{2,\;4,\;5,\;6\}. \end{aligned}$$

Therefore, $f$ is a $6$-D(2)-VDTC of $G$, and thus $\chi_{2vt}(G)=6$.

Lemma 7.

For a $3$ -regular graph $G$ with a perfect matching, $\chi_{2vt}(G)\leq11$ .

Proof.

If $G$ is the Petersen graph, then $\chi_{2vt}(G)=6<11$ by Lemma 6. Otherwise, we consider that $G$ is a $3$-regular graph but not isomorphic to the Petersen graph. We decompose $G$ as a perfect matching $M$ and a union of some cycles, denoted by $C_{n_{i}}^{(i)}=x_{1}^{i}x_{2}^{i}\cdots x_{n_{i}}^{i}x_{1}^{i}$ for $i=1, 2, \cdots, t$, where $n_{i}$ is the length of $C_{n_{i}}^{(i)}$. According to Corollary 1, one can see that $G$ has a $2$-distance vertex coloring with $8$ colors, suppose that $f_{1}: V(G)\rightarrow\{1,\;2,\;\cdots,\;8\}$ is a $2$-distance vertex coloring of $G$. Let $f_{2}: E(G)\rightarrow\{1,\;2,\;\cdots,\;11\}$ be a proper edge coloring of $G$. Without loss of generality, we may suppose that all the edges in $M$ are colored by $9$. Then we will color the edges of cycles $C_{n_{i}}^{(i)}$ where $i=1, 2, \cdots, t$. For clarity, we may suppose that $C_{n_{1}}^{(1)}$, $C_{n_{2}}^{(2)}$, $\cdots$, $C_{n_{r}}^{(r)}$ are even cycles, and $C_{n_{r+1}}^{(r+1)}$, $C_{n_{r+2}}^{(r+2)}$, $\cdots$, $C_{n_{s}}^{(s)}$, $C_{n_{s+1}}^{(s+1)}$, $\cdots$, $C_{n_{t}}^{(t)}$ are odd cycles, in which $C_{n_{r+1}}^{(r+1)}$, $C_{n_{r+2}}^{(r+2)}$, $\cdots$, $C_{n_{s}}^{(s)}$ satisfy that each vertex of one odd cycle is not adjacent to any vertex of the others, meanwhile, $C_{n_{s+1}}^{(s+1)}$, $C_{n_{s+2}}^{(s+2)}$, $\cdots$, $C_{n_{t}}^{(t)}$ satisfy that some vertices of one cycle are adjacent to some vertices of the others, where $r\leq s\leq t$.

Suppose that the edges of $C_{n_{1}}^{(1)}$, $C_{n_{2}}^{(2)}$, $\cdots$, $C_{n_{r}}^{(r)}$ are colored by $10$ and $11$ alternately. Now we color the edges of the cycles $C_{n_{r+1}}^{(r+1)}$, $C_{n_{r+2}}^{(r+2)}$, $\cdots$, $C_{n_{s}}^{(s)}$. For each cycle $C_{n_{i}}^{(i)}$ with $i=r+1, r+2, \cdots, s$, the edges $x_{1}^{i}x_{2}^{i}$, $x_{2}^{i}x_{3}^{i}$, $\cdots$, $x_{n_{i}-1}^{i}x_{n_{i}}^{i}$ of $C_{n_{i}}^{(i)}$ are colored alternately by $10$ and $11$, and the edge $x_{n_{i}}^{i}x_{1}^{i}$ is colored by a color $\alpha$, where $\alpha\in\{1,\;2,\;\cdots,\;8\}\backslash\{f_{1}(x_{1}^{i}),\;f_{1}(x_{n_{i}}^{i})\}$.

After that, we will color the edges of cycles $C_{n_{s+1}}^{(s+1)}$, $C_{n_{s+2}}^{(s+2)}$, $\cdots$, $C_{n_{t}}^{(t)}$. We construct a new graph $H$ with vertex set $V(H)=\{C_{n_{s+1}}^{(s+1)},\;C_{n_{s+2}}^{(s+2)},\;\cdots,\;C_{n_{t}}^{(t)}\}$ and edge set $E(H)$, where $E(H)$ equals to the set of all edges which connect the vertices of $C_{n_{i}}^{(i)}$ with the vertices of $C_{n_{j}}^{(j)}$ in $G$, where $i\not=j$ and $i, j=s+1, s+2, \cdots, t$. It is easy to see that $H$ may be disconnected. Let $H=H_{1}\cup H_{2}\cup\cdots\cup H_{m}$, where $H_{i}$$(i=1, 2, \cdots, m)$ are components of $H$.

We first color the edges of odd cycles corresponding to the vertices of $H_{1}$. For any $y\in V(H_{1})$, let $C_{n_{y}}^{(y)}=x_{1}^{y}x_{2}^{y}\cdots x_{n_{y}}^{y}x_{1}^{y}$ be the odd cycle corresponding to $y$ in $G$. Given a vertex $v\in V(H_{1})$, then the corresponding odd cycle is $C_{n_{v}}^{(v)}=x_{1}^{v}x_{2}^{v}\cdots x_{n_{v}}^{v}x_{1}^{v}$. We alternately color the edges $x_{1}^{v}x_{2}^{v}$, $x_{2}^{v}x_{3}^{v}$, $\cdots$, $x_{n_{v}-1}^{v}x_{n_{v}}^{v}$ by $10$ and $11$, and color the edge $x_{n_{v}}^{v}x_{1}^{v}$ by the color $\alpha$. For any $uv\in E(H_{1})$, we also color the edges $x_{1}^{u}x_{2}^{u}$, $x_{2}^{u}x_{3}^{u}$, $\cdots$, $x_{n_{u}-1}^{u}x_{n_{u}}^{u}$ of $C_{n_{u}}^{(u)}$ by $10$ and $11$ alternately, and color $x_{n_{u}}^{u}x_{1}^{u}$ by a color $\beta$, where $\beta\in \{1,\;2,\;\cdots,\;8 \}\backslash\{f_{1}(x_{n_{u}}^{u}),\;f_{1}(x_{1}^{u}),\;f_{1}(x_{n_{v}}^{v}),\; f_{1}(x_{1}^{v}),\;\alpha\}$. For any $w\in V(H_{1})$ with $d_{H_{1}}(v, w)\ge 2$, if $d_{H_{1}}(v, w)=2$, then we color the edges of $C_{n_{w}}^{(w)}$ by the coloring function that has dyed the edges of $C_{n_{v}}^{(v)}$; if $d_{H_{1}}(v, w)=3$, then we color the edges of $C_{n_{w}}^{(w)}$ by the coloring function that has dyed the edges of $C_{n_{u}}^{(u)}$. As an analogy, all edges of $C_{n_{w}}^{(w)}$, with $d_{H_{1}}(v, w)\ge 4$, can be colored in the same way, meanwhile, one can color the edges of odd cycles corresponding to the vertices of $H_{2}$, $H_{3}$, $\cdots$, $H_{m}$ by the coloring function which has dyed the edges of $H_{1}$. So far, all the edges of cycles $C_{n_{s+1}}^{(s+1)}$, $C_{n_{s+2}}^{(s+2)}$, $\cdots$, $C_{n_{t}}^{(t)}$ have been colored.

Thus, for any vertex of $G$, there are $5$ color sets under $f_{2}$, that is, $\{9,\;10,\;11\}$, $\{\alpha,\;9,\;10\}$, $\{\alpha,\;9,\;11\}$, $\{\beta,\;9,\;10\}$, and $\{\beta,\;9,\;11\}$, respectively.

Finally, we construct a total coloring $f: V(G)\cup E(G)\rightarrow\{1,\;2,\;\cdots,\;11\}$ of $G$ as follows:

$$ f(z)=\begin{cases} f_{1}(z), &z\in V(G),\\ f_{2}(z), &z\in E(G). \end{cases}$$

(1)

Obviously, $f$ is a proper total coloring of $G$. Under the coloring $f$, we show that any two vertices of $G$ with distance no more than $2$ are $D(2)$-vertex distinguishable.

Let $x_{k}^{i}\in V(C_{n_{i}}^{(i)})$ and $x_{l}^{j}\in V(C_{n_{j}}^{(j)})$ be two vertices with $d(x_{k}^{i}, x_{l}^{j})\leq2$, where $i$ and $j$ are not necessary distinct, and $i, j=1, 2, \cdots, t$. Let $S_{f}(x_{k}^{i})$ and $S_{f}(x_{l}^{j})$ be the color sets that correspond to $x_{k}^{i}$ and $x_{l}^{j}$, respectively. It is evident that $S_{f}(x_{k}^{i})=\{f_{1}(x_{k}^{i})\}\cup S_{f_{2}}(x_{k}^{i})$ and $S_{f}(x_{l}^{j})=\{f_{1}(x_{l}^{j})\}\cup S_{f_{2}}(x_{l}^{j})$. Moreover, we notice that $d(x_{k}^{i}, x_{l}^{j})\leq2$, from the coloring function $f_{2}$, one can see that

$$S_{f_{2}}(x_{k}^{i}), S_{f_{2}}(x_{l}^{j})\in\Big\{\{9,\;10,\;11\},\; \{\alpha,\;9,\;10\},\;\{\alpha,\;9,\;11\},\;\{\beta,\;9,\;10\},\;\{\beta,\;9,\; 11\}\Big\},$$

but $S_{f_{2}}(x_{k}^{i})=S_{f_{2}}(x_{l}^{j})\not\in\Big\{\{\alpha,\;9,\; 10\},\;\{\alpha,\;9,\;11\},$ $\{\beta,\;9,\;10\},\;\{\beta,\;9,\;11\}\Big\}$. Now we consider four cases in the following:

• 1. for $S_{f_{2}}(x_{k}^{i})=\{9,\;10,\;11\}$, if $S_{f_{2}}(x_{l}^{j})=\{9,\;10,\;11\}$, then one can see that $S_{f}(x_{k}^{i})\not=S_{f}(x_{l}^{j})$ since $f_{1}(x_{k}^{i})\not=f_{1}(x_{l}^{j})$; if $S_{f_{2}}(x_{l}^{j})\in \Big\{\{\alpha,\;9,\;10\},\;\{\alpha,\;9,\;11\},\;\{\beta,\;9,\;10\},\;\{\beta,\; 9,\;11\}\Big\}$, then we obtain $\{f_{1}(x_{k}^{i})\}\cup S_{f_{2}}(x_{k}^{i})\not=\{f_{1}(x_{l}^{j})\}\cup S_{f_{2}}(x_{l}^{j})$ since $\{\alpha,\;\beta,\;f_{1}(x_{k}^{i}),\;f_{1}(x_{l}^{j})\}\subset\{1,\;2,\; \cdots,\;8\}$ and, consequently, $S_{f}(x_{k}^{i})\not=S_{f}(x_{l}^{j})$;

• 2. for $S_{f_{2}}(x_{k}^{i})=\{\alpha,\;9,\;10\}$, if $S_{f_{2}}(x_{l}^{j})=\{\alpha,\;9,\;11\}$, then $\{f_{1}(x_{k}^{i}),\;\alpha,\;9,\;10\}\not=\{f_{1}(x_{l}^{j}),\;\alpha,$ $9,\;11\}$ due to $\{f_{1}(x_{k}^{i}),\;f_{1}(x_{l}^{j})\}\subset\{1,\;2,\;\cdots,\;8\}$, i.e., $S_{f}(x_{k}^{i})\not=S_{f}(x_{l}^{j})$; if

  $$S_{f_{2}}(x_{l}^{j})\in \Big\{\{\beta,\;9,\;10\},\;\{\beta,\;9,\;11\}\Big\},$$

  since $\beta\in\{1,\;2,\; \cdots,\;8\}\backslash\{f_{1}(x_{k}^{i}),\;\alpha\}$ we see that $\beta\not\in S_{f}(x_{k}^{i})$, and thus $S_{f}(x_{k}^{i})\not=S_{f}(x_{l}^{j})$;

• 3. for $S_{f_{2}}(x_{k}^{i})=\{\alpha,\;9,\;11\}$, if $S_{f_{2}}(x_{l}^{j})\in\Big\{\{\beta,\;9,\;10\},\;\{\beta,\;9,\;11\}\Big\}$ then $S_{f}(x_{k}^{i})\not=S_{f}(x_{l}^{j})$ as $\beta\not\in S_{f}(x_{k}^{i})$;

• 4. for $S_{f_{2}}(x_{k}^{i})=\{\beta,\;9,\;10\}$, if $S_{f_{2}}(x_{l}^{j})=\{\beta,\;9,\;11\}$, then we see that

  $$\{f_{1}(x_{k}^{i}),\;\beta,\;9,\;10\}\not=\{f_{1}(x_{l}^{j}),\;\beta,\;9,\; 11\}$$

  because $\{f_{1}(x_{k}^{i}),\;f_{1}(x_{l}^{j})\}\subset\{1,\;2,\;\cdots,\;8\}$, and hence, $S_{f}(x_{k}^{i})\not=S_{f}(x_{l}^{j})$.

Therefore, $f$ is an $11$-$D(2)$-VDTC of $G$. The proof completes.

3. Main Results

Theorem 1.

Let $G$ be a graph with maximum degree $\Delta(G)\le 3$ . Then $\chi_{2vt}(G)\leq11$ .

Proof.

Let $G$ be a graph with $\Delta(G)\le 3$. If $\Delta(G)\le 2$, then $G$ is a path, or a cycle, or a union of paths and cycles. From Lemmas 2 and 3, both the path and the cycle have a $5$-$D(2)$-VDTC, and it follows from Lemma 1 that the union of paths and cycles also has a $5$-$D(2)$-VDTC; if $\Delta(G)=3$, without loss of generality, by Lemma 1, we may suppose that $G$ is connected. Then we will prove that $G$ has an $11$-$D(2)$-VDTC by induction on $|E(G)|$.

When $|E(G)|=3$, then $G\cong K_{1, 3}$, it is easy to see that $G$ has a $7$-$D(2)$-VDTC, however $7<11$, the conclusion holds; when $|E(G)|\geq4$, suppose that for any connected graph $G^{'}$ with $\Delta(G^{'})\leq 3$ and $|E(G^{'})|<|E(G)|$, $G^{'}$ has an $11$-$D(2)$-VDTC. Now we consider two cases as follows.

Case 1. $G$ has a cut edge $uv$. Since $G$ is a connected graph with $\Delta(G)=3$, there is at most one pendant vertex in $\{u,\;v\}$. Thus, the following two subcases are considered.

Subcase 1.1. There is just one pendant vertex in $u$ and $v$. We may suppose that $d_{G}(v)=1$. Then $2\leq d_{G}(u)\leq3$. Let $u_{1}$ and $u_{2}$ (if exists) be the neighbors of $u$ different from $v$, and $u_{i1}$ and $u_{i2}$ (if exists) be the neighbors of $u_{i}$ different from $u$. Let $G^{'}=G-\{v\}$. Then $G^{'}$ has an $11$-D(2)-VDTC $f^{'}$ by induction. We will construct an $11$-D(2)-VDTC $f$ of $G$ by coloring $uv$ and $v$.

Setting $f(x)=f^{'}(x)$ for $\forall x\in V(G^{'})\cup E(G^{'})$, we first color the edge $uv$. We notice that the color set of $u$ should be distinguished from the color sets of vertices within distance $2$, there are $6$ vertices at most, that is, $\{u_{1}$, $u_{2}$, $u_{11}$, $u_{12}$, $u_{21}$, $u_{22}\}$ (if exists). In addition, by the definition of proper total coloring of graphs, there are at least $8$ colors in $\{1,\;2,\;\cdots,\;11\}$ which can be used to color $uv$. Since $8>6$ we can select one color from $\{1,\;2,\;\cdots,\;11\}\backslash\{f(u),\;f(uu_{1}),\;f(uu_{2})\}$ to dye $uv$ so that $S_{f}(u)\not=S_{f}(u_{i})$ and $S_{f}(u)\not=S_{f}(u_{ij})$, where $i, j=1, 2$. Next, we color the vertex $v$. Since there are $9$ colors which can be used to dye $v$ properly, and the color set of $v$ should be distinguished from the color sets of $3$ vertices at most, that is, $\{u,\;u_{1},\;u_{2}\}$ (if exists), there exists one color in $\{1,\;2,\;\cdots,\;11\}\backslash\{f(u),\;f(uv)\}$ for $v$, such that $S_{f}(v)\not=S_{f}(u)$ and $S_{f}(v)\not=S_{f}(u_{i})$ for $i=1, 2$. Besides those, the other vertices of $G$ are $D(2)$-vertex distinguishable. Thus, $f$ is an $11$-D(2)-VDTC of $G$.

Subcase 1.2. There is no pendent vertex in $u$ and $v$. Clearly, $2\leq d_{G}(u)\leq3$ and $2\leq d_{G}(v)\leq3$. Let $u_{1}$ and $u_{2}$ (if exists) be the neighbors of $u$ different from $v$, and $v_{1}$ and $v_{2}$ (if exists) be the neighbors of $v$ different from $u$. We suppose that $G-\{uv\}=G_{1} \dot{\cup} G_{2}$, where $u\in V(G_{1})$ and $v\in V(G_{2})$. Let $G^{'}=G_{1}+\{uv\}$ and $G^{''}=G_{2}+\{uv\}$. Then by the induction hypothesis, $G^{'}$ has an $11$-$D(2)$-VDTC $f_{1}$, and $G^{''}$ has an $11$-$D(2)$-VDTC $f_{2}$.

Without loss of generality, we let $f_{1}(u)=f_{2}(u)=1$, $f_{1}(uv)=f_{2}(uv)=2$, and $f_{1}(v)=f_{2}(v)=3$. Note that if $f_{1}(v)\in S_{f_{1}}(u)$, then one can recolor $v\in V(G^{'})$ to yield $f_{1}(v)\not\in S_{f_{1}}(u)$ since there are at least $7$ colors in $\{1,\;2,\;\cdots,\;11\}\backslash S_{f_{1}}(u)$ which can be used to dye $v$ so that the color set of $v$ is distinguished from the color sets of $3$ vertices at most, that is, $\{u,\;u_{1},\;u_{2}\}$ (if exists); if $f_{2}(u)\in S_{f_{2}}(v)$, similarly, the vertex $u\in V(G^{''})$ can also be recolored with $f_{2}(u)\not\in S_{f_{2}}(v)$, and thus, we may suppose that $f_{1}(v)\not\in S_{f_{1}}(u)$ and $f_{2}(u)\not\in S_{f_{2}}(v)$. Hence, we can assume that the colors assigned on $uu_{1}, uu_{2}\in E(G^{'})$ are $4$ and $5$, respectively, and the colors assigned on $vv_{1}, vv_{2}\in E(G^{''})$ are $6$ and $7$, respectively.

Now, we construct a proper total coloring $f^{*}$ of $G$ as follows: for any $z\in V(G)\cup E(G)$, define

$$ f^{*}(z)=\begin{cases} f_{1}(z), &z\in V(G^{'})\cup E(G^{'}),\\ f_{2}(z), &z\in V(G^{''})\cup E(G^{''}). \end{cases}$$

(2)

Since $6\not\in S_{f^{*}}(u)$, $7\not\in S_{f^{*}}(u)$, $6\in S_{f^{*}}(v)\cap S_{f^{*}}(v_{1})$, and $7\in S_{f^{*}}(v)\cap S_{f^{*}}(v_{2})$, we see that

$$S_{f^{*}}(u)\not=S_{f^{*}}(v) \qquad\text{and}\qquad S_{f^{*}}(u)\not=S_{f^{*}}(v_{i}) \quad\text{for}\;\; i=1, 2.$$

Since $4\not\in S_{f^{*}}(v)$, $5\not\in S_{f^{*}}(v)$, $4\in S_{f^{*}}(u)\cap S_{f^{*}}(u_{1})$, and $5\in S_{f^{*}}(u)\cap S_{f^{*}}(u_{2})$, we obtain

$$S_{f^{*}}(v)\not=S_{f^{*}}(u_{i}), \qquad\text{where}\quad i=1, 2.$$

Besides these relations, it is clear that the other vertices of $G$ are $D(2)$-vertex distinguishable. Therefore, $f^{*}$ is an $11$-D(2)-VDTC of $G$.

Case 2. $G$ has no cut edge. It follows that $G$ has no pendent vertex, that is, $2\leq d(x)\leq3$ for any $x\in V(G)$. If $G$ doesn’t contain vertex of degree-$2$, then $G$ should be a $3$-regular graph. Since $G$ has no cut edge, by Lemma 4, $G$ must have a perfect matching. Therefore, it follows from Lemma 7 that $\chi_{2vt}(G)\leq11$; if $G$ contains vertex of degree-$2$, let’s consider the following two subcases in terms of the distance between any two such vertices in $G$.

Subcase 2.1. There exist two vertices of degree-$2$ within distance $2$ in $G$.

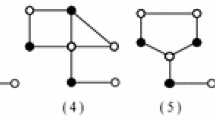
Subcase 2.1.1. The two vertices of degree-$2$ are adjacent in $G$. Let $P_{n+1}=u_{0}u_{1}\cdots u_{n}$$(n\geq3)$ be an internal path in $G$ including at least two vertices of degree-$2$. Let $u_{0}^{'}$ and $u_{0}^{''}$ be the neighbors of $u_{0}$ different from $u_{1}$, and let $u_{n}^{'}$ and $u_{n}^{''}$ be the neighbors of $u_{n}$ different from $u_{n-1}$. Now, we suppose that $G^{'}$ is the graph obtained by contracting $P_{n+1}(=u_{0}u_{1}\cdots u_{n})$ to $u_{0}vu_{n}$, see $F_{1}$ in Fig. 1. By the induction hypothesis, $G^{'}$ has an $11$-$D(2)$-VDTC $\varphi^{'}$. Without loss of generality, we suppose that $\varphi^{'}(u_{0}v)=1$, $\varphi^{'}(v)=11$, and $\varphi^{'}(u_{n}v)=2$. Next, we construct an $11$-$D(2)$-VDTC $\varphi$ of $G$.

Fig. 1.

The configuration in the proof of subcase $2.1$, where “$\bullet$” refers to the vertex whose degree is certain, and “$\circ$” refers to the vertex whose degree is uncertain and is at least 1.

For $3\leq n\leq4$, let $\varphi(u_{0}u_{1})=1$, $\varphi(u_{1})=11$, and $\varphi(u_{n-1}u_{n})=2$. If $n=3$, we first color the edge $u_{1}u_{2}$. Note that there are just $8$ colors for $u_{1}u_{2}$ to obtain a proper total coloring, meanwhile, the color set of $u_{1}$ should be distinguished from the color sets of at most $4$ vertices, that is, $\{u_{0},\;u_{0}^{'},\;u_{0}^{''},\;u_{3}\}$. Since $8>4$ we can select one color from $\{1,\;2,\;\cdots,\;11\}\backslash\{\varphi(u_{0}u_{1}),\;$ $\varphi(u_{1}),\;\varphi(u_{2}u_{3})\}$ to dye $u_{1}u_{2}$ such that $u_{1}$ and $\{u_{0},\;u_{0}^{'},\;u_{0}^{''},\;u_{3}$\} are $D(2)$-vertex-distinguishable. Next, we color the vertex $u_{2}$. Since there are at least $7$ colors in $\{1,\;2,\;\cdots,\; 11\}$ which can be used to dye $u_{2}$ properly, and the color set of $u_{2}$ should be distinguished from the color sets of at most $5$ vertices, that is, $\{u_{0},\;u_{1},\; u_{3},\;u_{3}^{'}$, $u_{3}^{''}\}$, we can select one color from $\{1,\;2,\;\cdots,\; 11\}\backslash\{\varphi(u_{1}u_{2}),$ $\varphi(u_{2}u_{3}),\;\varphi(u_{1}),\; \varphi(u_{3})\}$ for $u_{2}$, where $\varphi(u_{3})=\varphi^{'}(u_{3})$, such that $u_{2}$ and $\{u_{0},\;u_{1},\;u_{3},\;u_{3}^{'},\;u_{3}^{''}\}$ are $D(2)$-vertex-distinguishable; if $n=4$, by the same way, we can color $u_{1}u_{2}$, $u_{2}$, $u_{2}u_{3}$, and $u_{3}$ such that the vertices $u_{0}$, $u_{1}$, $u_{2}$, $u_{3}$, $u_{4}$, $u_{0}^{'}$, $u_{0}^{''}$, $u_{4}^{'}$, and $u_{4}^{''}$ are $D(2)$-vertex distinguishable.

For $n\geq5$, let $\varphi(u_{0}u_{1})=\varphi(u_{n-2}u_{n-1})=1$, $\varphi(u_{1})=\varphi(u_{n-1})=11$, and let

$$\varphi(u_{1}u_{2})=\varphi(u_{n-1}u_{n})=2.$$

We then circularly color $u_{2}$, $u_{2}u_{3}$, $u_{3}$, $\cdots$, $u_{n-3}u_{n-2}$ and $u_{n-2}$ by $3, 4, 5, 6$, and $7$. It is evident that the vertices of degree-$2$ and the vertices of degree-$3$ are $D(2)$-vertex distinguishable. Since $S_{\varphi}(u_{1})=S_{\varphi}(u_{n-1})=S_{\varphi^{'}}(v)=\{1,\;2,\;11\}$ we see that $S_{\varphi}(u_{1})\not=S_{\varphi}(u_{0}^{'})$, $S_{\varphi}(u_{1})\not=S_{\varphi}(u_{0}^{''})$, $S_{\varphi}(u_{n-1})\not=S_{\varphi}(u_{n}^{'})$, and $S_{\varphi}(u_{n-1})\not=S_{\varphi}(u_{n}^{''})$. Moreover, it follows from Lemma 2 that the vertices of $P_{n+1}$ are also $D(2)$-vertex distinguishable. Therefore, $\varphi$ is an $11$-D(2)-VDTC of $G$.

Subcase 2.1.2. The distance between any two vertices of degree-$2$ in $G$ is equal to $2$. Let $u, v\in V(G)$, $d(u)=d(v)=2$, and $d(u, v)=2$. Suppose that $u_{1}$ and $w$ are the neighbors of $u$, and $v_{1}$ and $w$ are the neighbors of $v$. Then $d(u_{1})=d(v_{1})=d(w)=3$. Let $u_{1}^{'}$ and $u_{1}^{''}$ be the neighbors of $u_{1}$ different from $u$, and let $v_{1}^{'}$ and $v_{1}^{''}$ be the neighbors of $v_{1}$ different from $v$, and $w_{1}$ the neighbor of $w$ different from $u$ and $v$. Note that $2\leq d(w_{1})\leq3$ (if exists), we may suppose that $w_{1}^{'}$ and $w_{1}^{''}$ are the neighbors of $w_{1}$ different from $w$. Let $G^{'}$ be the graph obtained by contracting $u_{1}uwvv_{1}$ to $u_{1}wv_{1}$, see $F_{2}$ in Figure 1. Then by induction hypothesis, $G^{'}$ has an $11$-$D(2)$-VDTC $\psi^{'}$. Let $\psi^{'}(ww_{1})=1$, $\psi^{'}(wu_{1})=2$, $\psi^{'}(wv_{1})=3$, and $\psi^{'}(w)=4$. Next, we will construct an $11$-$D(2)$-VDTC $\psi$ of $G$ by coloring $uu_{1}$, $u$, $uw$, $wv$, $v$, and $vv_{1}$.

Let $\psi(uu_{1})=2$ and $\psi(vv_{1})=3$. We then color $uw$ and $wv$ in turn. By the definition of proper total coloring of graphs, there are at least $8$ colors which can be used to dye $uw$, and $7$ colors that can be used to dye $wv$. We notice that the color set of $w$ should be distinguished from the color sets of $7$ vertices at most, that is, $\{u,\;u_{1},\;v,\;v_{1},\;w_{1},\;w_{1}^{'},\;w_{1}^{''}\}$ (if exists). Since $d(u)=d(v)=2$ and $d(w)=3$, any proper total coloring of $uw$ and $wv$ would enable that $w$ and $\{u,\;v\}$ are $D(2)$-vertex distinguishable. Thus, we only consider the color set of $w$ should be distinguished from the color sets of at most $5$ vertices, that is, $\{u_{1},\;v_{1},\;w_{1},\;w_{1}^{'},\;w_{1}^{''}\}$ (if exists). Since there are $8\times7$ assignments that can be colored the edges $uw$ and $wv$, and at most $5\times 2!$ combinations of them such that the color set of $w$ equals to the color sets of the vertices in $\{u_{1},\;v_{1},\;w_{1},\;w_{1}^{'},\;w_{1}^{''}\}$, however $8\times7>5\times 2!$, we can select two colors in $\{1,\;2,\;\cdots,\;11\}$ to dye $uw$ and $wv$ in turn, such that $w$ and $\{u_{1},\;v_{1},\;w_{1},\;w_{1}^{'},\;w_{1}^{''}\}$ are $D(2)$-vertex distinguishable. Then we color the vertex $u$. Note that there are at least $7$ colors which can be used to dye $u$ properly, and the color set of $u$ should be distinguished from the color sets of $5$ vertices, that is, $\{u_{1},\;u_{1}^{'},\; u_{1}^{''},\;w,\;w_{1}\}$ (if exists). Since $7>5$ we can select one color from $\{1,\;2,\;\cdots,\;11\}\backslash \{\psi(uw),\;\psi(uu_{1}),\;\psi(w),\;\psi(u_{1})\}$ for $u$ so that the vertex $u$ and $\{u_{1},\;u_{1}^{'},\;u_{1}^{''},\;w,\;w_{1}\}$ are $D(2)$-vertex distinguishable. We finally color the vertex $v$. Since there are at least $7$ colors which can be used to color $v$ properly, and the color set of $v$ should be distinguished from the color sets of $6$ vertices, that is, $\{u,\;w,\;w_{1},\;v_{1},\;v_{1}^{'},\;v_{1}^{''}\}$ (if exists), there exists one color in $\{1,\;2,\;\cdots,\;11\}\backslash\{\psi(w),\; \psi(wv),\;\psi(vv_{1}),\;\psi(v_{1})\}$ (note that $\psi(v_{1})=\psi^{'}(v_{1})$) for $v$ such that $v$ and $\{u,\;w,\;w_{1},\;v_{1},\;v_{1}^{'},\;v_{1}^{''}\}$ are $D(2)$-vertex distinguishable. Hence, we obtain an $11$-$D(2)$-VDTC $\psi$ of $G$.

Subcase 2.2. The distance between any two vertices of degree-$2$ in $G$ is no less than $3$. Let $G^{'}$ be the graph obtained by taking two copies of $G$ and joining their corresponding vertices of degree-$2$ by an edge. Then $G^{'}$ is a $3$-regular graph, and contains at most one cut edge. By Lemma 4, $G^{'}$ has a perfect matching. Hence $G^{'}$ admits an $11$-$D(2)$-VDTC $\phi^{'}$ by Lemma 7. We construct a proper total coloring $\phi$ of $G$. For any $x\in V(G)\cup E(G)$, set

$$\phi(x)=\phi^{'}(x).$$

Obviously, the vertices of degree-$2$ and the vertices of degree-$3$ are $D(2)$-vertex distinguishable if their distance is no more than $2$. Since the distance between any two vertices of degree-$2$ in $G$ is at least $3$, one doesn’t take the $D(2)$-vertex distinguishable of such vertices into account. In addition, for any two vertices $u$ and $v$ of degree-$3$, since $S_{\phi^{'}}(u)\not=S_{\phi^{'}}(v)$ while $d(u, v)\leq2$, we get $S_{\phi}(u)\not=S_{\phi}(v)$. Thus, $\phi$ is an $11$-$D(2)$-VDTC of $G$, as required.

Summing up the discussions above, the proof is completed.