Total Coloring of Planar Graphs Without Some Chordal 6-cycles

Abstract

A $k$-total-coloring of a graph $G$ is a coloring of vertex set and edge set using $k$ colors such that no two adjacent or incident elements receive the same color. In this paper, we prove that if $G$ is a planar graph with maximum $\Delta \ge 8$ and every 6-cycle of $G$ contains at most one chord or any chordal 6-cycles are not adjacent, then $G$ has a $(\Delta +1)$-total-coloring.

1 Introduction

All graphs considered in this paper are simple, finite and undirected, and we follow [2] for terminologies and notations not defined here. Let $G$ be a graph. We use $V(G)$, $E(G)$, $\Delta (G)$ and $\delta (G)$ (or simply $V$, $E$, $\Delta$ and $\delta$) to denote the vertex set, the edge set, the maximum degree and the minimum degree of $G$, respectively. For a vertex $v\in V$, let $N(v)$ denote the set of vertices adjacent to $v$ and let $d(v)=|N(v)|$ denote the degree of $v$. A $k$ -vertex, a $k^{-}$ -vertex or a $k^{+}$ -vertex is a vertex of degree $k$, at most $k$ or at least $k$, respectively. A $k$ -cycle is a cycle of length $k$. We use $(v_{1},v_{2},\ldots ,v_{d})$ to denote a cycle (or a face) whose boundary vertices are $v_{1},v_{2},\ldots ,v_{d}$ in the clockwise order. Note that all the subscripts in the paper are taken modulo $d$. We say that two cycles are adjacent (or intersecting) if they share at least one edge (or one vertex, respectively). Let $C=(v_1,v_2,\ldots ,v_k)(k\ge 4)$ be a cycle. If there is an edge $v_iv_j$ with $j\not \equiv i\pm 1\pmod {k}$, then the edge $v_iv_j$ is called a $chord$ of $C$.

A $k$ -total-coloring of a graph $G=(V,E)$ is a coloring of $V\cup {E}$ using $k$ colors such that no two adjacent or incident elements receive the same color. A graph $G$ is total- $k$ -colorable if it admits a $k$-total-coloring. The total chromatic number $\chi ^{\prime }(G)$ of $G$ is the smallest integer $k$ such that $G$ has a $k$-total-coloring. Clearly, $\chi ''(G)\ge \Delta +1$. Behzad [1] and Vizing [11] conjectured independently that $\chi ''(G)\le \Delta +2$ for each graph $G$. This conjecture was confirmed for graphs with $\Delta \le 5$. For planar graphs the only open case is that of $\Delta =6$ (see [6, 9]). In recent years, the study of total colorings planar graphs has attracted considerable attention. For planar graphs with large maximum degree, it is possible to determine $\chi ''(G)=\Delta +1$. This first result was given in [3] for $\Delta \ge 14$, which was finally extended to $\Delta \ge 9$ in [7]. Zhu [8] proved that if $G$ is a planar graph with maximum degree 8, and for each vertex $x$, there is an integer $k_x \in \{3, 4, 5, 6, 7, 8\}$ such that there is no $k_x$-cycle which contains $x$, then $\chi ''(G)=9$. Wang et al. [13] extended this result to that there is at most one $k_x$-cycle which contains $x$. Chang [4] proved that for planar graph $G$ with $\Delta \ge 7$, if there is an integer $k_x\in \{3,4,5,6\}$ such that there is no $k_x$-cycle which contains $x$ for each $x\in V(G)$, then $\chi ''(G)=\Delta +1$. Wang et al. [12] proved $\chi ''(G)=\Delta +1$ for some planar graphs with small maximum degree. Hou et al. [5] proved that every planar graphs with $\Delta \ge 8$ and without 6-cycles are total-9-colorable. Shen and Wang [10] extended this result to planar graphs without chordal 6-cycles. In this paper, we extend this result and get the following theorem.

Theorem 1

Let G be a planar graph with maximum degree $\Delta \ge 8$. If every $6$-cycle of $G$ contains at most one chord or chordal $6$-cycles are not adjacent in $G$, then $\chi ''(G)=\Delta +1$.

2 Proof of Theorem 1

First, we introduce additional notations and definitions here for convenience. Let $G$ be a planar graph having a plane drawing and let $F$ be the face set of $G$. For a face $f$ of $G$, the degree $d(f)$ is the number of edges incident with it, where each cut-edge is counted twice. A $k$ -face, a $k^{-}$ -face or a $k^{+}$ -face is a face of degree $k$, at most $k$ or at least $k$, respectively. Denote by $n_{d}(v)$ the number of $d$-vertices adjacent to the vertex $v$, $f_{d}(v)$ the number of $d$-faces incident with $v$.

Now, we begin to prove Theorem 1. According to [7], the theorem is true for $\Delta \ge 9$. So we assume in the following that $\Delta =8$. Let $G=(V,E)$ be a minimal counterexample to the planar graph $G$ with maximum degree $\Delta =8$, such that $|V|+|E|$ is minimal and $G$ has been embedded in the plane. Then every proper subgraph of $G$ is total-9-colorable. First we give some lemmas for $G$.

Lemma 1

[3]

• (a) $G$ is $2$-connected.

• (b) If $uv$ is an edge of $G$ with $d(u)\le 4$, then $d(u)+d(v)\ge \Delta +2=10$.

By Lemma 1(b), any two neighbors of a 2-vertex are 8-vertices.

Note that in all figures of the paper, vertices marked $\bullet$ have no edges of $G$ incident with them other than those shown and vertices marked $\circ$ are $3^+$-vertices.

Lemma 2

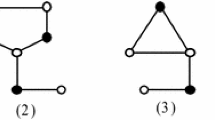
$G$ has no configurations depicted in Fig. 1, where v denotes the vertex of degree of 7.

Fig. 1

Forbidden configurations in G

Proof

The proof of (1), (2), (4) and (6) can be found in [14], (3) can be found in [10], (5) can be found in [7]. $\square$

Lemma 3

Suppose $v$ is a $d$-vertex of $G$ with $d\ge 5$. Let $v_{1},\ldots ,v_{d}$ be the neighbor of $v$ and $f_{1},f_{2},\ldots ,f_{d}$ be faces incident with $v$, such that $f_i$ is incident with $v_i$ and $v_{i+1}$, for $i\in \{1,2,\ldots ,d\}$. Let $d(v_1)=2$ and $\{v,u_1\}=N(v_1)$. Then $G$ does not satisfy one of the following conditions (see Fig. 2).

• (1) there exists an integer $k$ $(2\le k\le d-1)$ such that $d(v_{k+1})=2$, $d(v_i)=3$ $(2\le i\le k)$ and $d(f_j)=4$ $(1\le j\le k)$.

• (2) there exist two integers $k$ and $t$ $(2\le k<t\le d-1)$ such that $d(v_{k})=2$, $d(v_i)=3$ $(k+1\le i\le t)$, $d(f_t)=3$ and $d(f_j)=4$ $(k\le j\le t-1)$.

• (3) there exist two integers $k$ and $t$ $(3\le k\le t\le d-1)$ such that $d(v_i)=3$ $(k\le i\le t)$, $d(f_{k-1})=d(f_t)=3$ and $d(f_j)=4$ $(k\le j\le t-1)$.

Fig. 2

Forbidden configurations in G

Proof

Suppose $G$ satisfies all of the conditions (1)-(3). If $d(f_i)=4$, then let $u_i$ be adjacent to $v_i$ and $v_{i+1}$. By the minimality of $G$, $G'=G-vv_1$ has a $(\Delta +1)$-total-coloring $\phi$. Let $C(x)=\{\phi (xy): y\in N(x)\}\cup \{\phi (x)\}$. First we erase the colors on all $3^{-}$-vertices adjacent to $v$. We have $\phi (v_1u_1)\not \in C(v)$, for otherwise, the number of the forbidden colors for $vv_1$ is at most $\Delta$, so $vv_1$ can be properly colored and by properly recoloring the erased vertices, we get a $(\Delta +1)$-total-coloring of $G$, a contradiction. Without loss of generality, assume that $C(v)=\{1,2,\ldots ,d\}$ with $\phi (vv_i)=i$ $(i\in \{2,3,\ldots ,d\})$, $\phi (v_1u_1)=d+1$ and $\phi (v)=1$. Thus we have $d+1\in C(v_i)$ for all $i\in \{2,3,\ldots ,d\}$, for otherwise, we can recolor $vv_i$ with $d+1$ and color $vv_1$ with $i$, and by properly recoloring the erased vertices, we get a $(\Delta +1)$-total-coloring of $G$, a contradiction, too. In the following we consider (1)-(3) one by one.

• (1) Since $d+1\in C(v_i)$ for all $i\in \{2,3,\ldots ,d\}$, there is a vertex $u_s$ $(1\le s \le k)$ such that $d+1$ appears at least twice on $u_s$, a contradiction to $\phi$.

• (2) Since $d+1\in C(v_i)$ for all $i\in \{2,3,\ldots ,d\}$, $\phi (v_ku_k)=\phi (v_{k+1}u_{k+1})=\cdots =\phi (v_{t-1}u_{t-1})=\phi (v_{t}v_{t+1})=d+1$. We also have $\phi (v_{t}u_{t-1})=t+1$. For otherwise, we can recolor $v_tv_{t+1}$ with $t+1$, $vv_{t+1}$ with $d+1$ and color $vv_1$ with $t+1$. By properly recoloring the erased vertices, we get a $(\Delta +1)$-total-coloring of $G$, a contradiction. Similarly, $\phi (v_{t-1}u_{t-2})=\phi (v_{t-2}u_{t-3})=\cdots =\phi (v_{k+1}u_{k})=t+1$. So we can recolor $vv_{t+1}$ with $d+1$, $v_{t}v_{t+1}$ with $t+1$, $v_{t}u_{t-1}$ with $d+1$, $v_{t-1}u_{t-1}$ with $t+1$,$\ldots$, $v_{k+1}u_{k+1}$ with $t+1$, $v_{k+1}u_{k}$ with $d+1$, $v_{k}u_{k}$ with $t+1$ and color $vv_1$ with $t+1$. By properly recoloring the erased vertices, we get a $(\Delta +1)$-total-coloring of $G$, also a contradiction.

• (3) If $d+1\not \in \{\phi (v_{k-1}v_k)\cup \phi (v_{t}v_{t+1})\}$, then there is a vertex $u_s$ $(k\le s \le t-1)$ such that $d+1$ appears at least twice on $u_s$, a contradiction to $\phi$. So without loss of generality, assume $\phi (v_{k-1}v_k)=d+1$. If $\phi (v_{k+1}u_k)=d+1$, then $\phi (v_{k+2}u_{k+1})=\phi (v_{k+3}u_{k+2})=\cdots =\phi (v_{t}u_{t-1})=d+1$. By the discussion of (2), we also have $\phi (v_{k}u_{k})=\phi (v_{k+1}u_{k+1})=\cdots =\phi (v_{t-1}u_{t-1})=\phi (v_{t}v_{t+1})=k-1$. Then we can recolor $vv_{k-1}$ with $d+1$, $v_{k-1}v_k$ with $k-1$, $v_{k}u_k$ with $d+1$, $v_{k+1}u_k$ with $k-1$, $\ldots$, $v_{t-1}u_{t-1}$ with $d+1$, $v_{t}u_{t-1}$ with $k-1$, $v_{t}v_{t+1}$ with $t+1$, $vv_{t+1}$ with $k-1$ and color $vv_1$ with $t+1$. By properly recoloring the erased vertices, we get a $(\Delta +1)$-total-coloring of $G$, a contradiction. If $\phi (v_{k+1}u_{k+1})=d+1$, then $\phi (v_{k+2}u_{k+2})=\phi (v_{k+3}u_{k+3})=\cdots =\phi (v_{t-1}u_{t-1})=\phi (v_{t}v_{t+1})=d+1$. Similarly, we have $\phi (v_{t}u_{t-1})=\phi (v_{t-1}u_{t-2})=\cdots =\phi (v_{k+1}u_{k})=t+1$. Let $\phi (v_{k}u_{k})=s$. Then we can recolor $vv_{t+1}$ with $d+1$, $v_{t}v_{t+1}$ with $t+1$, $v_{t}u_{t-1}$ with $d+1$, $v_{t-1}u_{t-1}$ with $t+1$, $\ldots$, $v_{k+1}u_{k+1}$ with $t+1$, $v_{k+1}u_{k}$ with $s$, $v_{k}u_{k}$ with $t+1$, and color $vv_1$ with $t+1$. By properly recoloring the erased vertices, we get a $(\Delta +1)$-total-coloring of $G$, a contradiction, too.$\square$

By the Euler’s formula $|V|-|E|+|F|=2$, we have

$$\begin{aligned} \sum _{v\in V}(2d(v)-6)+\sum _{f\in F}(d(f)-6)=-6(|V|-|E|+|F|)=-12<0 \end{aligned}$$

We define $ch$ the initial charge that $ch(x)=2d(x)-6$ for each $x\in V$ and $ch(x)=d(x)-6$ for each $x\in F$. So $\sum _{x\in V\cup F}ch(x)=-12<0.$ In the following, we will reassign a new charge denoted by $ch^{\prime }(x)$ to each $x\in V \cup F$ according to the discharging rules. If we can show that $ch^{\prime }(x)\ge 0$ for each $x\in V \cup F$, then we get an obvious contradiction to $0\le \sum _{x\in V\cup F}ch^{\prime }(x)=\sum _{x\in V\cup F}ch(x)=-12$, which completes our proof. Now we define the discharging rules as follows.

• R1. Each 2-vertex receives 1 from each of its neighbors.

• R2. Let $f$ be a $3$-face. If $f$ is incident with a $3^-$-vertex, then it receives $\frac{3}{2}$ from each of its two incident $7^+$-vertices. If $f$ is incident with a $4$-vertex, then it receives $\frac{5}{4}$ from each of its two incident $6^+$-vertices. If $f$ is not incident with any $4^-$-vertex, then it receives 1 from each of its two incident $5^+$-vertices.

• R3. Let $f$ be a $4$-face. If $f$ is incident with two $3^-$-vertices, then it receives 1 from each of its two incident $7^+$-vertices. If $f$ is incident with only one $3^-$-vertex, then it receives $\frac{3}{4}$ from each of its two incident $7^+$-vertices; and $\frac{1}{2}$ from the left incident $4^+$-vertex. If $f$ is not incident with any $3^-$-vertex, then it receives $\frac{1}{2}$ from each of its incident $4^+$-vertices.

• R4. Each $5$-face receives $\frac{1}{3}$ from each of its incident $4^+$-vertices.

Next, we show that $ch^{'}(x)\ge 0$ for all $x\in V \cup F$. It is easy to check that $ch^{'}(f)\ge 0$ for all $f\in F$ and $ch^{'}(v)\ge 0$ for all 2-vertices $v\in V$ by the above discharging rules. If $d(v)=3$, then $ch^{'}(v)=ch(v)=0$. If $d(v)=4$, then $ch^{'}(v)\ge ch(v)-\frac{1}{2}\times 4=0$ by R2 and R3. For $d(v)\ge 5$, we need the following structural lemma.

Lemma 4

• (1) Suppose that every $6$-cycle of $G$ contains at most one chord. Then we have the following results.

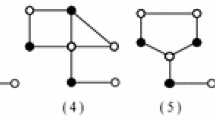
  • (a) $G$ has no configurations depicted in Fig. 3(1), Fig. 3(2) and Fig. 3(3);

  • (b) Suppose $G$ has a subgraph isomorphic to Fig. 3(4). Then $d(f_1)\ge 4$ and $d(f_2)\ne 4$. More over if $d(f_1)=4$, then $d(f_2)\ge 5$;

  • (c) If $G$ has a subgraph isomorphic to Fig. 3(5), then $d(f_1)\ge 5$ and $d(f_2)\ge 5$.

• (2) Suppose that all chordal $6$-cycles are not adjacent. Then we have the following results.

  • (d) If $G$ has a subgraph isomorphic to Fig. 3(5), then $\max \{d(f_1),~d(f_2)\}\ge 4$;

  • (e) $G$ has no configurations depicted in Fig. 3(6) and Fig. 3(7).

Fig. 3

Forbidden configurations in G

Suppose $d(v)=5$. Then $f_3(v)\le 4$ by Lemma 4. If $f_3(v)=4$, then $f_{6^+}(v)\ge 1$, so $ch^{'}(v)\ge ch(v)-1\times 4=0$. If $f_3(v)\le 3$, then $ch'(v)\ge ch(v)-1\times f_3(v)-\frac{1}{2}\times (5-f_3(v))=\frac{3-f_3(v)}{2}\ge 0$. Suppose $d(v)=6$. Then $f_3(v)\le 4$ and $ch^{'}(v)\ge ch(v)-\frac{5}{4}\times f_3(v)-\frac{1}{2}\times (6-f_3(v))=\frac{3(4-f_3(v))}{4}\ge 0$. Suppose $d(v)=7$. Then $f_3(v)\le 5$. By Lemma 2(1), $v$ is incident with at most two $3$-faces are incident with a $3^-$-vertex, that is, $v$ sends $\frac{3}{2}$ to each of the two $3$-faces and at most $\frac{5}{4}$ to each other $3$-face. If $f_3(v)=5$, then $f_{5^+}(v)\ge 1$, and $ch'(v)\ge ch(v)-\frac{3}{2}\times 2-\frac{5}{4}\times 3-\frac{3}{4}\times 1-\frac{1}{3}\times 1=\frac{1}{6}>0$. If $2\le f_3(v)\le 4$, then $ch'(v)\ge ch(v)-\frac{3}{2}\times 2-\frac{5}{4}\times (f_3(v)-2)-1\times (5-f_3(v))-\frac{3}{4}\times 2=\frac{4-f_3(v)}{4}\ge 0$. If $f_3(v)\le 2$, then $ch^{'}(v)\ge ch(v)-\frac{3}{2}\times f_3(v)-1\times (7-f_3(v))=\frac{2-f_3(v)}{2}>0$.

Suppose $d(v)=8$. Then $ch(v)=10$. Let $v_{1},\ldots ,v_{8}$ be neighbors of $v$ in the clockwise order and $f_{1},f_{2},\ldots ,f_{8}$ be faces incident with $v$, such that $f_i$ is incident with $v_i$ and $v_{i+1}$, for $i\in \{1,2,\ldots ,8\}$, and $f_{9}=f_1$.

Suppose $n_2(v)=0$. Then $f_3(v)\le 6$. If $f_3(v)=6$, then $f_{5^+}(v)\ge 2$, so $ch'(v)\ge 10-\frac{3}{2}\times 6-\frac{1}{3}\times 2=\frac{1}{3}>0$. If $f_3(v)=5$, then $f_{5^+}(v)\ge 1$, so $ch'(v)\ge 10-\frac{3}{2}\times 5-1\times 2-\frac{1}{3}\times 1=\frac{1}{6}>0$. If $f_3(v)\le 4$, then $ch'(v)\ge 10-\frac{3}{2}\times f_3(v)-1\times (8-f_3(v))\ge 0$.

Suppose $n_2(v)=1$. Without loss of generality, assume $d(v_1)=2$.

Suppose $v_1$ is incident with a 3-cycle $f_1$.

By Lemma 4, $f_3(v)\le 6$ and all $3$-faces incident with no $3^-$-vertex except $f_1$ by Lemma 2(6). If $f_3(v)=6$, then $f_{5^+}(v)\ge 2$, so $ch'(v)\ge 10-1-\frac{3}{2}\times 1-\frac{5}{4}\times 5-\frac{1}{3}\times 2=\frac{7}{12}>0$. If $4\le f_3(v)\le 5$, then $ch'(v)\ge 10-1-\frac{3}{2}\times 1-\frac{5}{4}\times (f_3(v)-1)-1\times (6-f_3(v))-\frac{3}{4}\times 2=\frac{5-f_3(v)}{4}\ge 0$. If $1\le f_3(v)\le 3$, then $ch'(v)\ge 10-1-\frac{3}{2}\times 1-\frac{5}{4}\times (f_3(v)-1)-1\times (8-f_3(v))=\frac{3-f_3(v)}{4}\ge 0$.

Suppose $v_1$ is not incident with a $3$-cycle.

Suppose every $6$-cycle of $G$ contains at most one chord. Then $f_3(v)\le 5$ by Lemma 2(2)–(4). If $4\le f_3(v)\le 5$, then $f_{5^+}(v)\ge 2$, so $ch'(v)\ge 10-1-\frac{3}{2}\times (f_3(v)-1)-1\times 1-1\times (6-f_3(v))-\frac{1}{3}\times 2=\frac{17-3f_3(v)}{6}>0$. If $f_3(v)=3$, then $f_{5^+}(v)\ge 1$, so $ch'(v)\ge 10-1-\frac{3}{2}\times 3-1\times 4-\frac{1}{3}\times 1=\frac{1}{6}>0$. If $f_3(v)=2$, then $ch'(v)\ge 10-1-\frac{3}{2}\times 2-1\times 6=0$. If $f_3(v)=1$, then without loss of generality, $d(f_2)=3$, i.e. $d(v_3)=3$ and $d(v_2)\ge 7$, so $ch'(v)\ge 10-1-\frac{3}{2}\times 1-1\times 6-\frac{3}{4}\times 1=\frac{3}{4}>0$. If $f_3(v)=0$, then $ch'(v)\ge 10-1-1\times 8=1>0$.

Suppose any two chordal $6$-cycles are not adjacent. Then $f_3(v)\le 5$ by Lemma 2(2)–(4). If $f_3(v)\ge 4$, then $ch'(v)\ge 10-1-\frac{3}{2}\times 2-\frac{5}{4}\times (f_3(v))-\frac{3}{4}\times (8-f_3(v))=\frac{5-f_3(v)}{2}\ge 0$. If $f_3(v)=3$, then $ch'(v)\ge 10-1-\frac{3}{2}\times 3-\frac{3}{4}\times 5=\frac{3}{4}>0$. If $1\le f_3(v)\le 2$, then $ch'(v)\ge 10-1-\frac{3}{2}\times f_3(v)-1\times (6-2f_3(v))-\frac{3}{4}\times (2+f_3(v))=\frac{6-f_3(v)}{4}>0$. If $f_3(v)=0$, then $ch'(v)\ge 10-1-1\times 8=1>0$.

Note that next Lemma 5 is also true for general planar graphs if we just use the above discharging rules.

Lemma 5

Suppose $d(v)=8$ and $2\le n_{2}(v)\le 8$. Then $ch'(v)\ge 0$.

Proof

Since $d(v)=8$, then $ch(v)=10$. First we give a Claim for convenience.

Claim

Suppose that $d(v_{i})=d(v_{i+k+1})=2$ and $d(v_{j})\ge 3$ for $i+1\le j\le i+k$. Then $v$ sends at most $\phi$ (in total) to $f_{i}$ and $f_{i+1}$, $f_{i+2}$, $\ldots$, $f_{i+k}$, where $\phi =\frac{5k+1}{4}$ $(k=1,2,3,4,5)$, see Fig. 4.

Fig. 4

Claim

By Lemma 2, $d(f_i)\ge 4$ and $d(f_{i+k})\ge 4$.

Case 1. $k=1$ By Lemma 3(1), we have $d(v_{i+1})\ge 4$ or $\max \{d(f_i),~d(f_{i+1})\}\ge 5$, so $\phi \le \max \{\frac{3}{4}\times 2,~1+\frac{1}{3}\}=\frac{3}{2}$ by R3.

Case 2. $k=2$ If $d(f_{i+1})=3$, then $\min \{d(v_{i+1}),~d(v_{i+2})\}\ge 4$ or $\max \{d(f_i),~d(f_{i+2})\}\ge 5$ by Lemma 3(2), and it follows that $\phi \le \max \{\frac{3}{4}+\frac{5}{4}+\frac{3}{4},~\frac{1}{3}+\frac{3}{2}+\frac{3}{4}\}=\frac{11}{4}$. Otherwise, $d(f_{i+1})\ge 4$, then $\min \{d(v_{i+1}),~d(v_{i+2})\}\ge 4$ or $\max \{d(f_i),~d(f_{i+1}),~d(f_{i+2})\}\ge 5$ by Lemma 3(1), and it follows that $\phi \le \max \{1+\frac{3}{4}\times 2,~1\times 2+\frac{1}{3}\}=\frac{5}{2}<\frac{11}{4}$.

Case 3. $k=3$ Suppose $d(f_{i+1})=d(f_{i+2})=3$. Then $d(v_{i+2})\ge 4$. If $d(v_{i+1})=d(v_{i+3})=3$, then $d(f_{i})\ge 5$ and $d(f_{i+3})\ge 5$, so $\phi \le \frac{3}{2}\times 2+\frac{1}{3}\times 2=\frac{11}{3}$. If $\min \{d(v_{i+1}),~d(v_{i+3})\}\ge 4$, then $\phi \le \frac{5}{4}\times 2+\frac{3}{4}\times 2=4$. Suppose $d(f_{i+1})=3$ and $d(f_{i+2})\ge 4$. If $d(v_{i+1})=3$, then $d(v_{i+2})\ge 7$ and $d(f_{i})\ge 5$, so $\phi \le \frac{1}{3}+\frac{3}{2}+\frac{3}{4}+1=\frac{43}{12}$. If $d(v_{i+2})=3$, then $d(v_{i+1})\ge 7$ and $d(v_{i+3})\ge 4$, so $\phi \le \frac{3}{4}+\frac{3}{2}+\frac{3}{4}+\frac{3}{4}=\frac{15}{4}$. If $\min \{d(v_{i+1}),~d(v_{i+2})\}\ge 4$, $\phi \le \frac{3}{4}+\frac{5}{4}+\frac{3}{4}+1=\frac{15}{4}$. It is similar with $d(f_{i+2})=3$ and $d(f_{i+1})\ge 4$. Suppose $\min \{d(f_{i+1}),~d(f_{i+2})\}\ge 4$. Then $\max \{d(v_{i+1}),~d(v_{i+2}),~d(v_{i+3})\}\ge 4$ or $\max \{d(f_i),~d(f_{i+1}),~d(f_{i+2}),~d(f_{i+3})\}\ge 5$, so $\phi \le \max \{1\times 2+\frac{3}{4}\times 2,~1\times 3+\frac{1}{3}\}=\frac{7}{2}$. So $\phi \le \max \{\frac{11}{3},~4,~\frac{43}{12},~\frac{15}{4},~\frac{7}{2}\}=4$.

Case 4. $k=4$ Suppose $d(f_{i+1})=d(f_{i+2})=d(f_{i+3})=3$. Then $\min \{d(v_{i+2}),~d(v_{i+3})\}\ge 4$. If $d(v_{i+1})=d(v_{i+4})=3$, then $d(f_{i})\ge 5$ and $d(f_{i+4})\ge 5$, so $\phi \le \frac{3}{2}\times 2+1\times 1+\frac{1}{3}\times 2=\frac{14}{3}$. If $\min \{d(v_{i+1}),~d(v_{i+4})\}\ge 4$, then $\phi \le \frac{5}{4}\times 3+\frac{3}{4}\times 2=\frac{21}{4}$. Suppose $d(f_{i+1})=d(f_{i+2})=3$, $d(f_{i+3})\ge 4$. Then $d(v_{i+2})\ge 4$. If $d(v_{i+1})=d(v_{i+3})=3$, then $d(v_{i+4})\ge 4$ and $d(f_{i})\ge 5$, so $\phi \le \frac{3}{2}\times 2+\frac{3}{4}\times 2+\frac{1}{3}\times 1=\frac{29}{6}$. If $\min \{d(v_{i+1}),~d(v_{i+3})\}\ge 4$, then $\phi \le \frac{5}{4}\times 2+1\times 1+\frac{3}{4}\times 2=5$. Similar with $d(f_{i+2})=d(f_{i+3})=3$, $d(f_{i+1})\ge 4$. Suppose $d(f_{i+1})=d(f_{i+3})=3$, $d(f_{i+2})\ge 4$. Then $\max \{d(v_{i+2}),~d(v_{i+3})\}\ge 4$ by Lemma 3(3), so $\phi \le \frac{3}{2}\times 1+\frac{5}{4}\times 1+\frac{3}{4}\times 3=5$. Suppose $d(f_{i+1})=3$, $d(f_{i+2})\ge 4$ and $d(f_{i+3})\ge 4$. If $d(v_{i+1})=3$, then $d(v_{i+2})\ge 7$ and $d(f_{i})\ge 5$, so $\phi \le \frac{3}{2}+1\times 2+\frac{3}{4}\times 1+\frac{1}{3}\times 1=\frac{55}{12}$. If $d(v_{i+2})=3$, then $d(v_{i+1})\ge 7$ and $\max \{d(v_{i+3}),~d(v_{i+4})\}\ge 4$, so $\phi \le \frac{3}{2}\times 1+1\times 1+\frac{3}{4}\times 3=\frac{19}{4}$. Otherwise, $\phi \le \frac{5}{4}\times 1+1\times 2+\frac{3}{4}\times 2=\frac{19}{4}$. It is similar with $d(f_{i+3})=3$, $d(f_{i+1})\ge 4$ and $d(f_{i+2})\ge 4$. Suppose $d(f_{i+2})=3$, $d(f_{i+1})\ge 4$ and $d(f_{i+3})\ge 4$. If $d(v_{i+2})=3$ or $d(v_{i+3})=3$, then $\phi \le \frac{3}{2}\times 1+1\times 1+\frac{3}{4}\times 3=\frac{19}{4}$. Otherwise, $\phi \le \frac{5}{4}\times 1+1\times 2+\frac{3}{4}\times 2=\frac{19}{4}$. Suppose $\min \{d(f_{i+1}),~d(f_{i+2}),~d(f_{i+3})\}\ge 4$. Then $\max \{d(v_{i+1}),~d(v_{i+2}),~d(v_{i+3}),~d(v_{i+4})\}\ge 4$ or $\max \{d(f_i),~d(f_{i+1}),~d(f_{i+2}),$ $d(f_{i+3}),~d(f_{i+4})\}\ge 5$, so $\phi \le \max \{1\times 3+\frac{3}{4}\times 2,~1\times 4+\frac{1}{3}\}=\frac{9}{2}$. So $\phi \le \max \{\frac{14}{3},~\frac{21}{4},~\frac{29}{6},~5,~\frac{55}{12},~\frac{19}{4},~\frac{9}{2}\}=\frac{21}{4}$.

Case 5. $k=5$ If $k=5$, then $\phi \le \frac{13}{2}$. It is similar to prove (e), we omit it here.

Next, we prove the Lemma.

If $n_2(v)=8$, then all faces incident with $v$ are $6^+$-faces by Lemma 2(2)–(4), that is, $f_{6^+}(v)=8$, so $ch^{'}(v)= 10-1\times 8=2>0$. If $n_2(v)=7$, then $f_{6^{+}}(v)\ge 6$ and $f_3(v)=0$, so $ch^{'}(v)\ge 10-1\times 7-\frac{3}{2}=\frac{3}{2}>0$ by Claim (a).

Fig. 5

$n_{2}(v)\le 6$

Suppose $n_2(v)\le 6$. The possible distributions of 2-vertices adjacent to $v$ are illustrated in Fig. 5. For Fig. 5(1), we have $f_{6^+}(v)\ge 5$ and $ch'(v)\ge 10-1\times 6-\frac{11}{4}=\frac{5}{4}>0$ by Claim (b).

For Fig. 5(2)–(4), we have $f_{6^+}(v)\ge 4$ and $ch'(v)\ge 10-1\times 6-\frac{3}{2}\times 2=1>0$. For Fig. 5(5), we have $f_{6^+}(v)\ge 4$ and $ch'(v)\ge 10-1\times 5-4=1>0$ by Claim (c). For Fig. 5(6)–(7), we have $f_{6^+}(v)\ge 3$ and $ch'(v)\ge 10-1\times 5-\frac{3}{2}-\frac{11}{4}=\frac{3}{4}>0$. For Fig. 5(8)–(9), we have $f_{6^+}(v)\ge 2$ and $ch'(v)\ge 10-1\times 5-\frac{3}{2}\times 3=\frac{1}{2}>0$. For Fig. 5(10), we have $f_{6^+}(v)\ge 3$ and $ch'(v)\ge 10-1\times 4-\frac{21}{4}=\frac{3}{4}>0$ by Claim (d). For Fig. 5(11) and (13), we have $f_{6^+}(v)\ge 2$ and $ch'(v)\ge 10-1\times 4-\frac{3}{2}-4=\frac{1}{2}>0$. For Fig. 5(12) and (16), we have $f_{6^+}(v)\ge 2$ and $ch'(v)\ge 10-1\times 4-\frac{11}{4}\times 2=\frac{1}{2}>0$. For Fig. 5(14) and (15), we have $f_{6^+}(v)\ge 1$ and $ch'(v)\ge 10-1\times 4-\frac{3}{2}\times 2-\frac{11}{4}=\frac{1}{4}>0$. For Fig. 5 (17), we have $ch'(v)\ge 10-1\times 4-\frac{3}{2}\times 4=0$. For Fig. 5(18), we have $f_{6^+}(v)\ge 2$ and $ch'(v)\ge 10-1\times 3-\frac{13}{2}=\frac{1}{2}>0$ by Claim (e). For Fig. 5(19), we have $f_{6^+}(v)\ge 1$ and $ch'(v)\ge 10-1\times 3-\frac{3}{2}-\frac{21}{4}=\frac{1}{4}>0$. For Fig. 5(20), we have $f_{6^+}(v)\ge 1$ and $ch'(v)\ge 10-1\times 3-\frac{11}{4}-4=\frac{1}{4}>0$. For Fig. 5(21), we have $ch'(v)\ge 10-1\times 3-\frac{3}{2}\times 2-4=0$. For Fig. 5(22), we have $ch'(v)\ge 10-1\times 3-\frac{3}{2}-\frac{11}{4}\times 2=0$. For Fig. 5(23), we have $f_{6^+}(v)\ge 1$. Suppose $d(f_{2})=d(f_{3})=d(f_{4})=d(f_5)=d(f_6)=3$. Then $\min \{d(v_{3}),~d(v_{4}),~d(v_{5}),~d(v_{6})\}\ge 4$. If $d(v_{2})=d(v_{6})=3$, then $d(f_{1})\ge 5$ and $d(f_{7})\ge 5$ by Lemma 3, so $ch'(v)\ge 10-1\times 2-\frac{3}{2}\times 2-\frac{5}{4}\times 2-1\times 1-\frac{1}{3}\times 2=\frac{5}{6}>0$. If $f_{2}$, $f_{3}$, $f_{4}$, $f_{5}$ and $f_{6}$ are incident with no $3^-$-vertex, then $ch'(v)\ge 10-1\times 2-\frac{5}{4}\times 5-\frac{3}{4}\times 2=\frac{1}{4}>0$. For Fig. 5(24), we have $ch'(v)\ge 10-1\times 2-\frac{3}{2}-\frac{13}{2}=0$. For Fig. 5(25), we have $ch'(v)\ge 10-1\times 2-\frac{11}{4}-\frac{21}{4}=0$. For Fig. 5(26), we have $ch'(v)\ge 10-1\times 2-4\times 2=0$. $\square$

Hence we complete the proof of the theorem.